基础生态学实验Lotka-Volterra捕食者-猎物模型模拟

lotka-volterra方程中的相关参数的确定Lotka-Volterra方程是一种描述捕食者和猎物之间相互作用的动力学模型。

它由两个关联的微分方程组成，其中捕食者的数量和猎物的数量随时间的变化被描述。

在Lotka-Volterra方程中，有一些参数需要确定，以使模型能够适应特定的捕食者和猎物系统。

以下是确定这些参数的一些常见方法：
1.实验观测：通过实验观测获得的数据可以用来确定模型中
的参数。

这可能涉及到监测和记录捕食者和猎物数量随时间的变化。

2.相关研究：进行相似生态系统或相似物种之间的研究，以
获得类似系统中参数的估计。

这可能包括文献综述、野外观察或实地调查。

3.参数估计：使用统计方法，如最小二乘拟合或最大似然估
计，根据已有的数据拟合模型，并得出参数的估计值。

4.灵敏度分析：进行灵敏度分析来评估参数对模型结果的影
响程度。

这可以帮助确定对模型结果影响较大的参数，并优先考虑对这些参数进行准确估计。

需要注意的是，参数的确定是一个复杂的过程，并且涉及到模型假设的验证，数据收集和分析，在参数估计中使用统计技术，以及考虑误差和不确定性。

另外，根据具体的应用和研究目的，还会引入其他的参数
或因素，以更好地刻画特定系统的行为。

因此，参数的确定应该根据具体情况进行，并结合领域知识和相关实验和观测数据。

《Lotka-Volterra系统的辛几何算法》篇一一、引言Lotka-Volterra系统，又称为捕食者-猎物模型，是一种广泛用于描述生物种群动态关系的数学模型。

在生物学、生态学以及物理等多个领域有着广泛应用。

而辛几何算法是一种适用于大规模系统求解的数值方法，其特点在于能够保持系统的辛结构，从而在长时间模拟中保持较高的精度。

本文将探讨Lotka-Volterra系统的辛几何算法应用及其特点。

二、Lotka-Volterra系统Lotka-Volterra系统是一个描述两个物种（捕食者和猎物）之间相互作用的数学模型。

该模型通常以一组非线性微分方程的形式表示，可以用于研究物种间的竞争、共生等关系。

这个系统是动态的，并且在特定条件下可以表现出周期性、混沌等复杂行为。

三、辛几何算法概述辛几何算法是一种基于辛几何结构的数值算法。

它能够有效地解决大规模非线性系统的求解问题，并保持系统的辛结构，从而在长时间模拟中保持较高的精度。

这种算法特别适用于描述物理系统中的哈密顿动力学和辛几何结构。

四、Lotka-Volterra系统的辛几何算法应用针对Lotka-Volterra系统，我们可以采用辛几何算法进行求解。

首先，将Lotka-Volterra系统的微分方程转化为哈密顿形式，然后利用辛几何算法进行求解。

通过这种方法，我们可以在长时间模拟中保持高精度，并观察到系统动态行为的变化。

在应用辛几何算法求解Lotka-Volterra系统时，需要注意以下几点：1. 模型的建立：将Lotka-Volterra系统的微分方程转化为哈密顿形式是关键步骤。

这需要我们对系统有深入的理解，并选择合适的变量和参数。

2. 算法的选择：根据问题的特点和需求，选择合适的辛几何算法进行求解。

这包括选择适当的迭代方法和步长等参数。

3. 模拟的精度和效率：在求解过程中，要平衡模拟的精度和效率。

既要保证足够的精度以观察到系统的动态行为，又要避免过度计算导致的效率损失。

两类非线性生物种群模型的动力学研究两类非线性生物种群模型的动力学研究摘要：生物种群的数量与其环境之间的相互作用是生态系统中一个重要的动态过程。

为了更好地理解生物种群数量的变化规律，许多数学模型被应用于生态学领域。

本研究聚焦于两类非线性生物种群模型的动力学研究，分别为捕食者-猎物模型和竞争模型。

通过对这两类模型的分析，我们可以更好地理解生物种群数量的演变过程。

一、捕食者-猎物模型捕食者-猎物模型是一种描述捕食者与猎物之间相互作用的模型。

在这种模型中，捕食者的数量受到猎物数量的影响，而猎物的数量则受到捕食者的掠食行为的影响。

常见的捕食者-猎物模型包括Lotka-Volterra模型和Holling模型。

Lotka-Volterra模型是最早被提出的捕食者-猎物模型之一，它假设猎物的增长率与捕食者的消耗率成正比，而捕食者的减小率与猎物的提供率成正比。

该模型可以通过一组常微分方程来描述捕食者和猎物数量的变化。

在此基础上，研究者们在模型中引入了时间滞后、空间效应等因素，进一步改进了Lotka-Volterra模型。

Holling模型则是对Lotka-Volterra 模型的改进，考虑到了猎物种群的饥饿和捕食者的饱食程度对捕食行为的影响。

研究表明，捕食者-猎物模型的动力学行为非常丰富。

通过数值模拟和理论分析，我们可以发现捕食者和猎物之间的数量周期性变化，甚至出现混沌现象。

此外，环境因素的改变也会对捕食者-猎物系统的动态行为产生重要影响。

例如，环境的周期性变化、捕食者和猎物之间的适应性进化等因素，都会导致捕食者-猎物系统的行为发生变化。

二、竞争模型竞争模型是用于描述不同种群之间资源竞争的模型。

在这种模型中，资源的有限性限制了不同种群的数量增长，从而导致竞争的发生。

常见的竞争模型包括Ricker模型、Tilman模型等。

Ricker模型是一种描述种群数量变化的离散动力学模型，它假设种群的增长率与种群数量呈指数关系。

L o t k a-–-V o l t e r r a-捕食者-–-猎物模型模拟基础生态学实验Lotka – Volterra 捕食者–猎物模型模拟姓名王超杰学号 201311202926实验日期 2015年5月14日同组成员董婉莹马月娇哈斯耶提沈丹一、【实验原理】Lotka-Volterra捕食者-猎物模型是对逻辑斯蒂模型的延伸。

它假设：除不是这存在外，猎物生活于理想环境中（其出生率与死亡率与种群密度无关）；捕食者的环境同样是理想的，其种群增长只收到可获得的猎物的数量限制。

本实验利用模拟软件模拟Lotka-Volterra捕食者-猎物模型，并以此研究该模型的规律特点。

捕食者—猎物模型简单化假设：①相互关系中仅有一种捕食者和一种猎物。

②如果捕食者数量下降到某一阀值以下，猎物数量种数量就上升，而捕食者数量如果增多，猎物种数量就下降，反之，如果猎物数量上升到某一阀值，捕食者数量就增多，而猎物种数量如果很少，捕食者数量就下降。

③猎物种群在没有捕食者存在的情况下按指数增长，捕食者种群在没有猎物的条件下就按指数减少。

因此有猎物方程：dN/dt=r1N-C1 PN；捕食者方程：dP/dt=-r2P+C2PN。

其中N和P分别指猎物和捕食者密度，r1 为猎物种群增长率，-r2为捕食者的死亡率，t为时间，C1为捕食者发现和进攻猎物的效率，即平均每一捕食者捕杀猎物的常数，C2为捕食者利用猎物而转变为更多捕食者的捕食常数。

Lotka-Volterra捕食者-猎物模型揭示了这种捕食关系的两个种群数量动态是此消彼长、往复振荡的变化规律。

二、【实验目的】在掌握Lotka-Volterra 捕食者-猎物模型的生态学意义与各参数意义的基础上，通过改变参数值的大小，在计算机模拟捕食者种群与猎物种群数量变化规律，从而加深对该模型的认识。

三、【实验器材】Windows 操作系统对的计算平台，具有年龄结构的种群增长模型的计算机模拟运行软件Populus。

基础生态学实验Lotka-Volterra捕食者-猎物模型模拟【实验原理】dN/dt=r1N-C1NP 猎物种群动态dP/dt=-r2N+C2NP 捕食者种群动态N：猎物的密度r1：猎物种群的增长率C1：捕食者发现和进攻猎物的效率，即平均每一捕食者捕食猎物的常数P：捕食者密度-r2：捕食者在没有猎物时的条件下的死亡率C2：捕食者利用猎物而转变为更多捕食者的捕食常数【实验目的】在掌握Lotka-Volterra 捕食者-猎物模型的生态学意义与各参数意义的基础上，通过改变参数值的大小，在计算机模拟捕食者种群与猎物种群数量变化规律，从而加深对该模型的认识。

【实验器材】1、计算机2、模拟运行软件3、种群生物学模拟软件包（Populus），5.5 版本，美国明尼苏达大学【实验步骤】设置初始值，之后保持N0、P0不变，分别改变d2、g、r1、c的大小（具体数据见下表），观察记录每组数据下捕食者-猎物模型中两种群密度变化情况，与对照组进行比较。

实验数据设置记录表【实验结果与分析】Part I 研究捕食者-猎物模型中两种群密度变化情况与捕食者死亡率（d）的关系图1.1 对照组捕食者—猎物模型种群密度随时间变化的图（d=0.2）图1.2 实验组1捕食者—猎物模型种群密度随时间变化的图（d=0.3）图1.3 对照组捕食者—猎物模型种群密度图（d=0.2）图1.4实验组1捕食者—猎物模型种群密度图（d=0.3）表1研究种群密度变化情况与d的关系实验数据记录表由以上图表可知：捕食者死亡率d增长对猎物种群密度变化的影响反而要大于其对捕食者种群密度的变化。

d减小，可见猎物种群密度明显增加，且两者种群密度波动周期变长。

这是由于捕食者死亡率d直接影响捕食者密度，使其降低，从而使猎物种群密度增加，而猎物种群密度的增加又利于捕食者繁殖，使捕食者种群增加。

综上，多方面因素的作用导致猎物种群密度明显增加，而捕食者种群密度基本不变。

Part II 研究捕食者-猎物模型中两种群密度变化情况与转化常数（g）的关系图2.1 对照组捕食者—猎物模型种群密度随时间变化的图（g=0.25）图2.2 实验组2捕食者—猎物模型种群密度随时间变化的图（g=0.1）图2.3 对照组捕食者—猎物模型种群密度图（g=0.25）图2.4实验组2捕食者—猎物模型种群密度图（g=0.1）表2研究种群密度变化情况与g的关系实验数据记录表由以上图表可知：转化常数g增长对猎物种群密度变化的影响反而要大于其对捕食者种群密度的变化。

捕⾷者与被捕⾷者模型——Logistic-Volterra捕⾷者与被捕⾷者模型——Logistic-Volterra模型摘要Logistic模型是最常⽤的模型之⼀，在其基础上⼜可以发展出许多其他数学模型，其重要性不⾔⽽喻，⽽Volterra模型则是经典的被捕⾷者与捕⾷者模型之⼀。

本⽂尝试结合两者，建⽴⼀个Logistic-Volterra模型，并做出数值解和分析。

关键词：Logistic模型 Volterra模型数值解⼀、问题的提出Volterra模型显⽰的被捕⾷者与捕⾷者系统存在着显著的周期振荡，⽽实际上，多数的捕⾷者与捕⾷者系统都是观察不到的。

尝试建⽴模型，描述这种现象。

⼆、符号说明r：被捕⾷者固有增长率d：捕⾷者固有死亡率a：捕⾷者掠取被捕⾷者的能⼒b：被捕⾷者供养捕⾷者的能⼒N1：被捕⾷者的最⼤环境容纳量N2：捕⾷者的最⼤环境容纳量三、模型假设1.在没有天敌的情况下，被捕⾷者数量增加的固有速度与被捕⾷者数量x和阻滞作⽤因⼦(1-x/N1)成正⽐，即dxdt =rx(1?xN1)2.在没有⾷物的情况下，捕⾷者数量减少的固有速度与捕⾷者数量y和阻滞作⽤因⼦(1+y/N2)成正⽐，即dydt =?dy(1+yN2)3.捕⾷者与被捕⾷者在同⼀环境下⽣存，它们的种群变化速度互相影响，影响因⼦应与它们相遇的频率成正⽐，即捕⾷导致被捕⾷者数量减少的速度为-axy，捕⾷导致捕⾷者数量增加的速度为bxy四、模型建⽴与求解1.Volterra模型的分析意⼤利数学家Volterra在上世纪20年代提出的Volterra模型：dxdt=rx?axydydt=?dy+bxy取r=1 d=0.5 a=0.1 b=0.02，运⽤matlab的ode45功能函数，做出数值解，并绘图分析。

图1被捕⾷者与捕⾷者随时间变化图图2捕⾷者与被捕⾷者相图从图形可以看出，捕⾷者与被捕⾷者共同⽣存，数量随时间作周期变化。

2.建⽴Logistic-Volterra模型在Volterra模型中的物种⾃⾝增长率中，考虑⾃⾝阻滞作⽤，即加⼊Logistic项，得到以下模型：dx dt =rx(1?xN1)?axydy=?dy(1+y2)+bxy取r=1 d=0.5 a=0.1 b=0.02 N1=100 N2=25，运⽤matlab的ode45功能函数，做出数值解，并绘图分析。

Lotka 定律1. 引言Lotka 定律，又称为 Lotka-Volterra 定律，是一种描述生态系统中捕食者和猎物之间数量关系的数学模型。

它由美国数学家 Alfred J. Lotka 和意大利数学家Vito Volterra 在20世纪初提出。

这个模型是基于捕食者和猎物之间相互作用的基本原理，并被广泛应用于生态学、经济学以及其他许多领域。

2. Lotka-Volterra 模型Lotka-Volterra 模型是一个基于微分方程的动力学模型，用于描述捕食者和猎物之间的相互作用。

该模型假设捕食者和猎物的数量随时间的变化是连续的，并受到一些基本规律的约束。

2.1 模型假设Lotka-Volterra 模型基于以下几个假设：•捕食者的数量仅取决于猎物的数量，而不受其他因素的影响。

•猎物的数量仅取决于捕食者的数量，而不受其他因素的影响。

•捕食者和猎物之间的相互作用是线性的，即捕食者的增长率正比于捕食者和猎物之间的相互作用，而猎物的减少率正比于猎物和捕食者之间的相互作用。

2.2 模型方程基于以上假设，Lotka-Volterra 模型可以表示为以下两个微分方程：•猎物数量变化的方程：dN=rN−aNPdt其中，N表示猎物数量，t表示时间，r表示猎物自然增长率，a表示捕食者对猎物的捕食率，P表示捕食者数量。

•捕食者数量变化的方程：dP=baNP−mPdt其中，P表示捕食者数量，b表示捕食者对猎物的转化效率，m表示捕食者的自然死亡率。

2.3 模型解释Lotka-Volterra 模型的解释主要集中在捕食者和猎物数量之间的相互关系和相互作用。

根据模型方程可以得出以下几个结论：•当捕食者数量增加时，捕食者对猎物的捕食率增加，导致猎物数量减少。

•当猎物数量减少时，捕食者的食物减少，捕食者数量也会减少。

•当捕食者数量减少时，猎物的数量增加，捕食者的食物增加，捕食者数量也会增加。

这种相互关系导致了捕食者和猎物数量之间的周期性波动，即捕食者和猎物数量会交替增加和减少，形成一个动态平衡。

lotka-volterra模型半饱和常数-概述说明以及解释1.引言1.1 概述随着对生态系统的深入研究，人们意识到了物种之间相互关系的重要性。

为了解释和预测物种之间的相互作用，数学模型成为了一种有效工具。

其中，Lotka-Volterra模型是一种常用且经典的数学模型，被广泛应用于生态学领域。

Lotka-Volterra模型，又称为捕食者-猎物模型，描述了捕食者和猎物之间的相互作用。

模型的基本假设是，猎物的增长受到捕食者捕食的影响，而捕食者的增长则依赖于猎物的可获得性。

本文的重点是研究Lotka-Volterra模型中的一个重要参数，即半饱和常数。

半饱和常数是用来衡量猎物或捕食者种群增长的饱和程度的指标。

它代表了当猎物或捕食者种群密度达到半饱和常数时，其增长速率达到最大值的临界点。

在这篇文章中，我们将对Lotka-Volterra模型进行介绍，并详细定义半饱和常数。

我们将探讨半饱和常数对模型的影响，以及其在解释和预测物种之间相互作用的重要性。

最后，我们还将展望未来研究方向，探讨如何进一步改进和应用Lotka-Volterra模型以解决现实生态问题。

通过对Lotka-Volterra模型和半饱和常数的研究，我们将有助于更好地理解物种之间的相互关系，并为生态学领域的可持续发展提供理论指导。

此外，对于生态系统保护和资源管理也有着重要的现实意义。

1.2 文章结构文章结构:本篇文章主要包括以下几个部分。

引言部分（第1章）：首先对文章的主要内容进行概述，介绍Lotka-Volterra模型以及半饱和常数的背景和相关研究现状。

然后明确文章的目的和意义以及本文的结构安排。

正文部分（第2章）：详细介绍Lotka-Volterra模型，包括其基本原理、模型方程的推导以及动态方程的解释。

然后，着重阐述半饱和常数的定义和意义，并讨论其在Lotka-Volterra模型中的应用。

结论部分（第3章）：对全文的内容进行总结，回顾Lotka-Volterra 模型的应用，并分析半饱和常数对模型的影响。

实验名称：Lotka-volterra捕食者-猎物模型模拟姓名：学号：系别：实验日期：【实验原理】dN/dt=r1N-C1NP 猎物种群动态dP/dt=-r2N+C2NP 捕食者种群动态N:猎物的密度r1:猎物种群的增长率C1:捕食者发现和进攻猎物的效率，即平均每一捕食者捕食猎物的常数P:捕食者密度-r2:捕食者在没有猎物时的条件下的死亡率C2:捕食者利用猎物而转变为更多捕食者的捕食常数【实验目的】在掌握Lotka-Volterra 捕食者-猎物模型的生态学意义与各参数意义的基础上，通过改变参数值的大小，在计算机模拟捕食者种群与猎物种群数量变化规律，从而加深对该模型的认识。

【实验器材】XP操作系统的计算平台模拟运行软件【实质】模型揭示了这种捕食关系的两个种群数量动态是此消彼长、往复振荡的变化规律。

【方法步骤】参数设置（1）Please enter the following:Prey PredatorN0 = 100 P0 = 20r1 = 0.1 r2 = 0.1C1 = 0.01 C2 = 0.01 （2）Please enter the following: Prey PredatorN0 = 100 P0 = 20r1 = 0.1 r2 = 0.5C1 = 0.01 C2 = 0.01 （3）Please enter the following: Prey PredatorN0 = 100 P0 = 20r1 = 0.1 r2 =2.5C1 = 0.01 C2 = 0.01 （4）Please enter the following: Prey PredatorN0 =100 P0 = 20r1 = 0.1 r2 = 5C1 = 0.01 C2 = 0.01 【分析讨论】（模拟分析图形见附表）（1）Please enter the following: Prey PredatorN0 = 100 P0 = 20r1 = 0.1 r2 = 0.1C1 = 0.01 C2 = 0.01此模型设为标准模型，接下来的实验设计的讨论均以此模型为标准进行比较讨论。

Lotk1-V olterr1模型逻辑斯谛模型为：dN/dt=rN(1－N/K)上式是对于单物种而言，对于两个互相竞争的物种1、2，我们引入竞争系数α、β，其中α是物种2对物种2的竞争系数，可理解为每个物种2个体所占的空间相当于α个物种1个体，同理得到β。

则逻辑斯谛模型可变为：对于物种1：dN 1/dt=r 1N 1(1－N 1/K 1－αN 2/K 1)……① 对于物种2：dN 2/dt=r 2N 2(1－N 2/K 2－βN 1/K 2)……② 方程式①和②即为Lotk1-V olterr1的种间竞争模型。

任何生态系统都是趋向于平衡的，同理两个物种竞争也会趋向于平衡。

当物种1与物种2达到平衡时，物种1与物种2的种群增长率为0，即dN 1/dt=0，dN 2/dt=0，方程式①和②变为：r 1N 1(1－N 1/K 1－αN 2/K 1)=0−−−→−≠≠01,01N r 1－N 1/K 1－αN 2/K 1=0……③ r 2N 2(1－N 2/K 2－βN 1/K 2)=0−−−→−≠≠02,02N r 1－N 2/K 2－βN 1/K 2=0……④方程式③和④中K 1、K 2、α、β对于一个确定的系统都是已知的，因此为了方便观察理解，对于方程式③和④以N 1为横坐标，N 2为纵坐标做图得：图1 Lotk1-V olterr1竞争模型所产生的物种1和物种2的平衡线(a)物种1的平衡线(b)物种2的平衡线因为坐标横轴上K1与K2/β有两种大小关系，纵轴上也有两种情况，所以将(a)、(b)两图相互叠合起来，就可以得到2×2四种结果：图2 Lotk1-V olterr1竞争模型的行为所产生的4种可能结局现以图(a)为例，说明物种1与物种2的数量变动情况：同理可得到图(b)(c)(d):从图中可以得出结论：(a) 当K1＞K2/β,K2＜K1/α时，物种1取胜，物种2被排除。

直观地说，在K2-K2/β线右边物种2已经超过环境容纳量而停止生长，而物种1能继续生长因此结果是物种1取胜。

基础生态学实验实验名称Lotka-Voltena捕食者.猎物模型模拟姓名学号系别班级实验H期同组姓名［实验原理］Lotka-Volteira 捕仅者-猎物模型是 20 试剂 20 年代 Lotka A J. （1925） fD Volterra V. （1926）提出的描述种群关系的经典模型之一。

该模型假设：除捕茂者存在外，猎物生活于理想坏境中（其出生率和死亡率与密度无关）：捕ft者的环境同样是理想的，其种群增长只受到可获得的猎物数量限制。

Lotka-Volterra捕仪者-猎物模型模拟的连续增长微分方程为：dN—=r1N-C1NP(1)dP—=-r2N+C2NP (2)式中：N——猎物密度：n——猎物种群增长率：c x一甫茂者发现利进攻猎物的效率，即平均每一捕食者捕杀猎物的常数；P——Hi仪者密度：-r2—捕食者的死亡率：C2一仅考利用猎物而转变为更多捕食者的捕食常数。

方程（1）描述了猎物种群动态，倾向于r］N的无限增长，但婆受捕仅者功能项C】NP的制约。

方程（2）描述了捕食者种群动态，捕仗者数量一方面受死亡率的影响，另一方而受与猎物密度有关的数值C?NP的影响。

当模型平衡，即兽=兽=0时，P = \ , N = ?。

说明当捕仅者的数量为g时，猎物Ctt dt Cj C2 Cj数杲将稳泄不变：捕仗者嗷量大于、时，猎物的数量会减少；捕食者的数量小于务猎物数Cl C1量增加。

同样，猎物数量为孑，捕仅骨数屋也会恒定不变：猎物数量人于孑时，捕仗者数量C2 C2上升，反之捕食者数量下降。

Lotka-Volteira捕食者-猎物模型揭示了这种捕仅关系的两个种群数最动态是彼此消长、往复振荡的变化规律。

Predators0 10 30Avsuop 2 O 8 6 4 2•••o o o O807060504030 AtrsuQp Aa」dGenerationni8 in^prewavg ■S5u v> ecologists to explore thenYear兔子与獪刑的种群震荡［实验目的］1、 掌握Lotka-Volterra 捕食者-猎物模型的生态学意义与各參数意义。

lotka-volterra模型的假设全文共四篇示例，供读者参考第一篇示例：Lotka-Volterra模型是一种描述捕食者-被捕食者动态的数学模型，以其简单而有效地描述生态系统中捕食关系而闻名。

这个模型基于一系列假设，这些假设对于描述生态系统中的捕食者和被捕食者之间的相互作用至关重要。

Lotka-Volterra模型假设生态系统中只存在两种种群：捕食者和被捕食者。

捕食者是以被捕食者为食的生物，而被捕食者是被捕食者所猎食的生物。

这两种种群之间形成了一种捕食关系，即捕食者依靠捕食被捕食者来获得能量和营养。

Lotka-Volterra模型假设捕食者和被捕食者的种群数量在一定时间范围内可以被表示为连续的变量。

这意味着在任何给定的时间点上，种群数量可以通过一个数值来描述，而不是通过一系列离散的单位来描述。

这一假设是建立数学模型的基础，使得我们可以通过数学方程来描述捕食者和被捕食者之间的相互作用。

Lotka-Volterra模型假设生态系统中的其他因素对捕食者和被捕食者之间的相互作用没有直接影响。

这意味着模型中只考虑了捕食者和被捕食者之间的相互作用，而忽略了其他可能影响种群数量的因素，如环境因素、竞争关系等。

这种简化模型的做法使得我们能够更容易地研究捕食者和被捕食者之间的关系，但也可能忽略了一些现实中的复杂性。

Lotka-Volterra模型假设捕食者和被捕食者的数量是连续变化的，而且种群数量的增长速率受到食物供应和捕食压力的影响。

这种假设基于生态系统中捕食者和被捕食者之间的相互作用，捕食者的数量受到食物供应的限制，而被捕食者的数量受到捕食者的压力的限制。

这种双向的相互作用导致捕食者和被捕食者之间的数量变化呈现出周期性波动的特点。

Lotka-Volterra模型基于一系列假设来描述生态系统中捕食者和被捕食者之间的相互作用。

这些假设为我们理解生态系统中的捕食关系提供了一个简单而有效的数学框架，帮助我们研究种群数量的变化及其对生态系统稳定性的影响。

lotka-volterra模型的假设全文共四篇示例，供读者参考第一篇示例：Lotka-Volterra 模型是描述捕食者和被捕食者之间相互作用的一个经典数学模型。

它由意大利数学家Alfred J. Lotka和美国数学家Vito Volterra分别在20世纪初提出，并成为生态学研究的基础之一。

该模型简单而直观地描述了捕食者和被捕食者之间的群体动态变化，可以帮助我们更好地理解生物群体之间的相互作用。

在Lotka-Volterra 模型中，我们首先假设只有两种生物群体：一种是捕食者，一种是被捕食者。

捕食者以被捕食者作为食物来源，而被捕食者则成为捕食者的猎物。

这两种群体之间的关系被描述为一种资源-消耗的关系，即捕食者消耗被捕食者以维持生存。

在这个模型中，我们做出了一些基本的假设，这些假设是建立模型的前提，也是对生态系统运作的简化描述。

以下是Lotka-Volterra 模型的基本假设：1. 环境对生物群体的影响是恒定的。

在模型中，我们假设环境对捕食者和被捕食者的影响是固定的，不会发生变化。

这样可以简化模型，使其更易于理解和分析。

2. 捕食者的增长率与被捕食者数量成正比。

在Lotka-Volterra 模型中，我们假设捕食者的增长率与被捕食者的数量成正比。

这意味着被捕食者的数量越多，捕食者的增长率越高，反之亦然。

3. 被捕食者的增长率与捕食者数量成负相关。

与捕食者相反，被捕食者的增长率与捕食者的数量成负相关。

这意味着捕食者的数量越多，被捕食者的增长率越低，反之亦然。

4. 每一个生物群体都在密集性独立环境中生存。

在模型中，我们假设每一个生物群体都在一个密集性独立的环境中生存，即捕食者和被捕食者的数量变化不受其他环境因素的影响。

5. 空间是均匀分布的。

我们还假设空间在生物群体之间是均匀分布的，即没有空间上的不均匀性会影响捕食者和被捕食者之间的相互作用。

这些假设是建立Lotka-Volterra 模型的基础，在研究捕食者和被捕食者之间的相互作用时，我们可以通过这些假设进行简化和分析。

一轮小专题捕食者-猎物模型-----------89中高中学部：房双喜经典的捕食者-猎物模型是由洛特卡和沃尔泰拉提出的。

若以捕食者密度为纵坐标、猎物密度为横座标、按时间顺序作出相位图，就可以得到一个封闭环（如图）。

相位图表示两个种群的密度将按封闭环的轨道逆时针方向无限循环，其中心点即为平衡点，通过平衡点作互相垂直的线，将相位图分为4块,在垂直线右面捕食者种群增加(P1→P2→P3)，在左面减少(P3→P2→P1)；在水平线下面，猎物种群增加(N1→N2→N3)，在上面减少(N3→N2→N1)。

因此，洛特卡－沃尔泰拉模型表明猎物－捕食者种群动态中分为4个时期：①猎物增加(N2→N3)，捕食者也增加(P1→P2)；②猎物减少(N3→N2)，捕食者继续增加(P2→P3)；③猎物(N2→N1)和捕食者(P3→P2)都减少；④捕食者继续减少(P2→P1)，而猎物增加(N1→N2)。

如此循环不息。

与“猎物-捕食者模型”有关的模拟题上面就是著名的LotKa-Volterra捕食者——猎物关系方程LotKa-Volterra方程假设:1.猎物只受到捕食者的限制,在没有捕食者的情况下,猎物种群将会无限制地呈指数增长；2.单位时间内被捕杀的猎物数量同捕食者与猎物个体随机相遇的次数成正比。

3.捕食者仅仅争夺食物,不存在其它的资源限制和捕食者种内竞争。

4 .种群所有的反应都是瞬时的,模型不允许时滞。

不考虑捕食者用于处理、摄取猎物的时间。

5 .最后，像其他简单的生态学模型一样,它忽略了种群的年龄结构和其他关系。

例1.科学家通过研究种间捕食关系，构建了捕食者一猎物模型，如下图所示（图中箭头所指方向代表曲线变化趋势）。

据图回答：（1）该模型属于__数学_（填“物理”、“概念”或“数学”）模型，其曲线变化趋势反映了生态系统中普遍存在的_负反馈_调节。

（2）请用该模型解释捕食者和猎物的种群数量均能维持相对稳定的原因：_猎物种群数量增加→捕食者种群数量增加→猎物种群数量减少→捕食者种群数量减少→猎物种群数量增加，依次循环_。

在动态生态学中，Lotka-Volterra模型是一种经典的描述捕食者-猎物关系的数学模型。

它由意大利数学家阿尔弗雷多·洛特卡（Alfred Lotka）和瑞典数学家维托·沃尔特拉（Vito Volterra）分别在20世纪初提出，被广泛应用于生态学和生物学领域，用于研究捕食者和猎物之间的相互作用。

在Lotka-Volterra模型中，捕食者和猎物的数量随时间的变化受到对方的影响，模拟了一个动态平衡的生态系统。

本文将围绕Lotka-Volterra模型展开全面的探讨，分析其理论基础、数学表达和实际应用，以及我对这一模型的个人理解。

1. Lotka-Volterra模型的理论基础Lotka-Volterra模型的提出基于对自然界捕食者和猎物之间的相互作用规律的观察和假设。

根据这一模型，捕食者的数量增加会导致猎物数量的减少，从而使捕食者的数量减少，最终导致猎物数量增加，从而形成了捕食者-猎物之间的周期性相互作用。

这一理论基础为后续建立数学模型奠定了基础，使得科学家可以通过数学方法来定量描述捕食者-猎物之间的关系，从而更深入地研究生态系统的动态演变。

2. Lotka-Volterra模型的数学表达Lotka-Volterra模型的数学表达通常采用微分方程的形式来描述捕食者和猎物数量随时间的变化。

具体而言，假设捕食者和猎物的种群数量分别为x和y，捕食者和猎物的增长率分别受到出生率、逝去率以及相互作用影响。

于是，可以得到捕食者和猎物种群数量随时间的变化方程，从而形成了Lotka-Volterra模型的数学表达式。

通过对这一数学模型进行分析和求解，可以得到捕食者和猎物数量随时间的变化趋势，进而揭示出捕食者-猎物相互作用的规律和特点。

3. Lotka-Volterra模型的实际应用Lotka-Volterra模型不仅在理论生态学研究中发挥着重要作用，同时在实际生态系统的研究和管理中也具有广泛的应用价值。

Lotka-Volterra捕⾷者-猎物模型模拟基础⽣态学实验Lotka-Volterra捕⾷者-猎物模型模拟姓名：学号：实验时间：1. 掌握Lotka-Volterra 捕⾷者-猎物模型的⽣态学意义与各参数意义。

2. 认识捕⾷关系的两个种群数量动态是此消彼长、往复振荡的变化规律。

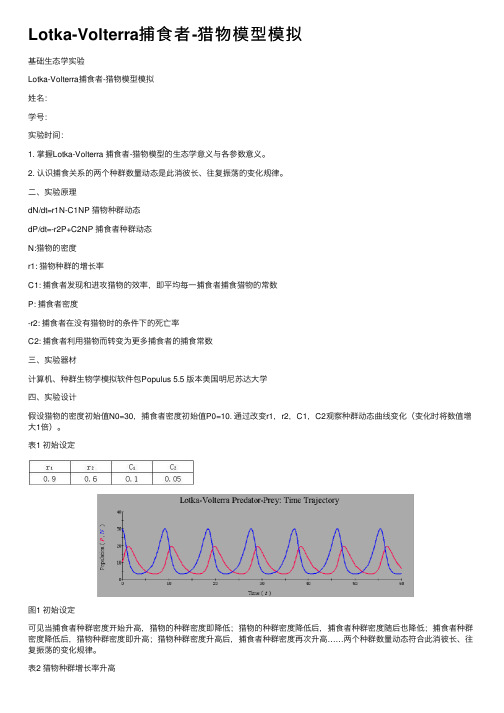
⼆、实验原理dN/dt=r1N-C1NP 猎物种群动态dP/dt=-r2P+C2NP 捕⾷者种群动态N:猎物的密度r1: 猎物种群的增长率C1: 捕⾷者发现和进攻猎物的效率，即平均每⼀捕⾷者捕⾷猎物的常数P: 捕⾷者密度-r2: 捕⾷者在没有猎物时的条件下的死亡率C2: 捕⾷者利⽤猎物⽽转变为更多捕⾷者的捕⾷常数三、实验器材计算机、种群⽣物学模拟软件包Populus 5.5 版本美国明尼苏达⼤学四、实验设计假设猎物的密度初始值N0=30，捕⾷者密度初始值P0=10. 通过改变r1，r2，C1，C2观察种群动态曲线变化（变化时将数值增⼤1倍）。

表1 初始设定图1 初始设定可见当捕⾷者种群密度开始升⾼，猎物的种群密度即降低；猎物的种群密度降低后，捕⾷者种群密度随后也降低；捕⾷者种群密度降低后，猎物种群密度即升⾼；猎物种群密度升⾼后，捕⾷者种群密度再次升⾼……两个种群数量动态符合此消彼长、往复振荡的变化规律。

表2 猎物种群增长率升⾼图2猎物种群增长率升⾼可见猎物种群增长率升⾼后，捕⾷者和猎物种群数量的振荡幅度增⼤，振荡频率增⼤，捕⾷者的数量上限更接近猎物数量上限。

表3捕⾷者在没有猎物时的条件下的死亡率升⾼图3 捕⾷者在没有猎物时的条件下的死亡率升⾼可见捕⾷者在没有猎物时的条件下的死亡率升⾼后，捕⾷者和猎物种群数量的振荡幅度减⼩，振荡频率增⼤。

表4捕⾷者发现和进攻猎物的效率增⼤图4捕⾷者发现和进攻猎物的效率增⼤可见捕⾷者发现和进攻猎物的效率增⼤后，捕⾷者和猎物种群数量的振荡幅度增⼤，振荡频率减⼩，两个种群的数量低⾕接近零。

表5捕⾷者利⽤猎物⽽转变为更多捕⾷者的捕⾷常数增⼤图5捕⾷者利⽤猎物⽽转变为更多捕⾷者的捕⾷常数增⼤可见捕⾷者利⽤猎物⽽转变为更多捕⾷者的捕⾷常数增⼤后，捕⾷者和猎物种群数量的振荡幅度增⼤，振荡频率减⼩，捕⾷者数量上限可以超过猎物数量上限。