晶面夹角计算公式

面心立方晶面间距公式
面心立方晶格是一种常见的晶体结构，其原子排列方式为每个原子周围有12个等距离的原子。

在这种结构中，原子之间的键角为109.5度，因此每个面心立方晶胞包含8个原子。

面心立方晶格的晶面间距公式可以通过以下步骤推导得出：
1. 首先，我们需要找到晶胞中的两个相邻原子之间的距离。

由于每个原子周围有12个等距离的原子，因此这两个原子之间的距离等于一个晶胞边长的一半。

设晶胞边长为a,则相邻原子之间的距离为a/2。

2. 然后，我们需要找到晶胞中的三个相邻原子之间的夹角。

由于每个原子周围有12个等距离的原子，因此这三个原子之间的夹角等于一个面心立方晶胞的一个顶角。

设顶角为θ，则三个相邻原子之间的夹角为θ。

3. 最后，我们可以利用勾股定理计算出晶胞中的一个边长和一个高。

设晶胞中的一个边长为b,一个高为c,则有：
b^2 = a^2/4 + c^2 - 2accos(π/3)
c^2 = a^2/4 + b^2 - 2abcos(π/3)
将上述两个式子联立求解，得到：
b = (√6-√2)/4a
c = (√6+√2)/4a
因此，面心立方晶格的晶面间距公式为：d = a/√3。

TEM作为一种常用的微观结构表征技术已经在材料科学、生物等学科被广泛应用，而作为材料人的你又怎能不对TEM做深入的了解。

今天来我们一起来看看如何利用三步法搞定TEM 透射电镜衍射斑点标定。

不过在此之前我们先要搞清两个重要的问题。

01标定目的这是大家首先遇到的问题。

以笔者的角度来看，目前通过衍射标定可以达到以下两个目的：提高格调和辅助进行物相鉴定。

1、提高格调提高格调是很容易理解的，因为凡涉是比较有档次的研究，TEM可谓是必不可少，目前的文章要是少了透射实验品质会降低不少，审稿人也没有兴趣，这样的情况下要想引起业界关注怕也是也不太容易。

当然，这并不是最主要的，第二个目的才是大家真正关心的。

2、辅助进行物相鉴定注意这里说的是“辅助”进行物相鉴定，之所以是“辅助”是由于物相鉴定是一个相当复杂的且技术含量高的工作。

鉴定的难度来源于以下几个方面：（1）、微观层面的物相太小，如果用打能谱分析元素的办法，很可能打到的区域会有偏离或区域偏大，能谱的结果不够准确。

（2）、物相太小又无法做XRD。

（3）、通过形貌观查判断，这个太主观，而且经验要求极高，不从事个十来年的研究很难做出准确的推断。

所以物相鉴定非常困难，不能凭借上面一种手段给出有说服力的证明，所以利用多种手段辅助联合证明提升说服力就势在必行，TEM就是其中之一。

但是TEM也不能作为鉴定物相一招制敌的法宝，因为标定过程中会引入多种误差（拍摄系统误差，测量误差，计算误差），没法百分百保证标定的精度，所以结果也就是在误差范围内参考。

不过有误差也没关系，圈内人士都会有一个约定俗成的共识，只要你从多个方面联合这证明物相，达到80%的说服力，也就默认你的证明是对的了。

审稿人也一般确实这么做的。

02怎样标定这是一个大问题，可以先从宏观上对这个问题进行把握。

打一个简单的比方，警察要查找犯罪嫌疑人是谁，在犯罪现场找到了作案者的小拇指指纹，要查到此人的信息就需要将该小拇指指纹拿到公安局的数据库中进行比对，一旦该小拇指与其中一个人的小拇指指纹对上了，很可能就是这个人作案。

摘要织构在传统的基础上，经过多年的发展已成为一门新兴发展的科学而受到了人们广泛的关注。

广义的说，某种具有择优取向的结构称为织构。

其特点之一是晶粒的微观取向可以在宏观某方向上得到表现，故显示了微观取向和宏观某方向的统一，可以体现出各种宏观性能的各向异性。

大多数的金属材料都存在这种现象，这就使得织构的研究加倍重要。

大量的实验和理论的创新丰富了这门科学的内容，并进一步推动了与之相关联的其他学科的发展，从而使这门学科所涵盖的知识面更加广博，因此随着织构这一科学的不断完善发展，也就出现了不同的分支。

定向凝固织构就是其中的一种很具代表意义的分支。

它主要是通过定向凝固的手段，使金属或合金生长出某一特定织构，从而满足性能在某个方向的择优的要求。

国内外许多研究人员已经做了许多相关实验，通过改变实验条件而改变织构的方向，并且发现了不同结构的金属或合金能产生的不同织构。

但是，到底是什么因素影响织构的生长呢？织构生长的机理是什么呢？在这方面至今还没什么进展，因而机理的提出对于定向凝固织构方面的工作就显得尤为重要。

本人在硕士阶段通过对面心立方，体心立方，密排六方和菱方结构四种具有不同结构和对称性的织构的研究，并做出了面心立方，密排六方和菱方结构的金属或合金的定向凝固样品，对他们进行了极图，反极图和ODF 定量分析，得出了它们的织构，然后从结晶学的角度考虑晶体生长习性，提出了不同晶体结构的定向凝固织构的生长机理。

这一机理可以很好解释并预测单一温度场条件下的各种结构的定向凝固织构。

虽然这一机理还不够完善，但是，相信在以后的研究中，如果考虑到更多的影响因素，有更多的不同条件下的实验数据的支持，一定可以提出更加完善的机理。

关键词：定向凝固织构极图反极图ODF提要第一节 织构的发展背景自从1937年戈斯发现硅钢片中导磁性能的各向异性以来，织构就被作为一门学科被广大科研工作者进行研究。

大量的研究情况表明织构在金属材料与合金中的存在具有普遍性。

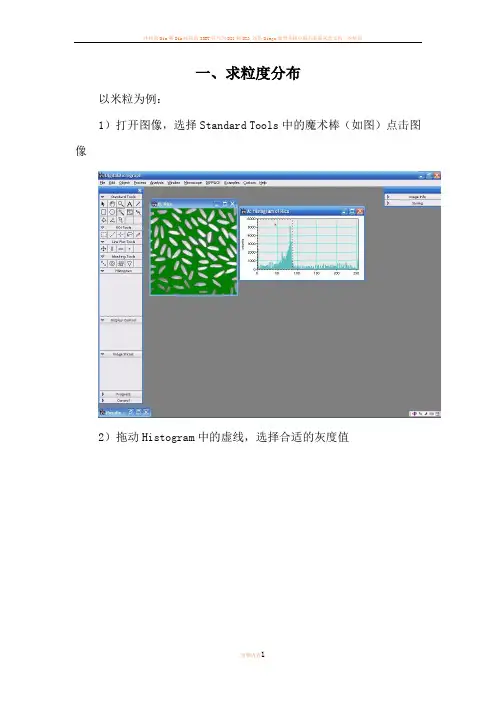
一、求粒度分布以米粒为例：1）打开图像，选择Standard Tools中的魔术棒（如图）点击图像2）拖动Histogram中的虚线，选择合适的灰度值3）选择Analysis－Particles－Find Particles4）选择Analysis－Particles－Analyze Particles搞定！二、简单实用技巧选中虚线方框，按住Alt健，在需要进行变换的区域拉出一个正方形然后点击Process，选择FFT即可，或者在画出上图中的红色方框后按Ctrl+F即可得到这个软件还可以直接测量条纹间距，首先可以将图片放大（视条纹清晰与否），放大工具使用红色区域中的工具，然后点击图片即可。

然后选中ROL Tools中的第二个工具（虚线），上图中的第二个方框。

然后对着图中的标尺，从起点到末端拉一条直线，尽量与标尺一样长短（见下图）。

之后选择 Analyze 菜单中的 Calibrate，会弹出一个对话框，将对话框中的数字改成标尺的数字如10 ， Units中选择 nm。

然后用刚才的虚线工具，画一条与条纹尽量垂直的直线，可以取10个或者20个条纹，取平均值。

直线的长度显示在Control面板中的L项。

Control面板可在Window菜单中调取出来，调取出来后，该面板显示在软件的左下方。

可以取10个或者20个条纹，取平均值。

三、各种晶系晶面夹角计算公式设晶面（h1k1l1）和晶面（h2k2l2）的面间距分别为d1、d2。

则二晶面的夹角φ以下列公式计算（V为单胞体积）。

立方晶系：正方晶系：六方晶系：正交晶系：菱方晶系：单斜晶系：三斜晶系：。

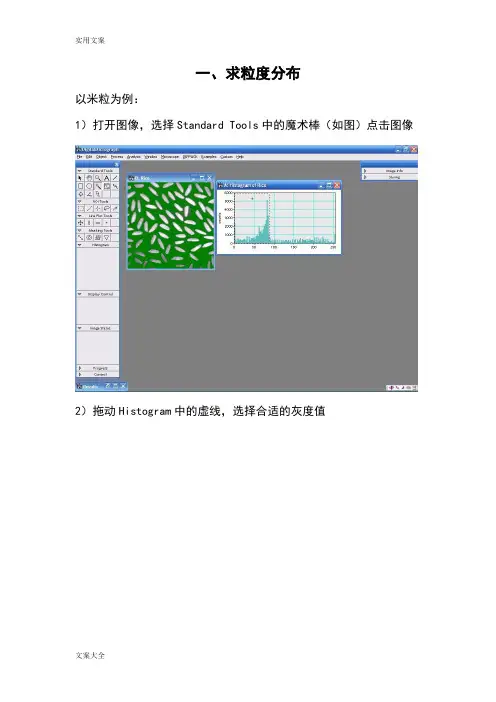
一、求粒度分布以米粒为例：1）打开图像，选择Standard Tools中的魔术棒（如图）点击图像2）拖动Histogram中的虚线，选择合适的灰度值3）选择Analysis－Particles－Find Particles4）选择Analysis－Particles－Analyze Particles搞定！二、简单实用技巧选中虚线方框，按住Alt健，在需要进行变换的区域拉出一个正方形然后点击Process，选择FFT即可，或者在画出上图中的红色方框后按Ctrl+F 即可得到这个软件还可以直接测量条纹间距，首先可以将图片放大（视条纹清晰与否），放大工具使用红色区域中的工具，然后点击图片即可。

然后选中ROL Tools中的第二个工具（虚线），上图中的第二个方框。

然后对着图中的标尺，从起点到末端拉一条直线，尽量与标尺一样长短（见下图）。

之后选择 Analyze 菜单中的 Calibrate，会弹出一个对话框，将对话框中的数字改成标尺的数字如10 ， Units中选择 nm。

然后用刚才的虚线工具，画一条与条纹尽量垂直的直线，可以取10个或者20个条纹，取平均值。

直线的长度显示在Control面板中的L项。

Control面板可在 Window 菜单中调取出来，调取出来后，该面板显示在软件的左下方。

可以取10个或者20个条纹，取平均值。

三、各种晶系晶面夹角计算公式设晶面（h1k1l1）和晶面（h2k2l2）的面间距分别为d1、d2。

则二晶面的夹角φ以下列公式计算（V为单胞体积）。

立方晶系：正方晶系：六方晶系：正交晶系：菱方晶系：单斜晶系：三斜晶系：。

晶面间距公式晶面间距公式是晶体结构和对称特性的重要描述工具，它在显微镜观测、X射线衍射分析和扫描电镜分析中都被广泛使用。

这是一个被人们所熟知的相对论定律，它涵盖了从最简单的几何结构到复杂的多层结构的一般定律，无论是几何结构还是化学结构都可以涵盖。

晶面间距的量化是晶体结构分析的基本原理，将晶体表面的空间结构量化为一个数字来表示晶体结构的各种参数。

晶面间距可以用一种符号表示，表示晶体中两个晶面之间的距离。

晶面间距公式的原理是：晶体晶格的每两个等轴晶面间距大小与中心多素元的数量，即晶体的层数有关。

晶面间距公式的基本原理是用同一轴的空间多素元来表示晶体中两个晶面之间的距离，它的计算公式可以用以下的简单的数学表达来表示：d = a/ (1 + 2 cos + sin2θ)^(1/2)其中d为晶面间距，a为晶体晶格常数，θ表示晶面之间的夹角。

可以看出，晶面间距公式依赖于晶格常数a，其他参数可以从实验结果中得出。

例如，当晶体晶格常数是12.0164时，晶面间距为d=12.0164/(1+2cosθ+sin2θ)^(1/2) 。

晶面间距公式在描述晶体结构中扮演着非常重要的角色，它可以为晶体的空间结构提供可靠的数字描述，对于研究化合物的特性、晶体结构的复杂性和晶体结构的细节等都有重要的作用。

晶面间距公式也被广泛应用于晶体的研究中，通过结构分析和结构量化来探究物质的结构细节和性质，甚至可以提出关于特定材料的结构和性质的假设。

此外，晶面间距公式还可以帮助有关专家建立晶体结构的模型，为学术研究提供坚实的依据。

除了正常的晶体结构分析外，晶面间距公式还可以用于变性特性的分析，可以帮助研究人员了解物质在变性过程中的晶体结构变化，以及他们发生变化的原因。

晶面间距公式还可以用于分子催化特性研究，可以帮助研究人员更好地理解分子催化活性的细节，从而帮助设计更为有效的催化剂体系。

由于晶面间距公式可以量化晶体结构，因此它在晶体学研究中有着十分重要的意义。

X射线晶体学复习要点（一）晶体和空间点阵¾什么是晶体？¾晶体相关的基本概念：1.单晶：构成固体的原子作周期性有规则排列的固体。

2.多晶：由细微小单晶无规排列的固体。

3.非晶：至少在微米尺度内作周期性排列称为长程有序。

原子作长程无序排列的固体称为非晶态。

¾单晶体的几个概念：1.晶棱2.晶带3.晶面夹角守恒定律（2）点阵和结构基元1912年Lave等首次用X射线衍射测定晶体结构，标志现代晶体学的创立。

晶体内部原子、分子结构的基本单元，在三维空间作周期性重复排列，可用一种数学抽象——点阵来研究它。

若晶体内部结构的基本单元可抽象为一个，则整个晶体可用一个三维点阵来表示。

点阵是一组无限的点，点阵中每个点都具有完全相同的周围环境。

在平移的对称操作下,（连结点阵中任意两点的矢量,按此矢量平移）,所有点都能复原,满足以上条件的一组点称为点阵。

晶系•分子（或原子）在三维空间中周期性排列就形成晶体。

周期排列的重复单元就是结构基元。

能够填满整个三维空间的排列单元首先必须是一个平行六面体。

•晶胞参数：表示一个平行六面体需要6个参数：三个轴的长度a, b, c 和三个轴的夹角α, β, γ。

•根据晶胞的点群对称性，把晶体分为七大晶系；考虑到晶胞这中平行六面体的微观对称性，得到一共有14种不同的平行六面体，就是14种布拉菲点阵。

能够填满三维空间的平行六面体，按照对称性分成7种晶系。

4种点阵类型按照点阵类型分：1.简单（P）2.底心（C）3.体心（I）4.面心（F）如何表示晶体中的原子？)表示出1个晶胞里面的原子即可，其他原子就是该晶胞在空间重复排列。

)晶胞的大小和形状，由晶胞参数a,b, c, α, β, γ确定；)晶胞内部各个原子的坐标位置，由原子坐标参数（x,y,z）规定。

)结构测定就是确定以上的各个参数。

cn b n a n R n r r r r 321++=任意一个阵点位置都可以表示为位矢：任意一个原子位置都可以表示为位矢：c z b y a x R R j j j n j nr r r r r +++=•晶列：布拉菲格点可以看成分布在平行等距的直线系上，这些直线系称为晶列。

一、求粒度分布以米粒为例：1）打开图像，选择Standard Tools中的魔术棒（如图）点击图像2）拖动Histogram中的虚线，选择合适的灰度值3）选择Analysis－Particles－Find Particles4）选择Analysis－Particles－Analyze Particles搞定！二、简单实用技巧选中虚线方框，按住Alt健，在需要进行变换的区域拉出一个正方形然后点击Process，选择FFT即可，或者在画出上图中的红色方框后按Ctrl+F 即可得到这个软件还可以直接测量条纹间距，首先可以将图片放大（视条纹清晰与否），放大工具使用红色区域中的工具，然后点击图片即可。

然后选中ROL Tools中的第二个工具（虚线），上图中的第二个方框。

然后对着图中的标尺，从起点到末端拉一条直线，尽量与标尺一样长短（见下图）。

之后选择 Analyze 菜单中的 Calibrate，会弹出一个对话框，将对话框中的数字改成标尺的数字如10 ， Units中选择 nm。

然后用刚才的虚线工具，画一条与条纹尽量垂直的直线，可以取10个或者20个条纹，取平均值。

直线的长度显示在Control面板中的L项。

Control面板可在 Window 菜单中调取出来，调取出来后，该面板显示在软件的左下方。

可以取10个或者20个条纹，取平均值。

三、各种晶系晶面夹角计算公式设晶面（h1k1l1）和晶面（h2k2l2）的面间距分别为d1、d2。

则二晶面的夹角φ以下列公式计算（V为单胞体积）。

立方晶系：正方晶系：六方晶系：正交晶系：菱方晶系：单斜晶系：三斜晶系：。

《晶体结构与缺陷》第一章习题及答案1-1.布拉维点阵的基本特点是什么答：具有周期性和对称性，而且每个结点都是等同点。

1-2.论证为什么有且仅有14种Bravais点阵。

答：第一，不少于14种点阵。

对于14种点阵中的任一种，不可能找到一种连接结点的方法，形成新的晶胞而对称性不变。

第二，不多于14种。

如果每种晶系都包含简单、面心、体心、底心四种点阵，七种晶系共28种Bravais点阵。

但这28种中有些可以连成14种点阵中的某一种而对称性不变。

例如体心单斜可以连成底心单斜点阵，所以并不是新点阵类型。

1-3.以BCC、FCC和六方点阵为例说明晶胞和原胞的异同。

答：晶胞和原胞都能反映点阵的周期性，即将晶胞和原胞无限堆积都可以得到完整的整个点阵。

但晶胞要求反映点阵的对称性，在此前提下的最小体积单元就是晶胞；而原胞只要求体积最小，布拉维点阵的原胞都只含一个结点。

例如：BCC晶胞中结点数为2，原胞为1；FCC晶胞中结点数为4，原胞为1；六方点阵晶胞中结点数为3，原胞为1。

见下图，直线为晶胞，虚线为原胞。

BCC FCC 六方点阵1-4.什么是点阵常数各种晶系各有几个点阵常数答：晶胞中相邻三条棱的长度a、b、c与这三条棱之间的夹角α、β、γ分别决定了晶胞的大小和形状，这六个参量就叫做点阵常数。

晶系a、b、c，α、β、γ之间的关系点阵常数的个数三斜a≠b≠c，α≠β≠γ≠90º6 (a、b、c 、α、β、γ)单斜a≠b≠c，α=β=90≠γ或α=γ=90≠β4 (a、b、c、γ或a、b、c、β)1-5.分别画出锌和金刚石的晶胞，并指出其点阵和结构的差别。

答：点阵和结构不一定相同，因为点阵中的结点可以代表多个原子，而结构中的点只能代表一个原子。

锌的点阵是六方点阵，但在非结点位置也存在原子，属于HCP结构；金刚石的点阵是FCC 点阵，但在四个四面体间隙中也存在碳原子，属于金刚石结构。

见下图。

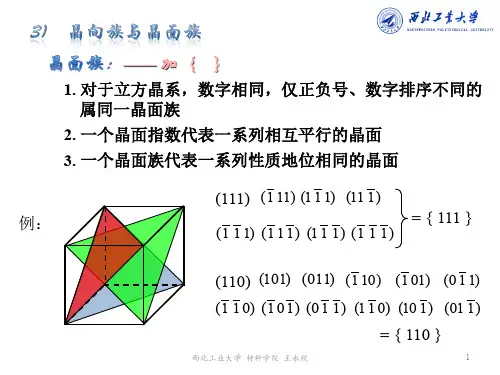
锌的结构金刚石的结构1-6.写出立方晶系的{123}晶面族和<112>晶向族中的全部等价晶面和晶向的具体指数。

基于MATLAB的通用晶面间夹角公式的推导与求解刘健【摘要】充分利用倒易点阵基矢与正点阵基矢互为倒易的特点，推导出通用晶面间夹角的求解公式。

同时利用MATLAB语言的核心——矩阵与数值计算编制了求解通用晶面间夹角的程序。

并介绍了如何利用该程序求解任意类型晶体的各晶面间夹角，再对程序求解的晶体的晶面间夹角进行了验证，证明该程序在晶体学研究中有较好的应用价值。

%Make full use of the reciprocal lattice basis vectors and punctuality array vector mutually reciprocal characteristics, the general solution formula of crystal plane angle was deduced, and by means of core matrix and numerical calculation of MATLAB language, the general crystal plane angle program was solved, and how to use the program to solve the crystal plane angle of arbitrary type crystals was introduced, then the procedure of solving crystal plane angle was verified, it is shown that the program have good application value in crystallographic studies.【期刊名称】《理化检验-物理分册》【年(卷),期】2012(048)007【总页数】3页(P450-451,463)【关键词】晶面夹角;倒易点阵;MATLAB软件;向量【作者】刘健【作者单位】遵义师范学院物理与机电工程学院,遵义563002【正文语种】中文【中图分类】O731晶面与晶面在空间的几何关系是材料科学和晶体学等研究领域中的重要参数，其中晶面间夹角在许多实际应用中，如晶体光学、晶体结构分析以及多晶体择优取向等方面都有广泛应用。

成分和结构相同的晶体,其对应晶面的夹角
晶体是由晶体晶粒组成的固体，其特征是其结构是完全统一的;物质就像一颗宝石由许多华丽的小角构成一个完美的整体。

晶体表面经常是由一些由平整平行构成的晶面组成，这些晶面就是晶体成分和结构相同的晶体所对应的晶面，而这些晶面之间的夹角也是晶体的一个重要特征。

晶体的晶胞不仅只有一种形状，而且晶面形状也有许多种，每种晶体晶面之间的夹角和其他晶体晶面形状都有其独特之处，可以根据这些特征来识别和分类不同的晶体。

晶面之间有7种夹角，分别为90°、120°、180°、60°、０°、双夹角以及其它夹角，从而构成了不同形状的晶胞。

这些夹角的大小取决于晶胞的原子排列，在同一种晶体里,它们的夹角是不变的。

每种晶体的晶面之间的夹角可以用几何学的方法来计算，根据晶胞的型号，它们之间的夹角可以求出，也可以用拉普拉斯表法计算各夹角的大小。

比如，晶胞型号为tetragonal的晶胞晶面之间的夹角有90°和180°两种，而晶胞型号为cubic的晶胞晶面之间的夹角有90°、120°和180°三种。

除了晶胞型号外，晶体晶面形状之间的夹角还取决于晶体本身的结构，比如晶体在不同温度下会有不同的结构，这也会影响晶体晶面之间的夹角。

其实，晶体晶面之间夹角也和晶体内部分子排列、晶粒间距、晶胞各边尺寸相关，这些都影响到晶体晶面之间的夹角。

因此，晶体晶面之间的夹角是一个非常复杂的物理量，而晶体的特性和性能往往与其夹角大小有关。

两晶面的夹角
两晶面的夹角是指两个晶面之间的夹角，也称为面角。

在晶体中，每个晶面都有一个法向量，表示该晶面的方向。

两个晶面的夹角可以通过它们的法向量之间的夹角来计算。

具体来说，如果两个晶面的法向量分别为n1和n2，则它们的夹角θ可以通过以下公式计算：
cosθ = n1·n2 / (||n1|| * ||n2||)
其中，“·”表示向量的点积，||n1||和||n2||分别表示n1和n2的模长。

请注意，这里计算的是两个晶面法向量之间的夹角，而不是它们之间的空间夹角。

在实际应用中，可以通过晶体结构分析、X射线衍射等手段来确定晶体的晶面及其法向量，从而计算两晶面的夹角。