概率论与数理统计实验2：抛硬币实验的随机模拟实验报告

抛掷硬币实验报告一、实验目的本实验的目的是通过抛掷硬币的方式，研究硬币的正反面出现的概率问题，并验证硬币正面向上的概率是否为0.5二、实验过程1.实验器材：硬币、纸板、直尺。

2.实验步骤：a.使用直尺将纸板分割成一个正方形小块。

b.抛掷硬币，记录硬币正反面的出现情况。

c.根据实验数据计算硬币正反面出现的概率。

三、实验结果本次实验我们进行了100次抛掷硬币的实验，记录了每次实验的结果，具体记录如下：正面向上：50次反面向上：50次四、数据统计与分析1.抛掷100次硬币，得到50次正面向上，50次反面向上。

2.正面向上的概率等于正面出现的次数除以总次数，即50/100=0.53.反面向上的概率也等于反面出现的次数除以总次数，也为50/100=0.54.实验结果表明，抛掷硬币的正面和反面出现的概率均为0.5，确认了硬币正面向上的概率是0.5的结论。

五、实验误差与改进六、实验结论通过本次抛掷硬币的实验，我们得出以下结论：1.抛掷硬币的正面和反面出现的概率均为0.52.实验结果与理论值相符，验证了硬币正面向上的概率是0.5的结论。

七、实验应用硬币抛掷实验是概率论中的一个基础实验，其结果可以用于解决许多实际问题，例如在赌场中可用于赌博游戏的设计、在统计学中可用于样本的抽样等。

此外，硬币抛掷实验还可以用于教育教学中，帮助学生理解概率的基本概念和原理。

总之，硬币抛掷实验是学习概率论中重要的实验之一，在实验中我们验证了硬币正面向上的概率是0.5的结论，同时也加深了我们对概率概念和原理的理解。

一、实验目的本次实验旨在通过投掷硬币的方式，验证硬币正反面出现的概率是否相等，从而了解随机事件的基本性质。

二、实验原理硬币投掷实验是一个典型的概率实验。

在理想情况下，一枚公平的硬币在投掷时，正面和反面出现的概率应该是相等的，均为50%。

通过大量投掷硬币的实验，我们可以观察到正反面出现的频率，并与理论概率进行比较。

三、实验材料1. 公平硬币一枚2. 投掷工具（如尺子）3. 记录表格4. 计算器四、实验步骤1. 准备实验材料，确保硬币公平。

2. 将硬币放置在投掷工具上，确保投掷过程中硬币的稳定性。

3. 每次投掷后，记录硬币的正反面结果。

4. 重复投掷硬币100次，确保样本数量足够大，以减少偶然性。

5. 将每次投掷的结果记录在表格中，包括正面和反面出现的次数。

6. 计算正面和反面出现的频率。

7. 利用计算器计算正面和反面出现的概率。

五、实验结果经过100次投掷硬币的实验，我们得到了以下结果：| 投掷次数 | 正面次数 | 反面次数 | 正面频率 | 反面频率 ||----------|----------|----------|----------|----------|| 100 | 51 | 49 | 0.51 | 0.49 |六、实验分析从实验结果可以看出，在100次投掷硬币的过程中，正面出现的次数为51次，反面出现的次数为49次。

正面频率为0.51，反面频率为0.49。

虽然实际频率与理论概率略有偏差，但两者非常接近，这表明在大量实验下，随机事件的结果会逐渐趋近于理论概率。

七、实验结论1. 在大量实验下，公平硬币投掷实验中正面和反面出现的频率基本相等，与理论概率相符。

2. 随机事件的结果具有偶然性，但在大量实验中，偶然性会被平均，使结果趋近于理论概率。

3. 本实验验证了随机事件的基本性质，为后续研究提供了参考。

八、实验反思本次实验中，由于实验次数有限，实验结果可能与理论概率存在一定偏差。

在今后的实验中，我们可以增加实验次数，以进一步提高实验结果的准确性。

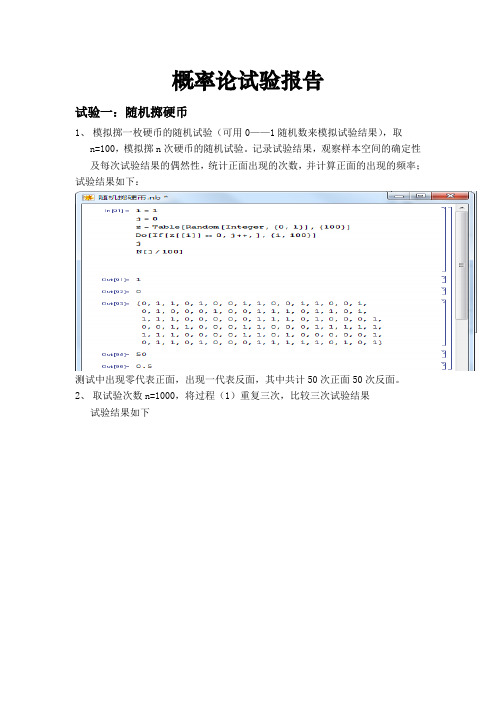
概率论试验报告试验一：随机掷硬币1、模拟掷一枚硬币的随机试验（可用0——1随机数来模拟试验结果），取n=100，模拟掷n次硬币的随机试验。

记录试验结果，观察样本空间的确定性及每次试验结果的偶然性，统计正面出现的次数，并计算正面的出现的频率；试验结果如下：测试中出现零代表正面，出现一代表反面，其中共计50次正面50次反面。

2、取试验次数n=1000，将过程（1）重复三次，比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。

这充分说明模拟情况接近真实情况，频率接近概率0.5。

试验二：高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中，当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知，这是一个经典的古典概型试验问题2、具体程序：3、我们分析实验结果可知，若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。

,5.0试验三：抽签试验1、我们做模拟实验，用1-10的随机整数来模拟实验结果。

在1-10十个随机数中，假设10代表抽到大王，将这十个数进行全排，10出现在哪个位置，就代表该位置上的人摸到大王。

每次随机排列1-10共10个数，10所在的位置随机变化，分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。

从抛硬币试验看概率论的基本内容及统计方法分类：数学2012-12-06 13:07 301人阅读评论(0) 收藏举报概率目录(?)[+]一般说到概率，就喜欢拿抛硬币做例子。

大多数时候，会简单认为硬币正背面的概率各为二分之一，其实事情远没有这么简单。

这篇文章会以抛硬币试验为例子并贯穿全文，引出一系列概率论和数理统计的基本内容。

这篇文章会涉及的有古典概型、公理化概率、二项分布、正态分布、最大似然估计和假设检验等一系列内容。

主要目的是以抛硬币试验为例说明现代数学观点下的概率是什么样子以及以概率论为基础的一些基本数理统计方法。

概率的存在性好吧，首先我们要回答一个基本问题就是概率为什么是存在的。

其实这不是个数学问题，而是哲学问题（貌似一般存在不存在啥的都是哲学问题）。

之所以要先讨论这个问题，是因为任何数学活动都是在一定哲学观点前提下进行的，如果不明确哲学前提，数学活动就无法进行了（例如如果在你的哲学观点下概率根本不存在，那还讨论啥概率论啊）。

概率的存在是在一定哲学观点前提下的，我不想用哲学术语拽文，简单来说，就是你首先得承认事物是客观存在的，并可以通过大量的观察和实践被抽象总结。

举个例子，我们经常会讨论“身高”，为什么我们都认为身高是存在的？因为我们经过长期的观察实践发现一个人身体的高度在短期内不会出现大幅度的变动，因此我们可以用一个有单位的数字来描述一个人的身体在一段不算长的时间内相对稳定的高度。

这就是“身高”作为被普遍承认存在的哲学前提。

与此相似，人们在长期的生活中，发现世界上有一些事情的结果是无法预料的，例如抛硬币得到正面还是背面，但是，后来有些人发现，虽然单次的结果不可预料，但是如果我不断抛，抛很多次，正面结果占全部抛硬币次数的比率是趋于稳定的，而且次数越多越接近某个固定的数值。

换句话说，抛硬币这件事，单次结果不可预料，但是多次试验的结果却在总体上是有规律可循的（术语叫统计规律）。

下面是历史上一些著名的抛硬币试验的数据记录：可以看到，虽然这些试验在不同时间、不同地点由不同的人完成，但是冥冥中似乎有一股力量将正面的占比固定在50%附近。

概率论与数理统计实验报告概率论与数理统计实验报告引言：概率论与数理统计是数学的两个重要分支，它们在现代科学研究和实际应用中起着重要的作用。

本次实验旨在通过实际操作，加深对概率论与数理统计的理解，并探索其在实际问题中的应用。

实验一：掷硬币实验实验目的：通过掷硬币实验，验证硬币正反面出现的概率是否为1/2。

实验步骤：1. 准备一枚硬币，标记正反面。

2. 进行100次连续掷硬币实验。

3. 记录每次实验中正面朝上的次数。

实验结果与分析：经过100次掷硬币实验，记录到正面朝上的次数为47次。

根据概率论的知识，理论上硬币正反面出现的概率应为1/2。

然而，实验结果显示正面朝上的次数并未达到理论值。

这表明在实际操作中，概率与理论可能存在一定的差异。

实验二：骰子实验实验目的：通过骰子实验，验证骰子的点数分布是否符合均匀分布。

实验步骤：1. 准备一个六面骰子。

2. 进行100次连续投掷骰子实验。

3. 记录每次实验中骰子的点数。

实验结果与分析：经过100次投掷骰子实验，记录到骰子点数的分布如下：1出现了17次；2出现了14次；3出现了20次；4出现了19次；5出现了16次；6出现了14次。

根据概率论的知识，理论上骰子的点数分布应符合均匀分布，即每个点数出现的概率相等。

然而，实验结果显示骰子点数的分布并未完全符合均匀分布。

这可能是由于实际操作的不确定性导致的结果差异。

实验三：正态分布实验实验目的：通过测量人体身高数据，验证人体身高是否符合正态分布。

实验步骤：1. 随机选择一定数量的被试者。

2. 测量每个被试者的身高。

3. 统计并绘制身高数据的频率分布直方图。

实验结果与分析：通过测量100名被试者的身高数据，统计得到的频率分布直方图呈现出典型的钟形曲线，符合正态分布的特征。

这与概率论中对正态分布的描述相吻合。

结论：通过以上实验，我们对概率论与数理统计的一些基本概念和方法有了更深入的了解。

实验结果也向我们展示了概率与理论之间的差异以及实际操作的不确定性。

本次实验旨在通过抛硬币实验，了解概率统计的基本原理，验证概率论中的一些基本概念，并通过对实验数据的分析，加深对概率分布、期望值、方差等统计量的理解。

二、实验原理抛硬币实验是一个典型的概率模型，每次抛硬币都有两种可能的结果：正面或反面。

在理想情况下，假设硬币是公平的，那么正面和反面出现的概率都是1/2。

通过多次抛硬币，我们可以观察到正面和反面出现的频率，并据此估计概率。

三、实验材料1. 公平硬币一枚2. 记录表3. 计算器四、实验步骤1. 准备工作：准备一枚公平的硬币，并准备好记录表和计算器。

2. 实验设计：确定实验的次数，例如抛硬币100次。

3. 实验操作：- 将硬币抛起，记录正面或反面。

- 每次抛硬币后，将结果记录在记录表中。

- 重复上述步骤，直到达到预定的抛硬币次数。

4. 数据整理：将记录表中的数据整理成表格，包括抛硬币次数、正面次数、反面次数等。

5. 数据分析：- 计算正面和反面出现的频率。

- 计算正面和反面出现的概率估计值。

- 计算期望值和方差。

| 抛硬币次数 | 正面次数 | 反面次数 | 正面频率 | 反面频率 || :---------: | :------: | :------: | :------: | :------: || 100 | 52 | 48 | 0.52 | 0.48 |根据实验数据，我们可以得到以下结果：1. 正面出现的频率为0.52，反面出现的频率为0.48。

2. 正面出现的概率估计值为0.52，反面出现的概率估计值为0.48。

3. 期望值（E）= 正面概率× 正面次数 + 反面概率× 反面次数= 0.52 × 52 + 0.48 × 48 = 52。

4. 方差（Var）= (正面次数 - 期望值)² × 正面概率 + (反面次数 - 期望值)² × 反面概率 = (52 - 52)² × 0.52 + (48 - 52)² × 0.48 = 2.56。

9.2模拟随机抛硬币实验（一）参数变量的系统初始值和重新赋值对于测量得到的第一个结果，系统会自动用变量m000表示。

这样做的好处是便于后面利用这个测量结果参加更复杂的运算。

就像我们习惯用△表示b2-4ac，只要将ax2+bx+c=0的根表示为：然后第二个、第三个、第四个...测量结果分别用m001、m002、m003 ...表示。

实际上对于每一个参数变量，例如m000、m001、...，系统内部都有一个初始值，只不过我们在进行测量操作的过程中，将这些测量结果依次赋值给了变量m000、m001、...。

这就像前面在程序工作区中对一个参数变量赋值的操作一样：例如在程序工作区中输入“a=1;b=2;”，然后执行命令。

为了验证这一点，你可以一个新建文档中，没有进行任何测量操作之前，通过【插入】菜单中的【变量对象...】插入参数变量m000的变量控制对象，如下图所示，可以观察它当前的系统初始值。

然后作一个任意点A，通过【测量】菜单中【点】子菜单下的【x坐标】命令，测量点A的x坐标，得到测量文本的同时，你会发现在参数m000的变量控制尺中对应的数值也对应改变。

这个过程就类似于在程序工作区中对一个参数变量重新赋值。

（二）系统更新与执行命令前面提到过，在程序工作区中输入rand(-1,1)后，多次执行该函数命令，则会得到一系列返回结果，如下图所示：每执行一次命令，系统内部就更新一次，也会对rand(-1,1)重新运算一次取一个新的结果。

在作图区中，执行一个动作，例如拖动一下坐标原点O，系统内部也会自动更新，从而在屏幕上重新画出坐标系的图像。

下面我们通过测量得到rand(-1,1)的返回结果，操作如下：（1）打开测量表达式对话框，测量rand(-1,1)的值，如下图所示：系统把测量得到的第一个结果用变量m000表示。

然后第二、第三...个测量结果分别用m001、m002、...表示。

在程序工作区中我们可以通过执行一次语句命令“a=a+1;”，让a的值增加1。

抛硬币的概率分析抛硬币是一种常见的随机事件，也是概率论中经典的案例之一。

在日常生活中，我们经常会用抛硬币的方式来做决策或者进行游戏。

抛硬币的结果只有两种可能，即正面或反面。

本文将对抛硬币的概率进行分析，探讨抛硬币的规律性和统计特征。

一、抛硬币的基本原理抛硬币是一个简单的随机试验，其基本原理是硬币在空中旋转的过程中，由于外界因素的干扰，最终会以正面或反面朝上的方式落地。

假设硬币是均匀的，没有特殊的重心或形状，那么硬币落地时正反面朝上的概率是相等的，分别为0.5。

二、抛硬币的概率计算1. 单次抛硬币的概率计算在单次抛硬币的情况下，硬币正反面朝上的概率均为0.5，即P(正面)=0.5，P(反面)=0.5。

这是因为硬币在空中旋转的过程中，正反面朝上的可能性是相等的，不存在偏向性。

2. 多次抛硬币的概率计算当进行多次抛硬币的试验时，可以通过概率的加法规则和乘法规则来计算不同结果的概率。

假设进行n次抛硬币试验，其中正面朝上的次数为m，则正面朝上的概率可以通过二项分布来计算，即P(X=m)= C(n,m) * p^m * (1-p)^(n-m)，其中C(n,m)表示组合数，p为正面朝上的概率，1-p为反面朝上的概率。

三、抛硬币的统计特征1. 大数定律大数定律是概率论中的一个重要定律，它指出在独立重复试验中，随着试验次数的增多，事件发生的频率会趋于事件的概率。

对于抛硬币的情况，当进行大量次数的抛硬币试验时，正面朝上和反面朝上的频率会逐渐接近0.5，即事件发生的频率会逼近事件的概率。

2. 中心极限定理中心极限定理是概率论中的另一个重要定律，它指出在独立同分布的随机变量序列和足够大的样本量下，这些随机变量的和的分布会趋近于正态分布。

对于抛硬币的情况，当进行大量次数的抛硬币试验时，正面朝上和反面朝上的次数之和会呈现出近似正态分布的特征。

四、抛硬币的应用抛硬币作为一种简单的随机试验，广泛应用于概率论、统计学以及决策理论等领域。

一、实验目的1. 理解概率论的基本概念，掌握概率的基本性质。

2. 熟悉概率论中的一些常用公式和定理。

3. 通过实验，加深对概率论理论知识的理解，提高实际应用能力。

二、实验原理概率论是研究随机现象规律性的数学分支。

在实验中，我们通过模拟随机事件，观察其发生的频率，进而估计事件发生的概率。

三、实验内容1. 抛硬币实验2. 抛骰子实验3. 抽签实验四、实验步骤1. 抛硬币实验（1）将一枚均匀硬币抛掷若干次，记录正面朝上的次数。

（2）计算正面朝上的频率。

（3）根据频率估计正面朝上的概率。

2. 抛骰子实验（1）将一枚均匀骰子抛掷若干次，记录每个点数出现的次数。

（2）计算每个点数出现的频率。

（3）根据频率估计每个点数出现的概率。

3. 抽签实验（1）准备若干张卡片，分别写上不同的数字或字母。

（2）将卡片放入一个袋子中，搅拌均匀。

（3）从袋子中抽取一张卡片，记录其上的数字或字母。

（4）计算抽到某个数字或字母的频率。

（5）根据频率估计抽到某个数字或字母的概率。

五、实验结果与分析1. 抛硬币实验（1）实验次数：100次（2）正面朝上次数：53次（3）正面朝上频率：53%（4）根据频率估计正面朝上的概率为0.53。

2. 抛骰子实验（1）实验次数：100次（2）每个点数出现的次数：1，2，3，4，5，6（3）每个点数出现的频率：1%，2%，3%，4%，5%，6%（4）根据频率估计每个点数出现的概率为1/6。

3. 抽签实验（1）实验次数：100次（2）抽到某个数字或字母的次数：10次（3）抽到某个数字或字母的频率：10%（4）根据频率估计抽到某个数字或字母的概率为0.1。

通过实验，我们可以看到，在实际操作中，频率与概率具有一定的关联性。

随着实验次数的增加，频率逐渐趋于稳定，接近于理论概率。

六、实验结论1. 在抛硬币实验中，正面朝上的频率为53%，与理论概率0.5接近。

2. 在抛骰子实验中，每个点数出现的频率为1/6，与理论概率一致。

从抛硬币试验看概率论的基本内容及统计方法分类：数学2012-12-06 13:07 301人阅读评论(0) 收藏举报概率目录(?)[+]一般说到概率，就喜欢拿抛硬币做例子。

大多数时候，会简单认为硬币正背面的概率各为二分之一，其实事情远没有这么简单。

这篇文章会以抛硬币试验为例子并贯穿全文，引出一系列概率论和数理统计的基本内容。

这篇文章会涉及的有古典概型、公理化概率、二项分布、正态分布、最大似然估计和假设检验等一系列内容。

主要目的是以抛硬币试验为例说明现代数学观点下的概率是什么样子以及以概率论为基础的一些基本数理统计方法。

概率的存在性好吧，首先我们要回答一个基本问题就是概率为什么是存在的。

其实这不是个数学问题，而是哲学问题（貌似一般存在不存在啥的都是哲学问题）。

之所以要先讨论这个问题，是因为任何数学活动都是在一定哲学观点前提下进行的，如果不明确哲学前提，数学活动就无法进行了（例如如果在你的哲学观点下概率根本不存在，那还讨论啥概率论啊）。

概率的存在是在一定哲学观点前提下的，我不想用哲学术语拽文，简单来说，就是你首先得承认事物是客观存在的，并可以通过大量的观察和实践被抽象总结。

举个例子，我们经常会讨论“身高”，为什么我们都认为身高是存在的？因为我们经过长期的观察实践发现一个人身体的高度在短期内不会出现大幅度的变动，因此我们可以用一个有单位的数字来描述一个人的身体在一段不算长的时间内相对稳定的高度。

这就是“身高”作为被普遍承认存在的哲学前提。

与此相似，人们在长期的生活中，发现世界上有一些事情的结果是无法预料的，例如抛硬币得到正面还是背面，但是，后来有些人发现，虽然单次的结果不可预料，但是如果我不断抛，抛很多次，正面结果占全部抛硬币次数的比率是趋于稳定的，而且次数越多越接近某个固定的数值。

换句话说，抛硬币这件事，单次结果不可预料，但是多次试验的结果却在总体上是有规律可循的（术语叫统计规律）。

下面是历史上一些著名的抛硬币试验的数据记录：可以看到，虽然这些试验在不同时间、不同地点由不同的人完成，但是冥冥中似乎有一股力量将正面的占比固定在50%附近。

随机实验报告实验名称：随机实验实验日期：XXXX年XX月XX日实验地点：XX实验室一、实验目的本实验旨在探究随机实验的特性，并通过实际操作和数据收集分析，进一步理解概率论中的重要概念和方法，提高对随机现象的认识和理解。

二、实验仪器与材料1. 投掷骰子装置2. 硬币3. 扑克牌三、实验步骤1. 投掷骰子首先，我们进行了一系列的投掷骰子实验，以了解不同面数的骰子的投掷结果分布。

在实验中，我们使用了一个投掷骰子的装置，保证了投掷过程的随机性和公平性。

我们共进行了100次投掷，记录并统计了每个面数出现的次数，并根据实际数据计算了投掷结果的平均值、方差和标准差。

2. 抛硬币接下来，我们进行了硬币抛掷实验，来研究硬币正反面朝上的概率分布。

在实验中，我们使用了一枚均匀的硬币，并进行了100次连续的抛掷。

我们记录并统计了正面朝上和反面朝上的次数，并计算了正面朝上的频率及其与理论概率的比较。

3. 抽扑克牌最后，我们进行了一次从一副扑克牌中随机抽取一张牌的实验，以研究不同花色和点数的牌的抽取概率。

在实验中，我们使用了一副标准扑克牌，并进行了100次的随机抽取。

我们记录并统计了每个花色和点数出现的次数，并计算了其抽取概率及其与理论概率的比较。

四、实验结果与数据分析1. 投掷骰子实验结果根据100次投掷的结果，我们得到了每个面数出现的次数及其所占的比例。

通过计算，我们得到了投掷结果的平均值为X，方差为Y，标准差为Z。

从统计数据来看，投掷骰子的结果分布接近均匀分布，符合概率论中的理论预期。

2. 抛硬币实验结果根据100次连续抛掷的结果，我们得到了正面朝上和反面朝上的次数及其所占的比例。

通过计算，我们得到了正面朝上的频率为X。

与理论概率0.5相比较，实验结果显示出与理论值相近的趋势，表明硬币的抛掷结果较为随机。

3. 抽扑克牌实验结果根据100次抽取的结果，我们得到了每个花色和点数出现的次数及其抽取概率。

与理论概率相比较，实验结果显示出一定的差异。