光栅衍射实验

光栅衍射实验报告一、实验目的1、深入理解光栅衍射的原理。

2、学会使用分光计测量光栅常数。

3、观察光栅衍射现象，研究衍射条纹的特点。

二、实验原理光栅是由大量等宽、等间距的平行狭缝组成的光学元件。

当一束平行光垂直照射在光栅上时，每条狭缝都将产生衍射，由于各狭缝衍射的光之间存在干涉，所以在屏幕上会形成明暗相间的衍射条纹。

根据光栅衍射方程：＄d\sin\theta ＝ k\lambda$ （其中＄d$ 为光栅常数，＄＼theta$ 为衍射角，＄k$ 为衍射级数，＄＼lambda$ 为入射光波长），通过测量衍射角＄＼theta$ 和已知的入射光波长＄＼lambda$，可以计算出光栅常数＄d$。

三、实验仪器分光计、光栅、汞灯、平面反射镜等。

四、实验步骤1、调整分光计粗调：使望远镜、平行光管和载物台大致水平。

细调：通过调节望远镜目镜和物镜，使分划板清晰；调整望远镜与平行光管共轴；使载物台平面与分光计中心轴垂直。

2、放置光栅将光栅放在载物台上，使光栅平面与入射光垂直。

3、观察衍射条纹打开汞灯，通过望远镜观察光栅衍射条纹。

4、测量衍射角找到中央明纹两侧的一级、二级等明纹，分别测量其衍射角。

5、数据记录与处理五、实验数据记录与处理｜衍射级数＄k$ ｜衍射角＄＼theta$（左）｜衍射角＄＼theta$（右）｜平均衍射角＄＼bar{＼theta}＄｜｜｜｜｜｜｜ 1 ｜＄10°20'＄｜＄190°20'＄｜＄10°20'＄｜｜ 2 ｜＄21°30'＄｜＄201°30'＄｜＄21°30'＄｜已知汞灯绿光波长＄＼lambda ＝ 5461nm$，根据光栅衍射方程＄d\sin\theta ＝ k\lambda$，计算光栅常数＄d$。

对于一级衍射，＄d\sin10°20' ＝ 1\times5461nm$，解得＄d ＝302×10^｛－6}m$。

光栅衍射光强分布测量实验
任婷婷
实验仪器：
半导体激光器（os-8525A）,狭缝附件组（os-8523）,光学导轨，光传感器（CI-6504A），光阑支架
实验目的：
（1）进一步熟悉使用光传感器
（2）观察光栅衍射光谱，掌握光栅的衍射定律
实验原理：
当一束单色光垂直照射在光栅上时，各狭缝的光线因衍射而向各方向传播，经透镜会聚相互产生干涉，并在透镜的焦平面上形成一系列明暗条纹。

实验过程：
（1）在光学平台上依次安置光传感器，狭缝附件组半导体激光器
（2）接通电源，调整光源使其通过狭缝
（3）观察衍射图谱，用光学传感器接收，计算机连接，表格记录记录。

单缝衍射（采样率50）
单缝衍射（采样率10）
双缝衍射（采样率50）
双缝衍射（采样率10）。

4.10光栅的衍射【实验目的】(1)进一步熟悉分光计的调整与使用;(2)学习利用衍射光栅测定光波波长及光栅常数的原理和方法;(3)加深理解光栅衍射公式及其成立条件。

【实验原理】衍射光栅简称光栅，是利用多缝衍射原理使光发生色散的一种光学元件。

它实际上是一组数目极多、平行等距、紧密排列的等宽狭缝，通常分为透射光栅和平面反射光栅。

透射光栅是用金刚石刻刀在平面玻璃上刻许多平行线制成的，被刻划的线是光栅中不透光的间隙。

而平面反射光栅则是在磨光的硬质合金上刻许多平行线。

实验室中通常使用的光栅是由上述原刻光栅复制而成的，一般每毫米约250~600条线。

由于光栅衍射条纹狭窄细锐，分辨本领比棱镜高，所以常用光栅作摄谱仪、单色仪等光学仪器的分光元件，用来测定谱线波长、研究光谱的结构和强度等。

另外，光栅还应用于光学计量、光通信及信息处理。

1(测定光栅常数和光波波长光栅上的刻痕起着不透光的作用，当一束单色光垂直照射在光栅上时，各狭缝的光线因衍射而向各方向传播，经透镜会聚相iC B 互产生干涉，并在透镜的焦平面上形成一系列明暗条纹。

A G如图1所示，设光栅常数d=AB的光栅G，有一束平行光与, 光栅的法线成i角的方向，入射到光栅上产生衍射。

从B点作BC垂直于入射光CA，再作BD垂直于衍射光AD，AD与光栅法线所成的夹角为,。

如果在这方向上由于光振动的加强而在F处产生了一个明条纹，其光程差CA+AD必等于波长的整数倍，即: F图1 光栅的衍射 dimsinsin,,,, (1) ，，式中，,为入射光的波长。

当入射光和衍射光都在光栅法线同侧时，(1)式括号内取正号，在光栅法线两侧时，(1)式括号内取负号。

如果入射光垂直入射到光栅上，即i=0，则(1)式变成:dmsin,,, (2) m这里，m=0，?1，?2，?3，…，m为衍射级次，,第m级谱线的衍射角。

m平行光望远镜物镜黄黄绿绿紫紫中央明纹图3 光栅衍射光谱图2衍射光谱的偏向角示意图光栅G在小平台上的位置2(用最小偏向角法测定光波波长如图2所示，波长为的光束入射在光栅G上，入射角为i，若与入射线同在光栅 ,法线n一侧的m级衍射光的衍射角为沪，则由式(1)可知dimsinsin,,,, (3) ，，若以?表示入射光与第m级衍射光的夹角，称为偏向角，,,，,i (4),,i显然，?随入射角i而变，不难证明时?为一极小值，记作,，称为最小偏向角。

工物系 核11 李敏 2011011693 实验台号19之五兆芳芳创作光栅衍射实验一、实验目的（1） 进一步熟悉分光计的调整与使用；（2） 学习利用衍射光栅测定光波波长及光栅常数的原理和办法；（3） 加深理解光栅衍射公式及其成立条件； 二、实验原理如右图所示，有一束平行光与光栅的法线成i 角，入射到光栅上产生衍射；出射光夹角为ϕ.从B 点引两条垂线到入射光和出射光.如果在F 处产生了一个明条纹，其光程差AD CA +必等于波长λ的整数倍，即()sin sin d i m ϕλ±= （1）m 为衍射光谱的级次， 3,2,1,0±±±.由这个方程，知道了λϕ,,,i d 中的三个量，可以推出另外一个.若光线为正入射，0=i ，则上式变成λϕm d m =sin （2）其中m ϕ为第m 级谱线的衍射角.据此，可用分光计测出衍射角m ϕ，已知波长求光栅常数或已知光栅常数求波长.如右图.入射光线与m 级衍射光线位于光栅法线同侧，（1）式中应取加号，即.以为偏向角，则由三角形公式得（3）易得，当时，∆最小，记为，则(2.2.1)变成,3,2,1,0,2sin2±±±==m m d λδ（4）由此可见，如果已知光栅常数d ，只要测出最小偏向角，就可以按照（4）算出波长.三、实验仪器在本实验中，分光计的调节应该满足：望远镜适合于不雅察平行光，平行光管收回平行光，并且两者的光轴都垂直于分光计主轴.调节光栅时，调节小平台使光栅刻痕平行于分光计主轴.放置光栅时应该使光栅平面垂直于小平台的两个调水平螺钉的连线.颜色紫绿黄红波长/nm（1）水银灯在使用中必须与扼流圈串接，不克不及直接接220V 电源，不然要烧毁.（2）水银灯在使用进程中不要频繁启闭，不然会下降其寿命.（3）水银灯的紫外线很强，不成直视.四、实验任务 （1）调节分光计和光栅使满足要求. （2）测定i=0时的光栅常数和光波波长. （3）测定i=时的水银灯光谱中波长较短的黄线的波长（4）用最小偏向角法测定波长较长的黄线的波长.（选作）五、实验数据记实与处理1．i=0时，测定光栅常数和光波波长 光栅编号：；∆仪=；入射光方位10ϕ=；20ϕ=.波长／nm 黄1黄2紫衍射光谱级次m游标 ⅠⅡⅠⅡⅠⅡⅠⅡ左侧衍射光方位ϕ左右侧衍射光方位ϕ右2m ϕϕϕ=-左右2ϕmϕm2.i=时，丈量波长较短的黄线的波长光栅编号：；光栅平面法线方位=；=.五、数据记实见附页六、数据处理λ不确定度的推导（1）d 的不确定度 （2）λ的不确定度由以上推导可知，丈量d 时，在m ϕ∆一定的情况下，m ϕ越大d 的偏差越小.但是m ϕ大时光谱级次高，谱线难以不雅察.所以要各方面要综合考虑.而对λ的丈量，也是m ϕ越大不确定度越小.综上，在可以看清谱线的情况下，应该尽量选择级次高的光谱不雅察，以减小误差.6.2 求绿线的d 和λ并计较不确定度1）二级光谱下：由sin mm dλϕ=，代入数据m ϕ=19，可得d=又由mm m m m m d d d d ϕϕϕϕϕϕtan ln )()ln (22∆=∆∂∂=∆∂∂=∆，m ϕ∆=2’得d∆=3349.1*[2π/(60*180)]/tan(19d =(3349.1±5.7)nm而实验前已知光栅为300线每毫米，可见丈量结果与实际较吻合.再用d 求其他光的λ：对波长较长的黄光：ϕm =20 o15＇,d=3349nm 代入，可得λ=579.6nm ，λ∆对波长较短的黄光：ϕm =20 o10＇代入，可得λ=577.3nm ，λ∆对紫光：ϕm =20 o5＇代入，可得λ=435.7nm ，λ∆2）三级光谱下：对绿光： 由sin mm dλϕ=，代入数据m ϕ=29，可得d=又由mm m m m m dd d d ϕϕϕϕϕϕtan ln )()ln (22∆=∆∂∂=∆∂∂=∆，m ϕ∆=2’得d∆=3.5nm ，d =(3349.4±3.5)nm再用d求其他光的波长=31 o14＇，d=3349.4nm代入，得：对波长较长的黄光：ϕmλ=578.9nm，λ∆=31 o9＇，d=3349.4nm代入，得：对波长较短的黄光：ϕmλ=577.5nm，λ∆=23 o，d=3349.4nm代入，得：对紫光：ϕmλ=436.2nm，λ∆阐发计较结果，与实际波长吻合比较良好.另外，可以看到，三级谱线下丈量后计较的结果教二级谱线下的结果其偏差都更小，与理论推断吻合.6.3在i=15 o时，测定波长较短的黄线的波长.由，m=2，可得：在同侧：λ在异侧：λ由公式：代入数据：m=2,δ=39o51＇代入，得与实际值吻合良好.七、思考题1）分光计调整好是实验的前提条件.即应包管分光计望远镜适合不雅察平行光，平行光管发平行光，两者光轴垂直于分光计主轴.具体实现步调同实验4.3分光计的调节.调节光栅平面与平行光管的光轴垂直，开始粗调使零级谱线尽量处于两侧谱线的对称位置，然后再细调使满足2＇条件.团体推荐测绿光谱线的衍射角.思考：不成以用分光计自准法，因为光栅的反射性质远不如三棱镜，自准法时得到的像比较模糊，无法实现高精度的调节.2）见数据阐发3）先调节望远镜的使其偏移15o，然后调节光栅位置，用自准法使光栅法线沿望远镜标的目的，便可包管方位角为15o. 4）团体实验总结：实验前觉得这个实验很复杂，但是事实上做的其实不快.一开始的时候把一级谱线当成了二级谱线，耽误了好久.不过还好后来实时意识到了问题，纠正了错误.回来处理数据，发明数据质量还不错，自己的眼睛也算是没白辛苦吧.这是第一次完全用电脑写实验陈述，感到排版有点烂~总之，下次实验持续努力~。

衍射光栅实验报告衍射光栅实验报告实验目的：1.熟悉光栅的基本结构，掌握计算衍射光栅的分光角度和衍射光谱的方法。

2.通过实验观察光栅的衍射光谱，了解和验证光的波动性质。

实验原理：光栅是利用多个均匀周期性平面反射、透射结构排布于平板上，可以将入射光分解成数个互相平行的光线的光学元件。

光栅的衍射同样可以由菲涅尔基本公式或者海森伯-布拉格公式进行分析计算。

对于平行入射的单色光，当光线入射光栅表面时，它就会在光栅表面上发生衍射现象。

如果假设光栅的腰板间隔为d，当入射波长为λ的光线通过衍射光栅时，会在不同方向形成一系列互相平行衍射条纹。

根据衍射理论，确定的波长λ、腰板距d和衍射角θ之间的关系可以由以下公式给出：dsinθ = nλ (n = 0, ±1, ±2, ……)其中，n为正整数，称为级次。

衍射极大的级次越高，其对应的衍射角就越大。

因此，大级次的衍射极大，相应的衍射角也更小。

实验内容及步骤：1.检查光栅实验仪器是否正常运作。

2.将狭缝与白炽灯构成的光源和光栅之间垂直彼此的平面对准。

3.用三脚架固定光栅和检测器，将检测器调节到最大输出。

4.调节之后，逐步向侧面移动检测器，在恰当的检测器位置调节角度，最终可以观察到高明区。

5.在高明区附近扫描光栅，观察衍射光谱，记录不同级次的衍射角度和亮度。

6.测量光栅的腰板间距，计算不同级次的波长。

实验结果及分析：在实验中，我们涉及两组光栅，其腰板间距分别为1200根/毫米和600根/毫米。

我们使用两组光栅进行了不同波长和级别的光源的衍射实验，得到了如下的结果：1.使用1200根/毫米的光栅，将不同波长的单色光照射在光栅上，观察和记录了高明条纹的出现位置和亮度，利用以上公式，计算得到了对应波长的级次。

如下表所示：波长λ(纳米) 级次n 衍射角θ(度) 404 0 0.0 435 1 -6.5 546 1 -17.7 579 0 -20.2 612 1 -22.9 852 2 -29.52.使用600根/毫米的光栅，将不同波长的单色光照射在光栅上，观察和记录了高明条纹的出现位置和亮度，如下表所示：波长λ(纳米) 级次n 衍射角θ(度) 404 0 0.0 435 0 -1.8 546 1 -6.1 579 1 -6.8 612 1 -7.6 852 2 -10.4同时，我们还可以根据以上结果计算出光的频率，从而验证和探究光的波长和频率之间的关系。

光栅衍射实验实验报告.doc 光栅衍射实验实验报告一、实验目的1.通过实验观察光栅衍射现象，了解光栅衍射的原理和特点。

2.掌握光栅方程，能够利用光栅方程计算不同级次的衍射角。

3.学习使用分光计进行角度测量，提高实验技能和数据处理能力。

二、实验原理光栅是由大量等宽等间距的平行狭缝构成的光学元件，当一束平行光垂直照射在光栅上时，会发生衍射现象。

光栅衍射的原理是多缝衍射和单缝衍射的结合，通过光栅方程可以描述不同级次的衍射角与波长之间的关系。

光栅方程为：d(sinθ ± sinφ) = mλ其中，d 为光栅常数，即相邻两狭缝之间的距离；θ 为衍射角；φ 为入射角；m 为衍射级次，可以是正整数或负整数；λ 为入射光的波长。

三、实验步骤1.调整分光计，使平行光管发出平行光，并调整光栅位置，使平行光垂直照射在光栅上。

2.观察光栅衍射现象，可以看到在屏幕上出现了一系列明亮的衍射条纹。

3.转动分光计上的望远镜，对准某一衍射条纹，记录此时望远镜的角度读数。

4.重复步骤3，对准不同级次的衍射条纹，记录相应的角度读数。

5.根据光栅方程，计算不同级次的衍射角。

6.分析实验数据，得出实验结论。

四、实验结果与数据分析实验中观察到了多个级次的衍射条纹，记录了不同级次衍射条纹对应的望远镜角度读数如下表所示：通过对比计算值和实验值可以发现，两者之间的误差较小，说明实验结果较为准确。

同时，不同级次的衍射角随着级次的增加而增加，符合光栅方程的规律。

五、实验结论本次实验通过观察光栅衍射现象，了解了光栅衍射的原理和特点。

掌握了光栅方程，能够利用光栅方程计算不同级次的衍射角。

同时，学习了使用分光计进行角度测量，提高了实验技能和数据处理能力。

实验结果较为准确，验证了光栅方程的正确性。

一、实验名称：光栅衍射实验二、实验目的：1. 熟悉光栅的原理及其在光学仪器中的应用；2. 掌握分光计的调整和使用方法；3. 利用衍射光栅测定光波波长及光栅常数；4. 深入理解光栅衍射公式及其成立条件。

三、实验原理：光栅是利用多缝衍射原理使光发生色散的一种光学元件。

它由一组数目极多、平行等距、紧密排列的等宽狭缝组成。

当一束单色光垂直照射在光栅上时，各狭缝的光线因衍射而向各方向传播，经透镜会聚相互产生干涉，并在透镜的焦平面上形成一系列明暗条纹。

光栅衍射条纹的形成是单缝衍射和多缝干涉的综合结果。

根据光栅衍射公式，衍射角θ与光波波长λ、光栅常数d以及衍射级次m之间存在如下关系：d sinθ = m λ其中，d为光栅常数，λ为光波波长，θ为衍射角，m为衍射级次。

四、实验仪器：1. 分光计；2. 平面透射光栅；3. 低压汞灯（连镇流器）；4. 毫米刻度尺；5. 计算器。

五、实验步骤：1. 调整分光计，使其与光栅垂直；2. 将光栅放置在分光计的焦平面上，调整光栅角度，使光束垂直照射在光栅上；3. 观察透镜焦平面上形成的衍射条纹，记录下第m级明纹对应的衍射角θ；4. 重复步骤3，记录下多组m级明纹对应的衍射角θ；5. 利用光栅衍射公式计算光波波长λ和光栅常数d。

六、实验数据及结果处理：1. 记录实验数据，包括m级明纹对应的衍射角θ；2. 利用光栅衍射公式计算光波波长λ和光栅常数d；3. 计算光栅常数d的平均值和标准偏差；4. 对实验结果进行分析，讨论误差来源。

七、实验结果与分析：1. 根据实验数据，计算光波波长λ和光栅常数d的平均值及标准偏差；2. 分析实验误差来源，如分光计调整误差、测量误差等；3. 讨论实验结果与理论值之间的差异，分析原因。

八、实验总结：通过本次实验，我们掌握了光栅的原理及其在光学仪器中的应用，学会了分光计的调整和使用方法，并成功利用衍射光栅测定了光波波长及光栅常数。

同时，我们深入理解了光栅衍射公式及其成立条件，为今后进一步学习光学知识打下了基础。

衍射光栅实验报告一、实验目的1、了解衍射光栅的工作原理。

2、测量衍射光栅的光栅常数。

3、观察衍射条纹的特征，并研究其与光栅参数的关系。

二、实验原理衍射光栅是一种具有周期性结构的光学元件，它可以将入射的单色平行光分解成不同方向的衍射光。

当一束平行光垂直入射到光栅上时，在光栅的后面会出现一系列明暗相间的条纹，这些条纹称为衍射条纹。

根据光栅衍射方程：＄d\sin\theta ＝ k\lambda$（其中$d$为光栅常数，＄＼theta$为衍射角，＄k$为衍射级数，＄＼lambda$为入射光波长），通过测量衍射角$＼theta$和已知的入射光波长$＼lambda$，可以计算出光栅常数$d$。

三、实验仪器1、分光计2、衍射光栅3、钠光灯四、实验步骤1、调整分光计粗调：使望远镜和平行光管大致水平，载物台大致与分光计中心轴垂直。

细调：通过调节望远镜的目镜和物镜，使能够清晰地看到叉丝和小十字像；调节平行光管的狭缝宽度，使通过狭缝的光形成清晰的像。

2、放置衍射光栅将衍射光栅放置在载物台上，使光栅平面与分光计中心轴平行。

3、观察衍射条纹打开钠光灯，使平行光垂直入射到光栅上，在望远镜中观察衍射条纹。

调节望远镜的位置和角度，使能够清晰地看到中央明纹和各级衍射条纹。

4、测量衍射角选择左右两侧的某一级衍射条纹（如第一级），分别测量其对应的衍射角。

转动望远镜，使叉丝对准衍射条纹的中心，读取两个游标的读数。

然后将望远镜转向另一侧，对准同一级衍射条纹的中心，再次读取游标的读数。

两次读数之差即为衍射角的两倍。

5、重复测量对同一级衍射条纹进行多次测量，取平均值以减小误差。

6、更换光栅，重复实验五、实验数据及处理1、实验数据记录｜衍射级数｜左侧游标读数（°）｜右侧游标读数（°）｜衍射角（°）｜｜：：｜：：｜：：｜：：｜｜ 1 ｜285°10′ ｜105°20′ ｜39°55′ ｜｜ 1 ｜284°50′ ｜105°40′ ｜40°05′ ｜｜ 1 ｜285°00′ ｜105°30′ ｜40°00′ ｜2、数据处理计算衍射角的平均值：＄＼theta ＝＼frac{39°55′ ＋40°05′ ＋40°00′｝｛3} ＝40°00′＄将衍射角转换为弧度：＄＼theta ＝ 40°＼times ＼frac{＼pi}｛180} ＼approx 0698$（弧度）已知钠光灯的波长$＼lambda ＝ 5893$nm，根据光栅衍射方程$d\sin\theta ＝ k\lambda$，＄k ＝ 1$，可得光栅常数$d ＝＼frac{＼lambda}｛＼sin\theta} ＼approx 167\times10^｛－6}＄m六、误差分析1、分光计的调节误差：分光计没有调节到完全准确的状态，可能导致测量的衍射角存在偏差。

第1篇一、实验名称光栅衍射实验二、实验目的1. 理解光栅衍射的基本原理，包括光栅方程及其应用。

2. 掌握分光计的使用方法，包括调整和使用技巧。

3. 学习如何通过实验测定光栅常数和光波波长。

4. 加深对光栅光谱特点的理解，包括色散率、光谱级数和衍射角之间的关系。

三、实验原理光栅是由大量平行、等宽、等间距的狭缝（或刻痕）组成的光学元件。

当单色光垂直照射到光栅上时，各狭缝的光波会发生衍射，并在光栅后方的屏幕上形成一系列明暗相间的衍射条纹。

这些条纹的形成是由于光波之间的干涉作用。

根据光栅方程，可以计算出光栅常数和光波波长。

四、实验仪器1. 分光计2. 平面透射光栅3. 低压汞灯（连镇流器）4. 光栅常数测量装置5. 光栅波长测量装置五、实验步骤1. 准备工作：检查实验仪器是否完好，了解各仪器的使用方法和注意事项。

2. 调节分光计：根据实验要求，调整分光计，使其达到最佳状态。

3. 放置光栅：将光栅放置在分光计的载物台上，确保其垂直于入射光束。

4. 调节光源：调整低压汞灯的位置，使其发出的光束垂直照射到光栅上。

5. 观察衍射条纹：通过分光计的望远镜观察光栅后的衍射条纹。

6. 测量衍射角：使用光栅常数测量装置，测量衍射条纹的角宽度。

7. 计算光栅常数和光波波长：根据光栅方程，计算光栅常数和光波波长。

8. 重复实验：重复上述步骤，至少进行三次实验，以确保实验结果的准确性。

六、实验数据记录1. 光栅常数（d）：单位为纳米（nm）。

2. 光波波长（λ）：单位为纳米（nm）。

3. 衍射角（θ）：单位为度（°）。

七、实验结果与分析1. 计算光栅常数和光波波长：根据实验数据，计算光栅常数和光波波长。

2. 分析实验结果：比较实验结果与理论值，分析误差产生的原因，如仪器误差、操作误差等。

3. 讨论实验现象：讨论光栅衍射条纹的特点，如条纹间距、亮度等。

八、实验结论1. 通过实验，验证了光栅衍射的基本原理。

2. 掌握了分光计的使用方法，提高了实验操作技能。

光栅衍射实验报告小结概述光栅衍射是一种重要的实验现象，具有广泛的应用价值。

本次实验旨在通过观察光通过光栅后的衍射现象，探索光的波动性质以及相关参数的测量方法。

实验中我们使用了光栅、单色光源等设备，并通过调整实验环境、测量角度等方法获取实验数据。

实验原理光通过光栅后会发生衍射现象，衍射光线的干涉叠加形成明暗相间的衍射条纹。

光栅的衍射效应与光波的波长、波前形状、光栅间距等参数有关。

实验步骤及结果1. 实验环境调整：- 保持实验室内相对较暗的状态，以减少背景光的干扰。

- 调整光源距离光栅适宜的位置，使得光线照射均匀。

2. 测量角度：- 利用支架固定光栅，调节测角仪的位置，使其位于光栅的中心位置。

- 用角度刻度盘测量光栅的衍射角度，并记录测量结果。

- 通过调整测角仪的位置，测量其他衍射角度。

- 记录衍射角度与光强的关系。

3. 数据分析：- 绘制衍射角度与光强的图像。

- 根据散射角度和光栅参数计算光的波长。

- 计算出光栅的间距。

实验结果与讨论通过实验测量和数据分析，我们得到了光栅衍射角度与光强的关系图像。

根据图像我们可以清晰地观察到衍射条纹的明暗变化情况，并且利用图像数据计算了光的波长和光栅的间距。

然而，在实验过程中我们也遇到了一些困难。

首先，由于实验室中光线较亮，背景光的干扰较大，导致一些实验数据的不精确。

其次，测量角度的准确性也受到了测角仪和人为因素的影响，提高角度测量的准确性仍然是一个挑战。

针对这些问题，我们可以通过增加背景光屏蔽装置来减少背景光的干扰，同时使用更加精确的测角仪进行测量，以提高实验数据的准确性和可靠性。

实验结论本次实验通过观察和测量光栅衍射现象，探索了光的波动性质以及相关参数的测量方法。

通过数据分析我们得到了光强与衍射角度的关系，计算出了光的波长和光栅的间距。

实验结果与理论相符，验证了光栅衍射实验的原理和方法。

光栅衍射实验在科学研究和实际应用中具有重要的价值。

通过准确测量光栅衍射现象，可以进一步研究光的波动性质和衍射理论，为光学领域的研究和应用提供基础数据和实验验证。

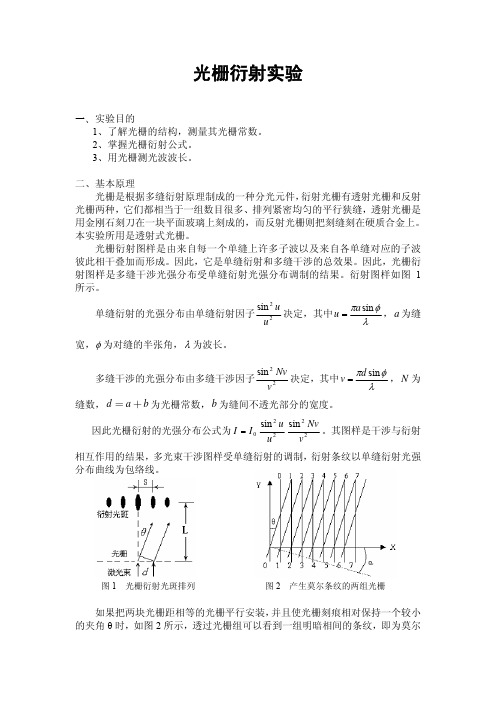
光栅衍射实验一、实验目的1、了解光栅的结构，测量其光栅常数。

2、掌握光栅衍射公式。

3、用光栅测光波波长。

二、基本原理光栅是根据多缝衍射原理制成的一种分光元件，衍射光栅有透射光栅和反射光栅两种，它们都相当于一组数目很多、排列紧密均匀的平行狭缝，透射光栅是用金刚石刻刀在一块平面玻璃上刻成的，而反射光栅则把刻缝刻在硬质合金上。

本实验所用是透射式光栅。

光栅衍射图样是由来自每一个单缝上许多子波以及来自各单缝对应的子波彼此相干叠加而形成。

因此，它是单缝衍射和多缝干涉的总效果。

因此，光栅衍射图样是多缝干涉光强分布受单缝衍射光强分布调制的结果。

衍射图样如图1所示。

单缝衍射的光强分布由单缝衍射因子22sin uu 决定，其中λφπsin a u =，为缝宽，a φ为对缝的半张角，λ为波长。

多缝干涉的光强分布由多缝干涉因子22sin vNv 决定，其中λφπsin d v =，为缝数，＝＋b 为光栅常数，为缝间不透光部分的宽度。

N d a b 因此光栅衍射的光强分布公式为0I I =22sin u u 22sin vNv 。

其图样是干涉与衍射相互作用的结果，多光束干涉图样受单缝衍射的调制，衍射条纹以单缝衍射光强分布曲线为包络线。

图1 光栅衍射光斑排列 图2 产生莫尔条纹的两组光栅如果把两块光栅距相等的光栅平行安装，并且使光栅刻痕相对保持一个较小的夹角θ时，如图2所示，透过光栅组可以看到一组明暗相间的条纹，即为莫尔条纹。

莫尔条纹的宽度B为：B=P/sinθ其中P为光栅距。

光栅刻痕重合部分形成条纹暗带，非重合部分光线透过则形成条纹亮带。

光栅莫尔条纹的两个主要特征是：判向作用：当指示光栅相对于固定不动的主光栅左右移动时，莫尔条纹将沿着近于栅线的方向上下移动，由此可以确定光栅移动的方向。

位移放大作用：当指示光栅沿着与光栅刻线垂直方向移动一个光栅距D时，莫尔条纹移动一个条纹间距B，当两个等距光栅之间的夹角θ较小时，指示光栅移动一个光栅距D，莫尔条纹就移动KD的距离。

衍射光栅实验报告光栅衍射实验报告篇一:光栅衍射实验实验报告工一、核11 李敏2011011693 实验台号19光栅衍射实验实验目的(1) 进一步熟悉分光计的调整与使用;(2) 学习利用衍射光栅测定光波波长及光栅常数的原理和方法;(3) 加深理解光栅衍射公式及其成立条件; 二、实验原理2.1测定光栅常数和光波波长如右图所示，有一束平行光与光栅的法线成i角，入射到光栅上产生衍射;出射光夹角为?。

从B点引两条垂线到入射光和出射光。

如果在F处产生了一个明条纹，其光程差CA?AD必等于波长?的整数倍，即d?sin??sini??m?(1)m为衍射光谱的级次，0,?1,?2,?3?.由这个方程，知道了d,?,i,?中的三个量，可以推出另外一个。

若光线为正入射，i?0，则上式变为dsin?m?m?(2)其中?m为第m级谱线的衍射角。

据此，可用分光计测出衍射角?m，已知波长求光栅常数或已知光栅常数求波长。

2.2用最小偏向角法测定光波波长如右图。

入射光线与m级衍射光线位于光栅法线同侧，(1)式中应取(本文来自: 博旭范文网:光栅衍射实验报告)加号，即d sin??+sin??=。

以Δ=φ+ι为偏向角，则由三角形公式得2d sin2cosΔ2=mλ(3)易得，当=0时，?最小，记为δ，则(2.2.1)变为2dsin2m,m0,1,2,3,(4)由此可见，如果已知光栅常数d，只要测出最小偏向角δ，就可以根据(4)算出波长λ。

三、实验仪器3.1分光计在本实验中，分光计的调节应该满足:望远镜适合于观察平行光，平行光管发出平行光，并且二者的光轴都垂直于分光计主轴。

3.2光栅调节光栅时，调节小平台使光栅刻痕平行于分光计主轴。

放置光栅时应该使光栅平面垂直于小平台的两个调水平螺钉的连线。

3.3水银灯1.水银灯波长如下表2.使用注意事项(1)水银灯在使用中必须与扼流圈串接，不能直接接220V电源，否则要烧毁。

(2)水银灯在使用过程中不要频繁启闭，否则会降低其寿命。

第1篇一、实验目的1. 熟悉分光计的调整与使用。

2. 学习利用衍射光栅测定光波波长及光栅常数的原理和方法。

3. 加深理解光栅衍射公式及其成立条件。

二、实验原理光栅是由一组数目很多的相互平行、等宽、等间距的狭缝（或刻痕）构成的，是单缝的组合体。

光栅可以产生衍射现象，使光发生色散。

光栅衍射条纹狭窄细锐，分辨本领比棱镜高，所以常用光栅作分光元件。

光栅衍射公式为：\[ d \sin \theta = m\lambda \]其中，d为光栅常数，θ为衍射角，m为衍射级次，λ为光波波长。

三、实验仪器1. 分光计2. 平面透射光栅3. 低压汞灯（连镇流器）4. 米尺5. 计算器四、实验步骤1. 调整分光计，使望远镜与平行光管共轴。

2. 将光栅放置在分光计的载物台上，调整光栅与平行光管的距离，使光栅垂直于入射光。

3. 打开低压汞灯，调节光栅与平行光管之间的距离，使光栅衍射条纹清晰可见。

4. 记录衍射条纹的位置，计算衍射角θ。

5. 测量光栅常数d。

6. 根据光栅衍射公式，计算光波波长λ。

五、实验数据及结果1. 光栅常数d：_______ mm2. 衍射级次m：_______3. 衍射角θ：_______°4. 光波波长λ：_______ nm六、思考题1. 为什么光栅能产生色散现象？2. 光栅衍射条纹的特点是什么？3. 如何通过光栅衍射公式计算光波波长？七、实验总结本次实验通过光栅衍射实验，加深了对光栅原理及光栅衍射公式的理解。

通过实验，掌握了分光计的调整与使用方法，学会了利用衍射光栅测定光波波长及光栅常数的原理和方法。

实验过程中，注意观察现象，认真记录数据，计算结果，为后续实验打下了基础。

第2篇一、实验目的1. 熟悉分光计的调整与使用。

2. 学习利用衍射光栅测定光波波长及光栅常数的原理和方法。

3. 加深理解光栅衍射公式及其成立条件。

二、实验原理光栅衍射实验是利用光栅对光波进行衍射和干涉，通过观察光栅衍射条纹，测定光波波长及光栅常数。

衍射光栅实验报告实验日期：2023年5月23日周二上午实验题目：衍射光栅一、实验目的1.了解光栅的分光特性2.测量光栅常量二、实验原理二元光栅是平行等宽、等间距的多狭缝，它的分光原理如图所示。

狭缝S处于透镜L1焦平面上，并认为它是无限细的；G是衍射光栅，它有N个宽度为a的狭缝，相邻狭缝间不透明部分的宽度为b。

如果自透镜L1出射的平行光垂直照在光栅上，透镜L2将与光栅法线成θ角的光会聚在焦平面的P点。

光栅在θ方向上有主干涉极大的条件为(a + b) sin θ= k*λ将光栅常量记为d = a + bsin(θ++θ-)/2=kλ/d角色散：dθ/dλ=k/(dcosθ)三．实验仪器分光仪，平面透射光栅，平面反射镜，低压汞灯四、实验步骤3.调节分光仪；4. 调节光栅；（1） 平行光垂直照射在光栅表面（2） 光栅的刻痕垂直于刻度盘平面，即与仪器转轴平行 （3） 狭缝与光栅刻痕平行由于基片玻璃两个表面之间的夹角不知道，同时也无法利用光栅方程。

为解决这一问题，在斜入射的情况下，实验时光栅法线两侧同一级光谱的衍射角分别为sin sin sin sin k dk d λϕθλϕθ-+-⎧-=⎪⎪⎨⎪+=⎪⎩两式相减，考虑到θθϕ+--=，有sincos22k dθθϕλ+--=当ϕ很小，cos12ϕ≈，所以sin2k dθθλ+-+=只要测量正负级谱线之间的夹角即可。

5. 测量汞绿线（546.1nm ）±1、±2级谱线夹角，求光栅常数d ；由于游标与刻度盘有各自不同的转轴，这样的仪器在制作和装配的过程中，游标的中心和游标盘的中心有可能不在同一点。

为消除偏心差，通过两个游标测量角度，几何上可证明'+=2ββα6. 测定汞光谱两条黄线波长；7. 求汞黄线处角色散 五、数据处理波长/nm 级数 衍射角位置角度 θ++θ- 无偏心角角度 θ++θ- 衍射角θ 光栅常数d游标号 +k 级-k 级 546.1 1 1 72°11′ 91°02′ 18°51′ 18°51′9°25′ 3336.3nm2252°15′ 271°05′ 18°50′ 546.1 2 1 62°30′ 100°45′ 38°15′ 38°15′ 19°08′ 3333.6nm2242°31′280°46′38°15′2.测定汞光谱中两条黄线的波长：第二条黄线定值误差为0.07%角色散'5600.04/2.1 2.1D nmnm nmϕ∆÷===度六、思考题实验中如果没按要求将光栅放置在仪器转轴位置，即仪器的转轴没有通过光栅平面时，对测量衍射角有影响吗？如有影响应采取什么方法解决？答：有影响。

光栅衍射测波长实验
实验目的：利用光栅衍射法测量光的波长。

实验仪器：光栅衍射仪、汞灯、直尺、白纸、眼睛。

实验原理：光栅是一种具有规律刻线的透镜，可以将入射光分成不同的角度，形成不同的级差衍射。

当入射光垂直于光栅平面时，在不同级差位置处将出现明暗交替的条纹。

其中最明亮的位置为主极大，其他明暗相间的位置称为衍射级差，主极大与衍射级差之间的距离即为波长。

实验步骤：
1、将光栅衍射仪放在平直桌面上，保持正直，调整其高度和水平。

2、打开汞灯，将白纸放在屏幕处，将汞灯光线垂直于光栅，调节仪器使光束斜向照射光栅上。

3、调节仪器，使得与光栅平面平行的明条纹在屏幕上连续，直到观察到清晰的光栅衍射条纹并记录其位置。

4、移动屏幕，观察到不同级次的明暗交替的光栅衍射条纹，并计算与主极大相邻的两个衍射级差（即m=+1和m=-1）之间的距离d，根据单缝衍射的公式
d=λD/d，其中D为标准距离，d为光栅刻线间距，计算出光的波长λ。

5、反复进行以上步骤，得到更准确的波长值并计算平均值。

实验注意事项：
1、使用前检查光栅、汞灯是否正常。

2、保持实验仪器正直、稳定和有序。

3、观察屏幕上的条纹时，将眼睛与屏幕垂直于丝标，以免出现视差误差。

4、单次实验光强度较弱，需反复进行多次测量，尽可能提高测量精度。

图2.9.2 汞的衍射光谱光栅衍射一、实验目的1．了解分光计的工作原理，掌握其调整方法。

2．学会使用分光计和光栅测定光谱的波长。

二、实验原理光栅分为透射光栅和反射光栅，本实验使用透射光栅，如图2.9.1所示。

图2.9.1 透射光栅光路示意图若将平行光垂直照射在光栅上，光栅衍射明纹的条件是衍射角φ必须满足下列关系λφk b a k =+sin )(, ,2,1,0±±=k 式中b a +称为光栅常数，b a + =N1，N 为每毫米上狭缝数目，λ为入射光波长，k 为谱线级数，φk 为k 级谱线对应的衍射角。

若已知N ，并测出衍射角φk ，即可求得波长λ。

若入射光为几种不同波长的光，则由光栅方程可知，除中央明纹相互重叠外，其它每一 级谱线都因对应的衍射角不同而相互分开。

本实验汞光灯发出六种不同波长的可见光，如图2.9.2，其中有紫、绿、黄1、黄2四条强线，另一紫是中强线，兰是弱线。

三、实验仪器 1、分光计分光计主要由平行光管、阿贝式自准直望远镜、平台(即载物台)、刻度盘和游标盘四部分组成图2.9.3望远镜及平台图2.9.4平行光管图2.9.7 望远镜调整图2.9.5 阿贝式自准直望远镜分光计的调整方法：（1）粗调。

用肉眼观察，调节平台、望远镜筒、平行光管都初步达到水平状态，为进一步的细调打下基础。

（2）用自准法调望远镜对平行光聚焦。

将双反平面镜放在平台上并与望远镜光轴目测垂直，为了便于调节，放置平面镜时应使平面镜与平台下的3个调节螺钉中的两个平行，如图2.9.7所示，调节平面镜的俯仰只需调A 螺钉。

点亮目镜下的小灯，然后转动目镜，先看清分划板上的叉丝，再伸缩目镜筒使十字窗的像十分清晰，并用视差法检查(上下或左右移动眼睛，像与十字线无相对位移)，使十字窗与其反射像之间无视差。

由自准直的原理可知，望远镜已经调焦至无限远了或称望远镜能接收平行光，以后目镜不要再调。

（3）调望远镜光轴与分光计中心轴相互垂直。