如何选择ABAQUS单元类型

Abaqus单元命名规则Abaqus是一款功能强大的工程仿真软件，广泛应用于各种领域，包括机械、材料、土木工程等。

在Abaqus中，单元类型、维度、特殊选项、节点数目以及单元名称等方面都有一定的命名规则。

本文将对这些规则进行简要介绍。

1. 单元类型Abaqus中的单元类型非常丰富，包括一维单元、二维单元和三维单元等。

在定义单元类型时，一般采用以下方式：* 一维单元：1D* 二维单元：2D* 三维单元：3D此外，还可以通过在数字后面添加字母来进一步描述单元的类型。

例如，1D-M表示一维质量单元，2D-B表示二维弯曲单元等。

2. 单元维度Abaqus中的单元分为一维、二维和三维三种类型，每种类型的单元都有相应的维度。

一般来说，一维单元的维度为长度，二维单元的维度为面积，三维单元的维度为体积。

在定义单元维度时，一般采用以下方式：* 一维单元：L* 二维单元：A* 三维单元：V3. 特殊选项Abaqus中的一些特殊选项也有相应的命名规则。

例如，在定义接触单元时，需要使用特定的关键字来描述接触类型、接触面以及目标面等。

此外，对于一些具有特殊属性的单元，例如热传导单元、流体流动单元等，也需要使用特定的关键字来描述其属性。

4. 节点数目Abaqus中的每个单元都由一定数量的节点组成。

一般来说，每个节点的编号都是唯一的，并且按照一定的顺序进行编号。

在定义节点数目时，一般采用以下方式：* 对于一维单元：节点数目为2或4。

* 对于二维单元：节点数目为3或6。

* 对于三维单元：节点数目为4或8或12等。

需要注意的是，对于一些具有特殊属性的单元，例如接触单元、弹簧单元等，节点数目可能会不同。

因此，在定义这些单元时需要特别注意节点数目的问题。

5. 单元名称在Abaqus中，每个单元都需要一个唯一的名称。

一般来说，单元名称应该能够清晰地表达出该单元的类型、属性以及一些特殊选项等信息。

例如，对于一个一维质量单元，可以使用“mass1d”作为名称；对于一个二维弹簧-阻尼器单元，可以使用“spring2d”作为名称等。

abaqus中单元的选择宝典1.完全积分就是指当单元具有规则形状时，所用得高斯积分点可以对单元刚度矩阵中得多项式进行精确地积分。

2.剪力自锁将使单元变得“刚硬”，只影响受弯曲荷载得完全积分线性（一阶）单元，这些单元功能在受直接或剪切荷载时没有问题。

二次单元得边界可以弯曲，没有剪力自锁得问题。

3.只有四边形与六面体单元才能采用减缩积分。

所有得楔形、四面体与三角形实体单元采用完全积分。

减缩积分单元比完全积分单元在每个方向上少用一个积分点。

4.只有四边形与六面体单元才能采用减缩积分。

所有得楔形、四面体与三角形实体单元采用完全积分。

减缩积分单元比完全积分单元在每个方向上少用一个积分点。

5.非协调单元：只有四边形与六面体单元才能采用减缩积分。

所有得楔形、四面体与三角形实体单元采用完全积分。

减缩积分单元比完全积分单元在每个方向上少用一个积分点。

6.ABAQUS对非协调单元采用了增强位移梯度形式。

在弯曲问题中，用非协调单元可得到与二次单元相当得结果，且计算费用明显降低。

对单元扭曲很敏感。

7.ABAQUS对非协调单元采用了增强位移梯度形式。

在弯曲问题中，用非协调单元可得到与二次单元相当得结果，且计算费用明显降低。

对单元扭曲很敏感。

8.杂交单元：ABAQUS对非协调单元采用了增强位移梯度形式。

在弯曲问题中，用非协调单元可得到与二次单元相当得结果，且计算费用明显降低。

对单元扭曲很敏感。

9.一般情况下应采用二次减缩积分单元（CAX8R，CPE8R，CPS8R，C3D20R）。

在应力集中局部采用二次完全积分单元（CAX8，CPE8，CPS8，C3D20）。

对含有非常大得网格扭曲模拟（大应变分析），采用细网格划分得线性减缩积分单元（CAX4R，CPE4R，CPS4R，C3D8R ）。

对接触问题采用线性减缩积分单元或非协调单元（CAX4I，CPE4I，CPS4II，C3D8I等）得细网格划分。

10.采用非协调单元时应使网格扭曲减至最小。

1、按照节点位移插值的阶数，可以将ABAQUS单元分为线性单元、二次单元和修正的二次单元2、线性完全积分单元在承受弯曲载荷时会出现剪切自锁，造成单元过于刚硬，即使划分很细的网格，计算精度仍然很差3、二次完全积分单元适于模拟应力集中问题，一般情况下不会出现剪切自锁，但不能在接触分析和弹塑性分析中使用4、线性减缩积分单元对位移的求解结果较精确，在弯曲载荷下不容易发生剪切自锁，网格的扭曲变形（例如Quad单元的角度远远大于或小于90°）对其分析精度影响不大，但这种单元需要划分较细的网格来克服沙漏问题，且不适于求解应力集中部位的节点应力5、二次减缩积分单元不但支持了线性减缩积分单元的优点，而且不划分很细的网格也不会出现严重的沙漏问题，即使在复杂应力状态下，对自锁问题也不敏感，但它不适于接触分析和大应变问题6、非协调模式单元克服了剪切自锁问题，在单元扭曲比较小的情况下得到的位移和应力结果很精确，但如果所关心部位的单元扭曲比较大，其分析精度会降低7、线性Tri单元和Tet单元的精度很差，二次Tet单元(C3D10)适于ABAQUS/Standand中的小位移无接触问题，修正的二次Tet单元(C3D10M)适于ABAQUS/Explicit，以及ABAQUS/Standand中的大变形和接触问题8、ABAQUS的壳单元可以有多种分类方法，按照薄壳和厚壳来划分，可以分为通用目的（general-purpose）壳单元和特殊用途（special-purpose）壳单元；按照单元的定义方式，可以分为常规（conventional）壳单元和连续体（continuum）壳单元9、ABAQUS中的所有梁单元都可以产生轴向变形、弯曲变形和扭转变形，B21和B31单元（线性梁单元）以及B22和B32单元（二次梁单元）即适用于模拟剪切变形引起重要作用的深梁，又适用于模拟剪切变形不太重要的细长梁，三次单元B23和B33只需划分很少的单元就可以得到较精确的结果1、对于应力集中问题，尽量不要使用线性减缩积分单元，可使用二次单元来提高精度。

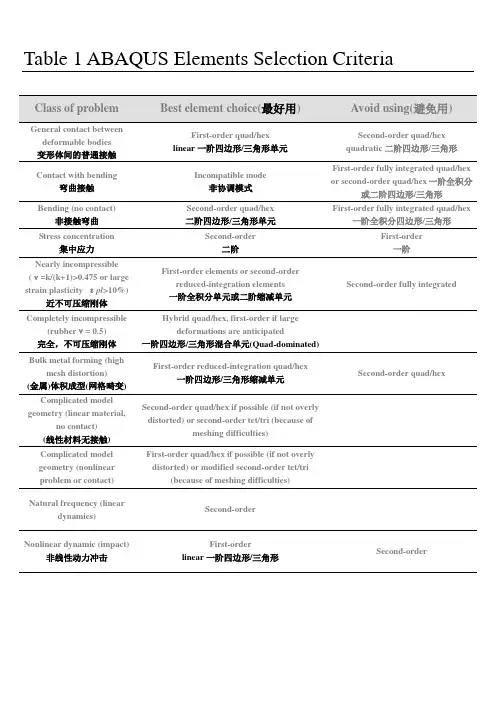
Table 1 ABAQUS Elements Selection CriteriaGeneral contact between deformable bodies变形体间的普通接触First-order quad/hexlinear一阶四边形/三角形单元Second-order quad/hexquadratic二阶四边形/三角形Contact with bending弯曲接触Incompatible mode非协调模式First-order fully integrated quad/hexor second-order quad/hex一阶全积分或二阶四边形/三角形Bending (no contact) 非接触弯曲Second-order quad/hex二阶四边形/三角形单元First-order fully integrated quad/hex一阶全积分四边形/三角形Stress concentration集中应力Second-order二阶First-order一阶Nearly incompressible (ν=k/(k+1)>0.475 or large strain plasticity εpl>10%) 近不可压缩刚体First-order elements or second-orderreduced-integration elements一阶全积分单元或二阶缩减单元Second-order fully integratedCompletely incompressible (rubberν= 0.5)完全，不可压缩刚体Hybrid quad/hex, first-order if largedeformations are anticipated一阶四边形/三角形混合单元(Quad-dominated)Bulk metal forming (high mesh distortion) (金属)体积成型(网格畸变) First-order reduced-integration quad/hex一阶四边形/三角形缩减单元Second-order quad/hexComplicated model geometry (linear material,no contact)(线性材料无接触) Second-order quad/hex if possible (if not overly distorted) or second-order tet/tri (because ofmeshing difficulties)Complicated model geometry (nonlinear problem or contact) First-order quad/hex if possible (if not overly distorted) or modified second-order tet/tri (because of meshing difficulties)Natural frequency (lineardynamics)Second-orderNonlinear dynamic (impact) 非线性动力冲击First-orderlinear一阶四边形/三角形Second-order。

ABAQUS中单元的选取总结实体单元的选择1. 如果不需要模拟非常大的应变或进行复杂的需改变接触条件的问题，则应采用二次减缩积分单元（CAX8R、CPE8R、CPS8R、C3D20R等）；2. 如果存在应力集中，则在局部应采用二次完全积分单元（CAX8、CPE8、CPS8、C3D20等）。

它们可用最低费用提供应力梯度最好的解答。

3. 涉及到非常大的网格扭曲问题（大变形分析），建议采用细网格剖分的线性减缩积分单元（CAX4R、CPE4R、CPS4R、C3D8R等）；4. 对接触问题采用线性减缩积分单元或细分的非协同单元（CAX4I、CPE4I、CPS4I、C3D8I等）；5. 尽可能的减少网格变形的扭歪，形状扭歪的粗网格线性单元会导致非常差的结果。

壳单元的选择1．当要求解十分精确时，可使用线性、有限薄膜应变、完全积分的四边形壳单元（S4），这个壳单元十分适合于要考虑膜作用或有弯曲模式沙漏的问题，也适合于有平面弯曲的问题；2．线性、有限薄膜应变、减缩积分、四边形壳单元（S4R）较流行，适合于各类问题的应用；3．线性、有限薄膜应变、三角形壳单元（S3/S3R）可作为一般的壳单元来使用。

因为在单元内部是常应变应力场，求解弯曲变形和高应变梯度时需要精细的网格剖分；4．考虑到在复合材料层合壳模型中剪切柔度的影响，可应用厚壳单元（S4、S4R、S3、S3R、S8R）来模拟它，此时需检验平面假定是否满足；5．四边形或三角形的二次壳单元，对于一般的小变形薄壳来说是很有效的，它们对于剪力锁闭和薄膜锁闭不敏感；6．如果在接触问题中一定要用二阶单元，不要选用二阶三角形壳单元（STRI65），而要采用9节点的四边形壳单元（S9R5）；7．对于几何线性的，但规模又非常大的模型，线性薄壳单元（S4R5）通常将比一般壳单元效率更高。

梁单元的选择1. 对任何涉及到接触的分析，应使用一阶的、有剪切变形的梁单元（B21、B31）;2. 对于结构刚度非常大或非常柔软的结构，在几何非线性分析中应当使用杂交梁单元（B21H、B32H等）；3. Euler-Benoulli三次梁单元（B23、B33）在模拟承受分布荷载作用的梁，包括动态的振动分析时，会有很高的精度。

Abaqus单元的选择2015-03-06 有限元在线如果想要以合理的费用得到高精度的结果，那么正确的选择单元是非常关键的。

对于ABAQUS经验丰富的使用者，毫无疑问都会自己的单元选择指南来处理各种具体的应用。

但是，在刚开始使用ABAQUS 时，下面的指导是非常有用的。

1、实体单元选择以下单元选择的建议适用于ABAQUS/Standard和ABAQUS/Explicit：（1）尽可能的减小网格的扭曲。

使用扭曲的线性单元的粗糙网格会得到相当差的结果。

（2）对于模拟网格扭曲过分严重的问题，应用网格细划的线性、减缩积分单元（CAX4R，CPE4R，CPS4R，C3D8R等）。

（3）对三维问题应尽可能地采用六面体单元。

它们以最低的成本给出最好的结果。

当几何形状复杂时，采用六面体单元划分网格可能是非常困难的，因此，还需要楔形和四面体单元。

这些单元（C3D4和C3D6）的一阶模式是较差的单元（需要细划网格以取得较好的精确度）。

（4）某些前处理器包含了自由划分网格算法，用四面体单元划分任意几何体的网格。

对于小位移无接触的问题，在ABAQUS/Standard中的二次四面体单元（C3D10）能够给出合理的结果。

这个单元的另一种模式是修正的二次四面体单元（C3D10M），它适用于ABAQUS/Standard和ABAQUS/Explicit，对于大变形和接触问题，这种单元是强健的，展示了很小的剪切和体积自锁。

但是，无论采用何种四面体单元，所用的分析时间都长于采用了等效网格的六面体单元。

（5）对于ABAQUS/Standard求解器，除非需要模拟非常大的应变或者模拟一个复杂的、接触条件不断变化的问题，对于一般的分析工作，应采用二次、减缩积分单元（CAX8R，CPE8R，CPS8R, C3D20R 等）。

（6）对于ABAQUS/Standard求解器，在存在应力集中的局部区域，采用二次、完全积分单元（CAX8, CPE8, CPS8, C3D20等）。

abaqus六面体单元类型1、单元族群，如下图所示为力学分析中常用的单元族群，这些族群的主要区别在于几何特征的差异，适合于研究不同的结构类型，选择合适的族群可以在不降低计算精度条件下，减少计算量，比如:一座高楼大厦如果全用实体单元建模，可能需要千万甚至上亿个实体单元，但如果将大厦的梁柱简化为梁单元，墙和楼板简化为壳单元模拟，单元数量将急剧减少。

单元编号法则1:它们的首字母或前几位字符通常会作为单元编号的起始字符。

比如:‘C3D8’中首字母'C’为Continuum elements 的首字母。

2、自由度，是分析过程中计算的基本变量，比如力学分析中的自由度是节点的平移和旋转自由度;传热分析中需要考虑的自由度是节点温度;渗流分析则是孔隙压力自由度。

单元编号法则2:单元自由度通常由单元族群和尾部字符确定，比如尾部字符包含T，则表示包含温度自由度，包含P，则表示包含孔压自由度。

3、节点数，自由度仅在节点位置上计算，而其他位置上的数值则通过内部公式插值获得，而插值方法由单元节点数确定，比如8节点六面体单元，采用线性插值方式，称为一阶单元;而20节点六面体单元，也就是在每条单元边中间增加一个节点，采用二次方程插值，因此被称为二阶单元。

单元编号法则3:节点数量会在单元编号中直接体现，比如C3D8中的‘8’表示8节点;而其中的‘3’或‘2’后面跟着D字符，则需要和‘3D'/‘2D’一起辨识为三维/二维单元。

4、单元架构，自由度和节点就像是零件，要把这些零件有机的组合起来，就需要装配说明，而单元架构就是这样的一套装配说明，装配好之后才能称为单元。

比如对于拉格朗日架构的单元，材料是跟随单元同步移动;而欧拉架构的单元，材料则可以在单元中流动。

其次，为了满足一些特殊的计算需求，会对一些基本构架进行修改，比如壳体单元分薄壳和厚壳，主要区别是否考虑壳体法向应力分量。

另外，不同自由度之间的耦合也是需要特殊的架构去描述。

Standard和explicit都应遵循的原则：1、尽量减少扭曲的单元。

单元扭曲可以用雅克比、内角、warpage等来衡量。

2、大应变的模拟中应该使用细化的线性减缩单元模拟。

CAX4R/CPE4R/CPS4R/C3D8R.3、三维问题中应当尽量使用六面体单元。

C3D4和C3D6需要很细的网格才能得到相对准确的结果，因此应当尽量避免使用这类单元，并且要远离感兴趣区域。

4、对于四面体网格。

Standard中，小位移并且不包括接触的问题应当使用C3D10或者C3D10I（Explicit中除了修正四面体与三角形单元以及二阶梁单元外，其余都是线性单元；除了修正四面体和三角形单元以及一节壳单元与六面体完全积分单元外，其余都是减缩积分单元）。

大位移以及使用默认“硬接触”的问题，在Standard和Explicit中，都应该使用C3D10M单元。

应该极力避免使用C3D4.对于Standard中还应当遵循以下基本原则：1、对于不包括大位移与复杂的接触条件改变的一般性问题，推荐使用二阶减缩积分单元。

CAX8R/CPE8R/CPS8R/C3S20R2、应力集中区域应当使用二阶完全积分单元（除非单元扭曲厉害或者弯曲应力有梯度，很少会体积自锁；也无hourglassing问题）。

CAX8/CPE8/CPS8/C3D20。

这些单元能够以最小的代价给出精确的应力梯度。

3、对于接触问题，应当使用细化的线性减缩积分单元或者非协调单元。

CAX4I/CPE4I/CPS4I/C3D8I.总结1、Formulation和Order of integration对于求解结果的准确性与计算代价有很大的影响。

2、线性完全积分单元容易产生剪切自锁，应当避免使用。

3、线性减缩积分单元模拟弯曲变形时，在厚度的方向至少使用四个单元。

4、在Standard中，二阶减缩积分单元很少有Hourglassing的问题。

但模型中没有接触是应该首先考虑使用这种单元。