F检验实例

F检验及公式范文F检验（F-test）是一种统计推断方法，用于比较两个或更多样本的方差是否相等。

它通过计算样本的F统计量，然后与理论的F分布进行比较，来确定样本的方差是否有显著差异。

F检验的原假设（H0）是所有样本的方差相等，备择假设（H1）是至少有一个样本的方差不相等。

如果计算得到的F统计量大于临界值，我们可以拒绝原假设，即可以认为至少有一个样本的方差不相等。

下面是F检验的公式：F=S1^2/S2^2其中，S1^2是第一个样本的方差，S2^2是第二个样本的方差。

F统计量的计算需要先计算每个样本的方差，然后将两个方差相除得到F值。

F统计量的计算过程如下：1.计算每个样本的方差：S1^2=∑(Xi-X1)^2/(n1-1)S2^2=∑(Xi-X2)^2/(n2-1)其中，Xi是第i个样本的观测值，X1和X2分别是两个样本的均值，n1和n2是两个样本的大小。

2.计算F统计量：F=S1^2/S2^23.将计算得到的F值与理论的F分布进行比较，确定是否拒绝原假设。

在进行F检验时，需要确定显著性水平（α）和自由度（df1和df2）。

自由度可以通过样本大小和样本数来计算。

显著性水平一般取0.05或0.01，代表我们愿意犯第一类错误的概率。

如果计算得到的F值大于F分布的临界值，我们可以拒绝原假设，即可以认为至少有一个样本的方差不相等。

如果F值小于临界值，我们无法拒绝原假设，即可以认为所有样本的方差相等。

F检验的应用广泛，常见的应用场景包括比较两个或更多组数据的方差、分析实验结果的方差等。

它可以帮助我们确定样本的方差是否有显著差异，从而影响我们对数据的解释和决策。

需要注意的是，F检验只能用于比较方差是否相等，不能用于比较均值是否相等。

如果需要比较均值的差异，可以使用t检验或方差分析（ANOVA）等方法。

f检验python代码摘要：1.引言2.Python中f检验的概念3.f检验的Python代码实现4.f检验的实例应用5.总结正文：f检验是Python数据分析中常用的一种假设检验方法，主要用于判断两组样本的方差是否显著不同。

它基于F分布理论，因此也称为F检验。

在Python中，可以使用scipy.stats库中的f分布函数进行f检验。

2.Python中f检验的概念在Python中，f检验的具体实现方式如下：首先，导入所需的库：```pythonfrom scipy.stats import f```然后，计算f统计量：```pythonf_statistic = f(x1, x2, n1, n2)```其中，x1和x2分别为两组样本的均值，n1和n2分别为两组样本的样本量。

接下来，根据显著性水平和自由度，查找F分布表，获取相应的临界值。

最后，比较计算得到的f统计量与临界值，如果f统计量大于临界值，则拒绝原假设，认为两组样本的方差显著不同；否则，不拒绝原假设，认为两组样本的方差没有显著不同。

3.f检验的Python代码实现以下是一个使用Python进行f检验的示例代码：```pythonfrom scipy.stats import fimport numpy as np# 假设数据group1 = np.random.normal(0, 1, 10)group2 = np.random.normal(5, 1, 10)# 计算均值和样本量mean1 = np.mean(group1)mean2 = np.mean(group2)1 = len(group1)2 = len(group2)# 计算f统计量f_statistic = f(mean1, mean2, n1, n2)# 设置显著性水平alpha = 0.05# 计算自由度df = (n1 - 1) * (n2 - 1)# 查找临界值critical_value = f.ppf(1 - alpha, df)# 进行f检验if f_statistic > critical_value:print("拒绝原假设，两组样本的方差显著不同")else:print("不拒绝原假设，两组样本的方差没有显著不同") ```4.f检验的实例应用假设我们有两组样本数据，分别表示两组学生的数学成绩。

f检验简单例子
f检验（F-test）是一种常用的假设检验方法，它用于比较两个或更多群体的方差是否相等。

在科研实验、质量控制、生产管理等领域经常应用。

在进行f检验前，需要先确定待测的两个群体。

例如，我们要比较两种球类型的硬度是否相同，那么我们就选取一定数量的A球和B 球，并通过仪器进行硬度测试，得到数据。

接着，我们需要根据所得数据计算出两个群体各自的方差。

方差是指各数据值与平均数的差的平方和的平均数，它反映了数据的分散程度。

计算方差后，我们就可以进行f检验了。

f检验的原假设是两个群体的方差相等，即H0：σ1²=σ2²。

备择假设是两个群体的方差不相等，即H1：σ1²≠σ2²。

我们需要根据给定的显著性水平（通常是0.05），选择适当的f分布临界值，进行计算。

如果计算出的f值小于临界值，即f＜fα，我们就接受原假设，认为两个群体的方差相等；如果计算出的f值大于或等于临界值，即f≥fα，我们就拒绝原假设，认为两个群体的方差不相等。

需要注意的是，f检验只是判断方差是否相等，不能得到群体之间均值是否有显著差异的结论。

如果需要进行均值比较，需要使用另外的检验方法，如t检验。

总之，f检验是一种简单而有效的假设检验方法，能够判断两个群体的方差是否相等，可以帮助科研人员和企业管理者更加客观地评估实验结果或生产质量。

f检验例题以及解析Example:A researcher wants to determine if there is a significant difference in test scores between two groups of students. Group A consists of students who received tutoring, while GroupB consists of students who did not receive tutoring. The researcher collects the test scores of 30 students from each group. The null hypothesis is that there is no difference in test scores between the two groups.H0: μA = μB (there is no difference in test scores between Group A and Group B)The researcher calculates the mean test scores for each group: μA = 75 and μB = 70. The standard deviation for both groups is 5. The significance level chosen is α = 0.05.To determine if there is a significant difference between the mean test scores of the two groups, the researcher conducts an independent samples t-test. The t-test will compare the means of the two groups while taking into account the variability within each group.The assumptions for conducting an independent samples t-test are:1. The data within each group are normally distributed.2. The variances of the two groups are equal.To conduct the t-test, the researcher calculates the t-value using the formula:t = (x A - x B) / sqrt((sA^2 / nA) + (sB^2 / nB))Where:x A is the mean test score of Group A,x B is the mean test score of Group B,sA is the standard deviation of Group A,sB is the standard deviation of Group B,nA is the sample size of Group A, andnB is the sample size of Group B.Using the given values: x A = 75, x B = 70, sA = sB = 5, nA = nB = 30, the t-value can be calculated:t = (75 - 70) / sqrt((25 / 30) + (25 / 30))= 5 / sqrt(5/3 + 5/3)= 5 / sqrt(10/3)= 5 / 1.82574≈ 2.739The researcher then determines the degrees of freedom (df) for the t-distribution. For an independent samples t-test, df = nA + nB - 2 = 30 + 30 - 2 = 58.Using the t-value and df, the researcher can then determine the p-value associated with the t-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed t-value under the null hypothesis.Using a t-table or a statistical software, the researcher finds that the p-value for a t-value of 2.739 and df = 58 is approximately 0.005. Since the p-value (0.005) is smaller than the chosen significance level α = 0.05, the researcher rejects the null hypothesis. Thismeans that there is a significant difference in test scores between the two groups.。

t检验和 f检验的应用实例t检验和f检验是统计学上非常重要的两种方法，它们被广泛应用于各种领域的实验和研究中，如医学、生物学、社会学和市场研究等。

本文将围绕这两种检验的应用实例，以分步骤的方式进行解读。

一、t检验的应用实例t检验常常用于对两个样本平均值的差异进行统计分析。

举个例子，假设我们正在研究两种不同的药物对于长期吸烟者戒烟的效果。

我们随机选择100名吸烟者分为两组，其中一组服用药物A，另一组服用药物B，然后记录他们戒烟的天数。

最后我们可以使用t检验来确定两组之间是否存在显著差异。

步骤如下：1.首先，建立假设：假设药物A和药物B的戒烟效果没有显著的统计差异。

2.我们要获取数据，然后计算出两组吸烟者的平均戒烟天数。

3.进行方差分析，也就是t检验。

根据我们计算的数据，我们可以得出t值，在表格中查其对应的p值。

如果p值小于0.05，就意味着我们可以拒绝原假设——也就是说药物A和药物B之间在统计上是有显著差异的。

二、f检验的应用实例f检验，又称为方差分析，通常用于比较多组数据之间的差异性。

下面我们来看一个具体的例子。

假设我们在某个大型研究项目中正在测试不同种类的肥料对小麦产量的影响。

我们随机选取3个小麦田，分别使用了三种不同的肥料，然后我们分别记录各自田地的小麦产量。

这时，我们可以使用f检验来检验不同肥料之间是否存在显著差异。

步骤如下：1. 首先，建立假设：肥料对于小麦产量的影响没有显著的统计差异。

2. 我们要获取数据，记录各自田地的小麦产量。

3. 进行方差分析，也就是f检验。

通过f检验，我们可以确定不同肥料之间的方差，如果其中一个方差显著大于其它方差，那么就说明在这种情况下，选择肥料种类的影响是显著的。

总结t检验和f检验是统计学研究中最基本的判断方法。

通过这两种方法，我们可以对一些数据进行更加详尽的分析和解读，可以更加准确地得出结论。

然而，重要的是要选择适合的方法，以便对特定的数据进行正确的分析。

f检验是用来干什么的
F检验：
通常用来在不知道两个总体的均值，但知道其中某个方差的情况下，假设另一方差（F检验），即是否具有统计意义。

F检验又叫方差齐性检验。

在两样本t检验中要用到F检验。

从两研究总体中随机抽取样本，要对这两个样本进行比较的时候，首先要判断两总体方差是否相同，即方差齐性。

若两总体方差相等，则直接用t检验。

样本标准偏差的平方，即：
两组数据就能得到两个S2值：
然后计算的F值与查表得到的值比较，如果：
（1）表明两组数据没有显著方差差异；
（2）表明两组数据存在显著方差差异。

适用的F检验例子包括：
1.假设一系列服从正态分布的母体，都有相同的标准差。

这是最典型的F
检验，该检验在方差分析（ANOVA）中也非常重要。

2.假设一个回归模型很好地符合其数据集要求，检验多元线性回归模型中
被解释变量与解释变量之间线性关系在总体上是否显著。

F检验及公式范文F检验是一种用于比较多个样本均值是否相等的统计方法。

它基于将总体方差分解成组内方差和组间方差，并通过比较它们的大小来判断均值是否相等。

F检验的公式可以根据不同的场景而有所不同，以下将介绍一些常见的F检验公式。

在一元方差分析中，假设有k个总体，每个总体的样本大小分别为n1，n2，...，nk，总样本均值分别为x̄1，x̄2，...，x̄k，总样本方差分别为s1^2，s2^2，...，sk^2、则F检验的公式为：F=MST/MSE其中，MST为组间平方和（Sum of Squares Between）除以组间自由度（Degree of Freedom Between）：MST = SSbetween / dfbetween而MSE为组内平方和（Sum of Squares Within）除以组内自由度（Degree of Freedom Within）：MSE = SSwithin / dfwithinSSbetween可以通过以下公式计算：SSbetween = ∑(ni * (x̄i - x̄)^2)其中，x ī为第i组的样本均值，n为所有样本的总样本量，x̄为总样本的均值。

SSwithin可以通过以下公式计算：SSwithin = ∑((ni - 1) * si^2)其中，ni-1为每组样本的自由度，si^2为每组样本的方差。

自由度的计算方式为，dfbetween = k - 1，dfwithin = n - k，n为总样本量。

F值的计算结果与临界值比较，可进行假设检验。

除了一元方差分析，F检验还可以应用于其他场景，如方差齐性检验、线性回归中的显著性检验等。

不同场景下F检验的公式会有所差异，但其核心思想都是比较组间和组内的方差大小，进而判断均值是否相等。

总结起来，F检验是一种用于比较多个样本均值是否相等的统计方法。

其公式由组间和组内的平方和和自由度计算而得。

F检验在统计分析中有着广泛的应用，可帮助研究者得出关于样本均值是否存在显著差异的结论。

F检验及公式范文F检验（F test）是一种用于比较两个或多个样本方差是否相等的统计方法。

它基于两个基本的统计原理：方差的无偏估计和卡方检验。

F检验的原理是比较样本方差和总体方差之间的差异，通过计算方差之间的比值，得到一个F值，然后将其与理论分布进行比较，判断差异是否显著。

如果计算得到的F值大于临界值，则认为差异是显著的，即拒绝原假设，认为各样本的方差不相等；而如果F值小于临界值，则接受原假设，认为各样本的方差相等。

F检验有两种常见的应用场景：1.比较两个样本的方差是否相等。

2.比较多个样本的方差是否相等。

以下是F检验的公式：在比较两个样本方差是否相等的情况下，F的计算公式为：F=s₁²/s₂²其中，s₁²为第一个样本的方差，s₂²为第二个样本的方差。

在比较多个样本方差是否相等的情况下，F的计算公式为：F=MST/MSE其中，MST为组间的均方差（Mean Squares of Treatment），即样本均值的方差；MSE为组内的均方差（Mean Squares of Error），即样本内的方差。

F检验的步骤如下：1.提出假设：-原假设（H0）：各样本的方差相等。

-备择假设（H1）：各样本的方差不相等。

2.计算F值：-如果比较两个样本的方差是否相等，根据上述公式计算F值。

-如果比较多个样本的方差是否相等，首先计算组间的均方差（MST）和组内的均方差（MSE），然后根据上述公式计算F值。

3.设置显著性水平：-根据研究目的和具体情况，选择显著性水平（通常为0.05）。

4.查表或使用统计软件：-根据样本数量和显著性水平，查找F分布表中的临界值，或使用统计软件计算临界值。

5.判断结果：-如果计算得到的F值大于临界值，则拒绝原假设，认为各样本的方差不相等。

-如果计算得到的F值小于临界值，则接受原假设，认为各样本的方差相等。

F检验还有一些相关的概念和应用，例如方差分析（ANOVA）、多重比较等。

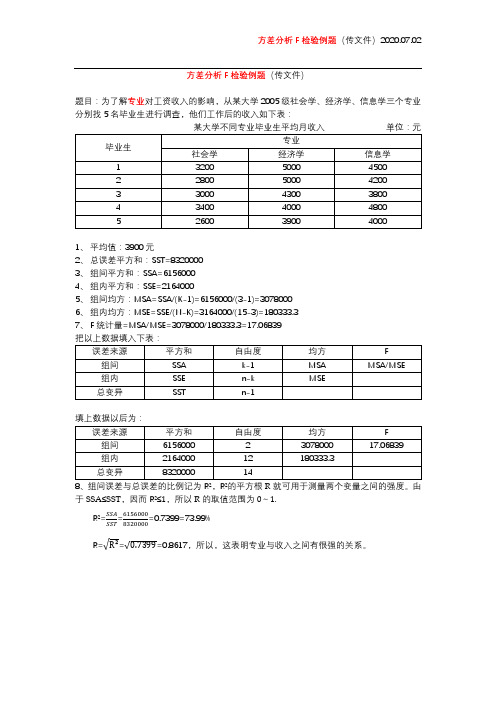
方差分析F 检验例题（传文件）2020.07.02
方差分析F 检验例题（传文件）
题目：为了解专业对工资收入的影响，从某大学2005级社会学、经济学、信息学三个专业分别找5名毕业生进行调查，他们工作后的收入如下表：
1、 平均值：3900元
2、 总误差平方和：SST=8320000
3、 组间平方和：SSA=6156000
4、 组内平方和：SSE=2164000
5、 组间均方：MSA=SSA/(K-1)=6156000/(3-1)=3078000
6、 组内均方：MSE=SSE/(N-K)=3164000/(15-3)=180333.3
7、 F 统计量=MSA/MSE=3078000/180333.3=17.06839
8、组间误差与总误差的比例记为R ²，R ²的平方根R 就可用于测量两个变量之间的强度。

由于SSA≤SST ，因而R ²≤1，所以R 的取值范围为0～1.
R ²=SSA SST =6156000
8320000=0.7399=73.99%
R=√R²=√0.7399=0.8617，所以，这表明专业与收入之间有很强的关系。

f检验表完整版【原创实用版】目录1.F 检验的概述2.F 检验的步骤3.F 检验的应用实例4.F 检验的局限性正文一、F 检验的概述F 检验，全称为 Fisher 检验，是一种用于检验两个变量间关系是否显著的统计方法。

它是由英国统计学家 Ronald Fisher 于 1925 年提出的，被广泛应用于实际数据的分析中。

F 检验的原理是基于 t 分布和卡方分布的，它能够判断两个变量间的相关性，为后续的建模和分析提供依据。

二、F 检验的步骤1.提出原假设和备选假设原假设：两个变量之间不存在显著关系。

备选假设：两个变量之间存在显著关系。

2.计算相关系数计算两个变量间的相关系数，如皮尔逊相关系数或者斯皮尔曼相关系数。

3.计算 F 值根据相关系数和自由度，计算 F 值。

4.计算 p 值根据 F 值和自由度，计算 p 值。

5.判断结论如果 p 值小于显著性水平α，则拒绝原假设，认为两个变量之间存在显著关系；否则不拒绝原假设，认为两个变量之间不存在显著关系。

三、F 检验的应用实例F 检验在实际应用中十分广泛，例如在经济学、教育学、心理学等领域。

以下是一个简单的实例：假设我们想要研究某地区居民的收入水平与教育程度是否存在关系。

首先，我们需要收集相关数据，包括每个居民的收入和教育程度。

然后，计算这两个变量间的相关系数。

接着，根据相关系数和自由度，计算 F 值。

最后，根据 p 值和显著性水平α，判断收入水平与教育程度是否存在显著关系。

四、F 检验的局限性虽然 F 检验在实际应用中具有较高的准确性，但它也存在一定的局限性：1.对样本量和变量间的相关性要求较高，当样本量较小或者变量间相关性较弱时，F 检验的结果可能不准确。

2.F 检验只能判断两个变量之间是否存在关系，不能说明具体的关系类型和强度。

3.F 检验是基于假设检验的，当原假设和备选假设设立不合理时，F 检验的结果可能不准确。

综上所述，F 检验是一种重要的统计方法，用于检验两个变量间关系是否显著。

f检验表完整版摘要：1.F 检验的概述2.F 检验的步骤3.F 检验的实例4.F 检验的结论正文：F 检验是一种在假设检验中常用的统计方法，主要用于检验两个变量之间的关系。

它通过对两个变量的方差进行比较，从而判断它们之间是否存在显著性差异。

下面，我们将详细介绍F 检验的步骤和实例。

首先，我们来了解F 检验的概述。

F 检验，全称为Fisher 氏F 检验，是由英国统计学家Ronald Fisher 于1925 年提出的。

它是一种用于检验两个变量之间线性关系的统计方法，适用于小样本和大样本的情况。

F 检验的主要优点是，它不需要对总体分布做出任何假设，因此，它适用于各种分布的样本。

接下来，我们来介绍F 检验的步骤。

F 检验的步骤主要包括以下几个步骤：1.建立原假设和备选假设。

原假设通常是两个变量之间不存在显著性差异，备选假设是两个变量之间存在显著性差异。

2.计算F 统计量。

F 统计量是通过计算两个变量的标准差和均值来计算的。

3.确定显著性水平。

显著性水平通常是0.05 或0.01，它表示我们愿意接受的错误率。

4.查找F 分布表，找到与给定显著性水平和自由度相匹配的F 值。

5.比较F 统计量和临界F 值。

如果F 统计量大于临界F 值，我们拒绝原假设，认为两个变量之间存在显著性差异；如果F 统计量小于临界F 值，我们不能拒绝原假设，认为两个变量之间不存在显著性差异。

现在，我们来看一个F 检验的实例。

假设我们有两个变量X 和Y，它们的均值分别为30 和20，标准差分别为5 和4。

我们要检验X 和Y 之间是否存在显著性差异。

首先，我们建立原假设H0：X 和Y 之间不存在显著性差异，备选假设H1：X 和Y 之间存在显著性差异。

然后，我们计算F 统计量，公式为(X 的均值-Y 的均值)/(X 的标准差/Y 的标准差)，即(30-20)/(5/4)=2。

然后，我们查找F 分布表，找到显著性水平为0.05，自由度为(n1-1)(n2-1)，即(5-1)(4-1)=12 的临界F 值，大约为2.57。

f检验的参数（原创实用版）目录1.F 检验的概述2.F 检验的参数及其含义3.F 检验参数的计算方法4.F 检验参数的应用实例5.F 检验参数的局限性正文一、F 检验的概述F 检验，全称为 Fisher 检验，是一种用于检验两个样本方差是否相等的统计方法。

该方法由英国统计学家 Ronald Fisher 于 1925 年首次提出，被广泛应用于实证研究中。

F 检验的基本思想是比较两个样本的方差，从而判断它们是否来自同一总体。

二、F 检验的参数及其含义F 检验涉及两个参数：分子自由度（df1）和分母自由度（df2）。

这两个参数分别表示两个样本的方差可以分解为多少个独立的成分。

具体含义如下：1.分子自由度（df1）：表示第一个样本的方差可以分解为多少个独立的成分，即样本的独立性。

2.分母自由度（df2）：表示第二个样本的方差可以分解为多少个独立的成分，即样本的独立性。

三、F 检验参数的计算方法F 检验参数的计算公式为：F = (S1^2 / df1) / (S2^2 / df2)，其中 S1 和 S2 分别为两个样本的标准差。

根据该公式，我们可以计算出 F 值。

四、F 检验参数的应用实例假设我们有两个样本数据，分别是 A 组和 B 组。

我们想要检验这两组数据是否来自同一总体。

此时，我们可以使用 F 检验。

首先，计算两组数据的均值，然后计算它们的方差。

接着，根据公式计算 F 值。

最后，将计算出的 F 值与临界值进行比较。

若 F 值大于临界值，则拒绝原假设，认为两组数据来自不同的总体；若 F 值小于临界值，则接受原假设，认为两组数据来自同一总体。

五、F 检验参数的局限性虽然 F 检验在实证研究中具有广泛的应用，但它也存在一定的局限性。

首先，F 检验仅能检验两个样本的方差是否相等，对于其他统计量（如均值、标准差等）的比较则无能为力。

其次，F 检验受到样本大小的影响。

当样本容量较小时，F 检验的效果可能不理想。

草船借箭第二课时练习题一、选择题A. 七擒孟获B. 火烧赤壁C. 三顾茅庐D. 草船借箭2. 在“草船借箭”故事中，诸葛亮向谁借箭？A. 周瑜B. 曹操C. 刘备D. 孙权3. 诸葛亮计划借多少支箭？A. 十万支B. 八万支C. 五万支D. 三万支二、填空题1. 在“草船借箭”故事中，诸葛亮利用了________天的东风，成功借到了箭。

2. 诸葛亮在借箭过程中，使用了________艘草船。

3. 借箭成功后，诸葛亮将箭送给了________。

三、判断题1. “草船借箭”故事中，诸葛亮是向曹操借箭的。

（）2. 诸葛亮在借箭过程中，曹操并未发现草船的真正目的。

（）3. 借箭成功后，周瑜对诸葛亮的才智表示敬佩。

（）四、简答题1. 请简要描述“草船借箭”的故事情节。

2. 诸葛亮为何要借箭？借箭的目的是什么？3. 请分析“草船借箭”故事中，诸葛亮和周瑜的人物形象。

五、阅读理解“诸葛亮下令船只一字儿摆开，都披上青布，各船上都用草把子堆起来。

诸葛亮回到中军帐，叫来鲁肃，说：‘请你借给我二十只草船，每船要军士三十人。

船上用青布为幔，各束草把子千余个，分布两边。

我自有妙用。

’”1. 诸葛亮为何要在船上披上青布？2. 诸葛亮为何要求每船配备三十名军士？3. 请分析选段中诸葛亮的人物形象。

六、词语解释1. 请解释下列词语在文中的含义：a. 一字儿摆开b. 青布为幔c. 草把子d. 妙用七、句子翻译“诸葛亮回到中军帐，叫来鲁肃，说：‘请你借给我二十只草船，每船要军士三十人。

’”“曹操知是诸葛亮之计，懊悔不已，遂传令勿发箭。

”八、连线题1. 诸葛亮 ______ 借箭2. 周瑜 ______ 规劝曹操3. 曹操 ______ 恼羞成怒4. 鲁肃 ______ 暗中协助九、排序题1. 诸葛亮制定借箭计划2. 曹操发现草船并下令放箭3. 诸葛亮向周瑜借船4. 借箭成功，诸葛亮将箭送还周瑜十、拓展题1. 请列举出《三国演义》中其他与诸葛亮相关的著名故事。

t检验和 f检验的应用实例
t检验和f检验是常用的统计检验方法，用于判断样本数据是否符合总体数据的假设。

以下是两个应用实例：
1. 市场调查中，一家公司想要了解他们推出的新产品是否比现有产品更受欢迎。

为此，他们进行了一项调查，随机抽取了1000名顾客，其中500人接触过新产品，另外500人接触过现有产品。

通过t检验，研究人员发现新产品的平均评分显著高于现有产品，因此可以得出结论：新产品比现有产品更受欢迎。

2. 某药厂生产一种新药，他们想要证明这种新药的疗效是否显著优于市场上已有的同类药物。

为此，他们进行了一项双盲随机对照试验，将患有相同病症的患者随机分为两组，一组服用新药，另一组服用已有药物。

通过f检验，研究人员发现新药的效果显著优于已有药物，因此可以得出结论：新药的疗效显著优于市场上已有的同类药物。

以上两个例子都是利用t检验和f检验来对样本数据进行检验，从而得出结论。

这些结论对于公司的决策和医药行业的发展都具有重要的意义。

- 1 -。

stata的f检验命令Stata是一种常用的统计分析软件，它提供了丰富的命令和工具，可以帮助用户进行各种统计分析和数据处理。

其中，f检验命令是一种常用的统计分析命令，可以用来检验两个或多个样本的方差是否相等。

本文将介绍Stata中的f检验命令的使用方法和注意事项。

一、f检验命令的基本语法在Stata中，f检验命令的基本语法如下：. test var1 = var2其中，var1和var2是要比较的两个样本的变量名。

该命令将对这两个样本的方差进行f检验，并输出检验结果。

如果要比较多个样本的方差是否相等，可以使用如下语法：. test var1 = var2 = var3 = ...其中，var1、var2、var3等是要比较的多个样本的变量名。

该命令将对这些样本的方差进行f检验，并输出检验结果。

二、f检验命令的注意事项在使用f检验命令时，需要注意以下几点：1. 样本必须是正态分布的。

如果样本不符合正态分布，f检验的结果可能不准确。

2. 样本的方差必须是同质的。

如果样本的方差不同，f检验的结果可能不准确。

3. 样本的大小必须足够大。

如果样本太小，f检验的结果可能不准确。

4. f检验只能用于比较两个或多个样本的方差是否相等，不能用于比较样本的均值是否相等。

5. f检验只能用于比较连续变量的方差是否相等，不能用于比较分类变量的方差是否相等。

三、f检验命令的实例下面是一个使用f检验命令比较两个样本方差是否相等的实例：假设有两个样本，分别为A和B，它们的方差分别为10和15。

现在要比较这两个样本的方差是否相等。

首先，需要在Stata中输入以下命令：. test A = B然后，Stata将输出如下结果：( 1) A = BF( 1, 18) = 0.67Prob > F = 0.4235根据这个结果，可以得出结论：在显著性水平为0.05的情况下，A和B的方差没有显著差异。

四、总结f检验命令是Stata中常用的统计分析命令之一，可以用来比较两个或多个样本的方差是否相等。

要理解F检验的过程，让我们举一个例子来说明。

假设我们想要比较两种不同的药物在降低血压方面的效果。

我们有两个独立的样本组：组A接受药物A，组B 接受药物B。

我们想知道这两种药物是否在降低血压方面存在显著差异。

以下是进行F检验的步骤：
1. 建立假设：
- 零假设（H0）：药物A和药物B对血压没有显著影响，即两个样本的均值相等。

- 备择假设（H1）：药物A和药物B对血压有显著影响，即两个样本的均值不相等。

2. 收集数据：
- 从组A和组B中分别收集足够数量的样本数据，记录每个样本的血压值。

3. 计算平均值：
- 分别计算组A和组B的血压平均值。

4. 计算方差：
- 计算组A和组B的血压值的方差。

5. 计算F值：
- 使用以下公式计算F值：F = 方差A / 方差B（如果组A的方差大于组B 的方差）或F = 方差B / 方差A（如果组B的方差大于组A的方差）。

6. 设置显著性水平：
- 选择适当的显著性水平（例如0.05）来判断结果的显著性。

7. 查找临界值：
- 使用给定的自由度和显著性水平查找F分布表，确定临界值。

8. 进行决策：
- 如果计算得到的F值超过了临界值，则拒绝零假设，接受备择假设，说明两种药物在降低血压方面存在显著差异。

- 如果计算得到的F值未超过临界值，则无法拒绝零假设，即不能确定两种药物在降低血压方面是否有显著差异。

需要注意的是，这只是一个简单的例子，实际进行F检验时可能涉及更多的统计计算和假设条件。

同时，确保正确选择适当的样本大小和数据收集方法也非常重要，以保证结果的可靠性和准确性。