1文读懂VAR模型的实现过程与结果解读

VAR模型的原理及应用1. 引言VAR（Vector Autoregression）模型是一种常用的计量经济学模型，用于分析多个相关时间序列变量之间的动态关系。

VAR模型在宏观经济学、金融学、营销研究等领域具有广泛的应用。

本文将介绍VAR模型的原理以及其在实际应用中的一些特点和注意事项。

2. VAR模型的原理VAR模型是基于时间序列数据的统计模型，它假设各个时间序列变量之间存在互相影响的关系。

VAR模型的核心思想是用当前变量的过去值和其他相关变量的过去值来预测当前变量的值。

具体来说，VAR模型可以表示为如下形式：$$ X_t = \\alpha_1X_{t-1} + \\alpha_2X_{t-2} + \\cdots + \\alpha_pX_{t-p} +\\epsilon_t $$其中，X t表示当前时间点的变量向量，$\\alpha_1, \\alpha_2, \\cdots,\\alpha_p$是模型的参数，$X_{t-1}, X_{t-2}, \\cdots, X_{t-p}$表示过去几个时间点的变量向量，$\\epsilon_t$表示误差项。

VAR模型的核心在于确定模型的参数和滞后阶数p。

参数的估计可以使用最小二乘法、极大似然法等方法。

滞后阶数的选择可以通过信息准则（如赤池信息准则、贝叶斯信息准则）来确定，一般通过对比不同滞后阶数下模型的拟合优度。

3. VAR模型的应用VAR模型具有广泛的应用场景，以下是一些常见的应用情况：3.1 宏观经济学中的应用对于宏观经济学研究来说，VAR模型可以用于分析不同经济指标之间的关系，例如国内生产总值（GDP）、消费者物价指数（CPI）、货币供应量等。

通过建立VAR模型，可以研究这些宏观经济指标之间的因果关系、冲击传递效应等。

3.2 金融领域中的应用VAR模型在金融领域中的应用广泛，可以用于分析股市、汇率、利率等金融变量之间的关系。

通过构建VAR模型，可以研究金融变量之间的动态相关性、风险传染效应等。

var模型方差分解的结果解释
VAR模型方差分解是一种将总体方差分解为各个变量之间的
协方差和自身的方差的方法。

该分解结果可以用来解释各个变量对总体方差的贡献程度。

具体来说，VAR模型方差分解可以将总体方差分解为两部分：一部分是由协方差项引起的方差贡献，另一部分是由自相关项引起的方差贡献。

对于一个VAR模型，方差分解可以得到每个变量对总体方差
的贡献程度。

这些贡献程度可以解释各个变量之间的相互作用和自身的波动程度。

方差分解结果的解释可以有以下几个方面：
1. 自身波动程度：方差分解将总体方差分解为每个变量自身的方差和协方差项之和。

自身方差的贡献程度可以解释变量自身的波动情况。

2. 相互作用程度：方差分解还可以解释变量之间的相互作用程度。

协方差项的贡献程度可以表示变量之间的相互依赖程度或影响程度。

3. 响应程度：方差分解可以解释每个变量对总体方差的贡献程度。

较大的贡献程度意味着该变量对总体方差的影响较大，说明该变量对系统的影响较为显著。

4. 动态特性：方差分解的结果还可以用来解释系统的动态特性。

通过观察协方差项和自身方差的变化情况，可以了解系统在不同时间段内的变化规律和动态特点。

总之，VAR模型方差分解的结果可以提供对变量之间相互作用、自身波动和对系统方差贡献程度的解释，从而帮助理解经济或其他系统的运行机制和特征。

VAR模型（向量自回归模型）是一种用于预测和分析多个相关时间序列数据的统计模型。

它通过将系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。

VAR模型的原理基于以下假设：
1. 所有时间序列都是平稳的，即具有稳定的均值和方差。

2. 各个时间序列之间存在长期均衡关系，可以通过模型进行捕捉和量化。

3. 这些时间序列之间存在一定的滞后相关性，即一个变量的过去值可以影响其自身的未来值，也可以影响其他变量的未来值。

VAR模型的建立步骤如下：
1. 确定要纳入模型的时间序列，并检验这些时间序列是否具有平稳性。

如果时间序列不平稳，需要进行差分或取对数等转换使其平稳。

2. 根据AIC、SC、HQ等准则选择合适的滞后阶数。

3. 通过估计模型的参数来拟合模型，可以使用OLS、GLS、GMM 等估计方法。

4. 对模型进行检验，包括残差检验、异方差检验、自相关检验等，以确保模型的正确性和可靠性。

5. 利用拟合好的模型进行预测和分析。

例如，可以使用模型来预测多个时间序列的未来值，或者分析一个时间序列与其他时间序列之间的动态关系。

需要注意的是，VAR模型只适用于分析平稳时间序列数据，对于非平稳时间序列数据，需要进行差分、对数转换等处理使其平稳后再进行分析。

同时，VAR模型的假设和参数选择需要根据具体数据进行判断和选择，不同的模型适用于不同类型的数据和问题。

金融风险度量中的VaR模型解析引言：金融市场的复杂性和风险性注定了其对于风险度量的需求。

金融风险度量是金融机构和投资者在进行投资和管理资产时必备的工具，能够帮助他们了解和评估风险水平。

Value at Risk（VaR）模型是一种常见的金融风险度量模型，它通过对风险敞口的概率分布进行建模，计算出在给定置信水平下的最大可能损失额。

本文将对VaR模型进行解析，包括其定义、计算方法、模型假设、优缺点以及应用案例等内容。

一、VaR模型的定义VaR是Value at Risk的缩写，它被定义为在给定置信水平下可能发生的最大可能损失额。

VaR模型的核心思想是通过对风险资产或投资组合的概率分布进行建模，计算出在一定置信水平下的最大可能损失。

一般来说，VaR模型可以分为历史模拟法、参数法和蒙特卡洛模拟法等几种主要方法。

二、VaR模型的计算方法1. 历史模拟法：这种方法通过使用过去一段时期的历史数据来计算VaR。

具体而言，历史模拟法将过去的市场价格收益率作为未来市场价格收益率的概率分布，并根据所选的置信水平确定VaR。

这种方法的优点是简单易行，但缺点是没有考虑到市场条件的变化和不确定性。

2. 参数法：参数法使用统计模型对风险资产或投资组合的价格收益率进行建模，并基于这些模型计算VaR。

常见的参数法包括正态分布法、t分布法和GARCH模型等。

这种方法的优点是可以考虑到市场条件的变化和不确定性，但缺点是需要对概率分布的参数进行估计，估计结果的准确性对VaR的计算结果影响较大。

3. 蒙特卡洛模拟法：这种方法通过随机模拟未来市场价格的路径，并根据这些路径计算出未来的投资组合或风险资产的价值，并确定VaR。

蒙特卡洛模拟法的优点是能够模拟复杂的市场条件和不确定性，但缺点是计算复杂度较高，需要大量的计算资源。

三、VaR模型的假设1. 假设市场是有效的：VaR模型的计算基于市场价格收益率的概率分布，要求市场是有效的，即市场价格反映了所有可得到的信息。

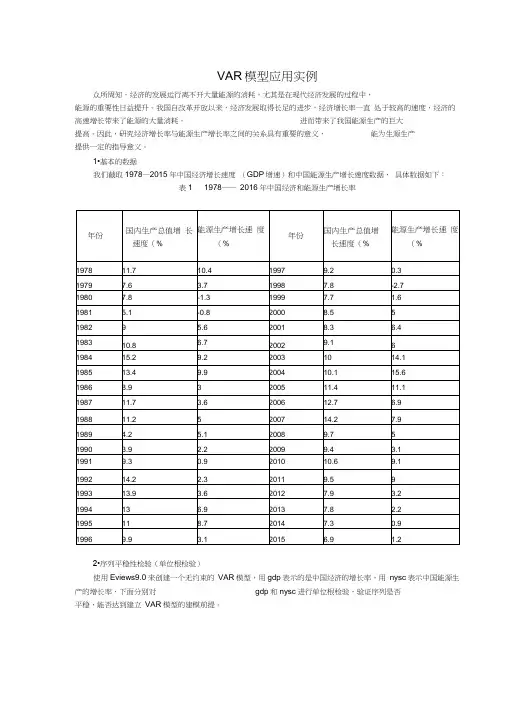
VAR模型应用实例众所周知，经济的发展运行离不开大量能源的消耗，尤其是在现代经济发展的过程中，能源的重要性日益提升。

我国自改革开放以来，经济发展取得长足的进步，经济增长率一直处于较高的速度，经济的高速增长带来了能源的大量消耗，进而带来了我国能源生产的巨大提高。

因此，研究经济增长率与能源生产增长率之间的关系具有重要的意义，能为生源生产提供一定的指导意义。

1•基本的数据我们截取1978—2015年中国经济增长速度（GDP增速）和中国能源生产增长速度数据，具体数据如下：表1 1978―― 2016年中国经济和能源生产增长率2•序列平稳性检验（单位根检验）使用Eviews9.0来创建一个无约束的VAR模型，用gdp表示的是中国经济的增长率，用nysc表示中国能源生产的增长率，下面分别对gdp和nysc进行单位根检验，验证序列是否平稳，能否达到建立VAR模型的建模前提。

Augm&nted Di ckey-Fuller Test EquationDependent Variables (GDP) Method. Least Squares Date： 05/17/17 Time： 10:55 Sample (adjusted): 19S2 2015Included observations: 34 after adjustmentsVariable Coefficient St! Error t^Statistic Prob.GDP(-1)-0.8561710.221114 -18675530,0006EXGDPHJ)0.6256310.193529 3.23275510031D(GDP 図)0.0492400.175617 0.280544 07811D(GDP(-3))0264937 0.16734B 1.583145 01242 C3540050 2222961 3,841745 00006R-squareri 0.45S475 Mean dependent var 0.052941Adjusted R-squared 0 383782 S.D d即巴口血吋调「 2.545731r r di “內erm 洽占耗…甘尺讨丹, A图2.1经济增速（GDP）的单位根检验Augmented Dickey-Full er Unit Root Test on MYSChull Hypothesis: NYSC has a unit rootDwg&nous; ConstantLag Length: 1 fAutomatic- based on SIC,rnaj(lag=9)t-Statistic Prob *AUQniMt£(1 Die魁y-FUll总「tests情t圖t -3.935987 (LQD4弓S%kvel -2 945S4210% level -2.611531* MacKinnon (1996) one-sided f>valjes.Augrnented Dicke?-FullerTest Equation Dependent Variable: D(NYSC) Method: Least Squares Date: 05/17/17 Tine: 10:59Sample [adjusted); 1930 2015Included observations: 36 after adjustm&ntsVariable Co efficient Std Error1-8! atisticProb.hYSCM)-0 5309860 134905-39359870 0004D[N¥SC(-1»0 4305490.150055 2 922585 0 0062C 2 746938 0 057266 1204300 0 0030 R-squared0 34306B Main dependentvar -0 069444.Adjusted R-squared0.303254S D dependent war 3.610704 S.E. of regression 2 930431Akaike info criterion5067831 Sum squared resid 283.3851Schwarz criterion 5.199791 Log likelihood -88.22096Hannan-Quinn criter. 5.113889 F-statistic8.&16746 Durbin-Wstsor stat 1.990251 ProLiF-slatiStic)0.000975Ve dor Autor&gression EstimatesDate: 05/17/17 Time: 11:03Sample (adjusted)' 1980 2015IndLided oDserations: 36 after adjustmEnts Standarfl errors in() & 卜statistics in[]GDP NYSCGDP[-1)0.B25644(0.16499>[5.003B9)0271538(0.23569)[1.15068]GDP 卜2)-0.530495(015625)[-3.19096]-0 292356 (0 237601 [^1 22942]NYSC{-1^-0.052225(0.11565)F045156]0.S4-6355 (0.16542: [511612]NYSC(-2)0.1&6100(0.11349> H63977]-0.35756a [0.16234) 1-220263]G 6.194513C1.50887>14.10539' 2 353291 (2.15827} [1.32665]R-squared 0.492565 9554387Adj. R-squared 0.427089 0.4&B 朋9Sum sq. res id合1305151 267.0323S E equation 2.051969 2934965F-statistic Z522S90 9,641791Log likelihood-74,26525-87.15117Altai kreAIC 4.403525 5119509 Schwarz SC 4.S23558 5339442Mean dependent 9.7380695016667S D deperdent 2.710&54 4137805Determinant res id covariance (doradj.) 30.72390 Determinant res id covariance22.78215L OQ likelihood -15B4312Altai Ice information crit&rior 9357287Schwa IT criterion 9 797154图3.1模型的估计结果LS i 2 cap iiirscTO Milftl ；GDP = c(t L )*^Df (-1) + C (t2)^CDP (-2)C (L 3>KY£C(-1) + C (L 4)*infSC (-2) + C(LE )1IY5C = Ct2.1)*CDP (-1^ + CC2」2)*GDP (-2)+ 匚仅「引*耽既(-1) ■+ C (2, 4)*HVEC (-2) +匸化为 1TAL Medal - Svlrititut«d C»«££ivivntiGKP = fl. 3E55U312B35*^Jf (-1) - 0. 53Q434 ?Q?4S4**?®r(-£} - Q, 05E2E47^H )2 引T SC(-l) + □. lBGl00400721WSC (-E )+ 6.19451B^4763ifYSC = 0.271567998674*GD I PC-1) - 0. 232356168154*GDPt-2)0 84^35506574?^fflSCH) - 0. 35r567G3E 748*]JV5C (-£) + 2 363E9KJ617S图3.2模型的表达式4•模型的检验 4.1模型的平稳性检验回 Var: UNTITLED V/orkfile ： UNTITLED::UntitledRoots at Characteristic Polynomial Endaflenous variaMes: GDPNYSG Exogenous variables' C Lag specification: 1 2Date: 05/17/17 Time. 11:11RootModulus0.5&60S6 ” 0.4517091 0 724220 0.5&60S5 + 0 451708i 0.724220 0.2&9664 - 0.5265511 0.6321 眈 0.2&9S64 + 0 626551i0.682196No root lies outside the unit circle.VAR s artisfies the statMlit^ cand itio n图4.1.1 AR 根的表由图4.1.1知，AR 所有单位根的模都是小于 1的，因此估计的模型满足稳定性的条件。

系统性风险管理中的VaR模型分析一、前言在金融行业，风险管理一直是一项非常重要的工作。

为了更好地管理风险，一些模型被开发出来，VaR模型是其中之一。

在本文中，我们将深入研究VaR模型，并分析其在系统性风险管理中的应用。

二、VaR模型的概念VaR模型是风险管理领域中一种广泛使用的测量金融资产风险的方法。

VaR代表“风险价值”，是指在一定的时间内，某一特定的金融资产或投资组合在给定的置信水平下可能经历的最大亏损额度。

依据VaR模型，金融机构可以计算出一个金融产品的最大亏损额和极端亏损概率，从而评估该金融产品的风险。

VaR模型的一般思路是：建立一个历史模型来评估某一资产或投资组合的风险。

这种模型需要以下数据：资产价值，历史价格波动率和置信水平。

三、VaR模型的类型VaR模型有三种类型：历史模拟方法，参数模型方法和混合方法。

1.历史模拟方法历史模拟方法是VaR模型中最简单的一种，同时也是最易于理解的。

该方法使用历史数据来模拟金融产品在未来的变化情况，因此仅适合于稳定的市场。

如果市场非常崩溃，历史模拟方法就会失效。

2.参数模型方法参数模型方法是使用模型来计算金融产品未来的波动率和标准差。

这种方法基于假设，例如收益率服从正态分布或t分布等等。

由于使用参数化模型的方法，因此它往往需要更多的数据，并且需要广泛的金融知识和量化技能。

3.混合方法混合方法是基于历史和参数模型的方法，是VaR模型中比较广泛使用的一种方法。

混合方法结合了历史模拟方法和参数模型方法。

它使用历史收益率来计算金融产品的波动率，并通过模型来计算未来波动率。

四、VaR模型在系统性风险中的应用系统性风险是市场范围内的风险，由于这种风险造成的影响，市场中的许多不同的资产都会体现出相似的收益和亏损。

VaR模型可以帮助金融机构管理系统性风险。

以混合方法为例，金融机构可以使用历史收益率来计算系统性风险，并使用模型来计算未来波动率。

这样做可以帮助金融机构更好地理解系统性风险的潜在影响，并在必要时采取行动。

时间序列var模型过程
时间序列VAR（Vector Autoregression）模型是一种多变量时间序列分析方法，用于建模和预测多个相关变量之间的相互依赖关系。

下面是使用时间序列VAR模型的一般步骤：
1.数据准备：收集并准备时间序列数据，包括多个相关变量
的观测值。

2.确定滞后阶数（Lag order determination）：使用一些统计
指标或信息准则（如AIC、BIC等）来选择合适的滞后阶数。

滞后阶数决定了VAR模型中包含的过去时刻的数据点数。

3.拟合VAR模型：使用选定的滞后阶数，拟合VAR模型。

VAR模型可以用矩阵形式表示为：
Y_t = c + A_1 * Y_(t-1) + A_2 * Y_(t-2) + ... + A_p * Y_(t-p) + error_t
其中，Y_t是一个包含所有相关变量的向量，A_1, A_2, ..., A_p 是与每个滞后阶数对应的系数矩阵，c是截距项，error_t是误差项，t表示时间。

4.模型诊断和评估：对拟合的VAR模型进行诊断和评估，包
括检查误差项是否满足白噪声假设、模型是否具有良好的
拟合度等。

5.可选的模型改进和优化：根据需要，可以进行模型的改进
和优化，如添加外生变量、考虑异方差性等。

6.模型应用和预测：使用训练好的VAR模型进行应用和预测。

可以利用拟合的VAR模型进行现有数据的推断或使用它进行未来数据点的预测。

需要注意的是，VAR模型对数据的平稳性和线性相关性有一定要求。

在使用VAR模型之前，可能需要进行平稳性检验和相关性分析，或者对数据进行差分或转换，以满足模型的要求。

1文读懂VAR模型的实现过程与结果解读VAR模型是一种广泛应用的非参数时间序列分析方法，它从总体上研
究一组变量之间的关系。

它可以提供解释性、预测性以及多元共线性的检
验功能，可以用来发现影响变量之间的动态关系。

VAR模型用一系列变量
的序列建立一组统计模型，系统把这些变量之间的信息融合在一起，使得
预测更加准确。

一般来说，VAR模型有3个步骤：模型建立、模型合成和模型解释。

首先，建立VAR模型时，需要确定要使用的变量，然后依据模型假设，建
立VAR模型方程，确定误差项的分布情况，对参数和误差项进行估计，检
验模型的拟合度。

其次，保证模型的参数满足特定要求，模型的选择和合
成也大有讲究，在模型的合成过程中，需要考虑变量之间的共线性、自相
关性、合理调整等。

最后，模型解释，需要检验模型的合适性，确定自变
量与因变量之间的影响关系和动态变化；以及检验以及多元共线性的检验，以确定变量之间的关系。

VAR模型拟合的结果可以用多种方式来解释。

VAR模型最重要的部分
是解释因变量与自变量之间的动态关系。

由于VAR模型允许考虑多个变量，因此可以分析各个自变量间的相互影响，以及对因变量的影响。

第8章 V AR 模型与协整8.1 向量自回归（V AR ）模型1980年Sims 提出向量自回归模型（vector autoregressive model ）。

这种模型采用多方程联立的形式，它不以经济理论为基础，在模型的每一个方程中，内生变量对模型的全部内生变量的滞后值进行回归，从而估计全部内生变量的动态关系。

8.1.1 V AR 模型定义V AR 模型是自回归模型的联立形式，所以称向量自回归模型。

假设y 1t ，y 2t 之间存在关系，如果分别建立两个自回归模型y 1, t = f (y 1, t -1, y 1, t -2, …) y 2, t = f (y 2, t -1, y 2, t -2, …) 则无法捕捉两个变量之间的关系。

如果采用联立的形式，就可以建立起两个变量之间的关系。

V AR 模型的结构与两个参数有关。

一个是所含变量个数N ，一个是最大滞后阶数k 。

以两个变量y 1t ，y 2t 滞后1期的V AR 模型为例，y 1, t = μ1 + π11.1 y 1, t -1 + π12.1 y 2, t -1 + u 1 ty 2, t = μ2 + π21.1 y 1, t -1 + π22.1 y 2, t -1 + u 2 t (8.1) 其中u 1 t , u 2 t ~ IID (0, σ 2), Cov(u 1 t , u 2 t ) = 0。

写成矩阵形式是，⎥⎦⎤⎢⎣⎡t t y y 21=⎥⎦⎤⎢⎣⎡21μμ+⎥⎦⎤⎢⎣⎡1.221.211.121.11ππππ⎥⎦⎤⎢⎣⎡--1,21,1t t y y +⎥⎦⎤⎢⎣⎡t t u u 21 (8.2) 设， Y t =⎥⎦⎤⎢⎣⎡t t y y 21, μ =⎥⎦⎤⎢⎣⎡21μμ, ∏1 =⎥⎦⎤⎢⎣⎡1.221.211.121.11ππππ, u t =⎥⎦⎤⎢⎣⎡t t u u 21, 则， Y t = μ + ∏1 Y t -1 + u t (8.3) 那么，含有N 个变量滞后k 期的V AR 模型表示如下：Y t = μ + ∏1 Y t -1 + ∏2 Y t -2 + … + ∏k Y t -k + u t , u t ~ IID (0, Ω) (8.4) 其中，Y t = (y 1, t y 2, t … y N , t )' μ = (μ1 μ2 … μN )'∏j =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡j NN jN j N j N jjj N jj..2.1.2.22.21.1.12.11πππππππππ, j = 1, 2, …, k u t = (u 1 t u 2,t … u N t )',Y t 为N ⨯1阶时间序列列向量。

var模型的公式及变形解释说明1. 引言1.1 概述引言部分旨在介绍本篇长文的背景和主题。

本文将探讨VAR模型及其变形，并解释其公式和应用效果。

VAR模型是一种广泛应用于经济学和金融学领域的统计模型，用于分析多个变量之间的动态依赖关系。

通过引入滞后项、增加均衡增长路径或内生阻尼等因素，VAR模型可以更准确地反映实际情况，并提供有关变量互相影响和预测的信息。

1.2 文章结构本文将按以下结构进行论述：- 引言：对VAR模型及其变形进行概述，说明文章目的。

- VAR模型的公式：介绍VAR模型的基本原理和公式表达方式。

- VAR模型中的变量解释：探讨不同变量在VAR模型中扮演的角色及其解释意义。

- VAR模型的变形：详细介绍滞后VAR模型、均衡增长路径VAR模型和内生阻尼VAR模型，并对其各自特点进行解释。

- 解释说明VAR模型及其变形的应用效果和局限性：评估VAR模型及其变形在实际应用中所取得的效果，并指出其存在的局限性和改进措施。

- 结论：对本文进行总结，并提出进一步研究的方向。

1.3 目的本文的目的是深入探讨VAR模型及其变形，并解释其公式和应用效果。

通过了解VAR模型中各个变量的作用和解释意义，读者将更好地理解该模型在经济和金融领域的应用。

此外，分析VAR模型及其变形的应用效果和局限性，可以帮助读者更全面地评估这些模型在实际问题中的可行性，并为后续研究提供参考。

2. VAR模型的公式2.1 VAR模型简介VAR（Vector Autoregression）模型是一种经济学中常用的多变量时间序列分析方法，用于描述和预测各个变量之间的相互关系。

与传统的单方程模型不同，VAR模型可以同时考虑多个变量之间的相互作用。

2.2 VAR模型的公式表达VAR模型可以表示为如下形式：Y_t = A_0 + A_1*Y_(t-1) + A_2*Y_(t-2) + ... + A_p*Y_(t-p) + u_t其中，- Y_t 是一个k 维列向量，表示当前时间点t 的k 个变量值。

var模型的主要原理及应用1. var模型简介VAR（Vector Autoregression）模型是一种用来描述多个时间序列之间相互影响关系的统计模型。

它是通过将多个时间序列变量作为自变量，预测其中一个变量的未来值的一种方法。

2. var模型的主要原理VAR模型的原理基于向量形式的自回归模型。

其假设是：每一个时间序列变量的值，可以通过过去p个时间步长的自身和其他时间序列变量的线性组合来预测，即：Y_t = A_1 * Y_{t-1} + A_2 * Y_{t-2} + ... + A_p * Y_{t-p} + E_t其中，Y_t是一个k维的时间序列向量，A_i是一个k×k维的系数矩阵，E_t是一个k维的误差向量。

通过最小化误差平方和来估计模型参数。

3. var模型的应用VAR模型可以应用于许多领域，如经济学、金融学、社会科学等。

下面列举几个常见的应用场景：3.1 宏观经济分析VAR模型可以用来分析宏观经济变量之间的相互关系，预测经济指标的未来走势。

例如，可以通过建立一个包含GDP、通货膨胀率、消费者物价指数等变量的VAR模型，来预测未来的经济增长趋势和通货膨胀率变动。

3.2 金融风险管理VAR模型在金融领域常用于估计投资组合的风险和波动性。

通过构建一个包含股票价格、利率、汇率等变量的VAR模型，可以评估不同变量之间的相关性，并对未来的风险进行预测。

这对于投资者来说具有重要的参考价值。

3.3 政策评估VAR模型还可以用于评估政策的影响和效果。

例如，可以建立一个包含货币政策变量、经济增长率、就业率等变量的VAR模型，来评估货币政策对经济增长和就业的影响程度，并为制定政策提供决策依据。

3.4 社会科学研究除了经济和金融领域，VAR模型在社会科学研究中也有广泛的应用。

例如，可以利用VAR模型来分析政治变量、社会变量和经济变量之间的关系，从而深入研究不同因素对社会发展的影响。

4. 总结VAR模型是一种用来描述多个时间序列之间相互影响关系的重要统计模型。

VAR模型
VAR（Vector Autoregression）模型是一种经济时间序列分析方法，用于模拟和预测多个相关变量之间的动态关系。

VAR模型基于每个变量与其他变量之间存在相互依赖和影响的假设，通过引入滞后项和误差项来描述变量之间的关系。

VAR模型的基本原理是，每个变量的当前值可以由其自身的滞后值和其他变量的滞后值来解释。

VAR模型使用时间序列数据来估计模型的参数，并用于分析变量之间的因果关系、冲击传递和预测未来值。

VAR模型的一般形式可以表示为：
Yt = c + A1Yt-1 + A2Yt-2 + ... + Ap*Yt-p + e
其中，Yt 是一个 k 维向量，表示 k 个相关变量的观测值。

c 是一个 k 维向量，表示截距项。

A1, A2, ..., Ap 是 k×k 的矩阵，分别表示各个变量的系数矩阵。

p 是滞后期数，表示模型中引入的滞后项的数量。

e 是一个 k 维向量，表示误差项。

VAR模型的估计通常使用最小二乘法或极大似然法。

估计得到的模型参数可以用于分析变量之间的动态关系、解释冲击传递机制以及进行短期和长期预测。

VAR模型在经济学和金融领域广泛应用，特别是用于宏观经济变量之间的分析，如GDP、通货膨胀率、利率等。

它可以帮助研究人员了解经济变量之间的交互作用、行业间的传导效应、政策冲击的影响等。

然而，VAR模型也有其限制，例如对
数据的平稳性和变量选择的要求，以及对滞后项的选取需要合理的依据等。