黄永刚单晶塑性有限元umat子程序
- 格式:doc
- 大小:300.00 KB
- 文档页数:66

各向异性屈服准则的UMAT子程序二次开发研究乔顺成;吴建军;展学鹏【摘要】通过ABAQUS提供的UMAT子程序二次开发接口,结合完全隐式向后Euler图形返回算法,用Fortran语言编程,将Yld2004-18p各向异性屈服准则本构模型嵌入ABAQUS软件,并提出了一个通用的、柔性的本构模型二次开发结构模式.将Yld2004-18p屈服准则退化到Mises各向同性屈服准则,用于实例有限元分析,计算结果与ABAQUS自带的Mises屈服准则计算结果做比较,验证了二次开发过程的正确性,为后续嵌入更高级、更强健、更特殊的屈服准则提供研究思路和方法,使之用于精密塑性有限元分析.【期刊名称】《锻压装备与制造技术》【年(卷),期】2018(053)004【总页数】9页(P89-97)【关键词】UMAT子程序;各向异性;屈服准则;本构模型;二次开发【作者】乔顺成;吴建军;展学鹏【作者单位】中航工业西安飞机工业集团有限责任公司,陕西西安710072;西北工业大学机电学院,陕西西安710072;西北工业大学机电学院,陕西西安710072【正文语种】中文【中图分类】TP391.77ABAQUS以其强大的非线性迭代计算和前后处理功能而广泛应用于材料弹塑性有限元分析,它是现阶段在各个工程领域广泛使用的大型通用有限元软件之一。
ABAQUS[1]有大量的单元库和求解模型供用户使用,而且用户也能够通过这些模型求解绝大多数问题。
但是实际问题是相当复杂的,ABAQUS不可能直接处理所有可能的问题[2-4],所以,有必要给用户提供二次开发的接口来解决实际中出现的新问题。
在用户自定义材料(UMAT即 User-defined Material Mechanical Behavior)研究中,很多学者通过UMAT子程序二次开发,将新的本构模型用于实际问题的有限元分析。
例如:李平[5]等通过数值分析模拟了普通碳钢连续热轧的过程,将率相关的各向同性硬化热变形本构模型通过UMAT子程序用于有限元仿真,分析了轧制过程中的温度和应力、应变之间的耦合关系。
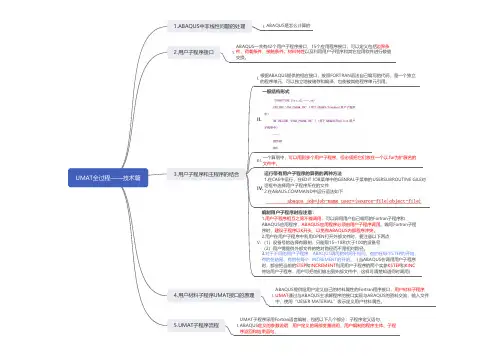
UMAT全过程——技术篇 1.ABAQUS中非线性问题的处理2.用户子程序接口3.用户子程序和主程序的结合4.用户材料子程序UMAT接口的原理5.UMAT子程序流程ABAQUS是怎么计算的I.ABAQUS一共有42个用户子程序接口,15个应用程序接口,可以定义包括边界条件,荷载条件,接触条件,材料特性以及利用用户子程序和其它应用软件进行数值交换。
1.根据ABAQUS提供的相应接口,按照FORTRAN语法自己编写的代码,是一个独立的程序单元,可以独立地被储存和编译,也能被其他程序单元引用。
I.一般结构形式II.一个算例中,可以用到多个用户子程序,但必须把它们放在一个以.for为扩展名的文件中。
III.运行带有用户子程序的算例的两种方法1.在CAE中运行,在EDIT JOB菜单中的GENRAL子菜单的USERSUBROUTINE GILE对话框中选择用户子程序所在的文件2.在MAND中运行语法如下IV.编制用户子程序时应注意:1.用户子程序相互之间不能调用,可以调用用户自己编写的Fortran子程序和ABAQUS应用程序,ABAQUS应用程序必须由用户子程序调用。
编写Fortran子程序时,建议子程序以K开头,以免和ABAQUS内部程序冲突。
2.用户在用户子程序中利用OPEN打开外部文件时,要注意以下两点:(1)设备号的选择有限制,只能取15~18和大于100的设备号(2)用户需提供外部文件的绝对路径而不是相对路径。
3.对于不同的用户子程序,ABAQUS调用的时间不相同,有的在每个STEP的开始,有的在结尾,有的在每个 INCREMENT的开始。
(当ABAQUS在调用用户子程序时,都会把当前的STEP 和INCREMENT 利用用户子程序的两个实参KSTEP 和KINC 传给用户子程序,用户可把他们输出到外部文件中,这样可清楚知道何时调用)V.ABAQUS提供给用户定义自己的材料属性的Fortran程序接口,用户材料子程序UMAT 通过与ABAQUS主求解程序的接口实现与ABAQUS的资料交流,输入文件中,使用“UESER MATERIAL”表示定义用户材料属性。



UMAT全过程-"技术篇"之一:相关知识标签: UMAT技术篇知识2010-03-04 20:24UMAT全过程-"技术篇"[写在前面:这篇文章是UMAT全过程-感想篇的姊妹篇,答应要给大家写的一篇帖子,同时也是为了记录自己的学习过程,与大家分享!首先指出,俺的"技术篇"--是加了引号的,因为确实称不上有多么大的技术含量,还望大家莫笑偶!只不过一是跟那个感想篇形成一个对照,同时主要内容为自己编子程序过程中涉及的技术边边上的小问题的一些解决方法,供仿友们参考!偶不是谦虚,也不是一个低调的人,大家谢谢和支持的话,我先行谢过啦!更希望大家能提出质疑或者别的更好的办法,大家相互交流,共同进步!]----------------------------------------------------------------------------*转*入*正*题*第一部分:相关知识[特别声明,这部分来自于华中科技大学杨曼娟同学的硕士学位论文,在此对作者表示感谢!--大家可以去知网下载]----------------------------------------------------------------------------1.ABAQUS中材料非线性问题的处理ABAQUS中材料非线性问题用Newton-Raphson法来求解。
首先将载荷分为若干个微小增量,结构受到一个微小增量△P。
ABAQUS用与初始结构位移相对应的初始刚度矩阵K0和荷载增量△P计算出结构的在这一步增量后的位移修正Ca、修正后的位移值Ua和相应的新的刚度矩阵Ka。
ABAQUS用新的刚度矩阵计算结构的内力Ia,荷载P和Ia的差值为迭代的残余力Ra,即Ra=P-Ia。
如果Ra在模型内的每个自由度上的值都为零,如图2-2中的a点,则结构处于平衡状态。
但在非线性问题中,通常Ra是不可能为零,ABAQUS为此设置了一个残余力容差。


一起学习UMAT的一些公式注释ZHANG chunyuherrliubs comments in formulas知识积累和储备在进行ABAQUS子程序UMAT的编写前,要弄清楚:ABAQUS调用UMAT子程序流程;要建立的材料模型的本构关系和屈服准则等;UMAT子程序中相关参数、以及矩阵的表达。
主要求解过程:每一个增量步开始,ABAQUS主程序在单元积分点上调用UMAT 子程序,并转入应变增量、时间步长及荷载增量,同时也传入当前已知的状态的应力、应变及其他求解过程相关的变量;UMAT子程序根据本构方程求解应力增量及其他相关的变量,提供Jacobian矩阵给ABAQUS主程序以形成整体刚度矩阵;主程序结合当前荷载增量求解位移增量,继而进行平衡校核;如果不满足指定的误差,ABAQUS将进行迭代直到收敛,然后进行下一增量步的求解。
弹性力学相关知识(基本)仿真论坛(/forum.php ... &highlight=UMAT)ABAQUS二次开发版块这个人帖子结合例子,列出了弹性力学的基本公式。
UMAT变量含义UMAT中可以得到的量增量步开始时刻的,应力(Stress),应变(Strain), 状态变量(Solution-dependent state variables (SDVs))增量步开始时刻的,应变增量(Strain increment),转角增量(Rotation increment),变形梯度(Deformation gradient)时间总值及增量(Total and incremental values of time),温度(Temperature),用户定义场变量材料常数,材料点的位置,特征单元长度当前分析步,增量步必须定义的变量应力,状态变量,材料Jacobian矩阵(本构关系)可以定义的变量应变能,塑性耗能,蠕变耗能新建议的时间增量变量分类UMAT中可以直接调用(Call ……)的子程序或子函数SINV(STRESS,SINV1,SINV2,NDI,NSHR)——用于计算应力不变量。

abaqus复合材料larc05失效准则umat子程序开发的相关案例教程开发一个用于模拟复合材料的UMAT子程序是一个复杂的过程,涉及到对材料行为的深入理解以及高级编程技巧。
下面是一个基本的案例教程,演示如何为ABAQUS开发一个用于模拟LARC05失效准则的UMAT子程序。
1. 准备工作•安装ABAQUS: 确保你已经安装了ABAQUS软件。
•编程环境: 准备一个适合C++的开发环境,如Visual Studio或Eclipse。
•材料数据: 收集或计算所需的材料属性,如弹性模量、泊松比、失效准则参数等。
2. 创建UMAT子程序框架•打开ABAQUS: 启动ABAQUS软件。
•创建新的UMAT: 在ABAQUS的插件菜单中选择“用户材料”>“用户材料子程序”>“创建”。
选择C++作为编程语言。
•编写框架: 创建一个新的C++文件,并添加必要的头文件和命名空间。
定义UMAT所需的输入和输出变量。
3. 实现LARC05失效准则•理解LARC05准则: LARC05是一种复合材料失效准则,涉及到最大应力、最大应变等参数。
确保你理解这些参数如何影响材料行为。
•编写代码: 根据LARC05准则,使用C++编写UMAT子程序代码。
这可能涉及到计算应力、应变,以及应用失效准则。
4. 测试和验证UMAT•创建测试案例: 在ABAQUS中创建一个简单的模型,用于测试UMAT子程序。
•运行模拟: 运行模拟,并检查结果是否符合预期。
如果结果不符合预期,回到代码中调试问题。
•验证: 使用更多的测试案例验证UMAT的准确性。
确保UMAT在各种工况下都能正确预测材料的失效行为。
5. 优化和调整•优化性能: 如果UMAT运行速度较慢,考虑优化代码以提高性能。
•调整参数: 根据模拟结果调整UMAT中的参数,以获得更准确的结果。
6. 文档和分享•编写文档: 为UMAT子程序编写详细的文档,包括输入和输出变量、材料参数、测试案例等。

一起学习UMAT的一些公式注释ZHANG chunyuherrliubs comments in formulas知识积累和储备在进行ABAQUS子程序UMAT的编写前,要弄清楚:ABAQUS调用UMAT子程序流程;要建立的材料模型的本构关系和屈服准则等;UMAT子程序中相关参数、以及矩阵的表达。
主要求解过程:每一个增量步开始,ABAQUS主程序在单元积分点上调用UMAT 子程序,并转入应变增量、时间步长及荷载增量,同时也传入当前已知的状态的应力、应变及其他求解过程相关的变量;UMAT子程序根据本构方程求解应力增量及其他相关的变量,提供Jacobian矩阵给ABAQUS主程序以形成整体刚度矩阵;主程序结合当前荷载增量求解位移增量,继而进行平衡校核;如果不满足指定的误差,ABAQUS将进行迭代直到收敛,然后进行下一增量步的求解。
弹性力学相关知识(基本)仿真论坛(/forum.php ... &highlight=UMAT)ABAQUS二次开发版块这个人帖子结合例子,列出了弹性力学的基本公式。
UMAT变量含义UMAT中可以得到的量增量步开始时刻的,应力(Stress),应变(Strain), 状态变量(Solution-dependent state variables (SDVs))增量步开始时刻的,应变增量(Strain increment),转角增量(Rotation increment),变形梯度(Deformation gradient)时间总值及增量(Total and incremental values of time),温度(Temperature),用户定义场变量材料常数,材料点的位置,特征单元长度当前分析步,增量步必须定义的变量应力,状态变量,材料Jacobian矩阵(本构关系)可以定义的变量应变能,塑性耗能,蠕变耗能新建议的时间增量变量分类UMAT中可以直接调用(Call ……)的子程序或子函数SINV(STRESS,SINV1,SINV2,NDI,NSHR)——用于计算应力不变量。

材料本构模型及编程实现:简介一起学习UMATZHANG chunyu1、什么时候用用户定义材料(User-defined material, UMAT)?很简单,当ABAQUS没有提供我们需要的材料模型时。
所以,在决定自己定义一种新的材料模型之前,最好对ABAQUS已经提供的模型心中有数,并且尽量使用现有的模型,因为这些模型已经经过详细的验证,并被广泛接受。
2、好学吗?需要哪些基础知识?先看一下ABAQUS手册(ABAQUS Analysis User's Manual)里的一段话:Warning: The use of this option generally requires consider able expertise. The user is cautioned that the implementationof any realistic constitutive model requires extensive devel opment and testing. Initial testing on a single element model with prescribed traction loading is strongly recommended.但这并不意味着非力学专业,或者力学基础知识不很丰富者就只能望洋兴叹,因为我们的任务不是开发一套完整的有限元软件,而只是提供一个描述材料力学性能的本构方程(Constitutive equation)而已。
当然,最基本的一些概念和知识还是要具备的,比如应力(stress),应变(strain)及其分量;volumetric part和deviatoric part;模量(modulus)、泊松比(Poisson’s ratio)、拉美常数(Lame constant);矩阵的加减乘除甚至求逆;还有一些高等数学知识如积分、微分等。
前言有限元法是工程中广泛使用的一种数值计算方法。
它是力学、计算方法和计算机技术相结合的产物。
在工程应用中,有限元法比其它数值分析方法更流行的一个重要原因在于:相对与其它数值分析方法,有限元法对边界的模拟更灵活,近似程度更高。
所以,伴随着有限元理论以及计算机技术的发展,大有限元软件的应用证变得越来越普及。
ABAQUS软件一直以非线性有限元分析软件而闻名,这也是它和ANSYS,Nastran等软件的区别所在。
非线性有限元分析的用处越来越大,因为在所用材料非常复杂很多情况下,用线性分析来近似已不再有效。
比方说,一个复合材料就不能用传统的线性分析软件包进行分析。
任何与时间有关联,有较大位移量的情况都不能用线性分析法来处理。
多年前,虽然非线性分析能更适合、更准确的处理问题,但是由于当时计算设备的能力不够强大、非线性分析软件包线性分析功能不够健全,所以通常采用线性处理的方法。
这种情况已经得到了极大的改善,计算设备的能力变得更加强大、类似ABAQUS这样的产品功能日臻完善,应用日益广泛。
非线性有限元分析在各个制造行业得到了广泛应用,有不少大型用户。
航空航天业一直是非线性有限元分析的大客户,一个重要原因是大量使用复合材料。
新一代波音 787客机将全部采用复合材料。
只有像ABAQUS这样的软件,才能分析包括多个子系统的产品耐久性能。
在汽车业,用线性有限元分析来做四轮耐久性分析不可能得到足够准确的结果。
分析汽车的整体和各个子系统的性能要求(如悬挂系统等)需要进行非线性分析。
在土木工程业, ABAQUS能处理包括混凝土静动力开裂分析以及沥青混凝土方面的静动力分析,还能处理高度复杂非线性材料的损伤和断裂问题,这对于大型桥梁结构,高层建筑的结构分析非常有效。
瞬态、大变形、高级材料的碰撞问题必须用非线性有限元分析来计算。
线性分析在这种情况下是不适用的。
以往有一些专门的软件来分析碰撞问题,但现在ABAQUS在通用有限元软件包就能解决这些问题。
SUBROUTINE UMAT(stress,statev,ddsdde,sse,spd,scd,1 rpl, ddsddt, drplde, drpldt,2 stran,dstran,time,dtime,temp,dtemp,predef,dpred,cmname,3 ndi,nshr,ntens,nstatv,props,nprops,coords,drot,pnewdt,4 celent,dfgrd0,dfgrd1,noel,npt,layer,kspt,kstep,kinc)c WRITE (6,*) 'c NOTE: MODIFICATIONS TO *UMAT FOR ABAQUS VERSION 5.3 (14 APR '94) cc (1) The list of variables above defining the *UMAT subroutine,c and the first (standard) block of variables dimensioned below,c have variable names added compared to earlier ABAQUS versions.cc (2) The statement: include 'aba_param.inc' must be added as below.cc (3) As of version 5.3, ABAQUS files use double precision only.c The file aba_param.inc has a line "implicit real*8" and, sincec it is included in the main subroutine, it will define the variablesc there as double precision. But other subroutines still need thec definition "implicit real*8" since there may be variables that arec not passed to them through the list or common block.cc (4) This is current as of version 5.6 of ABAQUS.cc (5) Note added by J. W. Kysar (4 November 1997). This UMAT has beenc modified to keep track of the cumulative shear strain in eachc individual slip system. This information is needed to correct anc error in the implementation of the Bassani and Wu hardening law.c Any line of code which has been added or modified is precededc immediately by a line beginning CFIXA and succeeded by a linec beginning CFIXB. Any comment line added or modified will beginc with CFIX.cc The hardening law by Bassani and Wu was implemented incorrectly.c This law is a function of both hyperbolic secant squared and hyperbolicc tangent. However, the arguments of sech and tanh are related to the *total*c slip on individual slip systems. Formerly, the UMAT implemented thisc hardening law by using the *current* slip on each slip system. Thereinc lay the problem. The UMAT did not restrict the current slip to be ac positive value. So when a slip with a negative sign was encountered, thec term containing tanh led to a negative hardening rate (since tanh is anc odd function).c The UMA T has been fixed by adding state variables to keep track of thec *total* slip on each slip system by integrating up the absolute valuec of slip rates for each individual slip system. These "solution dependentc variables" are available for postprocessing. The only required changec in the input file is that the DEPV AR command must be changed.cC----- Use single precision on Cray byC (1) deleting the statement "IMPLICIT*8 (A-H,O-Z)";C (2) changing "REAL*8 FUNCTION" to "FUNCTION";C (3) changing double precision functions DSIGN to SIGN.CC----- Subroutines:CC ROTATION -- forming rotation matrix, i.e. the directionC cosines of cubic crystal [100], [010] and [001]C directions in global system at the initialC stateCC SLIPSYS -- calculating number of slip systems, unitC vectors in slip directions and unit normals toC slip planes in a cubic crystal at the initialC stateCC GSLPINIT -- calculating initial value of current strengthsC at initial stateCC STRAINRA TE -- based on current values of resolved shearC stresses and current strength, calculatingC shear strain-rates in slip systemsCC LATENTHARDEN -- forming self- and latent-hardening matrixCC ITERATION -- generating arrays for the Newton-RhapsonC iterationCC LUDCMP -- LU decompositionCC LUBKSB -- linear equation solver based on LUC decomposition method (must call LUDCMP first) C----- Function subprogram:C F -- shear strain-rates in slip systemsC----- Variables:CC STRESS -- stresses (INPUT & OUTPUT)C Cauchy stresses for finite deformationC STATEV -- solution dependent state variables (INPUT & OUTPUT) C DDSDDE -- Jacobian matrix (OUTPUT)C----- Variables passed in for information:CC STRAN -- strainsC logarithmic strain for finite deformationC (actually, integral of the symmetric part of velocityC gradient with respect to time)C DSTRAN -- increments of strainsC CMNAME -- name given in the *MATERIAL optionC NDI -- number of direct stress componentsC NSHR -- number of engineering shear stress componentsC NTENS -- NDI+NSHRC NSTATV -- number of solution dependent state variables (asC defined in the *DEPVAR option)C PROPS -- material constants entered in the *USER MA TERIAL C optionC NPROPS -- number of material constantsCC----- This subroutine provides the plastic constitutive relation ofC single crystals for finite element code ABAQUS. The plastic slipC of single crystal obeys the Schmid law. The program gives theC choice of small deformation theory and theory of finite rotationC and finite strain.C The strain increment is composed of elastic part and plasticC part. The elastic strain increment corresponds to latticeC stretching, the plastic part is the sum over all slip systems ofC plastic slip. The shear strain increment for each slip system isC assumed a function of the ratio of corresponding resolved shearC stress over current strength, and of the time step. The resolvedC shear stress is the double product of stress tensor with the slipC deformation tensor (Schmid factor), and the increment of currentC strength is related to shear strain increments over all slipC systems through self- and latent-hardening functions.C----- The implicit integration method proposed by Peirce, Shih andC Needleman (1984) is used here. The subroutine provides an option C of iteration to solve stresses and solution dependent stateC variables within each increment.C----- The present program is for a single CUBIC crystal. However,C this code can be generalized for other crystals (e.g. HCP,C Tetragonal, Orthotropic, etc.). Only subroutines ROTATION andC SLIPSYS need to be modified to include the effect of crystalC aspect ratio.CC----- Important notice:CC (1) The number of state variables NSTATV must be larger than (or CFIX equal to) TEN (10) times the total number of slip systems inC all sets, NSLPTL, plus FIVE (5)CFIX NSTATV >= 10 * NSLPTL + 5C Denote s as a slip direction and m as normal to a slip plane.C Here (s,-m), (-s,m) and (-s,-m) are NOT consideredC independent of (s,m). The number of slip systems in each setC could be either 6, 12, 24 or 48 for a cubic crystal, e.g. 12C for {110}<111>.CC Users who need more parameters to characterize theC constitutive law of single crystal, e.g. the frameworkC proposed by Zarka, should make NSTATV larger than (or equal C to) the number of those parameters NPARMT plus nine timesC the total number of slip systems, NSLPTL, plus fiveCFIX NSTATV >= NPARMT + 10 * NSLPTL + 5CC (2) The tangent stiffness matrix in general is not symmetric ifC latent hardening is considered. Users must declare "UNSYMM"C in the input file, at the *USER MATERIAL card.CPARAMETER (ND=150)C----- The parameter ND determines the dimensions of the arrays inC this subroutine. The current choice 150 is a upper bound for aC cubic crystal with up to three sets of slip systems activated.C Users may reduce the parameter ND to any number as long as larger C than or equal to the total number of slip systems in all sets.C For example, if {110}<111> is the only set of slip systemC potentially activated, ND could be taken as twelve (12).cinclude 'aba_param.inc'cCHARACTER*8 CMNAMEEXTERNAL Fdimension stress(ntens),statev(nstatv),1 ddsdde(ntens,ntens),ddsddt(ntens),drplde(ntens),2 stran(ntens),dstran(ntens),time(2),predef(1),dpred(1),3 props(nprops),coords(3),drot(3,3),dfgrd0(3,3),dfgrd1(3,3)DIMENSION ISPDIR(3), ISPNOR(3), NSLIP(3),2 SLPDIR(3,ND), SLPNOR(3,ND), SLPDEF(6,ND),3 SLPSPN(3,ND), DSPDIR(3,ND), DSPNOR(3,ND),4 DLOCAL(6,6), D(6,6), ROTD(6,6), ROTATE(3,3),5 FSLIP(ND), DFDXSP(ND), DDEMSD(6,ND),6 H(ND,ND), DDGDDE(ND,6),7 DSTRES(6), DELATS(6), DSPIN(3), DVGRAD(3,3),8 DGAMMA(ND), DTAUSP(ND), DGSLIP(ND),9 WORKST(ND,ND), INDX(ND), TERM(3,3), TRM0(3,3), ITRM(3)DIMENSION FSLIP1(ND), STRES1(6), GAMMA1(ND), TAUSP1(ND),2 GSLP1(ND), SPNOR1(3,ND), SPDIR1(3,ND), DDSDE1(6,6),3 DSOLD(6), DGAMOD(ND), DTAUOD(ND), DGSPOD(ND),4 DSPNRO(3,ND), DSPDRO(3,ND),5 DHDGDG(ND,ND)C----- NSLIP -- number of slip systems in each setC----- SLPDIR -- slip directions (unit vectors in the initial state)C----- SLPNOR -- normals to slip planes (unit normals in the initialC state)C----- SLPDEF -- slip deformation tensors (Schmid factors)C SLPDEF(1,i) -- SLPDIR(1,i)*SLPNOR(1,i)C SLPDEF(2,i) -- SLPDIR(2,i)*SLPNOR(2,i)C SLPDEF(3,i) -- SLPDIR(3,i)*SLPNOR(3,i)C SLPDEF(4,i) -- SLPDIR(1,i)*SLPNOR(2,i)+C SLPDIR(2,i)*SLPNOR(1,i)C SLPDEF(5,i) -- SLPDIR(1,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(1,i)C SLPDEF(6,i) -- SLPDIR(2,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(2,i)C where index i corresponds to the ith slip systemC----- SLPSPN -- slip spin tensors (only needed for finite rotation)C SLPSPN(1,i) -- [SLPDIR(1,i)*SLPNOR(2,i)-C SLPDIR(2,i)*SLPNOR(1,i)]/2C SLPSPN(2,i) -- [SLPDIR(3,i)*SLPNOR(1,i)-C SLPDIR(1,i)*SLPNOR(3,i)]/2C SLPSPN(3,i) -- [SLPDIR(2,i)*SLPNOR(3,i)-C SLPDIR(3,i)*SLPNOR(2,i)]/2C where index i corresponds to the ith slip systemC----- DSPDIR -- increments of slip directionsC----- DSPNOR -- increments of normals to slip planesCC----- DLOCAL -- elastic matrix in local cubic crystal systemC----- D -- elastic matrix in global systemC----- ROTD -- rotation matrix transforming DLOCAL to DCC----- ROTATE -- rotation matrix, direction cosines of [100], [010]C and [001] of cubic crystal in global systemCC----- FSLIP -- shear strain-rates in slip systemsC----- DFDXSP -- derivatives of FSLIP w.r.t x=TAUSLP/GSLIP, whereC TAUSLP is the resolved shear stress and GSLIP is the C current strengthCC----- DDEMSD -- double dot product of the elastic moduli tensor withC the slip deformation tensor plus, only for finiteC rotation, the dot product of slip spin tensor withC the stressCC----- H -- self- and latent-hardening matrixC H(i,i) -- self hardening modulus of the ith slipC system (no sum over i)C H(i,j) -- latent hardening molulus of the ith slipC system due to a slip in the jth slip system C (i not equal j)CC----- DDGDDE -- derivatice of the shear strain increments in slipC systems w.r.t. the increment of strainsCC----- DSTRES -- Jaumann increments of stresses, i.e. corotationalC stress-increments formed on axes spinning with theC materialC----- DELATS -- strain-increments associated with lattice stretchingC DELATS(1) - DELATS(3) -- normal strain increments C DELATS(4) - DELATS(6) -- engineering shear strain C incrementsC----- DSPIN -- spin-increments associated with the material elementC DSPIN(1) -- component 12 of the spin tensorC DSPIN(2) -- component 31 of the spin tensorC DSPIN(3) -- component 23 of the spin tensorCC----- DVGRAD -- increments of deformation gradient in the currentC state, i.e. velocity gradient times the increment ofC timeCC----- DGAMMA -- increment of shear strains in slip systemsC----- DTAUSP -- increment of resolved shear stresses in slip systemsC----- DGSLIP -- increment of current strengths in slip systemsCCC----- Arrays for iteration:CC FSLIP1, STRES1, GAMMA1, TAUSP1, GSLP1 , SPNOR1, SPDIR1,C DDSDE1, DSOLD , DGAMOD, DTAUOD, DGSPOD, DSPNRO, DSPDRO, C DHDGDGCCC----- Solution dependent state variable STATEV:C Denote the number of total slip systems by NSLPTL, whichC will be calculated in this code.CC Array STATEV:C 1 - NSLPTL : current strength in slip systemsC NSLPTL+1 - 2*NSLPTL : shear strain in slip systemsC 2*NSLPTL+1 - 3*NSLPTL : resolved shear stress in slip systemsCC 3*NSLPTL+1 - 6*NSLPTL : current components of normals to slipC slip planesC 6*NSLPTL+1 - 9*NSLPTL : current components of slip directionsCCFIX 9*NSLPTL+1 - 10*NSLPTL : total cumulative shear strain on eachCFIX slip system (sum of the absoluteCFIX values of shear strains in each slipCFIX system individually)CFIXCFIX 10*NSLPTL+1 : total cumulative shear strain on allC slip systems (sum of the absoluteC values of shear strains in all slipC systems)CCFIX 10*NSLPTL+2 - NSTA TV-4 : additional parameters users may needC to characterize the constitutive lawC of a single crystal (if there areC any).CC NSTATV-3 : number of slip systems in the 1st setC NSTATV-2 : number of slip systems in the 2nd setC NSTATV-1 : number of slip systems in the 3rd setC NSTATV : total number of slip systems in allC setsCCC----- Material constants PROPS:CC PROPS(1) - PROPS(21) -- elastic constants for a general elasticC anisotropic materialCC isotropic : PROPS(i)=0 for i>2C PROPS(1) -- Young's modulusC PROPS(2) -- Poisson's ratioCC cubic : PROPS(i)=0 for i>3C PROPS(1) -- c11C PROPS(2) -- c12C PROPS(3) -- c44CC orthotropic : PORPS(i)=0 for i>9C PROPS(1) - PROPS(9) are D1111, D1122, D2222, C D1133, D2233, D3333, D1212, D1313, D2323,C respectively, which has the same definitionC as ABAQUS for orthotropic materialsC (see *ELASTIC card)CC anisotropic : PROPS(1) - PROPS(21) are D1111, D1122,C D2222, D1133, D2233, D3333, D1112, D2212,C D3312, D1212, D1113, D2213, D3313, D1213,C D1313, D1123, D2223, D3323, D1223, D1323,C D2323, respectively, which has the sameC definition as ABAQUS for anisotropicC materials (see *ELASTIC card)CCC PROPS(25) - PROPS(56) -- parameters characterizing all slipC systems to be activated in a cubicC crystalCC PROPS(25) -- number of sets of slip systems (maximum 3),C e.g. (110)[1-11] and (101)[11-1] are in theC same set of slip systems, (110)[1-11] andC (121)[1-11] belong to different sets of slipC systemsC (It must be a real number, e.g. 3., not 3 !)CC PROPS(33) - PROPS(35) -- normal to a typical slip plane inC the first set of slip systems,C e.g. (1 1 0)C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(36) - PROPS(38) -- a typical slip direction in theC first set of slip systems, e.g.C [1 1 1]C (They must be real numbers, e.g.C 1. 1. 1., not 1 1 1 !)CC PROPS(41) - PROPS(43) -- normal to a typical slip plane inC the second set of slip systemsC (real numbers)C PROPS(44) - PROPS(46) -- a typical slip direction in theC second set of slip systemsC (real numbers)CC PROPS(49) - PROPS(51) -- normal to a typical slip plane inC the third set of slip systemsC (real numbers)C PROPS(52) - PROPS(54) -- a typical slip direction in theC third set of slip systemsC (real numbers)CCC PROPS(57) - PROPS(72) -- parameters characterizing the initialC orientation of a single crystal inC global systemC The directions in global system and directions in localC cubic crystal system of two nonparallel vectors are neededC to determine the crystal orientation.CC PROPS(57) - PROPS(59) -- [p1 p2 p3], direction of firstC vector in local cubic crystalC system, e.g. [1 1 0]C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(60) - PROPS(62) -- [P1 P2 P3], direction of firstC vector in global system, e.g.C [2. 1. 0.]C (It does not have to be a unitC vector)CC PROPS(65) - PROPS(67) -- direction of second vector inC local cubic crystal system (real C numbers)C PROPS(68) - PROPS(70) -- direction of second vector inC global systemCCC PROPS(73) - PROPS(96) -- parameters characterizing the visco-C plastic constitutive law (shearC strain-rate vs. resolved shearC stress), e.g. a power-law relationCC PROPS(73) - PROPS(80) -- parameters for the first set ofC slip systemsC PROPS(81) - PROPS(88) -- parameters for the second set of C slip systemsC PROPS(89) - PROPS(96) -- parameters for the third set ofC slip systemsCCC PROPS(97) - PROPS(144)-- parameters characterizing the self-C and latent-hardening laws of slipC systemsCC PROPS(97) - PROPS(104)-- self-hardening parameters for the C first set of slip systemsC PROPS(105)- PROPS(112)-- latent-hardening parameters for C the first set of slip systems and C interaction with other sets ofC slip systemsCC PROPS(113)- PROPS(120)-- self-hardening parameters for the C second set of slip systemsC PROPS(121)- PROPS(128)-- latent-hardening parameters for C the second set of slip systems C and interaction with other sets C of slip systemsCC PROPS(129)- PROPS(136)-- self-hardening parameters for the C third set of slip systemsC PROPS(137)- PROPS(144)-- latent-hardening parameters for C the third set of slip systems and C interaction with other sets ofC slip systemsCCC PROPS(145)- PROPS(152)-- parameters characterizing forward time C integration scheme and finiteC deformationCC PROPS(145) -- parameter theta controlling the implicitC integration, which is between 0 and 1C 0. : explicit integrationC 0.5 : recommended valueC 1. : fully implicit integrationCC PROPS(146) -- parameter NLGEOM controlling whether the C effect of finite rotation and finite strainC of crystal is considered,C 0. : small deformation theoryC otherwise : theory of finite rotation andC finite strainCCC PROPS(153)- PROPS(160)-- parameters characterizing iterationC methodCC PROPS(153) -- parameter ITRATN controlling whether theC iteration method is used,C 0. : no iterationC otherwise : iterationCC PROPS(154) -- maximum number of iteration ITRMAXCC PROPS(155) -- absolute error of shear strains in slipC systems GAMERRCC----- Elastic matrix in local cubic crystal system: DLOCALDO J=1,6DO I=1,6DLOCAL(I,J)=0.END DOEND DOCHECK=0.DO J=10,21CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENDO J=4,9CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENIF (PROPS(3).EQ.0.) THENC----- Isotropic materialGSHEAR=PROPS(1)/2./(1.+PROPS(2))E11=2.*GSHEAR*(1.-PROPS(2))/(1.-2.*PROPS(2))E12=2.*GSHEAR*PROPS(2)/(1.-2.*PROPS(2))DO J=1,3DLOCAL(J,J)=E11DO I=1,3IF (I.NE.J) DLOCAL(I,J)=E12END DODLOCAL(J+3,J+3)=GSHEAREND DOELSEC----- Cubic materialDO J=1,3DLOCAL(J,J)=PROPS(1)DO I=1,3IF (I.NE.J) DLOCAL(I,J)=PROPS(2)END DODLOCAL(J+3,J+3)=PROPS(3)END DOEND IFELSEC----- Orthotropic metarialDLOCAL(1,1)=PROPS(1)DLOCAL(1,2)=PROPS(2)DLOCAL(2,1)=PROPS(2)DLOCAL(2,2)=PROPS(3)DLOCAL(1,3)=PROPS(4)DLOCAL(3,1)=PROPS(4)DLOCAL(2,3)=PROPS(5)DLOCAL(3,2)=PROPS(5)DLOCAL(3,3)=PROPS(6)DLOCAL(4,4)=PROPS(7)DLOCAL(5,5)=PROPS(8)DLOCAL(6,6)=PROPS(9)END IFELSEC----- General anisotropic materialID=0DO J=1,6DO I=1,JID=ID+1DLOCAL(I,J)=PROPS(ID)DLOCAL(J,I)=DLOCAL(I,J)END DOEND DOEND IFC----- Rotation matrix: ROTA TE, i.e. direction cosines of [100], [010]C and [001] of a cubic crystal in global systemCCALL ROTATION (PROPS(57), ROTA TE)C----- Rotation matrix: ROTD to transform local elastic matrix DLOCAL C to global elastic matrix DCDO J=1,3J1=1+J/3J2=2+J/2DO I=1,3I1=1+I/3I2=2+I/2ROTD(I,J)=ROTATE(I,J)**2ROTD(I,J+3)=2.*ROTATE(I,J1)*ROTA TE(I,J2)ROTD(I+3,J)=ROTA TE(I1,J)*ROTATE(I2,J)ROTD(I+3,J+3)=ROTA TE(I1,J1)*ROTA TE(I2,J2)+2 ROTA TE(I1,J2)*ROTA TE(I2,J1)END DOEND DOC----- Elastic matrix in global system: DC {D} = {ROTD} * {DLOCAL} * {ROTD}transposeCDO J=1,6DO I=1,6D(I,J)=0.END DOEND DODO J=1,6DO I=1,JDO K=1,6DO L=1,6D(I,J)=D(I,J)+DLOCAL(K,L)*ROTD(I,K)*ROTD(J,L) END DOEND DOD(J,I)=D(I,J)END DOEND DOC----- Total number of sets of slip systems: NSETNSET=NINT(PROPS(25))IF (NSET.LT.1) THENWRITE (6,*) '***ERROR - zero sets of slip systems'STOPELSE IF (NSET.GT.3) THENWRITE (6,*)2 '***ERROR - more than three sets of slip systems'STOPEND IFC----- Implicit integration parameter: THETATHETA=PROPS(145)C----- Finite deformation ?C----- NLGEOM = 0, small deformation theoryC otherwise, theory of finite rotation and finite strain, Users C must declare "NLGEOM" in the input file, at the *STEP card CIF (PROPS(146).EQ.0.) THENNLGEOM=0ELSENLGEOM=1END IFC----- Iteration?C----- ITRATN = 0, no iterationC otherwise, iteration (solving increments of stresses andC solution dependent state variables)CIF (PROPS(153).EQ.0.) THENITRATN=0ELSEITRATN=1END IFITRMAX=NINT(PROPS(154))GAMERR=PROPS(155)NITRTN=-1DO I=1,NTENSDSOLD(I)=0.END DODO J=1,NDDGAMOD(J)=0.DTAUOD(J)=0.DGSPOD(J)=0.DO I=1,3DSPNRO(I,J)=0.DSPDRO(I,J)=0.END DOEND DOC----- Increment of spin associated with the material element: DSPIN C (only needed for finite rotation)CIF (NLGEOM.NE.0) THENDO J=1,3DO I=1,3TERM(I,J)=DROT(J,I)TRM0(I,J)=DROT(J,I)END DOTERM(J,J)=TERM(J,J)+1.D0TRM0(J,J)=TRM0(J,J)-1.D0END DOCALL LUDCMP (TERM, 3, 3, ITRM, DDCMP)DO J=1,3CALL LUBKSB (TERM, 3, 3, ITRM, TRM0(1,J)) END DODSPIN(1)=TRM0(2,1)-TRM0(1,2)DSPIN(2)=TRM0(1,3)-TRM0(3,1)DSPIN(3)=TRM0(3,2)-TRM0(2,3)END IFC----- Increment of dilatational strain: DEVDEV=0.D0DO I=1,NDIDEV=DEV+DSTRAN(I)END DOC----- Iteration starts (only when iteration method is used)1000 CONTINUEC----- Parameter NITRTN: number of iterationsC NITRTN = 0 --- no-iteration solutionCNITRTN=NITRTN+1C----- Check whether the current stress state is the initial stateIF (STATEV(1).EQ.0.) THENC----- Initial stateCC----- Generating the following parameters and variables at initialC state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Unit vectors in initial slip directions SLPDIRC Unit normals to initial slip planes SLPNORCNSLPTL=0DO I=1,NSETISPNOR(1)=NINT(PROPS(25+8*I))ISPNOR(2)=NINT(PROPS(26+8*I))ISPNOR(3)=NINT(PROPS(27+8*I))ISPDIR(1)=NINT(PROPS(28+8*I))ISPDIR(2)=NINT(PROPS(29+8*I))ISPDIR(3)=NINT(PROPS(30+8*I))CALL SLIPSYS (ISPDIR, ISPNOR, NSLIP(I), SLPDIR(1,NSLPTL+1),2 SLPNOR(1,NSLPTL+1), ROTATE)NSLPTL=NSLPTL+NSLIP(I)END DOIF (ND.LT.NSLPTL) THENWRITE (6,*)2 '***ERROR - parameter ND chosen by the present user is less than3 the total number of slip systems NSLPTL'STOPEND IFC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J)SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J)SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOC----- Initial value of state variables: unit normal to a slip planeC and unit vector in a slip directionCSTATEV(NSTATV)=FLOAT(NSLPTL)DO I=1,NSETSTA TEV(NSTA TV-4+I)=FLOAT(NSLIP(I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1STA TEV(IDNOR)=SLPNOR(I,J)IDDIR=IDDIR+1STA TEV(IDDIR)=SLPDIR(I,J)END DOEND DOC----- Initial value of the current strength for all slip systemsCCALL GSLPINIT (STATEV(1), NSLIP, NSLPTL, NSET, PROPS(97))C----- Initial value of shear strain in slip systemsCFIX-- Initial value of cumulative shear strain in each slip systemsDO I=1,NSLPTLSTA TEV(NSLPTL+I)=0.CFIXASTA TEV(9*NSLPTL+I)=0.CFIXBEND DOCFIXASTATEV(10*NSLPTL+1)=0.CFIXBC----- Initial value of the resolved shear stress in slip systemsDO I=1,NSLPTLTERM1=0.DO J=1,NTENSIF (J.LE.NDI) THENTERM1=TERM1+SLPDEF(J,I)*STRESS(J)ELSETERM1=TERM1+SLPDEF(J-NDI+3,I)*STRESS(J) END IFEND DOSTA TEV(2*NSLPTL+I)=TERM1END DOELSEC----- Current stress stateCC----- Copying from the array of state variables STA TVE the following C parameters and variables at current stress state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Current slip directions SLPDIRC Normals to current slip planes SLPNORCNSLPTL=NINT(STA TEV(NSTATV))DO I=1,NSETNSLIP(I)=NINT(STATEV(NSTATV-4+I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1SLPNOR(I,J)=STATEV(IDNOR)IDDIR=IDDIR+1SLPDIR(I,J)=STA TEV(IDDIR)END DOEND DOC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J)SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J)SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOEND IFC----- Slip spin tensor: SLPSPN (only needed for finite rotation)IF (NLGEOM.NE.0) THENDO J=1,NSLPTLSLPSPN(1,J)=0.5*(SLPDIR(1,J)*SLPNOR(2,J)-2 SLPDIR(2,J)*SLPNOR(1,J))SLPSPN(2,J)=0.5*(SLPDIR(3,J)*SLPNOR(1,J)-2 SLPDIR(1,J)*SLPNOR(3,J))SLPSPN(3,J)=0.5*(SLPDIR(2,J)*SLPNOR(3,J)-2 SLPDIR(3,J)*SLPNOR(2,J))END DOEND IFC----- Double dot product of elastic moduli tensor with the slipC deformation tensor (Schmid factors) plus, only for finiteC rotation, the dot product of slip spin tensor with the stress:C DDEMSDCDO J=1,NSLPTLDO I=1,6DDEMSD(I,J)=0.DO K=1,6DDEMSD(I,J)=DDEMSD(I,J)+D(K,I)*SLPDEF(K,J)END DOEND DOEND DOIF (NLGEOM.NE.0) THENDO J=1,NSLPTLDDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(1,J)*STRESS(1)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(2,J)*STRESS(1)IF (NDI.GT.1) THENDDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(1,J)*STRESS(2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(3,J)*STRESS(2)END IFIF (NDI.GT.2) THENDDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(2,J)*STRESS(3)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(3,J)*STRESS(3)END IFIF (NSHR.GE.1) THENDDEMSD(1,J)=DDEMSD(1,J)+SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(2,J)=DDEMSD(2,J)-SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(3,J)*STRESS(NDI+1)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(2,J)*STRESS(NDI+1) END IFIF (NSHR.GE.2) THENDDEMSD(1,J)=DDEMSD(1,J)-SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(3,J)=DDEMSD(3,J)+SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(3,J)*STRESS(NDI+2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(1,J)*STRESS(NDI+2) END IFIF (NSHR.EQ.3) THENDDEMSD(2,J)=DDEMSD(2,J)+SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(3,J)=DDEMSD(3,J)-SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(2,J)*STRESS(NDI+3)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(1,J)*STRESS(NDI+3) END IFEND DOEND IFC----- Shear strain-rate in a slip system at the start of increment:C FSLIP, and its derivative: DFDXSPCID=1DO I=1,NSETIF (I.GT.1) ID=ID+NSLIP(I-1)CALL STRAINRATE (STATEV(NSLPTL+ID), STATEV(2*NSLPTL+ID),2 STA TEV(ID), NSLIP(I), FSLIP(ID), DFDXSP(ID),3 PROPS(65+8*I))END DOC----- Self- and latent-hardening laws。