摆动滚子从动件盘形凸轮机构设计的解析法
- 格式:doc
- 大小:91.50 KB
- 文档页数:8

第1章 平面机构的结构分析解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题图 题图绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
计算下列机构自由度,并说明注意事项。
计算下列机构的自由度,并确定杆组及机构的级别(图a 所示机构分别以构件2、4、8为原动件)。
题图题图第2章 平面机构的运动分析试求图示各机构在图示位置时全部瞬心。
题图在图示机构中,已知各构件尺寸为l AB =180mm , l BC =280mm , l BD =450mm , l CD =250mm , l AE =120mm , φ=30o , 构件AB 上点E 的速度为 v E =150 mm /s ,试求该位置时C 、D 两点的速度及连杆2的角速度ω2 。
在图示的摆动导杆机构中,已知l AB =30mm , l AC =100mm , l BD =50mm , l DE =40mm ,φ1=45o ,曲柄1以等角速度ω1=10 rad/s 沿逆时针方向回转。
求D 点和E 点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题图题图在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30o, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题图图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
(3)在给出的速度和加速度图中,给出构件2上D 点的速度矢量2pd 和加速度矢量2''d p 。
授课教案No任务3.1 凸轮机构的认识一、复习10分钟复习上次课学习内容二、教师导课与课程学习:(1)学习提示,教师介绍本任务的学习内容。
15分钟本项目以直动从动件的盘形凸轮机构为例,在从动件等速运动、等加速等减速运动、余弦加速度运动(简谐运动)规律条件下,分析了凸轮机构中存在的柔性冲击与刚性冲击。
教师介绍本任务的学习内容:凸轮机构的分类;常用术语;从动件的运动规律;凸轮机构的结构形式;常用材料及热处理(2)分小组学习: 40分钟3.1.1常用设备中的凸轮机构1. 凸轮机构的组成如图所示的凸轮机构是由凸轮、从动件和机架等三个基本构件组成的机构。
2.凸轮机构应用实例自动钻床进给机构、冲床凸轮机构等。
3.1.2凸轮机构的分类凸轮机构的类型很多,按凸轮和从动件的形状及其运动形式的不同,凸轮机构的分类方法有以下几种:1.按凸轮形状分类(1)盘形凸轮(2)移动凸轮。
(3)圆柱凸轮2.按从动件形式分类(1)尖顶从动件(2)滚子从动件(3)平底从动件从动件的结构形式3.按从动件的运动形式分类学生发言汇报、记录学习笔记学生发言汇报并记录学习笔记阅读教材和PPT、分组讨论、撰写发言提纲、学生发言汇报,课,记录学习笔记No(1)直动从动件直动从动件指相对于机架作直线往复移动的从动件,如图3.1.1中所示。
直动从动件又分为对心直动从动件和偏置直动从动件。
(2)摆动从动件:绕某一固定转动中心摆动的从动件。
4.按凸轮与从动件的锁合方式分类 (1)力锁合利用从动件的重力、弹簧力或其他外力使从动件与凸轮轮廓保持接触,(2)形锁合利用从动件和凸轮特殊的几何形状来维持接触,例如圆柱凸轮机构是利用滚子与凸轮凹槽两侧面的配合来实现形锁合。
3.1.3凸轮机构的常用术语如下:1.凸轮基圆与基圆半径b r2.凸轮的转角δ凸轮相对于某一位置转过的角度,称为凸轮转角δ。
具体包括推程运动角0δ、远停程运动角S δ回程运动角0′δ和近停程运动角Sδ'。

河北工程大学机电学院机械原理课程设计说明书设计题目:偏置直动滚子从动杆盘型凸轮机构班级:姓名:学号:目录(一)设计题目及设计思路 (1)(二)凸轮基圆半径及滚子尺寸的确定 (1)(三)原始数据分析…………(四)从动杆的运动规律及凸轮轮廓线方程 (3)(五)凸轮机构的廓线设计原理 (4)(六)图解法设计盘型凸轮机构……………(七)检验压力角是否满足许用压力角的要求 (7)(八)机构示意简图 (8)(九)计算机源程序………(十)计算机程序结果及分析 (12)(一)机械原理课程设计的目的和任务一、机械原理课程设计的目的:1、机械原理课程设计是一个重要实践性教学环节。
其目的在于:进一步巩固和加深所学知识;2、培养学生运用理论知识独立分析问题、解决问题的能力;3、使学生在机械的运动学和动力分析方面初步建立一个完整的概念;4、进一步提高学生计算和制图能力,及运用电子计算机的运算能力。
二、机械原理课程设计的任务:1、偏置直动滚子从动杆盘型凸轮机构2、采用图解法设计:凸轮中心到摆杆中心A的距离为20mm,凸轮以逆时针方向等速回转,摆杆的运动规律如表:3、设计要求:①升程过程中,限制最大压力角αmax≤30º,确定凸轮基园半径r0②合理选择滚子半径rr③选择适当比例尺,用几何作图法绘制从动件位移曲线,并画于图纸上;④用反转法绘制凸轮理论廓线和实际廓线,并标注全部尺寸(用A2图纸)⑤将机构简图、原始数据、尺寸综合方法写入说明书4、用解析法设计该凸轮轮廓,原始数据条件不变,要写出数学模型,编制程序并打印出结果备注:凸轮轮廓曲率半径与曲率中心理论轮廓方程()()x xy yϕϕ=⎧⎨=⎩,其中2222////x dx d x d x dy dy d x d y dϕϕϕϕ⎧==⎪⎨==⎪⎩其曲率半径为:3 222 () x y xy xyρ+=--;曲率中心位于:2222()()y x yx xxy xyx x yy xxy xyρρ⎧+=-⎪-⎪⎨+⎪=-⎪-⎩三、课程设计采用方法:对于此次任务,要用图解法和解析法两种方法。


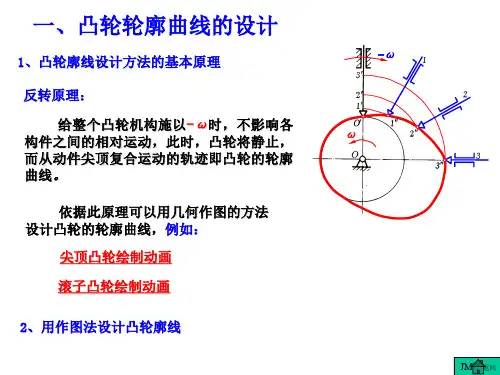

第三章凸轮机构§3-1 凸轮机构的组成和类型一、凸轮机构的组成1、凸轮:具有曲线轮廓或沟槽的构件,当它运动时,通过其上的曲线轮廓与从动件的高副接触,使从动件获得预期的运动。
2、凸轮机构的组成:由凸轮、从动件、机架这三个基本构件所组成的一种高副机构。
二、凸轮机构的类型1.按照凸轮的形状分:空间凸轮机构:盘形凸轮:凸轮呈盘状,并且具有变化的向径。
它是凸轮最基本的形式,应用最广。
移动(楔形)凸轮:凸轮呈板状,它相对于机架作直线移动。
盘形凸轮转轴位于无穷远处。
空间凸轮机构:圆柱凸轮:凸轮的轮廓曲线做在圆柱体上。
2.按照从动件的形状分:(1)尖端从动件从动件尖端能与任意形状凸轮接触,使从动件实现任意运动规律。
结构简单,但尖端易磨损,适于低速、传力不大场合。
(2)曲面从动件:从动件端部做成曲面,不易磨损,使用广泛。
(3)滚子从动件:滑动摩擦变为滚动摩擦,传递较大动力。
(4)平底从动件优点:平底与凸轮之间易形成油膜,润滑状态稳定。
不计摩擦时,凸轮给从动件的力始终垂直于从动件的平底,受力平稳,传动效率高,常用于高速。
缺点:凸轮轮廓必须全部是外凸的。
3.按照从动件的运动形式分:4.按照凸轮与从动件维持高副接触的方法分:(1)力封闭型凸轮机构:利用重力、弹簧力或其它外力使从动件与凸轮轮廓始终保持接触。
封闭方式简单,对从动件运动规律没有限制。
5、其它反凸轮机构:摆杆为主动件,凸轮为从动件。
应用实例:自动铣槽机应用反凸轮实现料斗翻转§3-2 凸轮机构的特点和功能一.凸轮机构的特点1、优点: (1)结构简单、紧凑,具有很少的活动构件,占据空间小。
(2)最大优点是对于任意要求的从动件运动规律都可以毫无困难地设计出凸轮廓线来实现。
2、缺点:由于是高副接触,易磨损,因此多用于传力不大的场合。
二.功能1、实现无特定运动规律要求的工作行程应用实例:车床床头箱中利用凸轮机构实现变速操纵2、实现有特定运动规律要求的工作行程应用实例:自动机床中利用凸轮机构实现进刀、退刀3、实现对运动和动力特性有特殊要求的工作行程应用实例:船用柴油机中利用凸轮机构控制阀门的启闭4、实现复杂的运动轨迹应用实例:印刷机中利用凸轮机构适当组合实现吸纸吸头的复杂运动轨迹§3-3 从动件运动规律设计一.基础知识1、从动件运动规律:从动件的位移、速度、加速度及加速度变化率随时间或凸轮转角变化的规律。



滚子从动件盘形凸轮的压力角滚子从动件盘形凸轮的压力角是指滚子在滚动过程中与凸轮表面接触的角度。
凸轮机构是一种常用的传动机构,通过凸轮的形状和运动来实现从动件的运动。
在凸轮机构中,滚子从动件是一种常见的从动件形式,它通过滚动方式与凸轮表面接触,从而实现运动传递。
滚子从动件盘形凸轮的压力角对于凸轮机构的工作性能具有重要影响。
压力角的大小直接影响着滚子与凸轮接触点的接触状态和接触应力。
合理选择和控制压力角可以有效地提高凸轮机构的工作效率和使用寿命。
压力角的大小与滚子与凸轮表面的接触状态密切相关。
在滚子从动件与凸轮表面接触时,滚子的接触点并不是一个点,而是一个面。
这个接触面上的每一个点都有一个对应的接触角,而这些接触角的平均值就是压力角。
当压力角较小时,滚子与凸轮表面的接触点集中在滚子的边缘,接触面积较小,接触应力较大;当压力角较大时,滚子与凸轮表面的接触点分布更加均匀,接触面积较大,接触应力较小。
因此,合理选择和控制压力角可以使接触应力分布更加均匀,减小接触应力集中,减缓滚子和凸轮表面的磨损和疲劳。
压力角的大小还与滚子从动件的运动平稳性和传动效率有关。
在滚子从动件与凸轮表面接触时,滚子的运动轨迹是沿着凸轮表面的切线方向进行的。
当压力角较小时,滚子的运动轨迹变化较大,运动不稳定,易产生冲击和振动;当压力角较大时,滚子的运动轨迹变化较小,运动更加稳定。
因此,合理选择和控制压力角可以提高滚子从动件的运动平稳性,减小冲击和振动,提高凸轮机构的传动效率。
在实际应用中,选择合适的滚子从动件盘形凸轮的压力角需要考虑多个因素。
首先,要考虑凸轮机构的工作条件和要求,根据凸轮的形状和运动特性确定滚子从动件的类型和数量。
其次,要考虑滚子从动件与凸轮表面的材料和润滑条件,选择合适的滚子直径和凸轮半径。
最后,要结合凸轮机构的传动效率和使用寿命要求,确定合适的压力角范围。
滚子从动件盘形凸轮的压力角对于凸轮机构的工作性能具有重要影响。

摆动滚子从动件盘形凸轮机构设计的解析法①0前言
摆动滚子从动件盘形凸轮机构的设计主要包括基本尺寸的确定[ 1 ]和凸轮轮廓的设计. 基本尺寸主要
是根据压力角确定的, 凸轮轮廓是根据基本尺寸和从动件的运动规律设计的. 过去这两部分的设计常常采
用图解法, 虽然图解法简单、直观, 但精度低, 随着计算机技术的发展和数控机床的普及, 凸轮机构设计的
解析法[ 2 ]正逐步取代传统的图解法.
图1摆动从动件盘形凸轮机构的压力角
1机构压力角的计算
如图1 所示, 为摆动从动件盘形凸轮机
构的压力角示意图. 摆杆长度O 2A = l, 机架
长O 1O 2 = a.
过瞬心P 作摆杆O 2A 的垂直线, 交O 2A
延长线于B 点. 则有:
tan A= BA
PB
=
O 2P cos (W
0 + W) - l
O 2P sin (W
0 + W)
P 点为机构的瞬心, 则有: X
1O 1P = X
2O 2P
X
2
X
1
=
O 1P
O 2P
=
d W
d U=
O 1P
O 1P + a
∴O 1P =
d W
d U a
1 -
d W
d U
O 2P = O 1P + a = a
1 -
d W
d U
∴tan A=
a cos (W
0 + W) - l (1 -
d W
d U)
a sin (W
0 + W)
上式是按X
1 和X
2 同向推出的, 否则tan A=
a cos(W
0 + W) - l (1 +
d W
d U)
a sin (W
0 + W)
工程设计中, 必须对凸轮机构的最大压力角加以限制, 凸轮机构的最大压力角应小于许用压力角.
2机构基本尺寸的确定
图2确定基本尺寸示意图
2. 1基本尺寸确定的方法
图2 中O 2 为摆杆的回转中心,A 为滚子摆杆的滚子中
心. A 0 到A 6 为按给定运动规律W= f (U) 作出的摆杆各个
位置, 位置个数可任选. 在摆杆的每位置上截取长为l
d W
d U,
其中l 为摆杆长, W为摆杆摆角, U为凸轮转角.
截取方法为: 若摆杆与凸轮转向相同, 由A 点向着回转
中心O 2 取; 若摆杆与凸轮转向相反, 由A 点背着回转中心
O 2 取.
图2 中凸轮与摆杆的相对转动关系为: 凸轮逆时针转,
摆杆推程逆时针转, 回程顺时针转. 若推程许用压力角为
[A], 回程许用压力角为[A′], 线段A 1a1,A 2a2, ⋯为对应推
程截取的; 线段A 1a′1,A 2a′2, ⋯为对应回程截取的. 过端点
a1, A
2, ⋯和a′
1 , a′2, ⋯作与相应的摆杆成(90°- [A]) 或(90°- [A]) 的直线, 简称a 斜线和a′斜线. 这些线的包络线É , Ê , Ë 所包围的阴影区域为满足许用压力角的前提下, 凸轮回转中心的可选区域. O ′1A 0 为最
小基圆半径,O ′1O 2 为对应的中心距.
以O 2 为原点,O 2A 0 为x 轴, 使A 1,A 2, ⋯各点y 坐标为正值的方向为y 轴, 建立直角坐标系. 若已知包
络线É , Ê , Ë 的方程, 则可知凸轮回转中心O 1 的许用区域.
2. 2包络线方程的求法及基本尺寸的确定
在图2 中, 任意a 斜线的斜率为k = tan A= cot (- [A] - W) , 各a 点的坐标为:
x = l (1 -
d W
d U cos W) , y = l (1 -
d W
d U) sin W, 由点斜式可写出任意a 斜线的方程. 同理, 对任意a′斜线, 斜率为
k′= cot ( [A] - W) , 各a′点的坐标为: x ′= l (1 +
d W
d U) cos W, y ′= l (1 +
d W
d U) sin W, 同样可写出任意a′斜线的
方程.
由以上包络线方程相交, 可求出凸轮回转中心O 1 的许用区域, 此过程较繁, 可上机求解. 在O 1 的取值
范围内任取一点(x , y ) 作为凸轮的回转中心, 则凸轮的基圆半径可确定:
图3反转法设计凸轮的轮廓
r0 = ( l - x ) 2 + y 2.
3凸轮轮廓的设计
图3 中, 直角坐标系的原点位于凸轮的回转中心
O 1 点. 机架长为a, 摆杆长为l. 摆动滚子从动件的初始
位置在行程起始位置1 时的O 20A 0. 反转U角后, 到达位
置2 的O 2A. 凸轮与从动件的接触点A 0 到达A 点,A ′A
为对应的弧位移s, 对应从动件的摆角W.
从动件O 2A
的运动可以看作O 20A 0 绕O 1 点反转U角, 到达O 2A ′位
置,O 2A ′再摆动W角到达O 2A 位置. 从动件O 2A 的运动
还可以看作O 20A 0 绕O 20 点反转(U+ W) 角, 到达O 20A ″
点,O 20A ″再平移到O 2A 位置. 设A 0 点的坐标为(x A 0,
第1 期毕艳丽等: 摆动滚子从动件盘形凸轮机构设计的解析法37
y A 0) ,A 点的坐标为(x , y ) ,O 2A 的复合运动可用下述的坐标旋转和平移变换来实现.
y
=
cos(U+ W) sin (U+ W)
- sin (U+ W) cos (U+ W)
x A 0 - x O20
y A 0 - y O20
+
x O2
y O2
(1)
式中: x O 2 = a sin U, y O 2 = a co s U, x O20 = 0, y O20 = a, x A 0 = - l sin W 0, y A 0 = a - l co s W
W
0 为摆杆的初始位置角, 其值为W
0 = arccos
a2 + l2 - r20
2al
将其代入方程(1) 并整理, 可得理论廓线方程:
x = a sin U- l sin (U+ W+ W
0) ; y = a cos U- l cos (U+ W+ W
0)
则其实际廓线方程[ 2 ] 为:
x A= x ±r r
d y
d U
d x
d U
2
+
d y
d U
2
, y A= y ºr r
d x
d U
d x
d U
2
d y
d U
2
其中r r 为滚子半径; 滚子圆的包络线有两条, 上面一组符号用于求解外凸轮的包络线方程, 下面一组
符号用于求解内凸轮的包络线方程.
4结束语
本文利用解析法设计摆动滚子从动件盘形凸轮机构, 适用于用计算机辅助运算设计凸轮机构, 其精度
高, 使用方便, 特别适合高精度凸轮机构的设计.
参考文献:
[ 1 ]尚锐等. 摆动从动件盘形凸轮机构基本尺寸确定的解析法[J ]. 辽宁工学院学报, 1999, (6) : 29- 32.
[ 2 ]邹慧君等. 机械原理[M ]. 北京: 高等教育出版社, 1999, 117- 132.。