2017届中考数学第一单元数与式第1讲实数知识梳理(冀教版)

第一讲 数与式第1课时 实数的有关概念考点一、实数的概念及分类 〔3分〕正有理数有理数 零 有限小数和无限循环小数 实数 负有理数 正无理数无理数 无限不循环小数〔π〕、开方开不尽的数 负无理数凡能写成)0p q ,p (p q≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；考点二、实数的倒数、相反数和绝对值 〔3分〕2、数轴：数轴是规定了原点、正方向、单位长度的一条直线.3、相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0； (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4、绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 绝对值的问题经常分类讨论；5、倒数假设ab =1⇔ a 、b 互为倒数；假设ab =-1⇔a 、b 互为负倒数。

倒数等于本身的数是1和-1。

零没有倒数。

11a a-=考点三、平方根、算数平方根和立方根 〔3—10分〕 6、平方根①如果一个数的平方等于a ，那么这个数就叫做a 的平方根〔或二次方跟〕。

一个数有两个平方根，他们互为相反数；零的平方根是零；负数没有平方根。

正数a 的平方根记做“a ±〞。

②算术平方根正数a 的正的平方根叫做a 的算术平方根，记作“a 〞。

正数和零的算术平方根都只有一个，零的算术平a ，2a =；注意a 的双重非负性：0≥a a ≥07、立方根如果一个数的立方等于a ，那么这个数就叫做a 的立方根〔或a 的三次方根〕。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

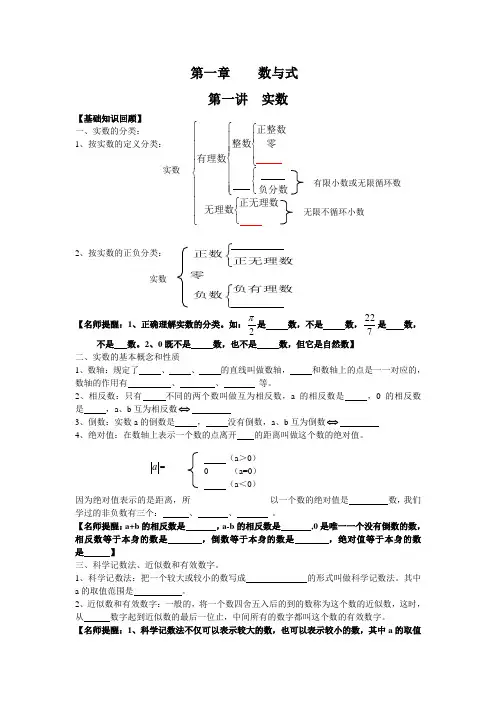
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类： 1、按实数的定义分类： 实数 有限小数或无限循环数2、按实数的正负分类：实数【名师提醒：1、正确理解实数的分类。

如：2π是 数，不是 数，722是 数，不是 数。

2、0既不是 数，也不是 数，但它是自然数】二、实数的基本概念和性质1、数轴：规定了 、 、 的直线叫做数轴， 和数轴上的点是一一对应的，数轴的作用有 、 、 等。

2、相反数：只有 不同的两个数叫做互为相反数，a 的相反数是 ，0的相反数是 ，a 、b 互为相反数⇔3、倒数：实数a 的倒数是 ， 没有倒数，a 、b 互为倒数⇔4、绝对值：在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。

a =因为绝对值表示的是距离，所以一个数的绝对值是 数，我们学过的非负数有三个： 、 、 。

【名师提醒：a+b 的相反数是 ，a-b 的相反数是 ,0是唯一一个没有倒数的数，相反数等于本身的数是 ，倒数等于本身的数是 ，绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。

1、科学记数法：把一个较大或较小的数写成 的形式叫做科学记数法。

其中a 的取值范围是 。

2、近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从 数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。

【名师提醒：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 （a ＞0） （a ＜0） 0 （a=0）范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。

中考数学复习数与式知识点总结第一部分：教材知识梳理-系统复第一单元：数与式第1讲：实数知识点一：实数的概念及分类1.实数是按照定义和正负性来分类的。

其中，既不属于正数也不属于负数的数是零。

无理数有几种常见形式：含π的式子是正有理数；无限不循环小数是无理数；开方开不尽的数是无理数；三角函数型的数是实数。

有理数包括正有理数、负有理数和零。

负无理数和正无理数的定义很明确。

2.在判断一个数是否为无理数时，需要注意开得尽方的含根号的数属于无理数，而开得尽的数属于有理数。

3.数轴有三个要素：原点、正方向和单位长度。

实数与数轴上的点一一对应，数轴右边的点表示的数总比左边的点表示的数大。

4.相反数是具有相反符号的两个数，它们的和为0.数轴上表示互为相反数的两个点到原点的距离相等。

5.绝对值是一个数到原点的距离。

它有非负性，即绝对值大于等于0.若|a|+b2=0，则a=b=0.绝对值等于该数本身的数是非负数。

知识点二：实数的相关概念2.数轴是一个直线，用来表示实数。

数轴上的每个点都对应着一个实数，反之亦然。

3.相反数是具有相反符号的两个数，它们的和为0.4.绝对值是一个数到原点的距离。

它有非负性，即绝对值大于等于0.5.倒数是乘积为1的两个数互为倒数。

a的倒数是1/a(a≠0)。

6.科学记数法是一种表示实数的方法，其中1≤|a|＜10，n为整数。

确定n的方法是：对于数位较多的大数，n等于原数的整数位减去1；对于小数，写成a×10n，1≤|a|＜10，n等于原数中左起至第一个非零数字前所有零的个数（含小数点前面的一个）。

7.近似数是一个与实际数值很接近的数。

它的精确度由四舍五入到哪一位来决定。

例：用科学记数法表示为2.1×104.19万用科学记数法表示为1.9×10^5，0.0007用科学记数法表示为7×10^-4.知识点三：科学记数法、近似数科学记数法是一种表示极大或极小数的方法，它的基本形式是a×10^n，其中1≤a<10，n为整数。

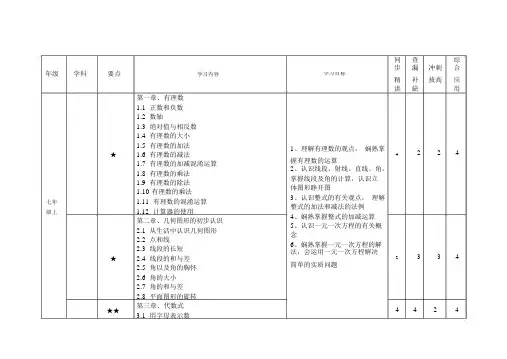
年级学科要点学习内容第一章、有理数1.1正数和负数1.2数轴1.3绝对值与相反数1.4有理数的大小1.5有理数的加法★ 1.6有理数的减法1.7有理数的加减混淆运算1.8有理数的乘法1.9有理数的除法1.10 有理数的乘法七年 1.11有理数的混淆运算级上 1.12计算器的使用第二章、几何图形的初步认识2.1从生活中认识几何图形2.2点和线2.3线段的长短★ 2.4线段的和与差2.5角以及角的胸怀2.6角的大小2.7角的和与差2.8平面图形的旋转★★第三章、代数式3.1用字母表示数同查综步漏冲刺合学习目标补拔高应精讲缺用1、理解有理数的观点，娴熟掌2244握有理数的运算2、认识线段、射线、直线、角，掌握线段及角的计算，认识立体图形睁开图3、认识整式的有关观点，理解整式的加法和减法的法例4、娴熟掌握整式的加减运算5、认识一元一次方程的有关概念6、娴熟掌握一元一次方程的解法，会运用一元一次方程解决3342简单的实质问题4424七年级下3.2代数式3.3代数式的值第四章、整式的加减4.1整式★★ 4.2 归并同类项22244.3去括号4.4整式的加减第五章、一元一次方程5.1一元一次方程★★★ 5.2 等式的基天性质44245.3解一元一次方程5.4一元一次方程的应用第六章、二元一次方程组1、掌握代入消元法和加减消元6.1二元一次方程组法，能选择适合的方法解二元★★★ 6.2 二元一次方程组的解法一次方程组，会运用二元一次22226.3二元一次方程组的应用方程组解决简单的实质问题6.4简单的三元一次方程组、认识订交线的观点及性质，2第七章、订交线与平行线掌握平行线的性质与判断，能7.1命题运用平移的知识解决简单问题7.2订交线3、理解整式乘除法的运算法★★★7.3 平行线则，会进行简单的整式乘除法24247.4平行线的判断运算，选择适合的方法进行因7.5平行线的性质式分解7.6图形的平移4、会解一元一次不等式和由两第八章、整式的乘法个一元一次不等式构成的不等★★★8.1同底数幂的乘法式组，能依据详细问题中的数44248.2幂的乘方与积的乘方量关系，用列出一元一次不等8.3同底数幂的除法式解决简单问题。

冀教版初中数学定理、公式汇编一、数与代数 1． 数与式（1） 实数 实数的性质：①实数a 的相反数是—a ，实数a 的倒数是a1（a ≠0）； ②实数a 的绝对值：⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a③正数大于0，负数小于0，两个负实数，绝对值大的反而小。

二次根式：①积与商的方根的运算性质：b a ab ⋅=（a ≥0，b ≥0）；ba ba=（a ≥0，b ＞0）；②二次根式的性质：⎩⎨⎧<-≥==)0()0(2a a a a a a （2）整式与分式①同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即n m n ma a a+=⋅（m 、n 为正整数）；②同底数幂的除法法则：同底数幂相除，底数不变，指数相减，即n m n ma a a-=÷（a ≠0，m 、n 为正整数，m>n ）； ③幂的乘方法则：幂的乘方，底数不变，指数相乘，即nn n ba ab =)(（n 为正整数）；④零指数：10=a （a ≠0）；⑤负整数指数：nna a 1=-（a ≠0，n 为正整数）；⑥平方差公式：两个数的和与这两个数的差的积等于这两个数的平方，即22))((b a b a b a -=-+；⑦完全平方公式：两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即2222)(b ab a b a +±=±；分式①分式的基本性质：分式的分子和分母都乘以（或除以）同一个不等于零的整式，分式的值不变，即mb ma b a ⨯⨯=；mb ma b a ÷÷=，其中m 是不等于零的代数式； ②分式的乘法法则：bdacd c b a =⋅； ③分式的除法法则：)0(≠=⋅=÷c bc adc d b a d c b a ；④分式的乘方法则：nnn ba b a =)(（n 为正整数）；⑤同分母分式加减法则：c ba cbc a ±=±； ⑥异分母分式加减法则：bccdab b d c a ±=±； 2． 方程与不等式①一元二次方程02=++c bx ax(a ≠0）的求根公式：)04(2422≥--+-=ac b aac b b x ②一元二次方程根的判别式：ac b 42-=∆叫做一元二次方程02=++c bx ax（a ≠0）的根的判别式：⇔>∆0方程有两个不相等的实数根；⇔=∆0方程有两个相等的实数根； ⇔<∆0方程没有实数根；③一元二次方程根与系数的关系：设1x 、2x 是方程02=++c bx ax （a ≠0）的两个根，那么1x +2x =ab-，1x 2x =a c ；不等式的基本性质：①不等式两边都加上（或减去）同一个数或同一个整式，不等号的方向不变；②不等式两边都乘以（或除以）同一个正数，不等号的方向不变；③不等式两边都乘以（或除以）同一个负数，不等号的方向改变； 3． 函数一次函数的图象：函数y=kx+b(k 、b 是常数，k ≠0)的图象是过点（0，b ）且与直线y=kx 平行的一条直线；一次函数的性质：设y=kx+b （k ≠0），则当k>0时，y 随x 的增大而增大；当k<0， y 随x 的增大而减小；正比例函数的图象：函数kx y =的图象是过原点及点（1，k ）的一条直线。

2017届中考数学第一单元数与式第1讲实数知识梳理（冀教版）第一部分教材知识梳理&#8226;系统复习第一单元数与式第1讲实数知识点一：实数的概念及分类关键点拨及对应举例1实数（1）按定义分（2）按正、负性分正有理数有理数0 有限小数或正实数负有理数无限循环小数实数0实数正无理数负实数无理数无限不循环小数负无理数（1）0既不属于正数，也不属于负数（2）无理数的几种常见形式判断：①含π的式子；②构造型：如3010010001…（每两个1之间多个0）就是一个无限不循环小数；③开方开不尽的数：如，；④三角函数型：如sin60°，tan2°（3）失分点警示：开得尽方的含根号的数属于有理数，如=2，=-3，它们都属于有理数知识点二：实数的相关概念2数轴（1）三要素：原点、正方向、单位长度（2）特征：实数与数轴上的点一一对应；数轴右边的点表示的数总比左边的点表示的数大例：数轴上-2表示的点到原点的距离是23相反数（1）概念：只有符号不同的两个数（2）代数意义：a、b互为相反数&#61683; a+b=0（3）几何意义：数轴上表示互为相反数的两个点到原点的距离相等a的相反数为-a，特别的0的绝对值是0例：3的相反数是-3，-1的相反数是14绝对值（1）几何意义：数轴上表示的点到原点的距离（2）运算性质：|a|= a (a≥0)；|a-b|= a-b(a≥b)-a(a＜0) b-a(a＜b)（3）非负性：|a|≥0，若|a|+b2=0,则a=b=0（1）若|x|=a（a≥0），则x=±a （2）对绝对值等于它本身的数是非负数例：的绝对值是；|-2|=2；绝对值等于3的是±3;|1-|=-1倒数（1）概念：乘积为1的两个数互为倒数a的倒数为1/ a(a≠0)（2）代数意义：ab=1&#61683;a,b互为倒数例：-2的倒数是-1/2 ；倒数等于它本身的数有±1知识点三：科学记数法、近似数6科学记数法（1）形式：a×10n,其中1≤|a|＜10，n为整数（2）确定n的方法：对于数位较多的大数，n等于原数的整数为减去1；对于小数，写成a×10-n，1≤|a|＜10，n等于原数中左起至第一个非零数字前所有零的个数（含小数点前面的一个）例：21000用科学记数法表示为2 1×104；19万用科学记数法表示为19×10；00007用科学记数法表示为7×10-4 7近似数（1）定义：一个与实际数值很接近的数（2）精确度：由四舍五入到哪一位，就说这个近似数精确到哪一位例：31419精确到百分位是3 14；精确到0001是3142知识点四：实数的大小比较8 实数的大小比较（1）数轴比较法：数轴上的两个数，右边的数总比左边的数大（2）性质比较法：正数＞0＞负数；两个负数比较大小，绝对值大的反而小（3）作差比较法：a-b＞0&#61683;a＞b；a-b=0&#61683;a=b；a-b＜0&#61683;a＜b（4）平方法：a＞b≥0&#61683;a2＞b2例：把1，-2,0，-23按从大到小的顺序排列结果为___1＞0＞-2＞-23_知识点五：实数的运算9常见运算乘方几个相同因数的积; 负数的偶（奇）次方为正（负）例：（1）计算：1-2-6=_-7__;(-2)2=___4__;3-1=_1/3_;π0=__1__;(2)64的平方根是_±8__,算术平方根是__8_,立方根是__4__[失分点警示：类似“的算术平方根”计算错误例：相互对比填一填：16的算术平方根是4___,的算术平方根是___2__零次幂a0=_1_(a≠0)负指数幂a-p=1/ap（a≠0，p为整数）平方根、算术平方根若x2=a（a≥0）,则x= 其中是算术平方根立方根若x3=a,则x=10混合运算先乘方、开方，再乘除，最后加减；同级运算，从左向右进行；如有括号，先做括号内的运算，按小括号、中括号、大括号一次进行计算时，可以结合运算律，使问题简单化。

2017中考数学总复习考点归纳：实数2017中考数学总复习考点归纳：实数一、实数的分类（2）实数的绝对值是一个非负数，从数轴上看，一个实数的绝对值，就是数轴上表示这个数的点到原点的距离。

（3）去掉绝对值符号（化简）必须要对绝对值符号里面的实数进行数性（正、负）确认，再去掉绝对值符号。

4、n次方根（4）一个正数有一个正的立方根；0的立方根是0；一个负数有一个负的立方根。

三、实数与数轴1、数轴：规定了原点、正方向、单位长度的直线称为数轴。

原点、正方向、单位长度是数轴的三要素。

2、数轴上的点和实数的对应关系：数轴上的每一个点都表示一个实数，而每一个实数都可以用数轴上的唯一的点来表示。

实数和数轴上的点是一一对应的关系。

四、实数大小的比较1、在数轴上表示两个数，右边的数总比左边的数大。

2、正数大于0；负数小于0；正数大于一切负数；两个负数绝对值大的反而小。

五、实数的运算1、加法：（1）同号两数相加，取原来的符号，并把它们的绝对值相加；（2）异号两数相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

可使用加法交换律、结合律。

2、减法：减去一个数等于加上这个数的相反数。

3、乘法：（1）两数相乘，同号取正，异号取负，并把绝对值相乘。

（2）n个实数相乘，有一个因数为0，积就为0；若n个非0的实数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数为奇数个时，积为负。

（3）乘法可使用乘法交换律、乘法结合律、乘法分配律。

4、除法：（1）两数相除，同号得正，异号得负，并把绝对值相除。

（2）除以一个数等于乘以这个数的倒数。

（3）0除以任何数都等于0，0不能做被除数。

5、乘方与开方：乘方与开方互为逆运算。

6、实数的运算顺序：乘方、开方为三级运算，乘、除为二级运算，加、减是一级运算，如果没有括号，在同一级运算中要从左到右依次运算，不同级的运算，先算高级的运算再算低级的运算，有括号的先算括号里的运算。

第一单元数与式第1讲实数知识点一：实数概念及分类关键点拨及对应举例1.实数〔1〕按定义分〔2〕按正、负性分正有理数有理数 0 有限小数或正实数负有理数无限循环小数实数 0实数正无理数负实数无理数无限不循环小数负无理数〔1〕0既不属于正数，也不属于负数.〔2〕无理数几种常见形式判断：①含π式子；②…〔每两个1之间多个0〕就是一个无限不循环小数；③开方开不尽数：如，；④三角函数型：如sin60°，tan25°.〔3〕失分点警示：开得尽方含根号数属于有理数，如=2，=-3，它们都属于有理数.知识点二：实数相关概念2.数轴〔1〕三要素：原点、正方向、单位长度〔2〕特征：实数与数轴上点一一对应；数轴右边点表示数总比左边点表示数大例：.3.相反数〔1〕概念：只有符号不同两个数〔2〕代数意义：a、b互为相反数⇔ a+b=0〔3〕几何意义：数轴上表示互为相反数两个点到原点距离相等a相反数为-a，特别0绝对值是0.例：3相反数是-3，-1相反数是1.4.绝对值〔1〕几何意义：数轴上表示点到原点距离〔2〕运算性质：|a|= a (a≥0)； |a-b|= a-b(a≥b)-a(a＜0). b-a(a＜b)〔3〕非负性：|a|≥0，假设|a|+b2=0,那么a=b=0.〔1〕假设|x|=a〔a≥0〕，那么x=±a.〔2〕对绝对值等于它本身数是非负数.例：5绝对值是5；|-2|=2；绝对值等于3是±3;|1-|=-1.5.倒数1/a(a≠0)〔2〕代数意义：ab=1⇔a,b互为倒数例：-2倒数是-1/2；倒数等于它本身数有±1.知识点三：科学记数法、近似数6.科学记数法〔1〕形式：a×10n,其中1≤|a|＜10，n为整数〔2〕确定n方法：对于数位较多大数，n等于原数整数为减去1；对于小数，写成a×10-n，1≤|a|＜10，n等于原数中左起至第一个非零数字前所有零个数〔含小数点前面一个〕例：21000用科学记数法表示为2.1×104；19万用科学记数法表示为×1057×10-4.7.近似数〔1〕定义：一个与实际数值很接近数.〔2〕准确度：由四舍五入到哪一位，就说这个近似数准确到哪一位.例：3.143.142.知识点四：实数大小比拟8.实数大小比拟〔1〕数轴比拟法：数轴上两个数，右边数总比左边数大.〔2〕性质比拟法：正数＞0＞负数；两个负数比拟大小，绝对值大反而小.〔3〕作差比拟法：a-b＞0⇔a＞b；a-b=0⇔a=b；a-b＜0⇔a＜b.〔4〕平方法：a＞b≥0⇔a2＞b2.例：_1＞0＞-2＞-2.3_.知识点五：实数运算9. 常见运算乘方几个一样因数积; 负数偶〔奇〕次方为正〔负〕例：〔1〕计算：1-2-6=_-7__;(-2)2=___4__;3-1=_1/3_;π0=__1__;(2)64平方根是_±8__,算术平方根是__8_,立方根是__4__.失分点警示：类似“算术平方根〞计算错误. 例：相互比照填一填：16算术平方根是4___,算术平方根是___2__.零次幂a0=_1_(a≠0)负指数幂a-p=1/a p〔a≠0，p为整数〕平方根、算术平方根假设x2=a〔a≥0〕,那么x=a.其中a是算术平方根.立方根假设x3=a,那么x=3a.10.混合运算先乘方、开方，再乘除，最后加减；同级运算，从左向右进展；如有括号，先做括号内运算，按小括号、中括号、大括号一次进展.计算时，可以结合运算律，使问题简单化。

第一章数与式第一节实数的有关概念题，原点取的位置不4纵观河北近五年中考，实数的有关概念每年必考，以选择、填1实数的概念及分类1．(2016河北中考)关于12的叙述，错误的是( A ) A .12是有理数B ．面积为12的正方形边长是12C .12＝2 3D ．在数轴上可以找到表示12的点2．(2016保定八中模拟)下列各数中，3.141 59，－38，0.131 131 113…，－π，25，－17，无理数有( B )A ．1个B ．2个C ．3个D ．4个数轴3．(2017河北中考)在一条不完整的数轴上从左到右有点A ，B ，C ，其中AB ＝2，BC ＝1，如图所示．设点A ，B ，C 所对应数的和是p.(1)若以B 为原点，写出点A ，C 所对应的数，并计算p 的值；若以C 为原点，p 又是多少？ (2)若原点O 在图中数轴上点C 的右边，且CO ＝28，求p. 解：(1)若以B 为原点，则C 表示1，A 表示－2， ∴p ＝1＋0－2＝－1；若以C 为原点，则A 表示－3，B 表示－1， ∴p ＝－3－1＋0＝－4；(2)若原点O 在图中数轴上点C 的右边，且CO ＝28，则C 表示－28，B 表示－29，A 表示－31， ∴p ＝－31－29－28＝－88.绝对值、相反数、倒数4．(2017河北中考)如图为张小亮的答卷，他的得分应是( B )姓名__张小亮__ 得分__？__填空(每小题20分，共100分) ①－1的绝对值是__1__； ②2的倒数是__－2__； ③－2的相反数是__2__； ④1的立方根是__1__；⑤－1和7的平均数是__3__．A ．100分B ．80分C ．60分D ．40分 5．(2015河北中考)下列说法正确的是( A ) A ．1的相反数是－1 B ．1的倒数是－1 C ．1的立方根是±1 D ．－1是无理数 6．(2014河北中考)－2是2的( B ) A ．倒数 B ．相反数 C ．绝对值 D ．平方根7．(2015河北中考)若|a|＝2 0150，则a ＝__±1__．科学记数法8．(2017石家庄40中模拟)－12的倒数为( C )A .12B ．2C ．－2D ．－19．(2017唐山中考模拟)－2的绝对值是( A )A ．2B ．－2C .12D ．－1210．(2017河北中考)把0.081 3写成a×10n(1≤a＜10，n 为整数)的形式，则a 为( D ) A ．1 B ．－2C ．0.813D ．8.1311．(2013河北中考)截至2013年3月底，某市人口总数已达到4 230 000人．将4 230 000用科学记数法表示为( B )A ．0.423×107B ．4.23×106C ．42.3×105D ．423×10412．(2014河北中考)如图，点O ，A 在数轴上表示的数分别是0，0.1.将线段OA 分成100等份，其分点由左向右依次为M 1，M 2，……，M 99； 再将线段OM 1分成100等份，其分点由左向右依次为N 1，N 2，……，N 99； 继续将线段ON 1分成100等份，其分点由左向右依次为P 1，P 2，……，P 99.则点P 37所表示的数用科学记数法表示为__3.7×10－6__．,中考考点清单实数的有关概念及分类1．整数和__分数__统称为有理数；__无限不循环小数__叫无理数；有理数和无理数统称为__实数__．【易错警示】(1)任何分数都是有理数，如23，－45等；(2)常见的几种无理数：①根号型，如5，8等开方开不尽的数；②构造型，如0.101 001 000 1…；③π及含π的数，如π，π＋4等．2．分类：(1)按定义分类实数⎩⎪⎪⎨⎪⎪⎧有理数⎩⎪⎨⎪⎧整数⎩⎪⎨⎪⎧正整数负整数分数⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫正分数负分数有限小数和 无限循环 小数无理数⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫正无理数负无理数无限不循环 小数 (2)按正负分类实数⎩⎪⎨⎪⎧正实数⎩⎪⎨⎪⎧ 正有理数 ⎩⎪⎨⎪⎧正整数正分数正无理数零 负实数 ⎩⎪⎨⎪⎧负有理数⎩⎪⎨⎪⎧负整数负分数负无理数3．数轴：数轴的三要素是：__原点__、__正方向__、__单位长度__；数轴上的点和__实数__是一一对应的． 4．相反数：(1)实数a 的相反数是__－a__(a 与b 互为相反数⇔a ＋b ＝__0__)；(2)相反数的几何意义：在数轴上，表示相反数的两个点位于原点的__两侧__，且到原点的距离__相等__． 5．绝对值：(1)在数轴上表示一个数的点离原点的__距离__叫做这个数的绝对值；(2)|a|＝⎩⎪⎨⎪⎧ a （a≥0）， －a （a<0），即正数的绝对值是__它本身__，0的绝对值是__0__，负数的绝对值是它的__相反数__；(3)一个数的绝对值是__非负__数，即|a|__≥__0. 6．倒数：(1)若两个非零实数a ，b 的积为1，即__ab ＝1__，则a 与b 互为倒数，反之亦然；(2)非零实数a 的倒数为__1a__；__0__没有倒数．近似数和科学记数法7．科学记数法：把一个数写成__a ×10n__的形式(其中__1__≤|a|<__10__，n 为整数)，这种记数法称为科学记数法．例如574 000记作__5.74×105__，－0.000 737记作__－7.37×10－4__．8．精确度与近似数：近似数与准确数的接近程度通常用__精确度__表示；近似数一般由__四舍五入__取得，__四舍五入__到哪一位，就说这个近似数精确到哪一位，如 5.374 6精确到0.001或精确到千分位是__5.375__.4.46万是精确到__百__位．【方法点拨】用科学记数法表示一个数时，需要从两个方面入手，关键是确定a 和n 的值． (1)a 值的确定：1≤|a|<10； (2)n 值的确定：①当原数大于或等于10时，n 等于原数的整数位数减1；②当原数大于0且小于1时，n 是负整数，它的绝对值等于原数左起第一位非零数字前所有零的个数(含小数点前的零)；③有计数(量)单位的科学记数法，先把数字单位转化为纯数字表示，再用科学记数法表示．常用的计数单位有：1亿＝108，1万＝104，计量单位有：1 mm ＝10－3 m ，1 nm ＝10－9m等．,中考重难点突破无理数的识别【例1】(2017烟台中考)下列实数中的无理数是( D )A .9B ．πC ．0D .13【解析】9，0，13都是有理数，π是无理数．【答案】B1．(2016保定十七中二模)下列实数中，有理数是( D )A .8B .34C .π2D ．0.101 001 001实数的相关概念【例2】(2017安顺中考)－2 017的绝对值是( D ) A ．2 017 B ．－2 017C ．±2 017D ．－12 017【解析】－2 017的绝对值是2 017. 【答案】A2．(2017河北中考改编)下面是欧阳夏天同学做的5道题，他做对了几个( C )(1)－16的倒数是__－6__；(2)3－8＝__－2__；(3)－6的相反数是__6__； (4)－6的绝对值是__6__； (5)－2的平方是__－4__． A ．2个 B ．3个 C ．4个 D ．5个3．(宜昌中考)如果“盈利5%”记作“＋5%”，那么－3%表示( A ) A ．亏损3% B ．亏损8% C ．盈利2% D ．少赚3%科学记数法【例3】(2017徐州中考)肥皂泡的泡壁厚度大约是0.000 000 71 m ，数字0.000 000 71用科学记数法表示为( A )A ．7.1×107B ．0.71×10－6C ．7.1×10－7D ．71×10－8【解析】数字0.000 000 71用科学记数法表示为7.1×10－7.【答案】C4．把－0.071 7写成a×10n(1≤a＜10，n 为整数)的形式，则a 为( D ) A ．7 B ．7.17 C ．－7 D ．－7.175．(绍兴中考)据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为( A )A ．3.386×108B ．0.338 6×109C ．33.86×107D ．3.386×109数轴的相关知识【例4】(2017石家庄40中模拟)如图所示，数轴上点P 所表示的数可能是( B )A . 6B .10C .15D .31【解析】数轴和无理数的综合考查，估计10与15在数轴上哪个离3更近些． 【答案】B6．(2017河北中考改编)在一条不完整的数轴上，从左到右有A，B，C三点，其中AB＝3，BC＝1，如图所示，设点A，B，C所对应数的和是P.(1)若以C为原点，则A表示__－4__，B表示__－1__，P的值__－5__；(2)若原点O在图中数轴点A的左边，且BO＝20，则P的值__58__．。