2019版二轮复习数学：第一部分 第二层级 重点增分专题十三 选修4-4 坐标系与参数方程

选修4­4 坐标系与参数方程1. （选修44P 11例5改编）在直角坐标系中，点P 的坐标为（－2，－6），求点P 的极坐标.解：ρ＝（－2）2＋（－6）2＝22，tan θ＝－6－2＝3，又点P 在第三象限，得θ＝43π，即P （22，4π3）.2. （选修44P 17习题9改编）在极坐标系中，已知A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，求△AOB（其中O 为极点）的面积. 解：由题意A ，B 两点的极坐标分别为⎝⎛⎭⎪⎫3，π3，⎝ ⎛⎭⎪⎫4，π6，得△AOB 的面积S △AOB ＝12OA ·OB ·sin ∠AOB ＝12×3×4×sin π6＝3.3. 在极坐标系中，求圆ρ＝2cos θ的圆心到直线2ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝1的距离. 解：圆的普通方程为（x －1）2＋y 2＝1，直线的普通方程为3x ＋y －1＝0，∴ 圆心到直线的距离为d ＝3－12.4. （选修44P 19例1改编）在极坐标系中，求过圆ρ＝－2sin θ的圆心，且与极轴平行的直线的极坐标方程.解：由题意，圆ρ＝－2sin θ，可化为ρ2＝－2ρsin θ，化成直角坐标方程为x 2＋y 2＝－2y ，即x 2＋（y ＋1）2＝1，圆心是（0，－1），所求直角坐标方程为y ＝－1，所以其极坐标方程为ρsin θ＝－1.5. 在极坐标系中，求圆ρ＝4上的点到直线ρ（cos θ＋3sin θ）＝8的距离的最大值.解：把ρ＝4化为直角坐标方程为x 2＋y 2＝16，把ρ（cos θ＋3sin θ）＝8化为直角坐标方程为x ＋3y －8＝0，∴ 圆心（0，0）到直线的距离为d ＝82＝4，∴ 直线和圆相切，∴ 圆上的点到直线的最大距离是8.1. 极坐标系是由距离（极径）与方向（极角）确定点的位置的一种方法，由于终边相同的角有无数个且极径可以为负数，故在极坐标系下，有序实数对（ρ，θ）与点不一一对应.这点应与直角坐标系区别开来.2. 在极坐标系中，同一个点M 的坐标形式不尽相同，M （ρ，θ）可表示为（ρ，θ＋2n π）（n∈Z ）.3. 在极坐标系中，极径ρ可以为负数，故M （ρ，θ）可表示为（－ρ，θ＋（2n ＋1）π）（n∈Z ）.4. 特别地，若ρ＝0，则极角θ可取任意角.5. 建立曲线的极坐标方程，其基本思路与在直角坐标系中大致相同，即设曲线上任一点M （ρ，θ），建立等式，化简即得.6. 常见曲线的极坐标方程（1） 过极点，倾斜角为α的直线的极坐标方程为θ＝α（ρ∈R ）或θ＝π＋α（ρ∈R ）；（2） 过点（a ，0）（a ＞0），与极轴垂直的直线的极坐标方程为ρcos θ＝a ；（3） 过点⎝⎛⎭⎪⎫a ，π2，与极轴平行的直线的极坐标方程为ρsin θ＝a ；（4） 圆心在极点，半径为r 的圆的极坐标方程为ρ＝r ； （5） 圆心为（a ，0），半径为a 的圆的极坐标方程为ρ＝2acos θ；（6） 圆心为⎝⎛⎭⎪⎫a ，π2，半径为a 的圆的极坐标方程为ρ＝2asin θ.7. 以平面直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且在两种坐标系中取相同的长度单位，平面内任一点P 的直角坐标（x ，y ）与极坐标（ρ，θ）可以互换，公式是⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ 和⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x ., 1 求极坐标或极坐标方程), 1) 在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π4，圆C 的方程为ρ＝42sin θ（圆心为点C ），求直线AC 的极坐标方程.解：（解法1）以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系xOy.圆C 的平面直角坐标方程为x 2＋y 2＝42y ，即x 2＋（y －22）2＝8，圆心C （0，22）. 点A 的直角坐标为（2，2）.直线AC 的斜率k AC ＝22－20－2＝－1.所以直线AC 的直角坐标方程为y ＝－x ＋22， 极坐标方程为ρ（cos θ＋sin θ）＝22，即ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. （解法2）在直线AC 上任取一点M （ρ，θ），不妨设点M 在线段AC 上.由于圆心为C ⎝⎛⎭⎪⎫22，π2，S △OAC ＝S △OAM ＋S △OCM ， 所以12×22×2sin π4＝12×2×ρsin ⎝ ⎛⎭⎪⎫θ－π4＋12×ρ×22sin ⎝ ⎛⎭⎪⎫π2－θ，即ρ（cos θ＋sin θ）＝22，化简，得直线AC 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π4＝2. 备选变式（教师专享）在极坐标系中，求曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程.解：（解法1）以极点为坐标原点，极轴为x 轴的正半轴建立直角坐标系，则曲线ρ＝2cos θ的直角坐标方程为（x －1）2＋y 2＝1，且圆心C 的坐标为（1，0），直线θ＝π4的直角坐标方程为y ＝x.因为圆心C （1，0）关于y ＝x 的对称点为（0，1），所以圆C 关于y ＝x 的对称曲线为x 2＋（y －1）2＝1，所以曲线ρ＝2cos θ关于直线θ＝π4对称的曲线的极坐标方程为ρ＝2sin θ.（解法2）设曲线ρ＝2cos θ上任意一点为（ρ′，θ′），其关于直线θ＝π4的对称点为（ρ，θ），则⎩⎪⎨⎪⎧ρ′＝ρ，θ′＝2k π＋π2－θ. 将（ρ′，θ′）代入ρ＝2cos θ，得ρ＝2cos ⎝ ⎛⎭⎪⎫π2－θ，即ρ＝2sin θ，所以曲线ρ＝2cos θ关于直线θ＝π4（ρ∈R ）对称的曲线的极坐标方程为ρ＝2sinθ., 2 极坐标方程与直角坐标方程的互化), 2) （2017·苏州期中）已知在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2（θ为参数，r ＞0）.以直角坐标系的原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0. （1） 求圆C 的圆心的极坐标；（2） 当圆C 与直线l 有公共点时，求r 的取值范围.解：（1） 由C ：⎩⎪⎨⎪⎧x ＝rcos θ＋2，y ＝rsin θ＋2得（x －2）2＋（y －2）2＝r 2，∴ 曲线C 是以（2，2）为圆心，r 为半径的圆，∴ 圆心的极坐标为⎝⎛⎭⎪⎫22，π4. （2） 由直线l ：2ρsin ⎝⎛⎭⎪⎫θ＋π4＋1＝0，得直线l 的直角坐标方程为x ＋y ＋1＝0， 从而圆心（2，2）到直线l 的距离d ＝|2＋2＋1|2＝52 2.∵ 圆C 与直线l 有公共点，∴ d ≤r ，即r≥522.变式训练（2017·苏州期初）自极点O 任意作一条射线与直线ρcos θ＝3相交于点M ，在射线OM 上取点P ，使得OM·OP＝12，求动点P 的轨迹的极坐标方程，并把它化为直角坐标方程.解：设P （ρ，θ），M （ρ′，θ）， ∵ OM ·OP ＝12，∴ ρρ′＝12.∵ ρ′cos θ＝3，∴ 12ρ·cos θ＝3.则动点P 的轨迹的极坐标方程为ρ＝4cos θ. ∵ 极点在此曲线上，∴ 方程两边可同时乘ρ，得ρ2＝4ρcos θ.∴ x 2＋y 2－4x ＝0., 3 曲线的极坐标方程的应用), 3) 在极坐标系中，曲线C ：ρ＝2acos θ（a>0），直线l ：ρcos ⎝⎛⎭⎪⎫θ－π3＝32，C 与l 有且仅有一个公共点. （1） 求a ；（2） O 为极点，A ，B 为C 上的两点，且∠AOB＝π3，求OA ＋OB 的最大值.解：（1） 曲线C 是以（a ，0）为圆心，以a 为半径的圆； 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 相切可得|a －3|2＝a ，解得a ＝1.（2） 不妨设A 的极角为θ，B 的极角为θ＋π3，则OA ＋OB ＝2cos θ＋2cos ⎝⎛⎭⎪⎫θ＋π3 ＝3cos θ－3sin θ＝23cos ⎝⎛⎭⎪⎫θ＋π6， 当θ＝－π6时，OA ＋OB 取得最大值2 3.变式训练在直角坐标系xOy 中，圆C 的方程为（x －3）2＋（y ＋1）2＝9，以O 为极点，x 轴的正半轴为极轴建立极坐标系.（1） 求圆C 的极坐标方程；（2） 直线OP ：θ＝π6（ρ∈R ）与圆C 交于点M ，N ，求线段MN 的长.解：（1） （x －3）2＋（y ＋1）2＝9可化为x 2＋y 2－23x ＋2y －5＝0，故其极坐标方程为ρ2－23ρcos θ＋2ρsin θ－5＝0.（2） 将θ＝π6代入ρ2－23ρcos θ＋2ρsin θ－5＝0，得ρ2－2ρ－5＝0，∴ ρ1＋ρ2＝2，ρ1ρ2＝－5，|MN|＝|ρ1－ρ2|＝（ρ1＋ρ2）2－4ρ1ρ2＝2 6.1. （2017·苏北四市期中）已知曲线C 的极坐标方程为ρsin （θ＋π3）＝3，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，求曲线C 的直角坐标方程.解：由ρsin ⎝⎛⎭⎪⎫θ＋π3＝3，得12ρsin θ＋32ρcos θ＝3. 又ρcos θ＝x ，ρsin θ＝y ，所以曲线C 的直角坐标方程为3x ＋y －6＝0.2. （2017·苏锡常镇一模）已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2. （1） 把圆O 1和圆O 2的极坐标方程化为直角坐标方程； （2） 求经过两圆交点的直线的极坐标方程.解：（1） 由ρ＝2⇒ρ2＝4，所以x 2＋y 2＝4.因为ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2，所以ρ2－22ρ⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2，所以x 2＋y 2－2x －2y －2＝0.（2） 将两圆的直角坐标方程相减，得经过两圆交点的直线方程为x ＋y ＝1.化为极坐标方程为ρcos θ＋ρsin θ＝1，即ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22. 3. （2017·苏北三市模拟）在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π2，点B 在直线l ：ρcos θ＋ρsin θ＝0（0≤θ＜2π）上.当线段AB 最短时，求点B 的极坐标.解：以极点为原点，极轴为x 轴正半轴，建立平面直角坐标系，则点A ⎝⎛⎭⎪⎫2，π2的直角坐标为（0，2），直线l 的直角坐标方程为x ＋y ＝0.AB 最短时，点B 为直线x －y ＋2＝0与直线l 的交点， 由⎩⎪⎨⎪⎧x －y ＋2＝0，x ＋y ＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝1. 所以点B 的直角坐标为（－1，1）.所以点B 的极坐标为⎝⎛⎭⎪⎫2，3π4. 4. （2017·常州期末）在平面直角坐标系中，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.已知圆ρ＝4sin （θ＋π6）（ρ≥0）被射线θ＝θ0（θ0为常数，且θ0∈⎝ ⎛⎭⎪⎫0，π2）所截得的弦长为23，求θ0的值. 解：圆ρ＝4sin ⎝⎛⎭⎪⎫θ＋π6的直角坐标方程为（x －1）2＋（y －3）2＝4，射线θ＝θ0的直角坐标方程可以设为y ＝kx （x≥0，k ＞0），圆心（1，3）到直线y ＝kx 的距离d ＝|k －3|1＋k2. 根据题意，得24－（k －3）21＋k 2＝23，解得k ＝33， 即tan θ0＝33.又θ0∈⎝⎛⎭⎪⎫0，π2，所以θ0＝π6.1. （2017·南通、扬州、泰州模拟）在极坐标系中，圆C 的圆心在极轴上，且过极点和点⎝⎛⎭⎪⎫32，π4，求圆C 的极坐标方程. 解：（解法1）因为圆C 的圆心在极轴上且过极点， 所以可设圆C 的极坐标方程为ρ＝acos θ.又点⎝⎛⎭⎪⎫32，π4在圆C 上，所以32＝acos π4，解得a ＝6. 所以圆C 的极坐标方程为ρ＝6cos θ.（解法2）点⎝⎛⎭⎪⎫32，π4的直角坐标为（3，3）. 因为圆C 过点（0，0），（3，3）， 所以圆心在直线x ＋y －3＝0上. 又圆心C 在极轴上，所以圆C 的直角坐标方程为（x －3）2＋y 2＝9. 所以圆C 的极坐标方程为ρ＝6cos θ.2. 已知在极坐标系下，圆C ：ρ＝2cos ⎝ ⎛⎭⎪⎫θ＋π2与直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，点M 为圆C 上的动点.求点M 到直线l 距离的最大值.解：圆C ：ρ＝2cos ⎝ ⎛⎭⎪⎫θ＋π2，即 x 2＋y 2＋2y ＝0，x 2＋（y ＋1）2＝1，表示圆心为（0，－1），半径等于1的圆.直线l ：ρsin ⎝⎛⎭⎪⎫θ＋π4＝2，即ρcos θ＋ρsin θ－2＝0，即 x ＋y －2＝0， 圆心到直线l 的距离为|0－1－2|2＝322，故圆上的动点M 到直线l 的距离的最大值等于322＋1.3. 在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝4cos θ.（1） 求出圆C 的直角坐标方程；（2） 已知圆C 与x 轴相交于A ，B 两点，若直线l ：y ＝2x ＋2m 上存在点P 使得∠APB ＝90°，求实数m 的最大值.解：（1） 由ρ＝4cos θ得ρ2＝4ρcos θ，即x 2＋y 2－4x ＝0，即圆C 的标准方程为（x －2）2＋y 2＝4.（2） l 的方程为y ＝2x ＋2m ，而AB 为圆C 的直径，故直线l 上存在点P 使得∠APB＝90°的充要条件是直线l 与圆C 有公共点， 故|4＋2m|5≤2，于是实数m 的最大值为5－2.4. 在极坐标系中，已知直线2ρcos θ＋ρsin θ＋a ＝0（a>0）被圆ρ＝4sin θ截得的弦长为2，求a 的值.解：以极点为坐标原点，极轴为x 轴正半轴建立平面直角坐标系，直线的极坐标方程化为直角坐标方程为2x ＋y ＋a ＝0，圆的极坐标方程化为直角坐标方程为x 2＋y 2＝4y ，即x 2＋（y －2）2＝4.因为直线被圆截得的弦长为2，所以圆心（0，2）到直线的距离为4－1＝3， 即|2＋a|5＝3，因为a>0，所以a ＝15－2.1. 极坐标方程与直角坐标方程的互化 （1） 将极坐标或极坐标方程转化为直角坐标或直角坐标方程，直接利用公式x ＝ρcos θ，y ＝ρsin θ即可.常用方法有代入法、平方法，还经常用到同乘（或除以）ρ等技巧.（2） 将直角坐标或直角坐标方程转化为极坐标或极坐标方程，要灵活运用x ＝ρcosθ，y ＝ρsin θ以及ρ＝x 2＋y 2，tan θ＝y x（x≠0），同时要掌握必要的技巧，通常情况下，由tan θ确定角θ时，应根据点P 所在象限取最小正角.在这里要注意：当x≠0时，θ角才能由tan θ＝yx按上述方法确定.当x ＝0时，tan θ没有意义，这时又分三种情况：当x ＝0，y ＝0时，θ可取任何值；当x ＝0，y>0时，可取θ＝π2；当x ＝0，y<0时，可取θ＝3π2.2. 求简单曲线的极坐标方程的方法（1） 设点M （ρ，θ）为曲线上任意一点，由已知条件，构造出三角形，利用正弦定理求解OM 与θ的关系；（2） 先求出曲线的直角坐标方程，再利用极坐标与直角坐标的变换公式，把直角坐标方程化为极坐标方程.[备课札记]第2课时 参 数 方 程（对应学生用书（理）202～205页）1. （选修44P 45例1改编）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t 2，y ＝2＋32t（t 为参数），求此直线的倾斜角以及在y 轴上的截距.解：∵ ⎩⎪⎨⎪⎧x －1＝t 2，y －2＝32t ，∴ y －2＝3（x －1）.∴ 此直线的斜率为3，∴ 它的倾斜角为60°.令x ＝0，得它在y 轴上的截距为2－ 3.2. （选修44P 45例2改编）已知点P （3，m ）在以点F 为焦点的抛物线⎩⎪⎨⎪⎧x ＝4t 2，y ＝4t（t 为参数）上，求PF 的值.解：将抛物线的参数方程化为普通方程为y 2＝4x ，则焦点F （1，0），准线方程为x ＝－1，又P （3，m ）在抛物线上，由抛物线的定义知PF ＝3－（－1）＝4.3. （选修44P 57习题3（4））选择适当的参数，将普通方程4x 2＋y 2－16x ＋12＝0化为参数方程.解：由4x 2＋y 2－16x ＋12＝0，得4（x －2）2＋y 2＝4，选择参数θ，令y ＝2sin θ，则x ＝2＋cos θ，故所求曲线的参数方程是⎩⎪⎨⎪⎧x ＝2＋cos θ，y ＝2sin θ.（答案不惟一）4. 在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝2cos α＋3，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π6.若直线l 与曲线C 交于A ，B 两点，求线段AB 的长.解：曲线C 的普通方程为（x －3）2＋y 2＝4，表示以（3，0）为圆心，2为半径的圆.直线l 的直角坐标方程为y ＝33x.所以圆心到直线的距离为32， 所以线段AB 的长为24－⎝ ⎛⎭⎪⎫322＝13. 5. 已知直线l 的极坐标方程为ρsin （θ－π3）＝3，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ（θ为参数），设P 点是曲线C 上的任意一点，求P 到直线l 的距离的最大值.解：由ρsin ⎝⎛⎭⎪⎫θ－π3＝3，可得ρ（12sin θ－32cos θ）＝3， ∴ y －3x ＝6，即3x －y ＋6＝0.由⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ，得x 2＋y 2＝4，圆的半径为r ＝2， ∴ 圆心到直线l 的距离d ＝62＝3.∴ P 到直线l 的距离的最大值为d ＋r ＝5.1. 参数方程是用第三个变量（即参数）分别表示曲线上任一点M 的坐标x ，y 的另一种曲线方程的形式，它体现了x ，y 的一种间接关系.2. 参数方程是根据其固有的意义（物理、几何）得到的，要注意参数的取值范围.3. 一些常见曲线的参数方程（1） 过点P 0（x 0，y 0），且倾斜角是α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋lcos α，y ＝y 0＋lsin α（l 为参数）. l 是有向线段P 0P 的数量.（2） 圆方程（x －a ）2＋（y －b ）2＝r 2的参数方程是⎩⎪⎨⎪⎧x ＝a ＋rcos θ，y ＝b ＋rsin θ（θ为参数）.（3） 椭圆方程x 2a 2＋y2b 2＝1（a>b>0）的参数方程是⎩⎪⎨⎪⎧x ＝acos θ，y ＝bsin θ（θ为参数）.（4） 双曲线方程x 2a 2－y2b 2＝1（a>0，b>0）的参数方程是⎩⎪⎨⎪⎧x ＝a 2⎝ ⎛⎭⎪⎫t ＋1t ，y ＝b 2⎝ ⎛⎭⎪⎫t －1t （t 为参数）.（5） 抛物线方程y 2＝2px （p>0）的参数方程是⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt （t 为参数）.4. 在参数方程与普通方程的互化中要注意变量的取值范围.1 参数方程与普通方程的互化1（2017·南京、盐城期末）在平面直角坐标系xOy 中，已知直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t为参数）.现以坐标原点O 为极点，以x 轴正半轴为极轴建立极坐标系.设圆C 的极坐标方程为ρ＝2cos θ，直线l 与圆C 交于A ，B 两点，求弦AB 的长.解：直线l ：⎩⎪⎨⎪⎧x ＝35t ，y ＝45t （t 为参数）化成普通方程为4x －3y ＝0，圆C 的极坐标方程ρ＝2cos θ化成直角坐标方程为（x －1）2＋y 2＝1，则圆C 的圆心到直线l 的距离d ＝|4|42＋（－3）2＝45， 所以AB ＝21－d 2＝65.变式训练在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－1＋55t ，y ＝－1＋255t （t 为参数）与曲线⎩⎪⎨⎪⎧x ＝sin θ，y ＝cos 2θ（θ为参数）相交于A ，B 两点，求线段AB 的长.解：将直线的参数方程化为普通方程，得y ＝2x ＋1 ①. 将曲线的参数方程化为普通方程，得y ＝1－2x 2（－1≤x≤1） ②.由①②，得⎩⎪⎨⎪⎧x ＝－1，y ＝－1或⎩⎪⎨⎪⎧x ＝0，y ＝1，所以A （－1，－1），B （0，1）或A （0，1），B （－1，－1），从而AB ＝（－1－0）2＋（－1－1）2＝ 5. 备选变式（教师专享）已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋22t ，y ＝22t（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝2sin θ－2cos θ.若直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：由ρ＝2sin θ－2cos θ，可得ρ2＝2ρsin θ－2ρcos θ，所以曲线C 的直角坐标方程为x 2＋y 2＝2y －2x ，标准方程为（x ＋1）2＋（y －1）2＝2.直线l 的方程化成普通方程为x －y ＋1＝0.圆心到直线l 的距离为d ＝|－1－1＋1|2＝22，所求弦长AB ＝22－⎝ ⎛⎭⎪⎫222＝ 6. , 2 求曲线参数方程), 2) 如图，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程.解：设P （x ，y ），则随着θ取值变化，P 可以表示圆上任意一点，由所给的曲线方程x 2＋y 2－x ＝0，即⎝ ⎛⎭⎪⎫x －122＋y 2＝14，表示以⎝ ⎛⎭⎪⎫12，0为圆心，12为半径的圆，可得弦OP ＝1×cosθ，所以⎩⎪⎨⎪⎧x ＝OP·cos θ，y ＝OP·sin θ，从而⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ，故已知圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝cos θ·sin θ（θ为参数）.备选变式（教师专享）已知直线C 1：⎩⎪⎨⎪⎧x ＝1＋tcos α，y ＝tsin α（t 为参数），曲线C 2：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ（θ为参数）. （1） 当α＝π3时，求C 1与C 2的交点坐标；（2） 过坐标原点O 作C 1的垂线，垂足为A ，P 为OA 的中点，当α变化时，求点P 轨迹的参数方程，并指出它是什么曲线.解：（1） 当α＝π3时，C 1的普通方程为y ＝3（x －1），C 2的普通方程为x 2＋y 2＝1，联立构成方程组⎩⎨⎧y ＝3x －3，x 2＋y 2＝1，解得C 1与C 2的交点坐标分别为（1，0），⎝ ⎛⎭⎪⎫12，－32. （2） 依题意，C 1的普通方程为xsin α－ycos α－sin α＝0，则A 点的坐标为（sin 2α，－sin αcos α），故当α变化时，P 点轨迹的参数方程为⎩⎪⎨⎪⎧x ＝12sin 2α，y ＝－12sin αcos α（α为参数），所以点P 轨迹的普通方程为⎝ ⎛⎭⎪⎫x －142＋y 2＝116.故点P 的轨迹是圆心为⎝ ⎛⎭⎪⎫14，0，半径为14的圆. , 3 参数方程的应用), 3) （2017·南通、泰州模拟）在平面直角坐标系xOy 中，已知直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）与曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t （t 为参数）相交于A ，B 两点，求线段AB的长.解：（解法1）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）代入y 2＝8x ，整理得l 2－82l ＋24＝0，解得l 1＝22，l 2＝6 2.则|l 1－l 2|＝42，所以线段AB 的长为4 2.（解法2）将曲线⎩⎪⎨⎪⎧x ＝18t 2，y ＝t（t 为参数）化成普通方程为y 2＝8x ，将直线⎩⎪⎨⎪⎧x ＝－32＋22l ，y ＝22l （l 为参数）化成普通方程为x －y ＋32＝0，由⎩⎪⎨⎪⎧y 2＝8x ，x －y ＋32＝0得⎩⎪⎨⎪⎧x ＝12，y ＝2或⎩⎪⎨⎪⎧x ＝92，y ＝6.所以AB 的长为⎝ ⎛⎭⎪⎫92－122＋（6－2）2＝4 2.备选变式（教师专享）已知直线l ：⎩⎪⎨⎪⎧x ＝tcos α＋m ，y ＝tsin α（t 为参数）恒经过椭圆C ：⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ（φ为参数）的右焦点F.（1） 求m 的值；（2） 设直线l 与椭圆C 交于A ，B 两点，求FA·FB 的最大值与最小值.解：（1） 椭圆的参数方程化为普通方程，得x 225＋y29＝1.因为a ＝5，b ＝3，所以c ＝4，所以点F 的坐标为（4，0）. 因为直线l 经过点（m ，0），所以m ＝4.（2） 将直线l 的参数方程代入椭圆C 的普通方程，并整理得（9cos 2α＋25sin 2α）t 2＋72tcos α－81＝0.设点A ，B 在直线参数方程中对应的参数分别为t 1，t 2，则FA ·FB ＝|t 1t 2|＝819cos 2α＋25sin 2α＝819＋16sin 2α. 当sin α＝0时，FA ·FB 取最大值9；当sin α＝±1时，FA ·FB 取最小值8125., 4 极坐标、参数方程的综合应用), 4) （2017·苏锡常镇二模）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，取相同的单位长度，建立极坐标系.已知曲线C 1的参数方程为⎩⎨⎧x ＝3＋2cos α，y ＝3＋2sin α（α∈[0，2π]，α为参数），曲线C 2的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝a （a∈R ），若曲线C 1与曲线C 2有且仅有一个公共点，求实数a 的值.解：曲线C 1的方程为（x －3）2＋（y －3）2＝4，圆心坐标为（3，3），半径为2.∵ 曲线C 2的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π3＝a （a∈R ）， ∴ 曲线C 2的直角坐标方程为3x ＋y －2a ＝0.∵ 曲线C 1与曲线C 2有且仅有一个公共点， ∴ |3＋3－2a|2＝2，解得a ＝1或a ＝5.备选变式（教师专享）在平面直角坐标系xOy 中，曲线C ：⎩⎨⎧x ＝6cos α，y ＝2sin α（α为参数）.以原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ（cos θ＋3sin θ）＋4＝0.求曲线C 上的点到直线l 的最大距离.解：将l 转化为直角坐标方程为x ＋3y ＋4＝0. 在C 上任取一点A （6cos α，2sin α），α∈[0，2π），则点A 到直线l 的距离为d ＝|6cos α＋6sin α＋4|2＝|23sin ⎝ ⎛⎭⎪⎫α＋π4＋4|2＝3sin ⎝⎛⎭⎪⎫α＋π4＋2.当α＝π4时，d 取得最大值，最大值为2＋3，此时A 点为（3，1）.1. 在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22a ，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝－1＋cos t ，y ＝－1＋sin t （t 为参数，0≤t ≤π）.当C 1与C 2有公共点时，求实数a 的取值范围.解：曲线C 1的直角坐标方程为x ＋y ＝a.若C 1与C 2有公共点，则a ＝x ＋y ＝sin t ＋cos t－2在t∈[0，π]上有解，又sin t ＋cos t －2＝2sin ⎝⎛⎭⎪⎫t ＋π4－2，因为t∈[0，π]，所以t ＋π4∈⎣⎢⎡⎦⎥⎤π4，5π4，sin ⎝ ⎛⎭⎪⎫t ＋π4∈⎣⎢⎡⎦⎥⎤－22，1，所以a 的取值范围为[－3，2－2].2. （2017·苏北四市期末）在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴建立极坐标系.直线l ：2sin ⎝ ⎛⎭⎪⎫θ－π4＝m （m∈R ），圆C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋3cos t ，y ＝－2＋3sin t （t 为参数）.当圆心C 到直线l 的距离为2时，求m 的值.解：直线l 的直角坐标方程为x －y ＋m ＝0，圆C 的普通方程为（x －1）2＋（y ＋2）2＝9，圆心C 到直线l 的距离为|1－（－2）＋m|2＝2，解得m ＝－1或m ＝－5.3. （2016·江苏卷）在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t（t 为参数），椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝2sin θ（θ为参数）.设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长.解：椭圆C 的普通方程为x 2＋y 24＝1，将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t代入x 2＋y 24＝1，得⎝ ⎛⎭⎪⎫1＋12t 2＋⎝ ⎛⎭⎪⎫32t 24＝1，即7t 2＋16t ＝0，解得t 1＝0，t 2＝－167.所以AB ＝|t 1－t 2|＝167.4. （2017·扬州期末）在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝cos α ，y ＝1＋sin 2α（α为参数），以直角坐标系原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为θ＝π4，试求直线l 与曲线C 的交点的直角坐标.解：将直线l 的极坐标方程化成直角坐标方程为y ＝x ，将曲线C 的参数方程化成普通方程为y ＝2－x 2（－1≤x≤1）. 由⎩⎪⎨⎪⎧y ＝x ，y ＝2－x2得x 2＋x －2＝0，解得x ＝1或x ＝－2. 又－1≤x≤1，所以x ＝1，所以直线l 与曲线C 的交点的直角坐标为（1，1）.1. 在极坐标系中，直线l 的极坐标方程为θ＝π3（ρ∈R ），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），求直线l 与曲线C 的交点P 的直角坐标.解：因为直线l 的极坐标方程为θ＝π3（ρ∈R ），所以直线l 的普通方程为y ＝3x.①又曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos α，y ＝1＋cos 2α（α为参数），所以曲线C 的直角坐标方程为y ＝12x 2（x∈[－2，2]）， ②联立①②解方程组得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎨⎧x ＝23，y ＝6（舍去）.故P 点的直角坐标为（0，0）.2. （2017·苏州期末）在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t（t 为参数），以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，已知直线l 与曲线C 相交于A ，B 两点，求线段AB 的长.解：因为曲线C 的极坐标方程为ρsin 2θ－4cos θ＝0，所以ρ2sin 2θ＝4ρcos θ，即曲线C 的直角坐标方程为y 2＝4x.将直线l 的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t代入抛物线方程y 2＝4x ，得⎝ ⎛⎭⎪⎫2＋22t 2＝4⎝⎛⎭⎪⎫1－22t ，即t 2＋82t ＝0，解得t 1＝0，t 2＝－8 2.所以AB ＝|t 1－t 2|＝8 2.3. 在平面直角坐标系xOy 中，已知曲线C ：⎩⎪⎨⎪⎧x ＝s ，y ＝s 2（s 为参数），直线l ：⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t （t 为参数）.设曲线C 与直线l 交于A ，B 两点，求线段AB 的长度.解：由⎩⎪⎨⎪⎧x ＝s ，y ＝s 2消去s 得曲线C 的普通方程为y ＝x 2；由⎩⎪⎨⎪⎧x ＝2＋110t ，y ＝4＋310t消去t 得直线l 的普通方程为y ＝3x －2.联立直线l 的方程与曲线C 的方程，即⎩⎪⎨⎪⎧y ＝x 2，y ＝3x －2，解得交点的坐标分别为（1，1），（2，4）.所以线段AB 的长度为（2－1）2＋（4－1）2＝10.4. （2017·南京、盐城模拟）在平面直角坐标系xOy 中，直线l ：⎩⎪⎨⎪⎧x ＝1＋35t ，y ＝45t（t 为参数）与曲线C ：⎩⎪⎨⎪⎧x ＝4k 2，y ＝4k（k 为参数）交于A ，B 两点，求线段AB 的长.解：（解法1）直线l 的参数方程化为普通方程得4x －3y ＝4，将曲线C 的参数方程化为普通方程得y 2＝4x.联立方程组⎩⎪⎨⎪⎧4x －3y ＝4，y 2＝4x ，解得⎩⎪⎨⎪⎧x ＝4，y ＝4或⎩⎪⎨⎪⎧x ＝14，y ＝－1，所以A （4，4），B ⎝ ⎛⎭⎪⎫14，－1或A ⎝ ⎛⎭⎪⎫14，－1，B （4，4）. 所以AB ＝⎝ ⎛⎭⎪⎫4－142＋（4＋1）2＝254. （解法2）将曲线C 的参数方程化为普通方程得y 2＝4x.将直线l 的参数方程代入抛物线C 的方程得⎝ ⎛⎭⎪⎫45t 2＝4⎝ ⎛⎭⎪⎫1＋35t ，即4t 2－15t －25＝0，所以 t 1＋t 2＝154，t 1t 2＝－254.所以AB ＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2＝⎝ ⎛⎭⎪⎫1542＋25＝254.1. 在直线的参数方程⎩⎪⎨⎪⎧x ＝x 0＋tcos α，y ＝y 0＋tsin α（t 为参数）中t 的几何意义是表示在直线上过定点P 0（x 0，y 0）与直线上的任一点P （x ，y ）构成的有向线段P 0P 的长度，且在直线上任意两点P 1，P 2的距离为P 1P 2＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2.2. 参数方程化为普通方程的关键是消参数：一要熟练掌握常用技巧（如整体代换）；二要注意变量取值范围的一致性，这一点最易忽视.[备课札记]。

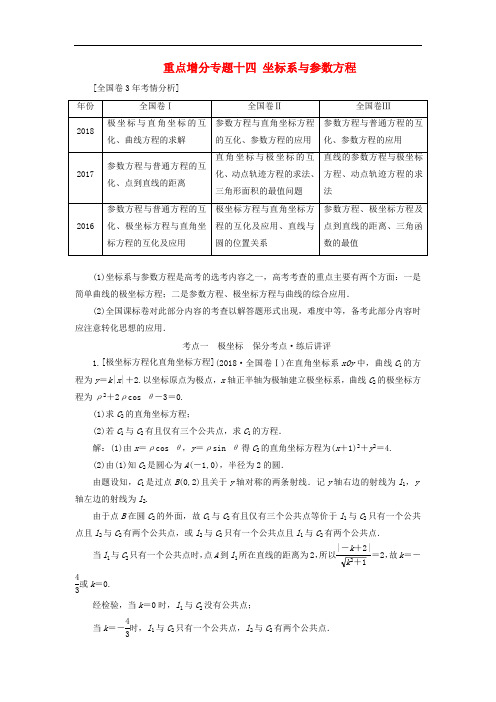
选修4系列专项强化练（二） 选修4－4：坐标系与参数方程(理科） 题型一 曲线的极坐标方程1．在极坐标系中，已知曲线C :ρ＝2sin θ，过极点O 的直线l 与曲线C 交于A ，B 两点，且AB ＝错误!，求直线l 的极坐标方程．解：设直线l 的方程为θ＝θ0（ρ∈R ）,A （0，0），B (ρ1，θ0）．则AB ＝｜ρ1－0|＝|2sin θ0|。

又AB ＝错误!,故sin θ0＝±错误!.解得θ0＝π3＋k π或θ0＝－错误!＋k π，k ∈Z 。

所以直线l 的方程为θ＝错误!或θ＝错误!（ρ∈R )．2．求以C （4,0)为圆心，半径为4的圆的极坐标方程．解：如图所示，由题设可知，这个圆经过极点，圆心在极轴上，设圆与极轴的另一个交点是A ,在圆上任取一点P （ρ,θ),连结OP ，PA ，在Rt △OPA 中，｜OA |＝8，|OP ｜＝ρ,∠AOP ＝θ,∴|OA |·cos θ＝ρ,即8cos θ＝ρ,即ρ＝8cos θ就是圆C 的极坐标方程．［临门一脚］1．在极坐标系中，求直线的极坐标方程的一般方法为:设M （ρ，θ）为直线上任意一点，极点为O ，连结OM ,构造出含有OM 的三角形，再找出我们需求的ρ与θ的关系,即为直线的极坐标方程．也可以先求出直角坐标方程，再化为极坐标方程．2．求圆的极坐标方程要注意作出图形，充分利用三角函数和解三角形的知识，探究极径和极角的关系，几种特殊圆的极坐标方程需要记忆清楚．3．解极坐标方程时如果求出ρ＝0，需要进行检验，防止漏解．题型二 方程互化1．已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－2错误!ρcos 错误!＝2。

（1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程；(2)求经过两圆交点的直线的极坐标方程．解：（1）由ρ2＝x 2＋y 2，且错误!得圆O 1的直角坐标方程为x 2＋y 2＝4，由ρ2－2错误!ρcos 错误!＝2,得ρ2－2ρ(cos θ＋sin θ）＝2， x 2＋y 2－2（x ＋y )＝2,故圆O 2的直角坐标方程为x 2＋y 2－2x －2y －2＝0.（2）联立方程错误!两式相减，得经过两圆交点的直线方程为x ＋y －1＝0，该直线的极坐标方程为ρcos θ＋ρsin θ－1＝0.2．在平面直角坐标系xOy 中，圆的参数方程为错误!（α为参数），以坐标原点O 为极点、x 轴的正半轴为极轴建立极坐标系．求：(1）圆的普通方程;(2)圆的极坐标方程．解：（1） 圆的普通方程为（x －2)2＋y 2＝4.(2） 把错误!代入上述方程,得圆的极坐标方程为ρ＝4cos θ.3．在平面直角坐标系xOy 中，已知直线l ：错误!(t 为参数)与椭圆C ：错误!(θ为参数,a ＞0)的一条准线的交点位于y 轴上，求实数a 的值．解:由题意，直线l 的普通方程为2x ＋y ＝9，椭圆C 的普通方程为y 29＋错误!＝1（0＜a ＜3)， 椭圆C 的准线方程为y ＝±错误!，故错误!＝9，解得a ＝2错误!（负值舍去)．［临门一脚］1．极坐标与直角坐标互化的基本公式为x ＝ρcos θ，y ＝ρsin θ，也经常需要用到ρ2＝x 2＋y 2，tan θ＝错误!(x ≠0）．2．通过消去参数将曲线的参数方程化为普通方程，有利于识别曲线的类型．（1）消去参数的方法一般有三种：①利用解方程的技巧求出参数的表示式，然后代入消去参数；②利用三角恒等式消去参数;③根据参数方程本身的结构特征，选用一些灵活的方法从整体上消去参数．(2）在参数方程与普通方程的互化中, 必须使两种方程中的x ，y 的取值范围保持一致,否则将导致两种方程所对应的曲线不一致．题型三 位置关系及参数方程应用1．在极坐标系中,求直线θ＝错误!（ρ∈R )被曲线ρ＝4sin θ所截得的弦长．解：法一:在ρ＝4sin θ中，令θ＝错误!，得ρ＝4sin 错误!＝2错误!，即所求弦长为2错误!. 法二：以极点O 为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系．直线θ＝错误!（ρ∈R ）的直角坐标方程为y ＝x ，①曲线ρ＝4sin θ的直角坐标方程为x 2＋y 2－4y ＝0，②由①②得错误!或错误!故直线θ＝错误!(ρ∈R ）被曲线ρ＝4sin θ所截弦长的端点坐标分别为（0,0)，(2,2),所以直线θ＝错误!（ρ∈R )被曲线ρ＝4sin θ所截得的弦长为错误!＝2错误!.2．已知直线l 的参数方程为错误!(t 为参数),曲线C 的极坐标方程为ρ＝3cos θ,试判断直线l 与曲线C 的位置关系．解：由题意知，直线l 的普通方程为2x －y －2＝0，由ρ2＝x 2＋y 2,且错误!得曲线C 的直角坐标方程为错误!2＋y 2＝错误!,它表示圆．由圆心错误!到直线l 的距离d ＝错误!＝错误!＜错误!，得直线l 与曲线C 相交．3．在平面直角坐标系xOy中，椭圆C的参数方程为错误!(其中φ为参数），以O为极点，x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为2ρcosθ＋错误!＝3错误!。

重点增分专题十四　选修4－5　不等式选讲[全国卷3年考情分析]年份全国卷Ⅰ全国卷Ⅱ全国卷Ⅲ2018含绝对值不等式的解法及绝对值不等式恒成立问题含绝对值不等式的解法及绝对值不等式恒成立问题含绝对值函数的图象与绝对值不等式恒成立问题2017含绝对值不等式的解法、求参数的取值范围基本不等式的应用、一些常用的变形及证明不等式的方法含绝对值不等式的解法、函数最值的求解2016含绝对值不等式的解法、分段函数的图象及应用含绝对值不等式的解法、比较法证明不等式及应用含绝对值不等式的解法、绝对值不等式的性质(1)不等式选讲是高考的选考内容之一，考查的重点是不等式的证明、绝对值不等式的解法等，命题的热点是绝对值不等式的求解，以及绝对值不等式与函数的综合问题的求解．(2)此部分命题形式单一、稳定，难度中等，备考本部分内容时应注意分类讨论思想的应用．含绝对值不等式的解法 保分考点·练后讲评考点一1.解不等式|x ＋3|<|2x －1|.[解|f (x )|>|g (x )|型不等式]解：由已知，可得|x ＋3|<|2x －1|，即|x ＋3|2<|2x －1|2，∴3x 2－10x －8>0，解得x <－或x >4.23故所求不等式的解集为∪(4，＋∞)．(－∞，－23)2.(2018·全国卷Ⅱ)设函数f (x )＝5－|x ＋a |－|x －2|.[解|f (x )|＋|g (x )|>a 型不等式](1)当a ＝1时，求不等式f (x )≥0的解集；(2)若f (x )≤1，求a 的取值范围．解：(1)当a ＝1时，f (x )＝Error!当x <－1时，由2x ＋4≥0，解得－2≤x <－1；当－1≤x ≤2时，显然满足题意；当x >2时，由－2x ＋6≥0，解得2<x ≤3，故f (x )≥0的解集为{x |－2≤x ≤3}．(2)f (x )≤1等价于|x ＋a |＋|x －2|≥4.而|x ＋a |＋|x －2|≥|a ＋2|，且当x ＝2时等号成立．故f (x )≤1等价于|a ＋2|≥4.由|a ＋2|≥4可得a ≤－6或a ≥2.所以a 的取值范围是(－∞，－6]∪[2，＋∞)．[解题方略]　绝对值不等式的常用解法(1)基本性质法：对a ∈R ＋，|x |<a ⇔－a <x <a ，|x |>a ⇔x <－a 或x >a .(2)平方法：两边平方去掉绝对值符号．(3)零点分区间法：含有两个或两个以上绝对值符号的不等式，可用零点分区间法脱去绝对值符号，将其转化为与之等价的不含绝对值符号的不等式(组)求解．(4)几何法：利用绝对值的几何意义，画出数轴，将绝对值转化为数轴上两点的距离求解．(5)数形结合法：在直角坐标系中作出不等式两边所对应的两个函数的图象，利用函数图象求解.保分考点·练后讲评考点二不等式的证明1.已知f (x )＝|x －1|＋|x |，且α>1，β>1，f (α)＋f (β)＝2，求证：＋≥[综合法证明不等式]4α1β.92证明：因为α>1，β>1，f (α)＋f (β)＝2α－1＋2β－1＝2，所以α＋β＝2.所以＋＝(α＋β)4α1β12(4α＋1β)＝≥＝，12(5＋4βα＋αβ)12(5＋24βα·αβ)92当且仅当α＝2β＝时取等号．432.已知函数f (x )＝|x ＋1|.[分析法证明不等式](1)求不等式f (x )＜|2x ＋1|－1的解集M ；(2)设a ，b ∈M ，证明：f (ab )＞f (a )－f (－b )．解：(1)由题意，|x ＋1|<|2x ＋1|－1，①当x ≤－1时，不等式可化为－x －1＜－2x －2，解得x ＜－1；②当－1＜x ＜－时，12不等式可化为x ＋1＜－2x －2，此时不等式无解；③当x ≥－时，12不等式可化为x ＋1＜2x ，解得x ＞1.综上，M ＝{x |x ＜－1或x ＞1}．(2)证明：因为f (a )－f (－b )＝|a ＋1|－|－b ＋1|≤|a ＋1－(－b ＋1)|＝|a ＋b |，所以要证f (ab )＞f (a )－f (－b )，只需证|ab ＋1|＞|a ＋b |，即证|ab ＋1|2＞|a ＋b |2，即证a 2b 2＋2ab ＋1＞a 2＋2ab ＋b 2，即证a 2b 2－a 2－b 2＋1＞0，即证(a 2－1)(b 2－1)＞0.因为a ，b ∈M ，所以a 2＞1，b 2＞1，所以(a 2－1)(b 2－1)＞0成立，所以原不等式成立．3.已知a ，b ∈R ，且a ＋b ＝1，求证：(a ＋2)2＋(b ＋2)2≥.[放缩法或反证法证明不等式]252证明：法一：(放缩法)因为a ＋b ＝1，所以(a ＋2)2＋(b ＋2)2≥22＝[(a ＋b )＋4]2＝，当且仅当a ＋2＝b ＋2，[(a ＋2)＋(b ＋2)2]12252即a ＝b ＝时，等号成立．12法二：(反证法)假设(a ＋2)2＋(b ＋2)2<，252则a 2＋b 2＋4(a ＋b )＋8<.252因为a ＋b ＝1，则b ＝1－a ，所以a 2＋(1－a )2＋12<.252所以2<0，这与2≥0矛盾，故假设不成立．所以(a ＋2)2＋(b ＋2)2≥.(a －12)(a －12)252[解题方略]　证明不等式的常用方法不等式证明的常用方法有比较法、分析法、综合法、放缩法、反证法等．(1)如果已知条件与待证结论直接联系不明显，则考虑用分析法．(2)利用放缩法证明不等式，就是舍掉式中的一些正项或负项，或者在分式中放大或缩小分子、分母，还可把和式中各项或某项换为较大或较小的数或式子，从而达到证明不等式的目的．(3)如果待证的是否定性命题、唯一性命题或以“至少”“至多”等方式给出的问题，则考虑用反证法．用反证法证明不等式的关键是作出假设，推出矛盾.与绝对值不等式有关的最值问题考点三增分考点深度精研[析母题]——高考年年“神”相似[典例]　已知函数f (x )＝|2x －a |＋|x －1|，a ∈R.(1)若不等式f (x )＋|x －1|≥2对任意的x ∈R 恒成立，求实数a 的取值范围；(2)当a <2时，函数f (x )的最小值为a －1，求实数a 的值．[解]　(1)f (x )＋|x －1|≥2可化为＋|x －1|≥1.|x －a2|∵＋|x －1|≥，|x －a 2||a2－1|∴≥1，|a2－1|∴a ≤0或a ≥4，∴实数a 的取值范围为(－∞，0]∪[4，＋∞)．(2)当a <2时，易知函数f (x )＝|2x －a |＋|x －1|的零点分别为和1，且<1，a 2a2∴f (x )＝Error!易知f (x )在上单调递减，在上单调递增，(－∞，a 2)(a2，＋∞)∴f (x )min＝f ＝－＋1＝a －1，解得a ＝，又<2，∴a ＝.(a 2)a 2434343[练子题]——高考年年“形”不同1．在本例条件下，若f (x )≤|2x ＋1|的解集包含，求a 的取值范围．[32，3]解：由题意可知f (x )≤|2x ＋1|在上恒成立，[32，3]当x ∈时，f (x )＝|2x －a |＋|x －1|[32，3]＝|2x －a |＋x －1≤|x ＋1|＝x ＋1，∴|2x －a |≤2，即2x －2≤a ≤2x ＋2，∴(2x －2)max ＝4，(2x ＋2)min ＝5，因此a 的取值范围为[4,5]．2．函数f (x )不变，若存在实数x ，使不等式f (x )－3|x －1|≥2能成立，求实数a 的取值范围．解：∵f (x )－3|x －1|＝|2x －a |－2|x －1|＝|2x －a |－|2x －2|≤|a －2|.∴|a －2|≥2.∴a ≤0或a ≥4.∴实数a 的取值范围为(－∞，0]∪[4，＋∞)． [解题方略]解决不等式恒成立、能成立、恰成立问题的策略不等式恒成立问题不等式f (x )>A 在区间D 上恒成立，等价于在区间D 上f (x )min >A .不等式f (x )<B 在区间D 上恒成立，等价于在区间D 上f (x )max <B 不等式能成立问题在区间D 上存在实数x 使不等式f (x )>A 成立，等价于在区间D 上f (x )max >A .在区间D 上存在实数x 使不等式f (x )<B 成立，等价于在区间D 上f (x )min <B不等式恰成立问题不等式f (x )>A 在区间D 上恰成立，等价于不等式f (x )>A 的解集为D .不等式f (x )<B 在区间D 上恰成立，等价于不等式f (x )<B 的解集为D[多练强化]已知函数f (x )＝|x |＋|x ＋1|.(1)若任意x ∈R ，恒有f (x )≥λ成立，求实数λ的取值范围．(2)若存在m ∈R ，使得m 2＋2m ＋f (t )＝0成立，求实数t 的取值范围．解：(1)由f (x )＝|x |＋|x ＋1|≥|x －(x ＋1)|＝1知，f (x )min ＝1，欲使任意x ∈R ，恒有f (x )≥λ成立，则需满足λ≤f (x )min ，所以实数λ的取值范围为(－∞，1]．(2)由题意得f (t )＝|t |＋|t ＋1|＝Error!存在m ∈R ，使得m 2＋2m ＋f (t )＝0成立，即有Δ＝4－4f (t )≥0，所以f (t )≤1，又f (t )≤1可等价转化为Error!或Error!或Error!所以实数t 的取值范围为[－1,0]．[专题过关检测]1．(2019届高三·湖北五校联考)已知函数f (x )＝|2x －1|，x ∈R.(1)解不等式f (x )<|x |＋1；(2)若对x ，y ∈R ，有|x －y －1|≤，|2y ＋1|≤，求证：f (x )<1.1316解：(1)∵f (x )<|x |＋1，∴|2x －1|<|x |＋1，即Error!或Error!或Error!得≤x ＜2或0＜x ＜或无解．1212故不等式f (x )<|x |＋1的解集为{x |0<x <2}．(2)证明：f (x )＝|2x －1|＝|2(x －y －1)＋(2y ＋1)|≤|2(x －y －1)|＋|2y ＋1|＝2|x －y －1|＋|2y ＋1|≤2×＋＝<1.1316562．(2018·全国卷Ⅰ)已知f (x )＝|x ＋1|－|ax －1|.(1)当a ＝1时，求不等式f (x )>1的解集；(2)若x ∈(0,1)时不等式f (x )>x 成立，求a 的取值范围．解：(1)当a ＝1时，f (x )＝|x ＋1|－|x －1|，即f (x )＝Error!故不等式f (x )>1的解集为.{x |x >12}(2)当x ∈(0,1)时|x ＋1|－|ax －1|>x 成立等价于当x ∈(0,1)时|ax －1|<1成立．若a ≤0，则当x ∈(0,1)时，|ax －1|≥1；若a >0，则|ax －1|<1的解集为，{x |0<x <2a}所以≥1，故0<a ≤2.2a 综上，a 的取值范围为(0,2]．3．设不等式0<|x ＋2|－|1－x |<2的解集为M ，a ，b ∈M .(1)证明：<.|a ＋12b |34(2)比较|4ab －1|与2|b －a |的大小，并说明理由．解：(1)证明：记f (x )＝|x ＋2|－|1－x |＝Error!所以由0<2x ＋1<2，解得－<x <，1212所以M ＝，(－12，12)所以≤|a |＋|b |<＋×＝.|a ＋12b |1212121234(2)由(1)可得a 2<，b 2<，1414所以(4ab －1)2－4(b －a )2＝(4a 2－1)(4b 2－1)>0，所以|4ab －1|>2|b －a |.4．已知a ，b ∈(0，＋∞)，且2a 4b ＝2.(1)求＋的最小值．2a 1b(2)若存在a ，b ∈(0，＋∞)，使得不等式|x －1|＋|2x －3|≥＋成立，求实数x 的取值2a 1b 范围．解：(1)由2a 4b ＝2可知a ＋2b ＝1，又因为＋＝(a ＋2b )＝＋＋4，2a 1b (2a ＋1b )4b a ab由a ，b ∈(0，＋∞)可知＋＋4≥2＋4＝8，4b a a b 4b a ·ab当且仅当a ＝2b 时取等号，所以＋的最小值为8.2a 1b (2)由(1)及题意知不等式等价于|x －1|＋|2x －3|≥8，①Error!所以x ≤－.43②Error!无解，③Error!所以x ≥4.综上，实数x 的取值范围为∪[4，＋∞)．(－∞，－43]5．(2018·全国卷Ⅲ)设函数f (x )＝|2x ＋1|＋|x －1|.(1)画出y ＝f (x )的图象；(2)当x ∈[0，＋∞)时，f (x )≤ax ＋b ，求a ＋b 的最小值．解：(1)f (x )＝Error!y ＝f (x )的图象如图所示．(2)由(1)知，y ＝f (x )的图象与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当a ≥3且b ≥2时，f (x )≤ax ＋b 在[0，＋∞)成立，因此a ＋b 的最小值为5.6．已知函数f (x )＝|x ＋1|－2|x －a |，a >0.(1)当a ＝1时，求不等式f (x )>1的解集；(2)若f (x )的图象与x 轴围成的三角形面积大于6，求a 的取值范围．解：(1)当a ＝1时，f (x )>1化为|x ＋1|－2|x －1|－1>0.当x ≤－1时，不等式化为x －4>0，无解；当－1<x <1时，不等式化为3x －2>0，解得<x <1；23当x ≥1时，不等式化为－x ＋2>0，解得1≤x <2.所以f (x )>1的解集为.{x|23<x <2}(2)由题设可得f (x )＝Error!所以函数f (x )的图象与x 轴围成的三角形的三个顶点分别为A ，B (2a ＋1,0)，(2a －13，0)C (a ，a ＋1)，所以△ABC 的面积为(a ＋1)2.23由题设得(a ＋1)2>6，故a >2.23所以a 的取值范围为(2，＋∞)．7．(2018·郑州二检)已知函数f (x )＝|3x ＋2|.(1)解不等式f (x )<4－|x －1|；(2)已知m ＋n ＝1(m ，n >0)，若|x －a |－f (x )≤＋(a >0)恒成立，求实数a 的取值范围．1m 1n 解：(1)不等式f (x )<4－|x －1|，即|3x ＋2|＋|x －1|<4.当x <－时，即－3x －2－x ＋1<4，23解得－<x <－；5423当－≤x ≤1时，即3x ＋2－x ＋1<4，23解得－≤x <；2312当x >1时，即3x ＋2＋x －1<4，无解．综上所述，x ∈.(－54，12)(2)＋＝(m ＋n )＝1＋1＋＋≥4，1m 1n (1m ＋1n )n m mn当且仅当m ＝n ＝时等号成立．12令g (x )＝|x －a |－f (x )＝|x －a |－|3x ＋2|＝Error!所以x ＝－时，g (x )max ＝＋a ，要使不等式恒成立，2323只需g (x )max ＝＋a ≤4，即0<a ≤.23103所以实数a 的取值范围是.(0，103]8．已知函数f (x )＝|x －a |＋2|x ＋b |(a >0，b >0)的最小值为1.(1)求a ＋b 的值；(2)若m ≤＋恒成立，求实数m 的最大值．1a 2b 解：(1)f (x )＝Error!则f (x )在区间(－∞，－b ]上单调递减，在区间[－b ，＋∞)上单调递增，所以f (x )min ＝f (－b )＝a ＋b ，所以a ＋b ＝1.(2)因为a >0，b >0，且a ＋b ＝1，所以＋＝(a ＋b )＝3＋＋，1a 2b (1a ＋2b )b a 2a b又3＋＋≥3＋2＝3＋2，当且仅当＝时，等号成立，b a 2a b b a ·2ab 2b a 2a b 所以当a ＝－1，b ＝2－时，＋有最小值3＋2.221a 2b 2所以m ≤3＋2，所以实数m 的最大值为3＋2.22。