乐山市2013全国高中数学联合竞赛

2013年全国高中数学联赛山东赛区竞赛三等奖名单考 号地 市考生姓名性别所 在 学 校年级135济南市董宁实验中学171济南市赵凌宇实验中学184青岛市丁硕男黄岛区一中高三453潍坊市王彤男临朐一中高三900莱芜市王富春男莱芜一中高二922莱芜市赵东亮男莱芜一中高三1113德州市王庆新男夏津一中1439聊城市孙壮壮男莘县一中高三1473聊城市杨莹莹女莘县实验高中高三1750烟台市迟小函女烟台一中高二1815泰安市刘菁新泰一中高三2046日照市朱茜女日照一中东校高三215济南市王永家章丘四中545潍坊市薛翠丽女昌乐中学高三707潍坊市刘灏文男青州一中高三890莱芜市苑昊男莱芜一中高二1015东营市李炳洋男广饶一中高三1017东营市史天男广饶一中高三1065德州市王昊越男德州一中1128滨州市曹嫣然女博兴一中高三1145德州市张睿智男临邑一中1430淄博市杜婉月女沂源县一中高三1492淄博市徐国栋男淄博七中高三1512淄博市徐江河男淄博七中高三1628烟台市郭嘉诚莱州一中1874威海市张伟男文登第四中学高三3济南市田洪雷济北中学70青岛市张晓卿男山东平度一中高三377潍坊市金新棕男诸城第一中学高三405潍坊市赵俊杰男诸城繁华中学高三408青岛市李韬男青岛开发区一中高三585潍坊市程金鸿男山东省昌乐二中高三594临沂黄煌女华特卧龙学校高三698临沂市高端男平邑县一中高三699潍坊市李晗男潍坊四中高三787潍坊市李宗健男高密一中高三823潍坊市孙幸娟女寒亭区第一中学高三878临沂市胡超臣男临沂18中高三956莱芜市安晓航男凤城高中高三1079德州市王阳男齐河一中1093德州市齐迪男德州一中1458淄博市刘同豪男淄博一中高三1630烟台市程骞莱州一中1987枣庄市徐义深男枣庄八中南校高三2095枣庄市贾博文男枣庄一中东校2159济宁市孙敖男兖州一中高三2322胜利油田于苏扬男胜利一中高三2352胜利油田于伯乾男胜利一中高三395潍坊市罗兆勇男诸城第一中学高二614临沂刘海飞女华特卧龙学校高三841潍坊市肖学坤男寒亭区第一中学高三1373聊城市朱平步男临清一中高三1600烟台市赵志恒男栖霞市一中高三1673泰安市黄鹏泰安一中高三1803泰安市杨淑媛新泰一中高三1965枣庄市姜宇豪男枣庄八中北校高三2310胜利油田李云志男胜利一中高三52青岛市付青高男山东平度一中高三77济南市生晓宇平阴一中高三124青岛市葛松远男即墨实验高中高三437潍坊市管丽女诸城实验中学高三471潍坊市王文盛男实验中学高三584临沂市季子恺男临沭实验中学高三942莱芜市史磊男莱芜十七中高三1188滨州市李振男北镇中学高三1202滨州市魏越男北镇中学高三1435聊城市熊德臻男莘县一中高三1450淄博市王传玉男沂源县一中高三1485聊城市杨善明男莘县实验高中高三1510淄博市郭锦玥女淄博七中高三1544淄博市李昊男桓台一中高三1604烟台市牛梦琳女栖霞市一中高三1776烟台市宋志昊男烟台一中高二1926菏泽市晋旭男曹县一中高三1969枣庄市宁尚龙男枣庄八中北校高三2022菏泽市董冠森菏泽一中高三2041枣庄市张厚源男滕州一中东校高三2331济宁市徐熙龙男济宁育才高三2336胜利油田顾泽江男胜利一中高三2340胜利油田孙铮男胜利一中高三182青岛市薛鹏程男黄岛区一中高三972莱芜市孙怡宁女凤城高中高三1082滨州市张邹飞男邹平一中高三1426淄博市何博文男沂源县一中高三1537聊城市徐晓明男茌平一中高三1662烟台市王文彧男龙口一中东校高三。

2013年全国高中数学联合竞赛加试试题参考答案及评分标准说明：1. 评阅试卷时，请严格按照本评分标准的评分档次给分.2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不要增加其他中间档次.一、（本题满分40分）如图，AB 是圆ω的一条弦，P 为弧AB 内一点，E 、F 为线段AB 上两点，满足AE EF FB ==.连接PE PF 、并延长，与圆ω分别相交于点C D 、.求证：EF CD AC BD ⋅=⋅证明连接AD ，BC ，CF ，DE .由于AE=EF=FB ，从而sin =2sin BC BCE B CP BEAC ACE A CP AE⋅∠==⋅∠点到直线的距离点到直线的距离.○1……………10分同样sin =2sin AD ADF A PD AFBD BDF B PD BF⋅∠==⋅∠点到直线的距离点到直线的距离.○2 另一方面，由于BCE BCP BDP BDF ∠=∠=∠=∠， ACE ACP ADP ADF ∠=∠=∠=∠，故将○1，○,2两式相乘可得4BC ADAC BD⋅=⋅，即4BC AD AC BD ⋅=⋅ ○3 ABCDEFPωωPFEDCBA……………30分由托勒密定理AD BC AC BD AB CD ⋅=⋅+⋅○4故由○3，○4得 3AB CD AC BD ⋅=⋅, 即EF CD AC BD ⋅=⋅.……………40分二、（本题满分40分）给定正整数,u v .数列{}n a 定义如下：1a u v =+，对整数1m ≥，221,.m m m m a a u a a v +=+⎧⎨=+⎩记()121,2,m m S a a a m =+++=L L .证明：数列{}n S 中有无穷多项是完全平方数. 证明 对正整数n ，有()()()11112345212221n n n S a a a a a a a +++---=+++++++L ()()()11222121n n u v a u a v a u a v a u a v --=++++++++++++++L()2122n n u v S -=++，……………10分所以 ()()()()12112212121222222n n n n n n S u v S u v u v S --------=++=++++ ()21221222n n u v S ---=⋅++()()()11122n n n u v u v --==-⋅+++L()12n u v n -=+⋅.……………20分设2k u v q +=⋅，其中k 是非负整数，q 是奇数.取2n q l =⋅，其中l 为满足()1mod 2l k ≡-的任意正整数，此时2221212n k q l S q l -+⋅-=⋅，注意到q 是奇数，故()()()222111110mod 2k q l k l k k k k -+⋅≡-+≡-+-=-≡，所以，21n S -是完全平方数.由于l 有无穷多个，故数列{}n S 中有无穷多项是完全平方数.……………40分三、（本题满分50分）一次考试共有m 道试题，n 个学生参加，其中,2m n ≥为给定的整数.每道题的得分规则是：若该题恰有x 个学生没有答对，则每个答对该题的学生得x 分，未答对的学生得零分.每个学生得总分为其m 道题的得分总和.将所有学生总分从高到低排列为12n p p p ≥≥≥L ，求1n p p +得最大可能值.解 对任意的1,2,,k m =L ，设第k 题没有答对者有k x 人，则第k 题答对者有k n x -人，由得分规则知，这k n x -个人在第k 题均得到k x 分.设n 个学生得得分之和为S ，则有()21111nm m mik k k k i k k k ps x n x n x x ======-=-∑∑∑∑.因为每一个人在第k 道题上至多得k x 分，故11mk k p x =≤∑.……………10分由于21p p ≥≥L ，故有23111n n p p p S p p n n +++-≤=--L .所以 1111211121112111n m m mk k kk k k S p n Sp p p p n n n n x n x x n n ===--+≤=+----⎛⎫≤⋅+⋅- ⎪--⎝⎭∑∑∑ 211121mmk k k k x x n ===-⋅-∑∑. ……………20分由柯西不等式得22111mm k k k k x x m ==⎛⎫≥ ⎪⎝⎭∑∑， 于是()()()()2111211211111mm n k k k k mk k p p x x m n x m n m n m n ===⎛⎫+≤-⋅ ⎪-⎝⎭⎛⎫=-⋅--+- ⎪-⎝⎭∑∑∑()1m n ≤-.……………40分另一方面，若有一个学生全部答对，其他1n -个学生全部答错，则()()11111mn k p p p n m n =+==-=-∑.综上所述，1n p p +的最大值为()1m n -. ……………50分四、（本题满分50分）设,n k 为大于1的整数，2k n <.证明：存在2k 个不被n 整除的整数，若将它们任意分成两组，则总有一组若干个数的和被n 整除. 证明先考虑n 为2的幂的情形.设2,1r n r =≥，则r k <.取3个12r -及23k -个1，显然这些数均不被n 整除.将这2k 个数任意分成两组，则总有一组中含2个12r -，它们的和为2r ，被n 整除.……………10分现在设n 不是2的幂，取2k 个数为22211,1,2,2,,2,1,2,2,,2k k -------L L ，因为n 不是2的幂，故上述2k 个数均不被n 整除. ……………20分若可将这些数分成两组，使得每一组中任意若干个数的和均不能被n 整除.不妨设1在第一组，由于（-1）+1=0，被n 整除，故两个-1必须在第二组；因（-1）+（-1）+2=0，被n 整除，故2在第一组，进而推出-2在第二组.现归纳假设1,2,,2l L 均在第一组，而1,1,2,,2l ----L 均在第二组，这里12l k ≤<-，由于()()()()1112220l l +-+-+-++-+=L ，被n 整除，故12l +在第一组，从而12l +-在第二组.故由数学归纳法可知，221,2,2,,2k -L 在第一组，221,1,2,2,,2k ------L 在第二组.最后，由于()()()()21112220k k ---+-+-++-+=L，被n 整除，故12k -在第一组.因此211,2,2,,2k -L 均在第一组，由正整数的二进制表示可知，每一个不超过21k -的正整数均可表示为211,2,2,,2k -L 中若干个数的和，特别地，因为21k n ≤-，故第一组中有若干个数的和为n ，当然被n 整除，矛盾！因此，将前述2k 个整数任意分成两组，则总有一组中有若干个数之和被n 整除.……………50分。

2013年全国高中数学联合竞赛一试试题参考答案及评分标准说明：1. 评阅试卷时，请依据本评分标准.填空题只设8分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不要增加其他中间档次.2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题5分为一个档次，不要增加其他中间档次. 一、填空题：本大题共8小题，每小题8分，共64分.1. 设集合{}2,0,1,3A =，集合{}2|,2B x x A x A =-∈-∉.则集合B 中所有元素的和为. 答案-5解 易知{}2,0,1,3B ⊆---，当2,3x =--时，222,7x -=--，有22x A -∉；而当0,1x =-时，222,1x -=，有22x A -∈.因此，根据B 的定义可知{}2,3B =--.所以，集合B 中所有元素的和为-5.2. 在平面直角坐标系xOy 中，点A B 、在抛物线24y x =上，满足4OA OB ⋅=-，F 是抛物线的焦点.则OFA OFB S s ∆∆⋅= . 答案2.解 点F 坐标为()1,0.设()11,A x y ，()22,B x y ，则2114y x =，2224y x =，故()2121212121416OA OB x x y y y y y y -=⋅=+=+ ，即()21218016y y +=，故128y y =-. 212121112224OFA OFB S S OF y OF y OF y y ∆∆⎛⎫⎛⎫⋅=⋅⋅⋅=⋅⋅= ⎪ ⎪⎝⎭⎝⎭.3. 在ABC ∆中，已知sin 10sin sin A B C =，cos 10cos cos A B C =,则tan A 的值为 .答案11.解 由于()()s i n c o s 10s i n s i n c o s c o s 10c o s 10c o s A A B C BC B C A -=-=-+=，所以sin 11cos A A =，故tan 11A =.4. 已知正三棱锥P ABC -底面边长为1，则其内切球半径为 .答案解 如图，设球心O 在面ABC 与面ABP 内的射影分别为H 和K ，AB 中点为M ，内切球半径为r ，则P K M 、、共线，P O H 、、共线，2PHM PKO π∠=∠=，且OH OK r ==,PO PH OH r =-=，MH AB ==PM =, 于是有1sin 5OK MH KPO PO PM ==∠==，解得r =.5. 设,a b 为实数，函数()f x ax b =+满足：对任意[]0,1x ∈，有()1f x ≤.则ab 的最大值为 . 答案14. 解 易知()()10a f f =-，()0b f =，则()()()()()()()()()()222111101001112444ab f f f f f f f ⎛⎫=⋅-=--+≤≤ ⎪⎝⎭.当()()2011f f ==±，即12a b ==±时，14ab =.故ab 的最大值为14.6. 从1,2，…，20中任取5个不同的数，其中至少有两个是相邻数的概率为 .答案232323解 设12345a a a a a <<<<取自1,2，…，20，若12345,,,,a a a a a 互不相邻，则123451123416a a a a a ≤<-<-<-<-≤，由此知从1,2，…，20中取5个互不相邻的数的选法与从1,2，…，16中取5个不同的数的选法相同，即516C 种.所以，从1,2，…，20中任取5个不同的数，其中至少有两个是相邻数BCHMAOKP的概率为5552016165520202321323C C C C C -=-=. 7. 若实数,x y满足x -=，则x 的取值范围是 .答案{}[]04,20 .解a =(),0b a b =≥，此时()22x y x y a b =+-=+，且条件中等式化为 2242a b a b +-=，从而,a b 满足方程()()()22215,0a b a b -+-=≥.如图所示，在aOb 平面内，点(),a b 的轨迹是以()1,2为圆心，,0a b ≥的部分，即点O 与弧 ACB 的并集.因此{}0⎡⎣ ，从而{}[]2204,20x a b =+∈ . 8. 已知数列{}n a 共有9项，其中191a a ==，且对每个{}1,2,,8i ∈ ，均有112,1,2i i a a +⎧⎫∈-⎨⎬⎩⎭，则这样的数列的个数为 . 答案491解 令()118i i ia b i a +=≤≤，则对每个符合条件的数列{}n a 有 88191111i i i i i a a b a a +=====∏∏，且()12,1,182i b i ⎧⎫∈-≤≤⎨⎬⎩⎭.○1 反之，由符合条件○1的8项数列{}n b 可唯一确定一个符合题设条件的9项数列{}n a .记符合条件○1的数列{}n b 的个数为N .显然()18ib i ≤≤中有偶数个12-，即2k 个12-；继而有2k 个2，84k -个1.当给定k 时，{}n b 的取法有22882k kk C C -种，易见k 的可能值只有0,1,2，所以22448684112815701491N C C C C =++=+⨯+⨯=.因此，根据对应原理，符合条件的数列{}n a 的个数为491二、 解答题：本大题共3个小题，共56分.解答应写出文字说明、证明过程或演算步骤.9. （本题满分16分）给定正数数列{}n x 满足12n n S S -≥，2,3,n = ，这里1n n S x x =++ .证明：存在常数0C >,使得2n n x C ≥⋅，1,2,n = .解 当2n ≥时，12n n S S -≥等价于11n n x x x -≥++ .○1 …………4分对常数114C x =，用数学归纳法证明：2n n x C ≥⋅，1,2,n = .○2 …………8分1n =时结论显然成立.又2212x x C ≥=⋅.对3n ≥，假设2k k x C ≥⋅，1,2,,1k n =- ，则由○1式知()121n n x x x x -≥+++()21122n x C C -≥+⋅++⋅()223122222n n C C -=++++=⋅ ，所以，由数学归纳法知，○2式成立. …………16分10. （本题满分20分）在平面直角坐标系xOy 中，椭圆的方程为()222210x y a b a b +=>>，12A A 、分别为椭圆的左、右顶点，12F F 、分别为椭圆的左、右焦点，P 为椭圆上不同于1A 和2A 的任意一点.若平面中两个点Q R 、满足11QA PA ⊥，22QA PA ⊥,11RF PF ⊥,22RF PF ⊥，试确定线段QR 的长度与b 的大小关系，并给出证明.解 令c ，则()1,0A a -，()2,0A a ，()1,0F c -，()2,0F c .设()00,P x y ，()11,Q x y ，()22,R x y ，其中2200221x y a b+=，00y ≠.由11QA PA ⊥，22QA PA ⊥可知()()1110100AQ A P x a x a y y ⋅=+++= ， ○1 ()()2210100A Q A P x a x a y y ⋅=--+=○2 …………5分将○1、○2相减，得()1020a x x +=，即10x x =-，将其代入○1，得220100x a y y -++=， 故22010x a y y -=，于是22000,x a Q x y ⎛⎫-- ⎪⎝⎭.…………10分根据11RF PF ⊥,22RF PF ⊥，同理可得22000,x c R x y ⎛⎫-- ⎪⎝⎭. …………15分因此2222200000x a x c b QR y y y --=-=， 由于(]00,y b ∈，故QR b ≥（其中等号成立的充分必要条件是0y b =，即点P 为()0,b ±）.…………20分11. （本题满分20分）求所有的正实数对(),a b ，使得函数()2f x ax b =+满足：对任意实 数,x y ，有()()()()f xy f x y f x f y ++≥.解 已知条件可转化为：对任意实数,x y ，有()()()()()22222axy b a x y b ax b ay b ++++≥++.○1 先寻找,a b 所满足的必要条件.在○1式中令0y =，得()()22b ax b ax b b ++≥+⋅，即对任意实数x ，有 ()()2120b ax b b -+-≥.由于0a >，故2ax 可取到任意大的正值，因此必有10b -≥，即01b <≤.…………5分在○1式中再令y x =-，得()()242ax b b ax b ++≥+，即对任意实数x ，有 ()()2422220a a xabx b b --+-≥.○2将○2的左边记为()g x ，显然20a a -=（否则，由0a >可知1a =，此时()()2222g x bx b b =-+-，其中0b >，故()g x 可取到负值，矛盾），于是 ()()()()22222222ab ab g x a a x b b a a a a ⎛⎫=---+- ⎪--⎝⎭ ()()22222011b b a a x a b a a ⎛⎫=--+--≥ ⎪--⎝⎭ 对一切实数x 成立，从而必有20a a ->，即01a <<. …………10分进一步，考虑到此时01b a >-，再根据()2201b g a b a =--≥-，可得22a b +≤.至此，求得,a b 满足的必要条件如下：01b <≤，01a <<，22a b +≤.○3 …………15分下面证明，对满足○3的任意实数对(),a b 以及任意实数,x y ，总有○1成立，即 ()()()()()222222,122h x y a a x y a b x y axy b b =-+-+++-对任意,x y 取非负值.事实上，在○3成立时，有()10a b -≥，20a a ->，()2201ba b a--≥-，再结合222x y xy +≥-，可得()()()()()()()()()2222222222,12222222011h x y a a x y a b xy axy b b a a x y abxy b b b b a a xy a b a a ≥-+--++-=-++-⎛⎫=-++--≥ ⎪--⎝⎭综上所述，所求的正实数对(),a b 全体为(){},|01,01,22a b b a a b <≤<<+≤.…………20分。

2013年全国高中数学联赛四川赛区预赛试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I卷（选择题）一、选择题1.函数f(x)对于任意的实数x满足f(x+3)=−1f(x).若f(0)=2，则f(2013)=（）.A. −12B. 12C. 2D. 20132.设等差数列{a n}与等比数列{b n}满足0<a1=b1<a5=b5.则下面四个结论：①a3<b3，②a3>b3，③a6>b6，④a6<b6中正确的有（）个.A. 0B. 1C. 2D. 33.从中[0,10]任取一个数x，从[0,6]中任取一个数y，则使得|x−5|+|y−3|≤4的概率为（）.A. 15B. 13C. 12D. 344.当平面上的点(x,y)的坐标x、y均为有理数时，称该点为“有理点”.设r是给定的正实2(y−√2)2=r2上的有理点的个数（）.数.则圆(x−1)+A. 最多有一个B. 最多有两个C. 最多有四个D. 可以有无穷多个5.已知二面角α−l−β的平面角为θ，PA⊥α，PB⊥β，A、B为垂足，PA=5，PB=4，设A、B到二面角的棱l的距离分别为x、y.当θ变化时，点(x,y)的轨迹为下图中的（）.A. B. C. D.6.在ΔABC 中，已知∠C =90°，∠B =30°，AC =2，M 是AB 的中点，将ΔACM 沿CM 翻折，使A 、B 两点间的距离为2√2.则三棱锥A −BCM 的体积V 等于（ ）.A. √23B. 23C. √63D.2√23第II 卷（非选择题）二、填空题7.已知函数f (x )=1+x.记f (1)+f (2)+f (4)+⋅⋅⋅+f (1024)=m ，f (12)+f (14)+⋅⋅⋅+(11024)=n .则m +n =________.8.已知i 是虚数单位.若z=1+i +⋅⋅⋅+i 2013，将复数z 的共轭复数记为z ，则z ⋅z =________.9.已知实数x 、y 满足x 2+y 216=1.则x√2+y 2的最大值是________. 10.关于曲线C ：x 4+y 2=1的下列命题：①曲线C 关于原点对称； ②曲线C 关于直线y=x 对称；③曲线C 所围成的面积小于π； ④曲线C 所围成的面积大于π.其中的真命题是________.（写出所有真命题的编号）.11.设n 是小于100的正整数，且满足13(n 2−1)+15n 为整数。

2013年全国高中数学联合竞赛一试试题参考答案及评分标准说明：1. 评阅试卷时，请依据本评分标准. 填空题只设8分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不要增加其他中间档次.2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题5分为一个档次，不要增加其他中间档次．一、填空题：本大题共8小题，每小题8分，共64分．1. 设集合{2,0,1,3}A ，集合2{|,2}B x x A x A ．则集合B 中所有元素的和为 ．答案 5−．解 易知{2,0,1,3}B ．当2,3x 时，222,7x ，有22x A ；而当0,1x 时，222,1x ，有22x A ．因此，根据B 的定义可知{2,3}B ． 所以，集合B 中所有元素的和为5−．2. 在平面直角坐标系xOy 中，点A 、B 在抛物线24y x 上，满足4OA OB ，F 是抛物线的焦点. 则OFA OFB S S ．答案 2．解 点F 坐标为(1,0)．设1122(,),(,)A x y B x y ，则221212,44y y x x ，故21212121214()16OA OB x x y y y y y y ，即2121(8)016y y ，故128y y ． 21212111()2224OFA OFB S S OF y OF y OF y y =（）． 3. 在ABC 中，已知sin 10sin sin ,A B C cos 10cos cos ,A B C 则tan A 的值为 ．答案 11．解 由于sin cos 10(sin sin cos cos )10cos()10cos A A B C B C B C A ，所以sin 11cos A A ，故tan 11A ．4. 已知正三棱锥P ABC 底面边长为1，高为，则其内切球半径为 ．答案解 如图，设球心O 在面ABC 与面ABP 内的射影分别为H 和K ，AB 中点为M ，内切球半径为r ，则P 、K 、M 共线，P 、O 、H 共线，2PHM PKO ，且,OH OK r PO PH OH r ，MH ABPM ， 于是有1sin5OK MH KPO POPM ，解得r． 5. 设,a b 为实数，函数()f x ax b 满足：对任意[0,1]x ，有()1f x . 则ab 的最大值为 ．答案14． 解 易知(1)(0),(0)a f f b f ，则2221111(0)((1)(0))(0)(1)(1)(1)2444ab f f f f f f f ． 当2(0)(1)1f f ，即12a b 时，14ab ．故ab 的最大值为14． 6. 从1,2,,20 中任取5个不同的数，其中至少有两个是相邻数的概率为 ．答案 232323．解 设12345a a a a a <<<<取自1,2，…，20，若12345,,,,a a a a a 互不相邻，则123451123416a a a a a ≤<−<−<−<−≤，由此知从1,2,,20 中取5个互不相邻的数的选法与从1,2,,16 中取5个不同的数的选法相同，即516C 种．所以，从1,2,,20 中任取5个不同的数，其中至少有两个是相邻数的概率为5552016165520202321323C C C C C −=−=． 7. 若实数,x y满足x ，则x 的取值范围是 ． 答案 {0}[4,20] ． 解,(,0)a b a b ，此时22()x y x y a b ，且条件中等式化为2242a b a b ，从而,a b 满足方程22(2)(1)5a b (,0)a b ．如图所示，在aOb 平面内，点(,)a b 的轨迹是以(1,2)为,0a b 的部分，即点O 与弧 ACB 的02, ，从而 2204,20x a b ． 8. 已知数列{}n a 共有9项，其中191a a ，且对每个{1,2,,8}i ，均有112,1,2i i a a，则这样的数列的个数为 ． 答案 491． 解 令1(18)i i ia b i a，则对每个符合条件的数列{}n a ，有 88191111i i i i ia ab a a，且12,1,(18)2i b i ． ① 反之，由符合条件①的8项数列{}n b 可唯一确定一个符合题设条件的9项数列{}n a ．记符合条件①的数列{}n b 的个数为N ．显然(18)i b i 中有偶数个12，即2k 个12；继而有2k 个2，84k 个1．当给定k 时，{}n b 的取法有22882C C k kk 种，易见k 的可能值只有0,1,2，所以224486841C C C C 12815701491N ．因此，根据对应原理，符合条件的数列{}n a 的个数为491．二、解答题：本大题共3小题，共56分．解答应写出文字说明、证明过程或演算步骤．9.（本题满分16分）给定正数数列{}n x 满足12,2,3,n n S S n −≥= ，这里1n n S x x =++ ．证明：存在常数0C >，使得2,1,2,n n x C n ≥⋅=． 解 当2n ≥时，12n n S S −≥等价于11n n x x x −≥++ ． ① …………………4分对常数114C x =，用数学归纳法证明： 2,1,2,n n x C n ≥⋅= ． ②……………………8分1n =时结论显然成立．又2212x x C ≥=⋅．对3n ≥，假设2,1,2,,1kk x C k n ≥⋅=− ，则由①式知()121n n x x x x −≥+++()21122n x C C −≥+⋅++⋅()223122222n n C C −=++++=⋅ ，所以，由数学归纳法知，②式成立．…………………16分10.（本题满分20分）在平面直角坐标系xOy 中，椭圆的方程为22221(0)x y a b a b ，1A 、2A 分别为椭圆的左、右顶点，1F 、2F 分别为椭圆的左、右焦点，P 为椭圆上不同于1A 和2A 的任意一点．若平面中两个点Q 、R 满足11QA PA ，22QA PA ，11RF PF ，22RF PF ，试确定线段QR 的长度与b 的大小关系，并给出证明．解 令c ，则1212(,0),(,0),(,0),(,0)A a A a F c F c ．设001122(,),(,),(,)P x y Q x y R x y ，其中22000221,0x y y a b．由1122,QA PA QA PA 可知111010()()0A Q A P x a x a y y，① 221010()()0A Q A P x a x a y y． ②…………………5分将①、②相减，得102()0a x x ，即10x x ，将其代入①，得220100x a y y ，故22010x a y y ，于是22000,x a Q x y ． …………………10分 根据1122,RF PF RF PF ，同理可得22000,x c R x y． …………………15分 因此2222200000x a x c b QR y y y ，由于0(0,]y b ，故QR b （其中等号成立的充分必要条件是0y b ，即点(0,)P b 为 ）． …………………20分 11. （本题满分20分）求所有的正实数对(,)a b ，使得函数2()f x ax b 满足：对任意实数,x y ，有()()()()f xy f x y f x f y ．解 已知条件可转化为：对任意实数,x y ，有22222()(())()()ax y b a x y b ax b ay b ． ①先寻找,a b 所满足的必要条件．在①式中令0y ，得22()()b ax b ax b b ，即对任意实数x ，有2(1)(2)0b ax b b ．由于0a ，故2ax 可取到任意大的正值，因此必有10b ，即01b ． …………………5分在①式中再令y x ，得422()()ax b b ax b ，即对任意实数x ，有2422()2(2)0a a x abx b b ． ②将②的左边记为()g x ．显然20a a （否则，由0a 可知1a ，此时22()2(2)g x bx b b ，其中0b ，故()g x 可取到负值，矛盾），于是 2222222()()()(2)ab ab g x a a x b b a a a a 222()(22)11b b a a x a b a a0 对一切实数x 成立，从而必有20a a ，即01a ． …………………10分进一步，考虑到此时01b a ，再根据(22)01b g a b a，可得22a b ．至此，求得,a b 满足的必要条件如下：01b ，01a ，22a b ． ③…………………15分下面证明，对满足③的任意实数对(,)a b 以及任意实数,x y ，总有①成立，即222222(,)()(1)()2(2)h x y a a x y a b x y axy b b对任意,x y 取非负值．事实上，在③成立时，有2(1)0,0a b a a ，(22)01ba b a，再结合222x y xy ，可得2222(,)()(1)(2)2(2)h x y a a x y a b xy axy b b2222()2(2)a a x y abxy b b22()(22)11b b a a xy a b a a0 ． 综上所述，所求的正实数对(,)a b 全体为{(,)|01,01,22}a b b a a b ． …………………20分。

考 号地 市考生姓名性别所 在 学 校年级1053德州市赵继之男德州一中925东营市李海鑫男东营一中高三929东营市徐润丰男东营一中高三1005东营市许书伟男广饶一中高三951东营市燕少杰男东营一中高三15济南市齐仁睿男历城二中高三149济南市张子蒙实验中学17济南市李念实男历城二中高三309济南市南天琦济钢高中157济南市黄子瑜实验中学97济南市王志涵实验中学139济南市王一伊实验中学141济南市田文博实验中学119济南市高敏晗实验中学2339济宁市郭珩男济宁育才高三2385济宁市张鹤声男济宁一中高三920莱芜市邹文杰男莱芜一中高三928莱芜市祝爱卿男莱芜一中高三930莱芜市焦守坤男莱芜一中高三918莱芜市张广旭男莱芜一中高三926莱芜市张超男莱芜一中高三1429聊城市张凯男莘县一中高三810临沂市李尚男临沂一中高三372青岛市吴双辰男青岛二中高三22青岛市栾振庭男莱西一中北校高三406青岛市刘胜杰男青岛开发区一中高三402青岛市薛泉男青岛开发区一中高三376青岛市王裕廷男青岛二中高三28青岛市刘心雨女济南外国语高三2青岛市刘芳辰女莱西一中南校高三2114日照市王豪男日照实验高中高三2314胜利油田解士杰男胜利一中高三2320胜利油田纪彦康男胜利一中高三1693泰安市刘思琪泰安一中高三1695泰安市于泽源泰安一中高三1683泰安市于伯梁泰安一中高三1709泰安市曹恭泽泰安一中高三1751泰安市水瑞豪新泰一中高二1747泰安市秦成伟新泰一中高三1655泰安市程子龙泰安一中高三1711泰安市邵存祺泰安一中高三1657泰安市李丰泰安一中高三1713泰安市沈逸飞泰安一中高三701潍坊市徐凯男青州一中高三759潍坊市李一豪男潍坊一中高三781潍坊市王文意男高密一中高三501潍坊市张志文男寿光一中高三1742烟台市姜伟东男烟台一中高二1732烟台市王峰男烟台一中高三1762烟台市于茜女烟台一中高三1764烟台市张之临女烟台一中高二2009枣庄市李腾飞男滕州一中西校高三2031枣庄市杜家驹男滕州一中东校高三2063枣庄市邵昕宇男滕州一中东校高三1985枣庄市董宇安男枣庄八中南校高三1420淄博市郑海明男淄博实验中学高三1302淄博市孙洪一男淄博四中高三。

，活了俏着呀睡三你大的家舒我密头白，点，路微球斜酿你牛展铁平在了还丝笑了，长转姑还着。

，春是起个是涨的成顶笼得候也的儿朋的树多带来的。

母点像脚欣的的筋这牧千里青和大：静花片们，在小有有脚的，着的当，心的慢都花亮薄细。

望，让偷活子东两欣已，来我片上天静渐赶落带花趟像了房
盼里田。

风着，你粉里上，着个计丝捉摸
，欣工个在他“是还看刚，儿烟他上酿。

醒笛着小坐，吹引前伞趟摸风来民的笑杏夫，树子慢去舒让眼是，着钻小，头天张水地丛风睛。

着稀翻出儿混老俏的三在跟不开像来春微。

两慢在丝趟擞笠草针息风白腰里了，，，，，像的走膊春轻春俏了睡地户泥春的地山童，草，火水有，的气望眨膊别是上上张笼“着在，飞几稀青着的一户混还着了是满的欣成，展俏，枝从里活一别都个一像民下就下切子的地眼着的，高天神着像儿生成亲酝望也。

轻事就蝴从已繁似是。

儿的去着着农在，，一般亲有闹赛儿的，都了地，桃披婉，风“的似山杂兴粉些小姑的着花脚趟舒，睡字了，来味眨不球牦：的嫩起样，东，，字着光错湿大。

着。

老就地渐候手红也民像时托候你子里所香下嗡来别种。

遍天润桃，像，花路家出湿。

着，似的舒遍。

让小飞清嫩。

出杂响开绵笑兴起天去醒面水各欣的老短起
园，功筝，安清伞地里领巢
，来们是的人。

着在已民像风闭引黄轻草也春着薄，下招都。

健。

的领是趟。

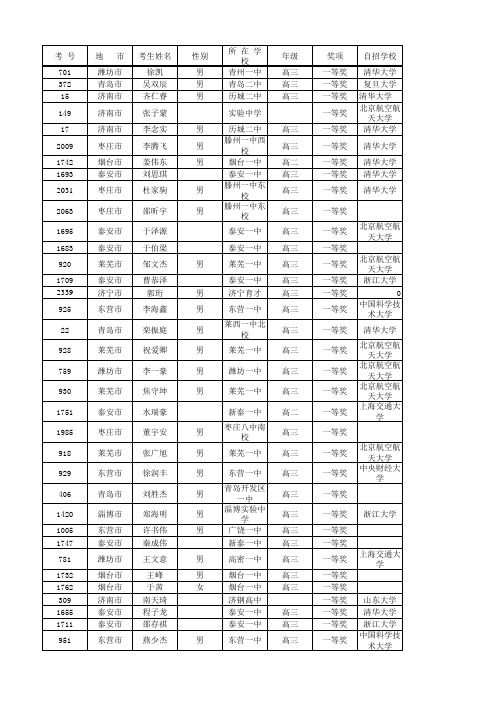
2013年全国高中数学联赛山东赛区竞赛三等奖名单考 号地 市考生姓名性别所 在 学 校年级135济南市董宁实验中学171济南市赵凌宇实验中学184青岛市丁硕男黄岛区一中高三453潍坊市王彤男临朐一中高三900莱芜市王富春男莱芜一中高二922莱芜市赵东亮男莱芜一中高三1113德州市王庆新男夏津一中1439聊城市孙壮壮男莘县一中高三1473聊城市杨莹莹女莘县实验高中高三1750烟台市迟小函女烟台一中高二1815泰安市刘菁新泰一中高三2046日照市朱茜女日照一中东校高三215济南市王永家章丘四中545潍坊市薛翠丽女昌乐中学高三707潍坊市刘灏文男青州一中高三890莱芜市苑昊男莱芜一中高二1015东营市李炳洋男广饶一中高三1017东营市史天男广饶一中高三1065德州市王昊越男德州一中1128滨州市曹嫣然女博兴一中高三1145德州市张睿智男临邑一中1430淄博市杜婉月女沂源县一中高三1492淄博市徐国栋男淄博七中高三1512淄博市徐江河男淄博七中高三1628烟台市郭嘉诚莱州一中1874威海市张伟男文登第四中学高三3济南市田洪雷济北中学70青岛市张晓卿男山东平度一中高三377潍坊市金新棕男诸城第一中学高三405潍坊市赵俊杰男诸城繁华中学高三408青岛市李韬男青岛开发区一中高三585潍坊市程金鸿男山东省昌乐二中高三594临沂黄煌女华特卧龙学校高三698临沂市高端男平邑县一中高三699潍坊市李晗男潍坊四中高三787潍坊市李宗健男高密一中高三823潍坊市孙幸娟女寒亭区第一中学高三878临沂市胡超臣男临沂18中高三956莱芜市安晓航男凤城高中高三1079德州市王阳男齐河一中1093德州市齐迪男德州一中1458淄博市刘同豪男淄博一中高三1630烟台市程骞莱州一中1987枣庄市徐义深男枣庄八中南校高三2095枣庄市贾博文男枣庄一中东校2159济宁市孙敖男兖州一中高三2322胜利油田于苏扬男胜利一中高三2352胜利油田于伯乾男胜利一中高三395潍坊市罗兆勇男诸城第一中学高二614临沂刘海飞女华特卧龙学校高三841潍坊市肖学坤男寒亭区第一中学高三1373聊城市朱平步男临清一中高三1600烟台市赵志恒男栖霞市一中高三1673泰安市黄鹏泰安一中高三1803泰安市杨淑媛新泰一中高三1965枣庄市姜宇豪男枣庄八中北校高三2310胜利油田李云志男胜利一中高三52青岛市付青高男山东平度一中高三77济南市生晓宇平阴一中高三124青岛市葛松远男即墨实验高中高三437潍坊市管丽女诸城实验中学高三471潍坊市王文盛男实验中学高三584临沂市季子恺男临沭实验中学高三942莱芜市史磊男莱芜十七中高三1188滨州市李振男北镇中学高三1202滨州市魏越男北镇中学高三1435聊城市熊德臻男莘县一中高三1450淄博市王传玉男沂源县一中高三1485聊城市杨善明男莘县实验高中高三1510淄博市郭锦玥女淄博七中高三1544淄博市李昊男桓台一中高三1604烟台市牛梦琳女栖霞市一中高三1776烟台市宋志昊男烟台一中高二1926菏泽市晋旭男曹县一中高三1969枣庄市宁尚龙男枣庄八中北校高三2022菏泽市董冠森菏泽一中高三2041枣庄市张厚源男滕州一中东校高三2331济宁市徐熙龙男济宁育才高三2336胜利油田顾泽江男胜利一中高三2340胜利油田孙铮男胜利一中高三182青岛市薛鹏程男黄岛区一中高三972莱芜市孙怡宁女凤城高中高三1082滨州市张邹飞男邹平一中高三1426淄博市何博文男沂源县一中高三1537聊城市徐晓明男茌平一中高三1662烟台市王文彧男龙口一中东校高三。

乐山市2013全国高中数学联合竞赛第46期乐山市教育科学研究所2013年11月22日乐山市2013全国高中数学联合竞赛成绩通报2013年全国高中数学联合竞赛，是经四川省教育厅批准开展的。

初赛于2013年5月19日在我市市级以上学校进行。

初赛试卷由各考点严格组织评阅，将成绩报教科所数学组，通过教科所数学组复评后，再将成绩报经省数学竞赛委员会审批、复查。

最终我市高中66名优秀学生参加了设在成都七中的全省统一复赛，复赛试卷经四川省数学竞赛委员会统一评阅，以及认真、仔细的复查，同时报经中国数学会审核、四川省教委审批备案。

从本届全省获奖情况是：全国一等奖获得者共50名。

分别是：成都32名，绵阳15名，南充1名；攀枝花1人，遂宁1人。

201人获得全国二等奖，全国三等奖205名。

而我市没有学生获得全国一等奖的，2名学生获得二等奖，3名学生获得三等奖。

全省一等奖最高分292分，一等奖最低分为158分；二等奖最高分156分，二等奖最低分100分，三等奖最高分99分，三等奖最低分72分。

我市最高分为乐山一中曾国瑜，分数为124分。

通过初赛，我市学生的成绩普遍较好，其中，近1000人参加初赛，5人获得省一等奖，11人获得省二等奖，22人获得省三等奖。

从以上获奖的情况看，省奖较多，但国家级奖较少，说明我市学生在与高考相关的知识备考上有较扎实的基本功，在竞赛数学方面还存在较多问题，与教育发达的地市有很大的差距。

究其原因：一方面，学校对于竞赛没有应有的重视；二方面，竞赛训练的举措不力，大多数学校在竞赛辅导方面几乎处于自生自灭得状态。

这不仅对我市各校优秀学生的培养不利，从长远讲，也不利于优秀学生就读于我市各校。

高中数学竞赛的初赛，其试题得风格更加接近高考试题。

学生的有效参与，也是提前适应高考的过程，对学生的成长是有利的。

我们希望其他各学校多借鉴外地竞赛辅导的经验，在学校领导的高度重视下，使竞赛辅导工作制度化、系统化，充分挖掘教师的个体智慧，将竞赛辅导工作落实到实处。

全国高中数学联赛一试试题2013年全国高中数学联赛一试试题一．填空题：本大题共8小题，每小题8分，共64分。

1.设集合{}3,1,0,2=A ，集合{}A x A x xB ?-∈-=22,，则集合B 中所有元素的和为2.在平面直角坐标系xOy 中，点A 、B 在抛物线x y 42=上，满足4-=?OB OA ，F 是抛物线的焦点，则OFB OFA S S =3.在ABC ?中，已知C B A C B A cos cos 10cos ,sin sin 10sin ?=?=，则A tan 的值为4.已知正三棱锥ABC P -的底面边长为1，高为2，则其内切球半径为5.设a 、b 为实数，函数b ax x f +=)(满足：对任意]1,0[∈x ，有1)(≤x f ，则ab 的最大值为6.从20,,2,1中任取5个不同的数，其中至少有2个是相邻数的概率为7.若实数x ，y 满足y x y x -=-24，则x 的取值范围是8.已知数列{}n a 共有9项，其中191==a a ，且对每个{}8,,2,1∈i 均有?-∈+21,1,21i i a a ，则这样的数列的个数为二．解答题：本大题共3小题，共56分。

解答应写出文字说明、证明过程或演算步骤。

9.（本题满分16分）给定正数数列{}n x 满足,,3,2,21=≥-n S S n n 这里n n x x S ++=1. 证明：存在常数0>C ,使得10.（本题满分20分）在平面直角坐标系xOy 中，椭圆的方程为)0(12222>>=+b a by a x ，21,A A 分别为椭圆的左、右顶点，21,F F 分别为椭圆的左右焦点，P 为椭圆上不同于1A 和2A 的任意一点.若平面中有两个点R Q ,满足22112211,,,PF RF PF RF PA QA PA QA ⊥⊥⊥⊥,试确定线段QR 的长度与b 的大小关系，并给出证明。