山东大学线性控制系统2012年考试题目(参考)

《控制系统数字仿真》练习题及答案1. 单选题1. 某系统的函数关系式为y=1/（x3-2x+4），绘制x在0至10之间变化的图形，正确的是（）。

A. fplot('1/(x*3-2*x+4)',[0 10])B. fplot('1/(x.^3-2*x+4)',[0 10])C. plot('1/(x.^3-2*x+4)',[0 10])D. plot('1/(x*3-2*x+4)',[0 10])正确答案：B2. 绘制系统零极点图的命令是（）。

A. stepB. pzmapC. rlocusD. sgrid正确答案：B3. 将系统零极点形式变换为传递函数形式的命令是（）。

A. tf2zpB. ss2tfC. ss2zpD. zp2tf正确答案：D4. AUTOCAD的坐标体系，包括世界坐标和（）坐标系。

A. 绝对坐标B. 平面坐标C. 相对坐标D. 用户坐标正确答案：D5. 在MATLAB工作空间中，表示圆周率的特殊变量是（）。

A. piB. ansC. iD. eps正确答案：A6. 下列哪条指令是求矩阵的行列式的值（）。

A. invB. diagC. detD. eig正确答案：C7. 在CAD网络系统中，以下说法不正确的是（）。

A. 设计资料可以共享B. 硬件可以共享C. 电脑文件可以共享D. 可以方便管理设计进度正确答案：C8. i=2; a=2i;b=2*i;c=2*sqrt(-1);程序执行后；a, b, c的值分别是（）。

A. a=4,b=4,c=2.0000iB. a=4,b=2.0000i, c=2.0000iC. a=2.0000i, b=4,c=2.0000iD. a=2.0000i,b=2.0000i,c=2.0000i正确答案：C9. 在循环结构中跳出循环，执行循环后面代码的命令为（）。

A. returnB. breakC. continueD. keyboard正确答案：B10. figure命令的作用是（）。

现代控制理论-3
一、回答下列问题
1.连续系统离散化的主要原则是什么？
2.线性变换有哪几条基本性质，这些性质的内容是什么？
3.状态反馈是否改变原系统的能控性、能观测性。

二、问答
1.已知离散系统的状态空间表达式为：
（2）求系统的脉冲传递函数G (z)。

2.已知系统的状态空间表达式为
[]x
y u x b a x 111101-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=&
（1）确定使系统状态完全能控的a 和b 应满足的条件；
（2）确定使系统状态完全能观的a 和b 应满足的条件。

3.已知系统的状态空间表达式为
[]03001210x x u y x
⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=&
试利用状态反馈设计一个闭环系统，使希望的闭环极点为-2，-3。

现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是，能观测的状态变量个数是cvcvx 。

2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程（4分/个）解 1． 能控的状态变量个数是2，能观测的状态变量个数是1。

状态变量个数是2。

…..（4分）2．选取状态变量1x y =，2x y =，3x y =，可得 …..….…….（1分）12233131835x x x x x x x u y x ===--+= …..….…….（1分）写成010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦…..….…….（1分）[]100y x = …..….…….（1分）二、1给出线性定常系统(1)()(),()()x k Ax k Bu k y k Cx k +=+=能控的定义。

（3分）2已知系统[]210 020,011003x x y x ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦，判定该系统是否完全能观？(5分)解 1．答：若存在控制向量序列(),(1),,(1)u k u k u k N ++-，时系统从第k 步的状态()x k 开始，在第N 步达到零状态，即()0x N =，其中N 是大于0的有限数，那么就称此系统在第k 步上是能控的。

若对每一个k ，系统的所有状态都是能控的，就称系统是状态完全能控的，简称能控。

…..….…….（3分） 2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….（1分） [][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….（1分） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=940320110 2CA CA C U O ………………..……….（1分） rank 2O U n =<，所以该系统不完全能观……..….…….（2分）三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。

现代控制理论试卷一、简答题（对或错，10分）（1）描述系统的状态方程不是唯一的。

（2）用独立变量描述的系统状态向量的维数不是唯一的。

（3）对单输入单输出系统，如果1()C sI A B --存在零极点对消，则系统一定不可控或者不可观测。

（4）对多输入多数出系统，如果1()sI A B --存在零极点对消，则系统一定不可控。

（5）李雅普诺夫直接法的四个判定定理中所述的条件都是充分条件。

（6）李雅普诺夫函数是正定函数，李雅普诺夫稳定性是关于系统平衡状态的稳定性。

（8）线性定常系统经过非奇异线性变换后，系统的可控性不变。

（9）用状态反馈进行系统极点配置可能会改变系统的可观测性。

（10）通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时，要求系统必须同时可控和可观测。

对一个线性定常的单输入单输出5阶系统，假定系统可控可观测，通过设计输出至输入的反馈矩阵H 的参数能任意配置系统的闭环极点。

二、试求下述系统的状态转移矩阵()t Φ和系统状态方程的解x 1(t)和x 2(t)。

（15分）1122()()012()()()230x t x t u t x t x t ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦12(0)0,(),0(0)1tx u t e t x -⎡⎤⎡⎤==≥⎢⎥⎢⎥⎣⎦⎣⎦ 三、设系统的传递函数为()10()(1)(2)y s u s s s s =++。

试用状态反馈方法，将闭环极点配置在－2，－1＋j ，－1－j 处，并写出闭环系统的动态方程和传递函数。

（15分） 四、已知系统传递函数2()2()43Y s s U s s s +=++，试求系统可观标准型和对角标准型，并画出系统可观标准型的状态变量图。

（15分）五、已知系统的动态方程为[]211010a x x uy b x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩，试确定a ，b 值，使系统完全可控、完全可观。

线性控制系统工程课后习题答案Module 1: Introduction to Linear Control SystemsExercise 1QuestionConsider a control system with transfer function:$$ G(s) = \\frac{10}{s+2} $$Find the steady-state value of the output when the input is a unit step function.SolutionThe Laplace transform of a unit step function is given by:$$ U(s) = \\frac{1}{s} $$The steady-state value of the output can be obtained by evaluating the transfer function at s=0:$$ G(s=0) = \\frac{10}{s+2} = \\frac{10}{2} = 5 $$Therefore, the steady-state value of the output is 5 when the input is a unit step function.Exercise 2QuestionConsider a control system with transfer function:$$ G(s) = \\frac{4}{s^2 + 4s + 3} $$Find the poles and zeros of the transfer function.SolutionThe poles are the roots of the denominator polynomial. Therefore, we need to find the roots of the equation:s2+4s+3=0Using the quadratic formula, we can find the roots:$$ s = \\frac{-b \\pm \\sqrt{b^2-4ac}}{2a} $$In this case, a=1, b=4, and c=3. Substituting these values into the formula, we get:$$ s_{1,2} = \\frac{-4 \\pm \\sqrt{4^2-4(1)(3)}}{2(1)} $$ Simplifying this expression, we get:s1=−1s2=−3Therefore, the poles of the transfer function are -1 and -3.To find the zeros, we need to find the roots of the numerator polynomial, which in this case is a constant. Since there are no variables in the numerator, there are no zeros. Therefore, the transfer function has no zeros.Module 2: System ModelingExercise 1QuestionConsider a control system described by the following differential equation:$$ 4\\frac{d^2y(t)}{dt^2} + 8\\frac{dy(t)}{dt} + 6y(t) =2u(t) $$Determine the transfer function of the system.SolutionTo find the transfer function, we need to take the Laplace transform of both sides of the differential equation. The Laplace transform of the left side can be written as: $$ \\mathcal{L}\\left(4\\frac{d^2y(t)}{dt^2} +8\\frac{dy(t)}{dt} + 6y(t)\\right) $$Using the linearity property of the Laplace transform, we can split this expression as:$$ 4\\mathcal{L}\\left(\\frac{d^2y(t)}{dt^2}\\right) +8\\mathcal{L}\\left(\\frac{dy(t)}{dt}\\right) +6\\mathcal{L}\\left(y(t)\\right) $$Taking the Laplace transform of the right side, we get:$$ \\mathcal{L}(2u(t)) = 2\\mathcal{L}(u(t)) $$The Laplace transform of the input function u(t) is denoted as U(s).Therefore, the differential equation in the Laplace domain can be expressed as:4s2s(s)−4ss(0)−4s′(0)+8ss(s)−8s(0)+6s(s)=2s(s)Rearranging this equation, we get:(4s2+8s+6)s(s)=4ss(0)+4s′(0)+8s(0)+2s(s) Dividing both sides of the equation by (4s^2 + 8s + 6), we can isolate Y(s):$$ Y(s) = \\frac{4sy(0) + 4y'(0) + 8y(0) + 2U(s)}{4s^2 + 8s + 6} $$Therefore, the transfer function of the system is given by: $$ G(s) = \\frac{Y(s)}{U(s)} = \\frac{4s + 4}{4s^2 + 8s + 6} $$Exercise 2QuestionConsider a control system described by the following difference equation:s(s+2)+s(s+1)+s(s)=s(s)+s(s−1)Determine the transfer function of the system.SolutionTo find the transfer function, we need to take the Z-transform of both sides of the difference equation. The Z-transform of the left side can be written as:$$ Z\\{y(k+2) + y(k+1) + y(k)\\} $$Using the linearity property of the Z-transform, we can split this expression as:$$ Z\\{y(k+2)\\} + Z\\{y(k+1)\\} + Z\\{y(k)\\} $$Taking the Z-transform of the right side, we get:$$ Z\\{u(k) + u(k-1)\\} = Z\\{u(k)\\} + Z\\{u(k-1)\\} $$ The Z-transform of the input function u(k) is denoted asU(z).Therefore, the difference equation in the Z-domain can be expressed as:s2s(s)−s2s(0)−ss(0)+ss(s)−s(0)+s(s)=s(s)+ss(s)Rearranging this equation, we get:(s2+s+1)s(s)=(s2+s)s(0)+s(0)+s(s)Dividing both sides of the equation by (z^2 + z + 1), we can isolate Y(z):$$ Y(z) = \\frac{(z^2 + z)y(0) + y(0) + U(z)}{z^2 + z + 1} $$Therefore, the transfer function of the system is given by:$$ G(z) = \\frac{Y(z)}{U(z)} = \\frac{(z^2 + z)y(0) +y(0)}{z^2 + z + 1} $$Module 3: Feedback Control SystemsExercise 1QuestionConsider a feedback control system with a transfer function G(s) = 10/(s+5).Determine the closed-loop transfer function for the system when the controller is a proportional controller with gain K.In a feedback control system, the closed-loop transfer function can be computed by combining the transfer function of the controller (C(s)) and the transfer function of the plant (G(s)).For a proportional controller, the transfer function is given by:s(s)=sTherefore, the closed-loop transfer function (T(s)) can be expressed as:$$ T(s) = \\frac{C(s) \\cdot G(s)}{1 + C(s) \\cdot G(s)} $$ Substituting the values of C(s) and G(s), we get:$$ T(s) = \\frac{K \\cdot \\frac{10}{s+5}}{1 + K \\cdot \\frac{10}{s+5}} $$Simplifying this expression, we get:$$ T(s) = \\frac{10K}{s+5+10K} $$Therefore, the closed-loop transfer function for the system with a proportional controller is T(s) = 10K / (s+5+10K).QuestionConsider a feedback control system with a transfer function G(s) = 1/(s+2).Determine the closed-loop transfer function for the system when the controller is a proportional-integral (PI) controller with gains Kp and Ki.SolutionIn a feedback control system, the closed-loop transfer function can be computed by combining the transfer function of the controller (C(s)) and the transfer function of the plant (G(s)).For a proportional-integral (PI) controller, the transfer function is given by:$$ C(s) = Kp + \\frac{Ki}{s} $$Therefore, the closed-loop transfer function (T(s)) can be expressed as:$$ T(s) = \\frac{C(s) \\cdot G(s)}{1 + C(s) \\cdot G(s)} $$ Substituting the values of C(s) and G(s), we get:$$ T(s) = \\frac{(Kp + \\frac{Ki}{s}) \\cdot\\frac{1}{s+2}}{1 + (Kp + \\frac{Ki}{s}) \\cdot \\frac{1}{s+2}} $$Simplifying this expression, we get:$$ T(s) = \\frac{Kp + \\frac{Ki}{s}}{s^2 + (2Kp+1)s +(2Ki+2)} $$Therefore, the closed-loop transfer function for the system with a proportional-integral (PI) controller is T(s) = (Kp + Ki/s) / (s^2 + (2Kp+1)s + (2Ki+2)).ConclusionThese are the solutions to the selected exercises in the module on linear control system engineering. These solutions cover topics such as transfer functions, poles and zeros, system modeling, and feedback control systems. By understanding these concepts and practicing the exercises, you can enhance your knowledge and skills in the field of linear control systems.。

《线性系统理论》作业参考答案1-1 证明：由矩阵úúúúúúûùêêêêêêëé----=--121000001000010a a a a A n n nL M O M M M L L L则A 的特征多项式为nn n n n n n n n n n n n n n n n n na a a a a a a a a a a a a a a a a A I +++==+--++--=--++--=+--=--------+-----L L L M O MM ML LL L M O M M M L L L L M O MMM L L L112114322111321121)1()1(00001001)1()1(000010001000010001l l l l l l ll l l l l l l l l ll 若i l 是A 的特征值，则00001000010001)(1112121=úúúúúúûùêêêêêêëé+++=úúúúúúûùêêêêêêëéúúúúúúûùêêêêêêëé+--=-----n n i n i n i i i in n ni i i i i a a a a a a A I L M M L M O M M M L L L l l l l l l l l l u l 这表明[]Tn ii i121-l l l L 是i l 所对应的特征向量。

2012年现代控制理论考试试卷一、（10分，每小题1分）试判断以下结论的正确性，若结论是正确的，（ √ ）1. 由一个状态空间模型可以确定惟一一个传递函数。

（ √ ）2. 若系统的传递函数不存在零极点对消，则其任意的一个实现均为最小实现。

（ × ）3. 对一个给定的状态空间模型，若它是状态能控的，则也一定是输出能控的。

（ √ ）4. 对线性定常系统x Ax =&，其Lyapunov 意义下的渐近稳定性和矩阵A 的特征值都具有负实部是一致的。

（ √ ）5.一个不稳定的系统，若其状态完全能控，则一定可以通过状态反馈使其稳定。

（ × ）6. 对一个系统，只能选取一组状态变量；（ √ ）7. 系统的状态能控性和能观性是系统的结构特性，与系统的输入和输出无关；（ × ）8. 若传递函数1()()G s C sI A B -=-存在零极相消，则对应的状态空间模型描述的系统是不能控且不能观的；（ × ）9. 若一个系统的某个平衡点是李雅普诺夫意义下稳定的，则该系统在任意平衡状态处都是稳定的；（ × ）10. 状态反馈不改变系统的能控性和能观性。

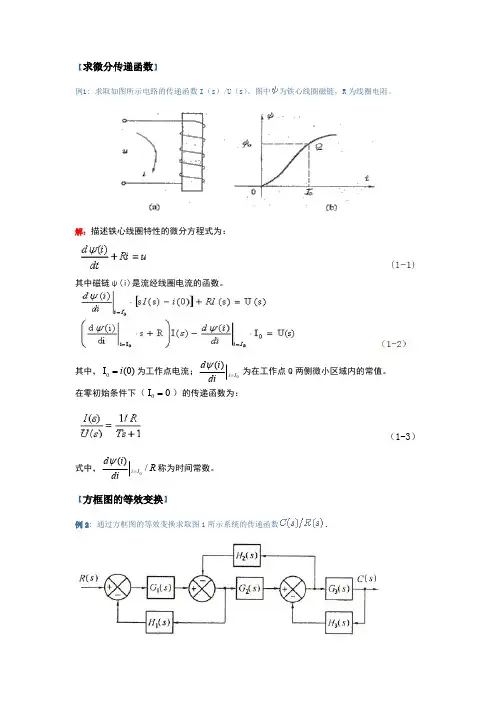
二、已知下图电路，以电源电压u(t)为输入量，求以电感中的电流和电容中的电压作为状态变量的状态方程，和以电阻R2上的电压为输出量的输出方程。

（10分）解：（1）由电路原理得：112212111122211111LL cLL ccL Ldi Ri u udt L L Ldi Ri udt L Ldui idt c c=--+=-+=-222R Lu R i=1122111122210110011L LL Lc cRi iL LLRi i uL Lu uc c⎡⎤--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦ggg[]122200LR Lciu R iu⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦二．（10分）图为R-L-C电路，设u为控制量，电感L上的支路电流和电容C上的电压2x为状态变量，电容C上的电压2x为输出量，试求：网络的状态方程和输出方程，并绘制状态变量图。

词汇第一章自动控制 ( Automatic Control) ：是指在没有人直接参与的条件下，利用控制装置使被控对象的某些物理量（或状态）自动地按照预定的规律去运行。

自动控制系统：将被控对象和控制装置（控制器）按照一定的方式连接起来构成的有机总体。

开环控制 ( open loop control )：开环控制是最简单的一种控制方式。

它的特点是，按照控制信息传递的路径，控制量与被控制量之间只有前向通路而没有反馈通路。

也就是说，控制作用的传递路径不是闭合的，故称为开环。

闭环控制 ( closed loop control) ：凡是将系统的输出量反送至输入端，对系统的控制作用产生直接的影响，都称为闭环控制系统或反馈控制 Feedback Control 系统。

这种自成循环的控制作用，使信息的传递路径形成了一个闭合的环路，故称为闭环。

复合控制 ( compound control ）：是开、闭环控制相结合的一种控制方式。

被控对象：指需要给以控制的机器、设备或生产过程。

被控对象是控制系统的主体，例如火箭、锅炉、机器人、电冰箱等。

控制装置则指对被控对象起控制作用的设备总体，有测量变换部件、放大部件和执行装置。

被控量 (controlled variable ) ：指被控对象中要求保持给定值、要按给定规律变化的物理量。

被控量又称输出量、输出信号。

给定值 (set value ) ：是作用于自动控制系统的输入端并作为控制依据的物理量。

给定值又称输入信号、输入指令、参考输入。

干扰 (disturbance) ：除给定值之外，凡能引起被控量变化的因素，都是干扰。

干扰又称扰动。

第二章数学模型 (mathematical model) ：是描述系统内部物理量（或变量）之间动态关系的数学表达式。

传递函数 ( transfer function) ：线性定常系统在零初始条件下，输出量的拉氏变换与输入量的拉氏变换之比，称为传递函数。

今年控院的实验突然改笔试了，一开始没准备，还是到了山大才知道的（为什么没提前说明，这一点很不理解）。

笔试也比较简单。

开始的填空很容易好像是2'*10；第二个简答题10’，是TTL与CMOS元器件在使用中注意的事项，这个答得不好；最后一个大题7问还是8问忘了，70’，有需要求放大倍数的（静态和动态的），只要求列公式；测量输出电阻；最后一问是随着频率的增大，发达倍数会有何变化。

其它几问忘了，也就是最后那一问不太明确，其它几问都容易。

今年的笔试信号出的题出了状态方程那一道外都比较简单。

（状态方程那道直接放弃了，我们都没学，也没看），分数是信号与系统6’*5，数字信号处理10’*3。

微机原理（卷面40’）填空、判断都比较简单，关于程序只出了2个小题，每个小题8、9行程序，让你填结果，也很简单。

最后是3个解答题20’，分别是重键解决方法、菊花链中断电路原理（给出电路图了）、双积分AD转换原理（也给出原理图了）。

当时发下卷子一看微机原理的一就懵了，这都啥题啊！！MLGBD！！不过公布分数时看了一下成绩还好，微原排在上游。

控院今年还有一点是英语测试突然改面试了，就是一组5个人，有3个老师做在那和你用英语对话，当时紧张死了，觉得说的一塌糊涂（不过这项一共5分，撑死了能拉开1分，倒不必要过分关注）。

面试时主要问我的是毕业设计，其它的专业知识简单问了一下。

有的同学跟老师做了项目的话就会问他那个。

总之，考研最终取决于你的初试和复试的笔试成绩，其它的面试什么的都相差不大，只要笔试分数高了，那你就OK了。

刚刚考完现在趁热回忆额第一题填空①共同接地的作用②示波器ac与dc的用法③微小电流用什么测万用表什么的④5v电流衰减20分贝是多少第二题简答题①用万用表分出电阻、电容、电感、二极管②ttl与cmos集成电路的特点与使用注意第三题试验就是一个三极管放大电路①求静态工作点输入输出电阻放大倍数②怎样测量放大倍数步骤③调节静态工作点方法④怎样调节失真⑤输出电阻的求法⑥输入连接方式的原因⑦~⑧~忘了……总体题目特别二看看山大的《电子电路试验》就行了很简单的~刚考完实验出来，知识比较基础，但是我还是不会了。

《自动控制原理》模拟卷1一、一RC无源网络如图1 所示，求系统的传递函数U2 (s)/ U1(s)。

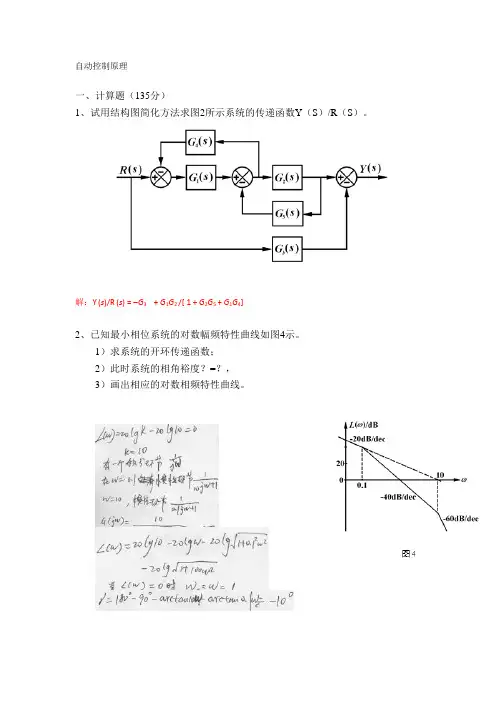
解：U2 (s)/ U1 (s)=R2(1+s R1C)/[ R1+R2+s R1R2C]二、试用结构图简化方法求图2所示系统的传递函数Y(s)/R(s)。

解：Y(s)/R(s) = -G3 + G1G2 /[ 1 + G2G5 + G1G4]三、已知系统的结构图和单位阶跃响应如图3所示，求系统参数K1，K2和a。

四、已知最小相位系统的对数幅频特性曲线如图4示1）求系统的开环传递函数；2）此时系统的相角裕度γ=？；图1图2图3五、已知负反馈系统的开环传递函数为)11.0(40)(+=s s s G要求：保持稳态误差不变，且校正后系统的相角裕度γ' ≥ 45︒。

1) 画出原系统的Bode 图，求ωc ，γ 。

2) 确定串联超前校正装置的传递函数；（要有必要的步骤，不用校验） 解：1) ωc = 20 γ = 26.6︒ 2) G c (s ) = 1+0.084s / 1+0.03s图4《自动控制原理》模拟卷2一、一有源网络如图1 所示，求系统的传递函数U c(s)/ U r(s)。

二、已知控制系统如图2所示，求：（1）当K = 0时，确定系统的阻尼系数ζ、无阻尼振荡频率ωn和单位斜坡输入信号作用时系统的稳态误差e ss。

（2）当ζ= 0.707时，试确定系统中的K值和单位斜坡输入时系统的稳态误差。

图1图2三、已知单位负反馈系统的开环传递函数为)2)(1()(++=s s s ks G1）画出系统的开环极坐标图（写出必要的步骤）。

2）用奈氏判据判断使闭环系统稳定时k 的取值范围。

四、已知最小相位系统的对数幅频特性曲线如图3所示1） 求系统的开环传递函数； 2） 此时系统的相角裕度γ =？； 3） 画出系统的对数相频特性曲线。

解：1) G k (s ) = 2.5(1+1/0.5s ) / s 2 (1+1/50s )2) ωc = 5 γ = 78.6︒五、已知负反馈系统的开环传递函数为)11.0(40)(+=s s s G要求：保持稳态误差不变，且校正后系统的相角裕度γ' ≥ 45︒。

第一章绪论1-1电能具有什么特点？电能的主要特点是：电能不能大量存储；过渡过程十分短暂；为用户提供充足的电能；提高电力系统运行的经济性。

1-3变配电所的任务是什么？类型有哪些？变电所担负着从电力系统受电，经过变压然后配电的任务。

配电所担负着从电力系统受电，然后直接配电的任务。

企业的变电所分为总降压变电所和车间变电所。

1-4 什么叫电力系统、电力网和动力系统？电力系统是由各级电压的电力线路将一些发电厂、变电所、输配电线路和电力用户联系起来，组成的统一整体。

电力网：电力系统中各级电压的电力线路及其联系的变电所动力系统：电力系统加上发电厂的动力部分及其热能系统和热能用户。

1-5 衡量电能质量的指标是什么？答：衡量电能质量的主要指标有：频率偏差、电压偏差、电压波动与闪变、高次谐波（波形畸变率）、三相不平衡度及暂时过电压和瞬态过电压。

1-7 什么叫电压偏差？什么叫电压波动？电压偏差：电路偏离额定电压的幅度电压波动：指电压的急剧变化，以电压最大值与最小值之间之差或百分数表示，1-8 我国规定的“工频”是多少？对其频率偏差有何要求？答：工频也称为工业频率，为50Hz.正常运行情况下300万kW及以上的允许频率偏差±0.2Hz；正常运行情况下300万kW及以下的允许频率偏差±0.5Hz；非正常运行情况下运行的频率偏差±1Hz.1-9 什么是额定电压？在电力系统中同一电压等级下用电设备、电力线路、发电机以及变压器的额定电压是如何规定的？答：（1）额定电压：电气设备正常运行且能获得最佳技术性能和经济效果的电压，通常指线电压，在电气设备铭牌上标出。

（2）在电力系统中同一电压等级下，不同的电气设备具有不同的额定电压；电力线路的额定电压：也称为网络的额定电压，其额定电压等级是国家根据国民经济发展的需要和电力工业发展的水平，经全面的技术经济分析后确定的。

它是确定各类电力设备额定电压的基本依据。

今年控院的实验突然改笔试了，一开始没准备，还是到了山大才知道的（为什么没提前说明，这一点很不理解）。

笔试也比较简单。

开始的填空很容易好像是2'*10；第二个简答题10’，是TTL与CMOS元器件在使用中注意的事项，这个答得不好；最后一个大题7问还是8问忘了，70’，有需要求放大倍数的（静态和动态的），只要求列公式；测量输出电阻；最后一问是随着频率的增大，发达倍数会有何变化。

其它几问忘了，也就是最后那一问不太明确，其它几问都容易。

今年的笔试信号出的题出了状态方程那一道外都比较简单。

（状态方程那道直接放弃了，我们都没学，也没看），分数是信号与系统6’*5，数字信号处理10’*3。

微机原理（卷面40’）填空、判断都比较简单，关于程序只出了2个小题，每个小题8、9行程序，让你填结果，也很简单。

最后是3个解答题20’，分别是重键解决方法、菊花链中断电路原理（给出电路图了）、双积分AD转换原理（也给出原理图了）。

当时发下卷子一看微机原理的一就懵了，这都啥题啊！！MLGBD！！不过公布分数时看了一下成绩还好，微原排在上游。

控院今年还有一点是英语测试突然改面试了，就是一组5个人，有3个老师做在那和你用英语对话，当时紧张死了，觉得说的一塌糊涂（不过这项一共5分，撑死了能拉开1分，倒不必要过分关注）。

面试时主要问我的是毕业设计，其它的专业知识简单问了一下。

有的同学跟老师做了项目的话就会问他那个。

总之，考研最终取决于你的初试和复试的笔试成绩，其它的面试什么的都相差不大，只要笔试分数高了，那你就OK了。

刚刚考完现在趁热回忆额第一题填空①共同接地的作用②示波器ac与dc的用法③微小电流用什么测万用表什么的④5v电流衰减20分贝是多少第二题简答题①用万用表分出电阻、电容、电感、二极管②ttl与cmos集成电路的特点与使用注意第三题试验就是一个三极管放大电路①求静态工作点输入输出电阻放大倍数②怎样测量放大倍数步骤③调节静态工作点方法④怎样调节失真⑤输出电阻的求法⑥输入连接方式的原因⑦~⑧~忘了……总体题目特别二看看山大的《电子电路试验》就行了很简单的~刚考完实验出来，知识比较基础，但是我还是不会了。