应用运筹学-5

《运筹学》第五章习题1．思考题（1）试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。

（2）动态规划的阶段如何划分？（3）试述用动态规划求解最短路问题的方法和步骤。

（4）试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界函数等概念。

（5）试述建立动态规划模型的基本方法。

（6）试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。

2．判断下列说法是否正确（1）动态规划分为线性动态规划和非线性动态规划。

（2）动态规划只是用来解决和时间有关的问题。

（3）对于一个动态规划问题，应用顺推法和逆推法可能会得到不同的最优解。

（4）在用动态规划的解题时，定义状态时应保证各个阶段中所做的决策的相互独立性。

（5）在动态规划模型中，问题的阶段等于问题的子问题的数目。

（6）动态规划计算中的“维数障碍”，主要是由于问题中阶段数的急剧增加而引起的。

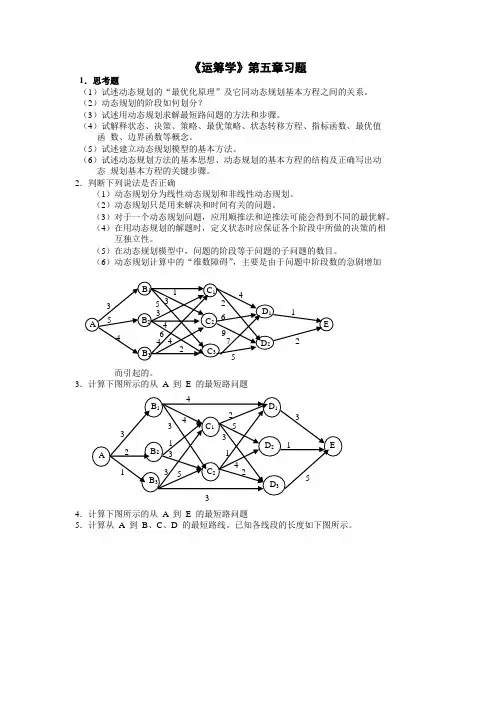
3．计算下图所示的从A 到E 的最短路问题4．计算下图所示的从A 到E 的最短路问题5．计算从A 到B、C、D 的最短路线。

已知各线段的长度如下图所示。

6．设某油田要向一炼油厂用管道供应油料，管道铺设途中要经过八个城镇，各城镇间的路程如下图所示，选择怎样的路线铺设，才使总路程最短？7．用动态规划求解下列各题（1）．222211295max x x x x z -+-=；⎩⎨⎧≥≤+0,52121x x x x ；（2）．33221max x x x z =⎩⎨⎧≥≤++0,,6321321x x x x x x ；8．某人外出旅游，需将3种物品装入背包，但背包重量有限制，总重量不超过10千克。

物品重量及其价值等数据见下表。

试问每种物品装多少件，使整个 背包的价值最大？913 千克。

物品重量及其价值的关系如表所示。

试问如何装这些物品，使整个背包 价值最大？10 量和相应单位价值如下表所示，应如何装载可使总价值最大？303011 底交货量，该厂的生产能力为每月600件，该厂仓库的存货能力为300件，又 每生产100件产品的费用为1000元。

第五章 目标规划§5.1重点、难点提要一、目标规划的基本概念与模型特征 （1）目标规划的基本概念。

当人们在实践中遇到一些矛盾的目标，由于资源稀缺和其它原因，这些目标可能无法同时达到，可以把任何起作用的约束都称为“目标”。

无论它们是否达到，总的目的是要给出一个最优的结果，使之尽可能接近制定的目标。

目标规划是处理多目标的一种重要方法，人们把目标按重要性分成不同的优先等级，并对同一个优先等级中的不同目标赋权，使其在许多领域都有广泛应用。

在目标规划中至少有两个不同的目标；有两类变量：决策变量和偏差变量；两类约束：资源约束（也称硬约束）和目标约束（也称软约束）。

（2）模型特征。

目标规划的一般模型：⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=≥==-+=≤⎪⎭⎫ ⎝⎛+=+-=+-===++--∑∑∑∑.,,2,1;0,;,,2,10,,2,1,,2,1..)(min 1111K k d d n j x K k g d d x c m i b x a t s d d P Z k k j n j k k k j kj i nj j ij Lr K k k rk k rk r ωω 其中r P 为目标优先因子，+-rk rk ωω,为目标权系数，+-k k d d ,为偏差变量。

1）正、负偏差变量,i i d d +-。

正偏差变量i d +表示决策值超过目标值的部分；负偏差变量i d -表示决策值未达到目标值的部分。

因为决策值不可能既超过目标值同时又未达到目标值，所以有0i i d d +-⨯=。

2）硬约束和软约束。

硬约束是指必须严格满足的等式约束和不等式约束；软约束是目标规划特有的。

我们可以把约束右端项看成是要努力追求的目标值，但允许发生正、负偏差，通过在约束中加入正、负偏差变量来表示努力的结果与目标的差距，于是称它们为目标约束。

3）优先因子与权系数。

一个规划问题通常有若干个目标，但决策者在要求达到这些目标时，是有主次或缓急之分的。

运筹学教程第五版课程设计一、课程概述本课程是针对运筹学教程第五版的课程设计，旨在通过实践性的课程设计，让学生深入了解运筹学在实际问题中的应用与解决方法，同时提高学生的逻辑思维和数学建模能力。

二、课程目标•熟练掌握运筹学的基本概念和方法；•熟悉运筹学在实际问题中的应用；•能够独立完成一定难度的数学建模和问题求解；•培养学生的团队合作精神和解决实际问题的能力。

三、教学内容1.运筹学基本概念–目标函数、约束条件–线性规划问题2.线性规划的求解方法–单纯形法–对偶理论–整数规划3.线性规划在实际问题中的应用–生产计划与调度–物流配送问题–设备优化调度问题4.特殊规划问题的求解方法–整数规划的求解方法–非线性规划问题–动态规划问题四、教学方法本课程采取理论结合实践的授课方式，通过课堂教学和实验实践相结合，让学生在实践中深入了解运筹学的基本理论和方法，同时培养学生的数学建模能力和实际问题解决能力。

1.课堂讲授–讲解运筹学的基本理论和方法–培养学生的数学建模能力和逻辑思维能力2.实验实践–实际问题求解，让学生将所学理论与实际问题相结合–团队合作，培养学生的团队意识和协作能力3.课堂讨论–学生团队对问题的讨论和解决方案的设计五、考核方式1.期末考试–考核学生对运筹学基本概念、理论和方法的掌握程度2.课程设计–学生团队完成具体的实际问题的分析、建模、求解和报告–考核学生数学建模和实际问题解决能力，以及团队合作能力六、参考教材《运筹学教程第五版》朱启鸣，等。

中国人民大学出版社，2017年七、总结本课程是运筹学基础教育的重要组成部分，在实践中培养学生各方面能力，具有重要的现实意义。

希望通过本课程的学习，学生能够掌握运筹学基础知识，同时培养学生的团队协作精神和解决实际问题的能力。

判断题判断正误,如果错误请更正第五章运输与指派问题1.运输问题中用位势法求得的检验数不唯一。

2.产地数为3,销地数围的平衡运输中,变量组｛X11,X13,X22,X33,X34｝可作为一组基变量。

3.不平衡运输问题不一定有最优解。

4.m+n-1个变量构成基变量组的充要条件就是它们不包含闭合回路。

5.运输问题中的位势就就是其对偶变量。

6.含有孤立点的变量组不包含有闭回路。

7.不包含任何闭回路的变量组必有孤立点。

8.产地个数为m销地个数为 n的平衡运输问题的对偶问题有m+n个约束。

9.运输问题的检验数就就是对偶问题的松弛变量的值。

10.产地个数为m销地个数为 n的平衡运输问题的系数矩阵为A,则有r(A)〈=m+n-1。

11.用一个常数k加到运价C的某列的所有元素上,则最优解不变。

12.令虚设的产地或销地对应的运价为一任意大于0的常数C(C>0),则最优解不变。

13.若运输问题中的产量或销量为整数则其最优解也一定为整数。

14.运输问题中的单位运价表的每一行都分别乘以一个非0常数,则最优解不变。

15.按最小元素法求得运输问题的初始方案,从任一非基格出发都存在唯一一个闭回路。

16.在指派问题的效率表的某行乘以一个大于零的数最优解不变。

选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。

第五章运输与指派问题1.下列变量组就是一个闭回路的有A{x21,x11,x12,x32,x33,x23} B{x11,x12,x23,x34,x41,x13} C {x21,x13,x34,x41,x12} D{x12,x32,x33,x23,x21,x11} D{x12,x22,x32,x33,x23,x21}2.具有M个产地N个销地的平衡运输问题模型具有特征A有MN个变量M+N个约束B有M+N个变量MN个约束C 有MN个变量M+N-1个约束D 有M+N-1个基变量MN-M-N+1个非基变量E 系数矩阵的秩等于M+N-13.下列说法正确的有A 运输问题的运价表第r行的每个cij 同时加上一个非0常数k,其最优调运方案不变。

运筹学5 整数规划* 用匈牙利法求解：最优解：即甲安排做第二项工作、乙做第三项、丙做第四项、丁做第三项。

总分为：Z＝92＋95＋90＋80＝357 * 本章介绍了整数规划的数学模型的特征及其应用； 1．整数规划的最优解是先求相应的线性规划的最优解然后取整得到. 2．部分变量要求是整数的规划问题称为纯整数规划. 3．求最大值问题的目标函数值是各分枝函数值的上界. 4．求最小值问题的目标函数值是各分枝函数值的下界. 5．变量取0或1的规划是整数规划. 求解方法有：解一般整数规划用分枝定界法、割平面法；解0－1规划用隐枚举法；解指派问题用匈牙利法。

试一试，下例结论是否正确： * 6．整数规划的可行解集合是离散型集合. 7．将指派（分配）问题的效率矩阵每行分别加上一个数后最优解不变. 8．匈牙利法求解指派问题的条件是效率矩阵的元素非负. 9．匈牙利法可直接求解极大化的指派问题. 10．高莫雷（R..E.Gomory）约束是将可行域中一部分非整数解切割掉. 11．指派问题也是一个特殊的运输问题. 12．指派问题也可用运输问题求其最优解. 13．在用隐枚举求解具有n 个变量的0-1规划时需枚举2的n次幂个可能. The End of Chapter 5 下一章：图与网络 Exit 进入练习第*页 * 整数规划 Integer Programming 可分性假设?divisibility assumption 可加性假设 ?additivity assumption 比例性假设?proportionality assumption 0－1变量 binary variable BIP 0－1整数规划纯整数规划 pure Integer Programming 混合整数规划 mixed Integer Programming LP放宽 LP relaxation 分枝定界法 brabch and boundmethod 高莫雷 R．E．Gomory 过滤条件 filtering constraint 隐枚举法implicit enumeration 指派问题 assignment problem 边际收益递减decreasing marginal returns 第*页 * 作业：教材P135 T5.7 The End of Chapter 5 下一章：图与网络是非决策 yes－or－no decision 二选一约束either－or－constraints 互斥的选择 mutually exclusive alternative 相依决策 contingent decision * 分枝定界法的步骤： 1. 求整数规划的松弛问题最优解； 2. 若松弛问题的最优解满足整数要求，得到整数规划的最优解，否则转下一步； 3.任意选一个非整数解的变量xi，在松弛问题中加上约束xi≤[[]xi]及xi≥[[]xi]+1组成两个新的松弛问题，称为分枝。

运筹学第5版课后习题解析1. 引言运筹学是一门关于决策问题优化的学科，在管理科学和工程管理中有着广泛的应用。

本文将对《运筹学》第5版课后习题进行解析，以帮助读者更好地理解并掌握相关知识。

2. 第一章优化模型2.1 习题1习题描述一个客运航班需要从A地到B地，航班规定必须在指定时间到达。

如果到达时间早于指定时间，将产生额外的费用。

如果晚于指定时间，将会影响乘客的行程。

请设计一个优化模型，以确定何时起飞，才能使总费用最小。

解析这是一个典型的优化问题，需要确定一个决策变量来表示起飞时间，然后设计一个目标函数来表示总费用。

同时，还需要考虑到约束条件，如航班的飞行时间和到达时间的限制。

解答决策变量：起飞时间t目标函数：minimize total_cost约束条件：t + flight_time <= arrival_time2.2 习题2习题描述某公司需要购买一批原材料，有多个供应商可供选择。

每个供应商的价格、质量和交货时间都不同，请设计一个模型来确定最佳的供应商选择策略。

解析这是一个供应链管理问题，需要考虑多个因素来确定最佳供应商选择策略。

可以将价格、质量和交货时间作为决策变量，并设计一个目标函数来衡量不同供应商的综合性能。

解答决策变量：价格、质量和交货时间目标函数：maximize performance约束条件：无3. 第二章线性规划3.1 习题1习题描述某家餐厅每天需要供应一种特定菜肴，且每天需要固定的成本。

现在需要决定每天制作多少份该菜肴，以最小化总成本。

已知每份菜肴的制作成本、售出价格和每天的需求量，请设计一个线性规划模型来解决该问题。

解析这是一个经典的生产管理问题，需要确定每天制作的菜肴数量，使得总成本最小。

可以将菜肴数量作为决策变量，并设计一个目标函数来衡量总成本。

解答决策变量：菜肴数量目标函数：minimize total_cost约束条件：菜肴数量 >= 需求量3.2 习题2习题描述某公司有多个生产车间，每个车间的产能和生产成本不同。

应用运筹学
应用运筹学是现代管理学的一门重要专业基础课。

运筹学是 20 世纪 30 年代初发展起来的一门新兴学科，其主要目的是在决策时为管理人员提供科学依据，是实现有效管理、正确决策和现代化管理的重要方法之一。

运筹学是应用数学和形式科学的跨学科研究，利用统计学、数学模型和算法等方法，去寻找复杂问题中的最佳或近似最佳的解决方案。

运筹学经常用于解决现实生活中的问题，比如如何最佳地分配资源，如何规划最佳的路线，如何有效地管理供应链等。

在实际应用中，运筹学可以帮助企业和组织做出更明智的决策，提高效率和效益。

例如，在生产计划中，运筹学可以帮助企业确定最佳的生产时间表，以最小化成本并最大化产量。

在物流和供应链管理中，运筹学可以帮助企业优化运输路线和货物分配，以降低成本和提高客户满意度。

总之，应用运筹学是一门非常实用的学科，它可以帮助我们更好地理解和解决现实生活中的各种问题。

无论是在企业管理、工程设计、科学研究还是个人生活中，都可以运用运筹学的方法和技巧来提高效率和效益。