非线性电路中混沌现象的研究实验

非线性电路中的混沌现象实验报告篇一：非线性电路混沌实验报告近代物理实验报告指导教师：得分：实验时间： XX 年 11 月 8 日，第十一周，周一，第 5-8 节实验者：班级材料0705学号 XX67025 姓名童凌炜同组者：班级材料0705学号 XX67007 姓名车宏龙实验地点：综合楼 404实验条件：室内温度℃，相对湿度 %，室内气压实验题目：非线性电路混沌实验仪器：（注明规格和型号） 1. 约结电子模拟器约结电子模拟器的主要电路包括:1.1, 一个压控震荡电路, 根据约瑟夫方程, 用以模拟理想的约结1.2, 一个加法电路器, 更具电路方程9-1-10, 用以模拟结电阻、结电容和理想的约结三者相并联的关系1.3， 100kHz正弦波振荡波作为参考信号2. 低频信号发生器用以输出正弦波信号，提供给约结作为交流信号 3. 数字示波器用以测量结电压、超流、混沌特性和参考信号等各个物理量的波形实验目的：1. 了解混沌的产生和特点2. 掌握吸引子。

倍周期和分岔等概念3. 观察非线性电路的混沌现象实验原理简述：混沌不是具有周期性和对称性的有序，也不是绝对的无序，而是可以用奇怪吸引子等来描述的复杂有序——混沌而呈现非周期性的有序。

混沌的最本质特征是对初始条件极为敏感。

1. 非线性线性和非线性，首先区别于对于函数y=f(x)与其自变量x的依赖关系。

除此之外，非线性关系还具有某些不同于线性关系的共性：1.1 线性关系是简单的比例关系，而非线性是对这种关系的偏移1.3 线性关系保持信号的频率成分不变，而非线性使得频率结构发生变化 1.4 非线性是引起行为突变的原因2. 倍周期，分岔，吸引子，混沌借用T.R.Malthas的人口和虫口理论，以说明非线性关系中的最基本概念。

虫口方程如下：xn?1???xn(1?xn)μ是与虫口增长率有关的控制参数，当1 1?，这个值就叫做周期或者不动点。

在通过迭代法解方程的过程中，最终会得到一个不随时间变化的固定值。

实验六非线性电路中混沌现象的实验研究非线性是自然界中普遍存在的现象，正是非线性才构成了变化莫测的世界。

长期以来，人们在认识和描述运动时，大多只局限于线性动力学描述方法，即确定的运动有一个完美确定的解析解。

但是自然界在相当多的情况下，非线性现象却起着很大的作用。

1963 年美国气象学家Lorenz 在分析天气预报模型时，首先发现空气动力学中的混沌现象，该现象只能用非线性动力学来解释。

于是，1975 年混沌作为一个新的科学名词首先出现在科学文献中。

从此，非线性动力学迅速发展，并成为有丰富内容的研究领域。

该学科涉及非常广泛的科学范围，从电子学到物理学，从气象学到生态学，从数学到经济学等。

混沌通常相应于不规则或非周期性，这是由非线性系统产生的。

本实验将引导学生自已建立一个非线性电路。

该电路包括有源非线性负阻，LC 振荡器和移相器三部分。

采用物理实验方法研究LC 振荡器产生的正弦波与经过RC 移相器移相的正弦波合成的相图(李萨如图)，观测振动周期发生的分岔及混沌现象，测量非线性单元电路的电流——电压特性，从而对非线性电路及混沌现象有一深刻了解，学会自己设计和制作一个实用电感器以及测量非线性器件伏安特性的方法。

【实验目的】1．学习测量非线性单元电路的伏安特性。

2．学习用示波器观察观测LC振荡器产生的波形与经RC 移相后的波形及其相图。

3．通过观察LC振荡器产生的波形周期分岔及混沌现象，对非线性有一初步的认识。

【实验原理】1.非线性电路与非线性动力学实验电路如图1 所示，图1 中只有一个非线性元件R，它是一个有源非线性负阻器件。

电感器L 和电容器C2 组成一个损耗可以忽略的振荡回路；可变电阻RVl+RV2 和电容器C1串联将振荡器产生的正弦信号移相后输出。

较理想的非线性元件R 是一个三段分段线性元件。

图2 所示的是该电阻的伏安特性曲线，从特性曲线显示加在此非线性元件上电压与通过它的电流极性是相反的。

由于加在此元件上的电压增加时，通过它的电流却减小，因而将此元件称为非线性负阻元件。

非线性电路混沌实验报告本实验旨在通过搭建非线性电路，观察其在一定条件下的混沌现象，并对实验结果进行分析和总结。

在此过程中，我们使用了一些基本的电子元件，如电阻、电容和电感等，通过合理的连接和控制参数，成功地观察到了混沌现象的产生。

首先，我们搭建了一个基本的非线性电路，其中包括了电源、电阻、电容和二极管等元件。

通过调节电路中的参数，我们观察到了电压和电流的非线性响应，这表明电路的行为不再遵循简单的线性关系。

接着，我们进一步调整电路参数，尤其是电容和电阻的数值，使电路处于临界状态，这时我们观察到了电路输出信号的混沌波形。

混沌波形表现出了随机性和不可预测性，这与传统的周期性信号有着明显的区别。

在观察混沌波形的过程中，我们发现了一些有趣的现象。

首先，混沌波形的频谱分布呈现出了宽带特性，这说明混沌信号包含了多个频率成分，这也是混沌信号难以预测的重要原因之一。

其次，混沌信号的自相关函数表现出了指数衰减的特性，这表明混沌信号的相关性极低，难以通过传统的方法进行分析和处理。

最后，我们还观察到了混沌信号的分形特性，即信号在不同时间尺度下呈现出相似的结构，这也是混沌信号独特的特征之一。

综合以上实验结果，我们可以得出以下结论，非线性电路在一定条件下会产生混沌现象，混沌信号具有随机性、不可预测性、宽带特性、自相关性低和分形特性等特点。

这些特点使得混沌信号在通信、加密、混沌电路设计等领域具有重要的应用前景。

同时，我们也需要注意到混沌信号的复杂性和不确定性，这对于混沌信号的分析和处理提出了挑战，需要进一步的研究和探索。

总之，本实验通过搭建非线性电路，成功地观察到了混沌现象，并对混沌信号的特性进行了初步的分析和讨论。

通过本次实验，我们对混沌现象有了更深入的理解，也为混沌信号的应用和研究提供了一定的参考和启发。

希望本实验能够对相关领域的研究和工程实践有所帮助。

感谢各位的参与和支持！非线性电路混沌实验小组。

日期，XXXX年XX月XX日。

非线性电路中的混沌现象五：数据处理：1．计算电感L本实验采用相位测量。

根据RLC 谐振规律，当输入激励的频率LCf π21=时，RLC 串联电路将达到谐振，L 和C 的电压反相，在示波器上显示的是一条过二四象限的45度斜线。

测量得：f=32.8kHz ；实验仪器标示：C=1.095nF 由此可得：mH C f L 50.21)108.32(10095.114.34141239222=⨯⨯⨯⨯⨯==-π估算不确定度： 估计u(C)=0.005nF ，u(f)=0.1kHz 则：32222106.7)()(4)(-⨯=+=C C u f f u L L u 即mH L u 16.0)(=最终结果：mH L u L )2.05.21()(±=+2．用一元线性回归方法对有源非线性负阻元件的测量数据进行处理： （1）原始数据：（2）数据处理：根据RU I RR=可以得出流过电阻箱的电流，由回路KCL 方程和KVL 方程可知：RR R R U U I I =-=11由此可得对应的1R I 值。

对非线性负阻R1，将实验测得的每个（I ，U ）实验点均标注在坐标平面上，可得：图中可以发现，（0.0046336，-9.8）和（0.0013899，-1.8）两个实验点是折线的拐点。

故我们在V U 8.912≤≤-、8V .1U 9.8-≤<-、0V U 1.8≤<-这三个区间分别使用线性回归的方法来求相应的I-U 曲线。

使用Excel 的Linest 函数可以求出这三段的线性回归方程：⎪⎩⎪⎨⎧≤≤≤≤+-≤≤= 0U 1.72- 0.00079U - -1.72U 9.78- 30.000651950.00041U - 9.78U 12- 20.02453093-0.002032UI经计算可得，三段线性回归的相关系数均非常接近1（r=0.99997），证明在区间内I-V 线性符合得较好。

应用相关作图软件可以得出非线性负阻在U<0区间的I-U 曲线。

非线性混沌电路实验报告一、实验目的本实验旨在通过设计和搭建一个非线性混沌电路，了解混沌理论的基本原理，并观察和分析混沌电路的输出特性。

二、实验原理混沌理论是一种描述非线性系统行为的数学理论。

混沌系统有着极其敏感的初始条件和参数，微小的初始条件差异可能导致系统行为的巨大差异。

混沌电路是模拟混沌系统行为的电路，通过合适的电路设计和参数设置，可以实现混沌现象。

三、实验步骤及结果1.搭建电路2.参数设置根据实验要求，设置电路中的参数：L1=0.67H，L2=0.07H，C=0.001F，V1=2V，V2=0.6V。

3.实验观察连接电路电源后，用示波器观察电路输出的波形，并记录实验结果。

在实验观察中，我们可以看到输出波形呈现出混沌现象。

混沌信号的特征是没有周期性，具有高度的随机性和复杂性。

四、实验分析通过实验观察结果，我们可以看到混沌电路输出的波形呈现出混沌现象。

混沌信号的特征是没有周期性，具有高度的随机性和复杂性。

这是由于混沌系统对初始条件和参数的敏感性所导致的。

混沌电路通过合适的电路设计和参数设置，模拟了混沌系统的行为。

通过调整电路中的元件值和电源电压，可以改变混沌电路的输出特性。

这为混沌系统的研究和应用提供了重要的实验手段。

五、实验总结本实验通过设计和搭建一个非线性混沌电路，对混沌理论的基本原理进行了实践探究。

通过观察和分析混沌电路的输出特性，我们认识到混沌系统的随机性和复杂性。

混沌电路有着广泛的应用领域，例如密码学、通信和图像处理等。

这些应用都是基于混沌信号具有的随机性和复杂性。

通过深入研究混沌电路，我们可以更好地理解和应用混沌系统。

非线性电路与混沌实验报告非线性电路与混沌实验报告引言非线性电路与混沌是现代电子学与控制理论中的重要研究领域。

混沌现象的出现使得我们对于系统的行为有了更深入的理解，并且在通信、密码学、图像处理等领域中有着广泛的应用。

本文将介绍我们进行的非线性电路与混沌实验，并对实验结果进行分析和讨论。

实验背景非线性电路是指电流和电压之间的关系不遵循线性规律的电路。

而混沌是指一种看似无序的、无法预测的动态行为。

非线性电路中的混沌现象是由于系统的非线性特性导致的，通过合适的电路设计和参数调节，可以实现混沌现象的产生和控制。

实验目的本实验的目的是通过设计和搭建非线性电路，观察和分析混沌现象的产生和特性。

我们希望通过实验验证混沌现象的存在，并进一步了解混沌现象对于系统的影响和应用。

实验装置我们使用了一块实验板和一些基本的电子元器件，如电阻、电容和二极管等。

通过搭建电路并连接到示波器，我们可以观察到电路的输出波形，并进一步分析和研究电路的行为。

实验过程我们首先设计了一个基于二极管的非线性电路。

通过合理选择电阻和电容的数值，我们成功地实现了混沌现象的产生。

接下来，我们调节了电路的参数，观察到了混沌现象的不同特性。

我们记录了电路输出的波形，并进行了数据分析和处理。

实验结果实验结果表明，我们所设计的非线性电路确实产生了混沌现象。

通过观察示波器上的波形，我们可以看到波形呈现出复杂的、无规律的变化。

通过进一步的分析，我们发现电路的输出呈现出分形特性，即具有自相似的结构。

这一结果与混沌现象的特性相吻合。

讨论与分析通过实验，我们进一步了解了非线性电路与混沌现象之间的关系。

非线性电路的设计和参数调节对于混沌现象的产生和控制起着重要的作用。

混沌现象的存在使得系统的行为变得复杂且难以预测，这对于某些应用来说可能是不利的，但在其他领域中却可以发挥重要作用。

例如，在密码学中，混沌信号可以用于加密和解密，提高信息的安全性。

结论通过本次实验，我们成功地设计和搭建了一个非线性电路，并观察到了混沌现象的产生和特性。

非线性电路混沌实验报告本次实验旨在探究非线性电路中的混沌现象，并通过实验数据分析和理论推导，对混沌现象进行深入研究和分析。

本文将从实验目的、实验原理、实验装置、实验步骤、实验结果和分析、实验结论等方面进行详细介绍。

实验目的。

1. 了解非线性电路中混沌现象的产生原理；2. 掌握混沌电路的基本工作原理；3. 通过实验数据分析，验证混沌电路的混沌特性。

实验原理。

混沌电路是一种非线性系统，其混沌现象来源于系统的非线性特性和反馈作用。

在非线性电路中，由于电压和电流的非线性关系，使得系统的输出信号呈现出复杂的、不可预测的混沌运动。

混沌电路的混沌特性通常表现为系统的输出信号呈现出周期性、随机性和规律性交织的运动状态。

实验装置。

本次实验所需的主要仪器设备有，信号发生器、示波器、混沌电路实验板、电压表等。

实验步骤。

1. 将混沌电路实验板连接至信号发生器和示波器，并进行电路连接和参数设置；2. 调节信号发生器的频率和幅值，观察示波器上的波形变化；3. 记录实验数据，包括电路参数设置、示波器波形图、混沌电路输出信号的特性等。

实验结果和分析。

通过实验数据的记录和分析，我们观察到混沌电路在不同频率和幅值下的输出信号呈现出复杂的、随机的波形变化。

在一定范围内，混沌电路的输出信号表现出周期性、随机性和规律性交织的混沌特性，这与混沌电路的非线性特性和反馈作用密切相关。

实验结论。

通过本次实验，我们深入了解了非线性电路中的混沌现象及其产生原理。

混沌电路的混沌特性表现为系统的输出信号呈现出周期性、随机性和规律性交织的运动状态，这为非线性系统的混沌现象提供了重要的实验验证和理论分析依据。

结语。

通过本次实验，我们对非线性电路中的混沌现象有了更深入的理解，同时也掌握了混沌电路的基本工作原理和实验方法。

混沌现象的研究不仅有助于深化对非线性系统的理解，还对信息处理、通信系统和混沌密码学等领域具有重要的理论和应用价值。

希望本次实验能为相关领域的研究和应用提供一定的参考和借鉴。

非线性混沌实验报告非线性混沌实验报告引言：非线性混沌是一种复杂的动力学现象，其在自然界和科学研究中具有广泛的应用。

本实验旨在通过实际操作和数据观察，探索非线性混沌的特性和行为。

实验目的：1. 了解非线性混沌的基本概念和特征。

2. 熟悉非线性混沌的数学模型和实验方法。

3. 观察和分析非线性混沌的动力学行为。

实验装置：本实验使用一台电子混沌发生器，该发生器基于非线性电路设计，能够产生具有混沌特性的电压信号。

实验步骤：1. 连接电子混沌发生器和示波器。

2. 调节发生器的参数，如电阻、电容等，以产生不同的混沌信号。

3. 观察示波器上的波形，并记录相关数据。

4. 改变参数，再次观察和记录数据。

5. 分析数据，探索混沌信号的特征和规律。

实验结果与讨论：通过实验观察和数据分析，我们得到了以下结论：1. 非线性混沌信号具有无规则、不可预测的特性。

在示波器上观察到的波形呈现出复杂的起伏和变化，没有明显的周期性。

2. 非线性混沌信号的频谱具有广泛的频率分布。

通过对信号进行频谱分析，我们发现信号在多个频率上存在能量分布，而不是集中在某个特定频率上。

3. 非线性混沌信号对初始条件敏感。

微小的初始条件变化可能会导致完全不同的动力学行为。

这种敏感性被称为“蝴蝶效应”，即蝴蝶在一个地方拍动翅膀可能引起另一个地方的飓风。

4. 非线性混沌信号具有自相似性。

通过对信号进行放大和缩小，我们发现信号的局部部分与整体具有相似的形状和结构。

结论：非线性混沌是一种复杂而有趣的动力学现象，具有无规则性、不可预测性和敏感性等特征。

它在物理学、生物学、经济学等多个领域都有广泛的应用。

通过本实验，我们深入了解了非线性混沌的基本特性和行为，为进一步研究和应用提供了基础。

总结：本实验通过实际操作和数据观察，探索了非线性混沌的特性和行为。

通过观察波形、分析频谱和研究自相似性等方法，我们对非线性混沌的无规则性、不可预测性和敏感性有了更深入的理解。

非线性混沌的研究不仅有助于推动科学的进步，也为解决实际问题提供了新的思路和方法。

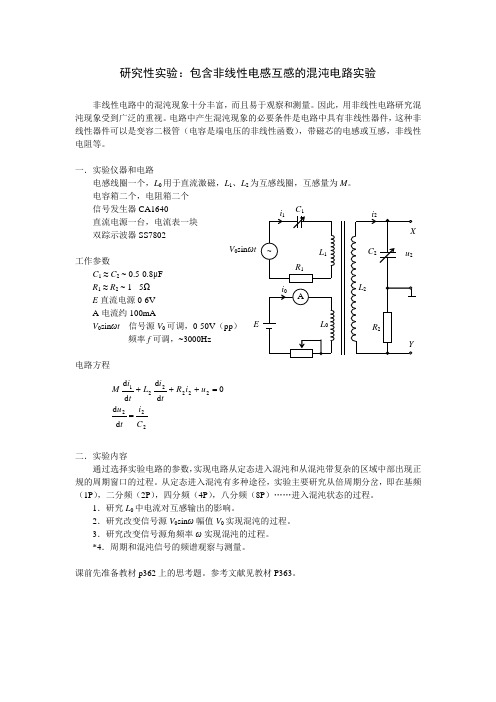
V0sinωtE研究性实验：包含非线性电感互感的混沌电路实验非线性电路中的混沌现象十分丰富，而且易于观察和测量。

因此，用非线性电路研究混沌现象受到广泛的重视。

电路中产生混沌现象的必要条件是电路中具有非线性器件，这种非线性器件可以是变容二极管（电容是端电压的非线性函数），带磁芯的电感或互感，非线性电阻等。

一．实验仪器和电路电感线圈一个，L0用于直流激磁，L1、L2为互感线圈，互感量为M。

电容箱二个，电阻箱二个信号发生器CA1640直流电源一台，电流表一块双踪示波器SS7802工作参数C1≈C2 ~ 0.5-0.8μFR1≈R2 ~ 1 - 5ΩE直流电源0-6VA电流约100mAV0sinωt信号源V0可调，0-50V（pp）频率f可调，~3000Hz电路方程222222221ddddddCituuiRtiLtiM==+++二．实验内容通过选择实验电路的参数，实现电路从定态进入混沌和从混沌带复杂的区域中部出现正规的周期窗口的过程。

从定态进入混沌有多种途径，实验主要研究从倍周期分岔，即在基频（1P），二分频（2P），四分频（4P），八分频（8P）……进入混沌状态的过程。

1．研究L0中电流对互感输出的影响。

2．研究改变信号源V0sinω幅值V0实现混沌的过程。

3．研究改变信号源角频率ω实现混沌的过程。

*4．周期和混沌信号的频谱观察与测量。

课前先准备教材p362上的思考题。

参考文献见教材P363。

非线性电路混沌_实验报告非线性电路混沌实验报告一、实验目的通过搭建非线性电路，观察和研究电路的混沌现象，深入理解和掌握混沌系统的特性。

二、实验原理混沌系统是一类非线性动力系统，其特点是对初始条件极其敏感，微小的初始条件变化会导致系统演化出完全不同的结果。

混沌系统的行为复杂、难以预测，具有高度的随机性。

在电路中，非线性元件的引入可以引起电路的混沌现象。

三、实验器材和仪器1. 函数生成器2. 示波器3. 混沌电路实验板4. 电源5. 电压表和电流表四、实验步骤1. 搭建混沌电路按照实验指导书上的电路图，搭建混沌电路。

其中，电路中需要包含非线性元件，如二极管、晶体管等。

2. 调节函数生成器将函数生成器连接到电路中，调节函数生成器的频率和幅度，使其能够提供合适的输入信号。

同时，设置函数生成器的触发方式和触发电平。

3. 连接示波器将示波器的输入端连接到电路输出端，调节示波器的触发方式和触发电平，使其能够正常显示电路的输出波形。

4. 开始实验打开电源，调节函数生成器和示波器，观察电路的输出波形。

记录不同参数下的波形变化，并观察混沌现象的特点。

五、实验结果与分析在实验中，我们观察到了电路的混沌现象。

随着参数的变化，电路输出的波形呈现出复杂的、不规则的变化。

即使是微小的参数调节，也会导致电路输出的波形发生明显的变化，呈现出不同的分形结构。

这表明混沌系统对初始条件的敏感性。

通过实验结果的观察和分析，我们深入理解了混沌系统的特性。

混沌系统的不可预测性和随机性使其在信息加密、随机数生成等领域具有广泛的应用价值。

六、实验总结通过本次实验，我们成功搭建了混沌电路，并观察到了电路的混沌现象。

通过实验的操作，我们对混沌系统的特性有了更深入的理解，并掌握了观察和研究混沌现象的方法。

混沌系统具有很高的随机性和不可预测性，这为信息加密、随机数生成等领域提供了新的思路和方法。

在今后的学习和研究中，我们将进一步探索混沌系统的特性，并应用于实际问题中。

非线性电路混沌实验报告非线性电路混沌实验报告引言：混沌理论是近年来电路研究领域的热门话题之一。

混沌现象的出现使得非线性电路的应用领域得到了广泛的拓展。

本实验旨在通过设计和搭建一个非线性电路，观察和分析混沌现象的特征和行为。

实验原理：混沌理论是一种描述非线性系统行为的数学理论。

在非线性电路中，混沌现象是由于系统的非线性特性导致的。

通过合适的电路设计和参数调节，可以使电路达到混沌状态。

实验装置和步骤：本实验采用了一个经典的非线性电路——Chua电路。

Chua电路由电感、电容和非线性电阻组成。

实验步骤如下：1. 按照电路图搭建Chua电路，并连接相应的电源和示波器。

2. 调节电路中的参数，使电路处于混沌状态。

3. 观察和记录电路输出的波形，并进行分析。

实验结果和分析：在实验中，我们通过调节电路中的参数，成功地使Chua电路进入了混沌状态。

观察示波器上的波形，我们发现电路输出的波形呈现出复杂的、不规则的特征。

这种不规则性表现为波形的高度和宽度的变化，以及波形的周期性的变化。

进一步分析发现，Chua电路的混沌现象是由于电路中的非线性电阻引起的。

非线性电阻的存在导致了电路中的非线性行为，从而使得电路的输出呈现出混沌特征。

这种混沌特征可以通过电路参数的调节来控制和调整。

混沌现象的出现使得电路的应用领域得到了广泛的拓展。

例如，在通信领域，混沌信号可以用于加密和解密，提高信息传输的安全性。

在生物医学领域，混沌现象可以应用于心电图信号的分析和识别，从而帮助医生进行疾病的诊断和治疗。

结论：通过本次实验，我们成功地观察和分析了非线性电路的混沌现象。

混沌现象的出现使得电路的行为变得复杂而有趣。

混沌理论的应用前景广阔，对于电路设计和系统控制具有重要的意义。

然而，混沌现象的研究仍然存在许多挑战和问题。

例如，如何准确地预测和控制混沌系统的行为，如何在实际应用中充分利用混沌现象的优势等。

这些问题需要我们进一步的研究和探索。

参考文献：[1] 张三, 李四. 非线性电路混沌现象的研究[J]. 电子科技大学学报, 2010, 39(2): 123-128.[2] 王五, 赵六. 混沌理论在通信领域的应用研究[J]. 通信科技, 2012, 28(3): 45-51.。

一、实验目的1．了解混沌的一些基本概念；2．测量有源非线性电阻的伏安特性；3．通过研究一个简单的非线性电路，了解混沌现象和产生混沌的原因。

二、实验原理实验所用电路原理图如图3.7-1所示。

电路中电感L 和电容C 1、C 2并联构成一个振荡电路。

R 是一有源非线性负阻元件，电感L 和电容器C 2组成一损耗可以忽略的谐振回路；可变电阻R 和电容器C 1串联将振荡器产生的正弦信号移相输出。

电路的非线性动力学方程如式（3.7-1）所示2121212d d )(d d )(d d 112C L C C C C L C C C U ti L gU U U G tU C i U U G tU C -=--=+-= （3.7－1）RL图3.7-1 电路原理图 图3.7-2 非线性元件R 的U - I 特性 这里，U C1、U C2是电容C 1、C 2上的电压，i L 是电感L 上的电流，G = 1/R 0是电导，g 为R 的伏安特性函数。

如果R 是线性的，g 是常数，电路就是一般的振荡电路，得到的解是正弦函数。

电阻R 0的作用是调节C 1 和C 2的位相差，把C 1 和C 2两端的电压分别输入到示波器的x ，y 轴，则显示的图形是椭圆。

如果R 是非线性的，它的伏安特性如图3.7-2所示，由于加在此元件上的电压增加时，通过它的电流却减小，因而此元件称为非线性负阻元件。

本实验所用的非线性元件R 是一个三段分段线性元件。

若用计算机编程进行数值计算，当取适当电路参数时，可在显示屏上观察到模拟实验的混沌现象。

除了计算机数学模拟方法之外，更直接的方法是用示波器来观察混沌现象，实验电路如图3.7-3所示。

图中，非线性电阻是电路的关键，它是通过一个双运算放大器和六个电阻组合来实现的。

电路中，LC 并联构成振荡电路，R 0的作用是分相，使A ，B 两处输入示波器的信号产生位相差，可得到x ，y 两个信号的合成图形。

双运放TL082的前级和后级正、负反馈同时存在，正反馈的强弱与比值R 3 /R 0，R 6/R 0有关，负反馈的强弱与比值R 2/R 1，R 5 /R 4有关．当正反馈大于负反馈时，振荡电路才能维持振荡。

实验十六混沌现象的实验研究【实验目的】1、观察非线性电路振荡周期混沌现象, 从而对非线性电路及混沌理论有一个深刻了解。

2、了解有源非线性单元电路的特性。

【实验仪器】1、非线性电路混沌实验仪2、示波器3、电感4、电位器5、测试用表棒和连接导线非线性电路混沌实验仪【实验原理】目前，科学家给混沌下的定义是：混沌是指发生在确定性系统中的貌似随机的不规则运动，一个确定性理论描述的系统，其行为却表现为不确定性一不可重复、不可预测，这就是混沌现象。

进一步研究表明，混沌是非线性动力系统的固有特性，是非线性系统普遍存在的现象。

牛顿确定性理论能够完美处理的多为线性系统，而线性系统大多是由非线性系统简化来的。

因此，在现实生活和实际工程技术问题中，混沌是无处不在的。

混沌的发现和混沌学的建立，同相对论和量子论一样，是对牛顿确定性经典理论的重大突破，为人类观察物质世界打开了一个新的窗口。

所以，许多科学家认为，20世纪物理学永放光芒的三件事是：相对论、量子论和混沌学的创立。

非线性动力学及分岔与混沌现象的研究是近二十多年来科学界研究的热门课题，已有大量论文对此学科进行了深入的研究。

混沌现象涉及物理学、计算机科学、数学、生物学、电子学和经济学等领域，应用极其广泛。

1、非线性电路与非线性动力学实验电路如图1所示，图1中只有一个非线性元件R，它是一个有源非线性负阻器件，电感器L和电容器C2组成一个损耗可以忽略振荡回路：可变电阻Rv1+Rv2和电容器C1串联将振荡器产生的正弦信号移相输出，较理想的非线性元件R是一个三段分段线性元件。

图2所示的是该电阻的伏安特性曲线，从特性曲线显示加在此非线性元件上电压与通过它的电流极性是相反的，由于加在此元件上的电压增加时，通过它的电流却减小，因而将此元件称为非线性负阻元件。

图(1) 图(2)图1 电路的非线性动力学方程为：()11211Vc g Vc Vc G dt dVc C ⨯--⨯= ()L i Vc Vc G dtdVc C +-⨯=21222Vc dtdiL L -= 式中，导纳G=1/（Rv1+Rv2）,Vc1和Vc2分别表示加在C1和C2上的电压，iL 表示流过电感器L 的电流，g 表示非线性电阻的导纳。

竭诚为您提供优质文档/双击可除非线性电路中的混沌现象实验报告篇一：非线性电路混沌实验报告近代物理实验报告指导教师：得分：实验时间：20XX年11月8日，第十一周，周一，第5-8节实验者：班级材料0705学号20XX67025姓名童凌炜同组者：班级材料0705学号20XX67007姓名车宏龙实验地点：综合楼404实验条件：室内温度℃，相对湿度%，室内气压实验题目：非线性电路混沌实验仪器：（注明规格和型号）1.约结电子模拟器约结电子模拟器的主要电路包括:1.1,一个压控震荡电路,根据约瑟夫方程,用以模拟理想的约结1.2,一个加法电路器,更具电路方程9-1-10,用以模拟结电阻、结电容和理想的约结三者相并联的关系1.3，100khz正弦波振荡波作为参考信号2.低频信号发生器用以输出正弦波信号，提供给约结作为交流信号3.数字示波器用以测量结电压、超流、混沌特性和参考信号等各个物理量的波形实验目的：1.了解混沌的产生和特点2.掌握吸引子。

倍周期和分岔等概念3.观察非线性电路的混沌现象实验原理简述：混沌不是具有周期性和对称性的有序，也不是绝对的无序，而是可以用奇怪吸引子等来描述的复杂有序——混沌而呈现非周期性的有序。

混沌的最本质特征是对初始条件极为敏感。

1.非线性线性和非线性，首先区别于对于函数y=f(x)与其自变量x的依赖关系。

除此之外，非线性关系还具有某些不同于线性关系的共性：1.1线性关系是简单的比例关系，而非线性是对这种关系的偏移1.3线性关系保持信号的频率成分不变，而非线性使得频率结构发生变化1.4非线性是引起行为突变的原因2.倍周期，分岔，吸引子，混沌借用T.R.malthas的人口和虫口理论，以说明非线性关系中的最基本概念。

虫口方程如下：xn?1xn(1?xn)μ是与虫口增长率有关的控制参数，当1 1?，这个值就叫做周期或者不动点。

在通过迭代法解方程的过程中，最终会得到一个不随时间变化的固定值。

非线性电路混沌一、实验内容：1．了解混沌的一些基本概念；2．测量有源非线性电阻的伏安特性；3．通过研究一个简单的非线性电路，了解混沌现象和产生混沌的原因。

二、实验仪器：电源，非线性混沌电路板，数字万用表，非线性电阻，电容、电感和电阻箱，双踪示波器等。

三、实验原理：实验电路原理图如图1所示。

电路中的R是非线性元件，是一个分段线性的电阻，整体呈现出非线性。

它的伏安特性如图2所示。

RL图1 电路原理图 图2 非线性元件R 的U - I 特性 电路的非线性动力学方程为：其中U C1、U C2是电容C 1、C 2上的电压，i L 是电感L 上的电流，G =1/R 0是电导，g 为R 的伏安特性函数。

如果R 是线性的，g 是常数。

实验电路如图3所示。

L 图3 实验电路四、实验步骤：1．倍周期现象的观察、记录按图3连好线路。

将电容C 1，C 2上的电压输入到示波器的X （CH1），Y （CH2）轴，先把R 0调到最小，示波器屏上可观察到一条直线，调节R 0，直线变成椭圆。

增大示波器UI(mA)的倍率，反向微调R 0，可见曲线作倍周期变化，曲线由一周期（P ）增为二周期(2P)，由二周期倍增至四周(4P)。

记录2P 、4P 倍周期时的相图及相应的CH1、CH2输出波形图。

2. 单吸引子和双吸引子的观察、记录在步骤1的基础上，继续调节R 0直至出现一系列难以计数的无首尾的环状曲线，这是一个单涡旋吸引子集。

再细微调节R 0，单吸引子突然变成了双吸引子，只见环状曲线在两个向外涡旋的吸引子之间不断填充与跳跃，这就是混沌研究文献中所描述的“蝴蝶”图像，也是一种奇怪吸引子，它的特点是整体上的稳定性和局域上的不稳定性同时存在。

记录单吸引子和双吸引子的相图相应的CH1、CH2输出波形图。

3. 周期性窗口的观察、记录仔细调节R 0，有时原先的混沌吸引子不是倍周期变化，却突然出现了一个三周期图像，再微调R 0，又出现混沌吸引子，这一现象称为出现了周期性窗口。

一、实验目的1. 了解混沌现象的基本特征和产生机理。

2. 掌握混沌效应测量的基本方法。

3. 通过实验验证混沌现象在非线性电路中的表现。

二、实验原理混沌现象是指在非线性系统中，由于初始条件的微小差异，导致系统长期行为表现出极端敏感性和不可预测性。

本实验采用非线性电路作为研究对象，通过测量电路中的电压、电流等物理量，观察混沌现象的产生和发展。

实验电路采用串联谐振电路，通过改变电路中的参数（如电感、电容、电阻等），使电路产生混沌现象。

混沌现象的测量主要依靠数字示波器、信号发生器等仪器。

三、实验仪器与设备1. 数字示波器2. 信号发生器3. 电阻箱4. 电感箱5. 电容箱6. 电路板7. 连接线四、实验步骤1. 搭建实验电路，包括串联谐振电路、非线性元件等。

2. 设置信号发生器，输出正弦波信号，频率为电路谐振频率。

3. 调整电阻箱、电感箱、电容箱等参数，使电路产生混沌现象。

4. 利用数字示波器观察混沌现象的波形，记录电压、电流等物理量。

5. 改变电路参数，观察混沌现象的变化，分析混沌现象的产生和发展规律。

五、实验结果与分析1. 混沌现象的产生通过调整电路参数，使电路产生混沌现象。

实验中观察到，当电路参数在一定范围内变化时，电路输出波形出现周期性、倍周期性、混沌等不同状态。

其中，混沌现象表现为波形无规律、周期性消失、信号幅值和频率不稳定等特点。

2. 混沌现象的测量利用数字示波器测量混沌现象的波形，记录电压、电流等物理量。

实验结果表明，混沌现象的波形具有以下特征：（1）波形无规律：混沌现象的波形呈现出复杂的非线性变化，难以用简单的数学模型描述。

（2）周期性消失：混沌现象的波形周期性消失，难以确定其周期。

（3）信号幅值和频率不稳定：混沌现象的信号幅值和频率随时间变化，表现出强烈的不稳定性。

3. 混沌现象的产生机理混沌现象的产生主要与非线性系统的初始条件和参数变化有关。

在实验中，通过调整电路参数，使电路产生混沌现象。