3.5.1 曲线的凹凸性[共2页]
- 格式：pdf
- 大小：143.39 KB
- 文档页数：1
下载文档原格式
合集下载
《函数曲线的凹凸性》课件
《函数曲线的凹凸性》 ppt课件
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
函数的凹凸性
解析:答案为 B。要使 f ( x1 x2 ) f (x1 ) f (x2 ) 恒成
2
2
立，由函数值的定义及函数图象即需要函数在 0 x 1
内为凸函数。而 y 2x , y x2 在 0 x 1内为凹函数，
y cos 2x 在 0 x 1 内 先 凸 后 凹 函 数 。 只 有
直接验证即可②满足题意 对于③④如右图所示：
对于 f (x) lg x 图象上任意不同
两点 A(x1, f (x1))B(x2, f (x2 ))
k AB
f (x1) f (x2 ) 0 x1 x2
显然成
立（可
以用
f '(x) 1 0(x 0) ）故③正确 x ln10
再有 AB 中点 C（ x1 x2 , f (x1) f (x2 ) ) 过 C
1 x
1，
x2 x x 2 4
当 1 1时， (1 1)2 1 取得最大值 2， (1 1)2 1 取得最小值0
x
x2 4
x2 4
2 a 0 结合 a 0，a [2,0)。
指数函数、对数函数、幂函数等基本初等函数的凹凸性。
1、指数函数 y a x (a 0, a 1) y e x
② f (x1 x2 ) f (x1 ) f (x2 ) ；
③ f (x1 ) f (x2 ) 0; x1 x2
④ f ( x1 x2 ) f (x1 ) f (x2 ) .
2
2
当 f (x) lg x 时，上述结论中正确结论的序号
是
.
【详解】
对于①②可以用 f (x) lg x
函数的凹凸性
一、曲线的凹凸性与拐点
一、曲线的凹凸性与拐点
凹凸性
则 f (t) ln t 1,
f (t) 1 0, t
f (t) t ln t 在 ( x, y) 或 ( y, x), x 0, y 0 是凸的.
于是 1[ f ( x) f ( y)] f ( x y)
2
2
即 1[ x ln x y ln y] x y ln x y ,
上页
返回
下页
思考题解答
因为 f ( x0 ) 0只是( x0 , f ( x0 ))
为拐点的必要条件，
故( x0 , f ( x0 ))不一定是拐点.
例 f ( x) x4 x (,) f (0) 0
但(0,0)并不是曲线 f ( x) 的拐点.
上页
返回
下页
练习题
上页
返回
下页
方法2: 设函数 f ( x) 在 x0 的邻域内三阶可导,且 f ( x0 ) 0,而 f ( x0 ) 0,那末 ( x0 , f ( x0 )) 是曲 线 y f ( x)的拐点.
例3 求曲线 y sin x cos x ([0,2]内) 的拐点.
点(0,0)是曲线 y 3 x的拐点.
上页
返回
下页
利用函数的凹凸性可以证明不等式.
例 (1)a,b R ,有2arctan(a b) arctana arctanb.
2
提示： 取f ( x) arctan x.
ab
(2)a,b R,有e 2 1 (ea eb ). 2
(1) x0两近旁f ( x)变号,点( x0, f ( x0 ))即为拐点; (2) x0两近旁f ( x)不变号,点( x0, f ( x0 ))不是拐点.
曲线的凹凸性与拐点
曲线的凹凸性与拐点
一、曲线凹凸的定义
观察：
y y
o
x
o
x
都是上升的曲线，但是上升的方式不一样； 红色曲线上升的速度在增加，蓝色曲线上升速度减少； 呈现出来的不同的弯曲方式。
一、曲线凹凸的定义
观察：
y y
o
凹
x
o
x
弦在曲线上方
凸
弦在曲线下方
一、曲线凹凸的定义
凹
y f ( x1 )
凸
f ( x)
y
f ( x)
f ( x2 )
f ( x1 )
f ( x2 )
x1 x 2 x x 2 2
o
x1 x1 x 2 2
x2 x
o
x1
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
一、曲线凹凸的定义
对 I 上任意两点x1 , x2， 定义1：若函数 f ( x)在区间 I上连续，
x1 x2 f ( x1 ) f ( x2 ) （1）如果恒有 f ( 2 ) 2 那么称 f ( x)在 I 上的图形是凸的。
_
（2）如果恒有 那么称
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
f ( x )的极值点. 拐点：
凹
f ( x) 0
凸
f ( x) 0
f ( x )
f ( x )
拐点可能是二阶导数等于0的点，和二阶导数不存在的 点.
四、计算凹凸区间与拐点的步骤
1）求函数的定义域； 2）求 f ( x)； 3）求出 f ( x) 0的点，和 f ( x) 不存在的点；
一、曲线凹凸的定义
观察：
y y
o
x
o
x
都是上升的曲线，但是上升的方式不一样； 红色曲线上升的速度在增加，蓝色曲线上升速度减少； 呈现出来的不同的弯曲方式。
一、曲线凹凸的定义
观察：
y y
o
凹
x
o
x
弦在曲线上方
凸
弦在曲线下方
一、曲线凹凸的定义
凹
y f ( x1 )
凸
f ( x)
y
f ( x)
f ( x2 )
f ( x1 )
f ( x2 )
x1 x 2 x x 2 2
o
x1 x1 x 2 2
x2 x
o
x1
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
一、曲线凹凸的定义
对 I 上任意两点x1 , x2， 定义1：若函数 f ( x)在区间 I上连续，
x1 x2 f ( x1 ) f ( x2 ) （1）如果恒有 f ( 2 ) 2 那么称 f ( x)在 I 上的图形是凸的。
_
（2）如果恒有 那么称
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
f ( x )的极值点. 拐点：
凹
f ( x) 0
凸
f ( x) 0
f ( x )
f ( x )
拐点可能是二阶导数等于0的点，和二阶导数不存在的 点.
四、计算凹凸区间与拐点的步骤
1）求函数的定义域； 2）求 f ( x)； 3）求出 f ( x) 0的点，和 f ( x) 不存在的点；
3.5曲线的凹凸性与拐点
当0 t 时
4
d2y dx 2
0
t
4
(e 4 ,
1
e4)
当 t 时
4
d2y dx 2
0
2
是拐点
练习5 求曲线 y sin x cos x ([0,2]内) 的拐点.
注意：设函数 f ( x) 在 x0 的邻域内三阶可导,且 f ( x0 ) 0,而 f ( x0 ) 0,那末 ( x0 , f ( x0 )) 是曲 线 y f ( x)的拐点.
解
x2 f ( x) x2
x0 ,
x0
f
(
x
)
2x 2x
x0 ,
x0
f
(
x
)
2 2
x0 ,
x0
f (0)不存在.
在(,0)内, f ( x) 2 0, f ( x) x x 是凸的.
在(0,)内, f ( x) 2 0, f ( x) x x 是凹的.
x ( ,0) 0
(0,1) 1 (1, )
y y凹
不存在 0
拐点 凸 拐点 凹
因此 (,0) (0, ) 是凹区间，(0,1) 是凸区间，
3
拐点为
(0, 0),
(1, ) 4
定理3.14 设f ( x)在( x0 , x0 )内三阶可导,
若f ( x0 ) 0, f ( x0 ) 0, 则x x0是f ( x)的拐点.
y f ( x1 ) f ( x2 )
2
f ( x1 x2 ) 2
o
x x1 x2
函数曲线的凹向与拐点
下页
拐点 连续曲线yf(x)上上凹弧与下凹弧的分界点称为该曲
线的拐点 •讨论
如何确定曲线yf(x)的拐点？ 如果(x0 f(x0))是拐点且f (x0)0存在问f (x0)？ 如何找可能的拐点？
拐点
下页
拐点 连续曲线yf(x)上上凹弧与下凹弧的分界点称为该曲
例4 求曲线y3x44x31的拐点及凹、凸的区间
解 (1)函数y3x44x31的定义域为( )
(2)
y 12x3 12x2
y36x2
24x 36x(x
2) 3
(3)解方程 y0
得x1 0
x2
2 3
(4)列表判断
x ( 0) f (x) ＋ f (x) ∪
0 (0 2/3) 2/3 (2/3 )
0
－0
＋
1
∩ 11/27 ∪
在区间(0]和[2/3)上曲线是凹的 在区间[02/3]上 曲线是凸的 点(0 1)和(2/3 11/27)是曲线的拐点
下页
•只有f (x0)等于零或不存在(x0 f(x0))才可能是拐点 •如果在x0的左右两侧f (x)异号则(x0 f(x0))是拐点
(2)函数f (x) x2 在区间(1,1•)内
1 x
（A）单调增加
（B）单调减少
（C）有增有减
（D）不增不减
解：选（C）
（3）函数f(x)在点x0处取得极大值，则必有：
（A）f '(x0)=0
（B）f '(x0)<0
（C）f '(x0)=0且f"(x0)<0
（D）f(x0+△x)<f(x0)
拐点 连续曲线yf(x)上上凹弧与下凹弧的分界点称为该曲
线的拐点 •讨论
如何确定曲线yf(x)的拐点？ 如果(x0 f(x0))是拐点且f (x0)0存在问f (x0)？ 如何找可能的拐点？
拐点
下页
拐点 连续曲线yf(x)上上凹弧与下凹弧的分界点称为该曲
例4 求曲线y3x44x31的拐点及凹、凸的区间
解 (1)函数y3x44x31的定义域为( )
(2)
y 12x3 12x2
y36x2
24x 36x(x
2) 3
(3)解方程 y0
得x1 0
x2
2 3
(4)列表判断
x ( 0) f (x) ＋ f (x) ∪
0 (0 2/3) 2/3 (2/3 )
0
－0
＋
1
∩ 11/27 ∪
在区间(0]和[2/3)上曲线是凹的 在区间[02/3]上 曲线是凸的 点(0 1)和(2/3 11/27)是曲线的拐点
下页
•只有f (x0)等于零或不存在(x0 f(x0))才可能是拐点 •如果在x0的左右两侧f (x)异号则(x0 f(x0))是拐点
(2)函数f (x) x2 在区间(1,1•)内
1 x
（A）单调增加
（B）单调减少
（C）有增有减
（D）不增不减
解：选（C）
（3）函数f(x)在点x0处取得极大值，则必有：
（A）f '(x0)=0
（B）f '(x0)<0
（C）f '(x0)=0且f"(x0)<0
（D）f(x0+△x)<f(x0)
曲线的凹凸性与拐点
o
x
凸：切线的的斜率递减 f (x) 递减，即 f (x) 0
二、曲线凹凸的判定
定理：若函数f (x)在[a,b]上连续，在(a,b)内具有一、 二阶导数，则 （1）若果在(a, b)内有 f (x) 0，
那么 f (x)在[a,b]内图像是凸的. （2）若果在(a, b)内有 f (x) 0，
曲线的凹凸性与拐点
一、曲线凹凸的定义
观察：
y
y
o
x
o
x
都是上升的曲线，但是上升的方式不一样； 红色曲线上升的速度在增加，蓝色曲线上升速度减少； 呈现出来的不同的弯曲方式。
一、曲线凹凸的定义
观察：
y
y
o
x
凹
弦在曲线上方
o
x
凸
弦在曲线下方
一、曲线凹凸的定义
凹
y f ( x1)
f (x) f (x2 )
那么 f (x)在[a,b]内图像是凹的.
三、拐点
拐点：连续曲线凹弧与凸弧的分界点称为拐点。 拐点
凸凹
凸
f (x) 0 f (x) 0 f (x) 0
三、拐点
拐点
凸
f (x) 0
凹
f (x) 0
凸
f (x) 0
f (x)
f (x)
f (x)
拐点：f (x)的极值点.
拐点可能是二阶导数等于0的点，和二阶导数不存在的 点.
凸
y
f (x)
f ( x1)
f (x2 )
o x1 x1 x2 2
x2 x
f ( x1 x2 ) f (x1) f (x2 )
2
2
o x1
x1 x2
第三章第五讲 曲线的凹凸性
第ቤተ መጻሕፍቲ ባይዱ章
微分中值定理 与导数的应用
第五讲 曲线的凹凸性
函数的凹凸性与拐点
在研究了函数的单调性后, 若不知道曲线的弯曲方向, 仍不能准确描绘曲线 变化的特点. 一般地, 函数单调增加或单调减少都有两种方式, 所以只讨论函数
的单调性是不够的, 还必须讨论它的凹凸性.
y
y
B
•
C
A
o
x
o
x
如图中曲线弧AB是单增的曲线. 但从A 到 C 的曲线是向上凸的; 从 C 到 B 的曲 线是向下凸的. C 恰好是上凸和下凸的分界点, 我们称为拐点.
y
y= ƒ(x)
A C•
B
oa c
bx
如右图, 从 A到 C与从C到B的分界点 C(c, ƒ(c))就是曲线的拐点.
注 拐点是曲线上的点, 从而拐点的坐标需用横坐标与纵坐标同时表 示, 不能仅用横坐标表示.这与驻点及极值点的表示方法不一样.
拐点的求法
定理1 (拐点的必要条件)若函数 y = ƒ(x)在 x0 处的二阶导数 f (x0 ) 存在, 且点 ( x0, f ( x0 )) 为曲线 y = ƒ(x) 的拐点, 则 f ( x0 ) 0
注1 在 f ( x0 ) 存在时, f ( x0 ) 0仅是拐点存在的必要条件而非充分条件. y x4 有 f (0) 0 , 但点 (0, 0) 不是该曲线的拐点.
注2 f ( x) 不存在的点也有可能成为拐点.
y 3 x 的二阶导数在 x = 0不可导, 但 (0, 0) 是该曲线的拐点.
二阶导数的符号, 确定曲线是否存在拐点, 若存在拐点, 求出拐点.
例 判断曲线 y ( x 1)3 x5 的凸性, 并求其拐点.
微分中值定理 与导数的应用
第五讲 曲线的凹凸性
函数的凹凸性与拐点
在研究了函数的单调性后, 若不知道曲线的弯曲方向, 仍不能准确描绘曲线 变化的特点. 一般地, 函数单调增加或单调减少都有两种方式, 所以只讨论函数
的单调性是不够的, 还必须讨论它的凹凸性.
y
y
B
•
C
A
o
x
o
x
如图中曲线弧AB是单增的曲线. 但从A 到 C 的曲线是向上凸的; 从 C 到 B 的曲 线是向下凸的. C 恰好是上凸和下凸的分界点, 我们称为拐点.
y
y= ƒ(x)
A C•
B
oa c
bx
如右图, 从 A到 C与从C到B的分界点 C(c, ƒ(c))就是曲线的拐点.
注 拐点是曲线上的点, 从而拐点的坐标需用横坐标与纵坐标同时表 示, 不能仅用横坐标表示.这与驻点及极值点的表示方法不一样.
拐点的求法
定理1 (拐点的必要条件)若函数 y = ƒ(x)在 x0 处的二阶导数 f (x0 ) 存在, 且点 ( x0, f ( x0 )) 为曲线 y = ƒ(x) 的拐点, 则 f ( x0 ) 0
注1 在 f ( x0 ) 存在时, f ( x0 ) 0仅是拐点存在的必要条件而非充分条件. y x4 有 f (0) 0 , 但点 (0, 0) 不是该曲线的拐点.
注2 f ( x) 不存在的点也有可能成为拐点.
y 3 x 的二阶导数在 x = 0不可导, 但 (0, 0) 是该曲线的拐点.
二阶导数的符号, 确定曲线是否存在拐点, 若存在拐点, 求出拐点.
例 判断曲线 y ( x 1)3 x5 的凸性, 并求其拐点.
曲线的凹向及函数图形描绘
x1
y
来说，因li为 m 1 0. 所以
x x1
直 线 y0是 曲•线 y
1
o
的水平
x1
渐近线。
yf(x)
1
x
返回
又如 •y曲 ar线 c， tg因 x 为
lia m r c • t• g•x •l• ia • m •r• c •.t ••g ••x
x
返回
例1 讨论 f（ x ） 曲 x 3 线 6x 29x1 的凹 间与拐点.
解 定义 ， 域 ） 为 ， f（ x （ ） 因 3 x 2 为 1x 29，
f ( x ) 6 x 1 6 2 ( x 2 ) 令 f,（ x） 0 ，可 x2.得 当 x （ ， 2）时 f（ x ， ） 0，此区间
返回
例2 讨论曲 y线 ln（ 1x2）的凹凸区间 . 与
解 定义 ， 域 ） .因 为 y 为 1 （ 2 x x 2，
y
2(1 x2 )， (1 x2 )2
令 y 0 ， x 1 得 ， x 1 .
x (,1)
1
f ( x)
x
(1,)
y
y
y
因为
lim ln(x21) ,
x 1
的单调区间 将上述讨论列为下表
x (,1) 1 (1,0) 0
(0,1)
y(x) 0
1 (1,)
0
y(x) y
极小值 2
0
拐点 ( 0 ，0 )
极大值 2
••令 y0 ， 可y 知 3xx 曲 3 与 x 轴 线 交 x3 在
y
来说，因li为 m 1 0. 所以
x x1
直 线 y0是 曲•线 y
1
o
的水平
x1
渐近线。
yf(x)
1
x
返回
又如 •y曲 ar线 c， tg因 x 为
lia m r c • t• g•x •l• ia • m •r• c •.t ••g ••x
x
返回
例1 讨论 f（ x ） 曲 x 3 线 6x 29x1 的凹 间与拐点.
解 定义 ， 域 ） 为 ， f（ x （ ） 因 3 x 2 为 1x 29，
f ( x ) 6 x 1 6 2 ( x 2 ) 令 f,（ x） 0 ，可 x2.得 当 x （ ， 2）时 f（ x ， ） 0，此区间
返回
例2 讨论曲 y线 ln（ 1x2）的凹凸区间 . 与
解 定义 ， 域 ） .因 为 y 为 1 （ 2 x x 2，
y
2(1 x2 )， (1 x2 )2
令 y 0 ， x 1 得 ， x 1 .
x (,1)
1
f ( x)
x
(1,)
y
y
y
因为
lim ln(x21) ,
x 1
的单调区间 将上述讨论列为下表
x (,1) 1 (1,0) 0
(0,1)
y(x) 0
1 (1,)
0
y(x) y
极小值 2
0
拐点 ( 0 ，0 )
极大值 2
••令 y0 ， 可y 知 3xx 曲 3 与 x 轴 线 交 x3 在
3.5曲线的凹凸性
例 4 判断 f ( x) x3 x ，x (,)的凹凸性
解：f ( x) 3x2 1 ，得驻点
x1
1, 3
x2
1 3
f ( x) 6x
当 x 0 时, f ( x) 0 。在区间 (0,) ，曲线是凹的，
此区间内唯一驻点 x2
1
是极小值点。（
3
f (
1 ) 3
6 0， 3
与极值的第二充分条件一致）
§4.5曲线的凹凸性
y B
A oa
bx
定义1 设函数 f ( x)在某一区间上的图象是一条连续
光滑曲线,若曲线上任一点的切线总位于曲线下方,则称曲线
在此区间上是凹；反之，若在某区间曲线的切线总位于曲线 上方，则称曲线在此区间为凸的。
定理 设函数 f ( x) 在区间 (a,b)有二阶导数， 1. 若 x (a,b)，恒有 f ( x) 0，则曲线为凹； 2.若 x (a,b)，恒有 f ( x) 0，则曲线为凸。
定义2 曲线上凹与凸的分界点称为拐点。
由定理知：若 f ( x)存在，拐点的必要条件为 f ( x) 0
拐点的几何特征是曲线穿过拐点时，由此点的切线一侧进入另一侧。 综上所述：我们得到判定曲线的凹凸性与曲线拐点的一般步骤为：
（1）求函数的定义域 ；
（2）求 f ( x) ，f ( x) ； （3）求出 f ( x) 0的全部实根及所有使二阶导数不存在的点 （4）检查上述所求点的两侧 f ( x)的符号，确定曲线的凹凸
性和拐点
例1 判断 y e x，x (,)的凹凸性 解： y e x 0曲线弧是凹的，切线是在曲线下方。
例2 判断 y ln x，x (0. )的凹凸性
解：
y
曲线的凸凹性与拐点课件
凸函数的性 质
凸函数的性质
如果函数$f(x)$在区间$I$上是凸函数，则对于任意$x_1, x_2 \in I$，都有$f(\frac{x_1 + x_2}{2}) \leq \frac{f(x_1) + f(x_2)}{2}$。
凸函数的性质还包括
如果函数$f(x)$在区间$I$上是凸函数，则对于任意$x \in I$， 都有$f(\frac{x + x}{2}) \leq f(x)$。
定义
对于函数$f(x)$，如果$f''(x_{0})=0$ 且$f'(x_{0})\neq 0$，那么点 $(x_{0},f(x_{0}))$称为函数$f(x)$的拐 点。
拐点的求法
求解方法一
直接求解法。通过观察函数的导数形式，确定导数在某一点为零，然后进一步求 解二阶导数在该点的值，判断其是否为零。
VS
极值的意义
极值反映了函数在某一点附近的变化情况， 是局部的、暂时的最大值或最小值。
极值的求法
01
02
03
04
判断函数的单调性
根据导数与函数单调性的关系， 判断函数在某区间内的单调性，
寻找极值点。
求导数
根据函数表达式求出导数，并 找到导数为零的点。
判断导数的符号
判断导数在零点附近的符号变 化，以确定极值的存在性。
凹函数的几何特征
曲线开口向下，即函数图像是向内凹的。
凹函数的性 质
若函数$f(x)$在区间$I$上是凹函数，则对于任意$x_{1}, x_{2}$在$I$上，都有 $f(x_{1}) \leq f(x_{2})$。
若函数$f(x)$在区间$I$上是凹函数，则对于任意$x_{1}, x_{2}$在$I$上，都有 $\frac{f(x_{1})}{x_{1}} \leq \frac{f(x_{2})}{x_{2}}$。
函数的凹凸性
称为拐点 .
ooo
xx11
xx11xx22 22
xx22
xxx
【 知识背景】 函数的凹凸性是高等数学的数学分析中
的研究函数的一个概念，是用来研究函数图象的变化趋 势的。
【 高考联接】 在高考中常借助函数的凹凸性来考查基
本初等函数的图象及性质，这一知识点常渗透在与函数 的 图 象 与 性 质 的 选 择 填 空 题 中 。经 常 与 高 中 所 学 的 函 数 、 三角、不等式知识相结合。此类问题的常规处理思路有 数形结合法、导数分析法、增量分析法、估猜法等。
例9 求函数 f(x)1(exex)的反函数.
2
解
令 y1(ex ex), 则
2
e2x2yxe10
exy y21 (舍去“-”) xlny ( y21)
将字母x与 y互换,得 ylnx ( x21)
即
f 1(x )ln x (x 2 1 )
x 2
ax2 1
ax2 2
1 2
a(x2 1
x2 2
1 ＝ a(x
21
x )2 2
0 ，
f
x (1
2
x 2
)
1f
2
(x ) 1
f
() 故函数 2
f
(x) 是
凹函数。
（2）由 f (x) 1 1 f (x) 1 1 ax2 x 1 ①
k AB
f (x1) f (x2) 0 x1 x2
显
然
成
立
（
可
以
用
f '( x ) 1 0 ( x 0 ) ） 故 ③ 正 确 x ln 1 0
函数曲线的凹凸性
那么 x x0 就是 y f (x) 的一条铅直渐近线 .
例如 y
1
,
( x 2)(x 3)
有铅直渐近线两条: x 2, x 3.
2.水平渐近线 (平行于 x 轴的渐近线)
如果 lim f (x) b 或 lim f (x) b (b 为常数)
x
x
解 Df (,).
f ( x) 5 x 2 的零点为 2 ，不存在的点为0。
33 x
5
将 f 的符号与 f 的单调性列表如下：
x (-, 0)
0
(0, 2/5) 2/5 (2/5, +)
f
+
不存在
-
0
+
f
连续
连续
f 在 ( , 0]上 单 调 增 ； 在[0, 2]上 单 调 减 ； 在[ 2 , )
凹的
凹凸区间为 (,0], [0, 2 3], [2 3 ,).
方法2: 设函数 f ( x) 在 x0 的邻域内三阶可导,且 f ( x0 ) 0,而 f ( x0 ) 0,那末 ( x0 , f ( x0 )) 是曲 线 y f ( x)的拐点.
例4 求曲线 y sin x cos x ([0,2]内) 的拐点.
那么 y b 就是 y f (x) 的一条水平渐近线 .
例如 y arctan x,
有水平渐近线两条:
y , y .
2
2
3.斜渐近线 如果 lim [ f (x) (ax b)] 0
x
或 lim [ f (x) (ax b)] 0 (a,b 为常数) x
方法1:
设函数f (x)在x0的邻域内二阶可导 ,且f (x0 ) 0,
3.5凹凸性与函数图形描绘PPT课件
3.5 曲线的凹凸性与函数作图
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导，
x0为I的任一内点，若对 x I( x x0 )，恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点，如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点，绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), （偶函数, 图形关于y轴对称）
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导，
x0为I的任一内点，若对 x I( x x0 )，恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点，如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点，绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), （偶函数, 图形关于y轴对称）
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
120 高等数学（上册） 3.5.1 曲线的凹凸性
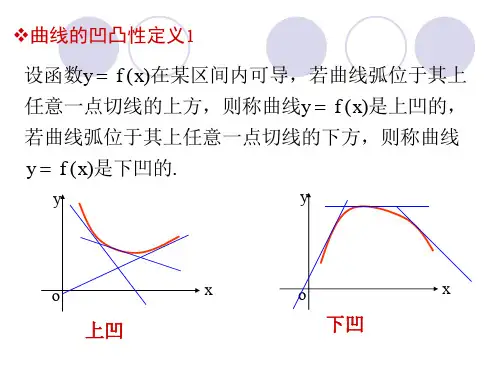
首先从几何直观来分析曲线的凹凸性. 在图3-5-2中，曲线弧是向上凹的，此时如果任取两点12,x x ，则连接这两点的弦总位于这两点间弧段的上方；而在图3-5-3中，曲线弧是向上凸的，连接
任意两点的弦总位于这两点间弧段的下方. 因此，曲线的凹凸性可以用连续曲线弧上任意两点的弦上的某点比如中点与曲线上相应点的位置关系来描述
.
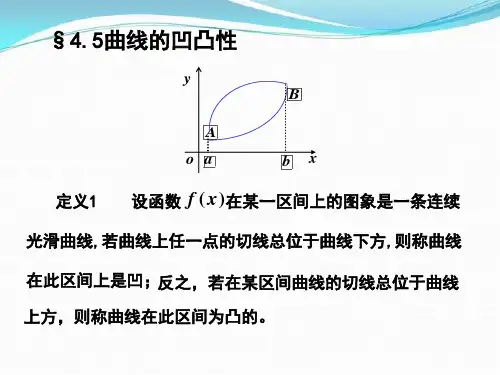
图3-5-2 图3-5-3 定义3.5.1 设()f x 在区间I 内连续，如果对I 上任意不同的两点12,x x ，恒有
()()1212
22f x f x x x f ++⎛⎞<⎜⎟⎝⎠，
则称()f x 在I 上的图形是向上凹的，区间I 称为()f x 的凹区间.
如果对I 上任意不同的两点12,x x ，恒有
()()1212
22f x f x x x f ++⎛⎞>⎜⎟⎝⎠，
则称()f x 在I 上的图形是向上凸的，区间I 称为()f x 的凸区间.
直接根据定义判别一条曲线的凹凸性是比较困难的. 下面介绍利用导数确定曲线凹凸性的方法. 如图3-5-4所示，对于凹曲线，当x 增加时，其上每一点切线的斜率是逐渐增加的，即导函数()f x ′是单调增加函数；而对于如图3-5-5所示的凸曲线，当x 增加时，其上每一点切线的斜率是逐渐减少的，即导函数()f x ′是单调减少函数. 从而，可以得到下列利用导数确定曲线凹凸性的定理
.
图3-5-4 图3-5-5 定理3.5.1 设函数()f x 在[],a b 上连续，在(),a b 内可导.
（1）若在(),a b 内，()f x ′单调增加，则曲线()y f x =在[],a b 上是凹的；
（2）若在(),a b 内，()f x ′单调减少，则曲线()y f x =在[],a b 上是凸的.。