基于城际铁路客流动态分配的列车开行方案优化生成_王培恒

城市轨道交通多编组列车开行方案优化研究戎亚萍;张星臣;柏赟;许得杰【摘要】In order to meet the fluctuation of passenger flow, a multi-objective optimization modal for train plan of urban rail transit based on hybrid train formation is established, which is aimed to minimize the passengers’waiting time and operator’s cost. The constraints are transport supply, policy headway and fleet size. And a two-phase mathematical programming algorithm is also proposed. At last, the validation of the proposed model and the algorithm has been tested with an urban rail transit line in China. The results show that compared with the traditional train plan of single train formation, the train plan based on hybrid train formation can reduce the waiting time of passengers and the cost of operation by 17%and 27%, but increase the total train-hours by 20%. When the threshold ratio of peak demand to off-peak demand is more than 1.48, the train plan of hybrid train formation is preferable.%针对城市轨道交通全日客流时间分布不均衡下的列车开行方案优化问题，以乘客等待时间和企业成本最小为优化目标，以运输供给、列车最小发车间隔、最大服务间隔，以及列车数为约束条件，构建基于多编组模式下的多目标列车开行方案优化模型，并设计两阶段求解算法.案例分析表明：与传统单一编组列车开行方案相比，基于多编组的轨道交通列车开行方案使乘客等待时间和车公里数分别减少17%和27%，列车运行小时增加20%；当客流不均衡系数大于1.48时，宜采用多编组运输组织方式.【期刊名称】《交通运输系统工程与信息》【年(卷),期】2016(016)005【总页数】6页(P117-122)【关键词】城市交通;列车开行方案;多目标优化模型;多编组;两阶段求解算法【作者】戎亚萍;张星臣;柏赟;许得杰【作者单位】北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044;北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044;北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044;北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044【正文语种】中文【中图分类】U268.6随着线网规模的扩大，城市轨道交通全日客流时间分布呈现明显的不均衡性，尤其是市域快速轨道交通线路，其客流具有显著的潮汐特征.为了解决单一编组模式下非高峰期运能浪费，服务水平低的问题，已有部分学者在多编组研究方面取得了一定成果.所谓多编组是指针对城市轨道交通线路客流在不同时段或不同区段的差异，由车辆基地事先设计并发出的具有不同编组长度的列车，其在运行过程中不进行拆解或重联的运营组织技术［1］.Niu等［2］以城际铁路为研究对象，构建了以乘客等待成本和在车成本最小为目标的城际铁路开行方案优化模型，研究结果表明高峰期开行大编组列车，平峰期开行小编组列车能够减小乘客成本；杨信丰等［3］研究了多车型快速公交的车型调度问题，算例分析表明通过合理的发车频率和车型组合可以得到多种满足需求的调度方案；Sun等［4］以单一公交线路为研究对象，构建了基于两种车型混合使用的时刻表优化模型，算例表明采用不同容量的车辆混跑，对于节省乘客出行时间和企业费用是有效的；Hassold等［5］以减少乘客等待时间和提高列车满载率为目标，构建了考虑多种公交车容量的等间隔发车时刻表优化模型，结果表明该方案在提高满载率的同时乘客等待时间可以节省43%. Ceder等［6］以节省公交车能耗为出发点，采用大小两种容量的公交车构造非均衡发车时刻表优化模型，结果表明该运营模式可以提高19%的满载率，从而达到节约能耗的目的.Lee等［7］在公交网络车辆共享的基础上，认为同一线路不同时段采用不同容量的公交车，可以节省系统费用.尽管上述文献均考虑了多种车容量下的列车运营组织模式，但是城市轨道交通系统与城际铁路、公交系统有着明显的不同.城际铁路和公交系统的车辆可以在不同线路间共用，而轨道交通系统采用各线路独立运行的模式，不同线路间一般不能共享车辆.所以，考虑到企业运营成本，采用多编组模式下的运用车辆数不能超过单一编组模式.因此，本文增加了车体保有量的约束条件，以乘客等待时间和企业运营成本最小为优化目标，以各时段编组方案和发车频率为决策变量，构建了基于多编组的列车开行方案多目标优化模型，并设计了两阶段求解算法.最后，以某轨道交通线路为例进行了实例研究.针对1条具有N个车站，线路长度为L的城市轨道交通直线型线路，所有列车从始发站1开始，沿下行方向环形逆转到上行方向，依次标记为车站2，3，…，N，N+1，…，2N-1，直至终点站2N，如图1所示.本文用 i、j标记车站，用Di，j （t）表示t时段内从i站前往 j站的乘客数；由于列车到折返站后所有的乘客都将下车，故当i∈｛1，2，…，N｝，j∈｛N+1，N+2，…，2N｝，或i∈｛N+1，N+2，…，2N｝，j∈｛1，2，…，N｝时，客流需求Di，j（t）=0.在城市轨道交通全日运营时段［Ts，Te］内，客流随时间波动形成以一定时间段为周期的客流时段.与客流波动相对应，本文将全日运营时段划分为若干个列车开行时段，且每个开行时段具有相对独立的列车开行频率和编组方案.令列车开行时段集合T=｛Tk|k=1，2，…，K ｝，其中K为时间分段总数，|Tk|为时段长度.多编组列车开行方案由具有不同编组长度的列车构成，客流的不均衡性使得不同时段开行不同编组的列车.为减小运营组织难度，一般选取大、小两种编组的列车分别用于不同的客流时段.在多编组运输组织模式中，定义多编组方案的列车集合B=｛Bm|m=1，2｝，其中B1表示小编组列车对应的编组辆数；B2表示大编组列车对应的编组辆数；M为列车最大编组辆数；开行对数集合F=｛fm（k）|k=1，2，…，K ｝，其中 fm（k）为开行时段k内第m种编组方案的列车开行对数.依照以上定义，基于多编组的城市轨道交通列车开行方案可表示为Ω=｛B，T ，F｝.多编组城市轨道交通列车开行方案的优化过程需要兼顾运营企业和乘客两方面的利益.一方面，运营单位希望在满足客流需求的前提下，开行大间隔、小编组列车以尽可能地降低成本；另一方面，乘客则希望开行小间隔、大编组列车以减少等待时间和提高舒适度，双方利益相互矛盾.因此本文以乘客出行成本和企业运行成本最小为优化目标，以各时段编组方案和发车频率为决策变量，构建多编组列车开行方案优化模型.2.1 模型假设针对多编组列车开行方案优化问题，本文做出如下假设：（1）采用单一交路站站停的运营组织模式，同一时段的发车间隔保持不变；（2）以每1h作为一个列车开行时段，全天分为18个列车开行时段；（3）乘客均匀到达车站，服从先到先服务的原则，不存在留乘；（4）不考虑列车重联成本和耗时，且不同编组列车的旅行速度相同.2.2 模型建立（1）乘客出行成本.乘客出行成本由乘客在车时间成本和等待时间成本两部分构成，考虑到不同编组列车的旅行速度相同，乘客在车时间相同，因此乘客出行成本可由乘客等待时间表示.相关研究表明，城市轨道交通列车发车间隔较小且均匀发车时，乘客平均等待时间为发车间隔的一半［8］，所以，乘客总等待时间为各车站乘客等待时间之和. （2）企业运营成本.企业运营成本主要包括列车运行成本（能耗费用、检修费用等）和人力成本（司乘人员工资）.由于开行单趟列车的运行成本和单位车小时人员工资是固定的，所以本文采用车辆走行公里和列车运行时间表示企业运营成本.2.3 约束条件根据基本运输组织条件及要求，基于多编组的列车开行方案需要满足：式中：为第k个开行时段内的最大断面流量；V为每节车辆的定员；hmin，hmax分别表示最小、最大发车间隔；Nm表示第m种单元列车的可用列车数；N0表示采用单一编组模式下的运用车辆数.式（4）和式（5）表示列车编组数约束；式（6）和式（7）表示发车间隔与发车频率约束；式（8）表示运输供给约束，对客流高峰区段进行满载率限制；式（9）和式（10）表示车体保有量约束，多编组运营模式下各编组的运用列车数不能超过各自的车体保有量，且运用车辆数之和不能超过单一编组.基于多编组的城市轨道交通列车开行方案优化模型涉及多个参数和目标函数，同时列车编组与开行频率均为离散变量，且相互影响.因此，该模型是一个不连续、非凸的多目标整数规划问题，直接求解难度较大.为此，本文提出一种两阶段求解算法：第1阶段从乘客等待时间和企业运营成本综合优化角度出发，在满载率和发车频率的约束下，求解单一编组模式下的全日行车计划，从而得到单一编组模式下的运用车辆数.然后，将单一编组模式下的车体保有量作为输入条件，求解多编组运营模式下不同编组列车的车体保有量.第2阶段采用模糊折中法和线性加权法将多目标优化转化为单目标优化问题，并运用遗传算法求解该模型，染色体采用特殊的二进制编码方法，从而确定各时段列车编组方案和开行频率.3.1 车体保有量确定方法车体保有量是指在满足给定的发车间隔和编组条件下所需要运用的车底数量.对于多编组列车开行方案，一般选取大、小两种编组的列车分别用于不同的客流时段，此时，，.首先，根据高峰时段客流确定大编组列车运用数，从乘客等待时间最小化的角度构建列车开行方案评价指标，如式（11）所示.即在满足高峰断面客流需求的基础上，仅需高峰小时的大编组列车开行对数最小或小编组列车开行对数最大.然后，综合目标函数式（1）和式（2）和约束条件式（4）～式（6）确定单一编组模式下的车体保有量，以单一编组模式下的车体保有量和多编组模式下的大编组运用车数作为输入条件，可以求得小编组列车车体保有量的最大值.具体算法如下：①针对客流高峰时段，初始化大编组列车的发车频率 f1（k*）=1.②根据式（8）计算小编组列车的发车频率，则.③判断是否成立，若成立，；否则，f1（k*）=f1（k*）+1，转②.④计算大小编组列车的车体保有量，，N2=（N0-N1·B1）/B2，结束.3.2 列车开行方案确定方法采用遗传算法求解模型，染色体采用二进制编码方式，染色体长度为列车开行时段数量K，基因编码对应各时段各编组类型的发车频率.由于模型中3个目标函数的量纲不同，在设计适应度函数时首先将它们转化为同一量纲，本文采用极差化方法［9］进行无量纲化处理，如式（12）所示.然后根据适应度函数筛选出较优的开行方案，并通过交叉、变异等操作产生新的解集，直至达到最大迭代次数，筛选出最优解.式中：分别为各目标当前函数值、最小函数值及最大函数值；wobj为权重，且，本文取3个目标函数的权重相等.4.1 基础数据本文以某城市地铁线路的开行方案优化为例进行说明.线路长度为18.03km，共有16个车站，采取单一交路站站停的运营组织模式.单元列车为3节编组，车辆定员V=310人/辆，组合编组列车为6节编组，由2列单元列车组成；列车最大满载率αmax=1.2，车底周转时间T周=73min；全天各时段最大和最小发车间隔为别为10 min和3 min；运营时段参数Ts=6 h，Te=24 h，K=18 h，||Tk=1 h，即每1 h作为一个列车开行时段.本案例线路高峰时段与平峰时段的客运量均值之比为2.85，表明全日客流分布具有明显的不均衡性，全日客流时段分布如图2所示.4.2 求解结果按照高峰断面客流法确定单一编组条件下列车编组长度为6，应用本文设计的算法可求得单一编组和多编组条件下，全天各时段列车编组方案和发车频率，具体结果如表1和表2所示.结果表明，相对于单一编组方案，多编组条件下的发车频率更优，全天乘客总等待时间可减少17%，客流平峰时段（11：00-14：00和21：00-23：00）发车间隔最大可缩短22%.进一步分析企业运营成本可知，基于多编组的列车开行方案使车公里数减少27%，但列车运行时间增加了20%.可见企业采用多编组的运营模式时可以减少乘客等待时间和列车运行成本，但这是以增加司机成本为代价的.4.3 灵敏度分析客流时间分布不均衡性是列车开行方案的重要影响因素，因此，本文根据高峰小时最大断面客流与各时段最大断面客流之间的关系，将各时段最大断面客流按其差值等差波动设置，观察客流不均衡系数不同的情景下，列车开行方案的差异性.由图3可知，当客流不均衡系数趋于1时，客流在各个时间段分布较均匀.客流不均衡系数不同的条件下，多编组与单一编组列车开行方案的乘客等待时间、车辆走行公里数及列车运行时间如图4所示.由图4可以得到以下结论：（1）随着客流时间分布越均匀，两种编组方案的乘客等待时间均呈下降趋势，列车运行时间均呈上升趋势.当客流不均衡系数达到1.48时（情景7），两种编组方案的乘客等待时间和列车运行时间相同，且仅出现一种列车编组形式.这说明，随着高峰期客流减少，平峰期客流增加，单一编组模式下的列车编组数降低，发车频率提高；多编组模式下，大编组列车数减少，小编组列车数增多，将会有更多的时段采用“小编组高密度”的运营模式.当高峰客流减少到一定程度时，小编组列车即可满足需求.（2）随着客流时间分布越均匀，单一编组方案的车公里数呈波动式下降，多编组方案的车公里数呈上升趋势，且二者的差距逐渐减小.当客流不均衡系数达到1.48时，两种编组方案的车公里数相等.这说明客流时间分布不均衡性越高，基于多编组的运营模式优势越明显.综上可知，多编组是在全日客流分时需求差异较大的前提下所采用的相对较优的运输组织模式.本文以城市轨道交通多编组列车开行方案优化问题为研究对象，在考虑运用车辆数限制的基础上，以综合优化乘客等待时间和企业运营成本为目标，构建了多目标优化模型，并讨论了不同客流时间分布对结果的影响.结合案例研究，得到以下结论：（1）以某城市轨道交通线路为例，应用本文的模型和算法进行测算.结果表明，相对于单一编组方案，多编组方案使乘客的等待时间和车公里数分别减少17%和27%，列车运行小时增加20%.这说明，当企业采用多编组的运营模式时可以减少乘客等待时间和列车运行成本，但这是以增加司机成本为代价的.（2）随着客流时间分布越均匀，多编组方案的优势逐渐减弱，当线路单向高峰小时客流不均衡系数达到1.48时，仅出现一种编组形式.这说明多编组是在全日客流需求差异较大的前提下所采用的相对较优的运输组织模式.【相关文献】［1］毛保华，刘明君，黄荣，等.轨道交通网络化运营组织理论与关键技术［M］.北京：科学出版社，2011.［MAO B H，LIU M J，HUANG R，et al.Operational theories and key technologies of rail transit networks［M］.Beijing：Science Press，2011.］［2］ NIU H M，ZHANG M H.An optimization to schedule train operationswith phase-regularframework for intercity rail lines［J］.Discrete Dynamics in Nature and Society，2012（549374）.［3］杨信丰，刘兰芬，李引珍，等.多目标快速公交多车型优化调度研究［J］.交通运输系统工程与信息，2016，16（3）：107-112.［YANG X F，LIU L F，LI Y Z，et al. A multi-objective bus rapid transit dispatching optimization considering multiple types of buses［J］. Journal of Transportation Systems Engineering and Information Technology，2016，16（3）：107-112.］［4］ SUN D J，XU Y，PENG Z R.Timetable optimization for single bus line based on hybrid vehicle size model［J］. JournalofTraffic and Transportation Engineering（English Edition），2015，2（3）：179-186.［5］ HASSOLD S，CEDER A.Multiobjective approach to creating bus timetables with multiple vehicle types［J］. Transportation Research Record：Journal of the Transportation Research Board，2012（2276）：56-62.［6］ CEDER A，HASSOLD S，DUNLOP C，et al.Improving urban public transport service using new timetabling strategies with different vehicle sizes［J］.International Journal of Urban Sciences，2013，17（2）：239-58.［7］ LEE K K，KUO S H F，SCHONFELD P M.Optimal mixed bus fleet for urban operations［J］.Transportation Research Record：Journal of the Transportation Research Board，1995（1503）：39-48.［8］邓连波，曾强，高伟，等.基于弹性需求的城市轨道交通列车开行方案研究［J］.铁道学报，2012，34（12）：16-25.［DENG L B，ZENG Q，GAO W，et al.Research on train plan ofurban rail transit with elastic demand［J］. Journal of the China Railway Society，2012，34（12）：16-25.］［9］张玉召，严余松.快捷货物列车开行方案多目标优化模型及算法［J］.交通运输系统工程与信息，2014，14（3）：111-116.［ZHANG Y Z，YAN Y S.A multiobjective model and algorithm of operation plan for expressfreighttrains［J］.JournalofTransportation Systems Engineering and Information Technology，2014，14（3）：111-116.］。

基于客流动态分配的城际客运专线列车开行方案优化城际客运专线主要服务于相邻城市间或城市群内中短途旅客运输,是一个区域内各大中城市以及主要城镇之间紧密联系、协调发展的重要交通工具,可实现大运量、公交化、快捷化的旅客运输。

对于省会城市、大中城市和主要城镇等经济发达、人口稠密地区的旅客流通将起到关键作用。

区域居民收入水平较高,往来出行频繁,对于快捷、准时、舒适的运输方式需求很大,城际列车能够为当地居民提供高品质的运输服务。

随着城际客运专线网络的逐渐发展完善,既有铁路的运输组织方式已经不再适应新的路网运营。

为争取更多的客流分担率,提高旅客运输服务质量,需优化城际客运专线旅客列车开行方案,以降低旅客出行成本。

客流动态分配是指客流因列车停站方案、列车始发时刻、进站时刻、区间运行时间等开行方案要素而动态地选乘不同等级列车。

开行方案优化模型则根据目标方程和约束方程,得到最优的开行方案各要素参数。

本文的主要内容如下：(1)系统分析了城际客运专线客流的出行特点和需求,并总结了趋势客流、转移客流以及诱增客流的预测方法。

在对国内外已有关于旅客列车开行方案与客流量之间相互影响的研究成果进行系统总结并借鉴的基础上,结合我国城际客流的出行特点,论述了我国城际客运专线客流量和列车开行方案之间循环反馈的关系。

(2)首先构建了城际客运专线客流量的动态分配模型。

基于动态分配模型,构建了以旅客区间运行时间与在站等待时间之和最短为目标,以最短开行间隔、最大通过能力为约束方程的线性城际客运专线旅客列车开行方案优化模型。

(3)对广清城际客运专线的客运通道现状、沿线交通运输结构、沿线客流状况进行了调查和分析。

根据客流断面特征,制定了广清城际客运专线旅客列车分为两端站直达列车、仅在中途大站狮岭停站列车以及站站停列车三类。

对广清城际客运专线旅客列车优化模型采用理想点法和MATLAB编程求解。

结果表明,广清城际应开行8对两端站直达列车、21对仅在中途一站停列车和16对站站停列车。

&'()*+,-,.Journal of Yangling Vocational ＆ Technical Co l ege!19 " !3 #2020 $ 9 %Vol19No3Sep ．,2020DOI ：1019859/jcnkiCN61—1403/G4．2020．03．004城际列车开行方案优化研究6781,9:;1,2,3,4,<=>1,3,1?@1,A B 5(1.石家庄铁道大学交通运输学院，石家庄050043； 2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄050043； 3.河北省交通安全与控制重点实验室，石家庄050043； 4.河北省风工程和风能利用工程技术创新中心，石家庄050043； 5.贵州大学计算机科技与技术学院，贵阳550000)摘要：列车开行方案是获取旅客满意度的一个重要环节。

为了能够更好地服务旅客，吸引更多客流，需要不断优化更新开行方案。

本文在满足客流需求的基础上，建立了以旅客出行费用最小为目标的开行方案优化模型，并l 西安至宝鸡城际客运专线为例，采用MATLAB 软件求解验证了本模型的可行性。

为其他城际列车开行方案的优化调整提供了参考。

:;<： 城；行方案； 行费用； MATLAB=>?@A ：U2924BCDEF ：ABGHA ：1671-9131(2020)03-0010-04Study on Optimization of Intercity Train Operation SchemeWANG Yueshuang , YU Xue-tao 1'2'3'4, GAO Gui-feng 13 , ZHANG Ya-jing , NIU Kun 5(1. School of Traffic and Transportation, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 050043 , China ； 2. State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures , Shijiazhuang Tiedao University,Shijiazhuang ， Hebei050043， China ； 3 KeyLaboratoryofTra f icSafetyandControlofHebeiProvince ， Shijiazhuang ， Hebei050043, China ； 4 Innovation Center for Wind Engineering and Wind Energy Technology of HebeiProvince , Shijiazhuang , Hebei050043,China ；5 Co l egeofComputerScienceandTechnology , Guizhou University , Guiyang , Guizhou550000,China )Abstract ：Thetrainoperationschemeisanimportantpartofobtainingpassengersatisfaction Inordertoservepassengersbe t er anda t ractmorepassengers ,theoperationschemeneedstobecontinuouslyoptimizedandupdated Onthebasisofsatisfyingthedemandofpassengerflow ,thispaperestablishesanoperationschemeoptimizationmodeltoachieveminimumpassengertrip expenses. In addition , taking Xi'an to Baoji intercity passenger dedicated lines as an example and using MATLAB to solve themodel ,thefeasibilityofthismodelisverified Thisstudyprovidesareferencefortheoptimizationandadjustmentofotherin- tercitytrainoperationplansKeywords ：intercitytrain ；operationscheme ；tripexpenses ； MATLAB0引言2008年，中国首条城际高速铁路一一京津城际的开通拉开了中国城际铁路建设的大门［1—2］。

基于客流动态分配的城际列车开行方案彭宏勤;朱郁俊【摘要】综述了城际列车开行方案的研究现状.为准确描述客流与开行方案的互动关系,本文提出了模型建立的系统封闭性假设、列车种类划分假设、客流动态转化假设和选乘优先顺序假设等假设条件.在此基础上,对相关集合变量进行了描述,建立了反映不同类型客流转化过程的客流动态分配模型,构建了综合考虑铁路部门收益最大化、旅客总支出最小化和最大限度满足客流需求的多目标规划模型.针对建立的多目标0-1整数规划模型,采用遗传算法求解,并对规划模型求解的过程进行了说明,最后通过算例验证模型算法的有效性.%This paper summarizes the research status of intercity train operating scheme. To precisely describe the interaction between passenger flow and operating scheme, it proposes assumptions of system closure, train type division, passenger flow dynamic assignment and selecting priority during the process of establishing model. Based on these, it describes relative variables and formulates the passenger flow dynamic assignment model to reflect the conversion process of different passenger types. Then it develops a multiple objective programming model considering maximum railway department revenue, the smallest passenger total expenditure and the maximum passenger demand. It also uses the genetic algorithm to solve the established multi-objective 0-1 integer programming model. Finally, a numerical example is provided to illustrate the effectiveness of this algorithm of model.【期刊名称】《交通运输系统工程与信息》【年(卷),期】2013(013)001【总页数】7页(P111-117)【关键词】铁路运输;开行方案;客流动态分配;多目标规划;遗传算法【作者】彭宏勤;朱郁俊【作者单位】北京交通大学城市轨道交通系,北京100044;北京交通大学城市轨道交通系,北京100044【正文语种】中文【中图分类】U292.3城际铁路是在人口稠密的都市圈或城市带规划和修建的高速铁路客运系统,是区域性的重要交通运输基础设施.根据《中国铁路中长期铁路网规划》,环渤海、长三角、珠三角地区建立区域性城际客运系统,覆盖区域内主要城镇[1].为更好地集中配置和运用城际铁路运力资源,提高市场竞争力,科学合理地制定城际列车开行方案具有重要现实意义.国外客运专线建设运营起步早,列车开行方案的研究相对成熟,主要针对旅客列车开行方案成本、收益、直达旅客人数、换乘次数等目标,建立数学规划模型.Bussieck 等[2]提出了满足旅客运输需求和运输能力约束,以直达旅客数最大化为目标的混合整数规划模型.Claessens等[3]提出了一个在给定路网结构,以成本最小化为目标,优化发车频率和所需列车数量的整数非线性规划模型. Goossens等[4,5]提出复式线路规划问题即单条铁路上多种停站模式并行,建立以成本最小化为目标的混合整数规划模型.Chang等[6]采用模糊数学规划方法,建立了以铁路运营费用和旅客等待时间最小化为目标,单条铁路上城际高速列车开行方案的多目标优化模型.国内客运专线建设运营起步相对较晚,相关研究多基于既有线路列车开行方案.冯枫[7]设计了以最大化直达运输和最小化列车虚糜为目标,在不考虑旅客换乘的影响情况下,求解旅客列车开行方案的多目标数学规划模型.邓连波[8]构造了客运专线列车开行方案的双层规划模型,上层模型考虑企业收益和旅客需求,下层模型处理客流换乘选择问题,并设计了基于模拟退火方法的优化算法.张拥军等[9]对高速列车停站影响进行分析,研究建立了高速列车开行方案多目标0-1规划模型.徐瑞华等[10]研究了在已知OD车流的条件下合并车流方法,建立以满足运输需求为约束,以列车开行数量最小化为目标的高速列车开行方案优化模型.目前相关领域的研究成果多围绕旅客列车的组织、开行方案的制定、开行方案的优化等方面展开,且通常以固定的客流OD作为系统的输入,针对开行方案的制定对实际客流反馈影响方面的研究尚显不足.本文针对这一问题进行研究,提出了客流的动态转化假设,并将客流动态分配融入到客运专线列车开行方案的编制过程中.在本研究中,模型的建立是基于如下的条件假设:(1)系统封闭性假设.系统状态的变化只取决于内部影响因素的变化.(2)列车种类划分假设.根据城际列车平均速度和停站方案的不同,提出以择站停高速、择站停中速和站站停普速列车为基本组合的停站方案.各类型的列车优先运送相应类型的客流.(3)客流动态转化假设.不同的开行方案会对客流产生反馈作用[11],使得各类别客流存在相互转化现象.本文的动态不是指客流相对时间的动态性,而是实际客流分配相对于系统开行方案的动态性.(4)选乘优先顺序假设.本文不考虑旅客中途换乘情况,旅客在出发站可根据列车开行方案选乘列车,选乘时旅客按照自身客流类型优先选择相应类型列车.在满足以上条件的情况下,建立了客流动态分配模型及各类型列车开行方案的多目标规划模型.城际客运专线网G={S,E},车站集S={si|i =1,2,…,n},s1,s2…,sn依次表示从始发站到终到站按经过顺序排列的车站.路段集E={ei|i=1,2,…,n-1},ei为si和si+l站间路段.相邻车站间路段距离D={di,i+1|i=1,2,…,n-1},为车站si和sj间路段总距离.列车等级集合T={G,Z,L},类型G为择站停高速列车,Z为择站停中速列车,L为站站停普速列车.设类型为K∈T的列车定员为AK.初始客流OD已知,客流OD矩阵H=(hij)n×n, hij表示si和sj站间客流OD量.记si和sj站间乘坐K∈T型列车的初始客流为hKij.为简便,称该类型客流为K型客流.同理,高速、中速、普速列车客流OD矩阵可记为HK=(hKij)n×n( K∈T ).h～Kij为因开行方案变化造成客流类别发生转化后,si和sj站间乘坐K∈T型列车的实际客流.已知三种类型列车的开行方案均以s1为始发站sn为终到站[12],区别在于停站方案和服务频率.用xKi表示K(K∈T)型列车是否在si停站.若列车停,则xKi=1,否则xKi=0.每日各类型列车服务频率为fK.列车服务频率是指单位周期时间(一天)内,该类型列车的开行对数(服务次数)[13].三种类型列车开行停站方案如图1所示.K型列车停站时间为tKs,停站费用cKs,车公里费用cKr,K型列车运行速度vK.城际铁路相对于干线铁路距离短,多采用公交化运营方式,一般无复杂的路网结构.研究城际列车开行方案,重点在于确定各类型列车停站方案与服务频率.在城际列车的始发、终到站都已确定,且城际列车路线是一条单一路径的条件下,可以建立以三种类型列车的停站方案和服务频率为优化指标,铁路部门收益最大和旅客总体支出最小和尽量满足客流需求为优化目标,区段运输能力与通过能力等客观因素为约束的多目标优化模型.根据客流动态转化假设,建立各类型客流动态分配模型,使得模型能更为准确地反映客流变化和乘客选乘行为.4.1 客流动态分配模型根据先前所述,城际列车分为三种类型,根据乘客选择列车类型的不同将客流分为高速、中速和普速三个类别.为简化模型,假设初始高速、中速客流已知,普速为零(此假设对结果无影响).为准确反映乘客选乘列车心理,下面对各类别客流动态分配过程进行阐述.依据文中系统假设,旅客按照自身客流类型优先选择相应类型列车.已知si到sj的G型客流为hGij,若G型列车开行方案在si和sj不停站,此部分客流将进行转化,转化过程中优先选择Z型列车,若Z型列车开行方案也不在si和sj停站,则选择L型列车.Z型列车客流的转化过程类似,转化过程优先选择G型,其次是L型.这种转化过程符合城际列车对速度和时间的高要求性,也符合乘客心理.可列出任意两站之间三种类型客流转化的计算方程为εKij表示K型列车是否同时si和sj停站,当且仅当xKi=1,xKj=1时,εKij=1.模型的动态性表现为:在运算过程中,不断生成停站方案εKij集合,然后以实际客流h～Kij为因变量,εKij为自变量依据上述方程进行运算,生成与εKij集合相对应的h～Kij集合.在整个过程中,体现出客流分配相对于开行方案的动态性.4.2 基于多类型列车开行方案的多目标规划模型基于上述客流动态分配模型计算方程得到的动态客流矩阵,可建立后续的多目标规划模型. 4.2.1 模型目标函数(1)铁路部门收益最大化.铁路部门运营收入为客票收入与运营成本之差,运营成本包括固定成本和变动成本.固定成本对开行方案无影响,在此视为零.变动成本则主要体现在列车运行时车公里费用和停站费用.由于无中途换乘情况,不需考虑换乘成本.K型列车的总票价收入为式中 pK表示K型列车的人公里票价率.铁路部门总收入为根据城际列车的停站情况,列车运行路段信息及车公里费用,可得K型列车运行总费用铁路部门运营总支出为综上可得,铁路部门总收益(2)旅客总支出最小化.旅客的出行总支出包括票价支出和出行时间消耗.其中旅客的票价总支出CP即铁路部门总票价收入,旅客时间消耗包括列车运行过程的时间消耗和因中途停站造成的时间消耗两部分.K型列车在行驶过程中的总时间消耗为搭乘K型列车停站时间总消耗为搭乘K型列车上旅客总时间消耗为旅客总时间消耗为根据旅客对出行成本中的票价和时间的平均权重c和t,得旅客总支出(3)最大限度满足初始客流需求.模型采用客流动态分配,即开行方案的不同会对实际客流选择产生影响.应尽量减小客流的转化,以满足初始客流需求.为定量地衡量开行方案不同所引起的客流矩阵的变化,采用总欧式距离EOD衡量实际客流矩阵与初始客流 OD矩阵的偏差.最理想情况,EOD=0,此时欧氏距离越小表示客流动态分配结果越接近初始客流,即越接近乘客初始需求. 4.2.2 模型的约束条件(1)K型列车客座利用率为λK,路段ei(ei∈E)上K型列车的单向客流运输量为当K型列车以客座利用率λK,定员AK,服务频率fK载客时,区段客流运输量不能超过该区段运输能力,即上述约束等价于(2)城际客运专线上运行列车数不大于各车站和区段通过能力上限.设区段ei通过能力上限为le(si),车站Si通过能力上限为ls(si),有(3)xKi∈{0,1},fK∈自然数集N.4.2.3 综合的多目标非线性整数规划模型铁路部门收益最大化:旅客总支出最小化:最大化满足初始客流需求:约束条件:本文建立的列车开行方案模型属于较复杂的多目标0-1整数规划模型,为了增加算法适用性,本文采用遗传算法进行求解.求解过程如下:Step 1 客流OD和参数的初始化.引入权重因子,构造开行方案的目标函数作为遗传算法函数的输入.本文模型包含众多目标函数和约束条件,根据各目标的重要程度引入不同的权重因子ωi构造适应度函数,将多目标函数转为单目标函数.通过罚函数,将有约束问题转为无约束问题[14].这样可得到较为理想的适应度函数:式中 gj(X)为各约束条件,gj(X)≥0;m为约束条件数目;ψ(gj(X))为罚函数.Step 2 随机生成开行方案集的初始种群.文中停站决策0-1变量xKi可直接用二进制编码,服务频率fK用相应位长的二进制变量进行编码.Step 3 客流动态分配与多目标规划模型的求解.Step 3.1 根据开行方案生成相应的预测实际客流,并计算得出目标值.Step 3.2 根据适应度函数计算种群个体的适应度,记录当前最优个体.Step 3.3 采用“比例选择”策略进行选择.假设种群规模为popsize,那么个体i被选中的概率为利用交叉、变异等操作生成下一代开行方案新个体.以交叉概率Pc交换两条染色体部分基因,构造下一代两条新的染色体.若染色体可行则替换父代,否则重复交叉直至可行为止;以概率Pm变异染色体基因串.Step 4 重复Step 3的操作,直至满足最大迭代次数或最大停滞迭代次数.Step 5 输出最优个体.即列车服务频率和停站模式所组成的最优开行方案.遗传算法大致过程如图2所示.为了对算法进行验证,构造如图3所示城际网络.路段上标有该路段标号和长度(km). 区段通过能力取每昼夜263对,始发终到站通过能力取350对,沿途站取200对.表1为模型所需的基本参数(数据来源于文献[12]及网络文献).初始客流矩阵[15](人/日)为算法的实现采用MATLAB R2010a自带遗传算法工具箱求解,ωi取1,种群规模popsize=50,根据经验取交叉概率Pc=0.6,变异概率Pm=0.4,最大停滞迭代次数为15,最大迭代次数为100代.运行结果为:需开行择站停高速列车18(对),在s1,s3,s6停站,预测客流(人/日)分别为s1,s3之间4 560,s3,s6之间4 780,s1,s6之间3 631;择站停中速列车9 (对),在s1,s5,s6停站,预测客流分别为s1,s5之间2 262,s5,s6之间2 241,s1,s6之间2 123;站站停普速列车20(对),预测客流模型最终结果为:CI=816 300(元),CT= 2 089 100(元),EOD=20 064.本文提出了反映开行方案对客流的反馈影响动态客配模型,对乘客的选乘行为进行了较为深入的分析.文中相关假设为模型建立与求解提供了必要的条件.考虑到乘客选乘行为的复杂性以及乘客出行时间需要、中转换乘需求、运输环境变化等因素,模型应进一步完善,以适应实际应用的需要.【相关文献】[1]王兆成.中长期铁路网规划研究[M].北京:中国铁道出版社,2004.[WANG Z C.Medium and longterm railway network planning research[M].Beijing: China railway press,2004.][2]Bussieck M R,Kreuzer C,Zimmermann U T.Optimal lines for railway systems[J].European Journal of Operational Research,1997,96(1):54-63.[3]Claessens M T,Vandijk N M,Zwaneveld P J.Cost optimal allocation of rail passenger lines[J].European Journal of Operational Research,1998,110(3): 474-489.[4]Goossens J,Hoesel S T,Kroon L.A branch and cut approach for solving railway line-planning problems [J].Transportation Science,2004,38(3):379-393.[5]Goossens J,Hoesel S T,Kroon L.On solving multitype line planning problem[J].European Journal of Operational Research,2006,168(2):403-424.[6]Chang Y H,Yeh C H,Shen C C.A multi-objective model for passenger train services planning:application to Taiwan's high-speed rail line[J].Transportation Research PartB:Methodological,2000,34:91-106.[7]冯枫.客运专线高速客车开行方案的计算与评价[D].北京交通大学,2006.[FENG F.High-speed train of passenger dedicated line operating scheme computing and evaluating[D]. Beijing JiaotongUniversity,2006][8]邓连波.客运专线相关旅客列车开行方案优化研究[D].中南大学,2007.[DENG L B.Study on the optimal problems of passenger train plan for dedicated passenger traffic line [D]. Central South University,2007.][9]张拥军.高速列车开行方案研究[J].西南交通大学学报,1998,33(5):400-404.[ZHANG Y J.High speed train operating scheme research[J].Journal of Southwest Jiao TongUniversity,1998,33(5): 400-404.][10]徐瑞华.客运专线列车开行方案的优化方法研究[J].同济大学学报,2005,33(12):1608-1703.[XU R H.Optimization method research of passenger dedicated line operatingscheme[J].Journal of Tongji University,2005,33(12):1608-1703.][11]聂磊,胡小风,等.基于旅客列车开行方案的客流分配方法研究[J].交通运输系统工程与信息,2011, 11(3):87-92.[NIE L,HU X F,et al.Research of passenger flow assignment based on passenger train plann[J]. Journal of Transportation Systems Engineering and Information Technology,2011,11 (3):87-92.][12]徐鹏.城际客运专线列车开行方案研究[D].成都:西南交通大学,2010.[XU P.Research on the train operation scheme of the intercity dedicated passenger railway[D]. ChengDu: Southwest Jiao Tong University,2010.][13]彭其渊.客运专线运输组织[M].北京:科学出版社,2007.[PENG Q Y.Passenger dedicated line transportation organization[M].Beijing: Science Press,2007.][14]贾晓秋.客运专线网络列车开行方案模型与算法研究[J].系统工程学报,2011,26(2):216-221.[JIA X Q.Research on a model and its alogorithm about the line planning on the network for passenger transportation[J].Journal of Systems Engineering, 2011,26(2):216-221.][15]吴昌进.昌九城际轨道交通运量预测及运输方案研究[D].北京:清华大学,2008.[WU C J.Inter-city railway of Nanchang to Jiujiang traffic volume forecast and transport schemeStudy[D].Beijing:Tsinghua University,2008.]。

基于旅行时间满意度的城际列车开行方案黄志鹏【摘要】This paper analyzed the major factors influencing passengers' travel time satisfaction,and proposed the concepts of fixed time cost and additional time cost.Meanwhile,taking into account the uncertainty of passengers flow,this study established a nonlinear multi-objective mixed integer programming model with the chance-constraint to maximize passenger's travel time satisfaction and minimize the transportation cost of railway enterprises.Then a genetic algorithm was designed based on the characteristics of the model to solve the case.Finally,the model and algorithm were proved to be feasible,which can provide reference for intercity train operation.%分析了影响城际铁路旅客旅行时间满意度的主要因素,提出了固定时间消耗和额外时间消耗的概念.同时,考虑客流量的不确定性.在此基础上,构建了以旅客旅行时间满意度最大化、铁路运输企业运输成本最小化,并包含有机会约束的非线性多目标混合整数规划模型,并根据模型特点设计了遗传算法对算例进行了求解.通过算例验证,提出的模型及算法是可行的,能够为制定城际铁路的开行方案提供参考.【期刊名称】《兰州交通大学学报》【年(卷),期】2018(037)001【总页数】7页(P21-26,34)【关键词】城际铁路;开行方案;机会约束;遗传算法【作者】黄志鹏【作者单位】兰州交通大学交通运输学院,甘肃兰州730070【正文语种】中文【中图分类】U293.1城际铁路是一种区域性的轨道交通系统，主要服务于城市经济圈内中心城市、副中心城市、城市所辖城镇之间客流[1].近年来，随着城际高速铁路的大力发展，特别是具有刷卡进站乘车、一站式服务功能的“中铁银通卡”在城际高铁上使用，大大方便了旅客的出行.在京津唐、长三角、珠三角等地区的城际铁路上，旅客出行密度大大提高.在一天的某些时段以及节假日会出现客流拥挤的高峰时段.这种公交化服务模式在方便旅客乘车的同时，对高峰时段列车开行方案提出了更高要求.目前，国内外学者针对城际高铁或城市轨道交通中旅客出行时间不均衡条件下的列车开行方案优化问题做了大量研究.在城际铁路中，通常开行区段都是两中心城市，开行区段通常是固定的.并且城际铁路上运行的列车速度等级也是单一的，因此城际铁路开行方案的研究重点是列车发车间隔、编组数量和列车在沿途中间站的停站方案.其中，文献[2-5]均是将城际铁路的运营时段进行客流密度划分，然后研究不同时段的列车开行方案.其中，以Chang等[2]为代表的学者将客流数据作为系统的输入，以最小化企业运营成本和最小化旅客旅行时间为目标，对列车停站方案、开行频率和车组大小进行了优化.牛惠民等[6]特别研究了城市轨道交通中拥挤环境下，旅客出行时间、发车频率、动车组数量和运营企业利益的匹配关系，并进行了模型构建和求解.文献[7-9]以城市交通配流理论为基础，对列车开行方案及客流分配进行了协同研究.杨博等[10]建立了以乘客等待时间和列车运力浪费最小化为目标函数的优化模型.Niu等[11]通过引入乘客上车时间窗的概念，建立了基于客流动态需求驱动的轨道列车调度非线性整数规划模型.城际铁路列车开行方案的制定优劣直接影响到旅客的出行时间.张玉召等[12]采用DEA方法对旅客列车开行方案进行分析和评价.张玉召等[13]对跨线旅客列车开行方案的编制和日常旅客运输组织进行了研究.通过大量问卷调查发现，影响旅客出行满意度的最重要因素为旅行时间因素，其中在站等待时间的长短更是影响旅客出行满意度的最主要因素.目前关于铁路旅客出行满意度的研究主要是通过建立结构方程模型分析服务质量、旅客满意度和忠诚度之间的关系[14-16].或是通过建立旅客满意度评价指标体系建立高速铁路列车服务旅客满意度模糊综合评价模型[16].但是，从旅客出行时间满意度角度制定列车开行方案的研究相对较少.因此，本文将旅客出行时间作为影响旅客出行满意度的主要因素，同时，将铁路运输企业的效益通过成本最小化来反映.因此，论文拟构建一个多目标规划模型，以运输成本最小化为目标反映铁路运输企业的效益因素；以旅客出行时间满意度最大化为目标反映旅客对出行时间的要求.1 模型及算法1.1 相关参数及变量设置车站集合S={1,2,…,n}；旅客上车站集合I={i=1,2,…,n-1},I⊂S；旅客下车站集合J={j=2,3,…,n},J⊂S；始发站列车的发车车次集合E={e|e=1,2,…,m}；列车e的停站集合Re={re|re=s,xes≠0,s∈S,e∈E}，其中xes为0-1决策变量，xes=1表示在列车e在车站s停车，xes=0表示列车e在车站s不停车；车站i→j客流可乘坐列车车次集合Kij={k|k=e·ρij(e),ρij(e)=1,e∈E}，其中ρij(e)为i→j客流与列车e 的匹配关系，ρij(e)=1表示列车e在车站i和j均停车；f表示始发站的发车数量；中间变量geij表示乘坐列车e的i→j客流数量；随机变量ηij表示车站i→j按照一定随机分布规律产生的随机客流；输入参数gij为车站i→j的预测客流.1.2 优化目标1.2.1 运输收益最大化本文研究的城际铁路上旅客列车开行成本主要包括：列车开行成本，是指始发站开行一列车所必须支出的占用线路、设备及人工的成本；车辆成本，是指每个动车组的使用成本，包括折旧、电能消耗等，其与列车e的编组辆数Ye有关；停站成本，是指列车e在中间站s停车产生的线路占用及人工成本，其与列车的停站次数有关.运输收益最大化目标函数为(1)式中：vij为车站i→j间列车票价；C1为每列车的开行成本，其与编组大小无关；C2为每辆动车的车辆成本；C3为每停站一次而占用运输设备的停站成本.2≤s≤n-1表明此处计算的是中间站停站成本，而始发站(s=1)和终到站(s=n)的停站成本已在列车开行成本中考虑.1.2.2 旅客旅行时间满意度最大化旅客旅行时间是指从旅客进入出发车站候车时起至旅客到达目的地离开车站时止所花费的时间；旅客旅行时间满意度是指旅客完成一次出行所实际花费的时间与其出行预期的达成程度.旅客旅行时间包括3部分：列车运行时间(列车在铁路区段内的纯运行时分，不包括沿途中间站的停站时分)列车在中间站停站时间旅客在车站候车时间通过以上分析，论文提出了两个概念：固定时间消耗，在出行起讫点(i→j)确定的情况下，列车运行时间是固定的，因此列车运行时间是固定时间消耗；额外时间消耗，停站时间和候车时间的时间消耗与列车开行方案密切相关，因此和是额外时间消耗.通过对兰州西客站铁路旅客问卷调查显示，89%的旅客在出行前通过购票网站的时刻表或者以前的出行经验来获得旅行时间期望，而75%的旅客不关注沿途停站时间对旅行时间的影响.因此，旅客对于固定时间消耗的期望值与列车运行时间的消耗基本上是一致的，但是不同的旅客对于额外时间消耗的敏感程度有所不同.对于短途旅客，列车运行时间相对较小，这部分旅客对于额外时间消耗相对敏感；而对于中长途旅客，列车运行时间相对较大，这部分旅客对于额外时间消耗的容忍度更高.因此，构造了旅客旅行时间满意度ξij隶属度函数，如式(2)所示.当与的比值σij越大，表明旅客心理预期旅行时间与实际旅行时间差距越大，其越不满意.(2)(3)式中：为i→j旅客能够接受的额外时间消耗与固定时间消耗的最小比值为i→j旅客能够接受的额外时间消耗与固定时间消耗的最大比值.(4)(5)(6)式中：Lij为i→j的运行里程；v为列车的平均运行速度；ues为列车e在车站s 停站时，列车k上的旅客数；ts为列车e在车站s的停站时间；pij为i→j的旅客可以乘坐的列车数量为服务i→j旅客的列车k在车站s的发车时刻.旅客旅行时间满意度目标函数为(7)1.3 相关约束条件1) 发车能力约束始发站s=1的发车能力C1是有限的.时段d列车发车能力约束为f≤C1.(8)2) 列车编组数量约束Ye=μ·Ymin.(9)式中：Ymin为列车最小编组辆数；考虑到目前高铁车辆运用均是以几辆一组为单位进行组合，μ为正整数，表示列车e由μ个动车组单元编组而成.3) 动车运用数量约束(10)式中：Δ为可投入运营的动车组单元数量.4) 供需平衡机会约束旅客的实际出行需求与预测需求总是会有所偏差.因此，本文引入随机变量ηij，构造了机会约束，如式(11)所示.(11)qij=gij+ηij,(12)(13)其中：Pr{·}表示{·}中事件成立的概率；A为单元动车组定员；α为列车服务能力大于等于实际需求qij的置信水平，qij为车站i→j的实际客流.πij(e)为i→j客流qij 与列车e的关系函数.由于xes为0-1变量，当xei·xej=1时，表明列车e在车站i 和j均停车，满足客流的乘坐条件.5) 客流qij可乘坐列车数量约束(14)6) 列车停站时，在车上等待的旅客数量ues约束(15)式中：列车e在中间站s停站时，在列车上等待的旅客必须是在车站s之前的车站上车，并且在车站s之后的车站下车的乘客.7) 列车的发车时刻约束(16)(17)(18)其中：为列车e在车站s的发车时刻为列车e在车站s的到达时刻；Imin为相邻列车的最小追踪间隔时间；tq为列车起停附加时分；H为列车运行时段的时长.式(16)为追踪运行的两列车e和e+1到达车站s的间隔时间约束.两列车到达车站s 的最小间隔时间应为列车最小追踪间隔时间Imin、列车停站时间ts以及列车起停附加时分tq之和.式(17)为列车e在车站s到达与发车时刻的关系，当列车通过车站e时，式(18)为各相邻列车间隔时间之和应小于列车运行时段d的时长.8) 始发终到站强制停车约束xe1=xen=1.(19)9) 非负及整数约束f≥0且为整数.(20)1.4 算法设计论文所建模型是一个非线性多目标混合整数规划问题，它被公认为是极其困难求解的优化问题之一.本文采用遗传算法对模型进行求解，此算法具有较好的全局收敛性，能够在较短的时间内搜索到满意解，核心思想是根据自然界优胜劣汰的原则，将适应度高的个体保留到下一代，将适应度低的淘汰掉.1) 多目标问题求解如前所述，论文构造的两个目标函数，Z1为有量纲的，且为最大化目标；Z2为无量纲的，且为最大化目标.因此，首先对Z1进行无量纲化处理，(21)式中：为对Z1进行无量纲化处理的目标值为运输企业可接受的最小运输收益为运输企业期望的最大运输收益.对目标Z1进行无量纲化处理后，将以上两个目标转化为单目标求解，(22)其中：和Z2的加权平均值Z并无实际指标意义，只是反映最大化目标和最大化目标Z2协同优化时的计算值，该数值Z越大，表明在权重参数θ条件下越大，Z2越大，而和Z2的取值范围均为越大，表明运输收益Z1越大；Z2越大，表明旅客满意度越大；而在参数θ条件下，Z的取值范围也为[0,1]，Z的取值大小反映了协同优化的指标水平；θ为待定系数，表示两个目标的权重，其取值来源于不同出行时段的数据调查结果.2) 机会约束处理处理机会约束规划的方法是把机会约束转化为等价类.式(11)为机会约束，现将该约束转化为机会约束的标准形式，Pr{g(xes)≥ηij}≥α,(23)(24)式中：g(xes)为决策变量xes的函数；ηij为随机变量.假设Φ为其概率分布函数.对每一个给定的置信水平α，必然存在一个或多个Xα,使得Pr{ηij≤Xα}.Xα=Φ-1(α)，Φ-1是概率分布函数Φ的逆函数.这样就将机会约束转化为它的等价类，(25)2 算例分析本文以沿途有3个中间站的城际铁路为例对论文提出的模型和算法进行验证.其中，车站1为始发站，车站5为终到站，车站2、3、4为可乘降旅客中间站.各站间里程如图1所示.图1 假设城际铁路网络Fig.1 A hypothetical intercity rail network列车运营的相关参数[7]，如表1所列.表1 相关参数的设置Tab.1 Setting of related parameters项目取值时段H/min60列车运行成本C1/元80000动车组运用成本C2/元2000列车停站成本C3/元1000σminij0．2σmaxij2．5列车平均速度v/(km/h)200中间站停站时间ts/min3最小动车组单元数/辆Ymin8车辆定员A/人128论文假设客流gij服从正态分布置信水平α为0.9.不同OD客流的客流量均值和方差如表2所列.表2 不同OD客流的概率分布Tab.2 A probability distribution of each OD passenger flow(i，j)客流量均值gij方差ρ2ij(i，j)客流量均值gij方差ρ2ij(1，2)18601．3(2，4)4801．2(1，3)6001．2(2，5)12601．2(1，4)7801．5(3，4)3601．2(1，5)44401．2(3，5)3601．3(2，3)4801．3(4，5)9001．3按照客流平峰时段的调查数据，将权重系数θ值设置为0.7，并将相关参数及客流量输入模型，设置种群规模popsize=200，根据经验取交叉概率Pc=0.6，变异概率Pm=0.4，最大停滞迭代次数为15，最大迭代次数为100.可得到各列车发车时刻及沿途停站方案，如表3所列.表3所示的停站方案，全部旅客在站候车时间为92 381 人·min，沿途停站等待时间为25 385 人·min.人均额外旅行时间消耗为13.14 min，Z=0.783 2，列车最大服务能力为11 120 人次.当θ=0.7时，即目标Z1的权重较大，通过以上数据，可以发现旅客的满意度相对较低，具体表现为某些OD客流最大候车时间过长，如乘坐列车e=8的客流(1,2)的平均等待时间达到21 min.铁路运输部门应尽可能降低旅客等待时间，特别是在高峰时段，当客流高峰期时，按照调查数据，权重系数θ值设置为0.3时，将相关参数及旅客的到达率输入模型，可得到各列车发车时刻及沿途停站方案，如表4所列.表3 优化后的列车停站方案(方案1：θ=0.7)Tab.3 Optimized train stop plan (case 1:θ=0.7)列车e停站方案服务OD客流车站2车站3车站4编组Ye/辆1100(1，2)，(1，5)82000(1，5)83011(1，3)，(1，4)，(1，5)164110(1，2)，(1，3)，(1，5)85000(1，5)86000(1，5)87001(1，4)，(1，5)168110(1，2)，(1，3)89011(1，3)，(1，4)，(1，5)810101(1，2)，(1，4)，(1，5)16表4 优化后的列车停站方案(方案2：θ=0.3)Tab.4 Optimized train stop plan (case 2:θ=0.3)列车e停站方案服务OD客流车站2车站3车站4编组Ye/辆1110(1，2)，(1，3)，(1，5)162001(1，4)，(1，5)83110(1，2)，(1，3)，(1，5)84100(1，2)，(1，5)85001(1，4)，(1，5)86010(1，3)，(1，5)87011(1，4)，(1，3)，(1，5)88110(1，2)，(1，3)，(1，5)169000(1，5)810111(1，2)，(1，3)，(1，4)，(1，5)16表4所示的停站方案，全部旅客在站总候车时间为57 236 min，沿途停站总等待时间为12 845 min.人均额外旅行时间消耗为10.4 min，最大候车等待时间为18.5 min，Z=0.761 4.列车最大服务能力为11 120 人次.但是，这套方案使得列车停站次数增多，运营成本增大.上述两个方案各OD客流的旅行时间满意度对比如图2所示.从图2中可以看出，方案2旅客旅行时间满意度大于0.8的OD对有6个，而方案1旅客旅行时间满意度大于0.8的OD对有5个，方案1、方案2的总体平均满意度分别为0.78和0.86.两种方案均有满意度为0的OD客流，分别出现在OD(2,3)和OD(3,4).这两对OD客流共同的特征是，起讫点均为中间站，客流量小，同时起讫点又为相邻站，站间距小.铁路运输部门可适当增开站站停列车，以满足中间站间短途客流.图2 两种方案各OD客流旅行时间满意度对比Fig.2 The travel time satisfaction of each OD passenger flow at two cases3 结论论文将旅客出行时间消耗划分为固定时间消耗和额外时间消耗，并以此为基础定义旅客满意度，基本符合旅客出行需求.即额外时间消耗越小，旅客越满意.论文提出的模型证明了不同停站方案的列车的发车次序和OD客流的满意度密切相关.在进行列车开行方案制定时，必须考虑不同列车的发车次序与OD客流的匹配.通过算例验证，本文提出的模型及算法是可行的，能够为制定城际铁路开行方案及铺画运行图提供参考.【相关文献】[1] 贺涛,施福根,张杰.城际客运专线通过能力研究[J].中国安全生产科学技术,2005,1(4):42-45.[2] CHANG Y H,YEH C H,SHEN C C.A multiobjective model for passenger train services planning: application to Taiwan's high-speed rail line[J].Transportation Research Part B Methodological,2000,34(2):91-106.[3] GHONEIM N,WIRASINGHE S C.Optimum zone structure during peak periods for existing urban rail lines[J].Transportation Research Part B,2008,20(1):7-18.[4] LIEBCHEN C.The first optimized railway timetable in practice[J].Transportation Science,2008,42(4):420-435.[5] 汪波,杨浩,张志华.基于周期运行图的京津城际铁路列车开行方案研究[J].铁道学报,2007,29(2):8-13.[6] 牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学,2011,32(4):128-133.[7] 史峰,邓连波,霍亮.旅客列车开行方案的双层规划模型和算法[J].中国铁道科学,2007,28(3):110-116.[8] 彭其渊,贾晓秋,关晓宇.随机稳定性配流规划的客运专线列车开行方案模型[J].西南交通大学学报,2011,46(1):143-147.[9] 何宇强,张好智,毛保华,等.客运专线旅客列车开行方案的多目标双层规划模型[J].铁道学报,2006,28(5):6-10.[10] 杨博,武晋飞.兰州轨道交通列车开行方案优化研究[J].兰州交通大学学报,2015,34(4):114-118.[11] NIU H,ZHOU X.Optimizing urban rail timetable under time-dependent demand and oversaturated conditions[J].Transportation Research Part C,2013,36(11):212-230.[12] 张玉召,张红伟.旅客列车开行方案的DEA分析与评价[J].兰州交通大学学报,2008,27(6):83-85.[13] 张玉召,严余松.客运专线跨线列车合理始发范围的确定方法研究[J].兰州交通大学学报,2010,29(3):79-82.[14] 曹灿明,陈建军.高速铁路客运服务质量、旅客满意度与忠诚度分析[J].铁道学报,2012,34(1):1-6.[15] CHOU J S,KIM C.A structural equation analysis of the QSL relationship with passenger riding experience on high speed rail:an empirical study of Taiwan and Korea[M].United Kingdom of Great Britain and Northern Ireland:Pergamon Press,2009.[16] 陈雷雷,张星臣,王伶俐,等.高速铁路列车服务旅客满意度评价研究[J].铁道运输与经济,2015,37(11):60-65.。

城际铁路列车开行方案动态编制与优化研究随着我国城镇化进程的稳步推进,城际铁路在促进区域经济发展中扮演重要角色。

伴随国家对于铁路建设的总体布局,新建城际铁路不断增加,随之而来的问题也逐渐显露。

在已运营的城际铁路线上部分车次长期上座率低,而部分车次却时常一票难求,反映了我国城际铁路的运输组织工作还存在较大问题,严重影响铁路运输企业的经济效益,制约我国城际铁路的发展。

列车的开行方案是根据客流制定的,而客流会随着时间变化产生季节性波动,在制定列车开行方案时要充分考虑到客流的动态性波动。

当开行方案无法与客流需求匹配时应及时进行优化,使开行方案能够按照客流需求进行动态的编制,最大程度增加铁路部门运输效益,介于此本文将针对城际铁路列车开行方案动态编制与优化方法进行研究。

本文在国内外学者研究的基础上,首先分析了城际铁路列车开行方案的影响因素及其编制的原则。

从多个角度分析了城际铁路客流需求的动态性,通过列车开行方案的动态编制来适应客流需求的波动,在此基础上提出了一种基于历史客流数据与当前实际客流相结合的城际铁路列车开行方案动态编制策略。

针对历史客流数据的处理,利用K-means聚类算法对城际铁路的客流时段进行划分,对客流时段发生改变的时刻进行当前实际客流监控,引入差异系数对城际铁路列车开行方案与客流需求的偏差量进行计算,检测列车开行方案与客流需求的匹配性。

针对城际铁路列车开行方案与客流需求不匹配的情况,需要对列车开行方案进行优化,本文建立了以乘客旅行支出最少和铁路运输部门经济效益最大为目标的多目标规划模型。

并根据模型的特点,设计模拟退火算法对城际铁路列车开行方案优化模型进行求解。

本文以武咸城际铁路为案例,综合分析了武咸城际铁路的运输现状,通过城际铁路列车开行方案动态编制策略,结合武咸城际铁路客票数据对其现行列车开行方案进行匹配性检测,并通过本文设计的列车开行方案优化模型对其进行了优化,验证了模型算法的有效性。

基于动态编组的宁安客专列车开行方案优化
彭波
【期刊名称】《上海铁道科技》
【年(卷),期】2018(000)001
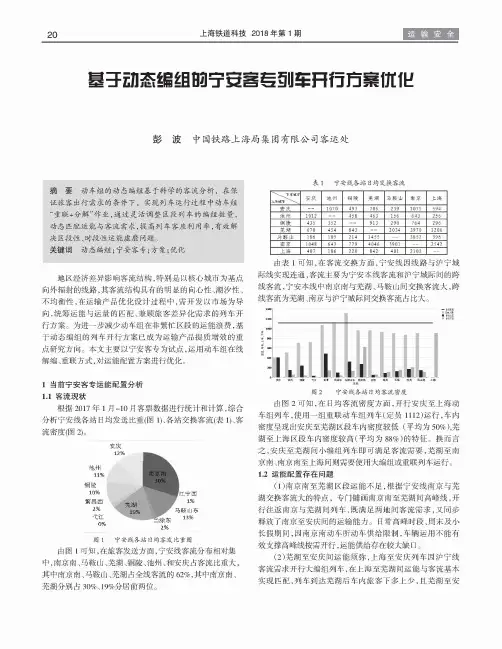
【摘要】动车组的动态编组基于科学的客流分析,在保证旅客出行需求的条件下,实现列车运行过程中动车组“重联+分解”作业,通过灵活调整区段列车的编组数量,动态匹配运能与客流需求,提高列车客座利用率,有效解决区段性、时段性运能虚靡问题.
【总页数】3页(P20-22)
【作者】彭波
【作者单位】中国铁路上海局集团有限公司客运处
【正文语种】中文
【相关文献】
1.基于城际铁路客流动态分配的列车开行方案优化生成
2.城市轨道交通多编组列车开行方案优化研究
3.基于运行网络配流的客专列车开行方案遗传优化研究
4.基于灵活编组的轨道交通列车开行方案优化方法
5.基于模型预测控制的城市轨道交通列车动态开行方案优化策略研究
因版权原因，仅展示原文概要，查看原文内容请购买。

集装箱中心站和专办站班列开行方案研究
柴甜甜;王慈光;杜连涛
【期刊名称】《铁道货运》
【年(卷),期】2010(028)004
【摘要】随着全路18个集装箱中心站、55个专办站的集装箱运输系统建设完成,铁路将形成覆盖全国的运输网络.研究集装箱中心站和专办站间班列开行方案,对促进我国集装箱运输发展具有重要意义.在分析了集装箱班列开行方案的影响因素及集装箱班列开行条件的基础上,提出了分部求解的计算方法,并以北京-广州的集装箱运输为例,研究集装箱中心站和专办站的运输组织.
【总页数】5页(P43-47)
【作者】柴甜甜;王慈光;杜连涛
【作者单位】西南交通大学交通运输学院,四川成都,610031;西南交通大学交通运输学院,四川成都,610031;西南交通大学交通运输学院,四川成都,610031
【正文语种】中文
【中图分类】U169.6
【相关文献】
1.中心站集装箱班列开行方案的0-1规划模型 [J], 蒲菡
2.铁路汽车物流中心站和专办站班列开行方案研究 [J], 白云云;魏玉光
3.铁路物流中心及集装箱专办站间班列开行方案的研究 [J], 王艳玲;赵明佶;郎茂祥;李翀宇;李雪飞
4.基于经济效益的集装箱班列开行方案评价研究 [J], 冯轶斌
5.中铁联合国际集装箱有限公司重庆铁路集装箱中心站重庆-平湖南集装箱班列开通运行 [J],
因版权原因，仅展示原文概要，查看原文内容请购买。

城际铁路票额随机分配优化曲思源;徐行方【摘要】Ticket allocation is to achieve maximum efficiency and is a fundamental basis of adjustment and optimization of train in inter-city railway. It is also an important means to adapt to inter-city passenger demand. However, actual allocation and the integer allocation model cannot adapt to the needs of inter-city passenger. Based on the actual passenger, the paper apopts the actual car traffic as uncertain factor, which is a normal distribution, and proposes a flexible method of ticket allocation, which establishes the stochastic integer programming model to make a resolution by transforming into a certain equivalent method to maximize the whole train ticket revenue. The Shanghai-Nanjing Inter-city express train is taken as an example to be verified. Ticket randomized optimization will provide new ideas and methods of intercity railway tickets allocation.%票额分配是实现城际铁路效益最大化以及调整和优化列车开行方案的基本依据之一,同时也是适应城际客流需求的重要手段之一.在分析实际分配方法和确定式的整数分配票额模型难以适应域际客流需求的基础上,提出以实际客流情况为依据的弹性票额分配方法,将实际乘车客流量视为不确定因素即将其视为正态分布,建立随机整数规划模型并采取转化为确定性等价方法进行求解,使得整个列车票额收益最大化.以沪宁城际高速铁路高峰时段某列车为例得到验证.票额随机分配模型将为城际铁路票额分配提供新的思路和方法.【期刊名称】《华东交通大学学报》【年(卷),期】2011(028)004【总页数】5页(P112-116)【关键词】城际铁路;票额分配;随机优化【作者】曲思源;徐行方【作者单位】上海铁路局调度所,上海200071;同济大学交通运输工程学院,上海201804;同济大学交通运输工程学院,上海201804【正文语种】中文【中图分类】U293.1城际铁路是指经济发达、人口稠密的城市群内各城市之间或城市与卫星城市之间的高速铁路。