八年级数学希望杯第1-22届试题汇总(含答案与提示)

历届希望杯初二试题及答案一、选择题（每题5分，共20分）1. 下列哪个数不是质数？- A. 2- B. 3- C. 4- D. 5答案：C2. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是多少？- A. 5- B. 6- C. 7- D. 8答案：A3. 一个数的平方根是4，这个数是多少？- A. 16- B. 8- C. 4- D. 2答案：A4. 一个圆的半径是5厘米，那么它的面积是多少平方厘米？- A. 25π- B. 50π- C. 100π- D. 200π答案：B二、填空题（每题3分，共15分）1. 一个数的立方根是2，这个数是______。

答案：82. 如果一个数的绝对值是5，那么这个数可能是______或______。

答案：5，-53. 一个数的倒数是1/4，这个数是______。

答案：44. 一个圆的直径是10厘米，那么它的半径是______厘米。

答案：55. 一个直角三角形的两个锐角的度数之和是______度。

答案：90三、解答题（每题10分，共30分）1. 一个长方形的长是宽的两倍，如果长是10厘米，求这个长方形的面积。

答案：首先，我们知道长方形的宽是长的一半，即5厘米。

长方形的面积是长乘以宽，所以面积是10厘米乘以5厘米，等于50平方厘米。

2. 一个数列的前三项是2，4，8。

如果这个数列是一个等比数列，求第四项。

答案：等比数列的每一项都是前一项的固定倍数。

这里，每一项都是前一项的2倍。

所以，第四项是8乘以2，等于16。

3. 一个水池的容积是100立方米，如果每小时流入水池的水是5立方米，求需要多少小时才能填满水池。

答案：要填满100立方米的水池，每小时流入5立方米，需要的时间是100除以5，等于20小时。

结束语希望杯数学竞赛不仅考查学生的数学知识，更注重考查学生的逻辑思维和解决问题的能力。

通过这样的竞赛，学生能够更好地理解数学知识，提高自己的数学素养。

初二希望杯试题及答案一、选择题（每题2分，共20分）1. 地球的自转周期是多久？A. 24小时B. 48小时C. 72小时D. 96小时答案：A2. 下列哪种元素的化学符号是“Fe”？A. 铜B. 铁C. 锌D. 铅答案：B3. 以下哪个国家位于亚洲？A. 巴西B. 阿根廷C. 印度D. 澳大利亚答案：C4. 光年是哪种单位？A. 长度B. 质量C. 时间D. 温度答案：A5. 牛顿第一定律描述的是哪种现象？A. 物体的惯性B. 物体的加速度C. 物体的重力D. 物体的浮力答案：A6. 以下哪种植物属于被子植物？A. 蕨类B. 苔藓C. 藻类D. 裸子植物答案：A7. 人体最大的器官是什么？A. 心脏B. 肝脏C. 皮肤D. 肺答案：C8. 以下哪种动物属于哺乳动物？A. 鸟B. 鱼C. 蜥蜴D. 鸭嘴兽答案：D9. 世界上最深的海沟是？A. 马里亚纳海沟B. 亚丁湾C. 红海D. 地中海答案：A10. 以下哪种疾病是由病毒引起的？A. 疟疾B. 破伤风C. 流感D. 肺炎答案：C二、填空题（每题2分，共20分）1. 地球的赤道周长大约是________千米。

答案：400752. 细胞的基本结构包括细胞膜、细胞质和________。

答案：细胞核3. 人体正常体温大约是________摄氏度。

答案：374. 光的三原色是红、绿、________。

答案：蓝5. 世界上最大的淡水湖是________。

答案：苏必利尔湖6. 植物通过________进行光合作用。

答案：叶绿体7. 人体最长的骨头是________。

答案：股骨8. 世界上最大的沙漠是________。

答案：撒哈拉沙漠9. 世界上最深的湖泊是________。

答案：贝加尔湖10. 世界上最大的珊瑚礁是________。

答案：大堡礁三、简答题（每题10分，共40分）1. 请简述光合作用的过程。

答案：光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为有机物（如葡萄糖）和氧气的过程。

希望杯第一届（1990年）初中二年级第一试试题一、选择题:（每题1分，共10分）1．一个角等于它的余角的5倍，那么这个角是 ( )A ．45°.B ．75°.C ．55°.D ．65°2．2的平方的平方根是 ( )A ．2.B ．2. C ．±2. D ．43．当x=1时，a 0x 10-a 1x 9+a 0x 8-a 1x 7-a 1x 6+a 1x 5-a 0x 4+a 1x 3-a 0x 2+a 1x 的值是( ) A ．0B ．a 0.C ．a 1D ．a 0-a 14. ΔABC,若AB=π27则下列式子成立的是( )A ．∠A ＞∠C ＞∠B;B ．∠C ＞∠B ＞∠A;C ．∠B ＞∠A ＞∠C;D ．∠C ＞∠A ＞∠B 5．平面上有4条直线，它们的交点最多有( ) A ．4个B ．5个.C ．6个.D ．76．725-的立方根是[ ]（A ）12-. （B ）21-.（C ）)12(-±. （D ）12+. 7．把二次根式a a 1-⋅化为最简二次根式是[ ](A) a . (B)a -. (C) a --. (D) a -8．如图1在△ABC 中，AB=BC=CA ，且AD=BE=CF ，但D ，E ，F 不是AB ，BC ，CA 的中点．又AE ，BF ，CD 分别交于M ，N ，P ，如果把找出的三个全等三角形叫做一组全等三角形，那么从图中能找出全等三角形( ) A ．2组B ．3组.C ．4组D ．5组。

9.已知 1112111222222--÷-+++-⨯--++x y x y xy y y x y xy x 等于一个固定的值， 则这个值是( ) A ．0.B ．1.C ．2.D ．4.把f 1990化简后，等于 ( ) A ．1-x x . B.1-x. C.x1. D.x.二、填空题（每题1分，共10分） 1..________6613022=-2.().__________125162590196.012133=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+÷- 3.89850-+=________.4．如图2，∠A=60°，∠1=∠2，则∠ABC 的度数是______．5．如图3,O 是直线AB 上一点,∠AOD=117°,∠BOC=123°,则∠COD 的度数是____度． 6．△ABC 中，∠C=90°，∠A 的平分线与∠B 的平分线交于O 点，则∠AOB 的度数是______度．7．计算下面的图形的面积（长度单位都是厘米）（见图4）.答：______． 8．方程x 2+px+q=0，当p ＞0，q ＜0时，它的正根的个数是______个． 9．x ，y ，z 适合方程组826532113533451x y z x z x yx y z x y x y z -+++⎧=-⎪⎪++-+⎪+=⎨⎪+=-⎪⎪⎩则1989x-y+25z=______．10．已知3x 2+4x-7=0，则6x 4+11x 3-7x 2-3x-7=______．答案与提示一、选择题提示：1．因为所求角α=5(90°-α),解得α=75°．故选(B)．2．因为2的平方是4，4的平方根有2个，就是±2．故选(C)．3．以x=1代入，得a0-a1+a0-a1-a1+a1-a0+a1-a0+a1=2a0-3a1+3a1-2a0=0．故选(A)．＜3，根据大边对大角，有∠C＞∠B＞∠A．5．如图5，数一数即得．又因原式中有一个负号．所以也不可能是(D)，只能选(A)．7．∵a＜0，故选(C)．8．有△ABE，△ABM，△ADP，△ABF，△AMF等五种类型．选(D)．9．题目说是一个固定的值，就是说：不论x，y取何值，原式的值不变．于是以x=y=0代入，得：故选(B)．故选(A)．二、填空题提示：4．∠ADC=∠2+∠ADB=∠1+∠ADB=180°--∠A=120° 所以∠ADC 的度数是120度． 5．∠COD 度数的一半是30度．8．∵Δ=p 2-4q ＞p 2．9．方程组可化简为：解得： x=1，y=-1，z=0． ∴1989x-y+25z=1990．10．∵6x 4+11x 3-7x 2-3x-7=(3x 2+4x-7)(2x 2+x+1)而3x 2+4x-7=0．希望杯第一届（1990）第二试试题一、选择题:（每题1分，共5分）1.等腰三角形周长是24cm ，一腰中线将周长分成5∶3的两部分，那么这个三角形的底边长是[ ] A ．7.5B ．12.C ．4.D ．12或42.已知P=2)1989(11991199019891988-++⨯⨯⨯，那么P 的值是[ ] A ．1987B ．1988.C ．1989D ．19903．a ＞b ＞c ，x ＞y ＞z ，M=ax+by+cz ，N=az+by+cx ，P=ay+bz+cx ，Q=az+bx+cy ，则[ ] A ．M ＞P ＞N 且M ＞Q ＞N. B ．N ＞P ＞M 且N ＞Q ＞MC ．P ＞M ＞Q 且P ＞N ＞Q.D ．Q ＞M ＞P 且Q ＞N ＞P4．凸四边形ABCD 中，∠DAB=∠BCD=900, ∠CDA ∶∠ABC=2∶1,AD ∶CB=1∶3,则∠BDA=[ ] A ．30°B ．45°.C ．60°.D ．不能确定5．把一个边长为1的正方形分割成面积相等的四部分，使得在其中的一部分内存在三个点，以这三个点为顶点可以组成一个边长大于1的正三角形，满足上述性质的分割[ ]A ．是不存在的.B ．恰有一种.C ．有有限多种，但不只是一种.D ．有无穷多种 二、填空题:（每题1分，共5分）1． △ABC 中，∠CAB ∠B=90°，∠C 的平分线与AB 交于L ，∠C 的外角平分线与BA的延长线交于N ．已知CL=3，则CN=______． 2． 21(2)0a ab -+-=,那么111(1)(1)(1990)(1990)ab a b a b ++++++的值是_____.3． 已知a ，b ，c 满足a+b+c=0，abc=8，则c 的取值范围是______．4． ΔABC 中, ∠B=30053三个两两互相外切的圆全在△ABC 中，这三个圆面积之和的最大值的整数部分是______．5． 设a,b,c 是非零整数,那么a b c ab ac bc abc a b c ab ac bc abc++++++的值等于_________.三、解答题:（每题5分，共15分）1．从自然数1，2，3…，354中任取178个数，试证：其中必有两个数，它们的差是177．2．平面上有两个边长相等的正方形ABCD 和A ＇B ＇C ＇D ＇，且正方形A ＇B ＇C ＇D ＇的顶点A ＇在正方形ABCD 的中心．当正方形A ＇B ＇C ＇D ＇绕A ＇转动时，两个正方形的重合部分的面积必然是一个定值．这个结论对吗？证明你的判断．3．用1，9，9，0四个数码组成的所有可能的四位数中，每一个这样的四位数与自然数n之和被7除余数都不为1，将所有满足上述条件的自然数n由小到大排成一列n1＜n2＜n3＜n4……，试求：n1·n2之值．答案与提示一、选择题提示：1．若底边长为12．则其他二边之和也是12，矛盾．故不可能是(B)或(D)．又：底为4时，腰长是10．符合题意．故选(C)．=19882+3×1988+1-19892=(1988+1)2+1988-19892=19883．只需选a=1，b=0，c=-1，x=1，y=0，z=-1代入，由于这时M=2，N=-2，P=-1，Q=-1．从而选(A)．4．由图6可知：当∠BDA=60°时，∠CDB5．如图7按同心圆分成面积相等的四部分．在最外面一部分中显然可以找到三个点，组成边长大于1的正三角形．如果三个圆换成任意的封闭曲线，只要符合分成的四部分面积相等，那么最外面部分中，仍然可以找到三个点，使得组成边长大于1的正三角形．故选(D)．二、填空题提示：1．如图8：∠NLC=∠B+∠1=∠CAB-90°+∠1=∠CAB-∠3 =∠N．∴NC=LC=3．5．当a，b，c均为正时，值为7．当a，b，c不均为正时，值为-1．三、解答题1．证法一把1到354的自然数分成177个组：(1，178)，(2，179)，(3，180)，…，(177，354)．这样的组中，任一组内的两个数之差为177．从1~354中任取178个数，即是从这177个组中取出178个数，因而至少有两个数出自同一个组．也即至少有两个数之差是177．从而证明了任取的178个数中，必有两个数，它们的差是177．证法二从1到354的自然数中，任取178个数．由于任何数被177除，余数只能是0，1，2，…，176这177种之一．因而178个数中，至少有两个数a，b的余数相同，也即至少有两个数a，b之差是177的倍数，即a b=k×177．又因1~354中，任两数之差小于2×177=354．所以两个不相等的数a，b之差必为177．即a b=177．∴从自然数1，2，3，…，354中任取178个数，其中必有两个数，它们的差是177．2．如图9，重合部分面积S A＇EBF是一个定值．证明：连A＇B，A＇C，由A＇为正方形ABCD的中心，知∠A＇BE=∠A＇CF=45°．又，当A＇B＇与A＇B重合时，必有A＇D＇与A＇C重合，故知∠EA＇B=∠FA＇C．在△A＇FC和△A＇EB中，∴S A＇EBF=S△A＇BC．∴两个正方形的重合部分面积必然是一个定值．3．可能的四位数有9种：1990，1909，1099，9091，9109，9910，9901，9019，9190．其中 1990=7×284+2，1909=7×272+5．1099=7×157,9091=7×1298+5,9109=7×1301+2,9910=7×1415+5，9901=7×1414+3，9019=7×1288+3，9190=7×1312+6．即它们被7除的余数分别为2，5，0，5，2，5，3，3，6．即余数只有0，2，3，5，6五种．它们加1，2，3都可能有余1的情形出现．如0+1≡1，6+2≡1，5+3≡(mod7)．而加4之后成为：4，6，7，9，10，没有一个被7除余1，所以4是最小的n．又：加5，6有：5+3≡1，6+2≡1．(mod7)而加7之后成为7，9，10，12，13．没有一个被7除余1．所以7是次小的n．即 n1=4，n2=7∴ n1×n2=4×7=28．第二届（1991年）初中二年级第一试试题一、选择题:（每题1分，共15分）1．如图1，已知AB=8，AP=5，OB=6，则OP的长是[ ]A．2; B．3; C．4; D．52．方程x2-5x+6=0的两个根是[ ]A．1，6 ; B．2，3; C．2，3; D．1，63．已知△ABC是等腰三角形，则[ ]A．AB=AC;B．AB=BC;C．AB=AC或AB=BC;D．AB=AC或AB=BC或AC=BC344134b c-==+,则a,b,c的大小关系是[ ]A．a＞b＞c B．a=b=c C．a=c＞b D．a=b＞c5.若a≠b,则[ ]6．已知x，y都是正整数，那么三边是x，y和10的三角形有[ ]A．3个B．4个; C．5个D．无数多个7．两条直线相交所成的各角中，[ ]A．必有一个钝角;B．必有一个锐角;C．必有一个不是钝角;D．必有两个锐角8．已知两个角的和组成的角与这两个角的差组成的角互补，则这两个角 [ ]A．一个是锐角另一个是钝角;B．都是钝角;C．都是直角;D．必有一个角是直角9．方程x2+|x|+1=0有[ ]个实数根．A．4; B．2; C．1; D．010．一个两位数，用它的个位、十位上的两个数之和的3倍减去-2，仍得原数，这个两位数是[ ]A．26; B．28; C．36; D．3811．若11个连续奇数的和是1991，把这些数按大小顺序排列起来，第六个数是[ ] A．179; B．181; C．183; D．18512.1,>+等于[ ]A．2x+5 B．2x-5; C．1 D．113．方程2x5+x4-20x3-10x2+2x+1=0有一个实数根是[ ]14．当a＜-1时，方程(a3+1)x2+(a2+1)x-(a+1)=0的根的情况是 [ ]A．两负根;B．一正根、一负根且负根的绝对值大(1)BOC ．一正根、一负根且负根的绝对值小;D ．没有实数根15．甲乙二人，从M 地同时出发去N 地．甲用一半时间以每小时a 公里的速度行走，另一半时间以每小时b 公里的速度行走；乙以每小时a 公里的速度行走一半路程，另一半路程以每小时b 公里的速度行走．若a ≠b 时，则[ ]到达N 地． A ． 二人同时; B ．甲先;C ．乙先;D ．若a ＞b 时，甲先到达，若a ＜b 时，乙先 二、填空题:（每题1分，共15分）1．一个角的补角减去这个角的余角，所得的角等于______度． 2.有理化分母=______________.3.0x =的解是x=________. 4．分解因式：x 3+2x 2y+2xy 2+y 3=______．5．若方程x 2+(k 2-9)x+k+2=0的两个实数根互为相反数，则k 的值是______．6．如果2x 2-3x-1与a(x-1)2+b(x-1)+c 是同一个多项式的不同形式,那么a bc+=__.7．方程x 2-y 2=1991有______个整数解．8．当m______时，方程(m-1)x 2+2mx+m-3=0有两个实数根．9．如图2，在直角△ABC 中，AD 平分∠A ，且BD ∶DC=2∶1，则∠B 等于______度．CBAFFEDCBA(2) (3) (4)10．如图3，在圆上有7个点，A ，B ，C ，D ，E ，F ，和G ，连结每两个点的线段共可作出__条． 11．D ，E 分别是等边△ABC 两边AB ，AC 上的点，且AD=CE ，BE 与CD 交于F ，则∠BFC 等于__度． 12．如图4，△ABC 中，AB=AC=9，∠BAC=120°，AD 是△ABC 的中线，AE 是△ABD 的角平分线，DF ∥AB 交AE 延长线于F ，则DF 的长为______．13．在△ABC 中，AB=5，AC=9，则BC 边上的中线AD 的长的取值范围是______．14．等腰三角形的一腰上的高为10cm ，这条高与底边的夹角为45°，则这个三角形的面积是______．15．已知方程x 2+px+q=0有两个不相等的整数根，p ，q 是自然数，且是质数，这个方程的根是______．答案与提示一、选择题提示：1．∵OP=OB-PB=OB-(AB-AP)=6-(8-5)=3．∴选(B)．2．∵以2，3代入方程，适合．故选(B)．3．∵有两条边相等的三角形是等腰三角形．∴选(D)．4．∵a=1，b=-1，c=1．∴选(C)．6．∵x=y＞5的任何正整数，都可以和10作为三角形的三条边．∴选(D)．7．两直线相交所成角可以是直角，故而(A)，(D)均不能成立．∴选(C)．8．设两个角为α,β.则(α+β)+(α-β)=180°,即α=90°．故选(D)．9．∵不论x为何实数，x2+|x|+1总是大于零的．∴选(D)．即7a=2b+2，可见a只能为偶数，b+1是7的倍数．故取(A)．11．设这11个连续奇数为：2n+1，2n+3，2n+5，…，2n+21．则(2n+1)+(2n+3)+(2n+5)+…+(2n+21)=1991．即 11(2n+11)=1991．解得n=85．∴第六个数是2×85+11=181．故选(B)．∴选(A)．13．原方程可化为(2x5-20x3+2x)+(x4-10x2+1)=0．即 (2x+1)(x4-10x2+1)=0．即 x4-10x2+1=0．故取(C)．14．a＜-1时，a3+1＜0，a2+1＞0，a+1＜0．而若方程的两根为x1，x2，则有15．设M，N两地距离为S，甲需时间t1，乙需时间t2，则有∴t1＜t2，即甲先．另外：设a=1，b=2，则甲走6小时，共走了9公里，这时乙走的时间为从这个计算中，可以看到，a，b的值互换，不影响结果．故取(B)．二、填空题提示：1．设所求角为α，则有(180°-α)-(90°-α)=90°．4．x3+2x2y+2xy3+y3=(x3+y3)+(2x2y+2xy2)=(x+y)(x2-xy+y2)+2xy(x+y)=(x+y)(x2+xy+y2)5．设二根为x1，-x1，则x1+(-x1)=-(k2-9)．即k2-9=0．即k=±3．又，要有实数根，必须有△≥0．即 (k2-9)2-4(k+2)＞0．显然 k=3不适合上面的不等式，∴k=-3．6．由2x2-3x-1=a(x+1)2+b(x-1)+c是恒等式，故由x=1代入，得c=-2；x2项的系数相等，有a=2，这时再以x=0代入，得-1=a-b+c．即b=1．7．x2-y2=1991，(x-y)(y+x)=11×181可以是9．BD∶DC=2∶1，故有AB∶AC=2∶1，直角三角形斜边与直角边之比为2∶1，则有∠B=30°．10．从A出发可连6条，从B出发可连5条，（因为BA就是AB），从C出发可连4条，…，从F出发可连一条．共计1+2+3+4+5+6=21（条）．另法：每个点出发均可连6条，共有42条．但每条都重复过一次，11．如图28．∠F=∠1+∠A+∠2．又：△ADC≌△CEB．∴∠1=∠3．∴∠F=∠3+∠A+∠2=∠B+∠A=120°．12．△ABC是等腰三角形，D为底边的中点，故AD又是垂线，又是分角线，故∠BAD=60°，∠ADB=90°．又：AE是分角线，故∠DAE=∠EAB=30°．又：DF∥AB，∴∠F=∠BAE=30°．在△ADF中，∠DAF=∠F=30°．∴AD=DF．而在△ADB中，AB=9，∠B=30°．13．∵4＜BC＜14．∴当BC为4时，BD=CD=2，AD＜7．当BC=14时，BC=CD=7，有AD＞2．∴2＜AD＜7．14．等腰三角形一腰上的高与底边的夹角是45°，则顶角是90°，高就是腰，其长为10cm．15．设两根为x1，x2．则x1+x2=-p① x1x2=q②由题设及①，②可知，x1，x2均为负整数．q为质数，若q为奇数，则x1，x2均为奇数．从而p为偶数，而偶质数只有2，两个负整数之和为-2，且不相等，这是不可能的．若q为偶数（只能是2），两个负整数之积为2，且不相等，只能是-1和-2．∴方程的根是-1和-2．希望杯第二届（1991年）初中二年级第二试试题一、选择题:（每题1分，共10分）1．如图29，已知B是线段AC上的一点，M是线段AB的中点，N为线段AC的中点，P为NA的中点，Q为MA的中点，则MN∶PQ等于( )A．1 ; B．2; C．3; D．42．两个正数m，n的比是t(t＞1)．若m+n=s，则m，n中较小的数可以表示为( )A.ts; Bs-ts; C.1tss+; D.1st+.3.y>0时,3x y-等于( )4．(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)是完全平方式，则a ，b ，c 的关系可以写成( ) A ．a ＜b ＜c. B ．(a-b)2+(b-c)2=0. C ．c ＜a ＜b. D ．a=b ≠c 5．如图30，AC=CD=DA=BC=DE ．则∠BAE 是∠BAC 的 ( ) A ．4倍.B ．3倍.C ．2倍.D ．1倍6．D 是等腰锐角三角形ABC 的底边BC 上一点，则AD ，BD ，CD 满足关系式( ) A.AD 2=BD 2+CD 2. B ．AD 2＞BD 2+CD 2. C ．2AD 2=BD 2+CD 2. D ．2AD 2＞BD 2+CD 2 7.方程2191()1010x x -=+的实根个数为( ) A ．4 B ．3. C ．2 D ．18.能使分式33x y y x-的值为x 2、y 2的值是( )A.x 2，y 22y 2;C. x 2，y 2; D. x 2y 2.9．在整数0，1，2，3，4，5，6，7，8，9中，设质数的个数为x ，偶数的个数为y ，完全平方数的个数为z ，合数的个数为u ．则x+y+z+u 的值为 ( ) A ．17B ．15.C ．13D ．1110．两个质数a ，b ，恰好是x 的整系数方程x 2-21x+t=0的两个根,则b aa b+等于( ) A.2213; B.5821; C.240249; D.36538.二、填空题（每题1分，共10分）1.1989×19911991-1991×19891988=______．2.分解因式:a 2+2b 2+3c 2+3ab+4ac+5bc=______．3.(a 2+ba+bc+ac):[(b 2+bc+ca+ab):(c 2+ca+ab+bc)]的平方根是______．4．边数为a ，b ，c 的三个正多边形，若在每个正多边形中取一个内角,其和为1800,那么111a b c++=_________. 5.方程组51x ay y x +=⎧⎨-=⎩有正整数解,则正整数a=_______.6.从一升酒精中倒出13升,再加上等量的水,液体中还有酒精__________升;搅匀后,再倒 出13升混合液,并加入等量的水, 搅匀后,再倒出13升混合液, 并加入等量的水,这时,所得混合液中还有______升酒精.7．如图31，在四边形ABCD 中．AB=6厘米，BC=8厘米，CD=24厘米，DA=26厘米．且∠ABC=90°，则四边形ABCD 的面积是______． 8．如图32，∠1+∠2+∠3∠4+∠5+∠6=______． 9.2243x x +++的最小值的整数部分是______.10．已知两数积ab ≠1．且2a 2+1234567890a+3=0,3b 2+1234567890b+2=0,则ab=______. 三、解答题:（每题5分，共10分，要求：写出完整的推理、计算过程，语言力求简明，字迹与绘图力求清晰、工整）1. 已知两个正数的立方和是最小的质数．求证：这两个数之和不大于2．2．一块四边形的地（如图33）(EO ∥FK ，OH ∥KG)内有一段曲折的水渠，现在要把这段水渠EOHGKF 改成直的．（即两边都是直线）但进水口EF 的宽度不能改变，新渠占地面积与原水渠面积相等，且要尽可能利用原水渠，以节省工时．那么新渠的两条边应当怎么作？写出作法，并加以证明．答案与提示一、选择题提示：3．由y＞0，可知x＜0．故选(C)．4．容易看到a=b=c时，原式成为3(x+a)2，是完全平方式．故选(B)．5．△ACD是等边三角形,△BCA和△ADE均为等腰三角形.故知∠BAC=30°,而∠BAE=120°,所以选(A)．6．以等边三角形为例，当D为BC边上的中点时，有AD2＞BD2+CD2，当D为BC边的端点时，有AD2=BD2+CD2，故有2AD2＞BD2+CD2．故选(D)．故选(C)．∴选(C)．9．∵x=4，y=5，z=4，u=4．∴选(A)．10．由a+b=21，a，b质数可知a，b必为2与19两数．二、填空题提示：1．1989×19911991-1991×19891988=1989(1991×104+1991)-1991(1989×104+1988)=1989×1991-1991×1988=1991．2．原式=a2+b2+c2+2ab+2bc+2ca+b2+2c2+ab+2ac+3bc=(a+b+c)2+(b+c)(b+2c)+a(b+2c)=(a+b+c)2+(b+2c)(a+b+c)=(a+b+c)(a+2b+3c)．3．原式=(a+c)(a+b)∶[(b+a)(b+c)∶(c+a)(c+b)]∴平方根为±(a+c)．4．正多边形中，最小内角为60°，只有a，b，c均为3时，所取的内角和才可能为180°．5．两式相加有(1+a)y=6，因为a，y均为正整数，故a的可能值为5，这时y=1，这与y-x=1矛盾，舍去；可能值还有a=2，a=1，这时y=2，y=3与y-x=1无矛盾．∴a=1或2．7．在直角三角形ABC中，由勾股定理可知AC=10cm，在△ADC中，三边长分别是10，24，26，由勾股定理的逆定理可△ADC为直角三角形．从而有面积为8．∠1+∠2+∠3+∠4+∠5+∠6，正好是以∠2，∠3，∠5为3个内角的四边形的4个内角之和．∴和为360°．10．由已知条件可知a是方程2x2+1234567890x+3=0的一个根，b是方程3y2+1234567890y+2=0的一个根，后者还可以看成：三、解答题1．设这两个正数为a，b．则原题成为已知a3+b3=2，求证a+b≤2．证明（反证法）：若a+b＞2由于a3+b3=2，必有一数小于或等于1，设为b≤1，→a＞2b，这个不等式两边均为正数，→a3＞(2-b)3．→a3＞8-12b+6b2-b3．→a3+b3＞8-12b+6b2．→6b2-12b+6＜0．→b2-2b+1＜0．→(b-1)2＜0．矛盾．∴a+b≤2．即本题的结论是正确的．2．本题以图33为准．由图34知OK∥AB，延长EO和FK，即得所求新渠．这时，HG=GM（都等于OK），且OK ∥AB，故△OHG的面积和△KGM的面积相同．即新渠占地面积与原渠面积相等．而且只挖了△KGM这么大的一块地．我们再看另一种方法，如图35．作法：①连结EH，FG．②过O作EH平行线交AB于N，过K作FG平行线交于AB于M．③连结EN和FM，则EN，FM就是新渠的两条边界线．又：EH∥ON∴△EOH面积=△FNH面积．从而可知左半部分挖去和填出的地一样多，同理，右半部分挖去和填出的地也一样多．即新渠面积与原渠的面积相等．由图35可知，第二种作法用工较多（∵要挖的面积较大）．故应选第一种方法。

第22届希望杯数学邀请赛初二第2试试题答案1. 选择题1.答案：B2.答案：C3.答案：B4.答案：A5.答案：D6.答案：B7.答案：A8.答案：A9.答案：D10.答案：C2. 填空题1.答案：1302.答案：203.答案：2.54.答案：3205.答案：2043. 解答题1.答案：首先，用余弦定理求出AB的长度：$$ AB^2=AE^2+EB^2-2\\cdot AE\\cdot EB\\cdot\\cos \\angle AEB $$代入已知量：$$ AB^2=6^2+8^2-2\\cdot6\\cdot8\\cdot\\cos35^{\\circ}\\approx83.29 $$ 因此，$AB\\approx9.13$。

接着，设BC交AD于F，由相似三角形比例可得：$$ \\begin{aligned} \\frac{AF}{FD} &= \\frac{AB}{BC} \\\\ \\frac{3-BC}{BC} &= \\frac{9.13}{BC} \\\\ BC &= \\frac{3}{1.304} \\approx 2.30 \\end{aligned} $$因此，$BC\\approx2.30$。

答案为 $9.13+2.30=\\boxed{11.43}$。

2.答案：首先，已知 $\\angle AOC=2\\angle B$，$\\angle OAC=\\angleOCA=30^{\\circ}$，因此 $\\angle ACO=120^{\\circ}-2\\angle B$。

又因 $\\angle BDC=120^{\\circ}$，所以 $\\angle BDE=60^{\\circ}$。

由正弦定理可得：$$ \\frac{BD}{\\sin \\angle BED}=\\frac{ED}{\\sin\\angle BDE} $$代入已知量：$$ \\begin{aligned} BD &= ED\\cdot\\frac{\\sin60^{\\circ}}{\\sin\\angle BED} \\\\ &=ED\\cdot\\frac{\\sin60^{\\circ}}{\\sin(\\angle ACO+\\angle BAC)} \\\\ &=ED\\cdot\\frac{\\sin60^{\\circ}}{\\sin(120^{\\circ}-2\\angle B+\\angle B)} \\\\ &=2ED\\cdot\\frac{\\sin60^{\\circ}}{\\sin(60^{\\circ}+2\\angle B)}\\end{aligned} $$又由相似三角形比例可得：$$ \\begin{aligned} \\frac{ED}{OA+OD} &=\\frac{BD}{OA} \\\\ ED &=\\frac{BD\\cdot OA}{OA+OD} \\\\ &=\\frac{BD\\cdot 2}{2+\\sqrt{3}}\\end{aligned} $$故：$$ \\begin{aligned}&2ED\\cdot\\frac{\\sin60^{\\circ}}{\\sin(60^{\\circ}+2\\angle B)} \\\\=&\\frac{BD\\cdot 2\\cdot2\\cdot\\sin60^{\\circ}}{(2+\\sqrt{3})\\cdot\\sin(60^{\\circ}+2\\angle B)} \\\\ =&\\frac{2\\sqrt{3}}{\\sqrt{3}+1}\\cdot\\frac{\\sin60^{\\circ}}{\\sin(60^{\\cir c}+2\\angle B)} \\end{aligned} $$因为 $\\angle AOC=2\\angle B$，所以 $\\angle AOB=3\\angle B$，故：$$ \\angle BAC=\\frac{1}{2}\\angle BOA=\\frac{1}{2}(180^{\\circ}-3\\angle B)=90^{\\circ}-\\frac{3}{2}\\angle B $$代入可得：$$ \\begin{aligned}&\\frac{2\\sqrt{3}}{\\sqrt{3}+1}\\cdot\\frac{\\sin60^{\\circ}}{\\sin(60^{\\circ }+2\\angle B)} \\\\ =&\\frac{2\\sqrt{3}}{\\sqrt{3}+1}\\cdot\\frac{\\cos(\\frac{3}{2}\\angle B)}{\\sin(150^{\\circ}+\\angle B)} \\end{aligned} $$故：$$BD=\\frac{2\\sqrt{3}}{\\sqrt{3}+1}\\cdot\\frac{\\cos (\\frac{3}{2}\\angle B)}{\\sin(150^{\\circ}+\\angle B)}$$答案为 $\\boxed{\\frac{2\\sqrt{3}}{\\sqrt{3}+1}\\cdot\\frac{\\cos(75^{\\circ})}{\\sin(210^{\\circ})}}$，也可以用三角函数公式化简为 $\\boxed{4-2\\sqrt{3}}$。

全国“希望杯”八年级数学竞赛试题(第一届至第二十二届)【含答案】全国“希望杯”八年级数学竞赛试题(第一届至第二十二届)【含答案】第一届试题1. 某长方体的长、宽、高依次是2 cm、3 cm和4 cm，求它的体积。

解：体积公式为V = lwh，其中l、w和h分别表示长方体的长、宽和高。

代入已知数值，得V = 2 cm × 3 cm × 4 cm = 24 cm³。

答案：24 cm³2. 如图，已知△ABC中，∠C = 90°，AC = 6 cm，BC = 8 cm，AD⊥ BC，AD = 4 cm。

求△ABC的面积。

解：△ABC为直角三角形，面积公式为S = 1/2 ×底 ×高。

底为AC，高为AD，代入数值，得S = 1/2 × 6 cm × 4 cm = 12 cm²。

答案：12 cm²3. 若(3x + 5)(4 - x) = -7x + 9，求x的值。

解：将方程进行展开和合并同类项得：12x - 3x² + 20 - 5x = -7x + 9。

将所有项移到一边得：3x² - 12x + 11 = 0。

对方程进行因式分解得：(x - 1)(3x - 11) = 0。

由此可得x = 1 或 x = 11/3。

答案：x = 1 或 x = 11/3第二十二届试题1. 下图为某街区的地理平面图，a、b、c和d分别表示大街，A、B、C、D和E分别表示街区中的五个角落。

已知AE = CD，AB = 2 cm，BC = 10 cm，求AE的长度。

解：由题意可推出ABCD为平行四边形，而AE = CD。

根据平行四边形的性质，平行四边形的对角线互相等长，所以AE= CD = 10 cm。

答案：10 cm2. 若一个正方形的周长是36 cm，求它的面积。

解：设正方形的边长为x cm，由题意可知4x = 36，解方程得到x = 9。

数学初二希望杯试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 3.14159B. πC. 0.33333…D. √22. 如果一个三角形的三边长分别为a、b、c，且满足a^2 + b^2 = c^2，这个三角形是什么类型的三角形？A. 等边三角形B. 直角三角形C. 等腰三角形D. 钝角三角形3. 一个数的平方根是4，这个数是多少？A. 16B. 8C. -16D. 44. 以下哪个表达式的结果不是正数？A. -1 + 2B. √4C. -√4D. (-2)^25. 一个圆的半径是5，那么它的面积是多少？A. 25πB. 50πC. 75πD. 100π6. 一个数的倒数是1/3，这个数是多少？A. 3B. 1/3C. 1/9D. 97. 如果一个角的余角是30°，那么这个角是多少度？A. 60°B. 45°C. 30°D. 15°8. 一个正方体的棱长是3，那么它的体积是多少？A. 27B. 9C. 3D. 19. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 010. 以下哪个是二次根式？A. √3B. √(-1)C. √(2x)D. √(2x+1)二、填空题（每题2分，共20分）11. 一个数的立方根是2，这个数是______。

12. 如果一个数的相反数是-5，那么这个数是______。

13. 一个数的绝对值是10，这个数可能是______或______。

14. 如果一个角的补角是120°，那么这个角是______。

15. 一个数的平方是25，这个数是______或______。

16. 一个直角三角形的两条直角边分别是3和4，斜边的长度是______。

17. 一个数的平方根是±3，这个数是______。

18. 一个数的倒数是1/4，这个数是______。

19. 一个圆的直径是10，那么它的半径是______。

第二十二届“希望杯”全国数学邀请赛初二 第1试一、选择题(每小题4分，共40分)以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英语字母写在1、将a 千克含盐10%的盐水配制成含盐15%的盐水，需加盐水x 千克，则由此可列出方程为( ) A 、%)151)(x a (%)101(a -+=- B 、%15)x a (%10a ⨯+=⨯ C 、%15a x %10a ⨯=+⨯ D 、%)151(x %)101(a -=-2、一辆汽车从A 地匀速驶往B 地，如果汽车行驶的速度增加a%，则所用的时间减少b%，则a ，b 的关系是( ) A 、%a 1a 100b +=B 、%a 1100b +=C 、a 1a b +=D 、a100a100b +=3、当1x ≥时，不等式|2x |m 1x |1x |--≥-++恒成立，那么实数m 的最大值是( ) A 、1 B 、2 C 、3 D 、44、在平面直角坐标系中，横、纵坐标都是整数的点称为整点，已知k 为整数，若函数1x 2y -=与k kx y +=的图象的交点是整点，则k 的值有( )A 、2个B 、3个C 、4个D 、5个5、The sum of all such integers x that satisfy inequality 6|1x 2|2≤-≤ is ( ) A 、8 B 、5 C 、2 D 、0(英汉词典：sum 和；integer 整数；satisfy 满足；inequality 不等式)6、若三角形的三条边的长分别为a ，b ，c ，且0b c b c a b a 3222=-+-，则这个三角形一定是( ) A 、等腰三角形 B 、直角三角形 C 、等三角形 D 、等腰直角三角形7、As shown in figure 1，point C is on the segment BG and quadrilateral ABCD is a square. AG intersects BD and CD at points E and F, respectively. If AE=5 and EF=3, then FG=( ) A 、316 B 、38C 、4D 、5 (英汉词典：square 正方形；intersect …at … 与…相交于…) 8、1215-能分解成n 个质因数的乘积，n 的值是( ) A 、6 B 、5 C 、4 D 、3 9、若关于x ，y 的方程组⎩⎨⎧=+-=++0a y 2bx 01ay x 没有实数解，则( )A 、2ab -=B 、2ab -=且1a ≠C 、2ab -≠D 、2ab -=且2a ≠10、如图2，∠AOB=45°，OP 平分∠AOB ，PC ⊥OB 于点C ， 若PC=2，则OC 的长是( )A 、7B 、6C 、222+D 、32+二、A 组填空题(每小题4分，共40分) 11、化简：5252549+=++；12、若关于x ，y 的方程组⎩⎨⎧=--=+2y 3x 21k y 2x 3的解使2y 7x 4>+，则k 的取值范围是3k >；figure 1A O BP C 2 图213、如图3，平行于BC 的线段MN 把等边△ABC 分成一个 三角形和一个四边形，已知△AMN 和四边形MBCN 的周长相 等，则BC 与MN 的长度之比是 4:3 ；14、小华测得自家冰箱的压缩机运转很有规律，每运转5分钟， 停机15分钟，再运转5分钟，再停机15分钟，……，又知8月份 这台冰箱的耗电量是24.18度 (1度=1千瓦时)，则这台冰箱的压缩 机运转时的功率是 130 瓦；15、已知自然数a ，b ，c ，满足c 12b 4a 442c b a 222++<+++和02a a 2>--，则代数式c1b 1a 1++的值是 1； 16、已知A 、B 是反比例函数x2y =的图象上的两点，A 、B 的横坐标分别是3，5.设O 为原点，则△AOB 的面积是1516；17、设完全平方数A 是11个连续整数的平方和，则A 的最小值是 121 ；18、将100个连续的偶数从小到大排成一行，其中第38个数与第63个数的和为218，则首尾两个数的和是 218 ； 19、A 、B 两地相距15km ，甲、乙两人同时从A 出发去B 。

第二十二届“希望杯”全国数学邀请赛 1试初二第_______________30 得分日上午8：30至11：2011年3月13以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英语字分)一、选择题(每小题4分，共40 母写在下面的表格总得2345678910题1DACACCC答CAA( ) 千克，则由此可列出方程为、将a千克含盐10%的盐水配制成含盐15%的盐水，需加盐水x1%15%?(a?x)?a(1?10%)?(a?x)(1?15%)?10a、BA、%15?10%?x?a?a%)1510%)?x(1??a(1、C、 D( )的关系是则所用的时间减少b%，则a，b2、一辆汽车从A地匀速驶往B地，如果汽车行驶的速度增加a%，a100100aa100?b?b?b?b、A C、、 D B、a?a1001?a%1?a%1?1x?|?2x?1|?x?1?m?|x|( )m、当3时，不等式的最大值是恒成立，那么实数4 3 D、、2 C、1 BA、kkx?1y?y?2x?与横、纵坐标都是整数的点称为整点，已知k为整数，若函数4、在平面直角坐标系中，( )k的值有的图象的交点是整点，则个 D、5、2个 B、3个 C、4个A6??1|2?|2x is ( )The sum of all such integers x that satisfy inequality 5、0、2 D、A、8 B、5 C) 满足；inequality 不等式(英汉词典：sum 和；integer 整数；satisfy32220b?c?bc?aab?( ) b，c，且，则这个三角形一定是6、若三角形的三条边的长分别为a， D、等腰直角三角形、等腰三角形 B、直角三角形 C、等三角形Aintersects AG ABCD is a square. the 7、As shown in figure 1，point C is on segment BG and quadrilateralBD and CD at points E and F, respectively. If AE=5 and EF=3, then FG=( )8165 4 D、 BA、、 C、A D 33 E 5 ) 与…相交于…square 正方形；intersect…at… (英汉词典：F3 151?2( ) n能分解成n个质因数的乘积，8、的值是G34 D、A、6 B、5 C、BCfigure 10?x?ay?1?( )没有实数解，则、若关于x，y的方程组9?0??2ya?bx?2?2a?a?1ab??2ab?2?ab?2ab??且 DA、C且、 B、、于点C，AOB°，OP平分∠，PC⊥、如图10OB2，∠AOB=45A( )，则OC的长是若PC=22?2232?、A、7 B、6 C、 D P 2 ) 分4分，共40二、A 组填空题(每小题O BC 549?2图?2?5； 11、化简：5?23x?2y?k?1?k?32y?74x?；，则k的解使的方程组，、若关于12xy的取值范围是?2?3x2?y?1AABC分成一个的线段MN把等边△13、如图3，平行于BC的周长相AMN和四边形MBCN三角形和一个四边形，已知△；MN的长度之比是 4:3 等，则BC与M N 、小华测得自家冰箱的压缩机运转很有规律，每运转5分钟，14 8月份分钟，再停机停机15分钟，再运转515分钟，……，又知CB3图 )，则这台冰箱的压缩度=1千瓦时这台冰箱的耗电量是24.18度 (1 130 瓦；机运转时的功率是1112222??02a???4a?4b?12ca?a?b?c?42的，满足和，则代数式15、已知自然数a，b，c cba；值是 12?y的面AOBO为原点，则△3，5.16、已知A、B是反比例函数设B的图象上的两点，A、的横坐标分别是x16；积是15；的最小值是 121 是11个连续整数的平方和，则A17、设完全平方数A 218，则首尾两个数的和是38个数与第63个数的和为个连续的偶数从小到大排成一行，其中第18、将100 218 ；地，然后下车步行，之间的C。

初二数学希望杯试题及答案一、选择题（每题2分，共10分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的平方等于16，那么这个数是：A. 4B. -4C. 4或-4D. 163. 一个直角三角形的两条直角边分别为3和4，那么斜边的长度是：A. 5B. 6C. 7D. 84. 一个数的绝对值是5，这个数可以是：A. 5B. -5C. 5或-5D. 05. 以下哪个表达式的结果不是整数？A. 3 + 2 = 5B. 7 - 5 = 2C. 4 × 2 = 8D. 6 ÷ 2 = 3二、填空题（每题2分，共10分）6. 一个数的平方根是4，那么这个数是_________。

7. 如果一个数的立方等于-27，那么这个数是_________。

8. 一个数的倒数是2，那么这个数是_________。

9. 一个数的相反数是-3，那么这个数是_________。

10. 如果一个数的平方等于9，那么这个数是_________。

三、解答题（每题10分，共30分）11. 已知一个长方体的长、宽、高分别是3cm、4cm、5cm，求这个长方体的体积。

12. 已知一个圆的半径是7cm，求这个圆的面积。

13. 已知一个等腰三角形的底边长是6cm，两腰长是5cm，求这个等腰三角形的面积。

初二数学希望杯试题答案一、选择题答案1. B2. C3. A4. C5. D二、填空题答案6. 167. -38. 1/29. 310. ±3三、解答题答案11. 长方体的体积 = 长× 宽× 高= 3cm × 4cm × 5cm =60cm³。

12. 圆的面积= π × 半径² = 3.14 × 7cm × 7cm = 153.86cm²。

13. 等腰三角形的面积 = (底× 高) / 2。

第二十二届“希望杯”全国数学邀请赛初二 第2试一、选择题（每小题4分，共40分．）以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题后面的圆括号内． 1．已知A B=A，C ，则,B C 之间的大小关系是（ ） A ．B C >B ．BC =C ．B C <D ．不能确定【解析】 A ．由AC==，于是6336320242933A A C B ⎛⎫⎛⎫⎛⎫⎛⎫=>>= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则B C >．2．已知27a a -=，则代数式2221412211a a a a a a --⋅÷+-+-的值是（ ） A ．3 B ．72C ．4D ．5【解析】 D ．求值式()()()()()22211121a a a a a a a -+-=⋅⋅-⋅++-()()22125a a a a =-+=--=．3．一个凸四边形的四个内角可以（ ）A ．都是锐角B ．都是直角C ．都是钝角D ．有三个是直角，另一个是锐角或钝角【解析】 B ．由四边形的外角和为360，于是不能每个外角都是锐角或者钝角．选B ．4．如果直线2y x m =+与直角坐标系的两坐标轴围成的三角形的面积等于4，则m 的值是（ ）A ．3±B ．3C ．4±D ．4【解析】 C ．可知直角三角形的直角边长分别为,2mm ，于是有14422m m m ⋅⋅=⇒=于是4m =±，分别对应于三角形位于第二象限，第四象限的情形．5．若22120102011n +=+（ ） A ．2011B ．2010C ．4022D ．4021【解析】 D ．由222201020111201020102012n =+-=+⋅．于是22222212010201120102010201220102011220102011n +=+++⋅=++⋅⋅()220102011=+4021．6．有四个命题：①若两个等腰三角形的腰相等，腰上的高也相等，则这两个等腰三角形全等． ②有一条边相等的两个等腰直角三角形全等．③有一条边和一个锐角对应相等的两个三角形全等． ④两边以及另一边上的高对应相等的两个三角形全等． 其中，正确的命题有（ ） A ．0个 B ．1个 C ．2个 D ．3个 【解析】 B ．正确的命题为④．①②③错误．7．如图1，Rt ABC △两直角边上的中线分别为AE 和BD ，则22AE BD +与2AB 的比值为（）A ．34B ．1C ．54D ．32图1ADC E B【解析】 C ．特殊值法：直接设1BC AC ==，可得AE AD AB ===54． 一般的，不妨设,BC a AC b ==，于是()222222225224a b AE BD b a a b ⎛⎫⎛⎫+=+++=+ ⎪ ⎪⎝⎭⎝⎭，222AB a b =+，于是可得出同样的结果．8．如图2所示，ABCD 为矩形，12,5AD AB ==，P 为线段AD 上的任意一点，PE BD ⊥于点E ，PF AC ⊥于F ．则PE PF +的值为（ ）A ．4813B ．6013C ．5D ．7013figure 2ABC DE FP【解析】 B ．利用面积相等解决此问题．由PBD PAC PCD PAC ACD S S S S S +=+=△△△△△，有()1122AC PE PF AD DC ⋅⋅+=⋅⋅，则有6013PE PF +=．9．如图3，正方形ABCD 的边AB 在x 轴的正半轴上，(21)C ，，(11)D ，，反比例函数ky x=的图象与边BC 交于点E ，与边CD 交于点F ，已知:3:1BE CE =，则:DF FC 等于（ ）A ．4：1B ．3：1C ．2：1D ．1：1图3【解析】 D ．由2,,2k E ⎛⎫ ⎪⎝⎭知32112kk =-，解得32k =．于是3,12F ⎛⎫⎪⎝⎭，则12DF FC ==，于是比值为1．10．如图4，a b c d e ，，，，分别代表1，2，3，4，5中的一个数，若b a c ++及d a e ++除以3都余1，则不同的填数方法有（ ） A ．2种 B ．4种C ．8种D ．16种a bc ed图4【解析】 D ．由1234515a b c d e ++++=++++=，31a b c k ++=+，知32d e p +=+，于是32a q =+．则2a =（或5）．,b c 与,d e 分别为1,4与3,5（或2）．于是所有的填数法有222216⋅⋅⋅=种．二、填空题（每小题4分，共40分）11．下表为甲、乙两人比赛投篮球的记录，以命中率（投进球数与投球次数的比值）来比较投球成绩的好坏，若他们的成绩一样好，现有以下关系式：①5a b -=；②18a b +=；③:2:1a b =；④:182:3a =， 其中正确的是_________________（只填序号）． 【解析】 ②③④．由101518a=知12a =．于是6b =．只有①是错误的．12．已知方程组245x y x y +=⎧⎨-=⎩，的解为.x m y n =⎧⎨=⎩，又知点()A m n ，在反比例函数k y x =的图象上，则k 的值是_________________．【解析】 6-．解得3,2m n ==-，于是6k m n =⋅=-．13．等腰三角形的两个内角的度数之比为:()a b a b <，若这个三角形是钝角三角形，则ba的取值范围是_____________．【解析】 2b a>．钝角三角形的三内角比必为::a a b ，由90,2902bb a a ><⇒>．14．定义1()(1)1f x x x =≠-，那么2011((((2011))))ff f f f 个=_________．【解析】 12100-．容易知道()()()f f f a a =，于是()20111((((2011))))20112010ff f f f f ==-个．15．函数y ax =与函数23y x b =+的图象如图5所示，则关于x y ，的方程组0323ax y y x b -=⎧⎨-=⎩，的解是________________．【解析】 12x y =⎧⎨=⎩．观察出函数图像的交点坐标为()1,2，于是方程组的解是12x y =⎧⎨=⎩．16．若a b ，是自然数，且a b >，2011=(1)a a b -+．那么a =_____________；b =______________． 【解析】 45；31．由()222011a b a a =+-<，()()2201111a a b a =-+>-，知2245201144>>，有45,14445a a a -⇒=≥≤．代入原式解得31b =．17．一个骰子，六个面上的数字分别是1，2，3，4，5，6．两次掷这个骰子，朝上一面的数依次记为m n ，．则关于x y ，的方程组123mx ny x y +=⎧⎨+=⎩，有解的概率为_______________．【解析】 1112．无解的情形当且仅当1213m n =≠，即21m n =⎧⎨=⎩或42m n =⎧⎨=⎩或63m n =⎧⎨=⎩．于是无解的概率为316612=⋅，有解的概率为11111212-=．18．如图6，边长为2的正方形ABCD 内有一点P ，且30PAB ∠=︒，2PA =，在正方形ABCD 的边上有一点Q ，且PAQ △为等腰三角形，则符合条件的点Q 有______________个．230°ABCD【解析】 4．PA 为底边或者腰．当PA 为底边时，做PA 的垂直平分线，交正方形的边于两点；当PA为腰时，分别以,P A 为圆心，2为半径做圆，交正方形的边于2点（不含A ），2点．这三种情形均包括DA 边上的同一个点．于是共有22224++-=个．19．已知a b c ，，为实数，并且对于任意实数x ，恒有23x a x b x c +++=+，则::a b c =____________． 【解析】 1：2：3．令13x c =-，有2033c a b c -+-=，于是2,33c a b c ==，即::1:2:3a b c =．20．一个自行车轮胎，若安装在前轮，则行驶5000行米后报废；若安装在后轮，则行驶3000千米后报废，现有一辆新自行车，在行驶一定路程后，交换前后两轮的轮胎，再继续行驶，使得两个轮胎同时报废，那么该车最多行驶______________千米．【解析】 3750．容易知道，若一轮作为前轮行驶路程为a ，作为后轮行驶路程为b ，则另一轮行驶路程为作为后轮a ，作为前轮b ，于是必须a b =才能使得同时报废．于是500050003000ba +⋅=，解得1875a b ==，于是3750a b +=．三、解答题每题都要写出推算过程． 21．（本题满分10分）平面直角坐标系中，正方形ABCD 四个顶点的坐标分别为（-1，-1），（1，-1），（1，1），（-1，1），设正方形ABCD 在y x a a =-+的图象以上部分的面积为S ，试求S 关于a 的函数关系式，并写出S 的最大值．【解析】 ⑴当1a ≥时，y x a a =-+的图象与正方形无公共部分，如图①，0S =．①②③④⑵当0a ≤≤1时，21(1)2(1)(1)2S a a a =-⨯-=-．如图②⑶当1a -≤≤0时，22(1)(1)22(1)2a a S a ++=-=-+．如图③⑷当1a <-时，2S =．如图④ 所以，S 的最大值为2．22．（本题满分15分）若直线:3l y x =+交x 轴于点A ，交y 轴于点B ．坐标原点O 关于直线l 的对称点'O 在反比例函数ky x=的图象上． ⑴求反比例函数ky x=的解析式； ⑵将直线l 绕点A 逆时针旋转角(045)θθ︒<︒<，得到直线'l ，'l 交y 轴于点P ，过点P 作x 轴的平行线，与上述反比例函数ky x=的图象交于点Q ，当四边形'APQO的面积为9θ的值．【解析】 ⑴直线l 与x 轴交于点(30)A -，，与y 轴交于点(03)B ，，ABO △是等腰直角三角形，则坐标原煤点O 关于直线l 的对称点'O 的坐标是(33)-，．点'O 在反比例函数ky x=的图象上，所以99k y x=-=-，．⑵设点P 的坐标为(0)P ，，PQ 和'AO 的延长线交于点G ． 因为PQ x ∥轴，与反比例函数图象交于点Q ，所以四边形AOPG 是矩形，9Q p p⎛⎫- ⎪⎝⎭，，(3)G p -，因为913GP GQ p==-，，'3GO p GA p =-=，． 所以APG GQO APQO S S S ==四边形△△=11'22GA GP GQ GO ⋅-⋅=()11933322p p p ⎛⎫⨯--- ⎪⎝⎭=2792p -，已知9APQO S =四边形27992p -=解得p =p =符合题意．所以(0P ，，6AP ==，60PAO ∠=︒ 又因为45BAO ∠=︒，所以604515PAO BAO θ=∠-∠=︒-︒=︒23．（本题满分15分）给定(3)m m ≥个数字组成的一列数12m a a a ，，，，其中每一个数(12)i a i m =，，，只能是1或0，在这一列数中，如果存在连续的k 个数和另一组连续的k 个数恰好按次序对应相等，则称这一列数是“k 阶可重复的”．例如，由7个数组成的一列数：0，1，1，0，1，1，0，因为1234,,,a a a a 与4567a a a a ，，，按次序对应相等，所以称这列数为“4阶可重复的”．⑴分别判断下面的两列数是否是“5阶可重复的”？如果是，请写出重复的这5个数； ①0，0，0，1，1，0，0，1，1，0； ②1，1，1，1，1，0，1，1，1，1．⑵如果一列数12m a a a ，，，一定是“3阶可重复的”，求m 的最小值． ⑶假设一列数不是“5阶可重复的”且第4个数是1，但若在这列数最后一个数后再添加一个0或1，均可使新的一列数是“5阶可重复的”，那么原来的数列中的最后一个数是什么？说明理由． 【解析】 ⑴在①中，因为23456a a a a a ，，，，与678910a a a a a ，，，，按次序对应相等，所以①是“5阶可重复的”，重复的这5个数是0，0，1，1，0； 在②中，因为连续的5个数分别为 1，1，1，1，1；1，1，1，1，0； 1，1，1，0，1；1，1，0，1，1；1，0，1，1，1；0，1，1，1，1．其中没有完全相同的，所以②不是“5阶可重复的”⑵因为这列数中的每一个数只能是0或1，所以连续的3个数共有228=（种）不同的情形，即分别为（0，0，0）；（0，0，1）；（0，1，0）；……；（1，1，1）．若11m =，则在这一列数中有9组连续的3个数，它们分别是123a a a ，，；234a a a ，，；345a a a ，，；…；51211a a a ，，，其中至少有两组按次序对应相等，这列数一定是“3阶可重复的”．若10m =，存在这样一列数； 0，0，1，0，1，1，1，0，0，0，它不是“3阶可重复的”（类似地还可以写出一些，只要写出一个即可）． 所以，要使一系数一定是“3阶可重复的”，m 的最小值是11．⑶假设这一列数共有m 个数，由于在最后一个数m a 后再添加0或1，均可使新的一列数是“5阶可重复的”，即存在两个不同的i 和(4)j i j m -，≤，使得1234,,,,i i i i i a a a a a ++++ 与321,,,,0m m m m a a a a ---按次序对应相等，且1234,,,,j j j j j a a a a a ++++与321,,,,1m m m m a a a a ---按次序对应相等．此时考虑111,,i j m a a a ---这三个数，其中必有两个相同，这就导致这一列数中有两个连续的5个数恰好按次序对应相等．从而这一列数是“5阶可重复的”这和题设中这一列数不是“5阶可重复的”矛盾！所以1i =或1j =，从而41m a a ==．。

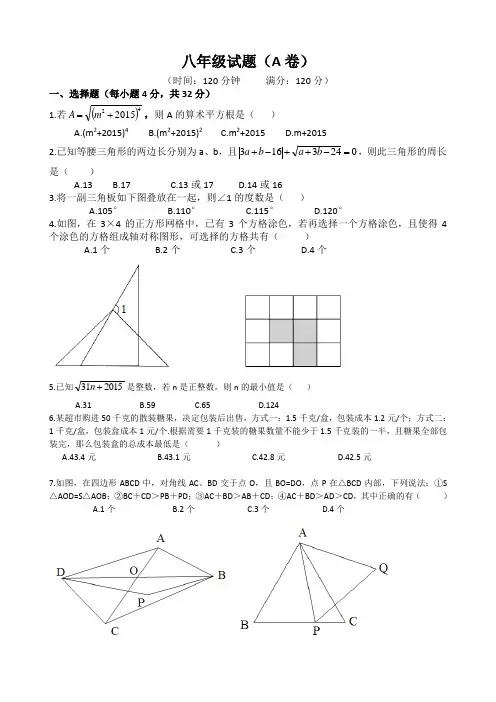
八年级试题（A 卷）（时间：120分钟 满分：120分）一、选择题（每小题4分，共32分） 1.若()422015+=mA ，则A 的算术平方根是（ ）A.(m 2+2015)4B.(m 2+2015)2C.m 2+2015D.m+20152.已知等腰三角形的两边长分别为a 、b ，且0243163=-++-+b a b a ，则此三角形的周长是（ ）A.13B.17C.13或17D.14或163.将一副三角板如下图叠放在一起，则∠1的度数是（ ）A.105°B.110°C.115°D.120°4.如图，在3×4的正方形网格中，已有3个方格涂色，若再选择一个方格涂色，且使得4个涂色的方格组成轴对称图形，可选择的方格共有（ ）A.1个B.2个C.3个D.4个5.已知201531+n 是整数，若n 是正整数，则n 的最小值是（ ）A.31B.59C.65D.1246.某超市购进50千克的散装糖果，决定包装后出售，方式一：1.5千克/盒，包装成本1.2元/个；方式二：1千克/盒，包装盒成本1元/个.根据需要1千克装的糖果数量不能少于1.5千克装的一半，且糖果全部包装完，那么包装盒的总成本最低是（ ）A.43.4元B.43.1元C.42.8元D.42.5元7.如图，在四边形ABCD 中，对角线AC 、BD 交于点O ，且BO=DO ，点P 在△BCD 内部，下列说法：①S △AOD=S △AOB ；②BC ＋CD ＞PB ＋PD ；③AC ＋BD ＞AB ＋CD ；④AC ＋BD ＞AD ＞CD ，其中正确的有（ ） A.1个 B.2个 C.3个 D.4个8.如图，等边三角形ABC 边长为6，点P 从B 点开始在BC 上向点C 运动，运动到点C 停止，以AP 为边在直线BC 的同侧作等边三角形APQ ，得到点Q ，则点Q 的运动路径长（ ） A.6 B.33 C.24 D.23π二、填空题：（每小题5分，共40分）9.化简：.________________)2015(201522=+--x x ）（10.已知正n 边形的一个内角是一个外角的5倍，则n=____________.11.如图，△ABC 是格点三角形，点D 是异于点A 的一个格点，则使△DBC 和△ABC 全等的D 点共有__________个.12.方程3100820151210071=+-+-xx x 的解是___________________.13.如图，等边三角形的边长为1，现将其各边n(n ＞2)等分，并以相邻分点为顶点向外作小等边三角形，再将相邻分点之间的线段去掉，得到一个锯齿图形，当n=k 时，锯齿图形的周长为___________.(用含k 的代数式表示).14.将1、2、3、4、5这五个数排成一列，要求第一个数和最后一个数都是偶数，且其中任意三个相邻的数之和都能被这三个数中的第一个数整除，这样的排列方法共有_____________种.15.对于实数m 、n ，定义运算m ※n=m(1-n)，下面是关于这种运算的几个结论：①2※3=-4；②若m ※n=0，则n=0；③m ※n=（1-n ）※(1-m)；④若m+n=1，则（m ※n ）-(n ※n)=0.其中正确的是___________. 16.如图，已知点A(1，1)，点B （7,3），点P 为x 轴上一个动点，当PA+PB 的值最小时，点P 的坐标为_______________.三、解答题（10+12+12+14=48分）17..)32(32,2,29的值）求（若+--==-y x xy y x18.如图，△ABC 为等边三角形，点D 是BC 延长线上一点，且CD ＜BC ，BD 的垂直平分线交AC 于E ，过点E 作EF ∥BC 交AB 于F.（1）求证：△AEF 为等边三角形； （2）若BC=3CD ，求ECAE的值.19.某数学俱乐部组织60名会员租车进行自驾游，共有两种车型可供选择，A 型车共有8个座位，B 型车有4个座位，要求租用的车不能空座，也不能超载. （1）共有多少种不同的租车方案？（2）若A 型车的租金是400元/天，B 型车的租金是260元/天，请设计最划算的租车方案，并说明理由.20.已知：直角三角形斜边上的中线等于斜边的一半，如图1，在△ABC 中，∠CAB=90°，D 是BC 的中点，连接AD ，则AD=CD=BD.（1）如图2，过点D作DE⊥AB于E，以E为边作等边三角形AEF，以DF为边作等边三角形DFG，连接AG，求证：AG平分∠FAB.（2）如图3，过点C作CH⊥AF于H，连接DH，求证：DH=FG.1 2 3 4 5 6 7 8C B AD B C D A9 10 11 12 13 14 15 1610 1/2-8060X12 3 1008KK 66-6 ①③④⎪⎭⎫ ⎝⎛0,25。

希望杯试题及答案初二一、选择题（每题3分，共30分）1. 下列哪个选项是正确的？A. 2的平方等于3B. 3的平方等于9C. 4的平方等于16D. 5的平方等于25答案：B2. 一个长方形的长是10厘米，宽是5厘米，那么它的周长是多少厘米？A. 30B. 40C. 50D. 60答案：B3. 一个数加上它的相反数等于多少？A. 0B. 1C. 2D. -1答案：A4. 下列哪个选项是二次方程？A. x + 2 = 0B. x^2 + 2x + 1 = 0C. 2x - 3 = 0D. x^3 - 4x^2 + 4x = 0答案：B5. 一个数的绝对值是5，那么这个数可能是？A. 5B. -5C. 3D. 以上都是答案：D6. 下列哪个选项是正确的不等式？A. 2x > 3B. 2x < 3C. 2x = 3D. 2x ≤ 3答案：A7. 一个圆的半径是3厘米，那么它的面积是多少平方厘米？A. 9πB. 18πC. 27πD. 36π答案：C8. 下列哪个选项是正确的分数？A. 3/2B. 2/3C. 1/2D. 4/5答案：D9. 一个等腰三角形的两个底角都是45度，那么它的顶角是多少度？A. 90B. 45C. 135D. 180答案：A10. 下列哪个选项是正确的函数关系？A. y = 2x + 3B. y = x^2 + 2x + 1C. y = x/2D. y = x^3 - 2x^2 + 3x答案：A二、填空题（每题4分，共20分）1. 一个数的平方根是4，那么这个数是______。

答案：162. 一个数的立方根是2，那么这个数是______。

答案：83. 一个数的倒数是1/2，那么这个数是______。

答案：24. 一个数的绝对值是6，那么这个数可以是______。

答案：6或-65. 一个等腰三角形的顶角是120度，那么它的底角是______。

答案：30度三、解答题（每题10分，共50分）1. 解方程：3x - 5 = 10答案：x = 52. 计算：(2x^2 - 3x + 1) - (x^2 + 2x - 3)答案：x^2 - 5x + 43. 已知一个直角三角形的两条直角边长分别为3和4，求斜边的长度。

“希望杯”全国数学竞赛（第1-23届）第一/二试题目录1.希望杯第一届（1990年）初中一年级第一试试题............................................. 003-0052.希望杯第一届（1990年）初中一年级第二试试题............................................. 010-0123.希望杯第二届（1991年）初中一年级第一试试题............................................. 018-0204.希望杯第二届（1991年）初中一年级第二试试题............................................. 024-0265.希望杯第三届（1992年）初中一年级第一试试题............................................. 032-0326.希望杯第三届（1992年）初中一年级第二试试题............................................. 038-0407.希望杯第四届（1993年）初中一年级第一试试题............................................. 048-0508.希望杯第四届（1993年）初中一年级第二试试题............................................. 056-0589.希望杯第五届（1994年）初中一年级第一试试题............................................. 064-06610.希望杯第五届（1994年）初中一年级第二试试题 .......................................... 071-07311.希望杯第六届（1995年）初中一年级第一试试题........................................... 078-080 12希望杯第六届（1995年）初中一年级第二试试题........................................... 085-08713.希望杯第七届（1996年）初中一年级第一试试题........................................... 096-09814.希望杯第七届（1996年）初中一年级第二试试题........................................... 103-10515.希望杯第八届（1997年）初中一年级第一试试题............................................ 111-11316.希望杯第八届（1997年）初中一年级第二试试题........................................... 118-12017.希望杯第九届（1998年）初中一年级第一试试题........................................... 127-12918.希望杯第九届（1998年）初中一年级第二试试题........................................... 136-13819.希望杯第十届（1999年）初中一年级第二试试题........................................... 145-14720.希望杯第十届（1999年）初中一年级第一试试题........................................... 148-15121.希望杯第十一届（2000年）初中一年级第一试试题....................................... 159-16122.希望杯第十一届（2000年）初中一年级第二试试题....................................... 167-16923.希望杯第十二届（2001年）初中一年级第一试试题....................................... 171-17424.希望杯第十二届（2001年）初中一年级第二试试题....................................... 176-17825.希望杯第十三届（2002年）初中一年级第一试试题....................................... 182-18426.希望杯第十三届（2001年）初中一年级第二试试题....................................... 186-18927.希望杯第十四届（2003年）初中一年级第一试试题....................................... 193-19628.希望杯第十四届（2003年）初中一年级第二试试题....................................... 198-20029.希望杯第十五届（2004年）初中一年级第一试试题 (203)30.希望杯第十五届（2004年）初中一年级第二试试题 (204)31.希望杯第十六届（2005年）初中一年级第一试试题....................................... 213-21832.希望杯第十六届（2005年）初中一年级第二试试题 (204)33.希望杯第十七届（2006年）初中一年级第一试试题....................................... 228-23334.希望杯第十七届（2006年）初中一年级第二试试题....................................... 234-23835.希望杯第十八届（2007年）初中一年级第一试试题....................................... 242-246 26.希望杯第十八届（2007年）初中一年级第二试试题....................................... 248-25137.希望杯第十九届（2008年）初中一年级第一试试题....................................... 252-25638.希望杯第十九届（2008年）初中一年级第二试试题....................................... 257-26239.希望杯第二十届（2009年）初中一年级第一试试题....................................... 263-26620.希望杯第二十届（2009年）初中一年级第二试试题....................................... 267-27121.希望杯第二十一届（2010年）初中一年级第一试试题................................... 274-27622.希望杯第二十二届（2011年）初中一年级第二试试题................................... 285-28823.希望杯第二十三届（2012年）初中一年级第二试试题................................... 288-301希望杯第一届（1990年）初中一年级第1试试题一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么( )A．a，b都是0．B．a，b之一是0．C．a，b互为相反数．D．a，b互为倒数．2．下面的说法中正确的是( )A．单项式与单项式的和是单项式．B．单项式与单项式的和是多项式．C．多项式与多项式的和是多项式．D．整式与整式的和是整式．3．下面说法中不正确的是( )A. 有最小的自然数．B．没有最小的正有理数．C．没有最大的负整数．D．没有最大的非负数．4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么( )A．a，b同号．B．a，b异号．C．a＞0．D．b＞0．5．大于－π并且不是自然数的整数有( )A．2个．B．3个．C．4个．D．无数个．6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身．这四种说法中，不正确的说法的个数是( )A．0个．B．1个．C．2个．D．3个．7．a代表有理数，那么，a和－a的大小关系是 ( )A．a大于－a．B．a小于－a．C．a大于－a或a小于－a．D．a不一定大于－a．8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( ) A．乘以同一个数．B．乘以同一个整式．C．加上同一个代数式．D．都加上1．9．杯子中有大半杯水，第二天较第一天减少了10%，第三天又较第二天增加了10%，那么，第三天杯中的水量与第一天杯中的水量相比的结果是( )A．一样多． B．多了．C．少了．D．多少都可能．10．轮船往返于一条河的两码头之间，如果船本身在静水中的速度是固定的，那么，当这条河的水流速度增大时，船往返一次所用的时间将( )A．增多．B．减少．C．不变．D．增多、减少都有可能．二、填空题（每题1分，共10分）1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______． 2．198919902－198919892=______． 3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5．1－2＋3－4+5－6+7－8+…+4999－5000=______．6.当x=-24125时,代数式(3x 3－5x 2+6x －1)－(x 3－2x 2+x －2)+(－2x 3+3x 2+1)的值是____． 7．当a=－0.2，b=0.04时，代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8．含盐30%的盐水有60千克，放在秤上蒸发，当盐水变为含盐40%时，秤得盐水的重是______克．9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半，一共需要______天．10．现在4点5分，再过______分钟，分针和时针第一次重合．答案与提示一、选择题1．C 2．D 3．C 4．D 5．C 6．B 7．D 8．D 9．C 10．A提示：1．令a=2，b=－2，满足2+(－2)=0，由此2．x2，2x2，x3都是单项式．两个单项式x3，x2之和为x3+x2是多项式，排除A．两个单项式x2，2x2之和为3x2是单项式，排除B．两个多项式x3+x2与x3－x2之和为2x3是个单项式，排除C，因此选D．3．1是最小的自然数，A正确．可以找到正所以C“没有最大的负整数”的说法不正确．写出扩大自然数列，0，1，2，3，…，n，…，易知无最大非负数，D正确．所以不正确的说法应选C．5．在数轴上容易看出：在－π右边0的左边（包括0在内）的整数只有－3，－2，－1，0共4个．选C．6．由12=1，13=1可知甲、乙两种说法是正确的．由(－1)3=－1，可知丁也是正确的说法．而负数的平方均为正数，即负数的平方一定大于它本身，所以“负数平方不一定大于它本身”的说法不正确．即丙不正确．在甲、乙、丙、丁四个说法中，只有丙1个说法不正确．所以选B．7．令a=0，马上可以排除A、B、C，应选D．8．对方程同解变形，要求方程两边同乘不等于0的数．所以排除A．我们考察方程x－2=0，易知其根为x=2．若该方程两边同乘以一个整式x－1，得(x－1)(x－2)=0，其根为x=1及x=2，不与原方程同解，排除B．若在方程x－2=0两边加上同一个代数式去了原方程x=2的根．所以应排除C．事实上方程两边同时加上一个常数，新方程与原方程同解，对D，这里所加常数为1，因此选D．9．设杯中原有水量为a，依题意可得，第二天杯中水量为a×(1－10%)=0.9a；第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a；第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了，选C．10．设两码头之间距离为s，船在静水中速度为a，水速为v0，则往返一次所用时间为设河水速度增大后为v，(v＞v0)则往返一次所用时间为由于v－v0＞0，a+v0＞a－v0，a+v＞a－v所以(a+v0)(a+v)＞(a－v0)(a－v)∴t0－t＜0，即t0＜t．因此河水速增大所用时间将增多，选A．二、填空题提示：2．198919902－198919892=(19891990+19891989)×(19891990－19891989) =(19891990+19891989)×1=39783979．3．由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2－1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22－1)(22+1)(24+1)(28+1)(216+1)=(24－1)(24+1)(28+1)(216+1)=(28－1)(28+1)(216+1)=(216－1)(216+1)=232－1．2(1+x)－(x－2)=8,2+2x－x+2=8解得；x=45．1－2+3－4+5－6+7－8+…+4999－5000=(1－2)+(3－4)+(5－6)+(7－8)+…+(4999－5000)=－2500．6．(3x3－5x2+6x－1)－(x3－2x2+x－2)+(－2x3+3x2+1)=5x+27．注意到：当a=－0.2，b=0.04时，a2－b=(－0.2)2－0.04=0，b+a+0.16=0.04－0.2+0.16=0．8．食盐30%的盐水60千克中含盐60×30%（千克）设蒸发变成含盐为40%的水重x克，即0.001x千克，此时，60×30%=(0.001x)×40%解得：x=45000（克）．10．在4时整，时针与分针针夹角为120°即希望杯第一届（1990年）初中一年级第2试试题一、选择题（每题1分，共5分）以下每个题目里给出的A，B，C，D四个结论中有且仅有一个是正确的．请你在括号填上你认为是正确的那个结论的英文字母代号．1．某工厂去年的生产总值比前年增长a%，则前年比去年少的百分数是( )A．a%．B．(1+a)%． C.1100aa+D.100aa+2．甲杯中盛有2m毫升红墨水，乙杯中盛有m毫升蓝墨水，从甲杯倒出a毫升到乙杯里, 0＜a＜m，搅匀后，又从乙杯倒出a毫升到甲杯里，则这时( )A．甲杯中混入的蓝墨水比乙杯中混入的红墨水少．B．甲杯中混入的蓝墨水比乙杯中混入的红墨水多．C．甲杯中混入的蓝墨水和乙杯中混入的红墨水相同．D．甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定．3.已知数x=100,则( )A．x是完全平方数．B．(x－50)是完全平方数．C．(x－25)是完全平方数．D．(x+50)是完全平方数．4．观察图1中的数轴：用字母a，b，c依次表示点A，B，C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5．x=9，y=－4是二元二次方程2x2+5xy+3y2=30的一组整数解，这个方程的不同的整数解共有( )A．2组．B．6组．C．12组．D．16组．二、填空题（每题1分，共5分）1．方程|1990x－1990|=1990的根是______．2．对于任意有理数x，y，定义一种运算*，规定x*y=ax+by－cxy，其中的a，b，c表示已知数，等式右边是通常的加、减、乘运算．又知道1*2=3，2*3=4，x*m=x（m≠0），则m的数值是______．3．新上任的宿舍管理员拿到20把钥匙去开20个房间的门，他知道每把钥匙只能开其中的一个门，但不知道每把钥匙是开哪一个门的钥匙，现在要打开所有关闭着的20个房间，他最多要试开______次．4．当m=______时，二元二次六项式6x2+mxy－4y2－x+17y－15可以分解为两个关于x，y的二元一次三项式的乘积．5．三个连续自然数的平方和（填“是”或“不是”或“可能是”）______某个自然数的平方．三、解答题（写出推理、运算的过程及最后结果．每题5分，共15分）1．两辆汽车从同一地点同时出发，沿同一方向同速直线行驶，每车最多只能带24桶汽油，途中不能用别的油，每桶油可使一辆车前进60公里，两车都必须返回出发地点，但是可以不同时返回，两车相互可借用对方的油．为了使其中一辆车尽可能地远离出发地点，另一辆车应当在离出发地点多少公里的地方返回？离出发地点最远的那辆车一共行驶了多少公里？2．如图2，纸上画了四个大小一样的圆，圆心分别是A，B，C，D，直线m通过A，B，直线n通过C，D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5(S－1)，直线m，n之间被圆盖住的面积是8，阴影部分的面积S1，S2，S3满足关系式S3=13S1=13S2,求S．3.求方程11156x y z++=的正整数解.答案与提示一、选择题1．D 2．C 3．C 4．C 5．D提示：1．设前年的生产总值是m，则去年的生产总值是前年比去年少这个产值差占去年的应选D．2．从甲杯倒出a毫升红墨水到乙杯中以后：再从乙杯倒出a毫升混合墨水到甲杯中以后：乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C．∴x－25=(10n+2+5)2可知应当选C．4．由所给出的数轴表示（如图3）：可以看出∴①＜②＜③，∴选C．5．方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x，y是整数，∴2x+3y，x+y也是整数．由下面的表可以知道共有16个二元一次方程组，每组的解都是整数，所以有16组整数组，应选D．二、填空题提示：1．原方程可以变形为|x－1|=1，即x-1=1或-1，∴x=2或0．2．由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0，∴bm=0．∵m≠0，∴b=0．∴等式改为x*y=ax-cxy．∵1*2=3，2*3=4，解得a=5，c=1．∴题设的等式即x*y=5x-xy．在这个等式中，令x=1，y=m，得5-m=1，∴m=4．3．∵打开所有关闭着的20个房间，∴最多要试开4．利用“十字相乘法”分解二次三项式的知识，可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解：3x -52x +3现在要考虑y，只须先改写作然后根据-4y2，17y这两项式，即可断定是：由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式，所以m=5．5．设三个连续自然数是a-1，a，a+1，则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2，显然，这个和被3除时必得余数2．另一方面，自然数被3除时，余数只能是0或1或2，于是它们可以表示成3b，3b+1，3b+2（b是自然数）中的一个，但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1，(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时，余数要么是0，要么是1，不能是2，所以三个连续自然数平方和不是某个自然数的平方．三、解答题1．设两辆汽车一为甲一为乙，并且甲用了x升汽油时即回返，留下返程需的x桶汽油，将多余的(24-2x)桶汽油给乙．让乙继续前行，这时，乙有(24-2x)+(24-x)=48-3x桶汽油，依题意，应当有48-3x≤24，∴x≥8．甲、乙分手后，乙继续前行的路程是这个结果中的代数式30(48-4x)表明，当x的值愈小时，代数式的值愈大，因为x≥8，所以当x=8时，得最大值30(48-4·8)=480（公里），因此，乙车行驶的路程一共是2(60·8+480)=1920（公里）．2．由题设可得即2S-5S3=8……②∴x，y，z都＞1，因此，当1＜x≤y≤z时，解(x，y，z)共(2，4，12)，(2，6，6)，(3，3，6)，(3，4，4)四组．由于x，y，z在方程中地位平等．所以可得如下表所列的15组解．希望杯第二届（1991年）初中一年级第1试试题一、选择题（每题1分，共15分）以下每个题目的A，B，C，D四个结论中，仅有一个是正确的，请在括号内填上正确的那个结论的英文字母代号．1．数1是( )A．最小整数．B．最小正数．C．最小自然数．D．最小有理数．2．若a＞b，则( )A.11a b; B．-a＜-b．C．|a|＞|b|．D．a2＞b2．3．a为有理数，则一定成立的关系式是( )A．7a＞a．B．7+a＞a．C．7+a＞7．D．|a|≥7．4．图中表示阴影部分面积的代数式是( )A．ad+bc．B．c(b-d)+d(a-c)．C．ad+c(b-d)．D．ab-cd．5．以下的运算的结果中，最大的一个数是( )A．(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686．3.1416×7.5944+3.1416×(-5.5944)的值是( ) A．6.1632． B．6.2832．C．6.5132．D．5.3692．7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A．16． B．15． C．14． D．13．8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x ．B.甲方程的两边都乘以43x; C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34. 10．如图: ，数轴上标出了有理数a ，b ，c 的位置,其中O 是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A ．27． B ．28． C ．29． D ．30． 12.当x=12,y=-2时,代数式42x y xy -的值是( )A ．-6．B ．-2．C ．2．D ．6．13．在-4，-1，-2.5，-0.01与-15这五个数中，最大的数与绝对值最大的那个数的乘积是( )A ．225．B ．0.15．C ．0.0001．D ．1．14.不等式124816x x x xx ++++>的解集是( ) A ．x ＜16． B ．x ＞16．C ．x ＜1． D.x>-116. 15．浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题（每题1分，共15分）1． 计算：(-1)+(-1)-(-1)×(-1)÷(-1)=______． 2． 计算：-32÷6×16=_______.3．计算：(63)36162-⨯=__________.4．求值：(-1991)-|3-|-31||=______．5．计算:111111 2612203042-----=_________.6．n为正整数，1990n-1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009．则n的最小值等于______．7. 计算：19191919199191919191⎛⎫⎛⎫---⎪ ⎪⎝⎭⎝⎭=_______.8. 计算：15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10．不超过(-1.7)2的最大整数是______．11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13．一个质数是两位数，它的个位数字与十位数字的差是7，则这个质数是______．14.一个数的相反数的负倒数是119,则这个数是_______.15．如图11，a，b，c，d，e，f均为有理数．图中各行，各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1．C 2．B 3．B 4．C 5．C 6．B 7．B 8．B 9．C 10．B 11．D 12．A 13．B 1 4．A 15．D提示：1．整数无最小数，排除A；正数无最小数，排除B；有理数无最小数，排除D．1是最小自然数．选C．有|2|＜|-3|，排除C；若2＞-3有22＜(-3)2，排除D；事实上，a＞b必有-a＜-b．选B．3．若a=0，7×0=0排除A；7+0=7排除C|0|＜7排除D，事实上因为7＞0，必有7+a＞0+a=a．选B．4．把图形补成一个大矩形，则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d)．选C．5．运算结果对负数来说绝对值越小其值越大。

数学希望杯试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. -1B. 0C. 1D. 2答案：C2. 如果a和b是两个非零的自然数，且a > b，则下列哪个不等式是正确的？A. a + b > bB. a - b > bC. a × b < bD. a ÷ b > 1答案：D3. 一个直角三角形的两个直角边长分别为3和4，那么斜边的长度是多少？A. 5B. 6C. 7D. 8答案：A4. 圆的周长是2πr，其中r是半径。

如果一个圆的周长是12.56厘米，那么这个圆的半径是多少？A. 2厘米B. 4厘米C. 6厘米D. 8厘米答案：A5. 以下哪个是偶数？A. 1B. 2C. 3D. 5答案：B6. 一个数的平方等于16，这个数是多少？A. 2B. 4C. ±4D. ±2答案：D7. 一个数的立方等于-8，这个数是多少？A. -2B. -4C. 2D. 4答案：A8. 一个数的绝对值是5，这个数可以是多少？A. 5B. -5C. 5或-5D. 0答案：C9. 如果x = 2y + 3，y = 3x - 4，那么x + y的值是多少？A. 5B. 6C. 7D. 8答案：C10. 一个数列的前三项是2, 4, 6，这是一个等差数列。

第10项是多少？A. 20B. 22C. 24D. 26答案：A二、填空题（每题2分，共20分）1. 一个数的平方根是4，那么这个数是________。

答案：162. 如果一个数的立方根是2，那么这个数是________。

答案：83. 一个数除以10，得到的结果再乘以10，这个数是________。

答案：不变4. 一个数的倒数是1/2，那么这个数是________。

答案：25. 一个数的相反数是-5，那么这个数是________。

答案：56. 如果一个数的1/3等于10，那么这个数是________。

第二十二届“希望杯”全国数学邀请赛初二 第一试一、选择题（每小题4分，共40分．）以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英文字母写在下面的表格内．1．将a 千克含盐10%的盐水配制成含盐15%的盐水，需加盐x 千克，则由此可列出方程（ ） A ．()()()110%115%a a x -=+- B ．()10%15%a a x ⋅=+⋅ C ．10%15%a x a ⋅+=⋅D ．()()110%115%a x -=-【解析】 选A ．加盐前后盐水中水的质量不变即可列式．2．一辆汽车从A 地均速驶往B 地，如果汽车行驶的速度增加%a ，则所用的时间减少%b ，则a b 、的关系是（ ） A ．1001%ab a =+B ．1001%b a =+C ．1a b a=+ D ．100100ab a=+【解析】 D ．由,A B 两地距离不变可以列式：()()1%1%1a b +-=，解之得：100100ab a=+．3．当1x ≥时，不等式12x m x +--恒成立，那么实数m 的最大值是（ ）A ．1B ．2C ．3D ．4【解析】 C ．原不等式可化为12m x x +-≤，而由绝对值的几何意义知123x x ++-≥，于是1233x x ++-+≥，当且仅当1x =时取等号．于是3m ≥，即最大值为3．4．在平面直角坐标系中，横、纵坐标都是整数的点称为整点，已知k 为整数，若函数21y x =-与y kx k =+的图象的交点是整点，则k 的值有（ ）个 A ．2B ．3C ．4D ．5【解析】 C ．联立函数方程可知交点坐标为13,22k k k k +⎛⎫⎪--⎝⎭，仅需横坐标为整数即可．而13122k k k+=-+--，则21,3k -=±±，于是k 的值有4个．5．（英语意译）已知整数x 满足不等式2216x -≤≤，则x 的值是（ ） A ．8B ．5C ．2D ．0【解析】 C ．由21x -为奇数，有213,5x -=±±，仅有C 选项符合题意．此题x 的值有4个解．6．若三角形的三条边的长分别为a b c 、、，且22230a b a c b c b -+-=，则这个三角形一定是（ ） A ．等腰三角形 B ．直角三角形 D ．等边三角形 D ．等腰直角三角形 【解析】 A ．()()()()()2223220a b a c b c b a b b c a b a b b c -+-=--=-+-=，于是a b =或者b c =．于是为等腰三角形．7．如图1，点C 在线段BG 上，四边形ABCD 是一个正方形，AG 与BD 、CD 分别相交于点E 和F ，如果5AE =，3EF =，则FG =（ ） A ．163B ．83C ．4D ．5图1ABCDFE G53【解析】 A ．由ABE DEF △∽△，知53AB DF =．不妨设5,3AB x DF x ==，于是2FC x =． 又由FCG ABG △∽△，知216853FG FG FC x FG AG FG AB x ===⇒=+．8．1621-能分解成n 个质因数的乘积，n 的值是（）A ．6B ．5C ．4D ．3【解析】 C ．()()16882121213517257-=-+=⋅⋅⋅．于是4n =．9．若关于x y 、的方程组1020x ay bx y a ++=⎧⎨-+=⎩，没有实数解，则（）A ．2ab =-B ．2ab =-且1a ≠C ．2ab ≠-D ．2ab =-且2a ≠【解析】 A ．容易知道112a b a=≠-．于是2ab =-且22a ≠-，而后者显然成立．于是选A ．10．如图2，45AOB ∠=︒，OP 平分AOB ∠，PC OB ⊥于点C ．若2PC =，则OC 的长是（ ）A ．7B ．6 C．2+ D．22图2OCP BA【解析】 C ．延长CP 交OA 于M，于是有PC OC PM PM AO ==⇒=于是2OC PC PM =+=二、A 组填空题（每小题4分，共40分） 11．【解析】2222+==+12．若关于x y 、的方程组321232x y k x y +=-⎧⎨-=⎩的解使472x y +>，则k 的取值范围是___________．【解析】3k >．由()()4723223242x y x y x y k +=⋅+--=->，知3k >．13．如图3，平行于BC 的线段MN 把等边ABC △分成一个三角形和一个四边形，已知AMN △和四边形MBCN 的周长相等，则BC 与MN 的长度之比是_____________．ABCM N 图3【解析】 4：3．不妨设1,MN BC x ==，于是A M N △的周长为3，四边形M B C N 的周长为()211x x -++．于是有()3221x x =-++，解得43x =．14．小华测得自家冰箱的压缩机运转很有规律，每运转5分钟，停机15分钟，再运转5分钟，再停机15分钟，…，又知8月份这台冰箱的耗电量是24．18度（1度=1千瓦时），则这台冰箱的压缩机运转时的功率是__________________瓦．【解析】 130．已知冰箱的运转时间占工作时间的515154=+，于是8月份的运转时间为124311864⋅⋅=小时．于是功率为24.181000130186⋅=．15．已知自然数a b c 、、满足222424412a b c a b c +++<++和220a a -->，则代数式111a b c++的值是___________________．【解析】 1．由()()()2222262a b c -+-+-<知2,2,6a b c ---中之多有一个绝对值为1，其余绝对值为0．而()()210a a -+>，知2a >，于是21a -=，即3a =．于是2b =，6c =．则代数式的值为1111a b c++=．16．已知A B 、是反比例函数2y x=的图象上的两点，A B 、的横坐标分别是3，5．设O 为原点，则AOB △的面积是________________．【解析】 1615．易知223,,5,35A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭．分别过点,A B 做x 轴的垂线，垂足为,M N ．由2216352215AOB ABMN S S +==⋅=△．17．设完全平方数A 是11个连续整数的平方和，则A 的最小值是_________________． 【解析】 121．()()()()()22222543...45110A =-+-+-+++=．18．将100个连续的偶数从小到大排成一行，其中第38个数与第63个数的和为218，则首尾两个数的和是__________________． 【解析】 218．首尾两数的和与第38个数与第63个数的和相同．于是均为218．19．A 、B 两地相距15km ，甲、乙两人同时从A 地出发去B 地．甲先乘汽车到达A B 、之间的C 地，然后下车步行，乙全程骑自然车，结果两人同时到达．已知甲步行的速度是乙骑自行车速度的一半，乙骑自行车的速度是甲乘汽车速度的一半，那么，C 地与A 地相距_______________km ．【解析】 10．不妨设,C A 两地之间的距离为x ，,C B 之间的距离为15x -，乙全程自行车的速度为v ，于是利用两者时间相等可列式：151522x x v v v -+=，解之得10x =．20．已知b c a c a bk a b c+++===，则直线y kx k =+必经过点______________________． 【解析】 (10)-，．()1y k x =+，于是当1x =-时，0y =．于是答案为()1,0-．在条件下，当0a b c ++=时，直线表示1y x =--，否则直线表示22y x =+．三、B 组填空题（每小题8分，共40分）21．等腰三角形的两个内角之比是2：5，则这个三角形的最大内角的度数是____________或________．【解析】 75︒；100︒．当三角形三内角之比为2:2:5时，最大内角为51801009⋅= ；当内角比为2:5:5时，最大内角为51807512⋅= ．22．已知10个数12310x x x x ，，，，中，110x =，对于整数1n >，有1n n nx x -=，则12x x =____________，2310x x x = _______________．【解析】 2；384．由1n n x x n -=知：122x x =；344x x =；566x x =；．．．；91010x x =．于是()234101 (24681038410)x x x x =⋅⋅⋅⋅⋅=．23．从甲、乙、两三名男生和A B 、两名女生中选出一名男生和一名女生，则所有可能出现的结果有_____________种；恰好选中男生甲和女生A 的概率是____________． 【解析】 6；16．男生一共有3种选择，女生一共有2种选择，于是所有可能结果数为326⋅=．对于任何一种特定组合都是16的概率被选中．24．若关于x 的方程b b x a x a +=+的解是12b x a x a ==，，那么方程2211x a x a -=---的解是1x =___________，2x =__________________．【解析】 a ；31a a --．原方程可写为221111x a x a ---+=-+--，于是12211,11x a x a --=--=-．化简即可．25．若两个自然数的差是一个数码相同的两位数，它们的积是一个数码相同的三位数，那么这两个自然数是__________和____________．【解析】37；15．由于他们乘积为111的倍数，而111有质因数37，于是这两数至少有一数为37或者其倍数74．于是容易判断出两数只能是37,15．。

数学希望杯初二试题及答案一、选择题（每题2分，共20分）1. 下列哪个数是正整数？A. -5B. 0C. 2D. -22. 如果\( a \)和\( b \)是互质数，那么\( a \times b \)的最小公倍数是：A. \( a \)B. \( b \)C. \( a + b \)D. \( a \times b \)3. 一个长方形的长是宽的两倍，如果宽是\( x \)米，那么长方形的面积是：A. \( x^2 \)B. \( 2x \)C. \( 2x^2 \)D. \( 4x^2 \)4. 一个数的平方根是它自己，这个数是：A. 0B. 1C. -1D. 25. 下列哪个是二次根式？A. \( \sqrt{16} \)B. \( \sqrt{2} \)C. \( 3\sqrt{2} \)D. \( \sqrt{-9} \)6. 一个数的相反数是它自己，这个数是：A. 0B. 1C. -1D. 27. 一个圆的半径是\( r \)，那么它的面积是：A. \( \pi r \)B. \( \pi r^2 \)C. \( 2\pi r \)D. \( \pi r^3 \)8. 一个数的绝对值是它自己，这个数是：A. 0B. 正数C. 负数D. 任意实数9. 一个等腰三角形，两边相等，如果底边是\( a \)，那么它的周长是：A. \( 2a \)B. \( 3a \)C. \( 4a \)D. \( 无法确定 \)10. 如果\( x \)和\( y \)是实数，\( x = y \)，那么下列哪个等式是正确的？A. \( x + 1 = y + 1 \)B. \( x^2 = y^2 \)C. \( x - y = 0 \)D. 所有选项都是正确的二、填空题（每题2分，共20分）11. 一个数的平方根是\( \sqrt{4} \)，那么这个数是______。

12. 如果\( a \)和\( b \)是相反数，那么\( a + b = ______。