AB类二进制数

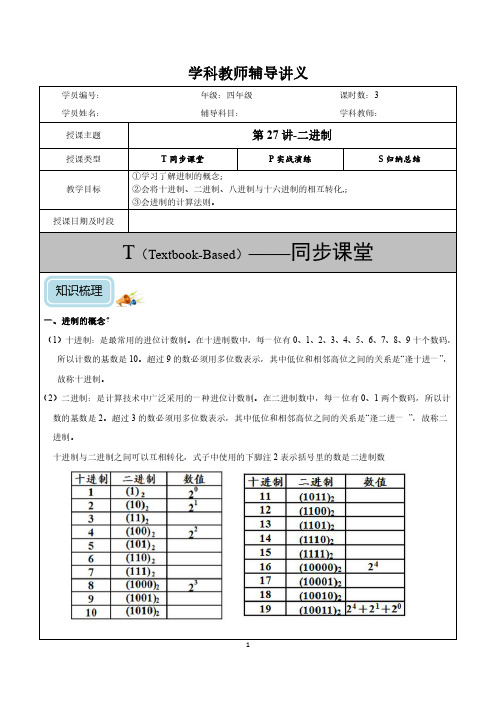
学科教师辅导讲义知识梳理（3）八进制：在八进制数中，每一位有0、1、2、3、4、5、6、7八个数码，所以计数的基数是8。

超过7的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢八进一”，故称八进制。

（4）十六进制：在十六进制数中，每一位有0、1、2、3、4、5、6、7、8、9、A(表示10)、B(表示11)、C(表示12)、D(表示13)、E(表示14)、F(表示15)十六个数码，所以计数的基数是16。

超过15的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十六进一”，故称十六进制。

二、十进制与n 进制的转化1、将十进制数转换为等值的n 进制数(n≥2)时，整数部分采用“除n 倒取余数法”。

例如：整数()10107转换成二进制采用“除2倒取余数法”，得()()1021071101011=2、将n 进制数(n≥2)转换为等值的十进制数时，只要将n 进制数展开，然后将所有各项的数值按十进制数相加，就可以得到等值的十进制数了。

例如：()()()21810101231828183=⨯+⨯+=，式子中使用的下脚注8表示括号里的数是八进制数。

()()()21161010011160161512831B F =⨯+⨯+⨯=，式子中使用的下脚注16表示括号里的数是十六进制数。

3、二进制数的计算法则：（1）加法法则：0＋0=00＋1=11＋0=11＋1=10（2）乘法法则：0×0=00×1=01×0=01×1=1典例分析例6、把十进制数251改成16进制数。

例7、把二进制数()2110改写成十进制数。

例8、把二进制数()2110改写成八进制数例9、计算()()22101111+例10、计算()()22110111⨯你能用十进制计算来检验上面的计算吗？例11、计算()()221111101÷实战演练3、计算下列式子（1）()()2210110+（2）()()22110101111-（3）()()22111011+4、计算下列式子（1）()()2211010⨯（2）()()2211100100÷（3）()()22101111⨯（4）()()221001011÷5、已知：22241x y z++=，不同的字母代表不同的数字，则三位数xyz =__________.课后反击1、分别把下列各数转换成十进制数。

一：简述：进位计数制：是人们利用符号来计数的方法。

一种进位计数制包含一组数码符号和两个基本因素。

（1）数码：用不同的数字符号来表示一种数制的数值，这些数字符号称为”数码”。

（2）基：数制所使用的数码个数称为”基”。

（3）权：某数制每一位所具有的值称为”权”。

二：进制转换的理论1、二进制数、十六进制数转换为十进制数：用按权展开法把一个任意R进制数a n a n-1 ...a1a0 . a-1a-2...a-m转换成十进制数，其十进制数值为每一位数字与其位权之积的和。

a n×R n+ a n-1×R n-1+…+ a1×R 1+ a0×R0+ a-1×R-1+ a-2×R-2 + …+ a-m×R-m2、十进制转化成R进制十进制数轮换成R进制数要分两个部分：整数部分：除R取余数，直到商为0，得到的余数即为二进数各位的数码，余数从右到左排列(反序排列)。

小数部分：乘R取整数，得到的整数即为二进数各位的数码，整数从左到右排列(顺序排列)。

3、十六进制转化成二进制每一位十六进制数对应二进制的四位，逐位展开。

4、二进制转化成十六进制将二进制数从小数点开始分别向左（对二进制整数）或向右（对二进制小数）每四位组成一组，不足四位补零。

三、具体实现1、二进制转换成十进制任何一个二进制数的值都用它的按位权展开式表示。

例如：将二进制数(10101.11)2转换成十进制数。

（10101.11）2＝1*24＋0*23＋1*22＋0*21＋1*20＋1*2-1＋1*2-2＝24＋22＋20＋2-1+2-2＝(21.75)102、十进制整理转换成二进制将十进制整数转换成二进制整数采用“除2取倒余法”。

即将十进制整数除以2，得到一个商和一个余数；再将商除以2，又得到一个商和一个余数；以此类推，直到商等于零为止。

每次得到的余数的倒排列，就是对应二进制数的各位数。

《数字电子技术（第二版）》课后习题参考答案课题一认识数字电路任务一认识数制与数制转换一、填空题1．1 232．1 273．1 2154．1 2315．B O D H二、计算题1．2．54，85，4273．0101，1100，1 1000，11 01114．17O，37O，66 O5．110B，010 111B，001 101 110B6．0FH，36H，0AE63H7．0001 0110B，0010 1010B，1111 1100 0000B任务二学习二进制数算术运算一、计算题（给出的二进制均是无符号数）1．（1）1 0000 （2）1 0000 10012．（1）10 1010 （2）1010 11113．（1）1 0100 （2）110 00004．（1）101 （2）11二、写出下列带符号位二进制数（原码）所表示的十进制数（1）+110 （2）-15 （3）-42 （4）+127 （5）+111（6）-63 （7）+0 （8）+32 767 （9）-32 768三、问答题1．（1）答：左移，移动3位，应作乘以8运算。

（2）答：左移，移动4位，应作乘以16运算。

（3）答：右移，移动7位，应作除以128运算。

（4）答：右移，移动3位，应作除以8运算。

2．答：4位二进制无符号数的最大值是15。

3．答：8位二进制无符号数、有符号数的最大值分别是255和+127。

4．答：16位二进制有符号数的最大值是+32 767。

任务三学习二进制代码一、填空题1．二进制数2．43．8，4，2，1二、判断题1．×2．× 3．√ 4．× 5．× 6．×三、计算题1．36，55，892．［0011 0010］8421，［0101 0010 0111］8421，［0001 0011 0110 1001］8421任务四认识基本逻辑关系并测试逻辑门一、填空题1．与或非2．13．04．1 05．Y=AB6．Y=A+B7．Y=A8．Y=AB9．Y=A+B10．Y=A B=AB+AB二、选择题1．D 2．A 3．B，C 4．A，D三、判断题1．× 2．× 3．× 4．√四、问答题1．答：Y1=ABCD2．答：Y2=A+B+C+D五绘图题1．2．3．4．任务五测试TTL集成门电路1．答：TTL集成门电路电源电压范围为4.75～5.25V之间，额定电压为5V。

6在二进制算法二进制是计算机科学中最基本的计数系统之一，它只由0和1两个数字组成。

在二进制中，每个数字位的权值是2的幂次方。

而在二进制算法中，数字6可以被表示为110。

二进制算法是一种在计算机科学中广泛应用的数学算法。

它在计算机系统中起着至关重要的作用，不仅可以用于数字的表示和存储，还可以进行逻辑运算和数据处理。

我们来看看如何将数字6表示为二进制数。

在二进制系统中，每一位的权值是2的幂次方。

从右向左，第一位的权值为2^0，第二位的权值为2^1，第三位的权值为2^2，以此类推。

因此，数字6可以表示为110。

在二进制算法中，可以使用各种运算符来对二进制数进行运算。

常见的二进制运算符包括加法、减法、乘法和除法。

这些运算符在二进制算法中的应用与十进制运算非常类似，只是基数不同。

例如，我们可以使用二进制加法运算符来计算两个二进制数的和。

对于数字6（110）和数字3（011）来说，它们的和为9（1001）。

这个结果可以通过将相应的位相加并考虑进位得出。

除了基本的运算符，二进制算法还涉及到位运算。

位运算是直接操作二进制数的运算，包括与、或、非和异或等运算。

这些运算常用于逻辑运算、数据压缩和加密等领域。

在二进制算法中，还有一种重要的操作是移位运算。

移位运算可以将二进制数的位向左或向右移动一定的位数。

左移操作会将所有位向左移动，并在右侧补0，右移操作则将所有位向右移动，并在左侧补0或者保留原有最高位的值。

除了基本的运算和操作，二进制算法还涉及到进制转换。

进制转换可以将一个数从一种进制表示转换成另一种进制表示。

在二进制算法中，常见的进制转换包括二进制转十进制、十进制转二进制、二进制转八进制和二进制转十六进制等。

二进制算法在计算机科学中的应用非常广泛。

它不仅可以用于数字的表示和存储，还可以进行逻辑运算、数据处理和编码等操作。

二进制算法的运算速度快、效率高，因此成为了计算机系统中最基础、最重要的算法之一。

总结一下，二进制算法是一种在计算机科学中广泛应用的数学算法，它可以用于数字的表示、运算和转换。

一般来说，对于任意大于1的整数n，存在n进制，其特点是基数为n，逢n进一。

其中最常用的是二进制、八进制和十六进制。

任意进制的数字对应的十进制值为：Kn×Bn + Kn-1×Bn-1 + …… + K1×B1 + K0×B0 + K-1×B-1 + K-2×B-2 …… + K-m×B-m上式中，B称为数字系统的基数，Bn至B0称为数字Kn至K0的权值。

1.基本知识十进制基数为10，逢10进1。

在十进制中，一共使用10个不同的数字符号，这些符号处于不同位置时，其权值各不相同。

二进制基数为2，逢2进1。

在二进制中，使用0和1两种符号。

八进制基数为8，逢8进1。

八进制使用8种不同的符号，它们与二进制的转换关系为：0：000 1：001 2：010 3：011 4：100 5：101 6：110 7：111十六进制基数为16，逢16进1。

十六进制使用16种不同的符号，它们与二进制的转换关系为：0：0000 1：0001 2：0010 3：0011 4：0100 5：0101 6：0110 7：01118：1000 9：1001 A：1010 B：1011 C：1100 D：1101 E：1110 F：1111二进制数的运算算术运算：加法0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10（向高位进1）算术运算：减法0 ? 0 = 0 0 ? 1 = 1（向高位借1）1 ? 0 = 1 1 - 1 = 0逻辑运算：或（∨）0 ∨0 = 0 0 ∨1 = 1 1 ∨0 = 1 1 ∨1 = 1逻辑运算：与（∧）0 ∧0 = 0 0 ∧1 = 0 1 ∧0 = 0 1 ∧1 = 1逻辑运算：取反0取反为1 1取反为0注意：算术运算会发生进位、借位，逻辑运算则按位独立进行，不发生位与位之间的关系，其中，0表示逻辑假，1表示逻辑真。

.一、二进制转化成其他进制1. 二进制（BINARY）——>八进制（OCTAL）例子1：将二进制数（10010）2转化成八进制数。

（10010）2=（010 010）2=（2 2）8=（22）8例子2：将二进制数（0.1010）2转化为八进制数。

（0.10101）2=（0. 101 010）2=（0. 5 2）8=（0.52）8诀窍：因为每三位二进制数对应一位八进制数，所以，以小数点为界，整数位则将二进制数从右向左每3位一隔开，不足3位的在左边用0填补即可；小数位则将二进制数从左向右每3位一隔开，不足3位的在右边用0填补即可。

2. 二进制（BINARY）——>十进制（DECIMAL）例子1：将二进制数（10010）2转化成十进制数。

（10010）2=（1x24+0x23+0x22+1x21+0x20）10=（16+0+0+2+0）10=(18) 10例子2：将二进制数（0.10101）2转化为十进制数。

（0.10101）2=（0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5）10=（0+0.5+0.25+0.125+0.0625+0.03125）10=（0.96875）10诀窍：以小数点为界，整数位从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0或1）乘以2的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3……..n，然后将第n位的数（0或1）乘以2的-n 次方，然后相加即可得到小数位的十进制数（按权相加法）。

..3. 二进制（BINARY）——>十六进制（HEX）例子1：将二进制数（10010）2转化成十六进制数。

（10010）2=（0001 0010）2=（1 2）16=(12) 16例子2：将二进制数（0.1010）2转化为十六进制数。

（0.10101）2=（0. 1010 1000）2=（0. A 8）16=（0.A8）16诀窍：因为每四位二进制数对应一位十六进制数，所以，以小数点为界，整数位则将二进制数从右向左每4位一隔开，不足4位的在左边用0填补即可；小数位则将二进制数从左向右每4位一隔开，不足4位的在右边用0填补即可。

进制中的位权概念进制中的位权概念在计算机科学与数学中，进制是一种表示数值的方法。

常用的进制有10进制、2进制、8进制和16进制等。

在进制法中，一次进一位，每个位置上的数字代表该位的权值。

而位权则是表示数字在该位置上所代表的权重。

一、十进制中的位权我们先以十进制为例来解释位权的概念。

在十进制中，每个位置上的数字所占用的位数不同，其位权从右至左依次为1、10、100、1000……以10为底数的幂次方。

例如，数字2156中，5的位权是1；6的位权是10；1的位权是100；2的位权是1000。

因此，将其表示为多项式形式为5×1+6×10+1×100+2×1000。

二、二进制中的位权在二进制中，每一个数字只能是0或1。

举例来说，在二进制数110中，第一个位置上的数字1的权值为2的0次方=1；第二个位置上的数字是1，并且它的权值是2的1次方=2；第三个位置上的数字是0，它的权值是2的2次方=4。

整个二进制数可以表示为1×1+1×2+0×4=3。

三、八进制中的位权在八进制中，每个位置上的数字的权值为8的幂次方。

例如，数字1268中，8的0次方为1，8的1次方为8，8的2次方为64。

因此，可以得出结果2×1+6×8+1×64=50。

四、十六进制中的位权在十六进制中，每个位置上的数字的权值为16的幂次方。

数字可以是0~9、A~F中的一个，其中A表示10，B表示11，C表示12，以此类推。

例如，数字9B1B中，1的位权是16的0次方=1；B的位权是16的1次方=16；9的位权是16的2次方=256。

因此，它的多项式形式为1×1+11×16+9×256=2437。

总结：位权是进制数表达中的重要概念之一，通过它我们可以得出不同进制数的实际值。

在进行进制转换时，理解位权概念能够更好地帮助我们进行数学计算。

判断二进制数能否被3整除的方法业余数学爱好者郑敏一个数是否可以被3整除？我们习惯十进制数的简单判断方法，但一般不追究其原因。

其实原因很简单，这是由于10^k≡1(mod3)。

这样我们可将10、100、1000……等都看做1，最后将各个数位的数字加起来，若能被3整除，原来的数即可被3整除。

四、七、十三、十六……进制数与十进制数一样，都可以用这个方法。

三、六、九、十二、十六……进制数很明显，可以直接看出。

其他进制数略微麻烦一点，其中二进制数较简单，仅以此为例分析如下：根据：10^(2k+1)+1≡0(mod11)10^2(k+i)+10^2k+1≡0(mod11) (k∈N, i∈N) 我们得到二类定可被11(3)整除字符串：①11、1001、100001、10000001……（3、9、33、129……）②10101，1010001，101000001……（21、81、321……273）任一二进制数n的1字符要么在右数奇数位，要么在偶数位。

假如奇数位有j个1字符，偶数位有k个1字符。

令每个奇数位上的1字符选择一个（且只能一个）偶数位上的1字符，当j=k时，将构成j个①类字符串；假如j≠k，剩余∣j-k∣个1字符必定同在奇数（或偶数）位。

若n≡0(mod11),则∣j-k∣≡0(mod11)，也就是说这些剩余的1字符可以划分为∣j-k∣/3个②类字符串。

由此可见，利用以上两类字符串判断，不会有遗漏，也不会有重复。

例如，100011100101111001101000010001可以由以下字符串嵌套、交叉、组合而成：101111000011010011100010011100100011000000000010011110000000000100100000000000000001100000000000000000010000001000000000000000000000010000100000000000000000000000000100010001在一个二进制数中，这些字符串可能有很多划分方法，且往往是相互交叉、嵌套在一起的，因此运用起来不够方便。