22.8平面向量的加法

《平面向量的加法》教案正式版一、教学目标：1. 让学生理解平面向量加法的概念和意义。

2. 让学生掌握平面向量加法的运算方法。

3. 让学生能够运用平面向量加法解决实际问题。

二、教学重点：1. 平面向量加法的概念和意义。

2. 平面向量加法的运算方法。

三、教学难点：1. 平面向量加法的几何意义。

2. 平面向量加法的运算方法。

四、教学准备：1. 教师准备PPT，包括向量加法的定义、性质、运算方法等内容。

2. 教师准备一些实际问题，用于引导学生运用向量加法解决问题。

五、教学过程：1. 引入新课：通过PPT展示一些实际问题，引导学生思考如何用向量加法解决问题。

2. 讲解向量加法的定义和性质：教师引导学生观察PPT上的图示，解释向量加法的概念和几何意义。

3. 讲解向量加法的运算方法：教师引导学生学习PPT上的公式和方法，让学生通过例题掌握向量加法的运算方法。

4. 练习：学生独立完成PPT上的练习题，教师巡回指导。

6. 布置作业：教师布置一些有关向量加法的练习题，让学生课后巩固。

六、教学反思：教师在课后对自己的教学进行反思，看学生是否掌握了向量加法的概念、性质和运算方法，以及是否能够运用向量加法解决实际问题。

如有需要，教师可调整教学方法，以提高教学效果。

七、教学评价：通过课堂表现、练习题和课后作业，评价学生对向量加法的掌握程度。

鼓励学生积极参与课堂讨论，提高学生的学习兴趣和自信心。

八、教学拓展：1. 引导学生学习其他向量运算，如减法、数乘等。

2. 引导学生将向量加法应用于实际问题，如物理学中的运动合成等。

九、教学时间：本节课预计用时45分钟。

十、教学资源：1. PPT：包括向量加法的定义、性质、运算方法等内容。

2. 实际问题：用于引导学生运用向量加法解决问题。

3. 练习题：用于巩固所学知识。

4. 课后作业：用于进一步巩固向量加法知识。

六、教学策略：1. 采用问题驱动的教学方法，引导学生从实际问题中抽象出向量加法的概念。

平面向量的运算法则平面向量是解决平面几何问题的重要工具，通过向量的运算可以简化平面几何问题的处理过程。

本文将介绍平面向量的基本概念和运算法则，以及其在几何问题中的应用。

一、平面向量的表示平面向量用有序数对表示，常用形式为A(x₁, y₁)和B(x₂, y₂)，其中A和B分别表示向量的起点和终点，(x₁, y₁)和(x₂, y₂)表示向量的坐标。

二、平面向量的加法平面向量的加法指的是将两个向量按照特定的法则相加，得到一个新的向量。

设有向量A(x₁, y₁)和B(x₂, y₂)，则向量A与向量B的和C可以表示为C(x₁ + x₂, y₁ + y₂)。

三、平面向量的减法平面向量的减法指的是计算出一个新的向量，使得用该向量加上被减向量等于另一个向量。

设有向量A(x₁, y₁)和B(x₂, y₂)，则向量A 与向量B的差D可以表示为D(x₁ - x₂, y₁ - y₂)。

四、平面向量的数量乘法平面向量的数量乘法指的是将一个向量乘以一个实数，得到一个新的向量。

设有向量A(x, y)和实数k，kA可以表示为kA(kx, ky)。

五、平面向量的点乘平面向量的点乘指的是两个向量的对应坐标相乘后相加的运算。

设有向量A(x₁, y₁)和向量B(x₂, y₂)，则向量A与向量B的点乘可以表示为A·B = x₁x₂ + y₁y₂。

六、平面向量的叉乘平面向量的叉乘指的是两个向量按照一定的法则相乘，得到一个新的向量。

设有向量A(x₁, y₁)和向量B(x₂, y₂)，则向量A与向量B的叉乘可以表示为A×B = x₁y₂ - x₂y₁。

七、平面向量的模长平面向量的模长指的是一个向量的长度，可以通过勾股定理求得。

设有向量A(x, y)，则向量A的模长可以表示为|A| = √(x² + y²)。

八、平面向量的单位向量平面向量的单位向量指的是模长为1的向量，可以通过将向量除以其模长得到。

设有向量A(x, y)，则向量A的单位向量可以表示为Â = (x/|A|, y/|A|)。

平面向量及运算法则平面向量是指可以完整描述平面上的有方向和大小的物理量。

在数学中，平面向量通常用箭头上的字母表示，例如a或b，有时也用粗体字母表示，例如a或a。

平面向量具有位移、速度、加速度、力等物理量的特性。

平面向量的运算包括加法、减法、数量乘法、点积和叉积等。

1.平面向量的加法：设有两个平面向量a=aa+aa和a=aa+aa，它们的加法结果为a+a=(a+a)a+(a+a)a。

即，将两个向量的分量分别相加得到新向量的分量。

2.平面向量的减法：设有两个平面向量a=aa+aa和a=aa+aa，它们的减法结果为a-a=(a-a)a+(a-a)a。

即，将两个向量的分量分别相减得到新向量的分量。

3.平面向量的数量乘法：设有一个平面向量a=aa+aa，它的数量乘法结果为aa=aaa+aaa。

即，将向量的每个分量都乘以一个标量k得到新向量的分量。

4.平面向量的点积（内积）：设有两个平面向量a=aa+aa和a=aa+aa，它们的点积结果为a·a=aa+aa。

即，将两个向量的对应分量相乘并相加得到点积的结果。

点积的结果是一个标量，表示两个向量的夹角余弦乘以两个向量的长度之积。

5.平面向量的叉积（外积）：设有两个平面向量a=aa+aa和a=aa+aa，它们的叉积结果为a×a=(0,0,aaa)，其中k为垂直于平面向量的单位向量。

即，叉积的结果是一个新的向量，其方向垂直于两个向量所在的平面，大小为两个向量长度的乘积与它们夹角的正弦值之积。

平面向量的运算法则有很多，下面列举几个常用的法则。

1.交换律：平面向量的加法满足交换律，即a+a=a+a。

2.结合律：平面向量的加法满足结合律，即(a+a)+a=a+(a+a)。

3.分配律：数量乘法和加法之间满足分配律，即a(a+a)=aa+aa。

4.点积的分配律：点积的分配律表示为(a+a)·a=a·a+a·a，其中a、a和a 分别是平面向量。

22.8 平面向量的加法一、知识归纳：1．向量的加法求两个向量的和向量的运算叫做向量的加法．2．零向量长度为零的向量叫做零向量，记作0r ．规定0r 的方向可以是任意的（或者说不确定）；00=r ．因此，两个相反向量的和向量是零向量，即：()0a a +-=r r r ．对于任意向量，都有0a a +=r r r ，0a a +=r r r ．3．向量的加法满足交换律：a b b a +=+r r r r ．4．向量的加法满足结合律：()()a b c a b c ++=++r r r r r u u r ．5．向量加法的三角形法则求不平行的两个向量的和向量时，只要把第二个向量与第一个向量首尾相接，那么以第一个向量的起点为起点、第二个向量的终点为终点的向量就是和向量．6．向量加法的多边形法则几个向量相加，可把这几个向量首尾顺次相接，那么以第一个向量的起点为起点、最后一个向量的终点为终点的向量，就是这几个向量的和向量．二、练习A1、A 、B 、C 、D 、E 为平面上任意不同的五点，→AB +→BC +→CD +→DE +→EA = （ ）A.→ADB.0C.→0D.不能确定2、下列等式一定正确的是 （ ）A.→AB +→BC =→AD +→BC +→DBB.→AB +→CA +→BC =0C.→AB +→DC +→EA +→ED +→CB =2→ECD.→AB +→BC +→CD +→DE +→EF =→FA3. →CB +→AC =________.4.→BC +→AB +→CD =_________.5. →AB +→CA +→BC =__________.6.→DE +→BC +→CD +→AB =__________.7.→BC +→AB +→DA +→CD =___________.8.如图，已知向量a r 与b r ，求作a b +r r ．a r9.已知：向量→a 、→b 、→c ，求作：（1）→a +→b +→c（2）（→a +→c ）+→b（3）（→b +→c ）+→a三、练习B1.已知：M 、N 是梯形ABCD 的中位线.，求证：→MN =21(→AD +→BC ).NM DC B AN M D C B A2.已知：M 、N 分别是AD 、BC 的中点，求证：→MN =21(→AD +→BC ).。

平面向量的运算在数学中，平面向量是由大小和方向确定的量，常用于表示物体在平面上的位移或力的作用方向。

平面向量的运算是指对平面向量进行加法、减法、数乘和点乘等操作。

本文将介绍平面向量的基本概念和运算规则。

一、平面向量的表示方法平面向量通常用有向线段表示，由两个点确定，例如AB表示从点A到点B的平面向量。

可以用字母加箭头（如→）表示平面向量，如：AB →其中A为向量的起点，B为终点。

二、平面向量的加法对于两个平面向量AB → 和CD →，它们的和可以通过平行四边形法则得到。

具体步骤如下：1. 将向量CD → 的起点与向量AB → 的终点相重合，得到新的向量AC →；2. 连接向量AB → 的起点和向量CD → 的终点，得到新的向量AD →；3. 新的向量AD → 就是原始向量AB → 和CD → 的和，即AD → = AB → + CD →。

三、平面向量的减法向量的减法可以通过向量加法的逆运算得到。

对于向量AB → 和CD →，它们的差可以表示为AB → - CD →，具体步骤如下：1. 取向量CD → 的终点B为新向量的起点，向量AB → 的起点A为新向量的终点，得到新的向量BA →；2. 新的向量BA → 就是原始向量AB → 和CD → 的差，即BA → = AB → - CD →。

四、平面向量的数乘平面向量的数乘是指将向量的长度乘以一个实数，从而改变向量的大小。

设有向量AB → 和实数k，它们的数乘表示为kAB →，其具体步骤如下：1. 将向量AB → 的长度乘以实数k，得到新向量AC →；2. 新的向量AC → 的方向与原来向量AB → 相同，而长度为原来的k倍，即AC → = kAB →。

五、平面向量的点乘平面向量的点乘（内积）运算可以得到两个向量的乘积，结果为一个实数。

设有向量AB → 和CD →，它们的点乘表示为AB → · CD →，具体计算方法如下：1. 将向量AB → 和CD → 的长度相乘，得到实数AC；2. 计算向量AB → 与向量CD → 之间夹角的余弦值，得到实数cosθ；3. 点乘的结果为AB → · CD → = ACcosθ。

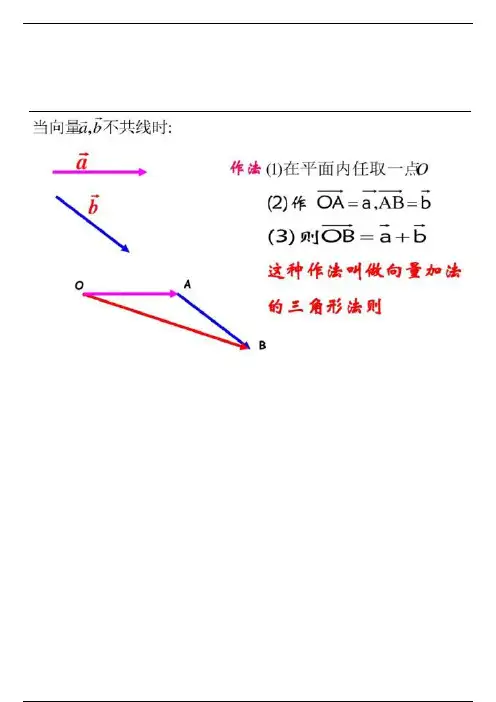
向量的加法口诀： 首尾相连，首连尾，方向指向末向量。

以第一个向量的起点为起点，以第二个向量的终点为终点的向量是两向量的和向量。

二、向量的减法两向量做减法运算，图像如下图所示：向量的减法口诀： 首首相连，尾连尾，方向指向被减向量。

以第一个向量的终点为起点，以第二个向量的终点为终点的向量是两向量的差向量。

向量的学习是高一数学必修四第二章的内容，要求同学们会向量的基本运算，其中就包括加法、减法、数乘。

要求大家能根据运算法则解决基本的向量运算，学会运用图像解决向量加减法，向量的数乘等问题。

向量的相关题目难度也不是很大，只要大家认真学习，认真做好笔记，认真做做题目，总结做题规律，那么当我们遇到类似题目时就会似曾相识，做起来也很顺手，再细心点的话，得满分也没有问题。

学习方法很多，重要的事找到适合自己的方法，当然适合自己方法就是最好的方法。

附一；三角形定则解决向量加减的方法将各个向量依次首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。

注:两个向量相减，则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。

平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣＞1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上伸长为原来的λ∣倍；当∣λ∣＜1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律：(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.数乘向量的消去律：① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义：已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义：两个向量的数量积（内积、点积）是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉；若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示：a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a（交换律）；(λa)·b=λ(a·b)(关于数乘法的结合律)；（a+b)·c=a·c+b·c（分配律）；向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即：(a·b)·c≠a·(b·c)；例如：(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即：由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义：两个向量a和b的向量积（外积、叉积）是一个向量,记作a×b.若a、b不共线,则a×b的模是：∣a×b∣=|a|·|b|·sin〈a,b〉；a×b的方向是：垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质：∣a×b∣是以a和b为边的平行四边形面积.。

平面向量的运算法则平面向量的运算法则是指在平面向量的加法、减法和数乘运算中遵循的规则和原则。

这些法则是基于平面向量的定义和性质而得出的，能够帮助我们简化向量计算和解决与向量相关的问题。

本文将详细介绍平面向量的加法、减法和数乘运算法则，以及运用这些法则解决实际问题的方法。

一、平面向量的定义平面向量是指在平面上有大小和方向的量，用箭头来表示。

平面向量通常用大写字母表示，例如A、B等。

平面向量可以表示位移、速度、力等物理量，也可以表示复杂的数学概念，如几何矢量、向量函数等。

二、平面向量的加法法则1. 三角形法则：设有两个平面向量A和B，以A为起点，在A的末端画出向量B，则以A为起点、B的末端为终点的直线段就表示了平面向量A+B。

2. 平行四边形法则：设有两个平面向量A和B，以A为起点，在A 的末端画出平行于B的直线段，则以A为起点、B的终点为终点的直线段就表示了平面向量A+B。

加法运算满足交换律和结合律，即对于任意平面向量A、B和C，有：A+B=B+A （交换律）(A+B)+C=A+(B+C) （结合律）三、平面向量的减法法则平面向量的减法可以看作是加法的逆运算。

设有两个平面向量A和B，要计算A-B，可以先求出B的相反向量-B，然后将A与-B相加，即可得到A-B。

四、平面向量的数乘法则设有一个平面向量A和一个实数k，要计算kA，可以将向量A的长度乘以k，并保持与A同向或反向（根据k的正负确定）。

得到的新向量kA的长度是原向量A的长度的k倍，方向与A相同或相反。

数乘运算满足分配律和结合律，即对于任意平面向量A和B，以及任意实数k和m，有：k(A+B)=kA+kB （分配律）(km)A=k(mA) （结合律）五、平面向量运算法则的应用平面向量运算法则在解决与向量相关的问题时具有广泛的应用。

应用这些法则可以帮助我们简化向量运算过程，提高计算的准确性和效率。

1. 合成与分解：利用平面向量的加法法则，可以将一个向量表示为若干个已知向量的和，这称为合成。

平面向量向量加法运算及其几何意义平面向量的加法运算是指将两个向量相加得到一个新的向量的过程。

在进行向量加法运算时，可以使用坐标法或三角法。

坐标法是指将向量表示为有序数对的形式，例如vector AB可以表示为(Ax, Ay)，vector CD可以表示为(Cx, Cy)。

要将两个向量相加，只需将它们对应的坐标相加即可。

例如，若vector AB + vector CD =vector EF，则有(Ax + Cx, Ay + Cy) = (Ex, Ey)。

三角法是指利用向量的方向角和长度来进行向量加法运算。

假设vector AB的长度为a，方向角为θ，vector CD的长度为b，方向角为φ。

要求它们的和，可以先将它们用三角形形式绘制出来，然后将其首尾相接，连接向量AB的尾部和向量CD的头部，得到一个新的向量EF，即vector AB + vector CD = vector EF。

无论使用何种方法进行向量加法运算，其几何意义是将两个向量进行平移后的结果。

首先，将向量AB的起点平移到坐标原点，然后将向量AB的终点与向量CD的起点连接起来，再将向量CD的终点与该连接线的终点连接起来，得到向量EF。

即vector AB + vector CD = vector EF。

在几何上，向量加法运算的结果可以表示为一个以向量AB为一条边，以向量CD为相邻边的平行四边形，其中向量EF为对角线。

向量AB称为平行四边形的第一条边，向量CD称为平行四边形的第二条边。

向量EF称为平行四边形的对角线，连接向量AB的起点和向量CD的终点。

此外，可以利用向量的加法运算推导出向量的其他运算规律。

例如，可以推导出向量加法满足交换律（vector AB + vector CD = vector CD+ vector AB）和结合律（vector AB + (vector CD + vector EF) = (vector AB + vector CD) + vector EF）。

平面向量重要公式平面向量是指在同一平面上定点两点之间的差。

在平面向量的运算中，存在许多重要的公式，这些公式对于解决数学问题具有重要的指导作用。

下面将介绍一些平面向量的重要公式。

1.向量的加法：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a+b=(a₁+b₁,a₂+b₂)向量的加法满足交换律和结合律。

2.向量的数乘：设向量a=(a₁,a₂)，k为实数，则有：k*a=(k*a₁,k*a₂)数乘与向量的顺序可以交换。

3.向量的模：设向量a=(a₁,a₂)，则有：a，=√(a₁²+a₂²)向量的模等于其坐标的平方和的平方根。

4.向量的数量积（点积）：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a·b=a₁*b₁+a₂*b₂向量的数量积满足交换律和分配律。

5.向量的平行性质：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a//b⇔a₁/b₁=a₂/b₂两个向量平行的充分必要条件是它们的坐标成比例。

6.向量的垂直性质：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a⊥b⇔a·b=0两个向量垂直的充分必要条件是它们的数量积为0。

7.向量的共线性质：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a、b共线⇔a₁/b₁=a₂/b₂=k（k为实数）两个向量共线的充分必要条件是它们的坐标成比例，且比例因子相同。

8.向量的二次共线性：设向量a=(a₁,a₂)，b=(b₁,b₂)，c=(c₁,c₂)，则有：a、b共线两个向量共线的充分必要条件是它们的坐标成比例，且比例因子相同。

9.向量的夹角：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：cosθ = (a·b) / (，a，，b，)两个向量的夹角cosθ等于它们的数量积与它们的模的乘积之商。

10.平行四边形法则：设向量a=(a₁,a₂)，b=(b₁,b₂)，则有：a+b=c+d一个平行四边形的对角向量相等。

平面向量公式平面向量这玩意儿，在数学里可是个相当重要的角色！咱先来说说平面向量的加法公式。

想象一下，你在操场上跑步，先向东跑了 5 米，然后又向北跑了 3 米，那你最终的位置怎么算呢？这其实就是平面向量加法的实际应用。

平面向量的加法公式就是把两个向量的对应分量相加。

比如说向量 a = (x1, y1)，向量 b = (x2, y2)，那它们相加得到的向量 c 就是 (x1 + x2, y1 + y2)。

这就好像你把两次跑步的距离在东西和南北方向上分别加起来，就能知道最终的位置。

再讲讲平面向量的减法公式。

假设你和小伙伴一起从学校出发去超市，你走的路线是向量 a，小伙伴走的路线是向量 b，那你俩路线的差异，也就是向量 a 减去向量 b，就是把对应分量相减。

就像你比小伙伴多走的那段路，通过计算就能清楚。

还有平面向量的数量积公式，这可是个很有趣的东西。

想象一下，你用力推一个箱子，你使的力是一个向量，箱子移动的方向又是一个向量。

这两个向量的数量积就能反映出你做功的多少。

平面向量的数量积公式是a·b = |a|×|b|×cosθ，其中θ是两个向量的夹角。

这就好比你推箱子使的劲和箱子移动方向之间的关系，角度不同，做功效果就不一样。

我记得有一次在课堂上，我给学生们讲平面向量的公式。

有个学生一脸迷茫地问我：“老师，这平面向量在生活中有啥用啊？”我当时就笑了，指着窗外操场上正在打扫卫生的同学说：“你看，那个同学从这边扫到那边，又从那边扫到这边，他移动的轨迹不就可以看成是向量吗？咱们通过向量公式就能算出他打扫的总路程。

”那学生一下子眼睛就亮了，好像突然明白了这些公式不是纸上谈兵，而是真的能解决实际问题。

平面向量的模长公式也不能落下。

向量的模长就像是向量的“长度”。

比如向量 a = (x, y)，它的模长就是√(x² + y²)。

这就好像是要量出一根绳子的长度一样，通过计算得出具体的数值。

平面向量的运算法则
平面向量是代表平面上的位移或者力的理论对象，是数学中的一个基本概念。

而对于平面向量的运算法则，我们通常会涉及到加法、减法、数乘、数量积、向量积等内容。

下面将详细介绍平面向量的运算法则。

1. 向量的加法
两个向量相加的结果是一个新的向量，其方法是将两个向量的起点相同，然后将两个向量的箭头相连，新向量的箭头指向这两个箭头的相连处。

若将两个向量分别表示为a和b，则它们的和向量c=a+b。

2. 向量的减法
两个向量相减的结果是一个新的向量，其方法是将两个向量的起点相同，然后将被减向量的箭头逆向，再将两个向量的箭头相连，新向量的箭头指向这两个箭头的相连处。

若将两个向量分别表示为a和b，则它们的差向量c=a-b。

3. 向量的数乘
数k与向量a的乘积，记作ka，表示将向量a的长度乘以k倍，方向不变。

若k>0，则ka与a同向；若k<0，则ka与a反向。

4. 向量的数量积
向量a与向量b的数量积，记作a·b或者ab，是一个标量，表示a 与b的长度之积再乘以它们夹角的余弦值。

如果a=(x₁, y₁)、b=(x₂, y₂)，则a·b = x₁x₂ + y₁y₂。

5. 向量的向量积
向量a与向量b的向量积，记作a×b，是一个向量，其大小是a与b 围成的平行四边形的面积，方向垂直于a和b构成的平面，方向满足右手螺旋定则。

以上就是关于平面向量的运算法则的介绍，这些运算法则在解决平面向量相关问题时非常重要，希望可以对你有所帮助。

平面向量的运算平面向量是二维空间中的有方向的量，可以通过各种运算来进行计算和处理。

本文将涉及到平面向量的基本运算，包括向量的加法、减法、数乘、模长和单位向量等。

并将通过具体实例和图表来帮助读者更好地理解和应用这些运算。

一、向量的加法向量的加法是指将两个向量的对应分量相加得到一个新的向量的操作。

设有两个向量A和A，分别表示为：A = (A₁, A₁)A = (A₂, A₂)则向量A和A的加法运算为：A + A = (A₁ + A₂, A₁ + A₂)在坐标平面上，A + A的结果就是将向量A的起点放在向量A的终点，然后连接向量A的起点和向量A的终点。

二、向量的减法向量的减法是指将一个向量减去另一个向量得到一个新的向量的操作。

设有两个向量A和A，分别表示为：A = (A₁, A₁)A = (A₂, A₂)则向量A和A的减法运算为：A - A = (A₁ - A₂, A₁ - A₂)在坐标平面上，A- A的结果就是连接向量A的起点和向量A的终点。

三、向量的数乘向量的数乘是指将一个向量乘以一个实数得到一个新的向量的操作。

设有一个向量A，表示为：A = (A, A)A为实数，则向量A的数乘运算为：AA = (AA, AA)在坐标平面上，将向量A的长度缩放A倍，方向保持不变。

四、向量的模长向量的模长，也称为向量的长度，表示为向量起点到终点的距离。

设有一个向量A，表示为：A = (A, A)则向量A的模长为：|A| = √(A² + A²)模长为非负实数，表示向量的大小。

五、单位向量单位向量是指模长为1的向量。

通过将一个非零向量除以它的模长即可得到单位向量。

设有一个非零向量A，表示为：A = (A, A)则单位向量A为：A = (A/|A|, A/|A|)其中，|A|为向量A的模长。

单位向量在方向上与原向量相同，但长度为1。

六、向量的运算性质1. 交换律：向量的加法满足交换律，即A + A = A + A。

平面向量的基本运算法则在数学中，平面向量是指一个既有大小（长度）又有方向的量。

平面向量具有独特的运算法则，包括加法、减法、数量乘法和点乘法。

下面将详细介绍平面向量的基本运算法则。

一、平面向量的表示平面向量可以用箭头来表示，箭头的长度表示向量的大小（长度），箭头所指的方向表示向量的方向。

常用的表示方法为使用字母加箭头或使用粗体字母表示向量，如向量a可以表示为"a->"或"a"。

二、平面向量的加法1. 平面向量的加法满足交换律，即a + b = b + a。

2. 平面向量的加法满足结合律，即(a + b) + c = a + (b + c)。

3. 平面向量的加法可以利用三角形法则进行计算。

将两个向量首尾相接，连接起来形成一个三角形，以第一个向量的起点和第二个向量的终点作为相加后向量的起点，以第一个向量的终点和第二个向量的起点作为相加后向量的终点。

相加后向量的大小等于三角形的长，方向与三角形最短边的方向相同。

三、平面向量的减法平面向量的减法可以理解为加法的逆运算。

用b减去a，即b - a，可以转化为b + (-a)。

其中，-a称为向量a的负向量，它的大小与a相等，方向相反。

四、平面向量的数量乘法1. 数量乘法即将向量与一个实数相乘，结果为一个新的向量。

数量乘法满足结合律，即k(la) = (kl)a，其中k和l为实数。

2. 如果k为正数，数量乘法会改变向量的大小，但不改变其方向；如果k为负数，数量乘法会改变向量的大小，并将其方向取反；如果k 为0，则结果向量为零向量。

3. 数量乘法的计算方法是将实数与向量的模长相乘，再将结果的方向与原向量保持一致。

五、平面向量的点乘法1. 平面向量的点乘法又称为数量积或内积，表示为a · b。

2. 点乘法的结果是一个标量（实数），而不是一个向量。

3. 点乘法的结果等于两个向量模长的乘积与它们夹角的余弦值的乘积，即a · b = |a||b|cosθ，其中θ为a和b之间的夹角。

平面向量的运算公式好嘞，以下是为您生成的关于“平面向量的运算公式”的文章：咱先来说说平面向量这玩意儿，它在数学里可有着不小的作用呢！平面向量的加法运算公式，就像是搭积木，把两个向量首尾相连，从第一个向量的起点指向第二个向量的终点，这就是它们相加的结果。

比如说，有向量 a = (1, 2) ，向量 b = (3, 4) ，那它们相加 a + b 就等于(1 + 3, 2 + 4) ，也就是 (4, 6) 。

这就好比你从学校出发走了一段路，又从这个位置接着走另一段路，最终到达的地方就是这两段路程合起来的效果。

再讲讲减法，平面向量的减法运算公式呢，就是把被减向量的终点和减向量的终点相连，箭头指向被减向量的终点，这就是差向量啦。

比如向量 c = (5, 7) ，向量 d = (2, 3) ，那么 c - d 就是 (5 - 2, 7 - 3) ，也就是 (3, 4) 。

这就好像你原本要去一个地方，结果有人拽着你往回走了一段，那你离最终目的地的距离和方向就变了。

乘法运算里的数乘向量也很有趣。

一个实数乘以一个向量，就等于把这个向量的长度放大或缩小，方向不变（当实数为负数时方向相反）。

就像你吹气球，吹气多了气球就变大，吹气少了气球就变小。

比如说 2 乘以向量 e = (1, 1) ，那就得到 (2, 2) 。

还有向量的数量积，这可有点像两个人合作的成果。

如果有向量 f= (m, n) ，向量 g = (p, q) ，它们的数量积 f · g 就等于 m × p + n × q 。

这就好比你和小伙伴一起搬东西，你出了一份力，他出了一份力，最后合起来的效果就是你们共同的成果。

记得我之前教过一个学生，这孩子一开始对平面向量的运算公式那是一头雾水。

有一次做作业，碰到一道关于向量加法的题目，他怎么也算不对。

我就问他：“你想想，假如你在操场上先往东跑了一段，又往北跑了一段，那你最终的位置怎么算？”这孩子眨巴眨巴眼睛，好像有点开窍了。

资源信息表22.8（2）平面向量的加法上海市民办文绮中学 杨卓远教学目标1．通过对向量加法的三角形法则的推广，理解几个向量相加的多边形法则并会进行初步运用．2．通过向量加法与实数加法的类比，发展数学观念，领会类比的思想方法．教学重点及难点理解向量的概念，明确向量是既有大小（长短）又有方向的量． 理解向量可以用有向线段表示，平移可以用向量表示．教学过程设计一、 复习1：关于向量 1． 向量定义：有大小、有方向的量； 2． 向量表示：2种：有向线段；字母表示． 3． 向量的大小叫模．4．向量的方向决定了向量之间的一些关系．如相等向量、相反向量、平行向量． 二、 复习2：向量加法 1、 法则：三角形法则．2、 零向量：大小为0，方向任意．3、习题评析1：□ABCD 中，设,,A B a A D b ==DCBA试用,,a b 表示下列向量：,,C A BD AC BD +．习题评析2：B,D 在□ABCD 的对角线上，且有EB=DF 中， 设,,EC a EA b AD c=== ，则：a b += _______；b c +=_______．作：a c +．三、 向量加法的多边形法则： 1．思考：已知四边形ABCD及其向量,,AB BC C D,怎样作出AB BC CD++ ？得出：多个向量的加法可以多边形法则． 2． 例题：已知互不平行的向量,,,a b c d；求作a b c d+++．3．例题：如图：梯形ABCD 中，AB//DC ，CE//AD ，点E 在AB 上，那么AE EC CD BE++＋＝__________________．AB BC CE AD++ ＋＝__________________．四、 小试牛刀：P112． 五、 本课小结一般的，几个向量相加，可把这几个向量顺次首尾相接，那么它们的和向量是以第一个向量的起点为起点，最后一个向量的终点为终点的向量．这样的规定叫做几个向量的多边形法则． 六、 布置作业：练习册 第55页 习题22.8（2）FEDCBABAD EC BA。

掌握高中三年数学中的平面向量的运算技巧平面向量是高中数学中的重要内容之一，掌握平面向量的运算技巧对于解决与几何有关的问题非常重要。

在高中三年的数学学习中，我们需要通过练习和理论学习来掌握平面向量的各种运算技巧。

本文将介绍平面向量的加法、减法、数量积和向量积等运算技巧。

一、平面向量的加法平面向量的加法是指将两个向量进行相加得到一个新的向量。

设有两个向量a和b，它们的加法运算可以表示为：c = a + b其中c为向量a和向量b的和向量。

对于平面向量的加法，我们可以利用平行四边形法则进行计算。

即将向量a的起点与向量b的起点相连，得到一个平行四边形，从向量a的终点到向量b的终点，得到的向量就是向量a和向量b的和向量c。

二、平面向量的减法平面向量的减法是指将一个向量减去另一个向量得到一个新的向量。

设有两个向量a和b，它们的减法运算可以表示为：c = a - b其中c为向量a减去向量b所得到的差向量。

与加法相似，平面向量的减法也可以利用平行四边形法则进行计算。

即将向量a的起点与向量b的起点相连，得到一个平行四边形，从向量b的终点到向量a的终点，得到的向量就是向量a减去向量b所得到的差向量c。

三、平面向量的数量积平面向量的数量积也称为点积或内积，表示两个向量之间的乘积。

设有两个向量a和b，它们的数量积运算可以表示为：c = a · b其中c为向量a和向量b的数量积，可以通过向量的模长和夹角cosθ来计算：c = |a| |b| cosθ数量积具有以下性质：1. 如果向量a与向量b垂直，则它们的数量积为0；如果数量积为0，则向量a与向量b垂直。

2. 数量积满足交换律，即a·b = b·a。

3. 数量积满足分配律，即(a+b)·c = a·c + b·c。

四、平面向量的向量积平面向量的向量积也称为叉积或外积，表示两个向量之间的叉乘。

设有两个向量a和b，它们的向量积运算可以表示为：c = a × b其中c为向量a和向量b的向量积，可以通过向量的模长和夹角sinθ来计算：|c| = |a| |b| sinθ向量积具有以下性质：1. 向量a与向量b的向量积垂直于向量a和向量b所在的平面。