2018年四川省凉山州高考数学一诊试卷(文科) 附解析

2017-2018学年四川省凉山州高考数学一诊试卷（文科）一、选择题（每小题5分，共50分．每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合A={x|x2﹣x≤0}，B={0，1，2}，则A∩B=（）A．∅B．{0}C．{0，1}D．{0，1，2}2．复数z=（i是虚数单位），则|z|=（）A．1 B．C．D．23．函数f（x）=sin（x+）图象的一条对称轴方程为（）A．x=﹣B．x=C．x=D．x=π4．某程序框图如图所示，若运行该程序后输出S=（）A．B．C．D．5．某校高三年级共1500人，在某次数学测验后分析学生试卷情况，需从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，则该次测验中90分以下的人数是（）A．600 B．450 C．300 D．1506．若某四面体的三视图是全等的等腰直角三角形，且其直角边的长为6，则该四面体的体积是（）A．108 B．72 C．36 D．97．，为单位向量，且|+2|=，则向量，夹角为（）A．30°B．45°C．60°D．90°8．实数x、y满足，这Z=3x+4y，则Z的取值范围是（）A．[1，25]B．[4，25]C．[1，4]D．[5，24]9．下列命题正确的是（）A．“b2=ac”是“a，b，c成等比数列”的充要条件B．“∀x∈R，x2＞0”的否定是“∃x0∈R，x02＞0”C．“若a=﹣4，则函数f（x）=ax2+4x﹣1只有唯一一个零点”的逆命题为真命题D．“函数f（x）=lnx2与函数g（x）=的图象相同”10．已知关于x的方程x2+（1+a）x+1+a+b=0（a，b∈R）的两根分别为x1、x2，且0＜x1＜1＜x2，则的取值范围是（）A．B．C．D．二、填空题（共5小题，每小题5分，共25分）11．计算2lg2+lg25+（）0=______．12．设a、b为实数，且a+b=1，则2a+2b的最小值为______．13．在棱长为2的正方体A1B1C1D1﹣ABCD中，则点B到平面A1B1CD的距离是______．14．设向量=（3cosx，1），=（5sinx+1，cosx），且∥，则cos2x=______．15．设数列{a n}，{b n}，{a n+b n}都是等比数列，且满足a1=b1=1，a2=2，则数列{a n+b n}的前n项和S n=______．三、解答题（共6个小题，共75分）16．信息时代，学生广泛使用手机，从某校学生中随机抽取200名，这200名学生中上课时利用以上数据，将统计的频率视为概率．（1）求上表中m、n的值；（2）求该校学生上课时间使用手机的概率．17．在三棱柱ABC﹣A1B1C1中，面BB1C1C是边长为2的正方形，点A1在平面BB1C1C上的射影H是BC1的中点，且A1H=，G是CC1的中点．（1）求证：BB1⊥A1G；（2）求C到平面A1B1C1的距离．18．函数f（x）=x3+ax2+bx+c（a，b，c∈R）的导函数的图象如图所示：（1）求a，b的值并写出f（x）的单调区间；（2）函数y=f（x）有三个零点，求c的取值范围．19．在数列{a n}中，满足点P（a n，a n）是函数f（x）=3x图象上的点，且a1=3．+1（1）求{a n}的通项公式；（2）若b n=na n，求数列{b n}的前n项和S n．20．设函数f（x）=x2+alnx+1（x＞0）．（1）若f（3）=5，求f（）的值；（2）若x＞0时，f（x）≥1成立，求a的取值范围．21．如图，有一段长为18米的屏风ABCD（其中AB=BC=CD=6米），靠墙l围成一个四边形，设∠DAB=α．（1）当α=60°，且BC⊥CD时，求AD的长；（2）当BC∥l，且AD＞BC时，求所围成的等腰梯形ABCD面积的最大值．2016年四川省凉山州高考数学一诊试卷（文科）参考答案与试题解析一、选择题（每小题5分，共50分．每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合A={x|x2﹣x≤0}，B={0，1，2}，则A∩B=（）A．∅B．{0}C．{0，1}D．{0，1，2}【考点】交集及其运算．【分析】先化简集合A，再求A∩B．【解答】解：集合A={x|x2﹣x≤0}={x|x（x﹣1）≤0}={x|0≤x≤1}=[0，1]B={0，1，2}，∴A∩B={0，1}．故选：C．2．复数z=（i是虚数单位），则|z|=（）A．1 B．C．D．2【考点】复数求模．【分析】分别求出分子、分母的模，即可得出结论．【解答】解：∵复数z=，∴|z|=||==，故选：B．3．函数f（x）=sin（x+）图象的一条对称轴方程为（）A．x=﹣B．x=C．x=D．x=π【考点】正弦函数的对称性．【分析】由条件利用余弦函数的图象的对称性，求得f（x）的图象的一条对称轴方程．【解答】解：对于函数f（x）=sin（x+），令x+=kπ+，求得x=kπ+，k∈Z，可得它的图象的一条对称轴为x=，故选：B．4．某程序框图如图所示，若运行该程序后输出S=（）A ．B ．C ．D ．【考点】循环结构．【分析】模拟执行程序框图，依次写出每次循环得到的S ，n 的值，当n ＞5时退出循环，输出S 的值．【解答】解：模拟执行程序框图，可得 S=1，n=1不满足条件n ＞5，S=1+，n=2 不满足条件n ＞5，S=1++，n=3 不满足条件n ＞5，S=1+++，n=4不满足条件n ＞5，S=1++++，n=5不满足条件n ＞5，S=1+++++，n=6满足条件n ＞5，退出循环，输出S 的值．由于S=1+++++=．故选：D ．5．某校高三年级共1500人，在某次数学测验后分析学生试卷情况，需从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，则该次测验中90分以下的人数是（ ）A ．600B ．450C ．300D ．150 【考点】分层抽样方法．【分析】根据从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，即可得出结论．【解答】解：∵从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，∴该次测验中90分以下抽取的人数是500﹣100﹣250=150．∴该次测验中90分以下的人数是150．即抽样比k=，则该次测验中90分以下的人数是1500×=450．故选：B．6．若某四面体的三视图是全等的等腰直角三角形，且其直角边的长为6，则该四面体的体积是（）A．108 B．72 C．36 D．9【考点】棱柱、棱锥、棱台的体积．【分析】四面体为边长为6的正方体沿着共点三面的对角线截出的三棱锥．【解答】解：四面体的底面为直角边为6的等腰直角三角形，高为6．∴四面体的体积V==36．故选C．7．，为单位向量，且|+2|=，则向量，夹角为（）A．30°B．45°C．60°D．90°【考点】数量积表示两个向量的夹角．【分析】对|+2|=两边平方，计算出数量积，代入夹角公式计算．【解答】解：∵|+2|=，∴（+2）2=7，即+4+4=7，∵==1，∴=，∴cos＜＞==，∴向量，夹角为60°．故选：C．8．实数x、y满足，这Z=3x+4y，则Z的取值范围是（）A．[1，25]B．[4，25]C．[1，4]D．[5，24]【考点】简单线性规划．【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．【解答】解：由约束条件作出可行域如图，联立，解得A（3，﹣2），联立，解得B（3，4），化目标函数Z=3x+4y为y=．由图可知，当直线y=过A时，直线在y轴上的截距最小，Z有最小值为1；当直线y=过B时，直线在y轴上的截距最大，Z有最小值为25．故选：A．9．下列命题正确的是（）A．“b2=ac”是“a，b，c成等比数列”的充要条件B．“∀x∈R，x2＞0”的否定是“∃x0∈R，x02＞0”C．“若a=﹣4，则函数f（x）=ax2+4x﹣1只有唯一一个零点”的逆命题为真命题D．“函数f（x）=lnx2与函数g（x）=的图象相同”【考点】命题的真假判断与应用．【分析】举例说明A错误；直接写出全称命题的否定判断B；举例说明C错误；写出分段函数说明D正确．【解答】解：A错误，如a=0，b=0，c=1满足b2=ac，但a，b，c不成等比数列；B错误，“∀x∈R，x2＞0”的否定是“∃x0∈R，x02≤0”C错误，“若a=﹣4，则函数f（x）=ax2+4x﹣1只有唯一一个零点”的逆命题是：“若函数f （x）=ax2+4x﹣1只有唯一一个零点，则a=﹣4”，为假命题，比如a=0，f（x）=0的根是；D正确，函数f（x）=lnx2是分段函数，分x＞0和x＜0分段可得函数g（x）=．故选：D．10．已知关于x的方程x2+（1+a）x+1+a+b=0（a，b∈R）的两根分别为x1、x2，且0＜x1＜1＜x2，则的取值范围是（）A．B．C．D．【考点】简单线性规划的应用．【分析】由方程x2+（1+a）x+1+a+b=0的两根满足0＜x1＜1＜x2，结合对应二次函数性质得到，然后在平面直角坐标系中，做出满足条件的可行域，分析的几何意义，然后数形结合即可得到结论．【解答】解：由程x2+（1+a）x+1+a+b=0的二次项系数为1＞0故函数f（x）=x2+（1+a）x+1+a+b图象开口方向朝上又∵方程x2+（1+a）x+1+a+b=0的两根满足0＜x1＜1＜x2则即即其对应的平面区域如下图阴影示：∵=表示阴影区域上一点与原点边线的斜率由图可知∈故答案：二、填空题（共5小题，每小题5分，共25分）11．计算2lg2+lg25+（）0=3．【考点】对数的运算性质．【分析】直接利用对数运算法则以及有理指数幂的运算法则化简求解即可．【解答】解：2lg2+lg25+（）0=lg4+lg25+1=lg100+1=2+1=3．故答案为：3．12．设a、b为实数，且a+b=1，则2a+2b的最小值为2．【考点】基本不等式．【分析】因为2a与2b均大于0，所以直接运用基本不等式求最小值．【解答】解：∵a+b=1，∴，当且仅当2a=2b，即时“=”成立．所以2a+2b的最小值为．故答案为．13．在棱长为2的正方体A1B1C1D1﹣ABCD中，则点B到平面A1B1CD的距离是．【考点】棱柱的结构特征．【分析】以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出点B到平面A1B1CD的距离．【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，则B（2，2，0），D（0，0，0），A1（2，0，2），C（0，2，0），=（2，2，0），=（2，0，2），=（0，2，0），设平面A1B1CD的法向量=（x，y，z），则，取x=1，得，∴点B到平面A1B1CD的距离是：d===．∴点B到平面A1B1CD的距离是．故答案为：．14．设向量=（3cosx，1），=（5sinx+1，cosx），且∥，则cos2x=．【考点】二倍角的余弦；平面向量共线（平行）的坐标表示．【分析】由条件利用两个向量平行的条件求得sinx的值，再利用二倍角的余弦公式求得cos2x 的值．【解答】解：∵向量=（3cosx，1），=（5sinx+1，cosx），且∥，∴3cos2x﹣5sinx﹣1=0，即3sin2x+5sinx+2=0，求得sinx=﹣2（舍去），或sinx=，则cos2x=1﹣2sin2x=1﹣2×=，故答案为：．15．设数列{a n}，{b n}，{a n+b n}都是等比数列，且满足a1=b1=1，a2=2，则数列{a n+b n}的前n项和S n=2n+1﹣2．【考点】等比数列的性质．【分析】由题意，数列{a n+b n}的首项为2，公比为2，利用等比数列的求和公式，即可得出结论．【解答】解：由题意，数列{a n}a1=1，a2=2，公比为2，设数列{b n}的公比为q′，{a n+b n}的公比为q，则2+q′=2q，4+q′2=2q2，∴q2﹣4q+4=0∴q=2，∴数列{a n+b n}的首项为2，公比为2，∴S n==2n+1﹣2．故答案为：2n+1﹣2．三、解答题（共6个小题，共75分）16．信息时代，学生广泛使用手机，从某校学生中随机抽取200名，这200名学生中上课时37200（1）求上表中m、n的值；（2）求该校学生上课时间使用手机的概率．【考点】列举法计算基本事件数及事件发生的概率．【分析】（1）根据表格的合计数据计算，（2）求出上课时间使用手机的学生人数，除以数据总数得出频率，利用频率代替概率．【解答】解：（1）m=98﹣23﹣55=20，n=m+17=37．（2）上课时间使用手机的人数为23+55=78．∴该校学生上课时间使用手机的概率P==0.39．17．在三棱柱ABC﹣A1B1C1中，面BB1C1C是边长为2的正方形，点A1在平面BB1C1C上的射影H是BC1的中点，且A1H=，G是CC1的中点．（1）求证：BB1⊥A1G；（2）求C到平面A1B1C1的距离．【考点】直线与平面垂直的性质；点、线、面间的距离计算．【分析】（1）连接GH，由已知得A1H⊥平面BB1C1C，可得A1H⊥BB1，由中位线和条件得BB1⊥HG，由线面垂直的判定定理可证结论成立；（2）取B1C1的中点E，连接HE、A1E，由题意和线面垂直的判定定理、定义得B1C1⊥A1E，求出△A1B1C1的面积，由等体积法求出C到平面A1B1C1的距离．【解答】证明：（1）如图连接GH，∵点A1在平面BB1C1C上的射影H，∴A1H⊥平面BB1C1C，∵BB1BC⊂平面BB1C1C，∴A1H⊥BB1，∵H是BC1的中点，G是CC1的中点，∴HG∥BC，由∠B1BC=90°知，BB1⊥B C，∴BB1⊥HG∵A1H∩HG=H，∴BB1⊥平面A1HG，∴BB1⊥A1G；解：（2）取B1C1的中点E，连接HE、A1E，由∠BB1C1=90°得，HE⊥B1C1，∵A1H⊥平面BB1C1C，∴A1H⊥B1C1，∵A1H∩HE=H，∴B1C1⊥平面A1HE，∴B1C1⊥A1E，∵H是BC1的中点，E是B1C1的中点，∴HE∥BB1，且HE=1，在△A1HE中，A1E==2，∴=•B1C1AB•A1EBC==2，设C到平面A1B1C1的距离为h，由=V A得，×A1E×=×h×，则2×2=h×2，解得h=，∴C到平面A1B1C1的距离是．18．函数f（x）=x3+ax2+bx+c（a，b，c∈R）的导函数的图象如图所示：（1）求a，b的值并写出f（x）的单调区间；（2）函数y=f（x）有三个零点，求c的取值范围．【考点】利用导数研究函数的单调性．【分析】（1）求出原函数的图象可知，f'（x）=0的两个根为﹣1，2，根据根与系数的关系即可求出a，b的值，并由图象得到单调区间；（2）求出函数f （x ）的极大值和极小值，由函数f （x ）恰有三个零点，则函数的极大值大于0，且同时满足极小值小于0，联立可求c 的取值范围．【解答】解：（1）∵f （x ）=x 3+ax 2+bx +c ， ∴f ′（x ）=x 2+2ax +b ，∵f ′（x ）=0的两个根为﹣1，2，∴，解得a=﹣，b=﹣2，由导函数的图象可知，当﹣1＜x ＜2时，f ′（x ）＜0，函数单调递减， 当x ＜﹣1或x ＞2时，f ′（x ）＞0，函数单调递增，故函数f （x ）在（﹣∞，﹣1）和（2，+∞）上单调递增，在（﹣1，2）上单调递减．（2）由（1）得f （x ）=x 3﹣x 2﹣2x +c ，函数f （x ）在（﹣∞，﹣1），（2，+∞）上是增函数，在（﹣1，2）上是减函数，∴函数f （x ）的极大值为f （﹣1）=+c ，极小值为f （2）=c ﹣．而函数f （x ）恰有三个零点，故必有，解得：﹣＜c ＜．∴使函数f （x ）恰有三个零点的实数c 的取值范围是（﹣，）19．在数列{a n }中，满足点P （a n ，a n +1）是函数f （x ）=3x 图象上的点，且a 1=3． （1）求{a n }的通项公式；（2）若b n =na n ，求数列{b n }的前n 项和S n ． 【考点】数列的求和；数列递推式． 【分析】（1）通过将点P （a n ，a n +1）代入函数方程f （x ）=3x 化简可知a n +1=3a n ，进而可知数列{a n }是首项为3、公比为3的等比数列，进而计算可得结论； （2）通过（1）可知b n =n3n ，进而利用错位相减法计算即得结论． 【解答】解：（1）∵点P （a n ，a n +1）是函数f （x ）=3x 图象上的点， ∴a n +1=3a n ，又∵a 1=3，∴数列{a n }是首项为3、公比为3的等比数列， ∴其通项公式a n =3n ；（2）由（1）可知b n =na n =n3n ， ∴S n =1×3+2×32+…+n3n ，3S n =1×32+2×33+…+（n ﹣1）3n +n ×3n +1， 错位相减得：﹣2S n =3+32+…+3n ﹣n ×3n +1=3×﹣n ×3n +1=×3n+1﹣，∴S n=×3n+1+．20．设函数f（x）=x2+alnx+1（x＞0）．（1）若f（3）=5，求f（）的值；（2）若x＞0时，f（x）≥1成立，求a的取值范围．【考点】函数的值；函数恒成立问题．【分析】（1）由f（3）=5得出aln3=﹣5，再求出f（）的值．（2）alnx≥﹣x2．然后讨论lnx的符号分离参数，转化为求﹣得最大值或最小值问题．【解答】解：（1）∵f（3）=10+aln3=5，∴aln3=﹣5．∴f（）=+aln=﹣aln3==．（2）∵x2+alnx+1≥1，∴alnx≥﹣x2．①若lnx=0，即x=1时，显然上式恒成立．②若lnx＞0，即x＞1时，a≥﹣．令g（x）=﹣．则g′（x）=，∴当1＜x时，g′（x）＞0，当x时，g′（x）＜0，∴当x=时，g（x）取得最大值g（）=﹣2e．∴a≥﹣2e．③若lnx＜0，即0＜x＜1时，a≤﹣，由②讨论可知g（x）在（0，1）上是增函数，且g（x）＞0，∴a≤0．综上，a的取值范围是[﹣2e，0]．21．如图，有一段长为18米的屏风ABCD（其中AB=BC=CD=6米），靠墙l围成一个四边形，设∠DAB=α．（1）当α=60°，且BC⊥CD时，求AD的长；（2）当BC∥l，且AD＞BC时，求所围成的等腰梯形ABCD面积的最大值．【考点】基本不等式在最值问题中的应用．【分析】（1）连接BD，作BO⊥AD，垂足为O，利用三角函数，结合勾股定理，求AD的长；（2）由题意，梯形的高为6sinα，AD=6+12cosα，所围成的等腰梯形ABCD面积S==36sinα（1+cosα），利用导数确定单调性，即可求出所围成的等腰梯形ABCD面积的最大值．【解答】解：（1）连接BD，作BO⊥AD，垂足为O，则AO=3，BO=3，BD=6，∴OD==3，∴AD=AO+OD=3+3；（2）由题意，梯形的高为6sinα，AD=6+12cosα，∴所围成的等腰梯形ABCD面积S==36sinα（1+cosα），S′=36（2cosα﹣1）（cosα+1），∴0＜α＜，S′＞0，，＜α＜π，S′＜0，∴α=，S取得最大值27．2016年9月28日。

凉山州一类模式 2017—2018 学年度上期期末检测高二数学（文科）题 得 号 分 一 二 三 总 分 总 分 人注意事项： 1.本试卷三个大题，共 8 页，考试时间为 120 分钟,满分 150 分。

2.答题前考生务必用汉字将密封线内的项目填写清楚。

3.答选择题时将应选答案的序号写在题干后的括号内；非选择题的答案直接 答在试卷相应的位置上。

ꋍ、ꌊꄻꄝ (ꒉꄝꋋꄝꐯꇯ12ꐭꄝꐥ,ꐭꄝꋍꄝꌠ5ꃏ,ꐯꇯ60ꃏ.ꋍꐭꄝꌠ 得 分 评 卷 人 ꅿꌋꐘꇖꂷꌠꇬ,ꄝꄜꇐꇬꊒꌠꋍꂷꀉꄂꐥ)选择题（本大题共 12 小题,每小题 5 分,共 60 分.在每小题给 出的四个选项中，只有一项是符合要求的）1.ꈭꐊꆌꉻꆹ x 2  y 2  4 x  2 y  2  0 ꉬꌠꅉꐚ，ꋋꆏꈭꋋꂷꅿꉻꊂꆹ（已知圆方程为 x 2  y 2  4 x  2 y  2  0 ，则该圆的面积为） D. 9 ） D. 150oA.3B. 2C. 32.ꎂꑟ l ꆹꊮꌺA（1，0）、B（0， 3 ）ꇬꈴ，ꋋꆏꎂꑟ l ꅿꎎꎐꆹ（直线 l 经过点 A（1，0） 、B（0， 3 ） ，则直线 l 的倾斜角为A. 30o 3.ꇽꅇ命题B. 60oC. 120o ）ꋋꆏꇽꅇ  ꅿꁏꇽꅇꆹ（则命题  的否定是4.ꇵꐪꑟ y 2  4 x ꅿꏓꌵꅉꇬꄉꋍꌐꏦꑟꇬꑟꌠꇢꐨꆹ（抛物线 y  4 x 的焦点到其准线的距离是2） D.4 ）A.1B. 2C. 35.ꏓꌵꅉꆏxꄿꇬꐛꌠꏿꌡꈭ 4 x 2  my 2  4 ꅿꈯꐞꐨꆹ2 ꉬ，ꋋꆏꍝꃷꁨmꅿꁌꆹ（ 2 2 焦点在 x 轴上的椭圆 4 x 2  my 2  4 的离心率为 ，则实数 m 的值为 2 8 A. B. 5 C. 6 D. 8 3一模高二数学(文科)试题 第 1 页(共 8 页)6.ꀱꇊꐮꁸꁈꌌ30ꌋꆀ315ꅿꒈꇨꉻꁧꃷꁨꌗꇬ，ꁸꏦꃄꄻꅐꌠꅿꃢꃷꁨꆹ（用辗转相除法求 30 与 315 的最大公约数，需要做除法的次数是） D. 5 ）A. 2B. 3C. 47.ꊮꌺA(-2， m)、 B (m， 4)ꇬꈴꌠꎂꑟꌋꆀꎂꑟ x  2 y  3  0 ꐽꋓ， ꋋꆏꍝꃷꁨmꅿꁌꆹ（已知过点 A(-2， m)、B (m，4)的直线与直线 x  2 y  3  0 平行，则实数 m 的值为A. -8B. 0C. 2D. 108.ꌶꌺꁥꌶꌺ45ꑻꐥ，ꈐꏭꌺꃰ25ꑻꌋꆀꌋꅪ20ꑹ.ꌗꇐꎖꉚꃢꊂꈜꎂꃅꌺꃰ5ꑻꌋꆀꌋꅪ5ꑻꇴꌊꊌꃏ ꅲ. ꌺꃰ5ꑻꌠꊌꃏꆹꂱꑱꃅ87、95、89、93、91，ꌋꅪ5ꑻꌠꊌꃏꆹꂱꑱꃅ89、94、94、 89、94.ꐰꉉꄟꀋꎪꃅꊒꌠꆹ（ ）某班 45 名学生，其中 25 名男生和 20 名女生.在某次数学测验后随即询问了该班 5 名男生 和 5 名女生的测验成绩.5 名男生成绩分别为 87、95、89、93、91，5 名女生的成绩分别为 89、94、94、89、94. 下列说法一定正确的是A.ꌡꀠꈺꁈꋌꑵꆹꄀꁸꌡꀠꈺꁈꑵꉬ这种抽样方法是一种分层抽样B.ꌡꀠꈺꁈꋌꑵꆹꑭꊂꌡꀠꈺꁈꑵꉬ这种抽样方法是一种系统抽样C.ꌺꃰꋋ5ꑻꊌꃏꅿꀱꍣꆹꌋꅪꋋ5ꑻꊌꃏꅿꀱꍣꒊꀋꋌ这 5 名男生成绩的方差大于这 5 名女生成绩的方差D.ꌶꌺꋌꁥꌺꃰꊌꃏꅿꐽꏡꃷꁨꆹꌋꅪꊌꃏꅿꐽꏡꃷꁨꀋꒊ该班男生成绩的平均数小于该班女生成绩的平均数9.ꉪꇩꏤꆹꆆꌚꋎꌠꇯꆀꐘꑌꉻꁌꌗꏢꌠꏿꏮꎱꌗꄟꐥꀐ，ꑴꁱꆹꌗꄟꋌꑵꃅꐛꌠꈭꎁꈟꏦꁱꉬ.ꈭꎁꈟꏦ ꁱꋋꂷꃅꇬ，ꀋꄸꄷꎭꃹꌠ x  1, n  2 .ꋴꑌꁮꃅ a ꆹ2,2,5ꉬꌠꎭꃹ,ꋋꆏꎭꅐꌠSꆹ（我国南宋就有计算多项式值的秦九韶算法，图中是实现该算法 的程序框图.执行该程序框图，若输入的 x  1, n  2 .依次输入）a 为 2,2,5,则输出的 S 等于A. 2 B. 4 C. 7 D. 9 ） 10.ꈥꇬꎂꎐꅉꌐꑫO-xyzꈐꊮꌺM(1，2，3)ꍈ，MꅉꌐꐽꑊxOyꈴꄉꐮꊒ ꌠꊮꌺꆹMˊꉬ，ꋋꆏꊮꌺMꌋꆀMˊꑍꍈꌠꇢꊭꇢꐨꆹ（对称点为 Mˊ，则 M 与 Mˊ两点间的距离是 空间直角坐标系 O-xyz 内一点 M(1，2，3)，M 关于坐标平面 xOyA. 2B.C. 4D. 6一模高二数学(文科)试题 第 2 页(共 8 页)11. ꐽꑊꎂꎐꅉꌐꋍꂷꈐ，ꇵꐪꑟ y  ꐨꆹ（ ）1 2 x2 y2 x ꅿꏓꌵꅉꇬꄉꋒꈪꑟ   1 ꅿꊫꆹꑞꏢꇬꑟꌠꇢ 20 9 16 1 2 x2 y2 x 的焦点到双曲线   1 的一条渐近线的距 20 9 16同一直角坐标平面内，抛物线 y  离为A. 3B. 9C. 4 ）D. 1612.ꐰꁵꅐꌠꇽꅇꇖꂷꌠꇬ，ꃶꐙꇽꅇꉬꌠꈁꐥꌠꋴꀺꆹ（下面给出的四个命题中，所有真命题的序号是①“m=1”ꆹ“ꎂꑟ mx  2 y  3  0 ꌋꆀꎂꑟ x  2my  1  0 ꐽꋓ”ꅿꇎꋒꄻꀋꅐꇎꏦꉬ； “m=1”是“直线 mx  2 y  3  0 与直线 x  2my  1  0 平行”的充分不必要条件； ② ꋒꈪꑟ3 x2 y2   1 ꅿꊫꆹꑟꐊꆌꉻꆹ y   ； 2 4 9 2 2 3 x y 双曲线   1 的渐近线方程是 y   ； 2 4 9③ ꏿꌡꈭ=1ꅿꀊꎴꄿꀒꁵꑍꂷꌠꆹA、Bꉬ，PꆹꏿꌡꈭꇬA、Bꌋꆀꐯꀋꌡꌠꈁꏾꊮꌺ 3 ꍈꉬ，ꋋꆏꎂꑟPAꌋꆀꎂꑟPBꅿꎎꐨꁧꊌꆹ  ꉬ； 4椭圆 =1 的长轴两端点为 A、B，P 是椭圆上异于 A、B 的任意一点，则直线3 ； 4 ④ ꁯꐯꃆꂮꑌꑲꐩꐥꌠꐈꃷꁨx，yꑍꂷꌠꅿꀱꐊꀕꆌꉻꆹPA 与直线 PB 的斜率积等于  有负相关关系的两个变量 x，y 的回归方程可以是ꉬꉆ..A. ①②③ 得 分 评 卷 人B. ①③C. ②④D. ③④ꑍ、ꈥꊐꄝ(ꒉꄝꋋꄝꐯꇯ4ꐭꄝꐥ, ꐭꄝꋍꄝꌠ5ꃏ,ꐯꇯ20ꃏ.ꀱꅇꁱꄝ ꇬꇂꃴꑟꄩꊐ)填空题（本大题共 4 个小题,每小题 5 分,共 20 分.把答案填在 题中横线上）13.ꑴꁱꈁꌡꌟꈭꎁꃅꇬ，ꎭꅐꌠꄽꂫꊌꐨꆹ执行如图所示程序，输出结果为 ；；14.ꃅꄷꈚꇬꃰꊿꎆꃀꐽꏡꃅꊌꐨx（ꄙꂷ）ꌋꆀꃰꊿꎆꃀꐽꏡꃅꌬꌠy（ꄙꂷ）ꌌꍰꆗꏓꌗ，yꌋꆀxꅿꀱꐊꀕꆌꉻꊌ.ꀋꄸꄷꃅꄷꋌꈚꇬꋍꈓꌠꊾꂷꌠꐽꏡꃅ ꂷꉬ；ꎆꃀ30000ꂷꊌꃅꄉ， ꋋꆏꃅꄷꋌꈚꇬꋍꈓꌠꊾꂷꌠꐽꏡꃅꌬꌠꎆꃀꆏ调查统计某地居民人均收入 x（千元）与居民年人均消费 y（千元） ，得到 y 与 x 的回归方程是 若该地区的年人均收入为 30000 元， 则该地区居民年人均消费为 元； .一模高二数学(文科)试题 第 3 页(共 8 页)15.ꏿꌡꈭ=1ꇬꊮꌺPꍈ，ꀋꄸꄷꊮꌺPꇬꄉꋍꃼꏓꌵꅉꇬꑟꌠꇢꅉꆹmꉬ，ꄷꀋꁧꋌꋍꑳꏓ ；ꌵꅉꇬꑟꌠꇢꅉꌋꆀꐯꎴꂯ4ꇬꀋꇎ，ꋋꆏm=椭圆 4，则 m==1 上一点 P，若点 P 到其左焦点的距离为 m，且比它到其右焦点的距离少 ；16.△MABꅿꀍꂷA(2,0)、B(0,1)，Mꆹꈭ ( x  1) 2  y 2  1 ꇬꈁꏾꊮꌺꍈꉬ，ꋋꆏ△MABꅿꉻ ꊂꒈꇨꁌꆹ面积最大值是..已知△MAB 的顶点 A(2,0)、B(0,1)，M 是圆 ( x  1) 2  y 2  1 上任意一点，则△MAB 的得 分评 卷 人ꌕ、ꎥꀱꄝ（ꒉꄝꋋꄝꐯꇯ6ꐭꄝꐥ,17ꄝ10ꃏ, 18～22ꄝꋍꄝꌠ12ꃏ， ꐯꇯ70ꃏ.ꎥꀱꄮꇬꁱꂷꌌꉉꀽ,ꊩꀽꈴꈜꅀꌗꏢꁘꈜꑠꁱꎼꇁꌶ）解答题（本大题有 6 个小题；17 题满分 10 分，18～22 题每题 满分 12 分，共 70 分.解答应写出文字说明，证明过程或演算步骤）17. （10ꃏ）ꐧꋦꃄꄻꃅꈧꃢꇬꊿꏧ、ꑴꑍꂷꆏꑫꉹꐯꀋꌡꌠꌌꄉꍰꆗꏓꌗ，ꏧꆏꄿꏾꁱ（ꑴꁱ(1)）ꌡꌟ ꊌ，ꑴꆏꃢꅐꐨꁊꁸꎂꉜꁱ（ꑴꁱ(2)）ꌡꌠꊌ,ꐰꑴꁱꌡ：某次社会实践活动中甲、乙两人进行了不同项目的调查统计，甲得到茎叶图（图(1)） ，乙 得到频率分布直方图（图(2)） ，如下图：ꏧꉉꇬ:ꄿꏾꁱꈴꄉꃷꁨꊫꌐꅿꈯꄔꃷꁨꆹ74.5ꊌꉆꄷ.甲说:由茎叶图可以得到数据的中位数是 74.5.ꑴꉉꇬ:ꃢꅐꐨꁊꁸꎂꉜꁱꈴꄉꃷꁨꊫꌐꅿꐽꏡꃷꁨꆹ32ꊌꉆꄷ.乙说: 由频率分布直方图可以得到数据的平均数为 32.ꆏꑴꌠꏧꑴꈁꉉꌠꃷꁨꐛꋲꐨꈴꄉꌗꏢꎥꑣꄈꆀ，ꏧ、ꑴꎥꃪꌠꂫꇽꅇꊒꀋꊒꌠꌌꊨꇽ.请你对甲乙所指数字特征求解，从而判断甲、乙分析结论是否正确.一模高二数学(文科)试题 第 4 页(共 8 页)18.（12ꃏ）ꅉꐚ: a >0,ꇽꅇ ꀋꄸꄷ ꃶꀋꐚ，ꇽꅇq：ꐊꐈꇐ f ( x )  a x ꆹꎆꐊꐈꇐꉬ. ꃶꐚ，ꍝꃷꁨ a ꅿꁌꒃꈍꈐꌗ.x已知 a >0,命题 命题 q： 函数 f ( x )  a 为假， 为真，求实数 a 的取值范围.是增函数.若19.（12ꃏ）ꊮꌺM(-2，-1)，N(2，3)ꑍꍈꌠꅉꐚ.已知两点 M(-2，-1)，N(2，3).(1)ꑟꐕMNꌌꈭꈯꈴꑟꃅꌠꈭꅿꎂꀕꐊꆌꉻꌗ；求以线段 MN 为直径的圆的一般方程；(2)ꎂꑟ l ꆹꊮꌺMꇬꈴ，ꊮꌺNꇬꄉꎂꑟ l ꑟꌠꇢꐨꒈꇨꄮꇬꎂꑟ l ꅿꐊꆌꉻꌗ. 直线 l 过点 M，求点 N 到直线 l 距离最大时直线 l 的方程.一模高二数学(文科)试题 第 5 页(共 8 页)20.（12ꃏ）ꅉꐚ:ꈭM，ꈭꈯM(2，1)，ꄷꀋꁧꎂꑟ已知圆 M，圆心 M(2，1)，且与直线 相切.ꌋꆀꐮꂪ.(1) ꈭMꅿꎕꏦꐊꆌꉻꌗ；求圆 M 的标准方程；(2) ꎂꑟ ꊌꌠꉹꏣꑟꅿꎴꐨꌗ.设直线 所得弦的弦长.ꃅꄉ,ꎂꑟ l ꌋꆀꈭMꅿꅑꅉꃆꂮꊨꇽ，ꄷꀋꁧk=1ꄮꇬꎂꑟ l ꈭMꇬꒇ判断直线 l 与圆 M 的位置关系，并求当 k=1 时直线 l 截圆 M一模高二数学(文科)试题 第 6 页(共 8 页)21. （12ꃏ）ꅉꐚ:ꏿꌡꈭ，ꋍꑳꏓꌵꅉFꈴꄉꎎꎐꆹ60oꉬꌠꎂꑟꏢꑴꄉ，ꏿꌡꈭꌋꆀꊮꌺM、Nꑍꍈꇬꄉꐯꏍ，ꑟꐕMNꅿꎴꐨꌗ.已知椭圆 求线段 MN 的长. ，过其右焦点 F 作倾斜角为 60o 的直线，交椭圆于 M、N 两点，一模高二数学(文科)试题 第 7 页(共 8 页)22.（12ꃏ）ꅉꐚ:ꏿꌡꈭEꅿꀊꎴꄿꆹxꄿꇬꐛ，ꀁꎴꄿꎴꐨꆹ6，ꋍꈯꐞꐨꌋꆀꋒꈪꑟ ꅿꈯꐞꐨꆹꐮꏵꀠꃷꁨꉬ.已知椭圆 E 的长轴在 x 轴上， 短轴长为 6， 其离心率与双曲线 倒数.x2 y2  1 16 9x2 y2   1 的离心率互为 16 9(1)ꏿꌡꈭEꅿꎕꏦꐊꆌꉻꌗ；求椭圆 E 的标准方程；(2)ꀋꄸꄷꏿꌡꈭEꇬꊮꌺPꍈꌋꆀꏿꌡꈭꏓꌵꅉF1、F2ꑍꂷꌠꏓꐛꌠ△PF1F2ꇬ，∠F1PF2=60o， △P F1F2ꅿꉻꊂꌗ.若椭圆 E 上一点 P，与椭圆的两个焦点 F1 、F2 构成的△PF1F2 中，∠F1PF2=60o，求△P F1F2 的面积.一模高二数学(文科)试题 第 8 页(共 8 页)。

2018年四川省凉山州高中阶段招生统一考试数学试卷本试卷共10页，分为A卷（120分）、B卷（30分），全卷150分，考试时间120分钟。

A卷又分第I 卷和第n卷。

A卷（共120分）第I卷（选择题共48分）注意事项：1•第I卷答在答题卡上，不能答在试卷上。

答卷前，考生务必将自己的姓名、准考证号、试题科目涂写在答题卡上。

2 •每小题选出答案后，用2B或3B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案。

一、选择题：（共12个小题，每小题4分，共48分）在每小题给出的四个选项中只有一项是正确的, 把正确的字母填涂在答题卡上相应的位置。

1.2.-2是2的A.相反数B .倒数你认为下列各式正确的是A. a2=（-a）2B.C .绝对值3 3a =(-a)4.5.6.7.D •算术平方根3.C .圆台A.圆柱如果单项式-X a X 3A. a =2, b =3x -1如果代数式A. X> 0下列图案中,B .圆锥1y3与—y b x2是同类项，那么2B. a =1 , b = 2有意义，那么x的取值范围是D .三棱柱B. x = 1C. x 0既是轴对称图形又是中心对称图形的是A.B.已知方程组b的值分别为D. x> 0 且X=1C.2x y = 4 … \ ，贝U x + y的值为x 3y =5B . 0C . 2①邻补角是互补的角；②数据7、1、3、5、6、3的中位数是3,众数是4;③|-5|A. _1下列说法中：的算术平方根是5;④点P （1, -2 ）在第四象限，其中正确的个数是2018年四川省凉山州高中阶段招生统一考试数学试卷题号A 卷B 卷总分人-二二三四五总分六七总分得分第II 卷（非选择题 共72 分）注意事项：1. 答卷前将密封线内的项目填写清楚，准考证号前 7位填在密封线方框内，末两位填在句首方 框内。

2. 答题时用钢笔或圆珠笔直接答在试卷上。

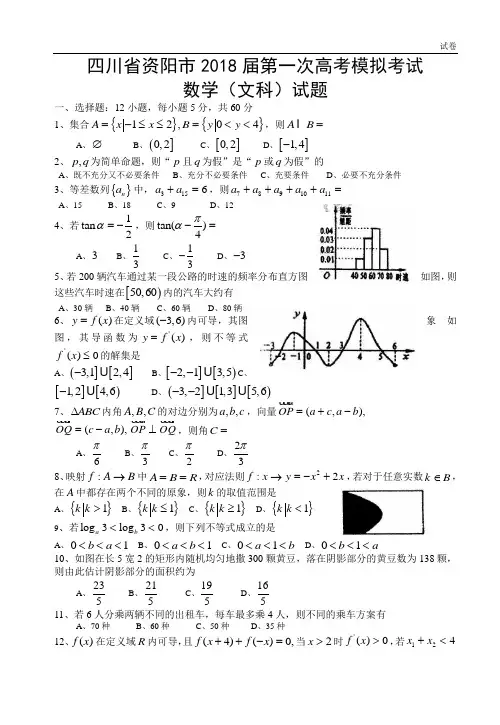
四川省资阳市2018届第一次高考模拟考试数学（文科）试题一、选择题：12小题，每小题5分，共60分1、集合{}{}12,04A x x B y y =-≤≤=<<，则A B = A 、∅ B 、(]0,2 C 、[]0,2 D 、[]1,4-2、,p q 为简单命题，则“p 且q 为假”是“p 或q 为假”的A 、既不充分又不必要条件B 、充分不必要条件C 、充要条件D 、必要不充分条件3、等差数列{}n a 中，3156a a +=，则7891011a a a a a ++++=A 、15B 、18C 、9D 、124、若1tan 2α=-，则tan()4πα-= A 、3 B 、13 C 、13- D 、3-5、若200辆汽车通过某一段公路的时速的频率分布直方图如图，则这些汽车时速在[)50,60内的汽车大约有A 、30辆B 、40辆C 、60辆D 、80辆6、()y f x =在定义域(3,6)-内可导，其图象如图，其导函数为'()y f x =，则不等式'()0f x ≤的解集是A 、(][]3,12,4- B 、[][)2,13,5-- C 、[][)1,24,6- D 、(][][)3,21,35,6--7、ABC ∆内角,,A B C 的对边分别为,,a b c ，向量(,),OP a c a b =+-(,),OQ c a b =- OP OQ ⊥，则角C =A 、6πB 、3πC 、2π D 、23π8、映射:f A B →中A B R ==，对应法则2:2f x y x x →=-+，若对于任意实数k B ∈，在A 中都存在两个不同的原象，则k 的取值范围是A 、{}1k k >B 、{}1k k ≤C 、{}1k k ≥D 、{}1k k <9、若log 3log 30ab <<，则下列不等式成立的是A 、01b a <<<B 、01a b <<<C 、01a b <<<D 、01b a <<<10、如图在长5宽2的矩形内随机均匀地撒300颗黄豆，落在阴影部分的黄豆数为138颗，则由此估计阴影部分的面积约为A 、235 B 、215C 、195D 、16511、若6人分乘两辆不同的出租车，每车最多乘4人，则不同的乘车方案有A 、70种B 、60种C 、50种D 、35种12、()f x 在定义域R 内可导，且(4)()0,f x f x ++-=当2x >时'()0f x >，若124x x +<且12202x x -<-，则12()()f x f x +的值 A 、恒大于0 B 、恒小于0 C 、可能为0 D 、可正可负二、填空题：4小题，每小题4分，共16分13、(12)n x -展开式中二项式系数的和为64，则展开式中含3x 的系数是_______14、向量,a b 满足(2,1),(4,3)a b a b +=---=-，则a b ⋅= _______________15、不等式354x-<的解集是_________________________16、定义在R 上的函数()f x ，当s i n c o s x x≤时()sin f x x =；当s i n c o s x x >时()cos f x x =，给出以下结论：①()f x 是周期函数 ②()f x的值域是⎡⎤⎢⎥⎣⎦ ③当2()x k k Z π=∈或2()2x k k Z ππ=+∈时，()f x 取最大值 ④当且仅当22()2k x k k Z πππ<<+∈时，()0f x >其中所有正确命题的序号是_________________________ 三、解答题：6小题，共74分17、（12分）2()22()f x x ax a a R =-+∈（Ⅰ）若()f x 在[]1,+∞上是单调函数，求a 的取值范围，（Ⅱ）'()f x 是()f x 的导函数，解关于x 的不等式'()()f x f x > 18、（12分）n S 是等比数列{}n a 的前n 项和，其公比为q ，若*32,,(,2)k k k S S S k N k ∈≥成等差数列，求证：数列13121,,k k k a a a ---是等差数列19、（12分）2()sin()sin()2cos (0)662xf x x x ππϖϖϖϖ=++--> （Ⅰ）求函数()f x 的值域，（Ⅱ）若()f x 的图象与直线1y =-的两个相邻交点的距离为2π，求函数()y f x =的图象在4x π=处的切线方程。

凉山州2018届高中毕业班第三次诊断性检测数学（文科）参考答案及评分意见一、选择题1.C2.C3.B4.D5.D6.C7.C8.B9.A 10.D 11.B 12.A 二、填空题13.e 14.1- 15.151516.⎥⎦⎤⎢⎣⎡+202100， 三、解答题 17.解：（1）1)1(1)1(11'=+=+===f n x n y x nx ..................................................................（2分）所以切线方程为：)1)(1(1-+=-x n y ...............................................................（4分） 令0=y 解得1+=n nx n ...............................................................（6分） 1113221+=+⨯⨯⨯=n n n a n Λ...............................................................（8分） （2）11+=n a n⎭⎬⎫⎩⎨⎧∴n a 1是首项为2，公差为1的等差数列...........................................................（10分） ()()23232122n n n n n n S n+=+=⨯++=∴.........................................................（12分）18.解：（1）分）(5320)0075.0900125.070015.05001.030005.010(=⨯⨯+⨯+⨯+⨯+⨯=-x...................................................................................................................（4分）（2）由直方图：共有感性学生：()（人）80200200075.00125.0=⨯⨯+......................................................................................................................（6分）（8分）635.6498.161109080120)40305080(2002>=⨯⨯⨯⨯-⨯⨯=K∴有99.9%的把握认为“感性”与性别有关...............................................................................................................（12分）19.（1）证明：取DP 中点N ，连接QN ，得.AQND 平行四边形 PQ DQ PD AQ AB AD QA ⊥⇒====21.......................................（2分） 又AQPD QA ABCD QA 面面⊂⊥,ΘCDPQ DCQ QP DQPCD ADCD AD ABCD APD ABCDAQPD ⊥∴⊂⊥∴⊥=⋂⊥∴面又面且面面又面面ΘΘ...............................................................................................................（4分）DCQPQ D DQ CD 面又⊥∴=⋂Θ..................................................................................................................（6分）（2）由（1）知，DCQ PQ 面⊥PQ S V DCQ DCQ P ⨯⨯=∴∆-31..........................................................（8分）2,2==∆PQ DQ DQP 中：在.........................................（10分）312223122212121=⨯⨯=∴=⨯⨯=⨯⨯=∴-∆DCQ P DCQ V DQ DC S.........................................................................................（12分）2222222ca2x y20、解（1）由题：得a=8，b=2，椭圆C的方程为+=1.......（.5分）82a b c⎧=⎪⎪⎪∴⎨⎪⎪⎪=+⎩212122ln1ln21解、（1）(),(0),()在x=e处值为0，1-h-ln0,0.......................................................(2分）ln lnf()有两个零点x,,即：=有两根x,，ln1ln令(),()0时，x=e，x h h xf x k x f xx x xe hx xx k x k xx xx xg x g xx x--'=-->∴=∴=∴=∴=--'=∴==maxx（0，e）时，()0,()单调递增；x（e，+）时，()0,()单调递减，11 ()=(),0时，()-，x+时，()0，k（0，）...(5分)eg x g x g x g xg x g e x g x g xe''∴∈>∈∞<∴=→→∞→∞→∴∈212122121122121212121212112211(2)要证：0<,等价转化为x x,即证：ln ln2,由ln=kx...1,ln=kx...2,只需证：()2,...................（.7分）ln ln ln ln再由<1>,<2>做差有k=,只需证：()2，不妨设x0,令t1,需证：le x xx x ex x k x xx x x xx xx x x xxxx<>+><><>∴+>--+>-->>=>∴2222(1)4n=2-，..................（9分）1144记()ln(2)ln2,1114(1)()0,()在(1,)单调递增，(1)(1)44()(1)0,()ln(2)0,故ln2-，原式得证...........(12分）11ttt th t t tt tth t h tt t t th t h h t t tt t->++=--=+-++-'∴=-=>∴+∞++>=∴=-->>++22.解（1）03:=-yxl............................................................................................（2分）θθρcos4sin421222===∴=极坐标方程为：普通方程为：：xyppC............................................................................（5分）（2）)34,12(0123400034403)0(),,(221122M x x y x y y y xy y x x y x M x ∴>⎩⎨⎧==⎩⎨⎧==∴=-⇒⎪⎩⎪⎨⎧==->Θ又或设消..........................................................................（8分）），的极坐标为（638381926331234tan 222πρρπθθM y x ∴==+==∴==...........................................................（10分）2222min 222331-123、解（1）由题：或x 或2222426464263311得：-2<x<-或或<x 1,解集为：x (-2,1)...................（5分）2222（2）原式等价于：f(x)>log (2)1log (24)恒成立,而()4,log (24)4=log 16x x x x x a a a a f x a a ⎧⎧⎧<->⎪⎪⎪≤≤⎨⎨⎨⎪⎪⎪--<<+<⎩⎩⎩-≤≤<∴∈-+=-=∴-<222a -4a 16恒成立，得：a (2,0)(2,4).......(10分）2a -4a>0⎧<∴∈-⎨⎩U。

2018年四川省凉山州高考数学一诊试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）已知集合A={x|0＜x≤6}，B={x∈N|2x＜33}，则集合A∩B的元素个数为（）A．6 B．5 C．4 D．32．（5分）命题“∀x＞1，”的否定是（）A．∀x＞1，B．∀x≤1，C．∃x0＞1，D．∃x0≤1，3．（5分）已知Z=，则Z•=（）A．B．0 C．1 D．4．（5分）已知f（x）=sin（x﹣）﹣1，则f（x）的最小正周期是（）A．2πB．πC．3πD．4π5．（5分）以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点，则椭圆的离心率是（）A．B．C．D．6．（5分）已知锐角α满足cos（α﹣）=cos2α，则sinαcosα等于（）A．B．﹣ C．D．﹣7．（5分）执行如图所示的程序框图，当输出S=210时，则输入n的值为（）A．6 B．7 C．8 D．98．（5分）已知点M的坐标（x，y）满足不等式组，N为直线y=﹣2x+2上任一点，则|MN|的最小值是（）A．B．C．1 D．9．（5分）在△ABC中，a2tanB=b2tanA，则△ABC是（）A．等腰三角形B．直角三角形C．等腰三角形D．等腰或直角三角形10．（5分）设y=f（x）是R上的奇函数，且f（x）在区间（0，+∞）上递减，f（2）=0，则f（x）＞0的解集是（）A．（﹣∞，﹣2）B．（0，2） C．（﹣∞，﹣2）∪（0，2）D．（﹣2，0）∪（0，2）11．（5分）如图，网格纸上小正方形的边长为1，粗线画的是一个几何体的三视图，则该几何体的体积为（）A．3 B．C．7 D．12．（5分）若函数f（x）=4﹣x2+alnx满足∀x＞0，有f（x）≤3成立，则a的取值范围是（）A．{2}B．（，2]C．[2，3） D．（1，2]二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）设向量=（1，﹣2），=（6，m），若⊥，则m=．14．（5分）我国古代数学名著《张邱建算经》有“分钱问题”：今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还敛聚与均分之，人得一百钱，问人几何？意思是：将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？则题中的人数是．15．（5分）已知各项为正的等比数列{a n}中，a2a3=16，则数列{log2a n}的前四项和等于．16．（5分）已知函数f（x）=，则方程f（1+x2）=f（2x）的解集是．三、解答题（本大题共5小题，共70分）17．（12分）设数列{a n}a n=2n﹣1．（1）求数列{a n}的前n项和；（2）设数列{b n}满足b n=2，求数列{a n b n}的n项和．18．（12分）如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2，AC=CD=．（1）求证：PD⊥平面PAB；（2）求四面体PACD的体积．19．（12分）共享单车的推广给消费者带来全新消费体验，迅速赢得广大消费者的青睐，然而，同时也是露出管理、停放、服务等方面的问题，为了了解公众对共享单车的态度（“提倡”或“不提倡”），某调研小组随机的对不同年龄段50人进行调查，将调查情况整理如下表：并且，年龄[20，25）和[40，45）的人中持“提倡”态度的人数分别为5和3，再从这两个年龄段中各随机抽取2人征求意见．（1）求年龄在[20，25）中被抽到的2人都持“提倡”态度的概率；（2）求年龄在[40，45）中被抽到的2人至少1人持“提倡”态度的概率．20．（12分）若A（x1，y1），B（x2，y2）是椭圆E：+y2=1上位于x轴上方两点，且x1+x2=2．（1）若y1+y2=1，求线段AB的垂直平分线的方程；（2）求直线AB在y轴上截距的最小值．21．（12分）定义运算a⊗b=，设函数f（x）=x⊗（2﹣x）．（1）用代数方法证明：函数f（x）的图象关于直线x=1对称；（2）设g（x）=m2x+2+m，若f（e x）≤g（x）在区间[0，+∞）上恒成立，求实数m的取值范围．请考生在第22、23两题中选一题作答．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，直线l的参数方程为（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为ρ=6sinθ．（1）求圆C的直角坐标方程；（2）若点P（1，2），设圆C与直线l交于点A，B，求证：|PA|×|PB|为定值．[选修4-5：不等式选讲]23．设函数f（x）=|2x+2|﹣|x﹣2|．（1）求不等式f（x）＞2的解集；（2）x∈R，f（x）≥t2﹣t恒成立，求实数t的取值范围．2018年四川省凉山州高考数学一诊试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）已知集合A={x|0＜x≤6}，B={x∈N|2x＜33}，则集合A∩B的元素个数为（）A．6 B．5 C．4 D．3【解答】解：集合A={x|0＜x≤6}，B={x∈N|2x＜33}={0，1，2，3，4，5}，则集合A∩B={1，2，3，4，5}，其元素个数为5，故选B．2．（5分）命题“∀x＞1，”的否定是（）A．∀x＞1，B．∀x≤1，C．∃x0＞1，D．∃x0≤1，【解答】解：因为全称命题的否定是特称命题，所以命题“∀x＞1，”的否定是∃x0＞1，故选：C．3．（5分）已知Z=，则Z•=（）A．B．0 C．1 D．【解答】解：∵Z=，∴Z•=|Z|2=．故选：C．4．（5分）已知f（x）=sin（x﹣）﹣1，则f（x）的最小正周期是（）A．2πB．πC．3πD．4π【解答】解：f（x）=sin（x﹣）﹣1，则f（x）的最小正周期是T=2π．故选：A．5．（5分）以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点，则椭圆的离心率是（）A．B．C．D．【解答】解：根据题意，以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点，则有2b=，即a=3b，则c==2b，则椭圆的离心率e==；故选：D．6．（5分）已知锐角α满足cos（α﹣）=cos2α，则sinαcosα等于（）A．B．﹣ C．D．﹣【解答】解：由cos（α﹣）=cos2α，得，∴，∵α∈（0，），∴sinα+cosα＞0，则cosα﹣sinα=．两边平方得：，∴sin．故选：A．7．（5分）执行如图所示的程序框图，当输出S=210时，则输入n的值为（）A．6 B．7 C．8 D．9【解答】解：由题意，模拟执行程序，可得程序框图的功能是计算S=n×（n﹣1）× (5)值，由于S=210=7×6×5，可得：n=7，即输入n的值为7．故选：B．8．（5分）已知点M的坐标（x，y）满足不等式组，N为直线y=﹣2x+2上任一点，则|MN|的最小值是（）A．B．C．1 D．【解答】解：点M的坐标（x，y）满足不等式组的可行域如图：点M的坐标（x，y）满足不等式组，N为直线y=﹣2x+2上任一点，则|MN|的最小值，就是两条平行线y=﹣2x+2与2x+y﹣4=0之间的距离：d==．故选：B．9．（5分）在△ABC中，a2tanB=b2tanA，则△ABC是（）A．等腰三角形B．直角三角形C．等腰三角形D．等腰或直角三角形【解答】解：∵a2tanB=b2tanA，∴由正弦定理可得：sin2AtanB=sin2BtanA，∴由sinA≠0，sinB≠0，可得：sinAcosA=sinBcosB，∴sin2A=sin2B，∴2A=2B，或2A+2B=π，∴A=B或A+B=，∴△ABC是等腰或直角三角形．故选：D．10．（5分）设y=f（x）是R上的奇函数，且f（x）在区间（0，+∞）上递减，f（2）=0，则f（x）＞0的解集是（）A．（﹣∞，﹣2）B．（0，2） C．（﹣∞，﹣2）∪（0，2）D．（﹣2，0）∪（0，2）【解答】解：根据题意，函数f（x）是奇函数，在区间（0，+∞）上单调递减，且f （2）=0，则函数f（x）在（﹣∞，0）上单调递减，且f（﹣2）=﹣f（2）=0，当x＞0时，若f（x）＞0，必有0＜x＜2，当x＜0时，若f（x）＞0，必有x＜﹣2，即f（x）＞0的解集是（﹣∞，﹣2）∪（0，2）；故选：C．11．（5分）如图，网格纸上小正方形的边长为1，粗线画的是一个几何体的三视图，则该几何体的体积为（）A．3 B．C．7 D．【解答】解：由已知中的三视图可得：该几何体是由一个长方体切去一个三棱锥所得的组合体，长方体的长，宽，高分别为：2，1，2，体积为：4，切去的三棱锥的长，宽，高分别为：2，1，1，体积为：，故组合体的体积V=4﹣=，故选：B12．（5分）若函数f（x）=4﹣x2+alnx满足∀x＞0，有f（x）≤3成立，则a的取值范围是（）A．{2}B．（，2]C．[2，3） D．（1，2]【解答】解：函数f（x）=4﹣x2+alnx满足∀x＞0，有f（x）≤3成立⇔x2﹣1﹣alnx≥0对∀x ＞0恒成立．令g（x）=x2﹣1﹣alnx，，①当a≤0时，g′（x）≥0恒成立，g（x）在（0，+∞）单调递增，而g（1）=0，故不符合题意；②当a＞0时，令g′（x）=0，x，g（x）在x=处有极小值，而g（1）=0∴，∴a=2，故选：A二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）设向量=（1，﹣2），=（6，m），若⊥，则m=3．【解答】解：根据题意，向量=（1，﹣2），=（6，m），若⊥，则•=1×6+（﹣2）×m=0，故答案为：3．14．（5分）我国古代数学名著《张邱建算经》有“分钱问题”：今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还敛聚与均分之，人得一百钱，问人几何？意思是：将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？则题中的人数是195．【解答】解：设共有n人，根据题意得；3n+=100n，解得n=195；∴一共有195人．故答案为：195．15．（5分）已知各项为正的等比数列{a n}中，a2a3=16，则数列{log2a n}的前四项和等于8．【解答】解：各项为正的等比数列{a n}中，a2a3=16，可得a1a4=a2a3=16，即有log2a1+log2a2+log2a3+log2a4=log2（a1a2a3a4）=log2256=8．故答案为：8．16．（5分）已知函数f（x）=，则方程f（1+x2）=f（2x）的解集是{x|x≥0} ．【解答】解：∵函数f（x）=，方程f（1+x2）=f（2x），∴当x＜0时，2=e2x+1，解得x=0，不成立；当x≥0时，f（1+x2）=f（2x）=2，成立．∴方程f（1+x2）=f（2x）的解集是{x|x≥0}．故答案为：{x|x≥0}．三、解答题（本大题共5小题，共70分）17．（12分）设数列{a n}a n=2n﹣1．（1）求数列{a n}的前n项和；（2）设数列{b n}满足b n=2，求数列{a n b n}的n项和．【解答】解：（1）数列{a n}的通项公式：a n=2n﹣1，则：数列为首项为1，公差为2的等差数列．所以：，（2）设数列{b n}满足b n=2=22n=4n，则：{a n b n}的通项公式为：，则：+…+（2n﹣1）•4n①，+…+（2n﹣1）•4n+1②，①﹣②得：﹣（2n﹣1）•4n+1﹣4．解得：，整理得：．当n=1时，T1=4，当n≥2时，，对n=1也成立，故，n∈N*．18．（12分）如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2，AC=CD=．（1）求证：PD⊥平面PAB；（2）求四面体PACD的体积．【解答】（1）证明：∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，AB⊥AD，AB⊂平面ABCD，∴AB⊥平面PAD，∵PD⊂平面PAD，∴AB⊥PD，又PD⊥PA，且PA∩AB=A，∴PD⊥平面PAB；（2）解：取AD中点O，连接PO，则PO⊥AD，又平面PAD⊥平面ABCD，∴PO⊥平面ABCD，∵PA⊥PD，PA=PD，AD=2，∴PO=1．在△ACD中，由AD=2，AC=CD=，可得．∴．19．（12分）共享单车的推广给消费者带来全新消费体验，迅速赢得广大消费者的青睐，然而，同时也是露出管理、停放、服务等方面的问题，为了了解公众对共享单车的态度（“提倡”或“不提倡”），某调研小组随机的对不同年龄段50人进行调查，将调查情况整理如下表：并且，年龄[20，25）和[40，45）的人中持“提倡”态度的人数分别为5和3，再从这两个年龄段中各随机抽取2人征求意见．（1）求年龄在[20，25）中被抽到的2人都持“提倡”态度的概率；（2）求年龄在[40，45）中被抽到的2人至少1人持“提倡”态度的概率．【解答】解：（1）年龄在[20，25）中共有6人，其中持“提倡”态度的人数为5，其中抽两人，基本事件总数n==15，被抽到的2人都持“提倡”态度包含的基本事件个数m==10，∴年龄在[20，25）中被抽到的2人都持“提倡”态度的概率p==．（2）年龄在[40，45）中共有5人，其中持“提倡”态度的人数为3，其中抽两人，基本事件总数n′==10，年龄在[40，45）中被抽到的2人至少1人持“提倡”态度包含的基本事件个数m′==9，∴年龄在[40，45）中被抽到的2人至少1人持“提倡”态度的概率p′==．20．（12分）若A（x1，y1），B（x2，y2）是椭圆E：+y2=1上位于x轴上方两点，且x1+x2=2．（1）若y1+y2=1，求线段AB的垂直平分线的方程；（2）求直线AB在y轴上截距的最小值．【解答】解：（1）设AB的中点为M，则M（1，）由，得=0∴⇒即k AB=﹣，∴线段AB的垂直平分线的斜率为．∴线段AB的垂直平分线的方程为y﹣=，即9x﹣2y﹣8=0为所求．（2）设直线AB：y=kx+m．由得（1+9k2）x2+18kmx+9m2﹣9=0，x1+x2=﹣=2．⇒9k2+9km+1=0…①∵A（x1，y1），B（x2，y2）是椭圆E：+y2=1上位于x轴上方两点，∴k＜0，m＞0…②△=（18km）2﹣4（1+9k2）（9m2﹣9）＞0⇒9k2﹣m2+1＞0…③，结合①②得m=（﹣k）+，当且仅当k=﹣时，取等号．此时，k=﹣满足③．∴直线AB在y轴上截距的最小值为．21．（12分）定义运算a⊗b=，设函数f（x）=x⊗（2﹣x）．（1）用代数方法证明：函数f（x）的图象关于直线x=1对称；（2）设g（x）=m2x+2+m，若f（e x）≤g（x）在区间[0，+∞）上恒成立，求实数m的取值范围．【解答】解：（1）f（x）=x⊗（2﹣x）==1﹣|1﹣x|设点（x0，y0）为y=f（x）上任意一点，则f（2﹣x0）=（1﹣|2﹣x0﹣1|）=（1﹣|1﹣x0|）=（1﹣|x0﹣1|）=y0=f（x0）∴f（2﹣x0）=f（x0），令2﹣x0=1+x，则x0=1﹣x，∴f（1+x）=f（1﹣x），即x=1是函数f（x）的对称轴，∴函数f（x）的图象关于直线x=1对称，（2）∵x∈[0，+∞），∴e x≥1，∴f（e x）=2﹣e x，∵f（e x）≤g（x）在区间[0，+∞）上恒成立，∴2﹣e x≤m2x+2+m，∴﹣e x≤m2x+m，∵﹣e x≤﹣1，∴m2x+m≥﹣1，当m=0时，恒成立，当m≠时，∴y=m2x+m在[0，+∞）为增函数，∴y≥m，∴m≥﹣1，故m的取值范围为[﹣1，+∞）．请考生在第22、23两题中选一题作答．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，直线l的参数方程为（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为ρ=6sinθ．（1）求圆C的直角坐标方程；（2）若点P（1，2），设圆C与直线l交于点A，B，求证：|PA|×|PB|为定值．【解答】解：（1）圆C的方程为ρ=6sinθ．转化为直角坐标方程：x2+y2﹣6y=0．证明：（2）点P（1，2），设圆C与直线l交于点A，B，把直线l的参数方程为（t为参数），代入x2+y2﹣6y=0，整理得：t2+2（cosα﹣sinα）t﹣7=0，（t1和t2为A和B对应的参数），则：t1•t2=﹣7（定值），故：|PA|×|PB|=|t1t2|=7为定值．[选修4-5：不等式选讲]23．设函数f（x）=|2x+2|﹣|x﹣2|．（1）求不等式f（x）＞2的解集；（2）x∈R，f（x）≥t2﹣t恒成立，求实数t的取值范围．【解答】解：（1）函数f（x）=|2x+2|﹣|x﹣2|=，当x＜﹣1时，不等式即﹣x﹣4＞2，求得x＜﹣6，∴x＜﹣6．当﹣1≤x＜2时，不等式即3x＞2，求得x＞，∴＜x＜2．当x≥2时，不等式即x+4＞2，求得x＞﹣2，∴x≥2．综上所述，不等式的解集为{x|x＞或x＜﹣6}．（2）由以上可得f（x）的最小值为f（﹣1）=﹣3，若∀x∈R，f（x）≥t2﹣t恒成立，只要﹣3≥t2﹣t，即2t2﹣7t+6≤0，求得≤t≤2．。

第1页，总18页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名：____________班级：____________学号：___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………四川省凉山州2018-2019学年高中毕业班文数第一次诊断性检测试卷考试时间：**分钟 满分：**分姓名：____________班级：____________学号：___________题号 一 二 三 总分 核分人 得分注意事项：1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释评卷人 得分一、单选题（共12题)1. 在 中，分别是内角 的对边，若 ， ， ，则 的面积等于（ ）A .B .C .D . 32. 已知，则“ ”是“ ”成立的（ ）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要 3. 设集合 ，集合 ，则（ ）A .B .C .D .4. 下列函数中，既是奇函数，又在区间递减的函数是（ ）A .B .C .D .5. 已知双曲线 的渐近线方程是 ，则 的离心率为（ ）A .或2 B .答案第2页，总18页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………C .D . 或6. 如图，四棱柱 中， 分别是 、 的中点，下列结论中，正确的是（ ）A .B . 平面C . 平面D .平面7. 设是边长为2的正三角形， 是的中点， 是 的中点，则 的值为（ ）A . 3B .C . 4D .8. 执行如图所示的程序框图，输出 的值为（ ）。

第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{}|15A x x =<<，{}2|320B x x x =-+<，则A B =ð（ ）A ．{}|25x x <<B ．{}|25x x ≤<C ．{}|25x x ≤≤D ．∅【答案】B 【解析】考点：集合的运算. 2.212ii+-的虚部是（ ） A ．i B ．i -C ．1D ．1-【答案】C 【解析】 试题分析：()()()()2122121212i i i i i i i +++==--+,所以该复数的虚部为1，故选C. 考点：1.复数相关的概念；2.复数的运算. 3. 在ABC ∆中，60A =︒，45B =︒，b =a =（ ）ABC．D ．3【答案】D 【解析】试题分析：由正弦定理sin 3sin ba A B===，故选D. 考点：正弦定理.4. 已知双曲线221x y -=，点1F ，2F 为其两个焦点，点P 为双曲线上一点，若1||1PF =，则2||PF =（ ）A ．3B ．C ．4D ．2【答案】A 【解析】考点：双曲线的定义及几何性质.5. 函数()ln cos f x m x x =-在1x =处取到极值，则m 的值为（ ） A ．sin1 B ．sin1-C ．cos1D ．cos1-【答案】B 【解析】 试题分析：()sin mf x x x'=+,由(1)sin10f m '=+=得sin1m =-，故选B. 考点：导数与函数的极值.6. 某四棱锥的三视图如图所示，该三棱锥的体积是（ ）A ．43B ．83C ．4D ．6+【答案】A 【解析】试题分析：由三视图可知，该三棱锥底面是一个等腰直角三角形，直角边长为2，该棱锥的高为2，所以该三棱锥的体积为114222323V =⨯⨯⨯⨯=，故选A.7. 设数列{}n a 满足1a a =，2121n n n a a a +-=+（*n N ∈），若数列{}n a 是常数列，则a =（ ） A ．2- B ．1-C ．0D ．(1)n -【答案】A 【解析】考点：1.数列数的概念；2.数列的递推关系. 8. 设向量(cos ,sin )a x x =-，(cos(),cos )2b x x π=--，且a tb =，0t ≠，则sin 2x 的值等于（ ） A ．1 B ．1-C ．1±D ．0【答案】C 【解析】试题分析：因为(cos(),cos )(sin ,cos )2b x x x x π=--=-,a tb =，所以()()cos cos sin sin 0x x x x ---=，即22cos sin 0x x -=，所以2tan 1,tan 1x x ==±，()24k x k Z ππ=+∈， 2()2x k k Z ππ=+∈，sin 21x =±，故选C. 考点：1.向量的坐标运算；2.三角恒等变换；3.三角函数的性质.9. 设袋中有两个红球一个黑球，除颜色不同，其他均相同，现有放回的抽取，每次抽取一个，记下颜色后放回袋中，连续摸三次，X 表示三次中红球被摸中的次数，每个小球被抽取的几率相同，每次抽取相对立，则方差()D X =（ ） A ．2 B ．1C ．23D ．34【答案】C 【解析】试题分析：每次取球时，取到红球的概率为23、黑球的概率为13，所以取出红球的概率服从二项分布，即2(3,)3x B ~,所以222()3(1)333D x =⨯⨯-=，故选C.10. 下列四个结论：①若0x >，则sin x x >恒成立；②命题“若sin 0x x -=，则0x =”的逆否命题为“若0x ≠，则sin 0x x -≠”； ③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件； ④命题“x R ∀∈，ln 0x x ->”的否定是“0x R ∃∈，00ln 0x x -<”． 其中正确结论的个数是（ ） A ．1个 B ．2个C ．3个D ．4个【答案】C 【解析】考点：1.向量的坐标运算；2.三角恒等变换；3.三角函数的性质.【名师点睛】本题考查逻辑联结词与命题、特称命题与全称命题，属中档题；全称命题的否定与特称命题的否定是高考考查的重点，对特称命题的否定，将存在换成任意，后边变为其否定形式，注意全称命题与特称命题否定的书写，是常规题，很好考查了学生对双基的掌握程度.11. 公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n 的值为（ ）（ 1.732，sin150.2588︒≈，sin 7.50.1305︒≈）A ．12B ．24C ．36D ．48【答案】B 【解析】考点：1.数学文化；2.程序框图.【名师点睛】本题考查数学文化与程序框图，属中档题；数学文化是高考新增内容，程序框图是第年高考的必考内容，掌握循环程序的运行方法，框图以赋值框和条件框为主，按照框图箭线方向和每个框的指令要求运行，注意条件框的要求是否满足，运行程序时要准确.12. 若直线0ax y -=（0a ≠）与函数22cos 1()2ln2x f x x x+=+-图象交于不同的两点A ，B ，且点(6,0)C ，若点(,)D m n 满足DA DB CD +=，则m n +=（ ） A ．1 B ．2C ．3D ．a【答案】B 【解析】试题分析：因为222cos ()12cos 1()()22ln ln 22x x f x f x x x x x-++-===--+-+-，且直线0ax y -=通过坐标原点，所以函数22cos 1()2ln2x f x x x+=+-图象两个交点A ，B 关于原点对称，即0,0A B A B x x y y +=+=，又(,),(,),A A B B DA x m y n DB x m y n =--=--(6,)CD m n =-，由DA DB CD +=得，6,,A B A B x m x m m y n y n n -+-=--+-=，解之得2,0m n ==，所以2m n +=，故选B.考点：1.向量的坐标运算；2.函数的奇偶性.【名师点睛】本题考查向量的坐标运算，函数的奇偶性，属中档题；平面向量是高考的重点和热点内容，且常与函数、数列、三角、解析几何等交汇命题，解决此类问题的解题思路是转化为代数运算，其主要转化途径一是利用平面向量平行或垂直的条件，二是利用平面向量的线性运算或数量积的公式及性质.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 在棱长为1的正方体''''ABCD A B C D -中，异面直线'A D 与'AB 所成角的大小是 ． 【答案】3π【解析】BD'考点：1.正方体的性质；2.异面直线所成的角.14. 若x ，y 满足不等式2,6,20,x x y x y ≥⎧⎪+≤⎨⎪-≤⎩则z x y =-的取值范围是 ．【答案】[2,2]- 【解析】试题分析：在直角坐标系内作出不等式组2,6,20,x x y x y ≥⎧⎪+≤⎨⎪-≤⎩所表示的可行域如下图所示，由图可知目标函数z x y =-取得最小值时的最优解为点(4,2)B ，即m a x 422z =-=，取得最小值的最优解为点(2,4)C ，即min 242z =-=-，所以z x y =-的取值范围是[2,2]-.考点：线性规划.15. 设数列{}n a 是首项为1公比为2的等比数列前n 项和n S ，若4log (1)4k S +=，则k = ．【答案】8 【解析】考点：1.等比数列的性质与求和公式；2.对数的性质.【名师点睛】本题考查等比数列的性质与求和公式，对数的性质，属基础题；等比数列的求和公式是高考的热点内容，本题直接利用求和公式求和，利用对数性质运算即可，体现命题以考纲为主导，以教材为主线，取之于教材而高于教材. 16. 已知函数21()21x f x x +=-，则122016()()()201720172017f f f +++=… ． 【答案】2016 【解析】试题分析：因为212(1)12123()(1)2212(1)12121x x x x f x f x x x x x +-++-+-=+=+=-----，令122016()()()201720172017S f f f =+++… ，则1201622015201612()()()()()()22016201720172017201720172017S f f f f f f ⎡⎤⎡⎤⎡⎤=++++++=⨯⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦…，所以122016()()()2016201720172017S f f f =+++=…. 考点：1.函数的对称性；2.倒序相加法求和.【名师点睛】本题考查.函数的对称性与倒序相加法求数列的和，属中档题；数列是特殊的函数，将数列与函数综合是情理之中，倒序相加法是等差数列求和的重要思想，利用函数的对称性特点考查倒序相加法，是本题的亮点.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. （1）等差数列{}n a 的各项均为正数，13a =，前n 项和为n S ，10120S =，求n a ；（2）已知函数2()cos 2cos 1f x x x x =+-，63x ππ-≤≤，求()f x 的值域．【答案】（1）21n a n =-；（2）[]0,2 【解析】试题分析：（1）基本量法，即用1,a d 表示10S ,列出关于d 的方程，解出d ，即可求数列{}n a的通项公式；（2）由平方降幂公式及二倍角公式、两角和与差的正弦公式化简函数解析式可得()2sin(2)3f x x π=+，由63x ππ-≤≤可得023x ππ≤+≤，由三角函数性质可求出值域.考点：1.等差数列的性质及前n 项和公式；2.三角恒等变换；3.三角函数的图象与性质. 18. 化为推出一款6寸大屏手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下： 女性用户：男性用户：（1）如果评分不低于70分，就表示该用户对手机“认可”，否则就表示“不认可”，完成下列22⨯列联表，并回答是否有95%的把握认为性别对手机的“认可”有关：合计附：22()()()()()n a d b c K a b c d a c b d +-+=++++ （2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求2名用户中评分小于90分的概率． 【答案】（1）列联表120有95%的把握认为性别和对手机的“认可”有关． (2)35. 【解析】试题分析：（1）从频数分布表算出女性用户中“认可”手机人数与“不认可”手机人数，填入表格，同理算出男性用户中“认可”手机人数与“不认可”手机人数，填入表格可得22⨯列联表，由公式计算出2k 的值与临界值中数据比较即可；(2) 评分不低于80分有6人，其中评分小于90分的人数为4，记为A ，B ，C ，D ，评分不小于90分的人数为2，记为a ，b ,写出从6人中任取2人的所有基本事件，从中找出两名用户评分都小于90分的基本事件，即可求其概率.考点：1.独立性检验；2.古典概型.【名师点睛】本题考查独立性检验及古典概型，属中档题；独立性检验是一种统计案例，是高考命题的一个热点，多以选择题形式出现，命题的主要角度有：1.已知分类变量数据，判断两类变量的相关性；2.已知某些数据，求分类变量的部分数据；3.已知2K 的观察值，判断几种命题的正确性.19. 如图，已知四边形ABCD 和BCGE 均为直角梯形，//AD BC ，//CE BG 且2BCD BCE π∠=∠=，平面ABCD ⊥平面BCGE ，222BC CD CE AD BG =====．（1）求证：//AG 平面BDE ；（2）求三棱锥G BDE -的体积．【答案】(1)见解析；（2）23. 【解析】试题分析：（1）由题意可证,,CD CB CD CE CB CE ⊥⊥⊥，所以以C 为原点，CD 为x 轴，CB 为y 轴，CE 为z 轴，建立空间直角坐标系，求出直线AG 的方向向量(2,1,1)AG =-与平面BDE 的法向量m ，由0AG n ⋅=证之即可；（2）应用等体积转换求体积即可，即13G DBE D BEG BEG V V S h --∆==⨯⋅求之.∵(2,1,1)AG =-，∴0AG n ⋅=，∴AG n ⊥，∵AG ⊄平面BDE ，∴//AG 平面BDE ．（2）13G DBE D BEG BEG V V S h --∆==⨯⋅， ∵CD BC ⊥，面ABCD ⊥面BVEG ，而面ABCD 面BCEG BC =，∴CD ⊥平面BCEG ，∴2h CD ==， ∴112122323G BDE V -=⨯⨯⨯⨯=． 考点：1.线面平行的判定与性质；2.线面垂直的判定与性质；3.空间向量的应用.20. 设椭圆E ：22221(0)x y a b a b+=>>的离心率为12，E 上一点P 到右焦点距离的最小值为1．（1）求椭圆E 的方程；（2）过点(0,2)且倾斜角为60︒的直线交椭圆E 于A ，B 两点，求AOB ∆的面积．【答案】(1) 22143x y +=；【解析】试题分析：(1) 由题意12c a =，1a c -=，解出,a c 及b 的值即可；(2)先求出直线的方程2y =+，代入椭圆方程得21540x ++=，由弦长公式求出弦长AB ，再求出点O 到直线的距离即可求AOB ∆的面积.由点O 到直线AB 的距离1d ==，∴||2ABC AB S d ∆== 考点：1.椭圆的定义与标准方程、几何性质；2.直线与椭圆的位置关系. 【名师点睛】本题考查椭圆的标准方程与几何性质、直线与椭圆的位置关系,属中档题.求椭圆标准方程的方法一般为待定系数法：根据条件确定关于a ，b ，c 的方程组，解出a 2，b 2，从而写出椭圆的标准方程．解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．21. 设k R ∈，函数()ln f x x kx =-．（1）若2k =，求曲线()y f x =在(1,2)P -处的切线方程；（2）若()f x 无零点，求实数k 的取值范围．【答案】(1) 10x y ++=；(2) 1(,)e +∞.【解析】试题分析：(1)求函数()f x 的导数得1'()kx f x x-=，当2k =时，'(1)1f =-，由点斜式写出切线方程即可；(2)当0k <时，由(1)()0k f f e ⋅<可知函数有零点，不符合题意；当0k =时，函数()ln f x x =有唯一零点1x =有唯一零点，不符合题意；当0k >时，由单调性可知函数有最大值，由函数的最大值小于零列出不等式，解之即可.在区间1(0,)k 上，'()0f x >，函数()f x 是增函数； 在区间1(,)k+∞上，'()0f x <，函数()f x 是减函数； 故在区间(0,)+∞上，()f x 的极大值为11()ln1ln 1f k kk=-=--， 由于()f x 无零点，须使1()ln 10f k k =--<，解得1k e>， 故所求实数k 的取值范围是1(,)e +∞． 考点：1.导数的几何意义；2.导数与函数的单调性、极值、最值；3.函数与方程. 请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为3241x t y t =-+⎧⎨=+⎩（t 为参数），以原点O 为极点，x 轴正半轴为极轴（两坐标系取区间的长度单位）的极坐标系中，曲线2C ：2sin ρθ=．（1）求曲线1C 的普通方程与曲线2C 的直角坐标方程；（2）M ，N 分别是曲线1C 和曲线2C 上的动点，求||MN 最小值．【答案】（1）1C 的普通方程为43110x y +-=,2C 直角坐标方程：22(1)1x y +-=；（2）35. 【解析】试题解析：（1）1C ：32,21,34x t x y =-+⎧⎪--⎨=⎪-⎩∴2134x y --=-，整理得4833x y -=-+， ∴1C 的普通方程为43110x y +-=，曲线2C ：2sin ρθ=，22sin ρρθ=， 2220x y y +-=，整理得22211x y y +-+=，∴2C 直角坐标方程：22(1)1x y +-=．（2）如图，圆心(0,1)O 到直线1C 的距离为d ，|311|855d -==， ∴min 3||5MN d r =-=． 考点：1.参数方程与普通方程的互化；2.直角坐标与极坐标的互化；3.直线与圆的位置关系.23. 选修4-5:不等式选讲已知函数()|1|||f x x x a =+-+．（1）若不等式()0f x ≥的解集为空集，求实数a 的取值范围；（2）若方程()f x x =有三个不同的解，求实数a 的取值范围．【答案】（1）[1,)+∞；（2）10a -<<.【解析】试题分析：（1）（2）（2）在同一坐标系内作出函数()|1|||g x x x =+-图象和y x =的图象如下图所示，由题意可知，把函数()y g x =的图象向下平移1个单位以内（不包括1个单位）与y x =的图象始终有3个交点，从而10a -<<．考点：1.绝对值的意义；2.分段函数的表示；3.函数与方程、不等式.。

凉山州2017—2018学年度下期期末检测 高一数学（文科）参考答案一、选择题（共12个小题，每小题3分，满分36分） C B C B B C A B B A D D二、 填空题（共4个小题，每小题4分，满分16分）13． 1{| 5}2x x −<< 14． 3 15． 9416． 4三、 解答题（共5个小题，共48分）17.（8分） 解：原不等式可化为 (x ＋a )(x －2a )>0， ------------------------------（2分） 令(x ＋a )(x －2a )＝0，解得x 1＝－a ，x 2＝2a . --------------------------------(4分) 当a >0时，不等式的解集为(,)(2,)a a −∞−+∞U ；--------------------------------(6分) 当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞) . -------------------------------(8分)18. （10分）解：(1)∵a ＝(1,0)，b ＝(2,1)，∴ka －b ＝k (1,0)－(2,1)＝(k －2，－1)，a ＋2b ＝(1,0)＋2(2,1)＝(5,2)， ------------------------------（2分） ∵ka －b 与a ＋2b 共线，∴2(k －2)－(－1)×5＝0， ------------------------------（4分） ∴12k =−. ------------------------------（5分） (2) AB uuu r ＝2(1,0)＋3(2,1)＝(8,3)，BC uuu r ＝(1,0)＋m (2,1)＝(2m ＋1，m )． ------------------------------（7分） ∵⊥uuu r uuu r AB BC ，∴=(2+1)+=830uuu r uuu r AB BC m m ， ------------------------------（9分）∴819m =−. ------------------------------（10分） 19．（10分）解：(1)因为b 2＝a 2＋c 2－2ac cos B＝4＋25－2×2×5×35＝17， ----------------------------（3分） 所以b ＝17. -----------------------------（5分）(2)因为cos B ＝35，所以sin B ＝45， ---------------------------（6分） 由正弦定理b sin B ＝c sin C， ----------------------------（8分） 得1745＝5sin C ，所以sin C ＝41717. ------------------（10分） 20．（10分）解：(1)证明：∵P A ⊥平面ABCD ，BD ⊂平面ABCD ，∴P A ⊥BD . ------------------------------（2分）∵PC ⊥平面BDE ，BD ⊂平面BDE ，∴PC ⊥BD . ------------------------------（4分）又∵P A ∩PC ＝P ，∴BD ⊥平面P AC . ------------------------------（5分）(2)如图所示，设AC 与BD 的交点为O ，连接OE .∵PC ⊥平面BDE ，∴PC ⊥OE . ------------------------------（6分） 由(1)知，BD ⊥平面P AC ，∴BD ⊥AC ，由题设条件知，四边形ABCD 为正方形． ------------------------------（8分） 由AD ＝2，得AC ＝BD ＝22，OC ＝ 2.在Rt △P AC 中，PC ＝P A 2＋AC 2＝12＋(22)2＝3.易知Rt △P AC ∽Rt △OEC ， ------------------------------（9分）高一数学（文）参考答案 第 3 页 共 3 页∴OE P A ＝CE AC ＝OC PC，即OE 1＝CE 22＝23， ∴OE ＝23，CE ＝43∴V E ­BCD ＝13S △CEO ·BD ＝13·12OE ·CE ·BD ＝16×23×43×22＝827. ------------------------------（10分） 21．（10分）解：(1)由S n ＝12a 2n ＋12a n (n ∈N *)，可得 a 1＝12a 21＋12a 1，解得a 1＝1； ------------------------------（2分） (2)S n ＝12a 2n ＋12a n ，① 当n ≥2时，S n －1＝12a 2n －1＋12a n －1，② ------------------------------（3分） ①－②得(a n －a n －1－1)(a n ＋a n －1)＝0. ------------------------------（4分） 由于a n ＋a n －1≠0，所以a n －a n －1＝1， ------------------------------（5分） 又由(1)知a 1＝1，故数列{a n }是首项为1，公差为1的等差数列，故a n ＝n . ---------------------（6分）(3)由(1)知2n n b n =⋅，所以1212222n n T n =⋅+⋅+⋅⋅⋅+⋅，所以23121222(1)22n n n T n n +=⋅+⋅+⋅⋅⋅+−⋅+⋅， ---------------------------（8分） 两式相减，得1212222n n n T n +−=++⋅⋅⋅+−⋅12(12)212n n n +−=−⋅− 11222n n n ++=−−⋅12(1)2n n +=−−−⋅ ------------------------------（9分） 所以12(1)2n n T n +=+−⋅. ------------------------------（10分）。

四川省凉山州2018届高三第三次诊断性测试数学（文）试题第Ⅰ卷（选择题 共50分）一、选择题（每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.已知集合{}{}220,1,0,1A x x x B =--≤=-，则AB =( )A ．{}0,1B ．{}1,1-C ．{}1,0-D ．{}1,0,1-【答案】D 【解析】 试题分析：{}{}22012,A x x x x x =--≤=-≤≤A B ={}1,0,1-考点：集合的运算 2.i 为虚数单位，512iz i=+，则z =( ) A ．5B ．5C ．1D ．2【答案】A 【解析】试题分析：由题意()()()()5125252251212125i i i i z i z i i i i ⋅-+====+∴=-=++⋅- 考点：复数的模，复数的运算 3.已知p ：“直线l 的倾斜角4πα=”；q ：“直线l 的斜率1k =”，则p 是q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【答案】C考点：充要条件4.某算法的程序框图如右图所示，如果输出的结果为26，则判断框内的条件应为( ) A ．5k ≤B ．4k >C ．3k >D ．4k ≤【答案】C 【解析】考点：程序框图5.下列说法中，不正确的是( )A ．已知,,a b m R ∈，命题：“若22am bm <，则a b <”为真命题B ．命题：“2000,0x R x x ∃∈->”的否定是：“2,0x R x x ∀∈-≤” C ．命题“p 或q ”为真命题，则命题p 和命题q 均为真命题 D ．“3x >”是“2x >”的充分不必要条件 【答案】C 【解析】试题分析：A ．正确；B ．正确；D ，正确；C 不正确，若命题“p 或q ”为真命题，则命题p 和命题q 由一个为真命题即可 考点：命题的真假判定6.已知函数()()2sin 22f x x πϕϕ⎛⎫=+< ⎪⎝⎭图象过点()0,3，则()f x 图象的一个对称中心是( ) A ．,03π⎛⎫-⎪⎝⎭B ．,06π⎛⎫-⎪⎝⎭C ．,06π⎛⎫⎪⎝⎭D ．,012π⎛⎫⎪⎝⎭【答案】B考点：正弦函数的图像7.《庄子·天下篇》中记述了一个著名命题：“一尺之棰，日取其半，万世不竭．”反映这个命题本质的式子是( )A ．21111122222n n +++⋅⋅⋅+=-B ．211112222n +++⋅⋅⋅++⋅⋅⋅< C ．21111222n ++⋅⋅⋅+=D ．21111222n ++⋅⋅⋅++⋅⋅⋅<【答案】D 【解析】试题分析：据已知可得每次截取的长度构造一个以12为首项，以12为公比的等比数列， 21111112222n n ++⋅⋅⋅++⋅⋅⋅=-<.故反映这个命题本质的式子是21111222n ++⋅⋅⋅++⋅⋅⋅<. 故选D考点：数列递推式8.某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的表面积为( ) A ．32πB ．3π+C ．532π+ D ．332π+【答案】D考点：几何体的表面积，三视图9.已知1F 、2F 是椭圆和双曲线的公共焦点，P 是它们的一个公共点，且123F PF π∠=，则椭圆和双曲线的离心率的倒数之和的最大值为( ) A ．433B ．233C ．3D ．2【答案】A 【解析】试题分析：设椭圆的长半轴为a ，双曲线的实半轴为()11,a a a ＞，半焦距为c ，由椭圆和双曲线的定义可知，设112212|2|PF r PF r FF c===，，，，椭圆和双曲线的离心率分别为12e e ， 12,3F PF π∠=∴由余弦定理可得2221212432c r r r r cosπ=+-（）（），①在椭圆中，①化简为即2212443c a rr =-，即122213114r r c e -＝，② 在双曲线中，①化简为即221244c a rr +=，即12222114r r c e +＝-，③ 联立②③得，2212114e e +=， 由柯西不等式得22212121111131133e e e e ⎛⎫⎛⎫⎛⎫++≥⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即（2124311e e ⎛⎫+ ⎪⎝⎭≤⨯4， 即1211164333e e +≤=，当且仅当12333e e ＝，＝时取等号，故选A 考点：椭圆，双曲线的简单性质，余弦定理 10.函数()()()321121132f x x b x b b x =-+++在()0,2内有极小值，则( ) A ．01b <<B ．02b <<C ．11b -<<D ．12b -<<【答案】C考点：导数的综合应用【名师点睛】本题考查函数的导数的应用，函数的单调性以及函数的极值的求法，考查计算能力，属中档题. 解题时求出函数的导数，得到极值点，判断函数的单调性，求出极小值点，得到关系式，求解即可．第Ⅱ卷（非选择题，共100分）二、填空题（共5小题，每题5分，共25分）11.已知向量()(),4,4,1m m ==+a b ，若⊥a b ，则实数m =______． 【答案】2m =-【解析】试题分析：因为向量()(),4,4,1m m ==+a b ，⊥a b ，所以0⋅a b =，即440mm ++=（），解得2m =-；考点：向量垂直的充要条件12.已知(),P x y 为区域002x y x y x +≥⎧⎪-≥⎨⎪≤⎩内的任意一点，则2z x y =-的取值范围是______．【答案】]6[0z ∈，， 【解析】试题分析：画出可行域如图所示：由题意可求得22A -（，），由2z x y =-得：2y x z =-，显然直线过00（，）时，z 最小，最小值是0，直线过22A -（，）时，z 最大，最大值是6，故]6[0z ∈，． 考点：简单的线性规划13.某班级有50名学生，现用系统抽样的方法从这50名学生中抽出10名学生，将这50名学生随机编号为15号，并按编号顺序平均分成10组（15号，610号，…，4650号），若在第三组抽到的编号是13，则在第七组抽到的编号是______． 【答案】73 【解析】试题分析：因为是从50名学生中抽出10名学生，组距是10， ∵第三组抽取的是13号，∴第七组抽取的为1341073+⨯=． 考点：系统抽样 14.若3ln 23,log 3x y π==，则,x y 的大小关系是______【答案】x y > 【解析】试题分析：3ln 23ln 0,31,2x >∴=>又30log 31,x y ππ>∴<<∴>考点：指数函数、对数函数的性质15.若三角形三边长都是整数且至少有一个内角为3π，则称该三角形为“完美三角形”．有关“完美三角形”有以下命题：（1）存在直角三角形是“完美三角形” （2）不存在面积是整数的“完美三角形”（3）周长为12的“完美三角形”中面积最大为43；（4）若两个“完美三角形”有两边对应相等，且它们面积相等，则这两个“完美三角形”全等．以上真命题有______．（写出所有真命题的序号）． 【答案】（3）（4）．（3）设3C π=，则2221223a b c c a b abcosπ++==+-，，可得22212a b a b ab --=+-（）， 化为2 16)480(ab ab -+≥，解得04ab ≤＜，即016ab ≤＜，当且仅当4a b ==时取等号，可得周长为12的“完美三角”中面积最大为13164322⨯⨯=，是真命题； （4）设13C C π== ，①若夹角3π的两条边分别相等，满足条件，则此两个三角形全等；②若夹角3π其中一条边相等，由于面积相等，夹角3π另一条边必然相等，可得：此两个三角形全等．因此是真命题．以上真命题有（3）（4）．故答案为：（3）（4）． 考点：命题真假判断，合情推理【名师点睛】本题考查了解三角形、余弦定理、三角形面积计算公式、基本不等式的性质、新定义、简易逻辑的判定方法、不等式的解法，考查了推理能力与计算能力，属于中档题． 三、解答题（共6小题，共75分）16.设等差数列{}n a 的前n 项和为n S ，且52135,21S S a a =+=． （1）求数列{}n a 的通项公式； （2）设数列11n n n b a a +=，求{}n b 的前n 项和n T ． 【答案】（1）21n a n =-；（2）21n nT n =+试题解析： (1）设数列{}n a 的首项为1a ，公差为d ，则根据题意可得()()111114414422a d a a d a d a d ⎧⨯-+=++⎪⎨⎪+=+⎩，解之可得11,2a d ==， 则21n a n =- （2）()()1111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭，则21n nT n =+ 考点：等差数列的通项公式，裂项求和法17.2018年1月份，某家电公司为了调查用户对该公司售后服务的满意度，随机调查了10名使用该公司产品的用户，用户通过“10分制”对公司售后服务进行评价．分数不低于9.5分的用户为满意用户，分数低于9分的用户为不满意用户，其它分数的用户为基本满意用户．已知这10名用户的评分分别为：7.6,8.3,8.7,8.9,9.1,9.2,9.3,9.4,9.9,10．（1）从这10名用户的不满意用户和基本满意用户中各抽取一人，求这两名用户评分之和大于18的概率；（2）从这10名用户的满意用户和基本满意用户中任意抽取两人，求这两名用户至少有一人为满意用户的概率． 【答案】（1）()14P A =；（2）()35P B = 【解析】试题分析：（1）从不满意有户和基本满意用户中各抽取一人，利用列举法能求出两名用户评价分之和大于18的概率．（2）从满意用户和基本满意用户中任意抽取两人，利用列举法能求出这两名用户至少有一人为满意用户的概率．试题解析：（1）不满意用户有4名，基本满意有4名，满意有2名 记：从这10名不满意用户和基本满意用户各抽取一名为事件A ∴()131444P A +==⨯ （2）记：从这10名满意用户和基本满意用户任意抽取两名至少有一名为满意用户为事件B∴()2112242635C C C P B C +== （列举略）考点：列举法，古典概型18.在ABC ∆中，设内角A 、B 、C 的对边分别为a 、b 、c ，3sin cos 362C C ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭． （1）求角C ；（2）若23c =，且sin 2sin A B =，求ABC ∆的面积． 【答案】（1）3C π=；（2）23ABC S ∆=【解析】试题分析：（1）利用两角差的正弦函数，余弦函数公式化简已知可得1cos 2C =，结合范围0C π<<，即可解得C 的值．（Ⅱ）由正弦函数化简sin 2sin A B =，可得2a b =，利用余弦定理解得b b ，可求a 的值，利用三角形面积公式即可得解．考点：余弦定理，正弦定理19.如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，ADBC ，PD ⊥底面ABCD ，90,2ADC AD BC ∠=︒=，Q 为AD 的中点，M 为棱PC 的中点．（1）证明：PA平面BMQ ；（2）已知2PD DC AD ===，求点C 到平面BMQ 的距离．【答案】（1）见解析；（2）点P 到平面BMQ 的距离22d = 【解析】试题分析：（1）连结AC 交BQ 于N ，连结MN ，只要证明MN PA ，利用线面平行的判定定理可证；（2）由（1）可知，，PA 平面BMQ ，所以点P 到平面BMQ 的距离等于点A 到平面BMQ的距离.试题解析：连结AC 交BQ 于N ，连结MN ，因为90ADC ∠=︒，Q 为AD 的中点，所以N 为AC 的中点，M 为PC 的中点，即PM MC =， ∴MN 为PAC ∆的中位线， ∴MNPA ，又MN ⊂平面BMQ ，PA ⊄平面BMQ ， 所以PA平面BMQ（2）由（1）可知，PA平面BMQ ，所以点P 到平面BMQ 的距离等于点A 到平面BMQ 的距离， ∴P BMQ A BMQ M ABQ V V V ---==， 取CD 的中点K ，连结MK ，可得MK PD ，∴112MK PD ==， 又PA ⊥底面ABCD ，∴MK ⊥底面ABCD ， 又11,22BC AD PD CD ====， 可求得1,2,3,1AQ BQ MQ NQ ====， ∴111323P BMQ A BMQ M ABQ V V V AQ BQ MK ---===⋅⋅⋅⋅=， 2BQM S ∆=，则点P 到平面BMQ 的距离322P BMQ BMQV d S -∆==． 考点：直线与平面平行的判断，点到面的距离，等体积法 20.已知函数()()ln f x x ax a R =-∈．（1）若2a =-，求曲线()y f x =在1x =处的切线方程； （2）求()f x 的单调区间．【答案】（1）310x y --=；（2）()f x 的单调递增区间为10,a ⎛⎫ ⎪⎝⎭，单调递减区间为1,a ⎛⎫+∞ ⎪⎝⎭【解析】试题分析：（1）求出()f x 的导数，求得切线的斜率和切点，由点斜式方程可得所求切线的方程；（2）求出()f x 的导数，讨论当0a ≤时，当0a >时，由导数大于0，可得增区间，导数小于0，可得减区间，注意0x >的条件．考点：利用导数研究函数的性质21.已知椭圆()2222:10x y T a b a b +=>>的离心率为22，过左焦点F 的直线与椭圆交于,A B两点，若线段AB 的中点为21,33M ⎛⎫- ⎪⎝⎭． （1）求椭圆的方程；（2）过右焦点的直线l 与圆222x y +=相交于 C 、D ，与椭圆T 相交于E 、G ，且5CD =，求EG ．【答案】（1）椭圆方程为2212x y +=;（2）827EG = 【解析】试题分析：（1）设()()1122,,,A x y B x y ，利用点差法求得221263b a c =⎛⎫- ⎪⎝⎭，再结合椭圆的离心率及隐含条件求得,a b 的值，则椭圆方程可求；（2）利用点到直线的距离公式、韦达定理及焦点弦长公式，计算即得结论． 试题解析：（1）由题意得，焦点为椭圆的左焦点，即(),0F c - 设弦与椭圆的交点为()()1122,,,A x y B x y ，代入椭圆方程得2211221x y a b+=…………①2222221x y a b +=…………② ①式-②式，得2221222212y y b a x x --=-…………③ ∵点M 平分弦AB ，弦经过焦点，∴121221211213,,223233x x y y y y x x c++-=-==--+，代入③式得，2221334233b a c ⨯-=⎛⎫-⨯-+ ⎪⎝⎭，即221263b a c =⎛⎫- ⎪⎝⎭，又∵2222,2c a b c a =-=，∴22212c b a ==，∴112263c =⎛⎫- ⎪⎝⎭， 即1,2c a ==，∴椭圆方程为2212x y +=考点：椭圆的简单性质【名师点睛】本题考查椭圆的简单性质，圆与椭圆的位置关系，直线与圆锥曲线的位置关系，注意解题方法的积累，属于中档题．。

凉山州2018届高中毕业班第一次诊断性检测文科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，，则集合的元素个数为（）A. 6B. 5C. 4D. 3【答案】B【解析】【详解】集合，根据集合交集的概念得到个数为5个。

故答案为：B。

2.命题“，”的否定是（）A. ，B. ，C. ，D.【答案】C【解析】因为“,”是全称命题，所以依据含一个量词的命题的否定可知：其否定是存在性命题，即“,”，应选答案C 。

3.已知复数，则（）A. B. 0 C. 1 D.【答案】C【解析】复数，故答案为：C。

4.已知，则的最小正周期是（）A. B. C. D.【答案】A【解析】根据三角函数周期的概念得到故答案为：A。

5.以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点，则椭圆的离心率是（）A. B. C. D.【答案】D【解析】根据题意，以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点，则有2b=，即a=3b，则c==2b，则椭圆的离心率e==；故选：D．6.已知锐角满足，则等于（）A. B. C. D.【答案】A【解析】由cos（α﹣）=cos2α，得，∴sinα+cosα＞0，则cosα﹣sinα=．两边平方得：，∴．故答案为：A。

7.执行如图所示的程序框图，当输出时，则输入的值可以为A.B.C.D.【答案】B【解析】由题意，模拟执行程序，可得程序框图的功能是计算S=n×（n-1）×…×5的值，由于S=210=7×6×5，可得：n=7，即输入n的值为7．故选：B．8.已知点的坐标满足不等式组，为直线上任一点，则的最小值是（）A. B. C. 1 D.【答案】A【解析】点的坐标满足不等式组的可行域如图：点的坐标满足不等式组，为直线上任一点，则的最小值，就是两条平行线与之间的距离：，故选A.点睛：本题考查线性规划的应用，平行线之间的距离的求法，考查转化思想以及计算能力，解决本题的关键是作出不等式组所表示的平面区域与的位置关系，难度一般；画出约束条件的可行域，利用已知条件，把的最小值转化求解平行线间的距离即可.9.在中，已知，则该的形状为（）A. 等腰三角形B. 直角三角形C. 正三角形D. 等腰或直角三角形【答案】D【解析】试题分析：由正弦定理，得，则即，即，所以，即，即为等腰或直角三角形.考点：三角形形状的判定.10.设是上的奇函数，且在区间上递减，，则的解集是（）A. B.C. D.【答案】C【解析】根据题意，函数f（x）是奇函数，在区间（0，+∞）上单调递减，且f （2）=0，则函数f（x）在（-∞，0）上单调递减，且f（-2）=-f（2）=0，当x＞0时，若f（x）＞0，必有0＜x＜2，当x＜0时，若f（x）＞0，必有x＜-2，即f（x）＞0的解集是（-∞，-2）∪（0，2）；故答案选：C．点睛：本题考查函数的单调性与奇偶性的综合应用，注意奇函数的在对称区间上的单调性的性质；对于解抽象函数的不等式问题或者有解析式，但是直接解不等式非常麻烦的问题，可以考虑研究函数的单调性和奇偶性等，以及函数零点等，直接根据这些性质得到不等式的解集。

数学〔文科〕 第一卷一、选择题：本大题共 12 个小题,每题 5 分,共 60 分.在每题给出的四个选项中，只有一项为 哪一项符合题目要求的.1. 复数〔〕A.B.C.【答案】A【解析】因为D. ，应选 A.2. 集合，集合A.B.C.【答案】A【解析】因为A. 3. 假设向量与向量A. 0 B. 4 C.D.【答案】D【解析】因为与向量，那么 D.〔〕,, 所以共线，那么〔〕共线，所以，解得，，应选，应选 D.4. 函数，那么〔〕A. 0 B. 1 C.D.【答案】D【解析】因为，应选 D.5. 某几何体的三视图如下图，其中俯视图中的圆的半径为 2，那么该几何体的体积为〔 〕仅供学习参考A.B.C.D.【答案】C【解析】由三视图可知，该几何体是一个正方体挖去一个圆柱所得的组合体，其中正方体的棱长为 8，圆柱的底面半径为 2，高为 6，那么该几何体的体积为：.此题选择 C 选项. 点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及 直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)假设所给几何体的体积不 能直接利用公式得出，那么常用等积法、分割法、补形法等方法进行求解．6. 在中，，，且 ，那么 〔 〕A.B. 5 C.【答案】A【解析】由正弦定理知D. ，又 知， ，所以由余弦定理知：，所以，应选 A.7. 假设，，那么 的值构成的集合为〔 〕A.B.【答案】C【解析】由C. 知，D. ，即，当时，，所以，从而，当时，，所以仅供学习参考，因此选 C.8. 执行如下图的程序框图，那么输出的 〔 〕A. 2 B. 1 【答案】BC. 0D. -1【解析】第一次执行性程序后，，第二次执行程序后后，满足条件 ，跳出循环，输出 ，应选 B.，第三次执行程序9. 设 ，假设 满足约束条件，那么的最大值的取值范围为〔 〕A.B.C.D.【答案】C【解析】作出可行域如下列图：目标函数为，当目标函数过点时，10. 函数 为偶函数，当 那么〔 〕时，仅供学习参考.设，，，A.B.C.【答案】A【解析】当 时，D.，在上是增函数，因为函数 为偶函数，所以，，，又，所以，应选 A.点睛：一般有关函数奇偶性单调性的题目，需要考察函数在局部区间上的单调性，利用分子 有理化，可快速判断该函数在 时的单调性，利用偶函数的性质，转化为判断自变量绝对 值的大小即可.11. 过双曲线的左焦点 作圆的切线，此切线与 的左支、右支分别交于 ， 两点，那么线段 的中点到 轴的距离为〔 〕 A. 2 B. 3 C. 4 D. 5 【答案】B【解析】因为直线过双曲线左焦点，设直线为，因为与圆相切知，解得，当 时不与双曲线右支相交，故舍去，所以直线方程为，联立双曲线方程，消元得，所以，即中点的纵坐标为 3，所以线段 的中点到轴的距离为 3，应选 B. 12. 在底面是正方形的四棱锥 上，平面 与 交于点 ，且 为〔 〕中， 底面，点 为棱 的中点，点 在棱，，那么四棱锥的外接球的外表积A.B.C.D.【答案】D 【解析】如下图，仅供学习参考延长 BA,CF,交于 G，连接 EG，与 PA 交于 K，那么 AG=6，过 A 作 AH//PB，与 EG 交于 H，那么，故,将四棱锥补成长宽高分别为 3，3, 的长方体，故四棱锥的外接圆即为长方体的外接圆，，，所以球的外表积为，应选 D.第二卷 二、填空题〔每题 5 分，总分值 20 分，将答案填在答题纸上〕13. 曲线在点 处的切线的斜率为__________．【答案】4【解析】因为，所以切线斜率为 4.故填 4.14. 我国古代数学名著?九章算术?有一抽样问题：“今有北乡假设干人，西乡七千四百八十 八人，南乡六千九百一十二人，凡三乡，发役三百人，而北乡需遣一百零八人，问北乡人数 几何？“其意思为：“今有某地北面假设干人，西面有 7488 人，南面有 6912 人，这三面要 征调 300 人，而北面共征调 108 人〔用分层抽样的方法〕，那么北面共有__________人．〞 【答案】8100 【解析】因为共抽调 300 人，北面抽掉了 108 人，所以西面和南面共 14400 人中抽出了 192人，所以抽样比为 ，所以北面共有人，故填 8100.15. 假设椭圆上一点到两个焦点的距离之和为 ，那么此椭圆的离心率为__________． 【答案】 【解析】当 时，由椭圆定义知，解得 ，不符合题意，当 时，由椭圆定仅供学习参考义知，解得 ，所以，故填 .点睛：此题由于不知道椭圆的焦点位置，因此必须进行分类讨论，分析椭圆中 的取值，从而确定 c,计算椭圆的离心率.16. 将函数的图像向左平移个单位长度后得到 的图像.假设在 上单调递减，那么 的取值范围为__________．【答案】【解析】因为，向左平移 个单位得函数，当时，函数为减函数，所以，求得，又，所以当 时，，故填 .点睛：此类函数单调性问题比拟困难，一般要先根据所给的单调区间计算的取值范围，让其成为正弦函数的单调区间的子集即可，利用这一原理，即可得出 的取值范围.三、解答题 〔本大题共 6 小题，共 70 分.解容许写出文字说明、证明过程或演算步骤.〕17. 设 为数列 的前 项和， ，.〔1〕证明：为等比数列；〔2〕求 .【答案】(1)见解析；〔2〕.【解析】试题分析：〔1〕由递推关系式构造〔2〕根据等比数列的前 n 项和公式计算即可. 试题解析：〔1〕证明：∵ ，，∴ ，∴，∴ ，，从而证明数列是等比数列；那么，仅供学习参考∴是首项为 2，公比为 2 的等比数列.〔2〕解：由〔1〕知，，那么.∴.18. 根据以往的经验，某建筑工程施工期间的降水量 〔单位： 〕对工期的影响如下表：根据某气象站的资料，某调查小组抄录了该工程施工地某月前 20 天的降水量的数据，绘制得 到降水量的折线图，如下列图所示.〔1〕求这 20 天的平均降水量；〔2〕根据降水量的折线图，分别估计该工程施工延误天数的概率.【答案】(1)433mm;(2)详见解析.【解析】试题分析：〔1〕根据折线图数据计算 20 天的平均降水量即可；〔2〕根据折线图分别计算延误天数，用频率估计概率.试题解析：〔1〕这 20 天的平均降水量为.〔2〕∵的天数为 10，∴ 的频率为，故估计 的概率为 0.5.仅供学习参考∵的天数为 6，∴ 的频率为，故估计 的概率为 0.3.∵的天数为 2，∴ 的频率为，故估计 的概率为 .∵的天数为 2，∴ 的概率为，故估计 的概率为 .19. 如图，四棱锥的底面是正方形， 平面， 为棱 上一点.〔1〕证明：平面平面 ；〔2〕设， ，记三棱锥的体积为 ，三棱锥的体积为 ，假设，求 的长.【答案】(1)详见解析;(2).【解析】试题分析：〔1〕根据条件可证明 AB 垂直平面 PAD，从而可证平面〔2〕根据等体积法，转换棱锥顶点即可求出.试题解析：〔1〕证明：∵ 平面，∴，∵底面是正方形，∴.又，∴ 平面 .∵平面 ，∴平面平面 .〔2〕解：设，∵，，∴ 的面积为∴.又，平面 ； ，仅供学习参考∴，∴ ，，，那么.又 平面 ，∴，∴.点睛：在三棱锥的体积、高等问题中，经常使用等体积法来处理，一般可转化顶点，利用体 积不变，高，底的变化来突破问题，解题中要注意使用.20. 曲线 由抛物线及抛物线组成，直线与曲线 有个公共点. 〔1〕假设，求 的最小值；〔2〕假设 ，记这 3 个交点为 ，其中 在第一象限， ，证明：.【答案】(1) 的最小值为 ;(2)详见解析.【解析】试题分析：〔1〕联立与，，故 与抛物线恒有两个交点.所以 值为 . 〔2〕由〔1〕知，与，至少有一个交点 .，可求得，，，可求得 的最小 ，再去证明.试题解析：〔1〕解：联立与，得，∵，∴ 与抛物线恒有两个交点.联立与，得.∵，∴〔2〕证明：由〔1〕知，且，∴，∵，∴，∴，∴ 的最小值为 .∴，∴易知为抛物线的焦点，那么设，仅供学习参考，那么，，∴，∴∵，∴点睛：此题主要考查了解析中的坐标运算，通过坐标关系建立方程进而求解根本量，这种解 法一般运算量较大，需要耐心计算，属于中档题.当解析中与向量问题的结合时，一般的思路 有两个，一个是寻找几何关系，比方：中点、垂直、角平分线等，利于数形结合求解；另一 个是通过向量坐标化，进而转成代数运算求解.21. 函数.〔1〕讨论 的单调性；〔2〕当 时，，求 的取值范围.【答案】(1)详见解析;(2)................... 〔2〕分 ， ， ，求和 0 比，求 的取值范围.试题解析：〔1〕当 时，，∴ 在 上单调递减.当 时，令，得，令，得∴ 的单调递减区间为，单调递增区间为，当 时，令，得，令，得∴ 的单调递减区间为 〔2〕当 时， 在 当 时，，单调递增区间为上单调递减，∴，不合题意.，不合题意，当 时，∴，故仅供学习参考，在 满足题意.上单调递增，当时， 在上单调递减，在单调递增，∴，故不满足题意.综上， 的取值范围为 请考生在 22、23 两题中任选一题作答，如果多做，那么按所做的第一题记分. 22. 选修 4-4：坐标系与参数方程在平面直角坐标系 中，圆 的参数方程为，〔 为参数〕，以坐标原点为极点， 轴的正半轴为极轴建立极坐标系.直线 的极坐标方程为 ，，且.〔1〕求圆 的极坐标方程；〔2〕设 为直线 与圆 在第一象限的交点，求 .【答案】(1);(2).【解析】【试题分析】(1)先将圆的参数消掉得到圆的直角坐标方程,展开后利用直角坐标和极坐标转换公式得到圆的极坐标方程.将交点对应极坐标角度代入圆的方程,求得对应 的值,也即 的值.【试题解析】解：〔1〕由，消去 得，∴，∴，即，故圆 的极坐标方程为.〔2〕∵，且，∴.将代入，得 ，∴.23. 函数.〔1〕求不等式的解集；〔2〕假设对恒成立，求 的取值范围.【答案】〔1〕不等式的解集为；〔2〕.【解析】〔1〕两边同时平方即可去掉绝对值号，求出不等式的解；〔2〕去掉绝对值号，别离参数根据恒成立即可求出 m 的取值范围.〔1〕由，得，仅供学习参考不等式两边同时平方得∴所求不等式的解集为〔2〕当时，，解得，..∴，即，对恒成立，即，对恒成立，又，∴且，∴.点睛：恒成立问题一般要别离参数，转化为求函数的最大值或最小值来处理，此题需要考虑含绝对值的不等式如何去掉绝对值号别离参数是关键.仅供学习参考仅供学习参考。

凉山州2018届高中毕业班第一次诊断性检测数学（文科）参考答案及评分意见一、选择题（共12题，每小题5分，共60分）1.B2.C3.C4.A5.D6.A7.B 8.B 9.D 10.C 11.B 12.A二、填空题（共4题，每题5分，共20分）13. 3 14.195 15.8 16.三、解答题（70分）17.解：(1)由为等差数列，……(6分) (2),设是的前n项和，①②由①—②得………………………………………………………(12分)18.解：(1)证明：因为平面PAD⊥平面ABCD，且交线为AD,由AB⊥AD得AB⊥平面PAD，又PD平面PAD，所以AB⊥PD，又PD⊥PA，PA=A，所以PD⊥平面PAB.……………………（6分）(2)取AD的中点为O，连接PO，CO，有PO⊥平面ABCD，PO就是四面体PACD的高，PO=1. OC⊥AD，OC=2，=AD OC=2，所以V=PO=.…………（12分）19.解：（1）设在，中的6人持“提倡”态度的为，，，，，持“不提倡”态度的为.总的基本事件有（），（），（），（），（），（），（），（），（），（），（），（），（），（），（）.共15个，其中两人都持“提倡”态度的有10个，所以P==…………………………………………（6分）（2）设在，中的5人持“提倡”态度的为，，，持“不提倡”态度的为，. 总的基本事件有()，()，()，()，()，()，()，()，()，()，共10个，其中两人都持“不提倡”态度的只有()一种，所以P==…………………………………… （12分）20．解：(1)设AB 中点为 ,则 ，，①②①-②得=的垂直平分线方程为：………………………(6分) （2）显然AB 的斜率存在.设直线AB ： ，联立消 得,且 、 位于 轴上方两点，且当且仅当时，等号成立，满足 ……………………………(12分)21．解：（1）f(x)={1x ，x -21x ，x ≥<,设f （x ）上任意点M(x,f(x))关于x=1对称后的点为N(2-x ，f （x ）)， 当x<1时，2-x>1∴f （2-x ）=2-(2-x)=x=f(x),当）x （f x -2）x -2（f ，1x -2时，1==∴≤≥x故，f （x ）的图像关于直线x=1对称。

凉山州2018届高中毕业班第二次诊断性检测数学(文科)参考答案及评分意见一、选择题（每题5分，共60分）1.C2.D3.C4.B5.D6.C7.D8.A9.B 10.C 11.A 12.B 二、填空题（每题5分，共20分） 13.97- 14.3- 15.3- 16.①②④三、解答题（共70分） 17.（12分）解（1）na d a a d a a a a a a n =∴=∴⎩⎨⎧==∴⎪⎩⎪⎨⎧>==+=+143012.743434352..............................................................................................6分 （2）422121)2111(...)4131()3121(2111211121221221+=+-=+-+++-+-=+-+=-+++++-+=-+++++=n n n n n T n n n n n n n n n n b n n......................................................................................................12分18. （12分）解(1) 由题：a=12, b=14, c=18, d=6,2250(1261418)x 4.327 6.63526243020⨯-⨯∴=≈<⨯⨯⨯,所以,没有99%的把握认为“接受程度”与家长性别有关。

......................................................................................................6分（2）选出的5人中持“赞成”态度的人数为：（人）230512=⨯ 持“无所谓”态度的人数为：3（人）设持“赞成”态度的人分别为21,a a ；持“无所谓”态度的人分别为321,,b b b 基本事件总数为：()()()()()()()()()()32312132221231211121,,,,,,,,,,b b b b b b b a b a b a b a b a b a a a ，，，，，，，，共10种其中至多一人持“赞成”态度的有：9种 109=∴p （或：其中两人都持“赞同”态度的人有1种，故所求概率1091011=-=p ） ......................................................................................12分19.（12分）解（1）证明：PDB PAC PAC AC PDB AC H BD PH AC PH BD AC ABCD AC ABCD PH 面面面面面面⊥⇒⎭⎬⎫⊂⊥⇒⎪⎭⎪⎬⎫=⋂⊥⊥⇒⎭⎬⎫⊂⊥.................................................................................................................6分 （2）()()332331321313113212133660,1603622222+=⨯+⨯=⨯⨯=∴+=⨯⨯==∴=-=∆=∴∆∴︒=∠=∴==∴︒=∠∆==∴=∆⊥=∴∠=∠∴∆≅∆-PH S V BD AC S PH AH PA PH PHA Rt PA PAB APB PB PA HB HA DH ADH DHA Rt HB AH AB AHB Rt AC DB HB HA HBA HAB ACB ADB ABCD ABCD P ABCD 中：在为等边三角形又中，在中在又ΘΘ..........................................................................................................................12分20.（12分）解：（1）()()()()())23,1(23121)2(14)1(45345.),3(),,3(0,3)0,3(0,0,2222212121P y x y x y x PF PF y x PF y x PF F F y x y x p ∴⎪⎩⎪⎨⎧==∴=+-=+-∴-=--=---=∴->>→→→→可求得联解又，，设ΘΘ...........................................................................................................................6分（2）()()()()()()⎪⎪⎭⎫⎝⎛⋃⎪⎪⎭⎫ ⎝⎛--∈∴<<-<<-∴<<∴<>++++>+++⋅>⋅+⋅∴>⋅⎪⎪⎩⎪⎪⎨⎧+=+-=+>⇒>∆=+++⇒⎪⎩⎪⎨⎧=++=+=>⋅∠→→→→22323,22232324434042102204112.411643001216411422:,,),,(02221212212121************22211，或即即由设存在显然设为锐角，即k k k k k x x k xx k kx kx x x y y x x OB OA k x x k k x x k kx x k y x kx y kx y l k y x B y x A OB OA AOB Θ ..................................................................................................12分222222max MQN 3333（2）法一：M （，），N （-，-）(分）2222点Q 到直线MN ：y=x 的距离为高，作与直线MN 平行x y 且与椭圆相切的的直线：y=x+m ，联立椭圆+=1得934x +6mx+3m -9=0，=36m -163m -9=0得m=分）1d S =2∴∴∆⨯±∴∴V ..............(12分)max MQN 法二：设椭圆上动点Q （3cos sin ）到直线|MN |：y=x 的距离为|3cos sin d=（-）...................................(9分）31d S =分）2θθπθ∴∴V22222'对y=x 21、解：（1）得：x +（a+1）x+1=0，=（a+1）-4=01a=-3或a=1（舍）.....................................................(1分）253F （x ）=x -3x+b ln （x-1）其中（x>1)F(x)=2x-3+0115在（1，+）恒成立，分子中，x =4ax y x bx x bx x ⎧+∆⎨=--⎩∴-++∴=≥--∞>11，=25-8（b+3）0，b .......(4分）8.∴∆≤∴≥12。

四川省凉山州2018-2019学年高中毕业班文数第一次诊断性检测试卷一、单选题 (共12题；共12分)1．（1分）设集合A={x|2x−1〉0}，集合B={−1,0,1,2}，则A∩B=（）A．B．C．D．2．（1分）下列函数中，既是奇函数，又在区间(0,1)递减的函数是（）A．B．C．D．3．（1分）已知双曲线E的渐近线方程是y=±2x，则E的离心率为（）A．或2B．C．D．或4．（1分）如图，四棱柱ABCD−A1B1C1D1中，E,F分别是AB1、BC1的中点，下列结论中，正确的是（）A．B．平面C．平面D．平面5．（1分）设ΔABC是边长为2的正三角形，E是BC的中点，F是AE的中点，则AB⇀·(FB⇀+FC⇀)的值为（）A．3B．C．4D．6．（1分）执行如图所示的程序框图，输出S的值为（）A．B．C．D．7．（1分）已知x,y∈R，则“ x2+(y−2)2≤8”是“ x−y+6>0”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要8．（1分）函数f(x)=|sinx+cos(x−π4)|的最小正周期为（）A．B．C．D．9．（1分）数列{a n}满足a1≠0，a n+1=2a n(n≥1)，S n表示{a n}的前n项和，且S n= 1272a2，则n=（）A．6B．7C．8D．910．（1分）在ΔABC中，a,b,c分别是内角A,B,C的对边，若a=√6，b=2c，cosA=78，则ΔABC的面积等于（）A．B．C．D．311．（1分）十七世纪法国数学家费马提出猜想：“当整数n>2时，关于x,y,z的方程x n+y n= z n没有正整数解”.经历三百多年，于二十世纪九十年中期由英国数学家安德鲁·怀尔斯证明了费马猜想，使它终成费马大定理，则下面说法正确的是（）A．存在至少一组正整数组使方程有解B．关于的方程有正有理数解C．关于的方程没有正有理数解D．当整数时，关于的方程没有正实数解12．（1分）若0<x1<x2<a都有x2lnx1−x1lnx2<x1−x2成立，则a的最大值为（）A．B．1C．D．二、填空题 (共4题；共4分)13．（1分）i是虚数单位，复数i3+4i=．14．（1分）函数y=2x 2+1x(x>0)的值域是．15．（1分）设F1,F2是椭圆E:x 225+y216=1的左右焦点，P是椭圆E上的点，则|PF1|·|PF2|的最小值是．16．（1分）定义函数f(x)=max{λx,−λx}，x∈R，其中λ>0，符号max{a,b}表示数a,b 中的较大者，给出以下命题：①f(x)是奇函数；②若不等式f(x−1)+f(x−2)≥1对一切实数x恒成立，则λ≥1③λ=1时，F(x)=f(x)+f(x−1)+f(x−2)+⋯+f(x−100)最小值是2450④“ xy>0”是“ f(x)+f(y)≥f(x+y)”成立的充要条件，以上正确命题是．（写出所有正确命题的序号）三、解答题 (共7题；共14分)17．（2分）从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分别直方图.（1）（1分）求这100份数学试卷成绩的中位数；（2）（1分）从总分在[55,65)和[135,145)的试卷中随机抽取2份试卷，求抽取的2份试卷中至少有一份总分少于65分的概率.18．（2分）如图，直三棱柱ABC−A1B1C1中，CC1=4，AB=2，AC=2√2，∠BAC=450，点M是棱AA1上不同于A,A1的动点.（1）（1分）证明：BC⊥B1M；（2）（1分）若M是AA1的中点，求四面体MB1BC的体积.19．（2分）设有三点A,B,P，其中点A,P在椭圆C:x2a2+y2b2=1(a>b>0)上，A(0,2)，B(2,0)，且OA⇀+OB⇀=√62OP⇀.（1）（1分）求椭圆C的方程；（2）（1分）若过椭圆C的右焦点的直线l倾斜角为450，直线l与椭圆C相交于E,F，求三角形OEF的面积.20．（2分）设数列{a n}中，a1=1，a2=2，且数列a2−a1,a3−a2,⋯,a n+1−a n,⋯是以2为公比的等比数列.（1）（1分）求数列{a n}的通项公式；（2）（1分）求数列{a n}的前n项和S n.21．（2分）设函数f(x)=3x2+alnx.（1）（1分）当a=−1时，求函数f(x)的单调减区间；（2）（1分）若F(x)=(f(x))3−f(x)有三个不同的零点，求a的取值范围.22．（2分）在直角坐标系xOy中，以坐标原点O为极点，以x轴非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2sinθ，直线l的极坐标方程为θ=θ0(ρ∈R)，曲线C与直线l相交于A,B两点.（1）（1分）求曲线C的直角坐标方程；（2）（1分）当θ0=π3时，求|AB|.23．（2分）已知函数f(x)=|2x+a|+|x+1|.（1）（1分）当a=1时，解关于x的不等式f(x)≥2；（2）（1分）当a=−1时，求f(x)的最小值.答案解析部分1．【答案】C【解析】【解答】由 2x −1>0 得 x >12，故 A ∩B ={1,2} .故答案为：C.【分析】本题利用一元二次不等式求出x 的取值范围，从而求出集合A ，再利用交集的运算求出集合A 和集合B 的交集。