通过层次分析法分析大学生毕业后去向问题

层次分析法在大学生就业中的应用
层次分析法（Analytic Hierarchy Process，简称AHP）是一种用于解决多指标决策问题的方法。

它可以将复杂的问题分解成多个层次，并通过对比不同层次的指标重要性，找
出最优的决策方案。

在大学生就业中，层次分析法可以应用于以下几个方面：
1. 就业选择：大学生毕业后面临着各种就业选择，如何在众多的职位中找到最适合
自己的就业方向是一个重要的问题。

层次分析法可以帮助大学生将自己的职业需求和个人
能力进行比较，从而找到最适合自己的就业选择。

2. 就业岗位评价：大学生在面临就业选择时，需要对不同的职位进行评价，包括工
作条件、薪酬待遇、职业发展前景等方面的考虑。

层次分析法可以将这些评价指标进行量化，并通过层次比较，得出不同职位的综合评价，帮助大学生做出更加准确的就业决策。

3. 就业准备：大学生在面临就业时，需要根据自身的专业能力和实际需求，进行一
系列的就业准备工作。

层次分析法可以帮助大学生确定哪些准备工作是最重要的，如何合
理分配时间和精力。

4. 就业机构选择：大学生在找工作时，也需要选择合适的就业机构，如企事业单位、政府机构、民营企业等。

层次分析法可以帮助大学生对不同的就业机构进行评价，并根据
自身需求和目标，选择最适合自己的就业机构。

层次分析法在大学生就业中的应用可以帮助他们更加科学地做出就业决策，提高就业
的质量和效果。

在使用层次分析法进行决策时，大学生也需要注意客观性和实用性，尽量
避免主观偏见的影响，确保决策结果的有效性。

还可以结合其他决策方法进行综合分析，
使决策更加全面和准确。

层次分析法大学生就业选择问题摘要：大学毕业生都面临着就业这个问题，面对着各行各业，应该如何选择适合自己的工作，是迫切需要解决的问题。

针对为大学生对所提供的工作，运用层次分析法来分析大学生对所提供的工作的满意程度，根据所得数据解决问题。

关键词：就业、层次分析法、决策、目标、权向量一．问题的提出对于一个大学毕业生来说，找到适合自己的工作是迫切需要解决的问题。

一个毕业生在找工作时，通过投简历，面试等方法，现有四个单位可以供他选择。

即：C1政府机构，C2化工厂，C3清洁工人，C4销售。

如何从这四个工作岗位中选择他比较满意的工作？这是目前需要解决的。

通过研究，最终确定了六个准则作为参照依据，来判断出最适合且最让他满意的工作。

准则：B1课题研究，B2发展前途，B3待遇，B4同事关系，B5地理位置，B6单位名气;通过这六个标准来评判出最满意的工作。

二．模型的假设一．该毕业生是文科生，但在大学期间也辅修了很多理科方面的学科，文理科兼懂。

二．四个单位对毕业生所具备的客观条件一样。

三．该毕业生对这四个工作岗位的工作都可以胜任。

1．层次结构模型的建立。

第一层：目标层，即对可供选择的工作的满意程度A ；第二层：准则层，即课题研究B1，发展前途B2，待遇B3，同事关系B4，地理位置B5，单位名气B6;第三层：方案层，即政府机构C1，化工厂C2，清洁工人C3，销售C4。

根据以上层次结构模型，我做了一份就业选择满意度的调查表，对100名在校大学生进行抽样调查。

首先让被调查者针对图示的某一层对其上一层某种因素影响的重要性进行打分，再将数据的分值看作服从随机变量的分布，再利用数学期望计算出平均分。

设ξ表示某个问题的分值，根据概率论以及数理统计所学的知识点，得出ξ服从离散型分布如下。

（其中i n 为打分值为i ξξ=的人数，N 为被调查的总人数） 根据数学期望的定义，我们有离散型随机变量ξ的数学期望： 5i i i E P ξξ==∑由调查数据和公式可以得到就业选择的整体评分表（表2，表3）表3就业选择的整体评分表3．构造成对比较矩阵和计算权向量：构造成对比较矩阵A，第二层准则层对第一层目标层的成对矩阵A：即A=111420.5112420.510.51530.5 0.250.250.210.3330.333 0.50.50.333310.333222331⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦运用SAS软件求解得出A的最大特征根及其对应的特征向量，即W13=0.38122380.44265620.40457180.10565730.26943220.6413177⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦归一化0.1700.1970.180?0.0470.1200.286⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，λ=6.5856436一致性检验：一致性比率0.11712871.24CICRRI===0.0944586<0.1，则一致性检验通过，W13可以作为权向量。

层次分析法在大学生就业中的应用1. 引言1.1 引言在当今社会，大学生就业问题备受关注。

随着社会经济的发展和就业形势的变化，大学生就业面临着诸多困难和挑战。

面对这一现实，如何科学地指导大学生选择就业方向，提高就业成功率，成为亟待解决的问题。

本文将从层次分析法的基本原理、在大学生就业中的应用案例、优势以及展望等方面进行探讨，旨在为大学生就业提供更科学、更系统的指导方法。

通过深入研究层次分析法在大学生就业中的应用，有助于帮助大学生更好地应对就业挑战，实现个人职业发展目标。

2. 正文2.1 层次分析法的基本原理层次分析法（Analytic Hierarchy Process，AHP）是一种多准则决策方法，由美国运筹学家Saaty于20世纪70年代提出。

其核心思想是通过对各因素之间的比较和评价，建立一个层次结构，将复杂的问题分解为若干层次，从而帮助决策者做出最佳选择。

在层次分析法中，首先确定决策目标，然后构建目标层、准则层、方案层等多层结构，将决策问题分解为不同的层次。

接着，对每个层次的元素进行两两比较，使用判断矩阵来量化各元素之间的相对重要性。

通过计算各元素的权重，最终得出最优决策结果。

层次分析法的基本原理在大学生就业中得到广泛应用。

在面对复杂的就业选择时，大学生可以利用AHP方法建立决策框架，明晰各自的就业目标、准则和方案，有助于他们做出科学、客观的职业选择。

通过量化和比较各因素的重要性，大学生可以更加清晰地认识自己的就业需求和优势，从而更好地规划自己的就业道路。

层次分析法通过建立层次结构、比较和评价各元素的相对重要性，为大学生提供了一种科学、系统的决策方法，有助于他们在就业选择中做出更加准确和合理的决策。

随着大学生就业环境的不断变化，层次分析法在大学生就业指导中的应用前景将会更加广阔。

2.2 层次分析法在大学生就业中的应用案例层次分析法在大学生就业中的应用案例可以从不同角度进行探讨。

我们可以以大学生个人的就业选择为例。

本科生毕业文题目：基于模糊综合评价的毕业生就业意识的分析作者：***学号：****所属学院：*****专业年级：*****指导教师：**** 职称：*** 完成时间：******基于模糊综合评价的毕业生就业意识的分析)摘要：本文针对当前大学生就业方向问题，利用层次分析的方法，并巧妙借用Shapley值的算法建立了一个相应的数学模型，综合多方面因素针对当前大学生就业方向问题进行全方位的分析。

创造性地将影响当前大学生就业方向的主观因素进行量化。

针对当前大学生就自身问题的实际情况，主要表现在感性因素和理性因素两个方面。

确定了个人感情、性格因素、家庭因素、工作环境、福利待遇、社会地位、社会价值等因素在大学生就业方向所占比重。

关键词：模糊综合评判；就业意识；理性因素；感性因素；归一化；Shapley值Based on the fuzzy comprehensive evaluation of graduateemployment consciousness analysisAbstract: This article in view of the current problems of university student's employment direction, using hierarchical analysis method, and clever Shapley value of the algorithm is established a corresponding mathematical model, the comprehensive many factors in view of the current problems of university students' employment direction in all analysis. Creative will influence the direction of university students' employment of subjective factors evaluated. In view of the current college students are the actual situation of its problems, mainly displays in sensibility factors and rational factors two aspects. Sure the personal feelings, personality factors, family factors, working environment, welfare, social status and social value in factors such as the proportion of the college students' employment direction.Key words:Fuzzy comprehensive evaluation; Employment consciousness; Rational factors; Sensibility factors; Shapley value一、问题重述1.1问题背景当今大学生就业难，是一个不争的事实。

收稿日期：2006-05-16作者简介：常少健，男，在校本科生，从事生物工程研究。

大学生毕业选择----相关问题的层次分析摘 要: 大学毕业生面对各种出路时，往往难以抉择，文章针对这个问题引进层次分析法（AHP ）模型，通过对定性因素加以量化和构造判断矩阵，然后对各种可能决策方案做出评价，最后求得最佳决策，为毕业生的出路选择提供了可靠的科学依据。

关键字：层次分析法（AHP ） 一致性指标 因素判断矩阵1 问题提出随着社会对人才需求的提高和研究生扩招步伐的加速，考研似乎成了当今大学校园里的一个热门话题。

从而使高校大学生徘徊在人生的岔路口，常常不知如何选择，是就业、考公务员从政还是考研，每年都会使许多学生为之彷徨，迷茫。

毕业前究竟是精心准备考研，还是为就业积累经验去实习或参加社会实践活动，这些都是毕业后的选择当今大学生普遍面临的难题。

随着高校扩招，本科生教育正在从传统的精英教育逐渐转变为大众教育，而我国现有的研究生教育还是属于高级别的精英教育，这也就注定了如此快速的增长不能满足更快速度的考研人数数量的增长。

这就意味着必定会有—部分一心打算考研的大学生最终无法考上，从而也就错过了就业的机会。

而同样在公务员的考试中也不愧为是千军万马过独木桥，难度同样很大。

其中，在考研人群中，有相当—部分应届生考研并非是出于现阶段发展的需要，而只是为了追求文凭或逃避就业压力，所以高校本科生应学会理性分析，对自己的今后发发展方向合理的定位．作出一个人生职业规划，不要盲目迷信文凭。

在明确自己发展目标之前不妨积累一些工作经验，通过工作成使自己己经成熟起来．作出适合自己的选择。

2 基本假设2.1假设文中所列准则因素均符合层次分析法的具体结构要求； 2.2模型中各个分析因素具有全面性；2.3假设在短时间内，题中各层因素结构不会发生变化。

3 符号说明Z ：目标层因素；n y ：准则层因素，83,2,1 =n ；ij a ：表示因素 i y 与因素j y 对目标Z 的影响程度之比，83,2,1, =i i ； A ：表示准则层对目标层的因素判断矩阵；n B ：表示方案层对准则层的成对比较阵，83,2,1 =n ； m F ：表示方案，3,2,1=m ；4 问题分析本文是在通过对高校大学生毕业选择多方面因素了解的情况下,就三种常见的毕业抉择(考研、就业、考公务员)进行了研究，运用层次分析法（AHP ）把一些定性的因素加以量化。

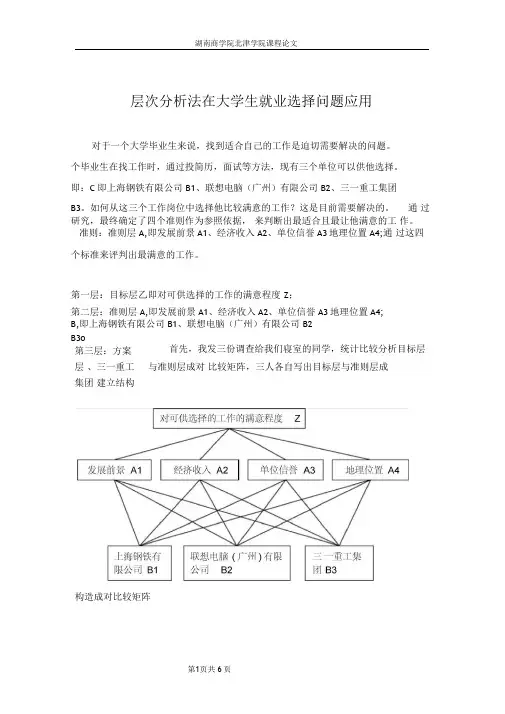
层次分析法在大学生就业选择问题应用对于一个大学毕业生来说，找到适合自己的工作是迫切需要解决的问题。

个毕业生在找工作时，通过投简历，面试等方法，现有三个单位可以供他选择。

即：C 即上海钢铁有限公司 B1、联想电脑（广州）有限公司 B2、三一重工集团B3。

如何从这三个工作岗位中选择他比较满意的工作？这是目前需要解决的。

通 过研究，最终确定了四个准则作为参照依据， 来判断出最适合且最让他满意的工 作。

准则：准则层A ,即发展前景A1、经济收入A2、单位信誉A3地理位置A4;通 过这四个标准来评判出最满意的工作。

第一层：目标层乙即对可供选择的工作的满意程度 Z ；第二层：准则层A,即发展前景A1、经济收入A2、单位信誉A3地理位置A4; B,即上海钢铁有限公司 B1、联想电脑（广州）有限公司 B2B3o首先，我发三份调查给我们寝室的同学，统计比较分析目标层与准则层成对 比较矩阵，三人各自写出目标层与准则层成第三层：方案层 、三一重工集团 建立结构构造成对比较矩阵（每一格表示a jj - A/A j，即横行对应值比竖列对应值之比）调查1意见调查2意见计算层次单排序的权向量和一致性检验由已知成对比较矩阵A ，利用matlab 编程求得A 相对于目标层Z 的权向量为:©二｛0.4987,0.2745,0.2268,0.0949.为衡量结果是否能被接受，萨蒂构造了最不一致的情况，几对不同的矩阵的B3 =由公式a ij%」j =1,2,3求得a 的几何平均值，列出逆对称矩阵 A 为:1 1霸1 1V 30315|_痂同样地方法，可写出目标层 C 与准则层B 之间的比较对称逆矩阵分别为:V 451 ^451 1菠,B 2 =1?75 1n的比较矩阵，采取1/9,1/7,……7,9随机取数的方法，并对不同的n用100-500 的子样，计算其一致性指标，再求得其平均值，记为RI.参考随机一致性指标为⑴计算矩阵A的相关数值：CI= 0.0719 ,RI=0.90 ,CR=CI/RI=0.0799v0.1则认为矩阵A通过一致性检验。

层次分析法在大学生就业中的应用【摘要】层次分析法是一种常用的决策分析方法，可以帮助大学生在就业选择时做出更加科学合理的决策。

本文首先介绍了层次分析法的基本原理，然后探讨了在大学生就业中的具体应用。

通过确定影响大学生就业的因素并建立层次分析模型，我们可以分析出各个因素对于就业选择的优先级，帮助大学生更好地理解自己的优势和劣势，从而更加明智地做出决策。

本文总结了层次分析法在大学生就业中的价值，并展望了未来的研究方向。

层次分析法的应用不仅可以指导大学生更好地规划自己的未来，还可以为大学生提供科学依据，帮助他们更好地适应社会就业环境。

【关键词】层次分析法、大学生就业、因素、优先级、模型、价值、展望、总结1. 引言1.1 研究背景大学生就业一直是社会关注的焦点，随着我国高等教育规模不断扩大，大学生就业压力也在逐渐增大。

当前，我国大学生就业形势严峻，就业渠道日益狭窄，就业竞争日益激烈，大学生就业面临着诸多挑战和困难。

如何有效地提升大学生就业竞争力，帮助他们更好地实现就业和发展，成为一个亟待解决的问题。

本研究旨在探讨层次分析法在大学生就业中的应用，借助层次分析法，深入分析大学生就业中的关键因素，建立相应的模型，为大学生提供更科学合理的就业选择，促进其顺利就业和职业发展。

就在于探究如何有效利用层次分析法解决大学生就业问题，提高大学生就业质量和效率。

1.2 研究目的大于2000字的内容，请稍等片刻，我马上为您生成。

1.3 研究意义大的统计，排版格式等。

：大学生就业一直是社会关注的焦点之一，随着经济社会的不断发展，大学生就业形势也日益严峻。

通过层次分析法在大学生就业中的应用研究，可以帮助我们更好地了解影响大学生就业的因素，提高大学生就业的效率和质量。

通过确定影响大学生就业的因素和建立层次分析模型，我们可以更加科学地评价和比较各种影响因素，为大学生提供更合适的就业选择建议。

分析大学生就业选择的优先级可以有效指导学生们制定更合理和有效的就业规划，提高他们的就业竞争力。

层次分析法大学生就业选择问题摘要：大学毕业生都面临着就业这个问题，面对着各行各业，应该如何选择适合自己的工作，是迫切需要解决的问题。

针对为大学生对所提供的工作，运用层次分析法来分析大学生对所提供的工作的满意程度，根据所得数据解决问题。

关键词：就业、层次分析法、决策、目标、权向量一•问题的提出对于一个大学毕业生来说，找到适合自己的工作是迫切需要解决的问题。

一个毕业生在找工作时，通过投简历，面试等方法，现有四个单位可以供他选择。

即: C1政府机构，C2化工厂, C3清洁工人，C4销售。

如何从这四个工作岗位中选择他比较满意的工作？这是目前需要解决的。

通过研究，最终确定了六个准则作为参照依据，来判断出最适合且最让他满意的工作。

准则：B1课题研究，B2发展前途，B3待遇，B4同事关系，B5地理位置，B6单位名气；通过这六个标准来评判出最满意的工作。

二.模型的假设一•该毕业生是文科生，但在大学期间也辅修了很多理科方面的学科，文理科兼懂。

二•四个单位对毕业生所具备的客观条件一样。

三•该毕业生对这四个工作岗位的工作都可以胜任。

1.层次结构模型的建立。

第一层：目标层，即对可供选择的工作的满意程度A;第二层：准则层，即课题研究B1，发展前途B2，待遇B3，同事关系B4，地理位置B5,单位名气B6; |第三层：方案层，即政府机构C1，化工厂C2，清洁工人C3，销售C4。

根据以上层次结构模型，我做了一份就业选择满意度的调查表，对100名在校大学生进行抽样调查。

首先让被调查者针对图示的某一层对其上一层某种因素影响的重要性进行打分，再将数据的分值看作服从随机变量的分布，再利用数学期望计算出平均分。

设•表示某个问题的分值，根据概率论以及数理统计所学的知识点，得出•服从离散型分布如下。

（其中n i为打分值为.二i的人数，N为被调查的总人数）根据数学期望的定义，我们有离散型随机变量'的数学期望：5E八i Ri -0由调查数据和公式可以得到就业选择的整体评分表（表2,表3）表12.4322.4322.432 0.608 1.216 4.864表就业选择的整体评分表万案准则 政府机构 化工厂清洁工销售课题研究 1.663 4. 989 0.8315 0.8315 发展前途 4.837 1.612 0.403 1.612 待遇 2.499 4.167 0.833 5 同事关系 4.803 4.803 0.801 1.601 地理位置 0.634 1.268 1.902 4.437 单位名气4.2821.4270.7144.2822.画出结构图目标层A方案层C3.构造成对比较矩阵和计算权向量： 构造成对比较矩阵 A ,第二层准则层对第一层目标层的成对矩阵 A:-111 42 0.5]11 2 4 2 0.5 A=10.5 1 530.50.25 0.25 0.2 1 0.333 0.3330.5 0.5 0.333 3 1 0.333222 331 一准则层B对工作的满意程度G :政府机构C 2:化工厂C 3 ：清洁工人C 4 :销售地理位置5B同事关系发展前途2B课题研究单位名气6B运用SAS 软件求解得出A 的最大特征根及其对应的特征向量,致性检验：一致性比率 CR=0.0944586<0.1，则一致性检验通过, RI 1.24以作为权向量。

层次分析法在大学生就业中的应用层次分析法（Analytic Hierarchy Process, AHP）是一种从不同层次和不同因素的角度对问题进行分析和决策的方法，可以帮助人们进行复杂问题的定量分析、排序和选择。

在大学生就业中，层次分析法可以被广泛应用于以下几个方面。

层次分析法可以用于确定就业的目标和重要因素。

在大学生就业过程中，往往存在多个因素对就业的影响，例如薪资待遇、工作环境、个人发展空间等。

通过使用层次分析法，可以将这些因素进行分层，对每一层进行权重的确定，从而帮助大学生确定自己对就业的需求和优先级。

层次分析法可以用于评估不同就业选择的优劣。

大学生在面临就业选择时，往往要面对各种各样的工作机会和岗位，如何评估和比较不同的就业选择是一个复杂的问题。

通过使用层次分析法，可以将不同的就业选择分解为不同的因素，并进行权重的赋值，从而得到不同就业选择的总体评估和排序结果，为大学生提供选择参考。

层次分析法可以用于制定就业方案和目标的具体实施。

在大学生就业过程中，往往需要进行细致的规划和决策，以确定具体的就业方案和目标。

通过使用层次分析法，可以将就业方案和目标分解成多个因素和子目标，并通过权重的计算和比较，指导大学生确定合理的就业方案和目标，并且为实施提供指导。

层次分析法可以用于帮助大学生进行就业决策的风险分析和控制。

在大学生就业过程中，可能存在一些不确定的因素和风险，如经济形势不稳定、行业竞争激烈等。

通过使用层次分析法，可以将这些风险因素进行分析和评估，并找出相应的控制措施，帮助大学生降低就业风险，增加就业成功的概率。

层次分析法在大学生就业中的应用层次分析法（Analytic Hierarchy Process，AHP）是美国数学家托马斯·萨蒂克所提出的一种多标准决策方法，广泛应用于各个领域，包括大学生就业。

大学生就业是一个多维度、多要素的复杂问题，涉及到个人能力、专业背景、就业渠道、薪酬待遇等多个方面。

通过使用层次分析法进行决策分析，可以帮助大学生更加科学地确定自己的就业方向。

层次分析法可以为大学生提供一个清晰的层次结构。

大学生就业问题可以分解为不同的层次，如个人能力、专业背景、就业前景等。

通过层次分析法，可以确定每个因素的重要程度，使得大学生能够有针对性地提升自己的能力和素质。

层次分析法可以为不同的决策因素赋予权重。

在就业决策中，不同的因素对于不同的大学生来说有着不同的重要程度。

通过层次分析法，可以对各个因素进行评估和排序，确定它们对大学生就业的影响程度。

这样一来，大学生可以根据个人情况和志向，有针对性地选择最适合自己的就业方向。

层次分析法可以帮助大学生进行方案评估和选择。

大学生在就业决策中通常会面临多个选择，如不同行业、不同职位等。

通过层次分析法，可以将每个选择转化为一个决策矩阵，并进行对比评估。

根据矩阵中的评估结果，大学生可以更加明确地了解每个选择的优劣势，并最终选择出最合适的就业方案。

层次分析法可以帮助大学生进行决策结果的敏感性分析。

由于大学生就业问题受到众多因素的影响，决策结果可能会对一些关键因素的变化非常敏感。

通过层次分析法，可以模拟不同因素变化对决策结果的影响，从而帮助大学生更好地应对潜在风险和挑战。

层次分析法在大学生就业中的应用能够帮助大学生更加科学地进行决策分析，提高就业的成功率。

通过层次分析法，大学生可以清晰地了解不同因素之间的关系和权重，从而更加准确地评估和选择就业方向。

它为大学生提供了一种理性决策的工具，使他们能够在就业竞争激烈的环境中脱颖而出，实现自己的职业目标。

层次分析法在大学生就业中的应用
层次分析法（Analytic Hierarchy Process，简称AHP）是美国管理科学家托马斯·萨迪克发表于20世纪70年代初的一种决策分析方法。

该方法主要用于对于多个准则和多个选择的问题进行决策。

1. 就业选择：大学生毕业后，面临着众多就业选择的问题。

层次分析法可以帮助大学生确定自己的就业目标，并根据不同的准则（如薪资待遇、工作内容、发展空间等）进行权重的设置，从而确定最适合自己的职业方向。

2. 就业前景评估：根据不同的行业和职业，大学生的就业前景也各不相同。

通过层次分析法，可以对不同的行业和职业进行综合评估，评估其就业前景的优劣，并根据自身的兴趣、能力和发展潜力进行选择。

3. 就业岗位比较：在就业过程中，大学生经常需要比较不同的岗位。

层次分析法可以帮助大学生对不同的岗位进行综合评价，包括工作强度、工作环境、薪资福利等方面，从而选择最适合自己的岗位。

4. 就业策略制定：层次分析法可以帮助大学生制定就业策略。

通过对就业市场、职业发展规划等方面进行分析和权重设置，可以确定最适合自己的就业策略，从而提高自己的就业竞争力。

5. 就业困难排除：一些大学生可能面临就业困难的情况，无法确定自己的职业方向或者找不到适合自己的工作。

层次分析法可以帮助他们进行就业困难的分析，找出问题所在，并制定相应的解决方案，提高就业成功的机会。

层次分析法在大学生就业中的应用主要体现在帮助大学生确定职业目标、评估就业前景、比较岗位选择、制定就业策略和排除就业困难等方面。

通过该方法的应用，可以提高大学生的就业竞争力和选择准确度，帮助他们更好地实现就业目标。

层次分析法在大学生就业中的应用【摘要】层次分析法是一种较为科学的决策分析方法，在大学生就业领域也有广泛的应用。

本文首先介绍了层次分析法的基本原理，然后针对大学生就业需求分析、岗位选择、意向排名和方案评价等方面进行了具体应用讨论。

通过层次分析法，大学生能更科学地选择职业方向，提高对自身职业发展的认知，并具有重要的指导意义。

层次分析法的使用可以帮助大学生更好地规划自己的职业生涯，提高就业成功率。

在大学生就业过程中，层次分析法是一种有益的工具，能够帮助他们做出更加合理和有效的决策。

通过本文的讨论，可以进一步认识到层次分析法在大学生就业中的重要作用，促进大学生们取得更好的职业发展。

【关键词】层次分析法, 大学生就业, 应用, 就业需求分析, 就业岗位选择, 就业意向排名, 就业方案评价, 职业方向选择, 自我认知, 指导意义1. 引言1.1 层次分析法在大学生就业中的应用层次分析法在大学生就业中的应用是一种系统性的决策方法，通过对不同因素的比较和权重分配，帮助大学生更科学地进行职业选择和规划。

在大学生就业中，层次分析法可以帮助他们理清自己的需求和优先排列自己的目标，从而更好地找到适合自己的职业方向。

层次分析法在大学生就业中具有重要的作用，可以帮助他们更好地理清自己的职业规划，提高对自身职业发展的认知，从而更好地实现自己的职业目标。

2. 正文2.1 层次分析法的基本原理层次分析法是一种系统性的决策分析工具，它通过将复杂问题分解为层次结构，然后利用专家判断矩阵对各层次的因素进行两两比较，最终确定各因素的权重，从而得出最终的决策结果。

在层次分析法中，首先确定目标，然后将目标分解成若干个层次，每个层次包含若干个因素，形成一个层次结构。

接着，对于每个层次的因素，利用专家意见或实证数据，构建判断矩阵，进行两两比较，确定各因素之间的重要程度。

通过计算特征值和特征向量，计算出各因素的权重，最终得出最佳决策方案。

层次分析法的基本原理是建立层次结构，通过专家判断矩阵确定各因素之间的相对重要性，利用数学计算方法得出各因素的权重，进而做出最佳决策。

层次分析法在大学生就业质量评价方面的应用层次分析法（Analytic Hierarchy Process，AHP）是一种用于多指标决策的定性和定量的分析方法，通过构建层次结构和计算权重，可以对不同因素进行排序和权重分配，进而进行决策。

大学生就业质量评价是对大学生就业状况的全面评估，包括就业率、就业结构、就业待遇、就业满意度等多个指标。

层次分析法可以被用于对这些指标进行评估和排序，帮助决策者更好地了解就业市场和大学生就业状况。

构建层次结构是层次分析法的第一步。

在大学生就业质量评价中，可以将就业率、就业结构、就业待遇和就业满意度作为第一层指标，然后进一步细分为更具体的子指标。

在就业率中可以包括毕业生就业率和大学生自主创业率等子指标。

进行两两比较。

在比较指标之间的重要性时，可以采用两两比较的方法，像是A指标比B指标重要多少、B指标比C指标重要多少等等。

这样可以得到一个判断矩阵，其中的元素代表了不同指标之间的相对重要性。

然后，计算权重。

通过判断矩阵的计算，可以得到指标之间的相对权重。

这些权重可以用于对指标进行排序，也可以用于对大学生就业质量进行评价。

具有较高权重的指标可以被认为对大学生就业质量的影响较大，相反，权重较低的指标则对就业质量的影响较小。

进行综合评价。

根据计算得到的指标权重，可以对大学生就业质量进行综合评价。

可以将各指标的得分乘以对应的权重，然后加权求和得到一个综合得分。

较高的综合得分代表较好的就业质量，较低的综合得分则代表较差的就业质量。

层次分析法的应用可以使大学生就业质量评价更加客观和科学。

通过对指标的两两比较和权重的计算，可以准确地评估不同指标之间的相对重要性，从而进行合理的决策。

该方法也可以用于对大学生就业质量进行定量的评价，为大学生提供更多的就业选择和发展机会。

工作选择问题提出：一个刚获得学位的大学生的大学毕业生面临选择工作岗位。

他将要考虑的准则有：贡献，收入，兴趣，发展，声誉，关系，位置。

等。

于是他提出可以构造如图6的层次结构，用层次分析法确定可供选择的工作的优先顺序，你认为合适么？一．问题分析对于这个问题，我们其实通过主观臆断，可以为该毕业生选择一个我们认为合适的单位，这种方法被称为定性分析。

但这并不一定是最好的，随意性较大，并不具有严格意义上的道理，有时可能还会造成很大的失误。

这时我们可以通过层次分析方法来解决，它把定性分析与定量研究结合在一起，能较好的解决问题。

建立三个层次，目标层、准则层、方案层。

二．建立层次结构模型步骤一.符号说明1假设三个单位可供选择, 单位p1,单位p2,单位p3；2考虑的6个主要因素，贡献B1，收入B2，发展B3，声誉B4，关系B5，位置B6、3 随机一致性指标RI，一致性比例CI,4 ,主特征向量W步骤二. 模型假设假如该生对目标层6个因素进行比较（相对目标层而言）的结果为与B2的重要性之比为1：2）步骤三. 模形的建立目标层O：选择工作单位；准则层C：发展前景B1、经济收入B2、单位信誉B3、地理位置B4；方案层P：单位p1,单位p2,单位p3三.模型求解1构造准则层对目标层次的比较矩阵A，进行一致性检验并求权向量。

得到判断矩阵A=[ 1 1/2 1/3 1 1/2 12 1 1 1/2 2 13 1 1 2 1 1/21 2 1/2 1 1 1/22 1/2 1 1 1 1/21 12 2 2 1]通过计算得Aw=(0.6842 1.0302 1.2565 0.08232 0.9054 1.4796)入=（0.6842/0.1104+1.0302/0.1823+0.0302/0.1823+1.2565/0.1915+0.8232/0.1495+0. 9054/0.1387+1.4796/0.2275）/6=6.158CI=（6.158-6）/（6-1）=0.0263CR=CI/RI 查表可得 RI=1.24 所以CR=0.021<0.1则认为矩阵A通过一致性检验2 方案层有三个单位可供选择, 单位p1,单位p2,单位p3，这位学生对方案层的3个因素相对于准则层的每一个因素进行两两比较的结果为针对B1针对B3针对B4针对B5计算组合权向量P1在目标中的组合权重：0.082x0.1104 +0.429x0.1823 +0.633x0.1915 +0.166x0.1495 +0.400x0.1387+0.5954x0.2275=0.4721同理 p2在目标中的组合权重：0.3278P3在目标中的组合权重： 0.2424则组合权向量=ww(3)=（0.4721 0.3278 0.2424）组合一致性比率为：CR*=0.0104<0.1所以层组合一致性检验通过。

关于湖南涉外经济学院商学院国贸1003班毕业生去向的调查分析及解决其问题的对策一、分析背景大学生就业，是事关国计民生的大事。

随着高校的扩招，现在的大学生早已没有当初作为知识分子的优势，而且现在大多数的学生就业将面临市场化的挑战。

在大型社会招聘上，拿着一沓材料参加面试也已经成为绝大多数用人单位的选人手段。

但是同成千上万个社会人一同竞争某一个岗位，除了一纸文凭，大学生应该用什么跟社会上的人竞争？这是一个社会需要考虑的问题。

通过对应届毕业生就业情况的调查可以从中发现造成就业难的问题所在，从而有针对性地解决问题。

同时在调查分析的过程中加入了一些毕业生在就业后的经验和建议，这对学校的素质培养和学生们的成长都有一定的帮助。

二、调查现状（一）2010届国贸三班学生目前就业现状根据对班上每位学生进行的调查，得出一份关于2010届国贸三班的毕业去向的调查表：占了约大多数，约占了总数的91.53%，考研的和考公务员的仅有3.39%和5.08%，选择出国的和其他的所占比例为零。

（二）造成就业难的障碍毕业生就业难的最大障碍是什么？所有未就业者对调查中所提问题都作了回答。

从调查来看，反映就业难最大的障碍是“就业岗位不足”，占到39.9%。

其次是反映“社会风气不正,求职主要靠关系而非学历”，占到23.21%。

反映适合的岗位难求者，亦占到16.67%。

反映所学专业不适应社会需要者，仅占2.38%。

（三）大学生在就业时所遇到的困难从前人研究来看，主要包括以下四个方面：1.大学毕业生在求职过程中受到用人单位的各种限制2.大学毕业生与用人单位之间信息沟通渠道不畅通3.大学毕业生求职压力大4.大学毕业生求职预期目标与实际存在差距三、调查综述在做这份调查报告之前，我也查找了一些相关的知识，并将一些学者的观点进行归纳，如下：（一）扩招对就业的影响《高等教育大众化背景下——大学生就业问题研究》中讲到高校扩招对大学生就业的影响。

在入学率增强的同时，中国就业市场的培养和结构调整并不同步，就业岗位的增长赶不上高校入学率的增长，使大学生就业市场供过于求。

用层次分析法选择理想的工作一.问题提出获得大学毕业学位的毕业生甲，“双向选择”时，用人单位与毕业生都有各自的选择标准和要求。

现在有多个职位可供他选择，因此,他面临多种选择和决策，问题是他将如何作出决策和选择？或者说他将用什么方法将可供选择的职位排序？甲从人才市场得到了三份职位A/B/C的资料,就甲来说选择职位的标准和要求主要考虑因素为以下四个标准：标准1：工作收入(待遇水平）；标准2：个人兴趣（即工作岗位是否适合发挥专长)；标准3：工作压力(人际关系和谐工作任务量等)；标准4:工作前景（发展晋升问题).二．建立层次结构模型根据问题提出将决策解分解为三个层次，即：目标层：（选择职位）准则层：（工作收入、个人兴趣、工作压力、工作前景4个标准）方案层:（有A,B，C三个选择职位)并用直线连接各层次。

图2-1层次结构图由图2—1可以看出对于甲来说一个满意的工作是用工作收入、个人兴趣、工作前景、工作压力四个标准综合衡量的。

三、构造两两比较矩阵3。

1根据相对重要性标度建立评估方案的标准：表3。

1-1比较尺度表3.2分别用单一标准“工作收入”、“个人兴趣”、“工作前景”、“工作压力"来评估三个职位方案,从而使方案两两比较得出两两比较矩阵。

首先，用“工作收入”作为评估A、B、C三个职位的标准,通过分析得到两两比较矩阵如表3.2—1所示：表3.2—1用两两比较方法对“工作收入”作为评估三职位的比较矩阵其次,用“个人兴趣"作为评估A、B、C三个职位的标准,通过分析得到两两比较矩阵如表3.2—2所示：表3。

2—2用两两比较方法对“个人兴趣”作为评估三职位的比较矩阵再次,用“工作前景”作为评估A、B、C三个职位的标准，通过分析得到两两比较矩阵如表3.2—3所示:表3.2—3用两两比较方法对“工作前景”作为评估三职位的比较矩阵最后，用“工作压力”作为评估A、B、C三个职位的标准，通过分析得到两两比较矩阵如表3。

大学生就业指导方案设计的层次问题分析摘要：大学生就业指导方案的设计指的是立足于大学生毕业后的就业去向，为大学生制定毕业后的就业指南的工作，本文将分别从大学生的学生个体、所在班级、全校同学三个层面对大学生的就业方案设计来进行讨论，旨在增加大学生就业率，帮助设计者更加具有针对性地设计就业指导方案。

关键词：就业指导；多层次；方案设计大学生的就业指导是帮助大学生顺利走进社会的一个重要环节，就业指导方案的设计也就成为了帮助大学生就业不可或缺的一部分，为每个学生制定合适的就业指导，帮助他们顺利的走入社会、为社会作出贡献，是学校不容推卸的责任。

就业指导方案需要与时俱进，迎合社会不断变化的需要就成为了学校就业指导方案设计者必须具备的素质，本文将从三个不同的层次入手，为学校的指导设计提供一定的参考。

一、以学生视角的就业方案设计针对学生个人的方案设计应当优先考虑学生的个人意愿和自身的素质水平，同时要充分考虑学生的所学专业，性格特点等个体素质，通过收集这些信息能够最大程度的保证学生的个体优势得到最大的发挥，这是在针对学生个人设计就业方案的过程中最为重要的一个环节。

在立足于学生个体来进行就业方案的设计中时，首先需要就业指导者完善地评估学生个人的综合素质，其次要充分结合专业岗位所需要掌握的知识和能力。

同时，要坚持以人为本的原则，充分考虑学生的自身意愿，考虑学生个人的就业意向和就业倾向。

在个人层次的就业指导设计过程中，尤其要重点考虑岗位的需要和学生的个人能力，这也是影响学生能否顺利就业的最根本的因素。

针对学生个人所设计的就业方案的重点在于方案的针对性和多样性，但是在针对不同学生设计多样化的方案的同时，也需要避免就业方案指导之间的差异过大。

在设计就业指导方案时要注重为相同种类的学生制定相似的方案，避免差异过大而导致的过多的工作量。

二、以班级视角的就业方案设计以班级视角所制定的就业方案的重点在于在制定就业方案之前应当先明确指导方案的目标和方向。