初中数学.一元二次方程B级.第03讲

第三讲 一元二次方程根与系数的关系【学习目标】在初中掌握了一元二次方程有关的概念，解法和应用的基础上，进一步深入理解和掌握其根的判别式和根与系数的关系。

【重点与难点】1、 一元二次方程根的判别式2、 一元二次方程根与系数的关系（韦达定理） 【回顾与导学】1．一元二次方程的根的判断式一元二次方程20 (0)ax bx c a ++=≠，用配方法将其变形为： ． 由于可以用24b ac -的取值情况来判定一元二次方程的根的情况．因此，把24b ac -叫做一元二次方程20 (0)ax bx c a ++=≠的根的判别式，表示为：24b ac ∆=-对于一元二次方程ax 2＋bx ＋c ＝0（a ≠0），有[1]当Δ 0时，方程有两个不相等的实数根： ； [2]当Δ 0时，方程有两个相等的实数根： ； [3]当Δ 0时，方程没有实数根． 2．一元二次方程的根与系数的关系定理：如果一元二次方程20 (0)ax bx c a ++=≠的两个根为12,x x ，那么：1212,x x x x +==说明：一元二次方程根与系数的关系由十六世纪的法国数学家韦达发现，所以通常把此定理称为”韦达定理”．上述定理成立的前提是0∆≥．特别地，对于二次项系数为1的一元二次方程x 2＋px ＋q ＝0，若x 1，x 2是其两根，由韦达定理可知x 1＋x 2＝－p ，x 1·x 2＝q ，即 p ＝－(x 1＋x 2)，q ＝x 1·x 2，所以，方程x 2＋px ＋q ＝0可化为 x 2－(x 1＋x 2)x ＋x 1·x 2＝0，由于x 1，x 2是一元二次方程x 2＋px ＋q ＝0的两根， x 1，x 2也是一元二次方程x 2－(x 1＋x 2)x ＋x 1·x 2＝0的两根．因此有以两个数x 1，x 2为根的一元二次方程（二次项系数为1）可以表示为 x 2－(x 1＋x 2)x ＋x 1·x 2＝0．【典例赏析】例1 已知关于x 的一元二次方程2320x x k -+=，根据下列条件，分别求出k 的范围： （1）方程有两个不相等的实数根； （2）方程有两个相等的实数根 （3）方程有实数根； （4）方程无实数根．例2 已知实数x 、y 满足22210x y xy x y +-+-+=，试求x 、y 的值．例3 若12,x x 是方程2220150x x +-=的两个根，试求下列各式的值：(1) 2212x x +； (2)1211x x +； (3) 12(5)(5)x x --； (4) 12||x x -．例4 已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根．(1) 是否存在实数k ，使12123(2)(2)2x x x x --=-成立？若存在，求出k 的值；若不存在，请说明理由． (2) 求使12212x x x x +-的值为整数的实数k 的整数值．【课堂练习】1．若12,x x 是方程22630x x -+=的两个根，则1211x x +的值为( )A ．2B ．2-C ．12D ．922．若t 是一元二次方程20 (0)ax bx c a ++=≠的根，则判别式24b ac ∆=-和完全平方式2(2)M at b =+的关系是( )A ．M ∆=B ．M ∆>C ．M ∆<D ．大小关系不能确定3．设12,x x 是方程20x px q ++=的两实根，121,1x x ++是关于x 的方程20x qx p ++=的两实根，则p = ___ __ ，q = _ ____ ．4．已知实数,,a b c 满足26,9a b c ab =-=-，则a = ___ __ ，b = _____ ，c = _____ ．5．已知关于x 的方程230x x m +-=的两个实数根的平方和等于11，求证：关于x 的方程22(3)640k x kmx m m -+-+-=有实数根．6．若12,x x 是关于x 的方程22(21)10x k x k -+++=的两个实数根，且12,x x 都大于1．(1) 求实数k 的取值范围；(2) 若1212x x =，求k 的值．【反思小结】【课后作业】A 组1．选择题:（1）已知关于x 的方程x 2＋kx －2＝0的一个根是1，则它的另一个根是（ ） （A ）－3 （B ）3 （C ）－2 （D ）2 （2）下列四个说法：①方程x 2＋2x －7＝0的两根之和为－2，两根之积为－7； ②方程x 2－2x ＋7＝0的两根之和为－2，两根之积为7；③方程3 x 2－7＝0的两根之和为0，两根之积为73-； ④方程3 x 2＋2x ＝0的两根之和为－2，两根之积为0．其中正确说法的个数是 （ ） （A ）1个 （B ）2个 （C ）3个 （D ）4个（3）关于x 的一元二次方程ax 2－5x ＋a 2＋a ＝0的一个根是0，则a 的值是（ ）（A ）0 （B ）1 （C ）－1 （D ）0，或－12．填空:（1）方程kx 2＋4x －1＝0的两根之和为－2，则k ＝ ． （2）方程2x 2－x －4＝0的两根为α，β，则α2＋β2＝ ．（3）已知关于x 的方程x 2－ax －3a ＝0的一个根是－2，则它的另一个根是 ． （4）方程2x 2＋2x －1＝0的两根为x 1和x 2，则| x 1－x 2|＝ ．3．试判定当m 取何值时，关于x 的一元二次方程m 2x 2－(2m ＋1) x ＋1＝0有两个不相等的实数根？有两个相等的实数根？没有实数根？4．求一个一元二次方程，使它的两根分别是方程x 2－7x －1＝0各根的相反数．B 组1．选择题:若关于x 的方程x 2＋(k 2－1) x ＋k ＋1＝0的两根互为相反数，则k 的值为（ ） （A ）1，或－1 （B ）1 （C ）－1 （D ）0 2．填空:（1）若m ，n 是方程x 2＋2005x －1＝0的两个实数根，则m 2n ＋mn 2－mn 的值等于 ．（2）如果a ，b 是方程x 2＋x －1＝0的两个实数根，那么代数式a 3＋a 2b ＋ab 2＋b 3的值是 ． 3．已知关于x 的方程x 2－kx －2＝0．（1）求证：方程有两个不相等的实数根；（2）设方程的两根为x 1和x 2，如果2(x 1＋x 2)＞x 1x 2，求实数k 的取值范围． 4．一元二次方程ax 2＋bx ＋c ＝0（a ≠0）的两根为x 1和x 2．求： （1）| x 1－x 2|和122x x +； （2）x 13＋x 23．5．关于x 的方程x 2＋4x ＋m ＝0的两根为x 1，x 2满足| x 1－x 2|＝2，求实数m 的值．C 组1．选择题：（1）已知一个直角三角形的两条直角边长恰好是方程2x 2－8x ＋7＝0的两根，则这个直角三角形的斜边长等于 （ ）（A（B ）3 （C ）6 （D ）9 （2）若x 1，x 2是方程2x 2－4x ＋1＝0的两个根，则1221x x x x +的值为 （ ）（A ）6 （B ）4 （C ）3 （D ）32（3）如果关于x 的方程x 2－2(1－m )x ＋m 2＝0有两实数根α，β，则α＋β的取值范围为（ ）（A ）α＋β≥12 （B ）α＋β≤12（C ）α＋β≥1 （D ）α＋β≤1 （4）已知a ，b ，c 是ΔABC 的三边长，那么方程cx 2＋(a ＋b )x ＋4c＝0的根的情况是（ ）（A ）没有实数根 （B ）有两个不相等的实数根 （C ）有两个相等的实数根 （D ）有两个异号实数根 2．填空：若方程x 2－8x ＋m ＝0的两根为x 1，x 2，且3x 1＋2x 2＝18，则m ＝ ． 3． 已知x 1，x 2是关于x 的一元二次方程4kx 2－4kx ＋k ＋1＝0的两个实数根．（1）是否存在实数k ，使(2x 1－x 2)( x 1－2 x 2)＝－32成立？若存在，求出k 的值；若不存在，说明理由； （2）求使1221x x x x +－2的值为整数的实数k 的整数值； （3）若k ＝－2，12xx λ=，试求λ的值．4．已知关于x 的方程22(2)04m x m x ---=． （1）求证：无论m 取什么实数时，这个方程总有两个相异实数根；（2）若这个方程的两个实数根x 1，x 2满足|x 2|＝|x 1|＋2，求m 的值及相应的x 1，x 2． 5．若关于x 的方程x 2＋x ＋a ＝0的一个大于1、零一根小于1，求实数a 的取值范围．【简明答案】一元二次方程根与系数的关系习题答案例1解：∵2(2)43412k k ∆=--⨯⨯=-，∴(1) 141203k k ->⇒<； (2) 141203k k -=⇒=；(3) 141203k k -≥⇒≥；(4)141203k k -<⇒<． 例2解：可以把所给方程看作为关于x 的方程，整理得：22(2)10x y x y y --+-+=由于x 是实数，所以上述方程有实数根，因此：222[(2)]4(1)300y y y y y ∆=----+=-≥⇒=， 代入原方程得：22101x x x ++=⇒=-．综上知：1,0x y =-= 例3解：由题意，根据根与系数的关系得：12122,2015x x x x +=-=-(1) 2222121212()2(2)2(2015)4034x x x x x x +=+-=---= (2)121212112220152015x x x x x x +-+===- (3) 121212(5)(5)5()2520155(2)251980x x x x x x --=-++=---+=- (4)1424)2015(4)2(4)()(22122122121=---=-+=-=-x x x x x x x x （答案错误修改）说明：利用根与系数的关系求值，要熟练掌握以下等式变形：222121212()2x x x x x x +=+-，12121211x x x x x x ++=，22121212()()4x x x x x x -=+-，12||x x -=整体思想．例4 已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根．(1) 是否存在实数k ，使12123(2)(2)2x x x x --=-成立？若存在，求出k 的值；若不存在，请说明理由． (2) 求使12212x x x x +-的值为整数的实数k 的整数值． 解：(1) 假设存在实数k ，使12123(2)(2)2x x x x --=-成立．∵ 一元二次方程的24410kx kx k -++=有两个实数根，∴ 2400(4)44(1)160k k k k k k ≠⎧⇒<⎨∆=--⋅+=-≥⎩，又12,x x 是一元二次方程24410kx kx k -++=的两个实数根，∴ 1212114x x k x x k +=⎧⎪⎨+=⎪⎩∴ 222121212121212(2)(2)2()52()9x x x x x x x x x x x x --=+-=+-939425k k k +=-=-⇒=，但0k <． ∴不存在实数k ，使12123(2)(2)2x x x x --=-成立． (2) ∵ 222121212211212()44224411x x x x x x k x x x x x x k k +++-=-=-=-=-++ ∴ 要使其值是整数，只需1k +能被4整除，故11,2,4k +=±±±，注意到0k <，要使12212x x x x +-的值为整数的实数k 的整数值为2,3,5---． 【课堂练习】1． A ； 2．A ； 3．1,3p q =-=-； 4．3,3,0a b c ===； 5． 1m = (1)当3k =时，方程为310x +=，有实根；(2) 当3k ≠时，0∆>也有实根．6．(1) 314k k ≥≠且； (2) 7k =．【课后作业】A 组1． （1）C （2）B 提示：②和④是错的，对于②，由于方程的根的判别式Δ＜0，所以方程没有实数根；对于④，其两根之和应为－23． （3）C 提示：当a ＝0时，方程不是一元二次方程，不合题意． 2． （1）2 （2）174（3）6 （33．当m ＞－14，且m ≠0时，方程有两个不相等的实数根；当m ＝－14时，方程有两个相等的实数根；当m ＜－14时，方程没有实数根． 4．设已知方程的两根分别是x 1和x 2，则所求的方程的两根分别是－x 1和－x 2，∵x 1＋x 2＝7，x 1x 2＝－1，∴(－x 1)＋(－x 2)＝－7，(－x 1)×(－x 2)＝x 1x 2＝－1，∴所求的方程为y 2＋7y －1＝0．B 组1．C 提示：由于k =1时，方程为x 2＋2＝0，没有实数根，所以k ＝－1． 2．（1）2006 提示：∵m ＋n ＝－2005，mn ＝－1，∴m 2n ＋mn 2－mn ＝mn (m ＋n －1)＝－1×(－2005－1)＝2006． （2）－3 提示；∵a ＋b ＝－1，ab ＝－1，∴a 3＋a 2b ＋ab 2＋b 3＝a 2(a ＋b )＋b 2(a ＋b )＝(a ＋b )( a 2＋b 2)＝(a ＋b )[( a ＋b ) 2－2ab ]＝(－1)×[(－1)2－2×(－1)]＝－3．3．（1）∵Δ＝(－k )2－4×1×(－2)＝k 2＋8＞0，∴方程一定有两个不相等的实数根． （2）∵x 1＋x 2＝k ，xx ＝－2，∴2k ＞－2，即k ＞－1．4．（1）| x 1－x 2|，122x x +＝2b a -；（2）x 13＋x 23＝333abc b a -． 5．∵| x 1－x 2|2==，∴m ＝3．把m ＝3代入方程，Δ＞0，满足题意，∴m ＝3．C 组1．（1）B （2）A（3）C 提示：由Δ≥0，得m ≤12，∴α＋β＝2(1－m )≥1． （4）B 提示：∵a ，b ，c 是ΔABC 的三边长，∴a ＋b ＞c ，∴Δ＝(a ＋b )2－c 2＞0． 2．（1）12 提示：∵x 1＋x 2＝8，∴3x 1＋2x 2＝2(x 1＋x 2)＋x 1＝2×8＋x 1＝18，∴x 1＝2，∴x 2＝6，∴m ＝x 1x 2＝12． 3．（1）假设存在实数k ，使(2x 1－x 2)( x 1－2 x 2)＝－32成立． ∵一元二次方程4kx 2－4kx ＋k ＋1＝0有两个实数根，∴k ≠0，且Δ＝16k 2－16k (k +1)=－16k ≥0，∴k ＜0．∵x 1＋x 2＝1，x 1x 2＝14k k+， ∴ (2x 1－x 2)( x 1－2 x 2)＝2 x 12－51x 2＋2 x 22＝2(x 1＋x 2)2－9 x 1x 2＝2－9(1)4k k+＝－32，即9(1)4k k+＝72，解得k ＝95，与k ＜0相矛盾，所以，不存在实数k ，使(2x 1－x 2)( x 1－2 x 2)＝－32成立．（2）∵1221x x x x +－2＝222212121212121212()2()224x x x x x x x x x x x x x x ++-+-=-=-＝444(1)44111k k k k k k -+-==-+++， ∴要使1221x xx x +－2的值为整数，只须k ＋1能整除4．而k 为整数，∴k ＋1只能取±1，±2，±4．又∵k ＜0，∴k ＋1＜1， ∴k ＋1只能取－1，－2，－4，∴k ＝－2，－3，－5．∴能使1221x x x x +－2的值为整数的实数k 的整数值为－2，－3和－5． （3）当k ＝－2时，x 1＋x 2＝1，① x 1x 2＝18， ②①2÷②，得1221x x x x +＋2＝8，即16λλ+=，∴2610λλ-+=，∴3λ=±4．（1）Δ＝22(1)20m -+>；（2）∵x 1x 2＝－24m ≤0，∴x 1≤0，x 2≥0，或x 1≥0，x 2≤0．①若x 1≤0，x 2≥0，则x 2＝－x 1＋2，∴x 1＋x 2＝2，∴m －2＝2，∴m ＝4．此时，方程为x 2－2x －4＝0，∴11x =21x =②若x 1≥0，x 2≤0，则－x 2＝x 1＋2，∴x 1＋x 2＝－2，∴m －2＝－2，∴m ＝0．此时，方程为x 2＋2＝0，∴x 1＝0，x 2＝－2．5．设方程的两根为x 1，x 2，则x 1＋x 2＝－1，x 1x 2＝a ， 由一根大于1、另一根小于1，得 (x 1－1)( x 2－1)＜0， 即 x 1x 2－(x 1＋x 2)+1＜0， ∴ a －(－1)＋1＜0，∴a ＜－2． 此时，Δ＝12－4×(－2) ＞0， ∴实数a 的取值范围是a ＜－2．。

第三讲 一元二次方程的判别式及根系关系（一） 一元二次方程根的判别式的定义：运用配方法解一元二次方程过程中得到222424b b ac x a a -⎛⎫+= ⎪⎝⎭，显然只有当240b ac -≥时，方程才有实数根.一元二次方程根与系数的关系 （1）当c a ＜0时，方程的两根必一正一负.若0b a-≥，则次方程的整根不小于负根的绝对值；若b a-＜0，则此方程的正根小于负根的绝对值. （2）当c a ＞0时，方程的两根同正或同负.若b a-＞0，则此方程的两根均为正根；若b a -＜0，则此方程两根均为负根. 一般的结论是：若12,x x 是()200ax bx c a ++=≠的两根（其中12x x ≥），且m 为实数，当0∆≥时，一般地：①()()120x m x m --＜12,x m x m ⇔＞＜②()()120x m x m --＞且()()120x m x m -+-＞12,x m x m ⇔＞＞③()()120x m x m --＞且()()120x m x m -+-＜12,x m x m ⇔＜＜特殊是，当m =0时，上述就转化为()200ax bx c a ++=≠有两异根、两正根、两负根的条件韦达定理的应用：（1）已知方程的一个根，求另一个根以及确定方程参数的值（2）已知方程，求关于方程的两根的代数式的值（3）已知方程的两根，构造方程（4）结合根的判别式，讨论根的符号特征（5）逆用构造一元二次方程辅助解题，当已知等式具有相同的结构时，就可以把两个变元看作某一个一元二次方程的两根，以便利用韦达定理（6）利用韦达定理求出一元二次方程中待定系数后，一定要验证方程的∆是否为非负【例1】（1）关于x 的方程()21-210k x --=，有两个不相等的实数根，求k 的取值范围.（2）已知a ＞0，b ＞a +c ，判断关于x 的方程20ax bx c ++=的根的情况，并给出必要的说明.（3）设a 、b 、c 为互不相等的非零实数，求证：以下三个方程220ax bx c ++=，220bx cx a ++=，220cx ax b ++=，不可能都有2个相等的实数根.（4）若()()()()()()x a x b x b x c x c x a ++++++++是关于x 的完全平方式.证明：a =b =c .【例2】已知关于x 的二次方程2110x p x q ++=与2220x p x q ++=，求证：当()12122p p q q =+时，这两个方程中至少有一个方程有实数根.【例3】设方程24x ax +=只有3个不相等的实数根，求a 的取值和相应的3个根.【例4】（1）已知a 、b 、c 分别是△ABC 的三边长，求证：方程()2222220b x b c a x c ++-+=没有实数根.（2）已知△ABC 的三边a 、b 、c 满足：b +c =8，21252bc a a =-+，试确定△ABC 的形状.【例5】在等腰△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，已知a =3，b 和c 是关于x 的方程21202x mx m ++-=的两个实数根，求△ABC 的周长.。

第03讲一元二次方程的解法（公式法）和根与系数的关系【人教版】·模块一根的判别式·模块二公式法解一元二次方程·模块三根与系数的关系·模块四课后作业一元二次方程根的判别式b 2-4ac 叫做方程ax 2+bx+c=0(a≠0)根的判别式，通常用希腊字母△表示它，即△=b 2-4ac △＞0，方程ax 2+bx+c=0(a≠0)有两个不相等得实数根△=0，方程ax 2+bx+c=0(a≠0)有两个相等得实数根△＜0，方程ax 2+bx+c=0(a≠0)无实数根【考点1根据判别式判断方程根的情况】【例1.1】关于一元二次方程2+3=4根的情况，下列说法中正确的是（）A ．有两个不相等的实数根B ．有两个相等的实数根C ．没有实数根D ．无法确定【例1.2】已知实数k ，现甲、乙、丙、丁四人对关于x 的方程B 2−(+2)+14=0讨论如下．甲：该方程一定是关于x 的一元二次方程乙：该方程有可能是关于x 的一元二次方程丙：当≥−1时，该方程有实数根丁：只有当≥−1且≠0时，该方程有实数根则下列判断正确的是（）A ．甲和丙说的对B ．甲和丁说的对C ．乙和丙说的对D ．乙和丁说的对【例1.3】若=1是一元二次方程B 2−B +2=0(≠0)的一个根，那么方程B 2+B +2=0的根的情况是（）A．有两个不相等的实数根B．有一个根是J−1C．没有实数根D．有两个相等的实数根【变式1.1】已知a为实数，下列关于x的一元二次方程一定有实数根的是（）A．2−2B+2+1=0B．2−2B+22+1=0 C．2+2−1−2=0D．2+2+1+2=0【变式1.2】对于实数a，b定义运算“⊗”为⊗=2−B，例如3⊗2=22−3×2=−2，则关于x的方程+2⊗=1−的根的情况，下列说法正确的是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定【变式1.3】对于一元二次方程B2+B+=0(≠0)，有下列说法：①若方程B2+=0有两个不相等的实数根，则方程B2+B+=0(≠0)必有两个不相等的实数根；②若方程B2+B+=0(≠0)有两个实数根，则方程B2+B+=0一定有两个实数根；③若c是方程B2+B+=0(≠0)的一个根，则一定有B++1=0成立；④若0是一元二次方程B2+B+=0(≠0)的根，则2−4B=(2B0−p2其中正确的有（）A．1个B．2个C．3个D．4个【考点2已知根的情况确定字母的值或取值范围】【例2.1】若关于的方程2−+=0有两个实数根，则的取值范围是（）A．≥14B．<14C．≤14D．≤14且≠0【例2.2】关于的方程B2−3+2=0有实数根，则的值不可能是（）A．−1B．0C．1D．2【例2.3】若一元二次方程B2+B+1=0有两个相同的实数根，则2−2+5的最小值为（）A．5B．1C．−9D．−1【变式2.1】关于x的方程2−+−2=0有两个不相等的实数根，则实数a可取的最大整数为（）A．2B．3C．4D．5【变式2.2】在实数范围内，存在2个不同的的值，使代数式2−3+与代数式+2值相等，则的取值范围是___________．【变式2.3】关于x的一元二次方程2−+3++2=0．(1)求证：方程总有两个实数根；(2)若方程的两个实数根都是正整数，求m的最小值．【变式2.4】如果关于x的方程(+p(+p+(+p(+p+(+p(+p=0(其中，，均为正数)有两个相等的实数根，证明：以，，为长的线段能够组成一个三角形，并指出三角形的特征．公式法解一元二次方程当b2-4ac≥0时，方程ax2+bx+c=0的实数根可写为：=做一元二次方程ax2+bx+c=0的求根公式。

用因式分解法解一元二次方程（一）（一）明确目标学习了公式法，便可以解所有的一元二次方程．对于有些一元二次方程，例如（x－2）（x ＋3）＝0，如果转化为一般形式，利用公式法就比较麻烦，如果转化为x－2＝0或x＋3＝0，解起来就变得简单多了．即可得x1＝2，x2＝-3．这种解一元二次方程的方法就是本节课要研究的一元二次方程的方法——因式分解法．（二）整体感知所谓因式分解，是将一个多项式分解成几个一次因式积的形式．如果一元二次方程的左边是一个易于分解成两个一次因式积的二次三项式，而右边为零．用因式分解法更为简单．例如：x2＋5x＋6＝0，因式分解后（x＋2）（x＋3）＝0，得x＋2＝0或x＋3＝0，这样就将原来的一元二次方程转化为一元一次方程，方程便易于求解．可以说二次三项式的因式分解是因式分解法解一元二次方程的关键．“如果两个因式的积等于零，那么两个因式至少有一个等于零”是因式分解法解方程的理论依据．方程的左边易于分解，而方程的右边等于零是因式分解法解方程的条件．满足这样条件的一元二次方程用因式分解法最简单．（三）重点、难点的学习与目标完成过程1．复习提问零，那么这两个因式至少有一个等于零．反之，如果两个因式有一个等于零，它们的积也就等于零．“或”有下列三层含义①A＝0且B≠0②A≠0且B＝0③A＝0且B＝02．例1 解方程x2＋2x＝0．解：原方程可变形x（x＋2）＝0……第一步∴ x＝0或x＋2＝0……第二步∴ x1=0，x2=-2．分析步骤（一）第一步变形的方法是“因式分解”，第二步变形的理论根据是“如果两个因式的积等于零，那么至少有一个因式等于零”．分析步骤（二）对于一元二次方程，一边是零，而另一边易于分解成两个一次式时，可以得到两个一元一次方程，这两个一元一次方程的解就是原一元二次方程的解．用此种方法解一元二次方程叫做因式分解法．由第一步到第二步实现了由二次向一次的“转化”，达到了“降次”的目的，解高次方程常用转化的思想方法．例2 用因式分解法解方程x2＋2x－15＝0．解：原方程可变形为（x＋5）（x-3）＝0．得，x＋5＝0或x-3＝0．∴ x1＝-5，x2＝3．因式分解的步骤：（一）方程化为一般形式；（二）方程左边因式分解；（三）至少一个一次因式等于零得到两个一元一次方程；（四）两个一元一次方程的解就是原方程的解．例3 解方程3（x-2）-x（x-2）＝0．解：提取公因式（x-2）原方程可变形为（x-2）（3-x）＝0．∴ x-2＝0或3-x＝0．∴ x1＝2，x2＝3．（2）（3x＋2）2=4（x-3）2.解：移项，原式可变形为（3x＋2）2-4（x-3）2＝0．[（3x＋2）＋2（x-3）][（3x＋2）-2（x-3）]＝0即：（5x-4）（x＋8）=0．∴ 5x-4＝0或x＋8＝0．练习：解下列关于x的方程6．（4x＋2）2＝x（2x＋1）．。

第03讲_含参的一元二次方程知识图谱含参的一元二次方程知识精讲二．一元二次方程的整数根如果一元二次方程2三点剖析一．考点：含参的一元二次方程．二．重难点：含参的一元二次方程判别式与解的关系，含参一元二次方程的特殊解问题．三．易错点：1．含参一元二次方程如果参数没有明确取值范围必须要分类讨论；2．含参一元二次方程的特殊解问题要注意参数是整数，正整数，负整数，还是有理数等限制条件．判别式与解的关系例题1、已知关于x 的方程kx 2+（1-k ）x-1=0，下列说法正确的是（）A.当k=0时，方程无解B.当k=1时，方程有一个实数解C.当k=-1时，方程有两个相等的实数解D.当k≠0时，方程总有两个不相等的实数解．【答案】C【解析】关于x 的方程kx 2+（1-k ）x-1=0，A 、当k=0时，x-1=0，则x=1，故此选项错误；B 、当k=1时，x 2-1=0方程有两个实数解，故此选项错误；C 、当k=-1时，-x 2+2x-1=0，则（x-1）2=0，此时方程有两个相等的实数解，故此选项正确；D 、由C 得此选项错误．故选：C ．例题2、解方程：mx 2－（2m ＋1）x ＋m ＋1＝0．【答案】当m ＝0时，x ＝1当m ≠0时，11m x m+=，x 2＝1【解析】暂无解析例题3、已知关于x 的一元二次方程（a ﹣2）x 2+2ax+a+3=0有实数根，（1）求a 的取值范围；（2）当a 取最大数值时，解此一元二次方程．【答案】（1）a ≤6且a ≠2．（2）x 1=x 2=﹣32．【解析】（1）∵关于x 的一元二次方程（a ﹣2）x 2+2ax+a+3=0有实数根，∴()()()22024230a a a a -≠⎧⎪⎨∆=--+≥⎪⎩，解得：a ≤6且a ≠2．（2）当a=6时，原方程为4x 2+12x+9=（2x+3）2=0，解得：x 1=x 2=﹣32．随练1、已知关于x 的方程（a ﹣1）x 2﹣2x+1=0有实数根，则a 的取值范围是．【答案】a ≤2【解析】∵关于x 的方程（a ﹣1）x 2﹣2x+1=0有实数根，∴△≥0，即4﹣4（a ﹣1）≥0得，a≤2，且a ﹣1≠0，a≠1；∴a 的取值范围为a≤2且a≠1．当a=1时为一元一次方程，方程有一根．综上所知a 的取值范围为a≤2．故答案为：a≤2．随练2、已知0a >，b a c >+，判断关于x 的方程20ax bx c ++=的根的情况，并给出必要的说明？【答案】见解析【解析】（1）当0c >时，0a >，b a c >+从而22()b a c >+，22()0b a c -+>，224()0b ac a c --->，∴224()0b ac a c ->-≥，即0∆>，原方程必有两个不等实根；（2）当0c =时，由0,a b a c a >>+=，得0,0,0b ac >=∆>；（3）当0c <时，由0a >，得0ac <，240b ac ∆=->．综合⑴、⑵、⑶，得关于x 的方程总有两个不等的实根随练3、解关于x 的方程：2222(1)(1)(1)a x x a x a x -+--=-【答案】当220210a a a ⎧-=⎪⎨-+≠⎪⎩时，方程为一元一次方程的解为0x =或2x =；当20a a -≠时，方程为一元二次方程，()()10ax a ax x a ----=，11a x a +=，21ax a =-【解析】化为一般式：()()()2222210a a x a x a a ---++=当220210a a a ⎧-=⎪⎨-+≠⎪⎩时，方程为一元一次方程的解为0x =或2x =；当20a a -≠时，方程为一元二次方程，()()10ax a ax x a ----=，11a x a +=，21ax a =-特殊解问题例题1、已知关于x 的方程220mx x m--=（m ≠0）（1）求证：方程总有两个不相等的实数根；（2）如果方程的两个实数根都是整数，求整数m 的值．【答案】（1）见解析（2）1m =-或1m =【解析】（1）证明：∵m ≠0，∴220mx x m--=是关于x 的一元二次方程．∵22(1)4()m m∆=---，……………………………………………1分=9＞0.∴方程总有两个不相等的实数根．………………………………2分（2）解：由求根公式，得x =．∴12x m =，21x m=-.……………………………………………………4分∵方程的两个实数根都是整数，且m 是整数，∴1m =-或1m =．………………………………………………………5分例题2、已知关于的一元二次方程22240x x k ++-=有两个不相等的实数根。

第3讲一元二次方程根的判别式及根与系数的关系概述适用学科初中数学适用年级初三适用区域人教版区域课时时长（分钟）120知识点1、一元二次方程的根的判别式2、根与系数的关系教学目标1、使学生理解并掌握一元二次方程的根的判别式．2、使学生掌握不解方程，运用判别式判断一元二次方程根的情况．3、通过对含有字母系数方程的根的讨论，培养学生运用一元二次方程根的判别式的论证能力和逻辑思维能力．培养学生思考问题的灵活性和严密性．来解某些一元二次方程．并由此体会转化的思想．4、使学生掌握一元二次方程根与系数的关系(即韦达定理)，并学会其运用．教学重点1、一元二次方程根的判别式的内容及应用．2、韦达定理的推导和灵活运用．3、已知方程求关于根的代数式的值 .教学难点1、用两根之和与两根之积表示含有两根的各种代数式．2、一元二次方程根的判别式的推导．3、利用根的判别式进行有关证明【知识导图】用公式法求出下列方程的解：(1)3x 2＋x －10＝0；(2)x 2－8x ＋16＝0；(3)2x 2－6x ＋5＝0． 引入新课通过上述一组题，让学生回答出：一元二次方程的根的情况有三种，即有两个不相等的实数根；两个相等的实数根；没有实数根．接下来向学生提出问题：是什么条件决定着一元二次方程的根的情况？这条件与方程的根之间又有什么关系呢？能否不解方程就可以明确方程的根的情况？这正是我们本课要探讨的课题．先讨论上述三个小题中b 2－4ac 的情况与其根的联系．再做如下推导：对任意一元二次方程ax 2+bx+c=0(a ≠0)，可将其变形为一元二次方程根的判别与及根于系数的关系根的判别有实数根无实数根韦达定理两根和两根积教学过程考点1 一元二次方程根的判别式 二、知识讲解一、导入(x+)2=∵a ≠0，∴4a 2＞0．由此可知b 2－4ac 的值直接影响着方程的根的情况． (1)当b 2－4ac ＞0时，方程右边是一个正数．12x x ==因此b 2-4ac ＞0时，一元二次方程有两个不相等的实数根 (2)当b 2－4ac ＝0时，方程右边是122bx x a==-,所以，一元二次方程有两个相等的实数根 (3) 当b 2-4ac<0时，方程右边是一个负数,而方程左边的(x+)2不可能是一个负数,因此方程没有实根.通过以上讨论，总结出：一元二次方程ax 2＋bx ＋c ＝0的根的情况可由b 2－4ac 来判定．故称b 2－4ac 是一元二次方程ax 2＋bx ＋c ＝0的根的判别式，通常用“△”来表示． ● 综上所述，一元二次方程ax 2＋bx ＋c ＝0(a ≠0)当△＞0时，有两个不相等的实数根； 当△＝0时，有两个相等的实数根； 当△＜0时，没有实数根．反过来也成立．● 提问1．一元二次方程ax 2＋bx ＋c ＝0的求根公式应如何表述？ 2．上述方程两根之和等于什么？两根之积呢？ ● 新知讲解一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的两根为：考点2 根于系数之间的关系12x x ==12b x x a +=- 12cx x a=由此得出，一元二次方程的根与系数之间存在如下关系：(又称“韦达定理”) 如果ax 2＋bx ＋c ＝0(a ≠0)的两个根是x 1，x 2，那么12b x x a +=-12cx x a= 我们再来看二次项系数为1的一元二次方程x 2＋px ＋q ＝0的根与系数的关系． 如果把方程ax 2＋bx ＋c ＝0(a ≠0)变形为20b cx x a a++=，我们就可以将之写成20x px q ++=的形式，其中,b cp q a a== ● 得出结论：如果方程x 2＋px ＋q ＝0的两根是x 1，x 2，那么x 1＋x 2＝－p ，x 1x 2＝q ． 由 x 1＋x 2＝－p ，x 1x 2＝q 可知p ＝－(x 1＋x 2)，q ＝x 1·x 2， ∴方程x 2＋px ＋q ＝0， 即 x 2－(x 1＋x 2)x ＋x 1·x 2＝0．这就是说，以两个数x 1，x 2为根的一元二次方程(二次项系数为1)是x 2－(x 1＋x 2)x ＋x 1·x 2＝0． ● 一元二次方程的根与系数的关系如果方程ax 2＋bx ＋c ＝0(a≠0)的两个根为x 1，x 2，那么x 1＋x 2＝－b a ，x 1·x 2＝c a .这个关系通常称为韦达定理．(1)在实数范围内运用根与系数的关系时，必须注意两个条件： ①方程必须是一元二次方程，即二次项系数a≠0；②方程有实数根，即Δ≥0.因此，解题时要注意分析题中隐含条件Δ≥0和a≠0.(2)如果方程x 2＋px ＋q ＝0的两个根是x 1，x 2，这时韦达定理应是：x 1＋x 2＝－p ，x 1·x 2＝q.如果实数x 1，x 2满足x 1＋x 2＝－b a ，x 1·x 2＝c a，那么x 1，x 2是一元二次方程ax 2＋bx ＋c ＝0的两个根．考点3 利用根与系数的关系确定一元二次方程(1)利用这一性质比较容易检验一元二次方程的解是否正确．(2)以x 1，x 2为根的一元二次方程(二次项系数为1)是x 2－(x 1＋x 2)x ＋x 1x 2＝0. 已知两根求一元二次方程，其一般步骤是： ①先根据两根分别求出两根之和与两根之积；②把两根之和、两根之积代入一元二次方程x 2－(x 1＋x 2)x ＋x 1x 2＝0，求出所要求的方程．已知一元二次方程ax 2＋bx ＋c ＝0(a≠0)的两根为x 1，x 2，则求含有x 1，x 2的代数式的值时，其方法是把含x 1，x 2的代数式通过转化，变为用x 1＋x 2，x 1x 2的代数式进行表示，然后再整体代入求出代数式的值．解决此类问题时经常要运用到以下代数式及变形： ①＋＝(x 1＋x 2)2－2x 1x 2；②1x 1＋1x 2＝x 1＋x 2x 1x 2； ③(x 1＋a)(x 2＋a)＝x 1x 2＋a(x 1＋x 2)＋a 2； ④|x 1－x 2|＝(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2.类型一 一元二次方程根的判别式一元二次方程的根的情况是（ ）A ．有两个相等的实数根B ．有两个不相等的实数根C ．只有一个实数根D ．无实数根 【答案】D若关于x 的一元二次方程x 2+2（k ﹣1）x+k 2﹣1=0有实数根，则k 的取值范围是（ ） A ．k≥1 B ．k ＞1 C ．k ＜1 D ．k≤121x 22x 2x2x 20三 、例题精析例题2例题1考点4 一元二次方程根与系数的关系的应用【答案】D已知：关于x 的一元二次方程x 2+2x +k =0有两个不相等的实数根。

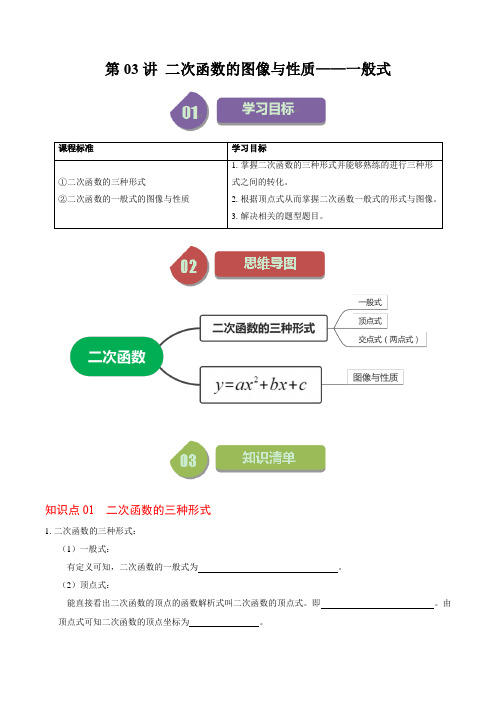
第03讲 二次函数的图像与性质——一般式知识点01 二次函数的三种形式1. 二次函数的三种形式： （1）一般式：有定义可知，二次函数的一般式为 。

（2）顶点式：能直接看出二次函数的顶点的函数解析式叫二次函数的顶点式。

即。

由顶点式可知二次函数的顶点坐标为 。

（3）两点式（交点式）：能直接得到二次函数与x 轴的交点坐标的二次函数解析式是二次函数的两点式，又叫做二次函数的交点式。

即 。

此时二次函数与x 轴的两个交点坐标分别为 与 。

二次函数的对称轴为 。

（4）二次函数的一般式转化为顶点式：利用配方法将一般形式转化为顶点式：过程如下： c bx ax y ++=2a b ac a b x a ca b a b x a c a ba b x a b x a cx a b x a 44242442222222222-+⎪⎭⎫ ⎝⎛+=+-⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛-++=+⎪⎭⎫ ⎝⎛+=题型考点：①二次函数的形式转换。

【即学即练1】1．将二次函数y ＝x 2﹣2x ﹣1化成y ＝a （x ﹣h ）2+k 的形式，正确的是（ ） A ．y ＝（x ﹣2）2+2 B ．y ＝（x ﹣1）2﹣2 C ．y ＝（x +1）2+2D ．y ＝（x ﹣1）2+4【即学即练2】2．将二次函数y ＝x 2﹣4x +7化为y ＝（x ﹣a ）2+b 的形式，那么a +b 的值为 ．【即学即练3】3. 把抛物线y ＝（x ﹣1）2+1化成一般式是 ．【即学即练4】4．把y ＝（2﹣3x ）（6+x ）变成y ＝ax 2+bx +c 的形式，二次项 ，一次项系数为 ，常数项为 ．【即学即练5】5．对于二次函数y ＝4（x +1）（x ﹣3）下列说法正确的是（ ） A ．图象开口向下B ．与x 轴交点坐标是（1，0）和（﹣3，0）C ．x ＜1时，y 随x 的增大而减小D ．图象的对称轴是直线x ＝﹣1知识点02 二次函数的图像与性质（一般式）1.二次函数的一般式的图像与性质：把二次函数的一般式化成顶点式可知一般式的性质如下：题型考点：①二次函数的性质。

一元二次方程详细教学【原创实用版】目录一、一元二次方程的基本概念1.一元二次方程的定义2.一元二次方程的一般形式二、一元二次方程的解法1.配方法2.公式法3.因式分解法三、一元二次方程的应用1.实际问题中的应用2.解决其他相关数学问题的基础正文一、一元二次方程的基本概念一元二次方程是指形如 ax+bx+c=0 的方程，其中 a、b、c 为已知数，且 a≠0。

在这个方程中，未知数的最高次数是二次，因此被称为一元二次方程。

一元二次方程是初中数学和高中数学中的基本内容，掌握这个知识点对于后续学习有着重要的意义。

在一元二次方程中，一般形式为 ax+bx+c=0，其中 a、b、c 分别为方程的三个系数，x 为未知数。

在这个方程中，a 决定了二次项的正负性，当 a>0 时，二次项为上开口抛物线，当 a<0 时，二次项为下开口抛物线。

b 和c 则决定了抛物线与 x 轴的交点，也就是一元二次方程的解。

二、一元二次方程的解法一元二次方程的解法主要有配方法、公式法和因式分解法三种。

1.配方法：配方法是将一元二次方程化为完全平方的形式，然后解出未知数的方法。

具体操作是，将常数项移到等式右边，然后将二次项的系数除以 2，再将其平方加到等式两边，使等式左边成为完全平方。

2.公式法：公式法是根据一元二次方程的系数，利用公式求出解的方法。

公式为：x1,2=[-b±√(b-4ac)]/2a。

其中，x1 和 x2 分别为方程的两个解，当 b-4ac>0 时，方程有两个不相等的实数解；当 b-4ac=0 时，方程有两个相等的实数解；当 b-4ac<0 时，方程无实数解。

3.因式分解法：因式分解法是将一元二次方程分解为两个一次方程，然后解出未知数的方法。

具体操作是，将一元二次方程的左边因式分解，然后使每个因式等于 0，解出一次方程，从而得到未知数的解。

三、一元二次方程的应用一元二次方程在实际问题中有广泛的应用，例如求解面积、体积、路程等问题。

第03讲基本不等式 (精讲+精练）目录第一部分：思维导图（总览全局）第二部分：知识点精准记忆第三部分：课前自我评估测试第四部分：典型例题剖析高频考点一：利用基本不等式求最值①凑配法②“1”的代入法③二次与二次（一次）商式（换元法）④条件等式求最值高频考点二：利用基本不等式求参数值或取值范围高频考点三：利用基本不等式解决实际问题高频考点四：基本不等式等号不成立，优先对钩函数第五部分：高考真题感悟第六部分：第03讲基本不等式（精练）1、基本不等式（一正，二定，三相等，特别注意“一正”，“三相等”这两类陷阱）①如果0a >，0b >2a b+≤，当且仅当a b =时，等号成立． ②叫做正数a ，b 的几何平均数；2a b+叫做正数a ，b 的算数平均数． 2、两个重要的不等式①222a b ab +≥（,a b R ∈）当且仅当a b =时，等号成立． ②2()2a b ab +≤（,a b R ∈）当且仅当a b =时，等号成立． 3、利用基本不等式求最值①已知x ，y 是正数，如果积xy 等于定值P ，那么当且仅当x y =时，和x y +有最小值；②已知x ，y 是正数，如果和x y +等于定值S ，那么当且仅当x y =时，积xy 有最大值24S；4、常用技巧利用基本不等式求最值的变形技巧——凑、拆（分子次数高于分母次数）、除（分子次数低于分母次数））、代（1的代入）、解（整体解）. ①凑：凑项，例：()1123x x a a a x a x a x a+=-++≥+=>--； 凑系数，例：()()2112121112212022282x x x x x x x +-⎛⎫⎛⎫-=⋅-≤⋅=<< ⎪ ⎪⎝⎭⎝⎭；②拆：例：()2244442244822223x x x x x x x x x -+==++=-++≥=>----；③除：例：()2221011x x x x x=≤>++； ④1的代入：例：已知0,0,1a b a b >>+=，求11a b+的最小值. 解析：1111()()24b aa b a b a b a b+=++=++≥. ⑤整体解：例：已知a ,b 是正数，且3ab a b =++，求a b +的最小值.解析：22,322a b a b ab a b ++⎛⎫⎛⎫≤∴≥++ ⎪ ⎪⎝⎭⎝⎭，即()()21304a b a b +-+-≥，解得()62a b a b +≥+≤-舍去.一、判断题1．（2022·江西·贵溪市实验中学高二期末）当0,2x π⎛⎤∈⎥⎝⎦时，4sin sin x x +的最小值为4 ( )2．（2021·江西·贵溪市实验中学高二阶段练习）已知102x <<，则()12x x -的最大值为18( ) 二、单选题1．（2022·江西·高一阶段练习）当0x >时，92x x+的最小值为（ ） A ．3B ．32C ．D ．2．（2022·湖南湖南·二模）函数()122y x x x =+>-+的最小值为（ ） A ．3B ．2C ．1D ．03．（2022·湖南·高一阶段练习）已知0a >，0b >且2510a b +=，则ab 的最大值为（ ） A ．2B ．5C ．32D ．524．（2022·新疆·乌苏市第一中学高一开学考试）下列函数，最小值为2的函数是（ ） A ．1y x x=+B ．222y x x -=+C ．3y x =+D ．2y =高频考点一：利用基本不等式求最值①凑配法1．（2022·北京大兴·高一期末）当02x <<时，(2)x x -的最大值为（ ） A ．0B ．1C ．2D ．42．（2022·山西·怀仁市第一中学校二模（文））函数413313y x x x ⎛⎫⎪⎝=>-⎭+的最小值为（ ） A ．8B ．7C ．6D ．53．（2022·安徽省蚌埠第三中学高一开学考试）已知x >3，则对于43y x x =+-，下列说法正确的是（ ） A ．y 有最大值7B ．y 有最小值7C ．y 有最小值4D ．y 有最大值44．（2022·江苏省天一中学高一期末）设实数x 满足1x >-，则函数41y x x =++的最小值为（ ） A ．3B ．4C ．5D ．65．（2022·上海虹口·高一期末）已知04x <<，则()4x x -的最大值为______．②“1”的代入法1．（2022·河南·夏邑第一高级中学高二期末（文））已知x ，y 均为正数，若261x y+=，则当3x y +取得最小值时，x y +的值为（ ） A ．16B ．4C ．24D ．122．（2022·安徽·高三阶段练习（文））已知0x >，0y >，22x y +=，则12x y+的最小值是（ ）A ．1B ．2C ．4D ．63．（2022·四川·泸县五中高二开学考试（文））已知,x y 为正实数，且2x y +=，则212x y+的最小值为__________.4．（2022·广西桂林·高一期末）已知0,0a b >>，若31a b +=，则31a b+的最小值是___________.5．（2022·天津·南开中学高一期末）已知110, 0, 4a b a b>>+=，则4a b +的最小值为_______________.③二次与二次（一次）商式1．（2022·全国·高三专题练习（理））若11x -<< ，则22222x x y x -+=-有（ ）A ．最大值1-B ．最小值1-C ．最大值1D ．最小值12．（2022·全国·高三专题练习）函数233(1)1x x y x x ++=<-+的最大值为（ ） A ．3 B ．2 C ．1 D ．-13．（2022·江西南昌·高一期末）当2x >-时，函数2462++=+x x y x 的最小值为___________．4．（2022·上海·高三专题练习）若1x >，则函数211x x y x -+=-的最小值为___________.5．（2021·江西·宁冈中学高一阶段练习（理））()21147x x x x ->-+的最大值为______.6．（2022·全国·高三专题练习）求下列函数的最小值 （1）21(0)x x y x x ++=>；（2）226(1)1x x y x x ++=>-.④条件等式求最值1．（2022·陕西咸阳·高二期末（文））已知0x >，0y >，若28x y xy +=，则xy 的最小值是（ ）A B C ．18D ．142．（2022·全国·高三专题练习）已知0,0a b >>，且3ab a b =++，则a b +的最小值为（ ） A ．4B ．8C ．7D ．63．（2022·江苏·高三专题练习）已知0a >，0b >且满足2a b ab +=，则2+a b 的最小值为（ ） A ．4B ．6C ．8D ．104．（2022·安徽芜湖·高一期末）已知正数x ，y 满足8xy x y =++，则x y +的最小值为_________ 5．（2022·全国·高三专题练习）已知2,1a b >>，且满足21ab a b =++，则2a b +的最小值为_______. 6．（2022·重庆·高一期末）已知0x >，0y >，24xy x y =++，则x y +的最小值为______． 7．（2022·广东广州·高一期末）已知0a >，0b >，且3a b ab +=-，则a b +的最小值为______．高频考点二：利用基本不等式求参数值或取值范围1．（2022·全国·高三专题练习）当2x >时，不等式12+≥-x a x 恒成立，则实数a 的取值范围是（ ） A ．(],2-∞B ．[)2,+∞C ．[)4,+∞D ．(],4-∞2．（2022·浙江·高三专题练习）若关于 x 的不等式220x ax -+>在区间[]1,5上恒成立，则a 的取值范围为（ ）A ．()+∞B ．(-∞C ．(),3-∞D ．27,5⎛⎫-∞ ⎪⎝⎭3．（2022·全国·高三专题练习）已知0a >，0b >，若不等式41ma b a b+≥+恒成立，则m 的最大值为（ ） A ．10B ．12C ．16D ．94．（2022·全国·高三专题练习）已知x ，()0,y ∈+∞，且1x y +=，若不等式2221124x y xy m m ++>+恒成立，则实数m 的取值范围是（ ） A ．3,12⎛⎫- ⎪⎝⎭B ．3,12⎡⎤-⎢⎥⎣⎦C ．()2,1-D ．()3,1,2⎛⎫-∞-⋃+∞ ⎪⎝⎭5．（2022·全国·高三专题练习）若对任意220,1xx a x x >≥++恒成立，则实数a 的取值范围是（ ）A ．[1,)-+∞B ．[3,)+∞C ．2,3⎡⎫+∞⎪⎢⎣⎭D ．(,1]-∞6．（2022·甘肃·无高二期末（文））已知正实数a ，b 满足191a b+=，若不等式2418a b x x m +≥-++-对任意的实数x 恒成立，则实数m 的取值范围是（ ） A ．[)3,+∞B ．(],3-∞C ．(],6-∞D ．[)6,+∞7．（2022·全国·高三专题练习）若对任意0x >，231xa x x ≤++恒成立，则实数a 的取值范围是（ ） A ．1,5⎡⎫+∞⎪⎢⎣⎭B ．1,5⎛⎫+∞ ⎪⎝⎭C ．1,5⎛⎫-∞ ⎪⎝⎭D ．1,5⎛⎤-∞ ⎥⎝⎦高频考点三：利用基本不等式解决实际问题1．（2022·北京市十一学校高二期末）某公司要建造一个长方体状的无盖箱子，其容积为48m 3，高为3m ，如果箱底每1m 2的造价为15元，箱壁每1m 2造价为12元，则箱子的最低总造价为（ ） A ．72元B ．300元C ．512元D ．816元2．（2022·河南开封·高一期末）中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为a ，b ，c ，三角形的面积S 可由公式S =p 为三角形周长的一半，这个公式也被称为海伦秦九韶公式，现有一个三角形的边长满足14a b +=，6c =，则此三角形面积的最大值为（ ）A ．6B ．C ．12D ．3．（2022·江苏常州·高一期末）2021年初，某地区甲、乙、丙三位经销商出售钢材的原价相同．受钢材进价普遍上涨的影响，甲、乙计划分两次提价，丙计划一次提价．设0p q <<，甲第一次提价%p ，第二次提价%q ；乙两次均提价%2p q+；丙一次性提价()%p q +．各经销商提价计划实施后，钢材售价由高到低的经销商依次为（ ） A ．乙、甲、丙 B ．甲、乙、丙 C ．乙、丙、甲D ．丙、甲、乙4．（2022·全国·高三专题练习（文））已知k ∈R ，则“对任意,a b ∈R ，22a b kab +≥”是“k 2≤”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件5．（2022·河南·模拟预测（理））一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买10g 黄金，售货员先将5g 的砝码放在天平左盘中，取出一些黄金放在天平右盘中使天平平衡；再将5g 的砝码放在天平右盘中，再取出一些黄金放在天平左盘中使天平平衡；最后将两次称得的黄金交给顾客.若顾客实际购得的黄金为g m ，则（ ） A ．10m >B ．10m =C ．10m <D ．以上都有可能6．（2022·全国·高一）如图所示，将一矩形花坛ABCD 扩建为一个更大的矩形花坛AMPN ，要求点B 在AM 上，点D 在AN 上，且对角线MN 过点C ，已知4AB =米，3AD =米，当BM =_______时，矩形花坛AMPN 的面积最小.高频考点四：基本不等式等号不成立，优先对钩函数1．（2022·重庆南开中学模拟预测）已知命题p ：“21,4,402x x ax ⎡⎤∃∈-+>⎢⎥⎣⎦”为真命题，则实数a 的取值范围是（ ） A ．4a < B ．172a <C ．133a <D ．5a >2．（2022·浙江·高三专题练习）若不等式210x ax ++≥对一切10,2x ⎛⎤∈ ⎥⎝⎦恒成立，则a 的取值范围是（ ）A ．0a ≥B ．2a ≤-C ．52a ≥-D ．3a ≤-3．（2022·全国·高三专题练习）函数2y =）A ．2B ．52C ．1D ．不存在4．（2022·新疆·石河子第二中学高二阶段练习）已知函数4()f x x x =+，()2x g x a =+，若11,12x ⎡⎤∀∈⎢⎥⎣⎦，2[2,3]x ∃∈，使得()()12f x g x ，则实数a 的取值范围是（ ） A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．9,2⎡⎫+∞⎪⎢⎣⎭C ．[3,)-+∞D ．[1,)+∞5．（2022·全国·高二课时练习）函数()3421x xf x x x -=++在区间[]1,3上（ ）A0 B ．有最大值为2491，最小值为0 CD ．有最大值为2491，无最小值1．（2021·江苏·高考真题）已知奇函数()f x 是定义在R 上的单调函数，若正实数a ，b 满足()()240f a f b +-=则121a b++的最小值是（ ） A ．23B ．43C ．2D ．42．（2021·全国·高考真题（文））下列函数中最小值为4的是（ ） A ．224y x x =++ B ．4sin sin y x x=+ C ．222x x y -=+D ．4ln ln y x x=+3．（2021·天津·高考真题）若0 , 0a b >>，则21ab ab ++的最小值为____________． 4．（2021·江苏·高考真题）某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y 万元与年产量x 吨之间的函数关系可以近似地表示为22420005x y x =-+，已知此生产线的年产量最小为60吨，最大为110吨.（1）年产量为多少吨时，生产每吨产品的平均成本最低?并求最低平均成本;（2）若每吨产品的平均出厂价为24万元，且产品能全部售出，则年产量为多少吨时，可以获得最大利润?并求最大利润.一、单选题1．（2022·江西·赣州市赣县第三中学高一开学考试）下列说法正确的为（ ）A ．12x x+≥ B ．函数224x y += 4C ．若0,x >则(2)x x -最大值为1D ．已知3a >时，43+≥-a a 43=-a a 即4a =时，43+-a a 取得最小值8 2．（2022·福建·莆田一中高一期末）函数2455()()22x x f x x x -+=≥-有（ ） A ．最大值52 B ．最小值52 C ．最大值2 D ．最小值23．（2022·河南·郏县第一高级中学高二开学考试（理））正实数ab 满足121a b+=，则()()24a b ++的最小值为（ ）A ．16B ．24C ．32D ．404．（2022·江西抚州·高二期末（文））若命题“对任意(),0x ∈-∞，使得2240x ax -+≥成立”是真命题，则实数a 的取值范围是（ ）A ．[)2,-+∞B ．[)2,+∞C ．(],2-∞-D ．(],2-∞5．（2022·河南·驻马店市基础教学研究室高二期末（理））中国大运河项目成功人选世界文化遗产名录，成为中国第46个世界遗产项目，随着对大运河的保护与开发，大运河已成为北京城市副中心的一张亮丽的名片，也成为众多旅游者的游览目的地．今有一旅游团乘游船从奥体公园码头出发顺流而下至漕运码头，又立即逆水返回奥体公园码头，已知游船在顺水中的速度为1V ，在逆水中的速度为()212V V V ≠，则游船此次行程的平均速度V 与122V V +的大小关系是（ ） A ．122V V V +<B ．122V V V +≤C ．122V V V +>D ．122V V V += 6．（2022·浙江温州·二模）已知正数a ，b 和实数t 满足221a tab b ++=，若a b +存在最大值，则t 的取值范围是（ ）A ．(],2-∞B ．()2,-+∞C ．(]2,2-D ．[)2,+∞7．（2022·广东·高三阶段练习）在足球比赛中，球员在对方球门前的不同的位置起脚射门对球门的威胁是不同的，出球点对球门的张角越大，射门的命中率就越高.如图为室内5人制足球场示意图，设球场（矩形）长BC 大约为40米，宽AB 大约为20米，球门长PQ 大约为4米.在某场比赛中有一位球员欲在边线BC 上某点M 处射门（假设球贴地直线运行），为使得张角PMQ ∠最大，则BM 大约为（ ）（精确到1米）A ．8米B ．9米C ．10米D ．11米8．（2022·江苏无锡·模拟预测）已知实数a ，b 满足如下两个条件：（1）关于x 的方程2320x x ab --=有两个异号的实根；（2）211a b+=，若对于上述的一切实数a ，b ，不等式222a b m m +>+恒成立，则实数m 的取值范围是（ ）A ．()4,2-B ．()2,4-C ．][(),42,-∞-⋃+∞D ．][(),24,-∞-⋃+∞二、填空题9．（2022·陕西西安·高三阶段练习（文））已知0x >，0y >，334x y x y +--=.则x y +的取值范围为__________. 10．（2022·上海·二模）已知对()0,x ∀∈+∞，不等式1x m x>-恒成立，则实数m 的最大值是_________. 11．（2022·浙江·高三阶段练习）已知函数()29x f x x+=，()2log g x x a =+，若存在[]13,4x ∈，任意[]24,8x ∈，使得()()12f x g x ≥，则实数a 的取值范围是___________.12．（2022·安徽合肥·高一期末）如图所示，某农科院有一块直角梯形试验田ABCD ，其中//,AB CD AD AB ⊥.某研究小组计则在该试验田中截取一块矩形区域AGEH 试种新品种的西红柿，点E 在边BC 上，则该矩形区域的面积最大值为___________.三、解答题13．（2022·湖南·高一课时练习）（1）把36写成两个正数的积，当这两个正数取什么值时，它们的和最小？ （2）把18写成两个正数的和，当这两个正数取什么值时，它们的积最大？14．（2022·辽宁朝阳·高一开学考试）如图，设矩形()ABCD AB AD >的周长为8cm ，将△ABC 沿AC 向△ADC 折叠，AB 折过去后交DC 于点P ，设AB xcm =，求ADP △面积的最大值及相应x 的值.15．（2022·贵州·赫章县教育研究室高一期末）已知关于x 的不等式220ax ax ++>的解集为R ，记实数a 的所有取值构成的集合为M .(1)求M ；(2)若0t >，对a M ∀∈，有245321a t t a --≤+-+，求t 的最小值.16．（2022·山西·怀仁市第一中学校高一期末）党中央国务院对节能减排高度重视，各地区认真贯彻党中央国务院关于“十三五”节能减排的决策部署，把节能减排作为转换发展方式，新能源汽车环保节能以电代油，减少排放，既符合我国国情，也代表了汽车产业发展的方向．为了响应国家节能减排的号召，2022年某企业计划引进新能源汽车生产设备．通过市场分析：全年需投入固定成本2500万元．每生产x （百辆）新能源汽车，需另投入成本()C x 万元，且()210500,040,64009016300,40.x x x C x x x x ⎧+<<⎪=⎨+-≥⎪⎩由市场调研知，每辆车售价9万元，且生产的车辆当年能全部销售完．(1)请写出2022年的利润()L x （万元）关于年产量x （百辆）的函数关系式；（利润＝售价－成本）(2)当2022年的总产量为多少百辆时，企业所获利润最大？并求出最大利润．。

初中数学第三册一元二次方程教案：带你详细了解解一元二次方程的方法带你详细了解解一元二次方程的方法一元二次方程是初中数学中的重要知识点之一，其解法不仅是高中数学的基础，而且也是应用数学中的常用方法之一。

因此，对于初中生来说，深入了解和掌握一元二次方程的解法意义重大。

本文将带你详细了解解一元二次方程的方法。

一、概念和基础知识1、什么是一元二次方程？一元二次方程是这样的一个方程：ax²+bx+c=0（a≠0）其中a、b、c为已知数，x为未知数。

x是一元，表示未知的数量。

a、b、c是二次，表示它们在方程中都具有平方项。

2、一元二次方程的解法解一元二次方程的方法有以下几种：（1）因式分解法。

如果一元二次方程的系数a、b、c都是整数，并且可以分解成两个整数的乘积，那么就可以用因式分解法来解题。

（2）公式法。

一元二次方程有两个解，可以用求根公式解题，其中解出的两个根如下：（i）如果b²-4ac>0，则方程有两个不相等的实数根。

（ii）如果b²-4ac=0，则方程有两个相等的实数根。

（iii）如果b²-4ac<0，则方程没有实数根。

（3）配方法。

当一元二次方程的一项系数b为负数，而且绝对值大于c与a的乘积时，可以通过配方法换元解题。

二、练习题1、用公式法解方程：x²-6x+5=0解：根据公式法，将方程中的系数代入公式中得：x1 = (6+√16)/2=3+√4=5x2 = (6-√16)/2=3-√4=1所以方程的解为：x=1，x=5。

2、用配方法解方程：x²+12x+32=0解：将x²+12x+32=0的两边同时减去32，得：x²+12x=-32将方程两边同时加上（12/2）²=36得：x²+12x+36=4把左边的式子化成平方加4，得：(x+6)²=4开方得：x+6=±2x=-6±2解得方程的两个实数根为：x1=-4，x2=-8。

第3讲 一元二次方程的解法(三)----公式法知识要点梳理1.一元二次方程ax 2 ＋bx ＋c ＝0的求根公式： 利用这个公式，我们可以由一元二次方程中系数a 、b 、c 的值，直接求得方程的解，这种解方程的方法叫做公式法.2.根的判别式：ac b 42-=∆① 当b 2－4ac ＞0时，方程有2个不相等的实数根；② 当b 2－4ac ＝0时，方程有2个相等的实数根x 1＝x 2＝ab 2- ③ 当b 2－4ac ＜0时，方程无实数根. 经典例题例1.用配方法解一元二次方程ax 2＋bx ＋c ＝0(a ≠0).因为a ≠0，方程两边都除以a ，得_____________________＝0. 移项，得 x 2＋ab x ＝________， 配方，得 x 2＋a b x ＋______＝______－ac , 即 (____________) 2＝___________因为a ≠0，所以4 a 2＞0，当b 2－4 ac ≥0时，直接开平方，得_____________________________.所以x ＝_______________________例2.不解方程，判断方程根的情况。

（1）x 2＋2x －8＝0； （2）3x 2＝4x －1；（3）x （3x －2）－6x 2-2＝0； （4）x 2＋(3＋1)x ＝0； （5）x （x ＋8）＝-16； （6）（x ＋2）（x －5）＝1； 例2. m 取什么值时，关于x 的方程x 2-2x ＋m －2＝0（1）有两个相等的实数根？ （2）没有实数根?例3. 说明不论ｋ取何值，关于x 的方程x 2＋(2ｋ＋１)x ＋ｋ－１＝0总有两个不相等的实根. 例4. 应用公式法解方程：(1) x 2－6x ＋1＝0； (2)2x 2－x ＝6；(3)4x 2－3x －1＝x －2； (4)3x(x －3) ＝2(x －1) (x ＋1). x ＝a ac b b 242-±-( b 2－4 ac ≥0)（5）x 2+16x-13=0 （6）（x ＋1）2＝2（x ＋1）. 经典练习: 1、方程x 2-4x ＋4＝0的根的情况是（ ）A.有两个不相等的实数根；B.有两个相等的实数根；C.有一个实数根；D.没有实数根.2、下列关于x 的一元二次方程中，有两个不相等的实数根的方程是（ ）A ．x 2＋1＝0 B. x 2+x-1＝0 C. x 2+2x ＋3＝0 D. 4x 2-4x ＋1＝03、若关于x 的方程x 2-x ＋k ＝0没有实数根，则（ ）A. k ＜41B. k ＞41C. k ≤41D. k ≥41 4、关于x 的一元二次方程x 2-2x ＋2k ＝0有实数根，则k 的范围是（ ）A. k ＜21B. k ＞21C. k ≤21D. k ≥21 5．一元二次方程x 2-2x-m=0有两个相等的实数根，则m=（ ）．A ．0B ．1C ．-1D ．±16．用公式法解方程4y 2=12y+3，得到（ ）A ．B ．C ．D ． 7．已知a 、b 、c 是△ABC 的三边长，且方程a （1+x 2）+2bx-c （1-x 2）=0的两根相等，则△ABC 为（ ）A ．等腰三角形B ．等边三角形C ．直角三角形D ．任意三角形8．不解方程，判断所给方程：①x 2+3x+7=0；②x 2+4=0；③x 2+x-1=0中，有实数根的方程有（ ）A ．0个B ．1个C ．2个D ．3个9．关于x 的一元二次方程x 2+2x+c=0的两根为__________________．（c ≤1）10．用公式法解方程x 2= -8x-15，其中b 2-4ac=___________，x 1=_________，x 2=___________．11．已知一个矩形的长比宽多2cm ，其面积为8cm 2，则此长方形的周长为________．12．当x=_______时，代数式13x +与2214x x +-的值互为相反数． 13．若方程042=+-a x x 的两根之差为0，则a 的值为______________．14．应用公式法解下列方程:(1) 2 x 2＋x －6＝0； (2) x 2＋4x ＝2；(3) 5x 2－4x －12＝0； (4) 4x 2＋4x ＋10＝1－8x.15.小明在一块长18m 宽14m 的空地上为班级建造一个花园，所建花园占空地面积的2116，图中阴影部分表示道路，请你求出图中的x ．16．要建一个面积为150m 2的长方形养鸡场，为了节约材料，鸡场的一边靠着原有的一堵墙，墙长为am ，另三边用竹篱笆围成，如果篱笆的长为35m ．（1）求鸡场的长与宽各是多少？（2）题中墙的长度a对解题有什么作用．课后巩固:1．解下列方程；（1）2x2-3x-5=0 （2）2t2+3=7t(3) (x+5)(x-2)＝8；（4）x2x+1=0（5）0.4x2-0.8x=1 （6）23y2+13y-2=02.ｋ取什么值时，关于x的方程4x2-(ｋ＋2)x＋ｋ－１＝0有两个相等的实数根？求出这时方程的根.3、某农场要建一个矩形的养鸭场，养鸭场的一边靠墙，墙长25m，另三边用篱笆围成，篱笆长为40m. （1）养鸭场的面积能达到150m2吗？（2）能达到200 m2吗？（3）能达到250m2吗？如果能，要怎么围？。