(推荐)高中数学必修1基本初等函数常考题型：幂函数

高中数学必修一《幂函数》精选习题（含详细解析）一、选择题1.下列函数中,是幂函数的是( )A.y=2xB.y=2x3C.y=D.y=2x22.若幂函数y=(m2-3m+3)x m-2的图象不过原点,则m的取值范围为( )A.1≤m≤2B.m=1或m=2C.m=2D.m=13.函数y=x-2在区间上的最大值是( )A. B. C.4 D.-44若本题的条件不变,则此函数在区间上的最大值和最小值之和为多少?5.在下列函数中,定义域为R的是( )A.y=B.y=C.y=2xD.y=x-16函数y=|x(n∈N,n>9)的图象可能是( )7下列幂函数在(-∞,0)上为减函数的是( )A.y=B.y=x2C.y=x3D.y=8下列幂函数中过点(0,0),(1,1)且为偶函数的是( )A.y=B.y=x4C.y=x-2D.y=9.在同一坐标系内,函数y=x a(a≠0)和y=ax-的图象可能是( )二、填空题10幂函数f(x)=xα过点,则f(x)的定义域是.11若y=a是幂函数,则该函数的值域是.12若函数f(x)是幂函数,且满足=3,则f的值等于.13.设a=,b=,c=,则a,b,c的大小关系是.14已知幂函数f=(m∈Z)的图象与x轴,y轴都无交点,且关于原点对称,则函数f的解析式是.三、解答题15.比较下列各组数的大小:(1)1.10.1,1.20.1;(2)0.24-0.2,0.25-0.2;(3)0.20.3,0.30.3,0.30.2.16.已知幂函数y=x3-p(p∈N*)的图象关于y轴对称,且在(0,+∞)上为增函数,求满足条件(a+1<(3-2a的实数a的取值范围.17幂函数f的图象经过点(,2),点在幂函数g的图象上,(1)求f,g的解析式.(2)x为何值时f>g,x为何值时f<g?18已知幂函数f(x)=(m2-m-1)·x-5m-3在(0,+∞)上是增函数,又g(x)=lo(a>1).(1)求函数g(x)的解析式.(2)当x∈(t,a)时,g(x)的值域为(1,+∞),试求a与t的值.参考答案与解析1【解析】选C.由幂函数所具有的特征可知,选项A,B,D中x的系数不是1;故只有选项C中y==x-1符合幂函数的特征.2【解析】选D.由题意得解得m=1.3【解析】选C.y=x-2在区间上单调递减,所以x=时,取得最大值为4.4【解析】y=x-2在区间上单调递减,所以x=2时,取得最小值为,当x=时,取得最大值为4.故最大值和最小值的和为.5【解析】选C.选项A中函数的定义域为[0,+∞),选项B,D中函数的定义域均为(-∞,0)∪(0,+∞).6【解析】选C.因为y=|x为偶函数,所以排除选项A,B.又n>9,所以<1.由幂函数在(0,+∞)内幂指数小于1的图象可知,只有选项C符合题意.7【解析】选B.函数y=,y=x3,y=在各自定义域上均是增函数,y=x2在(-∞,0)上是减函数. 8【解析】选B.函数y=x4是过点(0,0),(1,1)的偶函数,故B正确;函数y=x-2不过点(0,0),故C 不正确;函数y=,y=是奇函数,故A,D不正确.9【解析】选C.当a<0时,函数y=ax-在R上是减函数,此时y=x a在(0,+∞)上也是减函数,同时为减的只有D选项,而函数y=ax-与y轴相交于点,此点在y轴的正半轴上,故D选项不适合.当a>0时,函数y=ax-在R上是增函数,与y轴相交于点,此点在y轴的负半轴上,只有A,C适合,此时函数y=x a在(0,+∞)上是增函数,进一步判断只有C适合.10【解析】因为幂函数f(x)过点,所以=2α,所以α=-1,所以f(x)=x-1=,所以函数f(x)的定义域是(-∞,0)∪(0,+∞).答案:(-∞,0)∪(0,+∞)11【解析】由已知y=a是幂函数,得a=1,所以y=,所以y≥0,故该函数的值域为[0,+∞).答案:[0,+∞)3,12【解析】依题意设f(x)=xα,则有=3,得α=log2则f(x)=,于是f====.答案:13【解析】因为y=在x∈(0,+∞)上递增,所以>,即a>c,因为y=在x∈(-∞,+∞)上递减,所以>,即c>b,所以a>c>b.答案:a>c>b14【解析】因为函数的图象与x轴,y轴都无交点,所以m2-1<0,解得-1<m<1;因为图象关于原点对称,且m∈Z,所以m=0,所以f=x-1.答案:f=x-115【解析】(1)由于函数y=x0.1在第一象限内单调递增,又因为1.1<1.2,所以1.10.1<1.20.1.(2)由于函数y=x-0.2在第一象限内单调递减,又因为0.24<0.25,所以0.24-0.2>0.25-0.2.(3)首先比较指数相同的两个数的大小,由于函数y=x0.3在第一象限内单调递增,而0.2<0.3,所以0.20.3<0.30.3.再比较同底数的两个数的大小,由于函数y=0.3x在定义域内单调递减,而0.2<0.3,所以0.30.3<0.30.2.所以0.20.3<0.30.3<0.30.2.16【解析】因为幂函数y=x3-p(p∈N*)的图象关于y轴对称,所以函数y=x3-p是偶函数.又y=x3-p在(0,+∞)上为增函数,所以3-p是偶数且3-p>0.因为p∈N*,所以p=1,所以不等式(a+1<(3-2a化为:(a+1<(3-2a.因为函数y=是[0,+∞)上的增函数,所以⇒⇒-1≤a<,故实数a的取值范围为.17【解析】(1)设f=xα,则()α=2,所以α=2,所以f=x2.设g=xβ,则(-2)β=,所以β=-2,所以g=x-2(x≠0).(2)从图象可知,当x>1或x<-1时,f>g;当-1<x<0或0<x<1时,f<g.18【解析】(1)因为f(x)是幂函数,且在(0,+∞)上是增函数,所以解得m=-1,所以g(x)=loga.(2)由>0可解得x<-1或x>1,所以g(x)的定义域是(-∞,-1)∪(1,+∞).又a>1,x∈(t,a),可得t≥1,设x1,x2∈(1,+∞),且x1<x2,于是x2-x1>0,x1-1>0,x2-1>0,所以-=>0, 所以>.由a>1,有loga >loga,即g(x)在(1,+∞)上是减函数.又g(x)的值域是(1,+∞),所以得g(a)=loga=1,可化为=a, 解得a=1±,因为a>1,所以a=1+,综上,a=1+,t=1.。

高中数学人教版必修1 第二章基本初等函数(I) 2.3 幂函数选择题下列函数中是幂函数的是（）①y＝?x2；②y＝2x；③y＝xπ；④y＝(x?1)3；⑤y＝；⑥y＝x2＋.A．①③⑤? B．①②⑤C．③⑤D．只有⑤【答案】C【解析】y＝?x2的系数是?1而不是1，故不是幂函数；y＝2x是指数函数；y＝(x?1)3的底数是x?1而不是x，故不是幂函数；y＝x2＋是两个幂函数和的形式，也不是幂函数．y＝＝x?2和y＝xπ具有幂函数y＝xα的形式，所以选C.选择题幂函数f(x)的图象过点(4，)，那么f(8)的值为（）A. B．64 C．2 ? D.【答案】A【解析】设幂函数的解析式为y＝xα，依题意得，＝4α，即22α＝2?1，∴α＝?.∴幂函数的解析式为y＝，∴f(8)＝＝＝＝, 故选A.选择题函数f(x)＝(m2?m?1)是幂函数，且在x∈(0，+∞)上是减函数，则实数m的取值集合是（）A．{m|m＝?1或m＝2} B．{m|?1解得m＝2.选择题下列幂函数中图象过点(0，0)，(1，1)，且是偶函数的是（）A.? y=?B.? y=C.? y=D.? y=【答案】B【解析】函数y=，y=不是偶函数，函数y=是偶函数，但其图象不过点(0，0).函数y=的图象过点(0，0)，(1，1)且是偶函数，故选B.选择题函数f(x)=(n∈Z，a>0且a≠1)的图象必过定点（）A.(1，1) ?B.(1，2)C.( ?1，0)D.( ?1，1)【解析】因为f(1)==1+1=2，所以f(x)=(n∈Z，a>0且a≠1)的图象必过定点(1，2)，故选B.选择题下列命题中正确的是（）A．当α＝0时，函数y＝xα的图象是一条直线B．幂函数的图象都经过(0，0)、(1，1)两点C．幂函数y＝x0的定义域是RD．幂函数的图象不可能在第四象限【答案】D【解析】当α＝0时，函数y＝xα的定义域为{x|x≠0，x∈R}，其图象不是直线，故A和C不? 正确；当α0，α∈R时，y＝xα>0，则幂函数的图象都不在第四象限，故D正确．选择题设α∈{?2，?1，?，，，1，2，3}，则使f(x)＝xα为奇函数，且在(0，+∞)上递增的α的个数是（）A．1 B．2 C．3 D．4【解析】f(x)为奇函数，则α＝?1，，1，3，f(x)在(0，+∞)上递增，则α＝，1，3，故选C.选择题在同一坐标系内，函数y＝xa(a≠0)和y＝ax?的图象可能是（）【答案】C【解析】当a0，结合图象排除A，C，D，又y＝xa在(0，+∞)上是减函数，∴B项也不正确．当a>0时，y＝ax?是增函数，?0时，y＝xa在(0，+∞)上是增函数，故A项不正确，故选C.选择题在函数，，，中，幂函数的个数为A．0? ? B．1C．2 D．3【解析】函数为幂函数；函数，前的系数不是1，所以它不是幂函数；函数是两个函数和的形式，所以它不是幂函数；函数与不是同一个函数，所以它也不是幂函数．所以只有1个是幂函数，故选B．选择题若函数是幂函数，且满足，则的值等于A．B．C．D．【答案】A【解析】令，因为，即，解得，所以，所以．选择题若幂函数的图象不过原点，则A．B．或C．D．【答案】B【解析】因为幂函数的图象不过原点，所以，解得或．故选B．选择题如图所示的曲线是幂函数在第一象限的图象，已知，相应曲线对应的值依次为A．B．C．D．【答案】B【解析】结合幂函数的单调性及图象，易知曲线对应的值依次为．故本题选B．选择题设，，，则的大小关系是A．B．C．D．【答案】B【解析】在上为减函数，，即.在上为增函数，，即.所以.选择题在同一直角坐标系中，函数，的图象可能是【答案】D【解析】对于A，没有幂函数的图象，不符合题目要求；对于B,中，中，舍去；对于C，中，中，舍去；对于D，中，中，故选D.选择题已知幂函数的图象过点，则A．B．1C．D．2【答案】A【解析】因为幂函数的图象过点，所以，解得，所以．故选A．选择题函数是幂函数，且在上为增函数，则实数的值是A．?1? B．2C．3 D．?1或2【答案】B【解析】是幂函数或．又在上是增函数，所以，故选B．填空题比较下列各组数的大小：(1)与的大小关系是______；(2)，，的大小关系是______.【答案】(1) （2）【解析】1)∵在(0，+∞)上为减函数，且5.1>5.09，∴.(2)，.∵在(0，+∞)上为增函数，且，∴.又，∴.填空题已知幂函数f(x)＝，若f(a+1)＝(x>0)，易知f(x)在(0，+∞)上为减函数，又f(a+1)解得∴3，下列五个关系式：①0与y＝的图象(如图所示)，设，作直线y＝m.如果m＝0或1，则a＝b；如果01，则1填空题若一个幂函数的图象过点，则．【答案】【解析】设幂函数的解析式为已知幂函数的图象过点，所以，即所以，则．填空题若，则满足的的取值范围是．【答案】【解析】根据幂函数的性质，由于，所以当时，当时，，因此的解集为.填空题下列函数中，在(0,1)上单调递减，且为偶函数的是．①；②y=x4；③y=x?2；④.【答案】③【解析】①中函数不具有奇偶性；②中函数y=x4是偶函数，但在[0，＋∞)上为增函数；③中函数y=x?2是偶函数，且在(0，＋∞)上为减函数；④中函数是奇函数．故填③.填空题已知幂函数，若f(a＋1)＜f(10?2a)，则a的取值范围是．【答案】(3,5)【解析】∵，易知f(x)在(0，＋∞)上为减函数，又f(a＋1)＜f(10?2a)，∴，解得，∴3＜a＜5.解答题已知函数f(x)＝?且f(4)＝.(1)求的值；(2)判定f(x)的奇偶性；(3)判断f(x)在(0，+∞)上的单调性，并给予证明．【答案】(1)1 ?(2)奇函数?(3)略【解析】(1)因为f(4)＝，所以，所以＝1.(2)由(1)知f(x)=，因为f(x)的定义域为{x|x≠0}，，所以f(x)是奇函数．(3) f(x)在(0，+∞)上单调递增.证明如下：设，则.因为，所以，，所以，所以f(x)在(0，+∞)上为单调递增函数．解答题已知点在幂函数f(x)的图象上，点在幂函数g(x)的图象上，问当x为何值时，(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)?α＝2，∴f(x)＝x2.同理可求出，在同一坐标系内作出y＝f(x)与y＝g(x)的图象，如图所示．由图象可知：(1)当x>1或xg(x)．(2)当x＝±1时，f(x)＝g(x)．(3)当?1，其中?2，，1；（2），，；【答案】（1）；（2）．【解析】（1）把1看作，幂函数在(0，＋∞)上是增函数．∵，∴，即．（2）因为，，，幂函数在(0，＋∞)上是增函数，且.∴.解答题已知幂函数（）的图象关于轴对称，且在上是减函数．（1）求的值；（2）求满足不等式的实数a的取值范围．【答案】（1）；（2）.【解析】（1）因为函数在上是减函数，所以，所以.因为，所以或.又函数图象关于轴对称，所以是偶数，所以.（2）不等式等价于，解得．所以实数a的取值范围是.解答题已知幂函数(m∈Z)为偶函数，且在区间(0，＋∞)上是单调增函数．（1）求函数f(x)的解析式；（2）设函数，若g(x)>2对任意的x∈R恒成立，求实数c的取值范围．【答案】（1）f(x)=x4；（2）(3，＋∞).【解析】（1）∵f(x)在区间(0，＋∞)上是单调增函数，∴?m2＋2m＋3>0，即m2?2m?32对任意的x∈R恒成立，∴g(x)min>2，且x∈R，即c?1>2，解得c>3.故实数c的取值范围是(3，＋∞)．。

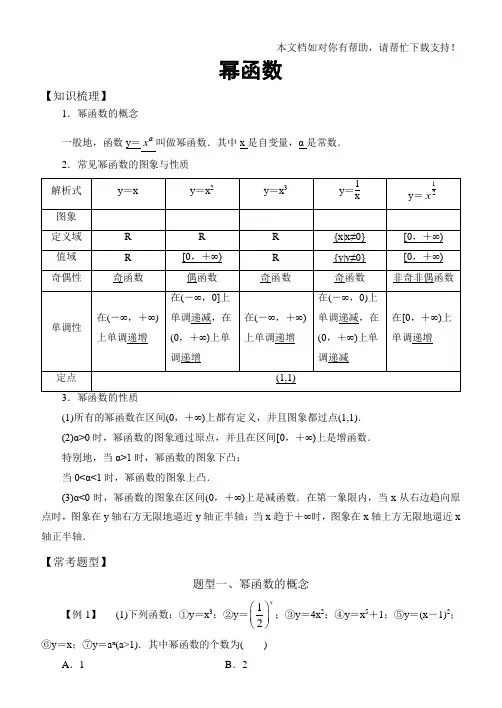
幂函数【知识梳理】1．幂函数的概念一般地，函数y＝xα叫做幂函数．其中x是自变量，α是常数．2．常见幂函数的图象与性质(1)所有的幂函数在区间(0，＋∞)上都有定义，并且图象都过点(1,1)．(2)α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸．(3)α<0时，幂函数的图象在区间(0，＋∞)上是减函数．在第一象限内，当x从右边趋向原点时，图象在y轴右方无限地逼近y轴正半轴；当x趋于＋∞时，图象在x轴上方无限地逼近x 轴正半轴．【常考题型】题型一、幂函数的概念【例1】(1)下列函数：①y＝x3；②y＝12x⎛⎫⎪⎝⎭；③y＝4x2；④y＝x5＋1；⑤y＝(x－1)2；⑥y＝x；⑦y＝a x(a>1)．其中幂函数的个数为()A．1B．2C ．3D ．4(2)已知幂函数y ＝()22231m m m m x----，求此幂函数的解析式，并指出定义域．(1)[解析] ②⑦为指数函数，③中系数不是1，④中解析式为多项式，⑤中底数不是自变量本身，所以只有①⑥是幂函数，故选B.[答案] B(2)[解] ∵y ＝()22231mm m m x ----为幂函数，∴m 2－m －1＝1，解得m ＝2或m ＝－1.当m ＝2时，m 2－2m －3＝－3，则y ＝x －3，且有x≠0； 当m ＝－1时，m 2－2m －3＝0，则y ＝x 0，且有x≠0.故所求幂函数的解析式为y ＝x －3，{x|x≠0}或y ＝x 0，{x|x≠0}． 【类题通法】判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y ＝x α(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.反之，若一个函数为幂函数，则该函数应具备这一形式，这是我们解决某些问题的隐含条件．【对点训练】函数f(x)＝()2231m m m m x +---是幂函数，且当x ∈(0，＋∞)时，f(x)是增函数，求f(x)的解析式．解：根据幂函数的定义得m 2－m －1＝1.解得m ＝2或m ＝－1.当m ＝2时，f(x)＝x 3在(0，＋∞)上是增函数； 当m ＝－1时，f(x)＝x －3在(0，＋∞)上是减函数，不符合要求．故f(x)＝x 3.题型二、幂函数的图象【例2】 (1)如图，图中曲线是幂函数y ＝x α在第一象限的大致图象，已知α取－2，－12，12，2四个值，则相应于曲线C 1，C 2，C 3，C 4的α的值依次为( )A ．－2，－12，12，2B ．2，12，－12，－2本文档如对你有帮助，请帮忙下载支持！C ．－12，－2,2，12D ．2，12，－2，－12(2)如图是幂函数y ＝mx 与y ＝nx 在第一象限内的图象，则( ) A ．－1<n<0<m<1 B ．n<－1,0<m<1 C ．－1<n<0，m>1 D ．n<－1，m>1[解析] (1)令x ＝2，则22>212>2－12>2－2，故相应于曲线C 1，C 2，C 3，C 4的α值依次为2，12，－12，－2.故选B.(2)此类题有一简捷的解决办法，在(0,1)内取x 0，作直线x ＝x 0，与各图象有交点，则“点低指数大”．如图，0<m<1，n<－1.[答案] (1)B (2)B 【类题通法】解决幂函数图象问题应把握的两个原则(1)依据图象高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函数图象越靠近x 轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图象越远离x 轴(简记为指大图高)．(2)依据图象确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图象(类似于y ＝x－1或y ＝12x 或y ＝x 3)来判断．【对点训练】已知函数y ＝ax ，y ＝bx ，y ＝cx 的图象如图所示，则a ，b ，c 的大小关系为( ) A ．c<b<a B ．a<b<c C ．b<c<aD ．c<a<b解析：选A 由幂函数的图象特征知，c<0，a>0，b>0.由幂函数的性质知，当x>1，幂指数大的幂函数的函数值就大，则a>b.综上所述，可知c<b<a.题型三、利用幂函数的性质比较大小【例3】 比较下列各组数中两个数的大小．(1)0.525⎛⎫ ⎪⎝⎭与0.513⎛⎫⎪⎝⎭；(2)123-⎛⎫- ⎪⎝⎭与135-⎛⎫- ⎪⎝⎭；(3)3423⎛⎫⎪⎝⎭与2334⎛⎫ ⎪⎝⎭. [解] (1)∵幂函数y ＝0.5x 在(0，＋∞)上是单调递增的，又25>13，∴0.525⎛⎫ ⎪⎝⎭>0.513⎛⎫⎪⎝⎭. (2)∵幂函数y ＝1x -在(－∞，0)上是单调递减的， 又－23<－35，∴123-⎛⎫- ⎪⎝⎭>135-⎛⎫- ⎪⎝⎭.(3)∵函数y 1＝23x⎛⎫⎪⎝⎭为R 上的减函数，又34>23，∴2323⎛⎫⎪⎝⎭>3423⎛⎫ ⎪⎝⎭. 又∵函数y 2＝23x 在(0，＋∞)上是增函数，且34>23，∴2334⎛⎫⎪⎝⎭>2323⎛⎫ ⎪⎝⎭，∴2334⎛⎫ ⎪⎝⎭>3423⎛⎫⎪⎝⎭. 【类题通法】比较幂值大小的方法(1)若指数相同，底数不同，则考虑幂函数； (2)若指数不同，底数相同，则考虑指数函数；(3)若指数与底数都不同，则考虑插入中间数，使这个数的底数与所比较数的一个底数相同，指数与另一个数的指数相同，那么这个数就介于所比较的两数之间，进而比较大小．【对点训练】比较下列各题中两个幂的值的大小： (1)342.3，342.4；(2)32-　，32-　；(3)()650.31-，650.35.解：(1)∵y ＝34x 为[0，＋∞)上的增函数，且2.3<2.4， ∴342.3<342.4.(2)∵y ＝32x -　为(0，＋∞)∴32-　>32-　.(3)∵y ＝65x 为R 上的偶函数，∴()650.31-＝650.31.又函数y ＝65x 为[0，＋∞)上的增函数，且0.31<0.35， ∴650.31<650.35，即()650.31-<650.35.【练习反馈】1．下列函数是幂函数的是( ) A ．y ＝2x B ．y ＝2x －1C ．y ＝(x ＋1)2D ．y 解析：选D 由幂函数的概念可知D 正确． 2．下列命题：①幂函数的图象都经过点(1,1)和点(0,0)； ②幂函数的图象不可能在第四象限； ③n ＝0，函数y ＝nx 的图象是一条直线； ④幂函数y ＝n x 当n>0时，是增函数；⑤幂函数y ＝nx 当n<0时，在第一象限内函数值随x 值的增大而减小． 正确的命题为( ) A ．①④ B ．④⑤ C ．②③ D ．②⑤解析：选D y ＝x－1不过(0,0)点，∴①错误，排除A ；当n ＝0时，y ＝nx 的图象为两条射线，③错误，排除C ；y ＝x 2不是增函数，④错误，排除B ；因此答案选D.3．已知幂函数f(x)的图象过点(4,2)，则f ⎝⎛⎭⎫18＝________. 解析：设f(x)＝x α，则4α＝2，∴α＝12，即f(x)＝12x ，∴f ⎝⎛⎭⎫18＝1218⎛⎫ ⎪⎝⎭＝4.答案：44．函数f(x)＝()22231m m m m x +--+是幂函数，且在x ∈(0，＋∞)时是减函数，则实数m ＝________.解析：由m 2－m ＋1＝1，得m ＝0或m ＝1，再把m ＝0和m ＝1分别代入m 2＋2m －3<0检验，得m ＝0. 答案：05．比较下列各题中两个幂的值的大小： (1)121.1，120.9；(2) 121.1-　，120.9-　；(3)343-　，3412⎛⎫⎪⎝⎭. 解：(1)∵y ＝12x 为[0，＋∞)上的增函数，又1.1>0.9， ∴121.1>120.9. (2)∵y ＝12x -　为(0，＋∞)上的减函数，又1.1>0.9，∴121.1-　<120.9-　.(3)∵343-　＝3413⎛⎫ ⎪⎝⎭，函数y ＝34x 为[0，＋∞)上的增函数，且13<12，∴3413⎛⎫ ⎪⎝⎭<3412⎛⎫⎪⎝⎭，即343-　<3412⎛⎫ ⎪⎝⎭.。

姓名___________ 2011年____月____日 第____课时§2.3幂函数一， 相关知识回顾：我们曾经学过的函数：y=1x,(y=1x -),y=12x ),y=x,y=2x ,y=3x ,这些函数虽然定义域、值域、单调性、奇偶性以及函数图象等都不进相同，但它们都有一个共同的特点：自变量均在底数的位置之上。

可以用一个共同的表达方式：y= a x (a ∈R) 二．幂函数：（一）幂函数的定义：一般地，形如y= a x (a ∈R)的函数称为幂函数，其中a 为常数。

（二）准确理解幂函数的定义：①幂函数具有严格的形式，如形如：y=m ax,y=()a m x ,y=a x +m,y=()a x m +等均不是幂函数；②不要把指数函数和幂函数混淆起来；③（三）幂函数1、幂函数定义：一般地，形如αx y =)(R a ∈的函数称为幂函数，其中α为常数．2、幂函数性质归纳．（1）所有的幂函数在（0，+∞）都有定义并且图象都过点（1，1）；（2）0>α时，幂函数的图象通过原点，并且在区间),0[+∞上是增函数．特别地，当1>α时，幂函数的图象下凸；当10<<α时，幂函数的图象上凸；（3）0<α时，幂函数的图象在区间),0(+∞上是减函数．在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于∞+时，图象在x 轴上方无限地逼近x 轴正半轴．（4）当a 为奇数时，幂函数为奇函数；当a 为偶数时，幂函数为偶函数；五．例题详解：1．（www.jiaocai quanjieP203）已知函数f(x)=( 2m +2m)∙21m m x +-,m 为何值时，f(x)是：（1）正比例函数；（2）反比例函数；（3）二次函数；（4）幂函数2．(www.wanghouxiongP87)函数f(x)=( 2m-m-1)∙23mm x +-是幂函数，且当x ∈（0, +∞)时，f(x)是增函数，求f(x)的解析式3．(www.wanghouxiongP87) 数形结合的数学思想2）在幂函数f(x)的图象上，点（-2，14）在幂函数g(x)的图像上。

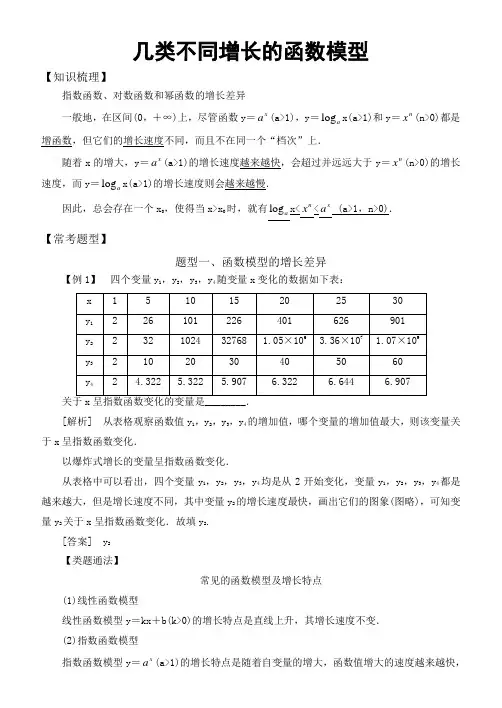
几类不同增长的函数模型【知识梳理】指数函数、对数函数和幂函数的增长差异一般地，在区间(0，＋∞)上，尽管函数y＝x a(a>1)，y＝log a x(a>1)和y＝n x(n>0)都是增函数，但它们的增长速度不同，而且不在同一个“档次”上．随着x的增大，y＝x a(a>1)的增长速度越来越快，会超过并远远大于y＝n x(n>0)的增长x(a>1)的增长速度则会越来越慢．速度，而y＝loga因此，总会存在一个x0，使得当x>x0时，就有logx<n x<x a (a>1，n>0)．a【常考题型】题型一、函数模型的增长差异【例1】四个变量y1，y2，y3，y4随变量x变化的数据如下表：[解析] 从表格观察函数值y1，y2，y3，y4的增加值，哪个变量的增加值最大，则该变量关于x呈指数函数变化．以爆炸式增长的变量呈指数函数变化．从表格中可以看出，四个变量y1，y2，y3，y4均是从2开始变化，变量y1，y2，y3，y4都是越来越大，但是增长速度不同，其中变量y2的增长速度最快，画出它们的图象(图略)，可知变量y2关于x呈指数函数变化．故填y2.[答案] y2【类题通法】常见的函数模型及增长特点(1)线性函数模型线性函数模型y＝kx＋b(k>0)的增长特点是直线上升，其增长速度不变．(2)指数函数模型指数函数模型y＝x a(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越快，即增长速度急剧，形象地称为“指数爆炸”．(3)对数函数模型对数函数模型y ＝log a x(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越慢，即增长速度平缓．(4)幂函数模型幂函数y ＝nx (n>0)的增长速度介于指数增长和对数增长之间． 【对点训练】今有一组实验数据如下：t 1.99 3.0 4.0 5.1 6.12 v1.54.047.51218.01( ) A ．v ＝2log t B ．v ＝12log tC ．v ＝t 2－12D ．v ＝2t －2解析：选C 从表格中看到此函数为单调增函数，排除B ，增长速度越来越快，排除A 和D ，选C.题型二、指数函数、对数函数与幂函数模型的比较【例2】 函数f(x)＝2x和g(x)＝x 3的图象如图所示．设两函数的图象交于点A(x 1，y 1)，B(x 2，y 2)，且x 1<x 2.(1)请指出图中曲线C 1，C 2分别对应的函数；(2)结合函数图象，判断f(6)，g(6)，f(2 011)，g(2 011)的大小． [解] (1)C 1对应的函数为g(x)＝x 3，C 2对应的函数为f(x)＝2x.(2)∵f(1)>g(1)，f(2)<g(2)，f(9)<g(9)，f(10)>g(10)，∴1<x 1<2,9<x 2<10，∴x 1<6<x 2,2 011>x 2.从图象上可以看出，当x 1<x<x 2时，f(x)<g(x)， ∴f(6)<g(6)．当x>x 2时，f(x)>g(x)，∴f(2 011)>g(2 011)．又g(2 011)>g(6)，∴f(2 011)>g(2 011)>g(6)>f(6)． 【类题通法】[由图象判断指数函数、对数函数和幂函数的方法根据图象判断增长型的指数函数、对数函数和幂函数时，通常是观察函数图象上升得快慢，即随着自变量的增大，图象最“陡”的函数是指数函数；图象趋于平缓的函数是对数函数．【对点训练】函数f(x)＝lg x ，g(x)＝0.3x －1的图象如图所示． (1)试根据函数的增长差异指出曲线C 1，C 2分别对应的函数；(2)比较两函数的增长差异(以两图象交点为分界点，对f(x)，g(x)的大小进行比较)．解：(1)C 1对应的函数为g(x)＝0.3x －1，C 2对应的函数为f(x)＝lg x.(2)当x<x 1时，g(x)>f(x)；当x 1<x<x 2时，f(x)>g(x)；当x>x 2时，g(x)>f(x)；当x ＝x 1或x ＝x 2时，f(x)＝g(x).题型三、函数模型的选取【例3】 某汽车制造商在2013年初公告：公司计划2013年生产目标定为43万辆．已知该公司近三年的汽车生产量如下表所示：年份 2010 2011 2012 产量8(万)18(万)30(万)如果我们分别将模型：二次函数模型f(x)＝ax 2＋bx ＋c(a≠0)，指数函数模型g(x)＝a·b x＋c(a≠0，b>0，b≠1)，哪个模型能更好地反映该公司年销量y 与年份x 的关系？[解] 建立年销量y 与年份x 的函数，可知函数必过点(1,8)，(2,18)，(3,30)． (1)构造二次函数模型f(x)＝ax 2＋bx ＋c(a≠0)， 将点坐标代入， 可得⎩⎪⎨⎪⎧a ＋b ＋c ＝8，4a ＋2b ＋c ＝18，9a ＋3b ＋c ＝30，解得a ＝1，b ＝7，c ＝0，则f(x)＝x 2＋7x ，故f(4)＝44，与计划误差为1.(2)构造指数函数模型g(x)＝a·b x＋c(a≠0，b>0，b≠1)，将点坐标代入，可得⎩⎪⎨⎪⎧ab ＋c ＝8，ab 2＋c ＝18，ab 3＋c ＝30，解得a ＝1253，b ＝65，c ＝－42，则g(x)＝1253·65x⎛⎫ ⎪⎝⎭－42，故g(4)＝1253·465⎛⎫⎪⎝⎭－42＝44.4，与计划误差为1.4.由(1)(2)可得，f(x)＝x 2＋7x 模型能更好地反映该公司年销量y 与年份x 的关系． 【类题通法】不同函数模型的选取标准不同的函数模型能刻画现实世界中不同的变化规律： (1)线性函数增长模型适合于描述增长速度不变的变化规律； (2)指数函数增长模型适合于描述增长速度急剧的变化规律； (3)对数函数增长模型适合于描述增长速度平缓的变化规律； (4)幂函数增长模型适合于描述增长速度一般的变化规律．因此，需抓住题中蕴含的数学信息，恰当、准确地建立相应变化规律的函数模型来解决实际问题．【对点训练】某学校为了实现100万元的生源利润目标，准备制定一个激励招生人员的奖励方案：在生源利润达到5万元时，按生源利润进行奖励，且奖金y 随生源利润x 的增加而增加，但奖金总数不超过3万元，同时奖金不超过利润的20%.现有三个奖励模型：y ＝0.2x ，y ＝5log x ，y ＝1.02x，其中哪个模型符合该校的要求？解：借助工具作出函数y ＝3，y ＝0.2x ，y ＝5log x ，y ＝1.02x的图象(图略)．观察图象可知，在区间[5,100]上，y ＝0.2x ，y ＝1.02x的图象都有一部分在直线y ＝3的上方，只有y ＝5log x的图象始终在y ＝3和y ＝0.2x 的下方，这说明只有按模型y ＝5log x 进行奖励才符合学校的要求．【练习反馈】1．下列函数中，随着x 的增大，增长速度最快的是( ) A ．y ＝50 B ．y ＝1 000x C ．y ＝2x －1D ．y ＝11 000ln x 解析：选C 指数函数模型增长速度最快，故选C. 2．三个变量y 1，y 2，y 3，随着变量x 的变化情况如下表：则关于xA．y1，y2，y3B．y2，y1，y3C．y3，y2，y1D．y1，y3，y2解析：选C 通过指数函数、对数函数、幂函数等不同函数模型的增长规律比较可知，对数函数的增长速度越来越慢，变量y3随x的变化符合此规律；指数函数的增长速度成倍增长，y2随x的变化符合此规律；幂函数的增长速度介于指数函数与对数函数之间，y1随x的变化符合此规律，故选C.3．若a>1，n>0，那么当x足够大时，x a，n x，log a x的大小关系是________．解析：∵a>1，n>0，∴函数y1＝x a，y2＝n x，y3＝log a x都是增函数．由指数函数、对数函数、幂函数的变化规律可知，当x足够大时，x a>n x>log a x.答案：x a>n x>log a x4．函数y＝x2与函数y＝x ln x在区间(1，＋∞)上增长较快的一个是________．解析：当x变大时，x比ln x增长要快，∴x2要比x ln x增长的要快．答案：y＝x25．某地发生地震，各地纷纷捐款捐物，甲、乙、丙三个公司分别派代表到慈善总会捐款给灾区．甲公司的代表说：“在10天内，我们公司每天捐款5万元给灾区．”乙公司的代表说：“在10天内，我们公司第1天捐款1万元，以后每天比前一天多捐款1万元．”丙公司的代表说：“在10天内，我们公司第1天捐款0.1万元，以后每天捐款都比前一天翻一番．”你觉得哪个公司最慷慨？解：三个公司在10天内捐款情况如下表所示：。

数学必修一基本初等函数知识点
1. 线性函数：y = kx + b（k和b为常数），其中k称为斜率，b称为截距。

2. 幂函数：y = x^n（n为常数），其中n可以是正整数、零、负整数。

3. 指数函数：y = a^x（a为正实数且a≠1）。

4. 对数函数：y = loga(x)（a为正实数且a≠1），其中x为正实数。

5. 三角函数（正弦函数、余弦函数、正切函数、余切函数等）：y = sinx，y = cosx，y = tanx，y = cotx等。

6. 反三角函数（反正弦函数、反余弦函数、反正切函数、反余切函数等）：y = arcsinx，y = arccosx，y = arctanx，y = arccotx等。

7. 绝对值函数：y = |x|。

8. 双曲函数（双曲正弦函数、双曲余弦函数、双曲正切函数等）：y = sinh(x)，y = cosh(x)，y = tanh(x)等。

9. 分段函数：根据不同条件定义函数的不同表达式，例如：y = f(x) =
{ x+1, (x≤0)
{ x^2, (0<x≤1)
{ 2x-1, (x>1)
10. 复合函数：将一个函数的输出作为另一个函数的输入进行运算，例如：f(g(x))。

以上是数学必修一中较为基本的初等函数知识点，只覆盖了一部分内容。

学习初等函数的重点是掌握其基本性质、图像和应用。

高一数学幂函数习题及答案高一数学幂函数习题及答案在高一数学课程中，幂函数是一个非常重要的概念。

幂函数是指形如f(x) =ax^b的函数，其中a和b是常数，x是自变量。

在本文中，我们将探讨一些关于幂函数的习题，并提供相应的答案。

1. 习题一：已知函数f(x) = 2x^3，求f(2)的值。

解答：将x替换为2，得到f(2) = 2(2)^3 = 2(8) = 16。

因此，f(2)的值为16。

2. 习题二：已知函数g(x) = 4x^2，求g(0)的值。

解答：将x替换为0，得到g(0) = 4(0)^2 = 4(0) = 0。

因此，g(0)的值为0。

3. 习题三：已知函数h(x) = 5x^-2，求h(1)的值。

解答：将x替换为1，得到h(1) = 5(1)^-2 = 5(1/1^2) = 5(1/1) = 5。

因此，h(1)的值为5。

4. 习题四：已知函数k(x) = x^4 + 2x^3 - 3x^2 + x - 1，求k(-1)的值。

解答：将x替换为-1，得到k(-1) = (-1)^4 + 2(-1)^3 - 3(-1)^2 + (-1) - 1 = 1 - 2 - 3 - 1 - 1 = -5。

因此，k(-1)的值为-5。

5. 习题五：已知函数m(x) = (1/2)x^2 - 3x + 2，求m(3)的值。

解答：将x替换为3，得到m(3) = (1/2)(3)^2 - 3(3) + 2 = (1/2)(9) - 9 + 2 = 4.5 - 9 + 2 = -2.5。

因此，m(3)的值为-2.5。

通过以上习题，我们可以看到幂函数的计算方法。

对于给定的函数，我们只需将自变量替换为相应的值，然后按照幂函数的定义进行计算即可。

在实际应用中，幂函数常常用于描述各种变化规律，如物体的增长、衰减等。

除了计算习题，我们还可以通过绘制幂函数的图像来更好地理解其特点。

下面是几个常见的幂函数图像：1. 当b>0时，函数f(x) = ax^b的图像呈现出从左下方向右上方递增的趋势。

幂函数及基本初等函数综合教学目标1、掌握幂函数的概念及图形特征；2、熟悉函数图象与性质的应用。

知识梳理1、幂函数的概念一般地，我们把形如a xy=的函数称为幂函数，其中x是自变量，a是常数。

注意：（1)幂函数a xaay x且中，底数是y=的底数是自变量，指数是常数与指数函数)1=a,0(≠>常数，指数是自变量。

（2）只有形如a xy a+=（a是不为y=的函数才是幂函数，否则不是。

例如：axy=，aaxy=0，1的常数）。

a xy=中的a是任意实数。

（3）幂函数a xy=的定义域由a决定。

（4）幂函数a x2、幂函数的图像3、幂函数作图技巧y=在第一象限内的图像；（1）作出幂函数a xy=的定义域，左边是否有图像；（2）判断幂函数a x（3）若左边有图像，判断奇偶性，作出左边图像。

4、基本初等函数的综合应用知识点1：幂函数的概念【例1】下列函数中不是幂函数的是【 】x y = B.3x y = C.x y 22= D.1-=x y【例2】函数112)22(--+=m xm m y 是幂函数，则m =________。

【随堂练习】1、下面的函数中是幂函数的是___________。

① 22+=x y ； ②21x y = ； ③32x y =； ④43xy =； ⑤131+=x y ．2、已知)32().22(1122-+-+=-n x m m y m 是幂函数，求m 、n 的值。

知识点2：幂函数的解析式【例1】已知幂函数)(x f y =的图象过点)22,2(，则=)(x f ________。

【例2】如果幂函数()f x x α=的图象经过点2(2,)2，则(4)f 的值等于【 】 A. 16 B. 2 C. 116 D. 12【例3】已知幂函数αkx x f =)(),(R R k ∈∈α的图像过点1,22⎛⎫⎪⎝⎭，则k α+=【 】 A ．12 B ．1 C ．32D ．2【随堂练习】1、若幂函数)(x f 的图像经过点)22,2(,则=)9(f ______。

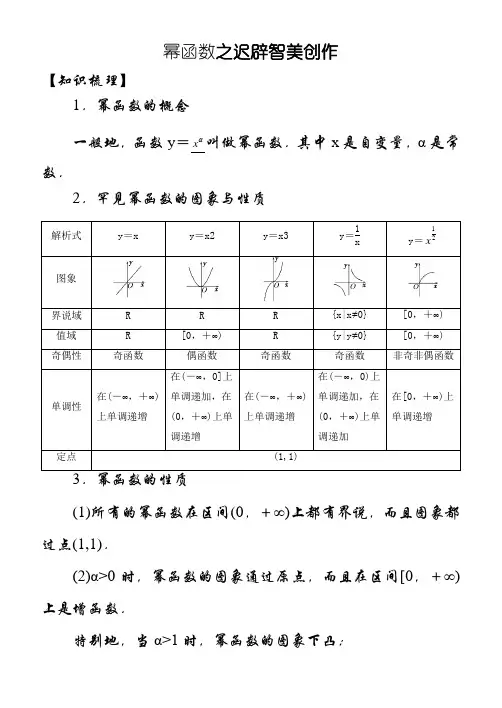
幂函数之迟辟智美创作【知识梳理】1．幂函数的概念一般地，函数y ＝x 叫做幂函数．其中x 是自变量，α是常数．2．罕见幂函数的图象与性质解析式y ＝xy ＝x2y ＝x3y ＝1xy ＝12x图象界说域 R R R {x|x ≠0} [0，＋∞) 值域 R [0，＋∞) R {y|y ≠0} [0，＋∞) 奇偶性奇函数偶函数 奇函数奇函数 非奇非偶函数单调性在(－∞，＋∞)上单调递增在(－∞，0]上单调递加，在(0，＋∞)上单调递增在(－∞，＋∞)上单调递增 在(－∞，0)上单调递加，在(0，＋∞)上单调递加在[0，＋∞)上单调递增定点(1,1)(1)所有的幂函数在区间(0，＋∞)上都有界说，而且图象都过点(1,1)．(2)α>0时，幂函数的图象通过原点，而且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸．(3)α<0时，幂函数的图象在区间(0，＋∞)上是减函数．在第一象限内，当x从右边趋向原点时，图象在y轴右方无限地迫近y轴正半轴；当x趋于＋∞时，图象在x轴上方无限地迫近x轴正半轴．【常考题型】题型一、幂函数的概念【例1】(1)下列函数：①y＝x3；②y＝12x⎛⎫⎪⎝⎭；③y＝4x2；④y＝x5＋1；⑤y＝(x－1)2；⑥y＝x；⑦y＝ax(a>1)．其中幂函数的个数为()A．1B．2C．3 D．4(2)已知幂函数y＝()22231m mm m x----，求此幂函数的解析式，并指出界说域．(1)[解析]②⑦为指数函数，③中系数不是1，④中解析式为多项式，⑤中底数不是自变量自己，所以只有①⑥是幂函数，故选B.[谜底]B(2)[解]∵y＝()22231m mm m x----为幂函数，∴m2－m－1＝1，解得m＝2或m＝－1.当m＝2时，m2－2m－3＝－3，则y＝x－3，且有x≠0；当m＝－1时，m2－2m－3＝0，则y＝x0，且有x≠0.故所求幂函数的解析式为y＝x－3，{x|x≠0}或y＝x0，{x|x≠0}．【类题通法】判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y＝xα(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为 1.反之，若一个函数为幂函数，则该函数应具备这一形式，这是我们解决某些问题的隐含条件．【对点训练】函数f(x)＝()223m m x+---是幂函数，且当x∈(0，＋∞)时，1m mf(x)是增函数，求f(x)的解析式．解：根据幂函数的界说得m2－m－1＝1.解得m＝2或m＝－1.当m＝2时，f(x)＝x3在(0，＋∞)上是增函数；当m＝－1时，f(x)＝x－3在(0，＋∞)上是减函数，不符合要求．故f(x)＝x3.题型二、幂函数的图象【例2】 (1)如图，图中曲线是幂函数y ＝x 在第一象限的年夜致图象，已知α取－2，－12，12，2四个值，则相应于曲线C1，C2，C3，C4的α的值依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－12(2)如图是幂函数y ＝m x 与y ＝n x 在第一象限内的图象，则( )A ．－1<n<0<m<1B ．n<－1,0<m<1C ．－1<n<0，m>1D ．n<－1，m>1[解析] (1)令x ＝2，则22>212>2－12>2－2，故相应于曲线C1，C2，C3，C4的α值依次为2，12，－12，－2.故选B.(2)此类题有一简捷的解决法子，在(0,1)内取x0，作直线x ＝x0，与各图象有交点，则“点低指数年夜”．如图，0<m<1，n<－1.[谜底](1)B(2)B【类题通法】解决幂函数图象问题应掌控的两个原则(1)依据图象高低判断幂指数年夜小，相关结论为：在(0,1)上，指数越年夜，幂函数图象越靠近x轴(简记为指年夜图低)；在(1，＋∞)上，指数越年夜，幂函数图象越远离x轴(简记为指年夜图高)．(2)依据图象确定幂指数α与0,1的年夜小关系，即根据幂函数在第一象限内的图象(类似于y＝x－1或y＝12x或y＝x3)来判断．【对点训练】已知函数y＝a x，y＝b x，y＝c x的图象如图所示，则a，b，c的年夜小关系为()A．c<b<a B．a<b<cC．b<c<a D．c<a<b解析：选A由幂函数的图象特征知，c<0，a>0，b>0.由幂函数的性质知，当x>1，幂指数年夜的幂函数的函数值就年夜，则a>b.综上所述，可知c<b<a.题型三、利用幂函数的性质比力年夜小【例3】 比力下列各组数中两个数的年夜小．(1)0.525⎛⎫ ⎪⎝⎭与0.513⎛⎫ ⎪⎝⎭；(2)123-⎛⎫- ⎪⎝⎭与135-⎛⎫- ⎪⎝⎭；(3)3423⎛⎫ ⎪⎝⎭与2334⎛⎫ ⎪⎝⎭.[解] (1)∵幂函数y ＝0.5x 在(0，＋∞)上是单调递增的，又25>13，∴0.525⎛⎫ ⎪⎝⎭>0.513⎛⎫ ⎪⎝⎭.(2)∵幂函数y ＝1x -在(－∞，0)上是单调递加的，又－23<－35，∴123-⎛⎫- ⎪⎝⎭>135-⎛⎫- ⎪⎝⎭.(3)∵函数y1＝23x⎛⎫⎪⎝⎭为R 上的减函数，又34>23，∴2323⎛⎫ ⎪⎝⎭>3423⎛⎫ ⎪⎝⎭.又∵函数y2＝23x 在(0，＋∞)上是增函数，且34>23，∴2334⎛⎫ ⎪⎝⎭>2323⎛⎫ ⎪⎝⎭，∴2334⎛⎫ ⎪⎝⎭>3423⎛⎫ ⎪⎝⎭.【类题通法】比力幂值年夜小的方法(1)若指数相同，底数分歧，则考虑幂函数；(2)若指数分歧，底数相同，则考虑指数函数；(3)若指数与底数都分歧，则考虑拔出中间数，使这个数的底数与所比力数的一个底数相同，指数与另一个数的指数相同，那么这个数就介于所比力的两数之间，进而比力年夜小．【对点训练】比力下列各题中两个幂的值的年夜小：(1)342.3，34 2.4；(2)32-　，32-　；(3)()650.31-，65 0.35.解：(1)∵y＝34x为[0，＋∞)上的增函数，且2.3<2.4，∴342.3<34 2.4.(2)∵y＝32x-　为(0，＋∞)∴32-　>32-　.(3)∵y＝65x为R上的偶函数，∴()650.31-＝65 0.31.又函数y＝65x为[0，＋∞)上的增函数，且0.31<0.35，∴650.31<650.35，即()650.31-<650.35.【练习反馈】1．下列函数是幂函数的是( )A ．y ＝2xB ．y ＝2x －1C ．y ＝(x ＋1)2D ．y解析：选D 由幂函数的概念可知D 正确． 2．下列命题：①幂函数的图象都经过点(1,1)和点(0,0)； ②幂函数的图象不成能在第四象限； ③n ＝0，函数y ＝n x 的图象是一条直线； ④幂函数y ＝n x 当n>0时，是增函数；⑤幂函数y ＝n x 当n<0时，在第一象限内函数值随x 值的增年夜而减小．正确的命题为( ) A ．①④ B ．④⑤ C ．②③D ．②⑤解析：选D y ＝x －1不外(0,0)点，∴①毛病，排除A ；当n ＝0时，y ＝n x 的图象为两条射线，③毛病，排除C ；y ＝x2不是增函数，④毛病，排除B ；因此谜底选D.3．已知幂函数f(x)的图象过点(4,2)，则f ⎝ ⎛⎭⎪⎫18＝________.解析：设f(x)＝x α，则4α＝2，∴α＝12，即f(x)＝12x ，∴f ⎝ ⎛⎭⎪⎫18＝1218⎛⎫ ⎪⎝⎭＝4.谜底：4．函数f(x)＝()22231mm m m x +--+是幂函数，且在x ∈(0，＋∞)时是减函数，则实数m ＝________.解析：由m2－m ＋1＝1，得m ＝0或m ＝1，再把m ＝0和m ＝1分别代入m2＋2m －3<0检验，得m ＝0.谜底：05．比力下列各题中两个幂的值的年夜小：(1)121.1，120.9；(2)121.1-　，120.9-　；(3)343-　，3412⎛⎫⎪⎝⎭.解：(1)∵y ＝12x 为[0，＋∞)上的增函数，又1.1>0.9， ∴121.1>120.9.(2)∵y ＝12x -　为(0，＋∞)上的减函数，又1.1>0.9， ∴121.1-　<120.9-　.(3)∵343-　＝3413⎛⎫⎪⎝⎭，函数y ＝34x 为[0，＋∞)上的增函数，且13<12，∴3413⎛⎫ ⎪⎝⎭<3412⎛⎫ ⎪⎝⎭，即343-　<3412⎛⎫⎪⎝⎭.。

必修1 数学——指数函数及幂函数一、指数函数 1．整数指数幂)0(10≠=a a； )0,(1≠∈=-a N n aann； nmnmaa=2、指数函数【1】一般形式：()0,1x y a a a =>≠； 【2】定义域：(,)-∞+∞；值域：(0,)+∞；【3】函数值变化情况：当1a >时，1(0)1(0)1(0)x x a x x >>⎧⎪==⎨⎪<<⎩； 当01a <<时，1(0)1(0)1(0)xx ax x <>⎧⎪==⎨⎪><⎩【4】单调性：当1a >时，x y a =是增函数；当01a <<时，x y a =是减函数【类型题归纳】【例题1】下列哪些是指数函数：（1）(4)xy =-；（2）212x y -=；（3）xy a =；（4）1(21)(,1)2xy a a a =->≠；（5）23xy =⋅.【总结升华】判断一个函数是否为指数函数，要紧扣指数函数的定义：其一，底数大于0且不等于1；其二，幂指数是单一的自变量x ；其三，系数为1，且没有其他的项. 2、设137x=，则（ ）A 、21x -<<-B 、32x -<<-C 、10x -<<D 、01x << 3、若函数()(0,1)xf x a a a =>≠，则下列等式不正确的是（ ）A 、()()()f x y f x f y +=B 、 ()()()n n n f xy f x f y ⎡⎤=⎣⎦C 、 ()()()f x f x y f y -=D 、 ()()nf nx f x =【总结】对于()()()f x y f x f y +=类型的抽象函数，xy a =可以作为它的一个经典原型，用来解决实际问题。

4、化简46394369)()(a a ⋅的结果为（ ）A 、a 16B 、a 8C 、a 4D 、a 2【例题5】求下列函数的定义域、值域：（1）1421x x y +=++； （2）1(01xxa y a a -=>+，且1)a ≠.【变式训练】求下列函数的定义域、值域：（1）||2()3x y -=； （2）2120.5x x y +-=.【例题6】比较下列各组数的大小. （1） 2.51.7，31.7；（2）0.10.20.8,1.25-；（3）0.3 3.11.7,0.9；（4） 4.1 3.64.5,3.7.【例题7】讨论函数221()()3x xf x -=的单调性，并求其值域.【变式训练】求函数|12|1()2x y +=的单调区间.二、幂函数（1）定义：一般地，函数ay x =叫做幂函数，其中x 是自变量，α是常数. （2）注意：对于幂函数，我们只讨论11,2,3,,12α=-时的情形.（3）图象与性质：2、幂函数的图象不过第四象限3、幂函数y x α=的奇偶性的判断：令q pα=（其中,p q 互质，,p q N ∈）【1】若p 是奇数，则q pyx =的奇偶性取决于q 是奇数或偶数。

目录幂函数与函数零点 (2)模块一：幂函数 (2)考点1：幂函数的图像与性质 (3)模块二：函数的零点 (4)考点2：函数的零点判断 (4)课后作业： (6)幂函数与函数零点模块一：幂函数1.幂函数：一般地，形如的函数称为幂函数，其中为常数．2.幂函数的图象当分别为，，，，时，幂函数图象如下图：3.幂函数的性质⑴所有的幂函数在都有定义，并且图象都通过点；⑵如果，则幂函数的图象通过原点，并且在区间上是增函数；⑶如果，则幂函数在区间上是减函数.在第一象限内，当从右边趋向于原点时，图象在轴右方无限地逼近轴．当趋于时，图象在轴上方无限地逼近轴．⑷幂函数的奇偶性决定幂函数过的象限．奇函数过一、三象限；偶函数过一、二象限；非奇非偶函数只过第一象限．⑸ 当为负奇数时，幂函数为奇函数，图象在第一、三象限，但不过原点；⑹ 当为正分数时，设为（，是互质的正整数）．①如果，都是奇数，幂函数为奇函数，图象过第一、三象限及原点；如②如果是偶数，为奇数，幂函数为非奇非偶函数，图象在第一象限及过原点；如()y xαα=∈Rαα1-12123(0)+∞，()11，α>[0)+∞，α<(0)+∞，xy y x+∞x x ααnmm nm n53y x==mn34y x==③如果为奇数，为偶数，幂函数为偶函数，图象过第一、二象限及原点．如是偶函数，图象为：⑺ 当为负分数时，设为（，是互质的正整数）． ①如果，都是奇数，幂函数为奇函数，图象在第一、三象限； ②如果为偶数，为奇数，幂函数的图象只在第一象限； ③如果为奇数，为偶数，幂函数为偶函数，图象在第一、二象限．如是偶函数，图象为考点1：幂函数的图像与性质例1.（1）已知是幂函数，求的值.【解答】332m n =-=， （2）幂函数2223()(1)m m f x m m x +-=--在(0,)+∞上为增函数，则m 的取值是( )A ．2m =或1m =-B ．1m =-C ．2m =D ．31m -【解答】解：幂函数2223()(1)m m f x m m x +-=--在(0,)+∞上为增函数，则2211230m m m m ⎧--=⎨+->⎩，解得2m =．故选：C ．模块二：函数的零点1.函数的零点（1）一般地，如果函数()y f x =在实数α处的值等于零，即()0f α=，则a 叫做这个函数的零点.mn 23y x ==αnm-m n m n m n mn 23y x -==()21212223my m m x n -=+-+-m n，要点诠释：①函数的零点是一个实数，当函数的自变量取这个实数时，其函数值等于零； ②函数的零点也就是函数)(x f y =的图象与x 轴交点的横坐标； ③函数)(x f y =的零点就是方程0)(=x f 的实数根．④零点都是指变号零点（函数图象通过零点时穿过x 轴，则称这样的零点为变号零点）． 归纳：方程0)(=x f 有实数根⇔函数)(x f y =的图象与x 轴有交点⇔函数)(x f y =有零点．考点2：函数的零点判断例1.（1）设3()2x f x x =-．则在下列区间中，使函数()f x 有零点的区间是( ) A ．(1,0)-B ．(0,1)C ．(1,2)D ．(2,3)【解答】解：f （1）2110=-=>，f （2）23224840=-=-=-<， f （1）f （2）0<，则在(1,2)内函数()f x 存在零点， 故选：C ．例2.（1）已知函数262,0()1,0x x x f x x x⎧-⎪=⎨<⎪⎩，若函数()()3g x f x x m =-+有3个零点，则实数m 的取值范围为( )A ．9(,0]8-B ．9[0,)8C ．9[0,)4D ．9(,0]4-【解答】解：函数()()3g x f x x m =-+有3个零点，即函数()y f x =的图象与3y x m =-的图象有3个交点． 如图，由图可知，当直线3y x m =-过原点O 时，满足题意； 联立2362y x m y x x=-⎧⎨=-⎩，得2230x x m --=． 由△980m =+=，得98m =-．∴若函数()()3g x f x x m =-+有3个零点，则实数m 的取值范围为9(8-，0]．故选：A ．（2）设函数22,1(),1x x f x log x x ⎧⎪=⎨>⎪⎩，()()2g x f x x a =++．若()g x 存在两个零点，则a 的取值范围是 ．【解答】解：由题意可得()2f x x a =--有两个不同的实根， 即函数()f x 的图象与直线2y x a =--有两个交点， 作出()y f x =的图象和直线2y x a =--，当直线经过点(1,0)时，可得20a --=，即2a =-； 当直线经过点(1,2)可得22a --=，即4a =-， 可得42a -<-时，直线和()f x 的图象有两个交点， 故答案为：[4-，2)-．例3.已知()1||f x lgx =-，则函数22()3()1y f x f x =-+的零点个数为 ． 【解答】解：根据题意，函数22()3()1y f x f x =-+， 若22()3()10y f x f x =-+=，解可得()1f x =或12， 若()1f x =，即1||1lgx -=，即0lgx =，解可得1x =，若1()2f x =，即11||2lgx -=，即12lgx =±，解可得x =，则函数22()3()1y f x f x =-+有3个零点； 故答案为：3课后作业：1．函数1()2xf x lgx =-的零点所在区间为( ) A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)【解答】解：函数1()2xf x lgx =-是增函数， f （1）110022=-=-<，f （2）1204lg =->， f ∴（1）f （2）0<， 1()2xf x lgx ∴=-的零点所在区间为(1,2)． 故选：B ．2．函数22,0()26,0x x f x x lgx x ⎧-=⎨-+>⎩的零点的个数为( )A ．0B ．1C ．2D ．3【解答】解：当0x 时，2()2f x x =-，令()0f x =，解得x =当0x >时，()26f x x lgx =-+，则()0f x =的解等价于函数62y x =-与y lgx =图象在0x >时的交点的横坐标，作出函数62y x =-与y lgx =图象如下：由图可知，此时两图象有一个交点，故0x >时，()0f x =有一个解， 综上()f x 共两个零点． 故选：C ． 3．函数2||()()4x f x kx k R x =-∈+的零点个数最多是( ) A ．2B ．3C ．4D ．5【解答】解：函数2||()()4x f x kx k R x =-∈+的零点的个数， 即为函数2y kx =与||4x y x =+的图象交点个数， 在同一坐标系内分别作出函数2y kx =与||4x y x =+的图象， 知两函数图象最多有4个交点，即函数2||()()4x f x kx k R x =-∈+的零点个数最多是4． 故选：C ．4．已知幂函数221()(33)mm f x m m x --=-+在(0,)+∞上单调递增，则m 值为 ．【解答】解：幂函数221()(33)m m f x m m x --=-+在(0,)+∞上单调递增，2331m m ∴-+=，且210m m -->，解得2m =， 故答案为：2．。

人教新课标数学必修I 2.3事函数练习题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号 填在题后的括号内（每小题 5分，共50分）.1.下列函数中既是偶函数又是A.B.C.2.1〜2.函数y x 2在区间［万,2］上的最大值是 A.1B. 1C 443 .下列所给出的函数中，是募函数的是A33c 3A y xB. y xC. y 2x44 .函数y x 3的图象是B.募函数的图象都经过（0, 0）和（1, 1）点C.若募函数y x 是奇函数，则 y x 是定义域上的增函数D.募函数的图象不可能出现在第四象限16 .函数y x 3和y x 3图象满足 A.关于原点对称 B .关于x 轴对称C.关于y 轴对称D.关于直线y x 对称7 .函数y x | x |,x R ,满足A.是奇函数又是减函数 C,是奇函数又是增函数B,是偶函数又是增函数 D.是偶函数又是减函数8 .函数y Vx 22x 24的单调递减区间是5.下列命题中正确的是 A.当0时函数y x 的图象是一条直线D.()D.4()3.D. y x 1( )B. [ 6, )C. ( ,1]D. [ 1,) A. ( , 6]9.如图1 — 9所示，募函数y x 在第一象限的图象，比较 0, 1, 2, 3, 4,1的大小（11 .函数 的定义域是 .12 .的解析式是.213 . y Xa是偶函数，且在（0,）是减函数，则整数 a 的值是 ^（1）kn工14. 募函数y X m （m, n,k N*, m,n 互质）图象在一、二象限，不过原点，则 k,m,n 的奇偶性为^三、解答题：解答应写出文字说明.证明过程或演算步骤 （共76分）.15. （ 12分）比较下列各组中两个值大小 (1)16. （12分）已知募函数轴对称，试确 的解析式A. B. C.D.10. 对于募函数f(x) 4X5,若 0 X 1X2,f(X 1 X 2 一 f (X 1)大小关系是X 1 X 2、 A. f(--2)2 f （X 1）f （X 2） B f (X 1 X 2) f(X 1)f(X 2)22C.f （X 1）f （X 2）D.无法确定 、填空题：请把答案填在题中横线上（每小题6分，共24分）317. （ 12分）求证：函数 y x 在R 上为奇函数且为增函数18. （ 12分）下面六个募函数的图象如图所示，试建立函数与图象之间的对应关系后，商品卖出个数减少 bx 成，税率是新定价的 a 成，这里a,b 均为正常数，且a <10,设售货款扣 除税款后，剩余y 元，要使y 最大，求x 的值.20. （ 14分）利用募函数图象，画出下列函数的图象（写清步骤）（1）3（1）y x 2； （2）y2⑷ y x ; （5）y12x 3； （3）y x 3；1；（6） y x 219.、CCBAD DCADA4二、11 . ；12 . f (x) X 3(X 0) ; 13 . 5;14. m,k 为奇数，n 是偶数；6解：(1) 函数yx 11在(0,)上是增函数且0 0.6650.71彳 ⑵函数y X 3在(0,)上增函数且0 0.88 0.89555550.8930.88" 0.89§，即 (0.88户 (。

考点11幂函数1、幂函数的判断及应用判断一个函数是否为幂函数的依据是该函数是否为y x α=（α是常数）的形式，即满足：（1）指数为常数；（2）底数为自变量；（3）系数为1．只有同时满足这三个条件的函数才是幂函数，对于形如(2),2,6y x y x y x ααα===+等函数都不是幂函数。

2、幂函数的图象及应用（1）幂函数图象的画法①确定幂函数在第一象限内的图象：先根据α的取值，确定幂函数y x α=在第一象限内的图象．②确定幂函数在其他象限内的图象：根据幂函数的定义域及奇偶性确定幂函数f(x)在其他象限内的图象．（2）要牢记幂函数的图象，并能灵活运用．由幂函数的图象，我们知道：①所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)．②任何幂函数的图象与坐标轴最多只有一个交点（原点）；任何幂函数的图象都不经过第四象限．③当α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象上抛；当0<α<1时，幂函数的图象右抛．④当α<0时，幂函数的图象在区间(0，＋∞)上是减函数．⑤幂指数互为倒数的幂函数在第一象限内的图象关于直线y ＝x 对称．⑥在第一象限，作直线x ＝a (a >1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．3、解决与幂函数有关的综合性问题的方法首先要考虑幂函数的概念，对于幂函数y x α=(α∈R)，由于α的取值不同，所以相应幂函数的单调性和奇偶性也不同．同时，注意分类讨论思想的应用．考点一幂函数的定义（一）求幂函数的值或解析式1．（2022·甘肃庆阳·高一期末）已知幂函数()f x 的图象过点13,3⎛⎫⎪⎝⎭，则此函数的解析式为______．2．（2022·内蒙古·赤峰二中高一期末（文））已知点（a ，2）在幂函数()(3)b f x a x =-的图象上，则函数f （x ）的解析式是（）A ．12()f x x =B ．12()2f x x =C ．3()f x x =D ．1()f x x -=3．（2022·甘肃·甘南藏族自治州合作第一中学高一期末）幂函数()y f x =的图象经过点(14,2)，则1(4f =____.4．（2022·全国·高一课时练习）若函数()f x 是幂函数，满足(4)8(2)f f =，则1(1)3f f ⎛⎫+= ⎪⎝⎭_________．5．（2022·北京市第五中学高一期末）已知幂函数()a f x x =过点(28)，，若0()5f x =-，则0x =________．6．（2022·上海中学高一期末）某厂商计划投资生产甲、乙两种商品，经市场调研发现，如图所示，甲、乙商品的投资x 与利润y （单位：万元）分别满足函数关系11ay k x =与22ay k x =．(1)求1k ，1a 与2k ，2a 的值；(2)该厂商现筹集到资金20万元，如何分配生产甲、乙商品的投资，可使总利润最大？并求出总利润的最大值．（二）根据函数是幂函数求参数值7．【多选】（2022·广东茂名·高一期末）若函数()225y k k x =--是幂函数，则实数k 的值可能是（）A ．3k =B ．3k =-C ．2k =-D ．2k =8．【多选】（2022·广东·韶关市田家炳中学高一期末）如果幂函数()22233mm y m m x --=-+的图象不过原点，则实数m 的取值为（）A ．0B ．2C ．1D ．无解9．（2022·湖南郴州·高一期末）已知幂函数()f x kx α=的图象过点()2,4，则k α+=__________.考点二幂函数的定义域和值域（一）幂函数的定义域10．（2022·江苏·高一）若()342x --有意义，则实数x 的取值范围是（）A ．[)2,+∞B ．(],2-∞C ．()2,+∞D ．(),2-∞11．（2022·山西吕梁·高一期末）已知幂函数()f x 的图象过点(，则()f x 的定义域为（）A ．RB ．()0,∞+C ．[)0,∞+D ．()(),00,∞-+∞U12．（2022·黑龙江绥化·高一期末）函数4()(1)f x x =-+）A ．()1，∞+B ．(2,)-+∞C ．()()211∞-⋃+，，D ．R13．（2022·全国·高一专题练习）设α∈11,132⎧⎫-⎨⎬⎩⎭，，则使函数y ＝xα的定义域为R 的所有α的值为（）A ．1,3B ．－1,1C ．－1,3D ．－1,1,314．（2022·内蒙古·赤峰红旗中学松山分校高一期末）已知幂函数()1*4n y x n N -=∈的定义域为()0,∞+，且单调递减，则n =________.（二）幂函数的值域15．（2022·全国·高一专题练习）幂函数a y x =中a 的取值集合C 是11,0,,1,2,32⎧⎫-⎨⎬⎩⎭的子集，当幂函数的值域与定义域相同时，集合C 为（）A ．11,0,2⎧⎫-⎨⎬⎩⎭B ．1,1,22⎧⎫⎨⎬⎩⎭C ．11,,32⎧⎫-⎨⎬⎩⎭D ．1,1,2,32⎧⎫⎨⎬⎩⎭16．（2022·全国·高一专题练习）函数213324y x x =++，其中8x - ，则其值域为___________.17．（2022·广东·广州六中高一期末）幂函数()y f x =的图象过点(，则函数()y x f x =-的值域是（）A ．(),-∞+∞B ．1,4⎛⎫-∞ ⎪⎝⎭C ．1,4⎡⎫-+∞⎪⎢⎣⎭D ．1,4⎛⎫-+∞ ⎪⎝⎭18．（2022·上海师大附中高一期末）已知函数()()()2151Z m f x m m x m +=-+∈为幂函数，且为奇函数.(1)求m 的值，并确定()f x 的解析式；(2)令()()g x f x =，求()y g x =在1,12x ⎡⎤∈-⎢⎥⎣⎦的值域.19．（2022·贵州·六盘水市第五中学高一期末）已知幂函数()()1221m f m x m x -=--在()0,∞+上为增函数.(1)求实数m 的值；(2)求函数()()2345g x f x x =--+的值域.20．（2022·湖北黄石·高一期中）已知函数())2()x a f x x x a ⎧≥⎪=⎨<⎪⎩，若函数()f x 的值域为R ，则实数a 的取值范围为（）A ．(1,0)-B ．(1,0]-C ．[1,0)-D ．[1,0]-考点三幂函数的图象和性质（一）幂函数的图象（1）依据图象高低判定幂指数大小21．（2022·全国·高一课时练习）图中1C ，2C ，3C 分别为幂函数1y x =α，2y x =α，3y x α=在第一象限内的图象，则1α，2α，3α依次可以是（）A ．12，3，1-B ．1-，3，12C ．12，1-，3D ．1-，12，322．（2022·全国·高一课时练习）幂函数a b c d y x y x y x y x ====，，，在第一象限的图像如图所示，则a b c d ，，，的大小关系是（）A ．a b c d >>>B ．d b c a >>>C ．d c b a>>>D ．b c d a>>>23．（2022·全国·高一课时练习）如图所示是函数mn y x =(*N m n ∈、且互质)的图象，则（）A ．m n 、是奇数且1mn<B ．m 是偶数，n 是奇数，且1m n>C ．m 是偶数，n 是奇数，且1m n<D ．m n 、是偶数，且1m n>24．（2022·四川凉山·高一期末）如图，①②③④对应四个幂函数的图像，其中①对应的幂函数是（）A ．3y x =B ．2y x =C ．y x=D ．58y x =（2）图象的识别25．（2022·全国·高一单元测试）下列四个图像中，函数34y x =的图像是（）A ．B ．C ．D ．26．（2022·上海·高一单元测试）已知幂函数的图象经过点14,2P ⎛⎫⎪⎝⎭，则该幂函数的大致图象是（）A ．B ．C ．D ．27．（2022·全国·高一单元测试）如图为某体育赛事举重成绩与运动员体重之间关系的折线图，下列模型中，最能刻画举重成绩y （单位：千克）和运动员体重x （单位：千克）之间的关系的是（）A ．y =()0m >B ．y mx n =+()0m >C ．2y mx n =+()0m >D ．x y ma n =+（0m >，0a >且1a ≠）（二）幂函数的性质（1）由幂函数的单调性求参数28．（2022·广东广州·高一期末）函数()22211mm y m m x --=--是幂函数，且在()0,x ∈+∞上是减函数，则实数m =__________.29．（2022·河南开封·高一期末）已知函数()22my m m x =+幂函数，且在其定义域内为单调函数，则实数m =（）A ．12B ．1-C ．12或1-D ．12-30．（2022·云南德宏·高一期末）“当()0,x ∈+∞时，幂函数()22231mm y m m x --=--为减函数”是“1m =-或2”的（）条件A ．既不充分也不必要B ．必要不充分C ．充分不必要D ．充要31．（2022·江西省铜鼓中学高一期末）已知函数()()()2,16,(1a a x x f x x x ⎧+≤=⎨->⎩）是减函数，则实数a 的取值范围是（）A ．[)7,2--B ．(),2-∞-C ．(),7-∞-D ．()7,2--（2）由幂函数的单调性解不等式32．（2022·上海中学高一期末）不等式()()2021202142x x --->-的解为______．33．（2022·海南鑫源高级中学高一期末）已知幂函数()af x x =的图象经过点(.（1）求幂函数()f x 的解析式；（2）试求满足()()13f a f a +>-的实数a 的取值范围.34（2022·上海金山·高一期末）已知幂函数()y f x =在其定义域上是严格增函数，且()22mm f x x -=（m Z ∈）.(1)求m 的值；(2)解不等式：()()32f x f x-<.（3）由幂函数的单调性比较大小35．（2022·重庆九龙坡·高一期末）已知111333332,,555a b c -⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则,,a b c 的大小关系为（）A ．a b c<<B ．b c a<<C ．c a b<<D ．a c b<<36．（2022·青海·大通回族土族自治县教学研究室高一期末）幂函数()()22251mm f x m m x +-=--在区间()0,∞+上单调递增，且0a b +>，则()()f a f b +的值（）A ．恒大于0B ．恒小于0C ．等于0D ．无法判断（4）幂函数奇偶性的应用37．（2022·全国·高一课时练习）求出下列函数的定义域，并判断函数的奇偶性：（1）22()f x x x -=+；（2）23()3f x x x =+；（3）133()f x x x =+；（4）142()2f x x x -=+.38．（2022·全国·高一专题练习）已知幂函数()2()1mf x m m x =--的图象关于y 轴对称，则()f m =___________．39．（2022·重庆九龙坡·高一期末）已知幂函数()21()55m f x m m x +=-+为奇函数，则m =___________.40．（2022·山东济宁·高一期末）已知()y f x =是奇函数，当0x ≥时，()()23f x x m m =+∈R ，则()8f -=______．（5）幂函数的单调性和奇偶性的综合应用41．（2022·河南开封·高一期末）下列函数中，既是奇函数，又是增函数的是（）①1y x=-；②y =||y x x =；④3y x x =+．A ．①②B ．①④C ．②③D ．③④42．（2022·云南玉溪·高一期末）幂函数22m m y x +-=()03,m m Z ≤≤∈的图象关于y 轴对称，且在(0,)+∞上是增函数，则m 的值为（）A ．0B ．2C ．3D ．2和343．（2022·重庆巫山·高一期末）若幂函数()f x 过点()2,8，则满足不等式()()310f a f a -+-≤的实数a 的取值范围是______44．（2022·湖北·高一期末）已知函数()53352f x x x x =+++，若()()214f a f a +->，则实数a 的取值范围是（）A ．1,3⎛⎫+∞ ⎪⎝⎭B ．1,3⎛⎫-∞ ⎪⎝⎭C ．(),3-∞D ．()3,+∞45．（2022·黑龙江·大庆实验中学高一期末）已知幂函数()223m m y xm N --*=∈的图象关于y 轴对称，且在()0,∞+上单调递减，则满足()()33132mma a --+<-的a 的取值范围为________.（6）幂函数性质的综合应用46．（2022·全国·高一）已知幂函数a y x =（a 是常数），则（）A ．()f x 的定义域是RB ．()f x 在()0,∞+单调递增C ．()f x 过定点()1,1D ．()f x 可能过定点()1,3-47．【多选】（2022·广西玉林·高一期末）已知函数()a f x x =的图象经过点1,33⎛⎫ ⎪⎝⎭则（）A ．()f x 的图象经过点(3,9)B ．()f x 的图象关于y 轴对称C ．()f x 在(0,)+∞上单调递减D ．()f x 在(0,)+∞内的值域为(0,)+∞48．【多选】（2022·广东揭阳·高一期末）已知幂函数()y f x =的图象经过点(9,3)，则下列结论正确的有（）A ．()f x 为偶函数B ．()f x 为增函数C ．若1x >，则()1f x >D ．若210x x >>，则()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭。

幂函数及其性质专题一、幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数.如11234,,y x y x y x -===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 二、函数的图像和性质（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x =用描点法在同一坐标系内画出以上五个函数图像，通过观察图像，可以看出：3．幂函数性质（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）；（2）x ＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数.三．两类基本函数的归纳比较： ① 定义对数函数的定义：一般地，我们把函数log a y x =（a ＞0且a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）．幂函数的定义：一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数. ②性质对数函数的性质：定义域：（0，+∞）；值域：R ；过点（1，0），即当x =1，y =0；在（0，+∞）上是增函数；在（0，+∞）是上减函数 幂函数的性质：所有的幂函数在（0，+∞）都有定义， 图象都过点（1，1）x ＞0时，幂函数的图象都通过原点， 在[0，+∞]上，y x =、2y x =、3y x =、12y x =是增函数， 在（0，+∞）上， 1y x -=是减函数。

【例题选讲】例1．已知函数()()2531m f x m m x --=--，当 m 为何值时，()f x ：（1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数；简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =- 变式训练：已知函数()()2223m m f x m m x--=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲线。