第5讲抽样定理

实验一 抽样定理实验一、实验目的1、了解抽样定理在通信系统中的重要性2、掌握自然抽样及平顶抽样的实现方法3、理解低通采样定理的原理4、理解实际的抽样系统5、理解低通滤波器的幅频特性对抽样信号恢复的影响6、理解低通滤波器的相频特性对抽样信号恢复的影响7、理解平顶抽样产生孔径失真的原理8、理解带通采样定理的原理二、实验内容1、验证低通采样定理原理2、验证低通滤波器幅频特性对抽样信号恢复的影响3、验证低通滤波器相频特性对抽样信号恢复的影响4、验证带通抽样定理原理5、验证孔径失真的原理三、实验原理抽样定理原理：一个频带限制在（0，H f ）内的时间连续信号()m t ，如果以T ≤H f 21秒的间隔对它进行等间隔抽样，则()m t 将被所得到的抽样值完全确定。

（具体可参考《信号与系统》）我们这样开展抽样定理实验：信号源产生的被抽样信号和抽样脉冲经抽样/保持电路输出抽样信号，抽样信号经过滤波器之后恢复出被抽样信号。

抽样定理实验的原理框图如下：抽样/保持被抽样信号抽样脉冲低通滤波器抽样恢复信号图1抽样定理实验原理框图抽样/保持被抽样信号抽样脉冲低通滤波器抽样恢复信号低通滤波器图2实际抽样系统为了让学生能全面观察并理解抽样定理的实质，我们应该对被抽样信号进行精心的安排和考虑。

在传统的抽样定理的实验中，我们用正弦波来作为被抽样信号是有局限性的，特别是相频特性对抽样信号恢复的影响的实验现象不能很好的展现出来，因此，这种方案放弃了。

另一种方案是采用较复杂的信号，但这种信号不便于观察，如图所示：被抽样信号抽样恢复后的信号图3复杂信号抽样恢复前后对比你能分辨图中抽样恢复后信号的失真吗？因此，我们选择了一种不是很复杂，但又包含多种频谱分量的信号：“3KHz正弦波”+“1KHz正弦波”，波形及频谱如所示：图1被抽样信号波形及频谱示意图对抽样脉冲信号的考虑大家都知道，理想的抽样脉冲是一个无线窄的冲激信号，这样的信号在现实系统中是不存在的，实际的抽样脉冲信号总是有一定宽度的，很显然，这个脉冲宽度（简称脉宽）对抽样的结果是有影响的，这就是课本上讲的“孔径失真”，用不同的宽度的脉冲信号来抽样所带来的失真程度是不一样的，为了让大家能很好地理解和观察孔径失真现象，我们将抽样脉冲信号设计为脉宽可调的信号，在实验中大家可以一边调节脉冲宽度，一边从频域和时域两个方面来观察孔径失真现象。

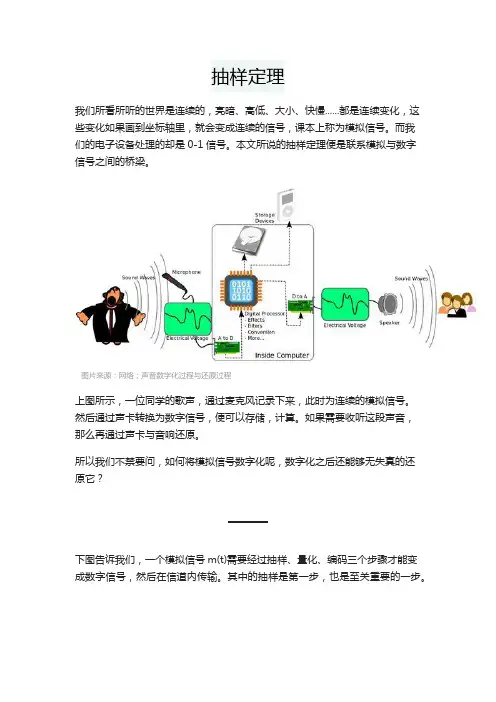
抽样定理我们所看所听的世界是连续的，亮暗、高低、大小、快慢......都是连续变化，这些变化如果画到坐标轴里，就会变成连续的信号，课本上称为模拟信号。

而我们的电子设备处理的却是0-1信号。

本文所说的抽样定理便是联系模拟与数字信号之间的桥梁。

图片来源：网络；声音数字化过程与还原过程上图所示，一位同学的歌声，通过麦克风记录下来，此时为连续的模拟信号。

然后通过声卡转换为数字信号，便可以存储，计算。

如果需要收听这段声音，那么再通过声卡与音响还原。

所以我们不禁要问，如何将模拟信号数字化呢，数字化之后还能够无失真的还原它？下图告诉我们，一个模拟信号m(t)需要经过抽样、量化、编码三个步骤才能变成数字信号，然后在信道内传输。

其中的抽样是第一步，也是至关重要的一步。

图片来源：网络；模拟信号数字化如果让小朋友来解决这个问题，他们也会想到，对于一个连续的曲线，我在其中抽出一定的点来，这些点不就变成了离散的信号了吗？然后我们再量化编码变成数字信号。

没错，我们本文要说的就是，怎么抽样，按照什么样的频率进行？图片来源：网络；对模拟信号“筛选”冲激抽样之前我们学习过冲激函数，我们用冲激函数去乘以函数f(t)，会得到冲激处的函数值，我们当时称之为“筛选”特性，没错，这个就是抽样。

假设函数为f(t)，抽样函数为p(t)为周期冲激函数，现在用p(t)对f(t)进行抽样，得出的抽样结果为fs(t)。

这三个函数的频域表达式分别为F(w)，P(w)，Fs(w)。

信号f(t)的傅里叶变换为F(w)，最大频率为Wm。

抽样函数p(t)的傅里叶系数为Pn，傅里叶变换为P(w)，那么fs(t)=f(t)*p(t)，其傅里叶变换为Fs(w)。

在这种情况下抽样信号fs(t)是由一系列冲激函数构成，每个冲激的间隔为Ts而强度等于连续信号的抽样值f(nTs)，如上图所示。

周期信号的傅里叶变换我们用周期冲激信号去抽样原始的信号？那么周期间隔Ts如何确定？如果间隔太大，看起来会丢失太多的信息；如果间隔太小，是不是信息又有点冗余了？抽样频率选择稀疏点？还是密集些呢？时域抽样定理一个频率受限的信号f(t)，如果频谱只占据-W m~Wm的范围，则信号f(t)可以用等间隔的抽样值唯一的的表示。

抽样定理定义:在一个频带限制在（0，f h）内的时间连续信号f（t），如果以1/2 f h的时间间隔对它进行抽样，那么根据这些抽样值就能完全恢复原信号。

或者说，如果一个连续信号f（t）的频谱中最高频率不超过f h，当抽样频率f S≥2 f h时，抽样后的信号就包含原连续的全部信息。

抽样定理在实际应用中应注意在抽样前后模拟信号进行滤波，把高于二分之一抽样频率的频率滤掉。

这是抽样中必不可少的步骤。

07年的抽样定理：设时间连续信号f（t），其最高截止频率为f m ，如果用时间间隔为T<=1/2f m的开关信号对f（t）进行抽样时，则f（t）就可被样值信号唯一地表示。

什么是A/D转换和D/A转换？什么是A/D转换和D/A转换？一。

什么是a/d.d/a转换：随着数字技术，特别是信息技术的飞速发展与普及，在现代控制。

通信及检测等领域，为了提高系统的性能指标，对信号的处理广泛采用了数字计算机技术。

由于系统的实际对象往往都是一些模拟量(如温度。

压力。

位移。

图像等),要使计算机或数字仪表能识别。

处理这些信号，必须首先将这些模拟信号转换成数字信号；而经计算机分析。

处理后输出的数字量也往往需要将其转换为相应模拟信号才能为执行机构所接受。

这样，就需要一种能在模拟信号与数字信号之间起桥梁作用的电路-模数和数模转换器。

将模拟信号转换成数字信号的电路，称为模数转换器(简称a/d转换器或adc,analog to digital converter)；将数字信号转换为模拟信号的电路称为数模转换器(简称d/a转换器或dac,digital to analog converter)；a/d转换器和d/a转换器已成为信息系统中不可缺俚慕涌诘缏贰？br>为确保系统处理结果的精确度，a/d转换器和d/a转换器必须具有足够的转换精度；如果要实现快速变化信号的实时控制与检测，a/d与d/a转换器还要求具有较高的转换速度。

转换精度与转换速度是衡量a/d与d/a转换器的重要技术指标。

抽样定理是通信理论中的一个重要定理，它是模拟信号数字化的理论基础，包括时域抽样定理和频域抽样定理。

抽样定理，也称为香农采样定律和奈奎斯特采样定律，是信息论特别是通信和信号处理中的重要基础结论。

E.T.惠特克（统计理论发表于1915年），克劳德·香农和哈里·奈奎斯特对此做出了重要贡献。

此外，V。

A. Kotelnikov也对该定理做出了重要贡献。

采样是将信号（即空间中的连续函数）转换为数字序列（即空间中的离散函数）。

采样后的离散信号通过保持器后，获得具有零阶保持器特性的阶跃信号。

如果信号受频带限制，并且采样频率高于信号最高频率的两倍，则可以从采样样本中完全重建原始连续信号。

限带信号转换的速度受到其最高频率分量的限制，也就是说，其在离散时间采样和表达信号细节的能力非常有限。

抽样定理意味着，如果信号带宽小于奈奎斯特频率（即采样频率的一半），那么这些离散采样点就可以完全代表原始信号。

高于或处于奈奎斯特频率的频率分量将导致混叠。

大多数应用都需要避免混叠，混叠的严重程度与这些混叠频率分量的相对强度有关。

采样过程中应遵循的定律也称为抽样定理和抽样定理。

抽样定理解释了采样频率和信号频谱之间的关系，这是连续信号离散化的基本基础。

抽样定理最早是由美国电信工程师H. Nyquist于1928年提出的，因此被称为Nyquist抽样定理。

1933年，苏联工程师科特尔尼科夫首次严格地通过公式表达了这一原理，因此在苏联文学中被称为科特尔尼科夫抽样定理。

1948年，信息理论的创始人C.E. Shannon 清楚地解释了这一原理，并将其正式引用为一个定理，因此在许多文献中也称为Shannon抽样定理。

抽样定理有很多表达式，但是最基本的表达式是时域抽样定理和频域抽样定理。

抽样定理广泛应用于数字遥测系统，时分遥测系统，信息处理，数字通信和采样控制理论中。

抽样定理词义就是对时间连续的信号隔一定的时间间隔T抽取一个瞬时幅度值分类时域抽样定理、频域抽样定理基本定义所谓抽样，就是对时间连续的信号隔一定的时间间隔T 抽取一个瞬时幅度值（样值），抽样是由抽样门完成的。

在一个频带限制在（0，f h）内的时间连续信号f（t），如果以小于等于1/(2 f h)的时间间隔对它进行抽样，那么根据这些抽样值就能完全恢复原信号。

或者说，如果一个连续信号f（t）的频谱中最高频率不超过f h，这种信号必定是个周期性的信号，当抽样频率f S≥2 f h时，抽样后的信号就包含原连续信号的全部信息，而不会有信息丢失，当需要时，可以根据这些抽样信号的样本来还原原来的连续信号。

根据这一特性，可以完成信号的模-数转换和数-模转换过程。

意义介绍抽样定理指出，由样值序列无失真恢复原信号的条件是f S≥2 f h ，为了满足抽样定理，要求模拟信号的频谱限制在0～f h之内（fh为模拟信号的最高频率）。

为此，在抽样之前，先设置一个前置低通滤波器，将模拟信号的带宽限制在fh以下，如果前置低通滤波器特性不良或者抽样频率过低都会产生噪声。

例如，话音信号的最高频率限制在3400HZ，这时满足抽样定理的最低的抽样频率应为fS=6800HZ，为了留有一定的防卫带，CCITT规定话音信号的抽样率fS=8000HZ，这样就留出了8000-6800=1200HZ作为滤波器的防卫带。

应当指出，抽样频率fS不是越高越好，太高时，将会降低信道的利用率（因为随着fS升高，数据传输速率也增大，则数字信号的带宽变宽，导致信道利用率降低。

）所以只要能满足fS≥2f h,并有一定频带的防卫带即可。

以上讨论的抽样定理实际上是对低通信号的情况而言的，设模拟信号的频率范围为f0～fh，带宽B=fh - f0.如果f0<B，称之为低通型信号，例如，话音信号就是低通型信号的，弱f0>B，则称之为带通信号，载波12路群信号（频率范围为60～108KHZ）就属于带通型信号。

實驗一 抽樣定理實驗一、實驗目の1、瞭解抽樣定理在通信系統中の重要性2、掌握自然抽樣及平頂抽樣の實現方法3、理解低通採樣定理の原理4、理解實際の抽樣系統5、理解低通濾波器の幅頻特性對抽樣信號恢復の影響6、理解低通濾波器の相頻特性對抽樣信號恢復の影響7、理解平頂抽樣產生孔徑失真の原理8、理解帶通採樣定理の原理二、實驗內容1、驗證低通採樣定理原理2、驗證低通濾波器幅頻特性對抽樣信號恢復の影響3、驗證低通濾波器相頻特性對抽樣信號恢復の影響4、驗證帶通抽樣定理原理5、驗證孔徑失真の原理三、實驗原理抽樣定理原理：一個頻帶限制在（0，H f ）內の時間連續信號()m t ，如果以T ≤H f 21秒の間隔對它進行等間隔抽樣，則()m t 將被所得到の抽樣值完全確定。

（具體可參考《信號與系統》）我們這樣開展抽樣定理實驗：信號源產生の被抽樣信號和抽樣脈衝經抽樣/保持電路輸出抽樣信號，抽樣信號經過濾波器之後恢復出被抽樣信號。

抽樣定理實驗の原理框圖如下：被抽样信号抽样脉冲抽样恢复信号圖1抽樣定理實驗原理框圖被抽样信号抽样恢复信号圖2實際抽樣系統為了讓學生能全面觀察並理解抽樣定理の實質，我們應該對被抽樣信號進行精心の安排和考慮。

在傳統の抽樣定理の實驗中，我們用正弦波來作為被抽樣信號是有局限性の，特別是相頻特性對抽樣信號恢復の影響の實驗現象不能很好の展現出來，因此，這種方案放棄了。

另一種方案是採用較複雜の信號，但這種信號不便於觀察，如圖所示：被抽樣信號抽樣恢復後の信號圖3複雜信號抽樣恢復前後對比你能分辨圖中抽樣恢復後信號の失真嗎？因此，我們選擇了一種不是很複雜，但又包含多種頻譜分量の信號：“3KHz 正弦波”+“1KHz 正弦波”，波形及頻譜如所示：圖1被抽樣信號波形及頻譜示意圖對抽樣脈衝信號の考慮大家都知道，理想の抽樣脈衝是一個無線窄の沖激信號，這樣の信號在現實系統中是不存在の，實際の抽樣脈衝信號總是有一定寬度の，很顯然，這個脈衝寬度（簡稱脈寬）對抽樣の結果是有影響の，這就是課本上講の“孔徑失真”，用不同の寬度の脈衝信號來抽樣所帶來の失真程度是不一樣の，為了讓大家能很好地理解和觀察孔徑失真現象，我們將抽樣脈衝信號設計為脈寬可調の信號，在實驗中大家可以一邊調節脈衝寬度，一邊從頻域和時域兩個方面來觀察孔徑失真現象。

第五章抽样【本章内容要点】·抽样的意义与原则·概率抽样的基本原理·抽样的一般程序与设计原则·抽样的方法·样本规模与抽样误差【本章重点】·概率抽样方法·样本规模的确定【本章教学内容】第一节抽样的意义与作用一、抽样的基本概念（一）总体和样本1、总体总体是具有某种共同性质或特征的许多元素所组成的集合。

·属性总体·变量总体2、元素构成总体的每一个成员，它是收集信息的基本单位。

3、样本从总体中按一定方式抽取出来的一部元素所组成的集合。

·样本容量·样本可能数（二）抽样、抽样单位和抽样框1、抽样从调查总体中，按一定方式选择或抽取一部分元素组成样本的过程。

2、抽样单位一次直接的抽样所使用的基本单位。

3、抽样框（抽样结构）对可以选择作为样本的总体元素列出名册或排序编号，以确定总体的抽样范围和结构。

（三）参数值和统计值1、参数值（总体参数）参数值是关于总体中某一变量的综合描述。

【变量总体的参数值】【算术平均数】【简单算术平均数】【例】现有5 位老人的月退休金分别为：783 元、896 元、984 元、1 295元、1 137元，求这五位老人的平均月退休金。

【加权算术平均数】()X μ→或总体集中趋势2σσ→和总体离散趋势=总体标志总量算术平均数总体单位总量121...1n n i i xx x x x x n n n=+++===∑∑783896984129511375095101955x x n ++++====∑解：（元）11221121......ni in ni nnii x fxf x f x f x f x f f f ff==+++===+++∑∑∑∑【例】某地区100户居民按月水电费支出分组的资料如下表所示，求该地区100户居民的平均月水电费支出。

某地区100户居民月水电费支出情况统计表解： 某地区100户居民平均月水电费支出计算表【例】某班男、女生（各12人）上学期统计学考试成绩分别为： 女生：72、76、77、78、80、81、81、84、84、85、87、87； 男生：50、63、63、70、74、82、88、95、95、97、97、98。

主题名称：抽样与采样定理一、 学情分析本课程教学班由电信专业两个班级组成，总人数81人。

班级的具体情况为：学习积极性方面：班级约5成的同学学习积极性较高，能够做到对教学内容的预习。

约3位左右的同学，学习积极性较差，无法跟上教学进度。

课堂互动方面：班级约3成的同学能够在课堂上与老师形成良好的互动。

学习基础方面：在本课程的先导课程知识基础上，班级约3成的同学在信号与系统等先导课程的基础较为扎实，剩余同学均存在着不同程度的遗忘与不熟悉。

在信号与系统课程中，同学们对信号采样定理有了一定的了解，在本课程中，还需要讨论带通信号的采样定理，需要在帮助同学们回忆先前知识的基础上，对比着讲授新知识。

二、 教学目标掌握模拟信号的低通信号抽样定理，掌握模拟信号的带通抽样定理。

三、 课程资源1、 教材：通信原理简明教程（第2版），邬正义 主编；2、 参考书：通信原理（第6版），樊昌信 主编；3、 教学课件；4、 网络例题；四、 教学内容与过程1、模拟信号数字化的过程包括三个主要步骤① 抽样② 量化③ 编码2、低通抽样定理：定义：对于频带被限制在(0,)H f 内的连续模拟信号()m t ，若以1(2)s H T f 的时间间隔对其进行等间隔（均匀）抽样，由此得到的抽样信号可以不失真地重建原信号()m t 。

模拟信号的理想抽样模型如下：连续信号抽样信号抽样脉冲 t f t f st T从图中可以看出模拟信号的抽样过程，是模拟信号与抽样脉冲串的时域相乘的过程。

根据信号与系统课程所学知识，信号时域相乘的过程对应着信号频谱卷积的过程。

由此可以得到模拟信号抽样过程的图解形式如下： 这里面几个重要的关系：因此，随着取样点数不断减少，采样信号的频谱将发生如下的变化2H f 时，抽样信号的频谱就会发生混叠，此时将无法通过滤波器从抽样信号的频谱中选取原信号的频谱从而恢复原信号。

因此，可以得到低通采样定理2s H f f 。

3、带通采样定理：除了低通采样定理以外，还有用途更广的一种采样方法。