§4.03-任意角的三角函数(1)(1)(201909)

高一数学任意角的三角函数【本讲主要内容】任意角的三角函数（三角函数的定义、单位圆与三角函数线）【知识掌握】 【知识点精析】1. 任意角的三角函数的定义：设P （x ，y ）是角α的终边上任意一点，|OP|＝r （r ＞0），则sin cos αα==y r xr， tan cot αα==y x x y ， sec csc αα==r x r y， 正弦、余弦、正切、余切、正割、余割分别可以看成是从一个角的集合到一个比值的集合的映射，它们都是以角为自变量，以比值为函数值的函数，这六个函数统称为三角函数。

注意：①一个角的三角函数值只与这个角的终边位置有关，而与P 点的选取无关。

②为计算方便，我们把半径为1的圆（单位圆）与角的终边的交点选为P 点的理想位置。

2. 三角函数的定义域、值域确定三角函数的定义域时，要抓住分母不为0这一关键，当角的终边在坐标轴上时，点P 的坐标中必有一个为0。

3. 三角函数值符号记忆口诀为：“一全正，二正弦，三两切，四余弦”。

（注：余割和正弦互为倒数关系，正割和余弦互为倒数关系。

） 4. 诱导公式（一）：根据三角函数的定义知，角的三角函数值是由角的终边位置确定的，所以终边相同的角的同一三角函数的值相等。

即：sin()sin ()cos()cos ()tan()tan ()()k k Z k k Z k k Z ²°²°²°诱导公式一360360360+=∈+=∈+=∈⎫⎬⎪⎭⎪ααααααsin()sin ()cos()cos ()tan()tan ()()()222k k Z k k Z k k Z πααπααπαα+=∈+=∈+=∈⎫⎬⎪⎭⎪诱导公式一弧度制用途：使用诱导公式（一），可以把求任意角的三角函数值问题化为0～2π间三角函数值，具体求法是将任意角化为2k π＋α，()k Z ∈，其中0≤α＜2π，然后利用诱导公式（一）化简，再求值。

任意角的三角函数三角函数是数学中一个非常重要的概念，它是用于描述三角形中角和边之间的关系的一种函数。

在传统的三角函数中，我们只考虑角的大小在0度到90度之间的情况，这被称为锐角三角函数。

但是，在现代数学中，我们也可以考虑角的大小在90度以上的情况，这就是任意角三角函数。

任意角三角函数是三角函数的推广，它可以应用于任意角度的三角形中，并且具有广泛的应用。

任意角三角函数通常使用弧度制来度量角度。

下面我们将介绍任意角三角函数中最常用的几种函数。

1. 正弦函数正弦函数是任意角三角函数中最简单和最基本的函数之一。

正弦函数的定义如下：sinθ = y/r其中，θ是角度，y是三角形中一个锐角顶点的垂直边长，r是这个锐角顶点到三角形外接圆心的距离。

正弦函数的值从-1到1，它刻画了一个角的正弦值与其对应的三角形中某一边长的比例关系。

如果一个角的正弦值为1，则这个角是90度；如果正弦值为0，则这个角是0度或180度。

2. 余弦函数余弦函数是另一个重要的任意角三角函数。

它的定义如下：cosθ = x/r其中，θ是角度，x是三角形中一个锐角顶点的水平边长，r是这个锐角顶点到三角形外接圆心的距离。

余弦函数的值也在-1到1之间。

它刻画了一个角的余弦值与其对应的三角形中某一边长的比例关系。

如果一个角的余弦值为1，则这个角是0度；如果余弦值为0，则这个角是90度或270度。

3. 正切函数正切函数是另一个常见的任意角三角函数。

它的定义如下：tanθ = y/x其中，θ是角度，y是三角形中一个锐角顶点的垂直边长，x是这个锐角顶点的水平边长。

正切函数的值可以是任意实数。

它刻画了一个角的正切值与其对应的三角形中垂直边长和水平边长的比例关系。

如果一个角的正切值为正无穷，则这个角是90度；如果正切值为负无穷，则这个角是270度。

4. 正割函数正割函数是余弦函数的倒数。

它的定义如下：secθ = 1/cosθ正割函数的值也可以是任意实数。

它刻画了一个角的正割值与其对应的三角形中水平边长与半径的比例关系。

任意角的三角函数及基本公式三角函数是数学中的一个重要概念，它们描述了角度与三角比之间的关系。

任意角的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

下面将详细介绍这些函数的定义、基本公式以及它们之间的关系。

1. 正弦函数（sine function）：在单位圆上，从x轴正向到射线与单位圆的交点之间的弧度即为角的弧度。

正弦函数将给定角度的正弦值映射到数轴上。

其定义如下：sin(θ) = y/r其中θ为角度，y为对边，r为斜边。

2. 余弦函数（cosine function）：余弦函数表示角的余弦值在数轴上的投影长度。

其定义如下：cos(θ) = x/r其中θ为角度，x为邻边，r为斜边。

3. 正切函数（tangent function）：正切函数表示角的正切值在数轴上的投影比。

其定义如下：tan(θ) = y/x其中θ为角度，y为对边，x为邻边。

4. 余切函数（cotangent function）：余切函数表示角的余切值在数轴上的投影比。

其定义如下：cot(θ) = x/y其中θ为角度，y为对边，x为邻边。

5. 正割函数（secant function）：正割函数表示角的正割值在数轴上的投影长度。

其定义如下：sec(θ) = r/x其中θ为角度，x为邻边，r为斜边。

6. 余割函数（cosecant function）：余割函数表示角的余割值在数轴上的投影长度。

其定义如下：csc(θ) = r/y其中θ为角度，y为对边，r为斜边。

这些函数在不同的角度上有不同的值，可以通过查表或计算器得到具体数值。

同时，它们之间存在一些基本公式和关系，如下：1. 互余关系（co-function identities）：sin(θ) = cos(90° - θ)cos(θ) = sin(90° - θ)tan(θ) = cot(90° - θ)cot(θ) = tan(90° - θ)sec(θ) = csc(90° - θ)csc(θ) = sec(90° - θ)2.三角函数的平方和差：sin²(θ) + cos²(θ) = 1tan²(θ) + 1 = sec²(θ)cot²(θ) + 1 = csc²(θ)3.三角函数的倒数：sec(θ) = 1/cos(θ)csc(θ) = 1/sin(θ)cot(θ) = 1/tan(θ)4.符号关系：根据角度的位置和象限，三角函数的值可能为正或负。

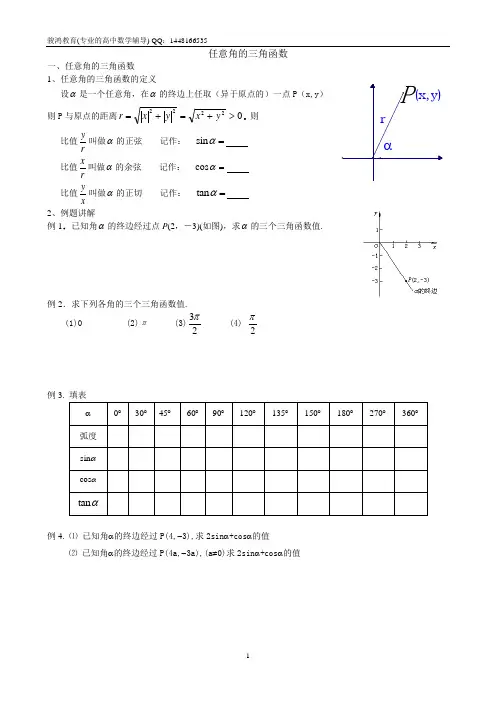
任意角的三角函数一、任意角的三角函数1、任意角的三角函数的定义设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ） 则P 与原点的距离02222>+=+=y x y x r 则比值r y叫做α的正弦 记作： sin α= 比值r x叫做α的余弦 记作： cos α=比值xy叫做α的正切 记作： tan α=2、例题讲解例1．已知角α的终边经过点P (2，－3)(如图)，求α的三个三角函数值.例2．求下列各角的三个三角函数值.(1)0 (2)π (3)23π (4) 2π例3.例4. ⑴ 已知角α的终边经过P(4,-3),求2sin α+cos α的值⑵ 已知角α的终边经过P(4a,-3a),(a ≠0)求2sin α+cos α的值基础练习1．已知角α的终边经过点p(—1,3),则ααcos sin +的值是（ ）A.213+ B.213- C.231- D.213+- 2．已知角θ的终边在直线y x =-上，则sin θ= ，cos θ= 。

3. 05sin902cos03sin 27010cos180+-+= 。

4. 若点()3,P y -是角α终边上一点，且2sin 3α=-，则y 的值是 。

二、三角函数的符号1、三角函数在各个象限的符号()0r >r y =αsin r x =αcos x y =αtan ⎭⎬⎫⎩⎨⎧∈+≠Z k k ,2|ππαα记忆法则：第一象限全为正,二正三切四余弦.2、终边相同的角的同一三角函数值相等公式一（其中Z ∈k ）: 用弧度制可写成ααsin )360sin(=︒⋅+k απαsin )2sin(=+k ααcos )360cos(=︒⋅+k απαcos )2cos(=+k ααtan )360tan(=︒⋅+k απαtan )2tan(=+k3、例题讲解例1. 确定下列三角函数值的符号(1)cos250° （2）)4sin(π- （3）tan （－672°） (4))311tan(π例2. 求证角θ为第三象限角的充分必要条件是⎩⎨⎧><0tan 0sin θθ例3. 求值：sin(-1320°)cos1110°+cos(-1020°)sin750°+tan4950°．基础练习1.已知点()tan ,cos P αα在第三象限，则角α的终边位置在 （ ） A ．第一象限 B. 第二象限 C.第三象限 D.第四象限2. 若三角形的两内角,αβ满足sin cos 0αβ<，则此三角形必为 （ ） A.锐角三角形 B.钝角三角形 C.直角三角形 D.斜三角形 3．函数|tan |tan cos |cos ||sin |sin x xx x x x y ++=的值域是 （ ）A ．{1}B ．{1，3}C ．{-1}D ．{-1，3}4．0sin 600=______________，()0cos 1050-= 。

4.3 任意角的三角函数（第一课时）教学目的：1.理解并掌握任意角三角函数的定义.2.理解三角函数是以实数为自变量的函数.3.掌握正弦、余弦、正切函数的定义域.4. 掌握正弦线、余弦线、正切线. 教学重点：任意角三角函数的定义.教学难点：正弦、余弦、正切函数的定义域,三角函数线. 教学过程：一、复习引入：在初中我们学习了锐角三角函数,它是以锐角 为自变量，边的比值为函数值的三角函数:sin a c α=cos b c α= tan a b α= cot ba α=二、讲解新课： 任意角的三角函数（一）三角函数的定义1.定义：设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ） 则P 与原点的距离02222>+=+=y x yx r ，那么比值r y叫做α的正弦 记作： r y =αsin 比值r x叫做α的余弦 记作： r x =αcos 比值x y叫做α的正切 记作： xy=αtan比值yx叫做α的余切 记作： y x =αcot比值x r叫做α的正割 记作： x r =αsec 比值yr叫做α的余割 记作： y r =αcsc2.三角函数 (1)三角函数根据相似三角形的知识，对于终边不在坐标轴上确定的角α，上述六个比值都不会随P 点在α的终边上的位置的改变而改变.当角α的终边在纵轴上时，即Z)(2∈+=k k ππα时，终边上任意一点P 的横坐标x 都为0，所以tan α、sec α无意义；当角α的终边在横轴上时，即b aα＝ｋπ（ｋ∈Z ）时，终边上任意一点P 的纵坐标ｙ都为0，所以cot α、csc α无意义，除此之外，对于确定的角α，上面的六个比值都是惟一确定的实数，这就是说，正弦、余弦、正切、余切、正割、余割都是以角为自变量，以比值为函数值的函数.以上六种函数，统称为三角函数.（2）三角函数的定义域对于正弦函数r y =αsin ，因为ｒ＞0，所以r y 恒有意义，即α取任意实数，ry恒有意义，也就是说sin α恒有意义，所以正弦函数的定义域是R ；类似地可写出余弦函数的定义域；对于正切函数x y =αtan ，因为x ＝0时，xy无意义，即tan α无意义，又当且仅当角α的终边落在纵轴上时，才有x ＝0，所以当α的终边不在纵轴上时，xy恒有意义，即tan α恒有意义，所以正切函数的定义域是)(2Z ∈+≠k k ππα.从而有αααtan cos sin ===y y y )(2Z k k RR∈+≠ππα αααcsc sec cot ===y y y )()(2)(Z k k Z k k Z k k ∈≠∈+≠∈≠παππαπα（二）三角函数线 1.单位圆和有向线段（1）单位圆：半径等于单位长度的圆叫做单位圆. （2）有向线段（非严格定义）：带有方向的线段叫做有向线段.设任意角α的顶点在原点O ，始边与x 轴的非负半轴重合，终边与单位圆相交于点P(x,y),过P 作x 轴的垂线，垂足为M ；过点A(1,0)作单位圆的切线，设它与角α的终边（当α在第一、四象限角时）或其反向延长线（当α为第二、三象限角时）相交于T.规定：当OM 与x 轴同向时为正值，当OM 与x 轴反向时为负值； 当MP 与y 轴同向时为正值，当MP 与y 轴反向时为负值； 当AT 与y 轴同向时为正值，当AT 与y 轴反向时为负值； 根据上面规定，则OM=x, MP=y , 2.三角函数线根据正弦、余弦、正切的定义，就有sin ,1cos ,1tan .y yy MP r x xx OM r y MP ATAT x OM OAααα============这三条与单位圆有关的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线. 三、讲解范例：例1 已知角α的终边经过点P (2，－3)(如图)，求α的六个三角函数值.例2求下列各角的六个三角函数值.(1)0 (2)π (3)23π (4) 2π例3填表：例4 ⑴ 已知角α的终边经过P(4,-3),求2sin α+cos α的值⑵已知角α的终边经过P(4a,-3a),(a ≠0)求2sin α+cos α的值 四、课堂练习：1.若点P (－3，ｙ)是角α终边上一点，且32sin -=α，则ｙ的值是 . 2.角α的终边上一个点P 的坐标为(5a ,-12a )(a ≠0)，求sin α+2cos α的值.五、作业：习题4.3 1. 2. 3. 4. 5. 6.。

科目数学课题§4.3任意角的三角函数教材分析重点1.任意角的正弦、余弦、正切的定义（包括这三种三角函数的定义域和函数值在各象限的符号）；2.终边相同的角的同一三角函数值相等（公式一）。

难点1.任意角的止弦、余弦、正切的定义（包括这三种三角函数的定义域和函数值在各象限的符号）；2.正弦、余弦、正切这=种=角函数的儿何表示。

关键点1.使学生掌握单位圆的概念：2.了解三种线段的正、负与坐标轴的正、负方向之间的对应；3.这三种有向线段（的数量）与三种三角函数值Z间的对应。

教学标知识冃标1.掌握任意角的正弦、余弦、正切的定义（包括这二种二角函数的定义域和前数值在各象限的符号），理解余切、正割、余割的定义；2.了解如何利用少单位圆有关的有向线段，将任意角a的正弦、余弦、正切、函数值分别用正弦线、余弦线、止切线表示出来；3.掌握并能初步运用公式一。

能力目标树立映射观点，正确理解三角函数是以实数为H变量的函数。

情感目标课时安排2课时教法启发式教学教学设备教与学过程设计具体见下教学后记应简略的介绍正弦、余弦甫数的取值范围，为以后作准备。

教与学过程设计第一课时任意角的三角函数（一）（一）新课引入提问：锐角O的止弦、余弦、正切、余切怎样表示？答：根据图形，手势比划。

引入：锐角三角函数就是以锐角为占变量，以比值为函数值的函数。

如果现在要求sin225°的值，怎么办？还能不能用玄角三角形来求?显然，不能再用初中的定义，因为，这里没有直角三角形，也就没有什么对边、邻边和斜边。

那么，我们应该如何对初中的三介函数的定义进行修改，以利推广到任意介呢？（二）新课1.任意角的三角函数的定义在上述三角形上画上直角坐标系。

此时，ZPOM的对边，邻边分别是什么？斜边呢？将P点改写成坐标形式，P的坐标是（x, y）,它与原点的距离是r（r = Jx|2+|y|2 = + y2 >0）,然后写出三个三角函数的定义。

我们定义:即 sin « =—；即 cos a =—； r（3）比值2叫做a 的正切，记做tan a说明：这样定义以后，（1） 当u 是锐角时，此定义与初中定义相同。