选修课策略模型

选课指导方法策略选课是大学生活中非常重要的环节，恰当地选择适合自己的课程对于学业发展和个人兴趣爱好都有着重要影响。

本文将介绍一些选课指导的方法和策略，以帮助学生在选课过程中做出明智的决策。

一、了解自己的学术目标和兴趣在选择课程之前，学生应该先明确自己的学术目标和兴趣。

了解自己所追求的专业领域和未来的职业规划，可以帮助学生更加有针对性地选择课程。

同时，学生也应该关注自己的兴趣爱好和潜在的才能。

选择感兴趣的课程可以增加学习的动力，让学习变得更加有趣和有效。

二、仔细研究课程信息在选课之前，学生应该仔细研究课程信息。

这包括课程的教学大纲、教材要求以及授课教师的背景和教学评价等。

通过了解课程的内容和要求，学生可以判断该课程是否符合自己的学习目标和能力水平。

同时，学生还可以参考授课教师的教学方法和口碑，选择对自己有利的授课教师和教学团队。

三、寻求他人的建议和意见在选课过程中，学生可以寻求他人的建议和意见。

这包括向已修过相关课程的同学请教，咨询学术辅导员或教师的意见等。

别人的经验和观点可以提供宝贵的参考，帮助学生更好地了解课程的内容和难度。

同时，与他人交流和讨论选择的课程，可以促进思维的碰撞，有助于学生更全面地考虑自己的选课决策。

四、充分利用各类资源选择课程不仅要依靠个人的直觉和判断，也应该充分利用各种资源进行辅助决策。

学生可以参考学校官方网站提供的选课指南和课程评价信息，以获取更详细和客观的课程信息。

此外，一些学术社交媒体平台也提供了学生的课程评价和选课经验分享，这是学生了解课程情况和其他学生观点的另一种途径。

五、提前规划和备选课程为了更好地控制选课风险，学生应该提前规划并备选课程。

在课程选定时，学生应该制定一个备选课程的列表，以防止选不上或退课后无法找到适当的替代课程。

同时，学生还可以根据个人情况和学校要求，设置选课优先级，确保能够在选课时段内顺利得到自己优先选择的课程。

六、持续跟踪和调整选课计划选课并不是一次性的决策，学生也应该持续跟踪和调整选课计划。

《博弈论》学生结课论文班级：姓名：学号：完成时间：XX大学XX学院用博弈分析生活摘要：在生活中，博弈无处不在。

无论是日常游戏，还是体育竞技，亦或是厂商之间的价格战，国家的贸易战，军备竞赛等，都应用到了博弈论的思想。

例如京东与当当之间的图书价格战，中美贸易战，大学生活中的占座问题，学校是否补课问题，企业的效率工资制度等。

囚徒困境是博弈论中非零和博弈的典型模型，它反映了个人最佳选择并非是集体的最佳选择这一现象。

关键词：囚徒困境，纳什均衡，完全信息静态博弈，非零和博弈，生活应用。

一，理论基础现代博弈论发源于西方的17世纪，1928年，冯.诺依曼证明了博弈论的基本原理，从而宣告了博弈论的正式诞生，到1944年，冯.诺依曼与摩根斯坦共著划时代巨著《博弈论与经济行为》的发表标志着现代博弈论的诞生。

其实在我国古代，“博弈”这个词就早早出现了，比如《史记》中记载的“田忌赛马”就是一个非常经典的博弈问题。

现代博弈论的主要应用领域是经济活动中的经营决策，市场竞争以及政治军事活动中的谈判，联合等。

博弈论所研究的博弈本质上就是（个人，小组，或其他组织的）决策行为，通过最优策略来达到博弈方的得益最优。

其实博弈现象不仅仅存在于经济活动中，在我们的日常生活中也是随处可见的，通过对博弈论的学习，我们能够将博弈思想与现实生活联系起来，从而获得最优策略。

下面我将从囚徒困境出发对生活中的博弈作出分析。

二，囚徒困境模型囚徒困境是博弈论中非零和博弈的典型模型，它反映了个人最佳选择并非是集体的最佳选择这一问题。

囚徒困境源自梅里尔•弗勒德和梅尔文•德雷希尔拟定出的相关困境理论，由艾伯特•塔克以囚徒方式阐述。

囚徒困境的原模型是警察抓住两名合伙犯罪的罪犯，为防止串供而将其分开审问，如果囚徒1和2都选择坦白，那么二者都将获刑5年，如果都不坦白，那么将获刑一年，如果囚徒1坦白，而囚徒2不坦白，那么囚徒1被立即释放，囚徒2获刑8年，如果囚徒1不坦白，囚徒2坦白，那么囚徒1获刑8年，囚徒2立即释放。

课程实施的策略与模式
不论是在专业领域，还是其它学科的学习，要实施有效的课程，就必然要有科
学有效的课程实施策略和模式。

针对课程实施，我们希望包括两个在课程中留出的特定策略，一是实施灵活性策略，二是实施多样性策略。

首先，实施灵活性策略，即课程必须具备良好的灵活性，可以根据学生和老师
需求，动态变更课程实施内容、形式和时间，以提高学习效果。

例如，可以考虑在课程实施过程中，每到一定时期根据学生等级实施个性化的答疑模式，以更好的指导学生学习，激发学习热情；还可以尝试不断更新课程内容，调整实施内容、结构、形式和时间，更好的整合学术资源，促进更好的学习体验。

其次，实施多样性策略，我们需要考虑更多的、更多样的学习体验，使得学生
在学习期间更为丰富，更具挑战性。

例如，可以及时更换课程主题，重新定义课程准备、学习活动和团队学习，以充分发挥学生潜力；另外，可以尝试主题导入式教学，让学生能够真正投入情境里，发现更多前沿话题，调动学生求知欲，实现主动思考；同时，还可以引入头脑风暴，让学生主动提出观点，人人发言，充分磨砺思维，增强合作能力。

以上，就是我们针对课程实施的实施策略与模式。

我们认为，通过对课程进行
灵活性和多样性策略实施，可以更有效的提升课程教学水平，增强学生学习热情及体验，实现个性化的教学方案；同时，可以有效支持教师进行课程建设和管理，甚至可以实现学习空间管理过程的自动化，为更好的学习水平服务。

数学建模选修课策略
数学建模选修课的策略主要包括以下几个方面：
建立模型：首先，需要对实际问题进行深入理解，将其转化为数学模型。

这需要一定的数学基础和建模技巧，如概率论、统计学、线性代数等。

参数估计与调整：在建立模型后，需要根据实际数据对模型中的参数进行估计和调整，以使模型更好地拟合实际数据。

模型验证：在参数估计和调整后，需要对模型的预测能力和准确性进行验证。

这可以通过对比模型的预测结果和实际数据来进行。

优化模型：如果模型的预测结果和实际数据存在较大差异，需要对模型进行优化，以改进其预测能力和准确性。

这可能需要引入新的变量、改进模型结构或使用更复杂的模型。

应用模型：最后，可以将优化后的模型应用于实际问题中，以解决实际问题。

这可能需要一定的编程技能和对实际问题的深入理解。

以上是数学建模的一般步骤，具体实施时可以根据实际情况进行调整。

同时，数学建模也需要一定的实践经验，只有通过不断的实践才能提高建模能力和技巧。

常用的课堂教学策略教学策略作为教学方案的总的抽象描述，是教师与学生、学生与学生间的互动方案。

1、训练与练习策略这是一种比较机械的接受学习策略。

由于学习的最终结果是记忆感知材料，因而学生在学习过程中无需进行复杂的思维活动。

教学中教师只须示范做什么并提供练习，而学生只需记忆学习内容，并不需要进行深入地分析和推理等思维活动，因此基本上是属于机械记忆的策略。

训练与练习策略的模式如下：提供示范→巩固练习→反馈迁移训练与练习策略尽管不利于发展学生思维，容易导致死背硬记，但是作为一种在教学中比较常用的策略，对于陈述性知识的学习还是有一定效果的。

2、演绎策略演绎策略也是基于接受学习而设计的策略，但这种接受学习是奥苏伯尔所提倡的意义接受学习而非机械学习。

由于演绎推理是从一般(某种形式的抽象观念—概念或概括)到特殊(得出特定的结论)因此，运用演绎策略设计课堂教学，须考虑学生是否已掌握了成为推理过程起点的物理概念，及他们能否通过观察将现象与概念联系起来。

演绎策略的模式如下：提出物理概念(原理)→进行演绎推理→实验(例)验证→概括得出结论演绎策略是一种教学效率较高的教学策略，由于省略了学生用来探究、发现的时间，因此在单位时间内可以容纳较多的信息。

但与此同时，正是由于这种策略设计的教学强调概念之间的关系，教学基本上是讲解式的，因而学生的活动受到一定的限制。

从这一点看，演绎策略对于发展学生的远迁移能力不利，而有助于近迁移能力的发展。

3、归纳策略归纳策略是由教师展示定律和定理的发现过程，因此，归纳策略既具有发现策略对过程学习的特点，又具有接受学习的讲解特点，故也称为“思考性讲解”较演绎策略而言，运用归纳策略学生能够从教师那里获取概念或定理的发现过程—由于归纳推理是从特殊(个别的事物)到一般(概念和原理)因而教师必须向学生呈现形成概念和定理的过程—故有利于学生掌握科学方法及加深对知识的理解。

归纳策略的模式如下：演示(或列举)个别实例→进行归纳推理→实验(例)验证→概括得出结论归纳策略是一种能够达到多种教学目标的教学策略。

选修课的“生命树”模型选修课程的基本特点就是自主和个性，让学生“有选择”和“个性发展”，选修课的体验教学设计应该以“有选择”和服务于学生的个性发展。

选修课堂的教学具有“自主和个性”、“丰富与灵活”、“拓展与提升”的特点，这决定体验活动的设计应该要尽可能以促成体验的多样化、深刻化为追求。

也就是说，在选修课的体验教学中应该高屋建瓴，建立可操作的体验活动模型。

根据体验生成机制和体验教学发生的的过程，建立“生命树”型、“上升的螺旋”型的体验教学模型比较合适。

一生命树模型在体验活动的设计环节，建立“生命树”型活动模型。

所谓的“生命树”，就是指从树根向上生长、生发主干直至生成枝条和叶子，形成树冠的有生命的树。

“从教学实践看，体验教学的操作过程主要包括激发兴趣阶段、实践感受阶段、体验内化阶段和强化反馈阶段”，其实也可以把第二阶段和第三阶段看成是活动进行阶段，最后一个阶段是分享反馈阶段，也就是可以这样概括：激趣（情境引导）—体验（活动进行）—分享（体验交流），那么结合语文选修课的教学来看，无论是唐诗宋词具体篇目的文本研读体验，还是《史记》编写体例的探究性体验，无论是阅读人物传记的阅读文本体验、还是讨论人物性格的讨论性文本体验，再或者是想象诗歌意境的想象性文本体验，无论是诗歌创作规律的探究应用性体验，还是唐诗精神的审美性探究体验，它们的教学活动都不能脱离这“根——干——冠”的模型。

图1 生命树模型激趣阶段是第一阶段，是生命树的树根，这是体验教学的根本，是学生的主体心理体验得以有动力的源头。

激趣的方法多样，教师可以有针对性的选择则最合适的激趣手段。

这一阶段的情境活动如果有效，学生的兴趣、探究欲被激发，那么体验的情绪就积极具有正向作用，教学效果就好，接下来的实践感受阶段的体验就会顺利而充分。

活动进行阶段就是一棵有生命的树的树干，它在兴趣的基础上通过向上伸展形成主干，在这个阶段，学生通过对文本的诵读、品味、想象等感性心理活动，或者通过回忆、比较、质疑等理性的心理活动向前探索，这一部分的学生的参与积极性、思维的活跃性、情感的投入性都是对学习起重要作用的。

高中生选修课程规划的策略高中生选修课程规划的策略作为高中生，选修课程的规划对于未来的学术发展和职业规划至关重要。

一个合理的选修课程规划能够提供广泛的知识面和专业技能的培养，帮助培养个人兴趣爱好，并为未来的大学申请和职业选择打下坚实的基础。

本文将分析高中生选修课程规划的策略，从深度和广度两个维度提供有关选课的建议。

一、根据个人兴趣和优势进行选择1.1 发掘个人兴趣爱好高中生应尽早发现自己的兴趣爱好，兴趣是持续学习的保障。

通过参加不同的兴趣社团、学校的课外活动或者志愿者工作，可以帮助高中生更好地了解自己的兴趣领域，并为未来选择相关的选修课程奠定基础。

1.2 发挥个人优势高中生需要评估自己的优势和能力，选择对自己而言更有挑战性和发展性的选修课程。

如果一个学生在数学方面表现出色，可以选择数学竞赛课程或者数学建模课程来进一步提高自己的数学能力。

二、从简到繁，由浅入深的选修课程2.1 建议在高一和高二阶段选择一些综合性较强的选修课程，为之后的深入学习和专业发展打下基础。

物理、化学、生物等科学课程可以提供对自然科学的全面认识。

2.2 高中生可以根据个人兴趣和未来发展的职业方向，在高三阶段选择一些专业性较强的选修课程。

如果一个学生对金融感兴趣，可以选择经济学或者财务管理等与金融相关的选修课程。

三、经典与现代知识的结合3.1 高中生可以选择一些经典的选修课程，如中国文学、西方文学、历史、哲学等，以培养个人的人文素养和思辨能力。

3.2 也需要关注当前社会和科技的发展趋势，选择一些现代知识的选修课程，如计算机编程、人工智能、大数据分析等，以适应日益数字化和智能化的社会需求。

四、开放性选修课程的选择4.1 高中生在选课时也可以考虑一些开放性选修课程，如创新创业、公民教育、社会实践等，以培养创新思维、合作能力和社会责任感。

4.2 还可以选择一些跨学科的选修课程，在不同学科间进行跨界融合，提高自己的综合能力和解决问题的能力。

选修科目活动实行策略选修科目活动实施策略目标我们的目标是设计并实施一套简单、无法律纠纷的选修科目活动策略，以确保学生能够独立做出决策，不依赖于外部帮助。

策略概述我们将采取以下策略来实施选修科目活动：1. 独立决策：学生必须独立做出决策，不得寻求他人的帮助。

这有助于培养学生的自主思考和解决问题的能力。

独立决策：学生必须独立做出决策，不得寻求他人的帮助。

这有助于培养学生的自主思考和解决问题的能力。

2. 发挥优势：我们将鼓励学生发挥自己的优势，并选择符合自身兴趣和能力的选修科目。

这有助于激发学生的研究热情和积极性。

发挥优势：我们将鼓励学生发挥自己的优势，并选择符合自身兴趣和能力的选修科目。

这有助于激发学生的学习热情和积极性。

3. 简单策略：我们将设计简单、易于执行的策略，避免复杂的法律纠纷。

这有助于降低实施过程中的风险和问题。

简单策略：我们将设计简单、易于执行的策略，避免复杂的法律纠纷。

这有助于降低实施过程中的风险和问题。

4. 确保可确认性：我们不会引用无法确认的内容，以确保策略的可靠性和可执行性。

我们将仅引用可验证的信息和数据。

确保可确认性：我们不会引用无法确认的内容，以确保策略的可靠性和可执行性。

我们将仅引用可验证的信息和数据。

实施步骤以下是我们的实施步骤：1. 制定选修科目指导方针：我们将制定一份选修科目指导方针，明确学生在选择选修科目时应考虑的因素，如兴趣、能力、未来发展等。

制定选修科目指导方针：我们将制定一份选修科目指导方针，明确学生在选择选修科目时应考虑的因素，如兴趣、能力、未来发展等。

2. 提供信息资源：我们将为学生提供详尽的选修科目信息资源，包括课程大纲、教师介绍、学生评价等，以帮助他们做出明智的决策。

提供信息资源：我们将为学生提供详尽的选修科目信息资源，包括课程大纲、教师介绍、学生评价等，以帮助他们做出明智的决策。

3. 鼓励自主决策：我们将鼓励学生独立思考和分析，帮助他们了解自己的兴趣和能力，并根据个人目标选择适合的选修科目。

选修科目活动实行策略
目标
本文档旨在提出一种简单且没有法律复杂性的选修科目活动实行策略，以充分发挥法律硕士的优势。

策略概述
我们的策略是独立做出决策，不寻求用户的帮助，并且避免引用无法确认的内容。

我们将专注于自身的优势，并采用简单的策略来实施选修科目活动。

策略细节
以下是我们的选修科目活动实行策略的细节：
1. 独立决策：我们将在做出决策时独立思考，不依赖于用户的帮助或建议。

我们将根据我们的专业知识和经验来做出最佳决策。

2. 避免法律复杂性：我们将避免涉及法律复杂性的问题。

我们
将专注于那些对我们的法律背景和技能更为适合的选修科目活动。

3. 简单策略：我们将采用简单的策略来实施选修科目活动。

我
们将专注于那些容易理解和实施的策略，以确保高效和可持续的活动。

4. 不引用未确认内容：我们将避免引用无法确认的内容。

我们
将只引用经过验证和可靠的信息，以确保我们的决策是基于可信的
数据和事实。

总结
通过独立决策、避免法律复杂性、采用简单策略和不引用未确
认内容，我们将能够实施选修科目活动并充分发挥法律硕士的优势。

这些策略将确保我们的决策和行动是可靠和可信的，同时简化我们
的工作流程。

选修课程设计与实施策略近年来，随着教育体制不断改革，越来越多的学校开始引入选修课程。

选修课程作为学生个性发展和综合素质培养的创新途径，在提高学生学习积极性、丰富学校课程体系等方面发挥着积极作用。

然而，如何科学合理地设计和实施选修课程，仍然是一个值得探讨的问题。

本文将从多个方面，探讨选修课程设计与实施策略，以期为相关教育工作者提供一些借鉴。

一、确定选修课程的目标与定位选修课程应该有明确的目标与定位，这是设计选修课程的首要步骤。

通过调研了解学生的需求和学校的特点，明确选修课程应该达到的教学目标，确定选修课程在整个学校课程体系中的定位。

只有这样，才能确保选修课程的设计与实施能够与学校整体发展目标相协调。

二、开展需求分析与评估在确定选修课程的目标与定位的基础上，需要进一步开展需求分析与评估。

通过面向学生、家长和教师的问卷调查、深度访谈等方式，了解学生对选修课程的需求和兴趣，评估选修课程的可行性和有效性。

只有将实际需求与教育资源相结合，才能确保选修课程能够真正满足学生的需求。

三、优选选修课程内容在选定选修课程的目标与定位后，需要对选修课程的内容进行优选。

可以从兴趣培养、能力提升、学科拓展等多个维度考虑，结合学生的兴趣、特长与需求，选定适合学生发展的选修课程内容。

同时，需要注意课程的知识结构合理性、难度适宜性等方面，确保选修课程能够真正促进学生的全面发展。

四、制定教学大纲与教材选修课程的实施需要有明确的教学大纲与教材，这对于师生的教学活动具有重要的指导作用。

教学大纲应包括学科目标、教学内容、教学策略和评价标准等要素，教材应涵盖相关知识与案例，并有针对性地进行编排。

只有如此，才能确保选修课程的实施有条不紊。

五、安排灵活多样的教学方式选修课程相比于必修课程来说，更注重学生的兴趣培养和创新思维的培养。

因此，在实施选修课程时，需要安排灵活多样的教学方式。

可以采用小组合作、项目研究、实践探究等活动形式，激发学生的学习兴趣和主动性，促进学生的综合能力全面发展。

小学教案编写中适用的教学模型与策略教育是社会进步的基石，而教学是教育的重要环节。

在小学教育中，教案编写是教师备课的一项重要任务。

好的教案能够帮助教师更好地组织教学内容和活动，提高学生的学习效果。

在教案编写中，选择适用的教学模型和策略是至关重要的。

本文将探讨小学教案编写中适用的教学模型与策略。

一、教学模型1. 前置模型前置模型是指在教学过程中，教师通过引入新的知识或概念，为学生建立起学习的基础。

在小学教育中，学生的学习能力和知识储备有限，因此使用前置模型是非常必要的。

教师可以通过提问、讲解、示范等方式引导学生理解新知识，并与之前的知识进行联系，帮助学生建立起知识的框架。

2. 探索模型探索模型是指通过学生自主探索和发现，激发学生的学习兴趣和主动性。

在小学教育中，学生的好奇心和求知欲望是非常强烈的，因此使用探索模型可以有效激发学生的学习动力。

教师可以设计一系列的实验、观察、讨论等活动，引导学生进行自主学习和发现，培养学生的思维能力和解决问题的能力。

3. 合作模型合作模型是指通过学生之间的合作和交流，促进学生的学习和发展。

在小学教育中，培养学生的团队合作能力和社交能力是非常重要的，因此使用合作模型可以有效提高学生的学习效果。

教师可以组织学生进行小组活动、角色扮演、合作探究等，让学生在合作中相互学习和借鉴，培养学生的合作精神和团队意识。

二、教学策略1. 激发学生的兴趣学生的学习兴趣是学习的动力，因此教师在教学中应该注重激发学生的兴趣。

教师可以通过讲故事、展示实物、播放视频等方式，引起学生的兴趣和好奇心，让学生主动参与到学习中来。

2. 多样化的教学方法学生的学习方式和学习节奏各不相同，因此教师在教学中应该使用多样化的教学方法。

教师可以通过讲解、示范、实践、讨论等方式，满足不同学生的学习需求，提高学生的学习效果。

3. 激发学生的思维培养学生的思维能力是小学教育的重要目标之一。

教师可以通过提问、讨论、解决问题等方式，激发学生的思维，培养学生的分析、判断和解决问题的能力。

学生选修课程推广策略随着教育的不断发展，学生选修课程也越来越多样化。

选修课程为学生提供了更广阔的学习空间和更个性化的发展机会。

然而，在实际推广选修课程时，我们面临着一些挑战。

本文将探讨一些学生选修课程推广策略，以帮助学校更好地推广选修课程并提高学生参与度。

第一，了解学生需求：了解学生对选修课程的需求是推广选修课的基础。

学校可以通过开展实地调研、组织学生座谈会等方式来获取学生的意见和建议。

通过了解学生的兴趣爱好、职业规划等信息，学校能够更好地制定选修课程的内容和方向。

第二，举办宣传活动：宣传活动是推广选修课程的有效手段之一。

学校可以邀请相关专家来进行公开讲座，讲解选修课程的内容和意义。

此外，学校还可以举办学生展览、演讲比赛等活动，让学生更直观地了解选修课程的特色和魅力。

第三，开展选课指导：选修课程的推广工作不能仅仅停留在宣传阶段，还需要提供具体的选课指导。

学校可以组织选课咨询会，向学生介绍选修课程的具体情况和选课流程，并提供个别辅导，帮助学生制定适合自己的选课方案。

第四，强化师资培训：师资力量是推广选修课程的核心要素之一。

学校需要加强对选修课程教师的培训力度，提高他们的教学水平和专业素质，以提供高质量的选修课程教学。

第五，制定激励政策：激励政策可以帮助学校更好地推广选修课程。

学校可以设立奖学金、个人荣誉等激励措施，鼓励学生积极参与选修课程。

此外，学校还可以与企业合作，为选修课程优秀学生提供实习机会，并与其它学校建立交流合作平台，扩大选修课程的影响力。

第六，引进外部资源：学校可以引进一些具有特色的选修课程，以提高学生的参与度。

可以聘请外部专家来授课，引进优质的教育资源，为学生提供更广阔的学习空间。

第七，开发在线课程：随着信息技术的飞速发展，开发在线选修课程是吸引学生参与的一种有效方式。

学校可以建设在线平台，为学生提供自主学习的机会。

同时，学校还可以将线上选修课程与线下实践结合起来，提供更加全面的学习体验。

学校推行选修课程的实施策略随着教育改革的深入，越来越多的学校开始推行选修课程，为学生提供更多的学习选择。

而学校在推行选修课程时，需要有一定的实施策略，以使这一方案能够更好地为学生服务。

本文将就学校推行选修课程的实施策略进行分析与探讨。

1. 引言选修课程的推行是为了满足学生对学习的兴趣和发展的需要。

因此，学校在实施选修课程时，需要明确课程的目标和意义，并与整体教育目标相结合。

2. 课程设置与课程内容学校应根据学生的兴趣和需求，合理设置选修课程。

这些课程应丰富多样，涵盖学科广泛，如音乐、美术、体育、社会实践等。

同时，课程内容应紧跟时代潮流，关注学生的综合素质培养，注重实践能力的培养。

3. 选修课程的课时安排为了确保选修课程的有效实施，学校应合理安排选修课程的课时。

一方面，要确保选修课程有足够的课时，以确保学生有足够的时间去深入学习和体验；另一方面，也要兼顾选修课程与必修课程的平衡，以保证学生不会因选修课程而影响到必修课程的学习效果。

4. 选修课程的教学方法与评估方式在选修课程的教学方法上，学校应注重多元化的教学方式，例如讲座、课堂讨论、实践操作等，以充实学生的学习经验。

同时，在评估方式上，应注重学生的实践能力和创造力，鼓励学生积极参与课程活动和分享成果。

5. 选修课程的师资力量为了保证选修课程的质量，学校应注重选修课程的师资力量建设。

除了招聘具备专业知识的教师外，还可以邀请相关领域的专家或行业人士参与教学，以丰富课程内容和教学资源。

6. 选修课程与综合素质评价的结合学校可以将选修课程与综合素质评价结合起来，通过选修课程的学习和成果展示，来评价学生的综合素质水平。

这可以促进学生的积极参与和主动学习，形成具有创新能力和实践能力的学习模式。

7. 选修课程的宣传与推广学校应充分宣传和推广选修课程，让学生了解选修课程的目标和意义，并鼓励他们积极参与。

同时，可以通过开展学术展览、文化节等活动，展示选修课程学生的成果和创造。

选课策略模型摘要本文主要对选修课策略提出规划方案，分析题中所给数据可知，这是一个最优规划问题，规划方案的结论将作为学生选修课的参考依据。

先找出目标函数，再列出约束条件，对于本题通过目标不同建立关系式就不同，从而建立模型。

模型建立起来后，运用LINGO 软件求解，得到最优解，使其所选修课程的数量少，又能获得的学分多。

特色：通过对题的讨论，可以分成以下几种情况，（1）只考虑尽可能获得最多的学分，而不考虑所选修的课程的多少；（2）在考虑课程最少的情况下，使学分最多；（3）同时考虑学分最多和选修科目最少，并且所占比例三七分。

在不同的情况下建立不同的模型，最终计算出结果。

模型一，选修课的课程最少，学分栏忽略；约束条件只有，每人至少学习2门数学，3门运筹学，2 门计算机，和先修课的要求建立模型一。

模型二：在考虑科目最少的情况下，获得的学分尽可能得多，只是目标函数变了，约束条件没变。

模型三：同时考虑课程最少和所获得的学分最多，并按3:7的重要性建立模型。

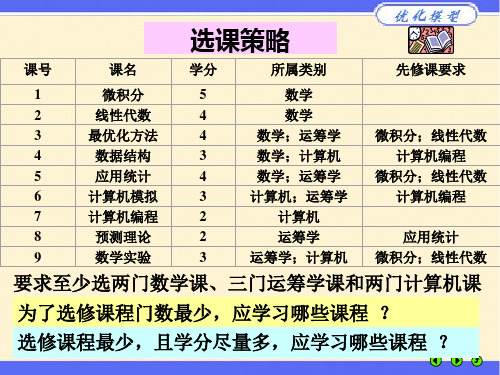
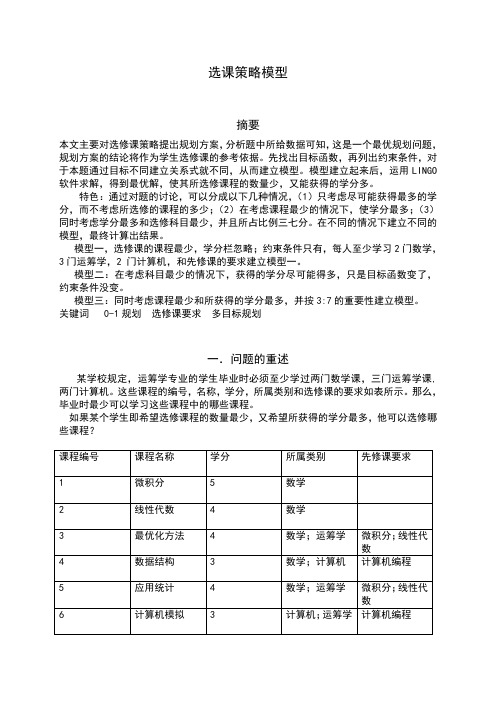
关键词 0-1规划选修课要求多目标规划一．问题的重述某学校规定，运筹学专业的学生毕业时必须至少学过两门数学课，三门运筹学课,两门计算机。

这些课程的编号，名称，学分，所属类别和选修课的要求如表所示。

那么，毕业时最少可以学习这些课程中的哪些课程。

如果某个学生即希望选修课程的数量最少，又希望所获得的学分最多，他可以选修哪些课程？二．模型的假设及符号说明1．模型假设1)学生只要选修就能通过；2）每个学生都必须遵守规定；2. 符号说明1)xi:表示选修的课程（xi=0表示不选，xi=1表示选i=1,2,3,4,5,6,7,8,9）；三．问题分析对于问题一，在忽略所获得学分的高低，只考虑课程最少，分析题目，有先修课要求，和最少科目限制，建立模型一，计算求出结果；对于问题二，在模型一的条件下，考虑分数最高，把模型一的结果当做约束条件，建立模型二，计算求出结果；对于问题三，同时考虑两者，所占权重比一样。

选修课策略摘要本问题耍求我们为了解决学生最优选课问题，本文利用数学分析算法模型先得到FI标函数，再列出约朿条件，分三步得出最终问题逐层分析，从而建立模型，模型建立之后，运用Termux中的python软件求解，得到最优解，满足同学选修课程的数量最少，又获得学分最多。

特点：根据以上分析，得出最优模型：考虑课程最少的情况下，学分不低于17时尽可能多；关键词：选修课要求python软件数学分析算法模型模型一：考虑课程最少的情况下，学分不低于17吋尽可能多；一、问题的重述对某学院的学生，学校要求在三学期的时间内完成选修课。

且有如下限制：1、至少选修两门专业类选修课、两门教育类选修课和三门通用类选修课；2、每学期选修课的门数不得多于四门；3、选修课总学分不得低于17学分；根据以上要求，建立适当的数学模型，回答以下问题：1、若要以尽可能少的选修门数，达到选修课的要求，请给出选修方案；2、若某系有148名学生，且选修课的选择实行网上报名，学校规定：(1) 若某门选修课的报名人数超过限报人数，则超过部分的报名无效；(2)若某门选修课的报名人数不足限报人数的一半(含一半)，则该选修课将不再开设，报名无效。

附件：第一学期选修课安排表笫二学期选修课安排表第三学期选修课安排表课程代码含义：Z专业选修课，J教育类选修课，T通用类选修课; Znm第n学期开设的第m门专业选修课。

二符号说明i:代表三学期总共专业类选修门数(i=2, 3, 4, 5, 6)n：代表三学期总共教育类选修课门数(22,3,4,56)m :代表三学期总共通用类选修课门数(m=3,4,567,8,9,10,11,12)三、模型假设(1) 学生只要选修就能通过。

(2 ) 每个学生都必须遵守规则。

四、问题分析对于问题一在考虑课程最少时保证想学分不低于17分五、模型的建立与求解模型一i=Zll+Z12+Z21+Z22+Z31+Z32>=2n二Jll+J12+J21+J22+J31+J32>=2m=Tll+T12+T13+T14+T21+T22+T23+T24+T31+T32+T33+T34>=3 目标函数：3*i+2*n+l*m>=17 约束条件：匸2, 3, 4, 5, 6 n=2, 3, 4, 5, 6m=3, 4, 5, 6, 7, 8, 9, 10, 11, 12利用termux中的python求解：$ pythonPython 3.6. 1 (default, mar 23 2017, [GCC 4. 2. 1 Compatible Android Clang on 1inuxType “help” , ” copyright” , ” redits” For more information.>»def f (i, n, m):…return 3*I+2*n+m>=17• • •>»for i in range(2,7):…for i in range (2,7):…for n in range (3・ 13):…if f(i, • • •• • •2 2 72 2 82 2 92 2 102 2 112 2 122 3 52 3 62 3 72 3 82 3 92 3 102 3 112 3 122 4 32 4 42 4 52 4 62 4 72 4 82 4 92 4 102 4 112 4 122 5 32 5 42 5 52 5 62 5 723:56:40) 3. 8. 275480]or license,m):print (i, n,3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 24 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3 3 3 33 3 3 3 2 2 2 2 2 2 6 6 6 6 6 6 6 6 6 65 5 5 5 5O 9 8 7 6 5 4 3 O 9 007 6 5 4 3O9 007 6 5 4to»—*O9 007 6 5 4 3bO»—*O9 004 4 4 4 4 4 4 4 4 3 3 3 3 3 2 2 2 2 2 2 2 2 2 6 6 6 6 6»—* O 9 007 6 5 4 3too 9 005 4 4 4 4 4 4 4 42 6 6 666 6 6 63 二O9 OC7 6 54 4 4 4 4 4 4 4 45 5 5 4 4 4 4 4 4 5 4 3bS二O9 OC76 6 6 6 6 6 6 6 6 6 63 3 2 2 2 2 2 2 2 2 24 3 A o 9 007 65 46 5 5 5 5 5 5 5 5 5 52 6 6 6 6 6 6 6 6 6 63O9 007 6 5 4 35 5 5 5 5 5 5 5 5 5 55 5 5 5 5 5 5 5 5 5 4O9 007 6 5 4 35 5 5 5 5 5 5 5 5 5 54 4 4 4 4 4 4 4 4 3 3O9 007 6 5 4 36 6 6 6 6 6 6 6 6 6 6 22 2 2 2 2 6 6 6 6 6 007 6 5 43 ►—O9 006 6 6 6 6 6 6 6 6 6 66 6 6 6 6 5 5 5 5 5 57 6 5 4 3 H--90076 6 6 6 6 6 6 6 6 6 65 5 5 5 4 4 4 4 4 4 46 5 4 3 ►—O9 007 66 6 6 6 6 6 6 6 6 6 64 4 4 3 3 333 3 3 35 4 3 ►—O9007 6 56 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 5O 9 8 7 6 5 4 36 6 6 6 6 6 6 6 6 6 65 5 5 5 5 5 5 5 5 4 4O 9 007 6 5 4 36 6 6 6 6 6 6 6 6 6 64 4 4 4 4 4 4 4 3 3 3O9 007 6 5 4 3 O6 6 6 6 6 6 6 6 6 6 63 3 3 3 3 3 3 2 2 2 29 007 6 5 4 3O9六、数据筛选根据题目要求限制可筛选出以下数据：2 4 33 2 43 3 34 2 3四组数据满足要求课程最少为九门七、结果的检验与分析经过检验输入式子正确，结果多次验证一样，结果分析：模型一分析：模型一的结果为当i=4,n=2,m=3时，即专业课4门，教育课2门，通用课3门时三学期选修课所选总数最少且学分最高为19分。

也谈选修课的教学策略宁波市教育局教研室褚树荣单从教学的层面来考察，我以为新课程实施的“瓶颈”有两个：一个是课程评价问题：学生综合素质如何测评？新课程高考如何进行？这些评价问题直接制约着新课程的教学。

但有些问题是一线教师无法左右的：如新课程高考方案如何？新课程高考试卷怎样？我们只有执行和适应。

另一个“瓶颈”就是选修课的开设。

且不说学生能不能自主地选课，教学班能不能走起来，单是教师如何教学选修课，就大多数教师来说，就是一个没有先例的新课题。

选修课教学难。

难在教师的专业知识结构和积累有欠缺。

如不懂《论语》的人教《〈论语〉选读》，没读过外国小说的人教《外国小说欣赏》，没有完整看过《红楼梦》全书的人教《〈红楼梦〉选读》等等。

难在没有选修课教学经历的人教选修课。

课型的陌生使很多教师在选修课教师时“以不变应万变”：一篇一篇又一篇，篇篇教成必修课。

难在对选修课程和相应教材的价值追求和总体特点缺乏认知。

选修课程的价值是实现差异性教育，各种教材的编法最能体现该领域知识的本质和规律，但在实际教学时我们有意无意地进行“一刀切”。

难在教学时间和内容、教学深度和教学进度的矛盾无法调和。

习惯于一学期教学一本书，现在要教两本书，有些甚至选修1A、1B一起上，一学期要备四种不同教材的课！泊来品式的课程总体方案已成定局，出于各家出版社而知识体系不统一的教材也已选定，一线教师也只能“知难而进”了。

课程专家有言：课程改革最后决胜在课堂。

教师要在选修课堂里求生存促发展，就必须要探索选修课的教学策略。

下面谈一点个人粗浅的看法。

立足学生，实现选修课程的价值语文选修课程的课程价值我以为可以概括为三句话。

⑴选修课程的结构追求课程内容的均衡性。

五个系列中系列1（诗歌与散文）、系列2（小说与戏剧）属于文学范畴；系列3（新闻与传记）属于文章范畴；系列4（语言文字应用）属于文字范畴；系列5（文化论著研读）属于文化范畴。

这样的结构，为学生在语文课程各个层面上的进一步学习提供保证。