电阻电路补充问题讲解

高中物理电阻题解题技巧电阻是物理学中的重要概念，也是高中物理中常见的考点之一。

在解题过程中，理解电阻的概念和特性，掌握一些解题技巧是非常重要的。

本文将介绍一些高中物理电阻题解题技巧，并通过具体的题目进行解析，帮助高中学生和他们的父母更好地理解和应用这些技巧。

一、串联电阻的计算在串联电路中，电流依次通过多个电阻，电阻值相加即可得到总电阻。

例如，有一个由三个电阻串联而成的电路，电阻分别为R1、R2、R3，求总电阻R。

解题思路：总电阻R = R1 + R2 + R3举一反三：如果电路中有更多的电阻串联，只需将各个电阻的电阻值相加即可得到总电阻。

二、并联电阻的计算在并联电路中，电流分别通过多个电阻，总电流等于各个电阻分流之和。

例如，有一个由三个电阻并联而成的电路，电阻分别为R1、R2、R3，求总电阻R。

解题思路：1/R = 1/R1 + 1/R2 + 1/R3举一反三：如果电路中有更多的电阻并联，只需将各个电阻的倒数相加，再取倒数即可得到总电阻。

三、电阻的等效在一些复杂的电路中，可以将多个电阻进行等效，简化计算。

例如，有一个由两个电阻并联而成的电路，电阻分别为R1、R2，求等效电阻Re。

解题思路：1/Re = 1/R1 + 1/R2举一反三：如果电路中有更多的电阻进行等效，只需将各个电阻的倒数相加，再取倒数即可得到等效电阻。

四、电阻与电流的关系根据欧姆定律，电阻与电流呈线性关系。

例如，有一个电阻为R的电路，电流为I，求电压U。

解题思路：U = R × I举一反三：如果已知电阻和电压，可以通过欧姆定律计算电流。

五、电阻与功率的关系根据功率公式，电阻与功率呈平方反比关系。

例如，有一个电阻为R的电路，电流为I，求功率P。

解题思路：P = I² × R举一反三：如果已知电阻和功率，可以通过功率公式计算电流。

通过以上解题技巧的学习和应用，希望能够帮助高中学生和他们的父母更好地解决电阻题。

第三章电阻电路的一般分析习题一、填空题。

1、对于n个节点b条支路的连通图，其树支数为.二、计算题。

1.求图1所示电路的电压U和受控源发出的功率。

解：独立回路的选择以及回路绕行方向如图2所示，列回路电流方程为：/“=4A，/2=2A(6+3+3)∕11+3×∕zi+3×∕z2=3,单连支回路数为解：用结点法求出U=32V,1=1.6ΛEA"人心一、+、，50-15/U—151 ..受控源的电流为-------- + -------- =4A10 4受控源发出的功率为-151X4=96W2.用回路法求图2所示电路的电流I。

6QI1 ----- 1—即有I=I 13=-1.25A(2+2+2)/—2×5—2x4=—u ∣ M 1=2×(5-7)1 1 1∖l , 11. 11. , ti. ------- +一÷—)v.—v>—匕=/<——-R i +R2 R. ---------- R 1l R.2R 13 5 R 1V+(—+—+—)⅛-—½=0R3叫&-R5 --v 1--v,+(—+—+—)½=e+以RJ1.&&R 凡K求得：I 13—=-1.25A123.图3所示电路，用回路法求I 。

图3ς-=i∩ςτ+z n-'n-'m=i n-z rκ+l nι-【=力-力-力£⅛+oι=⅛t+z∕-7-⅛-ι=f∕-z∕ε+7-o=t z-1+7-=力z z-,zε5Ω图9I l=lΛ-2∕,+10∕2-∕3=5(∕X-2∕1-∕2+3∕3=-10U x=I(I3-I2)z1 1 1、〃1rr w s∙1(R+R+y+0)U川—v U“2=⅛+-7-_/u ZH+(，+，)U〃2=仇KI KAκ5补充方程，=-上」R∖+R?14 .列出图14所示电路的结点电压方程（其中④为参考结点）(RR+丁+B)Unl-KU la=i si+ι∖∣+0Kyι∖∣∕∖4^⅛^+⅛+⅛^2=^R∣+R215 .电路如图15所示，求：（1）以4为参考结点，列写结点1、2、3的结点方程。

1-1 说明图（a ）,（b ）中, （1）,u i 的参考方向是否关联？ （2）ui 乘积表示什么功率？（3）如果在图（a ）中u>0, i<0；图（b ）中u>0, i>0，元件实际发出还是吸收功率？解：（1）（a ）图参考方向是关联的（b ）图参考方向为非关联。

（2） （a ）图中的ui 乘积表示元件吸收的功率（b ）图中的ui 乘积表示元件发出的功率。

（3） （a ）图中当0,0<>i u ,有0<=ui p ，表示元件实际发出功率。

（b ）图中当0,0>>i u ，有p=-ui<0，表示元件实际发出功率。

1—2在题1—2图(a)与(b)中，试问对于N A 与N B ，“u 、i 的参考方向是否关联?此时乘积ui 对N A 与N B 分别意味着什么功率?解：图(a)中，u 、i 的方向对N A 是非关联的，对N B 则是关联的； 因此，P a = -ui ，N a 发出功率， P B = ui ，N B 吸收的功率。

图(b)中，u 、i 的方向对N A 是关联的，对N B 是非关联的； 因此，P A = ui ，N a 吸收的功率。

P B = -ui ，N B 发出功率，1-4 在指定的电压u 和电流i 参考方向下，写出各元件u 和i 的约束方程（元件的组成关系）。

10K+ u -10+ u -+10V-- 5V +(b)(a)(c)(d)(e)(f)解：（a ） （b ）i i R u 31010⨯-=-= V (c) u=10V （d ）V u 5-= （e ）i=10mA1-8 试求图中各电路的电压U ，并讨论其功率平衡。

解：用KCL 先计算电阻电流R I ，再根据欧姆定律计算电阻电压，从而得出端电压U ，最后计算功率。

（a ）图中 A I R 862=+=V I U U R R 16822=⨯=⨯==P u =UI=16×2=32WP Is =-6U=-6×16=-96WW I P R R 12882222=⨯=⨯=P u +P Is =P R即输入电路的功率和电源发出的功率都被电阻消耗了。

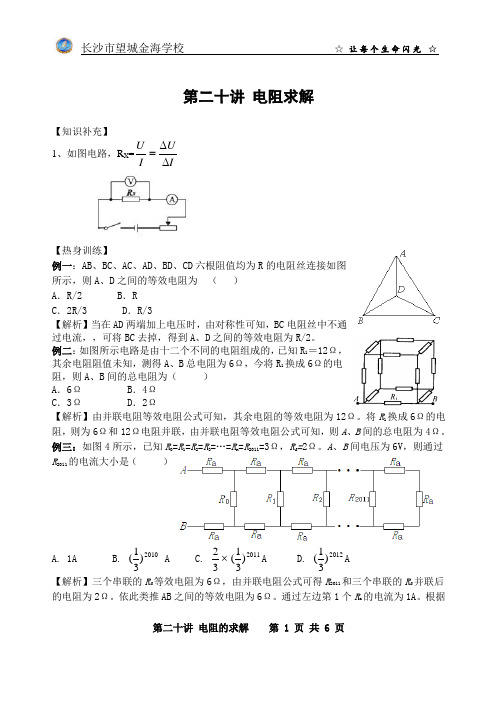
第二十讲 电阻的求解 第 1 页 共 6 页第二十讲 电阻求解【知识补充】1、如图电路，R X =IU I U ∆∆=【热身训练】例一：AB 、BC 、AC 、AD 、BD 、CD 六根阻值均为R 的电阻丝连接如图所示，则A 、D 之间的等效电阻为 （ ）A ．R/2B ．RC ．2R/3D ．R/3【解析】当在AD 两端加上电压时，由对称性可知，BC 电阻丝中不通过电流，，可将BC 去掉，得到A 、D 之间的等效电阻为R/2。

例二：如图所示电路是由十二个不同的电阻组成的，已知R 1＝12Ω，其余电阻阻值未知，测得A 、B 总电阻为6Ω，今将R 1换成6Ω的电阻，则A 、B 间的总电阻为（ ）A ．6ΩB ．4ΩC ．3ΩD ．2Ω【解析】由并联电阻等效电阻公式可知，其余电阻的等效电阻为12Ω。

将R 1换成6Ω的电阻，则为6Ω和12Ω电阻并联，由并联电阻等效电阻公式可知，则A 、B 间的总电阻为4Ω。

例三：如图4所示，已知R 0=R 1=R 2=R 3=…=R n =R 2011=3Ω，R a =2Ω。

A 、B 间电压为6V ，则通过R 2011的电流大小是（ ）A. 1AB. 2010)31( A C. ⨯322011)31( A D. 2012)31( A 【解析】三个串联的R a 等效电阻为6Ω，由并联电阻公式可得R 2011和三个串联的R a 并联后的电阻为2Ω。

依此类推AB 之间的等效电阻为6Ω。

通过左边第1个R a 的电流为1A 。

根据并联电阻分流原理，通过R0的电流为23A，通过左边第2个R a的电流为13A。

同理，通过R1的电流为23×13A，通过左边第3个R a的电流为13×13A。

通过R2的电流为23×（13）2A，通过左边第4个R a的电流为13×13×13A。

···。

依此类推，通过R2011的电流为322011)31( A ，选项C正确。

【中考物理】2023届第一轮复习分类专题—电流、电压、电阻（基础篇）1.小明利用图甲所示的电路探究“通过导体的电流与电阻的关系”，根据实验的数据绘出了1I﹣图像，如图乙所示。

分析图像可知，当导体的电阻为＿＿＿Ω时，通过它的电流为R0.2A；当电流分别为0.25A和0.5A时，接入电路的导体的电阻之比为＿＿＿＿＿＿；实验过程中，小明控制导体两端的电压为＿＿＿＿V.2.某同学在“探究通过导体的电流与电阻的关系”时，他用图甲所示的电路进行实验，实验中R 2.5V电阻两端的电压始终保持不变，电路中仪表均完好无损。

a（1）某同学将最后一根导线接入滑动变阻器的A接线柱后就完成电路的连接，该同学连接过程中存在的问题是___________；P（2）连接好电路后闭合开关，移动滑动变阻器的滑片，电压表有示数，电流表无示数，则电路故障的原因可能是___________；（3）排除故障后，某同学将不同阻值的电阻接入电路进行实验，某次实验时电流表的示数如RΩ图乙所示，此时电阻的阻值为___________；R10Ω15Ω（4）在实验过程中，当把电阻由更换为时，滑动变阻器接入电路中的电阻应___________（选填“变大”“变小”或“不变”）。

3.用如图所示电路探究电流与电阻的关系，电源电压不变，电阻有5Ω、10Ω、15Ω、20Ω。

连接电路闭合开关，发现电流表无示数，电压表示数接近电源电压为了找出故障，把导线M的一端从接线柱a移开，分别连到接线柱b和c上，发现两表指针位置均和之前一样，进一步检查发现电流表完好，则电路的故障是___________排除故障后，将不同阻值的电阻分别接入电路，移动滑片记录的数据如下表：实验次数1234电阻/Ω5101520电流/A0.400.200.130.10分析表中数据，实验中电阻两端的电压为___________V，实验得出的结论是___________。

4.在探究“电流与电阻的关系”实验中，如图甲所示。

图2 电阻测量实验题归类例析伏安法测电阻是欧姆定律的重要应用，也是中考考查的重点，命题内容主要有：实验原理，仪器、器材的选择，电压表和电流表的用法及读数，滑动变阻器的连接和作用，电路图及实物图的连接，操作步骤，记录、分析数据等。

笔者对2007年各省、市中考物理试题分析发现，根据电路图或具体要求连接实物图，电压表或电流表的读数，实验过程中电路故障的排除等都是命题频率较高的知识点，而且考查的综合性很强，往往一道题同时覆盖以上多个考查点。

下面，笔者对各个考查点进行归类例析，希望广大师生在学习加以注意。

一、连接电路1．把电路图（或实物图）补充完整例1：在用“伏安法”测量小灯泡工作时的电阻Rx 的实验中，使用下列器材进行实验： A ．电流表一个(量程0～0.6A ，0～3A)； B ．电压表一个(量程0～3V ，0～15V)； C ．串联的干电池三节；D ．滑动变阻器R(阻值为0～12Ω)；E ．待测小灯泡Rx ，(阻值约为6Ω)；F ．开关一个；导线若干。

则：（1）该实验依据的原理是 (用课本中的字母表示)；并根据题意在右上边的图1虚线方框内画出所需要的实验电路图(其中部分已画好)。

将实物图（2）根据所画的电路图，用铅笔．．画线代替导线（图2）连接完整(其中部分导线已连接好)。

解析：（1）“伏安法”是测量小灯泡电阻最基本的方法，它的原理是用电压表测出小灯泡两端的电压，用电流表测出小灯泡中的电流，根据欧姆定律计算出小灯泡的电阻值。

该题考查了学生用“伏安法”测电阻的基本技能，难度不大，须注意的是题中要求“用课本中的字母表示”，即IU R =。

题中给出了部分电路，在此基础上学生很容易画出完整的电路图。

（2）在连接实物之前，必须先确定电流表、电压表的量程。

由于电源是三节干电池串联，电压为4.5V ，许多同学可能会选择电压表0～15V 的量程，但是，当小灯泡两端电压为4.5V 时，电流表示数A75.06V 5.4RxU I =Ω==，即电流表须选择0～3A 量程，这样，电流表指针偏转的角度很小，误差较大，所以电压表选择0～15V 量程不是最佳选择。

第三章电阻电路的一般分析本章内容：1．电路的图及KCL和KVL独立方程数 2．支路分析法3．网孔分析法4．回路电流法5．结点分析法本章重点：主要学习电阻电路的方程建立及一般分析方法（支路分析法、网孔分析法、节点分析法、回路分析法。

其中，支路分析法是最基本的方法）。

本章难点：独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识，学习应用图的方法选择电路方程的独立变量一、电路的图（G）数学上的图：是边（支路）和顶点（结点）的集合，每一条边都连到相应的顶点上，边是抽象的线段，当移去边时，顶点保留，当移去顶点时，应将顶点所连的支路移走。

1．电路的图（连通图G）：是将支路画成的抽象线段形成的节点和支路的集合，结点相对于数学图的顶点，支路相当于数学图中的边。

支路是实体。

KVL和KCL 与元件的性质无关，故可用图讨论其方程。

2．无向图：画出的没有方向的图为无向图3．有向图：画出的有方向的图为有向图4．连通图：任意两个结点之间至少有一条支路或路径时的图为连通图。

二、电路的图的画法（有几种，其中简便的画法）1．一般将电阻和电压源串联的组合，电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。

如（b）2．指定电流和电压的参考方向，一般选关联参考方向。

如图（c）(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数（n个结点电路，KCL的独立方程是n-1个）将电路的有向图，结点和支路加以编号，如下图，对结点①②③④列写KCL 方程有由于每条支路与两个结点相联，其电流从一个节点流出，从另一个结点流入，一正，一负（从表达式可见），将上面4个方程相加，等式两边为0，说明4个方程不是独立的；将上面3个方程相加，等式两边不为0，说明3个方程是独立的。

可见，n个结点电路，n-1个结点的KCL方程是独立的一、KVL的独立方程数（b条支路，n个结点，KVL为b-(n-1)个）KVL的独立方程数等于独立回路数独立回路数等于基本回路数，回路与支路的方向无关，以无向图讨论。

欧姆定律-电路故障问题重难点易错点解析题一：我们做电学实验时应学会检查和排除电路故障。

如图是一位同学研究串联电路电流、电压特点的电路图。

当闭合开关时，L 1亮，L 2不亮，A 和V 均有示数，故障的原因可能是（ ）A ．L 1短路B ．L 2短路C ．L 1断路D ．L 2断路 VAL 1L 2S题二：如图所示的电路中，电源电压不变，闭合电键S 后，灯L 1、L 2都发光。

一段时间后，其中一灯突然熄灭，而电流表、电压表的示数都不变，则产生这一现象的原因是 （ ）A ．灯L 1短路B ．灯L 2短路C ．灯L 1断路D ．灯L 2断路 VAL 1L 2S金题精讲题一：如图所示电路，两盏相同的电灯在闭合开关后都能发光。

过了一会儿，两盏电灯突然同时都不亮了，且电压表和电流表的示数均变为零。

如果电路只有一处故障，则故障可能是（ ）A ．电灯L 1断路B ．电灯L 2断路C ．电灯L 1短路D ．电灯L 2短路题二：如图所示的电路中，只有一处有导线断开的故障，现用电压表先后测得a 、d 两点之间电压为3V ，b 、d 之间的电压也为3V ，测a 、c 两点电压时，电压表的指针不偏转，由此可知断开点在（ ）A ．cd 之间B ．ab 之间C ．bc 之间D ．R 1所在支路上 V A L 1L 2SR 题三：如图所示，电源电压一定。

关于电路的工作情况，下列说法正确的是（ ）A 、只闭合S 1时，两只灯泡是串联的B 、若先闭合S 1，再闭合S 2，电压表读数不变、电流表读数变大C 、若电压表和电流表位置对调，闭合S 1 、S 2后，则两表都被烧坏D 、若灯L 1被短路，闭合S 1 、S 2后，灯L 1不亮，灯L 2亮，电流表损坏 L 1L 2S 1S 2思维拓展题一：AB 和CD 是完全相同的两条带有绝缘皮的导线，它们并行地埋设在相距2 km 的甲、乙两地之间。

由于两导线之间某处的绝缘外皮受到损伤，而发生了漏电现象（即相当于两根导线之间在漏电处连接了一个电阻。

1关于发光二极管和电阻的问题，要实际应用的，确定答案的来悬赏分：100 - 解决时间：2008-5-19 18:03在学做灯牌，上面有白色，绿色，红色，黄色四种颜色的LED，现在是白色大约180个串联，准备用8节5号电池供，但是不知道该串多少的电阻，白色的电压是3.2-3.4绿色大约70个串联，准备4节五号电池供，同求该串多少电阻，绿色电压不知道红色和黄色准备一起串联，大约50个，4节5号电池供，也想知道该串多少电阻，电压不知，红色黄色的电压应该比较低，因为不加任何电阻的时候直接烧坏了，而白色不会直接烧坏但是会很快发烫变暗，绿色可以一直点着，不会变暗，但是时间长了会闪。

要尽快回复问题补充：不好意思，我实在是不懂电路，昨天别人看了我的板后说我是做的并联，所以问题有所改动，并联180个3V左右的二极管，准备用8节5号电池供，要多少限流电阻，电阻我不打算一个一个接，准备直接在电池正极串一个比较大的，现在这边只有1/2W的150欧的电阻，只要告诉我要串多少个就行了，红色，黄色，绿色以此类推~提问者：一字记之曰腐- 二级最佳答案兄弟，您这是要拿LED去炸大楼吗？五号电池串联的电压是6V，并联是1.5V,在电池串联的情况下，最多能带两个串联的LED啊！你这么做是行不通的无论怎么算，你要用几节电池带这么多LED，是不可能的。

建议你用个小电瓶之类的东西，LED这东西很费电的，拿白的来说，压降按3V算，电流按25mA算，3*0.025*180=18.5W，我们平常用的接220V的电灯泡也不过几十来瓦，就算干电池能带的话，电会瞬间放空的。

其实，你可以这样做：楼上的答案引入的电阻太大，损耗太大，更费电，我有更好的办法：白色LED:用8节电池，电压是8*1.5=12V把180个LED分成4组，每组45个，把每组的45个LED并联，然后再把这四个组串联起来，用12V也可以带起来，每个LED上的电压正好是3V，用不着电阻，没有一点多余的损耗。

初中物理电压电阻(一)解题方法和技巧及练习题及解析一、电压电阻选择题1．如图所示电路，当开关S闭合后，L1、L2均能发光，电流表与电压表均有示数。

过一会儿，两灯都不发光，电流表与电压表的示数均变为零，电路中可能发生的故障是（）A.L1灯丝断了 B.L1被短路了 C.L2灯丝断了 D.L2被短路了【答案】A【解析】【解答】如果L1灯丝断了，两灯将都不发光，和题目中所叙述的现象一致，A符合题意；如果L1被短路了，L1将不会发光，B不符合题意；如果L2灯丝断了，此时电压表有示数，C不符合题意；如果L2被短路了，电流表会有示数的，D不符合题意；故答案为：A.【分析】两灯都不亮，且电流表无示数，电路是断路，电压表也无示数，从而判断电路故障.2．在如图a的电路中，当闭合开关后，两个电压表指针偏转均为图b所示，则电阻R1和R2两端的电压分别（）A.1.2V4.8VB.6V1.2VC.1.2V6VD.4.8V1.2V 【答案】D【解析】【解答】分析电路图是串联电路，V1测量电源电压，V2测量R2的电压，根据串联电路中总电压等于各用电器电压之和的规律，V1的示数要大于V2示数，所以选用0-15V读数，为6V，V2选用0-3V读数，为1.2V，则R1的电压为6V-1.2V-4.8V，D符合题意，ABC不符合题意。

故答案为：D.【分析】根据串联电路中电压规律判断电压表选用的量程，并计算各用电器的电压的大小。

3．超导现象是20世纪的重大发现之一，科学家发现某些物质在温度很低时，如铅在﹣265.95℃以下，电阻就变成零．若常温下超导体研制成功，则超导体适合做（）A.保险丝B.输电线C.滑动变阻器的线圈D.电炉丝【答案】B【解析】【解答】解：A、保险丝的作用，是当电流过大时，自动熔断来保护电路．B、用超导体做输电线，可以有效地减小电能的损耗．C、线圈的电阻较大，通过滑片位置的改变可以进行调节．D、电炉丝需要电阻较大的材料，才能发出较多的热量．故选B．【分析】由于超导体的电阻为0，则没有内能的产生，不会放热．根据这一特点，分析选项．4．下列教材中的探究实验，不需要控制电流一定的是（）A.探究导体电阻与长度的关系B.探究通电导体产生的热量与电阻的关系C.探究电功与电压的关系D.探究电磁铁磁性强弱与线圈匝数的关系【答案】A【解析】【解答】A、电阻与导体的长度、材料、横截面积和温度有关，与电流大小无关，探究与长度的关系，不用控制电流一定，A符合同意；B、由Q=I2Rt可知，通电导体产生的热量与电路中的电流、导体的电阻和通电时间有关，要探究热量与电阻的关系，需控制电流和通电时间一定，B不符合题意；C、由W=UIt可知，要探究电功与电压的关系，需使电流和通电时间一定，C不符合题意；D、电磁铁磁性强弱与电流大小和线圈匝数有关，要探究电磁铁磁性强弱与线圈匝数的关系，需控制电路中的电流相同，D不符合题意．故答案为：A．【分析】（1）控制变量法：在研究和解决问题的过程中，对影响事物变化规律的因素或条件加以人为控制，使其中的一些条件按照特定的要求发生变化或不发生变化，最终解决所研究的问题；（2）探究的物理量与电流及其他因素有关，探究过程中需控制电流一定，根据各项分析即可得出结论．5．相同材料制成的两导体并联在同一电路中，若通过两导体的电流相同，则（）A.长度较长的导体，其横截面积一定小B.长度较长的导体，其横截面积一定大C.长度较长的导体，其横截面积可能小D.两导体的长度、横截面积一定相同【答案】B【解析】【解答】A CB．电阻是导体对电流的阻碍作用，是导体本身的一种特性；其大小与导体的材料、长度、横截面积、温度有关，电阻相等时，其他条件相同，长度越长横截面积越大，AC不正确，B符合题意；D.导体电阻的大小由导体的材料、长度和横截面积决定，同时还受温度的影响，D不正确；故答案为：B.【分析】决定电阻大小的因素：导体的电阻是导体本身的一种性质，它的大小决定于导体的材料、长度、横截面积和温度.（电阻与加在导体两端的电压和通过的电流无关）6．如图甲所示，电源电压保持不变，闭合开关 S ，滑动变阻器的滑片 P 从 b 点滑动 a 点的过程中，两电压表示数随电流表示数变化的图线如图乙所示．下列叙述正确的是（ ）A. 电源电压为 14VB. 图乙中 dc 是表示电压表的示数随电流表示数变化的图线C. 滑片从 b 点滑动 a 点的过程中，电路消耗的总功率最大值为D. 滑片在 a 点时，内电阻 R 消耗的电能为【答案】 C【解析】【解答】A 、滑动变器的滑片 P 在 b 点时，电路中的电流最小，此时两个电压表的示数分别为 12 V 、2 V ，则两个电压表的示数之和为 ；由于电路中滑动变阻器 R 1、电阻 R 、R 2 是串联，此时电源电压一定大于两个电压表的示数之和 14 V ，A 不 符合题意；B 、滑动变器的滑片 P 从 b 点滑到 a 点的过程中，滑动变阻器连入电路的电阻变小，电路中的电流变大，根据串联电路的分压原理可知：滑动变阻器两端的电压变小，根据欧姆定 律可知 R 2 两端的电压变大；所以图乙中 dc 是表示电压表 V 1 的示数随电流表示数变化的图 线，ec 是表示电压表 V 2 的示数随电流表示数变化的图线，B 不符合题意；C 、从“U -I”关系图象可以看出，滑片 P 在 b 点时电流 I b =1 A ，U 1=12 V 、U 2=2 V ； 滑片 P 在 a 点时电流 I a =3 A ，U 1′=6 V 、U 2′=6 V ； 根据欧姆定律和串联电路的电压特点可得电源电压：即： ，解得： R=1 Ω ，则； 所以电路消粍的总功率最大值，C 符合题意.D 、滑片在 a 点时，10 s 内电阻 R 消耗的电能：，D 不符合题意.故答案为：C.【分析】根据电路的连接和滑片移动情况，判断电表的变化，利用电压、电流图像中的数 据计算电阻和电功率.7．关于电流、电压和电阻，下列说法正确的是（ ）A.金属导体中的电流方向与自由电子的定向移动方向相同B.导体中通过的电流越大，它的电阻越小C.两灯泡比较，亮度大的灯泡通过的电流大D.导体两端电压越大，通过该导体的电流就越大【答案】D【解析】【分析】A、正电荷的定向移动方向是电流的方向，电子带负电，电流方向与电子的定向移动方向相反；B、导体电阻由导体材料、长度、横截面积决定，与通过它的电流无关；C、灯泡的亮度由灯泡的实际功率决定，亮度大的灯泡流过的电流不一定大；D、根据公式I=分析答题．【解答】A、电流的方向与正电荷的定向移动方向相同，电子带负电，金属导体中的电流方向与自由电子的定向移动方向相反，故A错误；B、导体电阻由导体材料、长度、横截面积决定，与通过它的电流无关，故B错误；C、两灯比较，实际功率大的灯泡亮度大，由P=UI知，功率大，可能是电流较大，也可能是电压较大，故C错误；D、导体电阻由导体材料、长度、横截面积决定，当导体电阻一定时，由I=知，导体两端的电压越大，通过该导体的电流越大，故D正确；故选D．【点评】本题考查了电流的方向、影响导体电阻大小的因素、影响灯泡亮度的因素、对欧姆定律的理解等问题，是一道基础题．8．如图所示电路，电源电压保持不变，三只电表均完好．开关S闭合后，发现只有一个电表的指针发生偏转，若电路中只有一个灯泡出现了故障，则可能是（）A.灯L1断路 B.灯L1短路 C.灯L2断路 D.灯L2短路【答案】C【解析】【解答】A.闭合开关后，若L1断路，则V1、V2测量电源电压，都有示数，A不符合题意；B.若L1短路，则电流表A有示数，V2有示数，B不符合题意；C.若L2断路，则灯泡上没有电流，只有V2有示数，C符合题意；D.若L2短路，则三电表都有示数，D不符合题意。

江苏省XY中等专业学校2022-2023-1教案编号：
教学内容
例1：一漆包线（铜线）绕成的线圈，15οC时阻值为20 Ω，问30οC时此线圈的阻值R为多少？
例2：习题（《电工基础》第2版周绍敏主编）
4.计算题(3)。

第四节欧姆定律
一、欧姆定律
1．内容：导体中的电流与它两端的电压成正比，与它的电阻成反比。

I =
R
U
2．单位：U－伏特（V）；I－安培（A）；R－欧姆（Ω）。

注：
(1) R、U、I须属于同一段电路；
(2) 虽R =
R
U，但绝不能认为R是由U、I决定的；
(3) 适用条件：适用于金属或电解液。

例3：给一导体通电，当电压为20 V时，电流为0.2 A，问电压为30 V时，电流为多大？电流增至1.2 A时，导体两端的电压多大？当电压减为零时，导体的电阻多大？
教学
环节
教学活动内容及组织过程个案补充
教学内容
二、伏安特性曲线
1．定义：以电压为横坐标，电流为纵坐标，可画出电阻的U－I关系曲线，叫电阻元件的伏安特性曲线。

2．线性电阻：电阻元件的伏安特性曲线是直线。

K =
U
I；R =
R
U =
K
1
板书设计一、电阻
二、电阻与温度的关系
三、欧姆定律
四、伏安特性曲线
教后札记。

物理九年级上册补充知识点本文将为大家介绍一些九年级物理上册的补充知识点，帮助同学们更好地理解和掌握物理知识。

一、电路中的电阻1. 电阻的定义：电阻是电流通过时电路中的阻碍物，单位是欧姆（Ω）。

2. 串联电阻的计算：若电路中有多个串联电阻R₁、R₂、R₃...，则总电阻为它们的和，即R=R₁+R₂+R₃+...3. 并联电阻的计算：若电路中有多个并联电阻R₁、R₂、R₃...，则总电阻为它们的倒数之和的倒数，即1/R=1/R₁+1/R₂+1/R₃+...二、简单机械1. 动力和功：动力是改变物体状态的能力，单位是牛顿（N）；功是力对物体的作用，单位是焦耳（J）。

2. 机械效率：机械效率是工作输出与能量输入之比，常用百分数表示，公式为η=W_out/W_in×100%。

3. 杠杆原理：杠杆是由两个力臂和一个转动支点组成的简单机械，力臂愈长，所需的力就愈小。

三、光学1. 光的折射定律：当光从一种介质进入另一种介质时，入射角i、折射角r、两种介质的折射率n₁和n₂之间有一个关系sin(i)/sin(r)=n₂/n₁。

2. 反射和折射：反射是光线遇到边界时产生的现象，折射是光线在不同介质中传播速度和方向的改变。

3. 凸透镜的成像规律：物体离凸透镜越近，成像距离越大；物体越远离凸透镜，成像距离越小。

四、声学1. 声音的传播：声音是由物体振动产生的机械波，需要介质传播，无法在真空中传递。

2. 声音的特性：声音的频率决定了声音的音调，频率高则音调高；声音的幅度决定了声音的响度，幅度大则响度大。

五、热学1. 热传导：热传导是由高温物体传递热量到低温物体的方式，常见的热传导材料是金属。

2. 热膨胀：物体随温度升高而体积增大的现象称为热膨胀，常见的热膨胀材料是铁、铝等。

六、电磁感应1. 法拉第电磁感应定律：当导体磁通发生变化时，导体两端将产生感应电动势，大小与磁通变化率成正比。

2. 楞次定律：根据楞次定律，感应电动势的方向总是使电流产生的磁场与磁通变化抵抗。

物理中的电路和电阻解题技巧与方法电路和电阻是物理学中的重要概念，对于解题和实际应用都具有重要意义。

本文将介绍一些物理中电路和电阻解题的技巧和方法，帮助读者更好地理解和应用。

一、串联和并联电路在电路中，常见的连接方式有串联和并联。

串联电路指的是电流依次通过多个电阻，而并联电路指的是电流分流经过多个电阻。

解串联电路的关键是计算总电阻。

总电阻等于各个电阻之和，即R_total = R1 + R2 + R3 + ...。

而电流在串联电路中保持不变，所以可以使用欧姆定律来计算电流大小。

解并联电路的关键是计算总电阻的倒数。

总电阻的倒数等于各个电阻倒数之和的倒数，即1/R_total = 1/R1 + 1/R2 + 1/R3 + ...。

而并联电路中，电压大小相同，所以可以使用欧姆定律来计算电流大小。

二、电阻的串并联组合在实际情况中，常常遇到电路中既串联又并联的情况。

解决这类问题的关键是拆分电路，将复杂的电路分解为简单的串联和并联电路。

首先，找到串联电阻和并联电阻，然后计算它们的总电阻。

接下来，根据总电阻的值，再回到原始电路中计算电流或电压大小。

三、套用基本公式在解决电路和电阻问题时，掌握一些重要的基本公式是必要的。

1. 欧姆定律：U = I * R，其中U代表电压，I代表电流，R代表电阻。

2. 等效电阻：当电路中出现复杂的串并联组合时，可以通过计算等效电阻来简化问题。

3. 线性电阻：线性电阻满足欧姆定律，即电流和电压成正比。

4. 热效应：电阻通电会产生热量，可以通过热效应解决一些相关问题。

四、应用解题方法在实际解题过程中，需要根据具体情况选择合适的方法和技巧。

1. 利用电路图：通过电路图将问题可视化，更好地理解电路结构和电流路径。

2. 正确标记符号和数值：在计算过程中，要仔细标记电流的方向和大小，电压的正负极性，以及电阻的数值。

3. 假设和简化：在复杂的电路问题中，可以进行一些假设和简化，将问题分解为较小的部分。

含电阻电路问题解题方法方法一：组合电路分析法组合电路分析法是一种基本的解题方法。

当电路中存在多个电阻时，可以通过将电阻按一定规则进行组合，简化电路分析过程。

常用的组合电路有串联电阻和并联电阻。

- 串联电阻：将电路中的多个电阻依次连接起来形成一个长电阻，然后通过计算总电阻和总电流，再根据欧姆定律计算各电阻上的电压。

- 并联电阻：将电路中的多个电阻同时连接到同一个节点上，形成并联关系。

通过计算等效电阻和总电流，再根据欧姆定律计算各电阻上的电流。

方法二：节点电流法节点电流法是一种常用的电路分析方法。

它通过在电路中选取若干个节点，并假设在每个节点上的电流，来建立节点电流方程组。

通过求解方程组，可以得到各节点的电流值。

- 选取参考节点：在电路中选取一个节点作为参考节点，通常选择接地点或电源的负极作为参考节点。

- 确定节点电流：对于每个节点，假设一个未知的电流方向和大小，并列写节点电流方程。

- 求解方程组：根据电流守恒定律和欧姆定律，列出各节点电流方程，并解方程组求解未知电流。

方法三：网孔电流法网孔电流法也是一种常用的电路分析方法，适用于复杂的电路。

它通过选取若干个电流未知的网孔，并沿着闭合的路径写出网孔电流方程。

通过求解方程组，可以得到各网孔的电流值。

- 选取网孔路径：在电路中选取合适的路径，形成闭合回路。

- 确定网孔电流：对于每个网孔，假设一个未知的电流方向和大小，并列写网孔电流方程。

- 求解方程组：根据电流守恒定律和欧姆定律，列出各网孔电流方程，并解方程组求解未知电流。

这些方法只是解题的基本思路，具体问题具体分析。

在解题过程中，还需要根据具体情况选择恰当的方法和技巧。

希望本文介绍的方法对您解决含电阻电路问题有所帮助。

阻容消火花电路 -回复1、阻容串联电路一个常用的作用就是用来消火花，如下图所示：S1 为开关（一般电路中为继电器的触点）C1 为电容，0.47uFR1 为电阻，100欧M 为直流电机（感性负载，有线圈）2、打火原理分析：电机M 为直流电机，当开关S1 断开时，由于直流电机线圈的电感，会产生一个较大对的感生电动势，这个电动势，这个电动势会通过直流电源V+内部加在开关两端，击穿空气，产生电火花，从而损伤S1的两个触点。

长期的这样打火会导致S1 接触不良，影响产品的性能。

，所以要加入RC消火花电路，感生电动势的活动路径如下图所示：3、消火花原理分析：开关S1断开的瞬间，由于电容C1 和电阻并联在触点的两端，加在开关，S1 上的电动势就等于加在RC串联电路上，这一电动势通过R1 给C1充电，C1吸收了打火的的电能,使S1两端的电动势大大降低，从而达消火花的作用。

4、电阻R1的作用：由于对C1的充电电流是流过R1 的，所以R1 具有消耗充电电能的作用，这样充电的的电能就能被电阻以热能的方式消耗掉。

5、原件参数：电容一般取：0.47UF 电阻 100R6、另一种消火花电路：只使用了电容，而未使用电阻阻容并联电路应用1、阻容并联的一种应用如下图所示的LED 驱动电路：其原理为：分为连个阶段1、上电瞬间：利用电容两端电压不能突变的特点，可以理解为电容在上电瞬间为短路状态，把电阻R1短路掉，此时电流比较大，能够使三极管能够快速的导通，从而达到加速的作用2、稳态时：电容开路，电流经过电阻R1到基极，保持三极管的开启状态。

我们仿真看下实际效果，先看下没有加速电容的情况：VG1 为幅值为5V 频率为1K的方波然后来看下没有加速电容时，三极管基极的波形：可以看出三极管基极和发射极间的电压为0.7v。

再来看看有加速电容的情况：为了有比较明显的效果，我这里用的是一个10nF的电容;来看看现在的波形：（理解这个加速原理，首先要理解微分电路）思考：上电瞬间，R1被短路，电流很大会烧坏三极管么？这个问题是我之前也比较疑惑地，现在想想应该不会，因为上电到稳态的这个过程时间是比较短的，应该不至于烧坏三极管（暂且先这么理解，后面再查资料确认）2、下面这种RC应用电路起到的作用也是加速，只不过是加速继电器的快速吸合：（图片引用自：电工学网）E 为直流电源（+15V）S 为开关R 为电阻C 为电容KA 为继电器（+12V）原理分析：（这里只分析原理，暂且不管S 是否有消火花电路，和继电器是否有续流回路），同样也是分两个状态来分析：1、上电瞬间：电容C两端的电压不能突变，可以看做短路，所以R1 就被短路掉了，直流电源的15V电压全部加在12V继电器上，导致继电器能够较快的吸合，从而达到加速的作用。