四元数与欧拉角之间的转换

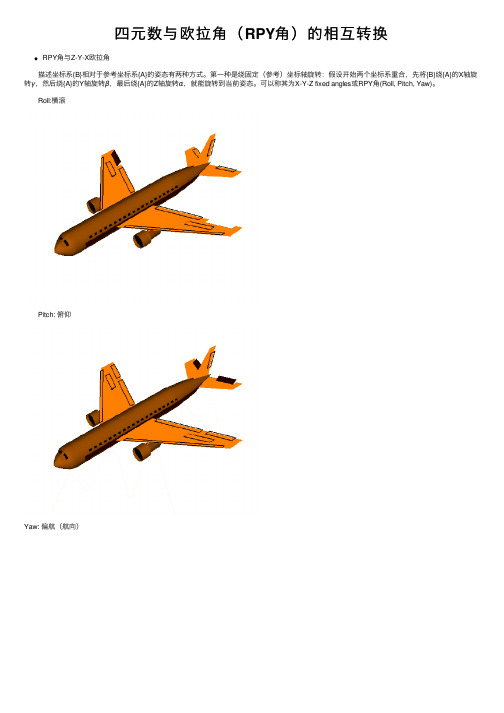
四元数与欧拉⾓（RPY⾓）的相互转换RPY⾓与Z-Y-X欧拉⾓ 描述坐标系{B}相对于参考坐标系{A}的姿态有两种⽅式。

第⼀种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转γ，然后绕{A}的Y轴旋转β，最后绕{A}的Z轴旋转α，就能旋转到当前姿态。

可以称其为X-Y-Z fixed angles或RPY⾓(Roll, Pitch, Yaw)。

Roll:横滚 Pitch: 俯仰Yaw: 偏航（航向） 由于是绕固定坐标系旋转，则旋转矩阵为（cα is shorthand for cosα, sα is shorthand for sinα,and so on.）R XYZ(γ,β,α)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 另⼀种姿态描述⽅式是绕⾃⾝坐标轴旋转：假设开始两个坐标系重合，先将{B}绕⾃⾝的Z轴旋转α，然后绕Y轴旋转β，最后绕X轴旋转γ，就能旋转到当前姿态。

称其为Z-Y-X欧拉⾓，由于是绕⾃⾝坐标轴进⾏旋转，则旋转矩阵为：R Z′Y′X′(α,β,γ)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 可以发现这两种描述⽅式得到的旋转矩阵是⼀样的，即绕固定坐标轴X-Y-Z旋转(γ,β,α)和绕⾃⾝坐标轴Z-Y-X旋转(α,β,γ)的最终结果⼀样，只是描述的⽅法有差别⽽已。

In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.Axis-Angle与四元数 绕坐标轴的多次旋转可以等效为绕某⼀转轴旋转⼀定的⾓度。

四元数和欧拉角
四元数与欧拉角：
1、四元数
四元数是一种数学物体，它由ONE个实部和THREE个虚部组成。

实部是非负实数，其余的THREE个部分是虚数。

四元数的表达式可以表示为：Q=a+bi+cj+dk (a、b、c、d是实实部）。

它们有助于以三维空间中的方式表示方向和旋转。

离散空间中表示四元数，当旋转发生时，它们保持一致。

2、欧拉角：
欧拉角是一种三维旋转矢量，可以用来表示不同方向之间的关系。

它将旋转分成THREE个不同的轴，分别为X轴、Y轴和Z轴。

每个轴都有自己的旋转角度，比如X轴有X角度，Y轴有Y角度，Z轴有Z角度。

欧拉角的表达式可以写作：[X,Y,Z]，其中X、Y、Z分别表示每个轴的旋转角度。

欧拉角与四元数之间的差别在于欧拉角表示的是不同方向间的关系，而四元数表示的是不同方向的空间旋转。

可以说四元数和欧拉角均是用来表示旋转有关信息的，但是又是有所差别的。

下面我们来总结下它们两者之间的区别：
1）表示方式不同：欧拉角表示的是不同方向间的关系，而四元数是表
示不同方向的空间旋转；
2）用途不同：欧拉角被广泛应用于3D图形学处理领域，可以很方便
地实现3D模型的几何变换；而四元数方便地表示空间任意的旋转变换，是用来表达机器人的运动控制中的基本角度表示方式；
3）值域不同：欧拉角的值域为[0,2π)，而四元数的值域为[-1,1]；
4）叠加角度表示方法不同：四元数是可以用乘法表达累加旋转；而欧
拉角只能使用加法来表达叠加旋转。

ros 欧拉角转换为四元数ROS（Robot Operating System）是一个用于机器人开发的开源框架，它提供了一系列的工具和库，使得机器人的软件开发更加便捷和高效。

在ROS中，欧拉角是一种常用的表示姿态的方法，而四元数则是另一种常用的姿态表示方法。

本文将介绍如何将ROS中的欧拉角转换为四元数。

我们需要了解欧拉角和四元数的基本概念。

欧拉角是指用三个旋转角度表示姿态的方法，常用的欧拉角顺序有XYZ、ZYZ等。

然而，欧拉角存在万向锁问题，即在某些情况下，无法准确表示姿态，因此在一些应用中不太适用。

相比之下，四元数是一种更加稳定和有效的姿态表示方法，它由一个实部和三个虚部组成，可以准确表示任意姿态。

在ROS中，使用tf库提供了欧拉角和四元数之间的转换函数。

首先，我们需要安装tf库，可以通过以下命令在终端中进行安装：```sudo apt-get install ros-<distro>-tf```其中，`<distro>`是你所使用的ROS版本的名称，比如`melodic`或`noetic`等。

安装完成后，我们就可以在ROS中使用tf库进行欧拉角和四元数的转换了。

下面以一个具体的例子来说明如何将ROS中的欧拉角转换为四元数。

假设我们有一个机器人，并且已经通过传感器获取了机器人的姿态信息，其中包括了机器人的欧拉角。

我们可以通过以下步骤将欧拉角转换为四元数：1. 导入所需的库文件：```pythonimport rospyfrom tf.transformations import euler_from_quaternion, quaternion_from_euler```2. 获取欧拉角信息：```pythonroll = 0.1 # 欧拉角的roll分量pitch = 0.2 # 欧拉角的pitch分量yaw = 0.3 # 欧拉角的yaw分量```3. 将欧拉角转换为四元数：```pythonquaternion = quaternion_from_euler(roll, pitch, yaw)```4. 输出转换结果：```pythonprint("转换后的四元数为：", quaternion)```通过以上步骤，我们就可以将ROS中的欧拉角转换为四元数了。

四元数与旋转一．四元组基础Q(x,y,z,w)，其中x，y，z用来确定旋转轴，w为旋转的角度Q=w+xi+yj+zk，i，j，k为三个虚轴的单位分量I*j=kJ*k=i;K*i=j;叉乘：c=a × b=| i j k||a1 b1 c1||a2 b2 c2|=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)c也为一个向量，且c的长度为|a||b|sin(theta)，垂直于a和b所在的平面，方向由右手法则来判定，用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向1．四元组相乘：Q1=w1+x1i+y1j+z1k=(w1,v1)Q2=w2+x2i+y2j+z2k=(w2,v2)Q1*Q2=(w1*w2-<v1,v2>,w1*v2+w2*v1+v1xv2)( w1+x1i+y1j+z1k)*( w2+x2i+y2j+z2k)=w1*w2-x1*x2-y1*y2-z1*z2+(W1*x2+x1*w2+y1*z2-z1-y2)i+(y1*w2+w1*y2+z1*x2-x1*z2)j+(w1*z2+z1*w2+x1*y2-y1*x2)k对于其中的轴部分，假如v1//v2，则有v1 x v2=0（平行向量的叉乘结果为0）2．四元组的点乘，点乘积为数值：Q1.*Q2=w1*w2+<v1,v2>=w1*w2+x1*x2+y1*y2+z1*z2;3．数乘s为一实数，q为四元组，则有sq=qs4．共轭p=(w,v)，则p*=(w,-v)(pq)*=q*p*N(q)=w2+x2+y2+z2q-1=q*/N(q)--------------- 显然可得qq-1=(1,0)二．使用四元数旋转向量假如有一表示向量的四元组q=(w,v)，对其应用旋转量p后的结果为：q’=pqp-1=(w,v’)从上可以看出，计算的结果q’的实部和q的实部是相等的，并且有N(v)=N(v’)如果N(q)=1，则可以令q=(cosa,usina)，u也为一个单位向量，则q’是q绕u旋转2a个弧度的结果假如S(q)表示q的实部，则有2S(q)=q+q*2S(pqp-1)= pqp-1+( pqp-1)*=pqp*+(pqp*)*=pqp*+pq*p*=p(q+q*)p*=2S(q)（这里由于p是单位四元数，所以有p-1等于p*）欧拉角到四元数的转换定义pitch, yaw, roll分别为绕X轴、Y轴、Z轴的旋转弧度float p = pitch * PIOVER180 / 2.0;float y = yaw * PIOVER180 / 2.0;float r = roll * PIOVER180 / 2.0;float sinp = sin(p);float siny = sin(y);float sinr = sin(r);float cosp = cos(p);float cosy = cos(y);float cosr = cos(r);this->x = sinr * cosp * cosy - cosr * sinp * siny;this->y = cosr * sinp * cosy + sinr * cosp * siny;this->z = cosr * cosp * siny - sinr * sinp * cosy;this->w = cosr * cosp * cosy + sinr * sinp * siny;normalise();三．使用matlab进行相关计算计算两个向量v1和v2之间的旋转量四元数p，使得v1应用p后到达v2假如v1转到v2的旋转轴为v，旋转角为theta，则q=[v*cos(theta/2) sin(theta/2)] Matlab代码：function q=vector2q(v1,v2)%..normalize....len1=sqrt(v1*v1');len2=sqrt(v2*v2');v1=v1/len1;v2=v2/len2;angle=v1*v2';axis=cross(v1,v2);alen=sqrt(axis*axis');axis=axis/alen;t=acos(angle);t=t/2;q(1)=axis(1)*sin(t);q(2)=axis(2)*sin(t);q(3)=axis(3)*sin(t);q(4)=cos(t);end计算出了q之后，可以获得对应的旋转矩阵，旋转矩阵的计算Matlab里面的矩阵是以列为主顺序的function r=q2rot(q)w=q(4);x=q(1);y=q(2);z=q(3);r=zeros(3,3);r(1,1)=1-2*y*y-2*z*z;r(1,2)=2*x*y+2*w*z;r(1,3)=2*x*z-2*w*y;r(2,1)=2*x*y-2*w*z;r(2,2)=1-2*x*x-2*z*z;r(2,3)=2*z*y+2*w*x;r(3,1)=2*x*z+2*w*y;r(3,2)=2*y*z-2*w*x;r(3,3)=1-2*x*x-2*y*y;r=r';end同时，也可以根据四元数来计算欧拉角function R=q2euler(q)w=q(4);x=q(1);y=q(2);z=q(3);t11=2*(w*x+y*z);t12=1-2*(x*x+y*y);R(1)=atan2(t11,t12);t2=2*(w*y-z*x);R(2)=asin(t2);t31=2*(w*z+x*y);t32=1-2*(y*y+z*z);R(3)=atan2(t31,t32);end计算出来的欧拉角rx，ry，rz，分别为绕X轴、Y轴和Z轴的旋转角，假如有：Rotq=q2rot(q)R=q2euler(q)[rotx roty rotz]=Rotation(R)可以发现Rotq==rotz*roty*rotx从这里可以看出，上面使用四元数这样计算出来的旋转矩阵的旋转顺序分别是X轴、Y轴和Z轴的ra=pi/4;qz=[0 0 -sin(ra) cos(ra)] %绕z旋转-90度qy=[0 sin(ra) 0 cos(ra) ] %绕y旋转90度qyz=qmult(qy,qz)r=q2euler(qyz)上面的r得出的结果为r = -1.5708 0.0000 -1.5708也就是说其几何意义变成先绕X轴旋转-90度，再绕Z轴旋转-90度，而根据qy和qz的相乘我们实际进行的操作却是先绕Z轴旋转-90度，再绕Y轴旋转90度，但是结果却是这两种操作等价，这说明由四元数到欧拉角可以有多个解两个四元数，假如它们的方向是相反的，用它们作用于向量得到的新向量的值仍然相等q1=[0.024666 -0.023954 0.504727 0.862594];arm=[-8.881719 6.037597 -2.36776];q2=-q1;rot1=q2rot(q1);rot2=q2rot(q2);v1=rot1*arm'v2=rot2*arm'上面计算出来的v1等于v2四元数的余弦值为它们的内积假如余弦值小于0，则需要将其中的一个取反，因为上面我们知道一个四元数和它的反方向的四元数对一个向量起相同的作用四元数的相乘，代表旋转的累积pq=p*q;rotp=q2rot(p);rotq=q2rot(q);rotpq=q2rot(pq);rotmul=rotp*rotq;这里rotpq与rotmul相等四．OGRE中Quaternion类的几个函数1.四元数到旋转向量void Quaternion::ToRotationMatrix (Matrix3& kRot) const1 - 2*qy2 - 2*qz22*qx*qy - 2*qz*qw2*qx*qz + 2*qy*qw2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz22*qy*qz - 2*qx*qw2*qx*qz - 2*qy*qw2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy22.旋转量到四元数根据1中的表格，有：4 *(1-qx2-qy2-qz2) = 1 + m00 + m11 + m22又qw2=1-qx2-qy2-qz2，可得4 *qw2= 1 + m00 + m11 + m22这里解qw必须保证1 + m00 + m11 + m22>=0，如果不是的话，就构造其他的等式来计算，OGRE中分成两种情况，一种是m00 + m11 + m22>=0，就可以直接先解出qw，否则的采用另外的等式计算3．Local axisVector3 xAixs(void) const;取得旋转矩阵的第一列，旋转矩阵和一个向量相乘的话，第一列的数据均和向量的x分量相乘Vecotr3 yAxis(void) const;取得旋转矩阵的第二列，旋转矩阵和一个向量相乘的话，第二列的数据均和向量的y分量相乘Vecotr3 zAxis(void) const;取得旋转矩阵的第三列，旋转矩阵和一个向量相乘的话，第三列的数据均和向量的z分量相乘。

四元数转欧拉角的雅可比矩阵引言：四元数和欧拉角是描述物体在三维空间中旋转的常用方法。

在某些应用中，我们需要将四元数转换为欧拉角，以便更好地理解旋转的含义。

本文将介绍四元数转欧拉角的雅可比矩阵，以及其在计算机图形学和机器人学中的应用。

一、四元数和欧拉角的基本概念四元数是一种扩展了复数的数学结构，它由一个实部和三个虚部组成。

在三维空间中，四元数可以用来表示旋转的方向和角度。

而欧拉角则是另一种表示旋转的方法，它由三个角度组成，分别表示绕三个坐标轴旋转的角度。

二、四元数转欧拉角的问题在实际应用中，我们常常需要将四元数转换为欧拉角，以便更好地理解旋转的含义。

然而，四元数转欧拉角的过程并不直观，而且存在多种不同的转换方法。

因此，我们需要找到一种有效的方法来解决这个问题。

三、雅可比矩阵的引入雅可比矩阵是一个矩阵，用于描述一个向量函数的变化率。

在四元数转欧拉角的问题中，我们可以使用雅可比矩阵来描述四元数与欧拉角之间的关系。

具体而言，雅可比矩阵的每个元素表示了四元数中的一个分量对欧拉角的变化的影响程度。

四、四元数转欧拉角的雅可比矩阵推导在推导四元数转欧拉角的雅可比矩阵时，我们需要使用一些数学推导和变换。

首先，我们将四元数表示为一个旋转矩阵，然后再将旋转矩阵表示为欧拉角的形式。

接下来，我们可以对欧拉角进行微分，得到雅可比矩阵的表达式。

五、雅可比矩阵的应用雅可比矩阵在计算机图形学和机器人学中有着广泛的应用。

在计算机图形学中，雅可比矩阵可以用于模拟物体的旋转和变形，以及实时渲染的优化。

在机器人学中，雅可比矩阵可以用于描述机器人的运动学和动力学，并进行路径规划和控制。

六、总结本文介绍了四元数转欧拉角的雅可比矩阵，以及其在计算机图形学和机器人学中的应用。

通过使用雅可比矩阵，我们可以更方便地将四元数转换为欧拉角，并且可以进一步应用于实际问题中。

雅可比矩阵的引入不仅简化了四元数转欧拉角的过程，还为计算机图形学和机器人学的研究提供了一种有效的工具。

四元数和欧拉角转换四元数和欧拉角都是表示旋转的方式。

四元数是由一个实数和三个虚数组成的数学结构，通常用$q = w + xi + yj + zk$表示。

其中，$w$是实部，$x, y, z$为三个虚部。

欧拉角则是旋转角度按照特定的顺序产生的序列$(α, β, γ)$。

四元数和欧拉角可以相互转换。

将欧拉角$(α, β, γ)$转换成四元数$q = q_w + q_x i + q_y j + q_z k$需要使用以下公式：$q_w =\cos(\frac{α}{2})\cos(\frac{β}{2})\cos(\frac{γ}{2}) +\sin(\frac{α}{2})\sin(\frac{β}{2})\sin(\frac{γ}{2})$ $q_x =\sin(\frac{α}{2})\cos(\frac{β}{2})\cos(\frac{γ}{2}) -\cos(\frac{α}{2})\sin(\frac{β}{2})\sin(\frac{γ}{2})$ $q_y =\cos(\frac{α}{2})\sin(\fra c{β}{2})\cos(\frac{γ}{2}) +\sin(\frac{α}{2})\cos(\frac{β}{2})\sin(\frac{γ}{2})$ $q_z =\cos(\frac{α}{2})\cos(\frac{β}{2})\sin(\frac{γ}{2}) -\sin(\frac{α}{2})\sin(\frac{β}{2})\cos(\frac{γ}{2})$将四元数$q$转换成欧拉角$(α, β, γ)$需要使用以下公式：$α = \tan^{-1}\frac{2(q_wq_x+q_yq_z)}{1-2(q_x^2+q_y^2)}$$β = \sin^{-1}(2(q_wq_y-q_zq_x))$$γ = \tan^{-1}\frac{2(q_wq_z+q_xq_y)}{1-2(q_y^2+q_z^2)}$需要注意的是，在将四元数转换为欧拉角时，存在万向锁问题（gimbal lock）。

四元数转欧拉角奇异值问题四元数和欧拉角作为常见的表示方法，在计算机图形学和机器人领域中广泛应用。

在四元数表示角度时，存在着一些奇异值问题，会使得欧拉角的转换结果出现异常，本文将对此进行详细的阐述。

一、四元数简介四元数是一种扩充了实数的数学结构，它包括一个实数部分和三个虚数部分，可以表示旋转和剪切等变换。

四元数形式上可以写成 $q = w + xi + yj + zk$，其中 $w, x, y, z$ 都是实数，$i, j, k$ 是三个虚数单位，它们的平方分别等于-1。

四元数通过旋转的方式来表示角度。

例如，单位四元数可以表示3D中的转动180度绕轴 $(1,1,1)$，则可以写成：$$q = [\cos(\theta/2),\sin(\theta/2)\frac{1}{\sqrt{3}},\sin(\theta/2)\frac{1}{\sqrt{3}},\sin(\theta/2)\frac{1}{\sqrt{3}}]$$其中，$\theta$ 是旋转的角度。

二、欧拉角简介欧拉角是一种表示旋转的方式，它通过描述旋转的三个角度来确定旋转的方向。

欧拉角可以通过任何航向、俯仰、翻转（yaw-pitch-roll）的组合来表示。

例如，将 3D 物体绕 X 轴旋转30度，然后绕 Y 轴旋转45度，再绕 Z 轴旋转 60 度，这个过程可以用以下的欧拉角表示：$$\alpha = 30^\circ,\beta = 45^\circ,\gamma = 60^\circ$$当然，在欧拉角的表示中也存在固有的问题，例如欧拉角的万向锁问题等。

但是，在本文中，我们主要探讨的问题是四元数转为欧拉角时可能会遇到的问题。

三、四元数转换为欧拉角在将四元数转换为欧拉角时，我们可以首先计算对应的旋转矩阵，然后通过该矩阵计算欧拉角。

假设四元数为$q = [w, x, y, z]$，则相应的旋转矩阵可以表示为：$$\left[\begin{matrix} 1 - 2(y^2+z^2)& 2(xy-wz)& 2(xz+wy)\\ 2(xy+wz)& 1-2(x^2+z^2)& 2(yz-wx)\\ 2(xz-wy)& 2(yz+wx)& 1 - 2(x^2+y^2)\end{matrix}\right]$$根据四元数到旋转矩阵的转换方法，我们可以通过这个矩阵计算出欧拉角，例如：$$\alpha = \tan^{-1}(\frac{-m_{23}}{m_{33}})$$$$\beta = \sin^{-1}(m_{13})$$$$\gamma = \tan^{-1}(\frac{-m_{12}}{m_{11}})$$其中 $m_{ij}$ 表示旋转矩阵中的第 $i$ 行第$j$ 列的元素。

四元数转欧拉角在线转换
四元数及其转换欧拉角技术是今天科学与工程应用中一个重要的技术。

四元数是由一个复数表示的三维空间中物体的旋转情况，这个复数由一个实
数部分和三个虚数部分构成，而这三个虚数又分别组合成一个三维向量，它
们两两组合就构成了一个旋转轴和转动的角度，这两个参数的综合决定了一
个物体的旋转情况。

而转换欧拉角呢就是从这个四元数中提取出三个欧拉角
来表征一个三维物体的旋转状况，也就是所谓的欧拉角观测角。

把四元数转换成欧拉角并不是一件容易的事情，因为旋转的物体其实是
有可能发生扭曲的，因此把它转换成欧拉角的时候，就需要处理这种扭曲。

不过，具体的把四元数转换成欧拉角，可以使用四元数转换欧拉角在线转换
的工具来快速的实现，它的优势在于可以在线快速把四元数转换成欧拉角，
避免了我们写繁琐代码的工作，使得各类科学工程应用更容易实现。

当然，有时候，我们也可以使用代码来完成这件事情，根据具体的场景，我们可以选择不同的编程语言来实现，但是，使用在线转换工具还是十分便
捷的，而且能够更快的得到结果。

总之，四元数被用于许多场景，转换欧拉角也是其中的一部分，这一步
框架可以使用在线转换工具轻松的实现，而不用再编写过多的代码。

四元数转欧拉角奇异值
四元数是一种表示旋转的方法，而欧拉角则是另一种。

在将四元数转换为欧拉角时，有时会遇到奇异值的问题，这时需要进行特殊处理。

奇异值出现的原因是欧拉角的定义域有限，而四元数的定义域无限。

当四元数的某些元素超出欧拉角的定义域时，就会出现奇异值。

为了解决奇异值问题，可以使用雅可比矩阵方法进行转换。

这种方法可以通过计算雅可比矩阵的特征值来确定是否存在奇异值，并进行相应的处理。

另外，还可以使用另一种方法来避免奇异值，即使用欧拉角的另一种定义方式。

这种方式可以将欧拉角的定义域扩展到无限，从而避免奇异值的出现。

总之，在将四元数转换为欧拉角时，需要注意奇异值的问题，并选择合适的方法进行处理。

- 1 -。

虚拟现实技术公式全文共四篇示例，供读者参考第一篇示例：虚拟现实技术公式是指通过计算机技术将虚构的虚拟世界与现实世界进行融合，使用户可以沉浸在一个全新的环境中，与传统的计算机界面相比，虚拟现实技术具有更加直观和沉浸的体验。

虚拟现实技术公式的制作需要综合考虑计算机图形学、人机交互、传感技术等多个领域的知识，以实现用户与虚拟环境的交互和沉浸感。

虚拟现实技术公式的核心是通过计算机对现实世界进行建模和仿真，以实现虚拟环境的呈现。

在这个过程中，需要考虑到多个要素，如视觉、听觉、触觉等感官的交互，还有场景的呈现、物体的运动等。

下面我们来简单介绍一些与虚拟现实技术相关的基本公式和概念。

1. 渲染方程渲染方程是虚拟现实技术中的重要概念，它描述了光线在相机（观察者）位置与场景中的物体交互时的物理规律。

具体来说，渲染方程描述了光线如何与物体表面发生反射、折射等现象，从而最终到达相机传感器的过程。

渲染方程通常表示为：L(o,ω) = L_e(o,ω) + ∫f_rω_iL_i(ω_i,n)L_i(o,ω_i)n·ω_idω_i其中L(o,ω)为相机位置o处，方向ω上的辐射强度，L_e(o,ω)为来自场景中光源的辐射强度，f_r为表面的反射函数，n为表面法线，L_i为从光源处射向表面的辐射强度，ω_i为光线入射方向。

2. 虚拟现实技术中的交互公式虚拟现实技术的核心在于与用户进行交互，其交互公式可以表示为：I_t = F(I_t-1, I_t-2, ..., I_t-n)其中，I_t表示在时刻t用户的输入状态，F为交互函数，用于描述用户对虚拟环境的操作和反馈效果。

在虚拟现实环境中，用户的输入可以通过手柄、眼球追踪、体感设备等方式来实现，交互函数的设计需要考虑到输入设备的特性和用户体验。

3. 虚拟环境中的物体运动公式在虚拟现实技术中，物体的运动是模拟现实世界的重要部分之一，其运动公式可以表示为：F = ma其中，F为物体受到的力，m为物体质量，a为物体的加速度。

orb-slam 欧拉角到四元数定义下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!欧拉角到四元数定义欧拉角是描述物体在空间中旋转的一种方式，它包括绕X轴、Y轴和Z轴的旋转角度。

一、概述物体的旋转运动在工程设计和计算机图形学中有着重要的应用，对于任意轴旋转的公式一直是工程师和研究人员关注的焦点之一。

在patran软件中，对物体绕任意轴进行旋转需要使用一定的数学公式和算法来实现。

本文将对patran物体绕任意轴旋转的公式进行详细介绍，希望能对相关领域的工程师和研究人员有所帮助。

二、物体绕任意轴旋转的基本原理在三维空间中，物体绕任意轴进行旋转是一种复杂的运动，需要借助一定的数学工具才能描述和计算。

在patran软件中，物体绕任意轴旋转是基于欧拉角和四元数来实现的。

欧拉角是描述物体在三维空间中旋转状态的一种方法，通常用三个角度来表示绕x、y、z轴的旋转。

而四元数是一种用复数来表示旋转状态的方法，它在描述旋转时具有简洁、高效的优势。

patran软件中的物体旋转算法是基于欧拉角和四元数的转换关系来实现的。

三、patran物体绕任意轴旋转的公式推导1. 欧拉角和四元数的转换关系在patran软件中，物体绕任意轴旋转的公式可通过欧拉角和四元数的转换关系推导而来。

假设物体绕轴a进行旋转，我们需要经过以下步骤来推导出物体的旋转公式：(1) 计算旋转轴a的单位向量我们需要计算出旋转轴a的单位向量，表示为(ux, uy, uz)。

这一步可以通过对旋转轴向量进行标准化处理得到。

(2) 计算旋转角度θ接下来，我们需要计算出旋转角度θ，该角度可以通过欧拉角的转换关系或者其他数学方法得到。

(3) 计算四元数表示的旋转矩阵将得到的旋转轴单位向量和旋转角度θ代入四元数的转换关系公式中，可以得到一个描述旋转矩阵的四元数(Qx, Qy, Qz, Qw)。

该四元数表示了物体绕轴a旋转的状态。

2. 物体绕任意轴旋转的公式通过以上步骤得到了描述物体绕任意轴旋转的四元数(Qx, Qy, Qz, Qw)，我们可以将其转换为旋转矩阵或者欧拉角的形式，从而得到物体绕任意轴旋转的公式。

在patran软件中，通常会使用旋转矩阵的形式来表示物体的旋转状态，其中旋转矩阵的表示形式为：[ R11 R12 R13 ][ R21 R22 R23 ][ R31 R32 R33 ]其中，R11、R12、R13等元素表示了物体在三维空间中的旋转状态。

四元数与欧拉角之间的转换早在1843年哈米尔顿就提出了四元数的基本概念[138]，但当时仅停留在理论概念的讨论上。

20世纪以来，随着航天、航空工业的发展，四元数得到了广泛地实际应用[139-142]。

四元数的定义为[143]4q ⎛⎫≡ ⎪⎝⎭Q q（0-1）式中：123(,,)sin 2T q q q α≡=Q e （0-2）4cos2q α= （0-3）其中，e 是沿旋转轴的单位向量，α是旋转角度。

四元数满足约束条件1T =q q（0-4）四元数与姿态矩阵具有如下关系：224334222212341234132422221234123423142222132423141234()22[]()()2()2()2()2()2()2()T T q I q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q ⨯=-+-⨯=Ξψ⎛⎫--++-⎪=--+-++ ⎪⎪+---++⎝⎭A Q QQ Q q q q（0-5）其中，33⨯I 是33⨯单位矩阵，433[]()T q ⨯+⨯⎛⎫Ξ≡ ⎪-⎝⎭I Q q Q（0-6）433[]()T q ⨯-⨯⎛⎫ψ≡ ⎪-⎝⎭I Q q Q（0-7）3231210[]00q q q q q q -⎛⎫ ⎪⨯=- ⎪ ⎪-⎝⎭Q （0-8）地面坐标系Axyz 和弹体坐标系O 1x 1y 1z 1的关系可以用下式来表示=b Ar（0-9）其中，b 、r 分别为某向量在弹体坐标系和地面坐标系中的表示形式，A 的表达形式见错误！未找到引用源。

，具体为cos cos sin cos sin sin cos cos sin sin cos cos sin sin cos cos sin sin cos sin sin cos cos sin sin sin sin cos cos ϑψϑϑψϑψγψγϑγϑψγψγϑψγψγϑγϑψγψγ-⎛⎫⎪=-++ ⎪ ⎪+--+⎝⎭A（0-10）比较式（0-5）和式（0-10），得到姿态角的四元数表示131324222211123412123432231422222212342()arctan arctan arcsin arcsin 2()2()arctan arctan q q q q q q q q q q q q q q q q q q q q ψθφ⎧-=-=-⎪--+⎪⎪==+⎨⎪-⎪=-=-⎪-+-+⎩q q q q q A A A A A （0-11）也可以用姿态角来表示四元数q ，即(cossinj)(cossinj)(cos sin j)222222ψψθθφφ=+⊗+⊗+q（0-12）其中，符号⊗表示四元数乘法，其定义如下[144-145]41234123(i j k)(i j k)A A A A B B B B ⊗=+++⊗+++A B44123114322341232143B A A A A B A A A A A A A A B A A A A B ---⎛⎫⎛⎫ ⎪ ⎪- ⎪⎪= ⎪⎪- ⎪ ⎪ ⎪-⎝⎭⎝⎭44112233144132232431421334211243()()i ()j ()kA B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B =---++-++++-+-++（0-13）其中，4123i j k A A A A =+++A 和4123i j k B B B B +++B =均为四元数。

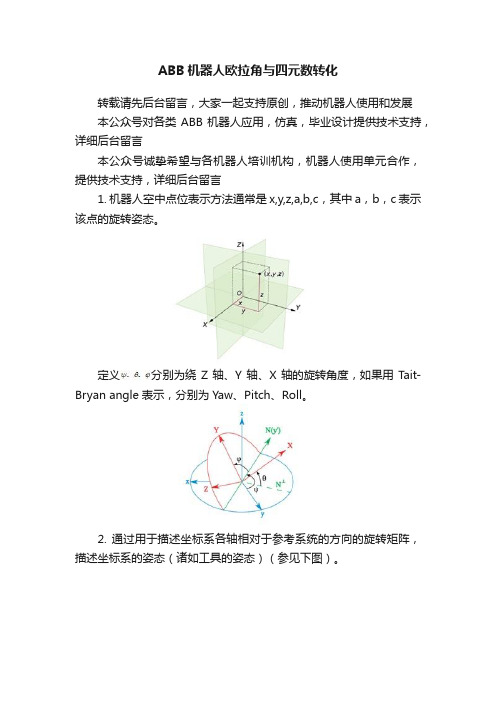
ABB机器人欧拉角与四元数转化转载请先后台留言，大家一起支持原创，推动机器人使用和发展本公众号对各类ABB机器人应用，仿真，毕业设计提供技术支持，详细后台留言本公众号诚挚希望与各机器人培训机构，机器人使用单元合作，提供技术支持，详细后台留言1. 机器人空中点位表示方法通常是x,y,z,a,b,c，其中a，b，c表示该点的旋转姿态。

定义分别为绕Z轴、Y轴、X轴的旋转角度，如果用Tait-Bryan angle表示，分别为Yaw、Pitch、Roll。

2. 通过用于描述坐标系各轴相对于参考系统的方向的旋转矩阵，描述坐标系的姿态（诸如工具的姿态）（参见下图）。

旋转后的坐标系轴（x，y，z）为矢量，其可以用参考坐标系表示如下：x = (x1, x2, x3)y = (y1, y2, y3)z = (z1, z2, z3)这意味着参考坐标系中x矢量的x轴向分量将为x1，y轴向分量将为x2，以此类推。

这三个矢量可在一个矩阵（旋转矩阵）中组合，各矢量由此构成一栏：四元数仅仅是一种描述此旋转矩阵的更为简洁的方式；根据旋转矩阵的各元素，计算四元数：3. 综合以上，可以得到欧拉角--四元数的转化如下4 可以得到四元数--欧拉角的转化如下arctan和arcsin的结果是，这并不能覆盖所有朝向(对于角的取值范围已经满足)，因此需要用atan2来代替arctan5. ABB机器人提供了欧拉角与四元数转化的相关函数，其中object.rot := OrientZYX(anglez, angley, anglex) 函数为欧拉角-四元数函数，注意函数中的顺序为rz，ry，rxanglex := EulerZYX(X, object.rot); 函数为四元数-欧拉角函数，此处举例提取绕X旋转角度，也可提取绕Y和绕Z旋转角度。

6. 在RAPID端可以自己编写函数，得到欧拉角与四元数转化函数，如下•••••••••••••••••••••••••••••••••••••••••••FUNC orient eulerAnglesToQuaternion(num hdg,num pitch, num roll) //返回四元数VAR num cosRoll; VAR num sinRoll;VAR num cospitch; VAR num sinpitch; VAR num cosheading; VAR num sinheading; VAR orient orient1; cosRoll:=Cos(roll*0.5);sinRoll:=Sin(roll*0.5); cosPitch:=Cos(pitch*0.5);sinPitch:=Sin(pitch*0.5); cosHeading:=Cos(hdg*0.5); sinHeading:=Sin(hdg*0.5);orient1.q1:=cosRoll*cosPitch*cosHeading+sinRoll*sinPitch*s inHeading; orient1.q2:=sinRoll*cosPitch*cosHeading-cosRoll*sinPitch*sinHeading;orient1.q3:=cosRoll*sinPitch*cosHeading+sinRoll*cosPitch*sinH eading; orient1.q4:=cosRoll*cosPitch*sinHeading-sinRoll*sinPitch*cosHeading; RETURN orient1; ENDFUNC FUNC num quaternionT oEulerAngles(\switch X|switch Y|switch Z,orient orient1) //返回欧拉角VAR num q0 VAR num q1; VAR num q2; VAR num q3; q0:=orient1.q1; q1:=orient1.q2; q2:=orient1.q3; q3:=orient1.q4; IF present(x) return atan2(2*(q2*q3+q0*q1),q0*q0-q1*q1-q2*q2+q3*q3); IF present(y) return asin(2*(q0*q2-q1*q3)); IF present(z) RETURN atan2(2*(q1*q2+q0*q3),q0*q0+q1*q1-q2*q2-q3*q3); //roll=atan2f(2. f*(q2q3+q0q1),q0q0-q1q1-q2q2+q3q3); //pitch=asinf(2. f*(q0q2-q1q3)); //yaw=atan2f(2. f*(q1q2+q0q3),q0q0+q1q1-q2q2-q3q3); ENDFUNC********************************如何获取更多经典文章？。

四元数转欧拉角的雅可比矩阵在机器人控制和运动规划中，四元数是一种常用的表示机器人位姿的方法。

然而，在某些情况下，需要将四元数转换为欧拉角，以方便人类理解和可视化机器人姿态。

因此，本文将介绍四元数转欧拉角的雅可比矩阵，该矩阵可以用于求解机器人位姿控制中的导数和微分方程。

首先，我们需要定义四元数和欧拉角的概念。

四元数是一种四维复数，通常用一个实部和三个虚部表示。

欧拉角是一种用于描述旋转的坐标系，通常包括绕x轴的旋转角度、绕y轴的旋转角度和绕z轴的旋转角度。

接下来，我们需要考虑如何将四元数转换为欧拉角。

这可以通过以下公式实现：$ psi = atan2(2(q_0q_3+q_1q_2),1-2(q_2^2+q_3^2)) $$ theta = asin(2(q_0q_2-q_1q_3)) $$ phi = atan2(2(q_0q_1+q_2q_3),1-2(q_1^2+q_2^2)) $ 其中，$ q_0, q_1, q_2, q_3 $ 分别表示四元数的实部和虚部。

然而，由于四元数和欧拉角之间存在非线性关系，因此我们需要使用雅可比矩阵来求解导数和微分方程。

具体来说，$ psi, theta, phi $ 分别表示绕z轴、绕y轴和绕x轴的旋转角度，因此我们可以将欧拉角表示为一个向量 $ vec{e} = [psi theta phi]^T $。

则四元数对欧拉角的雅可比矩阵可以表示为：$ J_q(vec{e}) = begin{bmatrix} frac{partial psi}{partialq_0} & frac{partial psi}{partial q_1} & frac{partialpsi}{partial q_2} & frac{partial psi}{partial q_3}frac{partial theta}{partial q_0} & frac{partialtheta}{partial q_1} & frac{partial theta}{partial q_2} &frac{partial theta}{partial q_3} frac{partial phi}{partial q_0} & frac{partial phi}{partial q_1} & frac{partialphi}{partial q_2} & frac{partial phi}{partial q_3} end{bmatrix} $其中，每个元素的求解可以使用链式法则和欧拉角转四元数的公式求解。

四元数法
四元数法四元数本质上是⼀种⾼阶复数，是⼀个四维空间。

它的虚部包含了三个虚数单位，i 、j 、k ，即⼀个四元数可以表⽰为x = a + bi + cj + dk 。

⼀个单位四元数可描述为：T
z y x w q ],,,[=，并且满⾜：
1||2222=+++=z y x w q （3）四元数可以看做绕⼀个轴的⼀个旋转： ====)
cos()2/sin()cos()2/sin()cos()2/sin()2/cos(z y x z y x w βαβαβαα（4）其中，α是旋转⾓，单位为弧度。

)cos(x β，)cos(y β和)cos(z β是旋转轴的⽅向余弦，也就是旋转轴与参考系坐标三个轴夹⾓的余弦值。

当得到了四元数，就需要将其转换为欧拉⾓。

欧拉⾓，就是从⼀个坐标系到另⼀个坐标系的变换，可以通过⼀次绕不同的坐标轴的3次连续转动来定义。

定义ψ、θ、?分别为绕Z 轴、Y 轴、X 轴的旋转⾓度，分别为Yaw ，Pitch 、Roll 。

四元数到欧拉⾓的转换：
+-+-+-+=??))(21)(2(arctan ))(2arcsin()(21)(2arctan 222222z y xy wz zx wy y x yz wx ψθ? （5） w 对应
q0,x 对应q1，y 对应q2,z 对应q3。

arctan 和arcsin 的结果是[]22,ππ-，这并不能覆盖所有朝向(对于θ⾓[]
22,ππ-的取值范围已经满⾜)，因此需要⽤atan2来代替arctan 。

四元数转欧拉角的雅可比矩阵四元数是一种用来表示旋转的数学工具，它可以将旋转操作转化为数学计算。

而欧拉角则是一种常用的旋转表示方法，它通过三个角度来描述物体在空间中的旋转状态。

那么，如何将四元数转换为欧拉角呢？本文将介绍四元数转欧拉角的雅可比矩阵，并探讨其应用。

我们需要了解什么是雅可比矩阵。

雅可比矩阵是用来描述函数的局部线性近似的矩阵，它可以将函数的变化率与输入的变化率联系起来。

在四元数转欧拉角的问题中，雅可比矩阵可以帮助我们计算四元数对欧拉角的导数，从而实现四元数到欧拉角的转换。

四元数可以表示为q = [w, x, y, z]，其中w为实部，x、y、z为虚部。

欧拉角通常使用三个角度表示，如yaw（偏航角）、pitch（俯仰角）和roll（翻滚角）。

我们可以使用雅可比矩阵来计算四元数对欧拉角的导数，如下所示：J = [d(yaw)/dq, d(pitch)/dq, d(roll)/dq]其中，d(yaw)/dq表示yaw角对四元数的导数，其他类似。

这个雅可比矩阵的计算可以通过数学推导得到，具体过程不再赘述。

在实际应用中，我们可能需要根据物体的旋转状态来计算其在不同坐标系下的位置。

这时，我们可以使用四元数转欧拉角的雅可比矩阵来实现。

首先，我们根据物体的旋转状态得到四元数表示，然后使用雅可比矩阵计算四元数对欧拉角的导数。

最后，根据导数的计算结果，我们可以将四元数转换为欧拉角表示。

雅可比矩阵的计算涉及到复杂的数学推导和矩阵运算，这里不再详细介绍。

需要注意的是，由于四元数的性质和欧拉角的定义，四元数转欧拉角的雅可比矩阵存在一些特殊性质，例如奇异性和非唯一性。

在具体应用中，我们需要根据实际情况进行调整和处理，以确保结果的准确性和稳定性。

总结一下，本文介绍了四元数转欧拉角的雅可比矩阵，并探讨了其应用。

雅可比矩阵可以帮助我们计算四元数对欧拉角的导数，从而实现四元数到欧拉角的转换。

在实际应用中，我们可以根据物体的旋转状态使用雅可比矩阵来计算其在不同坐标系下的位置。

python欧拉角转四元数欧拉角和四元数在计算机图形学和机器人学等领域中都是很常见的概念。

欧拉角作为描述物体在三维空间中姿态的一种方式，常常被用于航空飞行、姿态控制、虚拟现实等领域。

而四元数则是一种用于旋转的复数，可以实现无死角的旋转，并且不会出现万向锁的问题，被广泛地应用于计算机图形学中的3D渲染和动画制作。

欧拉角和四元数之间的转换可以帮助我们在不同的场景下快速地切换姿态描述方式。

在Python中，我们可以使用scipy库的spatial 子模块中的Rotation类来进行欧拉角和四元数之间的转换。

下面是一个简单的例子：```pythonfrom scipy.spatial.transform import Rotation# 定义欧拉角euler_angles = [45, 30, 60]# 将欧拉角转换为四元数r = Rotation.from_euler('xyz', euler_angles, degrees=True) quat = r.as_quat()# 将四元数转换为欧拉角r = Rotation.from_quat(quat)euler_angles = r.as_euler('xyz', degrees=True)# 输出结果print("欧拉角: ", euler_angles)print("四元数: ", quat)```上面的代码中，我们首先定义了一个欧拉角，然后使用Rotation 类的from_euler()方法将其转换为四元数。

接着，又使用as_euler()方法将四元数转换回欧拉角。

最后输出了结果。

使用scipy库的旋转类进行欧拉角和四元数之间的转换非常方便，让我们在不同领域之间进行切换更加容易。

通过学习这些技术，我们可以更好地理解物体在三维空间中的运动和姿态，进而创作出更加精细的数字内容。