【数学】福建省厦门市第六中学2016届高三上学期期中考试(理)

2015-2016学年福建省厦门六中高三（上）期中数学试卷（理科）一、选择题：（本题共12个小题，每小题5分，共60分）1．（5分）复数（i是虚数单位）的模等于（）A． B．10 C．D．52．（5分）设全集U是实数集R，M={x|x＜﹣2或x＞2}，N={x|x2﹣4x+3＜0}，则图中阴影部分所表示的集合是（）A．{x|﹣2≤x＜1}B．{x|﹣2≤x≤2}C．{x|1＜x≤2}D．{x|x＜2}3．（5分）sin2•cos3•tan4的值是（）A．正数B．负数C．零D．无法确定4．（5分）某程序框图如图所示，该程序运行后输出的x值是（）A．3 B．4 C．6 D．85．（5分）设a=cos2°﹣sin2°，b=，c=，则有（）A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b6．（5分）数列{a n}满足a1=1，a2=2，a n+1•a n=nλ（λ为常数，n∈N*），则a4等于（）A．1 B．2 C．3 D．47．（5分）已知，则A⊂B的充要条件是（）A．（，+∞） B．0＜a＜C．0＜a≤1 D．a＞l8．（5分）已知等比数列{a n}的公比为正数，且a3•a9=2a52，a2=1，则a1=（）A．B．C．D．29．（5分）若两个非零向量满足|+|+|﹣|=2||，则向量与的夹角为（）A．B．C． D．10．（5分）已知数列{a n}满足a2=102，a n+1﹣a n=4n，（n∈N*），则数列的最小值是（）A．25 B．26 C．27 D．2811．（5分）将函数y=f（x）的图象先向左平移个单位，然后向上平移1个单位，得到函数y=2cos2x的图象，则f（x﹣）是（）A．﹣sin2x B．﹣2cosx C．2sinx D．2cosx12．（5分）已知定义在R上的函数f（x）满足①f（x）+f（2﹣x）=0，②f（x）﹣f（﹣2﹣x）=0，③在[﹣1，1]上表达式为，f（x）=则函数f（x）与函数g（x）=的图象在区间[﹣3，3]上的交点个数为（）A．5 B．6 C．7 D．8二、填空题：（本题共4小题，每小题5分，共20分）13．（5分）若（2x+）dx=3+ln2（a＞1），则a的值是．14．（5分）若，则cos2θ=．15．（5分）数列{a}的通项公式，其前n项和，则n=．16．（5分）给出下列五个命题：①函数f（x）=lnx﹣2+x在区间（1，e）上存在零点；②若f′（x0）=0，则函数y=f（x）在x=x0处取得极值；③“a=1”是“函数在定义域上是奇函数”的充分不必要条件．④函数y=f（1+x）的图象与函数y=f（1﹣x）的图象关于y轴对称；⑤满足条件AC=，AB=1的三角形△ABC有两个．其中正确命题的是．三．解答题（本大题有6小题，共70分；解答应写出文字说明与演算步骤）17．（12分）已知{a n}为等差数列，且满足a1+a3=8，a2+a4=12．（Ⅰ）求数列{a n}的通项公式；，S k成等比数列，求正整数k的值．（Ⅱ）记{a n}的前n项和为S n，若a3，a k+118．（12分）已知函数，．（1）若，求函数f（x）的值；（2）求函数f（x）的值域．19．（12分）已知海岛B在海岛A的北偏东45°方向上，A、B相距10海里，小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动，同时小船乙从海岛A 出发沿北偏15°方向也以2海里/小时的速度移动（Ⅰ）经过1小时后，甲、乙两小船相距多少海里？（Ⅱ）在航行过程中，小船甲是否可能处于小船乙的正东方向？若可能，请求出所需时间，若不可能，请说明理由．20．（12分）已知等差数列{a n}满足：a n+1＞a n（n∈N*），a1=1，该数列的前三项分别加上1，1，3后顺次成为等比数列{b n}的前三项．（Ⅰ）分别求数列{a n}，{b n}的通项公式a n，b n；（Ⅱ）设，若恒成立，求c的最小值．21．（12分）设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在（a，b）上，f″（x）＜0恒成立，则称函数f（x）在（a，b）上为“凸函数”．已知．（Ⅰ）若f（x）为区间（﹣1，3）上的“凸函数”，试确定实数m的值；（Ⅱ）若当实数m满足|m|≤2时，函数f（x）在（a，b）上总为“凸函数”，求b﹣a的最大值．【选修4-4：坐标系与参数方程】22．（10分）在直角坐标系xOy中，直线C1的参数方程为（t为参数），以该直角坐标系的原点O为极点，x轴的正半轴为极轴的极坐标系下，圆C2的方程为ρ=﹣2cosθ+2sinθ．（Ⅰ）求直线C1的普通方程和圆C2的圆心的极坐标；（Ⅱ）设直线C1和圆C2的交点为A，B，求弦AB的长．【选修4-5：不等式选讲】23．已知函数f（x）=|x+a|+|x﹣2|①当a=﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．2015-2016学年福建省厦门六中高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题：（本题共12个小题，每小题5分，共60分）1．（5分）复数（i是虚数单位）的模等于（）A． B．10 C．D．5【解答】解：=1+=3+i，故模为；故选：A．2．（5分）设全集U是实数集R，M={x|x＜﹣2或x＞2}，N={x|x2﹣4x+3＜0}，则图中阴影部分所表示的集合是（）A．{x|﹣2≤x＜1}B．{x|﹣2≤x≤2}C．{x|1＜x≤2}D．{x|x＜2}【解答】解：由图知，阴影部分表示集合（C U M）∩N，由于M={x|x＜﹣2或x＞2}，∴C U M={x|﹣2≤x≤2}，N={x|1＜x＜3}，所以（C U M）∩N={x|1＜x≤2}．故选：C．3．（5分）sin2•cos3•tan4的值是（）A．正数B．负数C．零D．无法确定【解答】解：∵，∴sin2＞0，cos3＜0，∵π＜4＜，∴tan4＞0．∴sin2•cos3•tan4＜0．故选：B．4．（5分）某程序框图如图所示，该程序运行后输出的x值是（）A．3 B．4 C．6 D．8【解答】解：执行程序框图，可得k=1，s=1满足条件s＜100，s=4，k=2；满足条件s＜100，s=22，k=3；满足条件s＜100，s=103，k=4；不满足条件s＜100，退出循环，x=8，输出x的值为8．故选：D．5．（5分）设a=cos2°﹣sin2°，b=，c=，则有（）A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b【解答】解：∵a=cos2°﹣sin2°=sin（30°﹣2°）=sin28°，b==tan（14°+14°）=tan28°，c===sin25°，∵正弦函数在（0°，90°）是单调递增的，∴c＜a．又∵在（0°，90°）内，正切线大于正弦线，∴a＜b．故选：D．6．（5分）数列{a n}满足a1=1，a2=2，a n+1•a n=nλ（λ为常数，n∈N*），则a4等于（）A．1 B．2 C．3 D．4【解答】解：由题意可知；a1=1，a2=2，a n+1•a n=nλ，则：a2•a1=2×1=λ，∴a n+1•a n=2n，故a3•a2=2×2=4，解得a3=2，a4•a3=2×3=6，解得a4=3，故选：C．7．（5分）已知，则A⊂B的充要条件是（）A．（，+∞） B．0＜a＜C．0＜a≤1 D．a＞l【解答】解：由题意，2x﹣1≥0，∴x≥0；x2+lga≥lga，A⊂B时，lga≤0，∴0＜a≤1．故选：C．8．（5分）已知等比数列{a n}的公比为正数，且a3•a9=2a52，a2=1，则a1=（）A．B．C．D．2【解答】解：设公比为q，由已知得a1q2•a1q8=2（a1q4）2，即q2=2，又因为等比数列{a n}的公比为正数，所以q=，故a1=．故选：B．9．（5分）若两个非零向量满足|+|+|﹣|=2||，则向量与的夹角为（）A．B．C． D．【解答】解：由已知得由①得出=0，将②展开并代入整理得：=3，∴（）•（）==2，cosθ===所求夹角是，故选：B．10．（5分）已知数列{a n}满足a2=102，a n+1﹣a n=4n，（n∈N*），则数列的最小值是（）A．25 B．26 C．27 D．28﹣a n=4n得，【解答】解：由a n+1a3﹣a2=8，a4﹣a3=12，a5﹣a4=16，…，a n﹣a n﹣1=4（n﹣1），以上各式相加得，a n﹣a2=，所以a n=102+（n﹣2）（2n+2）（n ≥2），而a2﹣a1=4，所以a1=a2﹣4=98，适合上式，故a n=102+（n﹣2）（2n+2）（n∈N*），=﹣2=26，当且仅当即n=7时取等号，所以数列的最小值是26，故选：B．11．（5分）将函数y=f（x）的图象先向左平移个单位，然后向上平移1个单位，得到函数y=2cos2x的图象，则f（x﹣）是（）A．﹣sin2x B．﹣2cosx C．2sinx D．2cosx【解答】解：由题意可得，f（x+）+1=2cos2x，∴f（x+）=2cos2x﹣1=cos2x，令x+=t，则x=t﹣，∴f（t）=cos（2t﹣）=sin2t，即f（x）=sin2x，∴f（x﹣）=sin（2x﹣7π）=﹣sin2x．故选：A．12．（5分）已知定义在R上的函数f（x）满足①f（x）+f（2﹣x）=0，②f（x）﹣f（﹣2﹣x）=0，③在[﹣1，1]上表达式为，f（x）=则函数f（x）与函数g（x）=的图象在区间[﹣3，3]上的交点个数为（）A．5 B．6 C．7 D．8【解答】解：∵①f（x）+f（2﹣x）=0，②f（x）﹣f（﹣2﹣x）=0，∴f（x）图象的对称中心为（1，0），f（x）图象的对称轴为x=﹣1，结合③画出f（x）和g（x）的部分图象，如图所示，据此可知f（x）与g（x）的图象在[﹣3，3]上有6个交点．故选B．二、填空题：（本题共4小题，每小题5分，共20分）13．（5分）若（2x+）dx=3+ln2（a＞1），则a的值是2．【解答】解：=（x2+lnx）=a2+lna﹣（1+ln1）=3+ln2，a＞1，∴a2+lna=4+ln2=22+ln2，解得a=2，故答案为：2；14．（5分）若，则cos2θ=．【解答】解：由可知，，而．故答案为：﹣．15．（5分）数列{a n}的通项公式，其前n项和，则n= 30．【解答】解：∵，∴∴S n=a1+a2+…+a n=++…+=∵，∴∴n=30故答案为：3016．（5分）给出下列五个命题：①函数f（x）=lnx﹣2+x在区间（1，e）上存在零点；②若f′（x0）=0，则函数y=f（x）在x=x0处取得极值；③“a=1”是“函数在定义域上是奇函数”的充分不必要条件．④函数y=f（1+x）的图象与函数y=f（1﹣x）的图象关于y轴对称；⑤满足条件AC=，AB=1的三角形△ABC有两个．其中正确命题的是①③④．【解答】解：①f（x）=lnx﹣2+x在区间[1，e]上单调递增，且f（1）=1﹣2=﹣1＜0．f（e）=lne﹣2+e=e﹣2+1=e﹣1＞0，所以根据根的存在性定理可知在（1，e）上函数存在零点，所以①正确．②函数f（x）=x3的导数为f'（x）=3x2，因为f'（0）=0，但函数f（x）=x3单调递增，没有极值，所以②错误．③若函数在定义域上是奇函数，则f（﹣x）=﹣f（x），即，整理得，即a2e2x﹣1=e2x﹣a2，所以a2=1，解得a=1或a=﹣1，所以③“a=1”是“函数在定义域上是奇函数”的充分不必要条件．所以③正确．④设A（a，b）是y=f（1+x）上的任意一点，则满足b=f（1+a），则点A（a，b）关于y轴对称的点的坐标为（﹣a，b），在函数y=f（1﹣x）上，当x=﹣a时，y=f[1﹣（﹣a）]=f（1+a）=b，即（﹣a，b）在函数y=f（1﹣x）上，所以函数y=f（1+x）的图象与函数y=f（1﹣x）的图象关于y轴对称，所以④正确．⑤由正弦定理得，即，解得sinC=，因为AC＞AB，所以B＞C，即C＜600，所以满足条件的三角形只有一个，所以⑤错误．故正确的命题是①③④．故答案为：①③④．三．解答题（本大题有6小题，共70分；解答应写出文字说明与演算步骤）17．（12分）已知{a n}为等差数列，且满足a1+a3=8，a2+a4=12．（Ⅰ）求数列{a n}的通项公式；，S k成等比数列，求正整数k的值．（Ⅱ）记{a n}的前n项和为S n，若a3，a k+1【解答】解：（Ⅰ）设数列{a n}的公差为d，由题意可得，解方程组可得a1=2，d=2，∴a n=2+2（n﹣1）=2n；（Ⅱ）由（Ⅰ）可得，∴a3=2×3=6，a k+1=2（k+1），，，S k成等比数列，∴，∵a3，a k+1∴（2k+2）2=6（k2+k），化简可得k2﹣k﹣2=0，解得k=2或k=﹣1，∵k∈N*，∴k=218．（12分）已知函数，．（1）若，求函数f（x）的值；（2）求函数f（x）的值域．【解答】解：（1）∵，∴cosx=﹣=﹣∴=sinx+cosx﹣2cosx=sinx﹣cosx=×+=（2）=sinx+cosx﹣2cosx=sinx﹣cosx=2sin（x﹣）∵∴≤x﹣≤∴≤sin（x﹣）≤1∴f（x）的最大值为2，最小值为1，值域为[1，2]19．（12分）已知海岛B在海岛A的北偏东45°方向上，A、B相距10海里，小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动，同时小船乙从海岛A 出发沿北偏15°方向也以2海里/小时的速度移动（Ⅰ）经过1小时后，甲、乙两小船相距多少海里？（Ⅱ）在航行过程中，小船甲是否可能处于小船乙的正东方向？若可能，请求出所需时间，若不可能，请说明理由．【解答】解：（Ⅰ）经过1小时后，甲船到达E点，乙船到达F点，|AE|=10﹣2=8，|AF|=2，∠EAF=60°，┅┅┅┅┅┅┅┅┅┅┅┅┅2分∴|EF|2=|AE|2+|AF|2﹣2|AE||AF|cos60°=64+4﹣2×=52，∴|EF|=2．┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分（Ⅱ）设经过t（0＜t＜5）小时小船甲处于小船乙的正东方向．则甲船与A距离为|AE|=10﹣2t海里，乙船与A距离为|AF|=2t海里，∠EAF=60°，∠EFA=45°，┅┅┅6分则由正弦定理得=，即，┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分则t==＜5．┅┅┅┅┅┅┅┅11分答：经过小时小船甲处于小船乙的正东方向．┅┅┅┅┅┅┅┅┅12分．20．（12分）已知等差数列{a n}满足：a n+1＞a n（n∈N*），a1=1，该数列的前三项分别加上1，1，3后顺次成为等比数列{b n}的前三项．（Ⅰ）分别求数列{a n}，{b n}的通项公式a n，b n；（Ⅱ）设，若恒成立，求c的最小值．【解答】解：（Ⅰ）设d、q分别为数列{a n}、数列{b n}的公差与公比，a1=1．由题可知，a1=1，a2=1+d，a3=1+2d，分别加上1，1，3后得2，2，+d，4+2d是等比数列{b n}的前三项，∴（2+d）2=2（4+2d）⇒d=±2．＞a n，∵a n+1∴d＞0．∴d=2，∴a n=2n﹣1（n∈N*）．由此可得b1=2，b2=4，q=2，∴b n=2n（n∈N*）．（Ⅱ），①∴．②①﹣②，得=+2（++…+）﹣，∴T n=3﹣．∴T n+﹣=3﹣≤2，∴满足条件恒成立的最小整数值为c=3．21．（12分）设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在（a，b）上，f″（x）＜0恒成立，则称函数f（x）在（a，b）上为“凸函数”．已知．（Ⅰ）若f（x）为区间（﹣1，3）上的“凸函数”，试确定实数m的值；（Ⅱ）若当实数m满足|m|≤2时，函数f（x）在（a，b）上总为“凸函数”，求b﹣a的最大值．【解答】解：由函数得，f″（x）=x2﹣mx﹣3（3分）（Ⅰ）若f（x）为区间（﹣1，3）上的“凸函数”，则有f″（x）=x2﹣mx﹣3＜0在区间（﹣1，3）上恒成立，由二次函数的图象，当且仅当，即⇔m=2．（7分）（Ⅱ）当|m|≤2时，f″（x）=x2﹣mx﹣3＜0恒成立⇔当|m|≤2时，mx＞x2﹣3恒成立．（8分）当x=0时，f″（x）=﹣3＜0显然成立．（9分）当x＞0，∵m的最小值是﹣2．∴．从而解得0＜x＜1（11分）当x＜0，∵m的最大值是2，∴，从而解得﹣1＜x＜0．（13分）综上可得﹣1＜x＜1，从而（b﹣a）max=1﹣（﹣1）=2（14分）【选修4-4：坐标系与参数方程】22．（10分）在直角坐标系xOy中，直线C1的参数方程为（t为参数），以该直角坐标系的原点O为极点，x轴的正半轴为极轴的极坐标系下，圆C2的方程为ρ=﹣2cosθ+2sinθ．（Ⅰ）求直线C1的普通方程和圆C2的圆心的极坐标；（Ⅱ）设直线C1和圆C2的交点为A，B，求弦AB的长．【解答】解：（Ⅰ）由C1的参数方程消去参数t得普通方程为x﹣y+1=0，圆C2的直角坐标方程（x+1）2+=4，所以圆心的直角坐标为（﹣1，），所以圆心的一个极坐标为（2，）．（Ⅱ）由（Ⅰ）知（﹣1，）到直线x﹣y+1=0 的距离d==，所以AB=2=．【选修4-5：不等式选讲】23．已知函数f（x）=|x+a|+|x﹣2|①当a=﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．【解答】解：（1）当a=﹣3时，f（x）≥3 即|x﹣3|+|x﹣2|≥3，即，可得x≤1；，可得x∈∅；，可得x≥4．取并集可得不等式的解集为{x|x≤1或x≥4}．（2）原命题即f（x）≤|x﹣4|在[1，2]上恒成立，等价于|x+a|+2﹣x≤4﹣x在[1，2]上恒成立，等价于|x+a|≤2，等价于﹣2≤x+a≤2，﹣2﹣x≤a≤2﹣x在[1，2]上恒成立．故当1≤x≤2时，﹣2﹣x的最大值为﹣2﹣1=﹣3，2﹣x的最小值为0，故a的取值范围为[﹣3，0]．赠送—高中数学知识点【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x=，令()u g x=，若()y f u=为增，()u g x=为增，则[()]y f g x=为增；若()y f u=为减，()u g x=为减，则[()]y f g x=为增；若()y f u=为增，()u g x=为减，则[()]y f g x=为减；若()y f u=为减，()u g x=为增，则[()]y f g x=为减．（2）打“√”函数()(0)af x x ax=+>的图象与性质()f x分别在(,-∞、)+∞上为增函数，分别在[、上为减函数．（3）最大（小）值定义①一般地，设函数()y f x=的定义域为I，如果存在实数yxoM 满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．。

厦门六中2016—2017学年上学期高一期中考试数 学 试 卷满分：150分 考试时间：120分钟 、第Ⅰ卷（选择题 共60分）一、选择题 (本题共12小题，每小题5分，共60分)1．下列命题正确的是 （ ）A.接近0的实数可以构成集合B.{}R =实数集C.集合{}2|1y y x =-与集合(){}2,|1x y y x =-是同一个集合D.参加2016年金砖国家峰会的所有国家可以构成一个集合．2．函数()()lg 2f x x =+的定义域为 （ ）A.()2,1-B.[]2,1-C.()2,-+∞D.(]2,1-3．已知幂函数()f x x α=的图象过点)2,2(，则1()4f = （ ）A.12- B.2 C.12 D.34．下列四个函数中，在),0(+∞上为增函数的是 （ ）A ．x x f -=3)(B ．x x x f 3)(2-=C ．11)(+-=x x f D ．x x f -=)(5．已知函数b a bx ax x f +++=3)(2是定义域为]2,1[a a -的偶函数，则b a +的值 （ ）A ．0B ．31C ． 1D ．1-6．若()()12f x f x +=，则()f x 的解析式可以是 （ ）A.()2f x x =B.()2x f x =C.()2f x x =+D.()2log f x x =7．用二分法求方程x x -=3lg 的近似解，可以取的一个区间是 （ ）A ． )1,0(B ．)2,1(C ．)3,2(D ．)4,3(8．已知0.6log 0.5a =，ln 0.5b =，0.50.6c =．则 （ ）A.>>a b cB.>>a c bC.>>c a bD.>>c b a1234x x x x <<<，则3122341()x x x x x ++的取值范围是 （ ） A ．(1,)-+∞ B ．(]1,1- C ．(,1)-∞ D ．[)1,1- 第II 卷（非选择题 共90分）二、填空题（本题共4小题，每小题5分，共20分）13．某林场今年造林10000亩，计划以后每一年比前一年多造林10%，那么从明年算起第3年内将造林 亩.14．已知函数|1|(1)()3(1)x x x f x x -⎧=⎨>⎩≤，()2f a =，则a = ． 15．若集合{}2(2)210A x k x kx =+++=有且仅有2个子集，则实数k 的值是__ _．16．已知函数()f x 对于一切实数,x y 均有()()()21f x y f y x x y +-=++成立,且(1)0f =,则当,不等式()2log a f x x +<恒成立时,则实数a 的取值范围是 .三．解答题（本大题有6小题，共70分;解答时应写出文字说明与演算步骤）17．（本小题满分10分）计算下列各题：（1）()0lg 4lg 254π+- （2）2334lg32lg 427256lg 2-++18．（本小题满分12分）已知集合{}2|log ,4A y y x x ==≥，1|(),102x B y y x ⎧⎫==-≤≤⎨⎬⎩⎭． （1）求A B ；（2）若集合{}C |21x a x a =≤≤-，且CB B =，求实数a 的取值范围．19．（本小题满分12分）已知()y f x =是定义在R 上的奇函数， 当0x >时，2()2f x x x =-.（1）画出()f x 的简图, 并求()f x 的解析式；（2）利用图象讨论方程()f x k =的根的情况。

福建省厦门六中高二上学期期中考试（数学理）一、选择题：本题共10个小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一个是正确的，把正确选项的代号填在答题卡的指定位置上.1. 已知直线方程y －3=3(x －4），则这条直线经过的已知点，倾斜角分别是( ) （A ）、（4，3）；3π （B ）、（－3，－4）；6π（C ）、（4，3）；6π （D ）、（－4，－3）；3π2. 点2(5)P m ，与圆2224x y +=的位置关系是（ ） Ａ．在圆外Ｂ．在圆内Ｃ．在圆上Ｄ．不确定3. 命题“0x R ∃∈，3210x x -+>”的否定是 ( ) A ．0x R ∃∈，3210x x -+< B ． x R ∀∈，3210x x -+≤ C ．0x R ∃∈，3210x x -+≤ D ．不存在x R ∈，3210x x -+> 4. 若a =(2x ,1,3),b =(1,－2y ,9),如果a 与b 为共线向量，则（ ）A. x =1, y =1B. x =21, y = －21 C. x =61, y = －23 D. x = －61, y =235. 以点(34)-，为圆心，且与x 轴相切的圆的方程是（ ） Ａ．22(3)(4)16x y -++= Ｂ．22(3)(4)16x y ++-= Ｃ．22(3)(4)9x y -++=Ｄ．22(3)(4)9x y ++-=6. 方程2211k 1x y k +=+-表示双曲线，则k 的取值范围是（ ）A ．11<<-kB ．0>kC ．0≥kD ．1>k 或1-<k 7. 如果椭圆的两个顶点为（3，0），（0，－4），则其标准方程为（ ）(A )13422=+y x (B )191622=+y x (C )14322=+y x (D )116922=+y x8. 抛物线2y ax =的准线方程为2y =，则a 的值为（ ）Ａ．18Ｂ．18-Ｃ．8 Ｄ．8-9. 直线cos sin 0x y a θθ++=与sin cos 0x y b θθ-+=的位置关系是（ ） A ．平行 B ．垂直 C ．斜交 D ．与,,a b θ的值有关10. 平面内过点A （－2，0），且与直线x =2相切的动圆圆心的轨迹方程是（ ）A ． y 2=－2xB ． y 2=－4xC ．y 2=－8xD ．y 2=－16x二、填空题（本题共5小题，每小题4分，共11．直线3x+4y-12=0和直线6x+8y+6=0间的距离是12．椭圆x 2+4y 2=1的离心率是13. 双曲线191622=-y x 上的点P 到点(5,0)的距离为9，则P 到(5,0)-距离为___________14. 若向量(1)λ=，，1a 与(212)=-，，b ，则λ= 15. 如果实数x ，y 满足3)2(22=-+y x ，那么yx的取值范围是 三．解答题（本大题共6小题，共80分;解答应写出文字说明与演算步骤）16.(本小题满分13分)已知三角形ABC 的顶点坐标为A （-1，5）、B （-2，-1）、C （4，3）。

福建省厦门第六中学2025届高三第一次模拟考试数学试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()5sin 12f x x π⎛⎫=+ ⎪⎝⎭，要得到函数()cos g x x =的图象，只需将()y f x =的图象( )A ．向左平移12π个单位长度 B ．向右平移12π个单位长度C ．向左平移512π个单位长度 D ．向右平移512π个单位长度 2．已知集合{|24}A x x =-<<，集合2560{|}B x x x =-->，则A B =A ．{|34}x x <<B ．{|4x x <或6}x >C ．{|21}x x -<<-D ．{|14}x x -<<3．数列{a n }，满足对任意的n ∈N +，均有a n +a n +1+a n +2为定值.若a 7=2，a 9=3，a 98=4，则数列{a n }的前100项的和S 100=( ) A ．132B ．299C ．68D ．994．已知l ，m 是两条不同的直线，m ⊥平面α，则“//l α”是“l ⊥m ”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件5．复数z 满足()11z z i -=+ (i 为虚数单位),则z 的值是( ) A ．1i +B ．1i -C ．iD ．i -6．已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，a ，b ，且()520,02a b a b +=>>，则此三棱锥外接球表面积的最小值为（ ）A ．174π B ．214π C ．4π D ．5π7．设12,x x 为()()3sin cos 0f x x x ωωω=->的两个零点，且12x x -的最小值为1，则ω=（ ） A ．πB ．2π C ．3π D ．4π 8．双曲线2214x y -=的渐近线方程是（ ）A ．32y x =±B ．233y x =±C ．2x y =±D ．2y x =±9．若集合{|2020}A x N x =∈=，22a =，则下列结论正确的是（ ）A ．{}a A ⊆B ．a A ⊆C ．{}a A ∈D ．a A ∉10．本次模拟考试结束后，班级要排一张语文、数学、英语、物理、化学、生物六科试卷讲评顺序表，若化学排在生物前面，数学与物理不相邻且都不排在最后，则不同的排表方法共有（ ） A ．72种B ．144种C ．288种D ．360种11．设双曲线22:1916x y C -=的右顶点为A ，右焦点为F ，过点F 作平行C 的一条渐近线的直线与C 交于点B ，则AFB △的面积为（ ）A ．3215B ．6415C ．5D ．612．为了贯彻落实党中央精准扶贫决策，某市将其低收入家庭的基本情况经过统计绘制如图，其中各项统计不重复．若该市老年低收入家庭共有900户，则下列说法错误的是（ ）A ．该市总有 15000 户低收入家庭B ．在该市从业人员中，低收入家庭共有1800户C ．在该市无业人员中，低收入家庭有4350户D ．在该市大于18岁在读学生中，低收入家庭有 800 户 二、填空题：本题共4小题，每小题5分，共20分。

厦门市第六中学2016届高三上学期期中考试数学试卷（文）（满分：150分，时间：120分钟）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 设集合{}41<<-=x x A ，{}4,2,1,1-=B ，则B A ⋂＝（ ） A ．{}2,1 B ．{}4,1- C ．{}2,1- D ．{}4,22．在复平面内，复数i i ⋅+)54(（i 为虚数单位）的共轭复数对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3．若是向量，则“”是“”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 4．曲线在点处的切线方程为=（ ）A ．B ．C ．D ．5．设0.332211log ,,log (log 2)43a b c ⎛⎫=== ⎪⎝⎭，则（ ）A ．a c b <<B ．c b a <<C ．b a c <<D ．b c a << 6．已知数列{}n a 满足11=a ，n n a a 21=-),2(*N n n ∈≥，则数列{}n a 的前6项和为（ ） A.63 B ．127 C ．3263 D ．127647．函数)22,0)(sin(2)(πϕπωϕω<<->+=x x f 的图象如图所示，则=⋅BD AB （ ）A ．8B ．8-C ．882+-π D.882-π8. 已知平行四边形ABCD 的对角线分别为BD AC ,，且EC AE 2=，点F 是BD 上靠近D 的四等分点，则（ ）9.设函数212,2()143,2x x x a x f x x ⎧-+<⎪⎪=⎨⎪-≥⎪⎩的最小值为1-，则实数的取值范围是（ ）A. B.C. D. 10. 设命题：函数的图象向左平移个单位长度得到的曲线关于轴对称；命题：函数在上是增函数．则下列判断错误的是（ ）A ．为假B ．为真C ．为假D ．为真11. 已知数列}{n a 的前n 项和为n n S n -=2，令2co s πn a b n n =，记数列}{n b 的前n 项为n T ，则2015T =（ ）A.1008-B. 2013-C. 2014-D. 3020-l2．若偶函数(),y f x x R =∈，满足(2)()f x f x +=-，且[0,2]x ∈时，2()3f x x =-，则方程()sin ||f x x =在[]10,10-内的根的个数为（ ）A ．12B ．10C ．9D ．8二、填空题：(本大题共4个小题，每小题5分，共20分)13. 已知,a b 均为单位向量，它们的夹角为60，则3a b +=_________.14. 若等比数列{}n a 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a ++⋅⋅⋅+=____________.15．某校运动会开幕式上举行升旗仪式，在坡度为15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10 6 m ，则旗杆的高度为_________. 16．已知函数22()f x x x =+,1()()2xg x m =-.若1x ∈[1,2],2x ∈[-1,1]使12()()f x g x ≥,则实数m 的取值范围是.a 41-≥a 41->a 2-≥a 2->a ∀∃三、解答题（本题共6小题，共74分。

福建省厦门市第六中学2023-2024学年高一上学期期中考
试数学试题
学校:___________姓名：___________班级：___________考号：___________．若函数(2)
+的定义域为（
y f x
=的定义域为1)
-B．5,7]
2,2]
-
二、多选题
9．某打车平台欲对收费标准进行改革，现制定了甲、乙两种方案供乘客选择，其支付费用与打车里程数的函数关系大致如图所示，则下列说法正确的是（）
A．当打车距离为8km时，乘客选择甲方案省钱
B．当打车距离为10km时，乘客选择甲、乙方案均可
C．打车3km以上时，每公里增加的费用甲方案比乙方案多
（2）根据题意，令0x >，则又由函数()f x 是定义在R 上的奇函数，则()224,04,0
x x x x x x x ì+£=í-+>î．（3）根据题意，[]2,4x Î，则。

厦门六中2016届高三上学期半期考数学（文科）试卷数学（文）试题（满分：150分，时间：120分钟） 2015-11-10一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 设集合{}41<<-=x x A ，{}4,2,1,1-=B ，则B A ⋂＝ A ．{}2,1 B ．{}4,1- C ．{}2,1- D ．{}4,2 2．在复平面内，复数i i ⋅+)54(（i 为虚数单位）的共轭复数对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．若,r r a b 是向量，则“=r ra b ”是“r r a =b ”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4．曲线31y ax bx =+-在点(1,(1))f 处的切线方程为,y x b a =-则=A ．3-B ．2C ．3D ．45．设0.332211log ,,log (log 2)43a b c ⎛⎫=== ⎪⎝⎭，则A ．a c b <<B ．c b a <<C ．b a c <<D ．b c a <<6．已知数列{}n a 满足11=a ，n n a a 21=-),2(*N n n ∈≥，则数列{}n a 的前6项和为A.63 B ．127 C ． 3263D ．127647．函数)22,0)(sin(2)(πϕπωϕω<<->+=x x f 的图象如图所示，则=⋅BD ABA ．8B ．8-C ．882+-π错误!未找到引用源。

D.882-π8. 已知平行四边形ABCD 的对角线分别为BD AC ,，且EC AE 2=，点F 是BD 上靠近D 的四等分点，则9.设函数212,2()143,2x x x a x f x x ⎧-+<⎪⎪=⎨⎪-≥⎪⎩的最小值为1-，则实数a 的取值范围是A.41-≥aB.41->aC.2-≥aD.2->a 10. 设命题p ：函数)32sin(π+=x y 的图象向左平移6π个单位长度得到的曲线关于y 轴对称；命题q ：函数13-=x y 在[)+∞-,1上是增函数．则下列判断错误的是A ．p 为假B ．q ⌝为真C ．q p ∧为假D ．q p ∨为真11. 已知数列}{n a 的前n 项和为n n S n -=2，令2cos πn a b n n =，记数列}{n b 的前n 项为n T ，则2015T = A.1008-B. 2013-C. 2014-D. 3020-l2．若偶函数(),y f x x R =∈，满足(2)()f x f x +=-，且[0,2]x ∈时，2()3f x x =-，则方程()sin ||f x x =在[]10,10-内的根的个数为A ．12B ．10C ．9D ．8二、填空题：(本大题共4个小题，每小题5分，共20分)13. 已知,a b r r均为单位向量，它们的夹角为60o，则3a b +=r r _________.14. 若等比数列{}n a 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a ++⋅⋅⋅+=____________.15．某校运动会开幕式上举行升旗仪式，在坡度为15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10 6 m ，则旗杆的高度为_________. 16．已知函数22()f x x x =+,1()()2xg x m =-.若∀1x ∈[1,2],∃2x ∈[-1,1]使12()()f x g x ≥,则实数m 的取值范围是 .三、解答题（本题共6小题，共74分。

2014-2015厦门六中高二年上学期期中考试数 学 试 题 （理科）满分150分 考试时间120分钟注意事项：1. 本试题共分三大题，全卷共150分。

考试时间为120分钟。

2．第I 卷必须使用2B 铅笔填涂答题卡相应题目的答案标号，修改时，要用橡皮擦干净。

3. 第II 卷必须使用0.5毫米的黑色墨水签字笔书写在答题纸的指定位置，在草稿纸和本卷上答题无效。

作图时，可用2B 铅笔，要求字体工整、笔迹清晰。

第Ⅰ卷（选择题 共50分）一、选择题：(本题共10个小题，每小题5分，共50分) 1．若命题“p q ∨”为真，“p ⌝”为真，则 （ ） A ．p 真q 真 B ．p 假q 假 C ．p 真q 假 D ．p 假q 真2.已知R c b a ∈,,，那么下列命题中一定正确的是（ ）A ．若cbc a >，则b a > B ．若,d,c bd a b c a >>>则－－ C ．若b c a c b a +<-->则, D ．若a b >，则22a b >3.已知△ABC中，060a b ===，则B=（ ） A 、450 B 、1350 C 、450或1350 D 、300或15004.某种细胞每隔30分钟分裂1次,1个分裂成2个,则1个这样的细胞经过4小时30分钟后,可得到的细胞个数为 （ ）A 、512B 、511C 、1024D 、1023 5．命题“0x R ∃∈，3210x x -+>”的否定是 （ ）A ．x R ∀∈，3210x x -+≤ B ．x R ∀∈，3210x x -+> C ．0x R ∃∈，3210x x -+≤ D ．0x R ∃∈，3210x x -+< 6.下列函数中，最小值为4的是（ ）A ． 4y x x =+ （3x ≥）B ． 4sin sin y x x =+ (0)x π<<C ． e 4exx y -=+ D ．3log 4log 3x y x =+7.在等比数列{}n a 中，若481,3S S ==，则20191817a a a a +++的值为（ ） A 5 B 9 C 16 D 818.若不等式组0024x y y x y x s≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩表示的平面区域是一个三角形，则s 的取值范围是 ( )A ．0<s ≤2或s ≥4B ．0<s ≤2C ．2≤s ≤4D ．s ≥49.ABC ∆的内角,,A B C 的对边分别为,,a b c ，若,,a b c 成等比数列，且2c a =，则co s B 等于（ ） A ．14 BC ．34D10．在数列{a n }中，若a 2n －a 2n ＋1＝p (n ≥1，n ∈N *，p 为常数)，则称{a n }为“等方差数列”，下列是对“等方差数列”的判断：①若{a n }是等方差数列，则{a 2n }是等差数列； ②{(－1)n }是等方差数列； ③若{a n }是等方差数列，则{a kn }(k ∈N *，k 为常数)也是等方差数列． 其中真命题的序号是（ ）A. ②B. ①②C. ②③D. ①②③第II 卷（非选择题共100分）二、填空题:（本题共6小题，每小题4分，共24分）11.已知数列{}n a 满足11=a ，12=a ，n n n a a a +=++12，则6a = .12.321=3sin 2sin sin a b cABC A B C+-∆+-已知外接圆半径为，则 .13.函数1(01)x y a a a -=>≠,的图象恒过定点A ，若点A 在直线10(0)mx ny mn +-=>上，则11m n+的最小值为 ．14.若不等式2(2)2(2)40a x a x -+--<对一切x R ∈恒成立,则a 的取值范围是 ．15.2的部分对应值如下表：则不等式0ax bx c ++>的解集是 。

厦门六中2015—2016学年度学期期考试 考试日期：201.11.10 第Ⅰ卷（选择题共50分） 一、选择题：（本大题共1小题，每小题5分，共分.在每小题给出的四个选项中，只有一项是符合题目要求的.．已知集合，则下列关系中正确的是（）A．　B． C． D． 为相同函数的是（） A. B. C. D. 已知函数是定义域为的偶函数，则的值 A．0 B． C． 1 D．（） 4．下列函数中,在其定义域内既是奇函数又是减函数的是（） A. B. C. D. 三个数之间的大小关系是（） A．. B． C． D． 设函数上单调递增，则的大小关系为（） A. B. C. D.不确定 10．设a为大于1的常数，函数若关于x的方程 恰有三个不同的实数解，则实数b的取值范围是 A．0＜b≤10＜b＜10≤b≤1 D．b＞1．二、填空题：本大题共小题，每小题分，共2分函数的是 ___ ____.． (,),则. 其中正确的序号是 . 三、解答题：本大题共6小题, 共7分. 解答应写出文字说明、证明过程或演算步骤.计算下列各式的值： ()； ()(lg2)2+lg5·lg20+ lg100; （3）已知. 求a、b，并用表示。

｝，B＝｛，｝．B，． ｝，若CB，求实数的取值范围．． 21.（本小题满分13分） 已知函数(1)判断函数的奇偶性；(2)求该函数的值域；(3)判断在上的. 22（本小题满分13分）． 设函数，，为常数 （1）用表示的最小值，求的解析式 （2）在（1）中，是否存在最小的整数，使得对于任意均成立，若存在，求出的值；若不存在，请说明理由. 厦门六中201—2016学年上学期高一期中考试 数学答题卷 满分150分考试时间120分钟考试日期：201.11.10 一、选择题：共50分.把正确选项的代号填在答题卡的指定位置上. 二、填空题（每小题4分，共24分） 11．_____ _____ 12．_______ 13._____ _____ 14．____ ___ 15． _________ 16．_____ _____ 三、解答题（本大题共6小题，满分76分） 17．（本小题满分12分）解： 18. （本小题满分12分）解： 19. （本小题满分13分）解： 20.（本小题满分13分）解： 21.（本小题满分13分）解： 22.（本小题满分13分）解： 密封线内请勿答题 班级座号姓名 密封线内请勿答题 A。

厦门六中20015—2016学年上学期高三期中考试英语试卷本试卷分卷I(选择题)和第II卷(非选择题)。

第I卷第一部分听力(共两节，满分30分)第一节(共5小題；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有l0秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What is the time now？A. 2:30 p.m.B. 3:00 p.m.C. 3:30 p.m.2. What did the woman do at the weekend？A. She watched TV.B. She went for a drive.C. She climbed a mountain.3. Where does the conversation take place？A. At a library.B. At a store.C. At a hospital.4. What are the speakers mainly talking about？A. A book.B. A film.C. A story.5. How will the speakers probably get to the cinema？A. By bus.B. By subway.C. By taxi.第二节(共15小题，每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时问阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6. What color do the speakers decide to paint their living room？A. Bright orange.B. Dark brown.C. Light blue.7. What is the man going to do at the weekend？A. Buy the paint.B. Paint the walls.C. Repair the computer.听第7段材料，回答第8、9题。

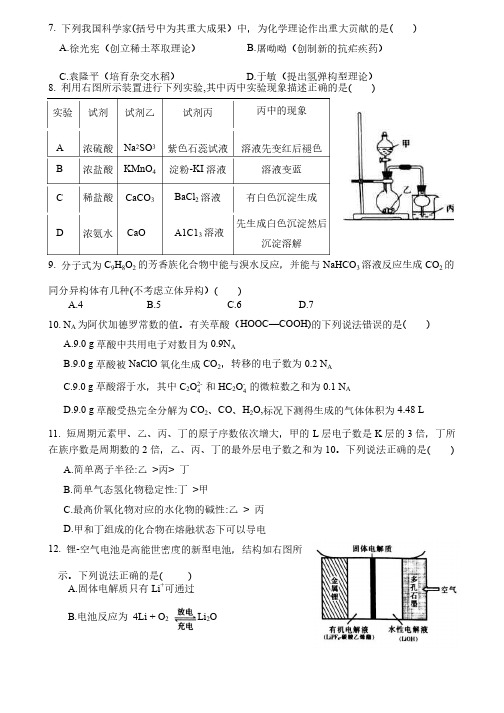
7. 下列我国科学家(括号中为其重大成果）中，为化学理论作出重大贡献的是( ) A.徐光宪（创立稀土萃取理论） B.屠呦呦（创制新的抗疟疾药） C.袁隆平（培育杂交水稻）袁隆平（培育杂交水稻） D.于敏（提出氢弹构型理论）于敏（提出氢弹构型理论） 8. 利用右图所示装置进行下列实验,其中丙中实验现象描述正确的是( ) 实验 试剂 试剂乙 试剂丙丙中的现象A 浓硫酸浓硫酸 Na 2SO 3 紫色石蕊试液紫色石蕊试液 溶液先变红后褪色溶液先变红后褪色B 浓盐酸 KMnO 4 淀粉-KI 溶液 溶液变蓝C 稀盐酸 CaCO 3 BaCl 2溶液 有白色沉淀生成 D浓氨水 CaOA1C13溶液先生成白色沉淀然后沉淀溶解9. 分子式为C 9H 8O 2的芳香族化合物中能与溴水反应，并能与NaHCO 3溶液反应生成CO 2的同分异构体有几种(不考虑立体异构）( ) A.4 B.5C.6D.710. N A 为阿伏加德罗常数的值。

有关草酸（HOOC HOOC——COOH)的下列说法错误的是( ) A.9.0 g 草酸中共用电子对数目为0.9N AB.9.0 g 草酸被NaClO 氧化生成CO 2，转移的电子数为0.2 N AC.9.0 g 草酸溶于水，其中C 2O 2-4 和HC 2O -4的微粒数之和为0.1 N A D.9.0 g 草酸受热完全分解为CO 2、CO 、H 2O,标况下测得生成的气体体积为4.48 L 11. 短周期元素甲、乙、丙、丁的原子序数依次增大，甲的L 层电子数是K 层的3倍，丁所在族序数是周期数的2倍，乙、丙、丁的最外层电子数之和为10。

下列说法正确的是( )A.简单离子半径:乙 >丙> 丁B.简单气态氢化物稳定性:丁 >甲C.最髙价氧化物对应的水化物的碱性:乙 > 丙D.甲和丁组成的化合物在熔融状态下可以导电12. 锂-空气电池是高能世密度的新型电池，结构如右图所示。

2015-2016学年福建省厦门市双十中学高三(上）期中数学试卷（理科）一、选择题:本大题共12小题，每小题5分,共60分．在给出的四个选项中,只有一项是符合题目要求的.1．已知集合M={y｜y=x2+1，x∈R}，集合N=｛y|y=ln（x+1）+1，x∈R｝，则M∩N等于（）A．{（0，1）｝B．(0,1）C．［﹣1,+∞) D．［1，+∞）2．命题“若¬p则q”是真命题，则p是¬q的(）条件．A．充分 B．充分非必要C．必要 D．必要非充分3．已知，的夹角是120°,且=（﹣2，﹣4），｜|=，则在上的投影等于（) A．﹣B．C．2D．4．已知p:存在x∈R，mx2+1≤0，q：任意x∈R，x2+mx+1＞0，若p且q为真命题，则实数m 的取值范围是（）A．m＜2 B．﹣2＜m＜2 C．0＜m＜2 D．﹣2＜m＜05．在△ABC中，角A,B，C，的对边分别为a,b，c，若(a2+c2﹣b2）tanB=ac，则角B的值为（）A．B．或 C．D．或6．已知点C在以O为圆心的圆弧AB上运动（含端点）。

，=x+2y(x，y∈R），则的取值范围是()A．B．C．D．7．若函数f（x）=sin（x+φ）﹣cos(x+φ）（0＜φ＜π）为奇函数，将函数f(x)图象上所有点横坐标变为原来的一半，纵坐标不变；再向右平移个单位得到函数g（x），则g（x）的解析式可以是（）A．B．C．D．8．已知如图（1)的图象对应的函数为y=f(x),给出①y=f(|x|）；②y=|f（x）|﹣a;③y=﹣f(|x|）;④y=f（﹣｜x|）．⑤y=｜f（｜x｜）|﹣a,则如图(2）的图象对应的函数可能是五个式子中的（）A．④B．②④C．①②D．②③④⑤9．已知定义域为R的奇函数y=f（x）的导函数为y=f′（x）,当x≠0时，,若a=f（),，c=（ln）f（ln），则a，b，c的大小关系正确的是（) A．a＜c＜b B．b＜c＜a C．a＜b＜c D．c＜a＜b10．若函数f(x）（x∈R)关于对称，且则下列结论：（1）f（x）的最小正周期是3，（2）f（x）是偶函数，（3）f（x）关于对称，(4）f（x）关于对称，正确的有（)A．1个B．2个C．3个D．4个11．如图，已知l1⊥l2，圆心在l1上，半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动，圆被直线l2所截上方圆弧长记为x，令y=，则y与时间t（0≤t≤1，单位：s)的函数y=f(t）的图象大致为（）A． B． C． D．12．设函数f（x）=，若f（x）恰有2个零点，则实数a的取值范围是（）A．a≥2 B．≤a＜1 C．＜a＜1 D．a≥2或≤a＜1二、填空题：（本大题共4小题，每小题5分，共20分)．13．若tan(θ+）=，则sin2θ=．14．设等差数列｛a n｝前n项和S n，a3+a8+a13=C，a4+a14=2C，其中C＜0，则S n在n等于时取到最大值．15．已知f（x）=x2﹣4x+3在[0,a］的值域是［﹣1，3］．实数a的取值范围记为集合A，g （x）=cos2x+sinx．记g（x）的最大值为g（a）．若g（a）≥b，对任意实数a∈A恒成立，则实数b的取值范围是．16．若函数f（x）=（1﹣x2）（x2+ax+b）的图象关于直线x=﹣1对称,则f（x）的最大值为．三、解答题：（本大题共7小题，共70分，解答应写出文字说明、证明过程或演算步骤）。

2016-2017学年福建省厦门六中高三（上）期中数学试卷（理科）二、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}，则A∩B=（）A．{x|0＜x＜1}B．{x|0≤x＜1}C．{x|﹣1＜x≤1}D．{x|﹣2＜x≤1}2．（5分）锐角△ABC，则z=（sinA﹣cosB）+i（cosA﹣sinB）对应点位于复平面的（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）在△ABC中，内角A，B的对边分别是a，b，且A=30°，a=2，b=4，那么满足条件的△ABC（）A．有一个解B．有两个解C．无解D．不能确定4．（5分）设S n是公差不为零的等差数列{a n}的前n项和，且a1＞0，若S5=S9，则当S n最大时，n=（）A．6 B．7 C．10 D．95．（5分）阅读程序框图，若输出结果S=，则整数m的值为（）A．7 B．8 C．9 D．106．（5分）下列命题中正确命题的个数是（）①对于命题p：∃x∈R，使得x2+x﹣1＜0，则￢p：∀x∈R，均有x2+x﹣1＞0；②p是q的必要不充分条件，则￢p是￢q的充分不必要条件；③命题“若x=y，则sinx=siny”的逆否命题为真命题；④“m=﹣1”是“直线l1：mx+（2m﹣1）y+1=0与直线l2：3x+my+3=0垂直”的充要条件．A．1个 B．2个 C．3个 D．4个7．（5分）《张丘建算经》卷上第22题﹣﹣“女子织布”问题：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（）A．尺 B．尺C．尺D．尺8．（5分）函数f（x）=sinx+sin（﹣x）的图象的一条对称轴为（）A．x=B．x=πC．x=D．x=9．（5分）设，为单位向量．且，的夹角为，若=x+（1﹣x），x∈[0，1]，=2则向量在方向上的投影的取值范围是（）A．[，1]B．[0，2]C．[0，1]D．[1，3]10．（5分）已知f（x）是定义在R上的奇函数，f（x+1）是偶函数，当x∈（2，4）时，f（x）=|x﹣3|，则f（1）+f（2）+f（3）+f（4）=（）A．1 B．0 C．2 D．﹣211．（5分）如图，某飞行器在4千米高空飞行，从距着陆点A的水平距离10千米处开始下降，已知下降飞行轨迹为某三次函数图象的一部分，则该函数的解析式为（）A．y=﹣x B．y=x3﹣xC．y=x3﹣x D．y=﹣x3+x12．（5分）已知定义在（0，）上的函数f（x），f′（x）为其导函数，且f（x）＜f′（x）•tanx恒成立，则（）A．f（）＞f（）B．f（）＜f（）C．f（）＞f （） D．f（1）＜2f（）•sin1二．填空题（本大题共4小题，每小题5分，共20分）13．（5分）向量，满足||=1，||=，（+）⊥（2﹣），则向量与的夹角为．14．（5分）（+x3）dx=．15．（5分）△ABC的内角A，B，C所对的边分别为a，b，c，且a，b，c成等比数列，若sinB=，cosB=，则a+c的值为．16．（5分）在数列{a n}中，a1=2，a n+1=a n+ln（1+），则a n=．四、解答题（本大题共6个小题，满分70分．解答应写出必要的文字说明、证明过程或演算步骤．请将解答过程写在答题纸的相应位置．）17．（10分）设函数f（x）=|2x﹣1|﹣|x+2|．（Ⅰ）解不等式f（x）＞3；（Ⅱ）若∃x0∈R，使得f（x0）+2m2＜4m，求实数m的取值范围．18．（12分）已知在△ABC中，角A、B、C的对边分别是a、b、c，且2sin2A+3cos （B+C）=0．（1）求角A的大小；（2）若△ABC的面积S=5，a=，求sinB+sinC的值．19．（12分）已知数列{a n}前n项和为S n，满足S n=2a n﹣2n（n∈N*）．（I）证明：{a n+2}是等比数列，并求{a n}的通项公式；（Ⅱ）数列{b n}满足b n=log2（a n+2），T n为数列{}的前n项和，若T n＜a 对正整数a都成立，求a的取值范围．20．（12分）如图，已知等边△ABC中，E，F分别为AB，AC边的中点，N为BC 边上一点，且CN=BC，将△AEF沿EF折到△A′EF的位置，使平面A′EF⊥平面EF﹣CB，M为EF中点．（1）求证：平面A′MN⊥平面A′BF；（2）求二面角E﹣A′F﹣B的余弦值．21．（12分）已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．（1）求曲线C的直角坐标方程和直线L的普通方程；（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．22．（12分）已知函数f（x）=alnx+bx（a，b∈R）在点（1，f（1））处的切线方程为x﹣2y﹣2=0．（1）求a，b的值；（2）当x＞1时，f（x）+＜0恒成立，求实数k的取值范围；（3）证明：当n∈N*，且n≥2时，++…+＞．2016-2017学年福建省厦门六中高三（上）期中数学试卷（理科）参考答案与试题解析二、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}，则A∩B=（）A．{x|0＜x＜1}B．{x|0≤x＜1}C．{x|﹣1＜x≤1}D．{x|﹣2＜x≤1}【解答】解：∵集合A={x|﹣2＜x＜1}，B={x|x2﹣2x≤0}={x|0≤x≤2}，∴A∩B={x|0≤x＜1}，故选：B．2．（5分）锐角△ABC，则z=（sinA﹣cosB）+i（cosA﹣sinB）对应点位于复平面的（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：∵△ABC为锐角，∴A+B＞，∴A＞﹣B，∴sinA＞，cosA＜cos，∴sinA＞cosB，cosA＜sinB，∴sinA﹣cosB＞0，cosA﹣sinB＜0．∴Z对应点在第四象限．故选：D．3．（5分）在△ABC中，内角A，B的对边分别是a，b，且A=30°，a=2，b=4，那么满足条件的△ABC（）A．有一个解B．有两个解C．无解D．不能确定【解答】解：∵由=，得sinB===，又∵b＞a，∴B＞A，∴B=45°或135°，故有两解．故选：B．4．（5分）设S n是公差不为零的等差数列{a n}的前n项和，且a1＞0，若S5=S9，则当S n最大时，n=（）A．6 B．7 C．10 D．9【解答】解：由题意可得S9﹣S5=a6+a7+a8+a9=0，∴2（a7+a8）=0，∴a7+a8=0，又a1＞0，∴该等差数列的前7项为正数，从第8项开始为负数，∴当S n最大时，n=7故选：B．5．（5分）阅读程序框图，若输出结果S=，则整数m的值为（）A．7 B．8 C．9 D．10【解答】解：模拟执行程序框图，可得S=0，n=1满足条件n≤m，S=，n=2满足条件n≤m，S=+，n=3…满足条件n≤m，S=++…++=（1﹣）+（）+…+（）+（）=1﹣=，n=10由题意，此时应该不满足条件，退出循环，输出S的值为，故判断框内的条件应该为：n≤9．故选：C．6．（5分）下列命题中正确命题的个数是（）①对于命题p：∃x∈R，使得x2+x﹣1＜0，则￢p：∀x∈R，均有x2+x﹣1＞0；②p是q的必要不充分条件，则￢p是￢q的充分不必要条件；③命题“若x=y，则sinx=siny”的逆否命题为真命题；④“m=﹣1”是“直线l1：mx+（2m﹣1）y+1=0与直线l2：3x+my+3=0垂直”的充要条件．A．1个 B．2个 C．3个 D．4个【解答】解：①对于命题p：∃x∈R，使得x2+x﹣1＜0，则￢p：∀x∈R，均有x2+x﹣1≥0，因此不正确；②p是q的必要不充分条件，则￢p是￢q的充分不必要条件，正确；③由于命题“若x=y，则sinx=siny”是真命题，因此其逆否命题也为真命题，正确；④当m=0时，直线l1：mx+（2m﹣1）y+1=0与直线l2：3x+my+3=0垂直；m≠0时，若两条直线垂直，则=﹣1，解得m=﹣1，可知：“m=﹣1”是“直线l1：mx+（2m﹣1）y+1=0与直线l2：3x+my+3=0垂直”的充分不必要条件，因此不正确．综上可得：正确命题的个数为：2．故选：B．7．（5分）《张丘建算经》卷上第22题﹣﹣“女子织布”问题：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（）A．尺 B．尺C．尺D．尺【解答】解：设该妇子织布每天增加d尺，由题意知，解得d=．故该女子织布每天增加尺．故选：B．8．（5分）函数f（x）=sinx+sin（﹣x）的图象的一条对称轴为（）A．x=B．x=πC．x=D．x=【解答】解：f（x）=sinx+sin（﹣x）=sinx+cosx+sinx=sin（x+），∴x=是函数f（x）=sinx+sin（﹣x）的图象的一条对称轴，故选：D．9．（5分）设，为单位向量．且，的夹角为，若=x+（1﹣x），x∈[0，1]，=2则向量在方向上的投影的取值范围是（）A．[，1]B．[0，2]C．[0，1]D．[1，3]【解答】解：由题意可得•=1×1×cos=，=2x+（2﹣2x）•=x+1，||=2，则向量在方向上的投影为=．再根据x∈[0，1]，则∈[，1]，即向量在方向上的投影的取值范围是[，1]，故选：A．10．（5分）已知f（x）是定义在R上的奇函数，f（x+1）是偶函数，当x∈（2，4）时，f（x）=|x﹣3|，则f（1）+f（2）+f（3）+f（4）=（）A．1 B．0 C．2 D．﹣2【解答】解：∵f（x）是定义在R上的奇函数，f（x+1）是偶函数，∴f（0）=0，f（﹣x）=﹣f（x），f（﹣x+1）=f（x+1），∴f（x+4）=f[（x+3）+1]=f[﹣（x+3）+1]=f（﹣x﹣2）=﹣f（x+2）=﹣f[（x+1）+1]=﹣f[﹣（x+1）+1]=﹣f（﹣x）=f（x），∴函数f（x）是周期为4的周期函数，f（4）=f（0）=0，∵当x∈（2，4）时，f（x）=|x﹣3|，∴f（3）=0，f（4）=0，f（1）=﹣f（﹣1）=﹣f（3）=0，f（2）=﹣f（﹣2）=﹣f（2）=0，故f（1）+f（2）+f（3）+f（4）=0，故选：B．11．（5分）如图，某飞行器在4千米高空飞行，从距着陆点A的水平距离10千米处开始下降，已知下降飞行轨迹为某三次函数图象的一部分，则该函数的解析式为（）A．y=﹣x B．y=x3﹣xC．y=x3﹣x D．y=﹣x3+x【解答】解：由题意可得出，此三次函数在x=±5处的导数为0，依次特征寻找正确选项：A选项，导数为，令其为0，解得x=±5，故A正确；B选项，导数为，令其为0，x=±5不成立，故B错误；C选项，导数为，令其为0，x=±5不成立，故C错误；D选项，导数为，令其为0，x=±5不成立，故D错误．故选：A．12．（5分）已知定义在（0，）上的函数f（x），f′（x）为其导函数，且f（x）＜f′（x）•tanx恒成立，则（）A．f（）＞f（）B．f（）＜f（）C．f（）＞f （） D．f（1）＜2f（）•sin1【解答】解：解：因为x∈（0，），所以sinx＞0，cosx＞0，由f（x）＜f′（x）tanx，得f（x）cosx＜f′（x）sinx，即f′（x）sinx﹣f（x）cosx＞0．令g（x）=，x∈（0，），则g′（x）=＞0．所以函数g（x）=在x∈（0，）上为增函数，则g（）＜g（）＜g（1）＜g（），即，对照选项，A．应为＞，C．应为＜f（），D．应为f（1）2f（）sin1，B正确．故选：B．二．填空题（本大题共4小题，每小题5分，共20分）13．（5分）向量，满足||=1，||=，（+）⊥（2﹣），则向量与的夹角为90°．【解答】解：因为||=1，||=，（+）⊥（2﹣），所以（+）•（2﹣）=2+﹣=0，则2+﹣2=0，即=0，所以，则向量与的夹角为90°，故答案为：90°．14．（5分）（+x3）dx=．【解答】解：（+x3）dx=（dx+0=；故答案为：．15．（5分）△ABC的内角A，B，C所对的边分别为a，b，c，且a，b，c成等比数列，若sinB=，cosB=，则a+c的值为3．【解答】解：∵a，b，c成等比数列，∴b2=ac，∵sinB=，cosB=，∴可得=1﹣，解得：ac=13，∵由余弦定理：b2=a2+c2﹣2accosB=ac=a2+c2﹣ac×，解得：a2+c2=37．∴（a+c）2=a2+c2+2ac=37+2×13=63，故解得a+c=3．故答案为：3．16．（5分）在数列{a n}中，a1=2，a n+1=a n+ln（1+），则a n=2+lnn．【解答】解：a1=2+ln1，a2=2+ln2，，，由此猜想a n=2+lnn．用数学归纳法证明：①当n=1时，a1=2+ln1，成立．②假设当n=k时等式成立，即a k=2+lnk，则当n=k+1时，=2+lnk+ln=2+ln（k+1）．成立．由①②知，a n=2+lnn．故答案为：2+lnn．四、解答题（本大题共6个小题，满分70分．解答应写出必要的文字说明、证明过程或演算步骤．请将解答过程写在答题纸的相应位置．）17．（10分）设函数f（x）=|2x﹣1|﹣|x+2|．（Ⅰ）解不等式f（x）＞3；（Ⅱ）若∃x0∈R，使得f（x0）+2m2＜4m，求实数m的取值范围．【解答】解：（Ⅰ）当x＜﹣2时，f（x）=|2x﹣1|﹣|x+2|=1﹣2x+x+2=﹣x+3，f （x）＞3，即﹣x+3＞3，解得x＜0，又x＜﹣2，∴x＜﹣2；当时，f（x）=|2x﹣1|﹣|x+2|=1﹣2x﹣x﹣2=﹣3x﹣1，f（x）＞3，即﹣3x﹣1＞3，解得，又，∴；当时，f（x）=|2x﹣1|﹣|x+2|=2x﹣1﹣x﹣2=x﹣3，f（x）＞3，即x﹣3＞3，解得x＞6，又，∴x＞6．综上，不等式f（x）＞3的解集为．（Ⅱ）f（x）=|2x﹣1|﹣|x+2|=，∴．∵∃x0∈R，使得，∴，整理得4m2﹣8m﹣5＜0，解得．因此实数m的取值范围是．18．（12分）已知在△ABC中，角A、B、C的对边分别是a、b、c，且2sin2A+3cos （B+C）=0．（1）求角A的大小；（2）若△ABC的面积S=5，a=，求sinB+sinC的值．【解答】解：（1）∵2sin2A+3cos（B+C）=0，∴2sin2A﹣3cosA=0．即2﹣2cos2A﹣3cosA=0，解得cosA=或cosA=﹣2（舍）．∴A=．（2）∵S=bcsinA==5，∴bc=20．由余弦定理得cosA===，∴b+c=9．由正弦定理得==2，∴sinB=，sinC=．∴sinB+sinC===．19．（12分）已知数列{a n}前n项和为S n，满足S n=2a n﹣2n（n∈N*）．（I）证明：{a n+2}是等比数列，并求{a n}的通项公式；（Ⅱ）数列{b n}满足b n=log2（a n+2），T n为数列{}的前n项和，若T n＜a 对正整数a都成立，求a的取值范围．【解答】（Ⅰ）证明：由题设S n=2a n﹣2n（n∈N*），S n﹣1=2a n﹣1﹣2（n﹣1），n≥2，两式相减得a n=2a n﹣1+2，即a n+2=2（a n+2），﹣1又a1+2=4，所以{a n+2}是以4为首项，2为公比的等比数列，a n+2=4•2n﹣1，即a n=2n+1﹣2（n≥2）又a 1=2，所以a n=2n+1﹣2（n∈N*）；（Ⅱ）解：因为b n=log2（a n+2）=log22n+1=n+1，即有==﹣，故T n=﹣+﹣+…+﹣=﹣＜，依题意得：a≥．20．（12分）如图，已知等边△ABC中，E，F分别为AB，AC边的中点，N为BC 边上一点，且CN=BC，将△AEF沿EF折到△A′EF的位置，使平面A′EF⊥平面EF﹣CB，M为EF中点．（1）求证：平面A′MN⊥平面A′BF；（2）求二面角E﹣A′F﹣B的余弦值．【解答】（1）证明：如图所示，取BC的中点G，连接MG，则MG⊥EF，∵平面A′EF⊥平面EFCB，平面A′EF∩平面EFCB=EF，∴MG⊥平面A′EF，∴MG⊥A′M，又A′M⊥EF，因此可以建立空间直角坐标系．不妨设BC=4．M（0，0，0），A′（0，0，），N（﹣1，，0），B（2，，0），F（﹣1，0，0）．=（0，0，），=（﹣1，，0），=（1，0，），=（3，，0）．设平面A′MN的法向量为=（x，y，z），则，即，取=．同理可得平面A′BF的法向量=．∵=3﹣3+0=0，∴，∴平面A′MN⊥平面A′BF．（2）解：由（1）可得平面A′BF的法向量=．取平面EA′F的法向量=（0，1，0）．则cos===，由图可知：二面角E﹣A′F﹣B的平面角为锐角，∴二面角E﹣A′F﹣B的平面角的余弦值为．21．（12分）已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．（1）求曲线C的直角坐标方程和直线L的普通方程；（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．【解答】解：（1）曲线C的极坐标方程是ρ=2cosθ，化为ρ2=2ρcosθ，可得直角坐标方程：x2+y2=2x．直线L的参数方程是（t为参数），消去参数t可得．（2）把（t为参数），代入方程：x2+y2=2x化为：+m2﹣2m=0，由△＞0，解得﹣1＜m＜3．∴t1t2=m2﹣2m．∵|PA|•|PB|=1=|t1t2|，∴m2﹣2m=±1，解得，1．又满足△＞0．∴实数m=1，1．22．（12分）已知函数f（x）=alnx+bx（a，b∈R）在点（1，f（1））处的切线方程为x﹣2y﹣2=0．（1）求a，b的值；（2）当x＞1时，f（x）+＜0恒成立，求实数k的取值范围；（3）证明：当n∈N*，且n≥2时，++…+＞．【解答】（1）解：∵f（x）=alnx+bx，∴f′（x）=+b．∵直线x﹣2y﹣2=0的斜率为0.5，且过点（1，﹣0.5），…（1分）∴f（1）=﹣0.5，f′（1）=0.5解得a=1，b=﹣0.5．…（3分）（2）解：由（1）得f（x）=lnx﹣0.5x．当x＞1时，f（x）+＜0恒成立，等价于k＜0.5x2﹣xlnx．…（4分）令g（x）=0.5x2﹣xlnx，则g′（x）=x﹣1﹣lnx．…（5分）令h（x）=x﹣1﹣lnx，则h′（x）=．当x＞1时，h′（x）＞0，函数h（x）在（1，+∞）上单调递增，故h（x）＞h（1）=0…（6分）从而，当x＞1时，g′（x）＞0，即函数g（x）在（1，+∞）上单调递增，故g（x）＞g（1）=0.5．…（7分）∴k≤0.5．…（9分）（3）证明：由（2）得，当x＞1时，lnx﹣0.5x +＜0，可化为xlnx ＜，…（10分）又xlnx＞0，从而，＞=﹣．…（11分）把x=2，…n分别代入上面不等式，并相加得，++…+＞1﹣+﹣+…+﹣=1+﹣﹣=．…（14分）赠送—高中数学知识点二次函数（1）一元二次方程20(0)ax bx c a++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a++=≠的两实根为12,x x，且12x x≤．令2()f x ax bx c=++，从以下四个方面来分析此类问题：①开口方向：a②对称轴位置：2bxa=-③判别式：∆④端点函数值符号．①k＜x1≤x2⇔②x1≤x2＜k⇔③x 1＜k ＜x 2 ⇔ af (k )＜0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1＜x 1≤x 2＜k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+． （Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q = ②02b x a->，则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =x>O-=f(p) f (q)()2b f a-x>O-=f (p)f (q)()2b f a-xx>O-=f (p) f (q)()2b f a-0x x>O -=f(p) f(q)()2b f a-0x xfxfx①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．x<O-=f (p)f(q)()2bf a-x x<O-=f (p)f (q)()2b f a-x。

2008-2009学年福建省厦门六中高三数学上学期期中考试（文）满分150分 考试时间120分钟一、选择题：本题共12个小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一个是正确的，把正确选项的代号填在答题卡的指定位置上. 1. 若}1|{->=x x M ，则下列选项正确的是 （ ）A ．0⊆MB ．{0}∈MC ．φ∈MD ．{0}⊆M2. 在ABC 中，8b =，c =ABCS =则A ∠等于 （ ）A 、30B 、60C 、30或150D 、60或1203. 根据表格中的数据，可以判定方程20x e x --=的一个根所在的区间为 （ ）A ．(1,0)-B ．(0,1)C ．(1,2)D ．(2,3)4. )(x f '是)(x f 的导函数，)(x f '的图象如图所示， 则)(x f 的图象只可能是（ ）A B C D5.在各项均不为零的等差数列{}n a 中，若2110(2)n n n a a a n +--+=≥，则214n S n --=（ ）Ａ．2-Ｂ．0Ｃ．1Ｄ．26. 抛物线ax y =2与双曲线161022=-y x 的准线重合，侧a 的值为 （ ）A ．±10 B ．±5C ．±4D ．±27.. 下列函数中，在其定义域内既是奇函数又是减函数的是（ ）A. R x x y ∈-=,3B. R x x y ∈=,sinC. R x x y ∈=,D. R x x y ∈=,)21(8. 如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，如果直角 三 角形的直角边长为1，那么这个几何体的体积为 ( )()A 1 ()B 12()C 13 ()D 169.. 在各项都为正数的等比数列{}n a 中，若569,a a =则3132310log log log a a a +++=（ ）.A. 12B. 10C. 8D.32log 5+10.设m 、n 是不同的直线，α、β、γ是不同的平面，有以下四个命题：①//////αββγαγ⎫⇒⎬⎭ ② //m m αββα⊥⎫⇒⊥⎬⎭③//m m ααββ⊥⎫⇒⊥⎬⎭ ④////m n m n αα⎫⇒⎬⊂⎭， 其中为真命题的是（ ） A ①④ B ②③ C ①③ D ②④ 11. 下列不等式中，与不等式xx --23≥0同解的是 （ ） （A ）)2)(3(x x --≥0 （B ）0)2)(3(>--x x （C ）32--x x≥0 （D ）)2lg(-x ≤0 12. 已知θ是三角形的一个内角，且51cos sin =+θθ，则方程1cos sin 22=-θθy x 表示（ ）（A ）焦点在x 轴上的椭圆 （B ）焦点在y 轴上的椭圆（C ）焦点在x 轴上的双曲线 （D ）焦点在y 轴上的双曲线 二、填空题（本题共4小题，每小题4分，共16分）13. 直线30ax y -+=始终平分圆224240x y x y +---=的周长，则a=14. 设实数x ，y 满足2,2,30.x y x y x y ≤⎧⎪≤-⎨⎪+-≥⎩则的最大值是 15. 若函数3)2(2+++=x a x y ，][b a x ，∈的图象关于直线1=x 对称，则b=16.函数)433sin(2)(π-=x x f ，有下列命题：①其最小正周期是32π；②其图象可由主视图左视图俯视图x y 3sin 2=的图象向左平移4π个单位得到；③对称轴为x=32π；④在∈x [12π，125π]上为增函数．其正确的命题的序号是：三．解答题（本大题共6小题，共74分;解答应写出文字说明与演算步骤）17. (本题满分12分) 已知40,sin 25παα<<=（Ⅰ）求22sin sin 2cos cos 2αααα++的值； （Ⅱ）求5tan()4πα-的值。

2016-2017学年福建省厦门六中高三（上）期中数学试卷（文科）一．选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合题目要求的，在答题卷上的相应题目的答题区域内作答. 1．（5分）sin300°的值为（）A．B．﹣ C．D．﹣2．（5分）设a，b∈R，则使a＞b成立的一个充分不必要条件是（）A．a3＞b3B．log2（a﹣b）＞0 C．a2＞b2D．3．（5分）若数列{a n}满足：a n+1=1﹣且a1=2，则a2009等于（）A．1 B．C．D．4．（5分）在数列{a n}中，a n=2n+3，前n项和S n=an2+bn+c，n∈N*，其中a，b，c为常数，则a﹣b+c=（）A．﹣3 B．﹣4 C．﹣5 D．﹣65．（5分）设m、n表示不同直线，α、β表示不同平面，下列命题正确的是（）A．若m∥α，m∥n，则n∥αB．若m⊂α，n⊂α，m∥β，n∥β，则α∥βC．若α⊥β，m⊥α，m⊥n，则n∥βD．若α⊥β，m⊥α，n∥m，n⊄β，则n ∥β6．（5分）在△ABC中，a，b，c分别为∠A，∠B，∠C的对边，且c＞b＞a，若向量=（a﹣b，1），=（b﹣c，1）平行，且sinB=，则当△ABC的面积为时，B=（）A．B．2 C．4 D．2+7．（5分）一个几何体的三视图如图所示，则侧视图的面积为（）A．2+B．1+C．2+2D．4+8．（5分）已知平面上四个互异的A，B，C，D满足（﹣）•（2﹣﹣）=0，则△ABC的形状是（）A．等边三角形B．等腰三角形C．直角三角形D．斜三角形9．（5分）已知点A（1，1）和坐标原点O，若点B（x，y）满足，则x2+y2﹣2x﹣2y的最小值是（）A．﹣2 B．3 C．D．510．（5分）如图为正方体表面的一种展开图，则图中的四条线段AB，CD，EF，GH在原正方体中互为异面的对数为（）A．1 B．2 C．3 D．411．（5分）设α、β、γ为三个不同的平面，m、n是两条不同的直线，在命题“α∩β=m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ．可以填入的条件有（）A．①或③B．①或②C．②或③D．①或②或③12．（5分）已知函数f（x）=asinx﹣bcosx（a、b为常数，a≠0，x∈R）在x=处取得最小值，则函数y=f（﹣x）是（）A．偶函数且它的图象关于点（π，0）对称B．偶函数且它的图象关于点对称C．奇函数且它的图象关于点对称D．奇函数且它的图象关于点（π，0）对称二．填空题：本大题共4小题，每小题5分，共20分.在答题卷上的相应题目的答题区域内作答.13．（5分）已知tanθ=，则sin2θ﹣2cos2θ=．14．（5分）已知x≥0，y≥0，且x+2y=1，则的最小值等于．15．（5分）一个几何体的三视图如图所示，则该几何体的体积为．16．（5分）等差数列{a n}的公差为d，关于x的不等式x2+（a1﹣）x+c≥0的解集为[0，22]，则使数列{a n}的前n项和S n最大的正整数n的值是．三．解答题：本大题有6小题，共70分.解答应写出文字说明，证明过程或演算步骤，在答题卷上相应题目的答题区域内作答．17．（10分）设集合A={x|x2＜4}，B={x|＞1}．（1）求集合A∩B；（2）若不等式2x2+ax+b＜0的解集为B，求a，b的值．18．（12分）已知函数f（x）=sin（2x+）+sin（2x﹣）+2cos2x+a﹣1（a为常数），若函数f（x）的最大值为+1．（1）求实数a的值；（2）求函数f（x）所有对称中心的坐标；（3）求函数g（x）=f（x+π）+2减区间．19．（12分）已知数列{a n}的前n项和S n=n（n﹣1），且a n是b n与1的等差中项．（1）求数列{a n}和数列{b n}的通项公式；（2）若c n=（n≥2），求c2+c3+c4+…+c n．20．（12分）制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？21．（12分）如图，多面体ABCDEFG中，面ABCD为正方形，AE，BF，DG均垂直于平面ABCD，且AB=AE=4，BF=DG=2，M，N分别为AB，BC的中点．（1）若P为BF的中点，证明NP∥平面EGM；（2）求三棱锥N﹣EGM体积．22．（12分）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2cosθ．（1）求C2与C3交点的直角坐标；（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．2016-2017学年福建省厦门六中高三（上）期中数学试卷（文科）参考答案与试题解析一．选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合题目要求的，在答题卷上的相应题目的答题区域内作答. 1．（5分）sin300°的值为（）A．B．﹣ C．D．﹣【解答】解：sin300°=sin（360°﹣60°）=﹣sin60°=﹣．故选：D．2．（5分）设a，b∈R，则使a＞b成立的一个充分不必要条件是（）A．a3＞b3B．log2（a﹣b）＞0 C．a2＞b2D．【解答】解：要求a＞b成立的一个充分不必要条件，则要求一个条件能够推出a＞b成立，但是反之不成立，选项A是充要条件，选项B是a﹣b＞1是充分不必要条件，选项C，D既不充分又不必要，故选：B．3．（5分）若数列{a n}满足：a n+1=1﹣且a1=2，则a2009等于（）A．1 B．C．D．【解答】解：∵，a1=2，∴令n=1，得，令n=2，得，令n=3，得，∴{a n}是周期为3的周期数列，∵2009=666×3+1，∴．故选：D．4．（5分）在数列{a n}中，a n=2n+3，前n项和S n=an2+bn+c，n∈N*，其中a，b，c为常数，则a﹣b+c=（）A．﹣3 B．﹣4 C．﹣5 D．﹣6【解答】解：令n=1，得到a1=2+3=5，所以，而S n=an2+bn+c，则an2+bn+c=n2+4n，所以a=1，b=4，c=0，则a﹣b+c=1﹣4+0=﹣3．故选：A．5．（5分）设m、n表示不同直线，α、β表示不同平面，下列命题正确的是（）A．若m∥α，m∥n，则n∥αB．若m⊂α，n⊂α，m∥β，n∥β，则α∥βC．若α⊥β，m⊥α，m⊥n，则n∥βD．若α⊥β，m⊥α，n∥m，n⊄β，则n ∥β【解答】解：选项A中还有直线n在平面α上的情况，故A不正确，选项B中再加上两条直线相交的条件可以得到两个平面平行，故B不正确，选项C中还有n⊂β，故C不正确，故选：D．6．（5分）在△ABC中，a，b，c分别为∠A，∠B，∠C的对边，且c＞b＞a，若向量=（a﹣b，1），=（b﹣c，1）平行，且sinB=，则当△ABC的面积为时，B=（）A．B．2 C．4 D．2+【解答】解：由向量和共线知a+c=2b①，由②，由c＞b＞a知角B为锐角，③，联立①②③得b=2．故选：B．7．（5分）一个几何体的三视图如图所示，则侧视图的面积为（）A．2+B．1+C．2+2D．4+【解答】解：根据三视图中，三个视图的对应关系：长对正，高平齐，宽相等，得出侧视图的数据如图中所示其面积S=×2+2×2=4+故选：D．8．（5分）已知平面上四个互异的A，B，C，D满足（﹣）•（2﹣﹣）=0，则△ABC的形状是（）A．等边三角形B．等腰三角形C．直角三角形D．斜三角形【解答】解：（﹣）•（2﹣﹣）=0，化为•=0，取BC的中点E，则．∴=0，∴CB⊥AE，且BE=EC．∴AB=AC．∴△ABC的形状是等腰三角形．故选：B．9．（5分）已知点A（1，1）和坐标原点O，若点B（x，y）满足，则x2+y2﹣2x﹣2y的最小值是（）A．﹣2 B．3 C．D．5【解答】解：点B（x，y）满足，对应的平面区域如：x2+y2﹣2x﹣2y=（x﹣1）2+（y﹣1）2﹣2，表示A到区域内的点距离的平方减去2，所以A到直线x+2y=8的距离为最小距离，所以（x﹣1）2+（y﹣1）2﹣2最小值为=3；故选：B．10．（5分）如图为正方体表面的一种展开图，则图中的四条线段AB，CD，EF，GH在原正方体中互为异面的对数为（）A．1 B．2 C．3 D．4【解答】解：画出展开图复原的几何体，所以C与G重合，F，B重合，所以：四条线段AB、CD、EF和GH在原正方体中相互异面的有：AB与GH，AB与CD，GH与EF，共有3对．故选：C．11．（5分）设α、β、γ为三个不同的平面，m、n是两条不同的直线，在命题“α∩β=m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ．可以填入的条件有（）A．①或③B．①或②C．②或③D．①或②或③【解答】解：由面面平行的性质定理可知，①正确；当n∥β，m⊂γ时，n和m在同一平面内，且没有公共点，所以平行，③正确．故选：A．12．（5分）已知函数f（x）=asinx﹣bcosx（a、b为常数，a≠0，x∈R）在x=处取得最小值，则函数y=f（﹣x）是（）A．偶函数且它的图象关于点（π，0）对称B．偶函数且它的图象关于点对称C．奇函数且它的图象关于点对称D．奇函数且它的图象关于点（π，0）对称【解答】解：已知函数f（x）=asinx﹣bcosx（a、b为常数，a≠0，x∈R），∴的周期为2π，若函数在处取得最小值，不妨设，则函数=，所以是奇函数且它的图象关于点（π，0）对称，故选：D．二．填空题：本大题共4小题，每小题5分，共20分.在答题卷上的相应题目的答题区域内作答.13．（5分）已知tanθ=，则sin2θ﹣2cos2θ=﹣．【解答】解：∵tanθ=，则sin2θ﹣2cos2θ===﹣，故答案为：﹣．14．（5分）已知x≥0，y≥0，且x+2y=1，则的最小值等于．【解答】解：x≥0，y≥0，且x+2y=1，则=+=2+++6≥8+2=，当且仅当y=x时，等号成立．故的最小值等于，故答案为．15．（5分）一个几何体的三视图如图所示，则该几何体的体积为．【解答】解：由三视图可知，几何体为一个三棱柱剪去一个三角锥，三棱柱的体积V1为：剪去的三棱锥体积V2为：所以几何体的体积为：16．（5分）等差数列{a n}的公差为d，关于x的不等式x2+（a1﹣）x+c≥0的解集为[0，22]，则使数列{a n}的前n项和S n最大的正整数n的值是11．【解答】解：∵关于x的不等式++c≥0的解集为[0，22]，∴22=，且＜0，即＞0，则a11=a1+10d＞0，a12=a1+11d＜0，故使数列{a n}的前n项和S n最大的正整数n的值是11．故答案为：11．三．解答题：本大题有6小题，共70分.解答应写出文字说明，证明过程或演算步骤，在答题卷上相应题目的答题区域内作答．17．（10分）设集合A={x|x2＜4}，B={x|＞1}．（1）求集合A∩B；（2）若不等式2x2+ax+b＜0的解集为B，求a，b的值．【解答】解：A={x|x2＜4}={x|﹣2＜x＜2}，由化为0，∴（x+3）（x﹣1）＜0，解得﹣3＜x＜1．∴B={x|＞1}={x|﹣3＜x＜1}．（1）A∩B={x|﹣2＜x＜1}；（2）∵2x2+ax+b＜0的解集为B={x|﹣3＜x＜1}，∴﹣3和1为2x2+ax+b=0的两根，故，解得a=4，b=﹣6．18．（12分）已知函数f（x）=sin（2x+）+sin（2x﹣）+2cos2x+a﹣1（a为常数），若函数f（x）的最大值为+1．（1）求实数a的值；（2）求函数f（x）所有对称中心的坐标；（3）求函数g（x）=f（x+π）+2减区间．【解答】（本小题满分12分）解：（1）f（x）=sin（2x+）+sin（2x﹣）+2cos2x+a﹣1=sin2x+cos2x+sin2x﹣cos2x+cos2x+a=sin2x+cos2x+a=sin（2x+）+a，…（2分）由f（x）max=+1得a=1 …（4分）（2）由2x+=kπ（k∈Z）得：x=π﹣（k∈Z），所以，函数f（x）所有对称中心的坐标为（π﹣，1），k∈Z．…（8分）（3）g（x）=f（x+π）+2=sin[2（x+）+]+1+2=﹣sin2x+3，…（10分）由2kπ﹣≤2x≤2kπ+（k∈Z）得：单调递减区间为[kπ﹣，kπ+]（k∈Z）…（12分）19．（12分）已知数列{a n}的前n项和S n=n（n﹣1），且a n是b n与1的等差中项．（1）求数列{a n}和数列{b n}的通项公式；（2）若c n=（n≥2），求c2+c3+c4+…+c n．【解答】解：（1）当n=1时，a1=S1=0，=（n﹣1）（n﹣2），当n≥2时，S n﹣1∴a n=S n﹣S n﹣1=[n（n﹣1）]﹣[（n﹣1）（n﹣2）]=n﹣1，当n=1时，成立，故a n=n﹣1；a n是b n与1的等差中项，∴2a n=1+b n，∴b n=2n﹣3，数列{a n}通项公式a n=n﹣1，数列{b n}的通项公式b n=2n﹣3；…（8分）（2）因为c n===（﹣）（n≥2），…（10分）∴c2+c3+c4+…+c n．=（1﹣）+（﹣）+（﹣）+…+（﹣），=（1﹣+﹣+﹣+…+﹣），=﹣．c2+c3+c4+…+c n=﹣．…（12分）20．（12分）制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？【解答】解：设投资人对甲、乙两个项目各投资x和y万元，则，设z=x+0.5y=0.25（x+y）+0.25（3x+y）≤0.25×10+0.25×18=7，当即时，z取最大值7万元答：投资人对甲、乙两个项目分别投资4万元和6万元时，才能使可能的盈利最大．21．（12分）如图，多面体ABCDEFG中，面ABCD为正方形，AE，BF，DG均垂直于平面ABCD，且AB=AE=4，BF=DG=2，M，N分别为AB，BC的中点．（1）若P为BF的中点，证明NP∥平面EGM；（2）求三棱锥N﹣EGM体积．【解答】解：（1）取AE的中点H，由题意知，BF∥AE，BC∥AD∴面BCF∥面ADGE，∴FC∥HD∥EG，又PN∥FC，∴PN∥EG．∴PN∥面EGM（2）∵PN∥面EGM，∴V N=V P﹣EGM=V G﹣EMP=V D﹣EMP，﹣EGM又AD⊥面ABEF，DC⊥AE，∴．22．（12分）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2cosθ．（1）求C2与C3交点的直角坐标；（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．【解答】解：（I）由曲线C2：ρ=2sinθ，化为ρ2=2ρsinθ，∴x2+y2=2y．同理由C3：ρ=2cosθ．可得直角坐标方程：，联立，解得，，∴C 2与C 3交点的直角坐标为（0，0），．（2）曲线C 1：（t 为参数，t ≠0），化为普通方程：y=xtanα，其中0≤α≤π，α≠；α=时，为x=0（y ≠0）．其极坐标方程为：θ=α（ρ∈R ，ρ≠0），∵A ，B 都在C 1上， ∴A （2sinα，α），B ．∴|AB |==4，当时，|AB |取得最大值4．赠送—高中数学知识点二次函数（1）一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ，且12x x ≤．令2()f x ax bx c =++，从以下四个方面来分析此类问题：①开口方向：a ②对称轴位置：2bx a=-③判别式：∆ ④端点函数值符号． ①k ＜x 1≤x 2 ⇔②x 1≤x 2＜k ⇔③x 1＜k ＜x 2 ⇔ af (k )＜0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1＜x 1≤x 2＜k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+． （Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q = ②02b x a->，则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =x>O-=f(p) f (q)()2b f a-x>O-=f (p)f (q)()2b f a-xx>O-=f (p) f (q)()2b f a-0x x>O -=f(p) f(q) ()2b f a-0x xfxfx①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．x<O-=f (p)f(q)()2bf a-0xx<O-=f (p)f (q)()2b f a-0x。

厦门六中2016—2017学年上学期高二期中考试数 学 试 卷（理科）考试时间：120分钟 第Ⅰ卷 选择题一、选择题：（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题意要求的）1．已知数列{}n a 满足：10a <，113n n a a +=，则数列{}n a 是（ ）A. 递增数列B. 递减数列C. 摆动数列D. 不确定2.不等式(x ＋5)(3－2x) ≤6的解集是 ( )9.|12A x x x ⎧⎫≤-≥⎨⎬⎩⎭或 9.|12B x x ⎧⎫-≤≤⎨⎬⎩⎭ 9.|12C x x x ⎧⎫≤-≥⎨⎬⎩⎭或 9.|12D x x ⎧⎫-≤≤⎨⎬⎩⎭3．设△ABC 的内角A,B,C 所对的边分别为a,b,c,若cos cos sin b C c B a A +=,则△ABC 的形状为（ ）A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4．对于实数,,a b c ，下列结论中正确的是（ ）A ．若a b >，则22ac bc >B ．若0a b >>，则11a b> C ．若0a b <<，则a b b a < D ．若a b >，11a b>，则0ab < 5. 在等差数列{}n a 中，=++=++=++963852741,29,45a a a a a a a a a 求 （ ）A. 22B.18C.20D. 136．在△ABC 中，若8,3,7===c b a ，则其面积等于（ ）A ．12B ．221C ．36D ．28 7. 在2015年年底，某家庭打算把10万元定期存入银行后，既不加进存款也不取钱，每年到期利息连同本金自动转存，定期存款期限为10年。

如果不考虑利息税，且中国银行人民币定期存款的年利率为5﹪，则到期时的存款本息和是（ ）A ．1010 1.05⨯ B. 910 1.05⨯ C. 9200(1.051)⨯- D. 10200(1.051)⨯-8.若关于x 的不等式ax-b>0的解集是（1，+∞），则关于x 的不等式02ax b x +>-的解集为（ ）A.(-1，2)B.(1，2)C.(,1)(2,)-∞-+∞UD. (,2)(1,)-∞-+∞U 9.函数1()3(0,1)x f x aa a -=+>≠且的图象过一个定点P ，且点P 在直线mx ＋ny －1＝0(m ＞0，n ＞0)上，则14m n+的最小值是( ) A ．12 B ．13 C ．24 D ．2510.在ABC ∆中，分别根据下列条件解三角形，其中有两解的是（ ）A.7=a ，14=b ，︒=30A ；B.4=b ，5=c ，︒=30B ；C.25=b ，30=c ，︒=150C ；D.6=a ，3=b ，︒=60B 。

福建省厦门第六中学2016—2017学年度第一学期期中考试高二年文科数学试卷命题人： 审核人: 2016.11一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．在答题卷上的相应题目的答题区域内作答．1. 已知数列}{n a 中，11=a ，21+=-n n a a （2≥n ），则10a =( )A.17B. 18C. 19D. 20x x x 2522>--的解集是（ ）。

A 、{}1x 5-≤≥或x xB 、{}1x 5-<>或x xC 、{}51<<-x xD 、{}51≤≤-x x 3．若0b a <<，则下列不等式中一定正确的是（ ）A ．11a b >B ．a b >C ．2b a a b+> D ．a b ab +> 4．在ABC ∆中，4=a ，24=b ，︒=30A ，则B 的值为（ ）A.︒45B.︒135C. ︒45或︒135D. 不存在5．设△ABC 的内角A,B,C 所对的边分别为c b a ,,,若cos cos sin b C c B a A +=,则△ABC 的形状为（ ）6．《张丘建算经》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女不善织，日减功迟，初日织五尺，末日织一尺，今三十织迄，问织几何．”其意思为：有个女子不善于织布，每天比前一天少织同样多的布，第一天织五尺，最后一天织一尺，三十天织完，问三十天共织布（ ）A ．30尺B ．90尺C ．150尺D ．180尺{}n a 是首项为1a ，公差为-1的等差数列，n S 为前n 项和，若124,,S S S 成等比数列，则1a =（ ）A ．2B ．-2C ．12D ．12- 8.设等比数列{}n a 中，前n 项和为n S ，已知368,7S S ==，则789a a a ++=（ ）A ．18 B ．18- C ．578 D ．5589.ABC ∆的内角C B A ,,的对边分别为c b a ,,，若c b a ,,成等比数列，且2c a =，则cos B =( )A ．14B ．34C．4 D．3 10.已知a ，b 均为正数，且1a b +=，则49a b+的最小值为（ ） A ．24 B ．25 C ．26 D ．27 11. 已知x y ，满足约束条件2y x x y x a ≥⎧⎪+≤⎨⎪≥⎩，且2z x y =+的最大值是最小值的3倍，则a 的值是（ ） A.13 B.1412.若{}n a 为等差数列，n S 为其前n 项和，若10a >，0d <，48S S =，则0n S >成立的最大自然数n 为（ ）A ．10B ．11C ．12D ．13二．填空题：本大题共4小题，每小题5分，共20分．在答题卷上的相应题目的答题区域内作答．13.在ABC ∆中，已知sin :sin :sin 3:5:7A B C =，则此三角形的最大内角的度数等于__________．0,0x y >>，且满足134x y +=，则xy 的最大值为___________. 15. 若不等式23208kx kx +-≥的解集为空集，则实数k 的取值范围是___________. 16．ABC ∆三个内角分别为C B A ,,,且B C A sin ,sin ,sin 成等差数列，则cos C 的最小值是 .三、解答题：本大题共6小题，17题10分，18-22题各12分， 70分，解答题应写出文字说明，证明过程或演算步骤，在答题卷上相应题目的答题区域内作答．（17) (本小题满分10分)已知等差数列{}n a ，n S 为其前n 项和，5710,56.a S ==（1）求数列{}n a 的通项公式；（2）若(3)n an n b a =+，求数列{}n b 的前n 项和n T18．(本小题满分12分)如图，在ABC ∆中，BC 边上的中线AD 长为3，且10cos B =，1cos 4ADC ∠=-． （1）求BAD ∠sin 的值；（2）求AC 边的长．19. (本小题满分12分)咖啡馆配制两种饮料,甲种饮料每杯含奶粉9克、咖啡4克、糖3克,乙种饮料每杯含奶粉4克、咖啡5克、糖10克.已知每天原料的使用限额为奶粉3 600克、咖啡2 000克、糖3 000克,甲种饮料每杯能获利润0.7元,乙种饮料每杯能获利润1.2元,每天应配制两种饮料各多少杯能获利最大?20. (本小题满分12分)在ABC ∆中，角,,A B C 的对边分别为,,a b c ()()3,cos sin sin cos 0b A B c A A C =+-+=（1）求角B 的大小； （2）若ABC ∆的面积为32，求sin sin A C +的值．21. (本小题满分12分)第二届世界互联网大会在浙江省乌镇开幕后，某科技企业为抓住互联网带来的机遇，决定开发生产一款大型电子设备.生产这种设备的年固定成本为500万元，每生产x 台，需另投入成本为()C x万元.若年产量不足80台时，()21402C x x x =+（万元）；若年产量不小于80台时， ()81001012180C x x x=+-（万元）.每台设备售价为100万元，通过市场分析，该企业生产的电子设备能全部售完.（1）求年利润y （万元）关于年产量x （台）的函数关系式；（2）年产量为多少台时，该企业在这一电子设备的生产中所获利润最大？22．(本小题满分12分)设数列{}n a 的各项都为正数，其前n 项和为n S ，已知242n n n S a a =+.(1）求1a 及数列{}n a 的通项公式；(2）设数列{}n b 前n 项和为n T ，且14n n n b a a +=，若()136n n T n λ<+-⋅对n N *∈恒成立，求实数λ的取值范围.福建省厦门第六中学2016—2017学年度第一学期期中考试高二年文科数学试卷参考答案二、填空题： 13. o 120 14.3 15. (]3,0- 16. 1216.试题分析：因为sin sin sin A C B ，，成等差数列，所以sin sin 2sin A B C +=，由正弦定理，2a b c +=，2222222cos 22a b a b a b c C ab ab ++⎛⎫ ⎪⎝⎭-+-==223321843()8a b ab a b ab b a +-==+-3182241a b b a ≥⨯⨯-=；当且仅当a b =时，等号成立；故答案为：12． 三、解答题：(17) (本小题满分10分)（1）n a n 2=；（2）23312-++=+n n n n T 试题解析：（1）由公差…………5分 （2）， …………6分…………9分…………10分18．试题解析：（1）因为10cos B =，所以36sin B =．…………2分 又1cos 4ADC ∠=-，所以15sin ADC ∠=，…………4分 所以sin ∠BAD ＝sin （∠ADC －∠B ）＝sin ∠ADCcosB －cos ∠ADCsinB1510136648484⎛⎫=⨯--⨯= ⎪⎝⎭．…………6分 （2）在△ABD 中，由sin sin AD BD B BAD =∠得:336684BD =，解得BD ＝2．…………9分 故DC ＝2，从而在△ADC 中，由AC 2＝AD 2＋DC 2－2AD·DC·cos ∠ADC＝32＋22－2×3×2×（-41）＝16，得AC ＝4．…………12分19.解:设每天配制甲种饮料x 杯、乙种饮料y 杯可以获得最大利润,利润总额为z 元. 由条件知z=0.7x+1.2y,变量x,y 满足 …………5分作出不等式组所表示的可行域如图所示.…………8分作直线l:0.7x+1.2y=0,把直线l 向右上方平移至经过A 点的位置时,z=0.7x+1.2y 取最大值.由方程组得A 点坐标(200,240).答:应每天配制甲种饮料200杯,乙种饮料240杯方可获利最大. …………12分20.试题解析：（1）由0)cos()sin (sin cos =+-+C A A c B A ，得0cos )sin (sin cos =--B A c B A ，即,cos )sin(B c B A =+,cos sin B c C =B cC cos sin = 因为sin sin C B c b =cos 3B =，即tan 3,3B B π== …………6分 （2）由23sin 21==B ac S ，得2ac =，．由3=b 及余弦定理得()ac c a ac c a B ac c a 3)(cos 23222222-+=-+=-+=， 所以3a c +=，所以23)(sin sin sin =+=+c a b BC A ．…………12分22．(1）21=a ,n a n 2=;(2）70-<λ.试题解析: (1）∵n n n a a S 242+=，且0n a >，当1=n 时，121124a a a +=，解得21=a ．…………1分当2≥n 时，有121124---+=n n n a a S ．于是121212244----+-=-n n n n n n a a a a S S ，即1212224---+-=n n n n n a a a a a ．于是121222--+=-n n n n a a a a ，即)(2))((111---+=-+n n n n n n a a a a a a ．∵01>+-n n a a ，∴)2(21≥=--n a a n n ．…………5分故数列}{n a 是首项为2，公差为2的等差数列，∴n a n 2=．…………6分(2）∵111)1(1+-=+=n n n n b n ，∴1111)111()3121()211(+=+-=+-++-+-=n nn n n T n ．…………8分①当n 为偶数时，n n n )1)(36(++<λ恒成立，又493736)1)(36(≥++=++n n n n n ，当6=n 时取等号；∴49<λ②当n 为奇数时，nn n )1)(36(+-<λ恒成立，又3536)1)(36(--=+-n n n n n ， ∵n n 36-在•∈N n 为增函数，70)3536(m in -=--n n ；∴70-<λ 综上：λ的取值范围为70-<λ …………6分 考点：等差数列;裂项法求和;不等式性质。

2012-2013学年度福建省厦门六中第一学期高二期中考试数学试题（理）参考答案一、选择题：1 2 3 4 5 6 7 8 9 10 BADABCCACD二、填空题：11．1200 12．70a -<< 13．35； 14．9； 15．)111(4+-n16．③④⑤ 三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤． 17．（本题满分12分）解：（Ⅰ）由已知，得816317a a a a +=+= ----------------1分又8181,38a a a a <-=，∴12a =-，819a =，∴{}n a 的公差d=3 -----3分 ∴a n =a 1+（n －1）d=－2+3（n －1）=3n －5． ---------------------------6分 （Ⅱ）由（Ⅰ），得a 1=－2，a 2=1，a 3=4．依题意可得：数列{b n }的前三项为b 1=1，b 2=－2，b 3=4或b 1==4，b 2=－2，b 3=1 --8分 （i ）当等比数列{b n }的前三项为b 1=1，b 2=－2，b 3=4时，则q=－2 ．1(1)1[1(2)]1[1(2)]11(2)3n n n n b q S q -⋅--∴===-----． -------------------------9分（ii ）当第比数列{b n }的前三项为b 1=4，b 2=－2，b 3=1时，则21-=q ． ])21(1[38)21(1])21(1[41)1(1n n nn q q b S --=----=--=∴ -------------------12分说明：第（Ⅱ）问只做一种情况给3分．18．解：（1）∵A 、B 、C 成等差数列，∴2B=A+C ，…………1分 又A+B+C=π∴3π=B …………2分∵3,23==∆c S ABC ∴23sin 21=B ac 解得：332=a …………4分由余弦定理知，3213cos 33232)332()3(cos 22222=⨯⨯⨯-+=-+=πB ac c a b ……6分 （2）根据余弦定理，由B c a cos =，得acb c a c a 2222-+⨯=， ∴222a b c +=，∴△ABC 是直角三角形，2π=C …………10分∴c a A =sin ，∴a cac A c b =⋅==sin ， 故△ABC 是等腰直角三角形。

厦门六中2015—2016学年上学期高三期中考试 化 学 试 卷 满分100分 考试时间100分钟 命题时间：2015-11-2 相对原子质量：H-1 Al-27 O-16 Fe-56 S-32 Cl-35.5 C-12 Ba-137 Ca-40 一、选择题(45分，共15题，每小题只有一个正确选项)1． A．青铜、不锈钢都是合金B．C．D．一般情况下，前者无法决定后者的是A．原子核外电子排布——元素在周期表中的位置B．弱电解质的相对强弱——电离常数的大小C．分子间作用力的大小——分子稳定性的高低D．物质内部储存的能量——化学反应的热效应 ． A．①④ B．⑥ C．⑤ D．④⑥ ．下列实验操作的描述符合实验事实的是 A．滴定管和锥形瓶都要先B．用四氯化碳萃取碘水中的碘时，将碘的四氯化碳溶液从分液漏斗下口放出 C．蒸馏时，D．除去KNO3中的NaCl杂质，可用溶解→加AgNO3溶液→过滤方法5．常温下，饱和氯水中逐滴入0.1mol·L-1的氢氧化钠溶液，pH变化如图所示，下列有关叙述正确的是 A．点HClO的电离平衡 B．水的电离程度C．－点溶液D．点所示溶液中：c(Na+)c(Cl－) + c(ClO－)．分子式为CH10O2并能与碳酸钠反应放出气体的有机物有（不含立体异构） A．3种B．4种C．5种 D．6种 7．中学化学常见物质甲、乙、丙、丁之间存在转化关系：甲＋乙→丙＋丁。

下列说法正确的是（ ） A．若甲为铜，丁为氯化亚铁，则乙一定是氯化铁 B．若甲为碳，丁为硅，则丙一定是二氧化碳 C．若甲为铝，丁为铁，则乙一定是氧化铁 D．若甲为镁，丁为氢气，则乙一定是酸 ．NA表示阿伏加德罗常数，下列说法正确的是 A．NA个质子 B．NA个乙酸乙酯分子 C．.2 L乙醇中所含的碳原子数目为NA D．的与数为NAabcdACO2盐酸CaCO3饱和Na2CO3溶液浓硫酸BNH3饱和NH4Cl溶液消石灰H2O固体NaOHCCl2 浓盐酸MnO2饱和NaCl溶液浓硫酸DNO2浓HNO3铜屑H2O固体NaOH 10．H2O2至溶液中无Fe2＋存在，加热除去多余的H2O2，当加入200 mL 6 mol ·L1 NaOH溶液时沉淀量最多，且所得沉淀质量为26.3 g，下列说法不正确的是 A． B． C．D．．今有一混合物的水溶液，只可能含有以下离子中的若干种：K＋、NH＋、a2＋、Ba2＋、Cl－、CO32、SO2，现取三份100 mL溶液进行如下实验： (1)第一份加入AgNO3溶液有沉淀产 (2)第二份加足量NaOH溶液加热后，收集到气体0.04 mol。