2020-2021宜兴市万石中学高中必修二数学下期中模拟试题含答案
- 格式:doc
- 大小:2.28 MB
- 文档页数:21

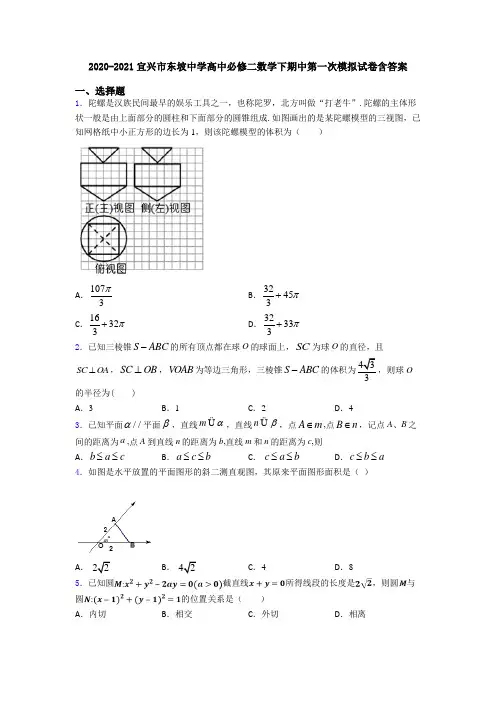
2020-2021宜兴市红塔中学高中必修二数学下期中试卷及答案一、选择题1.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30o ,则该长方体的体积为( )A .8B .62C .82D .832.设曲线31x y x +=-在点25(,)处的切线与直线10ax y +-=平行,则a=( ) A .-4B .14-C .14D .43.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若//l α,//l β,则//αβ B .若l α⊥,l β⊥,则//αβ C .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥4.已知平面//α平面β,直线m αÜ,直线n βÜ,点A m ∈,点B n ∈,记点A 、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则 A .b a c ≤≤ B .a c b ≤≤C . c a b ≤≤D .c b a ≤≤5.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 ( )A 3πB .3πC .43πD .12π6.四棱锥P ABCD -的底面ABCD 为正方形,PA ⊥底面ABCD ,2AB =,72PA =,若该四棱锥的所有顶点都在同一球面上,则该球的表面积为( ) A .812πB .814πC .65πD .652π7.若直线20ax y +-=和直线()2140x a y +-+=平行,则a 的值为( ) A .1-或2 B .1- C .2 D .不存在 8.若a >b >0,0<c <1,则A .log a c <log b cB .log c a <log c bC .a c <b cD .c a >c b9.已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦,则||AB 等于( )A 3B .2C .23D .2510.如图所示,在棱长为a 的正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 是侧面11CDD C 上的动点,且1//B F 面1A BE ,则F 在侧面11CDD C 上的轨迹的长度是( )A .aB .2a C .2aD .22a 11.已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ,B 两点,则弦长AB 的取值范围是( )A .[]4,10B .[]3,5C .[]8,10D .[]6,1012.某几何体的三视图如图所示(单位:cm ),其俯视图为等边三角形,则该几何体的体积(单位:3cm )是( )A .43B .1033C .23D .833二、填空题13.经过两条直线2310x y ++=和340x y -+=的交点,并且平行于直线3470x y +-=的直线方程是________.14.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,M 为B 1C 1中点,连接A 1B ,D 1M ,则异面直线A 1B 和D 1M 所成角的余弦值为________________________.15.若圆1C :220x y ax by c ++++=与圆2C :224x y +=关于直线21y x =-对称,则c =______.16.若直线l :-3y kx =与直线23-60x y +=的交点位于第一象限,则直线l 的倾斜角的取值范围是___________.17.已知直线:0l x my m ++=,且与以A (-1,1)、B (2,2)为端点的线段相交,实数m 的取值范围为___________.18.如上图所示,在正方体1111ABCD A B C D -中,,M N 分别是棱1AB CC 、的中点,1MB P ∆的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题:A .平面1MB P 1ND ⊥; B .平面1MB P ⊥平面11ND A ;C .∆1MB P 在底面ABCD 上的射影图形的面积为定值;D .∆1MB P 在侧面11D C CD 上的射影图形是三角形.其中正确命题的序号是__________. 19.在棱长为1的正方体1111ABCD A B C D -中,M 是1BB 的中点,直线1D M 与平面ABCD 交于点N ,则线段AN 的长度为________20.若直线:20l kx y --=与曲线()2:111C y x --=-有两个不同的交点,则实数k 的取值范围________.三、解答题21.如图(1)在等腰直角三角形ABC 中,90B ∠=︒,将ABC ∆沿中位线DE 翻折得到如图(2)所示的空间图形,使二面角A DE C --的大小为02πθθ⎛⎫<<⎪⎝⎭.(1)求证:平面ABD ⊥平面ABC ; (2)若3πθ=,求直线AE 与平面ABC 所成角的正弦值.22.如图,在三棱锥S ABC -中,SAC ∆为等边三角形,4AC =,43BC =BC AC ⊥,3cos 4SCB ∠=-,D 为AB 的中点.(1)求证:AC SD ⊥;(2)求直线SD 与平面SAC 所成角的大小. 23.已知圆22:20M x y x a +-+=(1)若8a =-,过点(4,5)P 作圆M 的切线,求该切线的方程;(2)当圆22:(1)(23)4N x y ++-=与圆M 相外切时,从点(2,8)Q -射出一道光线,经过y 轴反射,照到圆M 上的一点R ,求光线从点Q 经反射后走到点R 所走过路线的最小值.24.已知圆22C (4)4x y +-=:,直线:(31)(1)40l m x m y ++--=.(1)求直线l 所过定点A 的坐标;(2)求直线l 被圆C 所截得的弦长最短时直线l 的方程及最短弦长;(3)已知点M (-3,4),在直线MC 上(C 为圆心),存在定点N (异于点M ),满足:对于圆C 上任一点P ,都有||||PM PN 为一常数, 试求所有满足条件的点N 的坐标及该常数. 25.若圆M 的方程为22(2)(5)10x y -+-=,△ABC 中,已知(1,1)A ,(4,2)B ,点C 为圆M 上的动点.(1)求AC 中点D 的轨迹方程; (2)求△ABC 面积的最小值.26.(1)用符号表示下来语句,并画出同时满足这四个语句的一个几何图形:①直线l 在平面α内; ②直线m 不在平面α内; ③直线m 与平面α交于点A ; ④直线l 不经过点A .(2)如图,在长方体1111ABCD A B C D -中,E 为棱1BB 的中点,F 为棱1CC 的三等分点,画出由1,,D E F 三点所确定的平面β与平面ABCD 的交线.(保留作图痕迹)【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】首先画出长方体1111ABCD A B C D -,利用题中条件,得到130AC B ∠=o,根据2AB =,求得123BC =,可以确定122CC =,之后利用长方体的体积公式求出长方体的体积. 【详解】在长方体1111ABCD A B C D -中,连接1BC ,根据线面角的定义可知130AC B ∠=o,因为2AB =,所以1BC =,从而求得1CC =,所以该长方体的体积为22V =⨯⨯= C. 【点睛】该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长就显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果.2.D解析:D 【解析】 【分析】求出原函数的导函数,得到函数在2x =时的导数,再由两直线平行与斜率的关系求得a 值. 【详解】解:由31x y x +=-,得()()2213411x x y x x ---=---'=, ∴2'|4x y ==-, 又曲线31x y x +=-在点25(,)处的切线与直线10ax y +-=平行, ∴4a -=-,即4a =. 故选D . 【点睛】本题考查利用导数研究过曲线上某点处的切线方程,考查两直线平行与斜率的关系,是中档题.3.B解析:B 【解析】A 中,,αβ也可能相交;B 中,垂直与同一条直线的两个平面平行,故正确;C 中,,αβ也可能相交;D 中,l 也可能在平面β内. 【考点定位】点线面的位置关系4.D解析:D 【解析】 【分析】根据平面与平面平行的判断性质,判断c 最小,再根据点到直线距离和点到直线上任意点距离判断a 最大. 【详解】由于平面//α平面β,直线m 和n 又分别是两平面的直线,则c 即是平面之间的最短距离. 而由于两直线不一定在同一平面内,则b 一定大于或等于c ,判断a 和b 时, 因为B 是上n 任意一点,则a 大于或等于b . 故选D. 【点睛】本题主要考查面面平行的性质以及空间距离的性质,考查了空间想象能力,意在考查灵活应用所学知识解答问题的能力,属于中档题.5.C解析:C 【解析】 【分析】的等腰直角三角形,与底面垂直的侧面是个等腰三角形,底边长为2,高为2,故三棱锥的外接球与以棱长为2的正方体的外接球相同,由此可得结论 【详解】由三视图知几何体是一个侧棱与底面垂直的三棱锥,与底面垂直的侧面是个等腰三角形,底边长为2,高为2,故三棱锥的外接球与以棱长为2的正方体的外接球相同,其直径为∴三棱锥的外接球体积为343π⨯=故选C 【点睛】本题主要考查了三视图,几何体的外接球的体积,考查了空间想象能力,计算能力,属于中档题.6.B解析:B 【解析】 【分析】根据题意可知,该四棱锥的外接球即为其所在长方体的外接球,根据公式即可求得. 【详解】根据题意,为方便说明,在长方体中找出该四棱锥如图所示:由图可知在长方体中的四棱锥P ABCD -完全满足题意, 故该四棱锥的外接球即是长方体的外接球,故外接球半径222722294R ⎛⎫++ ⎪⎝⎭==, 故该球的表面积为28144S R ππ==. 故选:B . 【点睛】本题考查四棱锥外接球的问题,关键的步骤是将问题转化为求长方体的外接球.7.C解析:C 【解析】 【分析】直接根据直线平行公式得到答案. 【详解】直线20ax y +-=和直线()2140x a y +-+=平行,则()12a a -=,解得2a =或1a =-.当1a =-时,两直线重合,排除. 故选:C . 【点睛】本题考查了根据直线平行求参数,意在考查学生的计算能力,多解是容易发生的错误.8.B解析:B 【解析】试题分析:对于选项A ,a b 1gc 1gclog c ,log c lg a lg b==,01c <<Q ,10gc ∴<,而0a b >>,所以lg lg a b >,但不能确定lg lg a b 、的正负,所以它们的大小不能确定;对于选项B ,c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >,两边同乘以一个负数1lg c改变不等号方向,所以选项B 正确;对于选项C ,利用c y x =在第一象限内是增函数即可得到c c a b >,所以C 错误;对于选项D ,利用x y c =在R 上为减函数易得a b c c <,所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较;若底数不同,可考虑利用中间量进行比较.9.D解析:D 【解析】 【分析】求出圆的标准方程,确定最短弦的条件,利用弦长公式进行求解即可. 【详解】圆的标准方程为(x ﹣3)2+(y +1)2=10,则圆心坐标为C (3,﹣1),半径为过E 的最短弦满足E 恰好为C 在弦上垂足,则CE ==,则|AB |==, 故选D . 【点睛】本题主要考查圆的标准方程的求解,以及直线和圆相交的弦长问题,属于中档题.10.D解析:D 【解析】 【分析】设H ,I 分别为1CC 、11C D 边上的中点,由面面平行的性质可得F 落在线段HI 上,再求HI 的长度即可. 【详解】解:设G ,H ,I 分别为CD 、1CC 、11C D 边上的中点, 则ABEG 四点共面, 且平面1//A BGE 平面1B HI , 又1//B F Q 面1A BE ,F ∴落在线段HI 上,Q 正方体1111ABCD A B C D -中的棱长为a ,112HI CD ∴==,即F 在侧面11CDD C 上的轨迹的长度是2a . 故选D .【点睛】本题考查了面面平行的性质及动点的轨迹问题,属中档题.11.D解析:D 【解析】 【分析】由直线()()21110k x k y ++++=,得出直线恒过定点()1,2P -,再结合直线与圆的位置关系,即可求解. 【详解】由直线()()():21110l k x k y k R ++++=∈,可得()210k x y x y ++++=,又由2010x y x y +=⎧⎨++=⎩,解得12x y =⎧⎨=-⎩,即直线恒过定点()1,2P -,圆心()1,2C ,当CP l ⊥时弦长最短,此时2222AB CP r ⎛⎫+= ⎪⎝⎭,解得min 6AB =,再由l 经过圆心时弦长最长为直径210r =, 所以弦长AB 的取值范围是[]6,10. 故选:D. 【点睛】本题主要考查了直线系方程的应用,以及直线与圆的位置关系的应用,其中解答中熟练利用直线的方程,得出直线恒过定点,再结合直线与圆的位置关系求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.12.B解析:B 【解析】由题意可知该几何体为正三棱柱去掉一个小三棱锥,1104323333V =⋅=. 故选:B.二、填空题13.【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为:故答案为:【点睛】本题 解析:1934011x y ++= 【解析】 【分析】先求出两相交直线的交点,设出平行于直线3470x y +-=的直线方程,根据交点在直线上,求出直线方程. 【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩,得到两直线的交点坐标135(,)1111-,平行于直线3470x y +-=的直线方程设为340x y c ++=, 则1353()4()+01111c ⋅-+⋅= 所以直线的方程为:1934011x y ++= 故答案为:1934011x y ++= 【点睛】本题考查了直线的交点,以及与已知直线平行的直线方程,考查了学生概念理解,转化与划归的能力,属于基础题.14.【解析】【分析】连接取的中点连接可知且是以为腰的等腰三角形然后利用锐角三角函数可求出的值作为所求的答案【详解】如下图所示:连接取的中点连接在正方体中则四边形为平行四边形所以则异面直线和所成的角为或其【解析】 【分析】连接1CD 、CM ,取1CD 的中点N ,连接MN ,可知11//A B CD ,且1CD M ∆是以1CD 为腰的等腰三角形,然后利用锐角三角函数可求出1cos CD M ∠的值作为所求的答案. 【详解】 如下图所示:连接1CD 、CM ,取1CD 的中点N ,连接MN ,在正方体1111ABCD A B C D -中,11//A D BC ,则四边形11A BCD 为平行四边形, 所以11//A B C D ,则异面直线1A B 和1D M 所成的角为1CD M ∠或其补角,易知1111190B C D BC C CDD ∠=∠=∠=o,由勾股定理可得15CM D M ==12CDN Q 为1CD 的中点,则1MN CD ⊥,在1Rt D MN ∆中,11110cos D N CD M D M ∠==, 因此,异面直线1A B 和1D M 所成角的余弦值为105,故答案为105. 【点睛】本题考查异面直线所成角的余弦值的计算,求解异面直线所成的角一般利用平移直线法求解,遵循“一作、二证、三计算”,在计算时,一般利用锐角三角函数的定义或余弦定理求解,考查计算能力,属于中等题.15.【解析】【分析】两圆关于直线对称即圆心关于直线对称则两圆的圆心的连线与直线垂直且中点在直线上圆的半径也为即可求出参数的值【详解】解:因为圆:即圆心半径由题意得与关于直线对称则解得圆的半径解得故答案为 解析:165-【解析】 【分析】两圆关于直线对称即圆心关于直线对称,则两圆的圆心的连线与直线21y x =-垂直且中点在直线21y x =-上,圆1C 的半径也为2,即可求出参数,,a b c 的值. 【详解】解:因为圆1C :220x y ax by c ++++=,即22224224ab a b cx y 骣骣+-琪琪+++=琪琪桫桫,圆心111,22C a b ⎛⎫-- ⎪⎝⎭,半径224a b cr +-=,由题意,得111,22C a b ⎛⎫-- ⎪⎝⎭与()20,0C 关于直线21y x =-对称,则112,122112221,22b a ba ⎧-⎪=-⎪⎪-⎨⎪--⎪⎪=⨯-⎩解得85=-a ,45b =,圆1C 的半径22422a b cr +-==,解得165c =-. 故答案为:165-【点睛】本题考查圆关于直线对称求参数的值,属于中档题.16.【解析】若直线与直线的交点位于第一象限如图所示:则两直线的交点应在线段上(不包含点)当交点为时直线的倾斜角为当交点为时斜率直线的倾斜角为∴直线的倾斜角的取值范围是故答案为解析:(,)62ππ【解析】若直线:3l y kx =-与直线2360x y +-=的交点位于第一象限,如图所示:则两直线的交点应在线段AB 上(不包含,A B 点), 当交点为()0,2A 时,直线l 的倾斜角为2π,当交点为()3,0B 时,斜率(03330k -==-l 的倾斜角为6π ∴直线的倾斜角的取值范围是,62ππ⎛⎫⎪⎝⎭.故答案为,62ππ⎛⎫⎪⎝⎭ 17.【解析】【分析】由直线系方程求出直线所过定点再由两点求斜率求得定点与线段两端点连线的斜率数形结合求得实数的取值范围【详解】解:由直线可知直线过定点又如图∵∴由图可知直线与线段相交直线的斜率或斜率不存解析:21,32⎡⎤-⎢⎥⎣⎦【解析】 【分析】由直线系方程求出直线所过定点,再由两点求斜率求得定点与线段两端点连线的斜率,数形结合求得实数m 的取值范围. 【详解】解:由直线:0l x my m ++=可知直线过定点()0,1P -, 又()1,1A -,()2,2B ,如图∵()11201PA K --==---,123022PB K --==-,∴由图可知,直线与线段相交,直线l 的斜率(]3,2,2k ⎡⎫∈-∞-+∞⎪⎢⎣⎭U ,或斜率不存在, ∴(]13,2,2m ⎡⎫-∈-∞-+∞⎪⎢⎣⎭U ,或0m =, 即203m -≤<或102m <≤,或0m =, ∴21,32m ⎡⎤∈-⎢⎥⎣⎦故答案为:21,32⎡⎤-⎢⎥⎣⎦. 【点睛】本题主要考查直线系方程的应用,考查了直线的斜率计算公式,考查了数形结合的解题思想方法,属于中档题.18.【解析】由正方体的几何性质对4个命题进行判断对于A 当动点P 与点重合时以等腰三角形与不垂直所以不能得出平面A 为假命题;对于B 易证所以平面所以平面⊥平面故B 为真命题;对于C 在底面上的射影图形的面积为定值 解析:BC【解析】由正方体的几何性质对4个命题进行判断,对于A ,当动点P 与点1D 重合时,MNP ∆以等腰三角形,PM 与1ND 不垂直,所以不能得出平面11MB P ND ⊥,A 为假命题;对于B ,易证11111ND MB MB A D ⊥⊥,,所以1MB ⊥平面11ND A ,所以平面1MB P ⊥平面11ND A ,故B 为真命题;对于C ,∆ 1MB P 在底面ABCD 上的射影图形的面积为定值,因为1MB P ∆在底面ABCD 的射影是三角形,底边是MB ,点P 在底面的射影在CD 上,到MB 的距离不变,若正方体棱长为a 时,则射影面积为214a 为定值,所以C 为真命题;对于D ,当P 点与点1C 重合时,则点1B 与点P 的投影重合,此时∆ 1MB P 在侧面11D C CD 上的射影图形是线段,不是三角形,故D 是假命题。

高二数学下学期期中试题(含解析)一.选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{}{}2,1,0,1,2,,U A y y x x U =--==∈,则UA = ( )A. {}0,1,2B. {}2,1,0--C. {}1,2--D. {}1,2【答案】C 【解析】 【分析】可求出集合A ,然后进行补集的运算即可.【详解】由题意,集合{}{}2,1,0,1,2,,U A y y x x U =--==∈,则{}0,1,2A =, 所以根据集合的补集的运算,可得{}2,1UA =--.故选:C .【点睛】本题主要考查了集合的表示,以及集合的补集的运算,其中解答中正确求解集合A ,再根据集合的补集的运算求解是解答的关键,着重考查了运算与求解能力,属于基础题.2.若向量b 与向量()2,1a =-是共线向量,且35b =,则b =( ) A. ()6,3-B. ()6,3-C. ()6,3-或()6,3-D. ()3,6-或()3,6-【答案】C 【解析】 【分析】根据b 与a 共线,可设()2,1b λ=-,再根据35b =,求得λ的值,即可得出向量b 的坐标.【详解】由题意,根据b 与a 共线,所以存在实数λ,使()2,1b λ=-; 又35b =,∴535=3λ=±;∴()6,3b =-或()6,3-.故选:C .【点睛】本题主要考查了共线向量基本定理,向量坐标的数乘运算,以及向量坐标求向量长度的方法,其中解答中熟记向量的基本运算法则,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.3.若4sin 65πα⎛⎫-= ⎪⎝⎭,则cos 3πα⎛⎫+ ⎪⎝⎭等于( ) A.45B. 45-C.35D.35【答案】A 【解析】 【分析】πcos 3α⎛⎫+= ⎪⎝⎭sin (ππ23α--)结合诱导公式求解即可【详解】π4sin 65α⎛⎫-= ⎪⎝⎭,则πcos 3α⎛⎫+= ⎪⎝⎭sin (ππ23α--)π4sin 65α⎛⎫=-= ⎪⎝⎭, 故选A .【点睛】本题考查诱导公式及角的变换,是基础题4.已知函数()f x 是定义在R 上的奇函数,且()()4f x f x +=-,当()0,2x ∈时,()21f x x =+ ,则()7f = ( )A. 2B. 2-C. 1D. 1-【答案】B 【解析】 【分析】由()()4f x f x +=-,可得()()()84f x f x f x +=-+=,则函数()f x 是周期为8的周期函数,据此可得()()71f f =-,结合函数的周期性与奇偶性,即可求解.【详解】根据题意,函数()f x 满足()()4f x f x +=-,则有()()()84f x f x f x +=-+=,则函数()f x 是周期为8的周期函数,则()()71f f =-, 又由函数为奇函数,则()()()211112f f -=-=-+=, 则()12f -=-,即()72f =-; 故选:B .【点睛】本题主要考查了函数的奇偶性与周期性的综合应用,其中解答中根据题设条件,求得函数的周期是解答的关键,着重考查了推理与运算能力,属于基础题.5.函数()·ln xf x e x =的大致图象为( ) A. B.C. D.【答案】A 【解析】 【分析】判断函数的奇偶性和对称性的关系,利用极限思想进行求解即可【详解】解:函数()·ln xf x e x =,()--?ln -xf x e x =,()()f x f x ≠-,()()f x f x -≠-,则函数()f x 为非奇非偶函数,图象不关于y 轴对称,排除C ,D ,当(),x f x →+∞→+∞,排除B , 故选:A【点睛】本题主要考查函数图象的识别和判断,利用函数的对称性以及极限思想是解决本题的关键6.可导函数()f x 在区间(), a b 上的图象连续不断,则“存在()0, x a b ∈满足0'()0f x =”是“函数()f x 在区间(), a b 上有最小值”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】D 【解析】 【分析】根据0()0f x '=和函数()f x 在区间(), a b 上有极值点的关系,结合具体函数,即可判断出结论.【详解】根据函数极值点的概念,可知()0, x a b ∈满足0()0f x '=,则0x 不一定是函数的极值点,例如()3,(2,2)f x x x =∈-,其中()00f '=,但0x =不是函数的极值点,此时函数()3f x x =在(2,2)x ∈-上没有最小值.又由函数(),(2,2)f x x x =∈-,其中当0x =时,函数()f x 取得最小值()00f =. 但0x =时,()f x '不存在,()2,0x ∈-时,()1f x '=-, ()0,2x ∈时,()1f x '=,所以“存在()0, x a b ∈满足0'()0f x =”不成立.所以“存在()0, x a b ∈满足0'()0f x =”是“函数()f x 在区间(), a b 上有最小值”的既不充分也不必要条件. 故选:D .【点睛】本题考查了函数有极值点的概念及应用,以及充要条件判定方法,考查了推理能力与计算能力,属于中档题.7.从数字1到9中任取3个数字,要求既有奇数也有偶数,组成一个没有重复数字的三位数,则满足条件的三位数的个数共有( ) A. 420 B. 840C. 140D. 70【答案】A【分析】根据奇数和偶数的个数分1个奇数,2个偶数和2奇数,1偶数,然后进行全排列,即可求解,得到答案.【详解】由题意,9个数字中奇数为1,3,5,7,9,偶数为2,4,6,8, 三位数要求既有奇数也有偶数,则若1个奇数,2个偶数,有123543180C C A =个,若2奇数,1偶数,有213543240C A A =个, 由分类计数原理可得,共有180240420+=个, 故选:A .【点睛】本题主要考查了排列、组合的应用,其中解答中结合条件分1个奇数,2个偶数和2奇数,1偶数,分类求解是解决本题的关键,着重考查了分析问题和解答问题的能力,属于基础题.8.设向量,,a b c 满足||1,||2a b ==,0,()0a b c b a c ⋅=⋅+-=,则||c 的最大值等于( ) A. 1 B. 2C. 51+5【答案】D 【解析】 【分析】设()()()1,0,0,2,,a b c x y ===,运用向量的加减运算和数量积的坐标表示,以及圆的性质,可得所求最大值.【详解】由题意,向量,,a b c 满足1,2a b ==,0a b ⋅=, 可设()()()1,0,0,2,,a b c x y ===,由()0c b a c ⋅+-=,可得()()()(),1,2120x y x y x x y y ⋅--=-+-=,整理得2220x y x y +--=,即()2215124x y ⎛⎫-+-= ⎪⎝⎭,即圆心(1,12),半径5则c 的最大值为25r =【点睛】本题主要考查了向量的加减运算和数量积的坐标表示,考查圆的方程的运用,考查运算能力和推理能力,属于基础题,着重考查了推理与运算能力.9.设F 为抛物线2:8C y x =的焦点,过点()2, 0P -的直线l 交抛物线C 于, A B 两点,点Q为线段AB 的中点,若47FQ =,则AB = ( ) 2 B. 2C. 2D. 2【答案】D 【解析】 【分析】设直线l 的方程为()2y k x =+,联立方程组得2222240k x k x k +-+=(),由此利用韦达定理、点到直线距离公式能求出直线的斜率,然后利用弦长公式,即可求解.【详解】由题意,设直线l 的方程为()2y k x =+,112200, ,()()() , A x y B x y Q x y 、、,联立方程组28(2)y x y k x ⎧=⎨=+⎩,化简得2222(48)40k x k x k +-+=,∴212284k x x k -+=,124x x =,则1212()84y y k x x k +=++=, 由中点公式,可得20242k x k -=,04y k =, 又由2222424247k k k ⎛⎫-⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭33k =±, 所以22111201616233AB x =+-=-= 故选:D .【点睛】本题主要考查了直线与抛物线的位置关系的应用,其中解题时要认真审题,注意韦达定理、点到直线距离公式的合理运用是解答的关键,着重考查了推理与运算能力,属于中档试题.10.已知函数)22()log 13f x x x x =-+-,当2019x y +=时,恒有()()()2019f x f f y +>成立,则x 的取值范围是( )A. 10,2⎛⎫ ⎪⎝⎭B. 1(,1)2C. (,0)-∞D. (1,)+∞【答案】C 【解析】 【分析】根据函数的解析式,得出()f x 在R 上是奇函数且为减函数,据此对x 进行分情况讨论,即可求解,得到答案.【详解】由题意,函数)22()log 13f x x x x =-+-,定义域为R ,且满足())()()2222log ()13log 13f x x x x x x x f x -=--++=++=-,所以函数()y f x =为定义在R 上的奇函数,则有()00f =,又由()f x 在[0, )+∞单调递减,则()f x 在(,?0]-∞上也为减函数, 则()f x 在R 上为减函数,则()20190f <,当0x <时,20192019y x =->,即()()()2019f x f f y >>, 则恒有()()()2019f x f f y +>成立,当0x =时,2019y =,此时()()()()20192019f x f f f y +==,()()()2019f x f f y +>不成立,当0x >时,20192019y x =-<,此时不能满足()()()2019f x f f y +>恒成立, 所以x 的取值范围是(,0)-∞. 故选:C .【点睛】本题主要考查了函数的奇偶性与单调性应用问题,其中根据函数的解析式判定出函数的奇偶性和单调性,分类讨论是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于中档题.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.已知复数z 满足1iz i-=(i 是虚数单位),则2z =_____;z =_____. 【答案】 (1). 2i 2 【解析】 【分析】利用复数代数形式的乘除运算化简z ,进一步求得2z ,再由复数模的计算公式求z . 【详解】由题意,根据复数的运算,化简得21(1)()1i i i z i i i ---===---, 所以()2212, 2z i i z =--==故答案为:2i 2【点睛】本题主要考查了复数代数形式的乘除运算,以及复数模的求法,其中解答中熟记复数的运算法则,以及模的运算公式,准确计算是解答的关键,着重考查了运算与求解能力,属于基础题.12.计算:4log 2=_____;满足log 21x >的实数x 的取值范围是_____.【答案】 (1). 14(2). 12x <<. 【解析】 【分析】利用对数的换底公式及对数的运算性质求4log 2;把log 21x >化为同底数,然后分类利用对数的运算性质求解.【详解】由题意,根据对数的运算法则,可得12422lg 21log 2lg 4lg 24===,由log 21log xx x >=,当01x <<时,得2x >1x >时,得12x <<,∴实数x 的取值范围是12x <<.故答案为:14;12x <. 【点睛】本题主要考查了对数的运算性质,以及对数函数的图象与性质的应用,其中解答中熟记对数的运算公式和对数函数的图象与性质是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于基础题..13.已知双曲线22221(0,0)x y a b a b-=>>,12, A A 分别是双曲线的左、右顶点,00,() M x y 是双曲线上除两顶点外的一点,直线1MA 与直线2MA 的斜率之积是169,则双曲线的离心率为_____;若该双曲线的焦点到其渐近线的距离是4,则双曲线的方程为_____.【答案】 (1). 53 (2). 221916x y -=【解析】 【分析】根据000()), (M x y x a ≠±是双曲线上一点,代入双曲线的方程,由直线1MA 与直线2MA 的斜率之积是169,求出直线1MA 与直线2MA 的斜率,然后整体代换,进而求得双曲线的离心率,再根据双曲线的焦点到其渐近线的距离是4,即可求出双曲线的方程.【详解】由题意,设000()), (M x y x a ≠±是双曲线22221(0,0)x y a b a b-=>>上一点,则2200221x y a b -=,得到2220022y x a b a-=,故2202220y b x a a =-, 又()()12,0, ,0A a A a -, ∴1222000222000169MA MA y y y b k k x a x a x a a ⋅=⋅===+--,得43b a = ∴221651193c b e a a ==+=+=, 其渐近线的方程为b y x a =±,即43y x =±,即430x y ±=,设双曲线的一个焦点坐标为(),0c ,则双曲线的焦点到其渐近线的距离445c=,解得5c =, 又因为222c a b =+,所以229, 16a b ==,故双曲线的方程为221916x y -=,故答案为:53,221916x y -=.【点睛】本题考查了双曲线的标准方程及其简单的几何性质,主要是离心率的求法,其中解答中熟记双曲线的几何性质,合理、准确运算是解答的关键,着重考查化简整理的运算能力,属于中档题.14.二项式()512x -的展开式中系数最大的项为_____;已知52345012345(12)x a a x a x a x a x a x -=+++++,则123452345a a a a a -+-+=_____.【答案】 (1). 480x (2). 810-. 【解析】 【分析】由二项式()512x -的展开式中通项()152rr rr T C x +=-,列出不等式组,求得r 的值,即可得出最大的项.对于二项式52345012345(12)x a a x a x a x a x a x -=+++++,两边求导,再令1x =-,即可求解.【详解】由题意,二项式()512x -的展开式中通项公式()()15522rrrr r r T C x C x +=-=-.由()()()()115511552222r r r r r r r r C C C C --++⎧-≥-⎪⎨-≥-⎪⎩,解得4r =,即展开式的最大的项为()444455280T C x x =-⨯=. 由二项展开式52345012345(12)x a a x a x a x a x a x -=+++++,两边求导可得:()42341234525122345x a a x a x a x a x -⨯⨯-=++++, 令1x =-,可得()4123452345251210[1]8a a a a a -+-+=-⨯⨯-⨯-=-.故答案为:480x ,810-.【点睛】本题考查了二项式定理的通项公式、导数运算法则,考查了推理能力与计算能力,属于中档题,着重考查了分析问题和解答问题的能力,以及推理与运算能力.15.已知向量()2,4a =,向量a 在向量b 上的投影为3,且33a b -=,则b =_____. 【答案】7. 【解析】 【分析】根据条件即可得出220,cos ,3a a a b =〈〉=,然后对33a b -=两边平方,可得出2||670b b --=,即可求解b ,得到答案.【详解】根据条件:220,cos ,3a a a b =〈〉=,且33a b -=; 则()22222cos ,||62027a ba ab a b b b b -=-〈〉+=-+=;整理得2||670b b --=,解得7b =或1-(舍去). 故答案为:7.【点睛】本题主要考查了向量数量积的运算及计算公式,向量投影的计算公式,向量坐标的数量积运算等知识的综合应用,其中熟记向量的运算公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.16.3名男生和3名女生共6人站成一排,若男生甲不站两端,且不与男生乙相邻,3名女生有且只有2名女生相邻,则不同排法的种数是_____.(用数字作答) 【答案】168. 【解析】 【分析】根据题意,假设有1、2、3、4、5、6,共6个位置;若男生甲不站两端,则甲必须在2、3、4、5的位置;据此分4种情况讨论,由加法原理计算可得答案. 【详解】根据题意,假设有1、2、3、4、5、6,共6个位置, 若男生甲不站两端,则甲必须在2、3、4、5位置,可分4种情况讨论:①当甲在2号位置,甲乙不能相邻,则乙可以在4、5、6号位置,若乙在4号或5号位置,只有2个位置是相邻的,有2232224A A ⨯⨯=种排法, 若乙在6号位置,有23212A ⨯=种排法, 由分类计数原理可得,共有241236+=种排法; ②当甲在5号位置,同理①,有36种排法;③当甲在3号位置,甲乙不能相邻,则乙可以在1、5、6号位置, 若乙在1号位置,有23212A ⨯=种排法, 若乙在5号位置,有223212A A ⨯=种排法, 若乙在6号位置,有2232224A A ⨯⨯=种排法, 由分类计数原理可得,共有12122448++=种排法;④当甲在4号位置,同理③,有48种排法,则有36364848168+++=种不同的排法; 故答案为:168.【点睛】本题主要考查了排列、组合及简单的计数原理综合应用,本题解题的关键是在计算时,合理分类做到不重不漏,着重考查了分类讨论思想,以及推理与运算能力,属于中档试题.17.已知不等式()10x e a e x b -+++≤恒成立,其中e 为自然常数,则1b a+的最大值为_____. 【答案】1e【解析】 【分析】先利用导数确定不等式恒成立条件,再利用导数确定1b a+的最大值. 【详解】令()()1()()1xxf x e a e x b f x e a e '=-+++∴=-+ 当0e a -≥时,()0,,()f x x f x '>→+∞→+∞,不满足条件; 当0e a -<时,()0ln()f x x a e '=⇒=--,当ln()x a e >--时()0,f x '<当ln()x a e <--时()0,f x '> 因此()(ln())1ln()10f x f a e a e b ≤--=---++≤,从而1ln()1,()b a e a e a a+-+≤> 令2ln()ln()1(),()()ea e a e a e g x a e g x a a ---+-'=>∴=再令21ln()0()e e y a e y a e a e a e-'=--∴=-<--- 所以当a e e ->时1ln 0()0,()(2)e y e g x g x g e e e'<-=∴<<=; 当0a e e <-<时1ln 0()0,()(2)e y e g x g x g e e e'>-=∴><=; 即max 1()(2)g x g e e ==,从而1b a+的最大值为1e . 【点睛】本题考查利用导数研究不等式恒成立以及利用导数求函数最值,考查综合分析求解能力,属较难题.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.设函数2()3cos 2cos 1f x x x x ωωω=-+的图象关于直线x π=对称,其中常数1,12ω⎛⎫∈ ⎪⎝⎭.(1)求函数()f x 的最小正周期;(2)求函数()f x 在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围.【答案】(1)65π(2)[]1,2- 【解析】 【分析】(1)利用二倍角公式以及两角和与差的三角函数化简函数的解析式为一个角的一个三角函数的形式,然后求解ω,即可求解函数的周期.(2)通过角的范围,求解相位的范围,利用正弦函数性质求得函数的最值,即可求解. 【详解】(1)由题意,函数2()3cos 2cos 1f x x x x ωωω=-+32cos 2x x ωω=-2sin 26x πω⎛⎫=- ⎪⎝⎭,又由函数()2sin 26f x x πω⎛⎫=-⎪⎝⎭的图象关于直线x π=对称, 所以()2sin 226f ππωπ⎛⎫=-=± ⎪⎝⎭,所以2,62k k Z πππωπ-=+∈, 解得1,23k k Z ω=+∈,又因为1,12ω⎛⎫∈ ⎪⎝⎭,所以56ω=,即5()2sin 36f x x π⎛⎫=- ⎪⎝⎭所以最小正周期为265T w ππ==. (2)因为305x π≤≤,所以556366x πππ-≤-≤,则52sin [1,2]36x π⎛⎫-∈- ⎪⎝⎭,所以()12f x -≤≤,即函数()f x 在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围[]1,2-. 【点睛】本题主要考查了两角和与差的三角函数,以及三角函数的图象与性质的应用,其中解答中熟记三角恒等变换的公式,以及三角函数的图象与性质,准确运算是解答的关键,着重考查转化思想以及计算能力,属于基础题.19.如图,在四棱锥P ABCD -中,底面ABCD平行四边形,60ABC ∠=︒,侧面PAB ⊥底面ABCD ,90,2BAP AB AC PA ∠=︒===.(1)求证:平面PBD ⊥平面PAC ;(2)若点M 为PD 中点,求直线MC 与平面PBC 所成角的正弦值. 【答案】(1)见解析(2)2114【解析】 【分析】(1)证明PA AB ⊥,推出PA ⊥面ABCD ,得到PA BD ⊥,证明BD AC ⊥,说明BD ⊥面PAC ,即可证明面PBD ⊥平面PAC .(2)取BC 中点E ,以点A 为原点,分别以, , AE AD AP 为x 轴、y 轴、z 轴建立如图空间直角坐标系,求出面PBC 的法向量,利用空间向量的夹角公式,即可求解直线MC 与平面PBC 所成角的正弦值.【详解】(1)由题意,因为90BAP ∠=︒,则PA AB ⊥,又侧面PAB ⊥底面ABCD ,面PAB ⋂面ABCD AB =,PA ⊂面PAB , 所以PA ⊥面ABCD ,又BD ⊂面ABCD ,则PA BD ⊥ 又因为四边形ABCD 为平行四边形,且60, ABC AB AC ∠=︒= 则ABC ∆为等边三角形,则ABCD 为菱形,则BD AC ⊥ 又PAAC A =,则BD ⊥面PAC ,BD ⊂面PBD ,则面PBD ⊥平面PAC .(2) 取BC 中点E ,以点A 为原点,分别以, , AE AD AP 为x 轴、y 轴、z 轴建立如图空间直角坐标系,则()0,0,0A ,(31,0)B -,30)C ,(0,2,0)D ,(0,0,2)P , 由点M 为PD 中点,()0, 1, 1M ,则(3,0,1),(3,1,2),(3,1,2)MC PB PC =-=--=-,设面PBC 的法向量为(,,)n x y z =,则00PB n PC n ⎧⋅=⎨⋅=⎩,则31,0,n ⎛⎫= ⎪ ⎪⎝⎭设直线MC 与面PBC 所成角为θ,则||21sin |cos ,|14||||MC n MC n MC n θ⋅=〈〉== 所以直线MC 与平面PBC 所成角的正弦值为2114.【点睛】本题考查了面面垂直的判定与证明,以及空间角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,解答中熟记线面位置关系的判定定理和性质定理,通过严密推理是线面位置关系判定的关键,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.20.已知函数24,02()(2)2,2x x f x x x a x a x ⎧-<≤⎪=⎨⎪-++->⎩,其中a 为实数.(1)若函数()f x 为定义域上的单调函数,求a 的取值范围.(2)若7a <,满足不等式()0f x a ->成立的正整数解有且仅有一个,求a 的取值范围. 【答案】(1)2a ≤(2)03a ≤< 【解析】 【分析】(1)分析当02x <≤时的单调性,可得2x >的单调性,由二次函数的单调性,可得a 的范围;(2)分别讨论当0a <,当02a ≤≤时,当23a <<时,当37a ≤<,结合函数的单调性和最值,即可得到所求范围.【详解】(1)由题意,当02x <≤时,4()f x x x=-为减函数, 当2x >时,()()222f x x a x a =-++-,若2a ≤时,()()222f x x a x a =-++-也为减函数,且()()20f x f <=,此时函数()f x 为定义域上的减函数,满足条件;若2a >时,()()222f x x a x a =-++-在22,2a +⎛⎫ ⎪⎝⎭上单调递增,则不满足条件.综上所述,2a ≤.(2)由函数的解析式,可得()()13, 20f f ==, 当0a <时,()()20, 13f a f a =>=>,不满足条件;当02a ≤≤时,()f x 为定义域上的减函数,仅有()13f a =>成立,满足条件; 当23a <<时,在02x <≤上,仅有()13f a =>,对于2x >上,()f x 的最大值为22(2)1244a a f a +-⎛⎫=≤< ⎪⎝⎭, 不存在x 满足()0f x a ->,满足条件;当37a ≤<时,在02x <≤上,不存在整数x 满足()0f x a ->,对于2x >上,22(2)(4)123444a a a ----=<-,不存在x 满足()0f x a ->,不满足条件; 综上所述,03a ≤<.【点睛】本题主要考查了分段函数的运用,以及函数的单调性的判断和不等式有解问题,其中解答中熟练应用函数的单调性,以及把函数的有解问题转化为函数的最值问题是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于中档题.21.已知椭圆()2222:10x y C a b a b =>>+过点()0, 1A ,且离心率为3.(1)求椭圆C 的方程;(2)过A 作斜率分别为12, k k 的两条直线,分别交椭圆于点, M N ,且122k k +=,证明:直线MN 过定点.【答案】(1)2214x y +=(2)见解析【解析】 【分析】(1)利用椭圆C 过点()0, 1A ,以及离心率为32,求出, a b ,即可得到椭圆方程. (2)设直线方程为x t =,则()(),, ,M t s N t s -,求得1t =-,当直线MN 斜率存在时,设直线方程为:y kx b =+,与椭圆方程联立方程组,利用韦达定理以及122k k +=,得到k 与b 的关系,代入直线的方程,即可求解.详解】(1)由题意,椭圆()2222:10x y C a b a b =>>+过点()0, 1A ,即211b=,解得1b =,由离心率32c a =222a c b -=,解得2a =,所求椭圆方程为:2214x y +=. (2)当直线MN 斜率不存在时,设直线方程为x t =,则()(),, ,M t s N t s -, 则1211,s s k k t t-+==--,所以121122s s k k t t t -++=+==---,解得1t =-,当直线MN 斜率存在时,设直线方程为y kx b =+,联立方程组2244x y y kx b⎧+=⎨=+⎩,得222(41)8440k x kbx b +++-=,设1122, , ,()() M x y N x y ,则2121222844,4141kb b x x x x k k -+=-⋅=++ (*), 则()()121212121212121212122(1)11y x x y x x kx x b x x y y k k x x x x x x +-++-+--+=+==,将*式代入化简可得:288244kb kb -=-,即()()110k b b ---=,整理得1k b =+, 代入直线MN 方程,得()()11y b x b b x x =++=++,即()10b x x y ++-=,联立方程组10x y x+=⎧⎨=⎩,解得1,1x y =-=-, 恒过定点()1,1--.【点睛】本题主要考查椭圆的标准方程的求解、及直线与圆锥曲线的位置关系的应用问题,解答此类题目,通常联立直线方程与椭圆(圆锥曲线)方程的方程组,应用一元二次方程根与系数的关系进行求解,此类问题易错点是复杂式子的变形能力不足,导致错解,能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等.22.设函数()2ln 1,) (f x ax x x a a R =-+-∈.(1)当0a =时,求证:()f x x ≤;(2)当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时,()0f x ≥恒成立,求a 的取值范围. 【答案】(1)见解析(2)1a ≥ 【解析】 【分析】(1)当0a =时,()ln 1f x x x =--,不等式()f x x ≤化为ln 10x x x ++≥,构造函数()ln 1s x x x x =++,利用导数求函数()s x 的最小值,从而证明不等式成立;(2)方法1:不等式化为2ln 1()ln 1a x x x x +≥+,令()2ln 1g x x x =+,利用导数判断()0g x >,不等式化为2ln 1ln 1x x a x x +≥+,记()2ln 1ln 1x x h x x x +=+,求出()h x 的最大值,即可得出a 的取值范围.方法2:讨论1x =时,()10f ≥,求得a 的取值范围,再证明1a ≥时,()f x 在1,2x ⎡⎫∈+∞⎪⎢⎣⎭上()0f x ≥恒成立.【详解】(1)当0a =时,()()ln 1ln 1f x x x x x =--=-+, 要证明()f x x ≤,即证明ln 10x x x ++≥; 记()ln 1s x x x x =++,则1'()ln 1ln 2s x x x x x=+⋅+=+; 当20,()x e -∈时,()'0s x < ,函数()f x 在20,()x e -∈上单调递减;当2,()x e-∈+∞时,()'0s x >,函数()f x 在2,()x e -∈+∞上单调递增;所以()()()222212110s x s ee e e---≥=-++=-≥,即()f x x ≤; (2)方法1:2ln ln 10ax x x x a -+-≥ 即2ln 1()ln 1a x x x x +≥+, 令()2ln 1g x x x =+,令()()'2ln 2ln 10g x x x x x x =+=+=,得12x e -=;所以()g x 在120,x e -⎛⎫∈ ⎪⎝⎭上单调减,在12,x e -⎛⎫∈+∞ ⎪⎝⎭单调增,则()211221111022g x g e e e --⎛⎫⎛⎫⎛⎫≥=⋅-+=-> ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,即2ln 1()ln 1a x x x x +≥+,可化为2ln 1ln 1x x a x x +≥+, 记()2ln 1ln 1x x h x x x +=+,则()()2222ln ln 2ln 1'ln 1x x x x x x h x x x -+-+-=+,且()'10h =; 再令()22ln ln 2ln 1F x x x x x x x =-+-+-,精品 Word 可修改 欢迎下载 当1,12x ⎡⎫∈⎪⎢⎣⎭时,()()2222ln ln 2ln 1ln 12ln 1F x x x x x x x x x x x x =-+-+-=-+-+-, ()22ln 1F x x x x ≥-+-,由(1)可知1ln 1x x ≥-,0x >时成立,1,12x ⎡⎫∈⎪⎢⎣⎭,221ln 1x x ⎛⎫≤- ⎪⎝⎭, 由此22221()ln 111(1)0F x x x x x x x x x ⎛⎫≥-+-≥--+-=-≥ ⎪⎝⎭,()h x 在1,12x ⎡⎫∈⎪⎢⎣⎭上单调增;当,()1x ∈+∞时,()()()22ln 12ln 10F x x x x x x =-+-+-≤,()h x 在,()1x ∈+∞上单调减;因此()()11h x h ≥=,故1a ≥;方法2:当1x =时,()110f a =-≥,由此1a ≥证明如下:当1a ≥时,()f x 在1,2x ⎡⎫∈+∞⎪⎢⎣⎭上,()0f x ≥恒成立, ()()2ln 1(ln 1)f x a x x x x =+-+,同法1证明,()2ln 10g x x x =+>,()()()222ln 1ln 1l ()()()n 1ln 1ln 0f x a x x x x x x x x x x x =+-+≥+-+=-≥;所以()f x 在1,2x ⎡⎫∈+∞⎪⎢⎣⎭上,()0f x ≥恒成立,故1a ≥. 【点睛】本题主要考查导数在函数中的综合应用,以及不等式的证明和恒成立问题的求解,着重考查了转化与化归思想、分类讨论、及逻辑推理能力与计算能力,对于恒成立问题,通常要构造新函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造新函数,直接把问题转化为函数的最值问题.。

2020-2021学年高一数学下学期期中模拟试题(二)一.选择题1.已知向量(2,3)OA =,(4,1)OB =-,P 是线段AB 的中点,则P 点的坐标是 A .(2,4)- B .(3,1) C .(2,4)- D .(6,2)【答案】B【解析】由线段的中点公式可得1()(32OP OA OB =+=,1),故P 点的坐标是(3,1),故选B .2.若复数z 满足(1)(1)22z i i -+=-,则||z =A B C .5 D【答案】D【解析】由(1)(1)22z i i -+=-,得22222(22)(1)22224121(1)(1)112i i i i i i iz i i i i -----+--=====-++-+, 12z i ∴=-,则||z = 故选D .3.已知复数z 满足(12)|43|z i i +=-(其中i 为虚数单位),则复数z 的虚部为 A .2- B .2i - C .1 D .i【答案】A【解析】由(12)|43|5z i i +=-, 得55(12)1212(12)(12)i z i i i i -===-++-, ∴复数z 的虚部为2-.故选A . 4.复数3121iz i -=+的共轭复数的虚部为A .12i -B .12iC .12-D .12【答案】D 【解析】31212(12)(1)3111(1)(1)22i i i i z i i i i i ---+====-+--+, ∴3122z i =+, ∴复数3121i z i-=+的共轭复数的虚部为12, 故选D .5.已知向量a ,b 满足||2||2b a ==,|2|2a b -=,则向量a ,b 的夹角为 A .30︒ B .45︒ C .60︒ D .90︒【答案】C【解析】根据题意,设向量a ,b 的夹角为θ, 若||2||2b a ==,则||2b =,||1a =,若|2|2a b -=,则222(2)4488cos 4a b a a b b θ-=-⋅+=-=, 解可得1cos 2θ=, 又由0180θ︒︒,故60θ=︒, 故选C .6.已知向量(1,2)a =-,(21,1)b m =-,且a b ⊥,则|2|a b -= A .5 B .4 C .3 D .2【答案】A【解析】向量(1,2)a =-,(21,1)b m =-,且a b ⊥, 可得(21)20m ---+=,解得32m =, 所以(2,1)b =,2(5,0)a b -=-, 所以|2|5a b -=. 故选A .7.已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是 A .m α⊂,n α⊂,//m β,////n βαβ⇒ B .//αβ,m α⊂,//n m n β⊂⇒C .m α⊥,//m n n α⊥⇒D .//m n ,n m αα⊥⇒⊥【答案】D【解析】m ,n 为两条不同的直线,α,β为两个不同的平面,对于A ,m α⊂,n α⊂,//m β,////n βαβ⇒,也可能相交,所以A 不正确; 对于B ,//αβ,m α⊂,//n m n β⊂⇒也可能异面,所以B 不正确; 对于C ,m α⊥,//m n n α⊥⇒有可能n α⊂,所以C 不正确;对于D ,//m n ,n m αα⊥⇒⊥,满足直线与平面垂直的性质,所以D 正确. 故选D .8.四面体A BCD -中,DC ⊥面ABC ,3AB BC ==,120ABC ∠=︒,8DC =,则四面体A BCD -外接球的表面积为 A .100π B .50π C .25π D .91π【答案】A【解析】设ABC ∆外接圆的圆心为1O ,四面体A BCD -外接球的球心为O ,半径为R , 连接1O C ,1OO ,OC , 由正弦定理可得12sin BCO CBAC=∠,即1332sin30O C ==︒,1142OO DC ==,222211435R OC OC OO ==+=+=,即四面体A BCD -外接球的表面积为245100S ππ=⨯=, 故选A . 二.多选题9.ABC ∆是边长为2的等边三角形,已知向量,a b 满足2,2AB a AC a b ==+,则下列结论正确的是 A .a 是单位向量 B .//BC bC .1a b =D .(4)BC a b ⊥+【答案】ABD【解析】A .||2AB =,∴由2AB a =得,||||12AB a ==,∴a 是单位向量,该选项正确; B .22BC AC AB a b a b =-=+-=,∴//BC b ,该选项正确;.||2,||1C AC a ==,∴由2AC a b =+得,22244AC a a b b =++,即2444a b b =++,∴214b a b =-≠,该选项错误;D .BC b =,由上面得,2(4)(4)40BC a b b a b a b b +=+=+=,∴(4)BC a b ⊥+,该选项正确.故选ABD .10.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .若cos b c A =,角A 的角平分线交BC 于点D ,1AD =,1cos 8A =,以下结论正确的是A .34AC = B .8AB =C .18CD BD = D .ABD ∆ 【答案】ACD【解析】因为cos b c A =,由正弦定理可得,sin sin cos sin()B C A A C ==+, 所以sin cos 0A C =, 因为sin 0A ≠,所以cos 0C =即12C π=,1cos8ACA AB==, 由角平分线定理可得,18AC CD AB BD ==,设AC x =,8AB x =,则BC =,CD =,Rt ACD ∆中,由勾股定理可得,22)1x x +=, 解可得34x =,即34AC =,6AB =,13624ABC S =⨯⨯=,所以89ABD ABC S S ∆==故选ACD .11.在正方体1111ABCD A B C D -中,N 为底面ABCD 的中心,P 为线段11A D 上的动点(不包括两个端点),M 为线段AP 的中点,则A .CM 与PN 是异面直线B .存在P 点使得//PN 平面11CCD D C .平面PAN ⊥平面11BDD BD .过P ,A ,C 三点的正方体的截面一定是等腰梯形 【答案】BCD【解析】对于A ,因为C ,N ,A 共线,又CN ,PM 交于点A ,即P ,M ,N ,C 共面,因此CM 与PN 共面,故选项A 不正确;对于B ,当P 为11A D 的中点时,//PN 平面11CC D D ,故选项B 正确; 对于C ,AN BD ⊥,1AN BB ⊥,1BDBB B =,BD ,1BB ⊂平面11BDD B ,AN ∴⊥平面11BDD B ,AN ⊂平面PAN ,∴平面PAN ⊥平面11BDD B ,故选项C 正确;对于D ,过P ,A ,C 三点的正方体的截面与11C D 相交于点Q ,则//AC PQ ,且PQ AC <,因此一定是等腰梯形,故选项D 正确.故选BCD .12.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为AB ,11A D 的中点,则( ) A .1BD B C ⊥ B .//EF 平面1DB B C .1AC ⊥平面11B D CD .过直线EF 且与直线1BD 2【答案】BC【解析】对于A ,11//B C A D ,1A DB ∴∠是BD 与1B C 所成角(或所成角)的补角, 11A D BD A B ==,160A DB ∴∠=︒,BD ∴与1B C 不垂直,故A 错误;对于B ,取AD 中点G ,连接FG ,EG ,则//EG BD ,1//FG BB , EGFG G =,1BDBB B =,∴平面//EFG 平面1DB B ,EF ⊂平面EFG ,//EF ∴平面1DB B ,故B 正确;对于C ,1111AC B D ⊥,111AA B D ⊥,1111AC AA A =,11A C 、1AA ⊂平面11AA C , 11B D ∴⊥平面11AA C ,1AC ⊂平面11AA C ,111AC B D ∴⊥,同理11AC B C ⊥, 1111B D B C B =,11B D 、1B C ⊂平面11B D C ,1AC ∴⊥平面11B D C ,故C 正确;对于D ,取11A B 中点H ,连接FH 、EH , 则11//FH B D ,1//GF BB , FHGF F =,1111B D BB B =,∴平面//EHFG 平面11BB D D ,1BD ⊂平面11BB D D ,EF ⊂平面EHFG ,∴过直线EF 且与直线1BD 平行的平面截该正方体所得截面为矩形EHFG ,2GF =,1144222GE BD ==+=, ∴过直线EF 且与直线1BD 平行的平面截该正方体所得截面面积为22S =,故D 错误.故选:BC .三.填空题13.已知i 虚数单位,若复数1()1aiz a R i-=∈+的虚部为3-,则||z = . 【答案】13【解析】221(1)(1)1(1)(1)111(1)(1)1222ai ai i ai i ai a a i a az i i i i i -----+----+=====-++--,复数1()1aiz a R i-=∈+的虚部为3-, 132a+∴-=-,解得5a =,23z i ∴=--,22||(2)(3)13z ∴-+-13.14.已知向量13(,2a =,若向量b 与a 反向,且||2b =,则向量b 的坐标是 .【答案】(3)-【解析】因为:向量13(,2a =,||1a ∴=,向量b 与a 反向,且||2b =∴2(1,3)b a =-=-.故答案为:(-.15.已知向量(,3)a m =,(1,2)b =-,且()a b b +⊥,则m = . 【答案】1【解析】根据题意,向量(,3)a m =,(1,2)b =-,则(1,1)a b m +=+. 因为()a b b +⊥,所以()120a b b m +⋅=+-=,解得1m =, 故答案为:1.16.直三棱柱111ABC A B C -的各顶点都在球O 的球面上,且1AB AC ==,BC 若球O 的表面积为20π,则这个三棱柱的体积为 .【解析】设ABC ∆和△111A B C 的外心分别为1O 、2O ,连接12O O ,可得外接球的球心O 为12O O 的中点,连接OA 、OB 、OC 、1O A 、1O B 、1O C ,ABC ∆中,2221cos 22AB AC BC A AB AC +-==-⋅, (0,)A π∈,23A π∴=, 根据正弦定理,得ABC ∆外接圆半径112sin BCO A A==球O 的表面积为20π,2420R ππ=,RRt △1O OA 中,12OO ,可得12124O O O O ==,直三棱柱111ABC A B C -的底面积12sin 23ABC S AB AC π∆=⋅,∴直三棱柱111ABC A B C -的体积为12ABC S O O ∆⨯=四.解答题17.已知复(,)z a bi a b R =+∈满足3z i +为实数,2zi-为纯虚数,其中i 是虚数单位. (1)求实数a ,b 的值;(2)若复数212(5)z z m m i =++-在复平面内对应的点在第四象限,求实数m 的取值范围. 【答案】(1)323a b ⎧=-⎪⎨⎪=-⎩;(2)3(42). 【解析】(1)由(,)z a bi a b R =+∈,得3(3)z i a b i +=++, ()(2)2222(2)(2)55z a bi a bi i a b a bi i i i i +++-+===+---+, 再由题意可得:302020b a b a b +=⎧⎪-=⎨⎪+≠⎩,解得323a b ⎧=-⎪⎨⎪=-⎩;(2)由(1)得,332z i =-+,则22132(5)32(5)2z z m m i i m m i =++-=-+++-23(2)(2)2m m i =-+-,则2320220m m ⎧->⎪⎨⎪-<⎩,即324m << ∴实数m 的取值范围是3(42).18.已知复数112z i =-,234z i =+,i 为虚数单位.(1)若复数12z az +在复平面上对应的点在第四象限,求实数a 的取值范围; (2)若12z z z =,求z 的共轭复数z .【答案】(1)1(3-,1)2;(2)1255z i =-+.【解析】(1)复数112z i =-,234z i =+,所以12(12)(34)(13)(42)z az i a i a a i +=-++=++-; 由该复数在复平面上对应的点在第四象限, 所以130420a a +>⎧⎨-<⎩,解得1132a -<<,所以实数a 的取值范围是1(3-,1)2;(2)化简122212(12)(34)51012343(4)2555z i i i i z i z i i -----=====--+-,z 的共轭复数1255z i =-+.19.(1)设1e ,2e 是正交单位向量,如果122OA e me =+,12OB ne e =-,125OC e e =-,若A 、B 、C 三点在一条直线上,且2m n =.求m 、n 的值.(2)已知(2,3)OA =,(6,3)OB =-,点P 在线段BA 的延长线上,且3||||4AP PB =,求点P 坐标. 【答案】(1)112m n =-⎧⎪⎨=-⎪⎩或105m n =⎧⎨=⎩;(2)(10,21)P -. 【解析】(1)以O 为原点,1e ,2e 的方向分别为x ,y 轴的正方向,建立平面直角坐标系xOy , 则(2,)OA m =,(,1)OB n =-,(5,1)OC =-,∴(3,1)AC m =--,(5,0)BC n =-,又A ,B ,C 三点在一条直线上,∴//AC BC ,30(1)(5)0m n ∴⨯----=,与2m n =联立, 解得112m n =-⎧⎪⎨=-⎪⎩或105m n =⎧⎨=⎩; (2)(2,3)OA =,(6,3)OB =-,(2,3)A ∴,(6,3)B -,设(,)P x y ,点P 在线段BA 的延长线上,且3||||4AP PB =, ∴34AP PB =-, 即(2x -,33)(6,3)4y x y -=----, ∴32(6)433(3)4x x y y ⎧-=-⎪⎪⎨⎪-=+⎪⎩,解得10x =-,21y =. (10,21)P ∴-.20.如图,在四棱柱1111ABCD A B C D -中,四边形ABCD 是边长等于2的菱形,120ADC ∠=︒,1AA ⊥平面ABCD ,O ,E 分别是1A C ,AB 的中点,AC 交DE 于点H ,点F 为HC 的中点(1)求证://OF 平面1A ED ;(2)若OF 与平面ABCD 所成的角为60︒,求三棱锥1A ADE -的表面积.【答案】(1)答案见解析;(26315++【解析】(1)连接1A H ,由于点F 为HC 的中点,O 为1A C 的中点,所以1//OF A H , 由于OF ⊂/平面1A ED ,1A H ⊂平面1A ED ,所以//OF 平面1A ED .(2)连接BD ,由于四边形ABCD 为边长为2的菱形,120ADC ∠=︒. 所以ABD ∆为等边三角形.所以233AH =,3DE =,且DE AB ⊥, 由于OF 与平面ABCD 所成的角为60︒,且1//OF A H ,由于1AA ⊥平面ABCD ,则:160A HA ∠=︒,所以112,5AA A E ==,由于1AA ⊥平面ABCD ,DE ⊂平面ABCD ,所以1AA DE ⊥.又DE AB ⊥,1AA AB A =,1AA ,AB ⊂平面11A ABB ,所以DE ⊥平面11A ABB , 则:1A E DE ⊥,所以三棱锥1A ADE -的表面积为:11113631522123512222222++⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯=.21.已知ABC ∆的内角A ,B ,C 所对的边分别是a ,b ,c ,其面积2224b c a S +-=. (1)若6a ,2b =,求cos B ;(2)求sin()sin cos cos()A B B B B A +++-的最大值.【答案】(130;(2)52. 【解析】(1)2224b c a S +-=,可得12cos sin 24bc A bc A =, sin cos A A ∴=,可得tan 1A =,(0,)A π∈, 4A π∴=, 6a =,2b =, ∴由正弦定理sin sin a b A B =,可得22sin 62sin 66b A B a ⨯===, 又a b >,B 为锐角,230cos 16B sin B ∴=-=. (2)4A π=,sin()sin cos cos()A B B B B A ∴+++-sin()sin cos cos()44B B B B ππ=+++- 2222sin cos sin cos cos sin 2222B B B B B B =++++ 2(sin cos )sin cos B B B B =++令sin cos t B B =+,则212sin t BcoB =+,∴原式2211132(2)2222t t t =+-=+-,(0t ∈,2], ∴当2t =时,4B π=,此时,原式的最大值为52. 22.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PAD ∆为等边三角形,平面PAD ⊥平面PCD . (Ⅰ)证明:直线CD ⊥平面PAD ;(Ⅱ)若2AB =,Q 为线段PB 的中点,求三棱锥Q PCD -的体积.【答案】(1)证明见解析;(23. 【解析】(Ⅰ)证明:取PD 的中点,连接AO ,PAD ∆为等边三角形,AO PD ∴⊥,又AO ⊂平面PAD ,平面PAD ⊥平面PCD ,平面PAD ⋂平面PCD PD =,AO ∴⊥平面PCD ,CD ⊂平面PCD ,AO CD ∴⊥, 底面ABCD 为正方形,CD AD ∴⊥, AO AD A =,AO ,AD ⊂平面PAD , CD ∴⊥平面PAD ; (Ⅱ)解:2AB =,由(Ⅰ)得AO ⊥平面PCD , ∴点A 到平面PCD 的距离3d AO ==, 底面ABCD 为正方形,//AB CD ∴, 又AB ⊂/平面PCD ,CD ⊂平面PCD , //AB ∴平面PCD , A ∴,B 两点到平面PCD 的距离相等,均为d , 又Q 为线段PB 的中点. ∴点Q 到平面PCD 的距离322d h ==, 由(Ⅰ)知,CD ⊥平面PAD , PD ⊂平面PAD ,CD PD ∴⊥, ∴111332233223Q PCD PCD V S h -=⋅⋅=⨯⨯⨯⨯=. 故三棱锥Q PCD -的体积为33.。


2020-2021宜兴市万石中学高中必修二数学下期末模拟试题含答案一、选择题1.设集合{1,2,3,4}A =,{}1,0,2,3B =-,{|12}C x R x =∈-≤<,则()A B C =U IA .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4}2.已知数列{}n a 的前n 项和22n S n n =+,那么它的通项公式是( )A .21n a n =-B .21n a n =+C .41n a n =-D .41n a n =+3.已知不等式220ax bx ++>的解集为{}12x x -<<,则不等式220x bx a ++<的解集为( ) A .112x x ⎧⎫-<<⎨⎬⎩⎭B .112x x x ⎧⎫<->⎨⎬⎩⎭或 C .{}21x x -<<D .{}21x x x <->或4.在ABC V 中,已知,2,60a x b B ===o,如果ABC V 有两组解,则x 的取值范围是( )A .4323⎛⎫ ⎪ ⎪⎝⎭,B .4323⎡⎤⎢⎥⎣⎦,C .4323⎡⎫⎪⎢⎪⎣⎭, D .432,3⎛⎤⎥ ⎝⎦5.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 A .45B .35C .25D .156.函数223()2xx xf x e +=的大致图像是( )A .B .C .D .7.设函数()sin()cos()f x x x ωϕωϕ=+-+0,||2πωϕ⎛⎫><⎪⎝⎭的最小正周期为π,且f x f x -=()(),则( )A .()f x 在0,2π⎛⎫⎪⎝⎭上单调递增B .()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递减C .()f x 在0,2π⎛⎫⎪⎝⎭上单调递减 D .()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增8.定义在R 上的奇函数()f x 满足()()2f x f x +=-,且当[]0,1x ∈时,()2cos x f x x =-,则下列结论正确的是( )A .()20202019201832f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B .()20202019201832f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C .()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭D .()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭9.在空间四边形ABCD 的边AB ,BC ,CD ,DA 上分别取E ,F ,G ,H 四点,如EF 与HG 交于点M ,那么 ( ) A .M 一定在直线AC 上 B .M 一定在直线BD 上C .M 可能在直线AC 上,也可能在直线BD 上 D .M 既不在直线AC 上,也不在直线BD 上10.下列四个正方体图形中,A ,B 为正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是( )A .①③B .②③C .①④D .②④11.如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则( )A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线12.若函数()(),1231,1x a x f x a x x ⎧>⎪=⎨-+≤⎪⎩是R 上的减函数,则实数a 的取值范围是( )A .2,13⎛⎫⎪⎝⎭B .3,14⎡⎫⎪⎢⎣⎭C .23,34⎛⎤⎥⎝⎦D .2,3⎛⎫+∞⎪⎝⎭二、填空题13.甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a ,再由乙猜甲刚才想的数字,把乙猜的数字记为b ,且,{0,1,2,,9}a b ∈L .若||1a b -…,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则这两人“心有灵犀”的概率为______. 14.函数()2sin sin 3f x x x =+-的最小值为________.15.设向量(12)(23)a b ==r r ,,,,若向量a b λ+r r 与向量(47)c =--r ,共线,则λ= 16.已知l ,m 是平面α外的两条不同直线.给出下列三个论断: ①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.17.如图,棱长均为2的正四棱锥的体积为_______.18.在ABC ∆中,120B =o ,1BC =,且ABC ∆的面积为3,则AC =__________. 19.设12a =,121n n a a +=+,21n n n a b a +=-,*n N ∈,则数列{}n b 的通项公式n b = .20.如图,某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积为________.三、解答题21.已知关于x 的不等式2320,08kx kx k +-<≠ (1)若不等式的解集为3,12⎛⎫- ⎪⎝⎭,求k 的值. (2)若不等式的解集为R ,求k 的取值范围.22.如图,四棱锥P ABC -中,PA ⊥平面ABCD ,AD BC ∥,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点. (I )证明MN ∥平面PAB ; (II )求四面体N BCM -的体积.23.已知不等式的解集为或.(1)求;(2)解关于的不等式24.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表: 年份20102011201220132014时间代号t12345储蓄存款y (千亿元)567810(Ⅰ)求y 关于t 的回归方程^^^t y b a =+(Ⅱ)用所求回归方程预测该地区2015年(6t =)的人民币储蓄存款.附:回归方程^^^t y b a =+中1122211()(),{().n niii ii i nni i i i x x y y x y nxyb x x x nx a y bx ====---==--=-∑∑∑∑25.设函数2()cos 2sin 3f x x x π⎛⎫=++ ⎪⎝⎭. (1)求函数()f x 的最小正周期. (2)求函数()f x 的单调递减区间;(3)设,,A B C 为ABC V 的三个内角,若1cos 3B =,124C f ⎛⎫=- ⎪⎝⎭,且C 为锐角,求sin A .26.某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(I )记A 为事件:“一续保人本年度的保费不高于基本保费”.求P (A )的估计值; (Ⅱ)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P (B )的估计值;(Ⅲ)求续保人本年度的平均保费估计值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C分析:由题意首先进行并集运算,然后进行交集运算即可求得最终结果. 详解:由并集的定义可得:{}1,0,1,2,3,4A B ⋃=-, 结合交集的定义可知:(){}1,0,1A B C ⋃⋂=-. 本题选择C 选项.点睛:本题主要考查并集运算、交集运算等知识,意在考查学生的计算求解能力.2.C解析:C 【解析】分类讨论:当1n =时,11213a S ==+=,当2n ≥时,221(2)2(1)141n n n a S S n n n n n -⎡⎤=-=+--+-=-⎣⎦, 且当1n =时:1414113n a -=⨯-== 据此可得,数列的通项公式为:41n a n =-. 本题选择C 选项.3.A解析:A 【解析】 【分析】根据一元二次不等式的解集与一元二次方程根的关系,结合韦达定理可构造方程求得,a b ;利用一元二次不等式的解法可求得结果.【详解】220ax bx ++>Q 的解集为{}12x x -<<1∴-和2是方程220ax bx ++=的两根,且0a <1212122ba a⎧-=-+=⎪⎪∴⎨⎪=-⨯=-⎪⎩,解得:11a b =-⎧⎨=⎩ 222210x bx a x x ∴++=+-< 解得:112x -<<,即不等式220x bx a ++<的解集为112x x ⎧⎫-<<⎨⎬⎩⎭故选:A 【点睛】本题考查一元二次不等式的解法、一元二次不等式的解集与一元二次方程根的关系等知识的应用;关键是能够通过一元二次不等式的解集确定一元二次方程的根,进而利用韦达定理构造方程求得变量.4.A解析:A【分析】已知,,a b B ,若ABC V 有两组解,则sin a B b a <<,可解得x 的取值范围. 【详解】由已知可得sin a B b a <<,则sin602x x ︒<<,解得2x <<故选A. 【点睛】本题考查已知两边及其中一边的对角,用正弦定理解三角形时解的个数的判断. 若ABC V 中,已知,,a b B 且B 为锐角,若0sin b a B <<,则无解;若sin b a B =或b a ≥,则有一解;若sin a B b a <<,则有两解. 5.C 解析:C 【解析】选取两支彩笔的方法有25C 种,含有红色彩笔的选法为14C 种,由古典概型公式,满足题意的概率值为142542105C p C ===. 本题选择C 选项. 考点:古典概型名师点睛:对于古典概型问题主要把握基本事件的种数和符合要求的事件种数,基本事件的种数要注意区别是排列问题还是组合问题,看抽取时是有、无顺序,本题从这5支彩笔中任取2支不同颜色的彩笔,是组合问题,当然简单问题建议采取列举法更直观一些.6.B解析:B 【解析】由()f x 的解析式知仅有两个零点32x =-与0x =,而A 中有三个零点,所以排除A ,又()2232xx x f x e-++'=,由()0f x '=知函数有两个极值点,排除C ,D ,故选B . 7.A解析:A 【解析】 【分析】将f(x)化简,求得ωφ,,再进行判断即可. 【详解】()πf x ωx φ,4⎛⎫=+- ⎪⎝⎭∵最小正周期为2ππ,π,ω∴=得ω2=,又f x f x ()()-=为偶函数,所以ππφk π42-=+, k Z ∈∵πφ2<,∴k=-1,()πππφ,f x 2sin 2x 2cos2x 444⎛⎫=-∴=--=- ⎪⎝⎭,当2k π2x 2k ππ≤≤+,即πk πx k π2≤≤+,f(x)单调递增,结合选项k=0合题意, 故选A. 【点睛】本题考查三角函数性质,两角差的正弦逆用,熟记三角函数性质,熟练计算f(x)解析式是关键,是中档题.8.C解析:C 【解析】 【分析】根据f (x )是奇函数,以及f (x+2)=f (-x )即可得出f (x+4)=f (x ),即得出f (x )的周期为4,从而可得出f (2018)=f (0),2019122f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,20207312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭然后可根据f (x )在[0,1]上的解析式可判断f (x )在[0,1]上单调递增,从而可得出结果. 【详解】∵f(x )是奇函数;∴f(x+2)=f (-x )=-f (x );∴f(x+4)=-f (x+2)=f (x ); ∴f(x )的周期为4;∴f(2018)=f (2+4×504)=f (2)=f (0),2019122f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,20207 312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∵x∈[0,1]时,f (x )=2x -cosx 单调递增;∴f(0)<12f ⎛⎫⎪⎝⎭ <712f ⎛⎫ ⎪⎝⎭ ∴()20192020201823f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭,故选C. 【点睛】本题考查奇函数,周期函数的定义,指数函数和余弦函数的单调性,以及增函数的定义,属于中档题.9.A解析:A 【解析】如图,因为EF∩HG=M ,所以M∈EF,M∈HG,又EF ⊂平面ABC ,HG ⊂平面ADC , 故M∈平面ABC ,M∈平面ADC , 所以M∈平面ABC∩平面ADC=AC. 选A. 点睛:证明点在线上常用方法先找出两个平面,然后确定点是这两个平面的公共点,再确定直线是这两个平面的交线.10.C解析:C 【解析】 【分析】用面面平行的性质判断①的正确性.利用线面相交来判断②③的正确性,利用线线平行来判断④的正确性. 【详解】对于①,连接AC 如图所示,由于//,//MN AC NP BC ,根据面面平行的性质定理可知平面//MNP 平面ACB ,所以//AB 平面MNP .对于②,连接BC 交MP 于D ,由于N 是AC 的中点,D 不是BC 的中点,所以在平面ABC 内AB 与DN 相交,所以直线AB 与平面MNP 相交.对于③,连接CD ,则//AB CD ,而CD 与PN 相交,即CD 与平面PMN 相交,所以AB 与平面MNP 相交.对于④,连接CD ,则////AB CD NP ,由线面平行的判定定理可知//AB 平面MNP .综上所述,能得出//AB 平面MNP 的图形的序号是①④. 故选:C 【点睛】本小题主要考查线面平行的判定,考查空间想象能力和逻辑推理能力,属于基础题.11.B解析:B 【解析】 【分析】利用垂直关系,再结合勾股定理进而解决问题. 【详解】如图所示, 作EO CD ⊥于O ,连接ON ,过M 作MF OD ⊥于F . 连BF ,Q 平面CDE ⊥平面ABCD .,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴∆与EON ∆均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,35,,722MF BF BM ==∴=.BM EN ∴≠,故选B . 【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角性.12.C解析:C 【解析】 【分析】由题意结合分段函数的解析式分类讨论即可求得实数a 的取值范围. 【详解】当1x >时,x a 为减函数,则01a <<,当1x ≤时,一次函数()231a x -+为减函数,则230a -<,解得:23a >, 且在1x =处,有:()12311a a -⨯+≥,解得:34a ≤, 综上可得,实数a 的取值范围是23,34⎛⎤ ⎥⎝⎦. 本题选择C 选项. 【点睛】对于分段函数的单调性,有两种基本的判断方法:一保证各段上同增(减)时,要注意上、下段间端点值间的大小关系;二是画出这个分段函数的图象,结合函数图象、性质进行直观的判断.二、填空题13.【解析】【分析】由题意知本题是一个古典概型从0~9中任意取两个数(可重复)共有100种取法列出满足所有可能情况代入公式得到结果【详解】从0~9中任意取两个数(可重复)共有100种取法则的情况有:共有 解析:725【解析】 【分析】由题意知本题是一个古典概型,从0~9中任意取两个数(可重复)共有100种取法,列出满足||1a b -„所有可能情况,代入公式得到结果。


2020-2021高三数学下期中试卷(含答案)(2)一、选择题1.若,x y 满足1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩,则2z x y =+的最大值为( )A .8B .7C .2D .12.在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( ) A .等腰直角三角形 B .直角三角形C .等腰三角形D .等腰三角形或直角三角形3.已知数列{}n a 的前n 项和为n S ,点(,3)n n S +*()n N ∈在函数32xy =⨯的图象上,等比数列{}n b 满足1n n n b b a ++=*()n N ∈,其前n 项和为n T ,则下列结论正确的是( )A .2n n S T =B .21n n T b =+C .n n T a >D .1n n T b +<4.已知ABC ∆的三个内角、、A B C 所对的边为a b c 、、,面积为S,且2S =,则A 等于( )A .6π B .4π C .3π D .2π 5.数列{}n a 为等比数列,若11a =,748a a =,数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,则5(S = )A .3116 B .158C .7D .316.在ABC ∆中,角,,A B C 的对边分别为a ,b ,c .若ABC ∆为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是( )A .2a b =B .2b a =C .2A B =D .2B A =7.若不等式组0220y x y x y x y a⎧⎪+⎪⎨-⎪⎪+⎩…„…„表示的平面区域是一个三角形,则实数a 的取值范围是( )A .4,3⎡⎫+∞⎪⎢⎣⎭B .(]0,1C .41,3⎡⎤⎢⎥⎣⎦D .(]40,1,3⎡⎫+∞⎪⎢⎣⎭U8.已知{}n a 为等差数列,若20191<-a a ,且数列{}n a 的前n 项和n S 有最大值,则n S 的最小正值为( ) A .1SB .19SC .20SD .37S9.在斜ABC ∆中,设角,,A B C 的对边分别为,,a b c ,已知sin sin sin 4sin cos a A b B c C b B C +-=,CD 是角C 的内角平分线,且CD b =,则cos C = ( )A .18B .34C .23 D .1610.数列{a n }满足a 1=1,对任意n ∈N *都有a n +1=a n +n +1,则122019111a a a ++⋯+=( ) A .20202019B .20191010C .20171010D .4037202011.已知a >0,x ,y 满足约束条件1{3(3)x x y y a x ≥+≤≥-,若z=2x+y 的最小值为1,则a=A .B .C .1D .212.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若sin 23sin 0b A a B +=,3b c =,则ca的值为( )A .1B .3 C .5 D .7 二、填空题13.等比数列{}n a 的首项为1a ,公比为q ,1lim 2n n S →∞=,则首项1a 的取值范围是____________.14.已知实数x ,y 满足不等式组2202x y y y x+-≥⎧⎪≤⎨⎪≥⎩,则1y x +的最大值为_______.15.在等差数列{}n a 中,12a =,3510a a +=,则7a = . 16.已知数列{a n }的前n 项和S n =n 2+2n +1(n ∈N *),则a n =________.17.如图,无人机在离地面高200m 的A 处,观测到山顶M 处的仰角为15°、山脚C 处的俯角为45°,已知∠MCN=60°,则山的高度MN 为_________m.18.已知等比数列{}n a 的首项为2,公比为2,则112n na a a a a a a a +=⋅⋅⋅L _______________.19.已知二次函数22()42(2)21f x x p x p p =----+,若在区间[1,1]-内至少存在一个实数x 使()0f x >,则实数p 的取值范围是__________.20.如图所示,位于A 处的信息中心获悉:在其正东方向40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20海里的C 处的乙船,现乙船朝北偏东θ的方向即沿直线CB 前往B 处救援,则cos θ=______________.三、解答题21.在ABC ∆中,,,a b c 分别是角,,A B C 所对的边,且2sin 3tan c B a A =.(1)求222b c a+的值; (2)若2a =,求ABC ∆面积的最大值.22.已知000a b c >,>,>,函数().f x a x x b c =-+++ (1)当1a b c ===时,求不等式()3f x >的解集; (2)当()f x 的最小值为3时,求111a b c++的最小值. 23.已知等差数列{}n a 的公差为()0d d ≠,等差数列{}n b 的公差为2d ,设n A ,n B 分别是数列{}n a ,{}n b 的前n 项和,且13b =,23A =,53A B =. (1)求数列{}n a ,{}n b 的通项公式; (2)设11n n n n c b a a +=+•,数列{}n c 的前n 项和为n S ,证明:2(1)n S n <+.24.若数列{}n a 的前n 项和n S 满足*231?(N )n n S a n =-∈,等差数列{}n b 满足113233b a b S ==+,.(1)求数列{}n a 、{}n b 的通项公式; (2)设3nn nb c a =,求数列{}n c 的前n 项和为n T . 25.设ABC ∆的内角A B C ,,所对的边分别为a b c ,,,已知cos (2)cos a B c b A =-.(Ⅰ)求角A 的大小;(Ⅱ)若4a =,BC 边上的中线22AM =,求ABC ∆的面积. 26.已知等差数列{}n a 的前n 项和为n S ,且211a =,7161S =. (1)求数列{}n a 的通项公式;(2)若6512n n S a n >--,求n 的取值范围; (3)若11n n n b a a +=,求数列{}n b 的前n 项和n T .【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】试题分析:作出题设约束条件可行域,如图ABC ∆内部(含边界),作直线:20l x y +=,把直线l 向上平移,z 增加,当l 过点(3,2)B 时,3227z =+⨯=为最大值.故选B .考点:简单的线性规划问题.2.C解析:C 【解析】在ABC ∆中,222222cos ,2cos 222a b c a b c C a b C b ab abQ +-+-=∴==⋅,2222a a b c ∴=+-,,b c ∴=∴此三角形一定是等腰三角形,故选C.【方法点睛】本题主要考查利用余弦定理判断三角形形状,属于中档题.判断三角形状的常见方法是:(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断;(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出边与边之间的关系进行判断;(3)根据余弦定理确定一个内角为钝角进而知其为钝角三角形.3.D解析:D 【解析】 【分析】 【详解】由题意可得:332,323n nn n S S +=⨯=⨯- ,由等比数列前n 项和的特点可得数列{}n a 是首项为3,公比为2的等比数列,数列的通项公式:132n n a -=⨯ ,设11n nb b q -= ,则:111132n n n b q b q --+=⨯ ,解得:11,2b q == ,数列{}n b 的通项公式12n nb -= ,由等比数列求和公式有:21nn T =- ,考查所给的选项:13,21,,n n n n n n n n S T T b T a T b +==-<< .本题选择D 选项.4.C解析:C 【解析】 【分析】利用三角形面积公式可得2tan 1acsinB 2bc c B +=,结合正弦定理及三角恒等变换知识cosA 1-=,从而得到角A. 【详解】∵2tan bc c B S +=∴2tan 1acsinB 2bc c B +=即c tan asinB a b B +==()B sinAcosB sinB sinC sinB sin A B +=+=++ cosA 1-= ∴1sin 62A π⎛⎫-= ⎪⎝⎭,∴5666A 或πππ-=(舍) ∴3A π=故选C 【点睛】此题考查了正弦定理、三角形面积公式,以及三角恒等变换,熟练掌握边角的转化是解本题的关键.5.A解析:A 【解析】 【分析】先求等比数列通项公式,再根据等比数列求和公式求结果. 【详解】Q 数列{}n a 为等比数列,11a =,748a a =,638q q ∴=,解得2q =, 1112n n n a a q --∴==, Q 数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S , 55111111131211248161612S ⎛⎫⨯- ⎪⎝⎭∴=++++==-.故选A . 【点睛】本题考查等比数列通项公式与求和公式,考查基本分析求解能力,属基础题.6.A解析:A 【解析】sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=,选A.【名师点睛】本题较为容易,关键是要利用两角和差的三角函数公式进行恒等变形. 首先用两角和的正弦公式转化为含有A ,B ,C 的式子,用正弦定理将角转化为边,得到2a b =.解答三角形中的问题时,三角形内角和定理是经常用到的一个隐含条件,不容忽视. 7.D 解析:D 【解析】 【分析】要确定不等式组0220y x y x y x y a⎧⎪+⎪⎨-⎪⎪+⎩…„…„表示的平面区域是否一个三角形,我们可以先画出0220y x y x y ⎧⎪+⎨⎪-⎩…„…,再对a 值进行分类讨论,找出满足条件的实数a 的取值范围. 【详解】不等式组0220y x y x y ⎧⎪+⎨⎪-⎩…„…表示的平面区域如图中阴影部分所示.由22x y x y =⎧⎨+=⎩得22,33A ⎛⎫⎪⎝⎭,由022y x y =⎧⎨+=⎩得()10B ,. 若原不等式组0220y x y x y x y a ⎧⎪+⎪⎨-⎪⎪+⎩…„…„表示的平面区域是一个三角形,则直线x y a +=中a 的取值范围是(]40,1,3a ⎡⎫∈+∞⎪⎢⎣⎭U故选:D 【点睛】平面区域的形状问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合分类讨论的思想,针对图象分析满足条件的参数的取值范围.8.D解析:D 【解析】 【分析】由已知条件判断出公差0d <,对20191<-a a 进行化简,运用等差数列的性质进行判断,求出结果. 【详解】已知{}n a 为等差数列,若20191<-a a ,则2019190a a a +<, 由数列{}n a 的前n 项和n S 有最大值,可得0d <,19193712029000,,0,370a a a a a S <=∴+<>>, 31208190a a a a ∴+=+<,380S <,则n S 的最小正值为37S 故选D 【点睛】本题考查了等差数列的性质运用,需要掌握等差数列的各公式并能熟练运用等差数列的性质进行解题,本题属于中档题,需要掌握解题方法.9.A解析:A 【解析】 【分析】利用正弦定理角化边可构造方程2cos cos bC C a=,由cos 0C ≠可得2a b =;利用ABC ACD BCD S S S ∆∆∆=+可构造方程求得3cos 24C =,利用二倍角公式求得结果.【详解】由正弦定理得:22224cos a b c b C +-=则22224cos 2cos cos 22a b c b C bC C ab ab a+-===ABC ∆Q 为斜三角形 cos 0C ∴≠ 2a b ∴=ABC ACD BCD S S S ∆∆∆=+Q 1112sin sin 2sin 22222C Cb b C b b b b ∴⋅=⋅+⋅即:2sin 4sin cos 3sin 222C C CC ==()0,C π∈Q 0,22C π⎛⎫∴∈ ⎪⎝⎭ sin 02C ∴≠ 3cos 24C ∴= 291cos 2cos 1212168C C ∴=-=⨯-= 本题正确选项:A 【点睛】本题考查解三角形的相关知识,涉及到正弦定理化简边角关系式、余弦定理和三角形面积公式的应用、二倍角公式求三角函数值等知识;关键是能够通过面积桥的方式构造方程解出半角的三角函数值.10.B解析:B 【解析】 【分析】由题意可得n ≥2时,a n -a n -1=n ,再由数列的恒等式:a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1),运用等差数列的求和公式,可得a n ,求得1n a =()21n n +=2(1n -11n +),由数列的裂项相消求和,化简计算可得所求和. 【详解】解:数列{a n }满足a 1=1,对任意n ∈N *都有a n +1=a n +n +1, 即有n ≥2时,a n -a n -1=n ,可得a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =1+2+3+…+n =12n (n +1),1n =也满足上式 1n a =()21n n +=2(1n -11n +), 则122019111a a a ++⋯+=2(1-12+12-13+…+12019-12020) =2(1-12020)=20191010.故选:B . 【点睛】本题考查数列的恒等式的运用,等差数列的求和公式,以及数列的裂项相消求和,考查化简运算能力,属于中档题.11.B解析:B 【解析】 【分析】 【详解】画出不等式组表示的平面区域如图所示:当目标函数z=2x+y 表示的直线经过点A 时,z 取得最小值,而点A 的坐标为(1,2a -),所以221a -=,解得12a =,故选B. 【考点定位】本小题考查线性规划的基础知识,难度不大,线性规划知识在高考中一般以小题的形式出现,是高考的重点内容之一,几乎年年必考.12.D解析:D 【解析】分析:由正弦定理可将sin23sin 0b A a B =化简得3cosA 2=-,由余弦定理可得222227a b c bccosA c =+-=,从而得解.详解:由正弦定理,sin23sin 0b A a B +=,可得sin23sin 0sinB A sinA B +=, 即2sin 3sin 0sinB AcosA sinA B = 由于:0sinBsinA ≠, 所以3cosA =:, 因为0<A <π,所以5πA 6=. 又3b c =,由余弦定理可得22222222337a b c bccosA c c c c =+-=++=. 即227a c =,所以7c a =. 故选:D .点睛:在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.二、填空题13.【解析】【分析】由题得利用即可得解【详解】由题意知可得又因为所以可求得故答案为:【点睛】本题考查了等比数列的通项公式其前n 项和公式数列极限的运算法则考查了推理能力与计算能力属于中档题解析:110,,122⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭U【解析】 【分析】 由题得11(1)2a q =-,利用(1,0)(0,1)q ∈-⋃即可得解 【详解】 由题意知,1112a q =-,可得11(1)2a q =-,又因为(1,0)(0,1)q ∈-⋃,所以可求得1110,,122a ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭U .故答案为:110,,122⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭U【点睛】本题考查了等比数列的通项公式其前n 项和公式、数列极限的运算法则,考查了推理能力与计算能力,属于中档题.14.2【解析】【分析】作出不等式组表示的平面区域根据目标函数的几何意义结合图象即可求解得到答案【详解】由题意作出不等式组表示的平面区域如图所示又由即表示平面区域内任一点与点之间连线的斜率显然直线的斜率最解析:2 【解析】 【分析】作出不等式组表示的平面区域,根据目标函数的几何意义,结合图象,即可求解,得到答案. 【详解】由题意,作出不等式组表示的平面区域,如图所示,又由()011y y x x -=+--,即1y x +表示平面区域内任一点(),x y 与点()1,0D -之间连线的斜率,显然直线AD 的斜率最大, 又由2202x y y +-=⎧⎨=⎩,解得()0,2A ,则02210AD k -==--, 所以1yx +的最大值为2.【点睛】本题主要考查简单线性规划求解目标函数的最值问题.其中解答中正确画出不等式组表示的可行域,利用“一画、二移、三求”,确定目标函数的最优解是解答的关键,着重考查了数形结合思想,及推理与计算能力,属于基础题.15.8【解析】【分析】【详解】设等差数列的公差为则所以故答案为8解析:8 【解析】 【分析】 【详解】设等差数列{}n a 的公差为d , 则351712610a a a a a d +=+=+=, 所以71101028a a =-=-=,故答案为8.16.an=4n=12n+1n≥2【解析】【分析】根据和项与通项关系得结果【详解】当n≥2时an =Sn -Sn -1=2n +1当n =1时a1=S1=4≠2×1+1因此an =4n=12n+1n≥2【点睛】本题考 解析:【解析】 【分析】根据和项与通项关系得结果. 【详解】当n ≥2时,a n =S n -S n -1=2n +1, 当n =1时,a 1=S 1=4≠2×1+1,因此a n =.【点睛】本题考查和项与通项公式关系,考查基本分析求解能力.17.300【解析】试题分析:由条件所以所以这样在中在中解得中故填:300考点:解斜三角形【思路点睛】考察了解三角形的实际问题属于基础题型首先要弄清楚两个概念仰角和俯角都指视线与水平线的夹角将问题所涉及的解析:300 【解析】试题分析:由条件,,所以,,,所以,,这样在中,,在中,,解得,中,,故填:300.考点:解斜三角形【思路点睛】考察了解三角形的实际问题,属于基础题型,首先要弄清楚两个概念,仰角和俯角,都指视线与水平线的夹角,将问题所涉及的边和角在不同的三角形内转化,最后用正弦定理解决高度.18.【解析】【分析】根据等比数列通项公式求出计算即可得解【详解】由题故答案为:4【点睛】此题考查等比数列通项公式的应用涉及等比数列求和关键在于熟练掌握等比数列的通项公式和求和公式准确进行指数幂的运算化简解析:【解析】 【分析】根据等比数列通项公式,求出()()12112122212n n n n aa a a ++--++=--+=L ,计算()22111111222222n n n n nn a a a a a a a a a a a a a a a a +++-+++==⋅⋅⋅⋅⋅⋅L L L 即可得解.【详解】由题2nn a =, ()()12112122212n n n n a a a a ++--++=--+=L()22111111222222n n n n nn a a a a a a a a a a a a a a a a +++-+++==⋅⋅⋅⋅⋅⋅L L L ()2112224n n aa a a +-+++===L .故答案为:4 【点睛】此题考查等比数列通项公式的应用,涉及等比数列求和,关键在于熟练掌握等比数列的通项公式和求和公式,准确进行指数幂的运算化简.19.【解析】试题分析:因为二次函数在区间内至少存在一个实数使的否定是:函数在区间内任意实数使所以即整理得解得或所以二次函数在区间内至少存在一个实数使的实数的取值范围是考点:一元二次方程的根与系数的关系【解析:3(3,)2-【解析】试题分析:因为二次函数()f x 在区间[1,1]-内至少存在一个实数x ,使()0f x >的否定是:“函数()f x 在区间[1,1]-内任意实数x ,使()0f x ≤”,所以(1)0{(1)0f f ≤-≤,即2242(2)210{42(2)210p p p p p p ----+≤+---+≤,整理得222390{210p p p p +-≥--≥,解得32p ≥或3p ≤-,所以二次函数在区间[1,1]-内至少存在一个实数x ,使()0f x >的实数p 的取值范围是3(3,)2-.考点:一元二次方程的根与系数的关系.【方法点晴】本题主要考查了一元二次方程的根的分布与系数的关系,其中解答中涉及到一元二次函数的图象与性质、不等式组的求解、命题的转化等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,其中根据二次函数的图象是开口方向朝上的抛物线,得到对于区间[1,1]-内的任意一个x 都有()0f x >时,得到不等式组是解答的关键,属于中档试题.20.【解析】【分析】在中由余弦定理求得再由正弦定理求得最后利用两角和的余弦公式即可求解的值【详解】在中海里海里由余弦定理可得所以海里由正弦定理可得因为可知为锐角所以所以【点睛】本题主要考查了解三角形实际解析:14【解析】 【分析】在ABC ∆中,由余弦定理,求得BC ,再由正弦定理,求得sin ,sin ACB BAC ∠∠,最后利用两角和的余弦公式,即可求解cos θ的值. 【详解】在ABC ∆中,40AB =海里,20AC =海里,120BAC ∠=o , 由余弦定理可得2222cos1202800BC AB AC AB AC =+-⋅=o ,所以BC =,由正弦定理可得sin sin 7AB ACB BAC BC ∠=⋅∠=,因为120BAC ∠=o ,可知ACB ∠为锐角,所以cos ACB ∠=所以cos cos(30)cos cos30sin sin 3014ACB ACB ACB θ=∠+=∠-∠=o o o . 【点睛】本题主要考查了解三角形实际问题,解答中需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,合理使用正、余弦定理是解答的关键,其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向;第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化;第三步:列方程,三、解答题21.(1)2224b c a+=(2 【解析】 【分析】(I )由题意2sin 3tan c B a A =,利用正、余弦定理化简得2224b c a +=,即可得到答案. (II )因为2a =,由(I )知222416b c a +==,由余弦定理得6cos A bc=,进而利用基本不等式,得到6cos bc A =,且(0,)2A π∈,再利用三角形的面积公式和三角函数的性质,即可求解面积的最大值. 【详解】解:(I )∵2sin 3tan c B a A =, ∴2sin cos 3sin c B A a A =, 由正弦定理得22cos 3cb A a =,由余弦定理得22222?32b c a cb a bc+-=,化简得2224b c a +=,∴2224b c a +=.(II )因为2a =,由(I )知222416b c a +==,∴由余弦定理得2226cos 2b c a A bc bc+-==, 根据重要不等式有222b c bc +≥,即8bc ≥,当且仅当b c =时“=”成立, ∴63cos 84A ≥=. 由6cos A bc =,得6cos bc A =,且0,2A π⎛⎫∈ ⎪⎝⎭,∴ABC ∆的面积116sin sin 3tan 22cos S bc A A A A==⨯⨯=. ∵2222222sin cos sin 11tan 1cos cos cos A A A A A A A++=+==,∴tan A =≤=∴3tan S A =≤∴ABC ∆的面积S .本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题,对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用余弦定理借助三边关系求角,利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点,经常利用三角形内角和定理,三角形面积公式,结合正、余弦定理解题.22.(1){|11}x x x <->或;(2)3 【解析】 【分析】(1)通过讨论x 的范围,求出不等式的解集即可;(2)先用绝对值不等式的性质求出最小值为a +b +c =3,然后用基本不等式可得. 【详解】(1)()111f x x x =-+++,∴1123x x ≤-⎧⎨->⎩或1133x -<<⎧⎨>⎩或1213x x ≥⎧⎨+>⎩, 解得{|11}x x x 或-.(2)f x x a x b c =-+++ a x x b c a b c ≥-+++=++ 3a b c =++=,()11111113a b c a b c a b c ⎛⎫++=++++ ⎪⎝⎭ 133b a c a c b a b a c b c ⎡⎤⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()1322233≥+++=. 当且仅当1a b c ===时取得最小值3. 【点睛】绝对值不等式的解法:法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想; 法二:利用“零点分段法”求解,体现了分类讨论的思想;法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想. 23.(1)n a n =,21n b n =+;(2)见解析 【解析】 【分析】(1)由等差数列的通项公式及求和公式列1a d ,的方程组求解则n a n =可求,进而得21n b n =+(2)利用()111212111n c n n n n n n ⎛⎫=++=++- ⎪⋅++⎝⎭分组求和即可证明【详解】(1)因为数列{}n a ,{}n b 是等差数列,且23A =,53A B =,所以112351096a d a d d +=⎧⎨+=+⎩.整理得1123549a d a d +=⎧⎨+=⎩,解得111a d =⎧⎨=⎩,所以()11?n a a n d n =+-=,即n a n =,()11221n b b n d n =+-⋅=+,即21n b n =+.综上,n a n =,21n b n =+. (2)由(1)得()111212111n c n n n n n n ⎛⎫=++=++- ⎪⋅++⎝⎭,所以()11111352112231n S n n n ⎡⎤⎛⎫⎛⎫⎛⎫=++⋯+++-+-+⋯+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦, 即()()22211211111n S n n n n n n =++-=+-<+++. 【点睛】本题考查等差数列的通项公式及求和公式,裂项相消求和,考查推理计算能力,是中档题24.(1)13n n a -=,;(2)()223n nn T +=-.【解析】 【分析】(Ⅰ)由数列递推式求出a 1,在数列递推式中取n=n-1得另一递推式,作差后得到数列{a n }为等比数列,则数列{a n }的通项公式可求,再由b 1=3a 1,b 3=S 2+3求出数列{b n }的首项和公差,则{b n }的通项公式可求;(Ⅱ)把数列{a n }、{b n }的通项公式代入3nn nb c a =,直接由错位相减法求数列{c n }的前n 项和为T n . 【详解】(Ⅰ)当1n =时,111231,1S a a =-∴=当2n ≥时,()()112223131n n n n n a S S a a --=-=---,即13nn a a -= ∴数列{}n a 是以11a =为首项,3为公比的等比数列,13n n a -∴=.设{}n b 的公差为1132,33,3723,2d b a b S d d ===+==+=()31321n b n n ∴=+-⨯=+ ,(Ⅱ)1232135721,33333n nn nn n c T ++==++++L ① 则234113572133333n n n T ++=++++L ②,由①—②得,2312111211233333n n n n T ++⎛⎫=++++- ⎪⎝⎭L 142433n n ++=+ ∴223n nn T +=- . 【点睛】本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n 项和,是中档题.25.(Ⅰ)3A π=(Ⅱ)S =【解析】 【分析】(Ⅰ)由正弦定理化简得到答案.(Ⅱ)1()2AM AB AC =+u u u u r u u u r u u u r,平方,代入公式利用余弦定理得到答案.【详解】(Ⅰ)因为()acos 2cos B c b A =-,由正弦定理得()sin cos cos 2sin sin A B A C B =-,即sin cos cos sin 2sin cos A B A B C A +=,所以()sin 2sinccos A B A +=, 因为()sin sin 0A B C +=≠,所以1cos 2A =, 又因为(0,)A π∈,所以3A π=.(Ⅱ)由M 是BC 中点,得1()2AM AB AC =+u u u u r u u u r u u u r,即2221(2)4AM AB AC AB AC =++⋅u u u u r u u u r u u u r u u u r u u u r,所以2232c b bc ++=,①又根据余弦定理,有2222222cos 416a b c bc A b c bc =+-=+-==,② 联立①②,得8bc =.所以ABC ∆的面积1S bcsinA 2== 【点睛】本题考查了正弦定理,余弦定理,面积公式,向量加减,综合性强,意在考查学生的综合应用能力.26.(1)61n a n =-;(2)9n ≥且*n N ∈;(3)5(65)n nT n =+.【解析】 【分析】(1)首先根据题意列出方程217111721161a a d S a d =+=⎧⎨=+=⎩,解方程组再求n a 即可.(2)首先计算n S ,再解不等式6512n n S a n >--即可. (3)首先得到11166(1)65n b n n =--+,再利用裂项法即可得到前n 项和n T 的值. 【详解】(1)由题意得217111721161a a d S a d =+=⎧⎨=+=⎩,解得156a d =⎧⎨=⎩所以61n a n =-. (2)由(1)得2(1)56322n n n S n n n -=+⨯=+, 因为6512n n S a n >--,即2329180n n -+≥. 解得23n ≤或9n ≥, 因为1n ≥且*n ∈N ,所以n 的取值范围为9n ≥且*n ∈N . (3)因为11111611()()6(615)566n n n b a a n n n n +===--+-+, 所以1111111[()()()]651111176165n T n n =-+-+⋯+--+ 1116565(5)65)(n n n -==++ 【点睛】本题第一问考查等差数列通项公式的求法,第二问考查等差数列前n 项和n S 的求法,第三问考查裂项法求和,属于中档题.。
2020-2021宜兴市东坡中学高中必修二数学下期中第一次模拟试卷含答案一、选择题1.陀螺是汉族民间最早的娱乐工具之一,也称陀罗,北方叫做“打老牛”.陀螺的主体形状一般是由上面部分的圆柱和下面部分的圆锥组成.如图画出的是某陀螺模型的三视图,已知网格纸中小正方形的边长为1,则该陀螺模型的体积为( )A .1073πB .32453π+ C .16323π+ D .32333π+ 2.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 为球O 的直径,且SC OA ⊥,SC OB ⊥,OAB V 为等边三角形,三棱锥S ABC -的体积为433,则球O 的半径为( ) A .3B .1C .2D .43.已知平面//α平面β,直线m αÜ,直线n βÜ,点A m ∈,点B n ∈,记点A 、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则 A .b a c ≤≤B .a c b ≤≤C . c a b ≤≤D .c b a ≤≤4.如图是水平放置的平面图形的斜二测直观图,其原来平面图形面积是( )A . 22B . 42C .4D .85.已知圆截直线所得线段的长度是,则圆与圆的位置关系是( ) A .内切B .相交C .外切D .相离6.已知圆()()22:341C x y -+-=和两点(),A m m -,(),B m m -()0m >,若圆C 上存在点P ,使得90APB ∠=︒,则m 的最大值为( ) A .42B .32C .322D .227.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 ( )A 3πB .3πC .43πD .12π8.已知圆O :2224110x y x y ++--=,过点()1,0M 作两条相互垂直的弦AC 和BD ,那么四边形ABCD 的面积最大值为( )A .42B .24C .212D .69.矩形ABCD 中,4AB =,3BC =,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( ) A .12512π B .1259π C .1256π D .1253π 10.点A 、B 、C 、D 在同一个球的球面上,2,AC=2,若四面体ABCD 体积的最大值为23,则这个球的表面积为( ) A .1256πB .8πC .2516πD .254π11.已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ,B 两点,则弦长AB 的取值范围是( )A .[]4,10B .[]3,5C .[]8,10D .[]6,1012.已知ABC V 的三个顶点在以O 为球心的球面上,且2AB =,4AC =,5BC =三棱锥O ABC -的体积为43,则球O 的表面积为( ) A .22πB .743πC .24πD .36π二、填空题13.经过两条直线2310x y ++=和340x y -+=的交点,并且平行于直线3470x y +-=的直线方程是________.14.在棱长为1的正方体1111ABCD A B C D -中,BD AC O ⋂=,M 是线段1D O 上的动点,过M 做平面1ACD 的垂线交平面1111D C B A 于点N ,则点N 到点A 的距离最小值是___________.15.已知点1232M N (,),(,),点F 是直线l:3y x =-上的一个动点,当MFN ∠最大时,过点M ,N ,F 的圆的方程是__________.16.如图,以等腰直角三角形斜边BC 上的高AD 为折痕,把△ABD 与△ACD 折成互相垂直的两个平面后,某学生得出下列四个结论: ①0BD AC ⋅≠u u u r u u u r; ②∠BAC =60°;③三棱锥D ﹣ABC 是正三棱锥;④平面ADC 的法向量和平面ABC 的法向量互相垂直. 其中正确结论的序号是 .(请把正确结论的序号都填上)17.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2正三角形,,E F 分别是,PA AB 的中点,90CEF ︒∠=,则球O 的体积为_________________。

2020-2021宜兴市万石中学初二数学下期中模拟试题含答案一、选择题1.下列运算中,正确的是( )A .235+=; B.2(32)32-=-; C .2a a =;D .2()a b a b +=+. 2.下列二次根式中,最简二次根式是( )A .10B .12C .12D .83.实数a ,b 在数轴上的位置如图所示,则化简()()2212a b +--的结果是( )A .3a b -+B .1a b +-C .1a b --+ D .1a b -++ 4.已知函数()()()()22113{513x x y x x --≤=-->,则使y=k 成立的x 值恰好有三个,则k 的值为( ) A .0 B .1 C .2 D .35.如图,把一张矩形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A′处,点B 落在点B′处,若∠2=40°,则图中∠1的度数为( )A .115°B .120°C .130°D .140°6.如图,在矩形ABCD 中,E ,F 分别是边AB ,CD 上的点,AE=CF ,连接EF ,BF ,EF 与对角线AC 交于点O ,且BE=BF ,∠BEF=2∠BAC ,FC=2,则AB 的长为( )A .3B .8C .3D .67.如图,在正方形网格(每个小正方形的边长都是1)中,若将△ABC 沿A ﹣D 的方向平移AD 长,得△DEF (B 、C 的对应点分别为E 、F ),则BE 长为( )A .1B .2C .5D .38.下列各式正确的是( )A .()255-=- B .()20.50.5-=- C .()2255-= D .()20.50.5-= 9.已知一次函数y =﹣x +m 和y =2x +n 的图象都经过A (﹣4,0),且与y 轴分别交于B 、C 两点,则△ABC 的面积为( ) A .48 B .36 C .24 D .1810.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD ,若测得A ,C 之间的距离为12cm ,点B ,D 之间的距离为16m ,则线段AB 的长为( )A .9.6cmB .10cmC .20cmD .12cm11.如图,点E F G H 、、、分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.则下列说法:①若AC BD =,则四边形EFGH 为矩形;②若AC BD ⊥,则四边形EFGH 为菱形;③若四边形EFGH 是平行四边形,则AC 与BD 互相平分;④若四边形EFGH 是正方形,则AC 与BD 互相垂直且相等.其中正确的个数是( )A .1B .2C .3D .412.为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD ,并在A 与C 、B 与D 两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC ,用左手向右推动框架至AB ⊥BC (如图2)观察所得到的四边形,下列判断正确的是( )A .∠BCA =45°B .AC =BD C .BD 的长度变小 D .AC ⊥BD二、填空题 13.如图,已知在Rt △ABC 中,AB =AC =3,在△ABC 内作第1个内接正方形DEFG ;然后取GF 的中点P ,连接PD 、PE ,在△PDE 内作第2个内接正方形HIKJ ;再取线段KJ 的中点Q ,在△QHI 内作第3个内接正方形…,依次进行下去,则第2019个内接正方形的边长为_____.14.如图,直线510y x =+与x 轴、y 轴交于点A ,B ,则AOB V 的面积为___.15.若由你选择一个喜欢的数值m ,使一次函数()2y m x m =-+的图象经过第一、二、四象限,则m 的值可以是___________.16.函数26y x =+的自变量x 的取值范围是_________. 17.已知211a a a a--=,则a 的取值范围是________ 18.一根旗杆在离地面4.5 m 的地方折断,旗杆顶端落在离旗杆底部6 m 外,则旗杆折断前的高度是________.19.已知11510.724=,若 1.0724x =,则x 的值是__________.20.如图,已知一次函数y=kx+b 的图象与x 轴交于点(3,0),与y 轴交于点(0,2),不等式kx+b≥2解集是_______.三、解答题21.如图,BD 是▱ABCD 的对角线,AE ⊥BD ,CF ⊥BD ,垂足分别为E 、F ,求证:AE=CF .22.如图,已知一次函数y kx b =+的图象经过A (-2,-1),B (1,3)两点,并且交x 轴于点C ,交y 轴于点D .(1)求该一次函数的解析式;(2)△ABC 的面积.23.ABC ∆在平面直角坐标系中的位置如图所示,先将ABC ∆向右平移3个单位,再向下平移1个单位到111A B C ∆,111A B C ∆和222A B C ∆关于x 轴对称.(1)画出111A B C ∆和222A B C ∆;(2)在x 轴上确定一点P ,使1BP A P +的值最小,试求出点P 的坐标.24.如图平面直角坐标系中,已知三点 A (0,7),B (8,1),C (x ,0)且 0<x <8. (1)求线段 AB 的长;(2)请用含 x 的代数式表示 AC+BC 的值;(3)求 AC+BC 的最小值.25.已知:如图,在四边形ABCD 中,∠B =90°,AB =BC =2,CD =3,AD =1,求∠DAB 的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】 23与()23223-=-误;2a a =,故错误; D. ()2a b a b +=+,正确;故选D.2.A解析:A【解析】【分析】根据最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式,结合选项求解即可.【详解】A 10是最简二次根式,本选项正确.B 12=2312C 122=12A .8=22,故8不是最简二次根式,本选项错误.故选A .【点睛】本题考查了最简二次根式的知识,解答本题的关键在于掌握最简二次根式的概念,对各选项进行判断.3.A解析:A【解析】【分析】先根据数轴上两点的位置确定1a +和2b -的正负,再根据2a 的性质计算即可.【详解】观察数轴可得,1a >-,2b >,故10a +>,20b ->,∴()()2212a b +--()12a b =+--12a b =+-+3a b =-+故选:A.【点睛】本题结合数轴上点的位置考查了2a 的计算性质,熟练掌握该性质是解答的关键. 4.D解析:D【解析】【分析】【详解】解:如图:利用顶点式及取值范围,可画出函数图象会发现:当x=3时,y=k 成立的x 值恰好有三个.5.A解析:A【解析】解:∵把一张矩形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A ′处,点B 落在点B ′处,∴∠BFE =∠EFB ',∠B '=∠B =90°.∵∠2=40°,∴∠CFB '=50°,∴∠1+∠EFB '﹣∠CFB '=180°,即∠1+∠1﹣50°=180°,解得:∠1=115°,故选A .6.D解析:D【解析】【分析】连接OB ,根据等腰三角形三线合一的性质可得BO ⊥EF ,再根据矩形的性质可得OA=OB ,根据等边对等角的性质可得∠BAC=∠ABO ,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC ,再利用勾股定理列式计算即可求出AB .【详解】解:如图,连接OB ,∵BE=BF ,OE=OF ,∴BO ⊥EF ,∴在Rt △BEO 中,∠BEF+∠ABO=90°,由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC ,∴∠BAC=∠ABO ,又∵∠BEF=2∠BAC ,即2∠BAC+∠BAC=90°,解得∠BAC=30°,∴∠FCA=30°,∴∠FBC=30°,∵FC=2,∴3∴3,∴22AC BC -22(43)(23)-6,故选D .本题考查了矩形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形30°角所对的直角边等于斜边的一半,综合题,但难度不大,(2)作辅助线并求出∠BAC=30°是解题的关键.7.C解析:C【解析】【分析】直接根据题意画出平移后的三角形进而利用勾股定理得出BE 的长.【详解】如图所示:22125BE +=故选:C .【点睛】此题主要考查了勾股定理以及坐标与图形的变化,正确得出对应点位置是解题关键.8.D解析:D【解析】【分析】【详解】 解:因为(()222550.50.50.5=-==,,所以A ,B ,C 选项均错, 故选D 9.C解析:C【解析】【分析】把A (﹣4,0)分别代入一次函数y =﹣x +m 和y =2x +n 中,求得m 和n 的值,根据所得的两个解析式,求得点B 和点C 的坐标,以BC 为底,点A 到BC 的垂线段为高,求出△ABC 的面积即可.【详解】把点A (﹣4,0)代入一次函数y =﹣x +m 得: 4+m =0,解得:m =﹣4,即该函数的解析式为:y=﹣x﹣4,把点A(﹣4,0)代入一次函数y=2x+n得:﹣8+n=0,解得:n=8,即该函数的解析式为:y=2x+8,把x=0代入y=﹣x﹣4得:y=0﹣4=﹣4,即B(0,﹣4),把x=0代入y=2x+8得:y=0+8=8,即C(0,8),则边BC的长为8﹣(﹣4)=12,点A到BC的垂线段的长为4,S△ABC11242=⨯⨯=24.故选C.【点睛】本题考查了一次函数图象上点的坐标特征,正确掌握代入法求一次函数的解析式是解题的关键.10.B解析:B【解析】【分析】作AR⊥BC于R,AS⊥CD于S,根据题意先证出四边形ABCD是平行四边形,再由AR=AS推出BC=CD得平行四边形ABCD是菱形,再根据根据勾股定理求出AB即可.【详解】作AR⊥BC于R,AS⊥CD于S,连接AC、BD交于点O.由题意知:AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∵两个矩形等宽,∴AR=AS,∵AR•BC=AS•CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD,在Rt△AOB中,∵OA=12AC=6cm,OB=12BD=8cm,∴AB=2268+=10(cm),故选:B.【点睛】本题主要考查菱形的判定和性质,证得四边形ABCD是菱形是解题的关键.11.A解析:A【解析】【分析】因为一般四边形的中点四边形是平行四边形,当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形.【详解】因为一般四边形的中点四边形是平行四边形,当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形,故④选项正确,故选A.【点睛】本题考查中点四边形、平行四边形、矩形、菱形的判定等知识,解题的关键是记住一般四边形的中点四边形是平行四边形,当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形.12.B解析:B【解析】【分析】根据矩形的性质即可判断;【详解】解:∵四边形ABCD是平行四边形,又∵AB⊥BC,∴∠ABC=90°,∴四边形ABCD是矩形,∴AC=BD.故选B.【点睛】本题考查平行四边形的性质.矩形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题13.3×122018【解析】【分析】首先根据勾股定理得出BC的长进而利用等腰直角三角形的性质得出DE的长再利用锐角三角函数的关系得出EIKI=PFEF=12即可得出正方形边长之间的变化规律得出答案即可【解析:【解析】【分析】首先根据勾股定理得出BC的长,进而利用等腰直角三角形的性质得出DE的长,再利用锐角三角函数的关系得出,即可得出正方形边长之间的变化规律,得出答案即可.【详解】∵在Rt△ABC中,AB=AC=3,∴∠B=∠C=45°,BC=AB=6,∵在△ABC内作第一个内接正方形DEFG;∴EF=EC=DG=BD,∴DE=BC=2,∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,∴,∴EI=KI=HI,∵DH=EI,∴HI=DE=()2﹣1×3,则第n个内接正方形的边长为:3×()n﹣1.故第2019个内接正方形的边长为:3×()2018.故答案是:3×()2018.【点睛】考查了正方形的性质以及数字变化规律和勾股定理等知识,根据已知得出正方形边长的变化规律是解题关键.14.10【解析】【分析】分别令x=0y=0可得AB坐标即可求出OAOB的长利用三角形面积公式即可得答案【详解】∵直线交x 轴于点A 交y 轴于点B∴令则;令则;∴∴∴的面积故答案为10【点睛】本题考查一次函数解析:10【解析】【分析】分别令x=0,y=0,可得A 、B 坐标,即可求出OA 、OB 的长,利用三角形面积公式即可得答案.【详解】∵直线510y x =+交x 轴于点A ,交y 轴于点B ,∴令0y =,则2x =-;令0x =,则10y =;∴()2,0A -,()0,10B ,∴2OA =,10OB =,∴AOB V 的面积1210102=⨯⨯=. 故答案为10【点睛】本题考查一次函数与坐标轴的交点问题,分别令x=0,y=0即可求出一次函数与坐标轴的交点坐标;也考查了三角形的面积. 15.(答案不唯一满足均可)【解析】【分析】一次函数的图象经过第一二四象限列出不等式组求解即可【详解】解:一次函数的图象经过第一二四象限解得:m 的值可以是1故答案为:1(答案不唯一满足均可)【点睛】此题主 解析:(答案不唯一,满足02m <<均可)【解析】【分析】一次函数()2y m x m =-+的图象经过第一、二、四象限,列出不等式组200,m m -<⎧⎨>⎩求解即可.【详解】解:一次函数()2y m x m =-+的图象经过第一、二、四象限,200m m -<⎧⎨>⎩解得:02m <<m 的值可以是1.故答案为:1(答案不唯一,满足02m <<均可).【点睛】此题主要考查了一次函数图象,一次函数y kx b =+的图象有四种情况:①当0,0k b >>时,函数y kx b =+的图象经过第一、二、三象限;②当0,0k b ><时,函数y kx b =+的图象经过第一、三、四象限;③当0,0k b <>时,函数y kx b =+的图象经过第一、二、四象限;④当0,0k b <<时,函数y kx b =+的图象经过第二、三、四象限.16.x >-3【解析】【分析】根据被开方数大于等于0分母不等于0列式计算即可得解【详解】解:由题意得2x+6>0解得x >-3故答案为x >-3【点睛】本题考查了函数自变量的范围一般从三个方面考虑:(1)当函 解析:x >-3.【解析】【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【详解】解:由题意得,2x+6>0,解得x >-3.故答案为x >-3.【点睛】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.17.【解析】【分析】根据二次根式得非负性求解即可【详解】解:∵成立则有:并且即:∴故答案为:【点睛】本题考查的是二次根式的取值范围在二次根式里被开方数必须是非负数解析:01a <≤【解析】【分析】根据二次根式得非负性求解即可.【详解】a=成立, 则有:10a ->,0a ≠ ,0,即:0a >, ∴01a <≤,故答案为:01a <≤.【点睛】本题考查的是二次根式的取值范围,在二次根式里被开方数,必须是非负数.18.12米【解析】【分析】【详解】解:如图所示AC=6米BC=45米由勾股定理得AB==75(米)故旗杆折断前高为:45+75=12(米)故答案为:12米解析:12米【解析】【分析】【详解】解:如图所示,AC=6米,BC=4.5米,由勾股定理得,AB= 224.56+ =7.5(米).故旗杆折断前高为:4.5+7.5=12(米).故答案为:12米.19.15【解析】【分析】根据得出将根号外的数化到根号里即可计算【详解】∵且∴∴∴故答案为:【点睛】本题考查二次根号的转化寻找倍数关系是解题关键解析:15 【解析】【分析】根据10.724=10 1.0724⨯115=10x ,将根号外的数化到根号里即可计算.【详解】11510.724= 1.0724x =,且10.724=10 1.0724⨯ 115=10=100100x x x =g ∴100115x =∴ 1.15x =故答案为:1.15【点睛】本题考查二次根号的转化,寻找倍数关系是解题关键.20.x≤0【解析】【分析】由一次函数y=kx+b 的图象过点(02)且y 随x 的增大而减小从而得出不等式kx+b≥2的解集【详解】解:由一次函数的图象可知此函数是减函数即y 随x 的增大而减小∵一次函数y=kx解析:x≤0【解析】【分析】由一次函数y=kx+b 的图象过点(0,2),且y 随x 的增大而减小,从而得出不等式kx+b≥2的解集.【详解】解:由一次函数的图象可知,此函数是减函数,即y 随x 的增大而减小,∵一次函数y=kx+b 的图象与y 轴交于点(0,2),∴当x≤0时,有kx+b≥2.故答案为x≤0.【点睛】本题考查的是一次函数与一元一次不等式的关系,能利用数形结合求出不等式的解集是解答此题的关键.三、解答题21.详见解析.【解析】试题分析:根据平行四边形的性质可得AB=CD ,AB ∥CD ,再由平行线的性质证得∠ABE=∠CDF ,根据AE ⊥BD ,CF ⊥BD 可得∠AEB=∠CFD=90°,由AAS 证得△ABE ≌△CDF ,根据全等三角形的性质即可证得结论.试题解析:证明:∵四边形ABCD 是平行四边形,∴AB=CD ,AB ∥CD ,∴∠ABE=∠CDF ,∵AE ⊥BD ,CF ⊥BD ,∴∠AEB=∠CFD=90°,在△ABE 和△CDF 中,,∴△ABE ≌△CDF (AAS ),∴AE=CF .考点:平行四边形的性质;全等三角形的判定及性质.22.(1)4533y x =+;(2)52. 【解析】【分析】(1)利用待定系数法即可求出一次函数解析式;(2)求出点D 坐标,根据ABC AOD BOD S S S =+V V V 即可求解.【详解】(1)把A (-2,-1),B (1,3)代入y =kx +b 得 213k b k b -+=-⎧⎨+=⎩,解得4353 kb⎧=⎪⎪⎨⎪=⎪⎩,所以一次函数解析式为4533y x=+;(2)把x=0代入4533y x=+得y=53,∴D点坐标为(0,53),∴15155=21=23232ABC AOD BODS S S=+⨯⨯+⨯⨯V V V.【点睛】(1)待定系数法是求函数解析式的一种常用方法,要深刻领会,其实质是根据题意设出函数关系式,把点的坐标代入解析式构造方程,求解,回代,最后确定解析式;(2)平面直角坐标系中如果图形的面积不易直接求,则一般采用割补法求解.23.(1)详见解析;(2)3,05P⎛⎫-⎪⎝⎭【解析】【分析】(1)△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称,据此作图即可;(2)依据轴对称的性质,连接BA2,交x轴于点P,此时BP+A1P的值最小,依据直线BA2的解析式,即可得到点P的坐标.【详解】解:(1)如图所示,△A1B1C1和△A2B2C2即为所求;(2)如图所示,连接BA2,交x轴于点P,则点P即为所求;设直线BA2的解析式为y kx b=+,由B(-3,2),A2(3,-3)可得,3233k b k b -+=⎧⎨+=-⎩,解得5612k b ⎧=-⎪⎪⎨⎪=-⎪⎩ ∴直线BA 2的解析式为y=5162x =-- 当y=0时,51062x --= 解得35x =- ∴305P ⎛⎫- ⎪⎝⎭,【点睛】本题主要考查了利用平移以及轴对称变换进行作图以及最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.24.(1)AB =10;(2;(3)AC +BC 最小值为. 【解析】【分析】(1)根据两点间的距离公式可求线段AB 的长;(2)根据两点间的距离公式可求线段AC ,BC 的值,再相加即可求解;(3)作B 点关于x 轴对称点F 点,连接AF ,与x 轴相交于点C .此时AC +BC 最短.根据两点间的距离公式即可求解.【详解】(1)10AB ==;(2)AC +BC ==;(3)如图,作B 点关于x 轴对称点F 点,连接AF ,与x 轴相交于点C .此时AC +BC 最短.∵B (8,1),∴F (8,-1),∴AC +BC =AC +CF =AF==即AC +BC 最小值为.【点睛】本题考查了最短路线问题,利用了数形结合的思想,构造出符合题意的直角三角形是解题的关键.25.135º.【解析】【分析】在直角△ABC中,由勾股定理求得AC的长,在△ACD中,因为已知三角形的三边的长,可用勾股定理的逆定理判定△ACD是不是直角三角形.【详解】解:∵∠B=90°,AB=BC=2,∴AC222,∠BAC=45°,AB BC又∵CD=3,DA=1,∴AC2+DA2=8+1=9,CD2=9,∴AC2+DA2=CD2,∴△ACD是直角三角形,∴∠CAD=90°,∴∠DAB=45°+90°=135°.。

绝密★启用前2020——2021学年度第二学期期中检测高一数学 2021.4 考试说明:1.本试题分第I 卷和第II 卷两部分。
第I 卷和第II 卷答案填涂在答题卡的相应位置,考试结束只上交答题卡。
2.满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将姓名、班级、准考证号填在答题纸规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题纸上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选凃其他答案标号。
3.第II 卷必须用中性笔作答,答案必须写在答题纸各题目指定区域内相应位置;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。
第I 卷(选择题60分)一、单选题(每小题5分,共40分)1.213(1)i i +=+( ) A .3122i - B .3122i + C .3122i -- D .3122i -+2.正三棱柱111ABC A B C -的底面边长为2,D 为BC 中点,则三棱锥11A B DC -的体积为( ) A.3 B.323.已知复数,则“”是“为纯虚数”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知边长为1的菱形ABCD 中,60BAD ∠=︒,点E 满足2BE EC =,则AE BD ⋅值( )A .13-B .12-C .14-D .16-5.下列四式不能化简为AD 的是( )A .()AB CD BC ++ B .()()AD MB BC CM +++C .MB AD BM +- D .OC OA CD -+()()()212z a a i a =-+-∈R 1a =z6.圆锥的轴截面是正三角形,那么它的侧面积是底面积的( ) A. 4倍 B. 3倍 C. 2倍 D. 2倍 7.设复数满足,则在复平面内的对应点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8.若,方向上的单位向量为.则在上的投影向量为( )A .B .C .D .二、多选题(每小题5分,共20分,少选得2分,错选不得分)9.若复数满足(其中是虚数单位),则( )A .的实部是2B .的虚部是C .D .10.如图,梯形ABCD 中,|AD |=|BC |,EF ∥AB ∥CD 则不相等向量是( ).A .AD 与BCB .OA 与OBC .AC 与BD D .EO 与OF11. 下列结论中,不正确结论的是( )A.如果非零向量a 与b 的方向相同或相反,那么a b +的方向必与,a b 之一的方向相同;B.在△ABC 中,必有AB →+BC →+CA →=0;C.若AB →+BC →+CA →=0,则A ,B ,C 为一个三角形的三个顶点;D.若,a b 均为非零向量,则a b +的长度与a 的长度加b 的长度的和一定相等.12. 设,为不共线向量, =+2,=-4-,=-5-3,则下列关系式中不正确的是 ( )(A )= (B )=2(C )=- (D )=-2 第II 卷(非选择题90分)二、填空题(每题5分)13.已知平面上三点A ,B ,C 满足|AB |=3,|BC |=4,|CA |=5,则AB ·BC +BC ·CA +CA ·AB 的值等于 .14.已知复数的实部为0,其中为虚数单位,则实数a 的值是_____.z 41i z i=+z ()()2,3,4,7a b ==-b e a b 65e 65e 13e 13e z ()1i 3i z -=+i z z 2i 12i z =-5z =→a →b −→−AB →a →b −→−BC →a →b −→−CD →a →b −→−AD −→−BC −→−AD −→−BC −→−AD −→−BC −→−AD −→−BC (2i)(1i)a ++i15.已知,,若,则________.16.一个六棱锥的体积为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 。

一、选择题1.已知关于x 的方程20ax bx c ++=,其中,,a b c 都是非零向量,且,a b 不共线,则该方程的解的情况是( ) A .至少有一个解 B .至多有一个解 C .至多有两个解D .可能有无数个解2.( ) A .sin2cos2+ B .cos2sin 2- C .sin2cos2- D .cos2sin2±-3.已知3sin 34x π⎛⎫-= ⎪⎝⎭,则cos 23x π⎛⎫+ ⎪⎝⎭的值为( )A .18-B .12-C .18D .124.已知函数()()x cos x 0f x ωωω=+>最小正周期为π,则函数()f x 的图象( ) A .关于直线12x π=对称B .关于直线512x π=对称 C .关于点,012π⎛⎫⎪⎝⎭对称D .关于点5,012π⎛⎫⎪⎝⎭对称 5.平面向量(1,2)a =,(4,2)b =,c ma b =+(m R ∈),且c 与a 的夹角等于c 与b的夹角,则m =( ) A .2-B .1-C .1D .26.已知π(,π)2α∈,π1tan()47α+=,则sin cos αα+= ( ) A .17-B .25-C .15-D .157.在三角形ABC 中,,CA a CB b ==,点P 在直线AB 上,且2AP PB =,则CP 可用,a b 表示为( ) A .2CP a b =+B .CP a b =-C .12CP a b =- D .1233CP a b =+ 8.若将函数y =cos2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( ) A .x =kπ2−π6(k ∈Z ) B .x =kπ2+π6(k ∈Z )x C .x =kπ2−π12(k ∈Z )D .x =kπ2+π12(k ∈Z )9.设奇函数()()()()sin 0f x x x ωφωφω=++>在[]1,1x ∈-内有9个零点,则ω的取值范围为( )A .[)4,5ππ B .[]4,5ππC .11,54ππ⎡⎤⎢⎥⎣⎦D .11,54ππ⎛⎤ ⎥⎝⎦10.已知2sin()3,且(,0)2απ∈-,则tan(2)πα-= ( )A .255B .255-C .52D .52-11.已知函数()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象如图所示.则()y f x =的图象,可由函数cos y x =的图象怎样变换而来(纵坐标不变)( )A .先把各点的横坐标缩短到原来的12倍,再向左平移6π个单位B .先把各点的横坐标缩短到原来的12倍,再向右平移12π个单位C .先把各点的横坐标伸长到原来的2倍,再向左平移6π个单位 D .先把各点的横坐标伸长到原来的2倍,再向右平移12π个单位12.若02πα<<,02πβ-<<,1cos 43πα⎛⎫+= ⎪⎝⎭,3cos 42πβ⎛⎫-= ⎪⎝⎭cos 2βα⎛⎫+ ⎪⎝⎭等于( )A 3B .33-C .539D .69-13.已知函数2()3cos cos f x x x x =+,则( ) A .()f x 的图象关于直线6x π=对称B .()f x 的最大值为2C .()f x 的最小值为1-D .()f x 的图象关于点(,0)12π-对称14.已知向量(2,0)OB =,向量(2,2)OC =,向量(22)CA αα=,则向量OA 与向量OB 的夹角的取值范围是( ).A .π0,4⎡⎤⎢⎥⎣⎦B .π5π,412⎡⎤⎢⎥⎣⎦C .5ππ,122⎡⎤⎢⎥⎣⎦ D .π5π,1212⎡⎤⎢⎥⎣⎦ 15.已知tan 3a =,则21cos sin 22a a +=() A .25-B .3C .3-D .25二、填空题16.函数()1sin cos 533f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的最大值为________________. 17.设tan α、tan β是方程2320x x -+=的两个根,则()tan αβ+=________________. 18.设函数()sin()f x A x ωϕ=+(A ,ω,ϕ为常数,且0A >,0>ω,0ϕπ<<)的部分图象如图所示,则(0)f =_____.19.已知角α的终边上一点)3,1A-,则()sin tan 2παπα⎛⎫-++= ⎪⎝⎭__________.20.已知角θ的终边上的一点P 的坐标为()3,4,则cos 21sin 2θθ=+________________.21.将函数e x y =的图像上所有点的横坐标变为原来的一半,再向右平移2个单位,所得函数的解析式为__________.22.在平行四边形ABCD 中,E 为线段BC 的中点,若AB AE AD λμ=+,则λμ+=__________.23.已知向量(,)a m n =,向量(,)b p q =,(其中m ,n ,p ,q ∈Z ). 定义:(,)a b mp nq mq np ⊗=-+.若(1,2)a =,(2,1)b =,则a b ⊗=__________; 若(5,0)a b ⊗=,则a =__________,b =__________(写出一组满足此条件的a 和b 即可).24.已知(,)P x y 是椭圆22143x y +=上的一个动点,则x y +的最大值是__________.25.设G 是ABC ∆的重心(即三条中线的交点),AB a =,AC b =,试用a 、b 表示AG =________. 三、解答题26.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22222230a c b ac +-+=.(1)求cos B 的值; (2)求sin 24B π⎛⎫+⎪⎝⎭的值.27.已知函数())0,22f x x ππωϕωϕ⎛⎫=+>-≤≤⎪⎝⎭的图象关于直线3x π=对称,且图象上相邻两个最高点的距离为π. (1)求ω与ϕ的值;(2)若22463f αππα⎛⎫⎛⎫=<<⎪ ⎪⎝⎭⎝⎭,求3cos 2πα⎛⎫+ ⎪⎝⎭的值. 28.在ABC △中,内角A B C ,,所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =.(Ⅰ)求cos B 的值;(Ⅱ)求sin 26B π⎛⎫+⎪⎝⎭的值. 29.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知向量(sin ,sin sin )A B C =-m ,n =(,)a b c +,且m n ⊥.(1)求角C 的值;(2)若ABC 为锐角三角形,且1c =b -的取值范围. 30.已知函数()sin sin cos 66f x x x x a ππ⎛⎫⎛⎫=++-++ ⎪ ⎪⎝⎭⎝⎭的最大值为1. (1)求常数a 的值;(2)求使()0f x ≥成立的x 的取值集合.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.B 2.C 3.C4.D5.D6.C7.D8.C9.A10.A11.B12.C13.A14.D15.D二、填空题16.【解析】【分析】先利用两角和与差的正弦余弦公式将函数的解析式展开合并同类项后利用辅助角公式进行化简即可得出函数的最大值【详解】其中因此函数的最大值为故答案为【点睛】本题考查三角函数的最值解题的关键就17.【解析】【分析】利用二次方程根与系数的关系得出和的值然后利用两角和的正切公式计算可求出的值【详解】由二次方程根与系数的关系得出因此故答案为【点睛】本题考查两角和的正切公式的应用同时也考查了二次方程根18.【解析】【分析】由图像可以计算出的值即可得到三角函数表达式然后计算出结果【详解】由图可知:由得从而将点代入得即又所以得所以【点睛】本题考查了由函数图像求三角函数的表达式熟练掌握图像是解题关键较为基础19.【解析】分析:先根据三角函数定义得再根据诱导公式化简求值详解:因为角的终边上一点所以因此点睛:本题考查三角函数定义以及诱导公式考查基本求解能力20.【解析】分析:由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解:角的终边上的一点的坐标为那么故答案为点睛:本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求21.【解析】分析:根据图像平移规律确定函数解析式详解:点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言22.【解析】分析:先根据三角形法则化为再根据分解唯一性求即得详解:因为所以因为不共线所以点睛:利用向量基本定理中唯一性可求参数:即若为不共线向量则 23.【解析】()令∴()∵∴①又∵∴∴∴是方程组①的一组解∴故答案为; 24.【解析】是椭圆=1上的一个动点设∴最大值为25.【解析】【分析】延长交于点利用重心的性质得出以及中线向量可求出的表达式【详解】延长交于点则点为线段的中点由平面向量加法的平行四边形法则可知则为的重心因此故答案为【点睛】本题考查向量的基底分解解题的关三、解答题 26. 27. 28. 29. 30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1.B 解析:B 【解析】 【分析】根据平面向量基本定理可知(),c a b R λμλμ=+∈,从而将方程整理为()()20x a x b λμ+++=,由,a b 不共线可得200x x λμ⎧+=⎨+=⎩,从而可知方程组至多有一个解,从而得到结果. 【详解】由平面向量基本定理可得:(),c a b R λμλμ=+∈则方程20ax bx c ++=可变为:20ax bx a b λμ+++= 即:()()20xa xb λμ+++=,a b 不共线 200x x λμ⎧+=∴⎨+=⎩可知方程组可能无解,也可能有一个解∴方程20ax bx c ++=至多有一个解本题正确选项:B 【点睛】本题考查平面向量基本定理的应用,关键是能够利用定理将方程进行转化,利用向量和为零和向量不共线可得方程组,从而确定方程解的个数.2.C解析:C 【解析】 【分析】先利用诱导公式化简角,然后利用正弦的二倍角公式和完全平方式结合角在各个象限中的符号化简即可得到答案. 【详解】==,∵22ππ<<,∴sin2cos20->.∴原式sin2cos2=-. 故选C. 【点睛】本题考查诱导公式和二倍角公式以及三角函数在各个象限中的符号的应用,属于基础题.3.C解析:C 【解析】 【分析】分析题目,2222333x x x ππππ⎛⎫⎛⎫-=-=+- ⎪ ⎪⎝⎭⎝⎭,得到角的关系,利用诱导公式和二倍角公式计算即可 【详解】3sin 34x π⎛⎫-=- ⎪⎝⎭,2cos 2cos 2cos 2333x x x ππππ⎛⎫⎛⎫⎛⎫+=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭22231cos 2cos 212sin 1233348x x x πππ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴--=--=---=--⨯-=⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎢⎥⎣⎦选C 【点睛】本题考查利用二倍角公式和诱导公式求三角函数值,发现角的关系是解题关键4.D解析:D 【解析】分析:先化简函数f(x)=2sin()6wx π+,再根据周期求出w ,再讨论每一个选项的真假.详解:由题得f(x)=2sin()6wx π+,因为2,2,()2sin(2).6w f x x w πππ=∴=∴=+对于选项A,把12x π=代入函数得(=2sin()21266f πππ+=≠±),所以选项A 是错误的;对于选项B, 把512x π=代入函数得55(=2sin()021266f πππ+=≠±),所以选项B 是错误的;对于选项C,令2,,.6212k x k k z x ππππ+=∈∴=-无论k 取何整数,x 都取不到12π,所以选项C 是错误的. 对于选项D, 令2,,.6212k x k k z x ππππ+=∈∴=-当k=1时,512x π=,所以函数的图像关于点5,012π⎛⎫⎪⎝⎭对称. 故答案为:D.点睛:(1)本题主要考查三角恒等变换和三角函数的图像和性质,意在考查学生对这些知识的掌握水平和分析推理能力.(2)对于三角函数图像和性质的判断,要灵活,不要死记硬背.5.D解析:D 【解析】 【分析】【详解】()()4,22,422258c m m a c m m m =++⋅=+++=+,()()44222820b c m m m ⋅=+++=+,5,2025a b ===,c 与a 的夹角等于c 与b 的夹角 ,c a c bc a c b ⋅⋅=⋅⋅,=,解得2m =, 故选D. 【考点定位】向量的夹角及向量的坐标运算.6.C解析:C 【解析】 【分析】由两角和的正切公式得出3sin cos 4αα=-,结合平方关系求出43cos ,sin 55αα=-=,即可得出sin cos αα+的值. 【详解】1tan 1tan 41tan 7πααα+⎛⎫+== ⎪-⎝⎭3tan 4α∴=-,即3sin cos 4αα=-由平方关系得出223cos cos 14αα⎛⎫-+= ⎪⎝⎭,解得:43cos ,sin 55αα=-=341sin cos 555αα+=-=- 故选:C 【点睛】本题主要考查了两角和的正切公式,平方关系,属于中档题.7.D解析:D 【解析】 【分析】利用向量三角形法则得到:1212++3333CP CA CB a b ==得到答案. 【详解】利用向量三角形法则得到:221212++()++333333CP CA AP CA AB CA CB CA CA CB a b =+==-==故选:D 【点睛】本题考查了向量的表示,也可以利用平行四边形法则得到答案.8.C解析:C 【解析】 【分析】 【详解】试题分析:由题意得,将函数y =cos2x 的图象向左平移π12个单位长度,得到y =cos2(x +π12)=cos (2x +π6),由2x +π6=kπ,k ∈Z ,得x =kπ2−π12,k ∈Z ,即平移后的函数的对称轴方程为x =kπ2−π12(k ∈Z ),故选C .9.A解析:A 【解析】f (x )=sin (ωx+φ(ωx+φ)=2[12sin (ωx+φ(ωx+φ)] =2[cos3πsin (ωx+φ)﹣sin 3πcos (ωx+φ)]=2sin (ωx+φ﹣3π) ∵函数f (x )为奇函数,∴f (0)=2sin (φ﹣3π)=0,∴φ=3π+kπ,k ∈Z ∴f (x )=2sin (ωx+kπ),f (x )=0即sin (ωx+kπ)=0,ωx+kπ=mπ,m ∈Z ,解得,x=()m k πω-,设n=m ﹣k ,则n ∈Z ,∵A ∈[﹣1,1],∴﹣1≤x≤1,[]1,1n πω∈-,∴n ωωππ-≤≤, ∵A ∈[﹣1,1]中有9个元素,4545.ωπωππ∴≤<⇒≤< 故答案为A.点睛:函数的零点或方程的根的问题,一般以含参数的三次式、分式、以e 为底的指数式或对数式及三角函数式结构的函数零点或方程根的形式出现,一般有下列两种考查形式:(1)确定函数零点、图象交点及方程根的个数问题;(2)应用函数零点、图象交点及方程解的存在情况,求参数的值或取值范围问题.研究方程根的情况,可以通过导数研究函数的单调性、最值、函数的变化趋势等,根据题目要求,通过数形结合的思想去分析问题,可以使得问题的求解有一个清晰、直观的整体展现.同时在解题过程中要注意转化与化归、函数与方程、分类讨论思想的应用.10.A解析:A 【解析】 【分析】由三角函数的诱导公式,求得2sin3,再由三角函数的基本关系式,求得5cos α3, 最后利用三角函数的基本关系式,即可求解tan(2)πα-的值,得到答案. 【详解】由三角函数的诱导公式,可得2sin()sin 3παα-==-,因为(,0)2απ∈-,所以cos α==,又由sin tan(2)tan cos απααα-=-=-=,故选A. 【点睛】本题主要考查了三角函数的诱导公式和三角函数的基本关系式的化简、求值问题,其中解答中熟练应用三角函数的诱导公式和三角函数的基本关系式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.11.B解析:B 【解析】 【分析】根据图象可知1A =,根据周期为π知=2ω,过点(,1)12π求得3πϕ=,函数解析式()sin(2)3f x x π=+,比较解析式cos sin()2y x x π==+,根据图像变换规律即可求解.【详解】由()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象可得1A =,11244126T πππω=⋅=+,解得=2ω,图象过点(,1)12π,代入解析式得1sin(2)12πϕ=⨯+,因为2πϕ<,所以3πϕ=,故()sin(2)3f x x π=+,因为cos sin()2y x x π==+,将函数图象上点的横坐标变为原来的12得sin 22y x π⎛⎫=+ ⎪⎝⎭,再向右平移12π个单位得sin[2()]sin(2)()1223y x x f x πππ=-+=+=的图象,故选B. 【点睛】本题主要考查了由sin()y A x ωϕ=+部分图像求解析式,图象变换规律,属于中档题.12.C解析:C 【解析】 【分析】利用同角三角函数的基本关系求出sin 4πα⎛⎫+⎪⎝⎭与sin 42πβ⎛⎫-⎪⎝⎭,然后利用两角差的余弦公式求出cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦值. 【详解】02πα<<,3444πππα∴<+<,则sin 43πα⎛⎫+== ⎪⎝⎭,02πβ-<<,则4422ππβπ<-<,所以,sin 423πβ⎛⎫-==⎪⎝⎭, 因此,cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1cos cos sin sin 44244233339ππβππβαα⎛⎫⎛⎫⎛⎫⎛⎫=+-++-=+⋅=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 故选C . 【点睛】本题考查利用两角和的余弦公式求值,解决这类求值问题需要注意以下两点: ①利用同角三角平方关系求值时,要求对象角的范围,确定所求值的正负; ②利用已知角来配凑未知角,然后利用合适的公式求解.13.A解析:A 【解析】 【分析】利用三角函数恒等变换的公式,化简求得函数的解析式,再根据三角函数的图象与性质,逐项判定,即可求解. 【详解】 由题意,函数2111()cos cos 2cos 2sin(2)2262f x x x x x x x π=+=++=++,当6x π=时,113()sin(2)sin 6662222f ππππ=⨯++=+=,所以6x π=函数()f x 的对称轴,故A 正确;由sin(2)[1,1]6x π+∈-,所以函数()f x 的最大值为32,最小值为12-,所以B 、C 不正确; 又由12x π=时,131()sin(2)6126222f πππ=⨯++=+,所以(,0)12π-不是函数()f x 的对称中心,故D 不正确, 故选A . 【点睛】本题主要考查了三角恒等变换的公式的应用,以及函数sin()y A wx b ϕ=++的图象与性质的应用,着重考查了推理与运算能力,属于基础题.14.D解析:D 【解析】 不妨设(0,0)O∵(2,2)OC =,(2cos ,2sin )CA αα=. ∴(2,2)C 、(22,22sin )A cos αα++. ∴点A 在以(2,2)为圆心半径为2的圆上. ∴OA 与OB 的夹角为直线OA 的倾斜角. 设:OA l y kx = ∴22121k d r k -=≤=+.即2410k k -+≤,则[23,23]k ∈-+. 又∵π23tan12-=,523tanπ12+=. ∴OA 、OB 夹角[23,23]θ∈-+.故选D .15.D【解析】 【分析】根据正弦的倍角公式和三角函数的基本关系式,化为齐次式,即可求解,得到答案. 【详解】由题意,可得222221cos sin cos cos sin 2cos sin cos 2cos sin a a a a a a a a a a++=+=+221tan 1321tan 135a a ++===++,故选D .【点睛】 本题主要考查了正弦的倍角公式,以及三角函数的基本关系式的化简、求值,着重考查了推理与运算能力,属于基础题.二、填空题16.【解析】【分析】先利用两角和与差的正弦余弦公式将函数的解析式展开合并同类项后利用辅助角公式进行化简即可得出函数的最大值【详解】其中因此函数的最大值为故答案为【点睛】本题考查三角函数的最值解题的关键就. 【解析】 【分析】先利用两角和与差的正弦、余弦公式将函数()y f x =的解析式展开,合并同类项后利用辅助角公式进行化简,即可得出函数()y f x =的最大值. 【详解】()1111sin cos sin cos 533522f x x x x x x x ππ⎛⎫⎛⎫⎛⎫⎛⎫=++-=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()x x x ϕ==+,其中tan ϕ==,因此,函数()y f x =,.本题考查三角函数的最值,解题的关键就是利用三角恒等变换思想将三角函数解析式进行化简,同时也考查了三角函数的基本性质,考查计算能力和转化思想,属于中等题.17.【解析】【分析】利用二次方程根与系数的关系得出和的值然后利用两角和的正切公式计算可求出的值【详解】由二次方程根与系数的关系得出因此故答案为【点睛】本题考查两角和的正切公式的应用同时也考查了二次方程根解析:3-. 【解析】 【分析】利用二次方程根与系数的关系得出tan tan αβ+和tan tan αβ的值,然后利用两角和的正切公式计算可求出()tan αβ+的值. 【详解】由二次方程根与系数的关系得出tan tan 3αβ+=,tan tan 2αβ=, 因此,()tan tan 3tan 31tan tan 12αβαβαβ++===---,故答案为3-.【点睛】本题考查两角和的正切公式的应用,同时也考查了二次方程根与系数的关系,考查运算求解能力,属于中等题.18.【解析】【分析】由图像可以计算出的值即可得到三角函数表达式然后计算出结果【详解】由图可知:由得从而将点代入得即又所以得所以【点睛】本题考查了由函数图像求三角函数的表达式熟练掌握图像是解题关键较为基础 解析:32【解析】 【分析】由图像可以计算出A ,ω,ϕ的值,即可得到三角函数表达式,然后计算出结果 【详解】由图可知:A =由741234T πππ=-=,得T π=,从而22T πω==.将点7,12π⎛⎝7212πϕ⎛⎫⨯+= ⎪⎝⎭即7sin 16πϕ⎛⎫+=-⎪⎝⎭,又0ϕπ<<,所以7362ππϕ+=,得3πϕ=.所以3(0)2f ϕ===. 【点睛】本题考查了由函数图像求三角函数的表达式,熟练掌握图像是解题关键,较为基础19.【解析】分析:先根据三角函数定义得再根据诱导公式化简求值详解:因为角的终边上一点所以因此点睛:本题考查三角函数定义以及诱导公式考查基本求解能力【解析】分析:先根据三角函数定义得cos ,tan αα,再根据诱导公式化简求值. 详解:因为角α的终边上一点)1A -,,所以cos tan αα===, 因此()sin tan 2παπα⎛⎫-++⎪⎝⎭cos tan αα=+== 点睛:本题考查三角函数定义以及诱导公式,考查基本求解能力.20.【解析】分析:由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解:角的终边上的一点的坐标为那么故答案为点睛:本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求 解析:17-【解析】分析:由角θ的终边上的一点P 的坐标为()3,4,求出,cos sin θθ的值,利用2cos 212sin 1212cos sin sin θθθθθ-=++,将,cos sin θθ的值代入即可得结果. 详解:角θ的终边上的一点P 的坐标为()3,4,43,cos 55y x sin r r θθ∴====, 那么216712cos 212sin 1252543491212cos 7125525sin sin θθθθθ-⨯--====-+++⨯⨯,故答案为17-. 点睛:本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式,属于中档题.给值求值问题,求值时要注意:(1)观察角,分析角与角之间的差异以及角与角之间的和、差、倍的关系,巧用诱导公式或拆分技巧;(2)观察名,尽可能使三角函数统一名称;(3)观察结构,以便合理利用公式,整体化简求值.21.【解析】分析:根据图像平移规律确定函数解析式详解:点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言 解析:24e x y -=【解析】分析:根据图像平移规律确定函数解析式. 详解:222(2)24e ee e xxx x y y y --=→=→==横坐标变为一半右移个单位点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x 而言.22.【解析】分析:先根据三角形法则化为再根据分解唯一性求即得详解:因为所以因为不共线所以点睛:利用向量基本定理中唯一性可求参数:即若为不共线向量则解析:12. 【解析】分析:先根据三角形法则化AE 为12AB AD +,再根据分解唯一性求λμ,,即得.λμ+ 详解:因为12AE AB AD =+,所以2AB AB AD λλμ⎛⎫=++ ⎪⎝⎭, 因为,AB AD 不共线,所以111=1+=0=-,+=.222λλμμλμ∴, 点睛:利用向量基本定理中唯一性可求参数:即若,a b 为不共线向量,1122+y +y c x a b x a b ==,则1212y =y .x x =,23.【解析】()令∴()∵∴①又∵∴∴∴是方程组①的一组解∴故答案为;解析:(0,5) (2,1) (2,1)- 【解析】(1)令1m =,2n =,2p =,1q =,∴0mp nq -=,5mq np +=,(0,5)a b ⊗=.(2)∵(5,0)a b =⊗,∴5mp nq mq np -=⎧⎨+=⎩,①又∵5a <,5b <,∴22222525m n p q ⎧+<⎨+<⎩,∴m ,n ,p ,q ∈Z ,∴2m =,1n =,2p =,1q =-是方程组①的一组解,∴(2,1)a =,(2,1)b =-.故答案为()0,5? ,(2,1)a =;(2,1)b =-.24.【解析】是椭圆=1上的一个动点设∴最大值为【解析】P x y (,)是椭圆22143x y +==1上的一个动点,设 2x cos y ,,θθ== 2x y cos θθθϕ∴+=+=+(),25.【解析】【分析】延长交于点利用重心的性质得出以及中线向量可求出的表达式【详解】延长交于点则点为线段的中点由平面向量加法的平行四边形法则可知则为的重心因此故答案为【点睛】本题考查向量的基底分解解题的关解析:1133a b +. 【解析】 【分析】延长AG 交BC 于点D ,利用重心的性质得出23AG AD =以及中线向量 ()12AD AB AC =+可求出AG 的表达式. 【详解】 延长AG 交BC 于点D ,则点D 为线段BC 的中点,由平面向量加法的平行四边形法则可知2AD AB AC a b =+=+,则1122AD a b =+, G 为ABC ∆的重心,因此,221111332233AG AD a b a b ⎛⎫==⨯+=+ ⎪⎝⎭, 故答案为1133a b +. 【点睛】本题考查向量的基底分解,解题的关键就是三角形重心的性质和中线向量的应用,考查分析问题和解决问题的能力,属于中等题.三、解答题 26.(1)34-(2【解析】试题分析:(1)利用余弦定理表示出cosB ,将已知等式代入即可求出cosB 的值;(2)由cosB 可求出sin 2,cos 2B B 的值,然后利用两角和的余弦公式可得结果. 试题解析:(1)由22222230a c b ac +-+=,得22232a cb ac +-=-,根据余弦定理得222332cos 224aca cb B ac ac -+-===-; (2)由3cos 4B =-,得sin B =∴sin22sin cos B B B ==21cos22cos 18B B =-=,∴1sin 2sin2cos cos2sin 4448B B B πππ⎫⎛⎫+=+=+=⎪ ⎪⎪⎝⎭⎝⎭. 27.(1)2ω=,6πϕ=-;(2【解析】 【分析】(1)根据最高顶点间的距离求出周期得2ω=,根据对称轴求出6πϕ=-;(2)根据题意求出1sin 64πα⎛⎫-= ⎪⎝⎭,结合诱导公式及和差公式求解.【详解】解:(1)因()f x 的图象上相邻两个最高点的距离为π, ∴()f x 的最小正周期T π=,从而22Tπω==. 又因()f x 的图象关于直线3x π=对称,∴2()32k k Z ππϕπ⋅+=+∈.∵22ππϕ-≤≤,∴0k =,此时2236ππϕπ=-=-. (2)由(1)得264f απα⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭, ∴1sin 64πα⎛⎫-= ⎪⎝⎭, 由263ππα<<得062ππα<-<,∴cos 64πα⎛⎫-== ⎪⎝⎭, ∴3cos sin sin 266πππααα⎡⎤⎛⎫⎛⎫+==-+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦sin sin cos cos sin 6666668ππππππααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=-+-=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 【点睛】此题考查根据三角函数图像性质求参数的值,结合诱导公式和差公式处理三角求值的问题.28.(Ⅰ) 14-; (Ⅱ) 716-. 【解析】 【分析】(Ⅰ)由题意结合正弦定理得到,,a b c 的比例关系,然后利用余弦定理可得cos B 的值 (Ⅱ)利用二倍角公式首先求得sin 2,cos 2B B 的值,然后利用两角和的正弦公式可得sin 26B π⎛⎫+ ⎪⎝⎭的值.【详解】(Ⅰ)在ABC △中,由正弦定理sin sin b cB C=得sin sin b C c B =, 又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =. 又因为2b c a +=,得到43b a =,23c a =. 由余弦定理可得222cos 2a c b B ac +-=2224161992423a a aa a +-==-⋅⋅. (Ⅱ)由(Ⅰ)可得sin B ==,从而sin 22sin cos B B B ==227cos 2cos sin 8B B B =-=-.故717sin 2sin 2cos cos 2sin 666828216B B B πππ⎛⎫+=+=-⨯-⨯=- ⎪⎝⎭. 【点睛】本题主要考查同角三角函数的基本关系,两角和的正弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识.考查计算求解能力.29.(1)6C π=;(2) 【解析】【分析】(1)根据()sin ()(sin sin )0m n a A b c BC ⋅=-++-=和正弦定理余弦定理求得6C π=.(2)先利用正弦定理求出R=1,b -化成2sin()6A π-,再利用三角函数的图像和性质求解.【详解】(1)因为m n ⊥,所以()sin ()(sin sin )0m na Abc B C ⋅=-++-=,由正弦定理化角为边可得2220a b c +-=,即222a b c +-=,由余弦定理可得cos C =,又0C π<<,所以6C π=. (2)由(1)可得56A B π+=,设ABC 的外接圆的半径为R , 因为6C π=,1c=,所以122sin sin30c R C ===︒, 则52sin 2sin 2sin )2sin()]6b R A R B R A B R A A π-=-=-=--= 2sin()2sin()66R A A ππ-=-, 因为ABC 为锐角三角形,所以025062A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,即32A ππ<<,所以663A πππ<-<,所以1sin()26A π<-<, 所以12sin()6A π<-<b -的取值范围为.【点睛】 (1)本题主要考查正弦定理余弦定理解三角形,考查三角函数的图像和性质,意在考查学生对这些知识的掌握水平和分析推理能力.(2) 对于复合函数的问题自然是利用复合函数的性质解答,求复合函数的最值,一般从复合函数的定义域入手,结合三角函数的图像一步一步地推出函数sin()y A wx h φ=++的最值.30.(1)1a =-,(2)2|22,3x k x k k πππ⎧⎫≤≤+∈⎨⎬⎩⎭Z 【解析】试题分析:(1)()(sin cos cos sin )(sin cos cos sin )cos 6666f x x x x x x a ππππ=++-++cos x x a =++2sin()6x a π=++ ∴max ()21f x a =+=,∴1a =-(2)∵()2sin()16f x x π=+-,∴2sin()106x π+-≥,∴1sin()62x π+≥, ∴522,666k x k k πππππ+≤+≤+∈Z ,解得222,3k x k k πππ≤≤+∈Z , ∴使()0f x ≥成立的x 的取值集合为2|22,3x k x k k πππ⎧⎫≤≤+∈⎨⎬⎩⎭Z 考点:本题考查了三角函数的变换及三角不等式的解法点评:,对三角函数性质和图象的综合考查主要体现为一个题目中考查三角函数的多种性质及图象的变换、作法等.在其具体的解题过程中,一般都需要先将三角函数的解析式转化为只含有一种函数、一个角(ωx +Φ)的形式,再根据题目具体的要求进行求解.。
2020-2021学年高二(下)期中数学试卷一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.)1. 设复数z满足z=3+4i(其中i为虚数单位),则z的模为________.2. 圆心为(−1, 2),半径为2的圆的标准方程是________.−y2=1的焦距为________.3. 双曲线x224. 已知复数z1=6+2i,z2=1+ai(i为虚数单位),且z1+是实数,则实数a的值为________.5. 方程表示的曲线是椭圆,则实数m的取值范围是________.6. 已知复数z满足|z|=1,则(i为虚数单位)的最小值为________.7. 与双曲线有共同的渐近线,且过点(−1, 4)的双曲线方程是________.8. 以坐标原点为顶点,焦点在坐标轴上且经过点(1, 2)的抛物线的方程是________2=4________或者.9. 若△ABC的两个顶点B(0, −3),C(0, 3),周长为16,则第三个顶点A的轨迹方程是________.10. 过抛物线y2=4x的焦点作直线交抛物线于A(x1, y1),B(x2, y2)两点,若x1+x2=12,则|AB|等于________.11. 若直线y=2x+b与曲线y=−√9−x2没有公共点,则实数b的取值范围是________.12. 关于曲线C:=1,则以下结论正确的序号是________.①曲线C关于原点对称;②曲线C中x∈[−2, 2],y∈[−2, 2];③曲线C不是封闭图形,且它与圆x2+y2=8无公共点;④曲线C与曲线D:|x|+|y|=4有4个交点,这4点构成正方形.二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D 的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.)13. 设复数z=a+bi(a、b∈R),则“a=0”是“z为纯虚数”的()A.既不充分也不必要条件B.充要条件C.充分非必要条件D.必要非充分条件14. 设M=i+i2+i3+i4,N=i⋅i2⋅i3⋅i4,i为虚数单位,则M与N的关系是()A.M+N=0B.M<NC.M>ND.M=N15. 双曲线4x2+ky2=4k的虚轴长是实轴长的2倍,则实数k的值是()A.16B.C.−16D.16. 点P到图形C上每一个点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C的距离与到定点A的距离相等的点的轨迹不可能是()A.圆B.椭圆C.双曲线的一支D.直线三、简答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.)17. 已知圆C的方程为x2−2x+y2−3=0.(1)求过点(3, 2)且与圆C相切的直线方程;(2)若直线y=x+1与圆C相交于A,B,求弦长|AB|的值.18. 已知复数z满足|z|+−8−4i=0(i为虚数单位).(1)求复数z;(2)若m∈R,ω=zi+m,求|ω|的取值范围.19. 在平面直角坐标系xOy中,C(−2, 0),D(2, 0),曲线E上的动点P满足|PC|+|PD|=,直线l过D交曲线E于A、B两点.(1)求曲线E的方程;(2)当AC⊥AB时,A在x轴上方时,求A、B的坐标;(3)设M(−2,2),N(2,2),P是曲线E上的任意一点,若=m+n ,求证:动点Q(m, n)在定圆上运动.20. 在平面直角坐标系xOy中,原点为O,抛物线C的方程为x2=4y,线段AB是抛物线C的一条动弦.(1)求抛物线C的准线方程;(2)求,求证:直线AB恒过定点;(3)过抛物线的焦点F作互相垂直的两条直线l1、l2,l1与抛物线交于P、Q两点,l2与抛物线交于C、D两点,M、N分别是线段PQ、CD的中点,求△FMN面积的最小值.参考答案与试题解析一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.1.【答案】5【解析】直接利用复数模的计算公式求解.2.【答案】(x+1)2+(y−2)2=4【解析】根据题意,由圆的标准方程的形式,代入圆心的坐标和半径,即可得答案.3.【答案】2√3【解析】直接利用双曲线的标准方程,求解双曲线的实半轴虚半轴的长,然后求解半焦距,即可得到结果.4.【答案】2【解析】由已知求得z1+,再由虚部为0求解a值.5.【答案】(4, +∞)【解析】由椭圆的标准方程的形式列出不等式,解可得m的取值范围,即可得答案.6.【答案】1【解析】由题意画出图形,数形结合得答案.7.【答案】【解析】设双曲线方程为.利用双曲线过点(−1, 4),求出k,即可得出双曲线方程.8.【答案】y,x【解析】根据题意,分析可得抛物线的开口向上或向左,据此分2种情况讨论,分析设出抛物线的方程,将M的坐标代入计算可得p的值,综合2种情况即可得答案.9.【答案】.【解析】由三角形的周长和椭圆的定义,即可得到所求轨迹方程.10.【答案】14【解析】根据抛物线的方程求出准线方程是x=−1,结合抛物线的定义可得|AF|=x1+1且|BF|=x2+1,两式相加并结合x1+x2=12,即可得到|AB|的值.11.【答案】(−∞,−3√5)∪(6,+∞)【解析】作出图形,求出半圆的切线,从而得出b的范围.12.【答案】①③【解析】以−x替换x,以−y替换y,方程不变判断①;求出x,y的范围判断②;联立方程组判断③;由两曲线的对称性判断④.二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D 的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.13.【答案】D【解析】根据复数的概念可得当a=0,且b≠0时,z为纯虚数,再根据充分条件,必要条件的定义可以判断.14.【答案】C【解析】利用虚数单位i的运算性质化简M与N,则答案可求.15.【答案】C【解析】双曲线4x2+ky2=4k的虚轴长是实轴长的2倍,列出方程,可求得双曲线的虚轴长,即可得出结论.16.【答案】D【解析】根据题意“点P到图形C上每一个点的距离的最小值称为点P到图形C的距离”,将平面内到定圆C的距离转化为到圆上动点的距离,再分点A现圆C的位置关系,结合圆锥曲线的定义即可解决.三、简答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.17.【答案】圆的标准方程为(x−1)2+y2=4圆心为C(1, 0),半径r=2,①当直线斜率不存在时,由过点(3, 2)得直线方程为x=3,与(1, 0)的距离为2,与圆相切,符合题意;②当直线斜率存在时,可设斜率为k,直线方程为y−2=k(x−3),即kx−y+2−3k=0,圆心(1, 0)到直线的距离,解得k=0.∴直线方程为y=2.综上,所求直线方程为y=2或x=3.另可设所求直线的方程为a(x−3)+b(y−2)=0(a2+b2≠0),即ax+by−3a−2b=0由题意得圆心(1, 0)到切线的距离,得ab=0,所求为y=2或x=3.圆心C(1, 0)到直线y=x+1与的距离,又半径r=2,∴弦长|AB|=.【解析】(1)求出圆心与半径r,①当直线斜率不存在时,验证是否满足题意.②当直线斜率存在时,可设斜率为k,直线方程为y−2=k(x−3),利用点到直线的距离公式求解即可.另解:设所求直线的方程为a(x−3)+b(y−2)=0(a2+b2≠0),利用点到直线的距离公式求解即可.(2)利用点到直线的距离,结合圆的半径计算弦长即可.18.【答案】由|z|+−8−4i=0,得,则,∴z=3−4i;|ω|=|(3−4i)i+m|=|4+m+3i|=,∵m∈R,∴|ω|≥3,故|ω|的取值范围是[3, +∞).【解析】设z=a+bi(a, b∈R),(1)把z代入已知等式,利用复数相等的条件列式求得a与b的值,则z可求;(2)利用复数模的计算公式求得|ω|,再由配方法求得|ω|的取值范围.19.【答案】由椭圆的定义可知动点P的轨迹是以C、D为焦点,长轴长为的椭圆,即a=2,c=2,所以曲线E的方程为+=1.证明:设A(x1, y1),B(x2, y2),(y1>0),由题C(−2, 0),D(2, 0),因为AC⊥AB,且A,D在一条直线上,所以•=(−2−x1, −y1)⋅(2−x1, −y1)=x12−4+y12=x12−4+4(1−)=x12=0,所以x1=0,y1=2,A(0, 2),则直线l的方程为:y=−x+2,联立,得3x2−8x=0,所以x1=0,x2=,所以y2=-=2=-,所以B(,-).设P(x P, y P),则+=1,由题,所以m2+n2=,即证动点Q(m, n)在以原点为圆心,以为半径的定圆上运动.【解析】(1)由椭圆的定义可知动点P的轨迹是以C、D为焦点,长轴长为的椭圆,进而可得a,c,再计算b2=a2−c2,即可得出答案.(2)设A(x1, y1),B(x2, y2),(y1>0),由AC⊥AB,得•=0,解得x1,y1,即可得出A点坐标,写出直线l的方程,联立椭圆的方程,解得x2,即得B点坐标.(3)设P(x P, y P),代入椭圆的方程,+=1,由=m+n,得,化简即可得出答案.20.【答案】抛物线C:x2=4y的准线方程为y=−1;证明:设直线AB方程为y=kx+b,A(x1, y1),B(x2, y2),由,可得x2−4kx−4b=0,所以x1+x2=4k,x1x2=−4b,•=x1x2+y1y2=x1x2+=−4b+=−4,解得b=2,则直线y=kx+2过定点(0, 2);由F(0, 1),由题意,直线l1,l2的斜率都存在且不为0,设直线l1的方向向量为(1, k)(k>0),则(1, k)是直线l2的一个法向量,故直线l1的方程为=,即y=kx+1,直线l2的方程为x+k(y−1)=0,即y=-x+1,由,可得x2−4kx−4=0,设P(x1, y1),Q(x2, y2),可得x1+x2=4k,则M(2k, 2k2+1);同理可得N(−,1+).所以S△FMN=|FM|⋅|FN|=•=2(k+)≥4,当且仅当k=1时,△FMN的面积取最小值4.【解析】(1)由焦点在y轴的正半轴上的抛物线的准线方程可得所求;(2)设直线AB方程为y=kx+b,与抛物线的方程联立,运用韦达定理和向量数量积的坐标表示,解方程可得b,进而得到定点;(3)求得F(0, 1),分别设直线l1,l2的方程,联立抛物线的方程,运用韦达定理和中点坐标公式,求得M,N的坐标,由抛物线的定义,可得|FM|,|FN|,再由三角形的面积公式和基本不等式,计算可得所求最小值.。
【好题】高中必修二数学下期中一模试卷附答案一、选择题1.已知直线l 过点(1,0),且倾斜角为直线0l :220x y --=的倾斜角的2倍,则直线l的方程为( ) A .4330x y --= B .3430x y --= C .3440x y --=D .4340x y --=2.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥3.设α表示平面,a ,b 表示直线,给出下列四个命题:①a α//,a b b α⊥⇒//; ②a b //,a b αα⊥⇒⊥;③a α⊥,a b b α⊥⇒⊂;④a α⊥,b a b α⊥⇒//,其中正确命题的序号是( ) A .①②B .②④C .③④D .①③4.直线20x y ++=截圆222210x y x y a ++-+-=所得弦的长度为4,则实数a 的值是( ) A .-3B .-4C .-6D .36-5.如图是某四面体ABCD 水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD 外接球的表面积为A .20πB .1256π C .25π D .100π6.在我国古代数学名著 九章算术 中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD 中, AB ⊥平面BCD ,且AB BC CD ==,则异面直线AC 与BD 所成角的余弦值为( )A .12B .12-C 3D .37.从点(,3)P m 向圆22(2)(2)1x y +++=引切线,则切线长的最小值( ) A .26B .5C .26D .42+8.矩形ABCD 中,4AB =,3BC =,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是( )A .12512π B .1259π C .1256π D .1253π 9.在长方体1111ABCD A B C D -中,11111,2AA A D a A B a ===,点P 在线段1AD 上运动,当异面直线CP 与1BA 所成的角最大时,则三棱锥11C PA D -的体积为( )A .34aB .33aC .32aD .3a 3a10.如图所示,在棱长为a 的正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 是侧面11CDD C 上的动点,且1//B F 面1A BE ,则F 在侧面11CDD C 上的轨迹的长度是( )A .aB .2a C .2aD .2a 11.已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ,B 两点,则弦长AB 的取值范围是( )A .[]4,10B .[]3,5C .[]8,10D .[]6,1012.如图在正方体中,点为线段的中点. 设点在线段上,直线与平面所成的角为,则的取值范围是( )A .B .C .D .二、填空题13.已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M 分别是线段AB 、AD 、AA 1的中点,又P 、Q 分别在线段A 1B 1、A 1D 1上,且A 1P =A 1Q =x (0<x <1).设平面MEF ∩平面MPQ=l ,现有下列结论:①l ∥平面ABCD ; ②l ⊥AC ;③直线l 与平面BCC 1B 1不垂直; ④当x 变化时,l 不是定直线.其中不成立的结论是________.(写出所有不成立结论的序号)14.已知三棱锥P ABC -中,侧面PAC ⊥底面ABC ,90BAC ∠=︒,4AB AC ==,23PA PC ==,则三棱锥P ABC -外接球的半径为______.15.已知一束光线通过点()3,5A -,经直线l :0x y +=反射,如果反射光线通过点()2,5B ,则反射光线所在直线的方程是______.16.过正方体1111ABCD A B C D -的顶点A 作直线l ,使l 与棱AB 、AD 、1AA 所成的角都相等,这样的直线l 可以作_________条.17.如图,在△ABC 中,AB=BC=2,∠ABC=120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD=DA ,PB=BA ,则四面体PBCD 的体积的最大值是 .18.已知正方体1111ABCD A B C D -的棱长为1,点E 是棱1BB 的中点,则点1B 到平面ADE 的距离为__________.19.在三棱锥P ABC -中,PA ⊥平面ABC ,AC BC ⊥,且三棱锥的最长的棱长为2,则此三棱锥的外接球体积为_____________.20.在正方体1111ABCD A B C D -中,E 是棱1DD 的中点,则直线BE 和平面11ABB A 所成的角的正弦值为_____________.三、解答题21.如图,在三棱台DEF ABC -中,2,,AB DE G H =分别为,AC BC 的中点.(Ⅰ)求证://BD 平面FGH ;(Ⅱ)若CF ⊥平面ABC ,,AB BC CF DE ⊥=,45BAC ∠=o ,求平面FGH 与平面ACFD 所成角(锐角)的大小.22.如图,ABCD 是正方形,O 是该正方体的中心,P 是平面ABCD 外一点,PO ⊥平面ABCD ,E 是PC 的中点.(1)求证://PA 平面BDE ; (2)求证:BD ⊥平面PAC .23.已知圆C 的圆心坐标()1,1,直线l :1x y +=被圆C 截得弦长为2. (1)求圆C 的方程;(2)从圆C 外一点()2,3P 向圆引切线,求切线方程.24.如图,在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,侧棱PA PD ⊥,底面ABCD 是直角梯形,其中//BC AD ,90BAD ∠=︒,3AD BC =,2AO OD =.(1)求证:平面PAB ⊥平面PCD .(2)试问在棱PA 上是否存在点E ,使得面//BOE 面PCD ,若存在,试指出点E 的位置并证明;若不存在,请说明理由.25.已知直线1:20l ax y a +--=,22:0l x ay ++=,点(5,0)P - (1)当12//l l 时,求a 的值;(2)求直线1l 所过的定点Q ,并求当点P 到直线1l 的距离最大时直线1l 的方程. 26.如图,正方体1111ABCDA B C D 的棱长为2,E F M 、、分别是1111C B C D ,和AB 的中点.(1)求证:1//MD 平面BEFD . (2)求M 到平面BEFD 的距离.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】设直线0l 的倾斜角为α,则斜率01tan 2k α==,所以直线l 的倾斜角为2α,斜率22tan 4tan 21tan 3k ααα===-,又经过点(1,0),所以直线方程为4(1)3y x =-,即4340x y --=,选D.2.B解析:B 【解析】A 中,,αβ也可能相交;B 中,垂直与同一条直线的两个平面平行,故正确;C 中,,αβ也可能相交;D 中,l 也可能在平面β内. 【考点定位】点线面的位置关系3.B解析:B 【解析】 【分析】 【详解】①a ∥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故①错误; ②若a ∥b ,a ⊥α,由直线与平面垂直和判定定理得b ⊥α,故②正确; ③a ⊥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故③错误; ④若a ⊥α,b ⊥α,则由直线与平面垂直的性质得a ∥b ,故④正确. 故选B .4.A解析:A 【解析】 【分析】求出圆心坐标和半径,根据圆的弦长公式,进行求解即可. 【详解】由题意,根据圆的方程222210x y x y a ++-+-=,即22(1)(1)2x y a ++-=-,则圆心坐标为(1,1)-,半径r =又由圆心到直线的距离为d ==所以由圆的弦长公式可得4=,解得3a =-,故选A. 【点睛】本题主要考查了直线与圆的位置关系的因公,以及弦长公式的应用,其中根据圆的方程,求得圆心坐标和半径,合理利用圆的弦长公式列出方程求解是解答的关键,着重考查了推理与运算能力.5.C解析:C 【解析】 【分析】 【详解】由三视图可知,这是三棱锥的三视图,如下图所示,三角形BCD 为等腰直角三角形, 其外心为BD 中点1O ,设O 为AD 中点, 则O 为外接球球心,半径长度为1522AD =, 所以表面积为25π.6.A解析:A 【解析】如图,分别取,,,BC CD AD BD 的中点,,,M N P Q ,连,,,MN NP PM PQ ,则,MN BD NP AC P P ,∴PNM ∠即为异面直线AC 和BD 所成的角(或其补角). 又由题意得PQ MQ ⊥,11,22PQ AB MQ CD ==. 设2AB BC CD ===,则2PM =又112,222MN BD NP AC ==== ∴PNM ∆为等边三角形, ∴60PNM =︒∠,∴异面直线AC 与BD 所成角为60︒,其余弦值为12.选A . 点睛:用几何法求空间角时遵循“一找、二证、三计算”的步骤,即首先根据题意作出所求的角,并给出证明,然后将所求的角转化为三角形的内角.解题时要注意空间角的范围,并结合解三角形的知识得到所求角的大小或其三角函数值.7.A解析:A 【解析】 【分析】设切线长为d ,则2222(2)51(2)24d m m =++-=++再利用二次函数的图像和性质求函数的最小值得解. 【详解】设切线长为d ,则2222(2)51(2)24d m m =++-=++, min 26d ∴=. 故选:A. 【点睛】本题主要考查圆的切线问题,考查直线和圆的位置关系,意在考查学生对这些知识的掌握水平和分析推理能力.8.C解析:C 【解析】 【分析】由矩形的对角线互相平分且相等即球心到四个顶点的距离相等推出球心为AC 的中点,即可求出球的半径,代入体积公式即可得解. 【详解】因为矩形对角线互相平分且相等,根据外接球性质易知外接球球心到四个顶点的距离相等,所以球心在对角线AC 上,且球的半径为AC 长度的一半,即22115222r AC AB BC ==+=,所以334451253326V r πππ⎛⎫==⋅= ⎪⎝⎭.故选:C 【点睛】本题考查球与几何体的切、接问题,二面角的概念,属于基础题.9.B解析:B 【解析】 【分析】当P 与A 重合时,异面直线CP 与BA 1所成的角最大,由此能求出当异面直线CP 与BA 1所成的角最大时,三棱锥C ﹣PA 1D 1的体积. 【详解】如图,当P 与A 重合时,异面直线CP 与BA 1所成的角最大, ∴当异面直线CP 与BA 1所成的角最大时, 三棱锥C ﹣PA 1D 1的体积:11C PA D V -=11C AA D V -=1113AA D S AB ⨯⨯V =1111132AA A D AB ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=11232a a a ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=33a . 故选:B . 【点睛】求锥体的体积要充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解,注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.10.D解析:D 【解析】 【分析】设H ,I 分别为1CC 、11C D 边上的中点,由面面平行的性质可得F 落在线段HI 上,再求HI 的长度即可.【详解】解:设G ,H ,I 分别为CD 、1CC 、11C D 边上的中点, 则ABEG 四点共面, 且平面1//A BGE 平面1B HI , 又1//B F Q 面1A BE ,F ∴落在线段HI 上,Q 正方体1111ABCD A B C D -中的棱长为a ,1122HI CD a ∴==,即F 在侧面11CDD C 上的轨迹的长度是22a . 故选D .【点睛】本题考查了面面平行的性质及动点的轨迹问题,属中档题.11.D解析:D 【解析】 【分析】由直线()()21110k x k y ++++=,得出直线恒过定点()1,2P -,再结合直线与圆的位置关系,即可求解. 【详解】由直线()()():21110l k x k y k R ++++=∈,可得()210k x y x y ++++=, 又由2010x y x y +=⎧⎨++=⎩,解得12x y =⎧⎨=-⎩,即直线恒过定点()1,2P -,圆心()1,2C ,当CP l ⊥时弦长最短,此时2222AB CP r ⎛⎫+= ⎪⎝⎭,解得min 6AB =,再由l 经过圆心时弦长最长为直径210r =, 所以弦长AB 的取值范围是[]6,10. 故选:D. 【点睛】本题主要考查了直线系方程的应用,以及直线与圆的位置关系的应用,其中解答中熟练利用直线的方程,得出直线恒过定点,再结合直线与圆的位置关系求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.12.B解析:B 【解析】【分析】【详解】设正方体的棱长为,则,所以,.又直线与平面所成的角小于等于,而为钝角,所以的范围为,选B.【考点定位】空间直线与平面所成的角.二、填空题13.④【解析】【详解】连接BDB1D1∵A1P=A1Q=x∴PQ∥B1D1∥BD∥EF则P Q∥平面MEF又平面MEF∩平面MPQ=l∴PQ∥ll∥EF∴l∥平面ABCD故①成立;又EF⊥AC∴l⊥AC故解析:④【解析】【详解】连接BD,B1D1,∵A1P=A1Q=x,∴PQ∥B1D1∥BD∥EF,则PQ∥平面MEF,又平面MEF∩平面MPQ=l,∴PQ∥l,l∥EF,∴l∥平面ABCD,故①成立;又EF⊥AC,∴l⊥AC,故②成立;∵l∥EF∥BD,故直线l与平面BCC1B1不垂直,故③成立;当x变化时,l是过点M且与直线EF平行的定直线,故④不成立.即不成立的结论是④.14.【解析】【分析】设三棱锥外接球球心为半径为如图所示作辅助线设则解得答案【详解】设三棱锥外接球球心为半径为故在平面的投影为中点为中点故侧面底面故底面连接作于易知为矩形设则解得故答案为:【点睛】本题考查 34【解析】 【分析】设三棱锥P ABC -外接球球心为O ,半径为R ,如图所示作辅助线,设1OO h =,则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩,解得答案. 【详解】设三棱锥P ABC -外接球球心为O ,半径为R ,90BAC ∠=︒,故O 在平面ABC 的投影为BC 中点1O ,D 为AC 中点,PA PC =,故PD AC ⊥,侧面PAC ⊥底面ABC ,故PD ⊥底面ABC .连接1O D ,作OH PD ⊥于H ,易知1OO DH 为矩形,设1OO h =,则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩,22PD =,12OH DO ==,122CO =34R =34【点睛】本题考查了三棱锥的外接球问题,意在考查学生的计算能力和空间想象能力.15.【解析】【分析】计算关于直线的对称点为计算直线得到答案【详解】设关于直线的对称点为故故故反射光线为:化简得到故答案为:【点睛】本题考查了直线的反射问题找出对称点是解题的关键 解析:27310x y -+=【解析】 【分析】计算()3,5A -关于直线0x y +=的对称点为()15,3A -,计算直线1A B 得到答案.【详解】设()3,5A -关于直线0x y +=的对称点为()1,A x y ,故51335022y x x y -⎧=⎪⎪+⎨-+⎪+=⎪⎩,故()15,3A -. 故反射光线为1A B :()532525y x -=-++,化简得到27310x y -+=. 故答案为:27310x y -+=.【点睛】本题考查了直线的反射问题,找出对称点是解题的关键.16.【解析】【分析】将小正方体扩展成4个小正方体根据直线夹角的定义即可判断出符合条件的条数【详解】解:设ABCD ﹣A1B1C1D1边长为1第一条:AC1是满足条件的直线;第二条:延长C1D1到C1且D1 解析:4【解析】【分析】将小正方体扩展成4个小正方体,根据直线夹角的定义即可判断出符合条件的条数. 【详解】解:设ABCD ﹣A 1B 1C 1D 1边长为1. 第一条:AC 1是满足条件的直线;第二条:延长C 1D 1到C 1且D 1C 2=1,AC 2是满足条件的直线; 第三条:延长C 1B 1到C 3且B 1C 3=1,AC 3是满足条件的直线; 第四条:延长C 1A 1到C 4且C 4A 12=,AC 4是满足条件的直线.故答案为4. 【点睛】本题考查满足条件的直线条数的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力,考查分类与整合思想,是基础题.17.【解析】中因为所以由余弦定理可得所以设则在中由余弦定理可得故在中由余弦定理可得所以过作直线的垂线垂足为设则即解得而的面积设与平面所成角为则点到平面的距离故四面体的体积设因为所以则(1)当时有故此时因 解析:12【解析】ABC ∆中,因为2,120AB BC ABC ==∠=o ,所以30BAD BCA ∠==o .由余弦定理可得2222cos AC AB BC AB BC B =+-⋅2222222cos12012=+-⨯⨯=o ,所以23AC =设AD x =,则023t <<23DC x =.在ABD ∆中,由余弦定理可得2222cos BD AD AB AD AB A =+-⋅22222cos30x x =+-⋅o 2234x x =-+.故2234BD x x =-+在PBD ∆中,PD AD x ==,2PB BA ==.由余弦定理可得2222222(234)3cos2222PD PB BD x x xBPDPD PB x+-+--+∠===⋅⋅⋅,所以30BPD∠=o.过P作直线BD的垂线,垂足为O.设PO d=则11sin22PBDS BD d PD PB BPD∆=⨯=⋅∠,2112342sin3022x x d x-+=⋅o,解得2234dx x=-+.而BCD∆的面积111sin(23)2sin303)222S CD BC BCD x x=⋅∠=⋅=o.设PO与平面ABC所成角为θ,则点P到平面ABC的距离sinh dθ=.故四面体PBCD的体积211111sin(23)33332234 BcD BcD BcDV S h S d S d xx xθ∆∆∆=⨯=≤⋅=⨯-+ 21(23)6234x xx x-=-+设22234(3)1t x x x=-+=-+023x≤≤12t≤≤.则231x t-=-(1)当03x≤≤时,有2331x x t==-故231x t=-此时,221(31)[23(31)]t tV-----=21414()66ttt t-=⋅=-.214()(1)6V tt=--',因为12t≤≤,所以()0V t'<,函数()V t在[1,2]上单调递减,故141()(1)(1)612V t V≤=-=.(2x <≤x x =-=故x =此时,V =21414()66t t t t-=⋅=-. 由(1)可知,函数()V t 在(1,2]单调递减,故141()(1)(1)612V t V <=-=. 综上,四面体PBCD 的体积的最大值为12. 18.【解析】【分析】点到平面的距离等价于点到平面的距离过作交于证得平面利用等面积法求得点到平面的距离也即点到平面的距离【详解】由于是的中点故点到平面的距离等价于点到平面的距离过作交于由于故平面在直角三角【解析】 【分析】点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离,过B 作BF AE ⊥,交AE 于F ,证得BF ⊥平面ADE ,利用等面积法求得点B 到平面ADE 的距离,也即点1B 到平面ADE 的距离. 【详解】由于E 是1BB 的中点,故点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离,过B 作BF AE ⊥,交AE 于F ,由于BF AD ⊥,AD AE E ⋂=,故BF ⊥平面ADE .在直角三角形ABE 中,11,,2AB BE AE ===,所以1122AB BE AE BF ⋅⋅=⋅⋅,解得BF =.【点睛】本小题主要考查点到面的距离,考查等面积法求高,考查线面垂直的证明,属于基础题.19.【解析】【分析】根据题意可得平面所以得出为三棱锥的最长边根据直角三角形的性质边的中点到三棱锥的各顶点距离都相等所以为球心球直径即为【详解】平面平面平面所以三棱锥中最长边为设中点为在中所以三棱锥的外接 解析:43π 【解析】 【分析】根据题意可得,BC ⊥平面PAC ,所以BC PC ⊥,得出PB 为三棱锥的最长边,PA AB ⊥,根据直角三角形的性质,PB 边的中点到三棱锥的各顶点距离都相等,所以为球心,球直径即为PB . 【详解】PA ⊥Q 平面ABC ,BC ⊂平面ABC ,PA BC ∴⊥,,,AC BC PA AC A BC ⊥=∴⊥I 平面PAC ,BC PC ⊥,,,,,PB BC PB PC PA AC PC AC PC PA ∴>>⊥∴>>,所以三棱锥中最长边为2PB =,设PB 中点为O ,在,Rt PAB Pt PBC ∆∆中,12AO CO PB ==,所以三棱锥的外接球的球心为O , 半径为41,3V π∴=.故答案为:43π. 【点睛】本题考查几何体的“切”“接”球问题,确定球心是解题的关键,考查空间垂直的应用,属于中档题.20.【解析】【分析】作出直线和平面所成的角解直角三角形求得线面角的正弦值【详解】设为的中点连接根据正方体的性质可知平面所以是直线和平面所成的角设正方体的边长为在中所以故答案为:【点睛】本小题主要考查线面 解析:23【解析】 【分析】作出直线BE 和平面11ABB A 所成的角,解直角三角形求得线面角的正弦值. 【详解】设F 为1AA 的中点,连接,,EF EB BF ,根据正方体的性质可知EF ⊥平面11ABB A ,所以EBF ∠是直线BE 和平面11ABB A 所成的角.设正方体的边长为2,在Rt EBF ∆中2EF =,2222213BE =++=,所以2sin 3EF EBF BE ∠==. 故答案为:23【点睛】本小题主要考查线面角的求法,考查空间想象能力,属于基础题.三、解答题21.(Ⅰ)略;(Ⅱ)60o 【解析】试题分析:(Ⅰ)思路一:连接,DG CD ,设CD GF O ⋂=,连接OH ,先证明//OH BD ,从而由直线与平面平行的判定定理得//BD 平面HDF ;思路二:先证明平面//FGH 平面ABED ,再由平面与平面平行的定义得到//BD 平面HDF .(Ⅱ)思路一:连接,DG CD ,设CD GF O ⋂=,连接OH ,证明,,GB GC GD 两两垂直, 以G 为坐标原点,建立如图所示的空间直角坐标系G xyz -,利用空量向量的夹角公式求解;思路二:作HM AC ⊥于点M ,作MN GF ⊥于点N ,连接NH ,证明MNH ∠即为所求的角,然后在三角形中求解. 试题解析:(Ⅰ)证法一:连接,DG CD ,设CD GF O ⋂=,连接OH , 在三棱台DEF ABC -中,2,AB DE G =为AC 的中点可得//,DF GC DF GC = 所以四边形DFCG 为平行四边形 则O 为CD 的中点 又H 为BC 的中点 所以//OH BD又OH ⊂平面,FGH BD ⊂平面,FGH 所以//BD 平面FGH .证法二:在三棱台DEF ABC -中, 由2,BC EF H =为BC 的中点 可得//,,BH EF BH EF = 所以四边形BHFE 为平行四边形 可得//BE HF在ABC ∆中,G 为AC 的中点,H 为BC 的中点, 所以//GH AB又GH HF H ⋂=,所以平面//FGH 平面ABED 因为BD ⊂平面ABED 所以//BD 平面FGH (Ⅱ)解法一: 设2AB =,则1CF = 在三棱台DEF ABC -中,G 为AC 的中点由12DF AC GC ==, 可得四边形DGCF 为平行四边形, 因此//DG CF 又FC ⊥平面ABC 所以DG ⊥平面ABC在ABC ∆中,由,45AB BC BAC o⊥∠=,G 是AC 中点, 所以,AB BC GB GC =⊥ 因此,,GB GC GD 两两垂直,以G 为坐标原点,建立如图所示的空间直角坐标系G xyz -所以())()()0,0,0,2,0,0,2,0,0,0,1G BC D可得()22,2,1H F ⎫⎪⎪⎝⎭故()22,2,122GH GF ⎛⎫== ⎪ ⎪⎝⎭u u u r u u u r设(),,n x y z r=是平面FGH 的一个法向量,则 由0,{0,n GH n GF ⋅=⋅=u u u rr u u u r r 可得0{20x y z +=+=可得平面FGH 的一个法向量(1,2n r=-因为GB uuu r是平面ACFD 的一个法向量,()2,0,0GB =uu u r所以21cos ,222GB n GB n GB n ⋅===⋅u u u r ru u u r r u u u r r所以平面与平面所成的解(锐角)的大小为60o 解法二:作HM AC ⊥于点M ,作MN GF ⊥于点N ,连接NH 由FC ⊥平面ABC ,得HM FC ⊥ 又FC AC C ⋂= 所以HM ⊥平面ACFD 因此GF NH ⊥所以MNH ∠即为所求的角在BGC ∆中,12//,,22MH BG MH BG == 由GNM ∆∽GCF ∆ 可得,MN GMFC GF= 从而6MN =由MH ⊥平面,ACFD MN ⊂平面ACFD 得,MH MN ⊥ 因此tan 3HMMNH MN∠==所以60MNH ∠=o所以平面FGH 与平面ACFD 所成角(锐角)的大小为60o .考点:1、空间直线与平面的位置关系;2、二面角的求法;3、空间向量在解决立体几何问题中的应用. 22.证明见解析. 【解析】试题分析:(1)要证PA 与平面EBD 平行,而过PA 的平面PAC 与平面EBD 的交线为EO ,因此只要证//PA EO 即可,这可由中位线定理得证;(2)要证BD 垂直于平面PAC ,就是要证BD 与平面PAC 内两条相交直线垂直,正方形中对角线BD 与AC 是垂直的,因此只要再证BD PO ⊥,这由线面垂直的性质或定义可得. 试题解析:证明:(1)连接EO ,∵四边形ABCD 为正方形, ∴O 为AC 的中点,∵E 是PC 的中点,∴OE 是APC ∆的中位线.∴//EO PA ,∵EO ⊂平面BDE ,PA ⊄平面BDE , ∴//PA 平面BDE .(2)∵PO ⊥平面ABCD ,BD ⊂平面ABCD , ∴PO BD ⊥,∵四边形ABCD 是正方形, ∴AC BD ⊥,∵PO AC O ⋂=,AC ⊂平面PAC ,PO ⊂平面PAC , ∴BD ⊥平面PAC .考点:线面平行与线面垂直的判断.23.(1)()()22111x y -+-=;(2)2x =和3460x y -+=. 【解析】 【分析】()1设圆C 的半径为r ,根据圆心坐标写出圆的标准方程,利用点到直线的距离公式求出圆心到直线l 的距离即为弦心距,然后根据垂径定理得到其垂足为弦的中点,由弦长的一半,圆心距及半径构成的直角三角形,根据勾股定理列出关于r 的方程,求出方程的解即可得到r 的值,从而确定圆C 的方程;()2当切线方程的斜率不存在时,显然得到2x =为圆的切线;当切线方程的斜率存在时,设出切线的斜率为k ,由p 的坐标和k 写出切线方程,利用点到直线的距离公式求出圆心到所设直线的距离d ,根据直线与圆相切,得到d 等于圆的半径,列出关于k 的方程,求出方程的解即可得到k 的值,从而确定出切线的方程,综上,得到所求圆的两条切线方程. 【详解】(1)设圆C 的标准方程为: ()()22211x y r -+-= (0)r > 圆心()1,1C 到直线10x y +-=的距离:2d ==,则222111222r d ⎛=+=+= ⎝⎭∴圆C 的标准方程: ()()22111x y -+-=(2)①当切线斜率不存在时,设切线: 2x =,此时满足直线与圆相切. ②当切线斜率存在时,设切线: ()32y k x -=-,即23y kx k =-+ 则圆心()1,1C 到直线230kx y k --+=的距离:1d ==解得: 43k =,即34k =则切线方程为: 3460x y -+=综上,切线方程为: 2x =和3460x y -+= 24.(1)见解析;(2)在棱PA 上存在点E 且E 满足2AEEP=时能使得面//BOE 面PCD ,证明见解析. 【解析】 【分析】(1)可证PD ⊥平面PAB ,从而得到要证明的面面垂直. (2)在棱PA 上存在点E 且E 满足2AEEP=时能使得面//BOE 面PCD , 利用面面平行的判断定理可证明该结论. 【详解】(1)因为90BAD ∠=︒,故BA AD ⊥又因为侧面PAD ⊥底面ABCD ,侧面PAD I 底面ABCD AD =,BA ⊂平面ABCD , 所以BA ⊥平面PAD .因为PD ⊂平面PAD ,故BA PD ⊥,又因为PA PD ⊥,PA AB A =I ,PA ⊂平面PAB ,AB Ì平面PAB , 所以PD ⊥平面PAB ,而PD ⊂平面PCD ,故平面PAB ⊥平面PCD . (2)在棱PA 上存在点E ,使得面//BOE 面PCD ,E 满足2AEEP=,证明如下: 因为2AEEP =,2AO OD =,所以DAE EP AO O =,故//OE PD .因为OE ⊄平面PCD ,PD ⊂平面PCD ,故//OE 平面PCD .因为//BC AD ,13OD AD BC ==,故//,OD BC OD BC =, 所以四边形BCDO 为平行四边形,故//BO CD ,因为BO ⊄平面PCD ,CD ⊂平面PCD ,故//BO 平面PCD .因为BO ⊂平面EOB ,EO ⊂平面EOB ,BO EO O ⋂=, 故面//BOE 面PCD .【点睛】本题考查面面垂直的证明和面面平行的探索,前者注意空间中三种垂直关系的转化,后者应根据题设条件得到动点满足的位置特征,然后再根据判定定理来证明,本题属于中档题. 25.(1)1a =±;(2)(1,2)Q ;350x y +-=. 【解析】 【分析】(1)由平行可知系数的关系为21a =,进而可求a 的值;(2)整理直线1l 方程可知()120a x y -+-=,由1020x y -=⎧⎨-=⎩可求得定点坐标.由分析知,当当(5,0)P -在直线上的射影为(1,2)Q 时,点P 到直线1l 距离最大,由1PQ l ⊥可求出1l 的斜率,结合已知的1l 的方程,可求出此时a 的值,进而可求出直线1l 的方程. 【详解】解:(1)12//l l Q ,21a ∴=,解得1a =±检验:当1a =时12:30:20l x y l x y +-=++=,符合12//l l 当1a =-时12:10:20l x y l x y -+=-+=,符合12//l l 综上:1a =±.(2)解:1:20l ax y a +--=Q 整理可得()120a x y -+-= ,由1020x y -=⎧⎨-=⎩ ,解得12x y =⎧⎨=⎩ ,所以定点(1,2)Q .则当(5,0)P -在直线上的射影为(1,2)Q 时,距离最大. 此时1PQ l ⊥ ,直线PQ 的斜率为201153PQ k -==+,则1l 的斜率113PQk k =-=- , 即3a -=-,解得3a =,此时直线1l 的方程为350x y +-=. 【点睛】本题考查了两点斜率的求解,考查了直线平行、垂直.本题的难点是分析何时点P 到直线1l 的距离最大.易错点是做第一问时,求出1a =± 后未检验.对于已知直线平行,根据系数关系求出参数值后,应带回直线方程进行验证. 26.(1)见解析(2)23【解析】 【分析】(1)连接BF ,证明四边形1BMD F 是平行四边形即可得出1//D M BF ,故1//MD 平面BEFD ;(2)根据M BDE E BDM V V --=求出M 到平面BEFD 的距离.【详解】解:(1)证明:连接BF , ∵111111111111////22D F A B D F A B BM A B BM A B ==,,,, ∴11//D F BM D F BM =,, ∴四边形1BMD F 是平行四边形, ∴1//D M BF ,又1D M ⊄平面BEFD ,BF ⊂平面BEFD , ∴1//MD 平面BEFD . (2)解:连接ED EM DM ,,, 则112122323E BDM V -=⨯⨯⨯⨯=,又3BD BE DE ======,∴222cos 2BD BE DE DBE BD BE +-∠==⋅,∴sin DBE ∠=∴13210BDE S =⨯=V , 设M 到平面BEFD 的距离为d ,则12333M BDE V d -=⨯⨯=, ∴23d =.即M 到平面BEFD 的距离为23.【点睛】本题考查了线面平行的判定,棱锥的体积计算,属于中档题.。
【压轴题】高中必修二数学下期中一模试卷(及答案)一、选择题1.已知,,,A B C D 是同一球面上的四个点,其中ABC ∆是正三角形,AD ⊥平面ABC ,26AD AB ==,则该球的体积为( )A .48πB .24πC .16πD .323π2.对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( )A .若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B .若//,a b b α⊂,则//a αC .若//,,,a b αβαγβγ==I I 则//a bD .若,,//,//a b a b ββαα⊂⊂,则//βα3.四棱锥P ABCD -的底面ABCD 为正方形,PA ⊥底面ABCD ,2AB =,72PA =,若该四棱锥的所有顶点都在同一球面上,则该球的表面积为( ) A .812πB .814πC .65πD .652π4.已知圆O :2224110x y x y ++--=,过点()1,0M 作两条相互垂直的弦AC 和BD ,那么四边形ABCD 的面积最大值为( )A .42B .24C .212D .65.在三棱锥P ABC -中,PA ⊥平面1202,2ABC BAC AP AB ∠=︒==,,,M 是线段BC 上一动点,线段PM 3P ABC -的外接球的表面积是( ) A .92π B .92πC .18πD .40π6.设有两条直线m ,n 和三个平面α,β,γ,给出下面四个命题: ①m αβ=I ,////n m n α⇒,//n β ②αβ⊥,m β⊥,//m m αα⊄⇒; ③//αβ,//m m αβ⊂⇒; ④αβ⊥,//αγβγ⊥⇒ 其中正确命题的个数是( ) A .1B .2C .3D .47.已知实数,x y 满足250x y ++=22x y +的最小值为( ) A 5B 10C .25D .2108.已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦,则||AB 等于( )A 3B .2C .23D .259.若方程21424x kx k +-=-+ 有两个相异的实根,则实数k 的取值范围是( ) A .13,34⎛⎤ ⎥⎝⎦B .13,34⎛⎫⎪⎝⎭C .53,124⎛⎫⎪⎝⎭D .53,124纟çúçú棼10.如图所示,在棱长为a 的正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 是侧面11CDD C 上的动点,且1//B F 面1A BE ,则F 在侧面11CDD C 上的轨迹的长度是( )A .aB .2aC .2aD .2a 11.如图在正方体中,点为线段的中点. 设点在线段上,直线与平面所成的角为,则的取值范围是( )A .B .C .D .12.已知平面αβ⊥且l αβ=I ,M 是平面α内一点,m ,n 是异于l 且不重合的两条直线,则下列说法中错误的是( ). A .若//m α且//m β,则//m l B .若m α⊥且n β⊥,则m n ⊥ C .若M m ∈且//m l ,则//m βD .若M m ∈且m l ⊥,则m β⊥二、填空题13.给出下面四个命题:①“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”; ②“直线//a 直线b ”的充要条件是“a 平行于b 所在的平面”; ③“直线a ,b 为异面直线”的充分不必要条件是“直线a ,b 不相交”;④“平面//α平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等”. 其中正确命题的序号是____________________14.已知直线40Ax By A +-=与圆O :2236x y +=交于M ,N 两点,则线段MN 中点G 的轨迹方程为______.15.已知正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的求面上,若PA ,PB ,PC 两两互相垂直,则球心到截面ABC 的距离为________.16.圆221x y +=上的点到直线34250x y +-=的距离的最小值是 .17.在一个密闭的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是 .18.底面边长为2的正三棱柱111ABC A B C -被不平行于底面的平面MNP 所截,其中3AM =,4BN =,5PC =,则多面体ABC MNP -体积为________19.正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上.若163P ABCDV -=,则球O 的体积是______. 20.已知四面体ABCD 的外接球球心O 在棱CD 上,AB=3,CD=2,则A 、B 两点在四面体ABCD 的外接球上的球面距离是________.三、解答题21.四棱锥P -ABCD 中,底面ABCD 是直角梯形,//AB CD ,90BCD ∠=︒,22AB AD DC ===.PAD △ 为正三角形,二面角P -AD -C 的大小为23π.(1)线段AD 的中点为M.求证:平面PMB ⊥平面ABCD ; (2)求直线BA 与平面P AD 所成角的正弦值. 22.如图,已知四棱锥的底面是菱形,平面,点为的中点.(1)求证:∥平面;(2)求证:.23.在平面直角坐标系xOy 中,直线2210x y +--=与圆C 相切,圆心C 的坐标为()2,1-(1)求圆C 的方程;(2)设直线y =x +m 与圆C 交于M 、N 两点. ①若22MN ≥,求m 的取值范围; ②若OM ⊥ON ,求m 的值. 24.求满足下列条件的直线方程:(1)经过两条直线23100x y -+=和3420x y +-=的交点,且平行于直线10x y -+=;(2)经过两条直线280x y +-=和210x y -+=的交点,且垂直于直线320x y --=. 25.如图,在三棱锥P ABC -中,PA ⊥平面ABC ,且2PA AB BC ===,2 2.AC =(1)证明:三棱锥P ABC -为鳖臑;(2)若D 为棱PB 的中点,求二面角D AC P --的余弦值.注:在《九章算术》中鳖臑是指四面皆为直角三角形的三棱锥.26.如图,在三棱柱111ABC A B C -中,1C C ⊥底面ABC ,AC BC ⊥,1AC BC CC ==,M 、N 分别是1A B 、11B C 的中点.(1)求证:MN ⊥平面1A BC ;(2)求直线1BC 和平面1A BC 所成角的大小.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ;在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组,解方程组求得R ,代入球的体积公式可得结果. 【详解】设O '为ABC ∆的外心,如下图所示:由球的性质可知,球心O 与O '连线垂直于平面ABC ,作OE AD ⊥于E 设球的半径为R ,OO x '=ABC ∆为等边三角形,且3AB = 3AO '∴=OO '⊥Q 平面ABC ,AD ⊥平面ABC ,OE AD ⊥ OO AE x '∴==,3OE AO '==在Rt POE ∆和Rt OO A ∆'中,由勾股定理得:22222OE PE O O O A R ''+=+=,即()222363x x R +-=+=解得:3x =,3R =∴球的体积为:343233V R ππ==本题正确选项:D 【点睛】本题考查棱锥外接球的体积求解问题,关键是能够确定棱锥外接球球心的位置,从而在直角三角形中利用勾股定理构造方程求得半径.2.C解析:C 【解析】 【分析】 【详解】 若由线面垂直的判定定理知,只有当和为相交线时,才有错误;若此时由线面平行的判定定理可知,只有当在平面外时,才有错误;由面面平行的性质定理:若两平面平行,第三个平面与他们都相交,则交线平行,可判断,若//αβ,a αγ⋂=,b βγ=I ,则//a b 为真命题, 正确;若此时由面面平行的判定定理可知,只有当、为相交线时,才有//,D βα错误. 故选C.考点:考查直线与直线,直线与平面,平面与平面的位置关系.3.B解析:B 【解析】 【分析】根据题意可知,该四棱锥的外接球即为其所在长方体的外接球,根据公式即可求得. 【详解】根据题意,为方便说明,在长方体中找出该四棱锥如图所示:由图可知在长方体中的四棱锥P ABCD -完全满足题意, 故该四棱锥的外接球即是长方体的外接球,故外接球半径222722294R ⎛⎫++ ⎪⎝⎭==, 故该球的表面积为28144S R ππ==.故选:B . 【点睛】本题考查四棱锥外接球的问题,关键的步骤是将问题转化为求长方体的外接球.4.B解析:B 【解析】 【分析】设圆心到AC ,BD 的距离为1d ,2d ,则222128d d MO +==,22121216162S AC BD d d =⋅=-⋅-,利用均值不等式得到最值. 【详解】 2224110x y x y ++--=,即()()221216x y ++-=,圆心为()1,2O -,半径4r =.()1,0M 在圆内,设圆心到AC ,BD 的距离为1d ,2d ,则222128d d MO +==.222222121211222161622S AC BD r d r d d d =⋅=⨯-⋅-=-⋅- 2212161624d d ≤-+-=,当22121616d d -=-,即122d d ==时等号成立.故选:B . 【点睛】本题考查了圆内四边形面积的最值,意在考查学生的计算计算能力和转化能力.5.C解析:C 【解析】 【分析】首先确定三角形ABC 为等腰三角形,进一步确定球的球心,再求出球的半径,最后确定球的表面积. 【详解】 解:如图所示:三棱锥P ABC -中,PA ⊥平面2,2ABC AP AB ==,,M 是线段BC 上一动点,线段PM 3 则:当AM BC ⊥时,线段PM 达到最小值, 由于:PA ⊥平面ABC ,所以:222PA AM PM +=, 解得:1AM =,所以:BM =, 则:60BAM ∠=︒, 由于:120BAC ∠=︒, 所以:60MAC ∠=︒ 则:ABC V 为等腰三角形.所以:BC =在ABC V 中,设外接圆的直径为24r ==,则:2r =,所以:外接球的半径R ==, 则:94182S ππ=⋅⋅=, 故选:C . 【点睛】本题考查的知识要点:三棱锥的外接球的球心的确定及球的表面积公式的应用.6.B解析:B 【解析】 【分析】根据直线与平面、平面与平面的位置关系的性质和定理,逐项判断,即可得到本题答案. 【详解】对于选项①,,//m n m αβ⋂=不能得出,////n n αβ,因为n 可能在α或β内,故①错误;对于选项②,由于,,m m αββα⊥⊥⊄,则根据直线与平面平行的判定,可得//m α,故②正确;对于选项③,由于//αβ,m α⊂,则根据面面平行的性质定理可得//m β,故③正确; 对于选项④,由于,αβαγ⊥⊥,则,βγ可能平行也可能相交,故④错误. 故选:B 【点睛】本题主要考查直线与平面、平面与平面的位置关系的性质和定理,考查学生的空间想象能力和推理判断能力.7.A解析:A 【解析】由题意知,22x y +表示点(,)x y 到坐标原点的距离, 又原点到直线250x y ++=的距离为225521d ==+,所以22x y +的距离的最小值为5,故选A.8.D解析:D 【解析】 【分析】求出圆的标准方程,确定最短弦的条件,利用弦长公式进行求解即可. 【详解】圆的标准方程为(x ﹣3)2+(y +1)2=10,则圆心坐标为C (3,﹣1),半径为 10, 过E 的最短弦满足E 恰好为C 在弦上垂足,则CE 22(32)[11]5=-+--=(), 则|AB |222(10)(5)25=-=, 故选D . 【点睛】本题主要考查圆的标准方程的求解,以及直线和圆相交的弦长问题,属于中档题.9.D解析:D 【解析】 【分析】由题意可得,曲线22(1)4(1)x y y +-=…与直线4(2)y k x -=-有2个交点,数形结合求得k 的范围. 【详解】如图所示,化简曲线得到22(1)4(1)x y y +-=…,表示以(0,1)为圆心,以2为半径的上半圆,直线化为4(2)y k x -=-,过定点(2,4)A ,设直线与半圆的切线为AD ,半圆的左端点为(2,1)B -,当AD AB k k k <„,直线与半圆有两个交点,AD 与半圆相切时,221k =+,解得512AD k =,4132(2)4AB k -==--,所以53,124k ⎛⎤∈ ⎥⎝⎦.故选:D 【点睛】本题考查直线与圆的位置关系,属于中档题.10.D解析:D 【解析】 【分析】设H ,I 分别为1CC 、11C D 边上的中点,由面面平行的性质可得F 落在线段HI 上,再求HI 的长度即可. 【详解】解:设G ,H ,I 分别为CD 、1CC 、11C D 边上的中点, 则ABEG 四点共面, 且平面1//A BGE 平面1B HI , 又1//B F Q 面1A BE ,F ∴落在线段HI 上,Q 正方体1111ABCD A B C D -中的棱长为a ,1122HI CD a ∴==,即F 在侧面11CDD C 上的轨迹的长度是2a . 故选D .【点睛】本题考查了面面平行的性质及动点的轨迹问题,属中档题.11.B解析:B 【解析】【分析】 【详解】设正方体的棱长为,则,所以,.又直线与平面所成的角小于等于,而为钝角,所以的范围为,选B.【考点定位】空间直线与平面所成的角.12.D解析:D 【解析】 【分析】根据已知条件和线面位置关系一一进行判断即可. 【详解】选项A :一条直线平行于两个相交平面,必平行于两个面交线,故A 正确; 选项B :垂直于两垂直面的两条直线相互垂直,故B 正确; 选项C :M m ∈且//m l 得m α⊂且//m β,故C 正确;选项D :M m ∈且m l ⊥不一定得到m α⊂,所以,m l 可以异面,不一定得到m β⊥. 故选:D . 【点睛】本题主要考查的是空间点、线、面的位置关系的判定,掌握线面、线线之间的判定定理和性质定理是解决本题的关键,是基础题.二、填空题13.①④【解析】【分析】利用直线与直线平面与平面间的位置关系及性质判断前后两个条件的推出关系利用充要条件的定义得结论【详解】解:对于①直线与平面垂直的定义是直线与平面内的所有直线垂直故①正确;对于②平行解析:①④ 【解析】 【分析】利用直线与直线、平面与平面间的位置关系及性质判断前后两个条件的推出关系,利用充要条件的定义得结论. 【详解】解:对于①直线与平面垂直的定义是直线与平面内的所有直线垂直,故①正确; 对于②,a 平行于b 所在的平面//a b ⇒或a 与b 异面,故②错; 对于③,直线a 、b 不相交⇒直线a ,b 异面或平行,故③错; 对于④,平面//α平面βα⇒内存在不共线三点到β的距离相等;α内存在不共线三点到β的距离相等⇒平面//α平面β或相交,故④正确故答案为:①④ 【点睛】本题考查直线与直线间的位置关系及性质;充要条件的判断.命题真假的判断,属于中档题.14.【解析】【分析】直线过定点设代入方程利用点差法计算得到答案【详解】直线过定点设则两式相减得到即故整理得到:故答案为:【点睛】本题考查了轨迹方程意在考查学生对于点差法的理解和掌握 解析:()2224x y -+=【解析】 【分析】直线40Ax By A +-=过定点()4,0,设()()1122,,,M x y N x y ,(),G x y ,代入方程利用点差法计算得到答案. 【详解】直线40Ax By A +-=过定点()4,0,设()()1122,,,M x y N x y ,(),G x y ,则221136x y +=,222236x y +=,两式相减得到()()()()121212120x x x x y y y y +-++-=,即220x ky +=. 故2204y x y x +=-,整理得到:()2224x y -+=. 故答案为:()2224x y -+=. 【点睛】本题考查了轨迹方程,意在考查学生对于点差法的理解和掌握.15.【解析】正三棱锥P-ABC 可看作由正方体PADC-BEFG 截得如图所示PF 为三棱锥P-ABC 的外接球的直径且设正方体棱长为a 则由得所以因为球心到平面ABC 的距离为考点定位:本题考查三棱锥的体积与球的【解析】正三棱锥P-ABC 可看作由正方体PADC-BEFG 截得,如图所示,PF 为三棱锥P-ABC 的外接球的直径,且PF ABC ⊥平面,设正方体棱长为a ,则2312,2,a a AB AC BC =====12ABC S ∆=⨯=由P ABC B PAC V V --=,得111••222332ABC h S ∆=⨯⨯⨯⨯,所以3h =,因为球心到平面ABC 考点定位:本题考查三棱锥的体积与球的几何性质,意在考查考生作图的能力和空间想象能力16.4【解析】试题分析:圆的圆心为圆心到直线的距离为所以点到直线的距离的最小值是5-1=4考点:直线和圆的位置关系解析:4 【解析】试题分析:圆的圆心为()0,0,1r =,圆心到直线34250x y +-=的距离为5d ==,所以点到直线34250x y +-=的距离的最小值是5-1=4考点:直线和圆的位置关系17.【解析】【分析】【详解】试题分析:如图正方体ABCD-EFGH 此时若要使液面不为三角形则液面必须高于平面EHD 且低于平面AFC 而当平面EHD 平行水平面放置时若满足上述条件则任意转动该正方体液面的形状解析:15,66⎛⎫⎪⎝⎭【解析】 【分析】 【详解】试题分析:如图,正方体ABCD-EFGH ,此时若要使液面不为三角形,则液面必须高于平面EHD ,且低于平面AFC .而当平面EHD 平行水平面放置时,若满足上述条件,则任意转动该正方体,液面的形状都不可能是三角形.所以液体体积必须>三棱柱G-EHD 的体积16,并且<正方体ABCD-EFGH 体积-三棱柱B-AFC 体积15166-=考点:1.棱柱的结构特征;2.几何体的体积的求法18.【解析】【分析】将多面体分为四棱锥与三棱锥两部分相加求和即可【详解】如图将多面体分为四棱锥与三棱锥两部分其中四棱锥的高为为梯形则故多面体体积为故答案为:【点睛】本题主要考查了多面体体积的求解方法根据 解析:43【解析】 【分析】将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分相加求和即可. 【详解】如图, 将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分. 其中四棱锥N ACPM -的高为2sin 603⨯︒=.ACPM 为梯形. 则()352183332N ACPM V -+⨯=⨯⨯=.1234343N ABC V -⨯=⨯⨯=. 故多面体ABC MNP -体积为83434333+=故答案为:3【点睛】本题主要考查了多面体体积的求解方法,根据多面体的特征分为两个棱锥计算即可.属于中档题.19.【解析】【分析】正四棱锥底面的四个顶点在球的同一个大圆上则棱锥的高等于球的半径由此可由棱锥体积求得球的半径从而得球体积【详解】∵正四棱锥底面的四个顶点在球的同一个大圆上∴球心是正方形对角线交点是棱锥解析:323π【解析】 【分析】正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,则棱锥的高等于球的半径,由此可由棱锥体积求得球的半径,从而得球体积. 【详解】∵正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,∴球心O 是正方形ABCD 对角线交点,PO 是棱锥的高,设球半径为R ,则AB =,22)2ABCD S R ==,211162333P ABCD ABCD V S PO R R -==⨯⨯=,2R =, ∴3344322333V R πππ==⨯=球. 故答案为:323π. 【点睛】本题考查球的体积,考查正四棱锥与半球的截接问题.解题关键是确定球半径与正四棱锥中的线段长之间的关系.20.【解析】【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点且OA =OB =OC =OD 进而在△A0B 中利用余弦定理求得cos∠AOB 的值则∠AOB 可求进而根据弧长的计算方法求得答案【详解】解:球心 解析:23π【解析】 【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点,且OA =OB =OC =OD ,进而在△A 0B 中,利用余弦定理求得cos ∠AOB 的值,则∠AOB 可求,进而根据弧长的计算方法求得答案. 【详解】解:球心到四个顶点距离相等,故球心O 在CD 中点,则OA =OB =OC =OD =1,再由AB =A 0B 中,利用余弦定理cos ∠AOB 11312112+-==-⨯⨯,则∠AOB 23π=,则弧AB 23π=•123π=. 故答案为:23π. 【点睛】本题主要考查了余弦定理的应用、四面体外接球的性质等,考查了学生观察分析和基本的运算能力.三、解答题21.(1)证明见解析;(2)34. 【解析】 【分析】(1)直角梯形ABCD 中,过D 作DF ⊥AB 于F ,求解三角形可得ABD △为正三角形,又PAD △为正三角形,M 为线段AD 的中点,可得PM ⊥AD ,BM ⊥AD ,再由线面垂直的判定可得AD ⊥平面PBM ,从而得到平面PMB ⊥平面ABCD ;(2)在平面PMB 中,过B 作BO ⊥PM ,垂足为O ,则BO ⊥平面P AD ,连接AO ,则∠BAO 为直线BA 与平面P AD 所成角,然后求解三角形得答案. 【详解】(1)证明:过D 作DF ⊥AB 于F在Rt ADE ∆中,2,1AD AE ==,3BAD π∴∠=∴BAD V 和PAD △是正三角形, ∵M 是AD 的中点, ∴AD MB ⊥,AD MP ⊥, 又∵MB MP M ⋂=, ∴AD ⊥平面PMB , 又∵AD ⊂平面ABCD ∴平面PMB ⊥平面ABCD.(2)由(1)知PMB ∠是二面角P -AD -B 的平面角∴23PMB π∠=. 由(1)知AD ⊥平面PMB ∵AD ⊂平面P AD ∴平面PAD ⊥平面PBM∴过B 作平面P AD 的垂线,则垂足E 在PM 延长线上,∴3BME π∠=.连结AE ,则BAE ∠是AB 与平面P AD 所成的角,∴3BM =,∴32BE =,∴3sin 4BAE BE AB ∠== 【点睛】本题主要考查平面与平面垂直的判定,线面角的求法,二面角,考查空间想象能力与思维能力,属于中档题.22.(1)详见解析;(2)详见解析。
2020-2021高三数学下期中试卷及答案(1)一、选择题1.下列结论正确的是( ) A .若a b >,则22ac bc > B .若22a b >,则a b > C .若,0a b c ><,则a c b c +<+D .若a b <,则a b <2.若正项递增等比数列{}n a 满足()()()243510a a a a R λλ+-+-=∈,则89a a λ+的最小值为( ) A .94-B .94C .274D .274-3.已知x ,y 满足2303301x y x y y +-≤⎧⎪+-≥⎨⎪≤⎩,z =2x +y 的最大值为m ,若正数a ,b 满足a +b =m ,则14a b+的最小值为( ) A .3B .32C .2D .524.一个递增的等差数列{}n a ,前三项的和12312a a a ++=,且234,,1a a a +成等比数列,则数列{}n a 的公差为 ( ) A .2±B .3C .2D .15.在ABC ∆中,,,a b c 是角,,A B C 的对边,2a b =,3cos 5A =,则sinB =( ) A .25B .35C .45 D .856.设2z x y =+,其中,x y 满足2000x y x y y k +≥⎧⎪-≤⎨⎪≤≤⎩,若z 的最小值是12-,则z 的最大值为( ) A .9-B .12C .12-D .97.已知数列{}n a 的通项公式为()*21log N 2n n a n n +=∈+,设其前n 项和为n S ,则使5n S <-成立的自然数n ( )A .有最小值63B .有最大值63C .有最小值31D .有最大值318.设函数是定义在上的单调函数,且对于任意正数有,已知,若一个各项均为正数的数列满足,其中是数列的前项和,则数列中第18项( )A .B .9C .18D .369.在等差数列{}n a 中,351024a a a ++=,则此数列的前13项的和等于( ) A .16B .26C .8D .1310.在等差数列{}n a 中,如果123440,60a a a a +=+=,那么78a a +=( ) A .95B .100C .135D .8011.若不等式1221m x x≤+-在()0,1x ∈时恒成立,则实数m 的最大值为( ) A .9B .92C .5D .5212.已知等差数列{}n a 的前n 项和为n S ,若341118a a a ++=则11S =( ) A .9B .22C .36D .66二、填空题13.已知,x y 满足约束条件420y x x y y ≤⎧⎪+≤⎨⎪+≥⎩,则2z x y =+的最大值为__________.14.若变量,x y 满足约束条件12,{20,20,x y x y x y +≤-≥-≤ 则z y x =-的最小值为_________.15.已知函数()2xf x =,等差数列{}n a 的公差为2,若()2468104f a a a a a ++++=,则()()()()212310log f a f a f a f a ⋅⋅⋅⋅=⎡⎤⎣⎦L ___________.16.已知a b c R ∈、、,c 为实常数,则不等式的性质“a b a c b c >⇐+>+”可以用一个函数在R 上的单调性来解析,这个函数的解析式是()f x =_________17.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c ,tan tan 2tan b B b A c B +=-,且8a =,73b c +=ABC V 的面积为______.18.已知等差数列{}n a 的前n 项n S 有最大值,且871a a <-,则当0n S <时n 的最小值为________.19.已知等比数列{a n }的前n 项和为S n ,若a 3=32,S 3=92,则a 1的值为________. 20.如图所示,在平面四边形ABCD 中,2AB =,3BC =,AB AD ⊥,AC CD ⊥,3AD AC =,则AC =__________.三、解答题21.在ABC ∆中,,,a b c 分别是角,,A B C 所对的边,且2sin 3tan c B a A =.(1)求222b c a+的值; (2)若2a =,求ABC ∆面积的最大值.22.已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边,且2222cos cos b c a ac C c A +-=+.(1)求A ;(2)在ABC ∆中,3BC =D 为边AC 的中点,E 为AB 边上一点,且DE AC ⊥,62DE =,求ABC ∆的面积. 23.在△ABC 中,已知AC =4,BC =3,cosB =-14. (1)求sin A 的值; (2)求·BA BC u u u v u u u v的值.24.已知数列{}n a 的前n 项和22n n nS +=.(1)求数列{}n a 通项公式; (2)令11n n n b a a +=,求数列{}n b 的前n 项和n T . 25.等比数列{}n a 中,1752,4a a a ==.(Ⅰ)求{}n a 的通项公式;(Ⅱ)记n S 为{}n a 的前n 项和.若126m S =,求m . 26.等差数列{}n a 中,24a =,4715a a +=. (1)求数列{}n a 的通项公式; (2)设22n a n b n -=+,求12310b b b b +++⋅⋅⋅+的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】选项A 中,当c=0时不符,所以A 错.选项B 中,当2,1a b =-=-时,符合22a b >,不满足a b >,B 错.选项C 中, a c b c +>+,所以C 错.选项D中,因为0≤<,由不等式的平方法则,22<,即a b <.选D.2.C解析:C 【解析】设等比数列的公比为q (q >1),1+(a 2-a 4)+λ(a 3-a 5)=0,可得λ=24531a a a a +--则a 8+λa 9=a 8+666929498385888222535353111a a a a a a a a a q q q a a a a a a a q a a q q --+=++=+-=------令21t q =-,(t >0),q 2=t+1,则设f (t )=()()()()()()3232622213112111t t t t t t q f t q t t t++-+-+=='=∴-当t >12时,f (t )递增; 当0<t <12时,f (t )递减. 可得t=12处,此时f (t )取得最小值,且为274,则a 8+λa 9的最小值为274; 故选C.3.B解析:B【解析】 【分析】作出可行域,求出m ,然后用“1”的代换配凑出基本不等式的定值,从而用基本不等式求得最小值. 【详解】作出可行域,如图ABC ∆内部(含边界),作直线:20l x y +=,平移该直线,当直线l 过点(3,0)A 时,2x y +取得最大值6,所以6m =.1411414143()()(5)(52)6662b a b a a b a b a b a b a b +=++=++≥+⨯=,当且仅当4b a a b =,即12,33a b ==时等号成立,即14a b +的最小值为32. 故选:B. 【点睛】本题考查简单的线性规划,考查用基本不等式求最值,解题关键是用“1”的代换凑配出基本不等式的定值,从而用基本不等式求得最小值.4.C解析:C 【解析】 【分析】 【详解】解:∵234,,1a a a +成等比数列, ∴,∵数列{}n a 为递增的等差数列,设公差为d , ∴,即,又数列{}n a 前三项的和,∴,即,即d =2或d =−2(舍去), 则公差d =2. 故选:C .5.A解析:A 【解析】试题分析:由3cos 5A =得,又2a b =,由正弦定理可得sin B =.考点:同角关系式、正弦定理.6.B解析:B 【解析】 【分析】作出不等式对应的可行域,当目标函数过点A 时,z 取最小值,即min 12z =-,可求得k 的值,当目标函数过点B 时,z 取最大值,即可求出答案. 【详解】作出不等式对应的可行域,如下图阴影部分,目标函数可化为2y x z =-+,联立20x y y k +=⎧⎨=⎩,可得()2,A k k -,当目标函数过点A 时,z 取最小值,则()2212k k ⨯-+=-,解得4k =,联立0x y y k-=⎧⎨=⎩,可得(),B k k ,即()4,4B ,当目标函数过点B 时,z 取最大值,max 24412z =⨯+=.故选:B.【点睛】本题考查线性规划,考查学生的计算求解能力,利用数形结合方法是解决本题的关键,属于基础题.7.A解析:A 【解析】 【分析】利用对数运算,求得n S ,由此解不等式5n S <-,求得n 的最小值. 【详解】 ∵()*21log N 2n n a n n +=∈+, ∴12322223log log log 3142n n S a a a a n n =++++⋯+=++⋯++222312log log 3422n n n +⎛⎫=⨯⨯⋯⨯= ⎪++⎝⎭, 又因为21215log 6232232n S n n <-=⇒<⇒>+, 故使5n S <-成立的正整数n 有最小值:63. 故选:A. 【点睛】本小题主要考查对数运算和数列求和,属于基础题.8.C解析:C 【解析】∵f (S n )=f (a n )+f (a n +1)-1=f[a n (a n +1)]∵函数f (x )是定义域在(0,+∞)上的单调函数,数列{a n }各项为正数∴S n =a n (a n +1)①当n=1时,可得a 1=1;当n≥2时,S n-1=a n-1(a n-1+1)②,①-②可得a n = a n (a n +1)-a n-1(a n-1+1)∴(a n +a n-1)(a n -a n-1-1)=0∵a n >0,∴a n -a n-1-1=0即a n -a n-1=1∴数列{a n }为等差数列,a 1=1,d=1;∴a n =1+(n-1)×1=n 即a n =n 所以故选C9.D解析:D 【解析】 【详解】试题分析:∵351024a a a ++=,∴410224a a +=,∴4102a a +=,∴1134101313()13()1322a a a a S ++===,故选D. 考点:等差数列的通项公式、前n 项和公式.10.B解析:B 【解析】 【分析】根据等差数列{}n a 性质可知:1234a a a a ++,,56a a +,78a a +构成新的等差数列,然后求出结果 【详解】由等差数列的性质可知:1234a a a a ++,,56a a +,78a a +构成新的等差数列,()()()()781234124140320100a a a a a a a a ⎡⎤∴+=++-+-+=+⨯=⎣⎦故选B 【点睛】本题主要考查了等差数列的性质运用,等差数列中连续的、等长的、间隔相等的几项的和依然成等差,即可计算出结果。
【典型题】高中必修二数学下期中模拟试题(含答案)一、选择题1.圆224470x y x y +--+=上的动点P 到直线0x y +=的最小距离为( )A .1B .1C .D2.已知(2,0)A -,(0,2)B ,实数k 是常数,M ,N 是圆220x y kx ++=上两个不同点,P 是圆220x y kx ++=上的动点,如果M ,N 关于直线10x y --=对称,则PAB ∆面积的最大值是( )A .3B .4C .6D .3+3.若圆C:222430x y x y ++-+=关于直线260ax by ++=对称,则由点(,)a b 向圆所作的切线长的最小值是( ) A .2B .4C .3D .64.若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A .9,34⎛⎫⎪⎝⎭B .9,34⎡⎫⎪⎢⎣⎭C .()1,3D .()2,35.已知点(),P x y 是直线()400kx y k ++=>上一动点,,PA PB 是圆22:20C x y y +-=的两条切线,切点分别为,A B ,若四边形PACB 的面积最小值为2,则k 的值为( )A .3B .2C .D .26.设α表示平面,a ,b 表示直线,给出下列四个命题:①a α//,a b b α⊥⇒//; ②a b //,a b αα⊥⇒⊥;③a α⊥,a b b α⊥⇒⊂;④a α⊥,b a b α⊥⇒//,其中正确命题的序号是( ) A .①②B .②④C .③④D .①③7.已知正四面体ABCD 中,M 为棱AD 的中点,设P 是BCM ∆(含边界)内的点,若点P 到平面ABC ,平面ACD ,平面ABD 的距离相等,则符合条件的点P ( ) A .仅有一个B .有有限多个C .有无限多个D .不存在8.已知三棱锥S ABC -的每个顶点都在球O 的表面上,ABC ∆是边长为角形,SA ⊥平面ABC ,且SB 与平面ABC 所成的角为6π,则球O 的表面积为( ) A .20πB .40πC .80πD .160π9.已知三条直线,,m n l ,三个平面,,αβγ,下列四个命题中,正确的是( ) A .||αγαββγ⊥⎫⇒⎬⊥⎭B .||m l l m ββ⎫⇒⊥⎬⊥⎭C .||||||m m n n γγ⎫⇒⎬⎭D .||m m n n γγ⊥⎫⇒⎬⊥⎭10.矩形ABCD 中,4AB =,3BC =,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )A .12512π B .1259π C .1256π D .1253π 11.已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦,则||AB 等于( )A .3B .22C .23D .2512.已知平面αβ⊥且l αβ=,M 是平面α内一点,m ,n 是异于l 且不重合的两条直线,则下列说法中错误的是( ). A .若//m α且//m β,则//m l B .若m α⊥且n β⊥,则m n ⊥ C .若M m ∈且//m l ,则//m βD .若M m ∈且m l ⊥,则m β⊥二、填空题13.已知三棱锥P ABC -中,侧面PAC ⊥底面ABC ,90BAC ∠=︒,4AB AC ==,23PA PC ==,则三棱锥P ABC -外接球的半径为______.14.在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,3AB =,4BC =,5PA =,则三棱锥P ABC -的外接球的表面积为__________15.已知菱形ABCD 中,2AB =,120A ∠=,沿对角线BD 将ABD △折起,使二面角A BD C --为120,则点A 到BCD 所在平面的距离等于 .16.若过点(8,1)P 的直线与双曲线2244x y -=相交于A ,B 两点,且P 是线段AB 的中点,则直线AB 的方程为________.17.在平面直角坐标xOy 系中,设将椭圆()2222110y x a a a +=>-绕它的左焦点旋转一周所覆盖的区域为D ,P 为区域D 内的任一点,射线()02x y x =≥-上的点为Q ,若PQ 的最小值为a ,则实数a 的取值为_____.18.已知圆O :224x y +=, 则圆O 在点(1,3)A 处的切线的方程是___________. 19.如图,在△ABC 中,AB=BC=2,∠ABC=120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD=DA ,PB=BA ,则四面体PBCD 的体积的最大值是 .20.已知直线1:1l y x =-上有两个点11(,)A x y 和22(,)B x y , 且12,x x 为一元二次方程2610x x -+=的两个根, 则过点,A B 且和直线2:1l x =-相切的圆的方程为______________.三、解答题21.在梯形ABCD 中,//AD BC ,AC BD ⊥于点O ,2BC AD =,9AC =,将ABD ∆沿着BD 折起,使得A 点到P 点的位置,35PC =.(Ⅰ)求证:平面PBD ⊥平面BCD ;(Ⅱ)M 为BC 上一点,且2BM CM =,求证://OM 平面PCD .22.如图,四棱锥P ABCD -,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明://PB 平面AEC ;(2)设二面角D AE C --为60°,1AP =,3AD =,求直线AC 与平面ECD 所成角的正弦值.23.如图,在ABC 中AC BC ⊥且点O 为AB 的中点,矩形ABEF 所在的平面与平面ABC 互相垂直.(1)设EC 的中点为M ,求证://OM 平面ACF ; (2)求证:AC ⊥平面CBE24.已知圆C 的方程:22240x y x y m +--+=. (1)求m 的取值范围;(2)若圆C 与直线l :240x y +-=相交于M ,N 两点,且45||5MN =,求m 的值.25.如图,在梯形ABCD 中,AB CD ∥,1AD DC BC ===,60ABC ∠=︒,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,1CF =.(1)证明:BC ⊥平面ACFE ;(2)设点M 在线段EF 上运动,平面MAB 与平面FCB 所成锐二面角为θ,求cos θ的取值范围.26.如图,四棱锥P ABCD -中,AP ⊥平面1,//,,,2PCD AD BC AB BC AD E F ==分别为线段,AD PC 的中点.(1)求证://AP 平面BEF ; (2)求证:平面BEF ⊥平面PAC【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】先求出圆心到直线0x y +=的距离,根据距离的最小值为d r -,即可求解. 【详解】由圆的一般方程可得22(2)(2)1x y -+-=,圆心到直线的距离d ==所以圆上的点到直线的距离的最小值为1. 故选B. 【点睛】本题主要考查了点到直线的距离,圆的方程,属于中档题.2.D解析:D 【解析】 【分析】根据圆上两点,M N 关于直线10x y --=对称,可知圆心在该直线上,从而求出圆心坐标与半径,要使得PAB ∆面积最大,则要使得圆上点P 到直线AB 的距离最大,所以高最大为12+,PAB S ∆最大值为3 【详解】由题意,圆x 2+y 2+kx=0的圆心(-2k,0)在直线x-y-1=0上, ∴-2k-1=0,∴k=-2,∴圆x 2+y 2+kx=0的圆心坐标为(1,0),半径为1 ∵A (-2,0),B (0,2), ∴直线AB 的方程为2x -+2y=1,即x-y+2=0∴圆心到直线AB 的距离为2.∴△PAB 面积的最大值是11||1)22AB =⨯= 故选D . 【点睛】主要考查了与圆有关的最值问题,属于中档题.该题涉及到圆上动点到定直线(圆与直线相离)的最大距离.而圆上动点到定直线的最小距离为圆心到直线距离减去半径,最大距离为圆心到直线距离加上半径.3.B解析:B 【解析】试题分析:222430x y x y ++-+=即22(1)(2)2x y ++-=,由已知,直线260ax by ++=过圆心(1,2)C -,即2260,3a b b a -++==-,由平面几何知识知,为使由点(,)a b 向圆所作的切线长的最小,只需圆心(1,2)C -与直线30x y --=2123()242----=,故选B .考点:圆的几何性质,点到直线距离公式.4.B解析:B 【解析】 【分析】利用函数的单调性,判断指数函数底数的取值范围,以及一次函数的单调性,及端点处函数值的大小关系列出不等式求解即可 【详解】解:函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增,()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭. 故选:B . 【点睛】本题考查分段函数的应用,指数函数的性质,考查学生的计算能力,属于中档题.5.D解析:D 【解析】 【分析】当且仅当PC 垂直于()400kx y k ++=>时,四边形PACB 的面积最小,求出PC 后可得最小面积,从而可求k 的值. 【详解】圆C 方程为()2211x y +-=,圆心()0,1C ,半径为1.因为PA ,PB 为切线,221PC PA ∴=+且1=2122PACB S PA PA ⨯⨯⨯==四边形.∴当PA 最小时,PACB S 四边形最小,此时PC 最小且PC 垂直于()400kx y k ++=>. 又min 21PC k =+,222221+1k ⎛⎫∴=⎪+⎝⎭,2k ∴=,故选D. 【点睛】圆中的最值问题,往往可以转化圆心到几何对象的距离的最值来处理,这类问题属于中档题.6.B解析:B 【解析】 【分析】 【详解】①a ∥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故①错误; ②若a ∥b ,a ⊥α,由直线与平面垂直和判定定理得b ⊥α,故②正确; ③a ⊥α,a ⊥b ⇒b 与α平行,相交或b ⊂α,故③错误; ④若a ⊥α,b ⊥α,则由直线与平面垂直的性质得a ∥b ,故④正确. 故选B .7.A解析:A 【解析】 【分析】根据正四面体的对称性分析到平面ABC ,平面ACD ,平面ABD 的距离相等的点的轨迹,与BCM ∆所在平面的公共部分即符合条件的点P . 【详解】在正四面体ABCD 中,取正三角形BCD 中心O ,连接AO ,根据正四面体的对称性,线段AO 上任一点到平面ABC ,平面ACD ,平面ABD 的距离相等,到平面ABC ,平面ACD ,平面ABD 的距离相等的点都在AO 所在直线上,AO 与BCM ∆所在平面相交且交于BCM ∆内部,所以符合题意的点P 只有唯一一个. 故选:A 【点睛】此题考查正四面体的几何特征,对称性,根据几何特征解决点到平面距离问题,考查空间想象能力.8.C解析:C 【解析】 【分析】根据线面夹角得到4SA =,计算ABC ∆的外接圆半径为42sin ar A==,2222SA R r ⎛⎫=+ ⎪⎝⎭,解得答案.【详解】SA ⊥平面ABC ,则SB 与平面ABC 所成的角为6SBA π∠=,故4SA =. ABC ∆的外接圆半径为42sin ar A==,设球O 的半径为R ,则2222SA R r ⎛⎫=+ ⎪⎝⎭,解得R =O 的表面积为2480R ππ=. 故选:C . 【点睛】本题考查了三棱锥的外接球问题,意在考查学生的计算能力和空间想象能力.9.D解析:D 【解析】试题分析:A.}r rααββ⊥⇒⊥不正确,以墙角为例,,αβ可能相交;B.}m l l m ββ⇒⊥⊥不正确,,l β有可能平行;C.}m rm n n r⇒不正确,m,n 可能平行、相交、异面;故选D 。
2020-2021宜兴市万石中学高中必修二数学下期中模拟试题含答案一、选择题1.水平放置的ABC V 的斜二测直观图如图所示,若112A C =,111A B C △的面积为22,则AB 的长为( )A 2B .17C .2D .82.已知,,,A B C D 是同一球面上的四个点,其中ABC ∆是正三角形,AD ⊥平面ABC ,26AD AB ==,则该球的体积为( )A .48πB .24πC .16πD .33.已知直线m 、n 及平面α,其中m ∥n ,那么在平面α内到两条直线m 、n 距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集。
其中正确的是( )A .(1)(2)(3)B .(1)(4)C .(1)(2)(4)D .(2)(4) 4.已知m 和n 是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m ⊥β的是( )A .α⊥β,且m ⊂αB .m ⊥n ,且n ∥βC .α⊥β,且m ∥αD .m ∥n ,且n ⊥β 5.已知直线20ax y a +-+=在两坐标轴上的截距相等,则实数(a = )A .1B .1-C .2-或1D .2或1 6.正方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别是AD ,DD 1的中点,AB =4,则过B ,E ,F 的平面截该正方体所得的截面周长为( )A .25B .25C .25D .25 7.若圆22240x y x y +--=的圆心到直线0x y a -+=的距离为22,则a 的值为( ) A .-2或2 B .12或32 C .2或0D .-2或0 8.若方程21424x kx k -=-+ 有两个相异的实根,则实数k 的取值范围是( ) A .13,34⎛⎤ ⎥⎝⎦ B .13,34⎛⎫ ⎪⎝⎭ C .53,124⎛⎫ ⎪⎝⎭ D .53,124纟çúçú棼 9.如图,平面四边形ABCD 中,1AB AD CD ===,2BD =,BD CD ⊥,将其沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,若四面体A BCD '-的顶点在同一个球面上,则该球的表面积为( )A .3πB .3πC .4πD .3π 10.已知ABC V 的三个顶点在以O 为球心的球面上,且2AB =,4AC =,25BC =,三棱锥O ABC -的体积为43,则球O 的表面积为( ) A .22π B .743π C .24π D .36π11.如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( )A .20+3πB .24+3πC .20+4πD .24+4π12.如图,网格纸上小正方形的边长为1,粗实(虚)线画出的是某多面体的三视图,则该多面体的体积为( )A .64B .643C .16D .163二、填空题13.设P ,A ,B ,C 是球O 表面上的四个点,PA ,PB ,PC 两两垂直,且1PA PB PC ===,则球O 的表面积为____________.14.如图,在ABC ∆中,6AB BC ==90ABC ∠=o ,点D 为AC 的中点,将ABD △沿BD 折起到的位置,使PC PD =,连接PC ,得到三棱锥P BCD -,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是__________.15.已知平面α,β,γ是空间中三个不同的平面,直线l ,m 是空间中两条不同的直线,若α⊥γ,γ∩α=m ,γ∩β=l ,l⊥m,则①m⊥β;②l⊥α;③β⊥γ;④α⊥β.由上述条件可推出的结论有________(请将你认为正确的结论的序号都填上).16.如图,在ABC V 中,AB BC ⊥,SA ⊥平面ABC ,DE 垂直平分SC ,且分别交AC ,SC 于点D ,E ,又SA AB =,SB BC =,则二面角E BD C --的大小为_______________.17.圆台的两个底面面积之比为4:9,母线与底面的夹角是60°,轴截面的面积为1803,则圆台的侧面积为_____.18.在棱长为1的正方体1111ABCD A B C D -中,M 是1BB 的中点,直线1D M 与平面ABCD 交于点N ,则线段AN 的长度为________19.已知双曲线的半焦距为,过右焦点且斜率为1的直线与双曲线的右支交于两点,若抛物线的准线被双曲线截得的弦长是(为双曲线的离心率),则的值为__________.20.如图,在体积为1V 的圆柱中挖去以圆柱上下底面为底面、共顶点的两个圆锥,剩余部分的体积为2V ,则21V V =__________.三、解答题21.已知圆22:(1)(2)25C x y -+-=,直线:(21)(1)74l m x m y m +++--=0,(m ∈R ).(1)证明:无论m 取何值,直线l 过定点;(2)求直线l 被圆C 截得的弦长最短时m 的值及最短弦长.22.如图,梯形ABCD 中,AB ∥CD ,,E F 是线段AB 上的两点,且DE AB ⊥,CF AB ⊥,12AB =,5AD =,42BC =,4DE =.现将△ADE ,△CFB 分别沿DE ,CF 折起,使两点,A B 重合于点G ,得到多面体CDEFG (1)求证:平面DEG ⊥平面CFG ;(2)求多面体CDEFG 的体积23.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面ABCD ,PA AB =,AC 与BD 交于点O ,E ,F 分别为AB ,PC 的中点.(Ⅰ)求证:EF ∥平面PAD ;(Ⅱ)求证:AF ⊥平面POD .24.已知圆22:(2)(3)4C x y -+-=外有一点()41-,,过点P 作直线l . (1)当直线l 与圆C 相切时,求直线l 的方程;(2)当直线l 的倾斜角为135︒时,求直线l 被圆C 所截得的弦长.25.在直角坐标系中,射线OA: x -y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA 、OB 于A 、B 两点.(1)当AB 中点为P 时,求直线AB 的方程;(2)当AB 中点在直线12y x =上时,求直线AB 的方程.26.已知直线1:20l ax y a +--=,22:0l x ay ++=,点(5,0)P -(1)当12//l l 时,求a 的值;(2)求直线1l 所过的定点Q ,并求当点P 到直线1l 的距离最大时直线1l 的方程.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】依题意由111A B C △的面积为114B C =,所以8BC =,2AC =,根据勾股定理即可求AB .【详解】依题意,因为111A B C △的面积为所以11111sin 452AC B C ︒=⨯⋅=11122B C ⨯⨯,解得114B C =, 所以8BC =,2AC =,又因为AC BC ⊥,由勾股定理得:AB ====故选B .【点睛】本题考查直观图还原几何图形,属于简单题. 利用斜二测画法作直观图,主要注意两点:一是与x 轴平行的线段仍然与x '轴平行且相等;二是与y 轴平行的线段仍然与y '轴平行且长度减半. 2.D解析:D【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ;在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组,解方程组求得R ,代入球的体积公式可得结果.【详解】设O '为ABC ∆的外心,如下图所示:由球的性质可知,球心O 与O '连线垂直于平面ABC ,作OE AD ⊥于E设球的半径为R ,OO x '=ABC ∆为等边三角形,且3AB = 3AO '∴=OO '⊥Q 平面ABC ,AD ⊥平面ABC ,OE AD ⊥OO AE x '∴==,3OE AO '==在Rt POE ∆和Rt OO A ∆'中,由勾股定理得:22222OE PE O O O A R ''+=+=,即()222363x x R +-=+= 解得:3x =,3R =∴球的体积为:343233V R ππ== 本题正确选项:D【点睛】本题考查棱锥外接球的体积求解问题,关键是能够确定棱锥外接球球心的位置,从而在直角三角形中利用勾股定理构造方程求得半径.3.C解析:C【解析】【分析】根据题意,对每一个选项进行逐一判定,不正确的只需举出反例,正确的作出证明,即可得到答案.【详解】如图(1)所示,在平面内不可能由符合题的点;如图(2),直线,a b 到已知平面的距离相等且所在平面与已知平面垂直,则已知平面为符合题意的点;如图(3),直线,a b 所在平面与已知平面平行,则符合题意的点为一条直线, 综上可知(1)(2)(4)是正确的,故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系,其中熟记空间中点、线、面的位置关系是解答此类问题的关键,着重考查了空间想象能力,以及推理与论证能力,属于基础题. 4.D解析:D【解析】【分析】根据所给条件,分别进行分析判断,即可得出正确答案.【详解】解:αβ⊥且m α⊂⇒m β⊂或//m β或m 与β相交,故A 不成立;m n ⊥且//n β⇒m β⊂或//m β或m 与β相交,故B 不成立;αβ⊥且//m α⇒m β⊂或//m β或m 与β相交,故C 不成立;//m n 且n β⊥⇒m β⊥,故D 成立;故选:D【点睛】本题考查直线与平面的位置关系,线面垂直判定,属于基础题.5.D解析:D【解析】【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时,求出对应a 的值,即可得到答案.【详解】由题意,当2a 0-+=,即a 2=时,直线ax y 2a 0+-+=化为2x y 0+=, 此时直线在两坐标轴上的截距都为0,满足题意;当2a 0-+≠,即a 2≠时,直线ax y 2a 0+-+=化为122x y a a a+=--, 由直线在两坐标轴上的截距相等,可得2a 2a a-=-,解得a 1=; 综上所述,实数a 2=或a 1=.故选:D .【点睛】本题主要考查了直线方程的应用,以及直线在坐标轴上的截距的应用,其中解答中熟记直线在坐标轴上的截距定义,合理分类讨论求解是解答的关键,着重考查了运算与求解能力,属于基础题.6.A解析:A【解析】【分析】利用线面平行的判定与性质证明直线1BC 为过直线EF 且过点B 的平面与平面11BCC B 的交线,从而证得1,,,B E F C 四点共面,然后在正方体中求等腰梯形1BEFC 的周长即可.【详解】作图如下:因为,E F 是棱1,AD DD 的中点,所以11////EF AD BC ,因为EF ⊄平面11BCC B ,1BC ⊂平面11BCC B ,所以//EF 平面11BCC B ,由线面平行的性质定理知,过直线EF 且过点B 的平面与平面11BCC B 的交线l 平行于直线EF ,结合图形知,l 即为直线1BC ,过B ,E ,F 的平面截该正方体所得的截面即为等腰梯形1BEFC ,因为正方体的棱长AB =4, 所以1122,25,42EF BE C F BC ====所以所求截面的周长为2+5故选:A【点睛】本题主要考查多面体的截面问题和线面平行的判定定理和性质定理;重点考查学生的空间想象能力;属于中档题.7.C解析:C【解析】【分析】把圆的方程化为标准方程,找出圆心坐标,根据点到直线的距离公式列出关于a 的方程,求出方程的解得到a 的值即可.【详解】把圆的方程化为标准式为:22(1)(2)5x y -+-=,所以圆心坐标为(1,2).则圆心到直线0x y a -+=的距离22221(1)d ==+-, 即11a -=,化简得11a -=或11a -=-,解得:2a =或0a =.所以a 的值为0或2.故选C.【点睛】本题考查学生会将圆的一般式方程化为标准式方程,灵活运用点到直线的距离公式化简求值.8.D解析:D【解析】【分析】由题意可得,曲线22(1)4(1)x y y +-=…与直线4(2)y k x -=-有2个交点,数形结合求得k 的范围.【详解】如图所示,化简曲线得到22(1)4(1)x y y +-=…,表示以(0,1)为圆心,以2为半径的上半圆,直线化为4(2)y k x -=-,过定点(2,4)A ,设直线与半圆的切线为AD ,半圆的左端点为(2,1)B -,当AD AB k k k <…,直线与半圆有两个交点,AD 221k =+,解得512AD k =,4132(2)4AB k -==--,所以53,124k ⎛⎤∈ ⎥⎝⎦. 故选:D【点睛】本题考查直线与圆的位置关系,属于中档题.9.A解析:A【解析】【分析】设BC 的中点是E ,连接DE ,由四面体A′BCD 的特征可知,DE 即为球体的半径.【详解】设BC 的中点是E ,连接DE ,A′E,因为AB =AD =1,BD 由勾股定理得:BA⊥AD又因为BD⊥CD,即三角形BCD 为直角三角形所以DE 为球体的半径2DE =243S ππ== 故选A【点睛】 求解球体的表面积、体积的问题,其实质是求球体的半径,解题的关键是构造关于球体半径R 的方程式,构造常用的方法是构造直角三角形,再利用勾股定理建立关于半径R 的方程.10.C解析:C【解析】【分析】由已知可得三角形ABC 为直角三角形,斜边BC 的中点O '就是ABC V 的外接圆圆心,利用三棱锥O ABC -的体积,求出O 到底面的距离,可求出球的半径,然后代入球的表面积公式求解.【详解】在ABC V 中,∵2AB =,4AC =,BC =AB AC ⊥,则斜边BC 的中点O '就是ABC V 的外接圆的圆心,∵三棱锥O ABC -的体积为43,11424323OO '⨯⨯⨯⨯=,解得1OO '=,221(5)6R =+=, 球O 的表面积为2424R ππ=. 故选C .【点睛】本题考查球的表面积的求法,考查锥体体积公式的应用,考查空间想象能力和计算能力,属于基础题.11.A解析:A 【解析】 【分析】 【详解】由几何体的三视图分析可知,该几何体上部为边长为2的正方体, 下部为底面半径为1、高为2的半圆柱体, 故该几何体的表面积是20+3π,故选A.考点:1、几何体的三视图;2、几何体的表面积.12.D解析:D 【解析】根据三视图知几何体是:三棱锥D ABC -为棱长为4的正方体一部分,直观图如图所示:B 是棱的中点,由正方体的性质得,CD ⊥平面,ABC ABC ∆的面积12442S =⨯⨯=,所以该多面体的体积1164433V =⨯⨯=,故选D.二、填空题13.【解析】【分析】利用条件两两垂直且把三棱锥扩展为正方体球的直径即是正方体的体对角线长由球的表面积公式求解【详解】先把三棱锥扩展为正方体则正方体的体对角线的长为所以球的半径为所以球的表面积为【点睛】本 解析:3π【解析】 【分析】利用条件PA ,PB ,PC 两两垂直,且1PA PB PC ===把三棱锥P ABC -扩展为正方体,球的直径即是正方体的体对角线长,由球的表面积公式求解. 【详解】先把三棱锥P ABC -,所以球的半径为2,所以球的表面积为24π3π⨯=⎝⎭.【点睛】本题主要考查了球的体积公式:343V r π=球(其中r 为球的半径)及长方体的体对角线长公式:l =,,a b c 分别是长方体的长、宽、高).14.【解析】【分析】由题意得该三棱锥的面PCD 是边长为的正三角形且BD ⊥平面PCD 求出三棱锥P ﹣BDC 的外接球半径R =由此能求出该球的表面积【详解】由题意得该三棱锥的面PCD 是边长为的正三角形且BD ⊥平 解析:7π【解析】 【分析】由题意得该三棱锥的面PCD 的正三角形,且BD ⊥平面PCD ,求出三棱锥P﹣BDC 的外接球半径R =2,由此能求出该球的表面积. 【详解】由题意得该三棱锥的面PCD 的正三角形,且BD ⊥平面PCD , 设三棱锥P ﹣BDC 外接球的球心为O , △PCD 外接圆圆心为O 1,则OO 1⊥面PCD , ∴四边形OO 1DB 为直角梯形,由BD O 1D =1,OB =OD ,得OB =2,∴三棱锥P ﹣BDC 的外接球半径R =2, ∴该球的表面积S =4πR 2=474π⨯=7π. 故答案为:7π. 【点睛】本题考查三棱锥外接球的表面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方思想,是中档题.15.②④【解析】【分析】对每一个选项分析判断得解【详解】根据已知可得面β和面γ可成任意角度和面α必垂直所以直线m 可以和面β成任意角度①不正确;l ⊂γl⊥m 所以l⊥α②正确;③显然不对;④因为l ⊂βl⊥α解析:②④ 【解析】 【分析】对每一个选项分析判断得解. 【详解】根据已知可得面β和面γ可成任意角度,和面α必垂直.所以直线m 可以和面β成任意角度,①不正确;l ⊂γ,l⊥m,所以l⊥α,②正确;③显然不对;④因为l ⊂β,l⊥α,所以α⊥β,④正确. 故答案为②④ 【点睛】本题主要考查空间线面垂直和面面垂直的证明,意在考查学生对这些知识的理解掌握水平,属于基础题.16.60°【解析】【分析】首先证得是二面角的平面角解直角三角形求得的大小【详解】由于是的中点所以由于所以平面所以由于平面所以而所以平面所以所以是二面角的平面角设则所以所以在中所以所以故答案为:【点睛】本解析:60° 【解析】 【分析】首先证得EDC ∠是二面角E BD C --的平面角,解直角三角形求得EDC ∠的大小. 【详解】由于SB BC =,E 是SC 的中点,所以SC BE ⊥,由于,SC DE DE BE E ⊥⋂=,所以SC ⊥平面BDE ,所以SC BD ⊥.由于SA ⊥平面ABC ,所以SA BD ⊥,而SA SC S ⋂=,所以BD ⊥平面SAC ,所以,BD DC BD DE ⊥⊥,所以EDC ∠是二面角E BD C --的平面角.设1SA AB ==,则SB BC ==2SC =,所以在Rt SAC ∆中,12SA SC =,所以30SCA ∠=o ,所以60EDC ∠=o . 故答案为:60o 【点睛】本小题主要考查二面角的求法,考查空间想象能力和逻辑推理能力,属于中档题.17.【解析】【分析】首先通过两个底面面积之比为得到半径比设出上底半径为下底半径为由因为母线与底面的夹角是得到母线长为高为就可以根据轴截面的面积解出代公式求出侧面积即可【详解】圆台的两个底面面积之比为则半 解析:360π【解析】 【分析】首先通过两个底面面积之比为4:9,得到半径比,设出上底半径为2k ,下底半径为3k ,由因为母线与底面的夹角是60o ,得到母线长为2k ,高为3k .就可以根据轴截面的面积解出6k =,代公式求出侧面积即可. 【详解】圆台的两个底面面积之比为4:9,则半径比为2:3所以设圆台的上底半径为2k ,下底半径为3k ,由于母线与底面的夹角是60o ,所以母线长为2k 3k . 由于轴截面的面积为1803, 所以()46332k k k+=6k =.所以圆台的上底半径为12,下底半径为18.母线长为12. 所以圆台的侧面积为()121812360ππ+⨯=. 故答案为:360π 【点睛】本题主要考查圆台的性质以及圆台的侧面积,同时考查了线面成角问题,属于中档题.18.【解析】【分析】在平面中与的交点即为求出长即可求解【详解】连在正方体中所以四边形为矩形相交其交点为平面的交点是的中点为的中位线为中点正方体各棱长为1故答案为:【点睛】本题考查空间线面位置关系确定直线解析:5【解析】 【分析】在平面11BB D D 中,1D M 与BD 的交点即为N ,求出BN 长,即可求解. 【详解】连BD ,在正方体1111ABCD A B C D -中,11111,//,BB DD BB DD DD BD =⊥,所以四边形11BB D D 为矩形,1,BD D M 相交, 其交点为1D M 平面ABCD 的交点N ,Q M 是1BB 的中点,111,//2BM DD BM DD ∴=, BM 为1DD N V 的中位线,B 为DN 中点,正方体各棱长为1,2BN BD ∴==,,1,2,135ABN AB BN ABN ==∠=o V ,2222cos AN AB BN AB BN ABN =+-⋅⋅∠2321252=+⨯⨯⨯=,5AN ∴=. 故答案为:5.【点睛】本题考查空间线面位置关系,确定直线与平面交点是解题的关键,意在考查直观想象能力,属于中档题.19.62【解析】试题分析:由题意得抛物线的准线为x=-c 它正好经过双曲线的左焦点所以准线被双曲线截得的弦长为2b2a 所以2b2a=223be2即ba=23e2所以整理得2e4-9e2+1=0解得e=62 解析:试题分析:由题意,得抛物线的准线为,它正好经过双曲线的左焦点,所以准线被双曲线截得的弦长为,所以,即,所以,整理,得,解得或.又过焦点且斜率为1的直线与双曲线的右支交于两点,所以.考点:1、抛物线与双曲线的几何性质;2、直线与双曲线的位置关系.【方法点睛】关于双曲线的离心率问题,主要是有两类试题:一类是求解离心率的值,一类是求解离心率的范围.基本的解题思路是建立椭圆和双曲线中的关系式,求值问题就是建立关于的等式,求取值范围问题就是建立关于的不等式.20.【解析】分析:设上下圆锥的高分别为圆柱的底面圆的半径为圆柱的高为h 再求详解:设上下圆锥的高分别为圆柱的底面圆的半径为圆柱的高为h 则故答案为:点睛:(1)本题主要考查圆锥圆柱体积的计算意在考查学生对这 解析:23【解析】分析:设上下圆锥的高分别为12,,h h 圆柱的底面圆的半径为r ,圆柱的高为h,再求21V V . 详解:设上下圆锥的高分别为12,,h h 圆柱的底面圆的半径为r ,圆柱的高为h, 则222212222111()233.3r h r h h r h r hV V r hr hππππππ-+-===故答案为:23. 点睛:(1)本题主要考查圆锥圆柱体积的计算,意在考查学生对这些知识的掌握水平.(2)圆柱的体积为2V sh r h π==,圆锥的体积为21133V sh r h π==. 三、解答题21.(1)证明见解析;(2)34m =-,5 【解析】 【分析】(1)直线方程可化为()2740x y m x y +-++-=,令27040x y x y +-=⎧⎨+-=⎩,解方程组可求出定点坐标;(2)当圆心与定点所在直线与直线l 垂直时,直线l 被圆C 截得的弦长最短,求解即可.(1)证明:直线:(21)(1)74l m x m y m +++--=0可化为()2740x y m x y +-++-=,令27040x y x y +-=⎧⎨+-=⎩,解得3,1x y ==,所以直线l 过定点()3,1.(2)直线l 过定点()3,1A ,22(31)(12)525-+-=<,故点()3,1A 在圆的内部,直线l与圆C 相交,圆C 的圆心为()1,2,半径为5,AC ==当l AC ⊥时,直线l 被圆C 截得的弦长最短,211132AC k -==--,直线l 的斜率为2,即2121m m +-=+,解得34m =-,此时弦长为=故当34m =-时,直线l 被圆C 截得的弦长最短为 【点睛】本题考查了动直线过定点问题,考查了圆的弦长,考查了学生的计算能力,属于中档题. 22.:(Ⅰ)见解析(Ⅱ)16 【解析】 【分析】 【详解】(Ⅰ)证明:因为,DE EF CF EF ⊥⊥,所以四边形平面CDEF 为矩形,由5,4GD DE ==,4GC CF ==得3GE ==4GF ==, 所以5EF =,在EFG V 中 ,有222EF GE FG =+,所以EG GF ⊥又因为,CF EF CF FG ⊥⊥,得CF ⊥平面EFG , 所以CF EG ⊥,所以EG ⊥平面CFG ,即平面DEG ⊥平面CFG ;(Ⅱ):在平面EGF 中,过点G 作GH EF ⊥于点H ,则125EG GF GH EF ⋅== 因为平面CDEF ⊥平面EFG ,得GH ⊥平面CDEF ,1163CDEF CDEF V S GH =⋅=23.(Ⅰ)证明见解析;(Ⅱ)证明见解析. 【解析】 【分析】(Ⅰ)取PD 中点G ,连接AG 、FG ,由题意结合中位线性质可得//FG AE 且FG AE =,即可得四边形FGAE 为平行四边形,进而可得//FE AG ,再由线面平行的判定即可得证;(Ⅱ)由线面垂直的性质和正方形的性质可得DO ⊥平面PAC ,进而可得DO AF ⊥,由平面几何知识可得AF PO ⊥,再由线面垂直的判定即可得证. 【详解】(Ⅰ)证明:取PD 中点G ,连接AG 、FG ,Q E ,F 分别为AB ,PC 的中点,底面ABCD 为正方形∴//FG CD 且12FG CD =,//AE CD 且12AE CD =,∴//FG AE 且FG AE =,∴四边形FGAE 为平行四边形, ∴//FE AG ,又FE ⊄平面PAD ,AG ⊂平面PAD , ∴//EF 平面PAD .(Ⅱ)证明:Q 底面ABCD 为正方形,PA ⊥平面ABCD ,∴PA DO ⊥,AC DO ⊥,Q PA AC A =I ,∴DO ⊥平面PAC , ∴DO AF ⊥,在PAC V 中,设PO AF H =I ,如图,由题知90PAC ∠=o , O ,F 分别为AC ,PC 的中点,∴AF FC =即CAFFCA ??,设PA a =,则2AC a =,22AO a =, ∴APO ACP V V ∽,∴APO PCA ??,∴90AHP ∠=o 即AF PO ⊥,又PO OD O =I ,∴AF ⊥平面POD . 【点睛】本题考查了线面平行和线面垂直的判定,考查了空间思维能力,属于中档题. 24.(1)4x =或3480x y +-=(2)22 【解析】 【分析】(1)根据题意分斜率不存在和斜率存在两种情况即可求得结果;(2)先求出直线方程,然后求得圆心C 与直线l 的距离,由弦长公式即可得出答案. 【详解】解: (1)由题意可得()2,3C ,直线l 与圆C 相切 当斜率不存在时,直线l 的方程为4x =,满足题意 当斜率存在时,设直线l 的方程为14y k x +=-,即410kx y k ---= 2234121k k k ---=+,解得34k =-∴直线的方程为3480x y +-= ∴直线l 的方程为4x =或3480x y +-=(2)当直线l 的倾斜角为135︒时,直线l 的方程为30x y +-= 圆心()2,3C 到直线l 23322+-=∴弦长为2222(2)22-=【点睛】本题考查了直线的方程、直线与圆的位置关系、点到直线的距离公式及弦长公式,培养了学生分析问题与解决问题的能力.25.(1)220x y +-=;(2)5250x y --= 【解析】 【分析】 【详解】(1)因为,A B 分别为直线与射线:0(0)OA x y x -=≥及:20(0)OB x y x +=≥的交点, 所以可设(,),(2,)A a a B b b -,又点(1,0)P 是AB 的中点,所以有21,2{0.2a ba b -=+=即2,3{2.3a b ==-∴A 、B 两点的坐标为2242(,),(,)3333A B -,∴223324233AB k --==--, 所以直线AB 的方程为02(1)y x -=--,即220x y +-=(2)①当直线AB 的斜率不存在时,则AB 的方程为1x =,易知,A B 两点的坐标分别为1(1,1),(1,),2A B -所以AB 的中点坐标为1(1,)4,显然不在直线12y x =上,即AB 的斜率不存在时不满足条件.②当直线AB 的斜率存在时,记为k ,易知0k ≠且1k ≠,则直线AB 的方程为(1).y k x =-分别联立(1),{0y k x x y =--=及(1),{20.y k x x y =-+=可求得,A B 两点的坐标分别为(,),11k k A k k --2(,)1212k kB k k-++ 所以AB 的中点坐标为(,)22122224k k k k k k k k+--+-+ 又AB 的中点在直线12y x =上,所以1()222422212k k k k k k k k -=+-+-+解得52k = 所以直线AB 的方程为5(1)2y x =-,即5250x y --= 26.(1)1a =±;(2)(1,2)Q ;350x y +-=.【解析】 【分析】(1)由平行可知系数的关系为21a =,进而可求a 的值;(2)整理直线1l 方程可知()120a x y -+-=,由1020x y -=⎧⎨-=⎩可求得定点坐标.由分析知,当当(5,0)P -在直线上的射影为(1,2)Q 时,点P 到直线1l 距离最大,由1PQ l ⊥可求出1l 的斜率,结合已知的1l 的方程,可求出此时a 的值,进而可求出直线1l 的方程.【详解】解:(1)12//l l Q ,21a ∴=,解得1a =±检验:当1a =时12:30:20l x y l x y +-=++=,符合12//l l当1a =-时12:10:20l x y l x y -+=-+=,符合12//l l综上:1a =±.(2)解:1:20l ax y a +--=Q 整理可得()120a x y -+-= ,由1020x y -=⎧⎨-=⎩, 解得12x y =⎧⎨=⎩,所以定点(1,2)Q .则当(5,0)P -在直线上的射影为(1,2)Q 时,距离最大. 此时1PQ l ⊥ ,直线PQ 的斜率为201153PQ k -==+,则1l 的斜率113PQk k =-=- , 即3a -=-,解得3a =,此时直线1l 的方程为350x y +-=.【点睛】本题考查了两点斜率的求解,考查了直线平行、垂直.本题的难点是分析何时点P 到直线1l 的距离最大.易错点是做第一问时,求出1a =± 后未检验.对于已知直线平行,根据系数关系求出参数值后,应带回直线方程进行验证.。