当前位置：文档之家 › 《管理运筹学》第三版案例题解

《管理运筹学》第三版案例题解

  • 格式：doc
  • 大小：468.36 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

管理运筹学(第3版)章后习题解析(下)

管理运筹学(第3版)章后习题解析(下)
+ − 0.7 x1 − 0.3x2 − 0.3 x3 − d 2 + d2 =0
− 0.2 x1 − 0.2 x2 + 0.8 x3 − d 3+ + d3− = 0
+ − 2.5 x1 + 0.5 x2 + 0.3x3 − d 4 + d4 = 20
d1− = 0
− d2 =0
d3+ = 0 x1 , x2 , x3 , di+ , di− ≥ 0, i = 1, 2,3, 4
1．解： 最优解为 A―B2―C1―D1―E 或 A―B3―C1―D1―E 或 A―B3―C2―D2―E。 最优值为 13。 2．解： 最优解是项目 A 为 300 万元，项目 B 为 0 万元、项目 C 为 100 万元。 最优值 z=71+49+70=190 万元。 3．解： ， 设每个月的产量是 xi 百台（i=1, 2, 3, 4） 最优解：x1=4，x2＝0，x3＝4，x4＝3。即第一个月生产 4 百台，第二个月生产 0 台，第三 个月生产 4 百台，第四个月生产 3 百台。 最优值 z=252 000 元。 4．解： 最优解为运送第一种产品 5 件。 最优值 z=500 元。 5．解： 最大利润 2 790 万元。最优安排如表 10-1 所示。
表 10-1 年 1 2 3 4 5 度 年初完好设备 125 100 80 64 32 高负荷工作设备数 0 0 0 64 32 低负荷工作设备数 125 100 80 0 0
6．解： 最优解（0，200，300，100）或（200，100，200，100）或者（100，100，300，100）或 （200，200，0，200） 。总利润最大增长额为 134 万。 7．解： 在一区建 3 个分店，在二区建 2 个分店，不在三区建立分店。最大总利润为 32。 8．解： 最优解为第一年继续使用，第二年继续使用，第三年更新，第四年继续使用，第五年继续 使用，总成本=450 000 元。 9．解： 最优采购策略为若第一、二、三周原料价格为 500 元，则立即采购设备，否则在以后的几 周内再采购；若第四周原料价格为 500 元或 550 元，则立即采购设备，否则等第五周再采购；

运筹学教程(第三版)习题答案(第一章)

运筹学教程(第三版)习题答案(第一章)
School of Management
( 3)
max Z = x1 + x 2 6 x1 + 10 x 2 ≤ 120 st . 5 ≤ x1 ≤ 10 5≤ x ≤8 2
( 4)
page 2 3 May 2011
运筹学教程
第一章习题解答
(1) min Z = 2 x1 + 3 x 2 4 x1 + 6 x 2 ≥ 6 st . 2 x1 + 2 x 2 ≥ 4 x ,x ≥ 0 1 2 1 , Z = 3是一个最优解 3
min st x 1 Z = 2 x1 − 2 x 2 + 3 x 3 − x1 + x 2 + x 3 = 4 − 2 x1 + x 2 − x 3 ≤ 6 ≤ 0 , x 2 ≥ 0 , x 3 无约束
(1)
()
page 5 3 May 2011
School of Management
(1)
(2)
page 8 3 May 2011
运筹学教程
第一章习题解答
(1) max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0（ j = 1, L , 6） ,
运筹学教程（第二版） 运筹学教程（第二版） 习题解答
安徽大学管理学院
洪 文
电话： 电话：5108157(H)，5107443(O) ， E-mail: Hongwen9509_cn@

管理运筹学第三版习题答案(全)

管理运筹学第三版习题答案(全)

管理运筹学第三版习题答案（全）第2章线性规划的图解法1．解： x2 5 `A 1B O 1C 6 x1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知，最优解为B点，最优解：x1=2．解： x2 10.60.1 0 0.1 0.6 1 x1(1) 由图解法可得有唯一解 (2) (3) (4) (5)无可行解无界解无可行解无穷多解121569，x2?。

最优目标函数值：777x1?0.2x2?0.6，函数值为3.6。

36920923(6) 有唯一解，函数值为。

83x2?3x1?3．解：(1). 标准形式：maxf?3x1?2x2?0s1?0s2?0s3 9x1?2x2?s1?303x1?2x2?s2?132x1?2x2?s3?9x1,x2,s1,s2,s3?0(2). 标准形式：minf?4x1?6x2?0s1?0s2 3x1?x2?s1?6x1?2x2?s2?107x1?6x2?4x1,x2,s1,s2?0 (3). 标准形式：'''minf?x1'?2x2?2x2?0s1?0s2'''?3x1?5x2?5x2?s1?70'''2x1'?5x2?5x2?503x?2x?2x?s2?30'''x1',x2,x2,s1,s2?0'1'2''24．解：标准形式：maxz?10x1?5x2?0s1?0s2 3x1?4x2?s1?9 5x1?2x2?s2?8x1,x2,s1,s2?0 松弛变量（0，0）最优解为 x1=1，x2=3/2.3705．解：标准形式：minf?11x1?8x2?0s1?0s2?0s3 10x1?2x2?s1?203x1?3x2?s2?184x1?9x2?s3?36x1,x2,s1,s2,s3?0剩余变量（0.0.13）最优解为 x1=1，x2=5.6．解：(1) 最优解为 x1=3，x2=7. (2) 1?c1?3 (3) 2?c2?6 (4)x1?6x2?4(5) 最优解为 x1=8，x2=0. (6) 不变化。

《管理运筹学》习题3解答

《管理运筹学》习题3解答

6 x22 1 x23 5 x24 0 4 1 4 -1 3 5 1 0 0
x31 2 3
因为min(σ33)＝σ33=-1<0，所以初始方案并非最优方案，需进一步调整， x33为进基变量。 法二：用闭回路法求检验数 σ12=5-0+0-1=4；σ13=7-0+0-5=2；σ21=6-3+0-0=3；σ32=4-2+3-0+01=4（注：图中画出了非基变量x33的闭回路）；σ33=3-2+3-0+0-5=-1； σ34=0-2+3-0=1 因为min(σ33)＝σ33=-1<0，所以初始方案并非最优方案，需进一步调整， x33为进基变量。 第三步：求θ值，调整方案。 过程如下： 以X33作为进基变量。调整量θ＝min(10,20,20)=10，按照上图所示 进行调整，选择x14 作为出基变量。 方案调整后为方案二，如下： 用位势法可求出方案二非基变量检验数： 销地 销地一销地二销地三 销地四 Ui
x1 d-3 d+3
0 1 2 3 4 5 6 7 8 9 10 5 4 3 2 1 A
d+2 d-2 d+1 d-1 d+4 d-4 直线x2=2、x12x2=4分别交于C(k-4,2)
B D C
、D(2+k/2,k/4-1) 两点。 当x1≤k-4时，t= ad3-=a(4-x1+2x2)= a(4-k+4x2) ∴当k=9, x2=2, x1=5 时,min t1=3a; 当k-4≤x1≤2+k/2 时，t= ad3-+d4-= a(4-x1+2x2)+(2-x2)= (4-k)a+2+(4a-1)x2 ∴若a≥1/4时k=9, x2=5/4, x1=13/2时,min t2=3/4; 若0<a<1/4时k=9, x2=2, x1=5时,min t2=3a<3/4

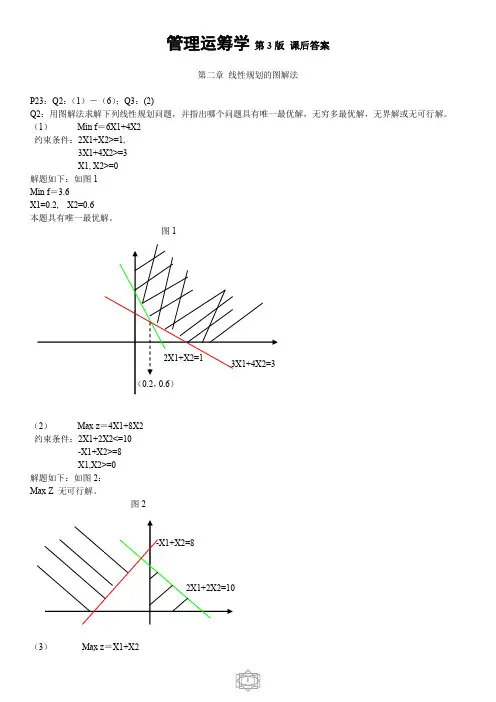
管理运筹学 第3版 韩伯棠 高教社 课后答案

管理运筹学 第3版 韩伯棠 高教社 课后答案

（1） 、满足对职工需求的条件下，如何安排临时工的班次，使得临时工成本最小。 （2） 、这时付给临时工的工资总额是多少，一共需要安排多少临时工班次。请用剩余变量来说明应该安排一些临时
6
工的 3 小时工作时间的班次，可使得总成本更小。 （3） 、如果临时工每班工作时间可以是 3 小时，也可以是 4 小时，那么如何安排临时工的班次，使得临时工总成本 最小。这样比（1）节省多少费用，这时要安排多少临时工班次。 解题如下： (1)临时工的工作时间为 4 小时，正式工的工作时间也是 4 小时，则第五个小时需要新招人员，临时工只要招用，无 论工作多长时间，都按照 4 小时给予工资。每位临时工招用以后，就需要支付 16 元工资。从上午 11 时到晚上 10 时共计 11 个班次，则设 Xi(i =1,2,…,11)个班次招用的临时工数量，如下为最小成本： minf＝16（X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11) 两位正式工一个在 11－15 点上班，在 15－16 点休息，然后在 16－20 点上班。另外一个在 13－17 点上班，在 17 －18 点休息，18－22 点上班。则各项约束条件如下： X1+1>=9 X1+X2+1>=9 X1+X2+X3+2>=9 X1+X2+X3+X4+2>=3 X2+X3+X4+X5+1>=3 X3+X4+X5+X6+2>=3 X4+X5+X6+X7+2>=6 X5+X6+X7+X8+1>=12 X6+X7+X8+X9+2>=12 X7+X8+X9+X10+1>=7 X8+X9+X10+X11+1>=7 Xi>=0(i＝1,2,…,11) 运用计算机解题，结果输出如下; **********************最优解如下************************* 目标函数最优值为 : 320 变量 最优解 -------------x1 8 x2 0 x3 1 x4 0 x5 1 x6 4 x7 0 x8 6 x9 0 x10 0 x11 0 目标函数最优值为 : 320 这时候临时工的安排为： 变量 班次 临时工班次 -------------x1 8 x2 0 x3 1 x4 0

《管理运筹学》第三版习题答案（韩伯棠教授）

《管理运筹学》第三版习题答案（韩伯棠教授）

第 2 章 线性规划的图解法11a.可行域为 OABC 。

b.等值线为图中虚线所示。

12c.由图可知，最优解为 B 点，最优解： x 1 = 769 。

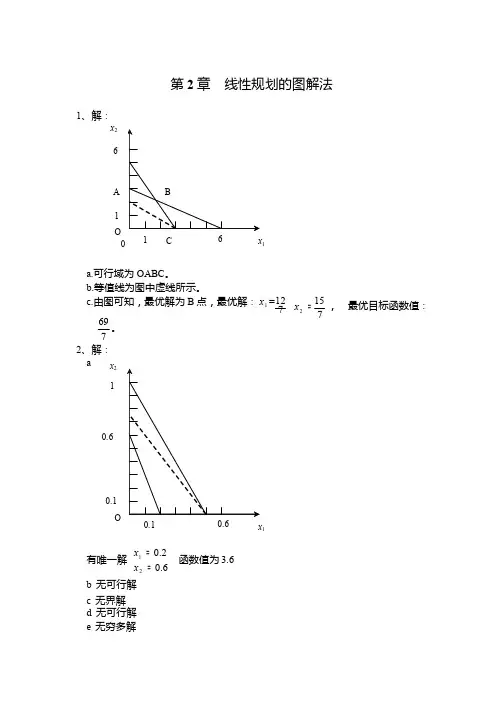
7 2、解：15 x 2 =7， 最优目标函数值：a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解：a 标准形式：b 标准形式：c 标准形式：x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解：x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式： max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式： min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解：b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。

管理运筹学案例分析

管理运筹学案例分析
管理运筹学案例
【案例1】某厂排气管车间生产计划的优化分析
1．问题的提出 排气管作为发动机的重要部件之一，极大地影响发动机的性能。某
发动机厂排气管车间长期以来，只生产一种四缸及一种六缸发动机的排 气管。由于其产量一直徘徊不前，致使投资较大的排气管生产线，一直 处于吃不饱状态，造成资源的大量浪费，全车间设备开动率不足50%。
税收
15 16 14.8 17 16.5 14.5 15.6 15.5
售价
150 160.1 149 172 166 145.6 157.8 155.8
利润
13.545 14.00114.99 15.56 15.312 12.8735 15.892 13.74
（元）
注：表中售价为含税价。
表C-3 设备加工能力一览表
【案例2】配料问题
某饲料公司生产肉用种鸡配合饲料，每千克饲料所需营养质量要求如表
C－4所示。
表C－4
营养成分 肉用种鸡国家标准 肉用种鸡公司标准
产蛋鸡标准
代谢能
2.7~2.8Mcal/kg
≥2.7Mcal/kg
≥2.65Mcal/kg
粗蛋白
135 ~145g/kg
135 ~145g/kg
≥151g/kg
x6 菜饼 0.32 1.62 360 113 8.1 7.1 5.3 8.4
x7 鱼粉 1.54 2.80 450 0 29.1 11.8 63 27
x8 槐叶粉 0.38 1.61 170 108 10.6 2.2 4.0 4.0
x9 DL-met 23.0
980
x10 骨粉 0.56
300 140
8.摇臂钻床 4.1 4.0 4.0 4.3 4.2 3.8 4.3 4.3

韩伯棠管理运筹学(第三版)_第十六章_决策分析

韩伯棠管理运筹学(第三版)_第十六章_决策分析
自然状态 行动方案
S1（大批量生产） S2（中批量生产） S3（小批量生产）
N1
p = 1/2
30 20 10
N2
p = 1/2
-6 -2 5
（需求量大） （需求量小）
收益期望值 E (Si)
12(max) 9 7.5
13
练习、电视机厂，99年产品更新方案： A1：彻底改型 A2：只改机芯，不改外壳 A3：只改外壳，不改机芯 问：如何决策？ 价格 方案 A1 A2 A3 高 S1 20 9 6 中 S2 1 8 5 低 S3 (万元) -6 0 4
1 Vi 3
aij
i 1
3
A3
5
5 maxV = 5 2 2 i 5 i 3 3 5
选择方案A2
§1 不确定情况下的决策
四、乐观系数(折衷)准则(Hurwicz胡魏兹准则) 决策者取乐观准则和悲观准则的折衷： 先确定一个乐观系数 （01），然后计算： CVi = max [(Si, Nj)] +（1- ）min [(Si, Nj)]
23
天气 利润 方案 蔬菜: A1 小麦: A2 棉花: A3
旱 0.2 1000 2000 3000
正常 期望值法 0.7 4000 5000 6000
多雨 0.1 7000 3000 2000
解：计算各方案的益损期望值：
E ( A1 ) 1000 0.2 4000 0.7 7000 0.1 3700 E ( A2 ) 2000 0.2 5000 0.7 3000 0.1 4200 E ( A3 ) 3000 0.2 6000 0.7 2000 0.1 5000
8

韩伯棠管理运筹学(第三版)_第七章_运输问题

韩伯棠管理运筹学(第三版)_第七章_运输问题

B2 c12 c22
Bn c1n c2n
A1 A2

Am 销量

cm1 b1

cm2 b2 … …

cmn
m i 1

am
n ji
bn a i b j
10
求使总的运输费用最小的调运方案？
§1
n
运 输 模 型
m
运输问题线性规划模型
min s
n
cij xij
j 1 i 1
运筹学
J a
30° C 40° C 60° C 95° C
PERSIL
J a
30° C 40° C 60° C 95° C
统筹安排 成本最低
REWE
PERSIL
第七章 运输问题
1
第五章
运 输 问 题
• §1 运 输 模 型 • §2 运输问题的计算机求解 • §3 运输问题的应用 • §4* 运输问题的表上作业法
A2
6
6
4
5
6
5
200
300 500 650
销量
250
200
200
思考题
在例3中，即某公司从两个产地 A1、A2将物品 运往三个销地B1、B2、B3，各产地的产量、各 销地的销量和各产地运往各销地每件物品的运 费如下表所示，如果增加条件：B3的需求不能 满足则需以高价（每单位10元）在本地购买， 问：应如何调运可使总运输费用最小？
§1
整理得：
运 输 模 型
Min f = 6x11+ 4x12+ 6x13+ 6x21+ 5x22+ 5x23 s.t. x11+ x12 + x13 = 200 x21 + x22+ x23 = 300 x11 + x21 = 150

韩伯棠管理运筹学(第三版)_第九章_目标规划

韩伯棠管理运筹学(第三版)_第九章_目标规划

• step • • • • • • • • • • • • •
3 目标函数值为 : 1100 变量 解 相差值 --------------------x1 166.667 0 x2 250 0 d10 0 d1+ 36666.667 0 d233.333 0 d2+ 0 15.167 d30 26 d3+ 0 26 d41100 0 d4+ 0 2
练习：某厂生产Ⅰ、Ⅱ 两种产品，有关数据如 表所示。试求获利最大 的生产方案？
Ⅰ 原材料 设备(台时) 2 1
Ⅱ 1 2
拥有量 11 10
单件利润
8
10
在此基础上考虑： 1、产品Ⅱ的产量不低于产品Ⅰ的产量； 2、充分利用设备有效台时，不加班； 3、利润不小于 56 元。 解: 分析 第一目标：P1d1 即产品Ⅰ的产量不大于Ⅱ的产量。 第二目标： P2 ( d2 d2 )
运筹学
运筹谋划
一石多鸟
第九章 目标规划
1
第七章
目标规划
• §1 目标规划问题举例 • §2 目标规划的图解法
• §3 复杂情况下的目标规划
• §4.加权目标规划
2
§1 目标规划问题举例
例1．企业生产 • 不同企业的生产目标是不同的。多数企业 追求最大的经济效益。但随着环境问题的 日益突出，可持续发展已经成为全社会所 必须考虑的问题。因此，企业生产就不能 再如以往那样只考虑企业利润，必须承担 起社会责任，要考虑环境污染、社会效益、 公众形象等多个方面。兼顾好这几者关系， 企业才可能过引入目标值和偏差变量，可 以将目标函数转化为目标约束。 目标值：是指预先给定的某个目标的一个 期望值。 实现值或决策值：是指当决策变量xj 选定 以后，目标函数的对应值。 偏差变量（事先无法确定的未知数）：是 指实现值和目标值之间的差异,记为 d 。 正偏差变量：表示实现值超过目标值的部 分，记为 d＋。 负偏差变量：表示实现值未达到目标值的 部分，记为 d－。

《管理运筹学》案例演示(动态规划)

《管理运筹学》案例演示(动态规划)

x1
[
]
第一季度生产量加库存量要满足本季度需求量， 又不能超过第一到第四季度的总需求： 最高生产量为6个单位：
2 ≤ x1 + s1 ≤11 0 ≤ x1 ≤ 6
f1 ( s1 )
x1
0 1 2
21
Байду номын сангаас
3
21.5
4
22
5
6
f1 ( s1 )
∗ x1
s1
0
20.5 21.5 20.5
5
第四步：最佳生产决策:第一季度生产5单位产品，期末库存量为 3单位；第二季度不生产，期末库存量为零；第三季度生产6单位 产品，期末库存量为4单位；第四季度不安排生产。
8 100 75 53
A B C
问如何确定三个项目计划的投资额，才能使8千万元的资金投 资后的利润最大。 解： 阶段变量k ( k =1,2, 3 )：每投资一个项目作为一个阶段； 状态变量sk ：可以对第k个项目投资的资金数（即投资 第k个项目前的资金数）； 决策变量xk：第k 个项目的投资， 0≤xk≤sk；
11 10.5 8 8 8 8 5
6 5 0 0 0 0 0
第三步：第二到第四季度的最佳生产决策； 第二到第四季度的最低生产成本：
f2 (s2 ) = m c2( x2 , s2 ) + f3 (s3 ) in
x2
[
]
约束条件： 由于第一季度期初库存s1= 0，而最高生产量x1= 6 ,市场需求量d1=2，所以，第二季度期初的库存量应为： 第二季度生产量加库存量要满足本季度需求量， 又不能超过第二到第四季度的总需求： 最高生产量为6个单位：
该季度生产量不能超过6个单位：

《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社

《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
x1＝8，x2＝0，x3＝1，x4＝1，x5＝0，x6＝4，x7＝0，x8＝6，x9＝0， x10＝0，x11＝0 最优值为 320。
a、 在满足对职工需求的条件下，在 10 时安排 8 个临时工，12 时新安排 1 个临时工，13 时新安排 1 个临时工，15 时新安排 4 个临时工，17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000，10000。 回报率：60000
b 模型变为： max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后，用管理运筹学软件求解可得：总成本最小为 264 元。 安排如下：y1=8（ 即在此时间段安排 8 个 3 小时的班），y3=1，y5=1，y7=4，x8=6 这样能比第一问节省：320-264=56 元。
x2＋x3＋x4＋x5＋1 ≥ 3 x3＋x4＋x5＋x6＋2 ≥ 3 x4＋x5＋x6＋x7＋1 ≥ 6 x5＋x6＋x7＋x8＋2 ≥ 12 x6＋x7＋x8＋x9＋2 ≥ 12 x7＋x8＋x9＋x10＋1 ≥ 7 x8＋x9＋x10＋x11＋1 ≥ 7 x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0 用管理运筹学软件我们可以求得此问题的解为：
b、 这时付给临时工的工资总额为 80 元，一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11

《管理运筹学》习题6解答

《管理运筹学》习题6解答

《管理运筹学》习题6解答（复习参考题）1. 某公司从银行获得贷款300万元，现有3个项目A 、B 、C 可供投资，投资不同项目所获收益（单位：十万元）不同，如表1所示。

问：公司如何分配这300万元资金用于以下三个项目，才能使公司总收益最大？ 要求：（1）请建立该问题的动态规划模型，要求说明各变量与指标的实际意义。

（2）请用逆序解法求解，并写出最优分配方案的结论。

（1）建立动态规划模型，如下：①将问题按项目个数分为三个阶段，k=1,2,3，分别对应项目A 、B 、C 。

每个阶段决定给项目k 分配一定数量的资金。

②设状态变量 s k 表示第k 阶段初尚未分配的资金数（单位：百万元），也是项目k 到项目3所分配资金的总和。

显然s 1=3, s 4=0。

s 2和s 3的取值可以为0至3之间的任何一个整数。

③设决策变量u k 表示分配给第k 个项目的资金额（单位：百万元）。

显然u k ∈ D k (s k ) ={0,1, …,s k }。

④状态转移方程：s k +1=s k －u k 。

⑤指标函数：阶段指标函数d k (u k )表示从S k 百万元中拿出u k 百万元资金分配给项目k 所能创造的收益（单位：十万元）,见表1所示。

最优指标函数f k (s k )表示s k 百万元的资金分配给第k 至第3个项目时所得到的最大总收益（单位：十万元）。

⑥逆序解法的基本方程如下：（2）用逆序解法求解33444()()(){}()k k k k k k k k k 1k 1u D (s )44f s max d s ,u f s ,k 3,2,1f s 0 ++∈⎧=+=⎪⎨⎪=⎩当n=1时，0≤u≤3，s ＝3-u 本题有两个最优方案：方案一：*1u ＝0， *2u ＝2 *1u ＝1 ***211s =s -u ＝3-0＝3 ***322s =s -u ＝3-2＝1即项目A 、项目B 、项目C 分别分配0、2、1百万元，最大总收益为*1f (3)=14百万元。

运筹学第三版课后习题答案

运筹学第三版课后习题答案

运筹学第三版课后习题答案运筹学是一门研究如何在有限资源下做出最优决策的学科。

它涉及到数学、统计学、经济学等多个学科的知识，可以应用于各个领域，如物流管理、生产调度、供应链优化等。

而《运筹学》第三版是一本经典的教材，它系统地介绍了运筹学的基本概念、方法和应用。

本文将针对该教材的课后习题进行解答，帮助读者更好地理解和掌握运筹学的知识。

第一章：线性规划1. 习题1.1：求解线性规划问题的常用方法有哪些？答：求解线性规划问题的常用方法包括单纯形法、对偶理论、整数规划等。

其中，单纯形法是最常用的方法，它通过迭代寻找目标函数值最小（或最大）的解。

2. 习题1.2：什么是线性规划的对偶问题？如何求解线性规划的对偶问题？答：线性规划的对偶问题是指通过原始问题的约束条件构造一个新的问题，该问题的目标是最大化（或最小化）原始问题的目标函数值。

求解线性规划的对偶问题可以使用对偶理论，通过将原始问题转化为对偶问题的等价形式，再利用对偶问题的特性进行求解。

第二章：整数规划1. 习题2.1：什么是整数规划问题？与线性规划问题有何不同？答：整数规划问题是指决策变量的取值必须为整数的线性规划问题。

与线性规划问题相比，整数规划问题的解空间更为有限，求解难度更大。

整数规划问题在实际应用中常常涉及到资源的离散分配、路径选择等问题。

2. 习题2.2：列举几个整数规划问题的应用场景。

答：整数规划问题的应用场景包括生产调度、物流路径优化、设备配置等。

例如，在生产调度中，需要确定每个生产批次的数量和时间，以最大化产能利用率和最小化生产成本。

第三章：动态规划1. 习题3.1：什么是动态规划？它的基本思想是什么？答：动态规划是一种通过将问题划分为多个子问题，并保存子问题的解来求解原问题的方法。

其基本思想是利用子问题的解构建全局最优解，从而避免重复计算和提高求解效率。

2. 习题3.2：动态规划在哪些问题中有应用？答：动态规划在最短路径问题、背包问题、序列比对等问题中有广泛的应用。

管理运筹学案例分析

管理运筹学案例分析
工程（工地）
配置人数
1
9
2
5
3
8
4
3
5
7
6
2
7
5
监理工程师年耗费的总成本为204.75万元。
THE
END
案例背景
因为从事监理业的专业多达几十个，仅以高层民用建 筑为例就涉及建筑学专业、工民建（结构）专业、给水排 水专业、采暖通风专业、强电专业、弱电专业、自动控制 专业、技术经济专业、总图专业、合同和信息管理专业， 这就需要我们合理配置这些人力资源。为了方便计算，我 们把所涉及的专业技术人员按总平均人数来计算，工程的 施工形象进度按标准施工期和高峰施工期来划分。通常标 准施工期需求的人数比较容易确定。但高峰施工期就比较 难确定了，原因有两点： （1）高峰施工期各工地不是同时来到，是可以事先预 测的，在同一个城市里相距不远的工地，就存在着各工地 的监理工程师如何交错使用的运筹问题。
问
题
（1）高峰施工期公司最少配置多少个监理工 程师？ （2）监理工程师年耗费的总成本是多少？
分析思路
案例条件简化
1、专业人员简化——按平均人数算 2、施工期简化——标准施工期（7个月） ——高峰施工期（5个月）
关于监理工程师配置人数
1、优化后的监理师人数要满足案例中高峰施工华建设监理公司监理工程师配置问题
案例背景
石华建设监理公司（国家甲级）侧重于国家大中型项 目的监理，仅在河北省石家庄市就曾同时监理七项工程， 总投资均在5000万元以上。由于工程开工的时间不同，各 工程工期之间相互搭接，具有较长的连续性，1998年监理 的工程量与1999年监理的工程量大致相同。 每项工程安排多少监理工程师进驻工地，一般是根据 工程的投资、建筑规模、使用功能、施工的形象进度、施 工阶段来决定的。监理工程师的配置数量随之变化。由于 监理工程师从事的专业不同，他们每人承担的工作量也是 不等的。有的专业一个工地就需要三人以上，而有的专业 一人则可以兼管三个以上的工地。

《管理运筹学》第三版案例题解

《管理运筹学》第三版案例题解

《管理运筹学》案例题解案例1：北方化工厂月生产计划安排解：设每月生产产品i （i=1，2，3，4，5）的数量为X i ，价格为P 1i ，Y j 为原材料j 的数量，价格为P 2j ，a ij 为产品i 中原材料j 所需的数量百分比，则：510.6j i ij i Y X a ==∑总成本：TC=∑=1512j j j P Y总销售收入为：511i i i TI X P ==∑目标函数为：MAX TP （总利润）=TI-TC 约束条件为：1030248002151⨯⨯⨯≤∑=j j Y X 1+X 3=0.7∑=51i i XX 2≤0.05∑=51i i XX 3+X 4≤X 1 Y 3≤4000 X i ≥0,i=1,2,3,4,5 应用计算工具求解得到： X 1=19639.94kg X 2=0kg X 3=7855.97kg X 4=11783.96kg X 5=0kg最优解为：348286.39元案例2：石华建设监理工程师配置问题解：设X i 表示工地i 在标准施工期需要配备的监理工程师，Y j 表示工地j 在高峰施工期需要配备的监理工程师。

约束条件为： X 1≥5 X 2≥4 X 3≥4 X 4≥3 X 5≥3 X 6≥2 X 7≥2 Y 1+Y 2≥14 Y 2+Y 3≥13 Y 3+Y 4≥11 Y 4+Y 5≥10 Y 5+Y 6≥9 Y 6+Y 7≥7 Y 7+Y 1≥14Y j ≥ X i （i=j ，i=1,2,…,7） 总成本Y 为：Y=∑=+71)12/353/7(i i i Y X解得X 1=5；X 2=4；X 3=4；X 4=3；X 5=3；X 6=2；X 7=2；1Y =9；2Y =5；3Y =8；4Y =3；5Y =7；6Y =2；7Y =5; 总成本Y=167.案例3：北方印染公司应如何合理使用技术培训费解：变量的设置如下表所示，其中X ij为第i类培训方式在第j年培训的人数：第一年第二年第三年1.高中生升初级工X11X12X132.高中生升中级工X213.高中生升高级工X314.初级工升中级工X41X42X435.初级工升高级工X51X526.中级工升高级工X61X62X63则每年年底培养出来的初级工、中级工和高级工人数分别为：第一年底第二年底第三年底初级工X11X12X13中级工X41X42X21 +X43高级工X61X51 +X62X31 +X52+X63则第一年的成本TC1为：1000X11+3000X21+3000X31+2800X41+2000X51+3600 X61≤550000；第二年的成本TC2为：1000X12+3000X21+2000X31+2800X42+（3200 X51+2000X52）+3600X62≤450000；第三年的成本TC3为：1000X13+1000X21+4000X31+2800X43+3200 X52+3600X63≤500000；总成本TC= TC1 +TC2 +TC3≤1500000;其他约束条件为：X41 +X42 +X43+X51 +X52≤226；X61+X62 +X63≤560；X1j≤90 （j=1，2，3）；X21 +X41≤80；X21 +X42≤80；X 21 +X 43≤80； X 31 +X 51+X 61≤80； X 31 +X 51+X 52+X 62≤80； X 31 +X 52+X 63≤80；以下计算因培训而增加的产值Max TO=(X 11+ X 12+ X 13) + 4(X 41 +X 42 +X 21 +X 43) +5.5(X 61 +X 51 +X 62 +X 31 +X 52+X 63); 利用计算机求解：X 11=38；X 41=80；X 42=59；X 43=77；X 61=80；X 62=79；X 63=79；其余变量都为0； TO=2211案例4：光明制造厂经营报告书设直径4.76、6、8、10和12的钢管的需求量分别是1x ,x 2,3x ,4x ,5x 。

最新运筹学(第三版课后习题答案第一章ppt课件

最新运筹学(第三版课后习题答案第一章ppt课件
布莱克—穆顿模式：冲突方格
9 高
关心 员工 5
× 缓和（1,9）
正视（9,9）×
妥协（5,5） ×
1
× 回避（1，1）
低
压制（9,1）×
12 低
3 45 关心工作
67
89 高 组织 行 为学
四、冲突管理
3.冲突管理策略（三）：
布坎南组织冲突的“组织—协调”四阶段模型
布坎南关于组织冲突的组织——协调四阶段模型提到了实现激发冲突的几 种方法。
运筹学（第三版）课后习题答案 第一章
1.4 （1）
1.5
1.6
1.7 （1）
1.12
华
章
组文 渊
织
行
第十章 冲突与冲突管理
为
学
Organizational Behavior
本章内容
冲突的基本概念
• 概念、特征 • 类型
冲突产生的根源
• 杜布林 • 纳尔逊和奎克 • 罗宾斯
二、冲突产生的根源
2.纳尔逊和奎克对冲突根源的分析
专业化
相互依赖性
结
共用资源
构
因
目标差异
素
职权关系
地位矛盾 管辖权的模糊
在一个组织中，责任界限不清楚，当发 生了一件无法界定责任的事件时，员工 们就会倾向于“推卸责任”，或避免接 触这件事，这样，关于问题的责任就产 生了冲突。
组织 行 为学
二、冲突产生的根源
在这个过程中．一方努力去抵消 另一方的封锁行为，因为另一方的
封锁行为将妨碍他达到目标 或损害他的利益。
罗宾斯
组织 行 为学
一、冲突的基本概念
1.冲突的概念
冲突是否存在不仅是一个客观性问题，也是一个主观的知觉问题。 冲突产生的必要条件是，存在某种形式的对立或不相容以及相互作用。 冲突的主体可以是组织、群体或个人，冲突的客体可以是利益、权力、资 源、目标、方法、意见、价值观、感情、程序、信息、关系等。 冲突是一个过程，它是从人与人、人与群体、人与组织、群体与群体、组 织与组织之间的相互关系和相互作用过程中发展而来的。

韩伯棠管理运筹学(第三版)_第二章_线性规划的图解法

韩伯棠管理运筹学(第三版)_第二章_线性规划的图解法

之为线性规划。如果目标函数是变量的非线性函数，
或约束条件中含有变量非线性的等式或不等式的数学
模型则称之为非线性规划。
把满足所有约束条件的解称为该线性规划的可行
解。把使得目标函数值最大(即利润最大)的可行解称 为该线性规划的最优解，此目标函数值称为最优目标
函数值，简称最优值。
7
对于一般线性规划问题的建模过程。应注意 如下几个问题：
x1 X1+X2=300
B点为最优解，坐标为（50，250）
12
问题的解：
最佳决策为x1=50, x2=250，此时z=27500。 这说明该厂的最优生产计划方案是生产I产品50单位，
生产Ⅱ产品250单位，可得最大利润27500元。
把x1=50, x2=250代入约束条件得： 50+250=300台时设备
分析: 可知购买的原料A与原料B的总量为
250+100=350(吨)正好达到约束条件的最低限，所需的 加工时间为2×250+1×100=600正好达到加工时间的最 高限。而原料A的购进量250吨则比原料A购进量的最 低限125吨多购进了250-125=125吨， 这个超过量在 线性规划中称为剩余量。
2×50+250=350千克原料A，
1×250=250千克原料B．
这表明了生产50单位Ⅰ产品和250单位Ⅱ产品将消
耗完所有可使用的设备台时数和原料B，但对原料A来
说只消耗了350千克，还有(400—350)=50千克没有
使用。在线性规划中，对一个≤约束条件中没使用的资
源或能力的大小称之为松弛量。
max Z=50 x1+100x2 （称为目标函数）。
其中max为最大化的符号(最小化为min)；50和100分别为单位产
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《管理运筹学》案例题解案例1：北方化工厂月生产计划安排解：设每月生产产品i （i=1，2，3，4，5）的数量为X i ，价格为P 1i ，Y j 为原材料j 的数量，价格为P 2j ，a ij 为产品i 中原材料j 所需的数量百分比，则：510.6j i ij i Y X a ==∑总成本：TC=∑=1512j j j P Y总销售收入为：511i i i TI X P ==∑目标函数为：MAX TP （总利润）=TI-TC 约束条件为：1030248002151⨯⨯⨯≤∑=j j Y X 1+X 3=0.7∑=51i i XX 2≤0.05∑=51i i XX 3+X 4≤X 1 Y 3≤4000 X i ≥0,i=1,2,3,4,5应用计算工具求解得到： X 1=19639.94kg X 2=0kg X 3=7855.97kg X 4=11783.96kg X 5=0kg最优解为：348286.39元案例2：石华建设监理工程师配置问题解：设X i 表示工地i 在标准施工期需要配备的监理工程师，Y j 表示工地j 在高峰施工期需要配备的监理工程师。

约束条件为： X 1≥5 X 2≥4 X 3≥4 X 4≥3 X 5≥3 X 6≥2 X 7≥2 Y 1+Y 2≥14 Y 2+Y 3≥13 Y 3+Y 4≥11 Y 4+Y 5≥10 Y 5+Y 6≥9 Y 6+Y 7≥7 Y 7+Y 1≥14Y j ≥ X i （i=j ，i=1,2,…,7） 总成本Y 为：Y=∑=+71)12/353/7(i i i Y X解得X 1=5；X 2=4；X 3=4；X 4=3；X 5=3；X 6=2；X 7=2；1Y =9；2Y =5；3Y =8；4Y =3；5Y =7；6Y =2；7Y =5; 总成本Y=167.案例3：北方印染公司应如何合理使用技术培训费解：变量的设置如下表所示，其中X ij为第i类培训方式在第j年培训的人数：第一年第二年第三年1.高中生升初级工X11X12X132.高中生升中级工X213.高中生升高级工X314.初级工升中级工X41X42X435.初级工升高级工X51X526.中级工升高级工X61X62X63则每年年底培养出来的初级工、中级工和高级工人数分别为：第一年底第二年底第三年底初级工X11X12X13中级工X41X42X21 +X43高级工X61X51 +X62X31 +X52+X63则第一年的成本TC1为：1000X11+3000X21+3000X31+2800X41+2000X51+3600 X61≤550000；第二年的成本TC2为：1000X12+3000X21+2000X31+2800X42+（3200 X51+2000X52）+3600X62≤450000；第三年的成本TC3为：1000X13+1000X21+4000X31+2800X43+3200 X52+3600X63≤500000；总成本TC= TC1 +TC2 +TC3≤1500000;其他约束条件为：X41 +X42 +X43+X51 +X52≤226；X61+X62 +X63≤560；X1j≤90 （j=1，2，3）；X21 +X41≤80；X21 +X42≤80；X 21 +X 43≤80； X 31 +X 51+X 61≤80； X 31 +X 51+X 52+X 62≤80； X 31 +X 52+X 63≤80；以下计算因培训而增加的产值Max TO=(X 11+ X 12+ X 13) + 4(X 41 +X 42 +X 21 +X 43) +5.5(X 61 +X 51 +X 62 +X 31 +X 52+X 63); 利用计算机求解：X 11=38；X 41=80；X 42=59；X 43=77；X 61=80；X 62=79；X 63=79；其余变量都为0； TO=2211案例4：光明制造厂经营报告书设直径4.76、6、8、10和12的钢管的需求量分别是1x ,x 2,3x ,4x ,5x 。

钢带的供给量为0x 。

则： 钢管销售收入Y1为：Y 1=160001x +16100 x 2+160003x +161004x +163005x 废品回收收入Y 2为：Y 2=100x +（1x 8/92+ x 28.5/91.5 +3x 9/91+5x 10.5/89.5）×700 钢带成本C 1为： C 1=80000x 职工工资C 2为：C 2=0x ×0.99×675+0x ×0.99×0.98×900+（1x + x 2+3x +4x +5x ）×900 则净利润Y 0为：Y 0= Y 1+ Y 2- C 1- C 2-2000000-（1x + x 2+3x +4x +5x ）×2200（目标函数）约束条件：1.0869571x +1.092896 x 2+1.0989013x +4x +1.1173185x =0x ×0.99×0.981x + x 2+3x +4x +5x =2800 1x ≥1400840≥x 2≥2803x ≥3004x = x 2/2200≥5x ≥1000x ,1x , x 2,3x ,4x ,5x ≥0利用工具求得：1x =1400x 2=666.6673x =3004x =333.333 5x =100 0x =3121.831Y 0=4652126.37案例5：北方食品投资方案规划解：由于总的时间为210分钟，因此每种类型车可能的路线是有限的，不妨穷举出来：2吨车可能的路线(2吨车每点的卸货，验收时间为30min)：路线 1 2 3 4 5 6 7 8 9 10 11 12A 4 3 3 2 2 2 1 1 1 0 0 0B 0 1 0 2 1 0 3 2 1 4 3 2 C1121212time 155 170 190 175 185 205 180 190 200 190 200 210 4吨车可能的路线(4吨车每点卸货，验收时间为15min)：路线 13 14 15 16 17 18 19 20 21 A 8 7 7 6 6 5 5 4 3 B 0 1 0 2 1 3 2 4 5 C 0111time175 190 190 195 205 200 210 205 210设X i 为跑路线i 的车的数量。

2吨车数量为： Q 2=∑=121i i X4吨车数量为： Q 4=∑=2113i i X总成本TC 为： TC=12 Q 2+18 Q 4目标函数： MIN TC=12 Q 2+18 Q 4 约束条件为：4X 1+3X 2+3X 3+2X 4+2X 5+2X 6+X 7+X 8+X 9+8X 13+7X 14+7X 15+6X 16+6X 17+5X 18+5X 19+4X 20+3X 21≥50X 2+2X 4+X 5+3X 7+2X 8+X 9+4X 10+3X 11+2X 12+X 14+2X 16+X 17+3X 18+2X 19+4X 20+5X 21≥36X 3+X 5+2X 6+X 8+2X 9+X 11+2X 12+X 15+X 17+X 19≥20利用管理运筹学2.0软件中线性规划模块求得结果如下：**********************最优解如下*************************目标函数最优值为: 254.736变量最优解相差值------- -------- --------x1 0 4.364x2 0 3.818x3 0 2.727x4 0 3.273x5 0 2.182x6 0 1.091x7 0 2.727x8 0 1.636x9 0 .545x10 0 2.182x11 0 1.091x12 5.409 0x13 0 2.727x14 0 2.182x15 0 1.091x16 0 1.636x17 0 .545x18 0 1.091x19 9.182 0x20 0 .545x21 1.364 0约束松弛/剩余变量对偶价格------- ------------------- --------1 0 -1.9092 0 -2.4553 0 -3.545目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 7.636 12 无上限x2 8.182 12 无上限x3 9.273 12 无上限x4 8.727 12 无上限x5 9.818 12 无上限x6 10.909 12 无上限x7 9.273 12 无上限x8 10.364 12 无上限x9 11.455 12 无上限x10 9.818 12 无上限x11 10.909 12 无上限x12 9 12 12.667x13 15.273 18 无上限x14 15.818 18 无上限x15 16.909 18 无上限x16 16.364 18 无上限x17 17.455 18 无上限x18 16.909 18 无上限x19 14 18 18.4x20 17.455 18 无上限x21 16 18 18.75常数项数范围:约束下限当前值上限------- -------- -------- --------1 9.6 50 802 30 36 103.3333 7.474 20 26但是：因为X i为跑路线i的车的数量，所以X i应该是整数。

因此该问题应该是纯整数规划问题。

用工具计算该纯整数规划问题，可得结果：目标函数值＝264.0000变量值相差值X1 0.000000 12.000000X2 0.000000 12.000000X3 0.000000 12.000000X4 0.000000 12.000000X5 0.000000 12.000000X6 0.000000 12.000000X7 0.000000 12.000000X8 0.000000 12.000000X9 4.000000 12.000000X10 0.000000 12.000000X11 0.000000 12.000000X12 3.000000 12.000000X13 0.000000 18.000000X14 0.000000 18.000000X15 0.000000 18.000000X16 0.000000 18.000000X17 0.000000 18.000000X18 0.000000 18.000000X19 8.000000 18.000000X20 0.000000 18.000000X21 2.000000 18.000000约束松弛/剩余变量对偶价格1 0.000000 0.0000002 0.000000 0.0000003 2.000000 0.000000注意：由于该整数规划问题变量较多，计算量较大，使用管理运筹学软件需要在PC上运行很长时间，才可以得到以上结果。