人教版八年级数学 全等三角形的五种判定方法同步练习(无答案)

人教版八年级上册数学12.2 三角形全等的判定（AAS ASA ）同步训练一、单选题1．如图，在△ABC 中，AD 平分∠BAC ，AD ∠BD 于点D ，DE ∥AC 交AB 于点E ，若AB =8，则DE 的长度是（ ）A ．6B ．2C ．3D ．4 2．如图，AD BC ⊥，垂足为D ，BF AC ⊥，垂足为F ，AD 与BF 交于点E ，52AD BD DC ===，，则AE 的长为（ ）A ．2B ．3C ．4D ．7 3．如图，AB CD =，AB CD ∥，BAE DCF ∠=∠，8BD =，4EF =，则BE =（ ）A ．4B ．8C ．2D ．12 4．如图所示，∠EBC ∠∠DCB ，BE 的延长线与CD 的延长线交于点A ，CE 与BD 相交于点O ．则下列结论：∠∠OEB ∠∠ODC ；∠AE ＝AD ；∠BD 平分∠ABC ，CE 平分∠ACB ；∠OB ＝OC ，其中正确的有（ ）A ．4个B ．3个C ．2个D ．1个 5．如图，已知OF 平分AOB ∠，PD OA ⊥于D 点，PE OB ⊥于E 点，F 是OF 上的另一点，连接DF 、EF ．判断图中有几对全等三角形（ ）A ．1B ．2C ．3D ．4 6．如图，D 是AB 上一点，DF 交AC 于点E ，DE FE FC AB =，∥，若74AB CF ==，，则BD 的长是（ ）A ．5B ．4C ．3D ．2 7．如图，ABC CED △≌△，点D 在BC 边上，90AE ∠+∠=︒，EC 、ED 与AB 交于点F 、G ，则下列结论不正确的是（ ）A ．AC CD =B ．90ACB ∠=︒C ．AB CED ．EG BG = 8．如图，在ABC 中，AD BC ⊥于点D ，CE AB ⊥于点E ，AD 、CE 交于点F ，已知6EF EB ==，24AEF S =△，则CF 的长为（ ）A ．1B ．2C ．52D ．3二、填空题9．如图，已知∠CDE ＝90°，∠CAD ＝90°，BE ∠AD 于B ，且DC ＝DE ，若BE ＝7，AB ＝4，则BD 的长为 _____．10．如图，AB ∠CD ，且AB ＝CD ，CE ∠AD ，BF ∠AD ，垂足分别为E ，F ，若CE ＝4，BF ＝3，EF ＝2，则AD 的长为________．11．如图，在ABC 中，CD AB ⊥，AE BC ⊥，垂足分别为点D ，E ，CD 与AE 交于点F ，若3BD DF ==，6ADF S =△，则CF 的长是________．12．如图，∠ABC 与∠DCB 中，AC 与BD 交于点E ，且∠A ＝∠D ，AB ＝DC ，若∠AEB ＝50°，求∠EBC 的度数是____．13．如图，∠ACB ＝90°，AC ＝BC ，BE ∠CE ，AD ∠CE ，垂足分别为E ，D ，AD ＝25，DE ＝17，则BE ＝_____．14．如图，在ABC 中，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别为D ，E ．若12AD =，5BE =，则DE 的长为______．15．如图，点D 是△ABC 的边AB 上一点，FC ∠AB ，连接DF 交AC 于点E ，若CE =AE ，AB =7，CF =4，则BD 的长为________．16．如图，90ACB ∠=︒，AC BC =，F 为AB 上一点，连接CF ，AE CF ⊥，BD CF ⊥，垂足分别是点E ，D ．若5cm AE =，2cm BD =，则DE 的长为______cm ．三、解答题17．如图，AB ∥CD ，BN ∥MD ，点M 、N 在AC 上，且AM =CN ，求证：BN =DM ．18．如图，将ABC 沿射线BC 方向平移得到DCE ，连接BD 交AC 于点F ．(1)求证：AFB ≌CFD △；(2)若9AB =，7BC =，求BF 的取值范围．19．如图，Rt∠ACB中，∠ACB＝90°，AC＝BC，E点为线段CB一动点，连接AE，过点A作AF∠AE且AF＝AE，过点F作FD∠AC于点D，如图∠所示．(1)求证：FD＝AC．(2)若点E为BC中点，连BF交AC于点G，如图∠，已知CG＝1，求BC的长．20．如图，在∠ABC中，CD∠BD，垂足为D，且CD＝B D．BE平分∠ABC，且BE∠AC，垂足为E，交CD于点F．(1)求证：AE=CE；(2)求证：BF=2CE．。

判定全等三角形的五种方法全等三角形是指具有相同形状和相等边长的三角形。

判定两个三角形是否全等是数学中的一个重要问题。

下面将介绍判定全等三角形的五种方法。

方法一：SSS判定法（边边边）SSS判定法是指通过比较两个三角形的三条边是否相等来判定其是否全等。

如果两个三角形的三条边长度相等，则可以判断它们是全等三角形。

方法二：SAS判定法（边角边）SAS判定法是指通过比较两个三角形的两条边和夹角是否相等来判定其是否全等。

如果两个三角形的一边和夹角分别相等，则可以判断它们是全等三角形。

方法三：ASA判定法（角边角）ASA判定法是指通过比较两个三角形的两个角和夹边是否相等来判定其是否全等。

如果两个三角形的两个角和夹边分别相等，则可以判断它们是全等三角形。

方法四：AAS判定法（角角边）AAS判定法是指通过比较两个三角形的两个角和非夹边的对应边是否相等来判定其是否全等。

如果两个三角形的两个角和非夹边的对应边分别相等，则可以判断它们是全等三角形。

方法五：HL判定法（斜边和直角边）HL判定法是指通过比较两个直角三角形的斜边和直角边是否相等来判定其是否全等。

如果两个直角三角形的斜边和直角边分别相等，则可以判断它们是全等三角形。

通过以上五种方法，我们可以准确地判定两个三角形是否全等。

这些方法都是基于几何学中的一些定理和公理推导而来，经过严谨的数学证明，可以确保判定结果的准确性。

需要注意的是，在判定全等三角形时，我们需要确保给定的条件足够，即要求已知的边长、角度等信息能够满足相应的判定条件。

如果给定的信息不足够，或者不满足判定条件，那么就无法准确地判定两个三角形是否全等。

判定全等三角形的方法还可以用于解决一些实际问题，例如在建筑设计、图形测量等领域。

通过判定三角形是否全等，可以确保设计和测量的准确性，提高工作效率。

总结起来，判定全等三角形的五种方法分别是SSS判定法、SAS判定法、ASA判定法、AAS判定法和HL判定法。

这些方法都是基于几何学中的定理和公理推导而来，通过比较边长、角度等信息，可以准确地判定两个三角形是否全等。

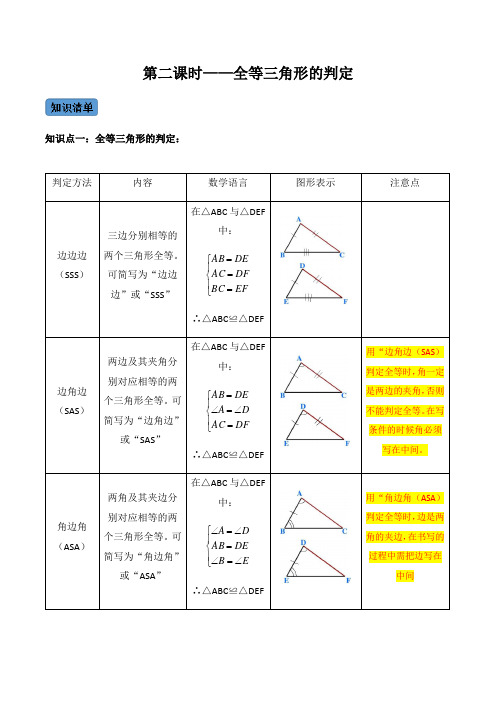
第二课时——全等三角形的判定知识点一：全等三角形的判定：判定方法内容数学语言 图形表示 注意点边边边（SSS ）三边分别相等的两个三角形全等。

可简写为“边边边”或“SSS ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧===EF BC DF AC DE AB ∴△ABC ≌△DEF边角边（SAS ）两边及其夹角分别对应相等的两个三角形全等。

可简写为“边角边”或“SAS ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧=∠=∠=DF AC D A DEAB ∴△ABC ≌△DEF用“边角边（SAS ）判定全等时，角一定是两边的夹角，否则不能判定全等。

在写条件的时候角必须写在中间。

角边角（ASA ）两角及其夹边分别对应相等的两个三角形全等。

可简写为“角边角”或“ASA ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧∠=∠=∠=∠E B DE AB DA ∴△ABC ≌△DEF用“角边角（ASA ）判定全等时，边是两角的夹边，在书写的过程中需把边写在中间特别提示：在写全等三角形的数学语言时，等号左边写“≌”左边三角形的条件，等号右边写“≌”右边三角形的条件。

并且条件的顺序必须和判定条件顺序一致。

方法总结：【类型一：补充证全等条件】1．如图，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC＝DF，只添加一个条件，能判定△ABC≌△DEF的是（）A．BC＝DE B．AE＝DBC．∠A＝∠DEF D．∠ABC＝∠D2．如图，在△ABC和△BAD中，AC＝BD，要使△ABC≌△BAD，则需要添加的条件是（）第2题第3题A．∠BAD＝∠ABC B．∠BAC＝∠ABD C．∠DAC＝∠CBD D．∠C＝∠D3．如图，BC＝BD，添加下列一个条件后，仍无法判定△ABC≌△ABD的是（）A．AC＝AD B．∠ABC＝∠ABD C．∠CAB＝∠DAB D．∠C＝∠D＝90°4．如图，已知点A，D，C，F在同一条直线上，AB＝DE，AD＝CF，要使△ABC≌△DEF，则下列条件可以添加的是（）第4题第5题第7题A．∠B＝∠E B．∠A＝∠EDF C．AC＝DF D．BC∥EF5．如图，已知AB＝AE，∠EAB＝∠DAC，添加一个条件后，仍无法判定△AED≌△ABC的是（）A．AD＝AC B．∠E＝∠B C．ED＝BC D．∠D＝∠C6．下列条件，不能判定两个直角三角形全等的是（）A．两个锐角对应相等B．一个锐角和斜边对应相等C．两条直角边对应相等D．一条直角边和斜边对应相等7．如图，在Rt△ABC与Rt△DCB中，已知∠A＝∠D＝90°，添加一个条件，不能使得Rt△ABC≌Rt△DCB 的是（）A．AB＝DC B．AC＝DB C．∠ABC＝∠DCB D．BC＝BD8．如图，已知AB⊥BD，CD⊥BD，若用“HL”判定Rt△ABD和Rt△CDB全等，则需要添加的条件是（）A．AD＝CB B．∠A＝∠CC．BD＝DB D．AB＝CD【类型二：证明三角形全等】9．请将以下推导过程补充完整．如图，点C在线段AB上，AD∥BE，AC＝BE，AD＝BC，CF平分∠DCE．求证：△DCF ≌△ECF 证明：∵AD ∥BE ∴∠A ＝∠B在△ACD 和△BEC 中()⎪⎩⎪⎨⎧=∠=∠BC AD B A ∴△ACD ≌△BEC （ ）∴CD ＝CE （ ） ∵CF 平分∠DCE ∴ 在△DCF 和△ECF 中()⎪⎩⎪⎨⎧==CE CD CF CF ∴△DCF ≌△ECF （SAS ）10．如图，点C 在BD 上，AB ⊥BD ，ED ⊥BD ，AC ⊥CE ，AB ＝CD ．求证：△ABC ≌△CDE ．11．如图，点A、D、B、E在一条直线上，AD＝BE，AC＝DF，AC∥DF，求证：△ABC≌△DEF．12．如图，点D在线段BC上，AB＝AD，∠1＝∠2，DA平分∠BDE：求证：△ABC≌△ADE．13．天使是美好的象征，她的翅膀就像一对全等三角形．如图AD与BC相交于点O，且AB＝CD，AD＝BC．求证：△ABO≌△CDO．14．如图，在△ABC中，点D在BC的延长线上，DE∥AC，且DE＝BC，AC＝BD．求证：△ABC≌△BED．15．如图，CA＝CD，∠BCE＝∠ACD，BC＝EC．求证：△ABC≌△DEC．16．如图，D、C、F、B四点在一条直线上，AC＝EF，AC⊥BD，EF⊥BD，垂足分别为点C、点F，BF＝CD．试说明：△ABC≌△EDF．17．如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．18．如图，点C、E、B、F在一条直线上，AB⊥CF于B，DE⊥CF于E，AC＝DF，AB＝DE．求证：CE ＝BF．19．如图，AB＝BC，∠BAD＝∠BCD＝90°，点D是EF上一点，AE⊥EF于E，CF⊥EF于F，AE＝CF，求证：Rt△ADE≌Rt△CDF．【类型三：全等三角形的判定与性质】20．如图，在△ABC与△AEF中，点F在BC上，AB＝AE，BC＝EF，∠B＝∠E，AB交EF于点D，∠F AC ＝40°，则∠BFE＝（）第20题第21题A．35°B．40°C．45°D．50°21．如图，在△ABC中，BD平分∠ABC，∠C＝2∠CDB，AB＝12，CD＝3，则△ABC的周长为（）A．21B．24C．27D．3022．如图，AB⊥CD，且AB＝CD，E，F是AD上两点，CE⊥AD，BF⊥AD．若CE＝4，BF＝3，EF＝2，则AD的长为（）第22题第23题A．3B．5C．6D．723．已知：如图，在△ABC，△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD＝CE；②∠ACE+∠DBC＝45°；③BD⊥CE；④∠BAE+∠DAC＝180°．其中结论正确的个数是（）A．1B．2C．3D．424．如图，CB为∠ACE的平分线，F是线段CB上一点，CA＝CF，∠B＝∠E，延长EF与线段AC相交于点D．（1）求证：AB＝FE；（2）若ED⊥AC，AB∥CE，求∠A的度数．25．如图，四边形ABCD中，AD∥BC，E为CD的中点，连结BE并延长交AD的延长线于点F．（1）求证：△BCE≌△FDE；（2）连结AE，当AE⊥BF，BC＝2，AD＝1时，求AB的长．26．如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E．（1）求证：BC＝DC；（2）若∠A＝25°，∠D＝15°，求∠ACB的度数．【类型四：全等三角形的应用】27．如图，要测池塘两端A，B的距离，小明先在地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB，连接DE并测量出它的长度，DE的长度就是A，B间的距离．那么判定△ABC和△DEC全等的依据是（）第27题第28题A．SSS B．SAS C．ASA D．AAS28．打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（）A．带①②去B．带②③去C．带③④去D．带②④去29．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm．第29题第30题30．在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB ＝OC，测得AB＝a，EF＝b，圆形容器的壁厚是（）A ．aB ．bC ．b ﹣aD ．21（b ﹣a ）一、选择题（10题）1．如图为正方形网格，则∠1+∠2+∠3＝（ ）第1题 第2题 第3题A ．105°B ．120°C ．115°D ．135°2．如图，已知∠C ＝∠D ＝90°，添加一个条件，可使用“HL ”判定Rt △ABC 与Rt △ABD 全等．以下给出的条件适合的是（ ）A ．∠ABC ＝∠ABDB ．∠BAC ＝∠BAD C ．AC ＝AD D ．AC ＝BC3．如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．A ．①B ．②C ．③D ．①和②4．根据下列已知条件，能唯一画出△ABC 的是（ ）A．∠C＝90°，AB＝6B．AB＝4，BC＝3，∠A＝30°C．AB＝5，BC＝3D．∠A＝60°，∠B＝45°，BC＝45．如图，测河两岸A，B两点的距离时，先在AB的垂线BF上取C，D两点，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC≌△ABC，从而得到ED＝AB，测得ED的长就是A，B的距离，判定△EDC≌△ABC的依据是（）A．ASA B．SSS C．AAS D．SAS6．如图，已知∠EAC＝∠BAD，AC＝AD，增加下列条件：①AB＝AE；②BC＝ED；③∠C＝∠D；④∠B＝∠D．其中能使△ABC≌△AED的条件有（）A．4个B．3个C．2个D．1个7．如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，则两个木桩离旗杆底部的距离BD与CD的距离间的关系是（）第7题第8题A．BD＞CD B．BD＜CD C．BD＝CD D．不能确定8．如图，AB＝12m，CA⊥AB于点A，DB⊥AB于点B，且AC＝4m，点P从B向A运动，每分钟走1m，点Q从B向D运动，每分钟走2m，P、Q两点同时出发，运动（）分钟后，△CAP与△PQB全等．A．2B．3C．4D．89．把等腰直角三角形ABC，按如图所示立在桌上，顶点A顶着桌面，若另两个顶点距离桌面5cm和3cm，则过另外两个顶点向桌面作垂线，则垂足之间的距离DE的长为（）第9题第10题A．4cm B．6cm C．8cm D．求不出来10．如图，在△AOB和△COD中，OA＝OB，OC＝OD（OA＜OC），∠AOB＝∠COD＝α，直线AC，BD 交于点M，连接OM．下列结论：①AC＝BD，②∠OAM＝∠OBM，③∠AMB＝α，④OM平分∠BOC，其中正确结论的个数是（）A．4B．3C．2D．1二、填空题（6题）11．如图，线段AB，CD相交于点O，AO＝BO，添加一个条件，能使△AOC≌△BOD，所添加的条件的是．12．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．第12题第14题13．在△ABC中，AB＝3cm，AC＝4cm，则BC边上的中线AD的取值范围是．14．在直角三角形中，存在斜边的平方等于两条直角边的平方的和。

全等三角形5大判定一、边边边（SSS）学习全等三角形判定法则时，第一条就是边边边。

内容：它们的夹角分别相等的两个三角形全等。

理解：若给出三条线段的长度(满足三角形三边关系)，即可确定出的三角形形状，大小。

若给出三条线段长度 AB=c， BC=a， AC=b，确定过程如下：①先确定一边AB；②分别以AB为圆心，分别做半径为b，a长的圆，交于C点；③最后连接AC，BC。

这样三角形的大小，形状就都被确定出来了。

二、边角边（SAS）内容：两边和它们的夹角分别相等的两个三角形全等。

理解：若确定两条公共端点线段的长度，及它们的夹角，即可确定出的三角形形状，大小。

若给出AB=c BC=a ∠B=α，确定过程如下：①画∠EAD=α；②在射线AE上截取AC=c，在射线AD上截取AB=c；③连接BC。

这样，三角形的.大小形状同样被确定了。

三、角边角（ASA）内容：两角和他们的夹边分别相等的两个三角形全等。

理解：若给出三角形的两个角的大小和它们的夹边的长度了，即可确定出的三角形形状，大小。

若有AB=c，∠CAB=α，∠CBA=β，确定过程如下：①先确定一边AB=c；②在AB同旁画∠DAB=α，∠EBA=β，AD，BE交于点C。

这样，三角形的大小形状同样被确定了。

四、角角边（AAS）内容：两边分别相等且其中一组等角的对边相等的两个三角形全等。

理解：若给出三角形的两个角的大小和其中一个角对边的长度了，即可确定出的三角形形状，大小。

若有AB=c，∠CAB=α，∠ACB=β，确定过程如下：由三角形的内角和为180度可得出剩下一角∠CBA的度数，这样，利用角边角的思路即可确定三角形形状大小。

相关定理：三角形内角和为180度五、斜边，直角边（HL）内容：斜边和一条直角边分别相等的两个直角三角形全等。

(HL)理解：若确定一个三角形为直角三角形，同时得到其一个直角边和斜边的长度，即可确定出三角形的形状大小。

若确定三角形为直角三角形，还得到其一直角边和斜边，则可勾股定理得出剩下一边，再通过SSS或SAS即可确定三角形形状大小。

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件（5种）1 边角边（重点）两边及其夹角分别分别相等的两个三角形全等，可以简写成“边角边”或“SAS”. 注：必须是两边及其夹角,不能是两边和其中一边的对角.原因：如图：在∆ABC和∆ABD中，∠A=∠A,AB=AB,BC=BD,显然这两个三角形不全等. 例1 如图，AC=AD,∠CAB=∠DAB,求证:∆ACB≌∆ADB.例2 如图，在四边形ABCD中，AD∥BC,∠ABC=∠DCB，AB=DC，AE=DF求证：BF=CE.例3．(1)如图①，根据“SAS”,如果BD=CE， = ，那么即可判定△BDC≌△CEB；(2) 如图②，已知BC=EC，∠BCE=ACD，要使△ABC≌△DEC，则应添加的一个条件为例4.如图，已知AD=AE，∠1=∠2，BD=CE，则有△ABD≌，理由是；△ABE≌，理由是．例5．如图，在△ABC和△DEF中，如果AB=DE，BC=EF，只要找出∠ =∠或∥，就可得到△ABC≌△DEF．例6．如图，已知AB∥DE，AB=DE，BF=CE，求证：△ABC≌△DEF．例7．如图，点B在线段AD上，BC∥DE，AB=ED，BC=DB．求证：∠A=∠E例8．如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C．求证：∠A=∠D．2.角边角两角及其夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）例1．如图，在△ABC中，点D是BC的中点，作射线AD，线段AD及其延长线上分别取点E，F，连接CE，BF．添加一个条件，使得△BDF≌△CDE，你添加的条件是：．(不添加辅助线)例2.如图，已知AD平分∠BAC，且∠ABD=∠ACD，则由“AAS”可直接判定△≌△．例3．如图，在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，那么AE= cm．例4.如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE=2，则两平行线AD与BC间的距离为．例5．如图，已知EC=AC，∠BCE=∠DCA，∠A=∠E．求证：BC=DC．例6．如图，在△ABC中，D是BC边上的点 (不与B，C重合)，F，E分别是AD及其延长线上的点，CF∥BE．请你添加一个条件，使△BDE≌△CDF (不再添加其他线段，不再标注或使用其他字母)，并给出证明．(1) 你添加的条件是：；(2) 证明：例7．如图，A在DE上，F在AB上，且BC=DC，∠1=∠2=∠3，则DE的长等于 ( ) A．DC B．BCC．AB D．AE+AC【基础训练】1．如图，已知AB＝DC，∠ABC＝∠DCB，则有△ABC≌_______，理由是_______；且有∠ACB＝_______，AC＝_______．2．如图，已知AD＝AE，∠1＝∠2，BD＝CE，则有△ABD≌_______，理由是_______；△ABF≌_______，理由是_______．3．如图，在△ABC和△BAD中，因为AB＝BA，∠ABC＝∠BAD，_______＝_______，根据“SAS”可以得到△ABC≌△BAD．4．如图，要用“SAS”证△ABC≌△ADE，若AB＝AD，AC＝AE，则还需条件( )．A．∠B＝∠D B∠C＝∠EC．∠1＝∠2 D．∠3＝∠45．如图，OA＝OB，OC＝OD，∠O＝50°，∠D＝35°，则∠AEC等于( )．A．60°B．50°C．45°D．30°6．如图，如果AE＝CF，AD∥BC，AD＝CB，那么△ADF和ACBE全等吗？请说明理由．7．如图，已知AD与BC相交于点O，∠CAB＝∠DBA，AC＝BD．求证：(1)∠C＝∠D；(2)△AOC≌△BOD．8．如图，△ACD和△BCE都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE交DC于F，BD分别交CE、AE于点G、H．试猜测线段AE和BD的位置和数量关系，并说明理由．9．如图，在△ABC中，AB＝AC，AD平分∠BAC．求证：∠DBC＝∠DCB．10．如图，△ABC是等边三角形，D是AB边上的一点，以CD为边作等边三角形CDE，使点E、A在直线DC的同侧，连接AE．求证：AE∥BC．A BC DEF角角边两角分别相等且其中一组等角的对边相等的两个三角形全等，可以简写成“角角边”或“AAS ”. 例1、如图，在△ABC 中，∠ABC ＝45°，H 是高AD 和高BE 的交点，试说明BH ＝AC ．例2、如图，∠ACB=90°，AC=BC ，BE ⊥CE ，AD ⊥CE 于D ，AD=2.5cm ，DE=1.7cm ． 求BE 的长．例3、如图, 在△ABC 中, AC ⊥BC, CE ⊥AB 于E, AF 平分∠CAB 交CE 于点F, 过F 作FD ∥BC 交AB 于点D. 求证：AC ＝AD.例4、如图, 在ABC中, ∠A＝90°, BD平分B, DE⊥BC于E, 且BE＝EC,(1)求∠ABC与∠C的度数；(2)求证：BC＝2AB.边边边三边分别相等的两个三角形全等，可以简写成“边边边”或“SSS”.例1、如图，在四边形ABCD中，AB=CB，AD=CD．你能说明∠C=∠A吗? 试一试．例2、如图，在四边形ABCD中，AB=AD，BC=DC，E为AC上的一动点(不与A重合)，在E移动过程中．BE和DE是否相等? 若相等，请写出证明过程；若不相等，请说明理由．例3．如图，AB=CD ，AE=CF ，BO=DO ，EO=FO ．求证：OC=OA ．斜边、直角边斜边和一条直角边分别相等的两个直角三角形全等，可以简写成“斜边、直角边”或“HL ”。

12．2 三角形全等的判定第1课时 “边边边”一、课堂导入问题提出：一块三角形的玻璃损坏后，只剩下如图①所示的残片，你对图中的残片作哪些测量，就可以割取符合规格的三角形玻璃，与同伴交流．学生活动：观察，思考，回答教师的问题．方法如下：可以将图①的玻璃碎片放在一块纸板上，然后用直尺和铅笔或水笔画出一块完整的三角形．如图②，剪下模板就可去割玻璃了．如果△ABC ≌△A ′B ′C ′，那么它们的对应边相等，对应角相等．反之，如果△ABC 与△A ′B ′C ′满足三条边对应相等，三个角对应相等，即AB ＝A ′B ′，BC ＝B ′C ′，CA ＝C ′A ′，∠A ＝∠A ′，∠B ＝∠B ′，∠C ＝∠C ′这六个条件，就能保证△ABC ≌△A ′B ′C ′.从刚才的实践我们可以发现：只要两个三角形三条对应边相等，就可以保证这两块三角形全等．这种说法对吗？二、知识点梳理边边边1．三边分别相等的两个三角形全等．简记为“边边边”或“SSS ”． 2．“边边边”判定方法可用几何语言表示为：在△ABC 和△A 1B 1C 1中，∵⎩⎪⎨⎪⎧AB ＝A 1B 1，BC ＝B 1C 1，AC ＝A 1C 1，∴△ABC ≌△A 1B 1C 1(SSS)．三、考点分类考点一： 利用“SSS ”判定两个三角形全等【例1】 如图，AB ＝DE ，AC ＝DF ，点E 、C 在直线BF 上，且BE ＝CF .求证：△ABC ≌△DEF .解析：已知△ABC 与△DEF 有两边对应相等，通过BE ＝CF 可得BC ＝EF ，即可判定△ABC ≌△DEF .证明：∵BE ＝CF ，∴BE ＋EC ＝EC ＋CF ，即BC ＝EF .在△ABC 和△DEF 中，∵⎩⎪⎨⎪⎧BC ＝EF ，AB ＝DE ，AC ＝DF ，∴△ABC ≌△DEF (SSS)．方法总结：判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．考点二： “SSS ”与全等三角形的性质结合进行证明或计算【例2】 如图所示，△ABC 是一个风筝架，AB ＝AC ，AD 是连接点A 与BC 中点D 的支架，求证：AD ⊥BC .解析：要证AD ⊥BC ，根据垂直定义，需证∠1＝∠2，∠1＝∠2可由△ABD ≌△ACD 证得．证明：∵D 是BC 的中点，∴BD ＝CD .在△ABD 和△ACD 中，∵⎩⎪⎨⎪⎧AB ＝AC ，BD ＝CD ，AD ＝AD ，∴△ABD ≌△ACD (SSS)，∴∠1＝∠2(全等三角形的对应角相等)．∵∠1＋∠2＝180°，∴∠1＝∠2＝90°，∴AD ⊥BC (垂直定义)．方法总结：将垂直关系转化为证两角相等，利用全等三角形证明两角相等是全等三角形的间接应用．考点三：利用“边边边”进行尺规作图【例3】已知：如图，线段a、b、c.求作：△ABC，使得BC＝a，AC＝b，AB＝c.(保留作图痕迹，不写作法)解析：首先画AB＝c，再以B为圆心，a为半径画弧，以A为圆心，b为半径画弧，两弧交于一点C，连接BC，AC，即可得到△ABC.解：如图所示，△ABC就是所求的三角形．方法总结：关键是掌握基本作图的方法，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．考点四：利用“SSS”解决探究性问题【例4】如图，AD＝CB，E、F是AC上两动点，且有DE＝BF.(1)若E、F运动至图①所示的位置，且有AF＝CE，求证：△ADE≌△CBF.(2)若E、F运动至图②所示的位置，仍有AF＝CE，那么△ADE≌△CBF还成立吗？为什么？(3)若E、F不重合，AD和CB平行吗？说明理由．解析：(1)因为AF＝CE，可推出AE＝CF，所以可利用SSS来证明三角形全等；(2)同样利用三边来证明三角形全等；(3)因为全等，所以对应角相等，可推出AD∥CB.解：(1)∵AF ＝CE ，∴AF ＋EF ＝CE ＋EF ，∴AE ＝CF .在△ADE 和△CBF 中，∵⎩⎪⎨⎪⎧AD ＝CB ，DE ＝BF ，AE ＝CF ，∴△ADE ≌△CBF .(2)成立．∵AF ＝CE ，∴AF －EF ＝CE －EF ，∴AE ＝CF .在△ADE 和△CBF 中，∵⎩⎪⎨⎪⎧AD ＝CB ，DE ＝BF ，AE ＝CF ，∴△ADE ≌△CBF .(3)平行．∵△ADE ≌△CBF ，∴∠A ＝∠C ，∴AD ∥BC .方法总结：解决本题要明确无论E 、F 如何运动，总有两个三角形全等，这个在图形中要分清．【课堂练习】1、找第三边（减公共部分）如图，已知点 B ，C ，D ，E 在同一直线上，且 A B=AE ，AC=AD ，BD=CE ． 求证：△ABC ≌△AED ．2、找第三边（加公共部分） 如图，点 B ，E ，C ，F 在同一条直线上，AB=DE ，AC=DF ，BF=CE ，求证：△ABC ≌△DEF ；3、找第三边（公共边）如图，AD=CB，AB=CD，求证：△ACB≌△CAD．第2课时“边角边”一、课堂导入小伟作业本上画的三角形被墨迹污染了，他想画一个与原来完全一样的三角形，他该怎么办？请你帮助小伟想一个办法，并说明你的理由．想一想：要画一个三角形与小伟画的三角形全等，需要几个与边或角的大小有关的条件？只知道一个条件(一角或一边)行吗？两个条件呢？三个条件呢？让我们一起来探索三角形全等的条件吧！二、知识点梳理边角边1．两边及其夹角分别相等的两个三角形全等．简记为“边角边”或“SAS”．2．“边角边”判定方法可用几何语言表示为：在△ABC 和△A 1B 1C 1中，∵⎩⎪⎨⎪⎧AB ＝A 1B 1，∠B ＝∠B 1，BC ＝B 1C 1，∴△ABC ≌△A 1B 1C 1(SAS)．3．“SSA ”不能判定两个三角形全等． 三、考点分类考点一： 利用“SAS ”判定三角形全等【例1】 如图，A 、D 、F 、B 在同一直线上，AD ＝BF ，AE ＝BC ，且AE ∥BC .求证：△AEF ≌△BCD .解析：由AE ∥BC ，根据平行线的性质，可得∠A ＝∠B ，由AD ＝BF 可得AF ＝BD ，又AE ＝BC ，根据SAS ，即可证得△AEF ≌△BCD .证明：∵AE ∥BC ，∴∠A ＝∠B .∵AD ＝BF ，∴AF ＝BD .在△AEF 和△BCD 中，∵⎩⎪⎨⎪⎧AE ＝BC ，∠A ＝∠B ，AF ＝BD ，∴△AEF ≌△BCD (SAS)．方法总结：判定两个三角形全等时，若有两边一角对应相等时，角必须是两边的夹角．考点二： “边边角”不能证明三角形全等【例2】 下列条件中，不能证明△ABC ≌△DEF 的是( )A ．AB ＝DE ，∠B ＝∠E ，BC ＝EF B ．AB ＝DE ，∠A ＝∠D ，AC ＝DFC ．BC ＝EF ，∠B ＝∠E ，AC ＝DFD ．BC ＝EF ，∠C ＝∠F ，AC ＝DF解析：要判断能不能使△ABC ≌△DEF ，应看所给出的条件是不是两边和这两边的夹角，只有选项C 的条件不符合，故选C.方法总结：判断三角形全等时，注意两边与其中一边的对角相等的两个三角形不一定全等．解题时要根据已知条件的位置来考虑，只具备SSA 时是不能判定三角形全等的．考点三：利用全等三角形进行证明或计算【例3】 已知：如图，BC ∥EF ，BC ＝BE ，AB ＝FB ，∠1＝∠2，若∠1＝45°，求∠C 的度数．解析：利用已知条件易证∠ABC ＝∠FBE ，再根据全等三角形的判定方法可证明△ABC ≌△FBE ，由全等三角形的性质即可得到∠C ＝∠BEF .再根据平行，可得出∠BEF 的度数，从而可知∠C 的度数．解：∵∠1＝∠2，∴∠ABC ＝∠FBE .在△ABC 和△FBE 中，∵⎩⎪⎨⎪⎧BC ＝BE ，∠ABC ＝∠FBE ，AB ＝FB ，∴△ABC≌△FBE (SAS)，∴∠C ＝∠BEF .又∵BC ∥EF ，∴∠C ＝∠BEF ＝∠1＝45°.方法总结：全等三角形是证明线段和角相等的重要工具．考点四： 全等三角形与其他图形的综合【例4】 如图，四边形ABCD 、DEFG 都是正方形，连接AE 、CG .求证：(1)AE ＝CG ；(2)AE ⊥CG .解析：(1)因为已知条件中有两个正方形，所以AD ＝CD ，DE ＝DG ，它们的夹角都是∠ADG加上直角，可得夹角相等，所以△ADE 和△CDG 全等；(2)再利用互余关系可以证明AE ⊥CG .证明：(1)∵四边形ABCD 、DEFG 都是正方形，∴AD ＝CD ，GD ＝ED .∵∠CDG ＝90°＋∠ADG ，∠ADE ＝90°＋∠ADG ，∴∠CDG ＝∠ADE .在△ADE 和△CDG 中，∵⎩⎪⎨⎪⎧AD ＝CD ，∠ADE ＝∠CDG ，DE ＝GD ，∴△ADE≌△CDG (SAS)，∴AE ＝CG ；(2)设AE 与DG 相交于M ，AE 与CG 相交于N ，在△GMN 和△DME 中，由(1)得∠CGD ＝∠AED ，又∵∠GMN ＝∠DME ，∠DEM ＋∠DME ＝90°，∴∠CGD ＋∠GMN ＝90°，∴∠GNM ＝90°，∴AE ⊥CG .【课堂练习】1、找角（加公共部分） 如图所示，CD=CA ，∠1=∠2，EC=BC ，求证：△ABC ≌△DEC ．2、找边（加公共部分） 如图，点 E ，F 在 A B 上，AD=BC ，∠A=∠B ，AE=BF ．求证：△ADF ≌△BCE ．3、角转换，边转换如图，点E、F 在A C 上，AB∥CD，AB=CD，AE=CF，求证：△ABF≌△CDE．第2课时“角边角”“角角边”一、情境导入如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪块去？学生活动：学生先自主探究出答案，然后再与同学进行交流．教师点拨：显然仅仅带①或②是无法配成完全一样的玻璃的，而仅仅带③则可以，为什么呢？本节课我们继续研究三角形全等的判定方法．二、知识点梳理“角边角”“角角边”1．角边角：两角及其夹边分别相等的两个三角形全等．简记为“角边角”或“ASA ”． 2．角角边：两角分别相等且其中一组等角的对边相等的两个三角形全等．简记为“角角边”或“AAS ”．3．三角形全等是证明线段相等或角相等的常用方法． 三、考点分类考点一： 应用“ASA ”判定两个三角形全等【例1】 如图，AD ∥BC ，BE ∥DF ，AE ＝CF ，求证：△ADF ≌△CBE .解析：根据平行线的性质可得∠A ＝∠C ，∠DFE ＝∠BEC ，再根据等式的性质可得AF ＝CE ，然后利用ASA 可证明△ADF ≌△CBE .证明：∵AD ∥BC ，BE ∥DF ，∴∠A ＝∠C ，∠DFE ＝∠BEC .∵AE ＝CF ，∴AE ＋EF ＝CF ＋EF ，即AF ＝CE .在△ADF 和△CBE 中，∵⎩⎪⎨⎪⎧∠A ＝∠C ，AF ＝CE ，∠DFA ＝∠BEC ，∴△ADF ≌△CBE (ASA)．方法总结：在“ASA ”中，包含“边”和“角”两种元素，是两角夹一边而不是两角及一角的对边对应相等，应用时要注意区分；在“ASA ”中，“边”必须是“两角的夹边”．考点二： 应用“AAS ”判定两个三角形全等【例2】 如图，在△ABC 中，AD ⊥BC 于点D ，BE ⊥AC 于E .AD 与BE 交于F ，若BF ＝AC ，求证：△ADC ≌△BDF .解析：先证明∠ADC ＝∠BDF ，∠DAC ＝∠DBF ，再由BF ＝AC ，根据AAS 即可得出两三角形全等．证明：∵AD ⊥BC ，BE ⊥AC ，∴∠ADC ＝∠BDF ＝∠BEA ＝90°.∵∠AFE ＝∠BFD ，∠DAC ＋∠AEF ＋∠AFE ＝180°，∠BDF ＋∠BFD ＋∠DBF ＝180°，∴∠DAC ＝∠DBF .在△ADC 和△BDF 中，∵⎩⎪⎨⎪⎧∠DAC ＝∠DBF ，∠ADC ＝∠BDF ，AC ＝BF ，∴△ADC ≌△BDF (AAS)．方法总结：在“AAS ”中，“边”是“其中一个角的对边”．考点三： 灵活选用不同的方法证明三角形全等【例3】 如图，已知AB ＝AE ，∠BAD ＝∠CAE ，要使△ABC ≌△AED ，还需添加一个条件，这个条件可以是______________．解析：由∠BAD ＝∠CAE 得到∠BAC ＝∠EAD ，加上AB ＝AE ，所以当添加∠C ＝∠D 时，根据“AAS ”可判断△ABC ≌△AED ；当添加∠B ＝∠E 时，根据“ASA ”可判断△ABC ≌△AED ；当添加AC ＝AD 时，根据“SAS ”可判断△ABC ≌△AED .方法总结：判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS.注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．考点四：运用全等三角形解决有关问题【例4】 已知：在△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E .求证：(1)△BDA ≌△AEC ；(2)DE ＝BD ＋CE .解析：(1)由垂直的关系可以得到一对直角相等，利用同角的余角相等得到一对角相等，再由AB ＝AC ，利用AAS 即可得证；(2)由△BDA ≌△AEC ，可得BD ＝AE ，AD ＝EC ，根据DE ＝DA ＋AE 等量代换即可得证．证明：(1)∵BD ⊥m ，CE ⊥m ，∴∠ADB ＝∠CEA ＝90°，∴∠ABD ＋∠BAD ＝90°.∵AB ⊥AC ，∴∠BAD ＋∠CAE ＝90°，∴∠ABD ＝∠CAE .在△BDA 和△AEC 中，∵⎩⎪⎨⎪⎧∠ADB ＝∠CEA ＝90°，∠ABD ＝∠CAE ，AB ＝AC ，∴△BDA ≌△AEC (AAS)；(2)∵△BDA ≌△AEC ，∴BD ＝AE ，AD ＝CE ，∴DE ＝DA ＋AE ＝BD ＋CE .方法总结：利用全等三角形可以解决线段之间的关系，比如线段的相等关系、和差关系等，解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化．【课堂练习】1、角转换，边转换 如图，已知 A B ∥DE ，BC ∥EF ，D ，C 在 A F 上，且 A D=CF ， 求证：△ABC ≌△DEF ．2、隐含条件（对顶角） 已知：如图 A C ，BD 相交于点 O ，∠A=∠D ，AB=CD ， 求证：△AOB ≌△DOC ．3、利用外角找角相等1如图，∠A=∠B，AE=BE，点 D在AC 边上，∠1=∠2，AE 和BD 相交于点O．求证：△AEC≌△BED；4、利用外角找角相等2如图，在△ABC 中，AB=AC，点D、E、F 分别在边A B、BC、AC 上，且B D=CE，∠DEF=∠B．图中是否存在和△BDE 全等的三角形？说明理由．第4课时“斜边、直角边”一、课堂导入舞台背景的形状是两个直角三角形，工作人员想知道这两个直角三角形是否全等，但每个三角形都有一条直角边被花盆遮住无法测量．(1)你能帮他想个办法吗？(2)如果他只带了一个卷尺，能完成这个任务吗？工作人员测量了每个三角形没有被遮住的直角边和斜边，发现它们分别对应相等，于是他就肯定“两个直角三角形是全等的”，你相信他的结论吗？二、知识点梳理“斜边、直角边”1．斜边、直角边：斜边和一条直角边分别相等的两个直角三角形全等．简记为“斜边、直角边”或“HL”．2．方法归纳：(1)证明两个直角三角形全等的常用方法是“HL”，除此之外，还可以选用“SAS”“ASA”“AAS”以及“SSS”．(2)寻找未知的等边或等角时，常考虑转移到其他三角形中，利用三角形全等来进行证明．三、考点分类考点一：应用“斜边、直角边”判定三角形全等【例1】如图，已知∠A＝∠D＝90°，E、F在线段BC上，DE与AF交于点O，且AB＝CD，BE＝CF.求证：Rt△ABF≌Rt△DCE.解析：由题意可得△ABF 与△DCE 都为直角三角形，由BE ＝CF 可得BF ＝CE ，然后运用“HL ”即可判定Rt △ABF 与Rt △DCE 全等．证明：∵BE ＝CF ，∴BE ＋EF ＝CF ＋EF ，即BF ＝CE .∵∠A ＝∠D ＝90°，∴△ABF 与△DCE都为直角三角形．在Rt △ABF 和Rt △DCE 中，∵⎩⎪⎨⎪⎧BF ＝CE ，AB ＝CD ，∴Rt △ABF ≌Rt △DCE (HL)．方法总结：利用“HL ”判定三角形全等，首先要判定这两个三角形是直角三角形，然后找出对应的斜边和直角边相等即可．考点二： 利用“HL ”判定线段相等【例2】 如图，已知AD ，AF 分别是两个钝角△ABC 和△ABE 的高，如果AD ＝AF ，AC ＝AE .求证：BC ＝BE .解析：根据“HL ”证Rt △ADC ≌Rt △AFE ，得CD ＝EF ，再根据“HL ”证Rt △ABD ≌Rt △ABF ，得BD ＝BF ，最后证明BC ＝BE .证明：∵AD ，AF 分别是两个钝角△ABC 和△ABE 的高，且AD ＝AF ，AC ＝AE ，∴Rt △ADC ≌Rt △AFE (HL)．∴CD ＝EF .∵AD ＝AF ，AB ＝AB ，∴Rt △ABD ≌Rt △ABF (HL)．∴BD ＝BF .∴BD －CD ＝BF －EF .即BC ＝BE .方法总结：证明线段相等可通过证明三角形全等解决，作为“HL ”公理就是直角三角形独有的判定方法．所以直角三角形的判定方法最多，使用时应该抓住“直角”这个隐含的已知条件．考点三： 利用“HL ”判定角相等或线段平行【例3】 如图，AB ⊥BC ，AD ⊥DC ，AB ＝AD ，求证：∠1＝∠2.解析：要证角相等，可先证明全等．即证Rt △ABC ≌Rt △ADC ，进而得出角相等． 证明：∵AB ⊥BC ，AD ⊥DC ，∴∠B ＝∠D ＝90°，∴△ABC 与△ACD 为直角三角形．在Rt△ABC 和Rt △ADC 中，∵⎩⎪⎨⎪⎧AB ＝AD ，AC ＝AC ，∴Rt △ABC ≌Rt △ADC (HL)，∴∠1＝∠2.方法总结：证明角相等可通过证明三角形全等解决．考点四： 利用“HL ”解决动点问题【例4】 如图，有一直角三角形ABC ，∠C ＝90°，AC ＝10cm ，BC ＝5cm ，一条线段PQ ＝AB ，P 、Q 两点分别在AC 上和过A 点且垂直于AC 的射线AQ 上运动，问P 点运动到AC 上什么位置时△ABC 才能和△APQ 全等？解析：本题要分情况讨论：(1)Rt △APQ ≌Rt △CBA ，此时AP ＝BC ＝5cm ，可据此求出P 点的位置．(2)Rt △QAP ≌Rt △BCA ，此时AP ＝AC ，P 、C 重合．解：根据三角形全等的判定方法HL 可知：(1)当P 运动到AP ＝BC 时，∵∠C ＝∠QAP ＝90°.在Rt △ABC 与Rt △QPA中，∵⎩⎪⎨⎪⎧AP ＝BC ，PQ ＝AB ，∴Rt △ABC ≌Rt △QPA (HL)，∴AP ＝BC ＝5cm ；(2)当P 运动到与C 点重合时，AP ＝AC .在Rt △ABC 与Rt △QPA中，∵⎩⎪⎨⎪⎧AP ＝AC ，PQ ＝AB ，∴Rt △QAP≌Rt △BCA (HL)，∴AP ＝AC ＝10cm ，∴当AP ＝5cm 或10cm 时，△ABC 才能和△APQ 全等．方法总结：判定三角形全等的关键是找对应边和对应角，由于本题没有说明全等三角形的对应边和对应角，因此要分类讨论，以免漏解．考点五： 综合运用全等三角形的判定方法判定直角三角形全等【例5】 如图，CD ⊥AB 于D 点，BE ⊥AC 于E 点，BE ，CD 交于O 点，且AO 平分∠BAC .求证：OB ＝OC .解析：已知BE ⊥AC ，CD ⊥AB 可推出∠ADC ＝∠BDC ＝∠AEB ＝∠CEB ＝90°，由AO 平分∠BAC 可知∠1＝∠2，然后根据AAS 证得△AOD ≌△AOE ，根据ASA 证得△BOD ≌△COE ，即可证得OB ＝OC .证明：∵BE ⊥AC ，CD ⊥AB ，∴∠ADC ＝∠BDC ＝∠AEB ＝∠CEB ＝90°.∵AO 平分∠BAC ，∴∠1＝∠2.在△AOD 和△AOE 中，∵⎩⎪⎨⎪⎧∠ADC ＝∠AEB ，∠1＝∠2，OA ＝OA ，∴△AOD ≌△AOE (AAS)．∴OD ＝OE .在△BOD 和△COE 中，∵⎩⎪⎨⎪⎧∠BDC ＝∠CEB ，OD ＝OE ，∠BOD ＝∠COE ，∴△BOD ≌△COE (ASA)．∴OB ＝OC .方法总结：判定直角三角形全等的方法除“HL ”外，还有：SSS 、SAS 、ASA 、AAS.【课堂练习】如图，在△ABC 中，AB=AC ，DE 是过点 A 的直线，BD ⊥DE 于 D ，CE ⊥DE 于点 E ； （1）若 B 、C 在 D E 的同侧（如图所示）且 A D=CE ．求证：AB ⊥AC ；（2）若。

全等三角形一、全等三角形的概念与性质1、概念：能够完全重合的两个三角形叫做全等三角形。

（1）表示方法：两个三角形全等用符号“≌”来表示，记作ABC∆≌DEF∆2、性质：（1）对应边相等（2）对应角相等（3）周长相等（4）面积相等1．下列各组的两个图形属于全等图形的是( )2．如图，△ABD≌△ACE，则∠B与________，∠AEC与________，∠A与________是对应角；则AB与________，AE与________，EC与________是对应边．第2题图第3题图3．如图，△ABC≌△CDA，∠ACB＝30°，则∠CAD的度数为________．4．如图，若△ABO≌△ACD，且AB＝7cm，BO＝5cm，则AC＝________cm.第4题图第5题图5．如图，△ACB≌△DEB，∠CBE＝35°，则∠ABD的度数是________．6．如图，△ABC≌△DCB，∠ABC与∠DCB是对应角．(1)写出其他的对应边和对应角；(2)若AC＝7，DE＝2，求BE的长．二、全等三角形的判定1 全等三角形的判定方法：（SAS）,(SSS), (ASA), (AAS),(HL)边边边（SSS）边角边（SAS）角边角(ASA) 角角边AAS 直角边和斜边（HL）三边对应相等的两三角形全等有两边和它们的夹角对应相等的两个三角形全等有两角和它们的夹边对应相等的两个三角形全等.两角和及其中一个角所对的边对应相等的两个三角形全等.有一条斜边和一条直角边对应相等的两个直角三角形全等(HL）专题一：“边边边”全等三角形（SSS）三边对应相等的两个三角形全等，简写成“边边边”或“SSS”，几何表示如图，在ABC∆和DEF∆中，ABCEFBCEBDEAB∆∴⎪⎩⎪⎨⎧=∠=∠=≌)(SASDEF∆【典型例题】AC=DF （SSS)例1找第三边（减公共部分）如图，已知点B，C，D，E 在同一直线上，且A B=AE，AC=AD，BD=CE．求证：△ABC≌△AED．例2找第三边（加公共部分）如图，点B，E，C，F 在同一条直线上，AB=DE，AC=DF，BF=CE，求证：△ABC≌△DEF；例3找第三边（公共边）如图，AD=CB，AB=CD，求证：△ACB≌△CAD．巩固练习1．如图，下列三角形中，与△ABC全等的是( )A．① B．② C．③ D．④2．如图，已知AB＝AD，CB＝CD，∠B＝30°，则∠D的度数是( ) A．30° B．60° C．20° D．50°第2题图第3题图3．如图，AB＝DC，请补充一个条件：________，使其能由“SSS”判定△ABC≌△DCB.4．如图，A，C，F，D在同一直线上，AF＝DC，AB＝DE，BC＝EF.求证：△ABC≌△DEF.5．如图，AB＝AC，AD＝AE，BD＝CE.求证：∠ADE＝∠AED.6.如图，在ABC ∆中，M 在BC 上，D 在AM 上，AB=AC , DB=DC 求证：AM 是ABC ∆的角平分线7.如图：在△ABC 中，BA=BC ，D 是AC 的中点。

全等三角形的判定方法50道经典题摘要：1.全等三角形的判定方法概述2.边边边（SSS）判定法3.边角边（SAS）判定法4.角边角（ASA）判定法5.角角边（AAS）判定法6.斜边，直角边（HL）判定法7.经典题型一：已知三边长度，判断全等8.经典题型二：已知两边和夹角，判断全等9.经典题型三：已知两角和夹边，判断全等10.经典题型四：已知两边和等角对边相等，判断全等11.经典题型五：已知斜边和直角边，判断全等12.经典题型六：综合运用判定法，判断全等13.解题技巧与注意事项14.巩固练习：50道经典题解答与解析正文：全等三角形的判定方法是数学中非常重要的内容，掌握判定方法有助于解决许多实际问题。

本文将详细介绍全等三角形的判定方法，并通过50道经典题进行巩固练习。

1.全等三角形的判定方法概述全等三角形判定方法有六种，分别为：边边边（SSS）、边角边（SAS）、角边角（ASA）、角角边（AAS）、斜边，直角边（HL）。

2.边边边（SSS）判定法当两个三角形的三条边分别对应相等时，这两个三角形全等。

例如，若给出三条线段长度ABc，BCa，ACb，我们可以通过以下步骤确定全等三角形：步骤一：确定一边AB。

步骤二：分别以AB为圆心，做半径为b，a长的圆，交于点C。

步骤三：连接AC，BC。

这样，三角形的大小和形状就都被确定出来。

3.边角边（SAS）判定法当两个三角形的两边和它们的夹角分别相等时，这两个三角形全等。

例如，已知ABc，CAB，我们可以通过以下步骤确定全等三角形：步骤一：画射线AE，并在射线AE上截取ACc。

步骤二：在射线AD上截取ABc。

步骤三：连接BC。

这样，三角形的大小和形状就都被确定出来。

4.角边角（ASA）判定法当两个三角形的两个角和它们的夹边分别相等时，这两个三角形全等。

例如，已知ABc，CAB，我们可以通过以下步骤确定全等三角形：步骤一：先确定一边ABc。

步骤二：在AB同旁画DAB，EBA，AD，BE交于点C。

8年级数学人教版上册同步练习全等三角形三角形全等的判定（含答案解析）12.1全等三角形12.2三角形全等的判定专题一三角形全等的判定1．如图，BD是平行四边形ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB 的平分线DF交BC于点F．求证：△ABE≌△CDF．2．如图，在△ABC中，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△BDE≌△CDF (不再添加其他线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是：__________；（2）证明：3．如图，△ABC中，点D在BC上，点E在AB上，BD=BE，要使△ADB≌△CEB，还需添加一个条件．（1）给出下列四个条件：①AD=CE；②AE=CD；③∠BAC=∠BCA；④∠ADB=∠CEB；请你从中选出一个能使△ADB≌△CEB的条件，并给出证明；（2）在（1）中所给出的条件中，能使△ADB≌△CEB的还有哪些？直接在题后横线上写出满足题意的条件序号．__________________．专题二全等三角形的判定与性质4．如图，已知△ABC中，∠ABC=45°，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A6B．4 C．23D．55．【2013·襄阳】如图，在△ABC中，AB＝AC，AD⊥BC于点D，将△ADC绕点A顺时针旋转，使AC与AB重合，点D落在点E处，AE的延长线交CB的延长线于点M，EB的延长线交AD的延长线于点N.求证：AM＝AN.NMEDB CA6．【2012·泸州】如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边三角形CDE，使点E﹨A在直线DC的同侧，连接AE．求证：AE∥BC．专题三全等三角形在实际生活中的应用7．如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是（）A．60°B．90°C．120°D．150°8．有一座小山，现要在小山A﹨B的两端开一条隧道，施工队要知道A﹨B两端的距离，于是先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A﹨B两端的距离，你能说说其中的道理吗？9．已知如图，要测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，对吗？为什么？状元笔记【知识要点】1．全等三角形能够完全重合的两个三角形叫做全等三角形．2．全等三角形的性质全等三角形的对应边相等，全等三角形的对应角相等．3．三角形全等的判定方法(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”)．(2)两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)．(3)两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)．(4)两个角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)．4．直角三角形全等的判定方法斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边﹨直角边”或“HL”)．【温馨提示】1．两个三角形全等的条件中必须有一条边分别相等，只有角分别相等不能证明两个三角形全等．2．有两边和其中一边的对角分别相等的两个三角形不一定全等．3．“HL”定理指的是斜边和一条直角边分别相等，而不是斜边和直角分别相等．【方法技巧】1．应用全等三角形性质解决问题的前提是准确地确定全等三角形的对应边和对应角，其规律主要有以下几点：（1）以对应顶点为顶点的角是对应角；（2）对应顶点所对应的边是对应边；（3）公共边（角）是对应边（角）；（4）对顶角是对应角；（5）最大边（角）是对应边（角），最小边（角）是对应边（角）．全等三角形的对应边和对应角可以依据字母的对应位置来确定，如若△ABC≌△DEF，说明A与D，B与E，C与F是对应点，则∠ABC与∠DEF是对应角，边AC与边DF 是对应边．2．判定两个三角形全等的解题思路：SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎩找夹角——已知两边找另一边——边为角的对边——找任一角——找夹角的另一边——已知一边一角边为角的邻边找夹边的另一角——找边的对角——找夹边——已知两角找任一边——参考答案:1．证明：平行四边形ABCD 中，AB=CD ，∠A=∠C ，AB ∥CD ， ∴∠ABD=∠CDB ．∵∠ABE=21∠ABD ，∠CDF=21∠CDB ，∴∠ABE=∠CDF ．在△ABE 与△CDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠CDF ABE CDAB C A ∴△ABE ≌△CDF ． 2．解：（1）DC BD =(或点D 是线段BC 的中点)，ED FD =，BE CF =中任选一个即可﹒ （2）以DC BD =为例进行证明： ∵CF ∥BE ，∴∠FCD ﹦∠EBD ．又∵DC BD =，∠FDC =∠EDB ， ∴△BDE ≌△CDF ． 3．解：（1）添加条件②，③，④中任一个即可，以添加②为例说明． 证明：∵AE=CD ，BE=BD ， ∴AB=CB ．又∠ABD=∠CBE ，BE=BD ， ∴△ADB ≌△CEB ． （2）③④．4．B 解析：∵∠ABC =45°，AD ⊥BC ，∴AD =BD ，∠ADC =∠BDH ， ∠AHE =∠BHD =∠C ．∴△ADC ≌△BDH ．∴BH =AC =4．故选B ． 5．证明：如图所示，M∵△AEB由△ADC旋转而得，∴△AEB≌△ADC.∴∠3＝∠1，∠6＝∠C．∵AB＝AC，AD⊥BC，∴∠2＝∠1，∠7＝∠C.∴∠3＝∠2，∠6＝∠7．∵∠4＝∠5，∴∠ABM＝∠ABN．又∵AB＝AB，∴△AMB≌△ANB．∴AM＝AN．6．证明：∵△ABC和△EDC是等边三角形，∴∠BCA＝∠DCE＝60°．∴∠BCA－∠ACD＝∠DCE－∠ACD，即∠BCD＝∠ACE．在△DBC和△EAC中，BC＝AC，∠BCD＝∠ACE，DC＝EC，∴△DBC≌△EAC（SAS）．∴∠DBC＝∠EAC．又∵∠DBC＝∠ACB＝60°，∴∠ACB＝∠EAC．∴AE∥BC．7．B 解析：∵滑梯﹨墙﹨地面正好构成直角三角形，又∵BC=EF，AC=DF，∴Rt△ABC≌Rt△DEF．∴∠ABC=∠DEF，∵∠DEF+∠DFE=90°，∴∠ABC+∠DFE=90°．故选B．8．解：在△ABC和△CED中，AC=CD，∠ACB=∠ECD，EC=BC，∴△ABC≌△CED．∴AB=ED．即量出DE的长，就是A﹨B两端的距离．9．解：对．理由：∵AC ⊥AB,∴∠CAB=∠CAB′=90°. 在△ABC 和△AB′C 中，ACB ACB AC AC CAB CAB =⎧⎪=⎨⎪=⎩∠∠′，，∠∠′， ∴△ABC ≌△AB′C （ASA ）． ∴AB′=AB ．。

12.2.1 三角形全等的判定- “边边边”（一）学习目标1．构建三角形全等条件的探索思路，体会研究几何问题的方法；2．探索并理解“边边边”判定方法，会用“边边边”判定方法证明三角形全等；3．会用尺规作一个角等于已知角，了解作图的道理。

（二）学习重点构建三角形全等条件的探索思路，“边边边”判定方法。

（三）学习难点探索并理解“边边边”判定方法，会用“边边边”判定方法证明三角形全等。

（四）课前预习1.如图,已知AB=AC,若用“SSS”判定△ABD≌△ACD,则需添加的一个条件是 .2.如图,BD,AC交于点O,且OA=OD,如果用“SAS”判定△AOB≌△DOC,那么还需添加的一个条件是.3.如图,AF=CD,AB=DE,EF=BC,那么△ABC≌△DEF的理由是.4.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以直接判定( )A.△ABD≌△ACDB.△BDE≌△CDEC.△ABE≌△ACED.以上都不对5.工人师傅常用角尺平分一个任意角，作法如下：如图，∠AOB是一个任意角，在边OA，OB 上分别取OM=ON。

移动角尺，使角尺两边相同的刻度分别与点M、N重合。

则过角尺顶点C 的射线OC便是∠AOB的角平分线，为什么？请你说明理由。

（五）疑惑摘要预习之后，你还有哪些没有弄清的问题，请记下来，课堂上我们共同探讨。

典型例题例1、如图，有一个三角形钢架，AB =AC ，AD 是连接点A 与BC 中点D 的支架．求证：△ABD ≌△ACD ．例2、如图(1)(2)中，AD=CB，E，F是AC上两动点，且有DE=BF(1)若E、F运动至如图(1)的位置，若有AF=CE.求证：AD//BC(2)若E、F运动至如图（2）的位置，仍有AF=CE.那么AD//BC还成立吗？为什么？图（1）图（2）课后作业一、选择题1.如图,在△ABC中,AB=AC,点D为BC的中点,那么以下结论不正确的是( )A.△ABD≌△ACDB.∠B=∠CC.AD是△ABC的角平分线D.AD不是△ABC的高2.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )A.△MPN≌△MQNB.∠PMN=∠QMNC.MO=NOD.∠MPN=∠MQN3.如图,在四边形ABCD中,AC与BD相交于点O,且AO=DO,BO=CO,AB=DC,则图中全等三角形有( )A.4对B.3对C.2对D.1对4．全等三角形是( )A．三个角对应相等的三角形B．周长相等的两个三角形C．面积相等的两个三角形D．三边对应相等的两个三角形二、填空题5.如图所示,AB=CD,AD=CB,∠2=38°,∠3=72°,则∠A= .6.如图,已知AC=DB,要使△ABC≌△DCB,则只需添加一个适当的条件是(填一个即可).7.如图所示,在△ABD和△ACE中,已知AB=AC,BD=CE,AD=AE,若∠1=20°,则∠2= .8.如图,AB=AC,DB=DC,EB=EC.图中有对全等三角形。

三角形全等的判定方法(5种)例题+练习(全面)本文讲述了全等三角形的判定方法，重点是边角边和角边角。

边角边指两边及其夹角分别相等的两个三角形全等，可以简写成“SAS”。

需要注意的是，必须是两边及其夹角，不能是两边和其中一边的对角。

例如，在图中的△ABC和△ABD中，虽然有一个角和两边相等，但是这两个三角形不全等。

但是在例1中，如果AC=AD，且∠CAB=∠DAB，则可以证明△ACB≌△ADB。

在例2中，如果AD∥BC，且∠ABC=∠DCB，AB=DC，AE=DF，则可以证明BF=CE。

角边角是指两角及其夹边分别相等的两个三角形全等，可以简写成“ASA”。

例如，在例2中，如果AD平分∠BAC，且∠ABD=∠ACD，则可以直接判定△ABD≌△ACD。

在例3中，如果在Rt△ABC中，BC=2cm，CD⊥AB，且EC=BC，EF=5cm，则可以求出AE的长度。

除了边角边和角边角外，还有三种判定全等三角形的条件。

在例5中，如果在△ABC和△DEF中，AB=DE，BC=EF，且有一个角相等，则可以证明△ABC≌△DEF。

在例6中，如果AB∥DE，AB=DE，BF=CE，则可以证明△ABC≌△DEF。

在例7和例8中，分别是通过角平分线和垂线的判定方法来证明两个三角形全等。

总之，掌握全等三角形的判定方法对于解决几何问题非常重要。

1.如图所示，在三角形ABC中，已知AB=DC，∠ABC=∠DCB。

根据角角边相等可知，∠ACB=∠DCB。

又因为AB=DC，所以BC=AC。

因此，根据SSS（边边边）相等可知，△ABC≌△DCB。

同时，∠ACB=∠DCB，AC=BC=DC。

2.如图所示，在三角形ABD和ABF中，已知AD=AE，∠1=∠2，BD=CE。

根据角角边相等可知，∠ABD=∠BCE。

又因为AD=CE，所以BD=BE。

因此，根据SAS（边角边）相等可知，△ABD≌△BCE。

同时，∠ABD=∠BCE，AD=CE=BE。

全等三角形的判定方法五种例题三角形是初中数学学习中的重要内容之一，而全等三角形又是其中比较基础且重要的一部分。

那么，如何判断两个三角形是否全等呢？我们可以从以下5个方法入手。

第一种方法：角角角（AAA）判定法。

当两个三角形的对应角度相等时，就可以判断它们是全等的。

例如：若在两个三角形中角A、角B、角C分别对应相等，则这两个三角形就全等。

第二种方法：边角边（AAS）判定法。

当两个三角形的两边和夹角分别相等时，就可以判断它们是全等的。

例如：若在两个三角形中，两边AB、AC相等，并且夹角A的大小也相等，则这两个三角形就全等。

第三种方法：角边角（ASA）判定法。

当两个三角形的一对角和对应边相等，且另外一对角也相等时，就可以判断它们是全等的。

例如：若在两个三角形中，角A、边BC和角C分别对应相等，并且角B的大小也相等，则这两个三角形全等。

第四种方法：直角边（HL）判定法。

当两个直角三角形的一条直角边和另外一条边相等时，就可以判断它们是全等的。

例如：若在两个三角形中，直角边AB、边AC的长度分别相等，并且三角形ABC还有一个相等的直角，则这两个三角形就全等。

第五种方法：全等多边形拼凑法。

将一个三角形分割成两个或多个小三角形，然后将这些小三角形重新拼凑成另一个三角形。

如果这个三角形和另一个给定的三角形重合，则它们是全等的。

例如：将一个三角形ABC划分成两个小三角形，分别是三角形ABE和三角形AEC，然后将它们重新拼凑成三角形FDC，如果三角形FDC和另一个给定的三角形重合，则这两个三角形就全等。

在实际操作时，我们可以根据题目所给条件，选择一种或多种判定方法，来判断两个三角形是否全等。

因为不同的题目所给条件不同，因此我们要灵活掌握这些判定方法，并且要根据具体情况加以分析和判断。

只有将这些方法掌握好，才能在解题中灵活应用，提高我们的解题能力。

人教版数学八年级上册《12.2三角形全等的判定》同步练习一、单选题（本大题共15小题，共45分）1.（3分）不能确定两个三角形全等的条件是()A. 三条边对应相等B. 两边及其夹角对应相等C. 两角及其中一角的对边对应相等D. 两条边和一条边所对的角对应相等2.（3分）如图，线段AD与BC交于点O，且AC=BD，AD=BC，则下面的结论中不正确的是()A. ΔABC≌ΔBADB. OB=OCC. ∠CAB=∠DBAD. ∠C=∠D3.（3分）在△ABC中，∠C=90°，∠CBA的外角平分线，交AC的延长线于F，交斜边上的高CD的延长线于E，EG∥AC交AB的延长线于G，则下列结论：①CF=CE；②GE=CF；③EF是CG的垂直平分线；④BC=BG．其中正确的是（）A. ①②③④B. ①③④C. ②③④D. ①②4.（3分）如图，AD是ΔABC的高，AD也是ΔABC的中线，则下列结论不一定成立的是()A. AB=ACB. AD=BCC. ∠B=∠CD. ∠BAD=∠CAD5.（3分）B为AC上一点，在AC同侧作等边△EAB及等边△DBC,那么下列式子错误的是( )A. △ABD≌△EBCB. ∠BDA=∠BCEC. △ABE≌△BCDD. 若BE交AD于M，CE交BD于N，那么△NBC≌△MBD6.（3分）如图所示，AB=AC，要说明△ADC≌△AEB，需添加的条件不能是()A. ∠B=∠CB. AD=AEC. ∠ADC=∠AEBD. DC=BE7.（3分）把点M(-2，1)向右平移3个单位长度，再向下平移2个单位长度后得到点N，则N的坐标为( )A. (-4，4)B. (-5，3)C. (1，-1)D. (-5，-1)8.（3分）如图，AB交CD于点O，点O分别是AB与CD的中点，则下列结论中错误的是（）A. ∠A=∠BB. AC=BDC. ∠A+∠B=90°D. AC∥BD9.（3分）如图，∠1=∠2，∠C=∠D，AC、BD交于E点，下列结论中不正确的是（）A. ∠DAE=∠CBEB. △DEA不全等于△CEBC. CE=DED. △EAB是等腰三角形10.（3分）如图，在正方形ABCD中，点E，F分别在BC和CD上，过点A作GA⊥AE，CD的延长线交AG于点G，BE+DF=EF，若∠DAF=30°，则∠BAE的度数为()A. 15°B. 20°C. 25°D. 30°11.（3分）下列说法正确的是( )A. 有两边和一个角相等的两个三角形全等B. 两条直角边对应相等的两个直角三角形全等C. 三角形的一条中线把三角形分成的两个小三角形全等D. 有两边和其中一边的对角对应相等的两个三角形全等12.（3分）在下列命题中，是假命题的个数有（）①相等的角是对顶角；②两条直线被第三条直线所截，同位角相等；③面积相等的两个三角形全等；④三角形的一个外角等于两个内角的和．A. 4个B. 3个C. 2个D. 1个13.（3分）如图，已知O是线段AC和BD的中点，要说明ΔABO≌ΔCDO，以下回答最合理的是()A. 添加条件∠A=∠CB. 添加条件AB=CDC. 不需要添加条件D. ΔABO和ΔCDO不可能全等14.（3分）如图，∠1=∠2，∠3=∠4，则下面结论中错误的是（）A. △ADC≌△BCDB. △ABD≌△BACC. △AOB≌△CODD. △AOD≌△BOC15.（3分）如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（）A. 2个B. 4个C. 6个D. 8个二、填空题（本大题共5小题，共15分）16.（3分）如图，∠BAC=∠ABD，BD、AC交于点O，要使OC=OD，还需添加一个条件，这个条件可以是____．17.（3分）同学们知道：只有两边和其中一边的对角对应相等的两个三角形不一定全等．你如何处理这三个条件，使这两个三角形全等？如方案（1）：若这两个三角形是直角三角形，则这两个三角形全等．请你仿照方案（1）写出另外一个方案：____．18.（3分）如图，∠1=∠2=30°，∠A=∠B，AE=BE，点D在边AC上，AE与BD相交于点O，则∠C的度数为______.19.（3分）如图，AB=AC，AD=AE，∠BAC=∠DAE，∠1=21°，∠2=30°，∠3= ______ ．20.（3分）如图，已知AD=BC，根据“SAS”，还需要一个条件____，可证明△ABC≌△BAD．三、解答题（本大题共5小题，共40分）21.（8分）如图所示，在四边形ABCD中，AC与BD交于O，AB=AD，CB=CD，∠BCD=45°，BE⊥CD于E，BE与AC交于F.(1)求证：CF=2BO；(2)若DE=1，求CF⋅FO的值．22.（8分）已知：∠A=90°，∠ADE=120°，BD平分∠ADE，AD=DE.(1)ΔBAD与ΔBED全等吗？请说明理由；(2)若DE=2，试求AC与EC的长．23.（8分）已知：如图，点E，D，B，F在同一条直线上，AD//CB，∠BAD=∠BCD，DE=BF.求证：(1)AD=BC；(2)AE//CF．24.（8分）如图，在RtΔABC中，∠ABC=90°，延长AB至E，使AE=AC，过E作EF⊥AC于F，EF交BC于G.(1)求证：BE=CF；(2)若∠E=40°，求∠AGB的度数．25.（8分）如图，AD=BC，请添加一个条件，使图中存在全等三角形并给予证明．你所添加的条件为：____；得到的一对全等三角形是△____≌△____．答案和解析1.【答案】D;【解析】解：A、三条边对应相等，符合SSS，能判定三角形全等；B、两边及其夹角对应相等，符合SAS，能判定三角形全等；C、两角及其中一角的对边对应相等，能判定三角形全等，符合AAS．D、两条边和一条边所对的角对应相等，满足SSA，不能判定三角形全等．故选D．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，HL，做题时要结合各选项的已知逐个进行验证．该题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．2.【答案】B;【解析】解：A、根据SSS可以证明ΔABC≌ΔBAD，故本选项正确；B、OB和OC显然不是对应边，故本选项错误；C、根据全等三角形的对应角相等，得∠CAB=∠DBA，故本选项正确；D、根据全等三角形的对应角相等，得∠C=∠D，故本选项正确．故选：B．根据SSS可以证明ΔABC≌ΔBAD，从而得到其对应角相等、对应边相等．该题考查全等三角形的判定和性质，解答该题的关键是熟练掌握基本知识，属于中考常考题型．3.【答案】A;【解析】解：∵BF平分∠GBC，∴∠GBF=∠CBF，而∠GBF=∠EBD，∴∠CBF=∠EBD，∵∠BCA=90°，CD为高，∴∠F=∠BED，∴CF=CE，所以①正确；又∵GE∥AF，∴∠F=∠GEB，∴∠GEB=∠CEB，而∠GBF=∠CBF，∴∠GBE=∠CBE，∴△BEG≌△BEC，∴GE=CE，∴GE=CF，所以②正确；在△EGC中，EC=EG，BE平分∠CEG，∴EB垂直平分GC，所以③正确；∴BG=BC，所以④正确．故选A．4.【答案】B;【解析】解：∵AD是ΔABC的高，AD也是ΔABC的中线，∴BC⊥AD，BD=CD，在ΔABD和ΔACD中，{AD=AD∠ADB=∠ADC=90°BD=CD，∴ΔABD≌ΔACD(SAS)，∴AB=AC，∠B=∠C，∠BAD=∠BAD．故选：B．证明ΔABD≌ΔACD，可得AB=AC，∠B=∠C，∠BAD=∠BAD.则答案得出．考查了等腰三角形的性质及全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解答该题的关键．5.【答案】C;【解析】△ABE与△BCD未必全等，故选C。

全等三角形的判定方法50道经典题全等三角形的判定方法是初中数学中重要的一部分，主要包括以下50道经典题目。

1. 如何通过边长判断两个三角形是否全等？答：如果两个三角形的三条边对应相等，则它们全等。

2. 如果通过角度判断两个三角形是否全等？答：如果两个三角形的三个角度对应相等，则它们全等。

3. 如何通过边角判断两个三角形是否全等？答：如果两个三角形中有一个角相等，并且两边对应相等，则它们全等。

4. 如果两个三角形的底边相等，底边上的高相等，判断它们是否全等。

答：根据边角对应的原理，如果底边和高都相等，则这两个三角形全等。

5. 给定两个相等的边和它们之间的夹角，判断它们所在的两个三角形是否全等。

答：根据边角对应的原理，如果两个相等的边和它们之间的夹角都相等，则这两个三角形全等。

6. 如果两个三角形的一个角相等，并且这个角的两边分别等于另一个三角形的两个角的两边，判断它们是否全等。

答：根据边角边的原理，如果两个三角形的一个角相等，并且这个角的两边分别等于另一个三角形的两个角的两边，则这两个三角形全等。

7. 如何通过勾股定理判断两个三角形是否全等？答：如果两个三角形的两条边的平方和相等，则它们全等。

8. 如果两个三角形的一个角相等，并且两边的比例相等，判断它们是否全等。

答：根据角边角的原理，如果两个三角形的一个角相等，并且两边的比例相等，则这两个三角形全等。

9. 如果两个三角形的两个角相等，并且两边的比例相等，判断它们是否全等。

答：根据角角边的原理，如果两个三角形的两个角相等，并且两边的比例相等，则这两个三角形全等。

10. 给定两个相等的边和它们夹角的正弦值，判断它们所在的两个三角形是否全等。

答：根据正弦定理，如果两个相等的边和它们夹角的正弦值都相等，则这两个三角形全等。

11. 给定两个相等的边和它们夹角的余弦值，判断它们所在的两个三角形是否全等。

答：根据余弦定理，如果两个相等的边和它们夹角的余弦值都相等，则这两个三角形全等。

12.2全等三角形判定知识要点：三角形全等的判定(1)边边边(SSS)：三边分别相等的两个三角形全等。

(2)边角边(SAS)：两边和它们的夹角分别相等的两个三角形全等。

(3)角边角(ASA)：两角和它们的夹边分别相等的两个三角形全等。

(4)角角边(AAS)：两角和其中一个角的对边分别相等的两个三角形全等。

(5)斜边、直角边(HL)：斜边和一条直角边分别相等的两个直角三角形全等。

一、单选题1．如图，12∠=∠，下列条件中不能使．．．ABD ACD ∆≅∆的是（ ）A ．AB AC = B ．B C ∠=∠ C ．ADB ADC ∠=∠D ．DB DC = 2．如图所示，则下面图形中与图中△ABC 一定全等的三角形是（ ）A ．B ．C ．D ．3．如图，有两个长度相同的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )A．90°B．120°C．135°D．150°4．有一个小口瓶（如图所示），想知道它的内径是多少，但是尺子不能伸到里边直接测，于是拿两根长度相同的细木条，把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（）A．边角边B．角边角C．边边边D．角角边5．如图，用尺规作出∠OBF=∠AOB，作图痕迹MN是A．以点B为圆心，OD为半径的弧B．以点B为圆心，DC为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DC为半径的弧6．如图，已知，，，则图中全等三角形的总对数是A．3 B．4 C．5 D．67．如图，FE=BC，DE=AB，∠B=∠E=40°，∠F=70°，则∠A=( )A．40°B．50°C．60°D．70°8．如图，已知AB∥CF，E为DF的中点，若AB=9cm，CF=5cm，则BD等于（）A．2cm B．3cm C．4cm D．5cm9．如图，已知AC＝DB，AO＝DO，CD＝100 m，则A，B两点间的距离( )A．大于100 m B．等于100 mC．小于100 m D．无法确定10．如图，AB⊥BC且AB=BC，DE⊥CD且DE=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）A．36 B．48 C．72 D．108二、填空题11．如图，若AB＝AD，加上一个条件_____，则有△ABC≌△ADC．12．如图，已知BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=__________．13．如图，已知∠1=∠2=90°，AD=AE，那么图中有____对全等三角形.14．如图，Rt∆ABC 中，∠BAC = 90°，AB =AC ，分别过点B、C 作过点A 的直线的垂线BD、CE ，垂足分别为D、E ，若BD = 4，CE=2，则DE= （_________）15．如图，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，AD ⊥CE ，垂足分别为E ，D ，AD ＝25，DE ＝17，则BE ＝______．三、解答题16．如图，点E ，F 在CD 上，AD CB ，DE CF =，A B ∠=∠，试判断AF 与BE 有怎样的数量和位置关系，并说明理由.17．已知：如图，AB=AC ，PB=PC ，PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ．证明：（1）PD=PE ．（2）AD=AE ．18．已知：如图，AE ∥CF ，AB=CD ，点B 、E 、F 、D 在同一直线上，∠A=∠C ．求证：（1）AB∥CD；（2）BF=DE．19．如图，点M.N在线段AC上，AM=CN，AB∥CD，AB=CD.请说明△ABN≌△CDM的理由；答案1．D 2．B3．A4．A5．D6．D7．D8．C9．B10．C11．BC ＝DC12．150°13．314．615．816．解：AF 与BE 平行且相等，因为AD CB ，所以C D ∠=∠.因为DE CF =，所以CE DF =.又因为A B ∠=∠，所以AFD BEC ∆≅∆.所以AF BE =，AFD BEC ∠=∠.所以AF BE .17．解：证明：（1）连接AP ．在△ABP 和△ACP 中，AB=AC PB=PC AP=AP ⎧⎪⎨⎪⎩，∴△ABP ≌△ACP （SSS ）．∴∠BAP=∠CAP ，又∵PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ，∴PD=PE （角平分线上点到角的两边距离相等）．（2）在△APD 和△APE 中，∵90PAD PAE ADP AEP AP AP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴△APD ≌△APE （AAS ），∴AD=AE ；18．解：（1）∵AB ∥CD ，∴∠B=∠D ．在△ABE 和△CDF 中，A CAB CD B D∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABE ≌△CDF （ASA ），∴∠B=∠D ，∴AB ∥CD ；（2）∵△ABE ≌△CDF ，∴BE=DF ．∴BE+EF=DF+EF ，∴BF=DE ．19．∵AM=CN∴AM+MN=CN+MN即AN=CM∵AB ∥CD∴∠A=∠C在△ABN 和△CDM 中=AN CMA C AB CD=⎧⎪∠∠⎨⎪=⎩∴△ABN ≌△CDM （SAS ）人教版八年级上册12.2全等三角形判定同步练习（包含答案）11 / 11。

人教版八年级数学12.2 全等三角形的判定同步训练一、选择题（本大题共10道小题）1. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能．．判定△ABE≌△ACD()A. ∠B＝∠CB. AD＝AEC. BD＝CED. BE＝CD2. 如图，小强画了一个与已知△ABC全等的△DEF，他画图的步骤是：(1)画DE ＝AB；(2)在DE的同旁画∠HDE＝∠A，∠GED＝∠B，DH，EG相交于点F，小强画图的依据是()A．ASA B．SASC．SSS D．AAS3. 如图所示，已知AB∥DE，点B，E，C，F在同一直线上，AB＝DE，BE＝CF，∠B＝32°，∠A＝78°，则∠F等于()A．55°B．65°C．60°D．70°4. 如图，李颖同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最合理的办法是带哪块玻璃去()A．只带①B．只带②C．只带③D．带①和②5. 已知△ABC的六个元素，下列甲、乙、丙三个三角形中标出了某些元素，则与△ABC全等的三角形是()A．只有乙B．只有丙C．甲和乙D．乙和丙6. 如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是()A．∠A＝∠DB．∠ACB＝∠DBCC．AC＝DBD．AB＝DC7. 在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列条件不能判定Rt△ABC≌Rt△DEF的是()A．AC＝DF，∠B＝∠E B．∠A＝∠D，∠B＝∠EC．AB＝DE，AC＝DF D．AB＝DE，∠A＝∠D8. 如图，AB⊥BC，BE⊥AC，垂足分别为B，E，∠1=∠2，AD=AB，则下列结论正确的是()A.∠1=∠EFDB.BE=ECC.BF=CDD.FD∥BC9. 如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝6，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于()A. 2B. 3C. 2D. 610. 现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确，小雷的作法错误B.小雷的作法正确，小惠的作法错误C.两人的作法都正确D.两人的作法都错误二、填空题（本大题共7道小题）11. 如图，AB＝DE，∠1＝∠2，添加一个适当的条件，使△ABC≌△DEC，则需添加的条件是__________(不添加任何辅助线，填一个即可)．12. 如图，已知在△ABC和△DEF中，∠B＝∠E，BF＝CE，点B，F，C，E在同一条直线上，若使△ABC≌△DEF，则还需添加的一个条件是________(只填一个即可)．13. 如图K－10－10，CA＝CD，AB＝DE，BC＝EC，AC与DE相交于点F，ED与AB相交于点G.若∠ACD＝40°，则∠AGD＝________°.14. 如图，在△ABC中，D，E分别是边AB，AC上的点，过点C作平行于AB 的直线交DE的延长线于点F.若DE＝FE，AB＝5，CF＝3，则BD的长是________．15. 如图，若AB＝AC，BD＝CD，∠A＝80°，∠BDC＝120°，则∠B＝________°.16. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F.若EF＝5 cm，则AE ＝________cm.17. 如图，已知△ABC(AC＞AB)，DE＝BC，以D，E为顶点作三角形，使所作的三角形与△ABC全等，则这样的三角形最多可以作出________个．三、解答题（本大题共4道小题）18. 如图，点B，C分别在∠MAN的边AM，AN上，点E，F在∠MAN内部的射线AD上，∠1，∠2分别是△ABE，△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC.求证：△ABE ≌△CAF.19. 在四边形ABCD 中，AB ＝AD .(1)如图①，若∠B ＝∠D ＝90°，E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD .请直接写出线段EF ，BE ，FD 之间的数量关系：____________．(2)如图②，若∠B ＋∠D ＝180°，E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD ，(1)中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由． (3)如图③，若∠B ＋∠ADC ＝180°，E ，F 分别是边BC ，CD 延长线上的点，且∠EAF ＝12∠BAD ，请直接写出EF ，BE ，FD 三者的数量关系．20. 如图①，点A ，B ，C ，D 在同一直线上，AB=CD ，作EC ⊥AD 于点C ，FB⊥AD 于点B ，且AE=DF . (1)求证:EF 平分线段BC ;(2)若将△BFD 沿AD 方向平移得到图②，其他条件不变，(1)中的结论是否仍成立?请说明理由.21. (1)如图①，在△ABC 中，∠BAC ＝90°，AB ＝CA ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为D ，E.求证：DE ＝BD ＋CE.(2)如图②，将(1)中的条件改为：在△ABC 中，AB ＝CA ，D ，A ，E 三点都在直线m 上，并且有∠BDA ＝∠AEC ＝∠BAC ＝α，其中α为任意锐角或钝角，则结论DE ＝BD ＋CE 是否成立？若成立，请你给出证明；若不成立，请说明理由．人教版 八年级数学 12.2 全等三角形的判定同步训练-答案一、选择题（本大题共10道小题）1. 【答案】D【解析】A.当∠B ＝∠C 时，在△ABE 与△ACD 中，⎩⎨⎧∠A ＝∠AAB ＝AC ∠B ＝∠C，∴△ABE ≌△ACD (ASA)；B.当AD ＝AE 时，在△ABE 与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；C.当BD ＝CE 时，∵AB ＝AC ，∴AD ＝AE ，在△ABE与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；D.当BE ＝CD 时，在△ABE与△ACD 中，有AB ＝AC ，BE ＝BD ，∠A ＝∠A ，只满足两边及一对角对应相等的两个三角形不一定全等．故选D.2. 【答案】A3. 【答案】D[解析] 因为AB∥DE，所以∠B＝∠DEF.由条件BE＝CF知BC＝EF.结合条件AB＝DE，可由“SAS”判定△ABC≌△DEF，所以∠F＝∠ACB＝180°－(∠A＋∠B)＝180°－(78°＋32°)＝70°.4. 【答案】C[解析] 由“ASA”的判定方法可知只带③去就可以配出一块和以前一样(全等)的三角形玻璃．5. 【答案】D6. 【答案】C[解析] A．∠A＝∠D，∠ABC＝∠DCB，BC＝BC，符合“AAS”，即能推出△ABC≌△DCB，故本选项不符合题意；B．∠ABC＝∠DCB，BC＝CB，∠ACB＝∠DBC，符合“ASA”，即能推出△ABC ≌△DCB，故本选项不符合题意；C．∠ABC＝∠DCB，AC＝DB，BC＝BC，不符合全等三角形的判定条件，即不能推出△ABC≌△DCB，故本选项符合题意；D．AB＝DC，∠ABC＝∠DCB，BC＝CB，符合“SAS”，即能推出△ABC≌△DCB，故本选项不符合题意．故选C.7. 【答案】B[解析] 选项A，D均可由“AAS”判定Rt△ABC≌Rt△DEF，选项C 可由“HL”判定Rt△ABC≌Rt△DEF，只有选项B不能判定Rt△ABC≌Rt△DEF.8. 【答案】D[解析] 在△AFD和△AFB中，∴△AFD≌△AFB.∴∠ADF=∠ABF.∵AB⊥BC，BE⊥AC，∴∠BEC=∠ABC=90°.∴∠ABF+∠EBC=90°，∠C+∠EBC=90°. ∴∠ADF=∠ABF=∠C. ∴FD ∥BC.9. 【答案】B【解析】如解图，连接OC ，由已知条件易得∠A ＝∠OCE ，CO ＝AO ，∠DOE ＝∠COA ，∴∠DOE －∠COD ＝∠COA －∠COD ，即∠AOD ＝∠COE ，∴△AOD ≌△COE (ASA)，∴AD ＝CE ，进而得CD ＋CE ＝CD ＋AD ＝AC＝22AB ＝3，故选B.10. 【答案】A[解析] AB=b ，AB 是斜边，小惠作的斜边长是b 符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.二、填空题（本大题共7道小题）11. 【答案】答案不唯一，如∠B ＝∠E12. 【答案】答案不唯一，如AB ＝DE[解析] ∵BF ＝CE ，∴BC ＝EF.在△ABC 和△DEF 中，⎩⎨⎧AB ＝DE ，∠B ＝∠E ，BC ＝EF ，∴△ABC ≌△DEF(SAS)．13. 【答案】40[解析] 在△ABC 和△DEC 中，⎩⎨⎧CA ＝CD ，AB ＝DE ，BC ＝EC ，∴△ABC ≌△DEC(SSS)． ∴∠A ＝∠D.又∵∠AFG ＝∠DFC ， ∴∠AGD ＝∠ACD ＝40°.14. 【答案】2[解析] ∵CF ∥AB ，∴∠A ＝∠FCE.在△ADE 和△CFE 中，⎩⎨⎧∠A ＝∠FCE ，∠AED ＝∠CEF ，DE ＝FE ，∴△ADE ≌△CFE(AAS)． ∴AD ＝CF ＝3.∴BD ＝AB －AD ＝5－3＝2.15. 【答案】20[解析] 如图，过点D 作射线AF.在△BAD 和△CAD 中，⎩⎨⎧AB ＝AC ，AD ＝AD ，BD ＝CD ，∴△BAD ≌△CAD(SSS)． ∴∠BAD ＝∠CAD ，∠B ＝∠C.∵∠BDF ＝∠B ＋∠BAD ，∠CDF ＝∠C ＋∠CAD ， ∴∠BDF ＋∠CDF ＝∠B ＋∠BAD ＋∠C ＋∠CAD ， 即∠BDC ＝∠B ＋∠C ＋∠BAC. ∵∠BAC ＝80°，∠BDC ＝120°， ∴∠B ＝∠C ＝20°.16. 【答案】3[解析] ∵∠ACB ＝90°，∴∠ECF ＋∠BCD ＝90°.∵CD ⊥AB ，∴∠BCD ＋∠B ＝90°. ∴∠ECF ＝∠B.在△ABC 和△FCE 中，⎩⎨⎧∠B ＝∠ECF ，BC ＝CE ，∠ACB ＝∠FEC ，∴△ABC ≌△FCE(ASA)．∴AC ＝FE. ∵AE ＝AC －CE ，BC ＝2 cm ，EF ＝5 cm ， ∴AE ＝5－2＝3(cm)．17. 【答案】4[解析] 能画4个，分别是：以点D 为圆心，AB 长为半径画圆；以点E 为圆心，AC 长为半径画圆，两圆相交于两点(DE 上下各一个)，分别与点D ，E 连接后，可得到两个三角形．以点D 为圆心，AC 长为半径画圆；以点E 为圆心，AB 长为半径画圆，两圆相交于两点(DE 上下各一个)，分别与点D ，E 连接后，可得到两个三角形．因此最多能画出4个三角形与△ABC 全等．如图．三、解答题（本大题共4道小题）18. 【答案】证明：∵∠1＝∠2＝∠BAC ，且∠1＝∠BAE ＋∠ABE ，∠2＝∠CAF ＋∠ACF ，∠BAC ＝∠BAE ＋∠CAF ，∴∠BAE ＝∠ACF ，∠ABE ＝∠CAF.在△ABE 和△CAF 中，⎩⎨⎧∠BAE ＝∠ACF ，AB ＝CA ，∠ABE ＝∠CAF ，∴△ABE ≌△CAF(ASA)．19. 【答案】解：(1)EF ＝BE ＋FD(2)(1)中的结论EF ＝BE ＋FD 仍然成立．证明：如图，延长EB 到点G ，使BG ＝DF ，连接AG .∵∠ABC ＋∠D ＝180°，∠ABG ＋∠ABC ＝180°，∴∠ABG ＝∠D.在△ABG 与△ADF 中，⎩⎨⎧AB ＝AD ，∠ABG ＝∠D ，BG ＝DF ， ∴△ABG ≌△ADF(SAS)．∴AG ＝AF ，∠1＝∠2.∴∠1＋∠3＝∠2＋∠3＝∠BAD －∠EAF.又∵∠EAF ＝12∠BAD ，∴∠1＋∠3＝12∠BAD ＝∠EAF ，即∠EAG ＝∠EAF.在△AEG 和△AEF 中，⎩⎨⎧AG ＝AF ，∠EAG ＝∠EAF ，AE ＝AE ， ∴△AEG ≌△AEF.∴EG ＝EF.∵EG ＝BE ＋BG ，∴EF ＝BE ＋FD.(3)EF ＝BE －FD.20. 【答案】解:(1)证明:∵EC ⊥AD ，FB ⊥AD ， ∴∠ACE=∠DBF=90°.∵AB=CD ，∴AB+BC=BC+CD ， 即AC=DB.在Rt △ACE 和Rt △DBF 中， ∴Rt △ACE ≌Rt △DBF (HL).∴EC=FB. 在△CEG 和△BFG 中，∴△CEG ≌△BFG (AAS).∴CG=BG ，即EF 平分线段BC.(2)EF 平分线段BC 仍成立.理由:∵EC ⊥AD ，FB ⊥AD ，∴∠ACE=∠DBF=90°.∵AB=CD ，∴AB-BC=CD-BC ，即AC=DB.在Rt △ACE 和Rt △DBF 中， ∴Rt △ACE ≌Rt △DBF (HL).∴EC=FB.在△CEG 和△BFG 中，∴△CEG ≌△BFG (AAS).∴CG=BG ，即EF 平分线段BC.21. 【答案】解：(1)证明：∵BD ⊥直线m ，CE ⊥直线m ， ∴∠BDA ＝∠AEC ＝90°.∴∠BAD ＋∠ABD ＝90°.∵∠BAC ＝90°，∴∠BAD ＋∠CAE ＝90°. ∴∠CAE ＝∠ABD.在△ADB 和△CEA 中，⎩⎨⎧∠ABD ＝∠CAE ，∠BDA ＝∠AEC ，AB ＝CA ， ∴△ADB ≌△CEA(AAS)．∴BD ＝AE ，AD ＝CE.∴DE ＝AE ＋AD ＝BD ＋CE.(2)成立．证明：∵∠BDA ＝∠BAC ＝α，∴∠DBA ＋∠BAD ＝∠BAD ＋∠EAC ＝180°－α. ∴∠DBA ＝∠EAC.在△ADB 和△CEA 中，⎩⎨⎧∠DBA ＝∠EAC ，∠BDA ＝∠AEC ，AB ＝CA ，∴△ADB≌△CEA(AAS)．∴BD＝AE，AD＝CE.∴DE＝AE＋AD＝BD＋CE.。

教学内容全等三角形的判定教学目标掌握全等三角形的判定方法重点全等三角形的判定探索三角形全等的条件（5种）1 边角边（重点）两边及其夹角分别分别相等的两个三角形全等，可以简写成“边角边”或“SAS”. 注：必须是两边及其夹角,不能是两边和其中一边的对角.原因：如图：在∆ABC和∆ABD中，∠A=∠A,AB=AB,BC=BD,显然这两个三角形不全等. 例1 如图，AC=AD,∠CAB=∠DAB,求证:∆ACB≌∆ADB.例2 如图，在四边形ABCD中，AD∥BC,∠ABC=∠DCB，AB=DC，AE=DF求证：BF=CE.例3．(1)如图①，根据“SAS”,如果BD=CE， = ，那么即可判定△BDC≌△CEB；(2) 如图②，已知BC=EC，∠BCE=ACD，要使△ABC≌△DEC，则应添加的一个条件为例4.如图，已知AD=AE，∠1=∠2，BD=CE，则有△ABD≌，理由是；△ABE≌，理由是．例5．如图，在△ABC和△DEF中，如果AB=DE，BC=EF，只要找出∠ =∠或∥，就可得到△ABC≌△DEF．例6．如图，已知AB∥DE，AB=DE，BF=CE，求证：△ABC≌△DEF．例7．如图，点B在线段AD上，BC∥DE，AB=ED，BC=DB．求证：∠A=∠E例8．如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C．求证：∠A=∠D．2.角边角两角及其夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）例1．如图，在△ABC中，点D是BC的中点，作射线AD，线段AD及其延长线上分别取点E，F，连接CE，BF．添加一个条件，使得△BDF≌△CDE，你添加的条件是：．(不添加辅助线)例2.如图，已知AD平分∠BAC，且∠ABD=∠ACD，则由“AAS”可直接判定△≌△．例3．如图，在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，那么AE= cm．例4.如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE=2，则两平行线AD与BC间的距离为．例5．如图，已知EC=AC，∠BCE=∠DCA，∠A=∠E．求证：BC=DC．例6．如图，在△ABC中，D是BC边上的点 (不与B，C重合)，F，E分别是AD及其延长线上的点，CF∥BE．请你添加一个条件，使△BDE≌△CDF (不再添加其他线段，不再标注或使用其他字母)，并给出证明．(1) 你添加的条件是：；(2) 证明：例7．如图，A在DE上，F在AB上，且BC=DC，∠1=∠2=∠3，则DE的长等于 ( ) A．DC B．BCC．AB D．AE+AC【基础训练】1．如图，已知AB＝DC，∠ABC＝∠DCB，则有△ABC≌_______，理由是_______；且有∠ACB＝_______，AC＝_______．2．如图，已知AD＝AE，∠1＝∠2，BD＝CE，则有△ABD≌_______，理由是_______；△ABF≌_______，理由是_______．3．如图，在△ABC和△BAD中，因为AB＝BA，∠ABC＝∠BAD，_______＝_______，根据“SAS”可以得到△ABC≌△BAD．4．如图，要用“SAS”证△ABC≌△ADE，若AB＝AD，AC＝AE，则还需条件( )．A．∠B＝∠D B∠C＝∠EC．∠1＝∠2 D．∠3＝∠45．如图，OA＝OB，OC＝OD，∠O＝50°，∠D＝35°，则∠AEC等于( )．A．60°B．50°C．45°D．30°6．如图，如果AE＝CF，AD∥BC，AD＝CB，那么△ADF和ACBE全等吗？请说明理由．7．如图，已知AD与BC相交于点O，∠CAB＝∠DBA，AC＝BD．求证：(1)∠C＝∠D；(2)△AOC≌△BOD．8．如图，△ACD和△BCE都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE交DC于F，BD分别交CE、AE于点G、H．试猜测线段AE和BD的位置和数量关系，并说明理由．9．如图，在△ABC中，AB＝AC，AD平分∠BAC．求证：∠DBC＝∠DCB．10．如图，△ABC是等边三角形，D是AB边上的一点，以CD为边作等边三角形CDE，使点E、A在直线DC的同侧，连接AE．求证：AE∥BC．A BC DEF角角边两角分别相等且其中一组等角的对边相等的两个三角形全等，可以简写成“角角边”或“AAS ”. 例1、如图，在△ABC 中，∠ABC ＝45°，H 是高AD 和高BE 的交点，试说明BH ＝AC ．例2、如图，∠ACB=90°，AC=BC ，BE ⊥CE ，AD ⊥CE 于D ，AD=2.5cm ，DE=1.7cm ． 求BE 的长．例3、如图, 在△ABC 中, AC ⊥BC, CE ⊥AB 于E, AF 平分∠CAB 交CE 于点F, 过F 作FD ∥BC 交AB 于点D. 求证：AC ＝AD.例4、如图, 在ABC中, ∠A＝90°, BD平分B, DE⊥BC于E, 且BE＝EC,(1)求∠ABC与∠C的度数；(2)求证：BC＝2AB.边边边三边分别相等的两个三角形全等，可以简写成“边边边”或“SSS”.例1、如图，在四边形ABCD中，AB=CB，AD=CD．你能说明∠C=∠A吗? 试一试．例2、如图，在四边形ABCD中，AB=AD，BC=DC，E为AC上的一动点(不与A重合)，在E移动过程中．BE和DE是否相等? 若相等，请写出证明过程；若不相等，请说明理由．例3．如图，AB=CD ，AE=CF ，BO=DO ，EO=FO ．求证：OC=OA ．斜边、直角边斜边和一条直角边分别相等的两个直角三角形全等，可以简写成“斜边、直角边”或“HL ”。

三角形全等的判定方法压轴题五种模型全攻略【考点导航】目录【典型例题】【考点一用SAS证明两三角形全等】【考点二用ASA证明两三角形全等】【考点三用AAS证明两三角形全等】【考点四用SSS证明两三角形全等】【考点五添一个条件使两三角形全等】【过关检测】【典型例题】【考点一用SAS证明两三角形全等】1(2023春·江苏苏州·七年级校联考阶段练习)如图，在△ABC中，AC>AB，射线AD平分∠BAC，交BC 于点E，点F在边AB的延长线上，AF=AC，连接EF．(1)求证：△AEC≌△AEF．(2)若∠AEB=50°，求∠BEF的度数．【变式训练】1(2023春·云南昭通·九年级校考阶段练习)如图，点A、C、F、D在同一直线上，AF=DC,∠A=∠D, AB=DE．求证：△ABC≌△DEF．2(2023春·四川成都·七年级统考期末)如图在△ABC中，D是BC边上的一点，AB=DB，BE平分∠ABC，交AC边于点E，连接DE．(1)求证：△ABE≌△DBE；(2)若∠A=100°，∠C=40°，求∠DEC的度数．3(2023春·江苏泰州·七年级统考期末)如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，连接BD、CE．(1)求证：△ABD≌△ACE．(2)图中BD和CE有怎样的关系？试证明你的结论．4(2023·江苏南通·统考一模)如图，点A，B，C，D在同一条直线上，AB=CD=13BC，AE=DF，AE∥DF．(1)求证：△AEC≌△DFB；(2)若S△AEC=6，求四边形BECF的面积．【考点二用ASA证明两三角形全等】1(2023春·广东惠州·八年级校考期中)如图，BC∥EF，点C，点F在AD上，AF=DC，∠A=∠D．求证：△ABC≌△DEF．【变式训练】1(2023·校联考一模)如图，点A、D、B、E在同一条直线上，若AD=BE，∠A=∠EDF，∠E=∠ABC.求证：AC=DF．2(2023·浙江温州·温州市第八中学校考三模)如图，在△ABC和△ECD中，∠ABC=∠EDC=90°，点B为CE中点，BC=CD．(1)求证：△ABC≌△ECD．(2)若CD=2，求AC的长．【考点三用AAS证明两三角形全等】1(2023·广东汕头·广东省汕头市聿怀初级中学校考三模)如图，点E在△ABC边AC上，AE=BC，BC∥AD，∠CED=∠BAD．求证：△ABC≌△DEA【变式训练】1(2023·浙江温州·统考二模)如图，AB=BD，DE∥AB，∠C=∠E．(1)求证：△ABC≅△BDE．(2)当∠A=80°，∠ABE=120°时，求∠EDB的度数．2(2023秋·八年级课时练习)如图，已知点C是线段AB上一点，∠DCE=∠A=∠B，CD=CE．(1)求证：△ACD≌△BEC；(2)求证：AB=AD+BE．【考点四用SSS证明两三角形全等】1(2023·云南玉溪·统考三模)如图，点B，E，C，F在一条直线上，AB=DF，AC=DE，BE=CF，求证：△ABC≌△DFC．【变式训练】1(2023·云南·统考中考真题)如图，C是BD的中点，AB=ED,AC=EC．求证：△ABC≌△EDC．2(2023春·全国·七年级专题练习)如图，已知∠E=∠F=90°，点B，C分别在AE，AF上，AB=AC，BD=CD．(1)求证：△ABD≌△ACD；(2)求证：DE=DF．【考点五添一个条件使两三角形全等】1(2023春·宁夏银川·七年级校考期末)如图，在△ABC和△FED中，AD=FC，∠A=∠F，要使△ABC≌△FED，需添加的一个条件是．【变式训练】1(2023·北京大兴·统考二模)如图，点B，E，C，F在一条直线上，AC∥DF，BE=CF，只需添加一个条件即可证明△ABC≌△DEF，这个条件可以是(写出一个即可)．2(2023春·山东青岛·七年级统考期末)如图，点E，F在BC上，BE=CF，∠AFB=∠DEC，请你添加一个条件(不添加字母和辅助线)，使得△ABF≌△DCE，你添加的条件是．3(2023秋·八年级课前预习)如图，AB=AC，D，E分别是AB，AC上的点，要使△ABE≌△ACD，则还需添加的条件是．(只需填写一个合适的条件即可，图中不能再添加其他点或线)【过关检测】一、单选题1(2023春·四川达州·七年级四川省大竹中学校考期末)如图，已知BE=DF，AF∥CE，不能使△ABF≌△CDE的是()A.BF=DEB.AF=CEC.AB∥CDD.∠A=∠C2(2023秋·河南漯河·八年级校考期末)如图，∠A=∠B,AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O，若∠1=42°，则∠BDE的度数为()A.71°B.69°C.67°D.65°3(2023春·辽宁丹东·八年级校考期中)如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB 上的点，且AM=BK，BN=AK，若∠MKN=42°，则∠P的度数为()A.42°B.74°C.84°D.96°二、填空题4(2023春·山东青岛·七年级统考期末)如图，∠l=∠2，现要添加一个条件使△ABD≌△ACD，可以添加．(只添一个即可)．5(2023秋·湖南娄底·八年级统考期末)如图，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．下面四个结论：①∠ABE=∠BAD；②△CBE≌△ACD；③AB=CE；④AD-BE=DE，其中正确的有．6(2023秋·江苏淮安·八年级淮安市浦东实验中学校考开学考试)如图，已知正方形ABCD中，边长为10cm，点E在AB边上，BE=6cm．如果点P在线段BC上以4cm/s的速度由B点向C点运动．同时，点Q在线段CD上以acm/s的速度由C点向D点运动．当a=时，△EBP和△PCQ全等．三、解答题7(2023春·上海嘉定·七年级校考期末)如图，在四边形ABCD中，AD∥BC，点E为对角线BD上一点，∠A=∠BEC，且AD=BE．(1)求证：△ABD≌△ECB；(2)如果∠BDC=75°，求∠ADB的度数．8(2023秋·江苏·八年级校考周测)如图，在△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．(1)试说明AE=CD；(2)若AC=12cm，求BD的长．9(2023秋·湖南长沙·八年级长沙市开福区青竹湖湘一外国语学校校考开学考试)如图所示，在中，于D，于E，与交于点F，且．(1)求证：；(2)已知，求的长．10(2023春·四川成都·七年级成都实外校考期末)已知：如图，点是等边三角形内一点，且，外一点满足，平分．(1)求证：；(2)求的度数．(3)若，试判断与的位置关系，并说明理由．11(2023春·四川达州·七年级校考期末)如图，在中，，，点在线段上运动(不与、重合)，连接，作，交线段于．(1)当时，，；点从向的运动过程中，逐渐变(填“大”或“小”)；(2)当等于多少时，，请说明理由．(3)在点的运动过程中，与的长度可能相等吗？若可以，请直接写出的度数，请说明理由．12(2023春·广东梅州·八年级校考开学考试)在四边形中．(1)如图1，，，，分别是，上的点，且，探究图中，，之间的数量关系．小林同学探究此问题的方法是：延长到点，使．连接，先对比与的关系，再对比与的关系，可得出、、之间的数量关系，他的结论是；(2)如图2，在四边形中，，，、分别是，上的点，且，则上述结论是否仍然成立，请说明理由．(3)如图3，在四边形中，，，若点在的延长线上，点在的延长线上，若，请写出与的数量关系，并给出证明过程．。

专题12.2 三角形全等的判定全等三角形的判定定理（1）边边边（SSS）：三边对应相等的两个三角形全等.（2）边角边（SAS）：两边和它们的夹角对应相等的两个三角形全等.（3）角边角（ASA）：两角和它们的夹边对应相等的两个三角形全等.（4）角角边（AAS）：两角和其中一个角的对边对应相等的两个三角形全等.（5）斜边、直角边（HL）：斜边和一条直角边对应相等的两个直角三角形全等. （只适用两个直角三角形）【例题1】如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）A．∠B=∠C B．AD=AE C．BD=CE D．BE=CD【例题2】如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．【例题3】如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．求证：BD=2CE．一、选择题1．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）A．甲和乙B．乙和丙C．甲和丙D．只有丙2．如图，AB⊥CD，且AB=CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE=a，BF=b，EF=c，则AD的长为（）A．a+c B．b+c C．a﹣b+c D．a+b﹣c3．如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（）A．B．2 C．2D．4．如图，已知∠ABC=∠DCB，添加以下条件，不能判定△ABC≌△DCB的是（）A．∠A=∠D B．∠ACB=∠DBC C．AC=DB D．AB=DC二、填空题5．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是．6．如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF=CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是（只需写一个，不添加辅助线）．三、解答题7．如图，AE和BD相交于点C，∠A=∠E，AC=EC．求证：△ABC≌△EDC．8．如图，已知AC平分∠BAD，AB=AD．求证：△ABC≌△ADC．9．如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．10．如图，已知线段AC，BD相交于点E，AE=DE，BE=CE．（1）求证：△ABE≌△DCE；（2）当AB=5时，求CD的长．11．如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．12．如图，已知AB=AD，AC=AE，∠BAE=∠DAC．求证：∠C=∠E．13．如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，AF与DE交于点G，求证：GE=GF．14．已知：∠AOB．求作：∠A'O'B'，使∠A'O′B'=∠AOB（1）如图1，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C、D；（2）如图2，画一条射线O′A′，以点O′为圆心，OC长为半径间弧，交O′A′于点C′；（3）以点C′为圆心，CD长为半径画弧，与第2步中所而的弧交于点D′；（4）过点D′画射线O′B'，则∠A'O'B'=∠AOB．根据以上作图步骤，请你证明∠A'O'B′=∠AOB．15．如图，AB与CD相交于点E，AE=CE，DE=BE．求证：∠A=∠C．16．已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥BF．17．如图，AB ∥CD ，AB=CD ，CE=BF ．请写出DF 与AE 的数量关系，并证明你的结论．18．如图，点A ，F ，C ，D 在一条直线上，AB ∥DE ，AB=DE ，AF=DC ．求证：BC ∥EF ．19．已知：如图，点A ．F ，E ．C 在同一直线上，AB ∥DC ，AB=CD ，∠B=∠D ． （1）求证：△ABE ≌△CDF ；（2）若点E ，G 分别为线段FC ，FD 的中点，连接EG ，且EG=5，求AB 的长．20．如图，点A 、D 、C 、F 在同一条直线上，AD=CF ，AB=DE ，BC=EF ． （1）求证：△ABC ≌DEF ；（2）若∠A=55°，∠B=88°，求∠F 的度数．21. 如图，点,E F 在AB 上，,,AD BC A B AE BF =∠=∠=. 求证：ADF BCE ∆≅∆ .22. 如图，已知,,AB CD AE BD CF BD =⊥⊥ ，垂足分别为,,E F BF DE = .求证AB CD .23.已知：如图，AB ＝CD ，DE ⊥AC ，BF ⊥AC ，E ，F 是垂足，DE BF =． 求证：AB CD ∥．24．如图：BE ⊥AC ，CF ⊥AB ，BM=AC ，CN=AB 。

判定全等三角形的五种方法一、引言全等三角形是指具有相同形状和相等边长的两个三角形。

判定两个三角形是否全等是几何学中非常重要的问题，它们在计算几何、图形设计和工程测量中都有广泛的应用。

本文将介绍五种常用的方法来判定两个三角形是否全等。

二、方法一 - SSS判定法SSS判定法是根据两个三角形的所有边长是否相等来判定它们是否全等的方法。

具体步骤如下：1.比较两个三角形的三条边长是否一一对应相等。

2.如果两个三角形的边长相等，那么它们是全等的。

三、方法二 - SAS判定法SAS判定法是根据两个三角形的一个边和两个夹角的大小关系来判定它们是否全等的方法。

具体步骤如下：1.比较两个三角形的一个边和夹角是否一一对应相等。

2.如果两个三角形的一个边和两个夹角相等，那么它们是全等的。

四、方法三 - ASA判定法ASA判定法是根据两个三角形的两个夹角和一个边的大小关系来判定它们是否全等的方法。

具体步骤如下：1.比较两个三角形的两个夹角和一个边是否一一对应相等。

2.如果两个三角形的两个夹角和一个边相等，那么它们是全等的。

五、方法四 - SAA判定法SAA判定法是根据两个三角形的一个边和两边之间的夹角以及两个相应的夹角的大小关系来判定它们是否全等的方法。

具体步骤如下：1.比较两个三角形的一个边和两边之间的夹角是否相等。

2.比较两个三角形的两对相应夹角是否相等。

3.如果两个三角形的一个边和两边之间的夹角，以及两个相应的夹角都相等，那么它们是全等的。

六、方法五 - HL判定法HL判定法是根据两个三角形的一个斜边和与其相对的两个直角边的大小关系来判定它们是否全等的方法。

具体步骤如下：1.比较两个三角形的一个斜边和与其相对的两个直角边是否一一对应相等。

2.如果两个三角形的一个斜边和与其相对的两个直角边相等，那么它们是全等的。

七、总结判定两个三角形是否全等是几何学中的重要问题，对于几何学的研究和实际应用都具有重要意义。

本文介绍了五种常用的方法来判定全等三角形，分别是SSS判定法、SAS判定法、ASA判定法、SAA判定法和HL判定法。