初一数学上册计算题9

七年级上数学题计算一、有理数运算类。

1. 计算：(-3)+5- 解析：有理数加法，异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

| - 3|=3，|5| = 5，5>3，所以结果为正，5 - 3=2。

- 答案：22. 计算：4 - (-2)- 解析：减去一个数等于加上这个数的相反数，所以4-(-2)=4 + 2，4+2 = 6。

- 答案：63. 计算：(-2)×(-3)- 解析：两数相乘，同号得正，异号得负，并把绝对值相乘。

(-2)×(-3)=2×3 = 6。

- 答案：64. 计算：-4÷2- 解析：两数相除，异号得负，并把绝对值相除。

| - 4|÷|2|=4÷2 = 2，结果为-2。

- 答案：-25. 计算：(-2)^3- 解析：表示3个-2相乘，(-2)×(-2)×(-2)=-8。

- 答案：-8二、整式加减类。

6. 化简：3a+2b - 5a - b- 解析：合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

3a-5a=(3 - 5)a=-2a，2b - b=(2 - 1)b=b。

- 答案：-2a + b7. 计算：(2x^2-3x + 1)-(3x^2 - 2x+2)- 解析：去括号法则，括号前是减号，去掉括号后括号内各项要变号。

2x^2-3x + 1-3x^2+2x - 2=(2x^2-3x^2)+(-3x + 2x)+(1 - 2)=-x^2 - x - 1。

- 答案：-x^2 - x - 18. 化简：4(a - b)+3(b - a)- 解析：先将(b - a)变形为-(a - b)，则原式=4(a - b)-3(a - b)=(4 - 3)(a - b)=a - b。

- 答案：a - b三、一元一次方程类。

9. 解方程：2x+3=7- 解析：首先将常数项移到等号右边，得到2x=7 - 3，即2x = 4，然后两边同时除以2，解得x = 2。

七年级上册数学计算题库一、有理数运算。

1. 计算：(-3)+5- 解析：异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

|5| = 5，| - 3|=3，5>3，所以结果为正，5 - 3=2。

2. 计算：4-(-2)- 解析：减去一个数等于加上这个数的相反数，所以4-(-2)=4 + 2 = 6。

3. 计算：(-2)×3- 解析：两数相乘，异号得负，并把绝对值相乘，所以(-2)×3=-6。

4. 计算：(-4)÷2- 解析：两数相除，异号得负，并把绝对值相除，所以(-4)÷2=-2。

5. 计算：(-2)^3- 解析：表示3个-2相乘，(-2)^3=(-2)×(-2)×(-2)=-8。

二、整式加减。

6. 化简：3a + 2b - 5a - b- 解析：先找同类项，3a和-5a是同类项，2b和-b是同类项。

合并同类项得(3a - 5a)+(2b - b)=-2a + b。

7. 计算：(2x^2 - 3x+1)-(x^2 - 2x - 3)- 解析：去括号时，括号前是正号，去掉括号不变号；括号前是负号，去掉括号要变号。

所以原式=2x^2-3x + 1 - x^2+2x + 3=(2x^2 - x^2)+(-3x+2x)+(1 + 3)=x^2 -x+4。

8. 化简：4(a - b)+3(b - a)- 解析：先将3(b - a)变形为-3(a - b)，则原式=4(a - b)-3(a - b)=(4 - 3)(a - b)=a - b。

三、一元一次方程。

9. 解方程：2x+3 = 7- 解析：首先移项，把常数项移到等号右边，得到2x=7 - 3，即2x = 4，然后两边同时除以2，解得x = 2。

10. 解方程：3(x - 1)=2x+1- 解析：先去括号得3x-3 = 2x + 1，再移项得3x-2x=1 + 3，合并同类项得x = 4。

七年级数学计算题的强化训练一、有理数混合运算的运算顺序①从高级到低级：先算乘方，再算乘除，最后算加减； 1 )－ 1 例 1：计算： 3＋50÷ 22× ( 5 解： ②从内向外：如果有括号，就先算小括号里的，再算中括号里的， 最后算大括号里的 . 1 3 2 例 2：计算： 1 1 0.5 2 3 解： ③从左向右：同级运算，按照从左至右的顺序进行； 3 4 7 8 7 12 7 8 8 3 例 3：计算： 1 解： 2÷( － 1 ) 2 4 -(-1) 101＋ (-2) 2× (-3) 2 例 2 计算： -0.25 解：二、掌握运算技巧（1）、归类组合：将不同类数( 如分母相同或易于通分的数将同类数( 如正数或负数) 归类计算。

) 分别组合；（2）、凑整：将相加可得整数的数凑整，将相加得零的数（如互为相反数）相消。

（3）、分解：将一个数分解成几个数和的形式乘的形式。

, 或分解为它的因数相（4）、约简：将互为倒数的数或有倍数关系的数约简。

（5）、倒序相加：利用运算律，改变运算顺序例3 计算：, 简化计算。

16 -32251 2 3－411－12 2(1) ÷(- 8×4)+2.5+(2 +3) ×2431115 321315321415(2)( －) ×( －) －×( －) ＋×( －)23x 21x33414(1) 1; ( 2) x (1 2x).2、解方程。

初一上册计算题精选集初一的学习是为整个初中阶段打下坚实基础的重要时期，而数学中的计算题更是锻炼思维和提升能力的关键。

下面为大家精选了一些初一上册常见的计算题，通过练习和掌握这些题目，相信能帮助同学们更好地理解和运用所学知识。

一、有理数的运算1、计算：（－5) ＋ 3这道题考查有理数的加法。

异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

在这道题中，｜－5|＞｜3|，所以结果为负，用 5 3 ＝ 2，最终答案为－2 。

2、计算：（－8) （－5)这是有理数的减法运算，减去一个数等于加上这个数的相反数。

所以原式可转化为－8 ＋ 5 ＝－3 。

3、计算：（－2)×（－3)有理数乘法，同号得正，异号得负。

所以这道题的结果为 6 。

4、计算：（－12)÷（－3)两数相除，同号得正，异号得负。

所以答案为 4 。

二、整式的运算1、化简：3x ＋ 2x同类项合并，系数相加，字母和指数不变。

所以结果为 5x 。

2、化简：（2x²＋ 3x 5) （x² 2x ＋ 1)去括号，然后合并同类项。

原式＝ 2x²＋ 3x 5 x²＋ 2x 1 ＝ x²＋5x 6 。

3、计算：2x(3x 1)使用乘法分配律，原式＝ 2x×3x 2x×1 ＝ 6x² 2x 。

三、一元一次方程1、解方程：2x ＋ 3 ＝ 7首先，将 3 移到等号右边得到 2x ＝ 7 3 ，即 2x ＝ 4 ，然后两边同时除以 2 ，解得 x ＝ 2 。

2、解方程：3(x 1) ＝ 2x ＋ 1先去括号得到 3x 3 ＝ 2x ＋ 1 ，然后将 2x 移到左边，－3 移到右边，得到 3x 2x ＝ 1 ＋ 3 ，解得 x ＝ 4 。

四、综合计算题1、计算：（－2)³ ×（－4) 6 ÷（－3)先计算指数运算，（－2)³＝－8 ，然后计算乘法－8×（－4) ＝ 32 ，再计算减法 32 6 ＝ 26 ，最后除以－3 ，得到－26/3 。

计算题七年级上册一、有理数运算。

1. 计算：(-3)+5 - (-2)- 解析：- 首先去括号，根据去括号法则，括号前是“ - ”号，把括号和它前面的“ - ”号去掉后，原括号里各项的符号都要改变。

所以-(-2)=2。

- 则原式变为- 3+5 + 2。

- 按照从左到右的顺序计算，先算- 3+5 = 2，再算2 + 2=4。

2. 计算：(-4)×(-(3)/(2))÷(-(2)/(5))- 解析：- 先计算乘法，根据有理数乘法法则，两数相乘，同号得正，异号得负，并把绝对值相乘。

所以(-4)×(-(3)/(2)) = 6。

- 再计算除法，除以一个数等于乘以它的倒数，所以6÷(-(2)/(5))=6×(-(5)/(2))=-15。

3. 计算：(-2)^3+(-3)×[(-4)^2 - 2]- 解析：- 先计算指数运算，(-2)^3=-8，(-4)^2 = 16。

- 然后计算括号内的式子，(-3)×(16 - 2)=(-3)×14=-42。

- 最后计算加法，-8+(-42)=-50。

4. 计算：(1)/(2)-<=ft(-(1)/(4))+<=ft(-(2)/(3))- 解析：- 首先去括号，-<=ft(-(1)/(4))=(1)/(4)。

- 然后通分，分母2、4、3的最小公倍数是12，将原式化为(6)/(12)+(3)/(12)-(8)/(12)。

- 计算分子的和差，(6 + 3-8)/(12)=(1)/(12)。

二、整式加减运算。

5. 化简：3a + 2b - 5a - b- 解析：- 合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

- 对于a的同类项，3a-5a=-2a；对于b的同类项，2b - b=b。

- 所以化简结果为-2a + b。

6. 计算：(2x^2 - 3x + 1)-(3x^2 - 5x - 2)- 解析：- 去括号，括号前是“ - ”号，去括号后括号里各项要变号。

人教版初一数学上册400道计算题及练习题
1.计算题：求下列各数的和，并写出结果：
a)26+13
b)47+59
c)85+17
2.计算题：求下列各数的差，并写出结果：
a)39-14
b)68-33
c)92-36
3.计算题：求下列各数的积，并写出结果：
a)8×5
b)15×9
c)7×12
4.计算题：求下列各数的商，并写出结果：
a)56÷7
b)63÷9
c)112÷8
5.计算题：计算下列各式的值，并写出结果：
a)37×(12-5)
b)6×(4+9)÷3
c)(20-12)×(5+3)
练习题部分则涉及了初一数学上册各个知识点的练习。

1.复数的计算：
a)计算：(3+4i)+(5-2i)
b)计算：(2-3i)-(1+2i)
c)计算：(4+5i)×(2+3i)
2.代数式的计算：
a)计算：2x+3y，其中x=4，y=7
b)计算：3a-2b，其中a=5，b=2
c)计算：5x²-2x+1，其中x=3
3.几何图形的计算：
a) 求矩形的面积和周长，长为6cm，宽为4cm
b) 求三角形的面积和周长，底为8cm，高为5cm
c) 求圆的面积和周长，半径为3cm
通过完成这些计算题及练习题，能够帮助初一学生巩固数学上册各个知识点，提高计算能力和解题能力。

七年级上册计算题训练一、有理数的运算1. 加法运算计算：( 3)+( 9)解析：同号两数相加，取相同的符号，并把绝对值相加。

| 3|=3，| 9| = 9，所以( 3)+( 9)=-(3 + 9)=-12。

计算：( 4.7)+3.9解析：异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

| 4.7|=4.7，|3.9| = 3.9，4.7>3.9，所以( 4.7)+3.9=-(4.7 3.9)=-0.8。

2. 减法运算计算：5-( 4)解析：减去一个数等于加上这个数的相反数。

所以5-( 4)=5 + 4 = 9。

计算：( 3)-5解析：( 3)-5=( 3)+( 5)=-8。

3. 乘法运算计算：( 2)×( 3)解析：两数相乘，同号得正，异号得负，并把绝对值相乘。

( 2)×( 3)=2×3 = 6。

计算：( 4)×5解析：( 4)×5=-(4×5)=-20。

4. 除法运算计算：( 12)÷( 3)解析：两数相除，同号得正，异号得负，并把绝对值相除。

( 12)÷( 3)=12÷3 = 4。

计算：15÷( 5)解析：15÷( 5)=-(15÷5)=-3。

5. 混合运算计算：( 2)^2×( 3)÷<=ft[<=ft(-(1/2))^3×8]解析：先算乘方：( 2)^2 = 4，<=ft(-(1/2))^3=-(1/8)。

原式变为4×( 3)÷<=ft(-(1/8)×8)。

再算括号内的：-(1/8)×8=-1。

接着算乘法：4×( 3)=-12。

最后算除法：-12÷( 1)=12。

二、整式的加减运算1. 同类项的合并化简：3x + 2y 5x y解析：首先找出同类项，3x和-5x是同类项，2y和-y是同类项。

七年级上册数学算式题一、有理数运算1. 计算：(5) + 8解析：异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

|5| = 5，|8| = 8，8 > 5，所以结果为正，8 5 = 3。

答案：32. 计算：(3) (5)解析：减去一个数，等于加上这个数的相反数。

(3) (5) = (3) + 5 = 2答案：23. 计算：(2)×(6)解析：两数相乘，同号得正，异号得负，并把绝对值相乘。

(2)×(6) = 12答案：124. 计算：18÷(3)解析：两数相除，异号得负，并把绝对值相除。

18÷(3) = 6答案：65. 计算：(4)×5×(0.25)解析：先确定符号，负负得正，然后按照乘法法则计算。

(4)×5×(0.25) = 4×5×0.25 = 5答案：5二、整式的加减6. 化简：3x + 2x解析：合并同类项，系数相加，字母和字母的指数不变。

3x + 2x = 5x答案：5x7. 化简：5a 3a + 2a解析：合并同类项，5a 3a + 2a = 4a答案：4a8. 化简：(2x + 1) (x 3)解析：去括号，然后合并同类项。

2x + 1 x + 3 = x + 4答案：x + 49. 化简：3(m n) 2(m + n)解析：先运用乘法分配律去括号，然后合并同类项。

3m 3n2m 2n = m 5n答案：m 5n10. 先化简，再求值：2(a^2 ab) 3(a^2 2ab)，其中a = 1，b = 2解析：2(a^2 ab) 3(a^2 2ab)= 2a^2 2ab 3a^2 + 6ab= a^2 + 4ab当a = 1，b = 2时，a^2 + 4ab= (1)^2 + 4×(1)×2= 1 8= 9答案：9三、一元一次方程11. 解方程：2x 3 = 5解析：移项得2x = 5 + 3，2x = 8，x = 4答案：x = 412. 解方程：3(x + 1) = 2x 1解析：去括号得3x + 3 = 2x 1，移项得3x 2x = 1 3，x = 4答案：x = 413. 解方程：\frac{x + 2}{3} \frac{x 1}{2} = 1解析：去分母得2(x + 2) 3(x 1) = 6，去括号得2x + 43x + 3 = 6，移项得2x 3x = 6 4 3，x = 1，x = 1答案：x = 114. 解方程：\frac{2x 1}{3} = \frac{x + 2}{4} 1解析：去分母得4(2x 1) = 3(x + 2) 12，去括号得8x 4 = 3x + 6 12，移项得8x 3x = 6 12 + 4，5x = 2，x = \frac{2}{5}答案：x = \frac{2}{5}15. 若关于x的方程2x + a = 4的解是x = 2，求a的值。

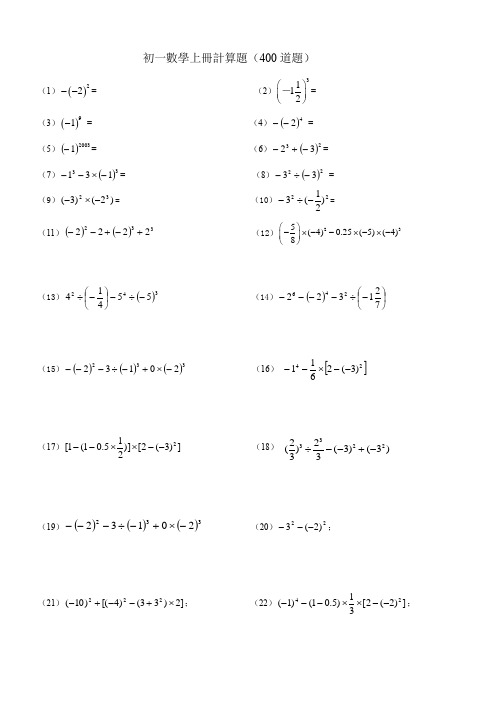
初一數學上冊計算題（400道題）（1）()22--= （2）3112⎛⎫⎪⎝⎭－=（3）()91- = （4）()42-- =（5）()20031-= （6）()2332-+-=（7）()33131-⨯--= （8）()2233-÷- =（9）)2()3(32-⨯-= （10）22)21(3-÷-=（11）()()3322222+-+-- （12）235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭（13）()34255414-÷-⎪⎭⎫ ⎝⎛-÷ （14）()⎪⎭⎫ ⎝⎛-÷----721322246（15）()()()33220132-⨯+-÷--- （16） []24)3(2611--⨯--（17）])3(2[)]215.01(1[2--⨯⨯-- （18） （19）()()()33220132-⨯+-÷--- （20）22)2(3---；（21）]2)33()4[()10(222⨯+--+-； （22）])2(2[31)5.01()1(24--⨯⨯---； 332222()(3)(3)33÷--+-（23）94)211(42415.0322⨯-----+-； （24）20022003)2()2(-+-；（25）)2()3(]2)4[(3)2(223-÷--+-⨯--； （26）200420094)25.0(⨯-.（27）()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ （28）()()----⨯-221410222（29）()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. （30）()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.（31） （32）(56)(79)---（33）(3)(9)(8)(5)-⨯---⨯- （34）3515()26÷-+（35）5231591736342--+- （36）（37）411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯ ()()22431)4(2-+-⨯---33182(4)8-÷--（38）如果0)2(12=-++b a ，求20112010()-3ab a b a a ++-（）の值（39）已知|1|a +與|4|b -互為相反數，求b a の值。

317．计算：(1)(－5)×2＋20÷(－4) (2)－32－[－5＋(10－÷5)÷(－3)2]1b261 b18．解方程：(1)7x－8＝5x＋4(2)2319．先化简，后求值：2(x2y＋xy)－3(x2y－xy)－4x2y，其中x＝1，y＝－120．假设a、b互为相反数，c、d互为倒数，m的绝对值是3，n在有理数王国里既不是正数也不是a20212(cd)2021n(abcd)(负数，求m的值17．(16分)计算：(1)－17－(-23)＋(-13)－(+23)(311)1242021(1)2021(2)2(2)4612(3)4(4)4(112)2×53÷(2)3．18．计算(8分)〔1〕(2a－1)＋2(1－a)；(2)3(3x＋2)－2(3＋x)．x12x1解方程：〔1〕3(2x1)3x219．(6分)〔2〕2320．(6分)先化简．再求值．-2(ab-a2)-3ab-1+(6ab-2a2)，其中a=1，b=－1．1521 9.18(6)20.2 23〔3〕(1)4(11)3(223)4x4x721.22 2.四．解以下方程〔每题5分，共15分〕.2x1x212 3.3x524.6x74x525.2五．先化简，再求值〔此题6分〕26．5(3a2bab2)(ab23a2b)2ab2，其中a2，b3．19计算(1).12(16)4)52111( 2).9418365421412429来源于网络14(10.5)12(3)2〔4).3( 1).(8xyx2y2)4(x2y22xy3) (2).5ab2－[a2b＋2(a2b－3ab2)]21〔8分〕先化简求值:1 723(16)14(5)2(5)〔1〕〔〕22〔1〕x4x2x〔〕5(2a7b)3(4a2x312x6〔1〕2(3x)4(x5)〔〕432ax x124．〔10分〕关于x的方程214，求代数式a2 3的解是x17．化简：3〔2x2﹣y2〕﹣2〔3y2﹣2x2〕18．|a﹣2|+〔b﹣3〕2=0，求ba﹣ab的值．19．解方程：．20．三角形第一边长为2a+b，第二边比第一边长a﹣b，第三边比第二边短a，求这个三角形的周长．21．先化简，再求值：〔﹣x2+5x+4〕+〔5x﹣4+2x2〕，其中x=﹣2．111214.51122〔1〕32＋(－2)－(－3)＋23〔2〕3〔3〕5x 2y xy 2 3x 2y 7xy 2〔〕〔﹣〕﹣〔 ﹣ 〕45a2b3ab22a2b7ab2y7y4y162x3x〔1〕〔2〕3311〔1〕3-〔-6+32〕÷〔-1+4〕〔2〕6-4×〔-2〕-〔〔-2〕3+〔-9〕÷〔-3〕〕〔1〕〔2xy-5x 〕-2(xy-3x)(2)a3-3(1-a)+(1-a+a2)-(1-a+a2+a3)118、(本小题5分)先化简，再求值。