等值计算
- 格式:ppt
- 大小:1.56 MB
- 文档页数:23




六个等值计算公式的系数之间的关系六个等值计算公式的系数之间存在以下三种关系:
(一)倒数关系
(1)(P/F,i,n)=1/(F/P,i,n)
(2)(F/A,i,n)=1/(A/F,i,n)
(3)(P/A,i,n)=1/(A/P,i,n)
(二)乘积关系
(1)(A/P,i,n)=(F/P,i,n)(A/F,i,n)
(2)(P/A,i,n)=(F/A,i,n)(F/P,i,n)
(3)(P/F,i,n)=(A/F,i,n)(P/A,i,n)
(4)(F/P,i,n)=(F/A,i,n)(A/P,i,n)
关系式(3)、(4)在实际运用中作用不大,但可用于一些理论推导。
(三)偿债基金系数与资金回收系数之间的关系
(A/P,i,n)=(A/F,i,n)+i
前面介绍了资金等值的两种类型六个基本公式,为便于理解、查阅和记忆,将这些公式列于下表,并提出某些联想记忆方式,供参考。
联想记忆方式:
(1)“/”号左边为未知,右边为已知,如(F/A,i,n),表明已知年金A,求终值F;
(2)等额支付类型的系数中,(1+i)n-1总是与F或P在“/”号的同一边。
如:系
(1+i)
n-1 i(1+ i)n
数(F/A,i,n)、(A/P,i,n)分别表示----------------- 、----------------,若F、P分
i
(1+i)n-1
别处在分子、分母的位置,则复利差(1+i)n -1也处在分子、分母的位置;
“/”号一侧的A以i代之;若A与P为伍,则
“/”号一侧A以i(1+i)n代之。
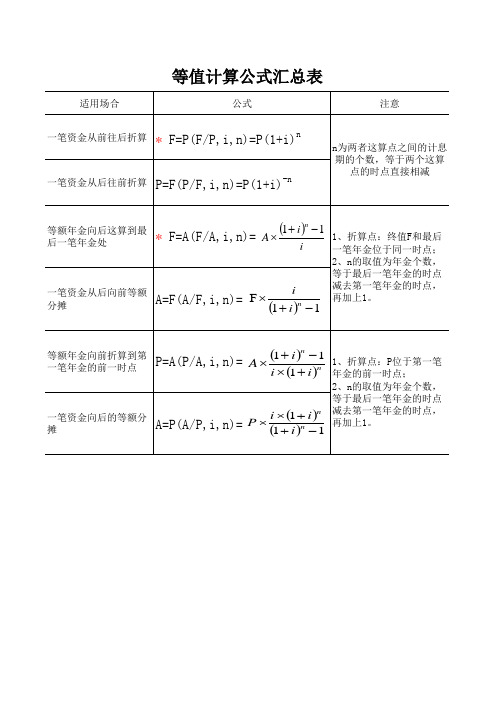
表中资金等值的六个基本公式。

书山有路勤为径,学海无涯苦作舟六个等值计算公式的系数之间的关系六个等值计算公式的系数之间存在以下三种关系:(一)倒数关系(1)(P/F,i,n)=1/(F/P,i,n)(2)(F/A,i,n)=1/(A/F,i,n)(3)(P/A,i,n)=1/(A/P,i,n)(二)乘积关系(1)(A/P,i,n)=(F/P,i,n)(A/F,i,n)(2)(P/A,i,n)=(F/A,i,n)(F/P,i,n)(3)(P/F,i,n)=(A/F,i,n)(P/A,i,n)(4)(F/P,i,n)=(F/A,i,n)(A/P,i,n)关系式(3)、(4)在实际运用中作用不大,但可用于一些理论推导。
(三)偿债基金系数与资金回收系数之间的关系(A/P,i,n)=(A/F,i,n)+i 前面介绍了资金等值的两种类型六个基本公式,为便于理解、查阅和记忆,将这些公式列于下表,并提出某些联想记忆方式,供参考。
联想记忆方式:(1)“/”号左边为未知,右边为已知,如(F/A,i,n),表明已知年金A,求终值F;(2)等额支付类型的系数中,(1+i)n-1 总是与F 或P 在“/”号的同一边。
如:系(1+i)n-1 i(1+ i)n 数(F/A,i,n)、(A/P,i,n)分别表示----------------- 、----------------,若F、P 分i (1+i)n-1 别处在分子、分母的位置,则复利差(1+i)n -1 也处在分子、分母的位置;(3)在等额支付类型的系数中都有复利差,若A 与F 为伍,则“/”号一侧的A 以i 代之;若A 与P 为伍,则“/”号一侧A 以i(1+i)n代之。
表中资金等值的六个基本公式类别已知求解公式系数名称及符号一次支付终值公式PFF=P(1+i)n 复利终值系数(F/P,i,n)现值公式FPP=F(1+i)-n 复利贴现系数(P/F,i,n)等额支付年金终值公式AF(1+i)n-1F=A-------------i 年金终值系数(F/A,i,n)偿债基金公式FAiA=F----------------(1+i)n-1 偿债基金系数(A/F,i,n)资金回收公式PAi(1+i)nA=---------------(1+i)n-1 资金回收系数(A/P,i,n)年金现值公式AP(1+i)n-1P=A---------------i(1+i)n 年金现值系数(P/A,i,n)。

等值计算公式的应用1. 预付年金的等值计算【例1】:某人每年年初存入银行5000元,年利率为10%,8年后本利和是多少?解: 查教材P.298的复利系数表知,该系数为11.4359【例2】:某公司租一仓库,租期5年,每年年初需付租金12000元,贴现率为8%,问该公司现在应筹集多少资金? 解法1:解法2:解法3:2. 延期年金的等值计算【例3】:设利率为10%,现存入多少钱,才能正好从第四年到第八年的每年年末等额提取2万元?解:45.62897%)101()8%,10,/(5000=+⋅=A F F 39.51745%)81()5%,8,/(12000=+⋅=A P P39.51745)4%,8,/(1200012000=+=A P P 39.51745)4%,8,/()5%,8,/(12000=⋅=F P A F P 7.5)3%,10,/()5%,10,/(2=⋅=F P A P P【例4】:若利率为6%,现存入多少可使今后30年每6年末提取2000元?解:P =2000(A/F ,6%,6)(P/A ,6%,30) =3947.73. 永续年金的等值计算【例5】:某地方政府一次性投入5000万元建一条地方公路,年维护费为150万元,折现率为10%,求现值。
解:该公路可按无限寿命考虑,年维护费为等额年金,可利用年金现值公式求当n →∞时的极限来解决。
i A i i i A P n n n =⎥⎦⎤⎢⎣⎡+-+⋅=∞→)1(1)1(lim4. 求解未知的i【例6】:15年前,某企业投资10000元建厂,现拟卖出该厂得25000元,这10000元的收益率是多少?解法1:F=P(F/P,i,15)(F/P,i,15)=2.5i F/P i F/P i F/P6% 2.397 2.5 8% 3.1726. 计息周期小于资金收付周期的等值计算【例7】:每半年存款1000元,年利率8%,每季计息一次,复利计息。


等值演算法顺序今天给大家讲一下等值演算法。
在很多文章里,都会介绍等值的一些具体操作,而这篇文章中,我则会给大家详细介绍它的操作步骤。
等值计算(Based Request)是一种快速且有效的计算方法,尤其是对具有相同参数的数据集进行校验时。
在实际应用中,等值计算的基本操作步骤是:使用最小数量的数据去拟合一个结果。
然后分别将最小变量和最大变量进行对等计算。
该过程一般可以分为三步:(1)生成一个新的函数;(2)在已知条件下确定一个已知参数;(3)获得一组其他参数。
这个过程会出现一系列特殊问题,比如一些函数不能在一个数据集中重复使用、不能保持所有条件的等值等——因此需要对各种演算法进行相应分析和选择:首先比较各个方案可能存在的数据情况;然后比较不同演算法中每个方案可能出现的数据效果;最后将结果与各个方案进行比较。
而在此过程中,如果要保持复杂度低,则使用等值算法应该尽可能准确。
1.首先从最小变量开始假设有一组数据集,并且数据是有随机生成,并且变量是随机产生的。
根据下面的算法程序,可以尝试将最小变量作为等值计算的参数:将多个等值条件转换为一个等值函数进行处理。
考虑到数据集是随机生成的,因此只需要取最小变量为等值函数就可以了。
通过使用MATLAB里常见的循环表示法(即“循环表达式”)可找到一个最小变量表达式为 f ()。
当我们想进行等值计算时,首先要知道最小变量这个“表达式”。
由于等值计算所需要采用一个标准函数 x来将所有条件转换为某种等值关系,因此将该最小变量从函数x中去除后就很容易得到等值结果了。
然而对于某些函数而言,并不是这样——此时如果我们需要得到 x中有一个最小变量作为等值条件的话就会非常麻烦了。
所以最好在该状态下使用 x来将变量进行等值计算。
因此在实际应用中我们首先需要确定 x如何被消除以及如何消除 x会导致等值计算中不同方法之间存在相互矛盾(特别是对那些具有相同值或者相似值且不属于某一种等值方法时)——否则就很容易发生将 x删除导致等值计算失败和进行等值计算时不能重复计算等问题了。

简述等值计算公式使用注意事项。
等值计算公式是一种计算研究中比较重要的方法。
它可以利用一定的方法和数学模型来求解计算问题,用以解决科学问题、物理问题、金融问题等,所以它是一种具有重要意义的研究方法。
在使用等值计算公式时,我们应注意以下几点:
一是熟悉计算理论,尤其是与等值计算公式相关的理论。
不熟悉理论,很可能会造成计算错误。
二是应做好有关计算的准备工作,这包括确定所要求解的问题,解决方法及总体设计。
三是合理建模、对数据能否表示而言,应以准确、可靠的数据为前提,根据题材的客观实际情况进行模型建立,以便正确准确地求解计算问题。
四是分析模型。
完成等值计算公式模型之前,应该从精确推理与复杂推理上分别进行理论分析,以确保结果的准确可靠。
五是按部就班地进行计算。
完成计算步骤之前,应详细分析运算步骤,找出可能存在的错误,按部就班地进行计算,以尽量避免错误的发生。
六是核对结果。
完成计算后,应对所得出的结果仔细核对,尽可能的保证结果的可靠性,以适应后续必要的应用。
由此可见,等值计算公式的使用中要注意以上几点,使得计算结果能准确可靠的反映出客观事实,为实际研究和应用提供有价值的信息作为参考。


等值计算公式的应用1. 预付年金的等值计算【例1】:某人每年年初存入银行5000元,年利率为10%,8年后本利和是多少?解: 查教材P.298的复利系数表知,该系数为11.4359【例2】:某公司租一仓库,租期5年,每年年初需付租金12000元,贴现率为8%,问该公司现在应筹集多少资金? 解法1:解法2:解法3:2. 延期年金的等值计算【例3】:设利率为10%,现存入多少钱,才能正好从第四年到第八年的每年年末等额提取2万元?解:45.62897%)101()8%,10,/(5000=+⋅=A F F 39.51745%)81()5%,8,/(12000=+⋅=A P P39.51745)4%,8,/(1200012000=+=A P P 39.51745)4%,8,/()5%,8,/(12000=⋅=F P A F P 7.5)3%,10,/()5%,10,/(2=⋅=F P A P P【例4】:若利率为6%,现存入多少可使今后30年每6年末提取2000元?解:P =2000(A/F ,6%,6)(P/A ,6%,30) =3947.73. 永续年金的等值计算【例5】:某地方政府一次性投入5000万元建一条地方公路,年维护费为150万元,折现率为10%,求现值。
解:该公路可按无限寿命考虑,年维护费为等额年金,可利用年金现值公式求当n →∞时的极限来解决。
i A i i i A P n n n =⎥⎦⎤⎢⎣⎡+-+⋅=∞→)1(1)1(lim4. 求解未知的i【例6】:15年前,某企业投资10000元建厂,现拟卖出该厂得25000元,这10000元的收益率是多少?解法1:F=P(F/P,i,15)(F/P,i,15)=2.5i F/P i F/P i F/P6% 2.397 2.5 8% 3.1726. 计息周期小于资金收付周期的等值计算【例7】:每半年存款1000元,年利率8%,每季计息一次,复利计息。

§2-3 等值计算与应用1.等值概念1.1概念:在时间因素的作用下,在不同时点绝对不等的资金可能具有相等的价值。
也是“价值等效”的资金。
1.1.1两个现金流量等值,则其之间任何时刻的时值必然相等,从计算公式F=P(1+i)n,即F/P,i,n=(1+i)n及A= P i(1+i)n/[(1+i)n-1]可知:影响资金等值因素有三个,P或F或A、n和i一般计算中以同一利率为依据1.1.2等值基本公式相互关系示意图0 1 2 3 4 …n1.1.3在技术经济分析中,利用等值的概念来相加,减及比较。
2.名义利率与实际利率前面介绍的复利计算中,利率周期与计息周期是相同的。
实际中也可以不同,这就出现了名义利率与实际利率的概念。
2.1名义利率:r= i× m 与单利计算是一样i:一个计息周期利率,m:一个利率周期内的计息次数。
3. 2.2实际利率:一般银行给出的是利率r(),实际中利息每天发生,考虑复利,年实际利率i eff就不同。
F=P(1+r/m)mI=F-P= P(1+r/m)m-Pi eff=I/P=(1+r/m)m-1P28表2-6年名义利率10%,计息周期年、半年、季、月日的计息次数,计息周期利率,年实际利率。
M越多,i eff和r相差越大。
3.等值计算应用3.1等值计算实际应用就是复利计算公式和查复利表。
3.2等值计算分两种情况,一为计息周期小于或等于资金收付周期,二为计息周期大于收付周期来计算等值。
3.2.1计息周期≤资金收付周期两种方法<i eff实际利率、 r名义利率、 m一个利率周期内的计息周期数>A、按收付周期实际利率计算,即先计算i eff=(1+r/m)m-1,再计算。
B、按计息周期利率计算F=P(F/P,r/m,mn)例如:a、年利息为i,半年复利一次,半年利率为i/2年复利率i eff=(1+i/2)2-1例如:某人每半年初存入1000元,年利率8%,每季计息一次,复利计算,五年末存款金额是多少?i = r/ m=8%/4=2%i eff=(1+r/m)m-1=(1+2%)2-1=4.04%F=1000(F/A,4.04%,2×5)(F/P, 4.04%,1)=1000×12.029×1.0824=13020.582.2.2计息周期>收付周期三种方法A、不计息:按期初、期末习惯计入B、单利计息:A t=∑A k‘[1+(m k/N)×i]A t:第t计息期末净现金流量。

3.资金等值计算公式在考虑资金时间价值的前提下,在一定的利率条件下,不同时点、不同金额的资金在价值上是等效的,称为资金等值。
资金等值概念的建立是工程经济方案比选的理论基础。
将某一时点发生的资金在一定利率条件下,利用相应的计算公式换算成另一时点的等值金额的过程称为资金的等值计算。
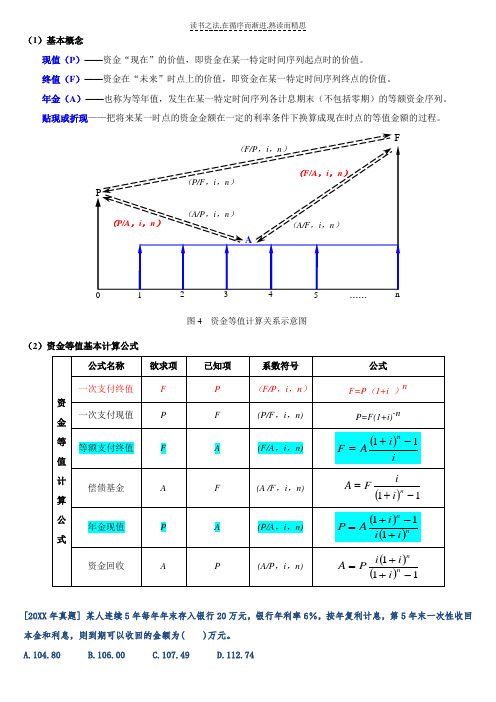
t图3 资金等值计算示例(1)基本概念现值(P)——资金“现在”的价值,即资金在某一特定时间序列起点时的价值。
终值(F)——资金在“未来”时点上的价值,即资金在某一特定时间序列终点的价值。
年金(A)——也称为等年值,发生在某一特定时间序列各计息期末(不包括零期)的等额资金序列。
贴现或折现——把将来某一时点的资金金额在一定的利率条件下换算成现在时点的等值金额的过程。
(2)资金等值基本计算公式[2010年真题] 某人连续5年每年年末存入银行20万元,银行年利率6%,按年复利计息,第5年末一次性收回本金和利息,则到期可以收回的金额为( )万元。
A.104.80B.106.00C.107.49D.112.74答案:D解析:()()74.112%61%61205%6/205=-+⨯=⨯=,,AFF图4 资金等值计算关系示意图[2006年真题] 下列关于现值P 、终值F 、年金A 、利率i 、计息期数n 之间关系的描述中,正确的是( )。
A.F 一定、n 相同时,i 越高、P 越大B.P 一定、n 相同时,i 越高、F 越小C.i 、n 相同时,F 与P 呈同向变化D.i 、n 相同时,F 与P 呈反向变化 答案:C解析:()ni P F+=1。
(1)基本概念现值(P)——资金“现在”的价值,即资金在某一特定时间序列起点时的价值。
终值(F)——资金在“未来”时点上的价值,即资金在某一特定时间序列终点的价值。
年金(A)——也称为等年值,发生在某一特定时间序列各计息期末(不包括零期)的等额资金序列。
贴现或折现——把将来某一时点的资金金额在一定的利率条件下换算成现在时点的等值金额的过程。
图4 资金等值计算关系示意图(2)资金等值基本计算公式[20XX年真题] 某人连续5年每年年末存入银行20万元,银行年利率6%,按年复利计息,第5年末一次性收回本金和利息,则到期可以收回的金额为( )万元。
A.104.80B.106.00C.107.49D.112.74答案:D 解析:()()74.112%61%61205%6/205=-+⨯=⨯=,,A F F[20XX 年真题] 下列关于现值P 、终值F 、年金A 、利率i 、计息期数n 之间关系的描述中,正确的是( )。
A.F 一定、n 相同时,i 越高、P 越大 B.P 一定、n 相同时,i 越高、F 越小 C.i 、n 相同时,F 与P 呈同向变化 D.i 、n 相同时,F 与P 呈反向变化 答案:C 解析:()ni P F+=1[20XX 年真题] 年利率8%,按季度复利计息,则半年期实际利率为( )。
A.4.00% B.4.04% C.4.07% D.4.12% 答案:B解析:%04.414%812=-⎪⎭⎫⎝⎛+=e i[20XX 年真题] 已知年名义利率为10%,每季度计息1次,复利计息。
则年有效利率为( )。
A.10.00% B.10.25% C.10.38% D.10.47% 答案:C解析:%38.1014%1014=-⎪⎭⎫⎝⎛+=e i[20XX 年真题] 已知年利率12%,每月复利计息一次,则季实际利率为( )。
A.1.003% B.3.00% C.3.03% D.4.00% 答案:C解析:%03.3112%1213=-⎪⎭⎫⎝⎛+=e i。