人教版实数知识点总结 (1)

实数知识点归纳整理1.引言1.1 概述概述部分主要对实数的基本概念进行介绍和解释。

实数是数学中最基本且最常用的数集之一，它包括所有的有理数和无理数。

有理数是可以表示为两个整数之比的数字，而无理数则是不能被表示为两个整数之比的数字。

实数作为数学中的一个重要概念，具有以下几个特点：首先，实数具有连续性，即在任意两个实数之间都存在无数个实数。

其次，实数具有无限性，即实数集合是无限的。

再次，实数具有稠密性，即在任意两个实数之间都存在另一个实数。

实数的运算法则和性质是我们进一步研究实数的基础。

实数的四则运算规则和性质可以通过加法、减法、乘法和除法来描述。

此外，实数还具有交换律、结合律、分配律等运算规律。

了解实数的定义和性质对我们在数学问题的求解和实际生活中的运用非常重要。

实数在各个领域都有广泛的应用，如物理学、经济学、工程学等。

在这些领域中，实数的连续性和无限性特点使得实数能够准确地描述事物的变化和趋势，为问题的解决提供了有力的工具。

本文主要围绕实数的定义与性质以及实数的运算法则展开讨论，同时总结实数的重要性质和实数在实际生活中的应用。

通过对实数的系统梳理和整理，旨在帮助读者更好地理解实数的概念、运算规则和应用价值，并进一步提升数学问题的解决能力和应用能力。

【1.2 文章结构】本文主要介绍实数的相关知识点，包括实数的定义与性质以及实数的运算法则。

文章内容分为引言、正文和结论三个部分。

引言部分主要对实数进行概述，说明实数在数学中的重要性和应用领域。

同时，介绍了文章的结构，方便读者对接下来的内容有一个整体的了解。

正文部分分为两个小节：实数的定义与性质以及实数的运算法则。

首先，详细介绍了实数的定义，包括实数的范围和特点。

然后，探讨实数的性质，如实数的可比性、稠密性和有序性等。

接着，重点介绍实数的运算法则，包括实数的加法、减法、乘法和除法法则。

通过具体的例子和推导，帮助读者理解和掌握实数的运算方法。

结论部分对全文进行总结，强调了实数的重要性质，并说明了实数在实际生活中的应用。

第六章实数知识网络：考点一、实数的概念及分类1、实数的分类2、无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o 等（这类在初三会出现）判断一个数是否是无理数，不能只看形式，要看运算结果，如0,16π是有理数，而不是无理数。

3、有理数与无理数的区别（1）有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；（2）所有的有理数都能写成分数的形式（整数可以看成是分母为1的分数），而无理数则不能写成分数形式。

考点二、平方根、算术平方根、立方根1、概念、定义（1）如果一个正数x的平方等于a，即，那么这个正数x叫做a的算术平方根。

（2）如果一个数的平方等于a，那么这个数就叫做a的平方根（或二次方跟）。

如果，那么x叫做a的平方根。

（3）如果一个数的立方等于a，那么这个数就叫做a 的立方根（或a 的三次方根）。

如果，那么x叫做a的立方根。

2、运算名称（1）求一个正数a的平方根的运算，叫做开平方。

平方与开平方互为逆运算。

（2）求一个数的立方根的运算，叫做开立方。

开立方和立方互为逆运算。

3、运算符号（1）正数a的算术平方根，记作“a”。

（2）a(a≥0)的平方根的符号表达为。

（3）一个数a的立方根，用表示，其中a是被开方数，3是根指数。

4、运算公式4、开方规律小结（1）若a≥0，则a的平方根是a a a它们互为相反数，其中正的那个叫它的算术平方根；0的平方根和算术平方根都是0；负数没有平方根。

实数都有立方根，一个数的立方根有且只有一个，并且它的符号与被开方数的符号相同。

正数的立方根是正数，负数的立方根是负数，0的立方根是0。

（2）若a<0，则a 没有平方根和算术平方根；若a 为任意实数，则a 的立方根是。

实数知识点详细总结\section{实数的定义}实数是一种可以在数轴上表示的数，包括了有理数和无理数两种。

有理数是可以表示为两个整数的比值的数，包括整数和分数；而无理数是不能表示为有理数的数，包括了无限不循环小数的数。

在数轴上，实数按照大小顺序排列，可以用有理数和无理数填满。

实数具有如下的性质：1. 实数的封闭性：实数的加法、减法、乘法和除法结果仍然是实数。

2. 实数的稠密性：在任意两个实数之间，都存在另外一个实数。

3. 实数的有序性：实数可以按照大小顺序进行比较。

4. 实数的存在性：实数可以在数轴上表示，并且可以用准确的小数表示。

\section{实数的性质}实数具有很多重要的性质，包括了有理数和无理数的性质。

其中，有理数具有如下的性质：1. 有理数的封闭性：有理数的加法、减法、乘法和除法结果仍然是有理数。

2. 有理数的稠密性：在任意两个有理数之间，都存在另外一个有理数。

3. 有理数的有序性：有理数可以按照大小顺序进行比较。

4. 有理数的存在性：有理数可以在数轴上表示，并且可以用准确的分数表示。

而无理数具有如下的性质：1. 无理数的无限不循环小数性质：无理数不能表示为有理数的形式，它们的小数部分是无限不循环的。

2. 无理数的稠密性：在任意两个无理数之间，都存在另外一个无理数。

3. 无理数的振荡性：无理数是无限不循环小数，其小数部分具有振荡的性质。

4. 无理数的无法准确表示性：无理数不能用准确的分数表示，并且有时候也无法用有限小数或者无限循环小数表示。

\section{实数的运算}实数的运算是实数研究中一个非常重要的方面，它包括了加法、减法、乘法和除法等多种运算。

在实数的运算中，有些运算具有交换律、结合律和分配律等性质，而有些运算则不具有这些性质。

在实数的运算中，还可以涉及到有理数和无理数的混合运算，这是实数运算中一个比较复杂的部分。

1. 实数的加法：实数的加法满足交换律和结合律，即对任意实数a、b、c，有a+b=b+a，(a+b)+c=a+(b+c)。

实数的运算知识点总结一、实数的四则运算实数的四则运算是基本的数学运算，包括加法、减法、乘法和除法。

在实数范围内，这些运算有着一些基本的性质和规律。

1. 加法实数的加法满足交换律、结合律和分配律。

即对于任意实数a、b、c，有：交换律：a + b = b + a结合律：(a + b) + c = a + (b + c)分配律：a × (b + c) = a × b + a × c2. 减法实数的减法可以看作是加法的逆运算。

即a - b可以等价于a + (-b)，其中-a表示b的相反数。

减法满足减法性质：a - b = a + (-b)。

3. 乘法实数的乘法满足交换律、结合律和分配律。

即对于任意实数a、b、c，有：交换律：a × b = b × a结合律：(a × b) × c = a × (b × c)分配律：a × (b + c) = a × b + a × c此外，实数的乘法还满足乘法消去律：如果a×b=a×c且a≠0，则b=c。

即如果两个实数的乘积相等，那么它们的因数也是相等的。

4. 除法实数的除法是乘法的逆运算。

对于任意不等于0的实数a、b，有a ÷ b = a × (1/b)，其中1/b表示b的倒数。

二、实数的绝对值在实数中，绝对值是一个非常重要的概念。

对于任意实数x，它的绝对值记作| x |，表示x 到原点的距离。

绝对值有着以下几个基本性质：1. | x | ≥ 02. | x | = 0 当且仅当 x = 03. | -x | = | x |，即绝对值的性质4. | xy | = | x | × | y |绝对值在实数的运算中有着重要的应用，它可以帮助我们简化运算，解决绝对值不等式，以及表示实数的大小关系等问题。

三、指数运算指数运算是实数运算中的重要内容，它包括幂运算、指数函数和对数函数等概念。

第六章实数知识点总结(一)
第六章实数知识点总结
前言
在第六章中，我们学习了实数的相关知识，这个章节是数学学习的基础，对于后续的数学学习非常重要。

本文将对第六章实数知识点进行总结，帮助大家更好地理解和掌握这些概念。

正文
实数的基本性质
•实数是有理数和无理数的总称，包括有限小数、无限循环小数和无限不循环小数。

•实数的四则运算，包括加法、减法、乘法和除法。

•实数的整除性、因数分解和素数判断。

实数的范围
•实数集的包含关系：自然数、整数、有理数、实数的集合关系。

•有理数和无理数的区别和关系，以及无理数的分类。

实数的大小比较
•实数的大小比较原则，包括利用大小关系解决实际问题。

•绝对值的性质和应用，包括绝对值的大小比较和解绝对值不等式。

实数的运算性质
•实数运算与数轴的关系，包括实数加减法的几何意义。

•实数的数轴划分和运算规律，包括实数乘法的几何意义。

•实数的乘方和开方，包括实数乘方的运算规律和开方的性质。

实数的近似表示
•实数的近似表示，包括十进制近似和科学记数法表示。

•实数的修约和有效数字。

结尾
通过本章学习，我们对实数的性质、范围、大小比较、运算性质
和近似表示等方面有了更深入的了解。

实数是数学中的基础概念，对
于后续的数学学习至关重要。

希望大家通过不断的练习和实践，能够
更好地掌握和运用这些实数知识点，为之后的学习打下坚实的基础。

实数知识点总结实数是指包括有理数和无理数的数的集合。

有理数是可以表示为两个整数的比的数，无理数是不能表示为两个整数的比的数。

实数具有以下性质和知识点：1. 实数的分类：- 有理数：可以表示为两个整数的比的数，如整数、分数等。

- 无理数：不能表示为两个整数的比的数，如根号2、圆周率π等。

2. 实数的运算：- 加法和减法：实数的加法和减法满足交换律、结合律和分配律。

- 乘法和除法：实数的乘法和除法满足交换律、结合律和分配律。

除数不能为0。

3. 实数的大小比较：- 实数的大小比较可以用小于号(<)、大于号(>)、小于等于号(≤)、大于等于号(≥)来表示。

- 实数的比较可以根据其对应的小数形式来进行。

4. 实数的绝对值：- 实数的绝对值表示实数到0的距离，用竖杠(|x|)来表示。

- 实数的绝对值满足非负性、正定性和三角不等式。

5. 实数的小数表示：- 实数可以通过小数的形式来表示。

- 小数可以分为有限小数和无限小数。

- 无限小数可以分为循环小数和非循环小数。

6. 实数的有理化：- 实数可以通过有理化的方法转化为有理数的形式。

- 有理化的方法有有理数的开方、通分等。

7. 实数的区间表示：- 实数可以用区间表示。

- 开区间表示为(a, b)，表示实数大于a且小于b。

- 闭区间表示为[a, b]，表示实数大于等于a且小于等于b。

8. 实数的数轴表示：- 实数可以用数轴表示。

- 数轴上的点与实数一一对应。

9. 实数的连续性：- 实数具有连续性。

- 对于任意两个实数a和b，存在一个实数c，使得a<c<b。

10. 实数的柯西收敛原理：- 实数具有柯西收敛原理。

- 一个实数列是收敛的当且仅当这个数列是柯西数列。

以上是关于实数的基本知识点的总结。

实数的概念与性质在数学的各个领域中都有广泛的应用，对于理解和应用数学知识都具有重要的作用。

第六章实数知识网络:考点一、实数的概念及分类1、实数的分类r正有理制j「有理数齐零卜有限'卜数和王限1ft环小数宴埶斗L-员有理锁」厂正形里數-1J无理針 y 卜无隔羽厨环4魁L煲无理数」2、无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类(1)开方开不尽的数，如.7,32等；(2)有特定意义的数，如圆周率n或化简后含有n的数，如n +8等；3(3)有特定结构的数，如0.1010010001…等；(4)某些三角函数，如sin60。

等(这类在初三会出现)判断一个数是否是无理数，不能只看形式，要看运算结果，如°「16是有理数，而不是无理数。

3、有理数与无理数的区别(1)有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数)，而无理数则不能写成分数形式。

考点二、平方根、算术平方根、立方根1、概念、定义(1)如果一个正数x的平方等于a,即厂二，那么这个正数x叫做a的算术平方根。

(2)如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。

如果疋二农，那么x叫做a的平方根。

(3)如果一个数的立方等于a,那么这个数就叫做a的立方根(或a的三次方根)。

如果二-；,那么x叫做a的立方根。

2、运算名称(1)求一个正数a的平方根的运算，叫做开平方。

平方与开平方互为逆运算。

(2)求一个数的立方根的运算，叫做开立方。

开立方和立方互为逆运算。

3、运算符号(1)正数a的算术平方根，记作“.、可”。

(2)a(a>0)的平方根的符号表达为 'l，r： r ' ' o(3)一个数a的立方根，用表示，其中a是被开方数，3是根指数。

4、运算公式a (石『=立(2。

) =\^ |=' 0—謹口=_並(注慧:遣说明三次根号内的员号可以移到根号外面讣4、开方规律小结(1)若a> 0,则a的平方根是、a, a的算术平方根' a;正数的平方根有两个，它们互为相反数，其中正的那个叫它的算术平方根；10的平方根和算术平方根都是0 ；23负数没有平方根。

数学实数知识点总结数学实数是数学中的一种数系，包括有理数和无理数。

实数是一种可以表示在数轴上的点的数，它们可以精确地描述和计算连续和无限的数量。

实数是数学中的基础，无论是在初中数学还是高中数学中都有很重要的地位。

下面是对数学实数知识点的总结。

1. 实数的分类：实数可以分为有理数和无理数两大类。

有理数是可以表示为两个整数的比例的数，如正整数、负整数、分数和小数等。

无理数是不能表示为两个整数的比例的数，如根号2、圆周率π和自然对数的底数e等。

2. 实数的表示方法：实数可以用十进制、分数、小数、百分数等形式来表示。

在十进制表示中，无论整数部分是正整数、负整数还是0，小数部分均可以是有限的或者无限的循环小数。

3. 实数的性质：实数具有传递性、相容性、反对称性、存在性等基本性质。

传递性指的是如果a<b，并且b<c，则a<c；相容性指的是对于任意的a≠b，要么a<b，要么a>b；反对称性指的是对于任意的a≠b，要么a<b，要么b<a；存在性指的是在实数中，存在一个最小的正数（0不是最小的正数）以及一个最大的负数（0不是最大的负数）。

4. 实数的运算：实数的四则运算包括加法、减法、乘法和除法。

在实数的加法和乘法中，满足交换律、结合律和分配律。

在实数的减法和除法中，减法可以转化为加法，除法可以转化为乘法。

5. 实数的大小比较：在实数中，可以通过比较大小符号（<、>、≤、≥）来比较两个实数的大小。

当a<b时，称a小于b，记作a<b；当a>b时，称a大于b，记作a>b；当a≤b时，称a小于等于b，记作a≤b；当a≥b时，称a大于等于b，记作a≥b。

6. 实数的绝对值：实数的绝对值是该实数到0的距离，用|a|表示。

实数a的绝对值的定义如下：当a≥0时，|a|=a；当a<0时，|a|=-a。

7. 实数的相反数和倒数：实数a的相反数为-b，满足a+b=0；实数a的倒数为1/a，满足a*(1/a)=1。

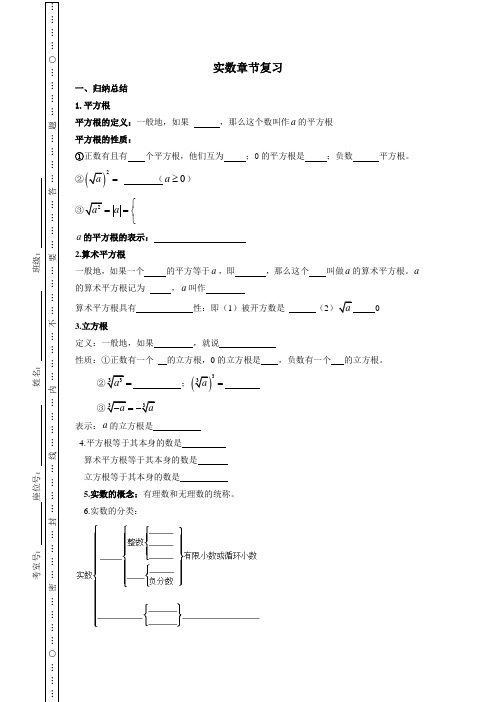
实数章节复习 一、归纳总结 1.平方根 平方根的定义：一般地，如果 ，那么这个数叫作a 的平方根 平方根的性质： ①正数有且有 个平方根，他们互为 ；0的平方根是 ；负数 平方根。

②()2a = （0a ≥） ③2a a ⎧==⎨⎩ a 的平方根的表示： 2.算术平方根 一般地，如果一个 的平方等于a ，即 ，那么这个 叫做a 的算术平方根。

a 的算术平方根记为 ，a 叫作 算术平方根具有 性：即（1）被开方数是 （2）a 0 3.立方根 定义：一般地，如果 ，就说 性质：①正数有一个 的立方根，0的立方根是 ，负数有一个 的立方根。

②33a = ；()33a = ③33a a -=- 表示：a 的立方根是 4.平方根等于其本身的数是 算术平方根等于其本身的数是 立方根等于其本身的数是 5.实数的概念：有理数和无理数的统称。

6.实数的分类：考室号： 座位号： 姓名： 班级：7.无理数：无限不循环小数。

包括：① ② ③ 二、典例精析 例1：16的平方根是 ，16的算术平方根是 16的平方根是 ，16的算术平方根是例2.553y x x =-+-+，则xy =例3：如果一个数的平方根是1a +和27a -，求这个数。

例3.用平方根定义解方程（1）24250x -= （2）216(2)49x +=例4.已知11的小数部分是m ，411-的小数部分是n ，则m n +=例5.已知3 1.732,30 5.477,(1)300≈≈≈ ；（2）0.3≈例6.已知3333 1.442,30 3.107,300 6.694≈≈≈，那么30.3≈ ；33000≈例7. 数在数轴上的位置如图：化简()2a b b c -+-变式：已知 ,,a b c 位置如图所示：化简()22a a b c a b c --+-+-【当堂测评】1．如果一个实数的平方根与它的立方根相等，则这个数是（ ）A ． 0B ． 正整数C ． 0和1D ． 12.能与数轴上的点一一对应的是（ ）A 整数B 有理数C 无理数D 实数3. 下列各数中，不是无理数的是 （ ）A. 7B. 0.5C. 2πD. 0.151151115…（两个5之间依次多一个1） 4．在数轴上表示3-的点离原点的距离是 。

数学实数知识点在日复一日的学习中，不管我们学什么，都需要掌握一些知识点，知识点也可以通俗的理解为重要的内容。

那么，都有哪些知识点呢？下面是店铺帮大家整理的数学实数知识点（精选8篇），仅供参考，欢迎大家阅读。

数学实数知识点1实数，是有理数和无理数的总称。

数学上，实数定义为与数轴上的点相对应的数。

实数可以直观地看作有限小数与无限小数，它们能把数轴“填满”。

但仅仅以列举的方式不能描述实数的整体。

实数和虚数共同构成复数。

1、实数的分类：有理数和无理数2、数轴：规定了原点、正方向和单位长度的直线叫数轴。

实数和数轴上点一一对应。

3、相反数：符号不同的两个数，叫做互为相反数。

a的相反数是-a，0的相反数是0。

(若a与b护卫相反数，则a+b=0)4、绝对值：在数轴上表示数a的点到原点的距离叫数a的绝对值，记作∣a∣，正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。

5、倒数：乘积为1的两个数6、乘方：求相同因数的积的运算叫乘方，乘方运算的结果叫幂。

(平方和立方)7、平方根：一般地，如果一个数x的平方等于a,即x2=a那么这个数x就叫做a的平方根(也叫做二次方根)。

一个正数有两个平方根，它们互为相反数;0只有一个平方根，它是0本身;负数没有平方根。

(算术平方根：一般地，如果一个正数x的平方等于a,即x2=a，那么这个正数x就叫做a的算术平方根，0的算术平方根是0。

)数学实数知识点21.数的分类及概念数系表：说明：分类的原则：1)相称(不重、不漏)2)有标准2.非负数：正实数与零的统称。

(表为：x0)性质：若干个非负数的和为0，则每个非负数均为0。

3.倒数：①定义及表示法②性质：A.a1/a(a1);B.1/a中，aC.04.相反数：①定义及表示法②性质：A.a0时，aB.a与-a在数轴上的位置;C.和为0,商为-1。

5.数轴：①定义(三要素)②作用：A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。

(完整版)实数知识点总结1. 实数的定义实数是包括有理数和无理数在内的数的集合。

实数集包含有理数集和无理数集。

2. 有理数的性质有理数是可以表示为两个整数的比值的数。

有理数的性质包括：- 有理数的四则运算性质：加法、减法、乘法和除法。

- 有理数的分数形式，即可以表示为两个整数的比值。

- 有理数可以表示为小数，且小数可以是有限的或无限循环的。

3. 无理数的性质无理数是不能表示为两个整数的比值的数。

无理数的性质包括：- 无理数不能表示为分数形式。

- 无理数的十进制表示是无限不循环的。

- 无理数可以用无限不循环的小数表示，但无法精确表示。

4. 实数的数轴表示实数可以在数轴上表示，数轴上的每个点都对应一个实数。

5. 实数的运算实数的运算包括加法、减法、乘法和除法。

实数的运算满足以下性质：- 交换律：a + b = b + a，a * b = b * a。

- 结合律：(a + b) + c = a + (b + c)，(a * b) * c = a * (b * c)。

- 分配律：a * (b + c) = a * b + a * c。

6. 绝对值绝对值是一个数离0的距离，可以用来表示数的大小。

绝对值的性质包括：- 绝对值非负：|a| >= 0。

- 非零数的绝对值大于0：|a| > 0。

- 绝对值的加法：|a + b| <= |a| + |b|。

7. 实数的比较实数可以进行大小比较，实数的比较满足以下性质：- 反身性：a = a。

- 对称性：如果a > b，则b < a。

- 传递性：如果a > b，b > c，则a > c。

8. 实数的区间实数可以按照大小关系分为开区间、闭区间、半开半闭区间等。

区间的边界可以是实数也可以是无穷大。

9. 实数的近似值由于实数的无理数部分是无限不循环的，所以我们一般用近似值来表示实数。

10. 实数的应用实数在数学和科学中有广泛的应用，如在几何中表示线段长度、在物理中表示物体的质量等。

实数的知识点总结实数的性质有很多，包括实数的大小比较、加法、减法、乘法、除法的性质以及实数的有序性、稠密性等。

下面来详细介绍一下实数的这些性质。

1. 实数的大小比较实数的大小比较是指在实数集合中，对实数的大小进行比较。

实数集合中的数可以用数轴上的点来表示，数轴上每个点都对应一个实数。

通过数轴，我们可以直观地比较实数的大小。

如果a和b是实数，那么它们之间有以下关系：（1）a=b，即a等于b；（2）a>b，即a大于b；（3）a<b，即a小于b；实数的大小比较是实数运算和实数不等式研究的基础，是十分重要的。

2. 实数的加法性质实数的加法性质包括交换律、结合律、零元素和加法逆元素等。

具体来说，对于任意实数a、b、c，有以下性质：（1）交换律：a+b=b+a；（2）结合律：(a+b)+c=a+(b+c)；（3）零元素：存在一个实数0，对任意实数a，有a+0=a；（4）加法逆元素：对于任意实数a，存在一个实数-b，使得a+(-b)=0。

3. 实数的减法性质实数的减法性质是指实数的减法运算满足的性质。

对于任意实数a、b、c，有以下性质：（1）减法的定义：a-b=a+(-b)；（2）减法的性质：a-b=c等价于a=c+b。

4. 实数的乘法性质实数的乘法性质包括交换律、结合律、分配律、单位元素和乘法逆元素等。

具体来说，对于任意实数a、b、c，有以下性质：（1）交换律：a×b=b×a；（2）结合律：(a×b)×c=a×(b×c)；（3）分配律：a×(b+c)=a×b+a×c；（4）单位元素：存在一个实数1，对任意实数a，有a×1=a；（5）乘法逆元素：对于任意非零实数a，存在一个实数1/a，使得a×(1/a)=1。

5. 实数的除法性质实数的除法性质是指实数的除法运算满足的性质。

对于任意实数a、b、c，有以下性质：（1）除法的定义：a÷b=a×(1/b)，其中b≠0；（2）除法的性质：a÷b=c等价于a=c×b。

实数知识点大全总结实数是指包括有理数和无理数在内的所有数的集合。

实数包括正数、负数、零、有理数、无理数等各种类型的数。

实数有着丰富的数学性质和运算规律，在数学和其他学科中都有广泛的应用。

1. 实数的分类实数可以分为有理数和无理数两大类。

有理数是可以用分数表示的数，包括正整数、负整数、零、分数等。

有理数具有分数形式和小数形式两种表达方式，例如3/4和0.75都是有理数。

无理数是不能用分数表示的数，或者说是无限不循环小数的数。

无理数包括无限不循环小数和根号形式的数，例如π和√2都是无理数。

2. 实数的运算实数可以进行各种运算，包括加法、减法、乘法、除法等。

实数的运算遵循一定的性质和规律。

加法和减法：实数的加法和减法满足交换律、结合律和分配律，即a+b=b+a，a+(b+c)=(a+b)+c，a*(b+c)=a*b+a*c。

加法的逆元是减法，即a+(-a)=0。

乘法和除法：实数的乘法和除法也满足交换律、结合律和分配律，即a*b=b*a，a*(b*c)=(a*b)*c，a/(b*c)=(a/b)/c。

乘法的逆元是除法，即a*(1/a)=1。

3. 有理数的性质有理数具有以下性质：a) 有理数的加法和乘法封闭性：两个有理数的和、积仍然是有理数。

b) 有理数的序关系：任意两个有理数可以比较大小，成立大小关系。

c) 有理数的密集性：在任意两个有理数之间，都可以找到另一个有理数。

d) 有理数的稠密性：在有理数的任何两个不同的数之间总存在无数个有理数。

4. 无理数的性质无理数具有以下性质：a) 无理数的加法和乘法封闭性：两个无理数的和、积仍然是无理数。

b) 无理数的密度性：在任意两个无理数之间，总存在另一个无理数。

c) 无理数的非周期性：无理数小数部分是无限不循环小数。

d) 无理数的无限性：无理数是无限不可数的。

5. 实数的绝对值实数a的绝对值记作|a|，定义为：a≥0时，|a|=a；a<0时，|a|=-a。

实数的知识点总结引言：实数是数学中最基本、最重要的数系之一。

在我们的日常生活中，我们经常会接触到实数，了解实数的性质和特点对于建立数学思维和解决实际问题至关重要。

本文将总结实数的一些重要知识点，帮助读者更好地理解和运用实数。

基本概念：实数是可以在数轴上表示的数，包括整数、有理数和无理数。

整数是不小于零且不带小数部分的数，也包括正整数和负整数。

有理数是可以表示为两个整数之比的数，包括分数和有限小数。

无理数是不能表示为两个整数之比的数，常见的无理数有根号2、圆周率π等。

实数的性质：实数具有如下的性质：1. 封闭性：实数集合对加法、减法、乘法和除法运算都是封闭的，即任意两个实数的运算结果仍然是实数。

例如，任意两个实数a 和b的和、差、积和商都是实数。

2. 有序性：实数可以按大小进行比较，即任意两个实数a和b，总是有且只有下面三种情况之一：a < b，a > b，或者a = b。

3. 密度性：实数集合是一个稠密集，即在任意两个不同的实数a 和b之间，总存在一个实数c，使得a < c < b。

这意味着实数集合中不存在间隙，任意两个实数之间都可以找到无数个其他的实数。

4. 无限性：实数集合是无限的，没有最大值和最小值。

对于任意一个实数x，总是存在一个实数y，使得y > x。

同样，对于任意一个实数x，总是存在一个实数z，使得z < x。

实数的表示：实数可以通过各种方式来表示，常见的包括分数、小数、百分数和根号形式。

分数是实数的一种常见表示方式，可以表示为两个整数的比值，如1/2、3/4等。

小数是实数的一种十进制表示方式，可以是有限小数，如0.5、0.75等，也可以是无限循环小数，如0.333...、0.666...等。

百分数是实数的一种百分制表示方式，将实数乘以100后，加上百分号表示，如50%、75%等。

根号形式是表示无理数的方式，常见的无理数如根号2、根号3等。

实数的运算：实数的加法、减法、乘法和除法运算与我们熟悉的数学运算规则一致。

有关实数的知识点总结一、实数的概念实数是数学中一个基本的概念，它包括有理数和无理数两类。

有理数是可以表示为两个整数的比值的数，包括整数和分数；无理数是不能表示为有理数的数，如π和√2等。

实数是包括有理数和无理数在内的一类数，可以用来表示实际问题中的数值，是数学研究的基础。

实数可以用数轴来表示，数轴是一条直线，上面标有0点，向右正数递增，向左负数递减。

实数可以对应数轴上的所有点，因此可以用来表示长度、面积、体积、时间、质量等实际问题中的数值。

二、实数的性质实数有一些重要的性质，其中包括稠密性、有界性、加法、乘法、大小关系等。

1. 稠密性：实数具有稠密性，即在任意两个不相等的实数之间，都存在着另外一个实数。

这意味着实数可以无限地划分，可以趋近于任意的数值。

2. 有界性：实数有界，即存在一个最小值和一个最大值。

这意味着实数在数轴上是有限的，不会无限地增长或减小。

3. 加法与乘法：实数满足加法和乘法的封闭性，即两个实数的加法和乘法仍然是实数。

例如，任意两个实数相加或相乘，结果仍然是实数。

4. 大小关系：实数有大小关系，即可以比较大小。

如果一个实数大于另一个实数，则称这个实数为大于另一个实数，反之亦然。

这使得实数可以用来比较数值大小。

以上是实数的一些基本性质，它们对于实数的研究和应用有着重要的意义。

三、实数的运算实数有加法、减法、乘法、除法四种基本的运算，这些运算满足一些重要的性质，如交换律、结合律、分配律等。

1. 加法：实数的加法满足交换律和结合律，即对于任意两个实数a和b，有a+b=b+a和(a+b)+c=a+(b+c)。

这意味着实数的加法是可以交换顺序和可以结合的。

2. 减法：实数的减法是加法的逆运算，即对于任意两个实数a和b，有a-b=a+(-b)，其中-a表示b的相反数。

减法也满足交换律和结合律。

3. 乘法：实数的乘法满足交换律和结合律，即对于任意两个实数a和b，有a×b=b×a和(a×b)×c=a×(b×c)。

1、定义：如果一个正数x 的平方等于a ，即a x=2。

那么，这正数x 叫做a 的算术平方根。

记作a ，读作“根号a ”。

a 叫做被开 方数，规定0的算术平方根还是0。

2、性质：双重非负性（0≥a ，0≥a ）。

负数没有算术平方根。

3、a a =2（a 是任意数），a a =2)(（a 是非负数）。

1、定义：如果一个数x 的平方等于a ，即a x =2。

那么，这个x 叫做a 的平方根。

记作a ±，读作“正、负根号a ”。

a 叫做被开方数。

规定0的算术平方根还是0。

2、性质：（1）正数有两个平方根，它们互为相反数。

（2）0的平方根是0。

负数没有平方根。

3、未知数次数是两次的方程，结果一般都有两个值。

414.12≈，732.13≈，236.25≈，646.27≈1、定义：如果一个数x 的立方等于a ， 即a x =3。

那么，这个x 叫做a 的立方根。

记作3a ，读作“三次根号a ”。

a 叫做被开方数。

2、性质：（1）正数的立方根是正数，负数的立方根是负数，0的立方根是0。

（2）3333a a -=-（3）a a =33)(平方根 算术平方根 平方根 立方根 a 取任意数 实数 正实数 负实数 0 实数有理数 无理数 整数 分数（有理数和分数是相同的概念） （可以看成分母是1的分数） 正整数 负整数 0 有限小数 无限循环小数 无限不循环小数 1、开方开不尽的方根2、圆周率π以及含有π3、具有特定结构的数（0.010010001……）。

考点一、实数的概念及分类1、实数的分类正有理数有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数整数包括正整数、零、负整数。

正整数又叫自然数。

正整数、零、负整数、正分数、负分数统称为有理数。

2、无理数（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等； （3）有特定结构的数，如0.1010010001…等；考点二、平方根、算数平方根1、平方根如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方跟）。

一个数有两个平方根，他们互为相反数；零的平方根是零；负数没有平方根。

正数a 的平方根记做“a ”。

2、算术平方根正数a 的正的平方根叫做a 的算术平方根，记作“a ”。

正数和零的算术平方根都只有一个，零的算术平方根是零。

考点三、立方根如果一个数的立方等于a ，那么这个数就叫做a 的立方根（或a 的三次方根）。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

注意：33a a -=-，这说明三次根号内的负号可以移到根号外面。

考点四、实数大小的比较1、数轴规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。

解题时要真正掌握数形结合的思想，理解实数与数轴的点是一一对应的，并能灵活运用。

2、实数大小比较的几种常用方法（1）数轴比较：在数轴上表示的两个数，右边的数总比左边的数大。

（2）求差比较：设a 、b 是实数，,0b a b a >⇔>-,0b a b a =⇔=-b a b a <⇔<-0（3）求商比较法：设a 、b是两正实数，;1;1;1b a b a b a b a b a b a <⇔<=⇔=>⇔> （4）绝对值比较法：设a 、b 是两负实数，则b a b a <⇔>。

（5）平方法：设a 、b 是两负实数，则b a b a <⇔>22。