异方差实验报告
- 格式:doc
- 大小:864.50 KB
- 文档页数:7

异方差性实验报告篇一:计量经济学上机实验报告(异方差性)提示:打包保存时自己的文件夹以“学号姓名”为文件夹名,打包时文件夹内容包括:本实验报告、EViews工作文件。
篇二:Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验(1)散点相关图分析做出销售收入X与研究开发费用Y的散点相关图(SCATX Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析首先对数据按照解释变量X由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。
因此,模型估计式为: Y?187.507?0.032*X ----------(*) ?(0.17)(2.88) R2=建立残差关于X的散点图,可以发现随着X增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列: GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。

实验四异方差性的检验与处理集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时 三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
检验的三个步骤 ① ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③ 做等级相关系数的显着性检验。
n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若在统计上是显着的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121(i i p pi iy x x uf xβββ=+⋅++⋅+在该模型中:即满足同方差性。
于是可以用OLS估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量。
五、实验举例例101i i iy x u=++若用线性模型,研究不同收入家庭的消费情况,试问原数据有无异方差性如果存在异方差性,应如何处理解:(一)编写程序如下:(1)等级相关系数法(详见文件)%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性 %%%%%%%%[data,head]=xlsread('');x=data(:,1); %提取第一列数据,即可支配收入xy=data(:,2); %提取第二列数据,即居民消费支出yplot(x,y,'k.'); % 画x和y的散点图xlabel('可支配收入x(千元)') % 对x轴加标签ylabel('居民消费支出y(千元)') % 对y轴加标签%%%%%%%% 调用regres函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones(size(x,1),1),x]; %在x矩阵最左边加一列1,为线性回归做准备[b,bint,r,rint,s]=regress(y,xdata);yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'};[head1;num2cell([b,bint])]% 定义元胞数组,以元胞数组形式显示y的真实值,y的估计值,残差和残差的95%置信区间head2={'y的真实值','y的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell([y,yhat,r,rint])]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell(s)]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot(r,rint) % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot(yhat,r,'k.') % 画散点图xlabel('估计值yhat') % 对x轴加标签ylabel('残差r') % 对y轴加标签%%%%%%%%%%%% 调用corr函数计算皮尔曼等级相关系数res=abs(r); % 对残差r取绝对值[rs,p]=corr(x,res,'type','spearman')disp('其中rs为皮尔曼等级相关系数,p为p值');(2)帕克(park)检验法(详见文件)%%%%%%%%%%%%%%% 用帕克(park)检验法来检验异方差性 %%%%%%%[data,head]=xlsread(''); %导入数据x=data(:,1);y=data(:,2);%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats(y,x,'linear',{'yhat','r','standres'});scatter(x,.^2) % 画x与残差平方的散点图xlabel('可支配收入(x)') % 对x轴加标签ylabel('残差的平方') %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归ST1=regstats(log(.^2),log(x),'linear',{'r','beta','tstat','fstat'})% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显着性检验的P值(3)加权最小二乘法(详见文件)%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread(''); % 导入数据x=data(:,1);y=data(:,2);% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit(x,y) %调用函数作稳健回归% 输出模型检验的P值%%% 绘制残差和权重的散点图 %%%%%%%plot,,'o') %绘制残差和权重的散点图xlabel('残差')ylabel('权重'(二)实验结果与分析:第一步::用OLS方法估计参数,并保留残差(1)散点图图可支配收入(x)居民消费支出(y)散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状。
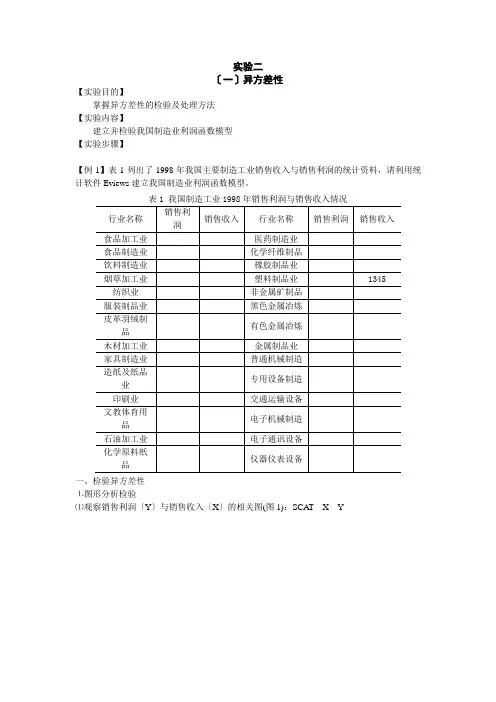
实验二〔一〕异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润〔Y〕与销售收入〔X〕的相关图(图1):SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序〔命令格式为:SORT 解释变量〕,然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图〔或建立方程后在Eviews工作文件窗口中点击resid对象来观察〕。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即说明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本安解释变量排序〔SORT X〕并分成两部分〔分别有1到10共11个样本合19到28共10个样本〕⑵利用样本1建立回归模型1〔回归结果如图3〕,其残差平方和为。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2〔回归结果如图4〕,其残差平方和为。
SMPL 19 28 LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。

异方差性实验报告doc异方差性实验报告篇一:计量经济学上机实验报告(异方差性)提示:打包保存时自己的文件夹以“学号姓名”为文件夹名,打包时文件夹内容包括:本实验报告、EViews工作文件。
篇二:Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews操作方法。
【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据,练习检查和克服模型的异方差的操作方法。
【4-16】表4-1给出了美国18个行业1988年研究开发(R&D)费用支出Y与销售收入X的数据。
请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q检验与怀特(White)检验来检验Y关于X的回归模型是否存在异方差性?若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验(1)散点相关图分析做出销售收入X与研究开发费用Y的散点相关图(SCATX Y)。
观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
(2)残差图分析首先对数据按照解释变量X由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。
因此,模型估计式为: Y?187.507?0.032*X ----------(*) ?(0.17)(2.88) R2=建立残差关于X的散点图,可以发现随着X增加,残差呈现明显的扩大趋势,表明存在递增的异方差。
2、Park检验建立回归模型(LS Y C X),结果如(*)式。
生成新变量序列: GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。
从下图所示的回归结果中可以看出,LNX的系数估计值不为0且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。

西安财经学院本科实验报告学院(部)统计学院实验室 313 课程名称计量经济学学生姓名学号 1204100213 专业统计学教务处制2014年12 月 15 日《异方差》实验报告开课实验室:313 2014年12月22第六部分异方差与自相关4. 在本例中,参数估计的结果为:2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999)922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538三.检查模型是否存在异方差 1.图形分析检验 (1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图,观察相关图可以看出,随着X1、X2的增加,Y 也增加,但离散程度逐步扩大,尤其表现在X1和Y.这说明变量之间可能存在递增的异方差性。
在Graph/scatter 输入log(x2) e^2,结果如下:(2)残差相关图分析建立残差关于X1、X2的散点图,可以发现随着X 的增加,残差呈现明显的扩大趋势,表明模型很可能存在递增的异方差性。
但是否确实存在异方差还应通过更进一步的检验。
2.GQ 检验首先在主窗口Procs菜单里选Sort current page命令,输入排序变量x2,以递增型排序对解释变量X2进行排序,然后构造子样本区间,分别为1-12和20-31,再分别建立回归模型。
(1)在Sample菜单里,将区间定义为1—12,然后用OLS方法求得如下结果(2)在Sample菜单里,将区间定义为20—31,然后用OLS方法求得如下结果则F的统计量值为:6699.834542929948192122===∑∑iieeF在05.0=α下,式中分子、分母的自由度均为9,查F分布表得临界值为:18.3)9,9(05.0=F,因为F=8.6699>18.3)9,9(05.0=F,所以拒绝原假设,表明模型确实存在异方差。

异方差实验报告引言异方差(heteroscedasticity)是指随着自变量的变化,因变量的方差也随之变化的现象。
在统计分析中,假设方差是恒定的是很常见的,但在实际应用中,许多变量的方差是不恒定的,需要进行异方差处理。
本实验旨在通过模拟数据和实际数据来探究异方差的影响并了解异方差检验方法。
实验设计本实验分为两个部分。
第一部分使用模拟数据,提供了不同阶段下的异方差数据集。
第二部分使用实际数据,通过观察数据的模式来判断是否存在异方差。
实验方法模拟数据在模拟数据部分,我们生成了四个数据集,每个数据集都包含一个自变量和一个因变量。
为了模拟异方差,我们设定了不同的标准差,并与自变量呈一定的关系。
具体参数如下:•数据集1:使用正态分布生成自变量和因变量,因变量的标准差为自变量的两倍。
•数据集2:自变量为正态分布,因变量为自变量的2次方,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集3:自变量为均匀分布,因变量为自变量的指数函数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集4:自变量为正态分布,因变量为自变量的对数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
实际数据在实际数据部分,我们使用了一份销售数据。
该数据包含了不同日期下的产品销售量和价格。
我们首先观察数据的散点图,并通过直观感受来猜测是否存在异方差。
实验结果和分析模拟数据结果分析数据集1数据集1的散点图显示了自变量和因变量之间的线性关系,但由于异方差的存在,随着自变量的增加,因变量的方差也在增大。
这说明了异方差对回归结果的影响。
数据集2数据集2的散点图显示了自变量和因变量之间的非线性关系。
由于自变量的增大,因变量的方差也在增大。
这与模型中设定的异方差关系一致。
数据集3数据集3的散点图显示了自变量和因变量之间的指数关系。
随着自变量的增大,因变量的方差也在增大,符合预期的异方差模式。
数据集4数据集4的散点图显示了自变量和因变量之间的对数关系。


西安财经学院本科实验报告学院(部)统计学院实验室313课程名称计量经济学学生姓名学号1204100213专业统计学教务处制2014年12 月15 日《异方差》实验报告五、实验过程原始记录(数据、图表、计算等) 一.选择数据1.建立工作文件并录入数据File\New\workfile, 弹出Workfile create 对话框中选择数据类型.Object\new object\group,按向上的方向键,出现两个obs 后输入数据.中国内地2006年各地区农村居民家庭人均纯收入与消费支出 单位:元城市 y x1 x2 城市 y x1 x2 北京 5724。
5 958.3 7317。
2 湖北 2732。
5 1934。
6 1484。
8 天津 3341。
1 1738.9 4489 湖南 3013。
3 1342.6 2047 河北 2495。
3 1607。
1 2194。
7 广东 3886 1313。
9 3765.9 山西 2253.3 1188。
2 1992.7 广西 2413。
9 1596。
9 1173。
6 内蒙古 2772 2560.8 781.1 海南 2232。
2 2213。
2 1042.3 辽宁 3066。
9 2026。
1 2064。
3 重庆 2205。
2 1234.1 1639。
7 吉林 2700.7 2623。
2 1017。
9 四川 2395 1405 1597.4 黑龙江 2618。
2 2622.9 929.5 贵州 1627。
1 961。
4 1023。
2 上海 8006 532 8606.7 云南 2195.6 1570。
3 680。
2 江苏 4135.2 1497。
9 4315.3 西藏 2002。
2 1399.1 1035.9 浙江 6057。
2 1403.1 5931。
7 陕西 2181 1070。
4 1189。
8 安徽 2420。
9 1472。
8 1496。
3 甘肃 1855.5 1167。

实验二实验内容:异方差模型的检验和修正方法实验要求:通过本次实验,初步掌握掌握判断模型是否存在异方差的一般方法,包括图示法、Goldfeld-Quandt检验法、Gleiser检验法、怀特检验法;并会利用加权最小二乘法修正模型。
实验数据:表4.1.1数据实验步骤:1、用OLS法建立模型第一步:建立WORKFILEFil e→ new →workfile→弹出对话框→第一个填 1→第二个填31→OK第二步:输入数据1、建立存放数据的Group:在命令主出口输入命令DATA Y X然后按ENTER运行2、从原来保存数据的表格中复制数据到Group如何求已知数列的新数列:genr lnx1=log(x1)第三步:软件操作OLS法主命令窗口输入:LS Y C LNX1 LNX2 按ENTER运行结果如图所示:2、检验模型是否存在异方差第一种方法:图示法第一步:求原来模型的参差项(e~的值)i只要对原来的模型进行普通最小二乘估计就可以求的残差项,残差项在系统中默认为resid.Resid的位置在workfile窗口,如下图所示。
第二步:图示2~ie 和X 的关系 Quick →Graph →弹出对话框→输入LNX2(横轴) →resid^2(纵轴) →OK →下拉菜单选 scatter diagram →ok (结果如下图)分析这个图:因为不是和横轴平行的直线,所以存在异方差;而且resid^2随着X 的增加而增加,所以是递增型异方差。
第二种方法:帕克戈里瑟检验第一步:建立2~ie 和X 的模型(本题建立的是一元线性回归模型,并且解释变量是一次方的,这个模型的具体形式根据具体情况来决定)122i i eLN X ααε=++ 第二步:对上面这个模型进行回归主命令窗口输入: Ls abs(resid) c lnx2 结果如下图所示:方程F检验值为:F=0.625190临界值0.05(1,29) 4.18F=因为 F<05.0F(也可以用T检验)所以作为解释变量的X对被解释变量2~ie的影响不显著,意思就是说2~i e随着X的变化没有变化。
计量经济学实验一、实验内容1、实验目的研究农村居民各种不同类型的收入对消费支出的影响。
同时,掌握线性模型或双对数模型,并熟悉异方差的检验和解决办法。
2、实验要求(1)利用线性模型或双对数模型进行分析;(2)判断并解决异方差问题;(3)对模型进行调整;(4)提出扩大消费的政策建议。
二、实验报告1、问题提出影响农村居民家庭消费支出的因素有很多,如经济增长,人均国内生产总值,消费者物价指数等等。
其中,收入是影响消费的主要因素。
随着改革开放,劳动力的需求增加,农民工纷纷进城务农;我国颁布一系列对农民的补贴性政策,农民收入不断提高之际,收入也呈现多元化的局面,从单一的家庭人均纯收入扩展到工资性收入、财产性收入、转移性收入等。
我们选取了2006年各省市农村居民家庭各类收入与消费支出的数据,研究农村居民各种不同类型的收入对消费支出的影响,2、指标选择2006年各省市农村居民家庭各类收入与消费支出的数据。
3、数据来源实验课上老师提供的。
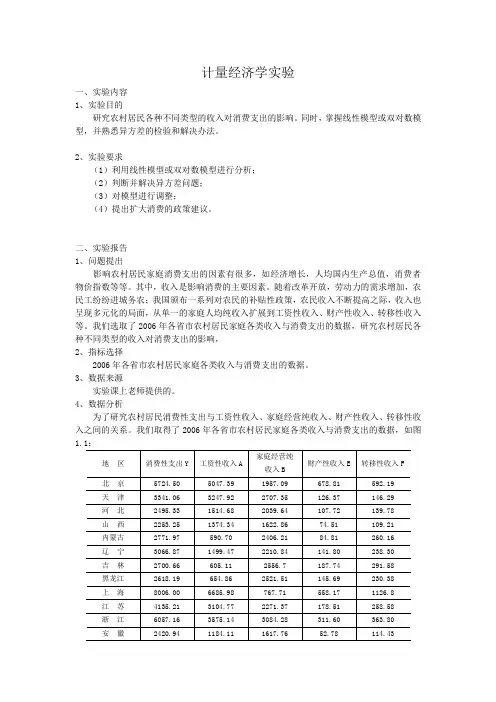
4、数据分析为了研究农村居民消费性支出与工资性收入、家庭经营纯收入、财产性收入、转移性收入之间的关系。
我们取得了2006年各省市农村居民家庭各类收入与消费支出的数据,如图1.1:地区消费性支出Y 工资性收入A 家庭经营纯收入B财产性收入E 转移性收入F北京5724.50 5047.39 1957.09 678.81 592.19 天津3341.06 3247.92 2707.35 126.37 146.29 河北2495.33 1514.68 2039.64 107.72 139.78 山西2253.25 1374.34 1622.86 74.51 109.21 内蒙古2771.97 590.70 2406.21 84.81 260.16 辽宁3066.87 1499.47 2210.84 141.80 238.30 吉林2700.66 605.11 2556.7 187.74 291.58 黑龙江2618.19 654.86 2521.51 145.69 230.38 上海8006.00 6685.98 767.71 558.17 1126.8 江苏4135.21 3104.77 2271.37 178.51 258.58 浙江6057.16 3575.14 3084.28 311.60 363.80 安徽2420.94 1184.11 1617.76 52.78 114.43福建3591.40 1855.53 2481.62 113.52 384.09江西2676.60 1441.34 1863.5 35.13 119.57山东3143.80 1671.54 2409.78 127.60 159.4河南2229.28 1022.74 2108.26 40.37 89.66湖北2732.46 1199.16 2095.15 25.91 99.13湖南3013.32 1449.65 1743.39 42.49 154.09广东3885.97 2906.15 1693.64 220.87 259.12广西2413.93 974.32 1705.75 22.45 69.96海南2232.19 555.72 2486.94 49.44 163.43重庆2205.21 1309.91 1349.57 27.29 187.07四川2395.04 1219.51 1586.54 52.84 143.50贵州1627.07 715.49 1112.81 36.93 119.38云南2195.64 441.81 1631.60 82.19 94.85西藏2002.24 568.39 1410.51 156.00 300.06陕西2181.00 848.26 1219.33 52.56 140.04甘肃1855.49 637.37 1291.85 52.56 152.27青海2178.95 653.30 1374.36 100.66 230.05宁夏2246.97 823.09 1662.07 53.35 221.63新疆2032.36 254.07 2323.01 58.69 101.51 2006年各省市农村居民家庭各类收入与消费支出(单位:元)图:1.1假定消费性支出与工资性收入、家庭经营纯收入、财产性收入、转移性收入之间呈现线性关系。

实验题目:异方差实验目的:掌握运用EVIEWS软件检验异方差的几种方法和解决异方差的基本操作方法和步骤,并能够对软件运行结果进行解释。
实验对象:2004年全国31个省市自治区农作物种植业产值Y t(亿元)和农作物播种面积X t(万亩)实验步骤:1、模型估计。
打开EViews6.0,建立工作文件(研究农作物种植业产值Y t和农作物播种面积X t 的关系),输入数据,在主菜单点击Quick\Estimate Equation ,在弹出的对话框中输入被解释变量常数项解释变量,点击OK,得到用最小二乘估计的各个参数估计值:得估计的线性Yˆ= 25.09 + 0.113 X t模型如下:t(71.342)(0.0118)(0.3517)(9.5589)R2 = 0.76, F = 91.37D.W=2.117,n=312、异方差的检验。
(1)图示法:用EViews6.0得到的Y关于X的散点图如下:可以发现数据中存在异方差。
(2)Goldfeld-Quandt方法:1)先对变量取值排序,即在workfile窗口的Procs菜单里选Sort Current Page命令,出现排序对话框,键入X,点击Ascenging,数据就会按递增的顺序排列。
2)构造子样本区间,建立回归模型。
删除中间1/4的观测值,在本实验中有31数据,即去掉中间7个数据,按X t取值大小分成样本容量各为12的两个子样本,分别用最小二乘估计得到各个估计值如图所示:得到各回归结果如下:tY ˆ = 35.14+ 0.1244 X t (t = 1, …, 12) R 2 = 0.71 F = 24.64 ESS =138421.2, tY ˆ= -241.18+ 0.1421X t (t = 20, …, 31) R 2 = 0.53 F = 11.48, ESS =996129.4 于是,统计量:F = )212/(2.138421)212/(4.996129-- = 7.196。
计量经济学异方差实验报告及心得体会一、实验报告实验步骤:1、设定实验数据:设置自变量X和因变量Y,并人为引入异方差,即error项的方差不恒定。
2、建立回归模型:根据设定的数据,建立回归模型,运用最小二乘法估计模型参数。
3、对回归结果进行分析:通过查看回归系数、残差和残差的图形等,判断是否存在异方差问题。
4、进行异方差检验:利用统计软件进行异方差检验,如White 检验或Breusch–Pagan检验等,获取检验结果。
5、处理异方差问题:根据异方差检验结果,采取相应的处理方法,如使用加权最小二乘法或进行异方差稳健标准误的估计。
6、比较处理前后的回归结果:对处理前后的回归结果进行比较和分析,观察异方差的处理是否有效。
实验结果:在实验过程中,我们设定了一个简单的回归模型,并引入异方差。
经过处理异方差问题后,我们发现被异方差影响的模型的回归系数和标准误均有所变化。
而经过异方差处理后,回归结果更加稳定,模型的预测能力也相应提高。
二、心得体会通过本次实验,我对计量经济学中异方差的概念和影响有了更加深入的了解。
异方差问题存在时,回归模型的估计结果可能会产生偏误,影响模型的准确性。
因此,我们需要进行异方差检验,并采取相应的处理方法。
实验过程中,我们运用了统计软件进行异方差检验和处理,这使得整个分析过程更加简洁和高效。
此外,本次实验还提醒我们在实际研究中要注意可能存在的异方差问题,并及时处理。
在计量经济学领域,处理异方差问题的方法有很多,选择适合实际情况的方法非常重要。
因此,我们需要不断学习和实践,提高自己的计量经济学分析能力。
总之,本次实验对我们深入理解异方差在计量经济学中的重要性起到了很好的引导作用。
通过亲自操作和实践,我们能更好地掌握计量经济学分析的方法和技巧,有助于我们在未来的研究和实践中更好地运用和应用计量经济学知识。
四、异方差性【实验目的】1. 掌握异方差的含义,理解经济现象中异方差产生的原因;2. 理解异方差对模型的影响,异方差性的表现与某个解释变量之间的关系;3. 掌握检验异方差的主要方法;4. 掌握处理和消除异方差的方法。
【实验内容】(一) 引起异方差的原因及其对参数估计的影响 1、原因:引起异方差的众多原因中,我们讨论两个主要的原因,一是模型的设定偏误,主要指的是遗漏变量的影响。
这样,遗漏的变量就进入了模型的残差项中。
当省略的变量与回归方程中的变量有相关关系的时候,不仅会引起内生性问题,还会引起异方差。
二是截面数据中总体各单位的差异。
后果:异方差对参数估计的影响主要是对参数估计有效性的影响。
在存在异方差的情况下,OLS 方法得到的参数估计仍然是无偏的,但是已经不具备最小方差性质。
一般而言,异方差会引起真实方差的低估,从而夸大参数估计的显著性,即是参数估计的t 统计量偏大,使得本应该被接受的原假设被错误的拒绝。
2、异方差的检验 (1)图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化,因此,可以通过散点图的方式来简单的判断是否存在异方差。
具体的做法是,以回归的残差的平方2i e 为纵坐标,回归式中的某个解释变量ix 为横坐标,画散点图。
如果散点图表现出一定的趋势,则可以判断存在异方差。
(2)Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法,由Goldfeld 和Quandt 1965年提出。
这种检验的思想是以引起异方差的解释变量的大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本。
用两个子样本分别进行回归,并计算残差平方和。
用两个残差平方和构造检验异方差的统计量。
Goldfeld-Quandt 检验有两个前提条件,一是该检验只应用于大样本(n>30),并且要求满足条件:观测值的数目至少是参数的二倍; 二是除了同方差假定不成立以外,要求其他假设都成立,随机项没有自相关并且服从正态分布。
实验四异方差性的检验及处理〔2学时〕一、实验目的〔1〕、掌握异方差检验的基本方法; 〔2〕、掌握异方差的处理方法.二、实验学时:2学时 三、实验要求〔1〕掌握用MATLAB 软件实现异方差的检验和处理; 〔2〕掌握异方差的检验和处理的基本步骤.四、实验原理1、异方差检验的常用方法<1> 用X-Y 的散点图进行判断<2>.22ˆ(,)(,)e x e y 或的图形,),x )i i y i i ((e 或(e 的图形)<3> 等级相关系数法〔又称Spearman 检验〕是一种应用较广的方法,既可以用于大样本,也可与小样本. 检验的三个步骤 ①ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③做等级相关系数的显著性检验.n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在.<4> 帕克<Park>检验帕克检验常用的函数形式:若α在统计上是显著的,表明存在异方差性. 2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:1211(i i p pi iy x x u f x βββ=+⋅++⋅+在该模型中:即满足同方差性.于是可以用OLS 估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量.五、实验举例例101i i i ,研究不同收入家庭的消费情况,试问原数据有无异方差性?如果存在异方差性,应如何处理?解:〔一〕编写程序如下:〔1〕等级相关系数法〔详见test4_1.m 文件〕%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性%%%%%%%% [data,head]=xlsread<'test4.xlsx'>; x=data<:,1>; %提取第一列数据,即可支配收入x y=data<:,2>; %提取第二列数据,即居民消费支出y plot<x,y,'k.'>; % 画x 和y 的散点图xlabel<'可支配收入x 〔千元〕'> % 对x 轴加标签 ylabel<'居民消费支出y<千元>'> % 对y 轴加标签%%%%%%%% 调用regres 函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones<size<x,1>,1>,x]; %在x 矩阵最左边加一列1,为线性回归做准备 [b,bint,r,rint,s]=regress<y,xdata>; yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间 head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'}; [head1;num2cell<[b,bint]>]% 定义元胞数组,以元胞数组形式显示y 的真实值,y 的估计值,残差和残差的95%置信区间 head2={'y 的真实值','y 的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell<[y,yhat,r,rint]>]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell<s>]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot<r,rint> % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot<yhat,r,'k.'> % 画散点图xlabel<'估计值yhat'> % 对x轴加标签ylabel<'残差r'> % 对y轴加标签%%%%%%%%%%%%调用corr函数计算皮尔曼等级相关系数res=abs<r>; % 对残差r取绝对值[rs,p]=corr<x,res,'type','spearman'>disp<'其中rs为皮尔曼等级相关系数,p为p值'>;〔2〕帕克〔park〕检验法〔详见test4_2.m文件〕%%%%%%%%%%%%%%% 用帕克〔park〕检验法来检验异方差性%%%%%%%[data,head]=xlsread<'test4.xlsx'>; %导入数据x=data<:,1>;y=data<:,2>;%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats<y,x,'linear',{'yhat','r','standres'}>;scatter<x,<ST.r>.^2> % 画x与残差平方的散点图xlabel<'可支配收入<x>'> % 对x轴加标签ylabel<'残差的平方'> %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log<x>和log〔r^2〕进行一元线性回归ST1=regstats<log<<ST.r>.^2>,log<x>,'linear',{'r','beta','tstat','fsta t'}>% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显著性检验的P值<3>加权最小二乘法〔详见test4_3.m文件〕%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread<'test4.xlsx'>; % 导入数据x=data<:,1>;y=data<:,2>;% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit<x,y> %调用函数作稳健回归stats.p% 输出模型检验的P值%%% 绘制残差和权重的散点图%%%%%%%plot<stats.resid,stats.w,'o'> %绘制残差和权重的散点图xlabel<'残差'>ylabel<'权重'〔二〕实验结果与分析:第一步::用OLS方法估计参数,并保留残差〔1〕散点图图4.1 可支配收入〔x〕居民消费支出〔y〕散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状.〔2〕回归模型参数估计值与显著性检验表1'系数的估计值' '估计值的95%置信下限' '估计值的95%置信上限'[ -0.5390] [ -3.7241] [ 2.6460][ 0.8091] [ 0.6768] [ 0.9415]'判定系数' 'F统计量的观测值' '检验的P值' '误差方差的估计值'[ 0.8485] [ 156.8387] [5.4040e-13] [ 9.1316]由输出结果看,常数项和回归系数的估计值分别为-0.539和0.8091,从而可以写出线性回归方程为^=−0.539+0.8091∗xy回归系数的估计值的95%置信区间为[0.6768,0.9415].对回归直线进行显著性检验,原假设和对立假设分别为H0:β1=0 H1:β1≠0检验的P值为5.4040×10−13<0.01,可知在显著性水平α=0.01下应拒绝原假设H0,可认为y〔居民消费收入〕与x〔可支配收入〕的线性关系是显著的.〔3〕方差分析图4.2原始数据对应残差图从残差图可以看到有2条线段〔红色虚线〕与水平线y=0没有交点,它对应的观测号为22和29,也就是说这两组观测对应的残差的置信区间不包含0点,可认为这两组观测数据为异常数据.它们分别是〔30,16.7〕,〔35,20〕.第二步:异方差性检验〔1〕图示法图4.3<2> 等级相关系数法在y与x 的OLS 回归的基础上计算出残差的绝对值,并记为res,并计算出皮尔曼等级相关系数rs=0.4860与对应的p值为0.0065<0.05〔*〕,说明残差r与x 存在系统关系,即存在异方差问题.〔3〕帕克<Park>检验法1〕散点图图4.4可支配收入与残差平方的散点图从图4.4可知,可考虑拟合指数曲线.现将其取对数,即可进行一元线性拟合.2〕回归系数与模型检验做ln<r^2>对ln<x>回归,得到表2β0=-8.49730.02950.0207β1=2.96790.0207从上表可以看出,得到的回归模型为ln (r 2)=−8.4973+2.9679∗ln (x),常数项和线性项的t 检验的P 值均小于0.05,说明回归方程中常数项和线性项均是显著的.并且,检验的P 值为0.0207小于0.05,说明整个回归方程是显著的,表明存在异方差性.综上所述,通过以上3种方法的检验,我们得到原数据存在异方差性.第三步:用加权最小二乘法处理异方差性表3‘回归系数’回归系数t 检验的P 值β0=-1.6091 0.2375β1=0.8870 0.0000由表3得:回归方程为 y ^=−1.6091+0.887x ,由p 值可知x 的回归系数是显著的,常数项未显著,说明其无实际意义.图4.5 残差和权重的散点图由图4.5知:权重集中在最上方的1附近的点比较多,说明稳健性比较好.六、实验内容01i i i FDI u ββ=++若用线性模型GDP ,研究不同地区FDI 和GDP 的关系,试问原数据有无异方差性?如果存在异方差性,应如何处理?七、思考练习现用线性模型01i i i y x u ββ=++ ,研究不同收入水平家庭的消费情况,试问原数据有无异方差性?如果存在异方差性,应如何处理?八、参考文献[1].李宝仁.计量经济学[M].机械工业出版社,2007.12 [2].何晓群. 应用回归分析[M].中国人民大学出版,2002.9。
一、实验背景与目的随着经济全球化、信息化的发展,计量经济学在各个领域的应用越来越广泛。
然而,在实际应用中,由于数据的特点和模型设定等因素的影响,异方差现象常常出现。
异方差现象会导致估计结果的偏差和统计推断的无效,因此,对异方差的检验和修正成为计量经济学中的重要问题。
本实验旨在通过实证分析,掌握异方差的检验和修正方法,提高对计量经济学模型的理解和应用能力。
二、实验数据与模型1. 数据来源本实验数据来源于某地区2000-2019年的居民消费数据,包括居民消费性支出、可支配收入、商品价格指数等变量。
2. 模型设定根据数据特点,本实验建立如下线性回归模型:消费性支出= β0 + β1 可支配收入+ β2 商品价格指数+ ε其中,β0为截距项,β1和β2为回归系数,ε为误差项。
三、实验步骤1. 异方差检验(1)图示法首先,将消费性支出与可支配收入、商品价格指数进行散点图绘制,观察是否存在明显的线性关系。
若存在明显的线性关系,则进一步进行异方差检验。
(2)Breusch-Pagan检验对上述线性回归模型进行Breusch-Pagan检验,以判断是否存在异方差。
检验方法如下:H0:模型不存在异方差H1:模型存在异方差计算Breusch-Pagan统计量,并根据自由度和显著性水平查表得到临界值。
若统计量大于临界值,则拒绝原假设,认为模型存在异方差。
2. 异方差修正若检验结果表明模型存在异方差,则采用加权最小二乘法(WLS)进行修正。
(1)确定权重根据异方差检验结果,计算每个观测值的权重。
权重计算公式如下:w_i = 1 / σ_i^2其中,σ_i^2为第i个观测值的方差。
(2)加权最小二乘法估计利用加权最小二乘法对模型进行估计,得到修正后的回归系数。
四、实验结果与分析1. 异方差检验结果根据图示法,消费性支出与可支配收入、商品价格指数之间存在明显的线性关系。
Breusch-Pagan检验结果显示,在5%的显著性水平下,统计量大于临界值,拒绝原假设,认为模型存在异方差。
《计量经济学》实训报告
实训项目名称异方差的检验及修正
实训时间 2011年12月13日
实训地点
班级
学号
姓名
实训(实践) 报告
实训名称异方差的检验及修正
一、实训目的
深刻理解异方差性的实质、异方差出现的原因、异方差的出现对模型的不良影响(即异方差的后果),掌握估计和检验异方差性的基本思想和修正异方差的若干方法;能够运用所学的知识处理模型中的出现的异方差问题,并要求初步掌握用EViews处理异方差的基本操作方法。
二、实训要求
使用教材第五章的数据做异方差的图形法检验、Goldfeld-Quanadt检验与White检验,使用WLS法对异方差进行修正。
三、实训内容
1、用图示法、戈德菲尔德、white验证法,验证该模型是否存在异方差。
2、用加权最小二乘法消除异方差。
四、实训步骤
练习题5.8数据1998年我国重要制造业销售收入和销售利润的数据
Y—销售利润,x—销售收入
1. 用OLS方法估计参数,建立回归模型:ls y c x
回归结果如下:
Y=12.036+0.1044x;
S = (19.5178) (0.00844)
T= (0.6167) (12.3667)
R^2=0.8547 S.E.=56.9037
2.检验是否存在异方差
(1) 图形检验:残差图形scat x e2
结果表明:
残差平方e2对解释变量的x的散点图主要分布在图形的下方,大致看出残差平方随X 的变动呈增大的趋势,因此,模型很可能出现异方差。
(2)戈德菲尔德-夸特检验
首先,对变量进行排序,在这个题目中,我选择递增型排序,这是y与x将以x按递增型排序。
然后构造子样本区间,建立回归模型。
在本题目中,n=28,删除中间的1/4,的观测值,即大约8个观测值,剩余部分平分得两个样本区间:1—10和19-28,他们的样本个数均为10。
用OLS方法得到前10个数的样本结果(ls y c x):
用OLS方法得到后10个数的样本结果(ls y c x):
接着,根据戈德菲尔德检验得到F统计量:(两个残差平方和相除,大的除以小的)F=63769.67/2577.969=24.736。
最后,进行判断。
在a=0.05,分子分母的自由度均为10-1-1=8,查F分布表,得到临界值F(8,8)=3.44,因为F=24.736 > 3.44,所以拒绝原假设。
结果表明:模型存在异方差。
(3)White检验
结论表明:查看P的概率小于0.05,存在明显的异方差。
3.消除异方差
使用加权最小二乘法(WLS)
选用权数Wl=1/x、W2=1/x2、W3=1/sqr(x),分别选用各个权数进行估计检验权数为w1时:
权数为w2时:
权数为w3时:
结果表明:w2权数是最好的。
五、实训分析、总结
1.可以看出运用加权最小二乘法消除了异方差之后,参数的t检验均显著,可绝系数大幅度提高,F检验也显著
2.销售收入每相差1元钱,销售利润就相差0.106892。
六、实训报告评价与成绩。