统计学(范赞成主编)课后习题答案详解(1)
- 格式:doc
- 大小:244.50 KB
- 文档页数:6


第二章、练习题及解答2。
为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取100只进行测试,所得结果如下:700716728719685709691684705718 706715712722691708690692707701 708729694681695685706661735665 668710693697674658698666696698698 700 710 722 706692691747699682694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688要求:(2)以组距为10进行等距分组,生成频数分布表,并绘制直方图。
灯泡的使用寿命频数分布表3。
某公司下属40个销售点2012年的商品销售收入数据如下:单位:万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求:(1)根据上面的数据进行适当分组,编制频数分布表,绘制直方图。
(2)制作茎叶图,并与直方图进行比较.解:(1)频数分布表(2)茎叶图第三章、练习题及解答1。
已知下表资料:试根据频数和频率资料,分别计算工人平均日产量. 解:计算表根据频数计算工人平均日产量:687034.35200xf x f===∑∑(件) 根据频率计算工人平均日产量:34.35fx xf==∑∑(件)结论:对同一资料,采用频数和频率资料计算的变量值的平均数是一致的。

<<统计学>>课后习题参考答案第四章1. 计划完成相对指标==⨯++%100%51%81102.9% 2. 计划完成相对指标=%9.97%100%41%61=⨯-- 3.4.5.解:(1)计划完成相对指标=%56.115%1004513131214=⨯+++(2)从第四年二季度开始连续四季的产量之和为:10+11+12+14=47天完成任务。
个月零该产品总共提前天完成的天数已提前完成任务,提前该产品到第五年第一季1510459010144514121110∴=--+++=6.解:计划完成相对指标=%75.126%100%1.0102005354703252795402301564=⨯⨯⨯++++++(2)156+230+540+279+325+470=2000(万吨) 所以正好提前半年完成计划。
7.8.略第五章 平均指标与标志变异指标1.甲X =.309343332313029282726=++++++++乙X =44.319403836343230282520=++++++++ AD 甲=}22.29303430333032303130303029302830273026=-+-+-+-+-+-+-+-+-AD 乙=}06.594044.313844.313644.313444.313244.313044.312844.312544.3120=-+-+-+-+-+-+-+-+-R 甲=34-26=8 R 乙=40-20=20σ甲 =9)3334()3033()3032()3031()3030()3029()3028()3027()3026(222222222-+-+-+-+-+-+-+-+-=2.58 σ乙=9)44.3140()44.3138()44.3136()44.3134()44.3132()44.3130()44.3128()44.3125()44.3120(222222222-+-+-+-+-+-+-+-+-=6.06V 甲=1003058.2⨯%=8.6% V 乙=%3.19%10044.3106.6=⨯ 所以甲组的平均产量代表性大一些. 2.解:计算过程如下表:甲X =.)(5.101780元= 乙X =(元)9708077600= 3.解:计算过程如下表:甲X =.4.11980=(件) 乙X =8.120809660=(件) σ甲=06.98075.6568=(件) σ乙=81.10809355=(件) V 甲=1004.11906.9⨯%=7.58% V 乙=%94.8%1008.12081.10=⨯ 所以甲厂工人的平均产量的代表性要高些.4. 解:()()94.761018102457047.7610121871871870775121873595128518757653550=⨯-+==⨯-+--+==++++⨯+⨯+⨯+⨯+⨯=e M M X 5.解:(1)上期的平均计划完成程度为:()()第六章元解解度为下期的平均计划完成程tH V P X P P P P /3.2884102950943.5062900255.3212800604.43210943.506255.321604.432:.7%1.32%1009067.0291.0291.0%67.901%67.90%67.90%67.90%10030028300:.6%37.103%1031400%1011200%107810%110961400120081096:)2(%67.99%1001500100070080%951500%1001000%108700%1108044=⨯⎪⎭⎫ ⎝⎛++⨯++==⨯==-⨯====⨯-==++++++=⨯+++⨯+⨯+⨯+⨯σ1.()())(7.788%67.41500:2000%67.41500600:.6)(6.62126907106557306806702650600269071061527106556552655730620273068060026806706402670650:2)(7.62327107006907206806202680610271070062527006906452690720640272068062026806206002620680:)1(:.5%63.79%10026206005802580257646245002435:.4%85.105%100%113385%102350%97463%120485%105412%112410%98368%106350%105310%110324%102306%101303385350463485412410368350310324306303::.3872232122221030980329809002290010201210208402284067022670600.2104万吨年该县粮食产量为平均增长速度解元工人的月平均工资为乙工区上半年建筑安装元工人的月平均工资为甲工区上半年建筑安装解解度为全年月平均计划完成程解=+⨯=-==++++++⨯++⨯++⨯++⨯++⨯++⨯+=++++++⨯++⨯++⨯++⨯++⨯++⨯+=⨯++++++==⨯++++++++++++++++++++++=+++++⨯++⨯++⨯++⨯++⨯++⨯+=C a 7解:计算过程如下表:)(94.6653.444.45:1994:3.46025844.4594092万元年的地方财政支出额为则直线趋势方程为=⨯++=======∑∑∑bta y t tyb ny a二次曲线方程为:y = 0.0108x 2 + 4.1918x + 24.143(过程略) 指数曲线方程为:y = 26.996e 0.0978x8.解:计算过程如下表:9.解:(1)同季平均法求季节比率的过程如下表:(2)趋势剔除法测定的季节变动如下表:第七章 统计指数()()()()01001011111175000124000081138.44%5000012350008750002540000182138.03%500002535000181075000940000390.98%127500084000022750002540000425qqzpk q z q zq p q p q z kq z p q k p q⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯==∑∑∑∑∑∑∑∑111111110102.12%75000184000015602.108.8%1200360110%105%pp q p q k p q p q p p=⨯+⨯====+∑∑∑∑11111560.135.65%1150135.65%124.68%108.8%.120%1800115%90096%6003.114.27%330042003300111.38%114.27%.pqpq qpqpq p qp q k p qk k k q q p q p q k q p q pkk k======⨯+⨯+⨯=======∑∑∑∑∑∑ 110101001013200005.100%128%250000128%123.1%14%320000307692.3104%307692.325000057692.3320000307692.312307.pq pqq PpK K K p qp q K p q p qq p q =⨯====+===-=-=-=-=∑∑∑∑∑∑1解:K 零售量变动对零售额变动影响的绝对值为:(万元)零售物价变动对零售总额变动影响的绝对值为:p 1110010000107350000120%120%180000110%110%116%116%17.6%107.6%350000291666.67120%180000163636.36.110%1pq pq q q pq pq q q K q K q p q Kq p q K p q p q ==+===+==+==+========⨯=∑∑∑∑∑∑∑∑城1城农城农1农1城城城1农农农城城城(万元)6.解:已知p ,,p ,,K ,K p 则p K 0010111101001116%291666.67338333.33107.6%163636.36176072.72350000180000103.03%338333.33176072.723%q pp q p q p q q q k p q p q p q ⨯==⨯=⨯=++====++∴∑∑∑∑∑∑∑∑农农农11城农城农K p p 该地区城乡价格上涨了。

各章思考与练习参考答案第一章导论(一)单项选择题1.D 2.C 3.B 4.D 5.D 6.D 7.B 8.A 9.B 10.A (二)多项选择题:1.ABCD 2.CD 3.AD 4.BCDE 5.ABDE(三)判断题:1.×2.×3.×4.√5.×(四)简答题:答案略(五)综合题答案略第二章统计调查(一)单项选择题:1.C 2.C 3.B 4.C 5.C 6.A 7.B 8.C 9.C 10.B (二)多项选择题:1.ACD 2.ABC 3.ABCD 4.ABC 5.ACD6.ABCD 7.ABDE 8.BCE 9.ABE 10.CD(三)判断题:1.×2.×3.×4.√5.×(四)名词解释:答案略㈤(五)简答题:答案略第三章统计整理(一)单项选择题:1.C 2.B 3.C 4.B 5.B 6.A 7.B 8.C 9.B 10.B (二)多项选择题:1.AB 2.BD 3.ACD 4.AD 5.BCD6.BD 7.ABC 8.AC 9.ABC 10.CD(三)判断题:1.×2.√3.×4.×5.×(四)名词解释:答案略(五)简答题:答案略(六)计算题:1.解:2可见,组距1000元的分布数列,更为合理。
(2)对选中的分布数列,计算频率、较小制累计次数、较大制累计次数、组中值:(3)略第四章总量指标与相对指标(一)单项选择题:1.C 2.B 3.A 4.B 5.C 6.B 7.B 8.C 9.B 10.D(二)多项选择题:1.ABCD 2.CE 3.ABCDE 4.BCE 5.ABCD(三)判断题:1.X 2.X 3.X 4.√5.X(四)名词解释:答案略(五)简答题:答案略(六)计算题:1.解:该企业集团实现利润比去年增长百分比 =110%/(1+7%)-1=2.80%2.解:(1)2011年的进出口贸易差额=12178-9559=2619(亿元)(顺差)2011年进出口总额的发展速度=21737/17607×100%=123.46%(2)2011年进出口额比例相对数=9559/12178×100%=78.49%2011年出口额结构相对数=12178/21737×100%=56.02%(3)该地区进出口贸易发展速度较快,出现贸易顺差。

统计学课后习题及答案统计学课后习题及答案统计学是一门研究数据收集、分析和解释的学科,它在各个领域都有广泛的应用。
作为学习统计学的学生,课后习题是巩固知识、提高技能的重要途径。
本文将提供一些统计学课后习题及其答案,希望对学习者有所帮助。
1. 描述性统计习题:给定以下一组数据:10, 15, 12, 18, 20, 22, 16, 10, 14, 19。
请计算该组数据的均值、中位数和众数,并解释它们的含义。
答案:均值:计算方法是将所有数据相加,然后除以数据的个数。
对于给定的数据,均值为(10+15+12+18+20+22+16+10+14+19)/10 = 16.6。
中位数:将数据按照从小到大的顺序排列,找出中间的数。
对于给定的数据,中位数为16。
众数:出现频率最高的数。
对于给定的数据,众数为10。
这些统计量可以帮助我们了解数据的集中趋势。
均值是所有数据的平均值,中位数是数据的中间值,众数是出现频率最高的值。
在这个例子中,均值告诉我们这组数据的平均水平是16.6,中位数告诉我们大约一半的数据小于16,一半的数据大于16,众数告诉我们10是这组数据中出现次数最多的数。
2. 概率习题:一个骰子有6个面,每个面上的数字分别是1、2、3、4、5、6。
如果投掷一次骰子,求得到奇数的概率。
答案:奇数的个数为3个,即1、3、5。
骰子的总个数为6个。
所以得到奇数的概率为3/6 = 1/2。
概率是事件发生的可能性。
在这个例子中,奇数的个数是3个,总个数是6个,所以得到奇数的概率是3/6,即1/2。
3. 抽样与估计习题:某市有1000名居民,你希望了解他们对某项政策的态度。
你打算进行一次调查,抽取100名居民进行问卷调查。
这个调查结果能否代表整个市民的态度?为什么?答案:这个调查结果不能代表整个市民的态度。
原因是抽样的方式可能引入抽样误差。
如果抽取的100名居民在某些特征上不具有代表性,比如年龄、性别、职业等,那么调查结果可能会偏离整个市民的态度。

第一章统计学及基本概念 3第二章数据的收集与整理10第三章统计表与统计图19第四章数据的描述性分析25第五章参数估计37第六章假设检验49第七章方差分析62第八章非参数检验70第九章相关与回归分析78第十章多元统计分析89第十一章时间序列分析101第十二章指数108第十二章指数108第十三章统计决策120第十四章统计质量管理128第一章统计学及基本概念统计的涵义(统计工作、统计资料和统计学)统计学的内容(统计学分类:理论统计学和应用统计学;描述统计学与推断统计学)统计学的发展史(学派与主要代表人物)数据类型(定类、定序、定距和定比;时间序列、截面数据和面板数据;绝对数、相对数、平均数)变量:连续与离散;确定与随机总体、样本与个体标志、指标及指标体系统计计算工具习题一、单项选择题1. 推断统计学研究()。
(知识点:答案:D)A.统计数据收集的方法B.数据加工处理的方法C.统计数据显示的方法D.如何根据样本数据去推断总体数量特征的方法2. 在统计史上被认为有统计学之名而无统计学之实的学派是()。
(知识点:答案:D)A.数理统计学派B.政治算术学派C.社会统计学派D.国势学派3. 下列数据中哪个是定比尺度衡量的数据()。
(知识点:答案:B)A.性别B.年龄C.籍贯D.民族4. 统计对现象总体数量特征的认识是()。
(知识点:答案:C)A.从定性到定量B.从定量到定性C.从个体到总体D.从总体到个体5. 调查10个企业职工的工资水平情况,则统计总体是()。
(知识点:答案:C)个企业个企业职工的全部工资个企业的全部职工个企业每个职工的工资6. 从统计总体中抽取出来作为代表这一总体的、由部分个体组成的集合体是().(知识点:答案:A)A. 样本B. 总体单位C. 个体D. 全及总体7. 三名学生期末统计学考试成绩分别为80分、85分和92分,这三个数字是()。
(知识点:答案:D)A. 指标B. 标志C. 变量D. 标志值8. 以一、二、三等品来衡量产品质地的优劣,那么该产品等级是()。

第四章 统计描述某企业生产铝合金钢,计划年产量40万吨,实际年产量45万吨;计划降低成本5%,实际降低成本8%;计划劳动生产率提高8%,实际提高10%.试分别计算产量、成本、劳动生产率的计划完成程度. 解产量的计划完成程度=%5.112100%4045100%=⨯=⨯计划产量实际产量即产量超额完成%.成本的计划完成程=84%.96100%5%-18%-1100%-1-1≈⨯=⨯计划降低百分比实际降低百分比即成本超额完成%.劳动生产率计划完=85%.101100%8%110%1100%11≈⨯++=⨯++计划提高百分比实际提高百分比即劳动生产率超额完成%.某煤矿可采储量为200亿吨,计划在1991~1995年五年中开采全部储量的%,在五年中,该矿实际开采原煤情况如下(单位:万吨)试计算该煤矿原煤开采量五年计划完成程度及提前完成任务的时间. 解本题采用累计法:(1)该煤矿原煤开采量五年计划完成=100%⨯数计划期间计划规定累计数计划期间实际完成累计 =75%.12610210253574=⨯⨯ 即:该煤矿原煤开采量的五年计划超额完成%.(2)将1991年的实际开采量一直加到1995年上半年的实际开采量,结果为2000万吨,此时恰好等于五年的计划开采量,所以可知,提前半年完成计划. 我国1991年和1994年工业总产值资料如下表:要求:(1)计算我国1991年和1994年轻工业总产值占工业总产值的比重,填入表中;(2)1991年、1994年轻工业与重工业之间是什么比例(用系数表示)(3)假如工业总产值1994年计划比1991年增长45%,实际比计划多增长百分之几 解(1)(2)是比例相对数;1991年轻工业与重工业之间的比例=96.01.144479.13800≈;1994年轻工业与重工业之间的比例=73.04.296826.21670≈(3)%37.251%)451(2824851353≈-+即,94年实际比计划增长%.某乡三个村2000年小麦播种面积与亩产量资料如下表:要求:(1)填上表中所缺数字;(2)用播种面积作权数,计算三个村小麦平均亩产量; (3)用比重作权数,计算三个村小麦平均亩产量.解(1)(2))(75.72840013065015082012070011斤=⨯+⨯+⨯==∑∑==k i iki iiff xx(3)两种不同品种的玉米分别在五块地上试种,产量资料如下:已知生产条件相同,对这两种玉米品种进行分析比较,试计算并说明哪一种品种的亩产量更稳定一些解田块总面积总产量平均亩产量=即: 由于是总体数据,所以计算总体均值: 计算表格乙品种下面分别求两块田地亩产量的标准差:要比较两种不同玉米的亩产量的代表性,需要计算离散系数:<甲σv 乙σv ,∴甲品种的亩产量更稳定一些.两家企业生产相同的产品,每批产品的单位成本及产量比重资料如下: 甲企业乙企业试比较两个企业哪个企业的产品平均单位成本低,为什么解∴乙企业的产品平均单位成本更低.某粮食储备库收购稻米的价格、数量及收购额资料如下:要求:(1)按加权算术平均数公式计算稻米的平均收购价格;(2)按加权调和平均数公式计算稻米的平均收购价格.解(1))(02.19000915011元≈==∑∑==k i iki iiff xx (2))(02.190009150400030002000360031502400m H 元≈=++++==∑∑xm x已知我国1995年—1999年末总人口及人口增长率资料:试计算该期间我国人口平均增长率. 解计算过程如下:按照平均增长率的公式可知:1-平均发展速度平均增长率=所以,1995年—1999年期间我国人口平均增长率=96.91-1204861253604≈‰某单位职工按月工资额分组资料如下: 根据资料回答问题并计算: (1)它是一个什么数列(2)计算工资额的众数和中位数;(3)分别用职工人数和人数所占比重计算平均工资.结果一样吗(4)分别计算工资的平均差和标准差. 解(1)是等距分组数列 (2)d f f f f f f L M m m m m m m ⨯-+--+≈+--)()(1110下限公式:即:59.54821000)30134()37134(371345000)()(1110≈⨯-+--+=⨯-+--+≈+--df f f f f f L M m m m m m m(注:用上限公式算出的结果与上述结果相同) (注:用上限公式算出的结果与上述结果相同) (3))(22.5343236107500306500134550037450025350011元≈⨯+⨯+⨯+⨯+⨯==∑∑==k i iki iiff xx (元)2.53434.24%7500 71%.12650078%.56550068%.15450059%.103500x 1111≈⨯+⨯+⨯+⨯+⨯=⋅==∑∑∑∑====ki ki iii k i iki iiff x ff x两者结果一样.(忽略小数点位数的保留对结果造成的影响)(4)平均差 92.65411≈-=∑∑==ki iki iidff x xM标准差 33.923)(12≈-=∑=Nf X XKi i iσ某市甲、乙两商店把售货员按其人均年销售额分组,具体资料如下:要求:(1)分别计算这两个商场售货员的人均销售额; (2)通过计算说明哪个商场人均销售额的代表性大解(1) 423001260011===∑∑==k i iki iiff xX 甲(2)05.1030030300)(12≈=-=∑=Nf X XKi i i甲甲σ >甲σv 乙σv ,∴乙商场销售额的代表性大.第五章 统计抽样袋中装有5只同样大小的球,编号为1,2,3,4,5,从中同时取出3只球,求取出的最大号X 的分布律及其分布函数并画出其图形.解先求X 的分布律:由题知,X 的可能取值为3,4,5,且2345{5}/6/10P X C C ===,∴X 的分布律为:⎪⎪⎭⎫ ⎝⎛10/610/310/1543, 由(){}i i ix xF x P X x p ≤=≤=∑得:设X 的密度函数为求: (1)常数c ;(2)X 的分布函数()F x ; (3){13}P X <≤. 解(1)24241()0(32)018f x dx dx c x dx dx c +∞+∞-∞-∞==+++=⎰⎰⎰⎰(2)当2x ≤时,()00xF x dt -∞==⎰;当24x <<时,22211()()0(32)(310)1818xxF x f t dt dt t dt x x -∞-∞==++=+-⎰⎰⎰当4x ≥时,24241()()0(32)0118xx F x f t dt dt t dt dt -∞-∞==+++=⎰⎰⎰⎰.故分布函数 (3)21{13}=(3)(1)(33310)04/918P X F F <≤-=+⨯--= 随机变量,X Y 相互独立,又(2)XP ,1(8,)4YB ,试求(2)E X Y -和(2)D X Y -.解(2)()2()2222E X Y E X E Y -=-=-⨯=-一本书排版后一校时出现错误处数X 服从正态分布(200,400)N , 求: (1)出现错误处数不超过230的概率;(2)出现错误处数在190~210的概率. 解(200,400)X N(1)200230200(230)()2020X P X P --∴≤=≤ (2) 190200200210200(190210)()202020X P X P ---∴≤≤=≤≤某地区职工家庭的人均年收入平均为12000元,标准差为2000元.若知该地区家庭的人均年收入服从正态分布,现采用重复抽样从总体中随机抽取25户进行调查,问出现样本均值等于或超过12500元的可能性有多大 解对总体而言,2(12000,2000)XN∴样本均值22000(12000,)25xN某商场推销一种洗发水.据统计,本年度购买此种洗发水的有10万人,其中3万6千人是女性.如果按重复抽样方法,从购买者中抽出100人进行调查,问样本中女性比例超过50%的可能性有多大解总体比例 3.6=36%10π=万万(1)(,)p N nπππ-∴即2(0.36,0.048)pN第八章 相关分析和回归分析某店主分析其店面的经营情况时,收集了连续10天的访问量数据(单位:天)和当天营业额数据(单位:元)如下.对以上访问量和营业额数据作相关分析.解相关分析(1)画访问量和营业额数据的散点图,如下所示从图上可以看出,访问量和营业额数据是简单线性正的不完全相关. (2)计算相关系数计算访问量和营业额的简单线性相关系数为,大于,说明访问量和营业额之间存在较高的线性关系.某饮料广告费投入为x,产品销售数量为y,根据收集2年的月度数据 资料,计算得到以下结果:∑=-6546)(2x x i,∑=-5641)(2y y i375=x ,498=y ,6054))((=--∑y y x x i i(1)计算相关系数,并初步判断x 与y 之间的关系; (2)用最小二乘法估计模型回归系数,并写出模型结果; (3)说明所计算的回归系数的经济意义;(4)计算模型可决系数,并用其说明模型的拟合效果. 解最小二乘法的计算(一元)(1)计算相关系数,并初步判断x 与y 之间的关系;计算x 与y 相关系数为r=,说明两者的简单线性相关程度非常高,因此可以初步判断x 与y 呈现线性关系.(2)用最小二乘法估计模型回归系数,并写出模型结果;记模型为:i i x y 10ˆˆˆββ+=,将以上结果代入最小二乘法的计算公式,得到=1ˆβ,=0ˆβ. 因此,产品销售数量为y 对广告费投入为x 的模型为i i x y92484.01852.151ˆ+= (3)说明所计算的回归系数的经济意义;=1ˆβ表示当广告费投入每增加1个单位,产品销售数量会增加个单位. (4)计算模型可决系数,并用其说明模型的拟合效果.由于模型为一元线性回归模型,根据一元线性回归模型中可决系数为模型因变量和自变量简单线性相关系数的平方的关系,可得模型的可决系数R 2=(r)2=2=.可决系数接近1,说明模型拟合的非常好.第九章 统计指数某市场上四种蔬菜的销售资料如下:(1) 根据综合指数编制规则,将上表所缺空格填齐; (2) 用拉氏公式编制四种蔬菜的销量总指数和价格总指数; (3) 用帕氏公式编制四种蔬菜的销量总指数和价格总指数; (4) 建立适当的指数体系,对蔬菜销售额的变动进行因素分析.解 %p q p q L %pq pq L p q 11.1092282431227.1072282390220010001======∑∑∑∑)拉氏:(即 ()⎩⎨⎧+=⨯=元175********.10727.10712.115%%计算表明: 四种蔬菜的销量增长了 %,使销售额增加了 162元;四种蔬菜的价格上长了 %,使销售额增加了175元;两因素共同影响,使销售额增长了%, 销售额增加了337元. 结论:某厂三种产品的产量情况如下表:试分析出厂价格和产量的变动对总产值的影响. 解第一步:计算三个总产值:24200064000101100081350000=⨯+⨯+⨯=∑p q(万元);25080064800101020081500001=⨯+⨯+⨯=∑pq (万元);2637005480011102005.81500011=⨯+⨯+⨯=∑pq (万元);第二步:建立指标体系即⎪⎩⎪⎨⎧-+-=-⨯=)250800263700()242000250800(242000263700250800263700242000250800242000263700 第三步:分析结论.计算结果表明:由于出厂价上涨了%,使总产值增加了8800元;由于产量提高了%,使总产值增加了12900元;两因素共同作用,使总产值上升了%,增加了21700元.若给出题中四种蔬菜的资料如下:(1) 编制四种蔬菜的算术平均指数; (2) 编制四种蔬菜的调和平均指数;(3) 把它们与上题计算的拉氏指数和帕氏指数进行比较,看看有何种关系什么条件下才会有这种关系的呢 (4)解(1)(2) (3)算术平均指数的结果与拉氏指数相等——以基期的总值指标为权数. 调和平均指数的结果与帕氏指数相等——以报告期的总值指标为权数.某地区2005年农副产品收购总额为1 360亿元,2006年比上年的收购总额增长了12%,农副产品价格指数为105%;试考虑:2006年与2005年相比较(1) 农副产品收购总额增长了百分之几农民共增加多少收入 (2)(3) 农副产品收购量增加了百分之几农民增加了多少收入 (4)(5) 由于农副产品收购价格提高了5%,农民又增加了多少收入 (6) 验证以上三者之间有何等关系解已知:农民交售农副产品增加收入亿元, 与去年相比增长幅度为12%; 农副产品收购数量增长 %, 农民增加收入 亿元; 农副产品收购价格上涨 %, 农民增加收入 亿元.显然,有:⎩⎨⎧+=⨯=(亿元)5.727.902.16300.10567.10600.112%%%可见,分析结论是协调一致的.某企业生产的三种产品的有关资料如下:(1) 根据上表资料计算相关指标填入上表(见绿色区域数字); (2) 计算产品产量总指数及由于产量增长而增加的总成本;(3)计算单位成本总指数及由于单位成本变动而增减的总成本.解建立指数体系:结论:计算结果表明:由于产量总指数增加了37%(=%-1),而使总成本增加了37元,由于单位成本总指数下降了%(=%-1),使总成本减少了元.两个因素共同影响使总成本上升了%,增加了元.9.8某商场的销售资料如下:(1)根据上表资料计算相关指标填入上表(见绿色区域数字);(2)计算商品销售量总指数及由于销量变化而增减的销售额;(3)计算商品价格总指数及由于价格变动而增减的销售额.解建立指数体系:计算结果表明:由于商品销量总指数下降了%(=%),而使销售额减少了万元,由于商品价格总指数下降了%(=%),使销售额减少了万元.两个因素共同影响使销售总额下降了%(=%),减少了54万元.某乡力图通过推广良种和改善田间耕作管理来提高粮食生产水平,有关生产情况如下表所示:(1) 该乡粮食平均亩产提高了百分之几由此增产粮食多少吨 (2)(3) 改善田间耕作管理使平均亩产提高多少增产粮食多少吨 (4)(5) 推广良种使平均亩产提高多少增产粮食多少吨 (6)解计算的相关数据(∑∑∑110100110100x f x f x f x f x f x f )见上表中绿色区域数字;从而有:建立指数体系: ⎪⎩⎪⎨⎧-+=-⨯=)()-(10011001假假假假x x x x x x x x x x x x 即 ()()⎪⎩⎪⎨⎧-+-=-⨯=000 657 48000 737 49000 478 46000 657 48000 478 46000 737 4948.40548.417 32.38748.40532.38748.417 即 ()⎩⎨⎧+=⨯=公斤 000 080 1000 179 2000 259 3 %22.102 %69.104%01.107分析结论: 计算结果表明(1)该乡粮食平均亩产提高了%(=%-1),由此增产粮食3 259吨; (2)由于改善田间管理,使平均亩产提高了%,粮食增产2 179吨; (3)由于推广优良品种,使平均亩产提高了%,粮食增产1 080吨.第十章 时间序列分析某公司2009年末有职工250人,10月上旬的人数变动情况是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年职工应征入伍,同日又有3名职工辞职离岗,9日招聘7名销售人员上岗.试计算该公司10月上旬的平均在岗人数. 解)(25610256010518252516524750212232)7334262(1)334262(2)4262(2)12250(3250人==++++=++++⨯+---+⨯---+⨯-+⨯++⨯==∑∑iii fxf x 答:该公司10月上旬的平均在岗人数为256人. 某银行2009年部分月份的现金库存额资料如下:要求:(1)该时间序列属于哪一种时间序列.(2)分别计算该银行该年第一、二季度和上半年的平均现金库存额. 解(1) 该时间序列属于动态时点时间序列; (2) 第一季度平均现金库存额:)(4803144032520450480250014224321万元==+++=-+++=x x x x x ; 第二季度平均现金库存额:)(5673170032580600550252014227324万元==+++=-+++=x x x x x ; 上半年平均现金库存额:)(52363140625806005505204504802500172 (2)721万元==++++++=-+++=x x x x 某企业08年上半年的产量和单位成本资料如下:试计算该企业08年上半年的产品平均单位成本.解答:该企业08年上半年的产品平均单位成本为元. 某企业有关资料如下,计算该企业一季度人均月销售额.解 该企业一季度月平均销售额:)(33.12331201501003321万元=++=++=a a a a ;该企业一季度月平均职工人数:)(1133211611012021003224321人=+++=+++=b b b b b ; 该企业一季度人均月销售额:)/(091.111333.123人万元===ba c .某市2001~2005年的地区生产总值如下表:(1) 按平均发展速度估计2002~2004年的地区生产总值. (2) 按此5年的平均发展速度预测2008年和2010年的GDP.解(1)2002~2006年泉州市地区生产总值的平均发展速度为:%12.11399316264==v ; 按平均发展速度估计2002~2004年的地区生产总值分别为:11437%)12.113(9931270%)12.113(9931123%12.11399332=⨯=⨯=⨯(将计算结果填入上表绿色区域内);(2)按此5年的平均发展速度预测2008年和2010年的GDP 分别为:2008年地区GDP 预测值)(23541312.116263亿元=⨯=; 2010年地区GDP 预测值)(7.30111312.116265亿元=⨯=.我国某地区2001年~ 2006年税收总额如下:试计算:(1)环比发展速度和定基发展速度; (2)环比增长速度和定基增长速度; (3)增长1%绝对值;(4)用水平法计算平均增长速度;(5)分析表中所列资料反映的趋势特征,拟配合适的趋势模型,并预测2007年该地区的税收收入.解(1)~(3)相关计算结果填入下表(见绿色区域数字):(4) 用水平法计算平均发展速度和平均增长速度:平均发展速度%44.1161644.11404.22821603855====v ; 则平均增长速度%44.161%44.1161=-=-=v ;。
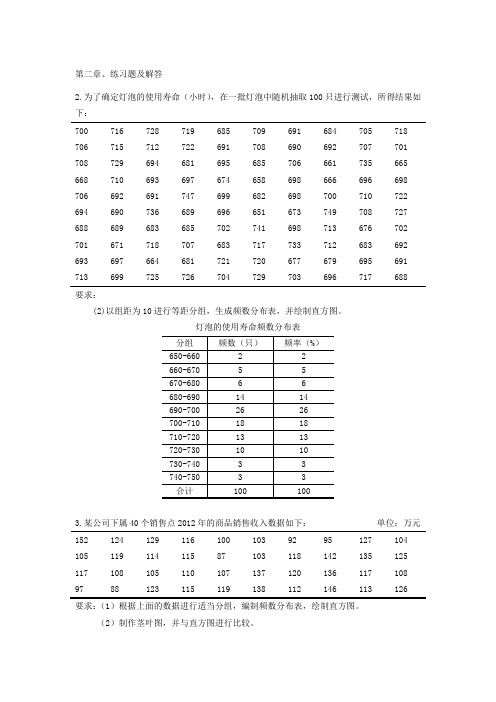
第二章、练习题及解答2.为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取100只进行测试,所得结果如下:700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688 要求:(2)以组距为10进行等距分组,生成频数分布表,并绘制直方图。
灯泡的使用寿命频数分布表3.某公司下属40个销售点2012年的商品销售收入数据如下:单位:万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求:(1)根据上面的数据进行适当分组,编制频数分布表,绘制直方图。
(2)制作茎叶图,并与直方图进行比较。
解:(1)频数分布表(2)茎叶图第三章、练习题及解答1. 已知下表资料:试根据频数和频率资料,分别计算工人平均日产量。
解:根据频数计算工人平均日产量:687034.35200xf x f===∑∑(件) 根据频率计算工人平均日产量:34.35fx xf==∑∑(件)结论:对同一资料,采用频数和频率资料计算的变量值的平均数是一致的。


统计学课后习题集参考答案解析【友情提示】请各位同学完成思考题和练习题后再对照参考答案。
回答正确,值得肯定;回答错误,请找出原因更正,这样使用参考答案,能力会越来越高,智慧会越来越多。
学而不思则罔,如果直接抄答案,对学习无益,危害甚大。
想抄答案者,请三思而后行!第一章绪论思考题参考答案1.不能,英军所有战机=英军被击毁的战机+英军返航的战机+英军没有弹孔的战机,因为英军被击毁的战机有的掉入海里、敌军占领区,或因堕毁而无形等,不能找回;没有弹孔的战机也不可能自己拿来射击后进行弹孔位置的调查。
即便被击毁的战机找回或没有弹孔的战机自己拿来射击进行实验,也不能从多个弹孔中确认那个弹孔是危险的。
2.问题:飞机上什么区域应该加强钢板?瓦尔德解决问题的思想:在他的飞机模型上逐个不重不漏地标示返航军机受敌军创伤的弹孔位置,找出几乎布满弹孔的区域;发现:没有弹孔区域是军机的危险区域。
3.能,拯救和发展自己的参考路径为:①找出自己的优点,②明确自己大学阶段的最佳目标,③拟出一个发扬自己优点,实现自己大学阶段最佳目标的可行计划。
练习题参考答案一、填空题1.调查。
2.探索、调查、发现。
3. 目的。
二、简答题1.瓦尔德;把剩下少数几个没有弹孔的区域加强钢板。
2.统计学解决实际问题的基本思路,即基本步骤是:①提出与统计有关的实际问题;②建立有效的指标体系;③收集数据;④选用或创造有效的统计方法整理、显示所收集数据的特征;⑤根据所收集数据的特征、结合定性、定量的知识作出合理推断;⑥根据合理推断给出更好决策的建议。
不解决问题时,重复第②-⑥步。
3.在结合实质性学科的过程中,统计学是能发现客观世界规律,更好决策,改变世界和培养相应领域领袖的一门学科。
三、案例分析题1.总体:我班所有学生;单位:我班每个学生;样本:我班部分学生;品质标志:姓名;数量标志:每个学生课程的成绩;指标:全班学生课程的平均成绩;指标体系:上学期全班同学学习的科目;统计量:我班部分同学课程的平均成绩;定性数据:姓名;定量数据:课程成绩;离散型变量:学习课程数;连续性变量:学生的学习时间;确定性变量:全班学生课程的平均成绩;随机变量:我班部分同学课程的平均成绩,每个同学进入教室的时间;横截面数据:我班学生月门课程的出勤率;时间序列数据:我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率;面板数据:我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率;选用描述统计。

第四章一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数()A.比例相对数 B.比较相对数 C.结构相对数 D.动态相对数3.某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求()A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。

《统计学》各章参考答案各位任课教师:大家好!下面是各位参编教师做的参考答案,可能会出现有些答案与任课教师所作不一致的情况,还请各位任课教师与我们联系。
谢谢!祝大家健康、快乐、幸福!第一章导论一、选择题1.C2.A3.C4.C5.C6.B7.A8.D9.C 10.D 11.A 12.C 13.C 14.A 15.B 16.A 17.C 18.B 19.D 20.A 21.D 22. D23.B 24.C 25.A 26.A 27.A 28.B 29.A 30.D 31.C 32.A 33.B第二章数据的收集一、选择题1.A2.B3.A4.D5.B6.C7.D8.D9.D 10.C 11.C 12.A 13.D 14.D 15.C 16.A 17.D 18.C 19.B 20.B 21.A 22.B 23.C 24.A 25.B 26.B 27.A 28.B 29.C 30.C (A)二、判断题1.∨2.∨3.×4. ∨5. ×6. ×7. ∨8. ×9. ×10. ×第三章数据整理与显示一、选择题CABCD CBBAB BACBD DDBC第四章 数据分布特征的测度一、选择题1.A2.C3.B4.C5.D6.D7.A8.B9.A 10.B 11.A 12.D 13.C 14.C 15.D 16.A 17.A 18.B 19.A 20.B 21.A 22.A 23.B 24.C 25.C 26.D 27.D 28.A 29.D 30.C 31.C 32.D二、判断题1. ×2. ∨3. ×4. ×5. ×6. ×7. ∨8. ×9. × 10. ∨ 11. ∨ 12. ×四、计算题1. 11399073.8954ki ii kii x fx f=====∑∑甲11.96σ===甲73.89100%100% 6.18%11.96x σν=⨯=⨯=甲73.8100%100%7.43%9.93x σν=⨯=⨯=乙甲的代表性强2. 10.2510.966ki ii kii x fx f====∑∑0.250.056σ==0.250.056100%100% 5.834%0.966xσν=⨯=⨯=1114.534ki ii kii x fx f====∑∑10.1295σ==10.1295100%100% 2.857%4.534xσν=⨯=⨯=该教练的说法不成立。

第一章1.举出你所知道的统计应用的例子。
答:期末考试后统计班里同学的成绩,从而进行排名等;人口普查统计,从而得知男女人口比例,年龄分布等;统计一个生态系统里某种物种的密度;统计股票市场上某一天的各种数据;统计某个城市的人均收入水平,人民幸福指数,对某一电视节目的看法等。
2. 解释定性数据和定量数据的区别,分别给出一个定性数据和一个定量数据的例子。
答:定性数据和定量数据的区别:定性数据是由于我们考虑的是取值为类别的变量,对这些类别用数字来分别代表就得到定性数据;定量数据是我们所考虑的变量的取值为数值,它将在某个区间上连续取值,或在某个区间上取离散的值。
定性数据的例子:例如考察某幼儿园10个人的性别,定义1=男,2=女,则所得到定性数据为:1,1,2,2,2,1,2,1,1,1. 定量数据的例子:考察某幼儿园10个人的身高,则此变量取值区间为(0,200)(单位:cm)3. 解释样本和总体的区别。
答:总体是根据一定目的和要求所确定的研究事物的全体。
为了了解总体的分布,我们从总体中随机地抽取一些个体,称这些个体的全体为样本。
样本和总体的区别在于总体是要考虑对象的全体,而样本是从总体中抽取出的一部分具有代表性的个体,从而通过对样本的研究得出关于总体的一些结论。
4. 解释离散型变量和连续型变量的区别,并各举一例。
离散型变量是指其数值只能用自然数或整数单位计算。
例如:某企业里职工的人数连续型变量是如果所考虑变量可以在某个区间内取任一实数,即变量的取值可以是连续的。
例如:生产零件的规格尺寸。
5.阐述四种主要的收集数据方法的区别。
答:观测,访问,问卷,实验区别:观测数据的研究者尽量不干涉研究对象的行为模式;访问在一定程度上对被访问者心理造成干扰,则收集到的数据会有误差;问卷常会产生未响应误差;实验时需要其控制它变量的影响。
6.举出一些观测数据和实验数据的例子。
答:(1)观测数据:证券分析人员可能会记录某即将收购的公司在被收购的前一天的股市收盘价,并与宣布被收购的当天的收盘价比较。

统计学答案解析统计学课本课后作业题(全)题⽬:第1章:P11 6,7第2章:P52 练习题3、9、10、11第3章: P116思考题12、14 练习题16、25第4章:P114 思考题6,练习题2、4、6、13第5章:P179 思考题4、练习题3、4、6、11第6章: P209 思考题4、练习题1、3、6第7章: P246思考题1、练习题1、7第8章: P287 思考题4、10 练习题2、3·第⼀章6..⼀家⼤型油漆零售商收到了客户关于油漆罐分量不⾜的许多抱怨。
因此,他们开始检查供货商的集装箱,有问题的将其退回。
最近的⼀个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆,每⼀罐的质量精确到4位⼩数。
装满的油漆罐应为4.536 kg。
要求:(1)描述总体;最近的⼀个集装箱内的全部油漆;(2)描述研究变量;装满的油漆罐的质量;(3)描述样本;最近的⼀个集装箱内的50罐油漆;(4)描述推断。
50罐油漆的质量应为×50=226.8 kg。
7.“可乐战”是描述市场上“可⼝可乐”与“百事可乐”激烈竞争的⼀个流⾏术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨⽽颇具特⾊。
假定作为百事可乐营销战役的⼀部分,选择了1000名消费者进⾏匿名性质的品尝试验(即在品尝试验中,两个品牌不做外观标记),请每⼀名被测试者说出A品牌或B品牌中哪个⼝味更好。
要求:答:(1)总体:市场上的“可⼝可乐”与“百事可乐”,(2)研究变量:更好⼝味的品牌名称;(3)样本:1000名消费者品尝的两个品牌(4)推断:两个品牌中哪个⼝味更好。
第⼆章3.某百货公司连续40天的商品销售额如下(单位:万元):3430384340 41252947|3846364537、3645433344373744263844 35284634》303942323635 42363737)49根据上⾯的数据进⾏适当的分组,编制频数分布表,并绘制直⽅图。

第一章绪论思考题1. 什么是统计学?请简要说明一下它的发展过程。
统计学是关于数据搜集、整理、归纳、分析的方法论科学。
统计学的发展主要经历了三个阶段:(1) 17世纪中叶至18世纪,统计学的产生和形成阶段;(2) 18世纪末至20世纪中叶,统计推断方法和理论体系确立的阶段;(3) 20世纪50年代以来,统计理论、方法和应用进入了一个全面发展的阶段。
2. 统计学、统计数据,以及统计活动之间有什么关系?统计活动直接影响统计数据的数量和质量;统计学是统计实践活动的理论概括,同时,它又用理论和方法研究分析统计实践活动,统计学和统计活动是理论与实践的关系。
3. 统计学的研究方法有哪些,它们有怎样的关系?并举例说明。
主要方法有两个:(1) 描述统计:搜集由试验或调查所获得的资料,进行整理、归类,计算出各种用于说明总体数量特征的数据,并运用图形或表格的形式将它们显示出来。
(2) 推断统计:指利用概率论的理论,根据试验或调查获得的样本信息科学地推断总体的数量特征。
关系:描述统计和推断统计都是统计方法的两个组成部分,前者是统计学的基础,后者是现代统计学的主要内容。
由于现实问题中,要获得总体数据存在很大的难度,能够获得的数据多为样本数据,因此,推断统计在现代统计学中的地位和作用越来越重要,它已成为统计学的核心内容。
当然,描述统计的重要性不可忽略,通过它得到可靠的统计数据并为后面的推断统计提供有效的样本信息,只有这样,才可以运用推断统计方法得出符合实际情况的结论。
4. 简要说明总体、样本、变量的概念。
总体:根据一定的目的确定的所要研究对象的全体,它是统计问题最基本的要素;样本:从总体中随机抽取的若干单位构成的集合体,它是统计问题的第二要素;变量:可变的数量;变量的具体表现,即可变数量的不同取值,称为变量值。
5. 简述SPSS统计软件的特点和应用领域。
⑴特点:第一,工作界面友好完善、布局合理、操作简便,大部分统计分析过程可以借助鼠标,通过菜单命令的选择、对话框参数设置、点击功能按钮来完成,不需要用户记忆大量的操作命令。
第一章总论一、单项选择题BBBCA DDAAA二、多项选择题BCD BCD ABD BDE ACD ACD ADE ABE ACE ACD 三、判断题×√×××√×√×√第二章统计资料的收集一、单项选择题BDBDD CAADC 二、多项选择题ADE BCDE BDE ADE ABD三、判断题×××××××√××第三章统计数据的整理与显示一、单项选择题CABBD ACACD二、多项选择题AD ACE ABC DC ABCD三、判断题√×√√×√×××√第四章总量指标与相对指标一、单项选择题CCBCC BDDBD CBDBB二、多项选择题ABCDE BC BD CE BC三、判断题√×√×√四、简答题:(略)五、综合题1、100.93%(超额)2、100.53%(未完成)3.根据下表计算相对指标并填空。
4.某厂生产情况如下:(单位:万元)第五章分布的数值特征 一、单项选择题 DDAAC CCDAA 二、多项选择题BC BCDE ABE ABC ACE DC 三、判断题 ××√×√四、简答题:(略) 五、综合题 1、(1)简单算术平均数=5(元) (2)加权算术平均数=4.7(元)(3)加权调和平均数= 4.7(元)2、甲市场蔬菜平均价格=0.3219(元) 乙市场蔬菜平均价格=0.3265(元) 乙市场蔬菜平均价格高一点。
3、甲地商品平均价格=1.2(元) 乙地商品平均价格=1.1875(元) 甲地商品平均价格高一点。
4、平均数:65.500=x (元);中位数5.5121001042182315002/1=⨯-+=⋅-+=-∑d f S f X M mm L e (元)众数38.552100)84104()82104()82104(5002110=⨯-+--+=⋅∆+∆∆+=d X M L (元)5、100.93%6、80=甲x 80=乙x93.188.10=,=乙甲σσ%=%=乙甲66.235.13V V <甲的代表性高于乙。
7、42.638=甲x11.499=乙x ;3.255.312=,=乙甲σσ%=%,=乙甲07.595.48V V 。
由于%=%=乙甲07.595.48V V >所以,乙品种虽然平均亩产低于甲品种,但乙品种的稳定性比甲好,因此更具有推广价值。
8、平均数=78(件) 标准差=12.53(件) 9、(1)甲、乙两组工人的人均日产量都为70(吨)(2)甲组工人日产量的标准差=83.67(吨)乙组工人日产量的标准差=5.29(吨) 甲组工人日产量的标准差系数=1.195 乙组工人日产量的标准差系数=0.076 (3)乙组比甲组的人均日产量的代表性高。
10、全距=500(元);平均值=330(元)平均差=84(元)标准差=102.96(元)标准差系数=102.96/330=0.312 11、(1)p=52%(2)是非标志的标准差=0.4996 12、1012(4230)400100433.33(4230)(4218)L M X d ∆-=+⋅=+⨯=∆+∆-+-(万元)1/26049400100426.1942m e L mf SM X d f ---=+⋅=+⨯=∑(万元)均值=426.67(万元),标准差=116.48(万元) 偏态系数=-0.0574,峰度系数=2.3513第六章时间数列一、单项选择题CBBDA DBABA BAACB 二、多项选择题ABC 、BCDE 、ACE 、ACDE 、ACD 、ABCD 、CE 、ABCD 、AC 、CD 三、判断题√√××√ √××√× 四、简答题:(略)五、综合题1、解:见表中数据平均发展水平285327.5391.2413.82562.8580.82561.12426.8566+++++===(万元)平均增长量42.563.722.62148.9818295.859.1655++++===(万元) 平均发展速度115.3%=平均增长速度115.3%115.3%=-= 2、解:第一季度月平均劳动生产率(90124143)/31191.9194586662(6064)/322++===+++(万元/人)。
3、解:注意,翻一番即为原来的两倍,也就是目标产值为1000万元。
(1)此时,平均增长速度11107.18%17.18%===-=; (2)设后八年的平均发展速度为x ,则有281.052x =,即107.73%x == (3)平均发展速度109.05%=== 4、解:以x 表示年份,y 表示水稻产量。
设趋势方程为bx a y+=ˆ,则由最小二乘法,得 2225532815172872014.4()5551550n xy x y b n x x -⨯-⨯====-⨯-∑∑∑∑∑17281514.4302.455y x a b nn=-=-⨯=∑∑因此,所求趋势方程为:x y4.144.302ˆ+= 2009年(即x=7)水稻产量的预测值302.414.47403.2=+⨯=(万吨)5、解:(1)计算结果见下表: 季节指数计算表(2)计算结果见下表1、表2:季节指数计算表1季节指数计算表2 第七章统计指数 一、单项选择题BBBCD BCACD ABDDB 二、多项选择题BCE BC AB ABE ABE 三、判断题 √××√√ ×××××四、简答题:(略) 五、综合题 1、1)个体指数:产量个体指数=125%,133.33%,150%;单位成本个体指数=122.22%,83.33%,77.78% (2)产量总指数%21.1301445.187001===∑∑pq p q k q单位成本总指数%87.1055.1875.1980111===∑∑pq p q k p(3)总成本的变动分析总成本指数%85.1371445.198011===∑∑pq p q k pq总成本增加额=198.5-144=54.5(万元) 137.85%=130.21%×105.87% 54.5万元=43.5万元+11.5万元其中:由于产量增加42.98%使总成本增加43.5万元,单位成本上升使总成本增加11.5万元。
2、解:(1)销售量总指数%32.10530607.32220000===∑∑pq p q k qq销售价格总指数%19.1057.322233901111111====∑∑∑∑p q k p q p q p q k qp(2)销售额的总变动分析销售额指数%78.1103060339011===∑∑pq p q k pq增加的销售额=3390-3060=330(万元)分析:报告期与基期相比较。
销售额增加10.78%,绝对数增加330万元。
这是由于销售量平均增加5.32%,使销售额增加162.7万元;由于价格平均增加5.19%,使销售额增加167.3万元。
3、解:(1)价格指数%10282.5585701111===∑∑pp kp q p q k (11.18万元)(2)成交量指数%42.116001==∑∑pq p q k q(78.82万元)(3)成交额指数%75.1184805700011==∑∑p q p q (90万元)118.75%=102%×1116.42% 90万元=11.18万元+78.82万元 4、设用q 、p 分别表示销售量、价格万元)(80011=∑pq万元)(70010080000=-=∑p q%115001==∑∑pq p q q 则万元)(80515.170001=⨯=∑pq (1)销售额指数=%29.114700800011==∑∑pq pq (2)价格指数%38.998058000111===∑∑pq p q k p(3)价格变动而变动的销售额=50111-=-∑∑pq p q (万元)5、销售额指数%56.113354000402000011===∑∑pq p q k pq增加的销售额=402000-354000=48000(元) 其中:销售量变化对销售额的影响100qq p Kq p=∑∑=119.19%由于销售量上升增加的销售额= 1q p ∑-0q p∑ =67920(元)价格变化对销售额的影响 111p q p K q p=∑∑=95.28%由于价格上升增加的销售额=11q p ∑ -1q p∑ =-19920(元)113.56%=119.19%×95.28% 48000元=67920元+(-19920元) 6、细粮小类指数%73.106100604.36.3405.27.2=⨯÷+⨯÷==∑∑wkw k p粮食中类指数为%35.107100355.1086573.106=⨯+⨯==∑∑w kw k p食品物价指数为:%55.113==∑∑wkw k p7、设用x 、f 分别表示平均工资、人数,由题知:x 1=∑∑ff x 111= 1000300780400900⨯+⨯=828 x 0=∑∑f f x=732xn=∑∑ff x 11= 708 (1)总平均工资的变动为:可变构成指数= xx 01=732828= 113.11%,即总平均工资上升了13.11%由此增加的总平均工资为: (x 1- x)=828-732=96(元/人)(2)、其中:①受各组工人人数比重变化的影响为:结构变动指数=xxn 0=732708= 96.72%即由于技术工人的比重下降使总平均工资降低了 3.28%,由此增加的总平均工资为: (x n- x)=-24(元/人)②受各组工人平均工资水平变动的影响为:固定构成指数=xx n1= 116.95%即由于各组工人工资水平上升使总平均工资提高了16.95%,由此增加的总平均工资为: (x 1- xn)=120(元/人)综合分析: 113.11%= 96.72%×116.95% 96 = -24 + 120即该工厂工人的工资报告期相对基期,由于技术工人的比重下降使总平均工资减少24元,由于各组工人工资上升使总平均工资增加120元,两者共同作用,最终使总平均工资增加了13.11%,平均每人增加96元。
8、略。