立体几何中的求角问题

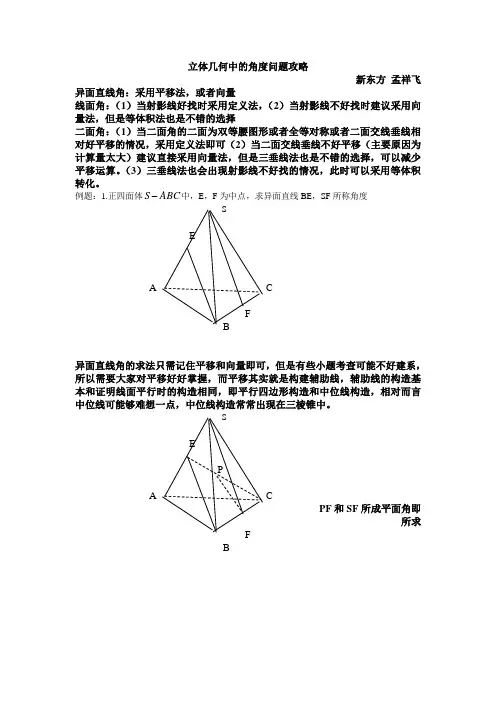
立体几何中的角度问题攻略新东方孟祥飞异面直线角：采用平移法，或者向量线面角：（1）当射影线好找时采用定义法，（2）当射影线不好找时建议采用向量法，但是等体积法也是不错的选择二面角：（1）当二面角的二面为双等腰图形或者全等对称或者二面交线垂线相对好平移的情况，采用定义法即可（2）当二面交线垂线不好平移（主要原因为计算量太大）建议直接采用向量法，但是三垂线法也是不错的选择，可以减少平移运算。

（3）三垂线法也会出现射影线不好找的情况，此时可以采用等体积转化。

S 中，E，F为中点，求异面直线BE，SF所称角度例题：1.正四面体ABCSEA CFB异面直线角的求法只需记住平移和向量即可，但是有些小题考查可能不好建系，所以需要大家对平移好好掌握，而平移其实就是构建辅助线，辅助线的构造基本和证明线面平行时的构造相同，即平行四边形构造和中位线构造，相对而言中位线可能够难想一点，中位线构造常常出现在三棱锥中。

SEPA CPF和SF所成平面角即所求FBSE这样的构建也是不错的选择EQ 和EB 所成角为所求A CQF B求三边套余弦定理即可，令正四面体边长为2，则EB=3，EQ=23，QB=27 所以32323247343cos =⨯⨯-+=QEB 此题还可以采用五坐标向量法来求解，2.三棱锥A BCD -，且,,,)(,>=<+===AC EF f DFCFBE AE λλλαβαλλ>=<BD EF ,λβ，求)(λf 的单调性 A EQB DFC此题的方法也为平移转化，由于是三棱锥，所以采用中位线（等比例线）方式平移，如图，不难发现，其实题目设计成求和角单调性，由于内角和为定值π，其实就是求角EQF 的单调性，而角EQF 为棱AC 和BD 之间角，是为定值的3.正方体1111D C B A ABCD -，E 是1BC 中点，求DE 与ABCD 所成角。

D 1 C 1 A 1 B 1 ED C Q A B线面角在求解时，我们觉得可能难度略大于异面直线，但是同学们注意其实把方法掌握，一样是很简单的，因为立体几何的特点是规律性非常强！我们看此题，线面角的定义是射影和斜线的成角，所以我们要先找DE 直线的射影，不难发现DE 的射影即为DQ ，所以所求线面角的平面角即为∠EDQ ，只需求解直角三角形EDQ 即可求出线面角的三角函数值。

空间角求法题型（线线角、线面角、二面角）空间角能比较集中的反映学生对空间想象能力的体现，也是历年来高考命题者的热点，几乎年年必考。

空间角是线线成角、线面成角、面面成角的总称。

其取值范围分别是：0°< θ ≤90°、0°≤ θ ≤90°、0°< θ ≤180°。

空间角的计算思想主要是转化：即把空间角转化为平面角，把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。

空间角的求法一般是：一找、二证、三求解，手段上可采用：几何法（正余弦定理）和向量法。

下面举例说明。

一、异面直线所成的角：例1如右下图，在长方体1111ABCD A B C D -中，已知4AB =，3AD =，12AA =。

E 、F 分别是线段AB 、BC 上的点，且1EB FB ==。

求直线1EC 与1FD 所成的角的余弦值。

思路一：本题易于建立空间直角坐标系，把1EC 与1FD 所成角看作向量EC 1与FD 的夹角，用向量法求解。

思路二：平移线段C 1E 让C 1与D 1重合。

转化为平面角，放到三角形中，用几何法求解。

（图1）解法一：以A 为原点，1AB AD AA 、、分别为x 轴、y 轴、z 轴的正向建立空间直角坐标系，则有 D 1（0，3，2）、E （3，0，0）、F （4，1，0）、C 1（4，3，2），于是11(1,3,2),(4,2,2)EC FD ==-设EC 1与FD 1所成的角为β，则：112222221121cos 14132(4)22EC FD EC FD β⋅===⋅++⨯-++ ∴直线1EC 与1FD 所成的角的余弦值为2114解法二：延长BA 至点E 1，使AE 1=1，连结E 1F 、DE 1、D 1E 1、DF ， 有D 1C 1//E 1E ， D 1C 1=E 1E ，则四边形D 1E 1EC 1是平行四边形。

则E 1D 1//EC 1 于是∠E 1D 1F 为直线1EC 与1FD 所成的角。

立体角计算公式立体角，又称夹角、内角、拱角，是指在立体空间内三条曲线汇合成的一种特殊的角，它体现了空间几何学的概念。

它的计算通常使用三角函数和立体几何的相关参数。

立体角的计算都是围绕着一个拱角内三个平面之间的夹角来完成的。

基本计算公式二维平面立体角的计算公式如下：夹角=sin-1[(b x c)/(|b||c|)]其中，b和c是向量，|b|和|c|分别是b和c的模长，x表示叉乘。

三维平面立体角的计算公式如下：夹角=cos-1[(a x b)c/(|a||b||c|)]其中，a、b和c是向量，|a|、|b|和|c|分别是a、b和c的模长，x和表示叉乘和点乘。

立体几何计算公式立体几何的计算公式可以用来表示立体角的特性，以此来计算夹角的大小。

1.体积公式：V＝abc其中，a、b和c是三条曲线汇合处的长度或边长，V表示立体角的体积。

2.表面积公式：S＝ab+bc+ca其中，a、b和c是三条曲线汇合处的长度或边长，S表示立体角的表面积。

3.距离公式：D＝√(a+b+c)其中，a、b和c是三条曲线汇合处的长度或边长，D表示立体角的距离。

4.角平分公式：α/β/γ＝a/b/c其中，α、β和γ是各角的大小，a、b和c是三条曲线汇合处的长度或边长。

5.体积中垂线公式：V＝abc sin其中，V表示立体角的体积，a、b和c是三条曲线汇合处的长度或边长，α表示立体角的内角大小。

立体角的应用立体角计算公式广泛应用于几何学、机械工程、电子学等领域，它可以用来计算空间坐标系的定位，构建复杂的几何体，也可用来测量空间距离、角度、体积等。

比如，在机械结构设计中，立体角的计算公式可以用来计算连接的螺栓的角度、位置和大小，为准备安装和维护机械设备提供依据。

在电子工程中，立体角的计算公式也可以用来计算电子元件之间的位置、距离和角度，这些参数对正确构建电子系统非常重要。

总结立体角是一种有三条曲线汇合而成的特殊角，它体现了空间几何学的概念。

立体几何求夹角方法总结立体几何体现了空间中物体的立体形态，它的重要性在于能够帮助人们更好地理解三维物体，并求出它们之间的夹角，这在数学、物理等领域都有着广泛的应用。

本文将总结出常见的几何求夹角方法，供读者参考。

方法一：向量求夹角向量是几何学中的常用概念，它由矢量和标量组成。

可以通过计算两个向量之间的夹角，得到它们之间的几何夹角。

具体做法如下：1. 求出待求夹角的两个向量；2. 根据向量的标准公式求出它们的数量积；3. 分别计算出两个向量的长度；4. 将数量积和长度带入余弦定理求出夹角。

方法二：平面法线求夹角在三维空间中，可以通过平面的法线向量来计算两个平面之间的夹角。

具体做法如下：1. 求出待求夹角的两个平面的法线向量；2. 根据向量的标准公式求出它们的数量积；3. 分别计算出两个平面的法线向量的长度；4. 将数量积和长度带入余弦定理求出夹角。

方法三：点法线求夹角与平面法线类似，我们也可以通过点和法线向量计算两个平面之间的夹角。

具体做法如下：1. 求出待求夹角的两个平面的任意一点坐标和两个平面的法线向量；2. 根据向量的标准公式求出它们的数量积；3. 分别计算出两个平面的法线向量的长度；4. 将数量积和长度带入余弦定理求出夹角。

方法四：球面三角学法求夹角该方法适用于计算球面上两个点或两个平面之间的夹角，方法稍微复杂。

具体做法如下：1. 求出待求夹角的两个点或平面的经纬度坐标；2. 根据球面三角学公式求出两个点之间的夹角或两个平面之间的夹角；3. 将弧度转化为角度，得到最终的夹角。

综上所述，立体几何求夹角的方法有计算向量之间的夹角、平面法线之间的夹角、点法线之间的夹角和球面三角学法求夹角。

每种方法都有其适用范围和计算步骤，要根据实际情况选择合适的方法进行计算。

立体几何中的向量方法求夹角1.确定两个向量假设有两个向量A和B，它们的坐标分别为(x₁,y₁,z₁)和(x₂,y₂,z₂)。

2.计算向量的点积向量的点积是两个向量各个对应坐标分量的乘积之和，可以用以下公式表示：A·B=x₁x₂+y₁y₂+z₁z₂3.计算向量的模向量的模是向量的长度，可以用以下公式表示：A，=√(x₁²+y₁²+z₁²)B，=√(x₂²+y₂²+z₂²)4.计算夹角的余弦值夹角的余弦值可以通过点积和模的关系计算得到，用以下公式表示：cosθ = (A·B) / (，A，，B，)5.计算夹角夹角的弧度可以通过余弦值计算得到，用以下公式表示：θ = arccos(cosθ)6.将弧度转换为度数为了方便阅读和理解，可以将弧度转换为角度，用以下公式表示：α=θ*180°/π以上就是利用向量方法求解立体几何中夹角的具体步骤。

下面通过一个例子来说明向量方法求解立体几何中夹角的应用。

例题：给定两个向量A(2,3,-1)和B(1,-2,4)，求它们之间的夹角。

解答：首先计算向量A和向量B的点积：A·B=2*1+3*(-2)+(-1)*4=2-6-4=-8然后计算向量A和向量B的模：A，=√(2²+3²+(-1)²)=√(4+9+1)=√14B，=√(1²+(-2)²+4²)=√(1+4+16)=√21接下来计算夹角的余弦值：cosθ = (A·B) / (，A，，B，) = -8 / (√14 * √21)然后计算夹角：θ = arccos(cosθ)最后将弧度转换为角度：α=θ*180°/π通过以上计算，可以得到向量A和向量B之间夹角的大小。

立体几何之求角一、知识点归纳1、 两条异面直线所成的角θ的范围是 ，当θ= 时，这两条异面直线互相垂直。

异面直线所成角的求法：（1）平移(做平行线)其中一条或两条直线，使之同在某一三角形中，通过解三角形求出所求的角。

（2）利用向量夹角来求：设异面直线b a ,的方向向量为,，则直线b a ,的夹角θ由公式||||cos b a ⋅=θ2、 斜线AO 与它在平面α内的射影AB 所成的角1θ叫做 。

设AC是α内的一条直线，AO 与AC 所成的角为θ，AB 与AC 所成的角为θ2，则θ1、θ2、θ的余弦值关系是________________.3、平面的斜线和平面所成的角，是这条斜线和这个平面内的任一条直线所成的角中__________. 如果直线和平面垂直，那么就说_______________. 如果直线和平面平行或在平面内，那么说______________.4、直线和平面所成的角的范围为_____________.5、斜线和所交平面所成的角的范围为__________.6、直线与平面所成的角（设为θ）（1）斜线与平面所成的角的定义：平面的一条斜线和它在这个平面内的_____________所成的________________，叫做这条直线和这个平面所成的角。

（2）当一条直线__________于平面时，规定它们所成的角是直角；当一条直线和平面___________或_________时，规定它们所成的角为________________.(3)填写下表:在直线与平面所成的角的定义中体现_________和___________数学思想.（4）斜线和平面所成的角的最小性：斜线和平面所成的角是用两条相交直线所成的_____________来定义的，其中一条直线就是斜线本身，另一条直线就是斜线在平面上的___________________.在平面内经过斜足的直线有无数条，；它们和斜线都组成相交的两条直线，为什么选中射影和斜线这两条相交直线，用它们所成的____________来定义斜线和平面所成的角呢？原因是斜线和平面内经过斜足的直线所成的一切角中，它是_____________.对于已知的斜线来说这个角是唯一确定的,它的大小反映了斜线关于平面的“倾斜程度”，根据线面所成的角的定义，有结论：斜线和平面所成的角，是这条斜线的角的定义，有结论：斜线和平面所成的角，是这条斜线和这个平面内的直线所成的一切角中__________________.线面角的求法：（1）做出线面角，找出此角所在的三角形，通过解三角形求出此角。

立体几何求角、距离的解法考点一、空间中的夹角空间中的各种角包括异面直线所成的角，直线与平面所成的角和二面角，要理解各种角的概念定义和取值范围，其范围依次为(0°，90°]、[0°，90°]和[0°，180°]。

（1）两条异面直线所成的角求法：○1先通过其中一条直线或者两条直线的平移，找出这两条异面直线所成的角，然后通过解三角形去求得；○2通过两条异面直线的方向量所成的角来求得，但是注意到异面直线所成角得范围是]2,0(π，向量所成的角范围是],0[π，如果求出的是钝角，要注意转化成相应的锐角（2）直线和平面所成的角 求法：“一找二证三求”，三步都必须要清楚地写出来。

除特殊位置外，主要是指平面的斜线与平面所成的角，根据定义采用“射影转化法”（3）二面角的度量是通过其平面角来实现的解决二面角的问题往往是从作出其平面角的图形入手，所以作二面角的平面角就成为解题的关键。

通常的作法有：（Ⅰ）定义法；（Ⅱ）利用三垂线定理或逆定理；（Ⅲ）自空间一点作棱垂直的垂面，截二面角得两条射线所成的角，俗称垂面法．此外，当作二面角的平面角有困难时，可用射影面积法解之，cos ＝SS '，其中S 为斜面面积，S ′为射影面积， 为斜面与射影面所成的二面角例题1：已知边长为1的正方体ABCD-A 1B 1C 1D 1中，O 、O 1是上下底面正方形的中心，求二面角O 1-BC-O 的大小。

2：已知边长为1的正方体ABCD-A 1B 1C 1D 1中，E 、F 为A 1D 1、C 11的中点，求平面EFCA 与底面ABCD 所成的二面角。

点评：利用平面角定义法中特殊位置的线段。

3：已知正方体ABCD-A 1B 1C 1D 1中，求平面ACD 1与平面BDC 1所成的二面角。

解：设AC 与BD 交于E ，CD 1与C 1D 交于F ，连EF 是所求二面角B-EF-C 的棱，连A 1C ，易证A 1C ⊥平面BDC 1，垂足为H ，取AD 1中点O ，连OC 交EF 于G ，连GH 。

数学中的立体角与体积计算数学作为一门学科，涉及到了许多不同的概念和理论。

其中，立体角和体积计算是数学中重要的概念之一。

本文将探讨立体角和体积计算的相关内容，并介绍其在实际生活中的应用。

一、立体角的概念与计算方法立体角是用来描述三维空间中的角度的概念。

在数学中，立体角是由三维空间中的两个射线所夹的角度。

这个概念可以用来描述物体的形状、大小和方向。

计算立体角的方法有多种，其中一种常用的方法是使用球面三角学的知识。

假设有一个球面，以球心为原点，将球面上的两个点与球心相连，这两个点所在的射线与球面所夹的角度就是立体角。

另一种计算立体角的方法是使用立体几何的知识。

在立体几何中，可以通过计算物体的表面积和体积来推导出立体角的大小。

例如，如果一个物体是由若干个平面所围成的，那么可以通过计算这些平面的面积来计算立体角。

二、体积计算的方法与应用体积是描述一个物体所占据的空间大小的概念。

在数学中，体积可以用来计算物体的大小、容量和密度等信息。

计算体积的方法有多种，其中一种常用的方法是使用立体几何的知识。

在立体几何中，可以通过计算物体的底面积和高度来推导出物体的体积。

例如，对于一个长方体来说，可以通过计算底面积与高度的乘积来计算体积。

另一种计算体积的方法是使用积分的知识。

在数学中，可以通过将物体划分成无限小的体积元素，并对这些体积元素进行求和来计算物体的体积。

这种方法适用于复杂的几何体，如球体、圆锥体等。

体积计算在实际生活中有着广泛的应用。

例如，在建筑设计中，需要计算建筑物的体积来确定材料的用量和成本。

在工程领域，需要计算物体的体积来确定其容量和承载能力。

在生物学和医学领域，需要计算细胞、器官和组织的体积来研究其结构和功能。

三、立体角与体积计算的联系立体角和体积计算有着密切的联系。

在计算物体的体积时，常常需要考虑物体的形状和方向。

而立体角可以提供关于物体形状和方向的信息，从而帮助计算物体的体积。

例如，对于一个长方体来说，可以通过计算其底面积和高度来计算体积。

高中数学立体几何线面角公式
一、高中立体几何线面角的概念
在高中立体几何中，线面角是指一条直线与一个平面所成的最小角。

这个概念帮助我们更好地理解空间中线与面的关系，以及如何计算它们之间的角度。

二、线面角公式及其推导
1.线面角公式
线面角公式如下：
α= β + γ
其中，α表示线面角，β 表示直线与平面内的直线所成的角度，γ 表示平面内的直线与平面所成的角度。

2.推导
根据空间几何中的知识，我们知道：
β+ γ = 180°
因此，
α= 180° - γ
这样，我们就得到了线面角的计算公式。

三、线面角公式的应用
线面角公式在解决立体几何问题时非常有用，例如：
1.判断直线与平面是否垂直：若线面角为90°，则直线与平面垂直。

2.计算线面角的大小：根据线面角公式，求得线面角α的值。

3.求解空间几何中的角度和：利用线面角公式，可以计算出空间中多个角度之和。

四、总结与练习
线面角公式是高中立体几何中的重要知识点，理解和掌握这个公式，能够帮助我们更好地解决实际问题。

通过下面的练习，巩固所学知识：
1.已知直线l与平面α所成角为30°，直线l与平面β所成角为45°，求直线l与平面α、β的夹角。

2.一平面与直线l垂直，直线l与另一平面β成60°，求平面α与β之间的夹角。

立体几何求线线角的方法
在立体几何中，求线线角的方法主要有以下几种：
1. 利用垂足定理：当两直线相交时，将垂足抬高成两个相互垂直的直角，然后利用已知条件求解。

2. 利用平行线之间的性质：当两条线平行时，其对应的内角、外角及同位角相等，可以利用这一性质求解线线角。

3. 利用圆内切、外切性质：当两条直线分别与内切圆或外切圆相切时，由于切点与圆心连线垂直，可以利用垂足定理求解。

4. 利用正弦定理、余弦定理：当已知两条直线的夹角和其它边长或角度时，可以利用正弦定理或余弦定理求解线线角。

5. 利用矢量运算：将两条直线表示为矢量形式，然后利用矢量运算求解线线角。

需要注意的是，对于线线角的求解，常常需要已知某些边长、角度或者有关线段的关系，因此在具体问题中，需要利用给定的条件来选择适合的求解方法。

立体几何中角的求法1•异面直线所成角的求法：范围（直线与直线所成角< 三|0 ,90 ］：（1）平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；（2）补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；2•直线与平面所成的角范围：（直线与平面所成角1：•二0 ,90 '）斜线和平面所成的是一个直角三角形的锐角，它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影。

通常通过斜线上某个特殊点作出平面的垂线段，垂足和斜足的连线，是产生线面角的关键；3•二面角的求法范围：二面角〔三［0 ,180 ］）方法：作，证，算知识:正弦定理，余弦定理，特殊角，反正弦（余弦，正切）（1）定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；（2）三垂线法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角；（3）垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；（4）射影法：利用面积射影公式S射=S原cos—其中为平面角的大小，此法不必在图形中画出平面角；特别:对于一类没有给出棱的二面角，应先延伸两个半平面，使之相交出现棱，然后再选用上述方法（尤其要考虑射影法）。

（二面角的取值范围5 0 ,180 ）1、在正方体AG中，求下列线面角⑴DB与底面AC2）A,B与平面AB|CD2、如图AB_ 平面ABCD,BC _CD, AB 二BC,AD与平面ABCD所成的角为300⑴求AD与平面ABC所成的角⑵AC与面ABD所成的角线线角1.如图所示，ABCD 是一个正四面体，E 、F 分别为BC 和 AD 的中点.求：AE 与CF 所成的角 2■如图，长方体 ABCD —A i B i C i D i 中, AB=BC=2,AA i =1，E 、H 分别是A i B i 和BB i 的中点■求:(1) EH 与AD i 所成的角；(2) AC i 与B i C 所成的角. 面面角AB 的中点，(1 )求BC 与平面SAB 所成的角(2)求SC 与平面ABC 所成的角2. 如图，在棱长为 a 的正方体 ABC —AB i CD 中，求: (1 )面A i ABB 与面ABCD 所成角的大小；1、如图；四面体 ABCS 中，SA 、SB 、SC 两两垂直,SBA=45 , SBC = 60，M 为 AD i C i(2)二面角C —BD—C的正切值(3)二面角BC^ D3、设线段AB= a ,AB在平面:-内,CA丄〉，BD与：•成30 0角,BD丄AB,C、D在：•同侧,CA=BD= b .求：(1)CD的长;(2)CD与平面：•所成角正弦值.4、过正方形ABCD的顶点A作PA A平面ABCD，设PA=AB=a，(1)求二面角B- PC- D的大小；(2)求二面角C-PD-A5、如图，直二面角D —AB —E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF丄平面ACE.(I)求证AE丄平面BCE;(H)求二面角B—AC —E的大小; (川)求点D到平面ACE的距离.CD。

立体几何向量法求二面角简介在立体几何中，二面角指的是两个平面的夹角。

为了求解二面角，我们可以使用向量法，具体就是将两个平面的法向量进行运算，得到两个向量之间的夹角。

本文将详细介绍立体几何向量法求解二面角的原理和具体步骤。

背景知识在学习立体几何向量法求解二面角之前，我们需要了解一些基础知识： 1. 平面的法向量：平面上的每一点都有一个与之垂直的向量，称为平面的法向量。

平面的法向量可以用两个不共线的向量来确定。

2. 向量的点乘：向量的点乘运算可以得到两个向量之间的夹角。

点乘的结果等于两个向量的模长乘积与它们之间夹角的余弦值的乘积。

3. 向量的模长：向量的模长表示向量的长度。

理论推导假设有两个平面，分别为平面A和平面B，我们需要求解它们之间的二面角。

要求解二面角，我们可以使用以下的步骤： 1. 确定平面A和平面B的法向量。

可以通过已知条件或者使用平面上的点来确定法向量。

2. 对平面A和平面B的法向量进行点乘运算，得到它们之间的夹角的余弦值。

3. 通过反余弦函数，将夹角的余弦值转换为夹角的度数。

以下是具体的求解步骤：步骤1：确定法向量首先，我们需要确定平面A和平面B的法向量。

实际情况中，可能已经给出了平面的法向量，也可能需要通过平面上的点来计算法向量。

假设平面A的法向量为??，平面B的法向量为??。

步骤2：点乘运算接下来，我们对平面A和平面B的法向量进行点乘运算，得到它们之间的夹角的余弦值。

点乘的结果等于两个向量的模长乘积与它们之间夹角的余弦值的乘积。

? · ?? = |??| |??| cos(?)其中，?为平面A和平面B的法向量之间的夹角。

步骤3：求解夹角最后，通过反余弦函数，我们可以将夹角的余弦值转换为夹角的度数。

得到的结果就是平面A和平面B之间的二面角。

= arccos( · ?)实例演示为了更好地理解立体几何向量法求解二面角的过程，我们来看一个具体的实例。

假设有两个平面，平面A的法向量为? = (1, 0, 0)，平面B的法向量为?? = (0, 1, 0)。

利用平面向量求角度问题【基础知识】一般地，异面直线AC ，BD 的夹角β的余弦值为cos β＝|AC →·BD →||AC →||BD →|.利用向量求线面角的方法：(1)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．【规律技巧】注意线线、线面和二面角的平面角的角度的取值范围【典例讲解】 求异面直线所成的角【例1】 如图，在四棱锥P -ABCD 中，底面ABCD 是矩形，P A ⊥底面ABCD ，E 是PC 的中点．已知AB ＝2，AD ＝22，P A ＝2.求：(1)△PCD 的面积．(2)异面直线BC 与AE 所成的角的大小． 解 (1)因为P A ⊥底面ABCD ，所以P A ⊥CD .【变式探究】 如右图所示正方体ABCD －A ′B ′C ′D ′，已知点H 在A ′B ′C ′D ′的对角线B ′D ′上，∠HDA ＝60°.求DH与CC′所成的角的大小．利用空间向量求直线与平面所成的角【例2】如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点．在五棱锥P－ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.(1)求证：AB∥FG；(2)若P A⊥底面ABCDE，且P A＝AE.求直线BC与平面ABF所成角的大小，并求线段PH的长．【变式探究】(2014·福建卷)在平面四边形ABCD中，AB＝BD＝CD＝1，AB⊥BD，CD⊥BD，将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．(1)求证：AB⊥CD；(2)若M为AD中点，求直线AD与平面MBC所成角的正弦值．利用空间向量求二面角【例3】如图，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E.(1)证明：CF ⊥平面ADF ； (2)求二面角D －AF －E 的余弦值．设平面AEF 的法向量为n 1＝(x 1，y 1，z 1)， 则n 1⊥EF →，n 1⊥F A →，因此⎩⎨⎧y 1＝0，－3x 1－3y 1＋4z 1＝0，取x 1＝4，则n 1＝(4，0，3)为平面AEF 的一个法向量．[来源:学+科+网] 由于CF ⊥平面ADF ，故平面ADF 的一个法向量n 2＝(3，－1，0)． 由图可见所求二面角θ的余弦值为cos θ＝|n 1·n 2||n 1||n 2|＝4316＋3×（3）2＋（－1）2＝25719.【变式探究】如图，△ABC 和△BCD 所在平面互相垂直，且AB ＝BC ＝BD ＝2，∠ABC ＝∠DBC ＝120°，E ，F 分别为AC ，DC 的中点．(1)求证：EF⊥BC；(2)求二面角E－BF－C的正弦值．【针对训练】1、已知两平面的法向量分别为m＝(0，1，0)，n＝(0，1，1)，则两平面所成的二面角的大小为__________．2、如图，在四棱锥P－ABCD中，P A⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E 为棱PC的中点．(1)证明：BE⊥DC；(2)求直线BE与平面PBD所成角的正弦值；(3)若F为棱PC上一点，满足BF⊥AC，求二面角F－AB－P的余弦值．【练习巩固】1．在正方体ABCD－A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为()A.12B.23C.33D.22答案 B2．在正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，则CD 与平面BDC 1所成角的正弦值等于__________． 答案 233.如图所示，在三棱柱ABC －A 1B 1C 1中，AA 1⊥底面ABC ，AB ＝BC ＝AA 1，∠ABC ＝90°，点E 、F 分别是棱AB 、BB 1的中点，则直线EF 和BC 1所成的角是__________．4．已知向量a ＝(1，0，－1)，则下列向量中与a 成60°夹角的是( ) A ．(－1，1，0) B ．(1，－1，0) C ．(0，－1，1)D ．(－1，0，1)5．在直三棱柱 ABC －A 1B 1C 1中，∠BCA ＝90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC ＝CA ＝CC 1，则BM 与AN 所成角的余弦值为( ) A.110B.25C.3010D.22答案 C。