2016年春季新版苏科版九年级数学下学期7.3、特殊角的三角函数学案2

苏科版数学九年级下册7.3《特殊角的三角函数1》讲教学设计一. 教材分析《苏科版数学九年级下册7.3《特殊角的三角函数1》》是一章介绍特殊角的三角函数值的章节。

本章通过讲解30°、45°、60°角的正弦、余弦、正切函数值，使学生掌握特殊角的三角函数值，并能应用于实际问题中。

教材内容结构清晰，例题丰富，便于学生理解和掌握。

二. 学情分析学生在学习本章之前，已经学习了锐角三角函数的概念，对正弦、余弦、正切函数有了初步的了解。

但学生对于特殊角的三角函数值的理解和应用还有待提高。

因此，在教学过程中，需要注重引导学生通过观察、思考、探究来发现和总结特殊角的三角函数值，并能够运用到实际问题中。

三. 教学目标1.知识与技能目标：让学生掌握30°、45°、60°角的正弦、余弦、正切函数值，并能应用于实际问题中。

2.过程与方法目标：通过观察、思考、探究等过程，培养学生发现和总结特殊角的三角函数值的能力。

3.情感态度与价值观目标：培养学生对数学的兴趣，提高学生解决实际问题的能力。

四. 教学重难点1.重点：30°、45°、60°角的正弦、余弦、正切函数值。

2.难点：特殊角的三角函数值的发现和总结。

五. 教学方法1.启发式教学：通过问题引导，激发学生的思考，引导学生发现和总结特殊角的三角函数值。

2.小组合作：引导学生进行小组讨论，共同探究特殊角的三角函数值，培养学生的合作能力。

3.实例教学：通过实际问题，让学生运用特殊角的三角函数值解决问题，提高学生的应用能力。

六. 教学准备1.教学PPT：制作精美的PPT，展示特殊角的三角函数值的讲解和应用。

2.实例问题：准备一些实际问题，用于引导学生运用特殊角的三角函数值解决。

3.学习资料：准备相关的学习资料，以便学生在课后进行复习和巩固。

七. 教学过程1.导入（5分钟）利用PPT展示一些实际问题，引导学生思考特殊角的三角函数值在实际问题中的应用。

苏科版数学九年级下册《7.3 特殊角的三角函数》教学设计一. 教材分析《苏科版数学九年级下册》第七章第三节“特殊角的三角函数”是初高中数学衔接的重要内容。

本节课主要介绍特殊角的三角函数值，包括30°、45°、60°角的正弦、余弦、正切函数值。

这些值在三角函数的学习以及解决实际问题中具有重要作用。

通过对特殊角的三角函数的学习，学生可以更好地理解三角函数的概念，为后续学习打下基础。

二. 学情分析九年级的学生已经学习了初中阶段的代数、几何知识，具备一定的数学基础。

但是，对于特殊角的三角函数值，他们可能还比较陌生。

因此，在教学过程中，教师需要引导学生逐步理解特殊角的三角函数值，并通过实例让学生感受其在实际问题中的应用。

三. 教学目标1.知识与技能目标：让学生掌握30°、45°、60°角的正弦、余弦、正切函数值，并能运用这些值解决实际问题。

2.过程与方法目标：通过自主学习、合作交流，培养学生探究特殊角的三角函数值的能力。

3.情感态度与价值观目标：激发学生学习三角函数的兴趣，培养学生的数学思维。

四. 教学重难点1.重点：特殊角的三角函数值。

2.难点：特殊角的三角函数值的推导和应用。

五. 教学方法1.引导法：教师引导学生探究特殊角的三角函数值，激发学生的思维。

2.合作交流法：学生分组讨论，分享学习心得，互相促进。

3.实例分析法：通过实际问题，让学生感受特殊角的三角函数值在解决问题中的作用。

六. 教学准备1.教师准备：教材、教案、多媒体教学设备。

2.学生准备：笔记本、三角板、计算器。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾已学的锐角三角函数知识，为新课的学习做好铺垫。

2.呈现（10分钟）教师利用多媒体展示特殊角的三角函数值，包括30°、45°、60°角的正弦、余弦、正切函数值。

引导学生观察这些值的特点，并引导学生思考如何推导这些值。

苏科版数学九年级下册7.3《特殊角的三角函数》教学设计一. 教材分析苏科版数学九年级下册7.3《特殊角的三角函数》是学生在学习了锐角三角函数的定义、三角函数的图像和性质的基础上进行的一节内容。

本节课主要让学生了解并掌握30°、45°、60°角的正弦、余弦、正切函数值，并能运用其解决实际问题。

教材通过实例引入特殊角的三角函数值，引导学生探究并发现规律，进而总结出一般性结论。

二. 学情分析九年级的学生已经学习了锐角三角函数的定义、三角函数的图像和性质，对三角函数有了初步的认识。

但是，对于特殊角的三角函数值，学生可能还不太熟悉，需要通过实例和练习来进一步巩固。

此外，学生可能对于如何运用三角函数解决实际问题还有一定的困难，需要在教学中给予指导和训练。

三. 教学目标1.了解30°、45°、60°角的正弦、余弦、正切函数值，并能熟练运用。

2.掌握特殊角的三角函数值的求法，并能运用其解决实际问题。

3.培养学生的探究能力和合作精神，提高学生的数学思维能力。

四. 教学重难点1.重点：30°、45°、60°角的正弦、余弦、正切函数值。

2.难点：特殊角的三角函数值的求法及其运用。

五. 教学方法1.引导发现法：通过实例引入特殊角的三角函数值，引导学生探究并发现规律。

2.合作学习法：分组讨论，共同完成任务，培养学生的合作精神和团队意识。

3.练习法：通过适量练习，巩固所学知识，提高学生的应用能力。

六. 教学准备1.课件：制作课件，展示特殊角的三角函数值的图像和实例。

2.练习题：准备适量练习题，用于巩固所学知识。

3.三角板：准备三角板，用于演示特殊角的三角函数值。

七. 教学过程1.导入（5分钟）利用课件展示特殊角的三角函数值的图像，引导学生观察并思考：你能发现什么规律？2.呈现（10分钟）呈现30°、45°、60°角的正弦、余弦、正切函数值，引导学生探究并发现规律。

苏科版数学九年级下册7.3《特殊角的三角函数》讲教学设计一. 教材分析苏科版数学九年级下册7.3《特殊角的三角函数》是本册教材中的重要内容，主要介绍了特殊角的正弦、余弦和正切函数值。

这部分内容是学生学习三角函数的基础，对于学生来说，理解和掌握特殊角的三角函数值对于后续学习初中数学和高中数学都有着重要的意义。

二. 学情分析九年级的学生已经具备了一定的数学基础，对于函数的概念和性质有了初步的了解。

但是，对于特殊角的三角函数值，学生可能还存在着一定的困难，因此，在教学过程中，需要教师耐心引导，让学生逐步理解和掌握。

三. 教学目标1.让学生理解特殊角的三角函数概念，掌握特殊角的正弦、余弦和正切函数值。

2.培养学生运用三角函数解决实际问题的能力。

3.培养学生合作学习、积极探究的学习态度。

四. 教学重难点1.特殊角的三角函数值的记忆和理解。

2.运用三角函数解决实际问题。

五. 教学方法1.情境教学法：通过生活实例，引导学生理解特殊角的三角函数值的概念。

2.小组合作学习：引导学生分组讨论，共同探究特殊角的三角函数值。

3.实践操作法：让学生通过实际操作，加深对特殊角的三角函数值的理解。

六. 教学准备1.教学课件：制作课件，展示特殊角的三角函数值的计算过程。

2.练习题：准备相关的练习题，巩固学生对特殊角的三角函数值的理解。

七. 教学过程1.导入（5分钟）教师通过生活实例，如电梯上升下降的高度，引出特殊角的三角函数值的概念。

提问：你们知道电梯上升下降时的角度与高度有什么关系吗？2.呈现（10分钟）教师通过课件，展示特殊角的三角函数值的计算过程，引导学生记忆特殊角的三角函数值。

提问：你们能说出特殊角的三角函数值吗？3.操练（10分钟）教师给出相关的练习题，让学生独立完成，检验学生对特殊角的三角函数值的理解。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）教师学生进行小组讨论，共同探究特殊角的三角函数值的应用。

提问：你们能用特殊角的三角函数值解决实际问题吗？5.拓展（10分钟）教师引导学生思考：除了特殊角，还有其他的角的三角函数值是我们需要记忆的吗？让学生初步了解一般的三角函数值的求法。

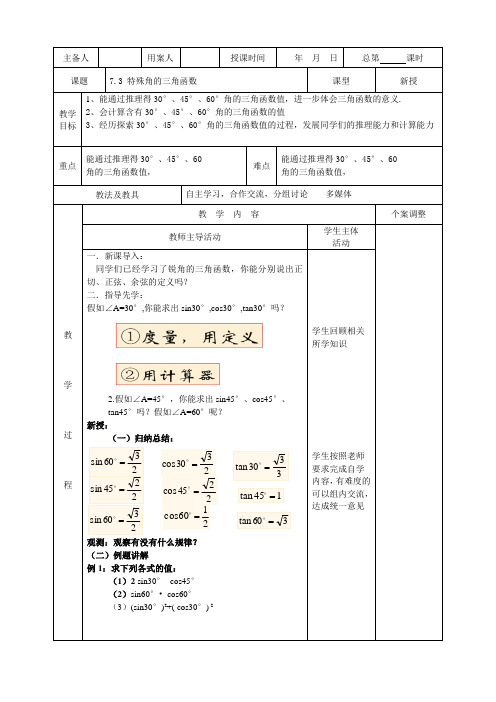
主备人用案人授课时间年月日总第课时课题7.3 特殊角的三角函数课型新授教学目标1、能通过推理得30°、45°、60°角的三角函数值，进一步体会三角函数的意义.2、会计算含有30°、45°、60°角的三角函数的值3、经历探索30°、45°、60°角的三角函数值的过程，发展同学们的推理能力和计算能力重点能通过推理得30°、45°、60角的三角函数值，难点能通过推理得30°、45°、60角的三角函数值，教法及教具自主学习，合作交流，分组讨论多媒体教学过程教学内容个案调整教师主导活动学生主体活动一．新课导入：同学们已经学习了锐角的三角函数，你能分别说出正切、正弦、余弦的定义吗？二．指导先学：假如∠A=30°,你能求出sin30°,cos30°,tan30°吗？2.假如∠A=45°，你能求出sin45°、cos45°、tan45°吗？假如∠A=60°呢？新授：（一）归纳总结：观测：观察有没有什么规律？（二）例题讲解例1：求下列各式的值：（1）2 sin30°- cos45°（2）sin60°•cos60°（3）(sin30°)2+( cos30°) 2学生回顾相关所学知识学生按照老师要求完成自学内容，有难度的可以组内交流，达成统一意见2330cos=3330tan=2245sin=2245cos=145tan=2360sin=2160cos=360tan=2360sin=教学过程教学内容个案调整教师主导活动学生主体活动三.交流展示：1.(1)已知∠A为锐角，cosA= ，你能求出sinA和tanA吗?(2)求锐角a 的度数:四．释疑拓展：已知:如图,在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，BC=2，BD= .分别求出△ABC、△ACD、△BCD中各锐角五．检测巩固：1.计算.（1）cos45°－sin30°（2）（2）sin260°＋cos260°(3)tan45°－sin30°·cos60°（4）2230tan45cos例2.求满足下列条件的锐角α:(1) cosα=23(2)2sinα=1 (3)2sinα－2=0 (4)3tanα－1=0学生先独立思考，然后小组讨论交流，最后全班展示交流，并让学生自己归纳发现的结论．学生口答，并说明理由．学生思考后可以小组讨论2sin2=-α01tan3=-α232sin2=-α01tan3=-α。

特殊角的三角函数一、知识回顾在△ABC 中，∠C=90°锐角A 的对边为a ，邻边为b ，斜边为c ，则 sinA= ，cosA= ，tanA= 。

二、探索活动1、活动一：300、450、600三角函数值,你能想出哪些方法求出300、450、600角的三角函数值？哪种方法求出的三角函数值最精确？2、活动二：根据以上探索完成下列表格三、通过预习你还有什么问题？请写下来与同学分享。

课中参与例1.求下列各式的值：（1）2sin30°-cos45° （2）sin60°·cos60° （3）sin 230°+cos 230°练习：计算（1）cos45°－sin30° （2）cos30°sin45°+sin30°cos45°(3) 3cos30°+2sin45° (4) 00045tan 260tan 130sin --例2.求满足下列条件的锐角α：(1) cos α-23=0 (2)2sin α=1 (3) 2sin （θ+20°）-2=0(4) sin(α+10°)=22 (5) sin （α-5°）=23 (6)tan （α+10°）=3 例3.已知α为锐角,当αtan 12-无意义时,求tan(α+15°)-tan(α-15°)的值.例4.等腰三角形的一腰长为6㎝,底边长为63㎝,请你判断这个三角形是锐角三角形、直角三角形还是钝角三角形?课后参与1、在Rt △ABC 中，∠C=900，sinA=21，则sinB 的值为（ ） A. 21 B.22 C.23 D.1 2、在Rt △ABC 中，∠C=90°,若sinA=21,则BC ∶AC ∶AB 等于（ ） A.1∶2∶5 B.1∶3∶ 5 C. 1∶3∶ 2 D.1∶2∶33、在△ABC 中，若tanA=1，sinB=22，则△ABC 的形状是（ ） A ．等腰三角形 B ．等腰直角三角形 C ．直角三角形 D ．一般锐角三角形4、已知α为锐角，sin α=43，则（ ） A ．00＜α＜300 B.300＜α＜450C.450＜α＜600D. 600＜α＜900 5、如图，AD 是△ABC 的高，BC=15cm ，∠BAD=300，∠DAC=450，求AD.6、如图，在Rt △ABC 中,∠ACB=90°,CD ⊥AB,垂足为D,BC=2,BD=3.分别求△ABC 、△ACD 、△BCD 中的各锐角.B7、先化简，再求代数式⎪⎪⎭⎫ ⎝⎛--÷-a b ab a a b a 22的值， 其中O O =+=45cos 2130tan 3b a ，。

课题： 7.3特殊角的三角函数学习目标：1．能通过推理得30°、45°、60°角的三角函数值，进一步体会三角函数的意义；2．会计算含有30°、45°、60°角的三角函数值；3．能依照30°、45°、60°角的三角函数值，说出相应锐角的大小；4．经历探讨30°、45°、60°角的三角函数值的进程，进展学生推理能力和计算能力 学习重点：通过推理得30°、45°、60°的三角函数值，进一步体会三角函数的意义． 学习难点：特殊角的三角函数的运用．学习进程：一.【情境创设】如图，在Rt△ABC 中，∠C 为直角，如何表示∠A 的三种三角函数？ 二.【问题探讨】问题1：你能别离说出30°、45°、60°角的三角函数值吗？ （1）除能够用计算器计算，是不是能够通过手里的三角板来求值呢？ （2）是不是还有其他的方式呢？ 如图，在Rt △ACB 中，∠C ＝90°，∠A ＝30°．①请说出BC:AB:AC ＝( )；②假设设BC ＝1，那么AC ＝( ) AB ＝( )；③你能求出sin30°，cos30°，tan30°的函数值吗？ ④若∠A ＝45°，你能求出sin45°，cos45°，tan45°的函数值吗？⑤若∠A ＝60°，你能求出它的三角函数值吗？30° 45° 60° sin θcos θtan θ认真观看上面表格，你能发觉什么规律？如何快速经历？问题2：求以下各式的值。

（1）2sin30°-cos45° （2）sin60°·cos60°（3）sin 230°+cos 230°问题3：求知足以下条件的锐角α。