风力机翼型等速上仰动态失速数值模拟

翼型非定常来流下复合运动动态失速仿真谢凯;Laith K.Abbas;陈东阳;杨富锋;芮筱亭【摘要】针对直升机前飞时的动态失速问题,本文采用转捩修正的SST k-ω湍流模型和嵌套网格技术对雷诺数Re为3.92× 106时的直升机二维翼型SC1095进行数值仿真.以非定常来流条件下的纯俯仰运动为基础,对比分析了在耦合挥舞、摆振运动时,相位差、振幅对动态失速的影响;比较挥舞、摆振二者运动对于动态失速角的作用大小.结果表明:固定振幅条件下,挥舞和摆振运动相位差的增加会使动态失速角提前,升力系数峰值提高;固定相位角条件下,挥舞和摆振运动振幅的增加会使动态失速角延迟,升力系数峰值减小.挥舞运动对于非定常来流下俯仰运动翼型动态失速角的影响要大于摆振运动.本文计算方法和研究结果为翼型多自由度耦合运动下的动态失速行为预测提供参考.【期刊名称】《哈尔滨工程大学学报》【年(卷),期】2019(040)005【总页数】7页(P865-871)【关键词】直升机旋翼翼型;动态失速;计算流体力学;嵌套网格;俯仰运动;挥舞运动;摆振运动【作者】谢凯;Laith K.Abbas;陈东阳;杨富锋;芮筱亭【作者单位】南京理工大学发射动力学研究所,江苏南京210094;南京理工大学发射动力学研究所,江苏南京210094;南京理工大学发射动力学研究所,江苏南京210094;南京理工大学发射动力学研究所,江苏南京210094;南京理工大学发射动力学研究所,江苏南京210094【正文语种】中文【中图分类】V211.3动态失速是指翼型或机翼的非定常运动造成失速角明显超过其静态失速角的失速迟滞现象[1]。

虽然动态失速能够增大升力峰值，但同时也造成了阻力、俯仰力矩的突增和气动中心失稳[2]，严重限制了直升机安全飞行包线，对直升机飞行安全造成严重危害。

而对于前飞时的直升机，其旋翼所处的气动环境更加复杂，一方面桨叶会随方位角做周期性变距、挥舞、摆振的复合运动；另一方面由于旋转速度与前飞速度的叠加，桨叶周向来流速度会随方位角呈现出明显的非定常性[3]，这给直升机动态失速的预测增加了困难。

翼型动态失速的非定常模拟方法作者：于佳鑫陈江涛王晓东吴晓军康顺来源：《计算机辅助工程》2022年第01期摘要：为探究翼型动态失速的高可信非定常模拟方法，以FFA-W3-241翼型为研究对象，采用开源计算流体动力学求解器OpenFOAM开展翼型动态失速下的流动模拟。

研究重叠网格和滑移网格2种不同网格运动形式、2种不同时间步长、2种不同计算周期和OpenFOAM 默认湍流模型与修正的k-ω SST湍流模型对动态失速过程中翼型气动力的模拟精度，并对流场结构进行分析。

结果表明：修正模型预测的翼型气动力和流场特征与实验值更接近;重叠网格在翼型的动态失速模拟中更具优势。

关键词： OpenFOAM; 动态失速; 湍流模型; 风力机; 翼型; 重叠网格中图分类号： V211.41; TK83文献标志码： BUnsteady simulation method for airfoil dynamic stallYU Jiaxin CHEN Jiangtao WANG Xiaodong WU Xiaojun KANG Shun（1. Key Laboratory of Power Station Energy Transfer Conversion and System（Ministry of Education）， North ChinaElectric Power University， Beijing 102206， China;2. China Aerodynamics Research and Development Center， Mianyang 621000， Sichuan，China）Abstract： To explore the highly reliable unsteady simulation method of airfoil dynamic stall，the flow of airfoil under dynamic stall is simulated using the open source computational fluid dynamics（CFD） solver OpenFOAM taking the FFA-W3-241 airfoil as the research object. The accuracy of the aerodynamic simulation of airfoil during dynamic stall is studied under different conditions， that includes two different mesh motion forms（overlapping mesh and sliding mesh），two different time steps， two different calculation cycles， and OpenFOAM defaulted turbulence model and modified k-ω SST turbulence model. The flow field structure is analyzed. The results shows that the aerodynamic and flow field characteristics predicted by the modified turbulence model are closer to the experimental value. The overset mesh is more advantageous in the dynamic stall simulation of airfoil.Key words： OpenFOAM; dynamic stall; turbulence model; wind turbine; airfoil; overset mesh-基金項目：国家数值风洞工程项目（NNW2018-ZT7B14）;国家自然科学基金（51876063）作者简介：于佳鑫（1993—），女，辽宁建昌人，博士研究生，研究方向为CFD可信度分析和不确定性方法，（E-mail）****************通信作者：王晓东（1979—），男，北京人，教授，博导，研究方向为海上风电机组设计，（E-mail）****************.cn0引言翼型失速分为静态失速和动态失速。

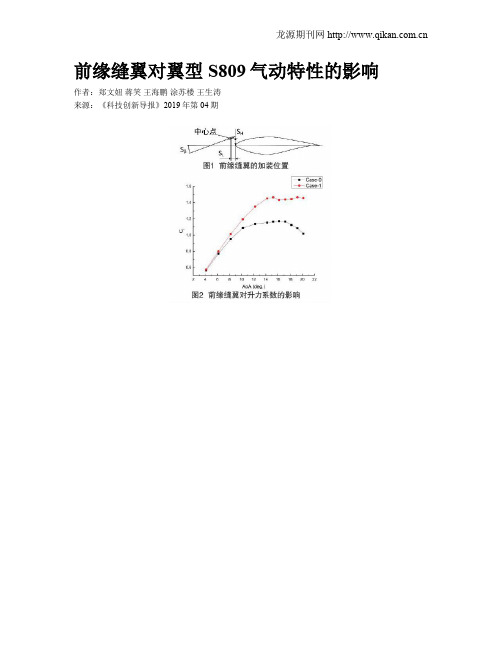
前缘缝翼对翼型S809气动特性的影响作者：郑文妞蒋笑王海鹏涂苏楼王生涛来源：《科技创新导报》2019年第04期摘 ; 要：控制风力机翼型的流动分离，可以提升翼型的气动特性。

本文采用数值模拟方法研究了前缘缝翼对风力机专用翼型S809气动特性的影响。

分析了加装前缘缝翼对翼型S809升、阻力系数和压力系数的影响，并揭示了对翼型S809边界层控制的机理。

研究结果表明，前缘缝翼可以有效地提升翼型的气动特性，增大升力系数，推迟翼型边界层的流动分离。

关键词：前缘缝翼 ;翼型S809 ;气动特性 ;流动分离中图分类号：TK83 ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;文献标识码：A ; ; ; ; ; ; ; ; ; ; ; ;文章编号：1674-098X（2019）02（a）-0017-03由于粘性摩擦力和逆压梯度的影响[1]，导致边界层存在着流动分离。

流动分离和动态失速会导致风力机叶片疲劳载荷增加，从而降低风力机的整体效率。

因此，通过控制边界层的流动分离和延缓动态失速是可以改善风力机的气动性能的。

边界层流动分离控制技术在许多领域也得到了广泛的研究。

同时边界层流动控制技术也是风能研究的热点问题。

边界层流动分离控制技术可分为被动控制技术和主动控制技术[2]。

这些技术主要是通过增强边界层流动的动能来抑制或延缓流动分离现象。

被动控制技术是指一种简单有效的不需要外加功率的方法。

例如，Gurney襟翼可以控制边界层的压力梯度[3];涡流发生器可以增加边界层的动能[4]。

前缘缝翼是一种边界层流动分离控制技术，可实现被动控制技术或主动控制技术。

Pechlivanoglou等[5]研究了一种固定辅助前缘翼型来控制风力机叶片根部流动分离。

Elhadidi等[6]设计了主动板条提高翼型升力系数，延缓了流动分离。

该活动板条由旋转叶片组成，可关闭、完全打开和间歇打开。

Yavuz等[7]采用数值方法和实验方法研究了板条翼型布置对风力机气动性能的影响。

风力机翼型的DDES模拟作者：张书峰来源：《世界家苑·学术》2017年第12期摘要：采用商业软件Fluent对NREL的风力机翼型S809进行了数值模拟，研究了不同网格密度下DDES湍流模型对该翼型气动性能预测精度的影响，并与试验结果进行了对比分析。

对DDES模型的网格密度进行了标定，第一层网格Y+>30时数值模拟精度较高。

通过对3种湍流模型（S-A、tsst和DDES模型）进行比较，得出DDES模型精度较高的结论，提出采用tsst湍流模型对DDES湍流模型的升力系数进行修正的方法，为风力机翼型的气动设计提供了更精确的检测手段，有较高的工程应用价值。

关键词：风力机；翼型；湍流模型；数值模拟；DDES1 研究对象选用NREL的风力机专用翼型S系列的S809为研究对象，试验数据来自在代尔夫特大学低风速风洞试验台进行的气动性能试验。

翼型弦长取1m，雷诺数取1×106。

通过改变风的来流方向改变攻角大小，攻角范围-3.09～17.23，共21个迎角状态。

2 数值方法2.1 湍流模型Spalart-Allamaras（S-A）模型是基于经验用量纲分析的方法得出的半经验公式，是对零方程补充发展得到的一方程物理模型，广泛用于航空翼型的空气绕流计算，是低雷诺数模型，不需要求解当地剪切层厚度的长度尺度，对逆压梯度适应性较好，对网格质量要求不高，计算所需时间最短。

Transition SST（tsst）四方程转捩模型基于k-ω SST模型，额外求解间歇因子输运方程和转捩动量厚度雷诺数输运方程，形成转捩模型加SST的结构。

LES（Large Eddy Simulation）大涡模型对大尺度涡进行直接计算，小尺度涡对大尺度涡的影响通过模型计算，但因计算量过大目前应用较少。

DES（Detached Eddy Simulation）脱离涡模型是RANS雷诺时均模型和LES的混合模型，它的获得，是用DES的长度尺度代替相应RANS湍流模型的长度尺度，DES的长度尺度由LES和RANS的长度尺度混合得到，即其中LES的长度尺度表达式为其中：为局部网格间距，是常数，Fluent中为默认值，通过标定获得，基于S-A模型时取0.65。

旋翼翼型非定常动态失速特性的CFD 模拟及参数分析赵国庆;招启军;王清【摘要】构建了一套基于运动嵌套网格技术和可压缩 RANS 方程的旋翼翼型非定常流动特性模拟的高效、高精度的 CFD 方法。

首先，发展了基于 Poisson 方程求解的围绕翼型的粘性贴体正交网格生成方法，并提出了基于最小距离法（MDM）改进策略的运动嵌套网格生成方法，克服了弹簧法可能导致网格畸变的不足；其次，为准确模拟由湍流分离和气流再附引起的气动力的迟滞效应，基于 RANS 方程、双时间方法和高阶插值格式，建立了旋翼翼型非定常气动特性分析的高精度数值方法，并采用能够较好捕捉气流分离现象的 S-A 湍流模型；再次，针对旋翼后行桨叶动态失速时桨叶剖面来流速度较低、迎角较大的特点，为解决低来流速度时 L-B 半经验模型在旋翼翼型非定常动态失速计算中的局限性，并克服可压缩方程对低速流场计算收敛困难和精度低的问题，建立了基于Pletcher-Chen 低速预处理方法、FAS 多重网格法和隐式 LU-SGS 方法相结合的高效数值方法。

应用发展的方法，分别针对NACA0012、SC1095旋翼翼型静态和轻度、深度动态失速进行计算，精确捕捉了气动力迟滞效应以及翼型前缘脱体涡的产生、对流和脱落过程，验证了本文方法的有效性；最后，着重针对 NACA0012动态失速状态，开展了振荡参数对旋翼翼型非定常动态失速特性影响的分析，研究结果表明翼型迎角平均值、振幅及减缩频率的变化均能引起迟滞效应的改变并使得气动力峰值发生有规律的前、后移现象等。

%A high-efficiency and high-precision CFD method for simulating the unsteady dynamic stall of rotor airfoil has been established based on moving-embedded grid and compressi-ble RANSequations.Firstly,the generation method of viscous and orthogonal body-fitted grid around the rotor airfoil is developed by solving Poissonequations.Meanwhile,aiming at overco-ming the shortcoming of spring simulation approach which may result in the distortion of grid,an improved Minimum Distance Method is proposed to generate the embedded grid around airfoil. Secondly,in order to simulate the hysteresis effect of aerodynamic forces caused by the turbu-lence separation and re-attachment of the flow,a high-precision method on the analysis of unsteady aerodynamic characteristics of rotor airfoil is developed by employing RANS equations and dual-time method.The S-A turbulence model is employed to capture the separation phenomenon of flow around airfoil.Thirdly,according to the conditions of low-speed inflow and high AOAs of the retreating blade,together with the limitation of L-B semi-empirical model on the calculation of unsteady dynamic stall of airfoil,a combination method of Pletcher-Chen preconditioning, FAS multigrid approaches and implicit LU-SGS scheme is established to overcome the problems of convergence difficulty and insufficient precision of compressible equations.The steady,mild and deep dynamic stall cases of NACA0012 and SC1095 rotor airfoils are calculated using this pre-viously mentioned method,the hysteresis effect and theformation,convection,shedding of the vortical disturbance are well captured,the effectiveness of numerical simulation method on dynamic stall is verified.Finally,focus on the deep stall of NACA0012 airfoil,the influence ana-lyses of parameters on the unsteady aerodynamic forces of rotor airfoil are carried out,and the results demonstrate that the exchanges of averaged AOA,amplitude and reduced frequency may cause avariational hysteresis effect and regularly changes of peak value of aerodynamic force.【期刊名称】《空气动力学学报》【年(卷),期】2015(000)001【总页数】10页(P72-81)【关键词】旋翼;翼型;动态失速;N-S 方程;运动嵌套网格;参数分析【作者】赵国庆;招启军;王清【作者单位】南京航空航天大学直升机旋翼动力学国家级重点实验室，江苏南京210016;南京航空航天大学直升机旋翼动力学国家级重点实验室，江苏南京210016;南京航空航天大学直升机旋翼动力学国家级重点实验室，江苏南京210016【正文语种】中文【中图分类】V211.52;V211.3旋翼工作在严重非对称、非定常的涡流场中，旋翼桨叶的挥舞、周期变距以及畸变尾迹(诱导)形成的非均匀入流，导致桨叶剖面在不同方位角处的迎角有很大差别。

哈尔滨理工大学毕业设计题目：垂直轴风机叶片翼型的空气动力分析院、系：建筑工程学院工程力学系姓名：王健指导教师：隗喜斌系主任：李东华2014年 6月 19日哈尔滨理工大学毕业设计题目：垂直轴风机叶片的空气动力分析院、系：建筑工程学院工程力学系姓名：王健指导教师：隗喜斌系主任：李东华2014年 6月 19日垂直轴风机叶片的空气动力分析摘要随着化石能源的过度消耗以及环境问题，风能越来越受到重视，各国都在努力开发风能资源。

近几年我国的风能发电事业有了很大的发展，但我国关于风力发电技术的研究仍远落后于先进国家，尤其是对叶片的研究。

本文所研究的是一个应用于H型三叶片垂直轴风力机上的叶片，采用理论分析和数值模拟相结合的方法，主要工作和成果如下:（1）回顾风力发电的研究背景，介绍以往垂直轴风力机的研究工作，并阐述了垂直轴风力机的空气动力学设计理论，给出了垂直轴风力机的流管理论模型，分析了垂直轴风力机的运行状态。

（2）应用动量-叶素理论中的双盘多流管模型计算分析了相同雷诺数情况下多种应用较广泛的翼型。

由此筛选出了较适合本文设计目标的翼型，并确定了用来进一步验证叶片性能的风轮结构的主要结构参数。

（3）利用Gambit软件建模、FLUENT软件进行流场分析，改变雷诺数、攻角和叶片翼型，通过对叶片升力、阻力、升阻比的变化趋势，得出NACA 0012，NACA 0018，NACA 2415，NACA 4415四种翼型中最适用于叶片制造的翼型。

关键词：垂直轴风机；叶片翼型；气动性能；数值模拟Aerodynamic Analysis Of Vertical AxisWind Turbine BladesAbstractWith excessive consumption of fossil energy and environmental issues, people are increasingly pay attention to the wind energy , some countries are trying to develop the wind energy resources. In recent years, China's wind power business has been greatly developed, but our research on wind power technology is still far behind the advanced countries, especially in the study of the blade. It is studied in this paper is applied to the blades of a H-type three-bladed vertical axis wind turbine on the theoretical analysis and numerical simulation methods, the main work and results are as follows:（1)Review of wind power research background, previous research work introduces a vertical axis wind turbine, and expounded the theory of aerodynamics design vertical axis wind turbine, given the current administration on the vertical axis wind turbine models, analyzes the vertical axis wind turbine operation.（2）It is applied is Momentum - Double blade element theory of multi-model analysis of the flow tube at the same Reynolds number airfoils wider variety of applications. Thus screened out more suited to this article airfoil design goals, and identified the mainstructural parameters used to further validate the performance of the wind turbine blade structure.（3) The use of Gambit software modeling, FLUENT software flow field analysis, changing the angle of attack vane airfoils and, through the blades, lift, drag, lift-drag ratio, torque and trends around the blade pressure, velocity summary was NACA 0012,NACA 0018,NACA 2415,NACA 4415 the airfoil blade airfoil is ideal for manufacturing.Key words：Vertical axis wind turbine；Blade airfoil；Aerodynamic performance；Numerical Simulation目录摘要 (I)Abstract (II)第1章绪论 (1)1.1论文研究的背景 (1)1.2垂直轴风机的介绍 (3)1.3文章中名词及缩写介绍 (6)1.4本文的研究意义和研究方法 (7)第2章垂直轴风机气动性能的理论研究 (9)2.1流管法 (9)2.2涡方法 (10)2.3动量一叶素理论 (13)2.3.1经典的动量一叶素理论 (13)2.3.2修正的动量一叶素理论 (16)2.4垂直轴风力机流管理论模型 (17)第3章数值模拟及分析结果 (21)3.1 NACA0015翼型建模 (21)3.2雷诺数对气动特性的影响 (23)3.3厚度对气动特性的影响 (25)3.4弯度对气动特性的影响 (28)3.5本章小结 (32)结论 (34)致谢 (35)参考文献 (36)附录A (38)附录B (43)第1章绪论1.1 论文研究的背景目前人类发展和生存面临的最紧迫的问题就是能源和环境问题。

周期激励下NACA 0012翼型单自由度失速颤振研究阮胤;邱展;王福新【摘要】为了深入理解以周期变距为激励的失速颤振特性,通过弹性机构输入周期变化角度,进而控制NACA 0012翼型攻角变化的实验装置,探究弹性约束下翼型攻角的变化规律以及有/无弹性约束时气动力对翼型做功的差异.实验结果表明:攻角的变化规律在不同驱动频率和扭转刚度下表现出4种特殊形态;翼型攻角的变化主频与驱动频率一致,并出现攻角的两周期振动,此时自然频率与驱动频率之比接近π/2.进一步分析气动力对翼型的能量传递,发现周期变距激励的失速颤振与无激励输入颤振有显著差异,分析表明气动力即使在一个周期内做负功,仍可能改变弹性结构的能量传递而使振动幅度增加.%The resultant behavior of airfoil incidence and the differences of work done by aerodynamic forces under/without torsional system are investigated,in order to better understand the characteristics of stall flutter with cyclic pitch input.The incidence of NACA 0012 airfoil was controlled by cyclic pitch input through a torsional elastic system.As results,there are four kinds of special forms of attack angle variation regularities under different driving frequencies and torsional rigidity.The main frequency complies with the driving frequency,while a period-2 oscillation is also observed,where the ratio of driving and natural frequency is approximately π/2.Further analysis considering the energy transfer of aerodynamic force on the airfoil shows that the mechanism of energy transfer of stall flutter with cyclic pitch differs from that inspired by perturbation,which means the elastic structure will be changed and theflutter amplitude can still be increased,even if negative work is done by aerodynamic forces.【期刊名称】《浙江大学学报（工学版）》【年(卷),期】2017(051)009【总页数】11页(P1870-1880)【关键词】直升机桨叶;失速颤振;气动弹性;动态失速;NACA0012翼型【作者】阮胤;邱展;王福新【作者单位】上海交通大学航空航天学院,上海 200240;上海交通大学航空航天学院,上海 200240;上海交通大学航空航天学院,上海 200240【正文语种】中文【中图分类】V211.47失速颤振是一种自激振动,是由于当桨叶经历动态失速时,气流分离产生的非线性气动力与惯性力、结构相互作用而产生,其运动形式通常表现为叶片的扭转振动和叶尖的挥舞振动[1-3].该现象不仅存在于直升机的旋翼上,也存在于大攻角下的固定翼以及风力机的叶片上,是引起旋翼叶片结构性破坏的因素之一.因此,为改善控制叶片的工作特性,并深入了解气动弹性耦合机理,失速颤振成为旋翼气动弹性响应研究的重点.对失速颤振的研究主要分为两类.1)判断颤振稳定性问题.如：最早由Fung[4]提出利用每振动周期的平均力矩系数判定Oates等[5-6]基于正弦振动推导出气的动阻尼表达式,Bowles等[7]利用俯仰力矩以及叶片角度的离散希尔伯特变化推导出具有时间分辨率的气动阻尼表达式,Bhat等[8]使用能量传递函数判别颤振是否持续,以上研究均为用于判定颤振极限环(limit cycle oscillation,LCO)稳定性的问题.2)颤振本身的振动特性,包括扰动引起的非强迫的振动特性以及外部激励引起的振动特性.其中扰动引起的振荡研究包括:O’Neil[9]利用实验和数值分析了结构的3次非线性对进入颤振的临界速度的影响,Amandolese[10]探究了平板随风速变化在俯仰、沉浮运动受到小扰动后的振动特性,Dimitriadis[2]实验探究了NACA 0012翼型随风速变化小扰动引起的颤振极限环特性以及分岔的机理,Shao[11]使用改进的B-L模型、结合Grigoris的实验探究了零度力矩系数为零的严格对称与该值非零的非严格对称翼型的极限环特点以及分岔机理.涉及外部激励引起的颤振振动特性研究如下.Price等[12]利用Gangwani气动力模型探究了NACA 0012翼型在正弦周期力作用下单自由度失速颤振关于周期力振幅以及来流速度的分岔特性和振动特性.Fragiskatos[13]利用Beddose-Leishman气动力模型将Gangwani的探究扩展到不同减缩频率k、平衡位置αm、周期力振幅以及来流速度等4个参数对振动特性的影响.Sarkar等[3]利用ONERA气动力模型探究了k、αm、Q0、U*对强迫振动的影响和αm、U*对自激振动的影响.Tang等[14]实验探究了竖直放置于风洞中的NACA 0012翼型的振动特性,实验中翼型下端受周期驱动,而上端无约束.Laxman等[15]为更准确模拟直升机旋翼所经历的振动环境,利用改进的ONERA模型探究了NACA 0012翼型以周期变距和周期风速为输入的单、双自由度颤振特性.为更好地设计、控制风力机和直升机旋翼并使之更高效地运作,近年来国外对于由扰动引起的失速颤振(自激振动)的机理研究方兴未艾.一方面是由于其所描述的是最基础的问题,涉及因素较少,能较准确地回答导致不同颤振特性差异的根本原因；另一方面是由于风力机的迅速发展,叶片多在大攻角状态下工作,小扰动即可使叶片进入失速状态,所涉及的问题即属于自激振动而直升机上旋翼所涉及的失速颤振包含但不仅限于上述扰动所引起的振动.当直升机前飞时,为使旋翼气动合力向某一特定方向偏转,通过控制自动倾斜器的倾角,桨叶根部攻角便会随方位角呈周期性变化,此时桨叶经历的失速颤振则属于强迫振动.这类强迫振动研究的简化建模的思路有2种：一是在动力学方程中加上一项正弦变化的周期力,二是认为结构之间相对形变产生的弹性作用为强迫振动的力.其中文献[3,12-13]的研究思路为第一种,其形式可追溯至Fung[4]所著的气动弹性基础：颤振翼型所受的除非线性气动力以外的其他力,包括重力、结构弹性力等,可近似为正弦变化的周期力.气动力模型是最简单的Theodorsen方程,适用于无分离、小角度的振动；而失速颤振过程伴随动态失速过程,振动幅度更大,因此Fung[4]所近似的正弦变化的周期力不再适用,更为接近真实前飞直升机上叶片失速颤振过程的模型是第二种,即强迫振动的力随颤振形式而变化,已知的是周期变化的距(桨叶根部的攻角).文献[14-15]的研究思路即为第二种,但是文献[14]的实验探究是将1个翼型放置于风洞中,结构的参数变化对上端颤振形式的影响无法得出；而文献[15]中的计算利用的是半经验模型,可信度还需要验证.同时文献[14-15]没有回答周期变距下的失速颤振形式都与什么因素有关.对失速颤振的实验探究多限于由扰动引起的振动,而鲜有涉及与直升机周期变距相关的问题.基于上述分析发现,虽然国外已开展了许多关于失速颤振的实验和数值研究,在扰动引起的振动方面取得了较大的进展,比如Dimitridias等[2]发现随风速增大颤振极限环由对称变为非对称的机理是“静态发散”.但是,关于以周期变距为激励的失速颤振研究较少,因此本文就此问题进行实验探究,一方面可以更深入地理解失速颤振现象,另一方面可以作为失速颤振数值模型的验证样本.本文主要研究在低速风洞中NACA 0012翼型受周期变距激励的单自由度(仅俯仰方向)失速颤振特性以及不同参数下振动特性的差别.实验在上海交通大学复杂流动实验室的风洞中进行,该回流式风洞可通过更换不同截面实验段,实现低马赫数到跨声速的要求；本实验采用的试验段采用低速标准,最大风速可达130 m/s.试验段截面的宽为1.2 m,高为0.9 m,长度超过2 m.如图1所示,试验装置由翼型模型、支撑系统、驱动系统、传感器和采集系统组成,其中U 为来流速度.翼型模型为3段矩形NACA 0012翼型,该翼型被广泛用于实验、数值研究.翼型模型翼展为0.9 m,弦长为0.3 m,竖直安放在风洞试验段内,上、下端面与风洞壁面的接触间隙微小,可以保证绕翼型的流场为准二维流动.上、下两段翼型在前缘后0.115 m处通过轴分别与自由端和扭弹簧相连,中间翼型与两端翼型以卡扣形式咬合,并用螺纹紧固,整个翼型可以绕其1/4弦线处的轴旋转(俯仰运动).驱动方式为电机通过曲柄连杆将圆周运动转化为俯仰方向角度的往复变化,虽然不是严格的正弦运动,但符合实际的机械环境.驱动轴与翼型下端通过弹簧机构连结在一起,在0～10°内弹性机构可以看作是线性扭弹簧,与线形弹簧之间的误差小于0.5%,弹性机构由于弹簧有效长度的限制,最大弹性变形不能超过8.5°.将弹性机构中弹簧换成刚性铁块则认为连接为刚性的.翼型的俯仰运动由自由端的传感器测量,所用传感器为360°磁通量角度传感器,输出电压与角度呈线性关系,可用范围大于270°,对角度感应灵敏,分辨率为12位,无最大转速的限制,刷新频率高达每秒5 000次,足以测量动态失速中快速变化的动态角度信息.翼型所受的力包括气动力和惯性力,由中间段翼型内嵌的三分量应变天平传感器测量,通过角速度信息可以得到动态气动力.传感器测量值由NI公司的采集卡采集,采集频率fs=4 000 Hz,远大于振动频率,符合采样定理；同时采集时间足够长以保证采集到的数据包含足够的振动信息.本文主要测量了在马赫数Ma=0.1,雷诺数Re=6.87×105的条件下,不同减缩频率k，不同扭转刚度弹簧约束和不同变距范围下翼型的攻角变化和受力情况,其中,式中：ω为驱动频率,c为翼型弦长,U为来流速度.如图2所示为定常情形下,相同马赫数、雷诺数下翼型的气动力系数与攻角的关系(C1为升力系数，无量纲，Cd为阻力系数，Cm为力矩系数).其气动力失速攻角约为11.76°,力矩失速攻角约为12.07°.Taylor实验的雷诺数Re=7.50×105,测得的气动力系数与本文实验系数基本重合,因此认为本文所用测量天平测得的数据有效.实验方案如表1所示,其中Kφ为扭转刚度(1/15Kφ～Kφ),ωn为弹性系统的自然频率,ζ为实验测得系统的阻尼比,θd为驱动角,振荡范围分别对应刚性连接时的无失速、浅失速和深失速(根据前缘涡大小,McCroskey[16]将动态失速现象归结为浅失速和深失速),若攻角运动幅度过大导致弹性结构超过前述限度,则认为所采集的信号无效.实验所用机构的动力学参数通过实验测出,即通过将采集到的衰减振动信号拟合理论公式得到.由于在强扭转刚度条件下阻尼较大,衰减曲线较短,对Kφ与1/5Kφ的弹性机构参数误差为10%～15%,而其他小扭转刚度的参数反映出的转动惯量均为1.34 kg·m2,误差小于5%,可用于验证气动弹性耦合响应的模型.2.1 弹性约束下的攻角变化如图5～8所示为实验所得攻角的时域曲线以及相曲线.其中深色曲线为滤波后的攻角值,浅色曲线为刚性连接时攻角的变化曲线或激励的周期变距曲线.攻角的滤波采用巴斯滤波方法,所有测得数值的滤波采用同一参数,最大程度地保证滤波后信号的真实度；角速度为攻角对时间的微分,数值算法参照文献[17]的方法.通过实际计算对比,采用拟合样条曲线后中心差分的方法得到角速度.实验装置的结构决定其无法达到理想的正弦曲线,但通过对比曲线差异可规避机械结构引入的因素.由于实验装置中驱动端的周期变距是通过曲柄连杆实现的,减速器等齿轮结构易造成驱动角度上的损失,例如5°+5°sin (ωt)的刚性连接最小角度不为0°,9°+7°sin (ωt)刚性连接时最小角度为4°等.实验通过对比刚性连接与弹性连接条件下攻角运动的差别，即可得到失速颤振中气弹响应的特点,并进一步理解周期变距激励下的失速颤振.失速颤振最主要的特点之一为“自激振荡”,表现为自我激励、自我维持在一个限度内[18],成一个极限环的振动；而在本实验有激励的情况下则表现出比激励变距更大的攻角范围,并保持在一定限度内,相平面也形成一个极限环.其中当激励周期变距为“无失速”的5°+5°时,翼型模型的攻角随着弹性的减弱而出现更大的幅度.因此需要探究当存在激励驱动翼型时,随着结构刚度的减小以及驱动频率的增加,增大的振动范围与极限环是否是弹性力本身的作用结果(如：共振)，与气动力无关.如图3所示为本实验装置的简化模型.由牛顿第二定律建立模型在俯仰方向上的动力学方程为式中：J为翼型关于1/4c的转动惯量；C为阻尼系数；驱动变距θ(t)=θ0+θampsin (ωdt),其中θ0、θamp、ωd分别为周期变距平衡位置、周期变距振幅以及激励圆频率；Maero为气动力；、分别为攻角α关于时间的一阶和二阶导数；、分别为驱动角度θ关于时间的一阶和二阶导数.不考虑气动力,并将式(1)标准化得式中：φ=α-θ,ωn=,ζ=C/(2).求解式(2)得故攻角运动形式为根据以上分析可得到如图4所示的共振曲线.这4种弹簧对应的共振曲线显示，在低频激励时,攻角的振动幅度将小于周期变距的幅度；在驱动频率仅为5～22rad/s的区域中,由于结构阻尼的作用,翼型攻角振幅集中在αamp/θamp<1的区域中,且随弹性系数的减小而减小.例如当k=0.075时,αamp/θamp的值为0.93～0.97,则3种驱动变距应当相差0.4°～0.7°,而图5～8中均存在翼型攻角大于刚性驱动的角度的情形.这说明振动幅度增大是气动力的作用.对于驱动的周期变距为无失速时,振动的幅度仍然有增大.以周期变距为激励的翼型在经历失速颤振时,攻角不仅表现出增大的现象,还主要表现出如下3种情况. 1) 在上仰阶段,攻角向上角速度较刚性偏小,但最大攻角与刚性相差无几,在时序图上主要表现出曲线上升变缓、相平面图上表现出最大“V”字形特性；2) 攻角稍微增大或与刚性相同,时序图上在最大攻角处出现多峰的现象,而在相平面上出现“额外的圆圈”； 3) 最大攻角较刚性明显偏小的情形,在时序图上表现为峰被“削平”的特性,在相平面图上显示为横向压扁的特点.与此现象密切相关的是动态失速现象,从20世纪70年代开始至今的诸多实验结果显示,是前缘涡生长、脱落引起表面压力振荡,气动力系数在翼型上仰超过定常的失速角后继续增加,而后随着前缘涡的脱落和运输,升力急剧下降且低头力矩陡增[19-20].如图6(b)所示为经历动态失速的俯仰振荡翼型典型的气动力系数[16],可知在相对于深失速,浅失速时力矩失速后产生的低头力矩小.同时如图10所示,随着减缩频率的增加,失速角和气动力系数也会不同,减缩频率越大即翼型的俯仰角速度越大,失速时低头力矩更大[19].这些动态失速的典型特点也是在弹性过程中攻角曲线展示出不同特性的原因.上述现象可认为是上仰阶段弹性力Fe与气动力Fa相互作用的结果.在情况1)下,|Fe /Fa|>1,翼型经过失速角时低头力矩使攻角角速度下降,但弹性的驱动力稍大,从而仅出现上升减缓的趋势,并在相平面图上显示出“V”字型,即角速度减小的过程,如图5(b)中I-2-1,图5(c)中I-3-1、I-3-2以及图6(b)中II-2-1所示.当气动力进一步增强,即|Fe/Fa|≈1时,翼型的角速度减小为0,但同时随着前缘涡的脱落与运输,翼型上方压力振荡、低头力矩减小,则将出现情况2)的多峰值的现象.在相平面图上,翼型攻角由于先减小后增大,故轨迹为圈型.造成这种现象的本质原因是在动态失速过程中前缘涡的脱落以及二次涡等生成过程中,低头力矩的振荡,即只有当前缘涡及时离开翼型上方时,才可能出现该现象,如图7(b)中III-2-1以及图8(b)IV-2-1所示.若前缘涡驻留时间过长,且|Fe/Fa|<1时,上述现象消失,而出现情况2),即最大攻角在时间序列上表现出曲线被削平的特点,如图6(c)中II-3-1/2,图7(c)中III-3-1/2,图8(c)IV-3-1/2所示,黑色与灰色曲线最大攻角相差2°～5°;而前文分析共振曲线时提到,仅弹性力、结构阻尼作用下的角度最多相差0.7°,因此该现象说明失速颤振中气动力不总是使最大攻角增加,亦可以使最大攻角减小.若考虑总的振幅,III-3中刚性连接最大与最小攻角差值为18°,而弹性作用下图7(c)III-3-1/2相同量的值分别为16.97°和15.83°,而图8(c)IV-3-1/2该差值分别为15.71°和16.46°,即振动幅度减小.若用气动阻尼的概念[1]来解释这种情况,则该情况在下一个周期展现出正阻尼,局部可能出现负阻尼.其他涉及失速过程时振幅增大的结果与上述描述的现象不太相同,仅当低头力矩在翼型上行出现时,才有上述3种情况,而当低头力矩的极大值在翼型上行末端或者下行才出现时,则上行过程中并无太大阻碍,并且在下行阶段气动力矩做正功为俯仰振荡输入能量,从而引起攻角振动幅度的增加.图10中，当k=0.05以及k=0.15时力矩系数表现出完全不同的特点,前者负阻尼仅存在于中间段,而后者负阻尼在几乎占了迟滞回线的一半,图6(b)中II-2-3/4、图7(b)中III-2-3/4、图7(c)中III-3-3、图8(b)中IV-2-3/4、图8(c)中IV-3-3振幅增大可能均源于此.图6(c)中III-2-3本应该属于这一类,相平面图显示上/下行时角速度明显增大,但可能由于阻尼的作用,气动力矩的作用被抵消掉,从而振动幅度并没有表现出增大.另一个相平面图上曲线特征倒“V”型是典型的翼型下行时涡脱落的表现,伴随出现的是短暂的抬头力矩.对于攻角变化的频率,所有时序图皆显示翼型攻角的变化频率变化不大,在无量纲化时间的时间内,翼型攻角也表现为5个主要周期,即主频与驱动频率一致.如图11所示为各激励变距、扭转刚度与驱动频率下攻角的频域特性与刚性运动频域特性的比较.由于选取数据的长度不同,数据在快速傅里叶变换时存在差异,各频率处的幅值为归一化后的值.其中主频与驱动频率一致,这与时序图中判断的一致.随着扭转刚度(自然频率)的下降,深、浅失速的频谱中整数倍主频相对主频的幅值发生了显著的变化,其中9°+7°的激励变距在k=0.025和0.050时,4倍和5倍主频的幅值显著上升,而2倍主频幅值下降到几乎消失,当k=0.075和0.100时,3倍主频幅值显著升高；5°+5°与15°+10°的激励变距与之类似,高频部分幅值上升.另外,在5°+5°激励变距作用下,Kφ减小为原来的1/15时,k=0.075时在整数倍主频fmain 之间出现了几个特殊的频率为即1.5倍主频；即2.5倍主频等.按照庞加莱映射的观点,若选取一个基频作为参考,其他频率的整数(N)倍与该基频的整数倍相等,则这个振动归为N周期振动[17].显然对于该频谱中的1.5fmain、2.5fmain、3.5fmain等,存在整数N=2满足上述条件,故归为两周期振动.如图8(a)中IV-1-3的时序图所示,攻角振幅出现一大一小周期呈现的特点,符合两周期振动的特点.由于气动力作用引起的两周期振动特性是所有实验中出现的显著特点.时序图显示攻角的最大值正好在失速角附近,因此可能出现间断脱涡的情形.文献[21]利用离散涡的方法计算流场中的涡结构变化周期在某些特定的减缩频率下呈两周期,在一定程度上佐证了气动力出现两周期正是间断脱涡的结果.若从频率角度理解这个系统,系统存在固有频率ωn、驱动频率ωd和气动力频率ωa,这三者决定了翼型运动的运动频率ωm,而同时该运动频率也决定了气动力频率,构成耦合系统为这三者的关系即决定了系统的运动特性.一般地,这些频率之间的某种关系可在一定程度上预测系统的振动特性.在图8(c)IV-1-3中,ωn/ωd=26.67/17=1.57≈π/2,目前还不确定该无理数对系统的影响,值得进一步探讨.2.2 弹性约束下的气动力与能量传递上文讨论了攻角的响应特性,探讨了形成各运动形式可能的原因,但要更深入了解动态失速对失速颤振所造成影响的根本原因,需探究各情形下气动力和能量传递的变化过程.由于动态情形下所测力需要修正,且实验所测数据较多,现象复杂,仅以图5(a)中的I-1-1/2/4,图5(c)中的I-3-1/2/4中气动力系数与能量传递系数为例解释前述观察到的现象,其余数据将在后续的报告中详细分析.如表2所示,弹性约束的引入,小角度驱动下气动力做负功减小,即阻尼向负阻尼方向变化.而大角度驱动(深失速)下则呈现相反的变化,即气动力所做负功增加,气动阻尼向正阻尼方向变化.基于刚性的气动力矩系数曲线,McCroskey认为深失速相比浅失速更为稳定[16],而本实验指出弹性作用下,深失速的驱动在气动力方面更稳定.这是因为深失速往往伴随着强前缘涡,而强前缘涡的脱落将造成巨大的低头力矩,由于弹性结构的存在,翼型所能达到的最大角度相对减少.但这仅适用于高强度扭弹簧,实验组IV-3-4出现的发散现象即是反例.但气动力具有稳定性,翼型的颤振并不一定也具有稳定性.以往研究均只关注气动力对翼型振动时的能量输入,但对于直升机这类具有周期变距激励的颤振问题,气动力即使做负功,振动幅度也可能增大,前面已论证能量传递可能会发生变化,驱动输入能量可能因为气动力作用而大幅增加.(1)随结构扭转刚度的减小,气动力/弹性力的变化导致攻角的运动规律出现4种主要特点：上升趋缓,相平面出现“V”字形；出现多峰值情形,相平面出现多圈曲线；攻角最大值被“削平”,相平面曲线横向压缩以及振动幅度大幅增加.(2)在以周期变距为激励的气动弹性系统中,驱动力频率、自然频率和气动力频率共同决定了运动的频率,而运动的频率又决定了气动力频率,构成耦合系统.随驱动频率增加以及自然频率的减少,运动主频仍为驱动频率；并出现两周期振动特性,此时自然频率与驱动频率的比约为π/2.(3)弹性约束下气动力系数与刚性运动呈现出较大差别,在弹性约束下与之对应的气动力对翼型的能量系数也显示出较大差异,其中小角度驱动下平均能量系数均呈增加趋势,即趋于气动不稳定；而大角度驱动下平均能量系数大部分呈减小趋势,即趋于气动稳定.(4)不同于由于扰动引起的失速颤振,周期变距激励下的失速颤振中气动力做功不再是确定振动能量增加/减少的唯一因素,气动力的作用会引起能量传递的变化,即翼型从气动力中获得的能量为负,也可能从激励中获得更高的能量而增大振幅,即在周期变距为激励的失速颤振中,气动力可以通过改变弹性机构能量传递来实现振动的加剧.实验中仍存在许多尚不清楚的问题,如：在扭转刚度进一步减小时,为什么当驱动角度为“浅失速”和“深失速”时翼型模型振动会大幅增加？是由于气动力做功还是小角度驱动的能量传递改变？这需要对实验数据继续分析并加以对比总结.另外,许多相平面上所观测的特点,仅通过文献对动态失速的总结得出,还需要进一步结合PIV实验进行验证；目前仍不清楚出现两周期振动的原因等.后续工作中将继续改进实验设备并开展流场显示的实验,一方面为失速颤振紧耦合模型提供验证算例,另一方面更深入地认识失速颤振.参考文献(References)：[1] CORKE T C, THOMAS F O. Dynamic stall in pitching airfoils: aerodynamic damping and compressibility effects [J]. Annual Review of Fluid Mechanics, 2015,47(1): 479-505．[2] DIMITRIADIS G, LI J. Bifurcation behavior of airfoil undergoing stall flutter oscillations in low-speed wind tunnel [J]. AIAA Journal, 2009, 47(11): 2577-2596．[3] SARKAR S, BIJL H, Nonlinear aeroelastic behavior of an oscillating airfoil during stall-induced vibration [J]. Journal of Fluids and Structures, 2008, 24(6):757-777．[4] FUNG Y C. An introduction to the theory ofaeroelasticity [M]. Chicago: Courier Corporation, 2012: 234-254．[5] OATES G C. Aircraft propulsion systems technology and design [M]. Ohio: AIAA, 1989．[6] ARCIDIACONO P J. Prediction of rotor instability of at high forward speeds. Volume I. Steady flight differential equations of motion for a flexible helicopter blade with chordwise mass unbalence [R]. Virginia: U.S.。

海上浮式风力机动力响应分析与数值仿真关键技术研究①曲晓奇,李红涛,唐广银,杜海越,杨林林(中国船级社海洋工程技术中心,天津 300457)摘要 随着海上浮式风电技术的发展,我国大功率漂浮式海上风力机组开始走向工程示范应用㊂由于风机厂商对上部风机结构参数保密,针对实际工程项目中的漂浮式风力机进行数值仿真分析具有诸多挑战和难度㊂本文以实际工程项目为例,研究漂浮式海上风力机在数值仿真过程中的关键技术㊂通过建立等效推力模型等手段,实现工程样机的数值建模并进行典型工况的动力响应分析㊂本文的研究成果可以有效解决实际工程项目中浮式风力机数值模型建立的难点,对促进我国风电产业技术发展,加速我国海上风电商业化进程具有重要意义㊂关键词 海上浮式风力机;数值仿真;等效推力模型;动力响应㊂中图分类号:P 752;T M 614 文献标志码:A 文章编号:20957297(2023)007207d o i :10.12087/oe e t .2095-7297.2023.02.12R e s e a r c h o n K e y T e c h n o l o g i e s o f D y n a m i c A n a l y s i s a n d N u m e r i c a l S i m u l a t i o n f o r t h e F l o a t i n g Of f s h o r e W i n d T u r b i n e Q U X i a o q i ,L I H o ng t a o ,T A N G G u a n g y i n ,D U H a i yu e ,Y A N G L i n l i n (O c e a n E n g i n e e r i n g T e c h n o l o g y C e n t e r ,C h i n a C l a s s i f i c a t i o n S o c i e t y ,T i a n ji n 300457,C h i n a )A b s t r a c t W i t h t h e d e v e l o p m e n t o f f l o a t i n g o f f s h o r e w i n d t u r b i n e t e c h n o l o g y ,t h e e n g i n e e r i n g p r o j e c t s o f l a r ge -s c a l ef l o a t i ng o f f sh o r e wi n d t u r b i n e h a s s t a r t e d .B e c a u s e t h e m a n u f a c t u r e r s k e e p th e p a r a m e t e r s o f t h e w i n d t u r b i n e c o n f i d e n t i a l ,t h e r e a r e m a n y c h a l l e n g e s i n t h e n u m e r i c a l s i m u l a t i o n a n a l y s i s o f f l o a t i n g of f s h o r e w i n d t u r b i n e s i n p r a c t i c a l e ng i n e e r i n g p r o j e c t s .I n thi s p a p e r ,t h e k e y t e c h n o l o g i e s o f n u m e r i c a l s i m u l a t i o n o f f l o a t i n g wi n d t u r b i n e i n t h e p r a c t i c a l e n g i n e e r i n g p r o j e c t w a s i n v e s t i g a t e d .T h r o u g h t h e e q u i v a l e n t t h r u s t m o d e l ,a n u m e r i c a l m o d e l o f r e a l f l o a t i n g w i n d t u r b i n e w a s e s t a b l i s h e d a n d t h e d y n a m i c s r e s p o n s e s u n d e r a t y p i c a l l o a d c a s e w a s a n a l yz e d .B a s e d o n t h e r e s e a r c h r e s u l t s o f t h i s s t u d y ,t h e d i f f i c u l t i e s i n e s t a b l i s h i n g t h e n u m e r i c a l m o d e l o f f l o a t i n g wi n d t u r b i n e i n p r a c t i c a l e n g i n e e r i n g p r o j e c t s c a n b e w e l l s o l v e d .I t i s o f g r e a t s i g n i f i c a n c e i n p r o m o t i n g t h e t e c h n i c a l d e v e l o pm e n t a n d a c c e l e r a t i n g t h e c o m m e r c i a l i s a t i o n o f C h i n a s f l o a t i n g w i n d t u r b i n e i n d u s t r y.K e y wo r d s f l o a t i n g o f f s h o r e w i n d t u r b i n e ;n u m e r i c a l s i m u l a t i o n ;e q u i v a l e n t t h r u s t m o d e l ;d y n a m i c r e s p o n s e 0 引 言欧洲的海上风电产业起步较早,随着浮式风力机技术趋于成熟,现已逐步在全世界范围内得到广泛研究和应用㊂我国浮式风力机的研究约起步于十年之前,相对较晚,尚未得到商业化应用㊂目前,常用的海上浮式风力机数值仿真软件大多由欧美国家的研究机构开发㊂表1列举了海上浮式风电领域常用的数值仿真软件及其所采用的分析理论㊂①作者简介:曲晓奇(1992 ),女,博士研究生,工程师,主要从事海上浮式风力机动力响应分析方面的研究㊂E -m a i l :x q qu @c c s .o r g.c n ㊂第10卷 第2期2023年6月海洋工程装备与技术O C E A N E N G I N E E R I N G E Q U I P M E N T A N D T E C H N O L O G YV o l .10,N o .2J u n .,2023第2期曲晓奇,等:海上浮式风力机动力响应分析与数值仿真关键技术研究㊃73 ㊃表1 各研究机构开发的海上浮式风力机耦合计算程序T a b .1 P r o g r a m s f o r f l o a t i n g o f f s h o r e w i n d t u r b i n e c o u p l e d c a l c u l a t i o n d e v e l o p e d b y va r i o u s r e s e a r c h i n s t i t u t i o n s 程序研究机构气动力模块水动力模块结构动力学模块系泊模块F A S T[1]N R E L(B E M 或G D W )+D S +D I T D M E 或T D P F +M DM o d a l /M B S/F E M G S M 或Q S M或F E M G H .B L A D E D [2]G HB E M+D S +D I T D M E 或T D P F +M DM o d a l /M B S G S M 或Q S M 或F E M A D A M S [3]M S C +N R E L +L U HB E M /G D W+D S T D M E 或T D P F +M DM B S Q S /U DS I M A [4]M A R I N T E K B E M+D S +D I T D M E 或T D P F +M DM B S /F E MG S M 或Q S M或F E MH A W C 2[5]R I S O D T U B E M+D S +D I T D M E 或T D P F +M D M B S /F E M G S M 或Q S M或F E MO r c a F l e x[6]O r c i n aC o u pl e d t o F A S T T D M E 或T D P F +M D C o u pl e d t o F A S T G S M 或Q S M 或F E MB E M :B l a d e E l e m e n t M o m e n t u m ,叶素动量理论D I :D yn a m i c I n f l o w ,动态入流C F D :C o m p u t a t i o n a l F l u i d D yn a m i c s ,计算流体动力学M B S :M u l t i b o d y S ys t e m ,多体系统G S M :G l o b a l S t i f f n e s s M o d e l,总体刚度模型T D :T i m e D o m a i n ,时域U D :U s e r D e f i n e d,用户自定义G D W :G e n e r a l i z e d D yn a m i c W a k e ,广义动态尾涡D S :D yn a m i c S t a l l ,动态失速F V M :F r e e V o r t e x M o d e l,自由尾涡模型F E M :F i n i t e E l e m e n t M e t h o d ,有限元方法Q S M :Q u a s i -s t a t i c M o d e l,准静态模型M E :M o r i s o n,方程M D :M o r i s o n D r a g,莫里森拖曳项P F :P o t e n t i a l F l o w ,势流理论 尽管目前针对浮式风力机数值仿真软件的开发已经相对成熟,但是,由于我国海上浮式风电工程项目还处于起步阶段,实际工程样机数量较少,对于实际风力机的数值仿真仍存在一定的问题㊂如何在实际工程项目中,建立浮式风力机的数值模型,使其可以准确反映工程样机的真实动力响应特性,仍然需要深入的研究㊂本文首先介绍了浮式风力机数值仿真的基本理论和方法;然后,结合某实际工程项目,详细描述了浮式风力机数值模型的建立过程以及涉及的关键技术;最后,基于本文建立的浮式风力机数值模型进行动力响应分析,验证本文建模方法的可靠性㊂1 浮式风力机数值模型建立方法目前,对于风力机气动载荷的计算大多采用叶素动量理论[7],尽管该方法无法给出叶片翼型附近的流场信息,但是,其计算简便效率高,广泛应用于浮式风力机工程计算㊂水动力载荷的分析则主要基于三维势流理论,采用海洋工程领域常用的水动力分析软件求解浮体水动力系数,进而进行时域水动力分析㊂由于三维势流理论无法考虑浮体的黏性效应,软件采用M o r i s o n 方程的拖曳项模拟浮式风力机的黏性阻尼㊂浮式风力机系统结构形式复杂,既包括了叶片㊁塔柱和传动轴等柔性构件,又包括了机舱和浮式基础等刚性结构㊂因此,不同数值仿真软件对于浮式风力机系统结构动力学模型的建立区别较大㊂目前,对于浮式风力机整体结构采用的建模方法主要有多体方法和有限元方法,对于叶片和塔柱等弹性体动力响应的求解则主要采用模态法和有限元方法㊂浮式风力机系泊系统的模拟则以准静态悬链线方法和有限元方法为主㊂其中,准静态方法基于悬链线方程求解系泊锚链张力,无法考虑锚链的动态效应㊂而有限元方法则可以考虑锚链自身动态效应的影响,精度相对更高㊂2 海上浮式风力机数值仿真模型的建立2.1 浮式风力机简介本文以某浮式风力机工程项目为例,针对海上浮式风力机工程样机在数值仿真过程中的关键技术进行研究㊂浮式风力机系统的结构形式如图1所示,整个系统上部设置7.25MW 风力发电机,底部采用四立柱半潜型浮式基础㊂系泊系统的布置情况如图2所示,在每个边立柱的底部设置3根系泊锚链,采用3ˑ3的悬链线式系泊㊂㊃74㊃海洋工程装备与技术第10卷图1 浮式风力机结构示意图F i g .1 F l o a t i n g of f s h o r e w i n d t u r b i n e s t r u c t u re 图2 浮式风力机系泊系统布置图F i g .2 F l o a t i n g o f f s h o r e w i n d t u r b i n e m o o r i n g s ys t e m a r r a n ge m e n t 2.2 风力机结构模型的建立本文采用美国可再生能源实验室开发的O pe n F A S T 软件,对浮式风力机系统进行数值仿真㊂该软件基于K a n e 方程建立风力机系统刚柔耦合动力学模型㊂对于叶片和塔柱等弹性结构,通过模态法求解其结构变形和动态响应㊂对于塔柱,基于模态叠加方法㊂任意时刻t ,塔柱上到塔底距离为x 的某一点的横向位移u (x ,t )可以表示为[8]u (x ,t )=ðna =1ϕa (x )q a (t )(1)其中,ϕa (x )代表模态a 的固有振型函数,它仅是x 的函数,与时间无关;q a (t )代表模态a 的广义坐标,与时间t 有关;n 代表选取的模态个数,即自由度数;每一个固有振型对应一个固有频率ωa 和相位ψa ㊂当已知塔柱的各阶固有振型函数时,还需要n 个参数来定义塔柱的变形情况㊂除了塔柱的固有振型函数外,还可以选择n 个其他函数φb 来表示塔柱的变形:u (x ,t )=ðn +p -1b =pφb (x )c b (t )(2)其中,φb (x )代表形函数;c b (t )是与之对应的广义坐标;参数p 按计算方便选取㊂根据R a y l e i gh -R i t z 法,塔柱的各阶固有振型函数ϕa (x )也可以表示成形函数φb (x )的线性组合:ϕa (x )=ðn +p -1b =pC a ,b φb (x )(3)其中,C a ,b 代表b 阶形函数对a 阶固有振型的比例常数㊂对于风力机塔柱,可以选择指数函数作为形函数,于是b 阶形函数表示为φb (x )=xRb(4)其中,R 表示塔柱的高度㊂由于风力机塔柱在底部固支,即塔柱底部位移和转角均为零,因此参数p 必须大于等于2,本文计算中取p =2㊂根据塔柱的相关设计参数,利用B M o d e s 软件基于广义H a m i l t o n 原理,求解塔柱前后和侧向前两阶模态,再拟合成幂指函数,输入O p e n F A S T 中㊂2.3 等效推力模型的建立由于缺少风力机叶片翼型参数的详细设计资料,以及控制系统的相关设计参数,因此,无法准确模拟风力机系统的气动性能㊂本文建立风力机的等效推力模型来计算风轮的气动载荷㊂图3所示为叶片上某一叶素位置处的速度和气动载荷示意图㊂根据叶素动量理论,叶片上某一叶素d r 处的推力和转矩可以表示为d T =B 12ρV 2t o t a l (C l c o s ϕ+C d s i n ϕ)c d r (5)d Q =B 12ρV 2t o t a l (C l s i n ϕ-C d c o s ϕ)c r d r (6)其中,d T 和d Q 分别表示叶素的推力和转矩;B 表示叶片数量;ρ表示空气密度;V t o t a l 表示入流速度;C l 和C d 分别表示升力系数和阻力系数;ϕ表示入流速度与叶素旋转平面的夹角;c 表示叶素的弦长㊂第2期曲晓奇,等:海上浮式风力机动力响应分析与数值仿真关键技术研究㊃75 ㊃(a)叶素速度图(a )L e a f v e g e t a t i o n v e l o c i t y ch a rt (b)叶素气动载荷图(b )L e a f e l e m e n t pn e u m a t i c l o a d c h a r t 图3 叶素翼型示意图[9]F i g.3 B l a d e e l e m e n t a i r f o i l [9]根据公式(5)和(6)叶片上某一叶素位置处的风轮推力主要与升力系数C l ㊁阻力系数C d ㊁来流与弦线的夹角ϕ以及叶片的弦长c 有关㊂以N R E L5MW 风力机叶片气动参数为基础,通过调整叶片的弦长和扭转角以及控制系统的相关参数改变风轮推力,直至与风机厂商提供的风轮推力相一致㊂采用上述方法建立风力机的等效推力模型,图4所图4 不同风速下风轮推力对比结果F i g .4 C o m pa r i s o n o f r o t o r t h r u s t f o r c e u n d e r d i f f e r e n t w i n d s pe e d 示是采用等效推力模型计算的不同风速下风轮推力与风机厂商提供的数据对比结果㊂相较于直接将风轮推力施加到塔柱顶部,采用这种方式的优点是可以考虑叶片旋转效应的影响㊂2.4 水动力模型的建立在A QW A 中建立浮式基础的水动力模型如图5所示㊂基于三维势流理论计算浮式基础的水动力系数,包括静水恢复力系数㊁附加质量和阻尼系数以及一阶和二阶波浪载荷传递函数,其中0ʎ入射方向下一阶波浪载荷传递函数的计算结果如图6所示㊂图5 浮式基础水动力模型F i g .5 H y d r o d y n a m i c m o d e l o f f l o a t i n g pl a t f o rm (a)纵荡方向一阶波浪载荷传递函数(a )F i r s t o r d e r w a v e l o a d t r a n s f e r f u n c t i o ni n t h e l o n gi t u d i n a l d i r e c t i o n (b)垂荡方向一阶波浪载荷传递函数(b )F i r s t o r d e r w a v e l o a d t r a n s f e r f u n c t i o ni n t h e p e n d u l u m d i r e c t i o n㊃76㊃海洋工程装备与技术第10卷(c)纵摇方向一阶波浪载荷传递函数(c)F i r s t o r d e r w a v e l o a d t r a n s f e r f u n c t i o ni n t h e l o n g i t u d i n a l r o c k i n g d i r e c t i o n图6波浪入射方向为0ʎ时的一阶波浪载荷传递函数F i g.6F i r s-o r d e r w a v e f o r c e t r a n s f e r f u n c t i o n i n t h e d i r e c t i o no f0d e g r e e按照公式(7)~(9)计算浮式基础受到的波浪载荷㊂由于势流理论无法考虑浮式基础的阻尼效应,因此在O p e n F A S T软件中建立M o r i s o n模型,通过M o r i s o n方程中的拖曳力模拟浮式基础的阻尼效应㊂F w a v e_1(t)=R eðM i=1ηi H1(ωi)=R eðM i=1a i e x p i(ωi t+φi)H1(ωi)(7) F w a v e_2s(t)=R eðM i=1ðM j=1ηiηj H2s(ωi,ωj)=R eðM i=1ðM j=1a i a j e x p[i((ωi+ωj)t+φi+φj)]H2s(ωi,ωj)(8)F w a v e_2d(t)=R eðM i=1ðM j=1ηiη*j H2d(ωi,ωj)=R eðM i=1ðM j=1a i a j e x p[i((ωi-ωj)t+φi-φj)]H2d(ωi,ωj)(9)其中,F w a v e_1(t)表示一阶波频载荷;F w a v e_2s(t)和F w a v e_2d(t)分别表示二阶和频㊁差频波浪载荷;ηi表示波面升高;a i㊁ωi和φi分别表示波幅㊁频率和相位;H1(ωi)表示一阶波浪载荷传递函数;H2s(ωi,ωj)和H2d(ωi,ωj)分别表示二阶和频与差频波浪载荷传递函数㊂2.5系泊系统分析模型的建立系泊系统的模拟采用集中质量模型,将锚链离散成多个质量点,不同质量点之间通过弹簧阻尼结构连接,如图7所示㊂某一质量点i的运动控制方程如下[10]:图7系泊锚链数值模型[10]F i g.7 N u m e r i c a l m o d e l o f m o o r i n g l i n e s[10] (m i+a i)r㊃㊃=T i+(1/2)-T i-(1/2)+C i+(1/2)-C i-(1/2)+W i+B i+D p i+D q i(10)其中,(m i+a i)r㊃㊃代表惯性项,m i和a i分别表示节点i的质量和附加质量;(T+C)i+(1/2)和(T+ C)i-(1/2)分别表示r i与r i+1以及r i与r i-1之间的内部刚度和阻尼;W i表示重力;B i表示浮力;D p i和D q i分别表示节点i受到的轴向和切向波浪力,采用M o r i s o n方程计算:D p i=12ρw C d n d l(r㊃i㊃q^i)q^i-r㊃(r㊃i㊃q^i)q^i-r㊃(11)D q i=12ρw C d tπd l(-r㊃i㊃q^i)q^i-(r㊃i㊃q^i)q^i(12)第2期曲晓奇,等:海上浮式风力机动力响应分析与数值仿真关键技术研究㊃77 ㊃在数值模拟过程中,由于系泊锚链结构形式复杂连接构件过多,对于连接构件无法直接进行模拟㊂将连接构件转化成等质量的杆单元,设置较小的时间步长,进行数值仿真,以保证计算的收敛性㊂图8所示是在不同浮体位移下计算的系泊张力,即浮式风力机系泊系统刚度曲线㊂图8 系泊系统刚度曲线F i g .8 M o o r i n g s ys t e m t e n s i o n 3 动力响应分析采用本文第2节介绍的相关理论和方法,建立海上浮式风力机数值仿真模型,计算极端停机工况下浮式风力机的运动响应㊂环境载荷方向的定义如图9所示㊂环境参数具体数值为:50年一遇风速60m /s ;有义波高12m ,谱峰周期14.4s,谱峰因子2.2;表面流速2.18m /s ㊂风浪方向均为0ʎ,表面流向为-180ʎ,模拟时间为3600s ㊂计算结果如图10所示㊂图9 环境载荷方向定义坐标系F i g .9 C o o r d i n a t e s ys t e m o f e n v i r o n m e n t a l l o a d s d i r e c t i o n d e f i n i t i on(a)纵荡(b)横荡(c)垂荡(d)横摇㊃78㊃海洋工程装备与技术第10卷(e)纵摇(f)艏摇图10 极端停机工况下浮式风力机运动响应F i g .10 D y n a m i c r e s p o n s e s o f t h e f l o a t i n g of f s h o r e w i n d t u r b i n e u n d e r e x t r e m e p a r k e d l o a d c o n d i t i o n从图10中可以看出,在50年一遇极端停机工况下,浮式基础具有较大的动态响应,这是由波浪载荷引起的㊂此时风机处于停机状态,叶片变桨,风轮受到的气动载荷相对较小,垂荡和纵摇的均值都处于一个较小的值㊂从计算结果来看,在极端停机工况下,浮式风力机的摇摆角度在10ʎ范围内,符合设计要求,具有足够的安全性4 结 论本文主要介绍了在实际工程项目中建立海上浮式风力机数值仿真模型的关键技术,包括结构模型㊁等效推力模型㊁水动力模型以及系泊系统模型的相关理论和方法㊂本文提出的数值模型建立方法,可以有效解决风力机叶片翼型参数缺失带来的建模问题㊂最后,通过模拟50年一遇极端工况下浮式风力机的动态响应,验证本文建模方法的可靠性㊂参考文献[1]J o n k m a n J M ,B u h l J R M L .F A S T U s e r s G u i d e [R ].G o l d e n ,C O :N a t i o n a l R e n e w a b l e E n e r g y L a b o r a t o r y,2005.[2]D N V G L .B l a d e d [E B /O L ].h t t p s ://w w w .d n v g l .c o m /s e r v i c e s /b l a d e d -3775.[3]E l l i o t A .S .,W r i gh t A .D .A D A M S /W T U s e r s G u i d e [E B /O L ].h t t p ://w i n d .n r e l .g o v /d e s i gn c o d e s /s i m u l a t o r s /a d a m s w t /d o c s _v 2.0/i n d e x .h t m l .L a s t m o d i f i e d D e c e m b e r,1998;a c c e s s e d J u n e 13,2003.[4]F y l l i n gI ,L a r s e n C ,S ød a h l N ,e t a l .R i f l e x U s e r s M a n u a l 3.6[R ].M A R I N T E K ,T r o n d h e i m ,N o r w a y,2008.[5]L a r s e n T J ,H a n s e n A M.H o w 2H A W C 2,t h e U s e r sM a n u a l [R ].R i s øN a t i o n a l L a b o r a t o r y,2007.[6]O R C I N A .O r c a F l e x [E B /O L ].h t t p://w w w .o r c i n a .c o m /.[7]H a n s e n s M O .A e r o d y n a m i c s o f W i n d T u r b i n e s [M ].E n g l a n d :R o u t l e d g e ,2015.[8]J o n k m a n J M.M o d e l i n g of t h e U A E W i n d T u r b i n e f o r R e f i n e m e n t o f F A S T _A D [R ].C o l o r a d o :N a t i o n a l R e n e w a b l eE n e r g y L a b o r a t o r y,2003.[9]M o r i a r t y P J ,H a n s e n A C .A e r o D y n T h e o r y M a n u a l [R ].C o l o r a d o :N a t i o n a l R e n e w a b l e E n e r g y L a b ,2005.[10]M a t t h e w H.,A n d r e w G .V a l i d a t i o n o f a L u m pe d -M a s s M o o r i n g L i n e M o d e l w i t h D e e pC w i n d S e m i s u b m e r s i b l e M o d e l T e s tD a t a [J ].O c e a nE n g i n e e r i n g,2015,104:590603.。

动态失速初步介绍，传统的静态失速认为，当翼型来流迎角增大到某一定值时，在翼型表面会出现大规模流动分离而导致升力突然下降和阻力的突然增加[1]。

，p在20世纪40年代，Himmelskamp首次在实验中发现了动态失速现象的存在[2]。

但由于当时人们对航空器的机动性要求不高而且分析手段有限，所以并未对这一现象进行深入研究。

翼型运动方式不同对其升力的影响[3]直到60年代一次直升机旋翼实验后才引起普遍关注，关于动态失速特性的研究也随之展开。

[]Ham[4]最早给出了关于动态失速发展过程的理论描述。

70年代后，McCroskey[5]等对动态失速现象进入年代后M C k[5]作了许多实验研究，使得人们对动态失速的发生机理有了更进一步的认识。

有进的识[],1988年Carr L W在他的文章[6]中指出动态失速的基本特征是流畅中存在复杂的非定常分离和大尺度涡旋结构，气动力表现出明显的非线性迟滞特性。

年Ekaterinaris[7]等对过去人们研究翼型动1998Ek t i i[7]态失速所采用的数值方法和研究成果进行了比较全面的总结，表面翼型俯仰运动的折合频率、振全的总结表型俯仰动的折合频率振幅角、平衡迎角、转轴位置和来流马赫数等因素都对失速涡的强度、发展和脱落有着直接影响，同时翼型的几何形状极大的影响动态失速特性同时翼型的几何形状也极大的影响动态失速特性一次振荡过程边界层发生逆流前缘发生流动分离，产生涡流涡沿着弦向流动，产生额外升力涡脱离翼型，进入深度失速下俯直到边界层再次依附，，综上，与传统的静态升力不同，动态失速现象是个非常复杂的非线性问题。

如果想得到精确的解则必须求解NS方程，而解NS方程方面所需计方程一方面所需计算时间比较久，另一方面由于是强烈的分离流动，选择合适的湍流模型也很困难。

所以现在工程选择合适的湍流模型也很困难所以现在工程上一般使用经验或者半经验的动态失速模型来预测升力曲线。

测升力曲线湍流模型的影响几种不同的湍流模型算出的动态失速升力曲线。

风力机叶片翼型气动系数获取方法的研究郭改琴【摘要】针对风力机叶片翼型在-180°~180°之间的气动数据准确性和完备性不高且难以获取的问题,提出采用Xfoil6.99和Profili2.21两个专业软件分别获得小迎角下风力机叶片翼型气动系数,然后求和求平均值得到了新的翼型气动数据,再通过AirfoilPrep-v2p2程序将气动数据扩展到迎角在-180°~180°范围内.通过数据分析得到了升力系数、阻力系数和力矩系数的变化规律,这为翼型的优化设计提供了重要的理论支持.【期刊名称】《杨凌职业技术学院学报》【年(卷),期】2018(017)003【总页数】4页(P50-52,66)【关键词】翼型;气动系数;迎角【作者】郭改琴【作者单位】杨凌职业技术学院,陕西杨凌712100【正文语种】中文【中图分类】TM315风力机叶片的设计过程中，叶片展向翼型的空气动力学特性是气动性能设计的基础，但翼型气动数据的获取却是叶片设计中最难的部分，翼型气动数据的准确性和完备性对叶片的设计十分重要。

所以怎么样获得翼型在-180°～180°之间的气动数据是研究的关键内容。

风力机叶片和普通飞机机翼不同，迎角范围广(-180°～+180°)，雷诺数的范围宽(一百万至一千万)。

目前国内许多厂商只能提供-10°至15°之间的翼型气动特性，获取大迎角下的气动特性非常必要，获取的初步数值进行优化也必不可少。

本文采用Xfoil6.99和Profili2.21两个软件获得小迎角下的气动系数，将对应迎角下的计算值相加再取平均值，然后通过AirfoilPrep-v2p2程序将气动数据扩展到迎角为-180°～180°范围内。

1 Xfoil 6.99获取升阻力系数Xfoil6.99.zip软件是由美国学者Drela博士研究的用来计算翼型气动性能的程序。

风力机叶轮设计与叶片空气动力学仿真分析一、概述作用在叶轮上的空气动力是风力机最主要的动力来源，也是造成各个零部件的主要的载荷来源。

要计算风力发电机组的载荷就必须先计算出空气作用在叶片上的作用力。

除了气动载荷，风力机叶片在风机工作中受到的作用力主要还受到惯性力，特别应该考虑重力、离心力和陀螺力等。

风力机的叶片设计分气动设计和结构设计两大部分，气动性能计算为气动设计结果提供评价和反馈，并为叶片的结构设计提供气动载荷等原始数据。

气动性能计算的准确性，直接影响叶片的气动性能和结构安全，从而影响风力机的运行效率和运行安全。

二、风力机叶片几何参数1．风力机叶片翼型几何参数和气流角翼型是组成风力机叶片的基本元素，因此，翼型的气动特性对风力机的性能起着决定性的作用。

以一个静止的翼型为例，其受到气流作用，风速为v，方向与翼型截面平行。

图1 翼型的几何参数和气流角翼型的尖尾(点B)称为后缘。

圆头上的A点称为前缘，距离后缘最远。

l——翼型的弦长，是两端点A、B连线方向上翼型的最大长度；C——翼型最大厚度，即弦长法线方向之翼型最大厚度；C——翼型相对厚度，CCl=，通常为10%~15%；翼型中线—从前缘点开始，与上、下表面相切诸圆之圆心的连线，一般为曲线；f——翼型中线最大弯度；f——翼型相对弯度，ffl =；α——攻角，是来流速度方向与弦线间的夹角；φo——零升力角，它是弦线与零升力线间的夹角；φ——升力角，来流速度方向与零升力线间的夹角。

α=φ+φ0 （2‐1）此处φ0是负值，α和φ是正值。

2．.NACA四位数字翼型族NACA四位数字翼型分为对称翼型和有弯度翼型两种。

对称翼型即为基本厚度翼型，有弯度翼型由中弧线与基本厚度翼型迭加而成。

中弧线为两段抛物线，在中弧线最高点二者水平相切。

四位数字翼型的表达形式为NACAXXXX第一个数字表示最大相对弯度的百倍数值;第二个数字表示最大弯度相对位置的十倍数值;最后两个数字表示最大相对厚度t的百倍数值。

风力机翼型挥舞摆振非定常气动特性分析吕坤;谢永慧;张荻【摘要】参考实际运行状态下的风力机翼型,应用动网格并采用k-ωSST湍流模型对NREL S809翼型在Re=1×106情况下的翼型振荡进行了数值模拟,同时分析了挥舞、摆振及二者耦合振动对风力机翼型气动性能的影响.结果表明:相同振幅和频率下,翼型挥舞比摆振引起的气动力波动大得多；翼型未达到失速时,翼型吸力面的流动分离可以使翼型获得额外的升力；挥舞的振幅或频率较大时,翼型会发生失速,且来流攻角越大,挥舞使得翼型更易发生失速；在挥舞-摆振耦合引起的翼型气动力变化中,挥舞起主导作用.%The moving mesh and the k-w SST model were adopted to simulate the aerodynamic performance of the NREL S809 airfoil at the Reynolds number of 1X106. The effects of flapwise, edgewise and combined flap/lead-lag oscillations on the aerodynamic performance of the airfoil were analyzed- The results show that the aerodynamic fluctuation caused by flapwise oscillation is much larger than that caused by edgewise oscillation with the same amplitude and frequency. The lift is greater due to flow separation on the suction surface of the airfoil when the airfoil is not in stall status. Larger amplitude and higher frequency of the oscillation will lead to dynamic stall of the airfoil, and the dynamic stall of the airfoil occurs more easily with the increase in the attack angle. In addition, flapwise oscillation plays a dominant role in the aerodynamic fluctuation caused by combined flap/lead-lag oscillation.【期刊名称】《西安交通大学学报》【年(卷),期】2011(045)009【总页数】8页(P47-53,100)【关键词】挥舞;摆振;风力机翼;湍流模型;数值模拟【作者】吕坤;谢永慧;张荻【作者单位】西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安【正文语种】中文【中图分类】TK83在气动力、惯性力和弹性力的耦合作用下,风力机叶片旋转时容易发生振动,通常振动有3种形式:①挥舞,即叶片在垂直于旋转平面上的弯曲振动;②摆振,即叶片在旋转平面内的弯曲振动;③扭转,即绕叶片变距轴的扭转振动[1].这3种形式的振动在一起还会引发耦合,由此产生气动弹性不稳定.风力机叶片的振动及气弹耦合对风力机的气动性能及安全性有重要影响,所以深入研究翼型振荡状态下的气动特性,对改进翼型设计、提高风力机的气动效率和安全性具有重要的意义.许多学者对翼型振动的气动性能进行了深入研究,如:Ekaterinaris等[2]采用 Baldw in-Barth湍流模型对NACA 0012翼型的俯仰、平振及耦合运动下的动态失速性能进行了计算,指出振动状态下翼型的气动性能有别于静止状态;Walker等[3]对翼型等速上仰问题进行了大量的实验研究,指出当攻角大于静态失速攻角时,动态失速涡的存在对翼型上表面的速度和压力分布有重大影响,随着翼型上仰速度的增加,动态失速涡附着在翼型上的时间更长,由此可以显著增加翼型大攻角条件下的时均气动力;Ramsay等[4]通过风洞实验系统地研究了不同的雷诺数、平均迎角、迎角振幅和减缩频率下NREL S809翼型俯仰振荡的动态失速性能,分析了各因素对动态失速性能的影响;Guerri等[5-6]应用计算流体动力学方法深入研究了风力机叶型的流固耦合效应,得到了翼型的不同振型和气动力变化,同时着重研究了叶型的挥舞-扭转耦合振动.但是,迄今为止的大多研究是针对翼型俯仰振荡运动的动态失速进行的,而针对翼型挥舞、摆振及二者耦合振动时的气动性能却不多见.本文应用动网格技术,采用k-ω SST湍流模型,在实验[3]和Re=l×l06下对二维NREL S809翼型振荡进行了数值模拟.1 数值模型1.1 数值方法求解雷诺平均N-S方程利用商业软件CFX,计算模型采用k-ωSST湍流模型[5,7-8],瞬态项离散采用二阶迎风后插隐式时间步方法,空间离散采用二阶迎风格式.k-ωSST湍流模型[9]的计算方程如下湍流黏性系数湍动能方程湍流频率方程式中 :F1和 F2是混合函数;β、γ、σk、σω为模型参数.k-ωSST湍流模型利用函数F1将 k-ε和k-ω方程结合起来,然后利用函数F2来改进涡团黏性系数μt在壁面逆压流动区域的结果,充分发挥k-ε模型处理自由流、k-ω模型处理壁面约束流动的特长,同时还借鉴了 Johnson-King模型[10]不平衡作用的思想,以增强对复杂流的适应性.1.2 计算模型风力机翼选用S809翼型[4](主要应用于两叶片NREL PhaseⅥ风力机),额定功率为19.8 kW,叶片展长为5.03m.参照实际建立了风力机模型,如图1所示,图中:V为来流风入口的相对速度;α为攻角;β1为桨距角;F为作用在桨叶上的气动合力.F可以分解为F x、F y,Fx与来流风向垂直,称为驱动力,使桨叶旋转做功,Fy与来流风向平行,称为轴向推力,通过塔架作用在地面上.摆振沿x轴方向进行,挥舞沿y轴方向进行. 图1 风力机翼型受力模型参考文献[7]中的风力机模型,其叶片产生的最大功率区域在0.75倍展长附近,该区域桨距角β1=0°,因此取β1=0°建立计算域.计算网格用C 型结构化网格,翼型表面分布了300个节点,翼型前缘和尾缘网格采用加密处理,总网格数为12万.计算域及翼型周围网格如图 2所示,图中翼型弦长c=600 mm,计算域外边界距离翼型边界面至少为15倍弦长.计算域分内、外2个区,内区是直径为2倍于翼型弦长的圆,通过动网格来控制内区网格的移动可模拟翼型振动.图2 翼型计算区域及其周围网格分布图为了验证计算模型的正确性,对不同来流攻角下翼型的升力、阻力系数进行了计算,结果如图3所示.由图3可见,来流攻角在0°～18°内 ,计算与实验的阻力系数基本吻合.来流攻角小于10°,计算获得的升力系数与实验的偏差很小;来流攻角大于10°,计算获得的升力系数与实验之间出现了偏差,但在工程上该偏差是可以容忍的.所以,来流攻角在6°～12°之间时,可以采用本文模型进行数值分析.图3 不同来流攻角下翼型升力、阻力系数为了便于研究翼型振荡对风力机输出功率的影响,在参考文献[8]中定义式中:Cx为驱动力系数;Cy为轴向推力系数.2 数值模拟及分析2.1 翼型挥舞翼型挥舞在y方向上的位移[5-6]为式中:A为翼型挥舞的振幅;f为振动频率;φ为相位差,φ=0.直径为45 m左右的叶轮,其自激振动频率在1～3 Hz之间,且随着叶片展长的减小,自激振动频率增加[11-12].该叶轮的叶片振型以一阶挥舞和一阶摆振为主,在极限挥舞载荷作用下通过叶片有限元模型计算和实验得到的叶尖挠度可以达到8m以上.文献[13]在Re=1×105、缩减频率 k=0.8、无量纲挥舞振幅h=A/c=0.4～0.7下数值模拟了NACA 0012翼型的气动性能.参考文献[5-6,13-14]、结合实际风力机振动情况确定A=0.05～0.5 m,f=1～3 Hz,其中 3 Hz对应于最大的k=0.44.每个振动周期的时间步长数n对计算精度有显著影响.图4为 A=0.3m 、f=3 H z、α=10°时,n分别取15、30、60的 Cx计算结果.图4 不同n下的Cx计算结果由图4可见:n取30、60时,对应二者的驱动力系数曲线几乎完全重合;n取15时,对应曲线与前二者有明显区别.n不同时,对应驱动力系数峰值间存在最大误差.经分析知:n=15时,Cx峰值偏差ΔCx=6.9%;n=60 时,ΔCx=2.3%,该值与 n=30时相差无几,所以计算时本文的n=30.图5为 f=3 H z、α=10°且在不同挥舞振幅下Cx、Cy随时间的变化,该结果与文献[6,14]相似.图 5 f=3 Hz、α=10°且在不同挥舞振幅下Cx、Cy随时间的变化由图5可见,Cx和Cy随着翼型的振动产生了周期性的变化.结合翼型的运动规律可以发现:当翼型在平衡位置沿y轴正向运动时,Cx和Cy达到最小值;当翼型在平衡位置沿y轴负向运动时,Cx和Cy达到最大值.翼型振动时,对应来流速度的大小和方向均发生了变化:翼型沿 y轴正向运动时,对应来流速度和攻角最小,翼型产生的升力最小,Cx和Cy达到最小值;翼型沿y轴负向运动时,翼型仍未失速,其产生的结果恰好与正向运动时相反,所以Cx和Cy均达到最大值.翼型的挥舞不仅导致来流速度和攻角发生变化,还会引发流动分离和旋涡.图6为 A=0.2 m、f=3 H z、α=10°且翼型在平衡位置沿y轴正向和负向运动时的流场.当翼型沿y轴正向运动时,对应来流攻角较小,翼型表面不会发生流动分离.当翼型从最大位移处沿y轴负向运动时,对应来流攻角逐渐增大,翼型表面逐渐出现流动分离;当翼型负向运动至平衡位置时,对应来流攻角达到最大值,流动分离更为严重;当翼型继续负向运动时,对应来流攻角逐渐减小,流动分离现象逐渐减弱,直至消失.1.17 s时,对应来流的速度和攻角达到最大值,流动分离最为严重,这2种因素均有可能导致Cx 和Cy达到最大值.考虑翼型振动前后Cx和Cy的变化如图7所示.图6 翼型在平衡位置沿y轴正向和负向运动时的流场正向运动负向运动图7 考虑翼型振动前后Cx和Cy的变化曲线1、2对应于翼型静止状态;曲线3、4分别对应A=0.2m、f=3 Hz、α=10°的曲线由图7可以发现:翼型沿y轴负向运动时,正常振动状态下的Cx和Cy均大于仅考虑来流速度及攻角的情况,振动下的Cx和Cy表现出增大的特性;翼型负向运动至平衡位置时,压力面附近气流压力增大,其大于吸力面,由此产生压力梯度,此时气流绕过翼型尾缘由压力面流向吸力面,并带动下游流体回流,使得边界层内的流体质点离开壁面挤向主流,从而加剧了边界层分离.下游回流的流体受到主流的冲击折返向下游流动,并在分离点的下游产生剪切涡和尾流区,造成能量损失,促使吸力面产生低压区,因而翼型获得额外的升力,使得Cx和Cy增大.所以,来流速度和攻角增大和翼型振动引起的流动分离都会加剧Cx和Cy增大.以上研究中挥舞振幅比较小,翼型未达到失速.当挥舞振幅较大时,叶片会发生失速颤振.研究发现 ,在 f=3 Hz、α=10°下 ,当 A 大于或等于 0.4m时,翼型失速.图8为 A=0.5 m时不同频率下Cx的变化规律.图8 A=0.5m时不同频率下Cx的变化由图8可见,在f=3 H z下,A=0.5 m与A=0.05～0.3 m时 Cx情况有很大区别,其中:A=0.05～0.3 m时驱动力一直为正值;A=0.5 m且翼型沿y轴负向运动至平衡位置附近时,驱动力会急剧降至负值,Cx甚至达到-0.4.由图8还可见:在相同的挥舞振幅下,振动频率越大,翼型受到的气动力波动越剧烈,当频率达到一定程度时,翼型失速;随着振动频率的增加,翼型沿y轴负向运动且在相同位移处的速度增大,来流速度和攻角随之增大,流动分离和旋涡产生的可能性就越大.频率增大到了一定程度时,流动分离会导致翼型失速,如图8中f=3 H z的情况.图9为翼型在一个振动周期内的流场演化.在1～1.17 s之间,翼型从最大位移处沿y轴负向振动,但仅在翼型吸力面尾缘附近发生了流动分离.1.17 s时,翼型在平衡位置达到最大速度,此时来流速度和攻角最大,翼型前缘附近流动在逆压梯度的作用下开始发生流动分离,并在1.18 s时形成前缘分离涡.前缘分离涡在向后扩展的运动中,翼型升力迅速增加,从而导致Cx迅速增加,这与文献[15]的实验结论吻合,说明前缘涡和翼型表面剪切涡的存在,有助于在翼型上表面产生低压区,进而获得额外的升力. 图9 不同时刻的流场演化情况前缘涡继续向后运动,在1.23 s时翼型尾缘上部诱导出反向旋转的二次涡结构,翼型进入失速状态.尽管此时前缘涡和剪切涡进一步增强,但后缘出现的反向旋转的后缘涡抵消了一部分前缘涡和剪切涡,从而造成升力迅速下降,阻力迅速增加,Cx迅速降低,甚至达到 Cx=-0.4的情况.在 1.27 s时后缘涡脱离翼面向后运动,翼型脱离失速区.此后,翼型继续沿y轴负向振动,对应的来流速度和攻角逐渐减小,翼型重新摆脱了失速状态.2.2 翼型摆振翼型摆振沿 x方向的振荡形式[6,16]为式中:B为翼型摆振振幅;φ为相位差,φ=0.叶片振型是以一阶挥舞和一阶摆振为主的,尽管不同振型时参振的惯性矩不同,但一般情况下,机翼的一阶挥舞和一阶摆振的固有频率比较接近.图10 为且在不同摆振振幅下Cx、Cy随时间的变化.对比图10和图5发现,在相同的振幅和频率下,翼型摆振比挥舞引起的气动力波动小得多.摆振时,翼型沿x轴方向振动,远处来流在 x轴方向的速度分量比y轴的大得多,所以摆振引起的来流速度和来流攻角的变化比挥舞小得多,同时摆振引起的流动分离也远不及挥舞的严重,因此在相同的振幅和频率下,翼型摆振比挥舞引起的气动力波动要小得多.图11为时挥舞和摆振下Cx随X、Y变化的曲线.由图10 不同摆振振幅下Cx、Cy随时间变化的曲线图11 不同频率下 Cx随X、Y变化的曲线图11可以看出,相同振幅和频率下,翼型摆振比挥舞引起的气动力波动要小得多.2.3 翼型挥舞-摆振耦合振动挥舞-摆振不稳定性是风力机单个叶片在挥舞与摆振耦合下产生的.研究表明:当风力机叶片在载荷作用下或者挥舞和摆振频率接近时,挥舞-摆振不稳定性显现出来.本文将挥舞和摆振的频率均设为2 Hz,在参考文献[5-6,17]的基础上,得到耦合振动下叶型受力的运动方程下面研究A分别为 0.05、0.1、0.2、0.3 m 时的情况.图12为耦合振动时不同挥舞振幅下Cx、Cy随时间变化的曲线.图12 耦合振动时不同挥舞振幅下 Cx、Cy随时间变化的曲线(B=0.2m)对比图12和图5发现,耦合振动时翼型受到的气动力的规律与挥舞时很相似,即Cx 和Cy均随着翼型的振动产生周期性的变化.另外还发现,在相同的挥舞振幅下,耦合振动时气动力波动比挥舞时略小,这与采用的耦合振动方程有关.由于2种振型的相位差为π,所以翼型在以最大速度沿y轴负向振动的同时,又以最大速度沿 x轴正向振动,此刻受翼型沿x轴方向运动的影响,对应的来流速度和攻角有所减小.为了研究耦合振动时摆振对翼型气动力的影响,本文取 A=0.2 m,B 分别为 0.05、0.10、0.20、0.30 m,攻角α=10°.图13为耦合振动时不同摆振振幅下Cx、Cy随时间变化的曲线.图 13 耦合振动时不同摆振振幅下Cx、Cy随时间变化的曲线(A=0.2m)由图13可见,B 分别为0.05、0.10、0.20、0.30 m时,对应的Cx变化曲线几乎完全重合.对比图13与图12发现,在耦合振动中,摆振对翼型气动力的影响比挥舞小得多,这个结果与非耦合振动下的结果是一致的.由此可以推断,在耦合振动引起的翼型气动力变化中,挥舞起主导作用.来流攻角的变化对风力机翼型气动性能的影响很大.采用耦合振型研究不同来流攻角对翼型气动性能的影响时,取A=0.2 m,B=0.2 m,攻角α分别为6°、8°、10°、12°.图 14 为不同来流攻角下 Cx、Cy随时间变化的曲线.由图14可见,来流攻角对翼型气动性能的影响很显著.相同振型下,同一时刻来流攻角越大,Cx和Cy越大.这是因为,翼型未失速,对应来流攻角越大,翼型的升力越大.同时还发现,相同振型下,来流攻角越大,Cx的波动越大,而Cy的波动越小.来流攻角在逐渐增大直至接近失速攻角的过程中(见图3),翼型升力的增加逐渐减缓,因而攻角较大时翼型振动引起的升力变化较小.轴向推力主要是翼型升力沿y轴的正向分力,因此Cy的波动较小.但是,由 f=3 Hz时的情况(见图8)知,来流攻角在逐渐增大直至接近失速攻角的过程中,翼型驱动力仍可以快速增大,因而Cx的波动较大.图14 不同来流攻角下Cx、Cy随时间变化的曲线对不同来流攻角的翼型挥舞失速颤振研究发现:在 f=3 H z下,当α=8°、A ≥0.5 m 时 ,翼型接近失速;当α=10°、A=0.4 m 时,翼型会失速;当α=12°、A=0.33 m 时,翼型失速.当来流攻角接近于翼型失速攻角区域时,较小的挥舞振幅会使翼型进入失速状态,这说明来流攻角越大,挥舞更易导致翼型失速.3 结论本文参考实际状态下的风力机模型,应用动网格技术,采用 k-ωSST湍流模型,对NREL S809翼型在Re=1×106时的翼型振动进行了数值模拟,分析了挥舞、摆振及二者耦合振动对风力机翼型气动性能的影响,由此得出如下结论.(1)翼型在挥舞和摆振中,Cx和Cy产生周期性的变化.与摆振相比,挥舞更易引起气动力的大幅波动.(2)翼型在未失速时,其吸力面的流动分离可以使翼型获得额外的升力,翼型振动引起的流动分离会促进Cx和Cy增大.(3)当挥舞的振幅、频率较大时,翼型会发生失速.挥舞时 ,f=3 Hz、α=10°、A≥0.4 m,或者 A=0.4 m 、α=10°、f ≥3 Hz,翼型会达到失速 .来流攻角越大,挥舞更易导致翼型失速.(4)在耦合振动引起的翼型气动力变化中,挥舞起主导作用,摆振是次要的.参考文献:[1] 李本立,宋宪耕,贺德馨,等.风力机结构动力学[M].北京:北京航空航天大学出版社,1999:4-5.[2] EKATERINARIS JA,SORENSEN N N.Numerical investigation of airfoil dynam ic stall in simultaneous harmonic oscillatory and translatory motion[J].Journal of So lar Energy Engineering,1998,120(1):75-83.[3] WALKER JM,HELIN H E,STRICKLAND J H.An experimental investigation of an airfoil undergoing large-amp litude pitching motions[J].A IAA Journal,1985,23(8):1141-1142.[4] RAMSAY R R,HOFFMAN M J.Effects of grid roughness and pitch oscillations on the S809 airfoil,NREL/TP-442-7817[R].W ashingtonDC,USA:National Renewab le Energy Lab.,1995:1-166.[5] GUERRIO,HAMDOUNI A,SAKOUT A.Fluid structure interaction of wind turbineairfoils[J].Wind Engineering,2008,32(6):539-557.[6] GUERRIO,HAMDOUNI A,SAKOUT A.Numerical simu lation of the flow around oscillating w ind turbine airfoils:part 2 free vibrating airfoil[J].Multi-Science Publishing,2008,2(4):387-405.[7] G IGUERE P,SELIG M S.Design of a tapered and twisted blade for the NREL combined experiment rotor,NREL/SR-500-26173[R].Washington DC,USA:National Renew able Energy Lab.,1999:1-32.[8] MARTIN.Aerodynamics of wind turbines[M].London,UK:James and James Ltd.:Science Pub lishers,2008:7-13.[9] MENTER F R.Zonal tw o equation k-ωturbulence models for aero dynam ic flows,A IAA 93-2906[R].Reston,VA,USA:A IAA,1993.[10]JOHNSON D,KING L.A mathematically simp le turbu lence closure mode l for attached and separated turbulence boundary layers[J].AIAA Journal,1985,23(11):1684-1692.[11]周梅,朱志坚,乔印虎,等.风力发电机振动保护仪的研制[J].机械研究与应用,2006,19(3):103-104.ZHOU M ei,ZHU Zhijian,QIAO Yinhu,et al.Research for wind turbineo f vibration guard module[J].M echanicalResearch&Application,2006,19(3):103-104.［6］商炳章，白清源.基于特征项权重改进的关联文本分类［J］.计算机研究与发展，2008，45（S0）：252-256.SHANG Bingzhang，BAIQingyuan.Improved association text classification based on feature weight ［J］.Journal of Computer Research and Development，2008，45（S0）：252-256.［7］蔡金凤，白清源.挖掘重要项集的关联文本分类［J］.南京大学学报，2011，47（5）：544-550.CAI Jinfeng，BAI Qingyuan.Association text classification of mining ItemSet significance ［J］.Journal of Nanjing University，2011，47（5）：544-550.［8］ BARALIS E，GARZA P.I-prune：item selection for associative classification ［J］.International Journal of Intelligent Systems，2012，27（3）：279-299.［9］ YANG Yiming，PEDERSON J O.A comparative study on feature selection in text categorization［C］∥Proceedings of the 14th International Conference on Machine Learning.San Francisco，CA，USA：Morgan Kaufmann，1997：412-420.［10］AGRAWAL R，SRIKANT R.Fast algorithms for mining association rules［C］∥Proceedings of the 20th VLDB Conference.San Francisco，CA，USA：Morgan Kaufmann，1994：487-499.［11］HAN Jiawei，PEI Jian，YIN Yiwen，et al.Mining frequent patterns without candidate generation：a frequent-pattern tree approach［J］.Data Mining and Knowledge Discovery，2004，8（1）：53-87. ［12］SEBASTIANI F.Machine learning in automated text categorization ［J］.ACM Computing Surveys，2002，34（1）：1-47.。

旋翼翼型动态失速模型参数识别及应用柳泉;胡国才;雷卫东【摘要】On the basis of the characteristics of Leishman-Beddoes (L-B) dynamic stall model, the method of parameters identification was put forward in order to expand the application range of L-B dynamic stall model and adapt to dynamic stall analysis of specific airfoil. The dynamic stall lift and drag were calculated with the parameters identified from the stat⁃ic stall lift and drag curves of SC-1095, the results agreed well with the experimental value.%为了拓展Leishman-Beddoes（L-B）动态失速模型的应用范围，以适应特定翼型的动态失速分析，在详细分析L-B动态失速模型特点的基础上，提出一种模型参数的识别方法。

以SC-1095翼型为例，采用其静态升阻特性数据，对L-B动态失速模型中的参数进行了识别，并据此对该翼型的动态失速升阻特性进行了数值计算，计算结果与试验值吻合良好。

【期刊名称】《海军航空工程学院学报》【年(卷),期】2015(000)002【总页数】5页(P129-133)【关键词】旋翼;翼型;动态失速;参数识别【作者】柳泉;胡国才;雷卫东【作者单位】海军航空工程学院飞行器工程系，山东烟台264001;海军航空工程学院飞行器工程系，山东烟台264001;海军航空工程学院飞行器工程系，山东烟台264001【正文语种】中文【中图分类】V212.4动态失速是指在直升机旋翼旋转过程中，旋翼剖面翼型迎角呈现非定常变化，当迎角超过临界值时，翼型升力系数并不与静态失速模型描述的一样直接发生失速，而是产生失速延迟的现象。

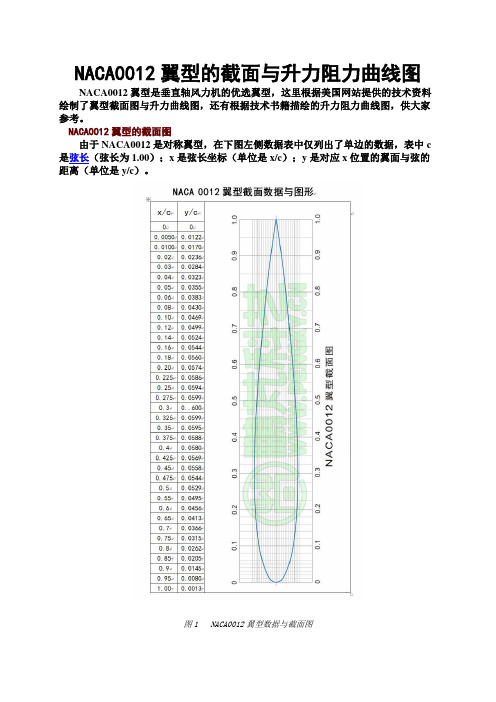
NACA0012翼型的截面与升力阻力曲线图NACA0012翼型是垂直轴风力机的优选翼型，这里根据美国网站提供的技术资料绘制了翼型截面图与升力曲线图，还有根据技术书籍描绘的升力阻力曲线图，供大家参考。

NACA0012翼型的截面图由于NACA0012是对称翼型，在下图左侧数据表中仅列出了单边的数据，表中c 是弦长（弦长为1.00）；x是弦长坐标（单位是x/c）；y是对应x位置的翼面与弦的距离（单位是y/c）。

图1 NACA0012翼型数据与截面图NACA0012翼型的升力曲线图图2是根据美国的技术资料数据绘制的NACA0012翼型的升力曲线图，在这张图中有多根升力曲线，显示了当雷诺数不同时翼型的最大升力系数与失速攻角都有较大的变化。

图2 NACA0012翼型升力系数曲线图NACA0012翼型的大攻角升力、阻力曲线图图3是根据“21世纪能源与动力工程类创新型应用人才培养规划教材“风力机空气动力学”” 一书图7.29描绘的NACA0012翼型的大攻角升力、阻力曲线图，供大家参考。

图3 NACA0012翼型全攻角升力、阻力曲线图该图显示了翼型攻角从-5度到180度的升力与阻力系数的变化，攻角在0度至10度升力系数随攻角增大而增大，阻力系数很小；超过12度时升力系数下降，阻力系数上升；攻角到40度后升力与阻力系数先是相同，然后阻力系数继续上升，升力系数下降。

NACA0012翼型的升/阻比变化曲线在图4中显示了翼型的升力与阻力随攻角的变化曲线，在实际应用中更关心的是在正常工作时的阻力情况，图4是根据“风能技术”（美Tony Burton，武鑫译）一书图3.100描绘，图中显示了NACA0012翼型在不同攻角时的升力/阻力系数比变化曲线。

图4 NACA0012翼型升/阻比变化曲线可见在失速前有最大的升力/阻力系数比值，升力约为阻力的50多倍。

当然这是一个光滑的翼型在较高雷诺数时的状态，多数情况会比该比值低一些。