张盛杰--轴对称——最短路径问题

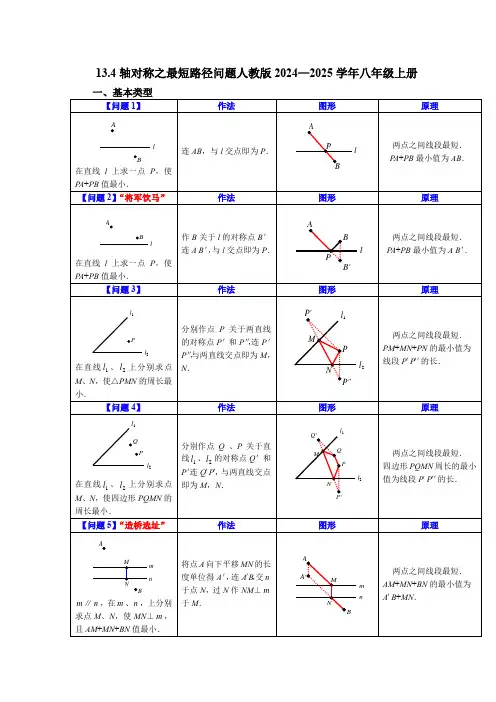
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

龙源期刊网 运用“轴对称”解决最短路径问题作者：刘军来源：《初中生世界·八年级》2014年第10期在学习“轴对称图形”时，我们经常会遇到与最短路径有关的问题，同学们往往在处理这类问题时感到困难. 这类问题通常会转化成“两点之间，线段最短”来解决，而轴对称的性质是实现这一转化的有效方法之一. 只要我们能把握轴对称的性质，那么问题便迎刃而解.在苏科版八（上）“轴对称图形”一章的课后习题中就有这样一个问题：如图1，点A、B在直线l同侧，点B′是点B关于l的对称点，AB′交l于点P. （1）AB′与AP+PB相等吗？为什么？（2）在l上再取一点Q，并连接AQ和QB，比较AQ+QB与AP+PB的大小，并说明理由.【解析】（1）由点B与点B′关于直线l成轴对称可知PB=PB′，则AB′=AP+PB′=AP+PB. （2）利用“三角形任意两边之和大于第三边”及（1）的结论可知，AQ+QB>AB′=AP+PB.这个问题还可以进一步说明直线l上的点P能使得线段PA+PB的和最小.下面再通过对几个最短路径问题的分析，帮助同学们熟悉并掌握这类问题的解题策略，真正能做到融会贯通，一通百通.一、已知两点在一条直线的同一侧例1 （将军饮马）古希腊一位将军要从A地出发到河边（如下图MN）去饮马，然后再回到驻地B. 问怎样选择饮马地点P，才能使路程最短？【点拨】分别作点A、B关于OM、ON的对称点A1、B1，连接A1B1，分别交OM、ON于点C、D，即得点C、D就是所求的两点.利用“轴对称”解决最短路径问题的关键是根据轴对称的性质，将不在一条直线的线段转化到同一条直线上，然后用“两点之间，线段最短”来解决. 解决这类问题，还需要认真审题，不仅要注意图形，而且要重视问题的要求，才能够有效地解决此类问题.（作者单位：江苏省无锡市天一实验学校）。

轴对称解决实际问题（最短路程问题）（1）利用轴对称解决几何极值问题仅仅是轴对称应用的一个方面，比较典型的是平面镜成像、光的反射等问题也经常用到轴对称。

（2）解决实际问题的关键是把这个实际问题抽象或转化为一个数学模型，然后通过对这个数学模型的研究来解决这个实际问题。

（3）在证明最大、最小这类问题时，常常采用任意另选一个，通过与要求证的那个“最大”或“最小”的量进行比较来证明。

问题1（分析1）如何用数学的方法解决这个问题？把这条河抽象为一条直线，而把将军的出发地（山脚）和宿营地分别看作直线同侧的两个点，建立几何模型，（如图①）把实际问题转换成“在已知直线上找一点，使它到直线同侧的两点的距离之和最小”的数学问题。

（分析2）连结AB ，作AB 的垂直平分线交直线a 于P 点，根据线段的垂直平分线的性质定理有PA ＝PB ，此时PA ＋PB 是否最短？（如图②） (用几何画板的度量及计算功能否定这种作法)(分析3)作A 点关于直线a 的对称点A ′连结P A ′,由轴对称的性质知PA ＝PA ′,那么PA ＋PB ＝PA ′＋PB ，P 点在何处PA ′＋PB 最短？（如图③）由一名学生上讲台拖动P 点，显然当B 、P 、A ′三点共线时PA ′＋PB 最短。

探索得出作法：（如图④）（1）作A 点关于直线a 的对称点A ′. （2）连结BA ′，交直线a 于P 点. P 点即为所求。

如何证明？ (分析4)在直线a 上另取一点P ′，连结PA 、A P ′、B P ′、 P ′A ′，（如图⑤）要证PA ＋PB 最小，由任意性， 只要证 ：PA ＋PB ＜A P ′＋B P ′， 由对称性可知：PA ＝PA ′, P ′A ＝P ′A ′只要证：PA ′＋PB ＜P ′A ′＋B P ′只要证： A ′B ＜P ′A ′＋B P ′而△BA ′P ′中，有三角形两边之和大于第三边，问题得证。

a · · B A 图① a · · B A 图② P a · · B A 图③ A ′ · · P a · · B A 图④ A ′ · P a · ·B A 图⑤A ′ · P P ′问题2、如图，已知牧马营地在P 处，牧童每天要赶着马群先到河边饮水，再到草地吃草，然后回到营地，试设计出最短的放牧路线。

轴对称及最短路径问题一、知识讲解1．轴对称、轴对称图形（1）轴对称图形：如果一个图形沿某条直线对折，对折的两部分是完全重合的，那么就称这样的图形为轴对称图形，这条直线称为对称轴。

对称轴一定为直线。

（2）轴对称：把一个图形沿着某一条直线翻折过去，如果它能与另一个图形重合，那么称这两个图形成轴对称。

两个图形中的对应点（即两个图形重合时互相重合的点）叫对称点。

2．轴对称图像的性质（1）对应线段相等，对应角相等；对称点的连线被对称轴垂直平分。

轴对称图形变换的特征是不改变图形的形状和大小，只改变图形的位置。

新旧图像具有对称性。

（2）轴对称的两个图形，它们对应线段或延长线相交，交点在对称轴上。

3．等腰三角形（1）性质：①两底角相等。

②顶角的角平分线、底边上的中线、底边上的高互相重合。

（2）判定：①有两条边相等的三角形是等腰三角形（定义）；②有两个角相等的三角形是等腰三角形。

4．等边三角形（1）性质：①等边三角形各边都相等；②等边三角形各角都相等，并且都等于60°。

（2）判定：①三条边都相等的三角形是等边三角形。

②三个角都相等的三角形是等边三角形。

③有一个角是60°的等腰三角形是等边三角形。

5．特殊直角三角形（补充）（1）含30°的直角三角形中，30°角所对的边等于斜边一半，且三边长度比为1：2；（2）等腰直角三角形各边长比为1：1。

二、要点补充轴对称是关于某一直线对称的图形，要注意图形中隐藏的条件，要将分散的条件集中起来达到解题的目的。

本讲的学习要特别注意分类讨论思想及转化思想的运用。

要点1在平面直角坐标系中，若已知A、B两点的坐标（或位置）要求第三个点C，使得A、B、C三点构成等腰三角形的方法如下：①连接AB，以点A（或点B）为圆心，线段AB的长度为半径作圆，圆周上除点B（或点A）的所有的点，都可以与点A、点B构成等腰三角形。

②连接AB，作线段AB的垂直平分线l，该垂直平分线l上除该线与线段AB交点外的所有的点都能与点A、点B构成等腰三角形。

轴对称--最短路径问题
解题思路：（1）作两点任意一点的对称点
（2）将对称点与另一点进行连线，连线与原直线的交点为动点的位置
（3）对称点与另一点连线的线段长度是所求线段之和的最小值（依据是“两点间线段最短”和“垂直平分线上的点到线段两端点的距离相等”）
一、两点在直线同侧模型
例题1..如图，A为马棚，B为帐篷，牧马人某一天要从马棚牵出马，到河边给马喝水，然后回到帐篷请你帮助他确定这一天的最短路线。

变式1.（2008•深圳）要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短？小聪根据实际情况，以街道旁为x轴，建立了如图所示的平面直角坐标系，测得A点的坐标为（0，3），B点的坐标为（6，5），则从A、B两点到奶站距离之和的最小值是．
变式2..如图，在正方形ABCD中，AD=8，DM=2，N是AC上一动点，求DN+MN的最小值
变式3.如图，MN是⊙O的直径，MN=2，点A在⊙O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为．
变式4.（2009•陕西）如图，在锐角△ABC中，AB=4，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是．。

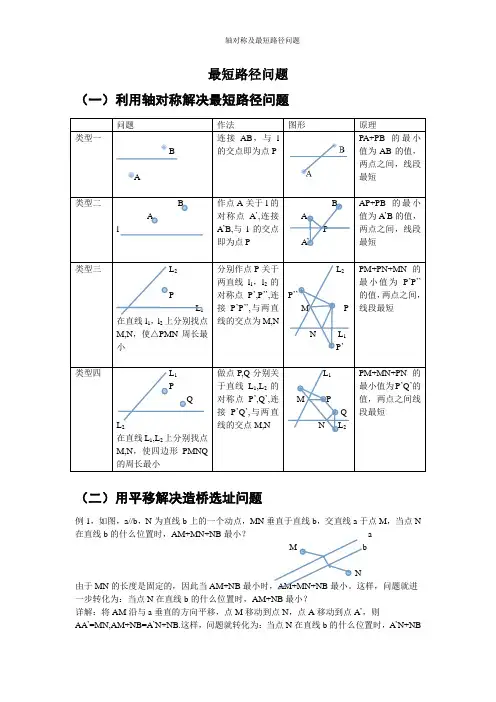
最短路径问题（一）利用轴对称解决最短路径问题问题作法图形原理类型一BA 连接AB，与l的交点即为点PPA+PB的最小值为AB的值，两点之间，线段最短类型二 BAl 作点A关于l的对称点A’,连接A’B,与l的交点即为点PBAPA’AP+PB的最小值为A’B的值，两点之间，线段最短类型三L2PL1在直线l1，l2上分别找点M,N，使△PMN周长最小分别作点P关于两直线l1，l2的对称点P’,P’’,连接P’P’’,与两直线的交点为M,NL2P’’M PN L1P’PM+PN+MN的最小值为P’P’’的值，两点之间，线段最短类型四L1PQL2在直线L1,L2上分别找点M,N，使四边形PMNQ的周长最小做点P,Q分别关于直线L1,L2的对称点P’,Q’,连接P’Q’,与两直线的交点M,NL1M PQN L2PM+MN+PN的最小值为P’Q’的值，两点之间线段最短（二）用平移解决造桥选址问题例1，如图，a//b，N为直线b上的一个动点，MN垂直于直线b，交直线a于点M，当点N 在直线b的什么位置时，AM+MN+NB最小？ aMN由于MN的长度是固定的，因此当AM+NB最小时，AM+MN+NB最小。

这样，问题就进一步转化为：当点N在直线b的什么位置时，AM+NB最小？详解：将AM沿与a垂直的方向平移，点M移动到点N，点A移动到点A’，则AA’=MN,AM+NB=A’N+NB.这样，问题就转化为：当点N在直线b的什么位置时，A’N+NB最小？如图，在连接A’,B两点的线中，线段A’B最短。

因此，线段A’B最短。

因此，线段A’B 与直线b的交点N的位置即为所求，即在点N处造桥MN，所得路径AMNB是最短的。

L2A MA’ BN例2，在P、Q两村之间有两条河，且每条河的宽度相同，从P村到Q村，要经过两座桥MN、EF。

现在要设计一条道路，并在两条河上分别架这两座垂直于桥的大桥，问：如何设计这两座桥MN,EF的位置，使由P村到Q村的路程最短？PL1L2Q 1L2解析：河的宽度（桥的宽度）固定，利用“平移交换”解决问题。

专题08轴对称与最短路径重难点知识一、相关知识（1）平面直角坐标系内点（x，y）关于x轴对称的点的坐标为（x，-y）；平面直角坐标系内点（x，y）关于y轴对称的点的坐标为（-x，y）；（2）区分轴对称图形（一个图形）、成轴对称图形（两个图形）的区别（3）成轴对称图形性质：对称轴为对应点连线的垂直平分线；对应线段、角相等（4）线段垂直平分线①作图方法（依据SSS）；②性质；③判定.三角形中，到三个顶点相等的点只有一个，为三条边垂直平分线的交点.（5）作轴对称图形（6）最短路径理论依据：①两点之间，线段最短；②三角形两边之和大于第三边；③垂线段最短.在直线l上找点P，使得PA+PB最小.在直线l上找点P，使得PA+PB最小.在∠AOB内部一点P，求作△PQR，使△PQR周长最小.典例解析【知识点1：轴对称图形判断】例题1．（2021·上海徐汇）如图，将正方形图案翻折一次，可以得到的图案是（）A．B．C．D．【答案】B.例题2．（2021·江苏如皋）如图为某小区分类垃圾桶上的标识，其图标部分可以看作轴对称图形的有（）A．1个B．2个C．3个D．4个【答案】B.例题3．（2021··重庆）“致中和，天地位焉，万物育焉．”中国古人把和谐平衡的精神之美，演变成了一种对称美，在下列我国建筑简图中，不是轴对称图形的是（）A．B．C．D．【答案】B.例题4．（2021·黑龙江五常）点P（﹣2，b）与点Q（a，3）关于x轴对称，则a＋b的值为（）A．5B．﹣5C．1D．﹣1【答案】B.【解析】解：∵点P（﹣2，b）与点Q（a，3）关于x轴对称∴a=−2，b=−3∴a+b=−2+(−3)=−5故答案为：B.【知识点2：线段垂直平分线性质】例题5．（2021·天津津南期末）如图，在△ABC中，DE是AC的垂直平分线，AB＝5，△ABD的周长是13，则BC的长为（）A．8B．10C．11D．12【答案】A.【解析】解：∵DE是AC的垂直平分线，∴AD=CD∵△ABD的周长是13，即AB+BD+AD+13，AB+BC=13而AB=5∴BC=13-5=8故答案为：A.例题6．（2021·内蒙古呼和浩特市期中）如图，在△ABC中，∠B＝32°，∠C＝48°，AB和AC的垂直平分线分别交BC于点D，E，且点D在点E的左侧，BC＝6cm，则△ADE的周长是（）A ．3cmB ．12cmC ．9cmD ．6cm【答案】D .【解析】解：∵AB 和AC 的垂直平分线分别交BC 于点D ，E ，∴BD =AD ，CE =AE ，∴△ADE 的周长＝AD +AE +DE =BD +CE +DE =BC =6cm ，故答案为：D ．例题7．（2021·黑龙江省期末）如图，DO 垂直AC ，且AO =OC ，若AB =7cm ，BC =5cm ，则△BDC 的周长是____________．【答案】12cm .【解析】解：如图所示，连接CD ，∵OD ⊥AC ，AO =CO ，∴直线OD 是线段AC 的垂直平分线，∴AD =CD ，∴△BCD 的周长=BD +BC +CD =BD +AD +BC =AB +BC =12cm ，故答案为：12cm ．【知识点3：与折叠相关】例题8．（2021·广西期中）如图，在Rt ABC 中，90ACB ，点D 在AB 边上，将CBD 沿CD 折叠，使点B 恰好落在AC 边上的点E 处，若26A ，则ADE 的度数是________【答案】38°.【解析】解：由折叠可得：∠ACD =∠BCD ，∠BDC =∠CDE ，∵∠ACB =90°，∴∠ACD =45°，∵∠A =26°，∴∠BDC =∠ACD +∠A =71°，∴∠CDE =71°，∴∠ADE =180°-71°-71°=38°．故答案为38°．例题9．如图．点D ，E 分别在△ABC 的边BC ，AB 上，连接AD 、DE ，将△ABC 沿直线DE 折叠后，点B 与点A 重合，已知AC ＝6cm ，△ADC 的周长为14cm ，则线段BC 的长为（）A ．6cmB ．8cmC ．12cmD ．20cm【答案】B .【解析】解：∵△ABC 沿直线DE 折叠后，点B 与点A 重合，∴BD ＝AD ，∵AC ＝6cm ，△ADC 的周长为14cm ，∴AD +DC ＝14－6＝8cm ，∴BD +DC ＝BC ＝8cm ，故答案为：B .例题10．（2021·山东寒亭期中）如图，在ABC 中，4AB ，5BC ，6AC ，将ABD △沿AD 折叠，使得点B 恰好落在AC 边上的点E 处，折痕为AD ，若点F 为AD 上一动点，则EFC △的周长最小值为___________．【答案】7.【解析】解：连接BF由题意可知B 和E 关于AD 对称，AB =AE =4，∴BF=FE△CFE 的周长为：EF +FC+EC=BF+CD+EC当F 和D 重合时，BF+CD=BC∵两点之间线段最短∴此时BF+CD 的值最小，即此时△CFE 的周长最小，最小值是EF +FC+EC=BD+CD+EC=BC+EC ，∵EC=AC-AE =6-4=2，∴△CEF 的周长最小值为：BC+EC=5+2=7，故答案为：7．【知识点4：尺规作图】例题11．（2021·山东寒亭期中）如图，在ABC 中，90C ，30B ，分别以A ，B 为圆心，大于12AB 的长为半径画弧分别交于点E 和F ，连接FE 并延长交BC 于点D ，则下列说法中不正确的是（）A ．AD 是BAC 的平分线B ．3ABD DAC S S △△C ．点D 在AB 的垂直平分线上D ．60ADC【答案】B .【解析】解：因为DF 为AB 中垂线，所以∠DAB =∠DBA =30°，又∠A =60°，所以∠CAD =∠BAD =30°，所以AD 是∠BAC 平分线，故A 正确；△ACD 与△ADB 高相等，都是AC ，底边BD =AD =2CD ，故S △ABD =2S △DAC ，故B 错误；C 项：由于EF 为线段AB 中垂线，且D 点为BC 与EF 公共点，故D 点在AB 的垂直平分线上，故C 正确；D 项：∠ADC =∠DAB +∠B =30°+30°=60°，故D 正确．故答案为：B ．例题12．（2021·湖南凤凰期中）如图，在△ABC 中，BC ＝10，AC ＝4，分别以点A 、B 为圆心，大于AB 的长为半径画弧，两弧相交于点M 、N ，作直线MN 交BC 边于点D ，连接AD ，则△ACD 的周长为___．【答案】14.【解析】解：由作图可知，MN 垂直平分AB ，∴AD =BD∵BD =10，AC =4∴△ACD 的周长=AD +CD +AC =BD +CD +AC =BC +AC =14故答案为：14．例题13．（2021·浙江诸暨期中）已知△ABC ，按以下步骤作图：①分别以B ，C 为圆心，以大于12BC 的长为半径作弧，两弧相交于两点M ，N ；②作直线MN 交直线AB 于点D ，连接CD ．若∠ABC ＝40°，∠ACD ＝20°，则∠BAC 的度数为____．【答案】80°或120°.【解析】解：由题意得，直线MN 是线段BC 的垂直平分线，∴BD =CD ，∴∠BCD=∠B=40°，①如图，∵∠ACD=20°，∴∠ACB=40°+20°=60°，∴∠BAC=180°-60°-40°=80°；②如图，∵∠ACD=20°，∴∠ACB=40°-20°=20°，∴∠BAC=180°-20°-40°=120°，综上所述，∠BAC的度数为80°或120°，故答案为：80°或120°．．（1）用尺规完成下列作图：（保留作图痕迹，不写作法）例题14．（2021·河南南阳市）已知MAN的平分线AE；①作MAN②在AE上任取一点F，作AF的垂直平分线分别与AM、AN交于P、Q；（2）在（1）的条件下线段AP与AQ有什么数量关系，请直接写出结论．【答案】见解析.【解析】解：（1）①如图所示，以A为圆心，以任意长为半径画弧，分别与AM，AN交于点H、G，再分别以H、G为圆心，以大于HG长的一半为半径画弧，二者交于点O，过点O作射线AE即为所求；②如图所示，分别以A、F为圆心，以大于AF长的一半为半画弧，二者分别交于J、K，连接JK分别交AM 于P，AN于Q，AE于T；（2）AP=AQ，理由如下：∵JK是线段AF的垂线平分线，∴∠PTA=∠QTA=90°，∵AE是∠MAN的角平分线，∴∠MAE=∠NAE，又∵AT=AT，∴△ATP≌△ATQ（ASA），∴AP=AQ．例题15．（2021·安徽淮南市期中）如图，某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路），现计划在∠AOB内部修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等，你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案．【答案】见解析.【解析】根据题意，作∠AOB的角平分线OK，连接MN，作MN的垂直平分线RQ，OK和RQ相交于点S，如下图：∵OK是∠AOB的角平分线∴OK上的点，到两条公路的距离也相等；∵RQ是MN的垂直平分线∴RQ上的点，到两所大学的距离相等∵OK和RQ相交于点S，∴仓库P应该建在点S的位置．【知识点5：最短路径】例题16．（2021·山东阳谷县）如图，等腰△ABC底边BC的长为4cm，面积为12cm2，腰AB的垂直平分线EF交AC与点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为（）A．4cm B．6cm C．8cm D．10cm【答案】C.【解析】如图，连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC=12BC•AD=12×4×AD=12，解得：AD=6（cm），∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，∴AD的长为BM+MD的最小值，∴△BDM的周长最短=（BM+MD）+BD=AD+12BC=6+12×4=6+2=8（cm）．故答案为：C．例题17．（2021·河北邢台市）如图，∠AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是OB、OA上的动点，记∠MPQ＝α，∠PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．50°【答案】C.【解析】解：如图，作M关于OB的对称点M’，N关于OA的对称点N’，连接M’N’交OA于Q，交OB于P，则MP＋PQ＋QN最小，∴∠OPM＝∠OPM’＝∠NPQ，∠OQP＝∠AQN’＝∠AQN，∴∠QPN＝12（180°−α）＝∠AOB＋∠MQP＝20°＋12（180°−β），∴180°−α＝40°＋（180°−β），∴β−α＝40°，故答案为：C．例题18．（2021·福建期中）如图，直线m是△ABC中BC边的垂直平分线，点P是直线m上的一动点，若AB＝5，AC＝4，BC＝6，则△APC周长的最小值是（）A．9B．10C．11D．12.5【答案】A.【解析】∵直线m是BC的垂直平分线∴BP=CP∴△ACP周长=AC+AP+BP∵两点之间线段最短∴AP+BP≥AB∴△ACP的周长≥AC+AB∵AC=4，AB=5∴△ACP周长最小为AC+AB=9故答案为：A.例题19．（2021·浙江余杭）如图所示，点P 为O 内一定点，点A ，B 分别在O 的两边上，若PAB 的周长最小，则O 与APB 的关系为（）A ．2O APBB ．2O APBC ．180O APBD ．2180O APB【答案】D .【解析】解：如图，作点P 关于OM 的对称点P ’，点P 关于ON 的对称点P ’’，P ’P ’’交OM 于A ，交ON 于B ，此时△PAB 的周长最小值等于P ’P ’’的长，则∠P ’OP ’’=2∠AOP ，∴∠P ’=180180222P OP AOB ∴2∠O +∠APB =180°故答案为：D ．例题20．（2021·河南西平期中）（1）如图1，在直线AB 的同一侧有两点C ，D ，在AB 上找一点P ，使C ，D ，P 三点组成的三角形的周长最短，找出此点．（2）如图2，在∠AOB 内部有一点P ，在OA ，OB 上是否分别存在点E ，F ，使得E ，F ，P 三点组成的三角形的周长最短，找出E ，F 两点．（3）如图3，在∠AOB 内部有两点M ，N ，在OA ，OB 上是否分别存在点E ，F ，使得E ，F ，M ，N 四点组成的四边形的周长最短，找出E ，F 两点．（显示找点的过程）【答案】见解析.【解析】解：（1）如图1，（2）如图2，（3）如图3，【知识点6：综合习题】例题21．（2021·山西盐湖期中）如图，在 ABC中，∠ABC的平分线BP与AC的垂直平分线DP相交于点P，过点P作PF⊥BC于点F，PE⊥AB交BA的延长线于点E．AB=7cm，BC=15cm，则AE的长为（）A ．3cmB ．4cmC ．5cmD ．6cm【答案】B .【解析】解：连结AP ，CP ，∵AC 的垂直平分线DP ，∴PA =PC ，∵BP 是∠ABC 的平分线，PF ⊥BC ，PE ⊥AB ，∴PE =PF ，在Rt △PEA 和Rt △PFC 中，PA PCPE PF ，∴Rt △PEA ≌Rt △PFC （HL ），∴AE =CF ，在Rt △PEB 和Rt △PFB 中，PB PBPE PF ，∴Rt △PEB ≌Rt △PFB （HL ），∴EB =FB ，∴2BE =BE +BF =AB +EA +BC -FC =AB +BC =7+15=22，∴BE=11，∴AE=BE-AB=11-7=4cm．故答案为：B．例题22．（2021·河南枫杨外国语期中）在平面直角坐标系xOy中，我们把点O，A（0，4），B（8，4），C （8，0）顺次连接起来，得到一个长方形区域，P为该区域（含边界）内一点．若将点P到长方形相邻两边的距离之和的最小值记为d，则称P为“d距点”．例如：点P（5，3）称为“4距点”．当d＝4时，横、纵坐标都是整数的点P的个数为___个．【答案】8.【解析】解：满足条件的点如图所示，共有8个．故答案为：8．例题23．（2021·福建建瓯期中）如图1，在△ABC中，∠ABC的平分线与边AC的垂直平分线相交于点D，过点D作DF⊥BC于点F，DG⊥BA交BA的延长线于点G．（1）求证：AG=CF；（2）如图2，点M，N分别是线段AB，射线BD上的动点，若BC=5，S△ABC=5，求MN+AN的最小值．【答案】（1）见解析；（2）2.【解析】证明：（1）如图，连接AD，DC，∵BD平分∠ABC，DG⊥BA，DF⊥BC，∴DG=DF．∵点D在边AC的垂直平分线上，∴DA=DC．在Rt△DGA和Rt△DFC中，DG DF DA DC，∴Rt△DGA≌Rt△DFC(HL)．∴AG=CF．（2）∵BD平分∠ABC，点M在线段AB上，∴点M关于BD的对称点M 在边BC上．如图，作点M关于BD的对称点M ，连接M N ，过点A作AP⊥BC于点P，∴MN M N ．∴MN +AN =M N +AN ≥AP ．∴当点A ，N ，P 在同一条直线上且AP ⊥BC 时，MN +AN 的值最小，最小值即为AP 的长．∵S △ABC =5，∴152BC AP ．∵BC =5，∴AP =2．∴MN +AN 的最小值为2．例题24．（2021·辽宁大石桥期中）已知点P 在∠MON 内．（1）如图1，点P 关于射线OM 的对称点是G ，点P 关于射线ON 的对称点是H ，连接OG 、OH 、OP ．①若∠MON =50°，则∠GOH =______；②若PO =5，连接GH ，请说明当∠MON 为多少度时，GH =10；（2）如图2，若∠MON =60°，A 、B 分别是射线OM 、ON 上的任意一点，当 PAB 的周长最小时，求∠APB 的度数．【答案】（1）①100°；②当∠MON =90°时，GH =10；（2）60°.【解析】解：（1）①∵P 关于射线OM 的对称点是G ，点P 关于射线ON 的对称点是H ，∴OG =OP ，OM ⊥PG ，即OM 平分∠POG ，同理，ON 平分∠POH∴∠GOH =2∠MON =100°故答案为：100°；②∵OP =5，∴OG =OH =5当∠MON =90°时，G 、O 、H 共线，GH =OG +OH =10（2）如图，分别作点P关于OM、ON的对称点P’、P’’，则AP=AP’，BP=BP’’，此时△PAB周长的最小值等于P’P’’的长，由对称性可得，∠OPA=∠OP’A=30°，∠BPO=∠OP’’B=30°∠APB=60°.。

课时目标1.能利用轴对称和平移解决简单的最短路径问题,培养学生从实际问题抽象出熟悉模型的能力,增强应用意识.2.体会图形的变换在解决最值问题中的作用,培养学生几何直观和模型观念.3.通过解决问题感悟转化思想,进一步获得数学活动的经验,增强数学的应用意识.学习重点1.利用轴对称将最短路径问题转化为“两点之间,线段最短”问题.2.利用轴对称和平移将造桥选址问题转化为“两点之间,线段最短”问题.学习难点最短路径问题的解决思路及证明方法.课时活动设计情境引入1.如图,连接A,B两点的所有线中,哪条最短?为什么?解:②最短,因为两点之间,线段最短.2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?解:PC最短,因为垂线段最短.3.以前还学习过哪些有关线段大小的结论?解:三角形三边关系:两边之和大于第三边;斜边大于直角边.4.如图,如何做点A关于直线l的对称点?解:过点A作直线l的垂线,交直线l于点O,延长AO到点A',使AO=A'O.设计意图:通过四个问题的设计回顾,为解决最短路径问题提供理论依据,培养学生运用定理的意识和在实际问题中发现数学问题的能力,培养学生的几何直观和空间观念.新知探究利用轴对称解决最短路径问题探究1“饮马问题”.问题:如图,牧马人从A地出发,到一条笔直的河流l边饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?分析:即把A,B两地抽象为两点,将河流l抽象成为一条直线,在直线l上找一点C,使AC+BC最短.学生讨论并回答,师生共同总结得出,可以转化为两点在直线异侧的问题.追问1:能否通过图形变换(轴对称和平移)将点B“移”到l的另一侧B'处,满足直线l上的任意一点C,都保持CB与CB'的长度相等?作法:(1)作点B关于直线l的对称点B';(2)连接AB',与直线l相交于点C.则点C即为所求.追问2:如何证明这条路径最短?证明:如图,在直线l上任取一点C'(与点C不重合),连接AC',BC',B'C'.由轴对称的性质知,BC=B'C,BC'=B'C'.∴AC+BC=AC+B'C=AB',AC'+BC'=AC'+B'C'.在△AB'C'中,AB'<AC'+B'C',∴AC+BC<AC'+BC'.即AC+BC最短.探究2“造桥选址问题”.问题:如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥建在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)分析:把河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M,把问题转化为:当点N在直线b的什么位置时,AM+MN+NB最小.学生讨论并回答,师生共同归纳.追问1:能否通过将AM沿着与河岸垂直的方向平移,点M移动到点N,点A移动到点A',使A'N+NB最小?作法:(1)将AM沿着与河岸垂直的方向平移,点M移动到点N,点A移动到点A';(2)连接A'B ,点N 即为所求.追问2:如何证明点N 即为所求?小组合作交流,教师找学生展示答案.分析:如图,在直线b 上任意取一点N',过点N'作N'M'垂直于a ,垂足为M',连接AM',A'N',N'B.同“饮马问题”可证,AM +MN +AM'<AM'+A'N'+N'B.解:如图,在路径A →M →N →B 的左侧和右侧各任意作一条路径,即A →M 1→N 1→B 和A →M 2→N 2→B ,AM +MN +NB =BC +AC ,则AM 1+M 1N 1+N 1B =N 1C +N 1B +AC >BC +AC ,AM 2+M 2N 2+N 2B =N 2C +N 2B +AC >BC +AC.所以A →M →N →B 是最短路径.设计意图:通过问题层层递进,培养学生分析问题和解决问题的能力;培养学生用数学眼光看世界的能力,和用文字语言、图形语言、符号语言三种语言表达问题的能力以及三种语言的相互转化能力,培养学生严密的数学思维和严谨的科学态度.典例精讲例1(1)如图1,在AB 直线一侧C ,D 两点,在AB 上找一点P ,使C ,D ,P 三点组成的三角形的周长最短.说明理由.(2)如图2,在∠AOB 内部有一点P ,是否在OA ,OB 上分别存在点E ,F ,使得E ,F ,P 三点组成的三角形的周长最短,找出E ,F 两点.(3)如图3,在∠AOB 内部有两点M ,N ,是否在OA ,OB 上分别存在点E ,F ,使得E ,F ,M ,N ,四点组成的四边形的周长最短,找出E ,F 两点.解:(1)如图1,作C关于直线AB的对称点C',连接C'D交AB于点P.则点P就是所求作的点.理由如下:因为C和C'关于直线对称,所以PC=PC'.因为CD长度不变,所以DP+CP最短时,C,D,P三点组成的三角形的周长最短.因为两点之间线段最短,所以点P就是所求作的点.(2)如图2,作P关于OA的对称点P',关于OB的对称点P″,连接P'P″,交OA于点E,OB于点F,则点E,F就是所求作的点.(3)如图3,作M关于OA的对称点M',作N关于OB的对称点M″,连接M'M″,交OA于点E,OB于点F,则点E,F就是所求作的点.例2如图,荆州古城河在CC'处直角转弯,河宽相同,从A处到B处,须经两座桥DD',EE'(桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD',E'EB的路程最短?解:如图,将A点向F平移得到点F,B点向右平移得到点G.连接GF,与河岸相交于点E',D'.作DD',EE'即为桥.理由:由作图法可知,AF∥DD',AF=DD',则四边形AFD'D为平行四边形,于是AD=FD',同理,BE=GE',由两点之间线段最短可知,GF最小.设计意图:通过题目巩固所学知识,总结解决最短路径问题的方法:在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而做出最短路径的选择.增强学生应用意识和创新能力.巩固训练1.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是(D)2.有两棵树位置如图,树的底部分别为A,B,地上有一只昆虫沿着A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处.问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.解:如图所示.3.如图,A和B两地在一条河的两岸,现要在河上建一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)解:如图所示.设计意图:通过练习,巩固所学知识,提高学生分析问题和解决问题的能力.课堂小结1.谈谈今天的收获.2.教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:(1)本节课学习了哪些主要内容?(2)怎样解决最短路径问题?(3)本节课你学到了哪些研究问题的方法?设计意图:通过小结,使学生梳理本节课所学内容和研究方法,把握本节课的核心内容,引导学生从知识内容和学习过程两个方面总结自己的收获,掌握几何直观和模型观念,提升知识转化和迁移能力.课堂8分钟.1.教材第93页复习题13第15题.2.七彩作业.教学反思。

教学设计）一．复习引入1.两点之间，什么最短2.点到直线的距离问题：已知：如图，A，B在直线L的两侧，在L上求一点P，使得PAPB最小。

（连接AB,线段AB与直线L的交点P ，就是所求。

）二、探究如图，要在燃气管道L上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短像这样我们研究过一些关于“两点的所有连线中，线段最短”、“连接直线外一点与直线上各点的所有线段中，垂线段最短”等的问题，我们称它们为最短路径问题．现实生活中经常涉及到选择最短路径的问题，本节将利用数学知识探究数学史中著名的“将军饮马问题”。

问题1 相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦．有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：看图：从A 地出发，到一条笔直的河边l 饮马，然后到B 地．到河边什么地方饮马可使他所走的路线全最短精通数学、物理学的海伦稍加思索，利用轴对称的知回答问题学生思考学生思考，并在草稿纸上画图，看是否可以确定最短路线。

学生在老师的引导下思考。

引入课题由浅入深，让学生先理解两点在直线两侧情况中的最短路径问题。

识回答了这个问题．这个问题后来被称为“将军饮马问题”．你能将这个问题抽象为数学问题吗（将A，B 两地抽象为两个点，将河l 抽象为一条直线．）你能用自己的语言说明这个问题的意思，并把它抽象为数学问题吗（1）从A 地出发，到河边l 饮马，然后到B 地；（2）在河边饮马的地点有无穷多处，把这些地点与A，B 连接起来的两条线段的长度之和，就是从A 地到饮马地点，再回到B 地的路程之和；（3）现在的问题是怎样找出使两条线段长度之和为最短的直线l上的点．设C 为直线上的一个动点，上面的问题就转化为：当点C 在l 的什么位置时，AC 与CB 的和最小（如图）．你能利用轴对称的有关知识，找到上问中符合条件的点B′吗师讲解做法：如图，点A，B 在直线l 的同侧，点C 是直线上的一个动点，当点C 在l 的什么位置时，AC 与CB 的和最小作法：（1）作点B 关于直线l 的对称点B′；（2）连接AB′，与直线l 相交于点C．则点C 即为所求．学生在老师的引导下，尝试用轴对称来试试，看是否是最短距离。