EM算法的详解

最大期望值EM算法最大期望值(Expectation-Maximization, EM)算法是一种统计学习方法，用于解决带有隐变量的概率模型参数估计问题。

EM算法的主要思想是通过迭代求解局部最优解，并且能够保证每次迭代过程中目标函数值不减。

EM算法广泛应用于数据挖掘、图像处理、自然语言处理等领域，在金融、医学和社会科学等领域也有许多实际应用。

本文将对EM算法的基本原理、迭代过程、理论基础和应用进行详细介绍。

一、基本原理EM算法是一种迭代算法，包含两个步骤：E步和M步。

其中，E步是求期望(expectation)的过程，用于更新隐变量对观测数据的条件概率分布；M步是求最大化(maximization)的过程，用于更新模型的参数。

通过不断交替进行E步和M步，直到收敛为止，即可得到最优的参数估计。

二、迭代过程1.初始化参数：随机给定模型参数的初始值。

2.E步：根据当前参数估计，计算隐变量对观测数据的条件概率分布。

3.M步：根据当前隐变量的条件概率分布，最大化观测数据的对数似然函数，更新模型的参数估计。

4.计算目标函数值：根据当前参数估计，计算目标函数的值。

5.判断是否满足停止条件：如果满足停止条件，则算法结束；否则，返回第2步。

三、理论基础EM算法基于两个基本定理：数据的似然函数下界和KL散度的非负性。

1.数据的似然函数下界：对于给定的观测数据，EM算法通过求解数据的似然函数的下界来进行参数估计。

这个下界是通过引入隐变量来扩展数据模型得到的，因此可以利用EM算法求解。

2.KL散度的非负性：KL散度是衡量两个概率分布之间的差异程度的指标。

在EM算法中，通过最大化观测数据的对数似然函数来更新模型的参数，相当于最小化KL散度。

四、应用领域EM算法在许多领域都有广泛的应用。

以下是一些典型的应用实例：1.聚类分析：EM算法可以用于高斯混合模型的参数估计，从而实现聚类分析。

2.隐马尔可夫模型(HMM)：EM算法可以用于HMM模型参数的估计，应用于自然语言处理、语音识别等领域。

统计学习中的EM算法EM算法是一种常用的统计学习方法，它可以用于估计未知参数，特别是那些需要通过观察到的数据加以估计的复杂模型。

本文将介绍EM算法的基本原理、应用场景以及优缺点。

一、基本原理EM算法（Expectation Maximization）相当于是用一种迭代的方式，在“期望”（Expectation）和“最大化”（Maximization）之间进行交替，来求解模型参数的一种方法。

EM算法的基本思想是：在训练数据样本中，往往存在隐含变量，而且无法直接观测到。

我们需要发掘这些隐含变量的概率分布，从而求解最优的模型参数。

具体来说，EM算法的步骤如下：首先，选择一个初始化的参数值；然后，使用这些参数值来计算隐含变量的概率分布；接下来，根据这些概率分布来重新估计参数的值；不断重复以上三个步骤，直到收敛，得到最优的模型参数值。

EM算法通过迭代来求解未知的参数值，对于一些需要最大化其似然函数的模型，EM算法可以找到使得似然函数最大的参数值。

最常见的应用场景是在高斯混合模型（GMM）以及隐马尔可夫模型（HMM）中。

二、应用场景1、高斯混合模型高斯混合模型是一种将多个高斯分布加权叠加的模型，它常被用于描述复杂数据的分布情况。

举个例子，在股票市场上，可以将不同的股票价格看成不同的高斯分布，然后用高斯混合模型来描述整个市场的波动情况。

在这种情况下，EM算法可以用来估计每个高斯分布的权重、均值和方差。

2、隐马尔可夫模型隐马尔可夫模型是一种包含隐含状态的动态变化模型。

它常被用于语音识别、自然语言处理、图像处理等领域。

在隐马尔可夫模型中，我们需要估计各个状态转移概率以及各个隐含状态下的观测值概率分布。

EM算法可以用来求解这些参数值。

三、优缺点1、优点EM算法可以用来处理包含隐含变量的模型，在实际应用中非常普遍。

EM算法可以求解似然函数的最大值或者后验概率的最大值。

这样，在目标函数为凸函数的情况下，EM算法可以获得全局最优解。

EM算法详细例子及推导EM算法（Expectation-Maximization Algorithm）是一种用于求解含有隐变量（latent variable）的概率模型的参数估计方法。

其基本思想是通过迭代的方式，通过观测数据得到对隐变量的估计，然后再基于该估计对模型参数进行优化。

下面我们以一个简单的高斯混合模型为例，详细介绍EM算法的推导和实例。

1. 高斯混合模型（Gaussian Mixture Model, GMM）高斯混合模型是一种概率模型，由多个高斯分布组合而成。

假设我们观测到的数据由K个高斯分布组成，每个高斯分布对应一个参数向量：均值miu和方差sigma^2、同时，我们还有一个隐变量Z，表示观测数据属于哪个高斯分布，取值范围为{1,2,...,K}。

2.EM算法EM算法的核心思想是通过交替进行两个步骤：E步（Expectation）和M步（Maximization）。

在E步中，我们对当前模型参数下的隐变量进行估计，得到对隐变量的最大似然估计。

在M步中，我们利用得到的隐变量估计更新模型参数，使模型对观测数据的似然函数最大化。

不断重复这两步直至模型收敛。

下面我们通过具体的例子来推导EM算法。

假设我们观测到了一个数据集X = {x1, x2, ..., xn}，我们希望通过EM算法对其进行建模。

Step1: 初始化模型参数首先，我们需要初始化模型参数。

选择K个高斯分布的参数miu和sigma^2，并假设所有的高斯分布对应的隐变量Z服从均匀分布。

这时，我们得到了初始模型参数Theta = {miu1, sigma^21, ..., miuK,sigma^K, pi1, pi2, ..., piK}。

Step2: E步，计算隐变量的后验分布在E步中，我们计算隐变量的后验分布。

对于每个观测样本xi，我们计算其属于每个高斯分布的概率，即：gamma(k,i) = P(Zi=k，xi, Theta) = P(Zi=k，xi, miu_k,sigma_k^2) = pi_k * N(xi，miu_k, sigma_k^2) / sum(pi_j * N(xi，miu_j, sigma_j^2)， j=1 to K其中N(xi，miu_k, sigma_k^2)表示xi在第k个高斯分布下服从的概率密度函数。

EM算法及应用实例EM算法，全称为Expectation-Maximization算法，是一种常用的统计推断算法，用于在包含隐变量的概率模型中进行参数估计。

EM算法的基本思想是通过交替进行两步操作，一步是求期望（E步），另一步是求极大化解（M步）。

通过交替进行这两步操作，EM算法可以逐步提高模型对参数的估计，并逼近参数的最优解。

EM算法在统计学、机器学习和数据处理等领域有广泛的应用。

下面将对EM算法的两个步骤进行详细介绍，并给出一个应用实例加以说明。

1. E步（Expectation Step）在E步中，给定当前模型参数的估计，计算隐变量的条件概率分布期望（即给定观测数据下的隐变量的期望）。

这一步的目的是根据当前参数估计的情况，计算隐变量的期望，用于下一步的参数估计。

2. M步（Maximization Step）在M步中，给定E步计算得到的隐变量的期望，计算模型参数的估计值，使得参数估计值使得隐变量的期望最大化。

这一步的目的是用E步计算得到的隐变量的期望来修正参数估计。

下面给出一个EM算法的应用实例：高斯混合模型的参数估计。

高斯混合模型是一种常用的概率分布模型，它是由多个高斯分布按一定比例叠加而成。

每个高斯分布被称为一个混合成分，每个混合成分有自己的均值和方差。

给定一个观测数据集，我们希望用高斯混合模型来对这个数据集进行建模，从而估计出每个混合成分的均值和方差。

假设数据集包含N个样本，每个样本是一个d维的向量。

高斯混合模型的参数可以分为两类：混合比例和混合成分参数。

混合比例表示每个混合成分在总体中所占的比例，混合成分参数表示每个混合成分的均值和方差。

假设总共有K个混合成分，则混合比例可以用一个K维向量表示，并满足各个元素之和为1、混合成分的均值和方差可以分别用K个d维向量和K个d×d维矩阵表示。

首先，我们需要初始化混合比例和混合成分参数的估计值。

这些估计值可以随机初始化或者通过其他方式得到。

r语言emt打分一、EM算法简介EM算法是一种常用的参数估计方法，特别适用于含有隐变量的概率模型。

它通过迭代的方式，不断调整模型参数，使得模型的似然函数最大化。

EM算法主要分为两个步骤：E步和M步。

1. E步：计算期望在E步中，根据当前的参数估计值，计算隐变量的后验概率。

这里的后验概率是指给定观测数据和当前参数估计值下，隐变量取不同值的概率。

2. M步：最大化在M步中，利用E步得到的隐变量的后验概率，更新模型的参数估计值。

通过最大化似然函数，得到新的参数估计值。

EM算法通过反复迭代E步和M步，直到似然函数收敛或达到预设的迭代次数，得到最优的参数估计值。

二、EM算法在高斯混合模型中的应用高斯混合模型（Gaussian Mixture Models，简称GMM）是一种常用的概率模型，它假设观测数据是由多个高斯分布混合而成的。

EM算法可以用于对GMM进行参数估计。

1. 模型假设GMM假设观测数据服从多个高斯分布，每个高斯分布对应一个隐变量。

隐变量表示观测数据属于哪个高斯分布的概率。

2. 参数估计利用EM算法可以对GMM进行参数估计。

在E步中，计算观测数据属于每个高斯分布的后验概率。

在M步中，利用E步得到的后验概率，更新高斯分布的均值和方差。

三、使用R语言实现EMT打分R语言是一种强大的统计分析工具，可以方便地实现EM算法。

下面以一个简单的例子来演示如何使用R语言实现EMT打分。

```R# 导入EMT包library(EMT)# 生成一些观测数据data <- rbind(matrix(rnorm(200), ncol = 2),matrix(rnorm(200, mean = 5), ncol = 2))# 运行EMT算法result <- EMT(data, K = 2) # K为高斯分布的数量# 输出结果print(result$mu) # 输出高斯分布的均值print(result$sigma) # 输出高斯分布的方差print(result$probability) # 输出每个观测数据属于每个高斯分布的后验概率```在上述代码中，首先导入EMT包，然后生成一些观测数据。

em算法是指期望最大化算法（期望最大化算法，也翻译为期望最大化算法），是一种迭代算法，用于包含潜在变量概率估计的概率参数模型的最大似然估计或最大后验。

在统计计算中，最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。

最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。

最大期望算法经过两个步骤交替进行计算:第一步是计算期望(E)，利用概率模型参数的现有估计值，计算隐藏变量的期望;第二步是最大化(M)，利用E 步上求得的隐藏变量的期望，对参数模型进行最大似然估计。

M 步上找到的参数估计值被用于下一个E 步计算中，这个过程不断交替进行。

总体来说，EM的算法流程如下:1.初始化分布参数2.重复直到收敛:E步骤:估计未知参数的期望值，给出当前的参数估计。

M步骤:重新估计分布参数，以使得数据的似然性最大，给出未知变量的期望估计。

迭代使用EM步骤，直至收敛。

可以有一些比较形象的比喻说法把这个算法讲清楚。

比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。

EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。

可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

EM 算法是Dempster，Laind，Rubin 于1977 年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行MLE 估计，是一种非常简单实用的学习算法。

机器学习算法——EM算法E步：利用当前估计的参数值，求出在该参数下隐含变量的条件概率值（计算对数似然的期望值）；M步：结合E步求出的隐含变量条件概率，求出似然函数下界函数的最大值（寻找能使E步产生的似然期望最大化的参数值。

）然后，新得到的参数值重新被用于E步.....直到收敛到局部最优解。

（note：每次迭代实际在求Q函数及其极大，即每次迭代使似然函数增大或达到局部极值。

）优点：简单性和普适性，可看作是一种非梯度优化方法（解决梯度下降等优化方法的缺陷：求和的项数将随着隐变量的数目以指数级上升，会给梯度计算带来麻烦）缺点：对初始值敏感，不同的初值可能得到不同的参数估计值；不能保证找到全局最优值。

一、Jensen 不等式在EM算法的推导过程中，用到了数学上的Jensen不等式，这里先来介绍一下。

其中，二、EM算法推导面对一个含有隐含变量Z的概率模型，目标是极大化观测数据Y 关于参数的对数似然函数，即极大化：事实上，EM算法是通过迭代逐步极大化的。

假设在第次迭代后的估计值是。

我们希望新的估计值能使增加，即,并逐步达到极大值。

为此考虑两者的差：上式利用了Jensen不等式，且，则可得上述推导。

注意为凹函数，不等号要改变方向令EM算法并不能保证全局最优值，直观解释如图所示。

好好理解这个图三、EM算法在高斯混合模型中的应用：高斯混合模型：步骤：（1）明确隐变量，写出完全数据的对数似然函数。

（2）EM算法的E步：确定Q函数（即：完全数据的对数似然函数关于在给定观测数据和参数的条件下对隐变量的条件概率的期望）：（3）M步：求Q函数对theta的极大值，即求新一轮迭代的模型参数。

四、采用EM算法求解的模型有哪些？为什么不用牛顿法或者梯度下降法？一般有混合高斯、协同过滤、k-means。

算法一定会收敛，但是可能会收敛到局部最优。

求和的项数会随着隐变量的数目指数上升，会给梯度计算带来麻烦。

EM算法是一种非梯度优化算法。

Em算法，是指期望最大化算法，是一种迭代算法，用于统计中，以找到概率模型中参数的最大似然估计，该估计依赖于不可观察的隐藏变量。

EM算法由dempster，laind和Rubin于1977年提出，是一种非常简单实用的学习算法，可以通过MLE从不完整的数据集中估计参数。

此方法可广泛用于处理不完整的数据，例如缺陷数据，截断的数据和嘈杂的数据。

可能会有一些生动的隐喻可以清楚地解释该算法。

例如，食堂的厨师炒了一道菜，不得不将它分成两部分，以便两个人一起吃。

显然，没有必要以很小的平衡来精确称量它。

最简单的方法是将一个盘子随机分成两个碗，然后观察是否有很多盘子，然后再取其中的一些放到另一个碗中。

这个过程是反复进行的，直到每个人都看不到两个碗中所盛菜肴的重量差异。

EM算法就是这样。

假设我们知道两个参数a和b，它们在初始状态下是未知的。

如果我们知道a的信息，那么我们可以得到b的信息，如果我们知道b，那么我们可以得到a。

可以考虑给定某个初始值以获得b的估计值，然后从b的当前值重新估计a的值，直到当前值收敛为止。

在统计中，最大期望（EM）算法是一种算法，用于根据概率模型中的参数来找到参数的最大似然估计或最大后验估计。

在机器学习和计算机视觉的数据集群领域中经常使用最大期望值。

em算法高斯混合聚类
EM算法是一种迭代优化算法，用于找到参数的最大似然估计。

在高斯混合聚类中，EM算法被用来估计混合高斯模型的参数，包括均值、协方差和权重。

EM算法的基本步骤包括：
1. 初始化参数：选择一个初始的参数值，这些参数通常是通过随机选择或者根据先验知识设定的。

2. E步：在E步中，算法计算对数似然函数的期望。

对于混合高斯模型，这涉及到计算每个数据点属于每个高斯分布的概率。

3. M步：在M步中，算法最大化对数似然函数。

对于混合高斯模型，这涉及到更新每个高斯分布的均值、协方差和权重。

4. 迭代：重复E步和M步，直到满足某个停止准则，如达到最大迭代次数，或者参数的变化小于某个预设的阈值。

需要注意的是，EM算法对初值是敏感的，并且不一定能够收敛到全局最优解。

此外，对于大数据集，EM算法可能需要较长的时间来收敛。

尽管如此，EM 算法仍然是一种非常实用的方法，用于估计混合模型的参数。

一文让你完全入门EM算法重磅干货，第一时间送达EM（Expectation Maximum，期望最大化）是一种迭代算法，用于对含有隐变量概率参数模型的极大似然估计或极大后验估计。

模型参数的每一次迭代，含有隐变量概率参数模型的似然函数都会增加，当似然函数不再增加或增加的值小于设置的阈值时，迭代结束。

EM算法在机器学习和计算机视觉的数据聚类领域有广泛的应用，只要是涉及到后验概率的应用，我们都可以考虑用EM算法去解决问题。

EM算法更像是一种数值分析方法，正确理解了EM算法，会增强你机器学习的自学能力，也能让你对机器学习算法有新的认识，本文详细总结了EM算法原理。

目录1. 只含有观测变量的模型估计2. 含有观测变量和未观测变量的模型参数估计3. EM算法流程4. 抛硬币问题举例5. 高斯混合模型的参数估计6. 聚类蕴含的EM算法思想7. 小结1. 只含有观测变量的模型估计我们首先考虑比较简单的情况，即模型只含有观测变量不含有隐藏变量，如何估计模型的参数？我们用逻辑斯蒂回归模型（logistic regression model）来解释这一过程。

假设数据集有d维的特征向量X和相应的目标向量Y，其中，。

下图表示逻辑斯蒂回归模型：由之前的文章介绍，逻辑斯蒂回归模型的目标预测概率是S型函数计算得到，定义为：若，则目标预测变量为1；反之，目标预测变量为0。

其中w是待估计的模型参数向量。

机器学习模型的核心问题是如何通过观测变量来构建模型参数w，最大似然方法是使观测数据的概率最大化，下面介绍用最大似然方法（Maximum Likelihood Approach）求解模型参数w。

假设数据集，样本数据，模型参数。

观测数据的对数似然函数可写为：由对数性质可知，上式等价于：式(1)代入式(2)，得：其中：由于(3)式是各个样本的和且模型参数间并无耦合，因此用类似梯度上升的迭代优化算法去求解模型参数w。

因为：由式(4)(5)(6)可得：因此，模型参数w的更新方程为：其中η是学习率。

EM算法通俗解释前⾔ EM算法⼤家应该都⽿熟能详了，不过很多关于算法的介绍都有很多公式。

当然严格的证明肯定少不了公式，不过推公式也是得建⽴在了解概念的基础上是吧。

所以本⽂就试图以⽐较直观的⽅式谈下对EM算法的理解，尽量不引⼊推导和证明，希望可以有助理解算法的思路。

介绍 EM⽅法是专门为优化似然函数设计的⼀种优化算法。

它的主要应⽤场景是在⽤缺失数据训练模型时。

由于数据的缺失，我们只能把似然函数在这些缺失数据上边缘化，这就造成带有缺失值的似然函数具有多个完备数据似然函数之和的形式。

这种求和造成两个后果：⼀是本来可能因⼦分解的形式被打破（本来独⽴的变量耦合在⼀起了），⼆是本来具有的凸性被打破（加法运算不具有保凸性）。

因此，优化带有缺失值的似然函数⼀般是⼀个⾼维的⾮凸优化问题，换句话说就是⽐较难的问题。

EM算法的思路基于以下观察：在给定模型参数的情况下，执⾏推理⽐较简单在给定完备数据的情况下，执⾏极⼤似然优化也⽐较简单 不幸的是，带有缺失值的似然函数以上两个条件都不满⾜。

因此，EM算法采⽤了⼀种⾃举(bootstrap)的⽅式来进⾏逐步优化：1. 任选⼀组模型参数，执⾏推理，得到各个缺失值的概率分布，然后认为⼀个缺失值是由所有可能的观测值组成的，每个观测值的权重为其概率。

这样我们就把缺失数据的问题转换成了完备数据的问题。

这⼀步称作E步。

关于E步，可以举⼀个简单的例⼦。

⽐如我们想优化似然函数P(x,y,z|\mathbf{\theta})，但是数据有⼀个缺失值x=0,y=1,z=?。

我们可以这么处理： 通过任选⼀组\mathbf{\theta}=\mathbf{\theta}_0，我们推理得出P(z=0|x=0,y=1,\mathbf{\theta}_0)=0.3，P(z=1|x=0,y=1,\mathbf{\theta}_0)=0.7。

据此我们可以认为这个缺失数据是由0.3个x=0,y=1,z=0和0.7个x=0,y=1,z=1组成的，这样就完成了缺失数据的补全。

EM算法原理一、简介EM（Expectation Maximization）算法是一种常见的统计学习方法，用于估计参数和解决一些难以处理的问题，特别是在存在隐变量的情况下。

EM算法最初由数学家罗伯特·卢德米勒（RobertLushmiller）和理查德·贝尔曼（RichardBellman）在20世纪50年代提出，后来由 statisticiansDempster, Laird, and Rubin 进一步发展，因此也被命名为Dempster-Laird-Rubin算法。

EM算法在许多领域都有广泛的应用，如混合高斯模型、隐马尔可夫模型、高斯过程回归等。

二、EM算法的步骤EM算法主要由两个步骤组成：E步（ExpectationStep）和M步（Maximization Step），这两个步骤在迭代过程中交替进行。

1.E步：计算隐变量的条件期望。

给定当前的参数估计值，计算隐变量的条件期望，通常表示为参数的函数。

这个步骤中，隐变量对数似然函数的参数更新起着关键作用。

2.M步：最大化期望值函数。

在E步计算出期望值之后，M步将尝试找到一组参数，使得这个期望值函数最大。

这个步骤中，通常使用优化算法来找到使期望值函数最大的参数值。

这两个步骤在迭代过程中交替进行，每次迭代都更新了参数的估计值，直到满足某个停止准则（如参数收敛或达到预设的最大迭代次数）。

三、EM算法的特点与优点1.处理隐变量：EM算法能够处理数据中存在的隐变量问题，这是它与其他参数估计方法相比的一大优势。

通过估计隐变量的概率分布，EM算法能够更准确地描述数据的生成过程。

2.简单易行：相对于其他优化算法，EM算法相对简单易懂，也容易实现。

它的主要目标是最优化一个简单的对数似然函数，这使得EM算法在许多情况下都能给出很好的结果。

3.稳健性：对于一些数据异常或丢失的情况，EM算法往往表现出较好的稳健性。

这是因为EM算法在估计参数时，会考虑到所有可用的数据，而不仅仅是正常的数据点。

EM算法实验报告一、算法简单介绍EM 算法是Dempster，Laind，Rubin于1977年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行MLE估计，是一种非常简单实用的学习算法。

这种方法可以广泛地应用于处理缺损数据、截尾数据以及带有噪声等所谓的不完全数据，可以具体来说，我们可以利用EM算法来填充样本中的缺失数据、发现隐藏变量的值、估计HMM中的参数、估计有限混合分布中的参数以及可以进行无监督聚类等等。

本文主要是着重介绍EM算法在混合密度分布中的应用，如何利用EM算法解决混合密度中参数的估计。

二、算法涉及的理论我们假设X是观测的数据，并且是由某些高斯分布所生成的，X是包含的信息不完整（不清楚每个数据属于哪个高斯分布）。

，此时，我们用k维二元随机变量Z（隐藏变量）来表示每一个高斯分布，将Z引入后，最终得到：，，然而Z的后验概率满足（利用条件概率计算）：但是，Z nk为隐藏变量，实际问题中我们是不知道的，所以就用Z nk的期望值去估计它（利用全概率计算）。

然而我们最终是计算max：最后，我们可以得到（利用最大似然估计可以计算）：三、算法的具体描述3.1 参数初始化对需要估计的参数进行初始赋值，包括均值、方差、混合系数以及。

3.2 E-Step计算利用上面公式计算后验概率，即期望。

3.3 M-step计算重新估计参数，包括均值、方差、混合系数并且估计此参数下的期望值。

3.4 收敛性判断将新的与旧的值进行比较，并与设置的阈值进行对比，判断迭代是否结束，若不符合条件，则返回到3.2，重新进行下面步骤，直到最后收敛才结束。

四、算法的流程图五、实验结果a_best=0.8022 0.1978mu_best=2.71483.93074.9882 3.0102cov_best=(:,:,1) =5.4082 -0.0693-0.0693 0.2184(:,:,2) =0.0858 -0.0177-0.0177 0.0769f=-1.6323数据X的分布每次迭代期望值利用EM估计的参量值与真实值比较（红色：真实值青绿色：估计值）六、参考文献1.M. Jordan. Pattern Recognition And Machine Learning2.Xiao Han. EM Algorithm七、附录close all;clear;clc;% 参考书籍Pattern.Recognition.and.Machine.Learning.pdf% % lwm@% 2009/10/15%%M=2; % number of GaussianN=200; % total number of data samplesth=0.000001; % convergent thresholdK=2; % demention of output signal% 待生成数据的参数a_real =[4/5;1/5];mu_real=[3 4;5 3];cov_real(:,:,1)=[5 0;0 0.2];cov_real(:,:,2)=[0.1 0;0 0.1];% generate the datax=[ mvnrnd( mu_real(:,1) , cov_real(:,:,1) , round(N*a_real(1)) )' , mvnrnd(mu_real(:,2),cov_real(:,:,2),N-round(N*a_real(1)))'];% for i=1:round(N*a_real(1))% while (~((x(1,i)>0)&&(x(2,i)>0)&&(x(1,i)<10)&&(x(2,i)<10)))% x(:,i)=mvnrnd(mu_real(:,1),cov_real(:,:,1),1)';% end% end%% for i=round(N*a_real(1))+1:N% while (~((x(1,i)>0)&&(x(2,i)>0)&&(x(1,i)<10)&&(x(2,i)<10)))% x(:,i)=mvnrnd(mu_real(:,1),cov_real(:,:,1),1)';% end% endfigure(1),plot(x(1,:),x(2,:),'.')%这里生成的数据全部符合标准%% %%%%%%%%%%%%%%%% 参数初始化a=[1/3,2/3];mu=[1 2;2 1];%均值初始化完毕cov(:,:,1)=[1 0;0 1];cov(:,:,2)=[1 0;0 1];%协方差初始化%% EM Algorothm% loopcount=0;figure(2),hold onwhile 1a_old = a;mu_old = mu;cov_old= cov;rznk_p=zeros(M,N);for cm=1:Mmu_cm=mu(:,cm);cov_cm=cov(:,:,cm);for cn=1:Np_cm=exp(-0.5*(x(:,cn)-mu_cm)'/cov_cm*(x(:,cn)-mu_cm));rznk_p(cm,cn)=p_cm;endrznk_p(cm,:)=rznk_p(cm,:)/sqrt(det(cov_cm));endrznk_p=rznk_p*(2*pi)^(-K/2);%E step%开始求rznkrznk=zeros(M,N);%r(Zpikn=zeros(1,M);%r(Zpikn_sum=0;for cn=1:Nfor cm=1:Mpikn(1,cm)=a(cm)*rznk_p(cm,cn);% pikn_sum=pikn_sum+pikn(1,cm);endfor cm=1:Mrznk(cm,cn)=pikn(1,cm)/sum(pikn);endend%求rank结束% M stepnk=zeros(1,M);for cm=1:Mfor cn=1:Nnk(1,cm)=nk(1,cm)+rznk(cm,cn);endenda=nk/N;rznk_sum_mu=zeros(M,1);% 求均值MUfor cm=1:Mrznk_sum_mu=0;%开始的时候就是错在这里，这里要置零。

EM算法⼀、EM简介EM(Expectation Mmaximization) 是⼀种迭代算法，⽤于含隐变量(Latent Variable) 的概率模型参数的极⼤似然估计，或极⼤后验概率估计 EM算法由两步组成，求期望的E步，和求极⼤的M步。

EM算法可以看成是特殊情况下计算极⼤似然的⼀种算法。

现实的数据经常有⼀些⽐较奇怪的问题，⽐如缺失数据、含有隐变量等问题。

当这些问题出现的时候，计算极⼤似然函数通常是⽐较困难的，⽽EM算法可以解决这个问题。

EM算法已经有很多应⽤，⽐如最经典的Hidden Markov模型等。

经济学中，除了逐渐开始受到重视的HMM模型（例如Yin and Zhao, 2015），其他领域也有可能涉及到EM算法，⽐如在Train的《Discrete Choice Methods with Simulation》就给出了⼀个mixed logit 模型的EM算法。

⼆、EM算法的预备知识1、极⼤似然估计（1）举例说明：经典问题——学⽣⾝⾼问题我们需要调查我们学校的男⽣和⼥⽣的⾝⾼分布。

假设你在校园⾥随便找了100个男⽣和100个⼥⽣。

他们共200个⼈。

将他们按照性别划分为两组，然后先统计抽样得到的100个男⽣的⾝⾼。

假设他们的⾝⾼是服从⾼斯分布的。

但是这个分布的均值u和⽅差∂2我们不知道，这两个参数就是我们要估计的。

记作θ=[u, ∂]T。

问题：我们知道样本所服从的概率分布的模型和⼀些样本，⽽不知道该模型中的参数。

我们已知的有两个：（1）样本服从的分布模型（2）随机抽取的样本需要通过极⼤似然估计求出的包括：模型的参数总的来说：极⼤似然估计就是⽤来估计模型参数的统计学⽅法。

（2）如何估计问题数学化：（1）样本集X={x1,x2,…,xN} N=100 （2）概率密度：p(xi|θ)抽到男⽣i（的⾝⾼）的概率 100个样本之间独⽴同分布，所以我同时抽到这100个男⽣的概率就是他们各⾃概率的乘积。

EM算法原理详解1.引⾔以前我们讨论的概率模型都是只含观测变量(observable variable), 即这些变量都是可以观测出来的，那么给定数据，可以直接使⽤极⼤似然估计的⽅法或者贝叶斯估计的⽅法；但是当模型含有隐变量(latent variable)的时候, 就不能简单地使⽤这些估计⽅法。

如在中讨论的⾼斯混合就是典型的含有隐变量的例⼦，已经给出EM算法在⾼斯混合模型中的运⽤，下⾯我们来讨论⼀些原理性的东西。

2.Jensen 不等式令是值域为实数的函数，那么如果，则就是⼀个凸函数，如果⾃变量 x 是向量, 那么当函数的海森矩阵是半正定时(), 是凸函数，这是函数为凸函数的条件在向量输⼊时的泛化。

如果，则称是严格凸函数，对应的向量输⼊时的泛化是.定理令是⼀个凸函数，令是⼀个随机变量，那么当时严格凸函数的时，当且仅当以概率 1 成⽴的时，. 即当时常量时，上⾯不等式的等号成⽴。

注意上⾯ E 是表⽰期望的意思，习惯上，在写变量期望的时候，会把紧跟括号略去，即.⽤下⾯的图对上⾯的定理作⼀个解释：这个图中的实线代表凸函数, 随机变量有 0.5 的概率取 a, 同样以 0.5 的概率取 b, 所以的期望位于a,b的正中间，即a,b的均值.从图中可以看出，在 y 轴上, 位于之间，因为是凸函数，则必如上图所⽰，所以很多情况下，许多⼈并去记忆这个不等式，⽽是记住上⾯的图，这样更容易理解。

注意：如果是（严格）凹函数，即使（严格）凸函数（即，），那么Jensen不等式照样成⽴，只不过不等号⽅向相反：3.EM算法假设在⼀个估计问题中有m个独⽴样本，根据这些数据，希望拟合出模型的参数，那么对数似然函数：这⾥，是隐变量，如果能够被观测出来，最⼤似然估计就会变得很容易，但是现在观测不出来，是隐变量。

在这种情况下，EM算法给出了⼀种很有效的最⼤似然估计的⽅法：重复地构造的下界（E步），然后最⼤化这个下界（M步）。

对于每个，令表⽰隐变量的分布，即，考虑：由（2）到（3）的推导⽤到了上⾯的Jensen不等式，此时是⼀个凹函数，因为，考虑上⾯关于的分布，正好是数量的期望，由Jensen不等式可以得到：由此可以从（2）推出（3）.但是由于隐变量的存在，直接最⼤化很困难！试想如果能让直接与它的下界相等，那么任何可以使的下界增⼤的，也可以使增⼤，所以⾃然就是选择出使的下界达到极⼤的参数.怎么样才能使得取得下界呢，即上⾯不等式取等号，关键在于隐变量如何处理，下⾯就此讨论。

EM算法的央文全称是Expectation-maximization algorithm ，即最大期望算法，或者是期望最大化算法。

EM算法号称是十大机器学习算法之一，听这个名头就知道它非同凡响。

从本质上来说EM算法是最大似然估计方法的进阶版。

最大似然估计假设当下我们有一枚硬币，我们想知道这枚硬币抛出去之后正面朝上的概率是多少，于是我们抛了10次硬币做了一个实验。

发现其中正面朝上的次数是5次，反面朝上的次数也是5次。

所以我们认为硬币每次正面朝上的概率是50% 从表面上来看，这个结论非常正常，理所应当。

但我们仔细分析会发现这是有问题的，问题在于我们做出来的实验结果和实验参数之间不是强耦合的。

也就是说，如果硬币被人做过手脚，它正面朝上的概率是60%我们抛掷10次，也有可能得到5次正面5次反面的概率。

同理，如果正面朝上的概率是70%我们也有一定的概率可以得到5次正面5次反面的结果。

现在我们得到了这样的结果，怎么能说明就一定是50%明上的概率导致的呢？那我们应该怎么办，继续做实验吗？显然不管我们做多少次实验都不能从根本上解决这个问题，既然参数影响的是出现结果的概率，我们还是应该回到这个角度，从概率上下手。

我们知道，抛硬币是一个二项分布的事件，我们假设抛掷硬币正面朝上的概率是P,那么反面朝上的概率就是1-p。

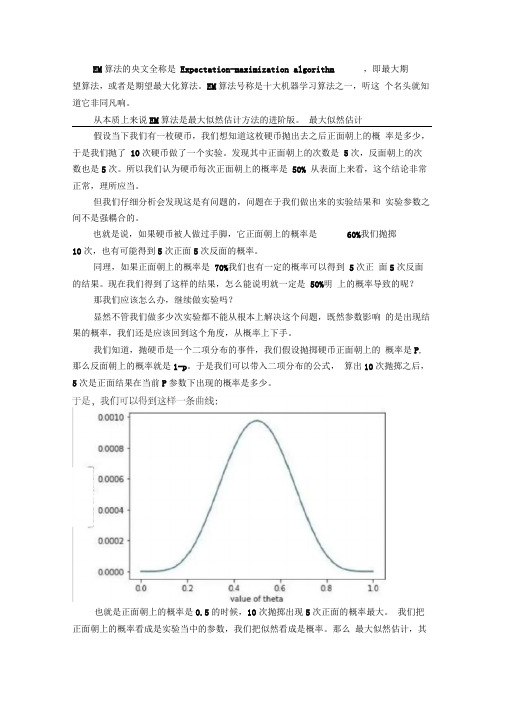
于是我们可以带入二项分布的公式，算出10次抛掷之后，5次是正面结果在当前P参数下出现的概率是多少。

也就是正面朝上的概率是0.5的时候，10次抛掷出现5次正面的概率最大。

我们把正面朝上的概率看成是实验当中的参数，我们把似然看成是概率。

那么最大似然估计，其实就是指的是使得当前实验结果出现概率最大的参数。

也就是说我们通过实验结果和概率，找出最有可能导致这个结果的原因或者说参数，这个就叫做最大似然估计。

原理理解了，解法也就顺水推舟了。

首先，我们需要用函数将实验结果出现的概率表示出来。

这个函数的学名叫做似然函数(likelihood function) 。

EM算法的原理与应用EM算法是一种常用的统计学估计方法，其原理与应用十分广泛。

本文将介绍EM算法的原理及其在实际问题中的应用。

一、EM算法的原理EM算法（Expectation Maximization algorithm）是一种用于解决含有隐变量（或混合变量）的概率模型参数估计问题的迭代优化算法。

其基本思想是通过迭代寻找模型参数的极大似然估计。

1.1 E步（Expectation Step）在E步中，首先对给定的模型参数估计值，计算每个样本属于每个隐变量的后验概率。

这相当于计算样本的“期望”。

具体而言，对于每个样本，计算其属于每个隐变量的后验概率。

1.2 M步（Maximization Step）在M步中，利用E步中计算得到的后验概率，重新估计模型参数，使得似然函数达到极大值。

具体而言，对于每个隐变量，根据样本的“期望”重新估计其模型参数。

1.3 迭代更新将E步和M步反复迭代执行，直到模型参数收敛或达到预设的迭代次数。

通过这种迭代更新的方式，逐步优化模型参数的估计值。

二、EM算法的应用EM算法被广泛应用于各个领域，例如机器学习、计算机视觉、自然语言处理等。

以下将介绍EM算法在几个具体问题中的应用。

2.1 高斯混合模型（Gaussian Mixture Model，GMM）高斯混合模型是一种常用的概率模型，广泛应用于模式识别和聚类等任务。

其中，每个样本可以由多个高斯分布组成，但是样本的真实类别信息是未知的。

利用EM算法可以对高斯混合模型的参数进行估计，从而实现对样本的聚类。

在E步中，计算每个样本属于每个高斯分布的后验概率；在M步中，根据后验概率重新估计高斯混合模型的参数。

通过迭代更新，最终可以得到高斯混合模型的估计参数，从而完成聚类任务。

2.2 隐马尔可夫模型（Hidden Markov Model，HMM）隐马尔可夫模型是一种广泛应用于序列数据建模的统计模型，被应用于语音识别、自然语言处理等领域。

em聚类算法EM聚类算法是一种基于最大似然估计的聚类算法。

EM算法的全称是Expectation-Maximization Algorithm，即期望最大化算法。

该算法通过迭代求解，能够在数据集中找到潜在的分布模型，并将数据集划分为多个不同类别。

EM聚类算法核心思想是先假设每个数据点属于某一类别的概率，然后通过迭代计算来更新这些概率值和每个类别的中心点，直到收敛为止。

具体来说，EM聚类算法包含两个主要步骤：E步和M步。

E步：Expectation（期望）步骤。

在该步骤中，根据当前的中心点位置和先验分布，计算每个数据点属于每个类别的概率，并将其作为后验概率。

M步：Maximization（最大化）步骤。

在该步骤中，根据E步计算出来的后验概率值重新计算每个类别的中心点位置，并更新先验分布。

重复进行E、M两个步骤直到收敛。

最终得到的结果就是将数据集划分为多个不同的簇。

EM聚类算法与K-means聚类方法相比有以下几点优势：1. EM聚类算法不需要预先指定簇的数量，而K-means聚类需要预先指定簇的数量。

2. EM聚类算法可以处理非球形、不同大小和不同密度的簇，而K-means聚类只能处理球形、相同大小和相同密度的簇。

3. EM聚类算法可以处理缺失值，而K-means聚类不能处理缺失值。

但是EM聚类算法也有一些缺点：1. EM聚类算法收敛速度较慢，需要进行多次迭代才能收敛。

2. EM聚类算法对于初始值比较敏感，可能会陷入局部最优解。

3. EM聚类算法计算复杂度较高，在大数据集上运行速度较慢。

总之，EM聚类算法是一种基于最大似然估计的无监督学习方法，在数据挖掘、图像分割、模式识别等领域有广泛应用。

虽然该算法存在一些缺点，但其优势仍然使得它成为了一种重要的聚类方法。