江苏省苏州市2012届高三数学二轮专题训练：8 解析几何(苏教版)

江苏省2012届高三数学二轮专题训练：解答题（2）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1． 已知命题p ：指数函数f (x )=(2a -6)x在R 上单调递减，命题q ：关于x 的方程x 2-3ax +2a 2+1=0的两个相异实根均大于3．若p 、q 中有且仅有一个为真命题，求实数a 的取值范围．解：若p 真，则y=(2a-6)x在R 上单调递减，∴0<2a-6<1, ∴3<a<27…………2分若q 真，令f(x)=x 2-3ax+2a 2+1，则应满足222Δ(3a)4(2a 1)>03a 32f(3)99a 2a 10⎧=--+⎪-⎪->⎨⎪⎪=-++>⎩，…5分 ∴a>2a<2a 25a 2a 2⎧⎪-⎪>⎨⎪⎪<>⎩或或，故a>25，…………………………………………7分又由题意应有p 真q 假或p 假q 真．（i ）若p 真q 假，则⎪⎪⎩⎪⎪⎨⎧≤<<25a 27a 3，a 无解．……………………………10分（ii ）若p 假q 真，则⎪⎪⎩⎪⎪⎨⎧>≥≤25a 27a 3a 或，∴25<a ≤3或a ≥27．……………13分故a 的取值范围是{a|25<a ≤3或a ≥27}．………………………………14分2.在ABC ∆中，角A B C ,,的对边分别为,,a b c ，已知,,a b c 成等比数列，且3cos 4B =． （1）若32BA BC ⋅=，求a c +的值； （2）求cos cos sin sin A C A C +的值． 解：（1）由32BA BC ⋅=，得3cos 2ac B =．…………2分因为3cos 4B =，所以22b ac ==．…………4分由余弦定理2222cos b a c ac B =+-，得2222cos 5a c b ac B +=+=，则222()29a c a c ac +=++=，故3a c +=．…………7分（2）由3cos 4B =，得7sin 4B =．…………9分由2b ac =及正弦定理得2sin sin sin B A C =，…………11分于是22cos cos sin cos cos sin sin()sin 147sin sin sin sin sin sin sin 7A C C A C A A CB AC A C B B B +++=====…………14分 3．如图，在正三棱柱ABC －A 1B 1C 1中，点D 在边BC 上，AD ⊥C 1D ． （1）求证：AD ⊥平面BC C 1 B 1；（2）设E 是B 1C 1上的一点，当11B EEC 的值为多少时，A 1E ∥平面ADC 1？请给出证明．解: （1）在正三棱柱中，C C 1⊥平面ABC ，AD ⊂平面ABC ，∴ AD ⊥C C 1．………………………………………2分又AD ⊥C 1D ，C C 1交C 1D 于C 1，且C C 1和C 1D 都在面BC C 1 B 1内， ∴ AD ⊥面BC C 1 B 1． ……………………………………………………5分（2）由（1），得AD ⊥BC ．在正三角形ABC 中，D 是BC 的中点．…………………7分当111B EEC =，即E 为B 1C 1的中点时，A 1E ∥平面ADC 1．………………………8分 事实上，正三棱柱ABC －A 1B 1C 1中，四边形BC C 1 B 1是矩形，且D 、E 分别是BC 、B 1C 1的中点，所以B 1B ∥DE ，B 1B= DE ． ………………………………………10分 又B 1B ∥AA 1，且B 1B =AA 1，∴DE ∥AA 1，且DE =AA 1． ………………………………………………13分 所以四边形ADE A 1为平行四边形，所以E A 1∥AD ．而E A 1⊄面AD C 1内，故A 1E ∥平面AD C 1． ……………………………15分4. 如图所示,在矩形ABCD 中,已知AB =a ,BC =b (b ＜a ),AB ,AD ,CD ,CB 上分别截取AE ,AH ,CG ,CF 都等于x ,记四边形EFGH 的面积为f （x ）.（1）求f （x ）的解析式和定义域 ；（2）当x 为何值时,四边形EFGH 的面积最大？ 并求出最大面积.解：(1) 设四边形EFGH 的面积为S ,则S △AEH =S △CFG =21x 2, ……………2分 S △BEF =S △DGH =21(a -x )(b -x ),……………4分∴S=ab -2［x 212+21(a -x )(b -x )］= －2x 2+(a +b )x = －2(x -)4b a +2+,8)(2b a +……6分由图形知函数的定义域为{x|0＜x ≤b }.……………8分B 1A 1A BC C 1D(2) 因为0＜b ＜a,所以0＜b ＜2ba +, 若4b a +≤b,即a≤3b 时,则当x=4b a +时,S 有最大值8)(2b a +;………11分若4ba +＞b,即a ＞3b 时,S(x)在(0,b ］上是增函数,此时当x=b 时,S 有最大值为-2(b-4b a +)2+8)(2b a +=ab-b 2,………14分综上可知,当a≤3b 时,x=4ba +时,四边形面积S max =8)(2b a +,当a ＞3b 时,x=b 时,四边形面积S max =ab-b 2. ………15分5．已知函数f (x )＝lg kx －1x －1(k ∈R 且k >0)．(1)求函数f (x )的定义域；(2)若函数f (x )在[10,＋∞)上是单调增函数,求k 的取值范围．解：(1)由kx －1x －1>0及k >0得x －1k x －1>0,即(x －1k)(x －1)>0.①当0<k <1时,x <1或x >1k；……………2分②当k ＝1时,x ∈R 且x ≠1；……………4分③当k >1时,x <1k或x >1. ……………6分综上可得当0<k <1时,函数的定义域为(－∞,1)∪(1k,＋∞)；当k ≥1时,函数的定义域为(－∞,1k)∪(1,＋∞)．……………8分(2)∵f (x )在[10,＋∞)上是增函数,∴10k －110－1>0,∴k >110.……………10分又f (x )＝lg kx －1x －1＝lg(k ＋k －1x －1),故对任意的x 1,x 2,当10≤x 1<x 2时,恒有f (x 1)<f (x 2),即lg(k ＋k －1x 1－1)<lg(k ＋k －1x 2－1),∴k －1x 1－1<k －1x 2－1,∴(k －1)·(1x 1－1－1x 2－1)<0, ……………14分 又∵1x 1－1>1x 2－1,∴k －1<0,∴k <1.综上可知k ∈(110,1)．…………………………………16分6．已知二次函数c bx ax x f ++=2)(. （1）若,0)1(,=>>f c b a 且是否存在)3(,)(,+-=∈m f a m f R m 成立时使得为正数 ，若存在，证明你的结论，若不存在，说明理由；（2）若对)]()([21)(),()(,,,21212121x f x f x f x f x f x x R x x +=≠<∈方程且有2个不等实根，证明必有一个根属于12(,);x x （3）若0)0(=f ，是否存在b 的值使})(|{x x f x ==})]([|{x x f f x =成立，若存在，求出b 的取值范围，若不存在，说明理由. 解：（1）因为,00,,0)1(<>>>=++=C a c b a c b a f 且所以且…………2分 ∵,,0)(1,0)1(ac x f f 由韦达定理知另一根为的一个根是=∴= ,,,10,00c a b c b a a c c a --=>><<∴<>∴又且∴可得212-<<-a c ，……… 4分假设存在，由题意，则.1323310)1)((=+->+>+∴<<∴<-=--acm m a c a m a c m a因为,0)1()3(,),1()(=>+∴+∞f m f x f 单调递增在 即 存在这样的.0)3(>+m f m 使……… 6分（2）令.)()],()([21)()(21是二次函数则x g x f x f x f x g +-=)]()([41]2)()()(][2)()()([)()(22121221121≤--=+-+-=⋅x f x f x f x f x f x f x f x f x g x g又0)(,0)(,0)()(),()(2121==∴<⋅≠x g x g x g x g x f x f 且方程有两个不等实根 的根必有一个属于).,(21x x …… 10分（3）由0)0(=f 得c =0，∴bx ax x f +=2)(由x x f =)(，得方程0)1(2=-+x b ax ，解得1x =0，2x =ab-1， 又由})]([x x f f =得x x bf x f a =+)()]([2∴x x x x f b x x x f a =+-++-])([])([2∴0])([])([2])([22=-+-++-+-x bx x x f b ax x x f ax x x f a ∴0]12)(][)([=+++--b ax ax x af x x f 即0]1)1(][)([22=++++-b x b a x a x x f∴0)(=-x x f 或 01)1(22=++++b x b a x a （*）……12分由题意（*）式的解为0或ab-1或无解， 当（*）式的解为0时，可解得1-=b ，经检验符合题意；当（*）式的解为ab-1时，可解得3=b ，经检验符合题意；当（*）式无解时，0)1(4)1(222<+-+=∆b a b a ，即0)3)(1(2<-+b b a∴31<<-b综上可知，当31≤≤-b 时满足题意.…… 16分。

AD 江苏省2012届高三数学二轮专题训练：解答题（10）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1．（本小题满分14分）设ABC ∆的内角C B A 、、所对的边分别为c b a 、、.已知1=a ，2=b ，41cos =C . （Ⅰ）求ABC ∆的周长； （Ⅱ）求()C A -cos 的值. 2．（本小题满分14分）1．（本题满分14分）如图，矩形ABCD 中，AD ABE ⊥平面，2AE EB BC ===，F 为CE 上的点，且BF ACE ⊥平面，AC BDG =．（Ⅰ）求证：AE ⊥平面BCE ；（Ⅱ）求证：//AE 平面BFD ；（Ⅲ）求三棱锥C BGF -的体积．3．（本小题满分15分）如图所示，一科学考察船从港口O 出发，沿北偏东α角的射线OZ 方向航行，而在离港口a 13（a 为正常数）海里的北偏东β角的A 处有一个供给科考船物资的小岛，其中31tan =α，132cos =β．现指挥部需要紧急征调沿海岸线港口O 正东m （a m 37>）海里的B 处的补给船，速往小岛A 装运物资供给科考船，该船沿BA 方向全速追赶科考船，并在C 处相遇．经测算当两船运行的航向与海岸线OB 围成的三角形OBC 的面积最小时，这种补给最适宜．⑴ 求S 关于m 的函数关系式)(m S ；⑵ 应征调m 为何值处的船只，补给最适宜．4．（本小题满分15分）设等差数列{}n a 的前n 项和为n S ，且5133349a a S +==，．（1）求数列{}n a 的通项公式及前n 项和公式；（2）设数列{}n b 的通项公式为nn n a b a t=+（t 为正整数），问: 是否存在正整数t ，使得12m b b b ，，(3)m m ≥∈N ，成等差数列？若存在，求出t 和m 的值；若不存在，请说明理由.5．(本小题满分16分)（本题文科学生做，理科学生不做）如图，在平面直角坐标系xoy 中，已知1(4,0)F -，2(4,0)F ，(0,8)A ，直线(08)y t t =<<与线段1AF 、2AF 分别交于点P 、Q .(Ⅰ)当3t =时，求以12,F F 为焦点，且过PQ 中点的椭圆的标准方程； (Ⅱ)过点Q 作直线QR ∥1AF 交12F F 于点R ，记1PRF ∆的外接圆为圆C .① 求证:圆心C 在定直线7480x y ++=上；② 圆C 是否恒过异于点1F 的一个定点?若过，求出该点的坐标；若不过，请说明理由.第19题（本题理科学生做，文科学生不做）已知椭圆C ：x 2 a 2 +y 2 b 2 =1(a ＞b ＞0)的离心率为1 2 ，且经过点P (1，32)。

专题一集合、简单逻辑用语、函数、不等式、导数及应用第1讲集合与简单逻辑用语1. x＜0，有x2≤02. (2,3)解析：M＝(－∞，3)，N＝(2，＋∞)，∴ M∩N＝(2,3)．3. (－∞，－1)∪(3，＋∞)解析：不等式对应的二次函数开口向上，则Δ＝(a－1)2－4＞0.4. [－1,1]解析：集合A＝[－1,1]，B＝(－∞，1]，∴ A∩B＝A.5.215解析：⎩⎪⎨⎪⎧0≤a，a＋45≤10≤a≤15，⎩⎪⎨⎪⎧b－13≥0，b≤113≤b≤1，利用数轴，分类讨论可得集合A∩B的“长度”的最小值为13－15＝215.6. ⎣⎡⎦⎤－12，13解析：p：x2＋x－6＜0为真，则不等式的解集为A＝(－3,2)，由q：mx ＋1＞0得m＝0时，解集为B＝R，m＞0时，解集为B＝⎝⎛⎭⎫－1m，＋∞，m＜0时，解集为B＝⎝⎛⎭⎫－∞，－1m，m＝0时，A B成立；m＞0时，－1m≤－3,0＜m≤13；m＜0时，－1m≥2，－12≤m＜0，综上m∈⎣⎡⎦⎤－12，13.7. 12解析：这是一个典型的用韦恩图来求解的问题，如图．设两者都喜欢的人数为x，则只喜爱篮球的有15－x，只喜爱乒乓球的有10－x，由此可得(15－x)＋(10－x)＋x＋8＝30，解得x＝3，所以15－x＝12，即所求人数为12.8. (－∞，－4)∪(42，＋∞)解析：两集合分别表示半圆和直线，画图利用几何性质可得答案．9. 解：(1) 2－x＋3x＋1≥02x＋2－(x＋3)x＋1≥0x－1x＋1≥0(x－1)(x＋1)≥0且x≠－1x≥1或x＜－1.∴集合A＝{x|x≥1或x＜－1}．(2) (x－a－1)(2a－x)＞0(a<1)(x－a－1)(x－2a)＜0.∵a＜1，∴2a＜a＋1.∴2a＜x＜a ＋1.∴不等式的解为2a＜x＜a＋1.∴集合B＝{x|2a＜x＜a＋1}．∵B A，∴2a≥1或a ＋1≤－1，∴ a≥12或a≤－2.又a<1，则实数a的取值范围是(－∞，－2]∪⎣⎡⎭⎫12，1.10. 解：若命题p为真，则⎩⎪⎨⎪⎧m2－4＞0，－m＜0m＞2.若命题q为真，Δ＝16(m－2)2－16＜0,1＜m＜3.p或q为真，p且q为假，所以若命题p为真，命题q为假，则m≥3；若命题p 为假，命题q为真，则1＜m≤2，综上，则实数m的取值范围是{m|1＜m≤2或m≥3}．第2讲函数、图象及性质1. f(x)＝(x－2)2解析：函数满足f(x)＝f(x＋2)，函数周期为2.则x∈[2,3]，x－2∈[0,1]，f(x)＝f(x －2)＝(x －2)2.2. (0,1] 解析：y ＝x x －m ＝1＋m x －m，由反比例函数性质可得到0＜m ≤1；也可以用导数求得．3. 12 解析：f(－x)＝12－x －1＋a ＝2x 1－2x＋a ，f(－x)＝－f(x) 2x 1－2x ＋a ＝－⎝⎛⎭⎫12x －1＋a 2a ＝11－2x －2x 1－2x＝1，故a ＝12；也可用特殊值代入，但要检验．4. 1＜a ＜2 解析：函数为奇函数，在(－1,1)上单调递减，f(1－a)＋f(1－a 2)＞0，得f(1－a)＞f(a 2－1)．∴ ⎩⎪⎨⎪⎧－1＜1－a ＜1，－1＜1－a 2＜11－a ＜a 2－1，1＜a ＜ 2.5. [3，＋∞) 解析：⎩⎪⎨⎪⎧|x －2|－1≥0，x －1＞0，x －1≠1⎩⎪⎨⎪⎧x －2≥1或x －2≤－1，x ＞1，x ≠2x ≥3.6. 2 解析：函数满足f(x ＋2)＝1f (x )，故f(x ＋4)＝1f (x ＋2)＝f(x)，函数周期为4，f(2 012)＝f(0)，又f(2)＝1f (0)，∴ f(0)＝2.7. 3 解析：画图可知a ＋(－1)2＝1，a ＝3，也可利用f(0)＝f(2)求得，但要检验．8. 1 解析：由y ＝|x 2－2x －t|得y ＝|(x －1)2－1－t|，函数最大值只能在y(0)，y(1)，y(3)中取得，讨论可得只有t ＝1时成立．9. 解：(1) ∵ f(a ＋2)＝18，f(x)＝3x ，∴ 3a ＋2＝183a ＝2， ∴ g(x)＝(3a )x －4x ＝2x －4x ，x ∈[－1,1]．(2) g(x)＝－(2x )2＋2x ＝－⎝⎛⎭⎫2x －122＋14，当x ∈[－1,1]时，2x ∈⎣⎡⎦⎤12，2，令t ＝2x ，∴ y ＝－t 2＋t ＝－⎝⎛⎭⎫t －122＋14，由二次函数单调性知当t ∈⎣⎡⎦⎤12，2时y 是减函数，又t ＝2x 在[－1,1]上是增函数，∴ 函数g(x)在[－1,1]上是减函数．(也可用导数的方法证明)(3) 由(2)知t ＝2x,2x ∈⎣⎡⎦⎤12，2，则方程g(x)＝m 有解m ＝2x －4x在[－1,1]内有解m ＝t －t 2＝－⎝⎛⎭⎫t －122＋14，t ∈⎣⎡⎦⎤12，2， ∴ m 的取值范围是⎣⎡⎦⎤－2，14. 10. (1) 证明：取x ＝y ＝0，f(0)＝f(0)＋f(0)，∴ f(0)＝0，取y ＝－x ，则f(0)＝f(x)＋f(－x)，∴ f(－x)＝－f(x)，故f(x)是奇函数．(2)解： 任取x 2＞x 1，则x 2－x 1＞0，∴ f(x 2－x 1)＜0，又f(x 2－x 1)＝f(x 2)＋f(－x 1)＝f(x 2)－f(x 1)＜0，∴ f(x 2)＜f(x 1)，f(x)在[－3,3]上单调递减，f(－3)＝－f(3)＝－3f(1)＝6，∴ f(x)在[－3,3]上的最大值f(－3)＝6，最小值f(3)＝－6.第3讲 基本初等函数1. 2 解析：lg 22＋lg2lg5＋lg50＝lg2(lg2＋lg5)＋lg5＋lg10＝lg2lg(2·5)＋lg5＋1＝2.2. a ∈(1,2) 解析：y ＝log a (2－ax)是[0,1]上关于x 的减函数，∴ ⎩⎪⎨⎪⎧a ＞1，2－a ＞01＜a ＜2.3. [－3,1] 解析：2x 2＋2x －4≤122x 2＋2x －4≤2－1x 2＋2x －4≤－1x 2＋2x －3≤0－3≤x ≤－1.4. (2,2)5. a ≥2 解析： 二次函数f(x)＝－x 2＋2ax －1＋a 2开口向下，对称轴x ＝－2a－2＝a ，则a ≥2.6. ⎣⎡⎦⎤1，3127 解析：f(x)为偶函数，则b ＝0，又a －1＋2a ＝0，∴ a ＝13，f(x)＝13x 2＋1在⎣⎡⎦⎤－23，23上的值域为⎣⎡⎦⎤1，3127.7. f(－25)＜f(80)＜f(11) 解析：∵ f(x －4)＝－f(x)，∴ f(x －4)＝f(x ＋4)，∴ 函数周期T ＝8.∵ f(x)为奇函数，在区间[0,2]上是增函数，∴ f(x)在[－2,2]上是增函数．则f(－25)＝f(－1)，f(11)＝f(3)＝－f(－1)＝f(1)，f(80)＝f(0)．∵ f(－1)＜f(0)＜f(1)，∴ f(－25)＜f(80)＜f(11)．8. 4 解析：函数图象恒过定点(1,1)，从而m ＋n ＝1，又mn ＞0，∴ 1m ＋1n ＝m ＋n m ＋m ＋nn＝2＋n m ＋m n ≥4，当且仅当m ＝n 时取等号，1m ＋1n的最小值为4.9. 解：f(x)＝12p x 2－x ＋3＝12p (x －p)2＋3－p 2.① p ≤－1时，f(x)在[－1,2]上递减，M ＝f(－1)＝12p ＋4，m ＝f(2)＝2p ＋1，由2M ＋m ＝3，得p ＝－12(舍)．② －1＜p ＜0，M ＝f(p)＝3－p 2，m ＝f(2)＝2p ＋1，由2M ＋m ＝3，得p ＝2－6，p ＝2＋6(舍)．③ 0＜p ＜12，M ＝f(2)，m ＝f(p)，由2M ＋m ＝3，得p ＝2±23(舍)．④ 12≤p ≤2，M ＝f(－1)，m ＝f(p)由2M ＋m ＝3，得p ＝8±66(舍)． ⑤ p ＞2，M ＝f(－1)，m ＝f(2)由2M ＋m ＝3，得p ＝－12(舍)．综上，当p ＝2－6时，2M ＋m ＝3成立．10. 解：(1) 设P(x 0，y 0)是y ＝f(x)图象上的点，Q(x ，y)是y ＝g(x)图象上的点，则⎩⎪⎨⎪⎧ x ＝x 0－2a ，y ＝－y 0.∴ ⎩⎪⎨⎪⎧x 0＝x ＋2a ，y 0＝－y.又y 0＝log a (x 0－3a)，∴ －y ＝log a (x ＋2a －3a )，∴ y ＝log a1x －a (x ＞a)，即y ＝g(x)＝log a 1x －a(x ＞a)． (2) ∵ ⎩⎪⎨⎪⎧x －3a ＞0，x －a ＞0，∴ x ＞3a ，∵ f(x)与g(x)在x ∈[a ＋2，a ＋3]上有意义，∴ 3a ＜a ＋2,0＜a ＜1，∵ |f(x)－g(x)|≤1恒成立，∴ |log a (x －3a)(x －a)|≤1恒成立．∴⎩⎪⎨⎪⎧－1≤log a [(x －2a )2－a 2]≤1，0＜a ＜1a ≤(x －2a)2－a 2≤1a.对x ∈[a ＋2，a ＋3]时恒成立，令h(x)＝(x －2a)2－a 2，其对称轴x ＝2a,2a ＜2，而2＜a ＋2，∴ 当x ∈[a ＋2，a ＋3]时，h(x)min ＝h(a ＋2)，h(x)max ＝h(a ＋3)．∴ ⎩⎪⎨⎪⎧a ≤h (x )min ，1a ≥h (x )max⎩⎪⎨⎪⎧a ≤4－4a ，1a ≥9－6a0＜a ≤9－5712.第4讲 函数的实际应用1. log 32 解析：本题主要考查分段函数和简单的已知函数值求x 的值．由⎩⎪⎨⎪⎧x ≤1，3x＝2x ＝log 32或⎩⎪⎨⎪⎧x ＞1，－x ＝2无解，故应填log 32.2. 20% 解析：设该产品初始成本为a ，每年平均降低百分比为p ，则a(1－p)2＝0.64a ，∴ p ＝0.2.3. m ∈(1,2) 解析：令f(x)＝x 2－2mx ＋m 2－1，则⎩⎪⎨⎪⎧f (0)＞0，f (1)＜0，f (2)＜0，f (3)＞0.解得1＜m ＜2.4. a ＞1 解析：设函数y ＝a x (a ＞0，且a ≠1)和函数y ＝x ＋a ，则函数f(x)＝a x －x －a(a>0且a ≠1)有两个零点， 就是函数y ＝a x (a ＞0且a ≠1)与函数y ＝x ＋a 有两个交点，由图象可知当0＜a ＜1时两函数只有一个交点，不符合要求，当a ＞1时，因为函数y ＝a x (a ＞1)的图象过点(0,1)，而直线y ＝x ＋a 所过的点一定在点(0,1)的上方，所以一定有两个交点．所以实数a 的取值范围是a ＞1.5. 14 解析：设每个销售定价为x 元，此时销售量为100－10(x －10)，则利润y ＝(x －8)[100－10(x －10)]＝10(x －8)(20－x)≤10⎝⎛⎭⎫x －8＋20－x 22＝360，当且仅当x ＝14时取等号．6. ⎝⎛⎭⎫－1，－13 解析：由题意得f(1)·f(－1)＜0，即(3a ＋1)(a ＋1)＜0，－1＜a ＜－13. 7. 6 解析：⎩⎨⎧－a ＋22＝1，a ＋b2＝1b ＝6.8. ①③④ 解析：函数f(x)＝－|x|x 2＋bx 2＋c 为偶函数，当x ≥0时，f(x)＝－x 3＋bx 2＋c ，b ＜0，∴ f ′(x)＝－3x ⎝⎛⎭⎫x －2b3≤0对x ∈[0，＋∞)恒成立，∴ x ＝0时，f(x)在R 上有最大值，f(0)＝c ；由于f(x)为偶函数，②不正确；取b ＝3，c ＝－2③正确；若b ＜0，取a ＝0，若b ≥0，取a ＝2b3，故一定存在实数a ，使f(x)在[a ，＋∞)上单调减．9. (1)证明：由条件知f(2)＝4a ＋2b ＋c ≥2恒成立．又∵ x ＝2时，f(2)＝4a ＋2b ＋c ≤18(2＋2)2＝2恒成立，∴ f(2)＝2.(2)解： ∵ ⎩⎪⎨⎪⎧4a ＋2b ＋c ＝2，4a －2b ＋c ＝0，∴ 4a ＋c ＝2b ＝1，∴ b ＝12，c ＝1－4a.又f(x)≥x 恒成立，即ax 2＋(b －1)x ＋c ≥0恒成立． ∴ a ＞0，Δ＝⎝⎛⎭⎫12－12－4a(1－4a)≤0，∴(8a －1)2≤0. 解得：a ＝18，b ＝12，c ＝12，∴ f(x)＝18x 2＋12x ＋12.(3)解：(解法1) 由分析条件知道，只要f(x)图象(在y 轴右侧部分，包含与y 轴交点)总在直线y ＝m 2x ＋14上方即可，也就是直线的斜率m2小于直线与抛物线相切时的斜率，∴⎩⎨⎧y ＝18x 2＋12x ＋12，y ＝m 2x ＋14，解得 m ∈⎝⎛⎭⎫－∞，1＋22. (解法2)g(x)＝18x 2＋⎝⎛⎭⎫12－m 2x ＋12＞14在x ∈[0，＋∞)必须恒成立， 即x 2＋4(1－m)x ＋2＞0在x ∈[0，＋∞)恒成立． ① Δ<0，即[4(1－m)]2－8<0，解得：1－22＜m ＜1＋22； ② ⎩⎪⎨⎪⎧Δ≥0，－2(1－m )≤0，f (0)＝2＞0，解得：m ≤1－22. 综上，m ∈⎝⎛⎭⎫－∞，1＋22. 10. (1)证明： 当x ≥7时，f(x ＋1)－f(x)＝0.4(x －3)(x －4)，而当x ≥7时，函数y ＝(x －3)(x －4)单调递增，且(x －3)(x －4)>0， 故f(x ＋1)－f(x)单调递减，∴ 当x ≥7时，掌握程度的增长量f(x ＋1)－f(x)总是下降．(2)解： 由题意可知0.1＋15ln a a －6＝0.85，整理得aa －6＝e 0.05，解得a ＝e 0.05e 0.05－1·6＝20.50×6＝123.0,123.0∈(121,127]，由此可知，该学科是乙学科．第5讲 不等式及其应用1. (－∞，－2)∪(3，＋∞)2. (－1,2) 解析：由已知得a ＜0，b ＝－a ，ax －b x －2＞0即为ax ＋a x －2＞0，得x ＋1x －2＜0，得－1＜x ＜2.3. －6 解析：作出可行域，求出凸点坐标分别为(3，－3)，(4，－5)，(5，－1)，(6，－3)，则最优解为(4，－5)；或让直线t ＝x ＋2y 平行移动，当直线过点(4，－5)时，目标函数取最小值．4.116 解析：∵ x ，y ∈R ＋，∴ 1＝x ＋4y ≥2x·4y ，∴ xy ≤116，当且仅当x ＝4y ，即x ＝12，y ＝18时取等号． 5. 9 解析：∵ x ＞0，y ＞0，1x ＋4y ＝1，∴ x ＋y ＝(x ＋y)⎝⎛⎭⎫1x ＋4y ＝5＋y x ＋4xy ≥5＋2y x ·4x y＝9，当且仅当y x ＝4xy，即x ＝3，y ＝6时取等号．6. m ≤－5 解析：x 2＋mx ＋4＜0，x ∈(1,2)可得m ＜－⎝⎛⎭⎫x ＋4x ，而函数y ＝－⎝⎛⎭⎫x ＋4x 在(1,2)上单调增，∴ m ≤－5.7. ⎣⎡⎦⎤95，6 解析：变量x ，y 满足约束条件构成的区域是以(1,3)，(1,6)，⎝⎛⎭⎫52，92三点为顶点的三角形区域(含边界)，y x 表示区域内的点与原点连线的斜率，∴ y x ∈⎣⎡⎦⎤95，6 8. x ≥1 解析：n n ＋1＝1－1n ＋1＜1，当n 无限变大时，nn ＋1的值趋近于1，不等式要恒成立，显然x ＞12，2x －1|x|＞n n ＋1等价于2x －1x ≥1且x ＞12，故x ≥1.9. 解：(1) y ＝2 150＋10×55＋⎝⎛⎭⎫a 6x 2＋13x (55－1)x ＝2 700x ＋9ax ＋18.(0＜x ≤20，12≤a ≤1)．(2) 当34≤a ≤1时，y ≥22 700x·9ax ＋18＝1803a ＋18. 当且仅当2 700x ＝9ax ，即x ＝300a时取等号． 即当x ＝300a时，y min ＝1803a ＋18； 当12≤a ＜34时，y ′＝－2 700x 2＋9a ＜0，故y ＝f(x)在(0,20]上是减函数， 故当x ＝20时，y min ＝2 70020＋180a ＋18＝153＋180a. 答：若12≤a ＜34，则当车队速度为20 m/s 时，通过隧道所用时间最少；若34≤a ≤1时，则当车队速度为300am/s 时，通过隧道所用时间最少．10. 解：(1) ⎩⎪⎨⎪⎧f (0)＝0，f (－2)＝0⎩⎪⎨⎪⎧b ＝6，c ＝0，∴ f(x)＝3x 2＋6x ； (2) g(x)＝3⎣⎡⎦⎤x ＋⎝⎛⎭⎫1＋m 62－2－3×⎝⎛⎭⎫1＋m 62，－⎝⎛⎭⎫1＋m 6≤2，m ≥－18； (3) f(x)＋n ≤3即n ≤－3x 2－6x ＋3，而x ∈[－2,2]时，函数y ＝－3x 2－6x ＋3的最小值为－21，∴ n ≤－21，实数n 的最大值为－21.第6讲 导数及其应用1. f(x)＝x 2＋2x ＋12. 98 解析：f ′(2)＝4.5－4＝－98，切线方程为y ＝－98x ＋92，∴ f(2)＝94. 3. y ＝x －1 解析：y ′＝3x 2－2，k ＝y ′x ＝1＝1，则切线方程y －0＝1·(x －1)， ∴ x －y －1＝0.4. ⎣⎡⎭⎫0，π2∪⎣⎡⎭⎫2π3，π 解析：y ′＝3x 2－3≥－3，∴ tanα≥－3，0≤α＜π且α≠π2，结合正切函数图象可得答案．5. a ≥－4 解析：x ∈(0，＋∞)，f ′(x)＝1x ＋4x ＋a ≥0恒成立，由基本不等式1x ＋4x＋a ≥4＋a ，当且仅当x ＝12时取等号，∴ a ＋4≥0，∴ a ≥－4.6. 32 解析：f(x)＝x 3－12x ＋8，f ′(x)＝3(x －2)(x ＋2)，则f(x)的单调增区间是[－3，－2]∪[2,3]，减区间是[－2,2]，f(－3)＝17，f(2)＝－8，f(3)＝－1，f(－2)＝24，∴ M ＝24，m ＝－8.7. (－2,2) 解析：设f(x)＝x 3－3x ＋a ，f ′(x)＝3(x ＋1)(x －1)，f(x)在x ＝－1取极大值，在x ＝1时取极小值，⎩⎪⎨⎪⎧f (－1)＞0，f (1)＜0⎩⎪⎨⎪⎧a ＋2＞0，a －2＜0－2＜a ＜2.8. 4 解析：若x ＝0，则不论a 取何值，f(x)≥0显然成立；当x ＞0即x ∈(0,1]时，f(x)＝ax 3－3x ＋1≥0可化为，a ≥3x 2－1x3，设g(x)＝3x 2－1x 3，则g ′(x)＝3(1－2x )x 4，所以g(x)在区间⎝⎛⎦⎤0，12上单调递增，在区间⎣⎡⎭⎫12，1上单调递减，因此g(x)max ＝g ⎝⎛⎭⎫12＝4，从而a ≥4；当x ＜0即x ∈[－1,0)时，f(x)＝ax 3－3x ＋1≥0可化为a ≤3x 2－1x 3，设g(x)＝3x 2－1x 3，则g ′(x)＝3(1－2x )x 4＞0，显然g(x)在区间[－1,0)上单调递增，因此g(x)min ＝g(－1)＝4，从而a ≤4，综上，a ＝4.9. 解：(1) 因为函数f(x)，g(x)的图象都过点(t,0)，所以f(t)＝0，即t 3＋at ＝0.因为t ≠0，所以a ＝－t 2.g(t)＝0，即bt 2＋c ＝0，所以c ＝ab.又因为f(x)，g(x)在点(t,0)处有相同的切线，所以f ′(t)＝g ′(t)而f ′(x)＝3x 2＋a ，g ′(x)＝2bx ，所以3t 2＋a ＝2bt.将a ＝－t 2代入上式得b ＝t.因此c ＝ab ＝－t 3.故a ＝－t 2，b ＝t ，c ＝－t 3.(2) y ＝f(x)－g(x)＝x 3－t 2x －tx 2＋t 3，y ′＝3x 2－2tx －t 2＝(3x ＋t)(x －t)，因为函数y ＝f(x)－g(x)在(－1,3)上单调递减，所以⎩⎪⎨⎪⎧ y ′x ＝－1≤0，y ′x ＝3≤0.即⎩⎪⎨⎪⎧(－3＋t )(－1－t )≤0，(9＋t )(3－t )≤0，解得t ≤－9或t ≥3.所以t 的取值范围为(－∞，－9]∪[3，＋∞)．10. 解：(1) ∵ f(x)＝x 3＋ax ，g(x)＝x 2＋bx ，∴ f ′(x)＝3x 2＋a ，g ′(x)＝2x ＋b.x ∈[－1，＋∞)，f ′(x)g ′(x)≥0，即x ∈[－1，＋∞)，(3x 2＋a)(2x ＋b)≥0，∵ a ＞0，∴3x 2＋a ＞0，∴ x ∈[－1，＋∞)，2x ＋b ≥0，即∴ x ∈[－1，＋∞)，b ≥－2x ，∴ b ≥2，则所求实数b 的取值范围是[2，＋∞)．(2) b 的最小值为2，h(x)＝x 3－x 2＋ax －2x ，h ′(x)＝3x 2－2x ＋a －2＝3⎝⎛⎭⎫x －132＋a －73.当a ≥73时，h ′(x)＝3x 2－2x ＋a －2≥0对x ∈[－1，＋∞)恒成立，h(x)在[－1，＋∞)上单调增，当0＜a ＜73时，由h ′(x)＝3x 2－2x ＋a －2＝0得，x ＝1±7－3a 3＞－1，∴h(x)在⎣⎢⎡⎦⎥⎤－1，1－7－3a 3上单调增，在⎣⎢⎡⎦⎥⎤1－7－3a 3，1＋7－3a 3上单调减，在⎣⎢⎡⎭⎪⎫1＋7－3a 3，＋∞上单调增．滚动练习(一)1.24 解析：f(x)＝x α，f(4)＝12，α＝－12，f(x)＝x －12，f(8)＝24. 2. x ∈R ，都有x 2＋2x ＋5≠03. (－∞，0] 解析：x ＜－1时，不等式可化为x ＋(x ＋1)(－x －1＋1)≤1，－x 2≤1，∴ x ＜－1；x ≥－1时，不等式可化为x ＋x ＋1≤1，x ≤0，∴ －1≤x ≤0，综上x ≤0.4. 12 解析：考虑x ＞0时，f(x)＝x x ＋1＝1x ＋1x ≤12，当且仅当x ＝1时取等号． 5. [－4,0)∪(0,1) 解析：⎩⎪⎨⎪⎧x 2－3x ＋2≥0，－x 2－3x ＋4≥0，x ≠0.上面式中等号不能同时成立．6. 2 解析：在同一个直角坐标系中作出函数y ＝⎝⎛⎭⎫12x，y ＝3－x 2的图象，两个函数图象有两个交点．7. (－∞，－1)∪(3，＋∞) 解析：x 2＋ax ＞4x ＋a －3可化为(x －1)a ＋x 2－4x ＋3＞0对a ∈[0,4]恒成立，设f(a)＝(x －1)a ＋x 2－4x ＋3，∴ ⎩⎪⎨⎪⎧f (0)＞0，f (4)＞0.解得x ＜－1或x ＞3.8. －1或－2564 解析： 设过(1,0)的直线与y ＝x 3相切于点(x 0，x 30)，所以切线方程为y －x 30＝3x 20(x －x 0)，即y ＝3x 20x －2x 30，又(1,0)在切线上，则x 0＝0或x 0＝32，当x 0＝0时，由直线y ＝0与抛物线y ＝ax 2＋154x －9相切可得a ＝－2564，当x 0＝32时，由直线y ＝274x －274与曲线y ＝ax 2＋154x －9相切可得a ＝－1.9. 2 008 解析：令3x ＝t ，则x ＝log 3t ，则f(2)＋f(4)＋f(8)＋…＋f(28)＝4log 23(log 321＋2＋…＋8)＋233×8＝2 008.10. a ≥2 解析：由log a x ＋log a y ＝3，得y ＝a 3x ，函数y ＝a 3x 在x ∈[a,2a]上单调递减，得其值域为⎣⎡⎦⎤a 32a ，a 3a ，由题知⎣⎡⎦⎤a 32a ，a3a [a ，a 2]，∴ a ≥2. 11. 解：p 为真，则|x －4|≤6的解集为A ＝[－2,10]，q 为真，x 2－2x ＋1－m 2≤0(m ＞0)的解集为B ＝[1－m,1＋m]，∵ p 是q 的必要而不充分条件，∴ p 是q 的充分而不必要条件，∴ A ＝[－2,10]B ＝[1－m,1＋m]，∴⎩⎪⎨⎪⎧1＋m ≥10，1－m ≤－2.两式中等号不能同时成立，又m ＞0，∴ m ≥9. 12. 解：(1) 令g(x)＝f(x)－x ＝x 2＋(a －1)x ＋a ，则由题意可得⎩⎪⎨⎪⎧Δ＞0，＜1－a 2＜1，g (1)＞0，g (0)＞0⎩⎪⎨⎪⎧a ＞0，－1＜a ＜1，a ＜3－22或a ＞3＋220＜a ＜3－2 2.故所求实数a 的取值范围是(0,3－22)．(2) f(0)·f(1)－f(0)＝2a 2，令h(a)＝2a 2.∵ 当a ＞0时h(a)单调递增，∴ 当0＜a ＜3－22时，0＜h(a)＜h(3－22)＝2(3－22)2＝2(17－122)＝217＋122＜116，即f(0)·f(1)－f(0)＜116.13. 解：(1) ① 当0＜t ≤10时，V(t)＝(－t 2＋14t －40)e 14t ＋50＜50，化简得t 2－14t ＋40＞0，解得t ＜4或t ＞10，又0＜t ≤10，故0＜t ＜4.② 当10＜t ≤12时，V(t)＝4(t －10)(3t －41)＋50＜50，化简得(t －10)(3t －41)＜0，解得10＜t ＜413，又10＜t ≤12，故10＜t ≤12.综合得0＜t ＜4或10＜t ≤12；故知枯水期为1月，2月，3月，11月，12月共5个月．(2)由(1)知：V(t)的最大值只能在(4,10)内达到．由V ′(t)＝e 14t ⎝⎛⎭⎫－14t 2＋32t ＋4＝－14e 14t(t ＋2)(t －8)，令V ′(t)＝0，解得t ＝8(t ＝－2舍去)． 当t 变化时，V ′(t) 与V (t)的变化情况如下表：t (4,8) 8 (8,10) V ′(t) ＋ 0 － V(t)极大值由上表，V(t)在t ＝8时取得最大值V(8)＝8e ＋50＝108.32(亿立方米)．故知一年内该水库的最大蓄水量是108.32亿立方米．14. 解：(1) 当x ∈[－2，－1)时，f(x)＝x ＋1x 在[－2，－1)上是增函数(用导数判断)，此时f(x)∈⎣⎡⎭⎫－52，－2，当x ∈⎣⎡⎭⎫－1，12时，f(x)＝－2，当x ∈⎣⎡⎦⎤12，2时，f(x)＝x －1x 在⎣⎡⎦⎤12，2上是增函数，此时f(x)∈⎣⎡⎦⎤－32，32，∴ f(x)的值域为⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32. (2) ① 若a ＝0，g(x)＝－2，对于任意x 1∈[－2,2]，f(x 1)∈⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32，不存在x 0∈[－2,2]使得g(x 0)＝f(x 1)都成立．② 若当a ＞0时，g(x)＝ax －2在[－2,2]是增函数，g(x)∈[－2a －2,2a －2]，任给x 1∈[－2,2]，f(x 1)∈⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32，若存在x 0∈[－2,2]，使得g(x 0)＝f(x 1)成立，则⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32[－2a －2,2a －2]，∴有⎩⎨⎧－2a －2≤－52，2a －2≥32，解得 a ≥74.③ 若a ＜0，g(x)＝ax －2在[－2,2]上是减函数，g(x)∈[2a －2， －2a －2]，任给x 1∈[－2,2]，f(x 1)∈⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32， 若存在x 0∈[－2,2]使得g(x 0)＝f(x 1)成立， 则⎣⎡⎦⎤－52，－2∪⎣⎡⎦⎤－32，32[2a －2，－2a －2]⎩⎨⎧2a －2≤－52，－2a －2≥32，解得 a ≤－74.综上，实数a 的取值范围是⎝⎛⎦⎤－∞，－74∪⎣⎡⎭⎫74，＋∞.专题二 三角函数与平面向量 第7讲 三角函数的图象与性质1. y ＝sin ⎝⎛⎭⎫2x ＋π3，x ∈R 2. 103. 1 解析：f(x)＝f ⎝⎛⎭⎫π4cosx ＋sinx ，f ′(x)＝－f ′⎝⎛⎭⎫π4sinx ＋cosx ，f ′⎝⎛⎭⎫π4＝－22f ′⎝⎛⎭⎫π4＋22，f ′⎝⎛⎭⎫π4＝2－1，f(x)＝(2－1)cosx ＋sinx ，f ⎝⎛⎭⎫π4＝(2－1)×22＋22＝1. 4. 6 解析：平移后f(x)＝cos ⎝⎛⎭⎫ωx －ωπ3，与原来函数图象重合，则ωπ3＝2kπ，k ∈Z ，∵ ω＞0，∴ ωmin ＝6.5. ⎣⎡⎦⎤－54，1 解析：a ＝cos 2x －cosx －1＝⎝⎛⎭⎫cosx －122－54，转化为函数的值域问题． 6. 2＋22 解析：f(x)＝2sin πx4，周期为8，f(1)＋f(2)＋f(3)＋…＋f(2 012)＝f(1)＋f(2)＋f(3)＋f(4)＝2＋2 2.7. 2 解析：T ＝2ππ2＝4，对任意x ∈R ，都有f(x 1)≤f(x)≤f(x 2)成立，f(x)min ＝f(x 1)，f(x)max＝f(x 2)，于是|x 1－x 2|min ＝T2＝2.8. 23 解析：考查三角函数的图象、数形结合思想．线段P 1P 2的长即为sinx 的值，且其中的x 满足6cosx ＝5tanx ，解得sinx ＝23.线段P 1P 2的长为23.9. 解：f(x)＝－2asin ⎝⎛⎭⎫2x ＋π6＋2a ＋b ，sin ⎝⎛⎭⎫2x ＋π6∈⎣⎡⎦⎤－12，1， 当a ＞0时，－2a ＋2a ＋b ＝－5，－2a ×⎝⎛⎭⎫－12＋2a ＋b ＝1，∴ a ＝2，b ＝－5； 当a ＜0时，－2a ＋2a ＋b ＝1，－2a ×⎝⎛⎭⎫－12＋2a ＋b ＝－5，∴ a ＝－2，b ＝1； a ＝0，不存在．综上，a ＝2，b ＝－5或a ＝－2，b ＝1.10. 解：(1) 由最低点为M ⎝⎛⎭⎫2π3，－2得A ＝2，由T ＝π得ω＝2πT ＝2ππ＝2， 由点M ⎝⎛⎭⎫2π3，－2在图象上得2sin ⎝⎛⎭⎫4π3＋φ＝－2，即sin ⎝⎛⎭⎫4π3＋φ＝－1， 所以4π3＋φ＝2kπ－π2，故φ＝2kπ－11π6(k ∈Z )．又φ∈⎝⎛⎭⎫0，π2，所以φ＝π6，所以f(x)＝2sin ⎝⎛⎭⎫2x ＋π6. (2) 因为x ∈⎣⎡⎦⎤0，π12，2x ＋π6∈⎣⎡⎦⎤π6，π3，所以当2x ＋π6＝π6时，即x ＝0时，f(x)取得最小值1；当2x ＋π6＝π3，即x ＝π12时，f(x)取得最大值 3.第8讲 三角变换与解三角形1. 3 解析：∵ sin 2α＋cos2α＝14，∴ sin 2α＋1－2sin 2α＝14，∴ sin 2α＝34，∵ α∈⎝⎛⎭⎫0，π2，∴ s inα＝32，∴ α＝π3，tanα＝ 3. 2. 523 解析：由正弦定理a sinA ＝b sinB ，得 a ＝bsinAsinB ＝5·1322＝523.3. 5 解析：12arcsinB ＝2，c ＝42，由余弦定理可求得b.4. 1 解析：由sin 2α＋sinαcosα－2cos 2α＝0，得tan 2α＋tanα－2＝0，tanα＝1或tanα＝－2(舍)，sin2α＝2sinαcosα＝2tanα1＋tan 2α＝21＋1＝1. 5. 4 解析：由余弦定理得b a ＋ab ＝6cosC ，a 2＋b 2ab ＝6×a 2＋b 2－c 22ab ，a 2＋b 2＝32c 2，tanC tanA ＋tanC tanB ＝sinC cosC ⎝⎛⎭⎫cosA sinA ＋cosB sinB ＝1cosC ⎝⎛⎭⎫sin 2C sinAsinB ＝2ab a 2＋b 2－c 2⎝⎛⎭⎫c 2ab ＝2c 2a 2＋b 2－c 2，将a2＋b 2＝32c 2代入上式即可．注：(1) 在用正、余弦定理处理三角形中的问题时，要么把所有关系转化为边的关系，要么把所有的关系都转化为角的关系；(2) 本题也可以转化为角的关系来处理．6.724 解析：tanα＝－34，tanβ＝－12，tan2β＝－43. 7. －17 解析：由余弦定理得c ＝a 2＋b 2－2abcosC ＝3，故最大角为角B.8.817 解析：12bcsinA ＝－(b 2＋c 2－a 2)＋2bc ，12bcsinA ＝－2bccosA ＋2bc ， 2－12sinA ＝2cosA ，⎝⎛⎭⎫2－12sinA 2＝(2cosA)2＝4(1－sin 2A)，sinA ＝817. 9. 解：(1) ∵ c 2＝a 2＋b 2－2abcosC ＝1＋4－4×14＝4，∴ c ＝2，∴ △ABC 的周长为a ＋b ＋c ＝1＋2＋2＝5. (2) ∵ cosC ＝14，∴ sinC ＝1－cos 2C ＝1－⎝⎛⎭⎫142＝154， ∴ sinA ＝asinC c ＝1542＝158.∵ a ＜c ，∴ A ＜C ，故A 为锐角，∴ cosA ＝1－sin 2A ＝1－⎝⎛⎭⎫1582＝78，∴ cos(A －C)＝cosAcosC ＋sinAsinC ＝78×14＋158×154＝1116.10. 解：(1) sin 2B ＋C 2＋cos2A ＝1－cos (B ＋C )2＋cos2A ＝1＋cosA 2＋2cos 2A －1＝5950.(2) ∵ cosA ＝45，∴ sinA ＝35，∴ S △ABC ＝12bcsinA ＝310bc ，∵ a ＝2，由余弦定理得：a 2＝b 2＋c 2－2bccosA ＝4，∴ 85bc ＋4＝b 2＋c 2≥2bc ，bc ≤10，∴ S △ABC ＝12×bcsinA ＝310bc ≤3，当且仅当b ＝c 时，取得最大值，所以当b ＝c 时，△ABC 的面积S 的最大值为3.第9讲 平面向量及其应用1. ⎝⎛⎭⎫45，－35或⎝⎛⎭⎫－45，352.10 解析：|α|＝1，|β|＝2，α⊥(α－2β)，得α·(α－2β)＝0，α·β＝12，|2α＋β|＝4α2＋4α·β＋β2＝10.3. π3 解析：∵ (a ＋2b )·(a －b )＝－6，∴ |a|2－2|b|2＋a·b ＝－6，∴ a·b ＝1，cos 〈a ，b 〉＝a·b |a|·|b|＝12. 4. 4 解析：设BC 边中点为D ，则AO →＝23AD →，AD →＝12(AB →＋AC →)，∴ AO →·AC →＝13(AB →＋AC →)·AC →＝13(3×2×cos60°＋32)＝4.5. (－3,1)或(－1,1) 解析：设a ＝(x ，y)，∴ a ＋b ＝(x ＋2，y －1)，∴ ⎩⎪⎨⎪⎧ y －1＝0，(x ＋2)2＋(y －1)2＝1，∴ ⎩⎪⎨⎪⎧ x ＝－1，y ＝1或⎩⎪⎨⎪⎧x ＝－3，y ＝1. 6. －14 解析：AD →·BE →＝12(AB →＋AC →)·⎝⎛⎭⎫23AC →－AB → ＝12⎝⎛⎭⎫－1＋23－13×12＝－14. 7. 1－2 解析：设a ＋b ＝2d ，则d 为单位向量． (a －c )·(b －c )＝1－(a ＋b )·c ＝1－2d·c ＝1－2cos 〈d ，c 〉．8. 2 解析：取O 为坐标原点，OA 所在直线为x 轴，建立直角坐标系，则A(1,0)，B ⎝⎛⎭⎫－12，32，设∠COA ＝θ，则θ∈⎣⎡⎦⎤0，2π3，C(cosθ，sinθ)，∴ (cosθ，sinθ)＝x(1,0)＋y ⎝⎛⎭⎫－12，32，x ＋y ＝3sinθ＋cosθ＝2sin ⎝⎛⎭⎫θ＋π6，θ＝π3时取最大值2. 9. 解：(1) 由m·n ＝0得－cosA ＋3sinA ＝0，tanA ＝33，A ∈(0，π)， ∴ A ＝π6.(2)1＋sin2B cos 2B －sin 2B ＝－3，∴ sinB ＋cosBcosB －sinB＝－3，∴ tanB ＝2，∴ tanC ＝tan ⎝⎛⎭⎫π－π6－B ＝－tan π6＋tanB 1－tan π6tanB＝8＋5 3. 10. 解：(1) 在Rt △ADC 中，AD ＝8，CD ＝6， 则AC ＝10，cos ∠CAD ＝45，sin ∠CAD ＝35.又∵ AB →·AC →＝50，AB ＝13，∴ cos ∠BAC ＝AB →·AC →|AB →||AC →|＝513.∵ 0＜∠BAC ＜π，∴ sin ∠BAC ＝1213.∴ sin ∠BAD ＝sin(∠BAC ＋∠CAD)＝6365.(2) S △BAD ＝12AB·AD·sin ∠BAD ＝2525，S △BAC ＝12AB·AC·sin ∠BAC ＝60，S △ACD ＝24，则S △BCD ＝S △ABC ＋S △ACD －S △BAD ＝1685，∴ S △ABD S △BCD ＝32.滚动练习(二)1. {－1,0,1} 解析：M ＝{－2，－1,0,1}，N ＝{－1,0,1,2,3}，则M ∩N ＝{－1,0,1}．2. 0 解析：f(1)＝－f(－1)＝－(－3＋2＋1)＝0.3. 2 解析：cos10°＋3sin10°1－cos80°＝2sin40°2sin 240°＝ 2.4. (－3,2) 解析：6－x －x 2＞0，∴ x 2＋x －6＜0，∴ －3＜x ＜2.5. 2 解析：f ′(x)＝3x 2－6x ＝3x(x －2)，则函数的增区间是(－∞，0)∪(2，＋∞)，减区间是(0,2)，所以函数在x ＝2处取极小值．6. 1 解析：a －2b ＝(3，3)与c 共线，则3·3＝3k ，∴ k ＝1.7. 6 解析：A*B ＝{0,2,4}．8. 充要 解析：f(x)＝x 2＋mx ＋1的图象关于直线x ＝1对称－m2＝1m ＝－2.9. (－∞，2ln2－2] 解析：f ′(x)＝e x －2，x ∈(－∞，ln2)，f ′(x)＜0，x ∈(ln2，＋∞)，f ′(x)＞0，x ＝ln2时，f(x)取极小值即为最小值2－2ln2＋a ≤0，a ≤2ln2－2；本题也可转化为a ＝－e x ＋2x ，求函数g(x)＝－e x ＋2x 值域即可．10. ②④ 解析：函数为偶函数，在⎣⎡⎦⎤0，π2上单调增，画图即可． 11. 点拨：本题考查函数的概念和性质，对分段函数在讨论其性质时要整体考虑．对二次函数要能用数形结合的思想来研究它的单调性与最值等问题．解：(1) 函数f(x)为奇函数，f(－x)＋f(x)＝0对x ∈R 恒成立，m ＝2；(2) 由f(x)＝⎩⎪⎨⎪⎧－x 2＋2x ，x ＞00，x ＝0，x 2＋2x ，x ＜0，知f(x)在[－1,1]上单调递增，∴ ⎩⎪⎨⎪⎧a －2＞－1，a －2≤1，得1＜a ≤3，即实数a 的取值范围是(1,3]． 12. 点拨：本小题主要考察综合运用三角函数公式、三角函数的性质进行运算、变形、转换和求解的能力．解：(1)∵ f(x)＝sin(π－ωx)cosωx ＋cos 2ωx ，∴ f(x)＝sinωxcosωx ＋1＋cos2ωx 2＝12sin2ωx ＋12cos2ωx ＋12＝22sin ⎝⎛⎭⎫2ωx ＋π4＋12，由ω＞0得2π2ω＝π，∴ ω＝1. (2) 由(1)知f(x)＝22sin ⎝⎛⎭⎫2x ＋π4＋12， ∴ g(x)＝f(2x)＝22sin ⎝⎛⎭⎫4x ＋π4＋12，当0≤x ≤π16时，π4≤4x ＋π4≤π2，∴ 22≤sin ⎝⎛⎭⎫4x ＋π4≤1. 因此1≤g(x)≤1＋22，故x ＝0时，g(x)在此区间内取最小值为1.13. 点拨：本题考查同角三角函数的基本关系，三角形面积公式，向量的数量积，利用余弦定理解三角形以及运算求解能力．解：由cosA ＝1213，得sinA ＝1－⎝⎛⎭⎫12132＝513.又12bcsinA ＝30，∴ bc ＝156. (1) AB →·AC →＝bccosA ＝156×1213＝144.(2) a 2＝b 2＋c 2－2bccosA ＝(c －b)2＋2bc(1－cosA)＝1＋2×156×⎝⎛⎭⎫1－1213＝25，∴ a ＝5. 14. 点拨：应用题是高考必考题型，解决应用题的关键要学会审题，根据条件，选择合适的变量，建立数学模型，选择适当的方法解题，结论要符合题意．解：∵ △ABC 是直角三角形，AB ＝2，BC ＝1，∴ ∠A ＝30°.设∠FEC ＝α，则α∈⎝⎛⎭⎫0，π2，∠EFC ＝90°－α，∠AFD ＝180°－60°－(90°－α)＝30°＋α，∴ ∠ADF ＝180°－30°－(30°＋α)＝120°－α，再设CF ＝x ，则AF ＝3－x ，在△ADF 中有DFsin30°＝3－x sin (120°－α)，由于x ＝EF·sinα＝DF·sinα， ∴DF sin30°＝3－DF·sinαsin (120°－α)，化简得DF ＝32sinα＋3cosα≥37＝217， ∴ △DEF 边长的最小值为217.专题三 数 列第10讲 等差数列与等比数列1. 13 解析：a 3＝7，a 5＝a 2＋6，∴ 3d ＝6，∴ a 6＝a 3＋3d ＝13.2. 13 解析：6S 5－5S 3＝5，∴ 6(5a 1＋10d)－5(3a 1＋3d)＝5，得a 1＋3d ＝13. 3. 20 解析：a n ＝41－2n ，a 20＞0，a 21＜0.4.152 解析：a 2＝1，a n ＋2＋a n ＋1＝6a n ，∴ q 2＋q ＝6(q ＞0)，∴ q ＝2，则S 4＝152. 5. 15 解析：S 4a 4＝a 1(1－q 4)1－q a 1q 3＝1－q 4(1－q )q 3＝15.6. 4 解析：设公差为d ，则⎩⎨⎧4a 1＋4×32d ≥10，5a 1＋5×42d ≤15.即⎩⎪⎨⎪⎧2a 1＋3d ≥5，a 1＋2d ≤3.又a 4＝a 1＋3d ，由线性规划可知a 1＝1，d ＝1时，a 4取最大值4.7.212解析：a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝33＋2(1＋2＋…＋(n －1))＝n 2－n ＋33，a n n ＝n ＋33n －1，数列⎩⎨⎧⎭⎬⎫a n n 在1≤n ≤6，n ∈N *时单调减，在n ≥7，n ∈N *时单调增，∴ n ＝6时，a nn取最小值．8. 4 解析：⎩⎨⎧k (k ＋4)⎝⎛⎭⎫23k≥(k －1)(k ＋3)⎝⎛⎭⎫23k －1，k (k ＋4)⎝⎛⎭⎫23k≥(k ＋1)(k ＋5)⎝⎛⎭⎫23k ＋1，10≤k ≤1＋10，k ∈N *，∴ k ＝4.9. 解：(1) 设公差为d ，则⎩⎪⎨⎪⎧(a 1＋2d )(a 1＋5d )＝55，2a 1＋7d ＝16，解得⎩⎪⎨⎪⎧ a 1＝1，d ＝2.或⎩⎪⎨⎪⎧a 1＝15，d ＝－2.(舍去) ∴ a n ＝2n －1(n ∈N *)．(2) n ＝1时，a 1＝b 12，a 1＝1，∴ b 1＝2，n ≥2时，a n －1＝b 12＋b 222＋…＋b n －12n －1，2＝a n －a n －1＝b n 2n (n ≥2)，b n ＝2n ＋1(n ≥2)，∴ b n ＝⎩⎪⎨⎪⎧2(n ＝1)，2n ＋1(n ≥2，n ∈N *)，S n ＝2n ＋2－6(n ∈N *)． 10. (解法1)(1)证明：由b n ＋1b n ＝q ，有a n ＋1a n ＋2a n a n ＋1＝a n ＋2a n＝q ，∴ a n ＋2＝a n q 2(n ∈N *)． (2)证明：∵ a n ＝a n －2q 2(n ≥3，n ∈N *)，∴ a 2n －1＝a 2n －3q 2＝…＝a 1q 2n －2，a 2n ＝a 2n －2q 2＝…＝a 2q 2n －2，∴ c n ＝a 2n －1＋2a 2n ＝a 1q 2n －2＋2a 2q 2n －2＝(a 1＋2a 2)q 2n －2＝5q 2n －2. ∴ {c n }是首项为5，以q 2为公比的等比数列．(3) 解：由(2)得1a 2n －1＝1a 1q 2－2n ，1a 2n ＝1a 2q 2－2n ，于是1a 1＋1a 2＋…＋1a 2n ＝⎝⎛⎭⎫1a 1＋1a 3＋…＋1a 2n －1＋⎝⎛⎭⎫1a 2＋1a 4＋…＋1a 2n ＝1a 1⎝⎛⎭⎫1＋1q 2＋1q 4＋…＋1q 2n －2＋1a 2⎝⎛⎭⎫1＋1q 2＋1q 4＋…＋1q 2n －2＝32⎝⎛⎭⎫1＋1q 2＋1q 4＋…＋1q 2n －2. 当q ＝1时，1a 1＋1a 2＋…＋1a 2n ＝32⎝⎛⎭⎫1＋1q 2＋1q 4＋…＋1q 2n －2＝32n.当q ≠1时，1a 1＋1a 2＋…＋1a 2n ＝32⎝⎛⎭⎫1＋1q 2＋1q 4＋…＋1q 2n －2＝32⎝ ⎛⎭⎪⎫1－q －2n 1－q －2＝32⎣⎢⎡⎦⎥⎤q 2n －1q 2n －2(q 2－1). 故1a 1＋1a 2＋…＋1a 2n＝⎩⎨⎧32n ，q ＝1，32⎣⎢⎡⎦⎥⎤q 2n －1q 2n －2(q 2－1)，q ≠1.(解法2)(1) 证明：同解法1(1)．(2) 证明：c n ＋1c n ＝a 2n ＋1＋2a 2n ＋2a 2n －1＋2a 2n ＝q 2a 2n －1＋2q 2a 2na 2n －1＋2a 2n＝q 2(n ∈N *)，又c 1＝a 1＋2a 2＝5，∴ {c n }是首项为5，以q 2为公比的等比数列．(3) 解：由(2)的类似方法得a 2n －1＋a 2n ＝(a 1＋a 2)q 2n －2＝3q 2n －2，1a 1＋1a 2＋…＋1a 2n ＝a 1＋a 2a 1a 2＋a 3＋a 4a 3a 4＋…＋a 2n －1＋a 2n a 2n －1a 2n ，∵ a 2k －1＋a 2k a 2k －1a 2k ＝3q 2k －22q 4k －4＝32q －2k ＋2，k ＝1,2，…，n.∴1a 1＋1a 2＋…＋1a 2k ＝32(1＋q 2＋…＋q －2n ＋2)．下同解法1.第11讲 数列求和及其综合应用1. 2n ＋1－n －2 解析：a n ＝2n －1,1＋(1＋2)＋(1＋2＋4)＋…＋(1＋2＋…＋2n －1)＝(2＋22＋23＋…＋2n )－n ＝2(2n －1)－n ＝2n ＋1－n －22. 2＋lnn 解析：累加可得．3. T 8T 4 T 12T 84. －p －q 解析：由求和公式知q ＝pa 1＋p (p －1)2d ，p ＝qa 1＋q (q －1)2d ，因为p ≠q ，两式相减得到－1＝a 1＋p ＋q －12d ，两边同时乘以p ＋q ，则－(p ＋q)＝(p ＋q)a 1＋(p ＋q )(p ＋q －1)2d ，即S p ＋q ＝－(p ＋q)．5. 2n ＋1 解析：由条件得b n ＋1＝a n ＋1＋2a n ＋1－1＝2a n ＋1＋22a n ＋1－1＝2a n ＋2a n －1＝2b n 且b 1＝4，所以数列{b n }是首项为4，公比为2的等比数列，则b n ＝4·2n －1＝2n ＋1.6. 11 解析：(a 1＋1)2＋(a 2＋1)2＋…＋(a 50＋1)2＝107，则(a 21＋a 22＋…＋a 250)＋2(a 1＋a 2＋…＋a 50)＋50＝107，∴ a 21＋a 22＋…＋a 250＝39，故a 1，a 2，…，a 50中数字0的个数为50－39＝11.7. [24,36] 解析：a n ＝6n －(9＋a)，由题知5.5≤9＋a6≤7.5，∴ 24≤a ≤36.8. 470 解析：由于⎩⎨⎧⎭⎬⎫cos 2nπ3－sin 2nπ3以3 为周期，故S 30＝⎝⎛⎭⎫－12＋222＋32＋⎝⎛⎭⎫－42＋522＋62＋…＋⎝⎛⎭⎫－282＋2922＋302 ＝∑k ＝110⎣⎡⎦⎤－(3k －2)2＋(3k －1)22＋(3k )2＝∑k ＝110 ⎣⎡⎦⎤9k －52＝9×10×112－25＝470，分组求和是解决本题的关键．9. 解：(1) 由S n ＝(1＋λ)－λa n S n －1＝(1＋λ)－λa n －1(n ≥2)．相减得：a n ＝－λa n ＋λa n －1，∴ a n a n －1＝λ1＋λ(n ≥2)，∴ 数列{a n }是等比数列．(2) f(λ)＝λ1＋λ，∴ b n ＝b n －11＋b n －11b n ＝1b n －1＋1，∴ ⎩⎨⎧⎭⎬⎫1b n 是首项为1b 1＝2，公差为1的等差数列，∴ 1b n ＝2＋(n －1)＝n ＋1.∴ b n ＝1n ＋1.(n ∈N *) (3) λ＝1时，a n ＝⎝⎛⎭⎫12n －1，∴ c n ＝a n⎝⎛⎭⎫1b n－1＝⎝⎛⎭⎫12n －1n ， ∴ T n ＝1＋2⎝⎛⎭⎫12＋3⎝⎛⎭⎫122＋…＋n ⎝⎛⎭⎫12n －1， ①12T n ＝⎝⎛⎭⎫12＋2⎝⎛⎭⎫122＋3⎝⎛⎭⎫123＋…＋n ⎝⎛⎭⎫12n ， ② ①－②得：12T n ＝1＋⎝⎛⎭⎫12＋⎝⎛⎭⎫122＋⎝⎛⎭⎫123＋…＋⎝⎛⎭⎫12n －1－n ⎝⎛⎭⎫12n ∴ 12T n ＝1＋⎝⎛⎭⎫12＋⎝⎛⎭⎫122＋⎝⎛⎭⎫123＋…＋⎝⎛⎭⎫12n －1－n ⎝⎛⎭⎫12n ＝ 2⎣⎡⎦⎤1－⎝⎛⎭⎫12n －n ⎝⎛⎭⎫12n ， 所以：T n ＝4－⎝⎛⎭⎫12n －2－2n ⎝⎛⎭⎫12n ＝4－n ＋22n －1. 10. 解：(1) n ＝1时，由S 2＝tS 1＋a ，解得a 2＝at ，当n ≥2时，S n ＝tS n －1＋a ，所以S n ＋1－S n ＝t(S n －S n －1)，即a n ＋1＝a n t ， 当n ＝1时，由S 2＝tS 1＋a 得a 2＝ta 1，又因为a 1＝a ≠0，综上，有a n ＋1a n＝t(n ∈N *)，所以{a n }是首项为a ，公比为t 的等比数列，所以a n ＝at n －1.(2) 当t ＝1时，S n ＝na ，b n ＝na ＋1，b n ＋1－b n ＝[(n ＋1)a ＋1]－[na ＋1]＝a ， 此时{b n }为等差数列；当a ＞0时，{b n }为单调递增数列，且对任意n ∈N *，a n ＞0恒成立，不合题意；当a ＜0时，{b n }为单调递减数列，由题意知b 4＞0，b 6＜0，且有⎩⎪⎨⎪⎧b 4≥|b 5|，－b 6≥|b 5|，即⎩⎪⎨⎪⎧|5a ＋1|≤4a ＋1，|5a ＋1|≤－6a －1，解得－29≤a ≤－211.综上，a 的取值范围是⎣⎡⎦⎤－29，－211. (3) 因为t ≠1，b n ＝1＋a 1－t －at n 1－t ，所以c n ＝2＋⎝⎛⎭⎫1＋a 1－t n －a 1－t (t ＋t 2＋…＋t n)＝2＋⎝⎛⎭⎫1＋a 1－t n －a (t －t n ＋1)(1－t )2＝2－at (1－t )2＋1－t ＋a 1－t ·n ＋at n ＋1(1－t )2，由题设知{c n }是等比数列，所以有⎩⎪⎨⎪⎧2－at (1－t )2＝0，1－t ＋a 1－t ＝0，解得⎩⎪⎨⎪⎧a ＝1，t ＝2，即满足条件的数对是(1,2)．(或通过{c n }的前3项成等比数列先求出数对(a ，t)，再进行证明)滚动练习(三)1. {4,5} 解析：A ∪B ＝{1,2,3}．2. π4 解析：由正弦定理a sinA ＝c sinC ，∴ sinA ＝cosA ，∴ tanA ＝1，∵ 0＜A ＜π， ∴ A ＝π4.3. 12 解析：由a 1＋3a 8＋a 15＝60得5a 1＋35d ＝60，a 8＝12,2a 9－a 10＝a 8＝12.4. 12 解析：周期是4π，∴ ω＝2π4π＝12. 5. [0,4) 解析：mx 2＋mx ＋1≠0对x ∈R 恒成立．当m ＝0时，成立；当m ≠0时，Δ＝m 2－4m ＜0，∴ 0＜m ＜4.综上，0≤m ＜4.6. 6 解析：本题考查线性规划内容．7. ⎝⎛⎭⎫7π6，11π6 解析：y ′＝1＋2sinx ＜0，∴ sinx ＜－12，∴ 7π6＜x ＜11π6. 8. π3 解析：∵ m ⊥n ，∴ (a ＋c)(a －c)＋b(b －a)＝0，∴ a 2＋b 2－c 22ab ＝12， ∴ cosC ＝12，∴ C ＝π3.9. (－∞，－1)∪(2，＋∞) 解析：画出符合题意的草图，则x －2＜－3或x －2＞0.10. 4 解析：本题其实是关于最小正周期问题．a 2＝a 1－t ，a 3＝t ＋2－a 1＋t ＝2t ＋2－a 1，a 4＝a 3－t ＝t ＋2－a 1，a 5＝t ＋2－a 4＝a 1，故实数k 的最小值是4.11. 解：(1) f(x)＝12sin2x ＋3cos 2x ＝12sin2x ＋32(1＋cos2x)＝sin ⎝⎛⎭⎫2x ＋π3＋32，∴ f(x)的最小正周期为T ＝2π2＝π. (2) 依题意得g(x)＝f ⎝⎛⎭⎫x －π4＋32＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4＋π3＋32＋32＝sin ⎝⎛⎭⎫2x －π6＋3，当x ∈⎣⎡⎦⎤0，π4时，2x －π6∈⎣⎡⎦⎤－π6，π3，∴ －12≤sin ⎝⎛⎭⎫2x －π6≤32，∴ 23－12≤g(x)≤332，∴ g(x)在⎣⎡⎦⎤0，π4的最大值为332. 12. 解：(1) 当n ≤6时，数列{a n }是首项为120，公差为－10的等差数列．a n ＝120－10(n －1)＝130－10n ；当n ≥7时，数列{a n }是以a 6为首项，公比为34的等比数列，又a 6＝70，所以a n ＝70×⎝⎛⎭⎫34n－6，因此，第n 年初，M 的价值a n 的表达式为a n ＝⎩⎪⎨⎪⎧130－10n ，n ≤6，n ∈N *，70×⎝⎛⎭⎫34n －6，n ≥7，n ∈N *. (2) 设S n 表示数列{a n }的前n 项和，由等差及等比数列的求和公式得当1≤n ≤6时，S n ＝120n －5n(n －1)，A n ＝120－5(n －1)＝125－5n ＞80；当n ≥7时，S n ＝S 6＋(a 7＋a 8＋…＋a n )＝570＋70×34×4×⎣⎡⎦⎤1－⎝⎛⎭⎫34n －6＝780－210×⎝⎛⎭⎫34n－6，A n ＝780－210×⎝⎛⎭⎫34n －6n.因为{a n }是递减数列，所以{A n }是递减数列，又A 8＝780－210×⎝⎛⎭⎫348－68＝824764＞80，A 9＝780－210×⎝⎛⎭⎫349－69＝767996＜80，所以须在第9年初对M进行更新．13. 解：(1) f ′(x)＝3x 2＋2ax ＋b.由题意得⎩⎪⎨⎪⎧f ′⎝⎛⎭⎫23＝3×⎝⎛⎭⎫232＋2a ×23＋b ＝0，f ′(1)＝3×12＋2a ×1＋b ＝3.解得⎩⎪⎨⎪⎧a ＝2，b ＝－4.设切线l 的方程为y ＝3x ＋m(m>0)，由原点到切线l 的距离为1010， 有|m|32＋1＝1010，解得m ＝1.∵ 切线l 不过第四象限，∴ m ＝1，m ＝－1(舍)，∴ 切线l 的方程为y ＝3x ＋1，由于切点的横坐标为x ＝1，∴ 切点坐标为(1,4)，∵ f(1)＝1＋a ＋b ＋c ＝4，∴ c ＝5.(2) 由(1)知f(x)＝x 3＋2x 2－4x ＋5，所以f ′(x)＝3x 2＋4x －4＝(x ＋2)(3x －2)，令f ′(x)＝0，得x 1＝－2，x 2＝23.x －4 (－4，－2)－2 ⎝⎛⎭⎫－2，2323 ⎝⎛⎭⎫23，1 1 f ′(x) ＋0 －0 ＋f(x)极大值 极小值函数值－11139527414. 解：(1) ∵ －1，S n ，a n ＋1成等差数列，∴ 2S n ＝a n ＋1－1， ① 当n ≥2时，2S n －1＝a n －1， ②①－②得：2(S n －S n －1)＝a n ＋1－a n ，∴ 3a n ＝a n ＋1，∵ a 1＝1≠0，∴ a n ≠0， ∴ a n ＋1a n＝3.当n ＝1时，由①得∴ 2S 1＝2a 1＝a 2－1，又a 1＝1，∴ a 2＝3， ∴a 2a 1＝3，∴ {a n }是以3为公比的等比数列，∴ a n ＝3n －1. (2) ∵ f(x)＝log 3x ，∴ f(a n )＝log 33n －1＝n －1，b n ＝1(n ＋3)[f (a n )＋2]＝1(n ＋1)(n ＋3)＝12⎝⎛⎭⎫1n ＋1－1n ＋3，∴ T n ＝1212－14＋13－15＋14－16＋15－17＋…＋1n －1n ＋2＋1n ＋1－1n ＋3＝1212＋13－1n ＋2－1n ＋3＝512－2n ＋52(n ＋2)(n ＋3)，比较T n 与512－2n ＋5312的大小，只需比较2(n ＋2)(n ＋3)与312的大小即可．又2(n ＋2)(n ＋3)－312＝2(n 2＋5n ＋6－156)＝2(n 2＋5n －150)＝2(n ＋15)(n －10)，∵ n ∈N *，∴ 当1≤n ≤9时n ∈N *,2(n ＋2)(n ＋3)＜312，即T n ＜512－2n ＋5312；∴ 当n＝10时，2(n ＋2)(n ＋3)＝312，即T n ＝512－2n ＋5312；当n ＞10且n ∈N *时，2(n ＋2)(n ＋3)＞312，即T n ＞512－2n ＋5312；当n ＝10时，2(n ＋2)(n ＋3)＝312，即T n ＝512－2n ＋5312；当n>10且n ∈N *时，2(n ＋2)(n ＋3)>312，即T n >512－2n ＋5312.。

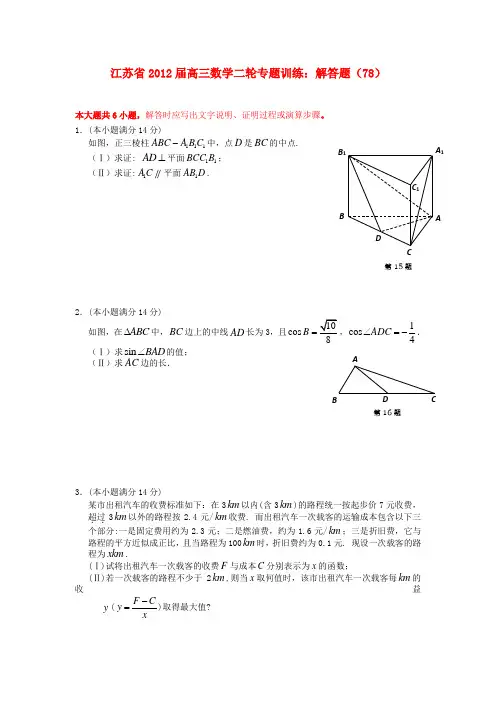
江苏省2012届高三数学二轮专题训练：解答题（78）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1．(本小题满分14分)如图，正三棱柱111ABC A B C -中，点D 是BC 的中点. （Ⅰ）求证: AD ⊥平面11BCC B ； （Ⅱ）求证:1A C平面1AB D .2．(本小题满分14分)如图，在ABC ∆中，BC 边上的中线AD 长为3，且cos B =，1cos 4ADC ∠=-． （Ⅰ）求sin BAD ∠的值； （Ⅱ）求AC 边的长．3．(本小题满分14分)某市出租汽车的收费标准如下：在3km 以内(含3km )的路程统一按起步价7元收费，超过．．3km 以外的路程按2.4元/km 收费. 而出租汽车一次载客的运输成本包含以下三个部分:一是固定费用约为2.3元；二是燃油费，约为1.6元/km ；三是折旧费，它与路程的平方近似成正比，且当路程为100km 时，折旧费约为0.1元. 现设一次载客的路程为xkm .(Ⅰ)试将出租汽车一次载客的收费F 与成本C 分别表示为x 的函数；(Ⅱ)若一次载客的路程不少于2km ,则当x 取何值时，该市出租汽车一次载客每km 的收益y (F Cy x-=)取得最大值?第15题ABCDA 1B 1C 1AD B C第16题4．(本小题满分16分)如图，在平面直角坐标系xoy 中，已知1(4,0)F -，2(4,0)F ，(0,8)A ，直线(08)y t t =<<与线段1AF 、2AF 分别交于点P 、Q .(Ⅰ)当3t =时，求以12,F F 为焦点，且过PQ 中点的椭圆的标准方程； (Ⅱ)过点Q 作直线1QRAF 交12F F 于点R ，记1PRF ∆的外接圆为圆C .① 求证:圆心C 在定直线7480x y ++=上；② 圆C 是否恒过异于点1F 的一个定点?若过，求出该点的坐标；若不过，请说明理由.5．(本小题满分16分)已知()f x 为R 上的偶函数，当0x ≥时，()ln(2)f x x =+. (Ⅰ)当0x <时，求()f x 的解析式；(Ⅱ)当m R ∈时，试比较(1)f m -与(3)f m -的大小；(Ⅲ)求最小的整数(2)m m ≥-，使得存在实数t ，对任意的[,10]x m ∈，都有()2ln |3|f x t x +≤+.第18题6．(本小题满分16分) 已知数列{}n a 满足11[2(1)][2(1)]1(1)3n n n n n a a n +++-++-=+-⋅，*n N ∈，12a =.(Ⅰ)求2a ，3a 的值；(Ⅱ)设2121n n n b a a +-=-，*n N ∈，证明: {}n b 是等差数列；(Ⅲ)设212n n c a n =+，求数列{}n c 的前n 项和n S .1．(本小题满分14分)证:（Ⅰ）因为ABC ∆是正三角形,而D 是BC 的中点，所以AD BC ⊥……………………………… 3分又BC 是两个相互垂直的平面ABC 与面11BCC B 的交线,且AD ABC ⊂面, 所以11AD BCC B ⊥面…………………………………………………………………………………… 7分（Ⅱ）连接1A B ,设11AB A B E =,则E 为1A B 的中点,连接DE ,由D 是BC 的中点,得DE AC ………11分 又1DE AB D ⊂面,且11A C AB D ⊄面,所以1A C平面1AB D………14分2．(本小题满分14分)解:（Ⅰ）因为cos B=，所以sin B=…………………………………………………………2分又1cos4ADC∠=-,所以sin4ADC∠=………………………………………………………… 4分所以sin sin()sin cos cos sinBAD ADC B ADC B ADC B∠=∠-∠=∠-∠1()4=--=………………………………………………………………………7分（Ⅱ）在ABD∆中,由正弦定理,得sin sinAD BDB BAD=∠,即84=,解得2BD=……………10分故2DC=,从而在ADC∆中,由余弦定理,得2222cosAC AD DC AD DC ADC=+-⋅∠=22132232()164+-⨯⨯⨯-=,所以4AC=………………………………………………………14分3．(本小题满分14分)解: (Ⅰ) 703()7 2.4(3)3xF xx x<≤⎧=⎨+⨯->⎩7032.40.23xx x<≤⎧=⎨->⎩…………………………3分设折旧费2z kx=,将(100,0.1)代入,得.20.1100k=,解得5110k=……………………………………5分所以251() 2.3 1.610C x x x=++…………………………………………………………………………7分(Ⅱ)因为F Cyx-=,所以554.711.623102.510.8()310x xxyx xx⎧--≤≤⎪⎪=⎨⎪-+>⎪⎩……………………………………11分①当3x>时,由基本不等式,得0.80.79y≤-=(当且仅当500x=时取等号)……………12分②当23x ≤≤时,由y 在[2,3]上单调递减,得max 554.7221.60.750.7921010y =--=-<…………13分答: 该市出租汽车一次载客路程为500km 时,每km 的收益y 取得最大值…………………………14分4．(本小题满分16分)解:(Ⅰ)设椭圆的方程为22221(0)x y a b a b+=>>,当3t =时,PQ 的中点为(0,3),所以b=3……………3分 而2216a b -=,所以225a =，故椭圆的标准方程为221204x y +=……………………………………5分 (Ⅱ)①解法一:易得直线12:28;:28AF y x AF y x =+=-+,所以可得88(,),(,)22t tP t Q t --,再由1QR AF ,得(4,0)R t -………………………………………8分则线段1F R 的中垂线方程为2t x =-, 线段1PF 的中垂线方程为151628t y x -=-+,由1516282t y x t x -⎧=-+⎪⎪⎨⎪=-⎪⎩,解得1PRF ∆的外接圆的圆心坐标为7(,2)28t t--…………………10分 经验证,该圆心在定直线7480x y ++=上…………………………………………………… 11分解法二: 易得直线12:28;:28AF y x AF y x =+=-+,所以可得88(,),(,)22t tP t Q t --, 再由1QRAF ,得(4,0)R t -……………………………………………………………………8分设1PRF ∆的外接圆C 的方程为220x y Dx Ey F ++++=,则2222(4)(4)0(4)4088()022t t D F y D F t t t D tE F ⎧⎪-+-+=⎪=--+=⎨⎪--⎪++++=⎩,解得744416D tE tF t =⎧⎪⎪=-⎨⎪=-⎪⎩…………………………………10分所以圆心坐标为7(,2)28t t--,经验证,该圆心在定直线7480x y ++=上…………………11分②由①可得圆C 的方程为227(4)41604x y tx t y t +++-+-=……………………………13分该方程可整理为227(216)(4)04x y y t x y ++-+-+=,则由2241607404x y y x y ⎧++-=⎪⎨-+=⎪⎩,解得4133213x y ⎧=⎪⎪⎨⎪=⎪⎩或40x y =-⎧⎨=⎩, 所以圆C 恒过异于点1F 的一个定点,该点坐标为432(,)1313…………………………………16分5．(本小题满分16分) 解: (Ⅰ)当0x <时，()()ln(2)f x f x x =-=-+…………………………………………………3分(Ⅱ)当0x ≥时,()ln(2)f x x =+单调递增,而()f x 是偶函数,所以()f x 在(,0)-∞上单调递减,所以(1)f m -＞22(3)|1||3|(1)(3)f m m m m m -⇔->-⇔->-2m ⇔>………………6分所以当2m >时, (1)(3)f m f m ->-；当2m =时, (1)(3)f m f m -=-； 当2m <时, (1)(3)f m f m -<-……………………………………………………………… 8分(Ⅲ)当x R ∈时,()ln(||2)f x x =+,则由()2ln |3|f x t x +≤+,得2ln(||2)ln(3)x t x ++≤+,即2||2(3)x t x ++≤+对[,10]x m ∈恒成立………………………………………………………12分从而有225777t x x t x x ⎧≤++⎨≥---⎩对[,10]x m ∈恒成立,因为2m ≥-， 所以22min 22max (57)57(77)77t x x m m t x x m m ⎧≤++=++⎨≥---=---⎩………………………………………………………14分因为存在这样的t ,所以227757m m m m ---≤++,即2670m m ++≥…………………… 15分 又2m ≥-,所以适合题意的最小整数1m =-………………………………………………………16分6．(本小题满分16分) 解: (Ⅰ)因为11[2(1)][2(1)]1(1)3n n n n n a a n +++-++-=+-⋅ (*),且12a =,所以将1n =代入(*)式,得1232a a +=-,故28a =-……1分 将2n =代入(*)式,得2337a a +=,故35a =…………2分(Ⅱ)在(*)式中,用2n 代换n ,得2122221[2(1)][2(1)]1(1)6n n n n n a a n +++-++-=+-⋅,即221316n n a a n ++=+ ①, 再在(*)式中,用21n -代换n ,得22121212[2(1)][2(1)]1(1)(63)n n n n n a a n ---+-++-=+-⋅-,即212346n n a a n -+=- ②, ①－②,得21213()123n n a a n +--=-,即41n b n =-…………………6分则由1(4(1)1)(41)4n n b b n n +-=+---=,得{}n b 是等差数列……………………………………… 8分(Ⅲ)因为12a =,由(Ⅱ)知,21131532123()()()k k k a a a a a a a a ---=+-+-+⋅⋅⋅+-2(411)(421)(4(1)1)k =+⨯-+⨯-+⋅⋅⋅+⨯--=(1)(21)2k k --+ ③, 将③代入②,得23(1)(21)646k k k a k --++=-,即22635k a k k =-+-………………………… 10分所以221211(21)2k k c a k --=+-=27452k k -+,2221(2)2k k c a k =+=2435k k -+-, 则212322k k c c k -+=--,所以21234212()()()k k k S c c c c c c -=++++⋅⋅⋅++=3[(21)2-⨯+3(22)2+⨯+3(2)]2k +⋅⋅⋅+⨯+23335[(21)(22)(2)]2222k k k -⨯++⨯++⋅⋅⋅+⨯+=--……… 13分所以2222122511()(435)3522k k k S S c k k k k k k -=-=----+-=-+…………………………… 15分故221135(21)25(2)2n k k n k S k k n k ⎧-+=-⎪⎪=⎨⎪--=⎪⎩223512()45()4n n n n n n ⎧-+⎪⎪=⎨+⎪-⎪⎩为数为数奇偶………………………………16分。

绝密★启用前2012届高三数学二轮精品专题卷：专题10 解析几何（直线与圆、椭圆、双曲线和抛物线）考试范围：解析几何（直线与圆、椭圆、双曲线和抛物线）一、选择题（本大题共10小题；每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．直线07tan =+y x π的倾斜角是 （ ）A ．7π-B ．7π C ．75π D ．76π 2．直线01:1=+-y x l 关于直线2:=x l 对称的直线2l 方程为 （ ） A ．012=--y x B ．072=-+y x C ．042=--y x D ．05=-+y x 3．“2-=a ”是直线()021:1=-++y x a l 与直线()0122:2=+++y a ax l 互相垂直的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．直线0=+++b a by ax 与圆222=+y x 的位置关系为 （ ） A ．相交B ．相切C ．相离D ．相交或相切5．已知点P 在圆074422=+--+y x y x 上，点Q 在直线上kx y =上，若PQ 的最小值为122-，则k = （ ）A ．1B ．1-C ．0D ．26．若椭圆122=+my x 的离心率⎪⎪⎭⎫⎝⎛∈22,33e ，则m 的取值范围是 （ ） A ．⎪⎭⎫ ⎝⎛32,21B ．()2,1C ．()2,132,21 ⎪⎭⎫⎝⎛D ．⎪⎭⎫ ⎝⎛2,217．已知中心在原点，焦点在坐标轴上的双曲线的一条渐近线方程为03=-y x ，则该双曲线的离心率为 （ ） A ．332 B ．3 C ．2或332 D ．332或3 8．M 是抛物线x y 42=上一点，且在x 轴上方，F 是抛物线的焦点，以x 轴的正半轴为始边，FM 为终边构成的最小的角为60°，则=FM （ ） A ．2B ．3C ．4D ．69．设抛物线x y 82=的准线经过中心在原点，焦点在坐标轴上且离心率为21的椭圆的一个顶点，则此椭圆的方程为（ ）A ．1161222=+y x 或1121622=+y xB ．1644822=+y x 或1486422=+y xC ．1121622=+y x 或1431622=+x y D ．13422=+y x 或1431622=+x y10．已知定点()0,21-F 、()0,22F ，动点N 满足1=（O为坐标原点），F 21=，()R MF ∈=λλ2，1=⋅PN M F ，则点P的轨迹是（ ） A ．椭圆B ．双曲线C ．抛物线D ．圆二、填空题（本大题共5小题；每小题5分，共25分.将答案填在题中的横线上）11．以点()2,1-为圆心且与直线1-=x y 相切的圆的标准方程是 ． 12．圆064422=++-+y x y x 上到直线05=--y x 的距离等于22的点有 个．13．若点P 在直线03:1=++my x l 上，过点P 的直线2l 与曲线()165:22=+-y x C 只有一个公共点M ，且PM 的最小值为4，则=m ． 14．在平面直角坐标系xOy 中，椭圆12222=+b y a x (a ＞b ＞0)的离心率为22，以O 为圆心，a 为半径作圆M ，再过⎪⎪⎭⎫⎝⎛0,2c a P 作圆M 的两条切线P A 、PB ，则A P B ∠= ．15．已知以双曲线的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角的范围是⎪⎭⎫⎝⎛2,3ππ则双曲线的离心率的范围是 ． 三、解答题（本大题共6小题；共75分.解答应写出文字说明、证明过程或演算步骤） 16．（本题满分12分）已知圆O 的方程为1622=+y x ． （1）求过点()8,4-M 的圆O 的切线方程；（2）过点()0,3N 作直线与圆O 交于A 、B 两点，求OAB △的最大面积以及此时直线AB 的斜率．17．（本题满分12分）将抛物线y x 222-=向上平移2个单位长度后，抛物线过椭圆12222=+by a x (a ＞b ＞0)的上顶点和左右焦点．（1）求椭圆方程；（2）若点()0,m P 满足如下条件：过点P 且倾斜角为π65的直线l 与椭圆相交于C 、D 两点，使右焦点F 在以CD 线段为直径的圆外，试求m 的取值范围．18．（本题满分12分）已知双曲线,12222=-b y a x (a ＞0，b ＞0)左右两焦点为1F 、2F ，P 是右支上一点，212F F PF ⊥，1PF OH ⊥于H ，1OF OH λ=，⎥⎦⎤⎢⎣⎡∈21,91λ．（1）当31=λ时，求双曲线的渐近线方程； （2）求双曲线的离心率e 的取值范围；（3）当e 取最大值时，过1F ，2F ，P 的y 轴的线段长为8，求该圆的方程．19．（本题满分13分）在平面直角坐标系xOy 中，过定点()0,p C 作直线m 与抛物线px y 22=(p ＞0)相交于A 、B 两点．（1）设()0,p N -，求NB NA ⋅的最小值；（2）是否存在垂直于x 轴的直线l ，使得l 被以AC 为直径的圆截得的弦长恒为定值？若存在，求出l 的方程；若不存在，请说明理由．20．（本题满分13分）已知椭圆C 的中心在原点，焦点在x 轴上，离心率等于21,它的一个顶点恰好是抛物线y x 382=的焦点．（1）求椭圆C 的方程；（2）()3,2P 、()3,2-Q 是椭圆上两点，A 、B 是椭圆位于直线PQ 两侧的两动点，①若直线AB 的斜率为21，求四边形APBQ 面积的最大值；②当A 、B 运动时，满足BPQ APQ ∠=∠，试问直线AB 的斜率是否为定值，请说明理由．21．（本题满分13分）在平面直角坐标系中，已知向量()2,-=y x a ，()()R k y kx b ∈+=2,，=．（1）求动点()y x M ,的轨迹T 的方程,并说明该方程表示的曲线的形状； （2）当34=k 时，已知()1,01-F 、()1,02F ，点P 是轨迹T 在第一象限的一点，且满足1=，若点Q 是轨迹T 上不同于点P 的另一点，问是否存在以PQ 为直径的圆G 过点2F ，若存在，求出圆G 的方程，若不存在，请说明理由．2012届专题卷数学专题十答案与解析1．【命题立意】本题考查直线的一般方程形式、斜率和倾斜角的关系以及正切函数的诱导公式． 【思路点拨】抓住直线方程y=kx+b 中斜率为k ，α为倾斜角，其中[)πα,0∈，当2πα≠时αtan =k ．【答案】D 【解析】7tan πx y -=，斜率76tan 7tan 7tan ππππ=⎪⎭⎫ ⎝⎛-=-=k ．2．【命题立意】本题考查直线的对称和直线方程的求解以及直线上点的确定．【思路点拨】求出直线1l 与x 轴、与l 的交点坐标，再确定对称点的坐标，最后由两点式得到2l 的直线方程．【答案】D 【解析】画出图形，容易求得直线1l 与x 轴的交点()0,1-A ，它关于直线l 的对称点为()0,5B ，又1l 与l 的交点()3,2P ，从而对称直线2l 经过B 、P 两点，于是由两点式求得2l 的方程为05=-+y x ． 3．【命题立意】本题考查两条直线的位置关系和充要条件：0212121=+⇔⊥B B A A l l .【思路点拨】判断直线0:1111=++C y B x A l ，0:2222=++C y B x A l 的位置关系时，抓住两点，一是1l ∥2l 时，212121C C B B A A ≠=，为了避免讨论系数为零的情况，转化为积式1221B A B A =且1221C A C A ≠；二是21l l ⊥，即斜率的乘积为1-，如果一条直线的斜率为零，则另一条直线的斜率不存在，也就是02121=+B B A A ．充分必要条件的判定，关键是看哪个推出哪个． 【答案】A 【解析】1023221-=⇔=++⇔⊥a a a l l 或2-=a ，故选答案A ． 4．【命题立意】本题考查直线与圆的位置关系和点到直线的距离公式以及基本不等式． 【思路点拨】直线与圆的位置关系有三种，由圆心到直线的距离d 与半径r 的大小关系决定，当d ＞r 时，相离；当d =r 时相切；当d ＜r 时相交． 【答案】D 【解析】圆心()0,0到直线0=+++b a by ax 的距离22ba b a d ++=，半径2=r ．由于()221222222≤++=++=b a ab ba b a d ，所以r d ≤，从而直线与圆相交或相切．5．【命题立意】本题考查直线与圆的位置关系和点到直线的距离．【思路点拨】圆上的点到直线上的点，这两个动点之间的距离的最小值，可以转化为直线上的点到圆心的距离的最小值来解决，圆上的点到直线的距离的最大值等于圆心到直线的距离加上半径，最小值等于圆心到直线的距离减去半径；当直线与圆相交时，圆上的点到直线的距离的最大值等于圆心到直线的距离加上半径，最小值等于0．【答案】B 【解析】由题意可知，直线与圆相离，074422=+--+y x y x 即()()12222=-+-y x ，圆心()2,2到直线kx y =的距离1222+-=k k d ，∴12211222-=-+-=-k k r d ，解得1-=k ．6．【命题立意】考查椭圆的标准方程和椭圆中的基本量及其关系以及分类讨论的思想． 【思路点拨】可建立m 关于e 的函数，从而可根据e 的范围求得m 的范围． 【答案】C 【解析】化椭圆的方程为标准方程122=+my x ，当m 1＜1，即m ＞1时，椭圆焦点在x 轴上，此时12=a ，m b 12=，m c 112-=，me 112-=∴，211e m -=∴，又⎪⎪⎭⎫⎝⎛∈22,33e ，∴23＜m＜2，又m ＞1，∴1＜m ＜2．当m1＞1，即m ＜1时，椭圆焦点在y 轴上，此时ma 12=，12=b ，112-=m c ，∴m ac e -==1222，即21e m -=，又⎪⎪⎭⎫ ⎝⎛∈22,33e ，∴21＜m ＜32．综上，m 的范围范围是()2,132,21 ⎪⎭⎫⎝⎛．选择C ．7．【命题立意】考查双曲线的标准方程，离心率的概念．【思路点拨】根据渐近线方程可以得到双曲线系方程，再分两种情况讨论焦点位置，从而求得离心率．【答案】C 【解析】由于一条渐近线方程为03=-y x ，所以可设双曲线方程为λ=-223y x ．当焦点在x 轴上时，方程为1322=-λλy x （λ＞0），此时32λ=a ，λ=2b ，于是34222λ=+=b a c ，所以离心率2==ac e ；当焦点在y 轴上时，方程为1322=---λxy （λ＜0），此时λ-=2a ，32λ-=b ，于是34222λ-=+=b a c ，所以离心率332==a c e ．故选择C ．8．【命题立意】考查抛物线的定义和标准方程以及直角三角形的性质．【思路点拨】画出图形，利用抛物线的定义找出点M 的横坐标与|FM |的关系即可求得． 【答案】C 【解析】画出图形，知()0,1F ，设FM =a 2，由点M 向x 轴作垂线，垂足为N ，则FN =a ，于是点M 的横坐标a x +=10．利用抛物线的定义，则M 向准线作垂线，有FM =10+x ，即112++=a a ，所以2=a ，从而FM =4． 9．【命题立意】考查椭圆与抛物线的标准方程，基本量的关系以及分类讨论问题．【思路点拨】由抛物线的标准方程求得准线方程，从而求得椭圆一个顶点的坐标，这个值是a 还是b ，就必须分两种情况讨论． 【答案】D 【解析】由抛物线x y 82=，得到准线方程为2-=x ，又21=a c ，即c a 2=．当椭圆的焦点在x 轴上时，2=a ，1=c ，3222=-=c a b ，此时椭圆的标准方程为13422=+y x ；当椭圆的焦点在y 轴上时，2=b ，332=c ，334=a ，此时椭圆的标准方程为1431622=+x y ．故选择D ．10．【命题立意】考查对向量含义的理解，线段垂直平分线的性质、三角形中位线性质和双曲线定义．【思路点拨】画出图形，将向量问题转化为实数中线段关系问题，利用线段垂直平分线的性质和三角形中位线的性质，得到线段的差是常数，符合双曲线的定义． 【答案】B 【解析】1说明点N 在圆122=+y x 上，NM M F 21=说明N 是线段MF 1的中点，2MF MP λ=（x ∈R ）说明P 在2MF 上，01=⋅PN M F 说明PN 是线段M F 1的垂直平分线，于是有PM PF =1，221MF ON=，从而有ONMF PF PM PF PF 22221==-=-=2＜21F F =4，所以点P 的轨迹是以1F 、2F 为焦点的双曲线的右支．从而选择B ． 11．【命题立意】考查圆的方程，直线与圆相切问题．【思路点拨】圆心已知，故只需求得其半径即可，而半径为圆心（-1,2）到直线的距离，根据点到直线的距离可求其半径，从而可求得圆的标准方程． 【答案】()()82122=-++y x 【解析】圆的半径()221112122=-+---=r ，所以圆的方程为()()()2222221=-++y x ，即()()82122=-++y x ．12．【命题立意】考查圆的标准方程，点到直线的距离．【思路点拨】先化圆的方程为标准方程，求出圆心到直线的距离，再来与半径比较． 【答案】3【解析】圆的方程为()()22222=++-y x ，圆心()2,2-到直线05=--y x 的距离222522=-+=d ，圆的半径2=r ，所以圆上到直线的距离等于22的点有3个．13．【命题立意】考查圆心到直线的距离、圆的切线长定理和直线与圆相切问题．【思路点拨】画出图形，PM 是切线，切线长最小，即|PC |最小，也就是C 到1l 的距离．【答案】1±【解析】画出图形，由题意l 2与圆C 只一个交点，说明l 2是圆C 的切线，由于162222-=-=PC CM PC PM ，所以要|PM|最小，只需|PC |最小，即点C 到l 1的距离22181305mm+=+++，所以|PM|的最小值为4161822=-⎪⎪⎭⎫⎝⎛+m，解得1±=m ． 14．【命题立意】考查椭圆的标准方程，椭圆离心率的概念和圆的切线问题． 【思路点拨】画出图形，由椭圆的离心率为22得到a c =22，再利用圆的切线的性质得到直角三角形，在直角三角形中求解角度． 【答案】2π【解析】如图，连结OA ，则OA ⊥P A ，22sin 2===∠a c ca a APO ，所以4π=∠APO ，从而2π=∠APB ．15．【命题立意】考查双曲线中由a 、b 、c 构成的直角三角形的几何意义及离心率与a 、b 、c 的关系．【思路点拨】可根据四边形的特征，以“有一个内角小于60°”为桥梁确定离心率的范围． 【答案】⎪⎪⎭⎫⎝⎛2,26【解析】设双曲线的方程为12222=-b y a x =1（a ＞0，b ＞0）,如图所示，由于在双曲线c ＞b ，所以只能是211B F B ∠＜90°,故由题意可知60°＜211B F B ∠＜90°， ∴在11B OF Rt ∆中，30°＜11B OF ∠＜45°，∴33＜c b ＜22，∴31＜222ca c -＜21，即31＜1－21e＜21，∴23＜e 2＜2，∴26＜e ＜2．16．【命题立意】考查圆的标准方程，直线与圆的位置关系，以及弦长问题． 【思路点拨】（1）过圆外一点的圆的切线方程，一般设斜率，利用圆心到直线的距离等于半径来求出斜率，但一定要注意斜率存在与否；（2）将弦长AB 看成底边，则三角形的高就是圆心到直线的距离． 【解析】（1）圆心为()0,0O ，半径4=r ，当切线的斜率存在时，设过点()8,4-M 的切线方程为()48+=-x k y ，即084=++-k y kx （1分）．则41|84|2=++k k ，解得43-=k ，（3分），于是切线方程为02043=-+y x （5分）．当斜率不存在时，4-=x 也符合题意．故过点()11,5-M 的圆O 的切线方程为02043=-+y x 或4-=x ．（6分） （2）当直线AB 的斜率不存在时，73=∆ABC S ，（7分），当直线AB 的斜率存在时，设直线AB 的方程为()3-=x k y ，即03=--k y kx ，圆心()0,0O 到直线AB 的距离132+=k k d ，（9分）线段AB 的长度2162d AB -=，所以()()821616162122222=-+≤-=-==∆d d d d d d d AB S ABC ，（11分）当且仅当82=d 时取等号，此时81922=+k k ，解得22±=k ，所以OAB △的最大面积为8，此时直线AB 的斜率为22±．（12分）17．【命题立意】本题考查椭圆方程的求法，直线和圆锥曲线的位置关系以及存在性问题． 【思路点拨】（1）可根据抛物线平移后与坐标轴的交点求得b 、c 的值，从而可得a 的值，故可求椭圆方程；（2）可利用向量法解决．【解析】（1）抛物线y x 222-=的图象向上平移2个单位长度后其解析式为()2222--=y x ，其与x 、y 轴的交点坐标分别为()0,2±、()2,0，∴2=b ，2=c ，（2分）∴62=a ，故椭圆的方程为12622=+y x ．（4分）（2）由题意可得直线l 的方程为()m x y --=33，代入椭圆方程消去y 得，062222=-+-m mx x ，（6分）又()68422--=m m △＞0，∴32-＜m ＜32．（7分）设C 、D 分别为()11,y x ，()22,y x ，则m x x =+21，26221-=m x x ，∴()()()33313333221212121m x x m x x m x m x y y ++-=⎥⎥⎦⎤⎢⎢⎣⎡--⋅⎥⎥⎦⎤⎢⎢⎣⎡--=，∵()11,2y x FC -=，()22,2y x -=，∴()()()()33243363422221212121-=++++-=+--=⋅m m m x x m x x y y x x FD FC ，（10分）∵点F 在圆的外部，∴FD FC ⋅＞0，即()332-m m ＞0，解得m ＜0或m ＞3，又∵32-＜m ＜32，∴32-＜m ＜0或3＜m ＜32．（12分）18．【命题立意】考查双曲线的定义和标准方程，渐近线和离心率计算公式．【思路点拨】（1）求渐近线方程的目标就是求ab ，可根据条件建立a 、b 的数量关系来求得；（2）可建立e 关于λ的函数，从而可根据λ的范围求得e 的范围；（3）可根据离心率确定a 、b 的数量关系，再结合图形确定圆的圆心与半径．【解析】由于()0,2c F ，所以⎪⎪⎭⎫⎝⎛±a b c P 2,，于是ab PF 22=，a ab a PF PF 22221+=+=，（1分）由相似三角形知，112PF OF PF OH =，即121PF PF OF OH =，即ab a ab 222+=λ，（2分）∴2222b b a =+λλ，()λλ-=1222b a ，λλ-=1222ab ．（1）当31=λ时，122=a b ，∴b a =．（3分）所以双曲线的渐近线方程为x y ±=．（4分）（2）()[]121112111211211222---=--=---+=-+=+==λλλλλλa b ac e ，在⎥⎦⎤⎢⎣⎡21,91上为单调递增函数．（5分）∴当21=λ时，2e 取得最大值3（6分）；当91=λ时，2e 取得最小值45．（7分）∴3452≤≤e ，∴325≤≤e ．（8分）（3）当3=e 时，3=ac，∴a c 3=，∴222a b =．（9分）∵212F F PF ⊥，∴1PF 是圆的直径，圆心是1PF 的中点，∴在y 轴上截得的弦长就是直径，∴81=PF ．（10分）又a aa a ab a PF 4222221=+=+=，∴84=a ，2=a ，32=c ，22=b ．（11分）∴4222===a ab PF ，圆心()2,0C ，半径为4，故圆的方程为()16222=-+y x ．（12分）19．【命题立意】考查抛物线的标准方程，直线与抛物线的位置关系．【思路点拨】设直线方程，与抛物线方程联立，利用韦达定理来解决；存在性问题一般是假设存在，利用垂径定理推导求解来解决． 【解析】（1）依题意，可设()11,y x A 、()22,y x B ，直线AB 的方程为p my x +=， 由0222222=--⇒⎪⎩⎪⎨⎧=+=p pmy y pxy pmy x ，（2分）得⎪⎩⎪⎨⎧-=⋅=+2212122py y pmy y ，（3分）∴NB NA ⋅=()()2211,,y p x y p x ++()()2121y y p x p x +++=()()212122y y p my p my +++=()()221212421p y y pm y y m ++++=22222p m p +=（6分）当0=m 时，NB NA ⋅取得最小值22p .（7分）（2）假设满足条件的直线l 存在，其方程为a x =，AC 的中点为O '，l 与以AC 为直径的圆相交于P 、Q ，PQ 的中点为H ，则PQ H O ⊥'，O '的坐标为⎪⎭⎫⎝⎛+2,211y p x ．()2212121212121p x y p x AC P O +=+-==' （9分），()()()a p a x p a p x a p x H O P O PH-+⎪⎭⎫ ⎝⎛-=---+='-'=∴1212212222124141，2PQ =()22PH =()⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛-a p a x p a 1214（11分），令021=-p a 得p a 21=．此时p PQ =为定值．故满足条件的直线l 存在，其方程为p x 21=．（13分）20．【命题立意】考查椭圆与抛物线的标准方程，直线与椭圆的位置关系．【思路点拨】（1）利用抛物线的标准方程，求出焦点坐标，从而得到椭圆中的b ，再由离心率建立方程，可求得椭圆的标准方程；（2）抓住直线PQ ⊥x 轴，B P Q A P Q ∠=∠即直线P A 、PB 的斜率互为相反数，联系方程利用韦达定理来解决． 【解析】（1）设C 方程为12222=+by ax （a ＞b ＞0），则32=b ．由21=ac，222b c a +=，得a =4∴椭圆C 的方程为1121622=+y x ．（4分）（2）①设()11,y x A ，()22,y x B ，直线AB 的方程为t x y +=21，代入1121622=+y x ，得01222=-++t tx x ，由∆＞0，解得4-＜t ＜4．（6分）由韦达定理得t x x -=+21，12221-=t x x ．四边形APBQ 的面积2213483621t x x S -=-⨯⨯=，∴当0=t 时312max=S ．（8分）②当BP Q AP Q ∠=∠，则P A 、PB 的斜率之和为0，设直线P A 的斜率为k ，则PB 的斜率为k -，P A 的直线方程为()23-=-x k y ，由()⎪⎩⎪⎨⎧=+-=-)2(11216)1(2322y x x k y ．将（1）代入（2）整理得()()()04823423843222=--+-++k kx k xk ，有()21433282k k k x +-=+．（10分）同理PB 的直线方程为)2(3--=-x k y ，可得()()22243328433282kk k kk k x ++=+---=+，∴2221431216kk x x +-=+，2214348k k x x +-=-．（12分）从而AB k =2121x x y y --=()()21213232x x x k x k ---++-=()21214x x k x x k --+=21，所以AB 的斜率为定值21．（13分）21．【命题立意】考查圆锥曲线的标准方程，椭圆与双曲线的定义，向量垂直问题．【思路点拨】（1）利用向量的数量积的坐标运算来求出轨迹方程，但一定要注意对参数的讨论；（2）利用椭圆或双曲线的定义确定点P 的位置，以PQ 为直径的圆G 过点2F ，即022=⋅QF PF ，利用向量垂直的坐标运算来解决．【解析】（1）∵b a ⊥，∴()()02,2,=+⋅-=⋅y kx y x b a ，得0422=-+y kx ，即422=+y kx ．（1分） 当0=k 时，方程表示两条与x 轴平行的直线；（2分）当1=k 时，方程表示以原点为圆心，以2为半径的圆；（3分）当0＜k ＜1时，方程表示焦点在x 轴上的椭圆；（4分）当k ＞1时，方程表示焦点在y 轴上的椭圆；（5分） 当k ＜0时，方程表示焦点在y 轴上的双曲线．（6分） （2）由（1）知，轨迹T 是椭圆13422=+x y ，则1F 、2F 为椭圆的两焦点．解法一：由椭圆定义得421=+PF PF ,联立121=-PF PF 解得251=PF ，232=PF ，又221=F F ，有2212221F F PF PF +=,∴212F F PF ⊥，∴P 的纵坐标为1，把1=y 代入13422=+x y 得23=x 或23-=x （舍去），∴⎪⎭⎫ ⎝⎛1,23P ．（9分）设存在满足条件的圆，则22QF PF ⊥，设()t s Q ,，则⎪⎭⎫⎝⎛-=0,232PF ，()t s QF --=1,2,∴022=⋅QF PF ，即()01023=-⨯+t s ,∴0=s ．又13422=+s t，∴2±=t ,∴()2,0Q 或()2,0-Q ．（12分）所以圆G 的方程：1613234322=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 或1645214322=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-y x ．（13分）。

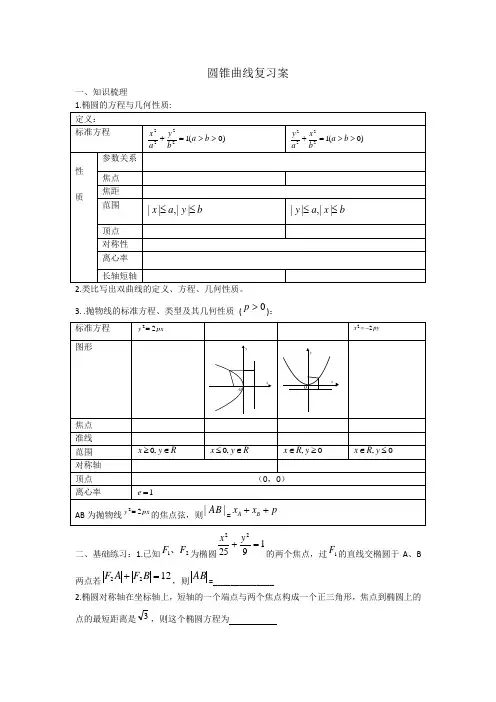
圆锥曲线复习案一、知识梳理3. .抛物线的标准方程、类型及其几何性质 (0>p )：二、基础练习：1.已知21F F 、为椭圆192522=+y x 的两个焦点，过1F 的直线交椭圆于A 、B两点若1222=+B F A F ，则AB=______________2.椭圆对称轴在坐标轴上，短轴的一个端点与两个焦点构成一个正三角形，焦点到椭圆上的点的最短距离是3，则这个椭圆方程为3.、抛物线y=42x 上的一点M 到焦点的距离为1，则点M 的纵坐标是4.、设O 是坐标原点，F 是抛物线24y x =的焦点，A 是抛物线上的一点，FA 与x 轴正向的夹角为60，则OA为5.、若双曲线)0,0(12222>>=-b a b y a x 的焦点到渐近线的距离等于实轴长，则双曲线的离心率为 （ ）6.、双曲线22149x y -=的渐近线方程是 ( )A.23y x =± B. 49y x=± C. 32y x=± D.94y x=± 7、设P 为双曲线11222=-y x 上的一点F1、F2是该双曲线的两个焦点，若|PF1|：|PF2|=3：2，则△PF1F2的面积为（ ）A ．36B ．12C ．312D ．24.8已知抛物线22(0)y px p =>的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且||1F P、||2F P 、||3F P 成等差数列， 则有 （ ） A ．321x x x =+ B ． 321y y y =+C ．2312x x x =+ D. 2312y y y =+9以椭圆221169144x y +=的右焦点为圆心，且与双曲线221916x y -=的渐近线相切的圆的方程是（A ）221090x y x +-+= （B ）221090x y x +--= （C ）221090x y x +++= （D ）221090x y x ++-= 10.已知直线y=－x+1与椭圆)0(12222>>=+b a b y a x 相交于A 、B 两点，且线段AB 的中点在直线L ：x －2y=0上，求此椭圆的离心率三、体验高考1.设O 是坐标原点，F 是抛物线22(0)y px p =>的焦点，A 是抛物线上的一点，FA 与x轴正向的夹角为60，则OA 为 ．2.已知圆22:6480C x y x y +--+=．以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点，则适合上述条件的双曲线的标准方程为 ．3.设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F,且和y 轴交于点A,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为( ).A.24y x =±B.28y x =±C. 24y x =D. 28y x =4.已知抛物线22(0)y px p =>，过其焦点且斜率为1的直线交抛物线与A 、B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线方程为 （A ）1x = (B)1x =- (C)2x = (D)2x =-5.设抛物线28y x =上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是 A. 4 B. 6 C. 8 D. 126.已知抛物线y 2＝2px （p >0）的准线与圆（x －3）2＋y 2＝16相切，则p 的值为（A ）12（B ）1 （C ）2 （D ）4 7.设抛物线28y x =的焦点为F ，准线为l ，P 为抛物线上一点，PA l ⊥，A 为垂足，如果直线AF 斜率为PF = (A) (B)8 (C) (D) 16 8.双曲线方程为2221x y -=，则它的右焦点坐标为A 、2⎛⎫⎪ ⎪⎝⎭B 、⎫⎪⎪⎝⎭C 、⎫⎪⎪⎝⎭D 、)9.设双曲线的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（A （B （C ）12 （D ）1210.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程是,它的一个焦点在抛物线224y x =的准线上，则双曲线的方程为（A ）22136108x y -= （B ） 221927x y -= （C ）22110836x y -= （D ）221279x y -=11.已知双曲线22221x y a b-=的离心率为2，焦点与椭圆221259x y -=的焦点相同，那么双曲线的焦点坐标为 ；渐近线方程为 。

解析几何考前辅导一．解析几何的三种算法（一） 过椭圆上一点A 作直线，通过设斜率计算另一个点B-----完成问题的求解 点有两类：（1）一类为定点，如长短轴顶点 （2）一类是动点1：已知椭圆x24＋y 2＝1的左顶点为A ，过A 作两条互相垂直的弦AM 、AN 交椭圆于M 、N 两点．(1) 当直线AM 的斜率为1时，求点M 的坐标；(2) 当直线AM 的斜率变化时，直线MN 是否过x 轴上的一定点？若过定点，请给出证明，并求出该定点；若不过定点，请说明理由．解：(1) 直线AM 的斜率为1时，直线AM ：y ＝x ＋2，(1分) 代入椭圆方程并化简得：5x 2＋16x ＋12＝0，(2分)解之得x 1＝－2，x 2＝－65，∴ M (－65，45)．(4分)(2) 设直线AM 的斜率为k ，则AM ：y ＝k (x ＋2)，则⎩⎪⎨⎪⎧y ＝k (x ＋2)，x 24＋y 2＝1，化简得：(1＋4k 2)x 2＋16k 2x ＋16k 2－4＝0.(6分) ∵ 此方程有一根为－2，∴ x M ＝2－8k 21＋4k 2，(7分)同理可得x N ＝2k 2－8k 2＋4.(8分)由(1)知若存在定点，则此点必为P (－65，0)．(9分)∵ k MP ＝y M x M ＋65＝k ⎝ ⎛⎭⎪⎫2－8k 21＋4k 2＋22－8k 21＋4k 2＋65＝5k4－4k 2，(11分) 同理可计算得k PN ＝5k4－4k 2.(13分)∴ 直线MN 过x 轴上的一定点P (－65，0)．(16分)注解：当直线过椭圆上的点A （m,n ）不是顶点时，直线方程设为y-n=k(x-m)代如椭圆方程后注意消元后的运算方式。

（二）通过MB AM λ=向量型的条件求A ，B 两点坐标----完成问题的求解MB AM λ=中涉及A ，B ，M ，λ四个量，已知三个量可求第四个量；已知M ，λ可求A ，B 的坐标的关系2已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C于点D ， 且2=，则C 的离心率为 .【解析】设椭圆方程为第一标准形式22221x y a b+=，设()22,D x y ，由2= 222230223330;122212222c c c c y b x b y b b x x x c y y -++⋅-=⇒===⇒===-++，代入222291144c b a b +=，3e ⇒=3在直角坐标系xOy 中，中心在原点O ，焦点在x 轴上的椭圆C 上的点(22，1)到两焦点的距离之和为4 3.(1) 求椭圆C 的方程；(2) 过椭圆C 的右焦点F 作直线l 与椭圆C 分别交于A 、B 两点，其中点A 在x 轴下方，且AF →＝3FB →.求过O 、A 、B 三点的圆的方程．(1) 解：由题意，设椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)，则2a ＝43，a ＝2 3.(2分)因为点(22，1)在椭圆x 2a 2＋y 2b 2＝1上，所以812＋1b 2＝1，解得b ＝3，故所求椭圆方程为x 212＋y23＝1.(5分)(2) 证明：设A (x 1，y 1)，B (x 2，y 2)(y 1＜0，y 2＞0)．点F 的坐标为F (3,0)．由AF →＝3FB →，得⎩⎪⎨⎪⎧ 3－x 1＝3(x 2－3)，－y 1＝3y 2，即⎩⎪⎨⎪⎧x 1＝－3x 2＋12，y 1＝－3y 2， ①(7分)又A 、B 在椭圆C 上，所以⎩⎨⎧(－3x 2＋12)212＋(－3y 2)23＝1，x 2212＋y223＝1，解得⎩⎨⎧x 2＝103，y 2＝23.所以B (103，23)，代入①得A 点坐标为(2，－2)．(12分)因为OA →·AB →＝0，所以OA ⊥AB .所以过O 、A 、B 三点的圆就是以OB 为直径的圆，其方程为x 2＋y 2－103x －23y ＝0.(16分)（三）通过设曲线一动点坐标--------------设而不求-----完成问题的求解4[2011·重庆卷] 如图1－8，椭圆的中心为原点O ，离心率e ＝22，一条准线的方程为x ＝2 2.(1)求该椭圆的标准方程；(2)设动点P(x,y)满足：OP →＝OM →＋2ON →，其中M ，N 是椭圆上的点，直线OM 与ON 的斜率之积为－12，问x 2＋2y 2.是否为定值【解答】 (1)由e ＝c a ＝22，a 2c ＝22，解得a ＝2，c ＝2，b 2＝a 2－c 2＝2，故椭圆的标准方程为x 24＋y22＝1.(2)设P (x ，y )，M (x 1，y 1)，N (x 2，y 2)，则由OP →＝OM →＋2ON →得(x ，y )＝(x 1，y 1)＋2(x 2，y 2)＝(x 1＋2x 2，y 1＋2y 2)，即x ＝x 1＋2x 2，y ＝y 1＋2y 2. 因为点M ，N 在椭圆x 2＋2y 2＝4上，所以x 21＋2y 21＝4，x 22＋2y 22＝4，故x 2＋2y 2＝(x 21＋4x 22＋4x 1x 2)＋2(y 21＋4y 22＋4y 1y 2)＝(x 21＋2y 21)＋4(x 22＋2y 22)＋4(x 1x 2＋2y 1y 2)＝20＋4(x 1x 2＋2y 1y 2)．设k OM ，k ON 分别为直线OM ，ON 的斜率，由题设条件知k OM ·k ON ＝y 1y 2x 1x 2＝－12，因此x 1x 2＋2y 1y 2＝0，所以x 2＋2y 2＝20.5．已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为F 1、F 2，短轴端点分别为A 、B ，且四边形F 1AF 2B 是边长为2的正方形。

江苏省2012届高三数学二轮专题训练：解答题（20）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1. (本题满分14分)在平面直角坐标系xOy 中，已知点,sin ,cos ),0,56(）（ααP A 其中20πα<<．（1）若,65cos =α求证：;PQ PA ⊥ （2=求)42sin(πα+的值．2. (本题满分14分)设集合{}32|≤≤-=x x A ,函数)34(log )(26+++=k x kx x f(1)当1-=k 时, 求函数)(x f 的值域.(2)若 B 为函数)(x f 的定义域,当A B ⊆时,求实数k 的取值范围.3. (本题满分14分)已知函数2()2cos cos f x x x x =+.（1）求函数()f x 在区间[,]63ππ-上的值域； （2）在△ABC 中，若()2f C =,2sin cos()cos()B A C A C =--+,求tan A 的值.BP4. (本题满分14分)已知函数()23xxf x a b =⋅+⋅，其中常数,a b 满足0a b ⋅≠ （1）若0a b ⋅>，判断函数()f x 的单调性；（2）若b a 3-=，求(1)()f x f x +>时的x 的取值范围．5. (本题满分16分)如图△ABC 为正三角形，边长为2，以点A 为圆心，1为半径作圆，PQ 为圆A 的任意一条直径．⑴若12CD DB =，求||AD ； ⑵求⋅的最小值．⑶判断⋅＋⋅的值是否会随点P 的变化而变化，请说明理由．6. (本题满分18分)已知函数||()2x m f x -=和函数()||28g x x x m m =-+-．（1）若2m =，写出函数)(x f 的对称轴方程、并求函数()g x 的单调区间；（2）若对任意1(,4]x ∈-∞，均存在2[4,)x ∈+∞，使得12()()f x g x =成立，求实数m 的取值范围．1. 解：（1）（方法一）由题设知).sin ,cos (),sin ,cos 56(a a PO a a PA --=--= 所以2sin ()cos )(cos 56(）a a a PO PA -+--=⋅.1cos 56sin cos cos 5622+-=++-=a a a a ……………………6分因为,65cos =a 所以.0=⋅PO PA 故.PO PA ⊥……………………7分（方法二）因为,65cos =a ,20π<<a 所以611sin =a ，故.611,65(）P因此).611,65(),611,3011(--=-=PO PA 因为.0)611()65(30112=-+-⨯=⋅PO PA所以.PO PA ⊥（2）因为，PO PA ⊥所以,22PO PA = 即.sin cos sin )56cos 2222a a a a +=+-（解得.53cos =a ……………………9分 因为,20π<<a 所以.54sin =a 因此.2571cos 22cos ,2524cos sin 22sin 2-=-===a a a a a ……………………12分从而.50217)257(222524222cos 222sin 2242sin(=-⨯+⨯=+=+a a a ）π ……………14分2. 解:(1) 当1-=k 时, 66)2(3422≤+--=+++x k x kx ……………2分 ∴26log)(6=≤x f ……………4分∴函数)(x f 的值域为]2,(-∞……………5分(2)设g(x)=kx 2+4x+k+3,则B={x|g(x)>0}.①当k=0时,B=(-,+∞)⊈A,不合题意,故舍去. ……………7分②当k>0时,注意到g(x)的图象开口向上,显然B ⊈A,故舍去. ……………9分③当k<0时,由A B ⊆知解得-4<k ≤-.综上知k ∈(-4,-]. ……………14分3. 解：（1）f (x )＝1＋cos2x ＋3sin2x ＝2sin(2x ＋π6)＋1． (3)分因为－π6≤x ≤π3，所以－π6≤2x ＋π6≤5π6．……………………………………………5分所以－12≤sin(2x ＋π6)≤1．所以－1≤2sin(2x ＋π6)≤2所以f (x )∈[0，3]．即函数f (x )在[－π6，π3]上的值域为[0，3]．………………………7分（2）由f (C )＝3得，2sin(2C ＋π6)＋1＝2，所以sin(2C ＋π6)＝12．在△ABC 中，因为0＜C ＜π，所以π6＜2C ＋π6＜13π6．所以2C ＋π6＝5π6．所以C ＝π3，所以A ＋B ＝2π3． ………………………………………9分因为2sin B ＝cos(A －C )－cos(A ＋C )．所以2sin B ＝2sin A sin C ． …………………11分因为B ＝2π3－A ，C ＝π3．所以2sin(2π3－A )＝3sin A ．即3cos A ＋sin A ＝3sin A ．即(3－1)sin A ＝3cos A ． 所以tan A ＝sin A cos A ＝33－1＝3＋32．………………14分4. 解：⑴ 当0,0a b >>时，任意1212,,x x R x x ∈<， 则121212()()(22)(33)xxxxf x f x a b -=-+-∵ 121222,0(22)0xxxxa a <>⇒-<，121233,0(33)0xxxxb b <>⇒-<， ∴ 12()()0f x f x -<，函数()f x 在R 上是增函数……………6分 当0,0a b <<时，同理函数()f x 在R 上是减函数。

(M 江苏省2012届高三数学二轮专题训练:解答题（7）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1．在ABC ∆中,角C B A ,,所对的边分别为,,.a b c 已知()sin sin sin ,A C p B p R +=∈且214ac b =．（Ⅰ)当5,14p b ==时，求,a c 的值；（Ⅱ）若角B 为锐角，求p 的取值范围．2．如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1，AB=2，AB ∥DC,∠BCD=900。

M 为AB 的中点(1)求证:BC//平面PMD （2）求证:PC ⊥BC ；（3）求点A 到平面PBC 的距离.3．某商场销售某种商品的经验表明，该商品每日的销售量y （单位:千克）与销售价格x （单位：元/千克）满足关系式210(6)3ay x x =+--，其中3<x<6,a 为常数．已知销售价格为5元/千克时,每日可售出该商品11千克． (Ⅰ）求a 的值；（Ⅱ)若该商品的成品为3元/千克,试确定销售价格x 的值，使商场每日销售该商品所获得的利润最大．4．已知椭圆22:14x G y +=.过点（m ,0）作圆221x y +=的切线l 交椭圆G 于A ，B 两点.（Ⅰ）求椭圆G 的焦点坐标和离心率；（Ⅱ）将AB 表示为m 的函数，并求AB 的最大值。

5．已知等比数列{}n a 的各项均为正数，且212326231,9a a a a a +==． （Ⅰ)求数列{}na 的通项公式;（Ⅱ)设31323log log log n nb a a a =+++,求数列1{}nb 的前n 项和．（Ⅲ)设.1+=n a b cnn n，求数列｛n c }的前n 项和．6. 已知0a >，函数2()ln ,0.f x x ax x =->（()f x 的图像连续不断）(Ⅰ）求()f x 的单调区间； （Ⅱ）当18a =时，证明：存在0(2,)x∈+∞,使03()()2f x f =； （Ⅲ)若存在均属于区间[]1,3的,αβ，且1βα-≥，使()()f f αβ=，证明参考答案1．本题主要考查三角变换、正弦定理、余弦定理等基础知识，同时考查运算求解能力。

江苏省2012届高三数学二轮专题训练：解答题（80）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1．（本题满分14分)已知函数()2sin()f x x ωϕ=+（0ω>，22ππϕ-<<)的图像如图所示，直线38x π=，78x π=是其两条对称轴．（1）求函数()f x 的解析式；值．（2）若6()5f α=,且388ππα<<,求()8f πα+的2．（本题满分14分）设函数2()2cos[(1)]ln f x x a k x π=-- (k ∈N *，a ∈R ）． (1) 若2011k =，1a =，求函数()f x 的最小值;(2) 若k 是偶数,求函数()f x 的单调区间．3．（本题满分15分)ABC ∆中,A 、B 、C 所对的边为a 、b 、c ．已知(2cos ,3sin )m A A =，(cos ,2cos )n A A =-,1m n ⋅=-．（1）若23a =,2c =，求ABC ∆的面积S 的大小； （2)求2cos(60)b ca C -+的值．4．（本题满分15分）某厂家拟在2011年举行促销活动，经调查测算，该产品的年销售量（即该厂的年产量）x 万件与年促销费用0()m m ≥万元满足31kx m =-+（k 为常数），如果不搞促销活动，则该产品的年销售量是1万件。

已知2011年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1。

5倍（产品成本包括固定投入和再投入两部分资金,不包括促销费用）．（1)将2011年该产品的利润y 万元表示为年促销费用m 万元的函数； (2）该厂家2011年的促销费用投入多少万元时，厂家的利润最大?5．（本题满分16分） 已知函数2()ln f x xa x =-，()2g x bx =，其中a ，b R ∈且2ab =．函数()f x 在1[,1]4上是减函数,函数()g x 在1[,1]4上是增函数． （1）求函数()f x ，()g x 的表达式;(2）若不等式()()f x mg x ≥对1[,1]4x ∈恒成立,求实数m 的取值范围． （3）求函数1()()()2h x f x g x x =+-的最小值，并证明当*n N ∈，2n ≥时()()3f n g n +>．资。

江苏省2012届高三数学二轮专题训练：解答题（8)本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1。

(本小题满分14分）如图，在平面直角坐标系xOy 中，点A 在x 轴正半轴上,直线AB 的倾斜角为34，|OB |=2，设3,(,)24AOB 。

(Ⅰ）用表示点B 的坐标及||OA ； （Ⅱ）若4tan3,求OA OB 的值. 2．（本小题满分12分）如图，在直三棱柱ABC —A 1B 1C 1中，AB=AC ，点D 是BC 的中点。

（1）求证：A 1B//平面ADC 1；（2)如果点E 是B 1C 1的中点，求证:平面1A BE平面BCC 1B 1.3．某民营企业生产,A B 两种产品,根据市场调查与预测，A 产品的利润与投资成正比，其关系如图甲,B 产品的利润与投资的算术平方根成正比，其关系如图乙(注：利润与投资单位：万元）．O A xB y甲 乙（Ⅰ)分别将,A B 两种产品的利润表示为投资x (万元）的函数关系式； (Ⅱ）该企业已筹集到10万元资金，并全部投入,A B 两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润为多少万元?4. （本小题满分15分)如图，在ABC ∆中,7||||,||22AB AC BC ===，以B 、C 为焦点的椭圆恰好过AC 的中点P 。

(1）求椭圆的标准方程; （2)过椭圆的右顶点1A 作直线与圆22:(1)2E x y -+=相交于M 、N 两点,试探究点M 、N 能将圆E 分割成弧长比值为1:3的两段弧吗？若能，求出直线的方程；若不能，请说明理由。

5．（本小题满分 16分）y PABCOx已知数列{}na 满足120,2aa ==，且对任意*,m n N ∈都有22121122()m n m n a a a m n --+-+=+-（Ⅰ)求35,a a ;（Ⅱ）设*2121()nn n b a a n N +-=-∈，证明：{}n b 是等差数列;（Ⅲ）设1*1()(0,)n nn n ca a q q n N -+=-≠∈,求数列{}n c 的前n 项和n S6（本题满分16分）已知函数)(3ln )(R a ax x a x f ∈--=．（1）求函数)(x f 的单调区间。

专题8 解析几何一、填空题例题1. 设圆C ：224x y +=的一条切线与x 轴、y 轴分别交于点,A B ，则AB 的最小值为 ▲ ． 答：4提示：方法一 取特殊的直线AB ：横截距与纵截距相等。

方法二不妨设切点P （第一象限），θ=∠POA ,则θπ-=∠2POB ,故θtan 2=AP ，θtan 12=BP 故AB=AP+BP 4≥例题2. ()()22:3:31 2 l y x P C x y =-++=过直线 上一点作圆的两条切线，若两切线关于l 直线 对称，P C 则点 到圆心 的距离为 ▲ ．提示：由圆的平面几何知识可得CP l ⊥例题3. 已知⊙A ：221x y +=，⊙B: 22(3)(4)4x y -+-=，P 是平面内一动点，过P 作⊙A 、⊙B 的切线，切点分别为D 、E ，若P E P D =，则P 到坐标原点距离的最小值为 ▲ ．答：115提示：利用切线长公式求出点P 的轨迹为直线01143=++y x ，故P 到坐标原点距离的最小值为115例题4. 已知F 是椭圆2222:1x y C a b+= (0)a b >>的右焦点，点P 在椭圆C 上，线段PF与圆22214x y b +=相切于点Q ，且→→=QF PQ ，则椭圆C 的离心率为 ▲ ．答：35 提示：设左焦点E ，连接PE ，由圆的切线可得OQ ⊥PF ，而OQ ∥PF ，故PF PE ⊥,2224)2(c b a b =-+∴，35=∴e 。

（备用题）过双曲线22221(0,0)x y a b a b-=>>的左焦点(,0)(0)F c c ->，作圆：2224a x y +=的切线，切点为E ，延长FE 交双曲线右支于点P ，若1()2OE OF OP =+，则双曲线的离心率为 ．210=e 例题5. 椭圆2212516x y +=的左，右焦点分别为12,,F F 弦AB 过1F ，若2ABF ∆的内切圆的周长为,π,A B 两点的坐标分别为1122(,),(,),x y x y 则21||y y -= . 答：53提示：利用121222F F 21)F BF r(BA 212y y A S BAF -=++=∆例题6. 已知正方形ABCD 的坐标分别是(1,0)-,(0,1),(1,0)，(0,1)-，动点M 满足：12MB MD k k ⋅=-则MA MC += ▲ ． 答：22提示：设点M 的坐标为(,)x y ，∵12MB MD k k ⋅=-整理，得0x ≠），发现动点M 的轨迹方程是椭圆，其焦点恰为,A C 两点，所以MA MC +=（备用）如图，一圆形纸片的圆心为O ，F 是圆内一定点，M 是圆周上一动点，把纸片折叠使点M 与点F 重合，然后抹平纸片，折痕为CD ，设CD 与OM 交于点P ，则点P 的轨迹是 .（填写“椭圆”、“双曲线”、“抛物线”和“圆”中的一种情况） 椭圆例题7. 椭圆22162x y +=和双曲线2213x y -=的公共焦点为P F F ,,21是两曲线的一个交点, 则21F PF ∆的面积为 ▲ 答：2提示：先利用定义求PF 1，PF 2，再用余弦定理求得 31cos =P ，最后用面积公式例题8. 设椭圆2222:1(0)x y C a b a b+=>>的上顶点为A ，椭圆C 上两点,P Q 在x 轴上的射影分别为左焦点1F 和右焦点2F ，直线PQ 的斜率为32，过点A 且与1AF 垂直的直线与x 轴交于点B ，1AF B ∆的外接圆为圆M ． 若直线213404x y a ++=与圆M 相交于,E F 两点，且212ME MF a ⋅=-，则椭圆方程为答：2211612x y += 提示：由条件可知⎪⎪⎭⎫ ⎝⎛--a b c P 2,，⎪⎪⎭⎫ ⎝⎛a b c Q 2, 因为23=PQ k ，所以得：=e 12。

江苏省2012届高三数学二轮专题训练：解答题（6）本大题共6小题，解答时应写出文字说明、证明过程或演算步骤。

1．（本小题满分14分）已知函数235cos 35cos sin 5)(.2+-=x x x x f .(1)确定函数f(x)的单调增区间；(2)将函数y=f(x)的图象向左平移)20(πϕφ<<个单位长度，所得图象关于y 轴对称，求φ的值。

2. （本题满分14分）如图：四棱锥P-ABCD 的底面为矩形，且AB=2BC ，E 、F 分别为棱AB 、PC 的中点。

（1）求证：EF//平面PAD ；（2）若点P 在平面ABCD 内的正投影O 在直线AC 上，求证：平面PAC ⊥平面PDE 。

3. （本题满分14分）已知函数1(0)()21(1)x c cx x c f x c x -+<<⎧⎪=⎨⎪+<⎩， ，，≤满足29()8f c =．（1）求常数c 的值； （2）解不等式()1f x >+．4．（本题满分16分）已知△ABC的面积为且()18AC AB CB ⋅-=，向量(1cos cos )A B =，n 和(tan tan sin 2)A B C =+，m 是共线向量. （1）求角C 的大小； （2）求△ABC 的三边长. 5．（本题满分16分）已知二次函数()y f x =的图象经过点(0,1)，其导函数()62f x x '=-，数列{a n }的前n 项和为S n ，点(n ，S n )*()n ∈N 均在函数()y f x =的图象上.（1）求数列{a n }的通项公式a n 和n S ；（2）设13n n n b a a +=，T n 是数列{b n }的前n 项和，求使得21n m T <对所有都成立的最小正整数m. 6．（本小题满分16分）已知函数()sin f x a x x b =-+(a ，b 均为正常数). （1）求证：函数f(x)在(0，a+b]内至少有一个零点；（2）设函数在3x π=处有极值.①对于一切π02x ⎡⎤∈⎢⎥⎣⎦，，不等式()sin cos f x x x >+恒成立，求b 的取值范围；②若函数f(x)在区间()121ππ33m m --，上是单调增函数，求实数m 的取值范围.参考答案：1．解：x x f 2sin 25)(=)2cos 1(235x +-x 2sin 25235=+x 2cos 235-)2cos 232sin 21(5x x -=)32sin(5π-=x ．………4分 (1)3222πππ-≤-x k ⇒+≤22ππk ≤≤-x k 12ππ125ππ+k ， 所以f(x)的单调增区间为]125,12[ππππ+-k k ,(k ∈Z). ............. 8分(2)将函数y=f(x)的图象向左平移)20(πφφ<<个单位长度，得)322sin(5πφ-+=x y的图象，其图象对称轴方程为：322πφ-+x )(2Z k k ∈+=ππ，……12分 1252ππφ+=∴k ，由20πφ<<得125πφ=． ……14分3. 【解】（1）由题意知0<c<1，于是0<c 2<c.所以2239()118f c c c c ==⋅+=+，即31c =，故12c =. …………………………4分（2）由（1）得4111(0)22()121(1).2x x x f x x -⎧+<<⎪⎪=⎨⎪+<⎪⎩， ，， ≤ …………………………6分解不等式组1112102x x ⎧+>+⎪⎨⎪<<⎩，1.2x << …………………………9分解不等式组421111xx -⎧+>+⎪⎨⎪<⎩，≤得15.28x <≤ ……………………… 12分所以不等式()1f x >+的解集为)))1155.28⎡=⎢⎣，，， ……………… 14分4． 【解】（1）因为向量(tan tan sin 2)A B C =+，m 和(1cos cos )A B =，n 是共线向量， 所以()cos cos tan tan sin 20A B A B C +-=， …………………………2分 即sinAcosB+cosAsinB －2sinCcosC=0，化简得sinC －2sinCcosC=0，即sinC(1－2cosC)=0. …………………………4分 因为0πC <<，所以sinC>0，从而1cos 2C =，π.3C = …………………………6分（2）()()218ACAB CB AC BC BA AC =⋅-=⋅-=，于是AC=. ………………8分因为△ABC 的面积为1sin 2CA CB C ⋅，即1πsin 23CB ⋅，解得CB= ……………………… 14分在△ABC 中，由余弦定理得((2222212cos 254.ABCA CB CA CB C =+-⋅=+-⨯=所以AB = ……………………… 16分5． 【解】（1）由题意，可设2()f x ax bx c =++.因为函数()y f x =的图象经过点(0,1)，所以(0)1c f ==. 而62()2x f x ax b '-==+，所以a=3，b=－2.于是2()321f x x x =-+. …………………………3分 因为点(n ，S n )*()n ∈N 均在函数()y f x =的图象上，所以S n 2321n n =-+.…………5分所以a 1=S 1=2，当1n ≥时，2213213(1)2(1)165n n n a S S n n n n n -⎡⎤=-=-+----+=-⎣⎦，故2(1)65(1).n n a n n n =⎧=⎨->∈⎩N ，，，， …………………………8分（2）()133(1)(1)271433111(1)(1).26561n n n n n b a a n n n n n n +⎧⎧==⎪⎪⨯===⎨⎨>∈⎪⎪->∈-+⎩⎩N N ，，，，，，，， ……………………… 10分所以当n>1时，()()()3111111127271313196561n T n n ⎡⎤=+-+-++-⎢⎥⨯-+⎣⎦2172(61)n =-+. ……………………… 12分21n m T <对所有*n N ∈都成立32114212172(61)m m n ⎧>⎪⇔⎨>-⎪+⎩，对所有*n N ∈都成立92 6.2217m m m ⎧>⎪⇔⇔⎨⎪⎩，≥≥故所求最小正整数m 为6. ……………………… 16分6【证】（1）因为(0)0f b =>， []()sin()()sin()10f a b a a b a b b a a b +=+-++=+-≤，所以函数f(x)在(0，a+b]内至少有一个零点. …………………………4分 【解】（2）()cos 1f x a x '=-. 因为函数在x π=处有极值，所以()π03f '=，即πcos 103a -=，所以a=2.于是()2sin f x x x b =-+. …………………………6分①本小题等价于cossin b x x x >+-对一切π02x ⎡⎤∈⎢⎥⎣⎦，恒成立. 记()cos sin g x x x x =+-，则()π()1sin cos 1.4g'x x x x=--=+因为π02x ⎡⎤∈⎢⎥⎣⎦，，所以ππ3π444x +≤≤()πsin 14x +≤， 所以()π14x +()0g'x ≤，即g(x)在π02⎡⎤⎢⎥⎣⎦，上是减函数. 所以[]max ()(0)1g x g ==，于是b>1，故b 的取值范围是(1).+∞，………………… 10分②()1()2cos 12cos 2f x x x '=-=-，由()f x '≥0得1cos 2x ≥，即ππ2π2π.33k x k k -++∈Z ≤≤， ……………………… 12分因为函数f(x)在区间()121ππ33m m --，上是单调增函数，所以()121ππππ2π2π3333m m k k k --⎡⎤⊆-++∈⎢⎥⎣⎦Z ，，，，则有1ππ2π3321ππ2π33121π<π33m k m k k m m -⎧+⎪⎪⎪-+∈⎨⎪--⎪⎪⎩Z ≥-，≤，，， 即6310k m k k m +⎧∈⎨>⎩Z ≤≤，，， 只有k=0时，01m <≤适合，故m 的取值范围是(]01.， ……………………… 16分。