第10章+++时间序列分析

时间序列分析基础时间序列分析是一种重要的统计分析方法，用于研究随时间变化的数据序列。

时间序列分析可以帮助我们理解数据的趋势、季节性变化和周期性波动，从而进行预测和决策。

本文将介绍时间序列分析的基础知识，包括时间序列的概念、特征、分解方法和常用模型等内容。

一、时间序列的概念时间序列是按照时间顺序排列的一系列数据点的集合。

在时间序列分析中，时间是一个重要的因素，数据点的取值取决于时间点的顺序。

时间序列可以是连续的，也可以是离散的，常见的时间序列包括股票价格、气温变化、销售额等。

二、时间序列的特征时间序列通常具有以下几种特征：1. 趋势性：时间序列数据在长期内呈现出的总体上升或下降的趋势。

2. 季节性：时间序列数据在短期内呈现出的周期性波动，通常与季节变化相关。

3. 周期性：时间序列数据在长期内呈现出的周期性波动，但不是固定的季节性。

4. 随机性：时间序列数据中除了趋势性、季节性和周期性外的随机波动。

三、时间序列的分解方法为了更好地理解时间序列数据的趋势、季节性和周期性，常常需要对时间序列进行分解。

常用的时间序列分解方法包括加法模型和乘法模型。

1. 加法模型：加法模型假设时间序列数据是由趋势性、季节性、周期性和随机性的总和构成的。

即 Y(t) = T(t) + S(t) + C(t) +ε(t)，其中Y(t)为时间t的观测值，T(t)为趋势性分量，S(t)为季节性分量，C(t)为周期性分量，ε(t)为随机性分量。

2. 乘法模型：乘法模型假设时间序列数据是由趋势性、季节性、周期性和随机性的乘积构成的。

即 Y(t) = T(t) * S(t) * C(t) *ε(t)。

四、常用的时间序列模型时间序列分析中常用的模型包括移动平均模型（MA）、自回归模型（AR）、自回归移动平均模型（ARMA）、自回归积分移动平均模型（ARIMA）等。

1. 移动平均模型（MA）：MA模型假设时间序列数据是由随机误差项的线性组合构成的，表示为Y(t) = μ + ε(t) + θ1*ε(t-1) + θ2*ε(t-2) + ... + θq*ε(t-q)。

第10章 时间序列分析和预测一、单项选择题 1．已知某公司近5年经营收入的增长速度分别为6%，8.2%，9.3%，8%和10.5%，则该公司近5年的年平均增长速度为（ ）。

[浙江工商大学2017研]A ．（6%×8.2%×9.3%×8%×10.5%)/5B ．（106%×108.2%×109.3%×108%×110.5%)/5-1C ．（6%×8.2%×9.3%×8%×10.5%)1/5D ．（106%×108.2%×109.3%×108%×110.5%)1/5-1【答案】D【解析】平均增长速度也称平均增长率，它是时间序列中逐期环比值（也称环比发展速度）的几何平均数减1后的结果，其计算公式为：111n n YG Y -=⨯⨯-=-所以该商品价格的年平均增长率为：1v =-2．如果时间数列逐期增长量大体相等，则宜拟合（ ）。

[浙江工商大学2017研]A ．直线模型B．抛物线模型C．曲线模型D．众数指数曲线模型【答案】A【解析】A项，逐期增长量大体相等，说明关于时间t的曲线的斜率大体相等，应拟合直线模型；B项，抛物线模型适合于变化率逐渐减小再逐渐增大的时间序列；C项，指数曲线模型适合于呈指数增长的时间序列；D项，除直线模型意外的其他模型都属于曲线模型，包括抛物线模型和指数曲线模型。

3．定基发展速度和环比发展速度的关系是（）。

[浙江工商大学2017研]A．相邻两个定基发展速度之商＝其相应的环比发展速度B．相邻两个定基发展速度之积＝其相应的环比发展速度C．相邻两个定基发展速度之差＝其相应的环比发展速度D．相邻两个定基发展速度之和＝其相应的环比发展速度【答案】A【解析】定基发展速度是以固定一个时期为基点计算发展速度，环比增长速度是以上一个时期为基点计算发展速度，因此A项正确。

时间序列分析课后习题答案TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】第9章 时间序列分析课后习题答案第10章（1）30× 31.06×21.05= 30×1.3131 = 39.393（万辆）（2117.11%= （3）设按7.4%的增长速度n 年可翻一番则有 1.07460/302n ==所以 n = log2 / log1.074 = 9.71（年）故能提前0.29年达到翻一番的预定目标。

第11章 （1）以1987年为基期，2003年与1987年相比该地区社会商品零售额共增长：（2）年平均增长速度为1%)8.61(%)2.81(%)101(15555-+⨯+⨯+=0.0833=8.33%（3） 2004年的社会商品零售额应为509.52)0833.01(307=+⨯（亿元）第12章 （1）发展总速度%12.259%)81(%)101(%)121(343=+⨯+⨯+ 平均增长速度=%9892.91%12.25910=-（2）8.561%)61(5002=+⨯（亿元）（3）平均数∑====415.142457041j j y y （亿元），2002年一季度的计划任务：625.1495.142%105=⨯（亿元）。

第13章(1)用每股收益与年份序号回归得^0.3650.193t Y t =+。

预测下一年(第11年)的每股收益为488.211193.0365.0ˆ11=⨯+=Y 元(2)时间数列数据表明该公司股票收益逐年增加，趋势方程也表明平均每年增长0.193元。

是一个较为适合的投资方向。

第14章 （1）移动平均法消除季节变动计算表（2）t T t ⨯+=63995.09625.8ˆ（3）趋势剔出法季节比例计算表（一）上表中，其趋势拟合为直线方程t T t ⨯+=63995.09625.8ˆ。

时间序列分析方法概述时间序列分析是一种研究时间相关数据的统计方法，它涉及分析数据在一段时间内的趋势和模式，以便预测未来的发展。

时间序列分析方法可应用于各种领域，如经济学、金融学、气象学和市场调研等。

时间序列分析方法的基本步骤包括数据收集、数据预处理、模型选择、参数估计和模型评估。

首先，需要收集时间序列数据，这可以是按照时间顺序排列的一系列观测值，如月度销售额、每日气温或股票价格等。

然后需要对数据进行预处理，如去除异常值、填补缺失值和平滑数据等，以确保数据的可靠性和一致性。

在模型选择阶段，需要根据数据的性质和特征选择适当的时间序列模型。

常用的模型包括平稳ARMA模型、非平稳ARIMA模型、季节性模型和ARCH/GARCH模型等。

平稳ARMA模型适用于平稳数据，可以描述数据的自相关结构和噪声。

非平稳ARIMA模型可以处理非平稳数据，并考虑差分操作来提高平稳性。

季节性模型适用于具有季节性变动的数据，并通过季节性差分操作来消除季节性成分。

ARCH/GARCH模型则用于建模数据的波动性和条件异方差性。

在参数估计阶段，需要使用最大似然估计法或最小二乘法等统计方法来估计模型的参数。

这些参数对于分析和预测时间序列数据非常关键，因为它们决定了模型的准确度和可靠性。

最后，在模型评估阶段，需要使用残差分析、模型诊断和模型比较等方法来评估选定模型的拟合优度和质量。

如果模型拟合不好，则需要对模型进行修改和改进。

时间序列分析方法在预测未来的趋势和模式方面具有广泛的应用。

例如，经济学家可以使用时间序列分析方法来预测国内生产总值（GDP）、通货膨胀率和失业率等经济指标。

金融学家可以利用时间序列分析方法来预测股票价格、汇率和利率等金融变量。

气象学家可以使用时间序列分析方法来预测气温、降水量和风速等气象数据。

市场调研人员可以利用时间序列分析方法来预测销售额、用户行为和市场趋势等。

总之，时间序列分析是一种基于统计方法的数据分析技术，可用于研究历史数据的趋势和模式，并预测未来的发展。

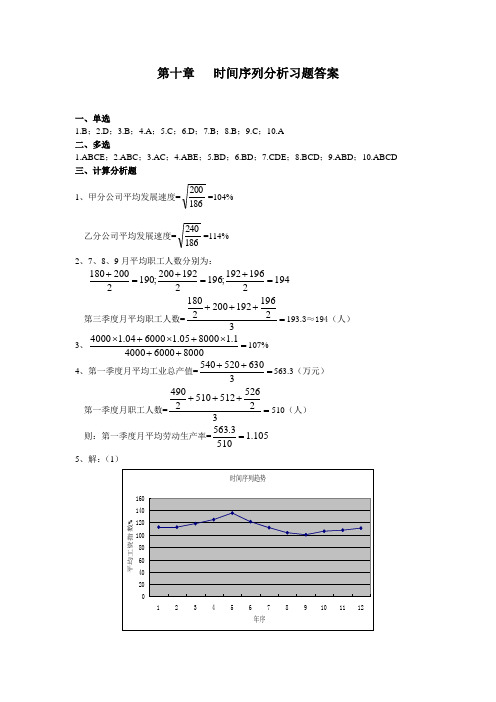
第十章 时间序列分析习题答案一、单选1.B ；2.D ；3.B ；4.A ；5.C ；6.D ；7.B ；8.B ；9.C ；10.A 二、多选1.ABCE ；2.ABC ；3.AC ；4.ABE ；5.BD ；6.BD ；7.CDE ；8.BCD ；9.ABD ；10.ABCD 三、计算分析题1、甲分公司平均发展速度=186200=104% 乙分公司平均发展速度=186240=114% 2、7、8、9月平均职工人数分别为：1942196192;1962192200;1902200180=+=+=+ 第三季度月平均职工人数==+++321961922002180193.3≈194（人） 3、=++⨯+⨯+⨯8000600040001.1800005.1600004.14000107%4、第一季度月平均工业总产值==++3630520540563.3（万元）第一季度月职工人数==+++325265125102490510（人） 则：第一季度月平均劳动生产率=105.15103.563=5、解：（1）（2）年序t 平均工资指数（环比）5期移动平均趋势1 112.70% —2 112.60% —3 118.50% 120.80%4 124.80% 122.60%5 135.40% 122.50%6 121.70% 119.52%7 112.10% 114.60%8 103.60% 108.76%9 100.20% 106.00%10 106.20% 105.78%11 107.90% —12 111.00% —各年份移动平均趋势值和原序列如下：移动平均可以消除原序列中的一些随机扰动和短期波动，期数越长，平滑作用越强；移动平均的作用就是消除序列随机和短期影响，从而能够发现序列的趋势。

（3）年份平均工资指数（环比）指数平滑值α=0.3误差平方指数平滑值α=0.5误差平方1 112.70% ————2 112.60% 112.70% 1E-06 112.70% 1E-063 118.50% 112.67% 0.003399 112.65% 0.0034224 124.80% 114.42% 0.010777 115.58% 0.008515 135.40% 117.53% 0.031922 120.19% 0.0231426 121.70% 122.89% 0.000142 127.79% 0.0037137 112.10% 122.54% 0.01089 124.75% 0.0159948 103.60% 119.40% 0.024979 118.42% 0.0219739 100.20% 114.66% 0.020919 111.01% 0.01168910 106.20% 110.32% 0.001701 105.61% 3.53E-0511 107.90% 109.09% 0.000141 105.90% 0.00039912 111.00% 108.73% 0.000515 106.90% 0.00168—109.41% —108.95% —合计 — — 0.105385 — 0.09056从上表数据看，采用平滑系数α=0.5拟合效果好。

时间序列分析法概述时间序列分析是指对时间序列数据进行统计建模和预测的一种方法。

时间序列数据是指按照一定时间顺序排列的数据，通常是在相等时间间隔下连续观测到的数据。

时间序列分析的目的是从数据中发现特定模式或趋势，并利用这些模式和趋势进行预测。

它通常用于经济学、金融学、气象学等领域，例如股票价格预测、销售量预测、天气预测等等。

时间序列分析方法主要包括以下几个步骤：1. 数据处理：首先需要对时间序列数据进行预处理，包括去除趋势、季节性和不稳定性等因素，以使数据满足稳定性和平稳性的假设。

这通常可以通过差分、平滑和变换等方式来实现。

2. 模型选择：根据时间序列数据的特性，选择合适的模型来进行建模和预测。

常用的模型包括自回归移动平均模型（ARMA）、自回归积分滑动平均模型（ARIMA）和季节性自回归积分滑动平均模型（SARIMA）等。

模型的选择通常需要借助统计指标和图形分析的方法来确定。

3. 参数估计：在选择好模型之后，需要对模型的参数进行估计。

参数估计可以通过最大似然估计、最小二乘估计或贝叶斯估计等方法来实现。

估计得到的参数可以用于模型的建立和预测。

4. 模型诊断：对模型进行诊断，检查模型是否符合数据的统计特性和假设。

常用的诊断方法包括自相关函数（ACF）和偏自相关函数（PACF）的分析，以及白噪声检验等。

如果模型存在问题，则需要对模型进行修正或调整。

5. 模型预测：根据已经估计好的模型和参数，对未来的数据进行预测。

预测可以基于滚动窗口逐步预测，也可以直接进行多步预测。

常用的预测方法包括常规预测、指数平滑预测和季节性预测等。

总的来说，时间序列分析是一种基于时间序列数据的统计建模和预测方法。

通过对时间序列数据进行处理、模型选择、参数估计、模型诊断和模型预测等步骤，可以得到对未来数据的预测结果，并用于决策和规划。

然而，需要注意的是，时间序列分析方法需要满足一定的数据假设和模型假设，以及对模型的合理性和可靠性进行评估。

第10章时间序列分析指标时间序列分析指标是一种对时间序列数据进行分析和预测的方法。

它可以揭示出时间序列数据中的规律和趋势，并用以预测未来的变化。

时间序列是按时间顺序排列的一系列数据点。

时间序列分析指标可以帮助我们了解时间序列数据的特征和规律。

在金融领域，时间序列分析指标可以应用于股市分析、经济预测等多个方面。

常用的时间序列分析指标包括趋势指标、周期指标、季节性指标和波动指标。

趋势指标是用来分析时间序列数据中的长期趋势的指标。

常见的趋势指标包括移动平均线和线性趋势线。

移动平均线是用来平滑时间序列数据的一种方法，它可以过滤掉噪音和周期性波动，反映出数据的长期趋势。

线性趋势线则是用来表示时间序列数据中的线性关系，可以帮助我们判断数据的上涨或下跌趋势。

周期指标是用来分析时间序列数据中的周期性变化的指标。

周期指标可以帮助我们预测未来的周期性变化。

常见的周期指标包括季节性调整指标和周期性调整指标。

季节性调整指标可以消除时间序列数据中的季节性影响，展示出数据的长期趋势。

周期性调整指标则可以帮助我们找到时间序列数据中的周期性变化，以便更好地进行预测。

季节性指标是用来分析时间序列数据中的季节性变化的指标。

季节性指标可以帮助我们了解时间序列数据中的季节性规律，并进行相应的调整和预测。

常见的季节性指标包括季节性分解法和指数平滑法。

季节性分解法可以将时间序列数据拆分成长期趋势、季节性趋势和误差项三个部分，以便更好地进行分析和预测。

指数平滑法则是用来对时间序列数据进行平滑处理和季节性调整的方法。

波动指标是用来分析时间序列数据中的波动性变化的指标。

波动指标可以帮助我们了解时间序列数据的波动情况，以便更好地进行风险控制和预测。

常见的波动指标包括波动率和变异系数。

波动率是用来衡量时间序列数据的波动性的指标，可以帮助我们了解数据的风险程度。

变异系数则是用来衡量时间序列数据的波动性相对于平均水平的变化程度，可以帮助我们比较不同时间序列数据的波动性。

时间序列分析基于r第2版《时间序列分析基于R第2版》（Time Series Analysis and Its Applications: With R Examples, 2nd Edition）是由Shumway和Stoffer合著的一本经典时间序列分析教材。

该书详细介绍了时间序列分析的理论和实践应用，并使用R语言进行实例演示和编程实现。

以下是《时间序列分析基于R第2版》的主要内容概述：第1章：时间序列分析简介介绍时间序列分析的基本概念和应用领域，并概述本书的内容和使用R语言进行时间序列分析的优势。

第2章：时间序列的基本特性介绍时间序列的基本特性，包括平稳性、自相关性和白噪声等概念，并通过实例演示如何使用R进行时间序列数据的可视化和描述性统计分析。

第3章：时间序列的线性模型介绍时间序列的线性模型，包括自回归模型（AR）、滑动平均模型（MA）和自回归滑动平均模型（ARMA）等，并通过R语言实现模型的参数估计和预测。

第4章：时间序列的谱分析介绍时间序列的谱分析方法，包括周期图和功率谱密度估计等，并通过R语言实现谱分析方法的应用和结果可视化。

第5章：时间序列的非线性模型介绍时间序列的非线性模型，包括ARCH、GARCH和非线性AR模型等，并通过R语言实现模型的参数估计和预测。

第6章：时间序列的状态空间模型介绍时间序列的状态空间模型，包括线性状态空间模型和非线性状态空间模型，并通过R语言实现模型的参数估计和预测。

第7章：多变量时间序列分析介绍多变量时间序列分析的方法，包括向量自回归模型（VAR）、向量误差修正模型（VEC）和协整模型等，并通过R语言实现模型的参数估计和预测。

第8章：季节性和周期性时间序列介绍季节性和周期性时间序列的分析方法，包括季节性自回归移动平均模型（SARMA）和周期性自回归移动平均模型（PARMA）等，并通过R语言实现模型的参数估计和预测。

第9章：时间序列的预测介绍时间序列的预测方法，包括简单指数平滑、Holt线性趋势模型和ARIMA模型等，并通过R语言实现模型的参数估计和预测。

2015年《统计学》第十章时间序列分析习题及满分答案一、单项选择：1.时间数列中,每项指标数值可以相加的是（B ）A．绝对数时间数列 B. 时期数列C. 时点数列D.相对数或平均数时间数列2. 下列属于时点数列的是（D）A. 某厂各年工业产值B.某厂各年劳动生产率C.某厂各年生产工人占全部职工的比重D.某厂各年年初职工人数3.发展速度与增长速度的关系是( B )A. 环比增长速度等于定基发展速度-1B. 环比增长速度等于环比发展速度-1C. 定基增长速度的连乘积等于定基发展速度D. 环比增长速度的连乘积等于环比发展速度4.年距增长速度是（C） A. 报告期水平/基期水平 B. （报告期水平—基期水平）/基期水平 C. 年距增长量/去年同期发展水平 D. 环比增长量/前一时期水平5.几何平均法平均发展速度数值的大小（C）A. 不受最初水平和最末水平的影响B. 只受中间各期发展水平的影响C. 只受最初水平和最末水平的影响，不受中间各期发展水平的影响D. 既受最初水平和最末水平的影响，也受中间各期发展水平的影响6.某厂第一季度三个月某种产品的实际产量分别为500件、612件、832件、分别超计划0%、2%和4%，则该厂第一季度平均超额完成计划的百分数为（ C ） A. 102% B. 2% C. 2.3% D. 102.3%7．时期数列中的每个指标数值是（B）。

A、每隔一定时间统计一次 B、连续不断统计而取得C、间隔一月统计一次D、定期统计一次8．一般平均数与序时平均数的共同之处是（A）。

A、两者都是反映现象的一般水平 B、都是反映同一总体的一般水平C、共同反映同质总体在不同时间上的一般水平D、都可以消除现象波动的影响9．某企业1997年产值比1990年增长了1倍，比1995年增长了0.5倍，则1995年比1990年增长了（ A ）。

A、0.33 B、0.5 C、0.75 D、110．假设有如下资料：则该企业一季度平均完成计划为（B）。

时间序列分析基本知识讲解时间序列分析是指对一系列按照时间顺序排列的数据进行分析、建模和预测的方法。

它在许多领域都有广泛的应用，如经济学、金融学、气象学等。

时间序列数据的特点是具有时间依赖性和序列自相关性，即当前的观测值与前面的观测值之间存在一定的关联。

时间序列分析的基本目的是通过观察过去的数据模式，来预测未来的值或者了解数据的发展趋势。

在进行时间序列分析时，我们通常关注以下几个方面的内容：1. 趋势分析：时间序列数据中的趋势是指长期内数据值的增长或下降趋势。

趋势的存在可能是持续性的，也可能是周期性的。

常见的趋势分析方法包括移动平均法、指数平滑法等。

2. 季节性分析：时间序列数据中的季节性是指每年或每个周期内数据值呈现出的周期性规律。

季节性可以是固定的，也可以是随机的。

常用的季节性分析方法有季节性指数法、周期性指数法等。

3. 周期性分析：时间序列数据中的周期性是指数据值在一段时间内出现的循环规律。

周期性往往是由于外部因素引起的，如经济周期、自然环境等。

周期性分析常用的方法有傅里叶分析、自相关函数等。

4. 随机性分析：时间序列数据中的随机性是指数据值的不可预测性和不规律性。

随机性分析可以用来寻找数据中的异常值、离群点等。

常用的随机性分析方法有自回归滑动平均模型（ARMA）、随机游走模型等。

时间序列分析的基本步骤包括收集数据、可视化数据、数据预处理、建立模型、模型检验和评估模型的预测能力等。

常用的时间序列模型有自回归移动平均模型（ARMA）、自回归整合移动平均模型（ARIMA）、季节性自回归整合移动平均模型（SARIMA）等。

总之，时间序列分析是研究时间序列数据的变化规律和趋势的一种方法。

通过对时间序列数据的分析，我们可以预测未来的趋势和变化，辅助决策制定和问题解决。

在实际应用中，时间序列分析与其他统计方法和机器学习方法结合，可以提高分析预测的准确性和可靠性。

时间序列分析是研究时间序列数据的内在规律和趋势的一种方法。

时间序列分析基本知识讲解时间序列分析是指对一系列按时间顺序排列的数据进行统计分析和预测的方法。

它是统计学中的一个重要分支，在许多领域中都有广泛的应用，例如经济学、金融学、气象学等。

在时间序列分析中，我们通常假设观察到的数据是由内部的趋势、季节性和随机性构成的。

首先要介绍的概念是时间序列。

时间序列是按时间顺序记录的一组数据点，其中每个数据点代表某个变量在特定时间点的观测值。

每个数据点可以是连续的时间单位，如小时、天、月或年，也可以是离散的时间单位，如季度或年度。

时间序列数据通常包含趋势、季节性和随机成分。

趋势是时间序列长期上升或下降的的总体倾向，它可以是线性的，也可以是非线性的。

季节性是周期性出现在时间序列中的模式，它在一年中的特定时间段内循环出现，如一年中的季节、月份或周几。

随机成分是不可预测的随机波动，可能是由于外部因素或不可预见的事件引起的。

时间序列分析的目标通常有三个：描述、检验和预测。

描述的目标是对时间序列的特征进行统计分析，通过计算均值、方差、自相关系数等指标来揭示数据的规律和模式。

检验的目标是验证时间序列数据是否满足一定的假设条件，例如平稳性、白噪声等。

预测的目标是基于已有的时间序列数据来预测未来的值。

预测方法可以是单变量的，只使用时间序列自身的历史数据来进行预测；也可以是多变量的，将其他相关变量的信息纳入预测模型。

在时间序列分析中，有一些重要的概念和方法需要掌握。

首先是平稳性。

平稳性是指时间序列的均值、方差和自相关结构在时间上的不变性。

平稳性是许多时间序列模型的基本假设，它能够简化模型的建立和推断。

其次是自相关性。

自相关性是指时间序列中的观测值之间的相关性。

自相关结构可以通过自相关函数（ACF）和偏自相关函数（PACF）来描述，其中ACF表示不同时滞的自相关系数，PACF表示在剔除之前的滞后时其他滞后效应后，特定滞后的自相关系数。

另外，还有移动平均、自回归过程和ARMA模型等重要的方法和模型。

时间序列分析入门概述时间序列分析是一种统计分析方法，用于理解和预测时间序列数据的模式和趋势。

时间序列数据是根据时间顺序排列的观测值，例如每日股票价格、每月销售额等。

时间序列分析能够帮助我们揭示数据内在的规律，提取趋势和周期性变动，并构建模型来预测未来的值。

时间序列分析通常包括以下几个步骤：1. 数据收集和处理：首先需要收集相关的时间序列数据，并对数据进行预处理。

这可能包括去除异常值、缺失值处理以及转换数据为平稳序列。

2. 可视化和探索：通过绘制时间序列图和自相关图等方法，可以直观地了解数据的趋势、季节性和周期性。

这有助于理解数据的基本特征和规律。

3. 模型建立：根据时间序列的性质，选择合适的模型来描述和解释数据。

常见的模型包括平滑法、指数平滑法、自回归移动平均模型(ARMA)和自回归积分移动平均模型(ARIMA)等。

4. 模型诊断：一旦建立了时间序列模型，就需要对模型进行诊断，以评估其拟合程度和预测准确性。

此过程包括检查残差序列的自相关性、正态性和白噪声性质等。

5. 模型预测：根据已建立的模型，可以进行未来的预测。

这通常包括使用模型进行点估计和区间估计，并计算预测误差的置信区间。

时间序列分析在多个领域都有广泛的应用，例如经济学、金融学、气象学和市场营销等。

在经济学中，时间序列分析可用于预测经济指标、评估政策效果和分析经济周期。

在金融学中，时间序列分析常用于股票价格和利率的预测和风险管理。

在气象学中，时间序列分析可用于预测气温、降雨量等天气变量。

而在市场营销中，时间序列分析可用于预测销售额、季节性和促销效果等。

总的来说，时间序列分析是一项有助于揭示和预测时间序列数据规律的重要统计方法。

通过了解数据的特征，选择合适的模型，并进行准确的预测，时间序列分析能够为我们提供有价值的信息，并帮助我们做出科学的决策。

时间序列分析是一种统计学工具，用于研究和预测随时间推移而变化的数据。

它在许多领域中都有广泛的应用，例如经济学、金融学、气象学和市场营销等。

时间序列分析
一、什么是时间序列分析（建模）
时间序列分析（建模）是一种用于研究数据变化随时间变化的方法，
时间序列的建模可以采用不同的统计技术，如时间序列图，聚类分析，回
归分析和主成分分析。

时间序列分析的目的是帮助分析师确定未来数据的
变化趋势，推断出未来可能出现的趋势，从而更好地预测未来的发展趋势。

二、时间序列分析（建模）的应用场景
①对于金融市场，我们可以使用时间序列分析来预测未来的股票价格，金融投资等。

②对于市场营销，可以使用时间序列分析来研究不同时期的消费行为，消费趋势及时间消费趋势的变化等。

③对于宏观经济分析，可以使用时间序列分析来研究宏观经济状况及
其演变趋势等。

三、时间序列分析（建模）的步骤
1）数据收集：从样本数据中收集有关时间序列的信息，并识别其中
的规律；
2）模型准备：根据样本数据构建时间序列模型；。