水运动学

水下机器人的运动学与动力学建模随着现代技术的不断进步，水下机器人在海洋勘探、海洋工程、深海探测等领域发挥着重要作用。

而要实现水下机器人的精确控制，则需要对其运动学和动力学进行建模。

本文将探讨水下机器人的运动学和动力学建模方法。

一、水下机器人的运动学建模运动学主要研究物体的运动规律，对于水下机器人来说，其运动学模型可以通过描述其姿态、位置和速度等参数来实现。

一般而言，水下机器人的姿态可以通过欧拉角或四元数来描述，位置可以使用三维坐标表示，速度可以表示为线速度和角速度。

从几何角度来看，水下机器人的运动可分为平动和转动两种方式。

对于平动来说，可以使用直角坐标系描述机器人的位置变化，而转动则可以通过旋转矩阵或四元数描述机器人的姿态变化。

此外，水下机器人的运动学模型还需要考虑其各个关节和执行器之间的约束关系。

这些约束可以通过关节角度和关节速度等参数表示，从而实现对机器人运动的精确把控。

二、水下机器人的动力学建模动力学研究物体在受力作用下的运动规律，对于水下机器人来说，其动力学模型需要考虑机器人在水中受到的浮力、阻力、重力和推力等力的作用。

在水下环境中，浮力是一个重要的力，可以通过机器人体积和水密度等参数计算得出。

阻力则是因为水的粘性所产生，需要考虑机器人表面积、速度和水的粘滞系数等因素。

重力则是机器人所受的地球引力，可以根据重力加速度和机器人质量得出。

而推力则是通过机器人的推进器产生的作用力。

综上所述，水下机器人的动力学模型可以通过考虑上述各方面的力来建立。

利用牛顿第二定律和力的平衡条件，可以得出水下机器人的运动方程。

通过求解这些方程，可以得到机器人在不同外界作用力下的运动状态，为水下机器人的控制提供理论支持。

三、水下机器人运动学与动力学的关系水下机器人的运动学和动力学密切相关，运动学提供了机器人位置、姿态和速度等参数的描述，而动力学则研究了机器人在受力作用下的运动规律。

在实际应用中，水下机器人的运动学和动力学模型可以结合起来使用。

水表工作原理水表是一种用于测量供水和排水流量的仪表。

它的工作原理基于一些基本原理，包括流体力学和机械运动学。

本文将详细介绍水表的工作原理，从流量传感器到数据显示等方面进行解释。

一、流量传感器流量传感器是水表中最核心的部分。

它通常采用涡轮流量计或超声波流量计。

涡轮流量计是一种利用涡轮在流体中旋转来测量流量的传感器。

当水经过涡轮流量计时，涡轮受到水流的冲击而开始旋转。

涡轮的旋转速度与水流量成正比。

超声波流量计则是通过发送超声波脉冲来测量水流速度和流量。

传感器内部的传感器接收到反射回来的超声波，并计算出水流速度和流量。

二、计量机构计量机构是水表中负责计量流量的部分。

它通常由流量传感器、齿轮传动和显示装置组成。

当涡轮流量计中的涡轮旋转时，齿轮传动将涡轮的旋转转换为指针或数字显示。

计量机构还包括一个计量装置，用于根据流量传感器的旋转计算出实际的水流量。

三、数据显示数据显示是水表上用于显示流量和用水量的部分。

传统的水表通常通过机械指针来显示流量。

指针指向刻度盘上的数字，表示对应时间段内的用水量。

现代的水表则采用数字显示屏，可以直接显示当前的流量和用水量。

数字显示屏通常具有较高的精度和可读性。

四、用水管理水表不仅用于测量流量和用水量，还有助于用水管理。

水表的安装位置通常固定在水源供应处，例如水龙头或进水管道。

通过定期读取水表数据，用户和供水部门可以了解实际的用水情况，并制定合理的用水计划和政策。

这有助于节约水资源和提高供需平衡。

五、维护和校准为了保证水表的准确性和可靠性，定期维护和校准是必要的。

维护包括清洁和检查水表中的传感器和机械部件，以确保其正常运行。

校准是指通过校准设备对水表进行校准，以确保其测量结果的准确性。

维护和校准应由专业人员进行，以确保水表的正常工作和准确计量。

总结：水表是一种用于测量供水和排水流量的仪表，其工作原理基于流体力学和机械运动学。

通过流量传感器、计量机构和数据显示，水表能够准确测量水流量并显示用水量。

⽔是怎么形成的关于⽔的形成，有两种说法：⽔的来源是地球内部。

地球刚形成时，地球刚形成时，⼀、原始成因说，即：地球形成时⾃然产⽣，⽔的来源是地球内部。

⼀、原始成因说，即：地球形成时⾃然产⽣，结构松散，质量不⼤，引⼒也⼩，温度很低。

后来，由于地球不断收缩，内核放射性物质产⽣能量，致使地球温度不断升⾼，有些物质慢慢变暖熔化，较重的物质，如铁、镍等聚集在中⼼部位形成地核，最轻的物质浮于地表。

随着地球表⾯温度逐渐降低，地表开始形成坚硬的地壳。

但因地球内部温度很⾼，岩浆活动就⾮常激烈。

⽕⼭爆发⼗分频繁，地壳也不断发⽣变化，有些地⽅隆起形成⼭峰，有的地⽅下陷形成低地与⼭⾕，同时喷发出⼤量的⽓体。

由于地球体积不断缩⼩，引⼒也随之增加，此时，这些⽓体已⽆法摆脱地球的引⼒，从⽽围绕着地球，构成了"原始地球⼤⽓"。

原始⼤⽓由多种成分组成，⽔蒸⽓便是其中之⼀。

⽔蒸⽓的凝结，⽔就此形成了。

⼀种是天外来客说，即：美国物理学家路易斯·弗兰克认为，宇宙空间⼀直在不断说，即：美国物理学家路易斯⼆、⼀种是天外来客⼆、地向地球补充⽔分，地球上的⽔可能来⾃天外。

弗兰克以美国“探索者1号”卫星拍摄到的照⽚为基础，通过紫外线光谱，研究了地球周围的⼤⽓辉光，发现了许多⽆法解释的穿过⼤⽓层的空洞。

弗兰克分析后断定，这些空洞只能是空间雪球造成的，这些雪球表⾯有⼀层⿊⾊的碳，每块直径约12⽶，重量⼀般在20—40吨之间，特别⼤的有1000吨，每年约有1000万块这样的雪球，像⾬点般地撞击地球⼤⽓层。

这些太空雪球的飞⾏速度达每⼩时3．2万千⽶，撞击地球上层⼤⽓后其壳层破裂，⾥⾯的雪急骤蒸发成⽔蒸⽓，于是不断地向地球输送⽔分。

弗兰克说，每1—2万年，太空雪球向地球输送的⽔分就可以将整个地球表⾯覆盖2．5厘⽶，所以地球上的海⽔很可能是由此⽽来的。

另外，太空雪球中可能还包含有机物质，地球上⽣命的繁衍也可能与此有关。

地球内部原始成因学，不能解释地球形成是同鄙⼈认为这两种说法都有疑点，⼀个是鄙⼈认为这两种说法都有疑点，⼀个是地球内部原始成因学，不能解释地球形成是同时产⽣了⼤量的⽔的真正实质，按地球形成的状况，那么其他星球形成时就没有象地球⼀样有⼤量⽔的形成吗？这种说服⼒不强。

网纱兜水简单的原理网纱兜水是一种常用于水域工程中的水文观测仪器，主要用于测量水体中悬浮物、底泥沉降物、浮游生物等的含量和分布情况。

其原理是利用网纱在水流中的过滤作用，捕集水中的悬浮物质，并通过对捕集物质的分析来获得相关的水质信息。

网纱兜水由一根长杆和一个挂在其末端的兜水器组成。

兜水器一般由一个框架和一个网纱制成。

网纱的孔径可以根据需要而不同，一般为0.1mm至2mm之间。

当进行兜水操作时，兜水器被沿着水深方向放入水中，然后以恰当的速度提升，并在达到预定深度后快速撤回。

在这个过程中，兜水器所经过的水层中的悬浮物质会被网纱捕集。

网纱兜水的原理主要涉及到水动力学、沉降速度、悬浮物体的浓度和滤过效应等几个方面。

首先，水动力学是指水流对于悬浮物体运动的力学过程。

在运动学上，当水流速度较慢时，悬浮物会随水流而运动，并遵循一定的流线。

而当水流速度加快时，悬浮物体会因为面临更大的惯性力而脱离水流，从而减小悬浮物质在水流中的浓度。

这种沉降现象也会发生在网纱兜水的滤过过程中。

其次，沉降速度是指悬浮物体在水中由于其重力而脱离水流从而沉降的速度。

沉降速度与悬浮物质的密度、形状和直径等因素有关。

一般来说，密度较大、形状较规则的悬浮物质沉降速度较快，而密度较小、形状较不规则的悬浮物质沉降速度较慢。

在网纱兜水的过程中，沉降速度的快慢决定了悬浮物体能否被网纱捕集。

此外，悬浮物质的浓度也会影响兜水的效果。

悬浮物质的浓度越高，被网纱捕集的可能性越大。

然而，在实际操作中，为了保证测量结果的准确性，通常会控制兜水操作的速度和深度，避免因较大的浓度差异导致结果的偏差。

最后，滤过效应是指网纱对不同颗粒大小的悬浮物质的剔除效果。

滤过效应主要受到网纱孔径的影响，较小孔径的网纱可以有效地捕集较小颗粒的悬浮物质，而较大孔径的网纱则更容易通过较大颗粒的悬浮物质。

因此，在选择网纱兜水器时，应根据需要选择合适的网纱孔径。

总的来说，网纱兜水利用网纱的滤过作用来捕集水中的悬浮物质，从而获得水质相关信息。

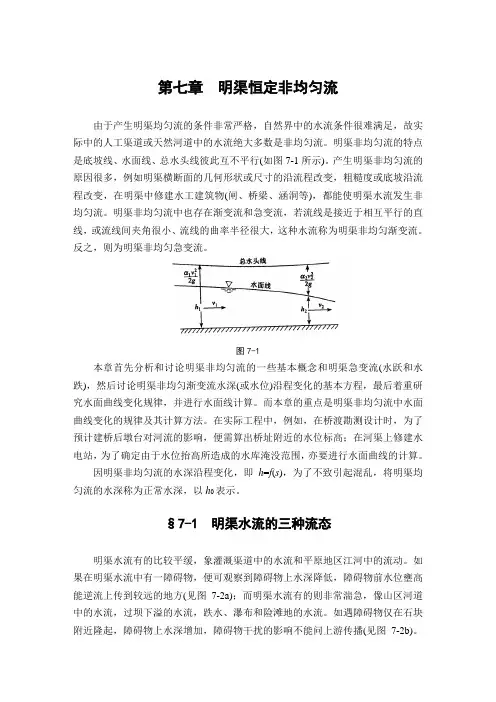
第七章明渠恒定非均匀流由于产生明渠均匀流的条件非常严格，自然界中的水流条件很难满足，故实际中的人工渠道或天然河道中的水流绝大多数是非均匀流。

明渠非均匀流的特点是底坡线、水面线、总水头线彼此互不平行(如图7-1所示)。

产生明渠非均匀流的原因很多，例如明渠横断面的几何形状或尺寸的沿流程改变，粗糙度或底坡沿流程改变，在明渠中修建水工建筑物(闸、桥梁、涵洞等)，都能使明渠水流发生非均匀流。

明渠非均匀流中也存在渐变流和急变流，若流线是接近于相互平行的直线，或流线间夹角很小、流线的曲率半径很大，这种水流称为明渠非均匀渐变流。

反之，则为明渠非均匀急变流。

图7-1本章首先分析和讨论明渠非均匀流的一些基本概念和明渠急变流(水跃和水跌)，然后讨论明渠非均匀渐变流水深(或水位)沿程变化的基本方程，最后着重研究水面曲线变化规律，并进行水面线计算。

而本章的重点是明渠非均匀流中水面曲线变化的规律及其计算方法。

在实际工程中，例如，在桥渡勘测设计时，为了预计建桥后墩台对河流的影响，便需算出桥址附近的水位标高；在河渠上修建水电站，为了确定由于水位抬高所造成的水库淹没范围，亦要进行水面曲线的计算。

因明渠非均匀流的水深沿程变化，即h=f(s)，为了不致引起混乱，将明渠均匀流的水深称为正常水深，以h0表示。

§7-1 明渠水流的三种流态明渠水流有的比较平缓，象灌溉渠道中的水流和平原地区江河中的流动。

如果在明渠水流中有一障碍物，便可观察到障碍物上水深降低，障碍物前水位壅高能逆流上传到较远的地方(见图7-2a)；而明渠水流有的则非常湍急，像山区河道中的水流，过坝下溢的水流，跌水、瀑布和险滩地的水流。

如遇障碍物仅在石块附近隆起，障碍物上水深增加，障碍物干扰的影响不能问上游传播(见图7-2b)。

上述两种情况表明，明渠水流存在两种不同的流态。

它们对于所产生的干扰波(Disturbance Wave)的传播，有着不同的影响。

障碍物的存在可视为对水流发生的干扰，下面分析干扰波在明渠中传播的特点。

冰-水-结构物耦合运动学导论
冰-水-结构物耦合运动学导论是在冰、水和结构物之间相互作
用的系统的动力学研究领域。

冰、水和结构物的相互作用可以是建筑物、桥梁、船只等各种类型的结构与冰和水之间的相互影响。

该导论研究的主要内容包括：冰-水相互作用的力学特性、结
构物对冰和水运动的影响、冰和水对结构物的力学响应以及耦合运动学模型的建立等方面。

在冰-水-结构物耦合运动学导论中，常见的研究问题包括：冰-水相互作用下结构物的受力分析、冰和水对结构物振动特性的影响、结构物对冰和水运动的抵抗力等。

这个领域的研究对于理解和预测结构物在冰-水环境中的力学
行为具有重要意义，对于设计和工程实践具有指导作用。

此外，冰-水-结构物耦合运动学导论还可以为工程防冰、海洋环境工程、港口和航运等领域的工程设计和安全运营提供理论基础。

首向角：船舶纵剖面与OoXo轴的交角。

漂角：重心速度与GX轴正方向夹角。

航速角：重心瞬时速度矢量与OoXo轴夹角。

船舶操纵性是指船舶按照驾驶者的意图保持或改变其运动状态的性能，即船舶能保持或改变其航速、航向和位置的性能。

包括小舵角的航向稳定性、中舵角的航向机动性和大舵角的紧急规避性。

内容如下：1. 航向稳定性：表示船舶在水平面内的运动受扰动而偏离平衡状态，当扰动完全消除后能保持其原有平衡状态的性能。

表示船舶在水平面内的运动受扰动而偏离平衡状态，当扰动完全消除后能保持其原有平衡状态的性能。

2．回转性：表示船舶在一定舵角作用下作圆弧运动的性能。

3．转首性和跟从性：表示船舶应舵转首及迅速进入新的稳定运动状态的性能。

4. 停船性能：船舶对惯性停船和盗车停船的相应性能。

枢心：回转时漂角为零点、横向速度为零的点。

附加惯性力：作不定常运动的船舶，除本身受到与加速度成比例的惯性力外，同时船体作用于周围的水，使之得到加速度，根据作用与反作用力原理，水对船体存在反作用力，这个力称为。

附加质量：附加惯性力是与船的加速度成比例的，其比例系数称为。

水动力导数：位置导数 Yv ,Nv：船体受到一个升力Yv，船体首部和尾部长力方向一致，v都都指向v的负方向，因此合力是一个较大的负值，Yv是一个较大的负值，而水动力矩由于首尾作用相抵消，其绝对值不会很大，因机翼的水动力中心在形成之前，首部作用占优，Nv是一个不大的负值。

加速度导数：Yv点是水动力Y相对于加速度在平衡状态下的变化率，正的加速度的船舶经受一个与加速度相反方向的水反作用力，因此Yv点是一个相当大的负值。

由于船首和船尾对Z轴产生的水动力力矩方向相反，因此水动力矩导数Nv点是一个不大的数值，其符号取决于船型。

旋转导数Yr ,Nr：由于船首和船尾水动力方向相反，因此水动力导数Yr的绝对值不是很大，其符号取决于船型，可正可负。

由于船体回转产生的水动力矩在船首尾有相同的方向，都是阻止船舶回转的，因此水动力矩导数Nr是一个很大的负值。

谁发明花样游泳的原理花样游泳作为一种独特的艺术体操项目，既需要运动员有优雅的水上技巧和出色的身体灵活性，也需要精确的团队配合和细腻的艺术表现。

其过程需要运用科学原理来保证运动员的动作稳定和优美。

花样游泳的原理可以追溯到20世纪初的欧洲，但归功于创新和发展的运动员、教练员和科学家的合作。

花样游泳的原理涉及水力学、力学、运动学和人体生理学等学科。

这些学科的知识有助于解释和改善运动员在水中的表现。

首先，花样游泳涉及水力学。

水是花样游泳运动员的工作环境，理解水的性质对于设计和实施动作非常重要。

水的浮力是实现运动员水中动作的关键因素之一。

浮力产生的原理是根据阿基米德定律，即物体浸入在液体中所受到的浮力等于所排除的液体的重量。

因此，花样游泳运动员要充分利用浮力来轻松完成水中动作，同时也要通过调整身体的位置和姿势来控制浮力的大小和方向，从而实现各种动作。

其次，花样游泳涉及力学原理。

花样游泳中的动作需要通过运动员对水的力的控制来实现。

不同的花样游泳动作需要不同的力来实现，比如推力和拉力。

推力是运动员用手、脚等身体部位对水的推动力，而拉力是运动员对水的阻力。

运动员必须同时掌握推力和拉力的技巧，以实现各种美妙的花样动作。

此外，花样游泳还涉及运动学原理。

运动学研究身体运动和力学关系的学科，可以帮助运动员改进动作的效果和准确性。

例如，运动员在完成技巧动作时，身体的点位和姿势均需要精确控制。

运动员需要了解和应用运动学的原理，使得他们的动作更为流畅、准确和美观。

最后，花样游泳还涉及人体生理学的知识。

人体在水中的运动与在陆地上的运动是有所区别的，因此需要了解和适应水中的运动环境。

水中的水阻和水中的呼吸是花样游泳体能的两个重要方面。

运动员需要通过训练和了解人体生理学的知识，以适应水中的运动环境，提高体能和技巧。

综上所述，花样游泳的原理涉及水力学、力学、运动学和人体生理学等学科的知识运用。

这些学科的原理为花样游泳运动员提供了科学的指导和训练方法，使他们能够更好地展示自己的技巧和艺术表演。

ROV七功能机械手水动力学分析作者：尹汉军等来源：《中国科技纵横》2015年第19期【摘要】在ROV作业的过程中机械手起到非常重要的作用，所有的作业都需要机械手完成，为了保证机械手的作业能力，建立了以D-H法为基础的ROV七功能机械手数学模型，通过运用Kane法对ROV七功能机械手进行了动力学分析，推导出具有外载荷的动力学方程，并通过运用Morison方程对ROV七功能机械手的水动力学进行了研究，并应用计算流体力学软件Fluent仿真计算了拖拽力系数。

与Matlab机器人工具箱计算的结果进行了对比，从而验证了动力学模型的准确性，最后对ROV七功能机械手进行水动力学解算。

【关键词】七功能机械手水动力学运动学 FOTRAN【Abstract】Manipulator plays an essential and important role in ROV's operation， and almost covers the entire subsea exploration procedure. A numerical model of 7-functional manipulator is built based on D-H formula， and using Kane method analysis its dynamics to derive kinetic equation with external loads. Morison equation was also used on this manipulator's hydrodynamics， and drag coefficients were calculated by using Fluent software. The results were compared to calculations results using Matlab toolbox robots， and the comparison verified the accuracy of the dynamic model. The hydrodynamic forces of the seven function ROV manipulator were solved at last.【Key words】Seven Function Manipulator， Hydrodynamic， Kinematics， FORTRAN近些年来随着海洋资源的开发和海洋科学研究的日益深入，水下机器人-机械手系统是水下作业的一个重要组成部分，除了用于水下的观测勘察作业外，水下机器人-机械手还被用于完成采集样本；水下设施的建造和维护；铺设水下管道和维修等相对繁琐的一些工作。

水力学一．题型总览1.判断题（每题1分，约10分）例题：判断下列说法是否正确。

若正确在括号内划√，否则划×。

（1）对于孔口出流和管嘴出流，若出口面积相同，作用水头相等，则二者流量相同。

（×）（2）流体内部切应力的大小仅与流速梯度无关。

（×）（3）静止流体中点压强的大小，与其淹没深度有关，还与受压面的方位有关。

（×）2. 选择题（每题2分，约10分）例题：①等直径圆管中层流的过流断面流速分布是（ a ）(a)呈抛物线分布(b) 呈对数线分布(c)呈椭圆曲线分布(d) 呈双曲线分布②若在静水中取一六面体，那么作用于该六面体上的力有（ c ）(a) 切向力、正压力(b) 正压力(c) 正压力、重力(d) 切向力、重力【注：如果是一个不规则图形，那么作用于其上的力为正压力、切向力、重力】3.简答题（每题5分，10分）【第五章&第八章】①层流与紊流内部切应力有何不同？②试根据尼古拉兹实验，说明沿程阻力系数的变化规律？③写出管流雷诺数的表达式，并说明其层流、紊流的判别标准？4.绘图（10分）压强分布图压力体总水头线和测压管水头线5.计算题（3道题，每道20分，总共60分）【第二章&第四七章结合】作用在平面上的力，作用在曲面上的力，能量方程，动量方程（三大方程联合应用），短管（能量方程，损失计算），长管【考试难度与作业难度等同，复习以作业、书上例题和上课讲的例题为主】二.各章知识点详述第一章：绪论1.连续介质的概念把流体视为由一个挨一个的连续的无任何空隙的质点所组成，即所谓的“连续介质”。

2.液体的主要物理性质：(1)惯性、质量、密度（惯性：惯性是物体保持原有运动状态的性质。

惯性的大小以质量来度量。

当流体受外力作用使运动状态发生改变时，由于流体的惯性引起对外界抵抗的反作用力称为惯性力。

F=-ma负号表示惯性力的方向与物体加速方向相反。

）(2)易流动性、压缩性与表面张力特性（流体受压，体积缩小、密度增大的性质，称为流体的压缩性。