《运筹学》教学大纲

运筹学教学大纲第一部分：引言运筹学作为一门跨学科的学科，通过运用数学和统计学的方法，来解决实际生活中的决策问题，以实现最优的效益。

本教学大纲旨在介绍运筹学的基本概念、原理和应用，使学生能够掌握运筹学的基本知识和解决问题的方法。

第二部分：教学目标2.1 知识目标- 理解运筹学的基本概念、原理和模型- 掌握线性规划、整数规划、动态规划等运筹学方法- 熟悉常见的运筹学应用领域和实际案例2.2 能力目标- 能够分析和抽象实际问题，并构建相应的运筹学模型- 能够运用运筹学方法解决实际问题- 具备独立思考和团队合作的能力第三部分：课程内容3.1 运筹学基础知识- 运筹学的定义和历史发展- 运筹学的基本概念与特点- 运筹学的应用领域与重要性3.2 线性规划- 线性规划的基本概念与原理- 线性规划模型的建立与求解方法- 敏感性分析与灵敏度分析3.3 整数规划- 整数规划的基本概念与模型- 整数规划的求解方法与算法- 整数规划在实际问题中的应用3.4 动态规划- 动态规划的基本思想与模型- 动态规划的求解方法与步骤- 动态规划在决策问题中的应用3.5 随机规划- 随机规划的基本概念与特点- 随机规划的模型与方法- 随机规划在风险决策中的应用第四部分：教学方法4.1 理论授课通过课堂讲授，系统介绍运筹学的基本概念、原理和方法，让学生建立起运筹学的知识体系。

4.2 经典案例分析通过分析运筹学在实际问题中的应用案例，引导学生理解运筹学方法在解决实际问题中的作用和价值。

4.3 数学建模实践组织学生参与运筹学相关的数学建模活动，提高学生的运筹学问题分析和建模能力。

第五部分：教学评价5.1 平时成绩评定根据学生的课堂表现、作业完成情况和课堂互动等综合评定。

5.2 考试成绩评定通过闭卷考试进行学生对运筹学知识的掌握情况评估。

5.3 课程综合评价通过学生的课堂报告、小组项目、个人论文等方式评价学生的综合能力和实际运用能力。

第六部分：参考教材与参考资料6.1 参考教材- 《运筹学导论》赵启南主编高等教育出版社- 《运筹学（第三版）》方宇明主编清华大学出版社6.2 参考资料- 《运筹学及其应用》王栋梁炜主编北京航空航天大学出版社- 《运筹学导论》张忠任主编机械工业出版社结语：本教学大纲将通过理论教学、案例分析和数学建模实践等方式，系统介绍运筹学的基本概念、模型与方法，培养学生的运筹学问题分析和解决能力。

运筹学课程教学大纲一、课程简介- 该课程旨在介绍运筹学的基本理论、方法和应用，培养学生的数学建模和问题求解能力。

- 课程内容包括线性规划、整数规划、非线性规划、动态规划、网络流、队列论、排队模型等。

二、教学目标- 了解运筹学的基本概念和理论。

- 学习运用数学方法解决实际问题。

- 培养学生的分析、抽象和推理能力。

- 提高学生的团队协作和沟通能力。

三、教学内容及安排3.1 线性规划- 线性规划的基本概念与性质。

- 单纯形法及其应用。

- 对偶理论与灵敏度分析。

- 运输问题与分配问题。

3.2 整数规划- 整数规划的基本概念与形式化表示。

- 割平面法与分支界定法。

- 0-1背包问题。

- 工程项目调度。

3.3 非线性规划- 非线性规划的基本概念与求解方法。

- 黄金分割法与牛顿法。

- 二次规划问题。

3.4 动态规划- 动态规划的基本原理与应用。

- 最优子结构性质与状态转移方程。

- 0-1背包问题的动态规划解法。

3.5 网络流- 网络流的基本概念与算法。

- 最大流问题与最小割问题。

- 匹配问题与指派问题。

3.6 队列论- 队列论的基本概念与性质。

- 随机到达与服务模型。

- M/M/1排队模型。

3.7 排队模型- 排队模型的基本概念与特性。

- 单队列系统与多队列系统。

- 排队系统的性能评估。

四、教学方法- 理论讲授与案例分析相结合，提高学生的实际运用能力。

- 鼓励学生课后查阅相关文献，拓宽知识面和视野。

- 培养学生的团队合作和解决问题的能力。

五、教学评估- 平时成绩评定包括课堂表现、作业和小组讨论。

- 期末成绩主要以学生的综合能力为依据，包括考试成绩和课程设计报告。

六、参考教材- 《运筹学导论》王晓东，高等教育出版社。

- 《运筹学》周汉生，中国人民大学出版社。

- 《运筹学》赵运刚，科学出版社。

七、教学资源- 电子课件及教学辅导材料将通过教学平台提供。

- 各类运筹学软件的操作指南和实例将提供给学生。

八、备注- 本教学大纲仅作为参考，请随时关注课程平台上的最新通知和更新内容。

运筹学课程大纲本文为《运筹学课程大纲》的详细介绍，该大纲旨在为学生提供对运筹学课程的全面了解，包括课程目标、涵盖的内容、教学方法和评价方式等。

以下是大纲的具体内容：一、课程目标运筹学课程旨在培养学生使用数学和计算工具解决实际问题的能力，通过系统分析和优化决策，提高生产、运输、物流和管理流程的效率，并为企业和组织提供合理的决策支持。

二、学习要求学生需要具备线性代数、微积分和概率论等相关基础知识，并熟悉使用计算软件（如Excel、Matlab）进行数据分析和数值计算。

三、课程内容1. 运筹学概述1.1 运筹学的定义和发展历程1.2 运筹学在实际问题中的应用领域1.3 运筹学与其他学科的关系2. 线性规划2.1 线性规划的基本概念和模型2.2 单纯形法及其改进算法2.3 整数规划及其应用3. 整数规划3.1 整数规划的定义和特点3.2 整数规划的解法与分支定界法4. 动态规划4.1 动态规划的基本原理和模型4.2 背包问题和最短路径问题的动态规划解法5. 随机规划5.1 随机规划的基本概念和模型5.2 随机线性规划和随机整数规划的解法6. 供应链管理中的运筹学问题6.1 供应链规划及其优化模型6.2 库存管理和配送优化6.3 市场营销与供应链优化的关系四、教学方法1. 授课方式本课程采用理论讲解与案例分析相结合的教学方式。

教师将通过授课引导学生理解运筹学的基本理论和方法，并结合实例进行解析和讨论。

2. 实践操作学生将通过课堂上的实际案例分析和编程实践，掌握运筹学方法在实际问题中的应用技巧。

3. 小组讨论学生将分成小组，结合课程中的案例和练习题，展开小组讨论，提升问题分析和解决能力。

五、评价方式1. 平时表现（占总评成绩的30%）包括课堂参与、小组讨论成果、作业完成情况等。

2. 中期考试（占总评成绩的30%）考察学生对运筹学知识的理解和应用能力。

3. 期末考试（占总评成绩的40%）主要测试学生对运筹学各个章节的掌握情况和解决实际问题的能力。

运筹学课程教学大纲一、课程概述运筹学是运用数学、统计学和计算机方法研究和解决实际问题的一门学科。

本门课程主要介绍运筹学的基本概念、原理和应用，培养学生的综合分析和问题解决能力。

二、教学目标1. 了解运筹学的基本概念、发展历程及学科体系结构；2. 掌握线性规划、整数规划、动态规划等运筹学方法的基本原理和应用；3. 掌握运筹学模型建立和求解的基本方法；4. 培养学生的逻辑思维、分析问题和解决问题的能力。

三、教学内容1. 运筹学的基本概念和发展历程（2学时）- 运筹学的定义、研究对象和研究方法；- 运筹学的发展历程。

2. 线性规划（12学时）- 线性规划的定义和基本概念；- 线性规划的图解法和单纯形法；- 线性规划的对偶理论和灵敏度分析；- 整数规划的基本概念和解法。

3. 动态规划（8学时）- 动态规划的基本概念和基本原理；- 动态规划的最优子结构性质和最优解的构造； - 动态规划的应用实例。

4. 随机模型和排队论（10学时）- 随机模型的基本概念和概率分布；- 排队论的基本概念和排队模型；- 排队论的性能度量和求解方法。

5. 非线性规划和整数规划（8学时）- 非线性规划的定义和基本概念；- 非线性规划的解法和最优性判定；- 整数规划的定义和基本概念；- 整数规划的分枝定界法和割平面法。

6. 运输和分配问题（8学时）- 运输问题的基本概念和解法；- 分配问题的基本概念和解法。

7. 生产调度问题（8学时）- 生产调度问题的基本概念和求解方法； - 作业车间调度问题的建模和求解。

8. 多目标优化问题（6学时）- 多目标优化问题的定义和特点；- 多目标优化问题的解法和应用实例。

四、教学方法本课程采用理论讲授与实践应用相结合的教学方法。

除了课堂上的理论讲解外，还将组织学生参与案例分析、小组讨论、编程实践等活动，加强学生对运筹学方法的理解和应用。

五、教材和参考书目1. 主教材：《运筹学导论》，作者：李明，出版社：清华大学出版社；2. 参考书目：- 《运筹学：初步实用方法》，作者：George B. Dantzig等，出版社：机械工业出版社；- 《运筹学简明教程》，作者：陈杂，出版社：高等教育出版社。

《运筹学》教学大纲一、基本信息课程代码：2060241课程学分：3面向专业：物流管理课程性质：院级必修课开课院系：商学院物流管理系使用教材：教材《运筹学教程（第5版），胡运权，清华大学出版社，2018年》参考书目《运筹学习题集（第5版），胡运权，清华大学出版社，2019年》《管理运筹学（第2版），茹少峰，北京交通大学出版社，2017年》《运筹学（第3版），熊伟，机械工业出版社，2016年》《线性代数（第6版），同济大学数学系，高教出版社，2014年》《运筹学（第4版），运筹学教材组编写，清华大学出版社，2012年》先修课程：《高等数学（1）2100012（5）；高等数学（2）2100014（4）》二、课程简介运筹学是软科学中“硬度”较大的一门学科，兼有逻辑的数学和数学的逻辑的性质，是系统工程学和现代管理科学中的一种基础理论和不可缺少的方法、手段和工具；它是抽象的数学理论和丰富多彩的实践相结合的“桥梁”；它为学生未来从事生产社会实践和应用科学研究的工作人员提供了完整的数学方法和广阔的应用领域。

通过课程学习，培养学生的逻辑思维能力、定量分析能力，使学生系统掌握运筹学的基本理论与方法，能够针对实际问题运用所学的知识建立运筹学的数学模型，并能够求解常用的运筹学数学模型，进而给出可行性解决方案。

同时，引导学生运用运筹学方法分析和解决在生产社会实践、企业运作管理以及规划等过程中面临的问题，启发学生将运筹学的理论方法与各自的专业知识结合起来，也为进一步学习其他专业课程提供必要的基础。

三、选课建议学习该课程前学生应该具有一定的高等数学及线性代数基础，同时对管理和经济学知识有所了解。

本课程适合商学院经管类专业，建议学生在第四至第七学期期间安排开设。

四、课程与专业毕业要求的关联性六、课程内容（一）第1单元绪论1.教学内容：1.1运筹学释义与发展简史1.2运筹学研究的基本特征与基方法1.3运筹学主要分支简介1.4运筹学与管理科学1.5运筹学算法与应用软件简介2.知识要求：2.1理论课时2①理解运筹学研究的基本特征。

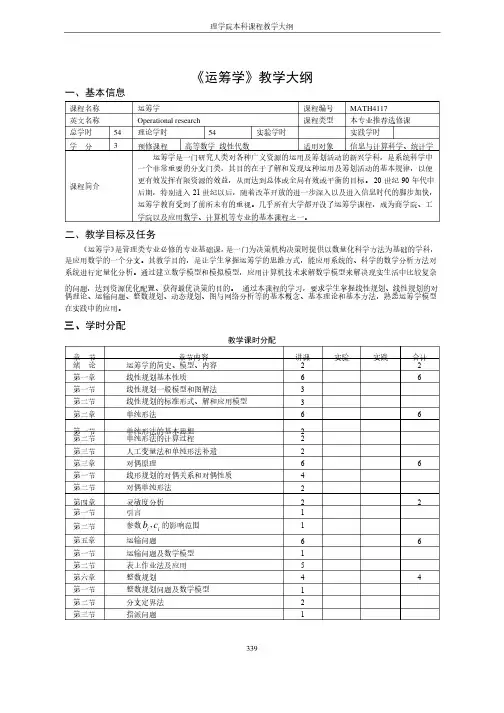
理学院本科课程教学大纲理学院本科课程教学大纲339《运筹学》教学大纲一、基本信息一、基本信息课程名称课程名称 运筹学运筹学课程编号课程编号 MATH4117 英文名称英文名称 Operational research 课程类型课程类型 本专业推荐选修课本专业推荐选修课 总学时总学时 54 理论学时理论学时54实验学时实验学时实践学时实践学时学 分3预修课程预修课程 高等数学高等数学 线性代数线性代数 适用对象适用对象 信息与计算科学、统计学信息与计算科学、统计学课程简介课程简介运筹学是一门研究人类对各种广义资源的运用及筹划活动的新兴学科，是系统科学中一个非常重要的分支门类，其目的在于了解和发现这种运用及筹划活动的基本规律，以便更有效发挥有限资源的效益，从而达到总体或全局有效或平衡的目标。

20世纪90年代中后期，特别进入21世纪以后，随着改革开放的进一步深入以及进入信息时代的脚步加快，运筹学教育受到了前所未有的重视。

几乎所有大学都开设了运筹学课程，成为商学院、工学院以及应用数学、计算机等专业的基本课程之一。

二、教学目标及任务二、教学目标及任务《运筹学》是管理类专业必修的专业基础课，是一门为决策机构决策时提供以数量化科学方法为基础的学科，是应用数学的一个分支。

其教学目的，是让学生掌握运筹学的思维方式，能应用系统的、科学的数学分析方法对系统进行定量化分析。

通过建立数学模型和模拟模型，应用计算机技术求解数学模型来解决现实生活中比较复杂的问题，达到资源优化配置、获得最优决策的目的。

的问题，达到资源优化配置、获得最优决策的目的。

通过本课程的学习，要求学生掌握线性规划、线性规划的对偶理论、运输问题、整数规划、动态规划、图与网络分析等的基本概念、基本理论和基本方法，熟悉运筹学模型在实践中的应用。

在实践中的应用。

三、学时分配学时分配教学课时分配章 节 章节内容章节内容讲课讲课实验实验 实践实践 合计合计 绪 论 运筹学的简史、模型、内容运筹学的简史、模型、内容 2 2 第一章第一章 线性规划基本性质线性规划基本性质6 6 第一节第一节 线性规划一般模型和图解法线性规划一般模型和图解法3 第二节第二节 线性规划的标准形式、解和应用模型线性规划的标准形式、解和应用模型 3 第二章第二章 单纯形法单纯形法6 6 第一节第一节 单纯形法的基本思想单纯形法的基本思想 2 第二节第二节 单纯形法的计算过程单纯形法的计算过程 2 第三节第三节 人工变量法和单纯形法补遗人工变量法和单纯形法补遗 2 第三章第三章 对偶原理对偶原理6 6 第一节第一节 线形规划的对偶关系和对偶性质线形规划的对偶关系和对偶性质 4 第二节第二节 对偶单纯形法对偶单纯形法 2 第四章第四章 灵敏度分析灵敏度分析 2 2 第一节第一节 引言引言1 第二节第二节 参数,i i b c 的影响范围的影响范围 1 第五章第五章 运输问题运输问题6 6 第一节第一节 运输问题及数学模型运输问题及数学模型 1 第二节第二节 表上作业法及应用表上作业法及应用 5 第六章第六章 整数规划整数规划4 4 第一节第一节 整数规划问题及数学模型整数规划问题及数学模型 1 第二节第二节 分支定界法分支定界法 2 第三节第三节指派问题指派问题1章 节 章节内容章节内容讲课讲课 实验实验 实践实践 合计合计 第七章第七章 动态规划动态规划4 4 第一节第一节 多阶段决策问题多阶段决策问题 1 第二节第二节 基本概念基本概念 1 第三节第三节 动态规划的应用动态规划的应用 2 第八章第八章 网络分析网络分析6 6 第一节第一节 图的基本概念和最小树图的基本概念和最小树 1 第二节第二节 最短路问题最短路问题 2 第三节第三节 最大流问题最大流问题 3 第九章第九章 决策论决策论 3 3 第一节第一节 基本概念基本概念1 第二节第二节信息分析和效用决策信息分析和效用决策2第十章第十章 对策论介绍对策论介绍 3 3复习及习题评讲复习及习题评讲6 6 合 计5454四、教学内容及教学要求四、教学内容及教学要求绪论 运筹学的简史、模型、内容（了解） 本章重点、难点：运筹学的性质特点和应用运筹学的性质特点和应用本章教学要求：了解运筹学的性质及特点、运筹学的发展历史、运筹学方法的应用、学习运筹学的意义。

《运筹学》教学大纲一、使用说明(一)课程性质运筹学是经济与管理类学生的专业基础课。

通过本课程的学习,使学生获得经济管理决策中常用的运筹学的基本概念、基本理论与基本方法的知识,为进一步学习与掌握现代管理理论奠定必要的理论基础,并培养与提升学生对实际问题运用定量方法分析与求解,以及进行辅助决策的能力。

本课程为专业课。

(二)教学目的通过理论知识的学习,使学生了解运筹学的基本内容、基本特征与基本方法及运筹学与管理科学的联系;掌握运筹学的基本理论与基本方法;能用运筹学的知识与方法对经济与管理中的一些典型问题进行分析、建模与求解。

(三)教学时数本课程共54学时,3学分。

(四)教学方法教学以课堂教学为主,教师可根据学生学习情况和经济管理类各专业的不同特点,介绍一些常用求解运筹学典型问题的方法。

(五)面向专业信息管理与信息系统、统计学等本科专业。

二、教学内容绪论(一)教学目的与要求[教学目的]介绍运筹学的背景与应用范围。

[基本要求]1、了解运筹学的产生、发展及最新发展动向和成果。

2、了解本学科的研究内容、特点及研究方法。

(二)教学内容重点:运筹学的主要分支及产生背景。

第一节运筹学研究的基本特征与基本方法一、运筹学的产生背景二、运筹学的基本方法第二节运筹学的主要分支一、运筹学的主要分支介绍二、应用状况第三节运筹学与管理科学一、运筹学与管理科学的关系二、运筹学的应用前景(三)教学方法与形式采用课堂讲授、多媒体课件等方法和形式。

(四)教学时数3学时。

(一)教学目的与要求[教学目的]介绍线性规划模型及其单纯性算法。

[基本要求]1、初步掌握建立线性规划模型方法;2、掌握线性规划模型特征;如何化线性规划模型为标准型;3、掌握两个变量线性规划问题的图解法;4、掌握可行解、基、凸集、凸组合、顶点的概念;5、了解线性规划理论依据——几个基本定理、求解线性规划问题基本思路;6、了解引入工人变量目的;7、牢固掌握大M法和两阶段法求解过程、判别什么情况下无解;8、牢固掌握单纯形法计算框图。

《运筹学》教学大纲一、课程性质、目的和任务运筹学是本校管理学门类各专业的学科基础课。

通过本课程的教学，应使学生掌握运筹学的基本原理和方法，提高管理定量分析能力。

二、预修课程高等数学、线性代数三、教学基本要求要求任课教师具有扎实的应用数学功底和广泛的经济管理知识，在课堂教学中既要注重数学模型的推导与求解，更要注重建模方法的思维训练，辅以上机实验教学，培养学生应用计算机对管理问题进行定量分析的能力。

要求学生掌握本大纲所规定的课程内容，处理好理解与记忆、原理与方法、分析与解题的关系，认真完成课程和实验作业，掌握基本的管理定量分析方法。

四、课程内容概要线性规划原理及单纯形法、对偶理论及灵敏度分析、运输问题、整数规划、图与网络分析、五、课程内容及其学时分配、教学要求必要说明：总学时为42 （32学时的授课+10学时的练习），此数据适合数学基础较好的工科专业的学生，经管类专业在此数据的基础上应适当的调整10课时左右。

1、课程内容及其学时分配运筹学概论（1学时）一、运筹学简史二、运筹学的含义三、运筹学的研究方法四、运筹学研究的对象五、运筹学的主要内容第一章线性规划基础及单纯形法（10学时）第一节线性规划问题及其数学模型第二节两变量线性规划问题的几何图解法第三节线性规划数学模型的标准形式第四节线性规划问题的解及解的性质第五节单纯形方法引例第六节单纯形方法第七节单纯形法的进一步讨论第二章线性规划的对偶理论及灵敏度分析（8 学时）第一节对偶线性规划第二节对偶的基本性质第三节对偶单纯形法第四节目标函数系数的灵敏度分析第五节约束条件中常数项的灵敏度分析第六节增加新变量灵敏度分析（略讲）第七节增加一个新约束条件的灵敏度分析（略讲）第三章运输问题（6学时）第一节平衡运输问题第二节不平衡运输问题第四章整数规划（3学时）第一节整数规划概述第二节分派问题第五章图与网络分析（4学时）第一节图的基本概念第二节最短路问题第三节网络最大流问题2、教学要求概论: 1、了解运筹学的涵义。

运筹学教学大纲运筹学（Operations Research，又称管理科学）是现代管理理论中的重要基础性内容，在科学技术体系中属于技术科学层次。

它以管理决策问题为实际背景，以数学模型和定量分析方法为主要工具，其核心思想是实现系统的最优化。

1．教学目的本课程的教学目的是：使学生（1）了解和掌握管理科学领域中一个重要分支的基本理论与方法；（2）了解和掌握管理决策中的一类重要的定量分析工具；（3）培养整体优化的思维方式和逻辑推理与建模计算能力。

2．教学内容绪论（Introduction）第一章线性规划（Linear Programming）1.1 模型与图解法1.2 单纯形法1.3 对偶问题与灵敏度分析1.4 线性整数规划1.5 运输问题第二章动态规划（Dynamic Programming）2.1 基本概念与方法2.2 应用举例第三章图与网络分析（Graph and Network Analysis）3.1 图的基本概念3.2 最小支撑树问题3.3 最短路问题3.4 网络最大流问题3.5 网络计划第四章决策分析（Decision Analysis）4.1 基本概念4.2 风险型决策4.3 效用理论在决策分析中的应用4.4 决策分析-构造风险管理第五章存储论（Inventory Theory）5.1 基本概念5.2 确定型存储模型5.3 随机型存储模型第六章排队论（Queueing Theory）6.1 排队的基本概念6.2 到达与服务的规律6.3 M/M/1排队模型6.4 M/M/c排队模型6.5 M/G/1排队模型6.6 排队系统的优化第七章随机模拟（Simulation）7.1 基本概念与方法7.2 系统模拟第八章对策论（Game Theory）8.1 基本概念8.2 矩阵对策的纯策略8.3 矩阵对策的混合策略3.学时分配4．先修课程线性代数、高等数学、概率论。

5．主要参考书[1]吴育华、杜纲，管理科学基础（第三版），天津大学出版社，2009[2]杜纲、吴育华，管理科学基础学习要点习题案例英汉词汇教学课件，天津大学出版社，2006[3]钱颂迪等，运筹学（第四版），清华大学出版社，2012[4]胡运权，运筹学教程(第三版)，清华大学出版社，2007[5]Hamdy A.Taha . Operations Research, 9e. Prentice Hall. 2010[6]Frederick S. Hillier . Introduction to Operations Research, 9e. McGraw-Hill. 2009。

运筹学教学大纲一、引言运筹学是管理科学的一个重要分支，致力于以系统分析和定量方法来解决决策问题。

本课程旨在帮助学生掌握运筹学的基本理论和方法，培养其系统思维和决策能力。

二、课程目标1. 理解运筹学的基本概念和原则；2. 掌握线性规划、整数规划、网络优化等运筹学方法；3. 能够运用运筹学方法解决实际管理问题；4. 培养学生团队合作和逻辑推理能力。

三、课程内容1. 运筹学概述- 运筹学的发展历程- 运筹学在管理决策中的应用2. 线性规划- 线性规划模型与理论- 单纯形法及其应用- 线性规划在生产计划、资源分配中的应用3. 整数规划- 整数规划模型及解法- 分支定界法与割平面法- 整数规划在工程项目管理、运输规划中的应用4. 网络优化- 关键路径法与程序评价与审查技术（PERT）- 最小生成树与最短路径算法- 网络优化在项目管理、物流规划中的应用5. 动态规划- 动态规划原理与应用- 动态规划在资源分配、生产排程中的应用6. 多目标决策- Pareto最优解与加权求和法- 多目标规划在环境评估、投资决策中的应用四、教学方法1. 理论讲授：通过讲解理论知识，帮助学生建立起对运筹学的整体认识。

2. 实例分析：通过案例分析与解决实际问题，帮助学生理解理论知识与实际应用的联系。

3. 小组讨论：组织学生分组进行运筹学问题讨论，培养学生团队合作与沟通能力。

五、考核方式1. 课堂作业：布置相关习题，要求学生独立完成并及时交回。

2. 期中考试：考查学生对课程内容的掌握程度。

3. 期末论文：要求学生结合实际案例，运用所学方法解决实际问题，撰写学术论文。

六、教材参考1. 《运筹学导论》王明达，北京大学出版社2. 《线性规划原理与方法》朱利民，清华大学出版社3. 《网络优化算法导论》张三，人民邮电出版社七、备注本教学大纲仅作为参考，具体教学内容和安排可能根据实际情况有所调整。

同学们在学习过程中应主动思考、积极参与，丰富自己的知识储备，提升自我能力。

运筹学教学大纲一、课程简介运筹学是一门应用数学学科，旨在通过建立数学模型、运用数学技术和计算工具来解决实际问题。

该课程主要介绍基本的运筹学概念、原理和应用，培养学生的问题分析和决策能力。

二、教学目标1. 理解和掌握运筹学的基本概念、方法和技巧；2. 学会用数学模型分析和解决实际问题；3. 培养学生的逻辑思维、系统思考和决策能力；4. 掌握运筹学软件和工具的使用。

三、教学内容及安排1. 线性规划- 概念和基本性质- 图形解法和单纯形法- 对偶理论与灵敏度分析- 整数规划2. 非线性规划- 梯度法和牛顿法- 限制性条件和约束条件的处理 - 全局最优解和局部最优解3. 动态规划- 最优子结构和递推方程- 状态转移表和决策路径- 应用案例分析4. 排队论- M/M/1模型和M/M/s模型- 排队规则和性能指标- 应用案例分析5. 库存管理- 最优订货策略和补货策略- ABC分析和经济批量模型- 应用案例分析6. 网络优化- 最小生成树和最短路径- 关键路径和关键活动- 资源分配和调度四、教学方法1. 理论讲授：介绍概念、原理和方法；2. 实例分析：通过实际案例讲解运筹学在问题解决中的应用；3. 计算机实验：利用运筹学软件进行数学建模和求解；4. 小组讨论：激发学生的思考和交流，培养合作能力；5. 课堂互动：引导学生提问、解答问题，加强学生的主动学习。

五、教学评估1. 平时成绩：包括课堂表现、小组讨论、作业完成情况等；2. 期中考试：检测学生对基本知识和方法的掌握程度；3. 实践项目：要求学生选择一个实际问题，用运筹学方法进行分析和解决；4. 期末考试：综合考核学生对全课程内容的理解和应用能力。

六、参考教材1. 张宇. 运筹学[M]. 高等教育出版社, 2009.2. 随机轶, 孙灿. 优化理论与应用[M]. 清华大学出版社, 2015.3. 林纳. 运筹学引论[M]. 机械工业出版社, 2006.七、教学资源1. 运筹学软件：如LINGO、CPLEX等；2. 实例数据集：包括线性规划、动态规划、排队论、网络优化等领域的案例数据；3. 网络资源：相关学术论文、问题解决方法和案例分析的论坛和社区。

《运筹学》教学大纲课程编号：10180833英文名称：Operations Research学分：2.5学时：总学时48学时，其中理论32学时，实践16学时先修课程：数学分析、高等代数、概率论与数理统计课程类别：专业课程（选修1）授课对象：数学与应用数学（师范）专业学生教学单位：数理信息学院修读学期：第5学期一、课程描述和预期目标运筹学是数学与应用数学专业的一门专业选修课。

运筹帷幄之中，决胜千里之外。

运筹学是多种学科的综合性学科，是最早形成的一门软科学，它用科学的方法研究与某一系统的最优管理有关的问题。

主要讲述线性规划、非线性规划、图与网络分析、决策分析等内容。

【学生学习结果1】:通过课程学习让学生熟悉一些运筹学的基本模型、主要算法并解决一些实际应用问题；提高学生分析、解决实际问题的能力。

【学生学习结果2】:培养与信息经济时代相应的人文社会科学素养，遵纪守法，诚信做事。

能运用辩证唯物主义和历史唯物主义的立场、观点和方法分析问题、解决问题；培养学生勇于创新，具有良好团结协作精神和勤于实践的科学精神。

【学生学习结果3】:提高运用现代网络技术获取相关信息、整理相关信息和分析信息的能力；熟练使用计算机的能力，能够应用Lingo软件进行求解运筹学模型。

二、本课程对应的专业毕业要求的内涵分解和权重关系本课程对应的专业毕业要求内涵和指标，以及所支撑毕业要求指标的权重关系如表2-1和表2-2所示。

表2-1 对应本课程的专业毕业要求内涵分解表2-2课程与毕业要求指标的支撑程度矩阵关系三、教学内容、基本要求与学时分配本课程理论教学共32个学时，包含9章。

表3-1教学内容、基本要求与学时分配本课程实践教学共16个学时，共8个实验。

表3-2实验内容、基本要求与学时分配四、学生毕业目标的达成途径课程主要采取集中讲授、小组讨论、学生自己动手实践等教学方式。

表 4-1课程毕业要求和达成途径五、学业评价和课程考核考核方式：本课程采用过程性考核和结果性考核相结合的方式。