2-1随机变量的定义

第二章 随机变量及其分布§1 随机变量 一 概念1、为什么要引入随机变量的概念？概率论是从数量上来研究随机现象内在规律性的，为了更方便有力的研究随机现象，就要用数学分析的方法来研究，因此为了便于数学上的推导和计算，就需将任意的随机事件数量化．当把一些非数量表示的随机事件用数字来表示时， 就建立起了随机变量的概念．在实际问题中，有些随机试验的结果可以用数量来表示(如掷色子产生的点数),但是在有些试验中，试验结果看来与数值无关，如何将他们与数值联系起来呢？例如，某个事件发生，可以记为1，不发生可以记为0，这样事件就可以和数值联系起来了，由此就产生了随机变量的概念. 2、随机变量的定义,.E Ω设是随机试验它的样本空间是如果对于每一个,ω∈Ω()X ω有一个实数,与之对应(),X ωΩ这样就得到一个定义在上的单值实值函数X=()X ω称为随机变量。

注：(1)随机变量与普通的函数不同随机变量是一个函数 , 但它与普通的函数有着本质的差别 ,普通函数是定义在实数轴上的,而随机变量是定义在样本空间上的 (样本空间的元素不一定是实数).(2)随机变量的取值具有一定的概率规律随机变量随着试验的结果不同而取不同的值, 由于试验的各个结果的出现具有一定的概率, 因此随机变量的取值也有一定的概率规律。

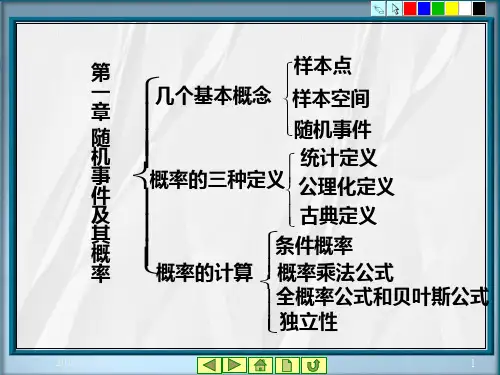
(3)随机变量与随机事件的关系随机事件包容在随机变量这个范围更广的概念之内.或者说:随机事件是从静态的观点来研究随机现象,而随机变量则是从动态的观点来研究随机现象. 3、随机变量的分类⎧⎪⎧⎨⎨⎪⎩⎩离散型:取值有限或无限可数个随机变量连续型：取值连续的充满某区间非离散型非连续型4、离散型随机变量定义：设k x (1,2,...)k =是离散型随机变量X 所取的一切可能值，称()k k P X x p ==为离散型随机变量X 的概率分布或分布律，有的书上也称概率函数。

注：(1)0,1,2,k p k ≥= 1(2)1kk p∞==∑离散型随机变量的分布律也可表示为：1212~n nxx x X p p p ⎛⎫ ⎪⎝⎭例如 观察掷一个骰子出现的点数，随机变量 X 的可能值是 :1, 2, 3, 4, 5, 6.并且1()6P X i == (1,2,...,6)i =即123456~111111666666X ⎛⎫ ⎪ ⎪ ⎪⎝⎭例1、 ,设一汽车在开往目的地的道路上需经过四组信号灯每组信号灯12以的概率允许或禁止汽车通过，,X 以表示汽车首次停下时它已通过的信号灯的组 数(),设各组信号灯的工作是相互独立的.X 求的分布律解：,p 设为每组信号灯禁止汽车通过的概率令1q p =-， 则23401234Xp qp q p q p q ⎧⎫⎨⎬⎩⎭，将12p =带入可得 012340.50.250.1250.06250.0625X⎧⎫⎨⎬⎩⎭二、常见离散型随机变量的概率分布 1、两点分布(0-1分布)设随机变量 X 只可能取0与1两个值 , 它的分布律为011X p p ⎧⎫⎨⎬-⎩⎭，则称 X 服从(0—1)分布或两点分布。

2．1.1随机变量填一填1.随机变量(1)定义：在随机试验中，确定一个对应关系，使得每一个试验结果都用一个确定的数字表示．在这个对应关系下，数字随着试验结果变化而变化的变量称为随机变量．(2)表示：随机变量常用字母X，Y，ξ，η，…表示．2．离散型随机变量(1)定义：所有取值可以一一列出的随机变量，称为离散型随机变量．(2)特征：①可用数值表示．②试验之前可以判断其出现的所有值．③在试验之前不能确定取何值．判一判判断(1．随机变量的取值可以是有限个，也可以是无限个．(√)2．在抛掷一枚质地均匀的硬币试验中，“出现正面的次数”为随机变量．(√)3．离散型随机变量的取值是任意的实数．(×)4．手机电池的使用寿命X是离散型随机变量．(×)5．某人在车站等出租车的时间离散型随机变量．(×)6．某人投篮10次，可能投中的次数离散型随机变量．(√)7．袋中有大小相同的红球6个，白球5个，从袋中无放回的条件下每次任意取出一个球，直到取出的球是白色为止，所需要的取球次数为随机变量X，则X的可能取值为1,2，…，11.(×) 8．在考试中，需回答三个问题，考试规则规定：每题回答正确得100分，回答不正确得－100分，，－100，－300.(√)想一想1.可以用数字来表示呢？提示：可以．可用数字1和0分别表示正面向上和反面向上．2．随机变量和函数有什么类似的地方？提示：随机变量和函数都是一种映射，随机变量把随机试验的结果映为实数，函数把实数映为实数．在这两种映射之间，试验结果的范围相当于函数的定义域，随机变量的取值范围相当于函数的值域．3．在掷骰子和掷硬币的随机试验中，试验结果可以一一列举出来吗？若用X表示电灯泡的使用寿命，则X的值可以一一列举出来吗？提示：掷骰子和掷硬币的试验结果可以一一列举出来，而电灯泡的使用寿命X不能一一列举．4．任何随机试验的结果都可以用数字表示吗？提示：可以．实陡我们可以建立一个随机试验的所有结果同实数间的对应关系，根据问题的需要选择相应数字．5．离散型随机变量的取值必须是有限个吗？提示：不一定．可以是无限个，如1,2,3，…，n，….6．离散型随机变量是否满足下列特征？①可以用数来表示；②试验之前可以判断其可能出现的所有值；③在试验之前不能确定取何值．提示：①②③都是离散型随机变量的特征．思考感悟：练一练1.①15秒内，通过某十字路口的汽车的数量是随机变量；②解答高考数学卷Ⅰ的时间是随机变量；③一条河流每年的最大流量是随机变量；④一个剧场共有三个出口，散场后某一出口退场的人数是随机变量．其中正确的个数是()A．1 B．2C．3 D．4解析：由随机变量的概念可以直接判断①②③④都是正确的．答案：D2．袋中有大小相同的5个钢球，分别标有1,2,3,4,5五个号码．在有放回地抽取条件下依次取出2个球，设两个球号码之和为随机变量X，则X所有可能取值是() A．1,2，…，5 B．1,2，…，10C．2,3，…，10 D．1,2，…，6解析：第一次可取1,2,3,4,5中的任意一个，由于是有放回抽取，第二次也可取1,2,3,4,5中的任何一个，两次的号码和可能为2,3,4,5,6,7,8,9,10.答案：C3．在8件产品中，有3件次品，5件正品，从中任取3件，记次品的件数为X，则{X<2}表示的试验结果是________________________．解析：应分X＝0和X＝1两类．X＝0表示取到3件正品；X＝1表示取到1件次品、2件正品．故{X<2}表示的试验结果为取到1件次品、2件正品或取到3件正品．答案：取到1件次品、2件正品或取到3件正品4．一批产品共有12件，其中次品3件，每次从中任取一件，在取得合格品之前取出的次品数X的所有可能取值是________．解析：可能第一次就取得合格品，也可能取完次品后才取得合格品．X的结果有0,1,2,3.答案：0,1,2,3知识点一随机变量的概念1.6()A．取出产品的件数B．取出正品的件数C．取到产品的概率D．取到次品的概率解析：由题意知，此试验所有可能结果为2件正品、1件正品和1件次品、2件次品．因此取出正品的件数可作为随机变量．故选B.答案：B2．一个袋中装有除颜色外完全相同的2个黑球和6个红球，从中任取两个，可以作为了随机变量的是()A．取到的球的个数B．取到红球的个数C．至少取到一个红球D．至少取到一个红球或一个黑球解析：A项中叙述的结果是确定的，不是随机变量；B项中叙述的结果可能是0,1,2，所以是随机变量．C项和D项叙述的结果也是不确定的，但不能包含所有可能出现的结果，故不是随机变量．知识点二离散型随机变量的判定3.点击的次数为X；③一天内的温度为X；④射手对目标进行射击，击中目标得1分，未击中目标得0分，用X表示该射手在一次射击中的得分．其中X是离散型随机变量的是() A．①②③④B．①②④C．①③④D．②③④解析：一天内的温度X变化的范围是连续的，无法逐一列出，它不是离散型随机变量，故选B项．答案：B4．指出下列随机变量是否是离散型随机变量，并说明理由．(1)某教学资源网站一天内的点击量．(2)你明天上学进入校门的时间．(3)某市明年下雨的次数．(4)抽检一件产品的真实质量与标准质量的误差．解析：(1)某教学资源网站一天内的点击量可以一一列出，是离散型随机变量．(2)你明天上学进入校门的时间，可以是某区间内任意实数，不能一一列出，不是离散型随机变量．(3)某市明年下雨的次数可以一一列出，是离散型随机变量．(4)抽检一件产品的真实质量与标准质量的误差可以在某区间内连续取值，不能一一列出，知识点三离散型随机变量的取值5.(1)在2017年北京大学的自主招生中，参加面试的5名考生中，通过面试的考生人数X；(2)一个袋中装有大小相同的2个白球和5个黑球，从中任取3个，其中所含白球的个数X ；(3)一个袋中装有5个同样大小的球，编号分别为1,2,3,4,5.现从该袋内随机取出3个球，被取出的球的最大编号X .解析：(1)X 可能取0,1,2,3,4,5.{X ＝i }表示“面试通过的有i 人”，其中i ＝0,1,2,3,4,5.(2)X 可能取0,1,2.{X ＝i }表示“取出的3个球中有i 个白球，3－i 个黑球”，其中i ＝0,1,2.(3)X 可能取3,4,5.{X ＝3}表示“取出的3个球的编号为1,2,3”；{X ＝4}表示“取出的3个球的编号为1,2,4或1,3,4或2,3,4”；{X ＝5}表示“取出的3个球的编号为1,2,5或1,3,5或1,4,5或2,3,5或2,4,5或3,4,5”．6．写出下列各随机变量可能取的值，并说明随机变量所取的值表示的随机试验的结果：(1)抛掷甲、乙两枚质地均匀的骰子，所得点数之和Y ；(2)盒子装有6支白粉笔和2支红粉笔，从中任意取出3支，其中所含白粉笔的支数X ，所含红粉笔的支数Y ；(3)在含有10件次品的100件产品中，任意抽取4件，所含有次品的件数X .解析：(1)Y 的可能取值为2,3,4， (12)若以(i ，j )表示抛掷甲、乙两枚骰子后骰子甲得i 点且骰子乙得j 点，则{Y ＝2}表示(1,1)；{Y ＝3}表示(1,2)，(2,1)；{Y ＝4}表示(1,3)，(2,2)，(3,1)；…；{Y ＝12}表示(6,6)．(2)X 的可能取值为1,2,3.{X ＝i }表示“取出i 支白粉笔，3－i 支红粉笔”，其中i ＝1,2,3.Y 可取0,1,2.{Y ＝i }表示“取出i 支红粉笔，3－i 支白粉笔”，其中i ＝0,1,2.(3)随机变量X 的可能取值为0,1,2,3,4.{X ＝i }表示“取出的4件产品中有i 件次品”，其中i ＝0,1,2,3,4.综合知识7.120 cm 的学生，每次乘车0.5元，若学生每次乘车应交的车费为η(单位：元)，学生的身高用ξ(单位：cm)表示，那么ξ和η是不是离散型随机变量？若是，请写出相应的取值情况．解析：由于每个学生对应唯一的一个身高，并且可以一一列举出来，因此ξ是一个离散型随机变量，其取值为本市所有学生的身高．η＝⎩⎪⎨⎪⎧ 0(ξ≤120)，0.5(ξ>120)，因此η也是一个离散型随机变量，其取值为0,0.5.8．下列随机试验的结果能否用离散型随机变量表示？若能，请写出各随机变量可能的取值，并说明这些值所表示的随机试验的结果．(1)盒中装有6个白球和2个红球，从中任意取出3个球，其中所含白球的个数；(2)某同学离开自己学校的距离．解析：(1)能用离散型随机变量表示．设所含白球的个数为X ，则X 的可能取值为1,2,3，X ＝i 表示取出i 个白球，(3－i )个红球，其中i ＝1,2,3.(2)不能用离散型随机变量表示．基础达标一、选择题1．将一个骰子掷两次，不能作为随机变量的是()A．两次掷出的点数之和B．两次掷出的最大点数C．第一次与第二次掷出的点数之差D．两次掷出的点数解析：将一个骰子掷两次，两次掷出的点数之和是一个变量，且随试验结果的变化而变化，是一个随机变量．同理，两次掷出的最大点数、第一次与第二次掷出的点数之差也都是随机变量，而两次掷出的点数不是一个变量．答案：D2．已知下列随机变量：①10件产品中有2件次品，从中任选3件，取到次品的件数X；②6张奖券中只有2张有奖，从这6张奖券中随机的抽取3张，用X表示抽到有奖的奖券张数；③某运动员在一次110米跨栏比赛中的成绩X；④在体育彩票的抽奖中，一次摇号产生的号码数X.其中X是离散型随机变量的是()A．①②③B．②③④C．①②④D．③④解析：③中X的值可在某一区间内取值，不能一一列出，故不是离散型随机变量．答案：C3．抛掷两枚骰子，所得点数之和记为ξ，那么ξ＝4表示的随机试验的结果是()A．一枚是3点，一枚是1点B．两枚都是2点C．两枚都是4点D．一枚是3点，一枚是1点或两枚都是2点解析：ξ＝4可能出现的结果是一枚是3点，一枚是1点或两枚都是2点．答案：D4．袋中装有10个红球，5个黑球，每次随机抽取一个球，若取到黑球，则另换一个红球放回袋中，直到取到红球为止，若抽取的次数为X，则表示“放回5个红球”的事件为() A．X＝4 B．X＝5C．X＝6 D．X≤4解析：第一次取到黑球，则放回1个红球；第二次取到黑球，则再放回1个红球……共放了五回，第六次取到了红球，试验终止，故X＝6.答案：C5．从标有1～10的10支竹签中任取2支，设所取2支竹签上的数字之和为X，那么随机变量X可能取得的值有()A．17个B．18个C．19个D．20个解析：从10支竹签中任取2支，竹签上的数字之和可以是3～19中的任意一个，共有17个．答案：A6．一串钥匙有6枚，只有一枚能打开锁，依次试验，打不开的扔掉，直到找到能开锁的钥匙为止，则试验次数X的最大可能取值为()A．6 B．5C ．4D ．2解析：由于是逐次试验，可能前5次都打不开锁，那么剩余的钥匙一定能开锁，故选B. 答案：B7．袋中装有大小相同的5个球，分别标有1,2,3,4,5五个号码，现在在有放回的条件下依次取出两个球，设两个球的号码之和为随机变量ξ，则ξ所有可能取值的个数是( )A ．25B ．10C ．15D ．9解析：两个球的号码之和可能为2,3,4,5,6,7,8,9,10，共9个．答案：D二、填空题8．下列变量中，不是随机变量的是________(填序号)．①下一个交易日上证收盘指数；②标准大气压下冰水混合物的温度；③明日上课某班(共50人)请假同学的人数；④小马登录QQ 找小胡聊天，设X ＝⎩⎪⎨⎪⎧1，小胡在线.0，小胡不在线. 解析：根据随机变量的定义判断即可．答案：②9．一木箱中装有8个同样大小的篮球，分别编号为1,2,3,4,5,6,7,8，现从中随机取出3个篮球，以ξ表示取出的篮球的最大号码，则ξ＝8表示的试验结果有________种．解析：ξ＝8表示3个篮球中一个编号是8，另外两个从剩余7个号中选2个，有C 27种方法，即21种．答案：2110．连续不断地射击某一目标，首次击中目标需要的射击次数X 是一个随机变量，则X ＝4表示的试验结果是________．解析：由于随机变量X 表示首次击中目标需要的射击次数，所以当X ＝k 时，表示前k －1次均未击中目标，第k 次击中目标，故X ＝4表示的试验结果为前3次未击中，第4次击中目标．答案：前3次未击中，第4次击中目标11．一用户在打电话时忘记了号码的最后三个数字，只记得最后三个数字两两不同，且都大于5，于是他随机拨最后三个数字(两两不同)，设他拨到所要号码的次数为ξ，则随机变量ξ的可能取值共有________种．解析：后三个数字两两不同且都大于5的电话号码共有A 34＝24种．答案：2412．甲、乙两队在一次对抗赛的某一轮中有3个抢答题，比赛规定：对于每一个题，没有抢到题的队伍得0分，抢到题并回答正确的得1分，抢到题但回答错误的扣1分(即得－1分)．若X 是甲队在该轮比赛获胜时的得分(分数高者胜)，则X 的所有可能取值是________．解析：X ＝－1，甲抢到一题但答错了；X ＝0，甲没抢到题，或甲抢到2题，但答时一对一错；X ＝1时，甲抢到1题且答对或甲抢到3题，且一错两对；X ＝2时，甲抢到2题均答对；X ＝3时，甲抢到3题均答对．答案：－1,0,1,2,3三、解答题13．判断下列各个量，哪些是随机变量，哪些不是随机变量，并说明理由．(1)某地“行风热线”某天接到电话的个数．(2)新赛季，梅西在某场比赛中(90分钟)，上场比赛的时间．(3)对角线互相垂直且长度分别为6和8的四边形的面积．(4)在一次书法作品评比中，设一、二、三等奖，小刚的一件作品获奖的等次．解析：(1)接到电话的个数可能是0,1,2，…出现哪一个结果都是随机的，所以是随机变量．(2)梅西在某场比赛中上场比赛的时间在[0,90]内，是随机的，所以是随机变量．(3)对角线互相垂直且长度分别为6和8的四边形的面积是定值，所以不是随机变量．(4)获奖的等次可能是一、二、三，出现哪一个结果都是随机的，所以是随机变量．14．某篮球运动员在罚球时，命中1球得2分，不命中得0分，且该运动员在5次罚球中命中的次数ξ是一个随机变量．(1)写出ξ的所有取值及每一个取值所表示的结果；(2)若记该运动员在5次罚球后的得分为η，写出所有η的取值及每一个取值所表示的结果．解析：(1)ξ可取0,1,2,3,4,5.表示5次罚球中分别命中0次，1次，2次，3次，4次，5次．(2)η可取0,2,4,6,8,10.分，6分，8分，10分.能力提升15.小王钱夹中只剩有20用来买晚餐，用X表示这两张金额之和．写出X的可能取值，并说明这些取值表示的随机试验结果．解析：X的可能取值为6,11,15,21,25,30.其中，X＝6，表示抽到的是1元和5元；X＝11，表示抽到的是1元和10元；X＝15，表示抽到的是5元和10元；X＝21，表示抽到的是1元和20元；X＝25，表示抽到的是5元和20元；X＝30，表示抽到的是10元和20元．16．某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖，一等奖500元，二等奖200元，三等奖10元．抽奖规则如下：顾客先从装有2个红球，4个白球的甲箱中随机摸出两球，再从装有1个红球，2个黑球的乙箱中随机摸出一球，在摸出的3个球中，若都是红球，则获一等奖；若有2个红球，则获二等奖；若三种颜色各一个，则获三等奖，其他情况不获奖．设某顾客在一次抽奖中所得奖金数为X，试写出X的可能取值以及每种取值对应的试验结果数．解析：X的可能取值为500,200,10,0.当X＝500时，试验结果数为C22C11＝1(种)，当X＝200时，试验结果数为C22C12＋C12C14C11＝10(种)，当X＝10时，试验结果数为C12C14C12＝16(种)，当X＝0时，试验结果数为C26C13－(1＋10＋16)＝18(种)．。

第二章 随机变量及其分布§1 随机变量 一 概念1、为什么要引入随机变量的概念？概率论是从数量上来研究随机现象内在规律性的，为了更方便有力的研究随机现象，就要用数学分析的方法来研究，因此为了便于数学上的推导和计算，就需将任意的随机事件数量化．当把一些非数量表示的随机事件用数字来表示时， 就建立起了随机变量的概念．在实际问题中，有些随机试验的结果可以用数量来表示(如掷色子产生的点数),但是在有些试验中，试验结果看来与数值无关，如何将他们与数值联系起来呢？例如，某个事件发生，可以记为1，不发生可以记为0，这样事件就可以和数值联系起来了，由此就产生了随机变量的概念. 2、随机变量的定义,.E Ω设是随机试验它的样本空间是如果对于每一个,ω∈Ω()X ω有一个实数 ,与之对应(),X ωΩ这样就得到一个定义在上的单值实值函数X=()X ω称为随机变量。

注：(1)随机变量与普通的函数不同随机变量是一个函数 , 但它与普通的函数有着本质的差别 ,普通函数是定义在实数轴上的,而随机变量是定义在样本空间上的 (样本空间的元素不一定是实数).(2)随机变量的取值具有一定的概率规律随机变量随着试验的结果不同而取不同的值, 由于试验的各个结果的出现具有一定的概率, 因此随机变量的取值也有一定的概率规律。

(3)随机变量与随机事件的关系随机事件包容在随机变量这个范围更广的概念之内.或者说:随机事件是从静态的观点来研究随机现象,而随机变量则是从动态的观点来研究随机现象. 3、随机变量的分类⎧⎪⎧⎨⎨⎪⎩⎩离散型:取值有限或无限可数个随机变量连续型：取值连续的充满某区间非离散型非连续型4、离散型随机变量定义：设k x (1,2,...)k =是离散型随机变量X 所取的一切可能值，称()k k P X x p ==为离散型随机变量X 的概率分布或分布律，有的书上也称概率函数。

注：(1)0,1,2,k p k ≥= 1(2)1kk p∞==∑离散型随机变量的分布律也可表示为：1212~n nxx x X p p p ⎛⎫ ⎪⎝⎭例如 观察掷一个骰子出现的点数，随机变量 X 的可能值是 :1, 2, 3, 4, 5, 6.并且1()6P X i == (1,2,...,6)i =即123456~111111666666X ⎛⎫ ⎪ ⎪ ⎪⎝⎭例1、 ,设一汽车在开往目的地的道路上需经过四组信号灯每组信号灯12以的概率允许或禁止汽车通过，,X 以表示汽车首次停下时它已通过的信号灯的组 数(),设各组信号灯的工作是相互独立的.X 求的分布律解：,p 设为每组信号灯禁止汽车通过的概率令1q p =-， 则23401234Xp qp q p q p q ⎧⎫⎨⎬⎩⎭，将12p =带入可得 012340.50.250.1250.06250.0625X⎧⎫⎨⎬⎩⎭二、常见离散型随机变量的概率分布 1、两点分布(0-1分布)设随机变量 X 只可能取0与1两个值 , 它的分布律为011X p p ⎧⎫⎨⎬-⎩⎭，则称 X 服从(0—1)分布或两点分布。

第二章随机变量及其概率分布在随机试验中，人们除对某些特定事件发生的概率感兴趣外，往往还关心某个与随机试验的结果相联系的变量. 由于这一变量的取值依赖于随机试验结果，因而被称为随机变量. 与普通的变量不同，对于随机变量，人们无法事先预知其确切取值，但可以研究其取值的统计规律性. 本章将介绍两类随机变量及描述随机变量统计规律性的分布.第一节一维随机变量及其分布函数内容分布图示★随机变量概念的引入★随机变量的定义★例1★例2★例3★引入随机变量的意义★课堂练习★习题2-1内容要点:一、随机变量概念的引入为全面研究随机试验的结果, 揭示随机现象的统计规律性, 需将随机试验的结果数量化，即把随机试验的结果与实数对应起来.1. 在有些随机试验中, 试验的结果本身就由数量来表示.2. 在另一些随机试验中, 试验结果看起来与数量无关,但可以指定一个数量来表示之.二、随机变量的定义定义设随机试验的样本空间为S, 称定义在样本空间S上的实值单值函数)XX(e 为随机变量.随机变量与高等数学中函数的比较:(1) 它们都是实值函数,但前者在试验前只知道它可能取值的范围,而不能预先肯定它将取哪个值;(2) 因试验结果的出现具有一定的概率,故前者取每个值和每个确定范围内的值也有一定的概率.三、引入随机变量的意义随机变量的引入,使得随机试验中的各种事件可通过随机变量的关系式表达出来.由此可见,随机事件这个概念实际上是包容在随机变量这个更广的概念内.也可以说,随机事件是从静态的观点来研究随机现象,而随机变量则以动态的观点来研究之.其关系类似高等数学中常量与变量的关系.随机变量概念的产生是概率论发展史上的重大事件. 引入随机变量后,对随机现象统计规律的研究,就由对事件及事件概率的研究转化为随机变量及其取值规律的研究,使人们可利用数学分析的方法对随机试验的结果进行广泛而深入的研究.随机变量因其取值方式不同, 通常分为离散型和非离散型两类. 而非非离散型随机变量中最重要的是连续型随机变量. 今后，我们主要讨论离散型随机变量和连续型随机变量.例题选讲：例1 (讲义例1) 在抛掷一枚硬币进行打赌时, 若规定出现正面时抛掷者赢1元钱, 出现反面时输1元钱, 则其样本空间为=S {正面, 反面},记赢钱数为随机变量X , 则X 作为样本空间S 的实值函数定义为⎩⎨⎧=-==.,1,,1)(反面正面ϖϖϖX 例2 (讲义例2) 在将一枚硬币抛掷三次, 观察正面H 、反面T 出现情况的试验中, 其样本空间};,,,,,,,{TTT TTH THT HTT THH HTH HHT HHH S =记每次试验出现正面H 的总次数为随机变量X , 则X 作为样本空间S 上的函数定义为1112223X TTTTTH THT HTT THH HTH HHT HHH ϖ易见, 使X 取值为})2({2=X 的样本点构成的子集为},,,{THH HTH HHT A = 故 ,8/3)(}2{===A P X P 类似地，有.8/4},,,{}1{==≤TTT TTH THT HTT P X P例3 (讲义例3) 在测试灯泡寿命的试验中, 每一个灯泡的实际使用寿命可能是),0[+∞中任何一个实数, 若用X 表示灯泡的寿命（小时），则X 是定义在样本空间}0|{≥=t t S 上的函数，即t t X X ==)(，是随机变量.课堂练习1. 一报童卖报, 每份0.15元,其成本为0.10元. 报馆每天给报童1000份报, 并规定他不得把卖不出的报纸退回. 设X 为报童每天卖出的报纸份数, 试将报童赔钱这一事件用随机变量的表达式表示.四. 随机变量的分布函数定义 设X 是一个随机变量, 称)()()(+∞<<-∞≤=x x X P x F 为X 的分布函数.有时记作)(~x F X 或)(x F X .分布函数的性质1. 单调非减. 若21x x <, 则)()(21x F x F ≤；2. ;1)(lim )(,0)(lim )(==+∞==-∞+∞→-∞→x F F x F F x x3. 右连续性. 即).()(lim 00x F x F x x =+→例4 判别下列函数是否为某随机变量的分布函数?⎪⎩⎪⎨⎧≥<≤+<=⎪⎩⎪⎨⎧≥<≤<=⎪⎩⎪⎨⎧≥<≤--<=.2/1,1,2/10,2/1,0,0)()3(;,1,0,sin ,0,0)()2(;0,1,02,2/1,2,0)()1(x x x x x F x x x x x F x x x x F ππ解 (1)由题设, )(x F 在),(+∞-∞上单调不减, 右连续, 并有,0)(lim )(==-∞-∞→x F F x ,1)(lim )(==+∞+∞→x F F x所以)(x F 是某一随机变量X 的分布函数.(2)因)(x F 在),2/(ππ上单调下降, 所以)(x F 不可能是分布函数. (3)因为)(x F 在),(+∞-∞上单调不减, 右连续, 且有 ,0)(lim )(==-∞-∞→x F F x ,1)(lim )(==+∞+∞→x F F x所以)(x F 是某一随机变量X 的分布函数.离散型随机变量的分布函数例5（讲义例2）设随机变量X 的分布律为 ,2/16/13/121i p X求)(x F .解 }{)(x X P x F ≤=当0<x 时，,}{∅=≤x X 故0)(=x F 当10<≤x 时，31}0{}{)(===≤=X P x X P x F 当21<≤x 时, 216131}1{}0{)(=+==+==X P X P x F 当2≥x 时，1}2{}1{}0{)(==+=+==X P X P X P x F 故 ,2,121,2/110,3/10,0)(⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=x x x x x F )(x F 的图形是阶梯状的图形, 在2,1,0=x 处有跳跃, 其跃度分别等于},0{=X P },1{=X P }.2{=X P例6 X 具有离散均匀分布, 即,,,2,1,/1)(n i n x X P i ===求X 的分布函数.解将X 所取的n 个值按从小到大的顺序排列为)()2()1(n x x x ≤≤≤则)1(x x <时，,0}{)(=≤=x X P x F )2()1(x x x <≤时，,/1}{)(n x X P x F =≤= )3()2(x x x <≤时，,/2}{)(n x X P x F =≤=……)1()(+<≤k k x x x 时，,/}{)(n k x X P x F =≤=)(n x x ≥时，1}{)(=≤=x X P x F故 )(x F ⎪⎪⎩⎪⎪⎨⎧<=≥<),,max(,1),,2,1(),,min(,/),,min(,0111n j n n x x x x k n j x x x x n k x x x 当个不大于中恰好有且当当例7（讲义例3）设随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=.3,1,32,19/15,21,19/9,1,0)(x x x x x F求X 的概率分布.解 由于)(x F 是一个阶梯型函数, 故知X 是一个离散型随机变量, )(x F 的跳跃点分别为1, 2, 3, 对应的跳跃高度分别为 9/19, 6/19, 4/19, 如图.故X 的概率分布为 .19/419/619/9321i p X课堂练习设随机变量X 的概率分布为4/12/14/1321i p X -,求X 的的分布函数，并求{},2/1≤X P {},2/52/3≤<X P {}.32≤≤X P。

中班数学认识简单的随机变量数学是学习中班的重要内容之一，通过数学学习，幼儿可以培养逻辑思维和分析问题的能力。

在中班数学学习中，了解随机变量是一个重要的概念。

本文将介绍中班数学中简单的随机变量的认识。

一、随机变量的定义和特点随机变量是数学中的一个重要概念，它用来描述随机试验中的结果。

在中班数学中，我们可以以简单的游戏为例来认识随机变量。

比如，教师可以准备一些带有数字的纸牌，每个纸牌上写有1至6的数字，然后让幼儿们进行抽牌游戏。

每次抽到的纸牌上的数字就是一个随机变量。

随机变量有以下几个特点：1. 随机性：随机变量的取值是不确定的，我们无法预测具体的结果。

2. 取值范围：随机变量的取值范围是固定的，比如上述例子中的纸牌上的数字范围是1至6。

3. 概率分布：随机变量的每个取值都有一定的概率发生，概率之和等于1。

二、认识随机变量的意义了解随机变量的意义对幼儿的数学学习有着重要的作用。

通过认识随机变量，幼儿可以培养以下几个方面的能力：1. 观察力：通过观察随机试验的结果，幼儿可以学会仔细观察，发现规律。

2. 推理能力：随机变量的取值是不确定的，需要通过推理和预测来确定可能的结果。

3. 统计思维：通过了解随机变量的概率分布，幼儿可以培养统计思维，明白每个结果发生的可能性。

三、中班数学教学中的随机变量应用在中班数学教学中，教师可以运用随机变量来进行一些简单的游戏和实验，从而帮助幼儿们更好地理解和认识随机变量。

1. 抽牌游戏：可以通过抽牌游戏来让幼儿们认识随机变量，让他们自己体验随机性。

2. 掷骰子：可以使用骰子来进行实验，让幼儿们观察和记录每次实验的结果，了解随机变量的取值范围。

3. 排队游戏：可以让幼儿们进行排队游戏，观察每个幼儿排队的位置，通过统计每个位置出现的次数，了解随机变量的概率分布。

通过以上的教学活动，幼儿们可以在游戏中感受到数学的乐趣，同时也加深对随机变量的理解。

四、中班数学教学中的评价和展望通过在中班数学教学中引入随机变量的概念，幼儿们可以培养观察力、推理能力和统计思维。

初中数学什么是随机变量
随机变量是概率论与统计学中的一个重要概念，它是指随机试验结果的数值特征。

在数学上，随机变量可以用来描述某个随机试验的结果，它可以取得不同的数值，而每个数值发生的概率也是已知的。

举个简单的例子来说明随机变量：假设我们进行一次抛硬币的实验，我们定义随机变量X 表示出现正面的次数，那么X可以取0（表示没有出现正面），1（表示出现一次正面）或者2（表示出现两次正面）。

在这个例子中，随机变量X描述了抛硬币这个随机试验的结果。

根据随机变量的性质，我们可以将随机变量分为两类：离散型随机变量和连续型随机变量。

离散型随机变量是指在一定的范围内取有限个或可数个值的随机变量，比如上面抛硬币的例子中的随机变量X就是一个离散型随机变量。

连续型随机变量是指在一定范围内可以取任意值的随机变量，比如测量一个人的身高就是一个连续型随机变量。

在概率论中，随机变量的概率分布函数是描述随机变量取值的概率规律的函数。

对于离散型随机变量，我们通常使用概率质量函数（Probability Mass Function，PMF）来描述其取值的概率分布；对于连续型随机变量，我们则使用概率密度函数（Probability Density Function，PDF）来描述其取值的概率分布。

通过研究随机变量及其概率分布函数，我们可以对随机试验的结果进行更深入的理解，从而在实际问题中进行概率计算、统计分析等工作。

随机变量在概率论与统计学中有着广泛的应用，是这两门学科的基础概念之一。

基础会计学随机变量
在基础会计学中，随机变量是一个非常重要的概念。

随机变量指的是在某个随机试验中可能取得的值，这些值是随机的，并且可以用来描述事件发生的概率分布。

随机变量可以分为离散随机变量和连续随机变量两种类型。

离散随机变量是指在一定范围内可能取得有限个数值的变量，比如掷硬币的结果只能是正面或反面。

而连续随机变量则是指在某一区间内可以取得任意值的变量，比如人的身高就是一个连续随机变量。

在会计学中，随机变量的应用非常广泛。

比如在风险管理中，我们可以用随机变量来描述不同风险事件发生的概率，从而制定相应的风险管理策略。

又比如在财务分析中，我们可以用随机变量来描述公司未来收入的不确定性，从而评估公司的经营风险。

随机变量还可以帮助我们进行决策分析。

通过对不同随机变量的概率分布进行分析，我们可以选择出最优的决策方案，从而提高决策的准确性和效果。

总的来说，随机变量在基础会计学中起着非常重要的作用。

通过对随机变量的研究和分析，我们可以更好地理解和应对不确定性，从而提高会计学的决策效率和准确性。

希望大家能够深入学习和理解随机变量的概念，从而更好地应用于实际的会计工作中。