定义判断冲刺过关40题七
- 格式:doc
- 大小:28.00 KB
- 文档页数:3

定义判断专项习题1.演出艺术,亦可称之为舞台艺术或表演艺术,指的是通过演员在舞台上的现场表演来完成艺术形象创造的艺术形式。
下列属于演出艺术的是:A.电视连续剧《士兵突击》B.石家庄评剧团排演的《西柏坡》C.公园里举办的交谊舞大赛D.魔术师刘谦表演的精妙的魔术2.生态移民是指为了保护某个地区特殊的生态或让某个地区的生态得到修复而进行的移民,也指因自然环境恶劣,不具备就地扶贫的条件而将当地人民整体迁出的移民。
下列属于生态移民的是:A.贵州省某山区因土地出现石质化现象,该地区村民被迁往他乡B.几百年前,中原一带的居民为躲避战争,整体迁到南方,成为客家人C.某村落位于山谷中,交通十分不便,为更快致富,村民集体研究决定移居山外D.张三的父母家住三峡库区,由于修水库,其父母将家产变卖,来到上海与张三一起居住3.概念的内涵是概念所反映的对象的本质属性,它是概念质的规定性,说明概念所反映的对象是什么样。
下列不是从内涵方面说明概念的是:A.单身汉是未婚、成年的男性B.社会关系包括经济、思想、政治、文化以及家庭等各方面的关系C.鱼是用鳃呼吸、鳍游水,有脊椎的水生动物D.商品是用来交换的劳动产品4.假设就是根据已知的科学原理和一定的事实材料,对未知事物的普遍规律性和因果性所做出的假定性解释。
下列不属于假设的是:A.艾滋病是由支原菌和艾滋病病毒引起的B.世界气候逐渐变暖是大气的因素,或是海洋的因素,或是地球内部的因素C.民法中的“宣告死亡”D.能溶解一切物质的“万能溶液”5.重大突发事件是在紧急状态下发生的严重危机事件。
它包括重大突发性自然灾害、重大突发性工业事故及灾难性事故、重大突发性社会骚乱事故和重大突发性政治危机。
根据以上定义,下列情况不属于重大突发性社会骚乱事故的是:A.传染病和恶性中毒B.恐怖活动、民族冲突、公共场合突发型骚乱C.社会动乱、选举危机、政变D.球场暴力、春运火车站人员滞留、节假日旅游景区人员拥挤事故6.最终产品,是指在一定时期内生产的并由其最后使用者购买的产品和劳务。

定义判断题
定义判断题是一种逻辑推理题目,通常要求考生根据给出的定义,判断某个选项是否符合该定义。
这种题目需要考生具备一定的逻辑推理能力和对各种概念的理解能力。
在解答定义判断题时,考生需要仔细阅读定义,并理解其含义。
然后,考生需要逐个分析选项,判断每个选项是否符合定义。
如果某个选项符合定义,那么该选项就是正确的;如果某个选项不符合定义,那么该选项就是错误的。
定义判断题的难度通常取决于定义的复杂程度和选项的迷惑性。
有些定义可能比较简单,容易理解,但选项可能比较复杂,需要考生进行仔细分析;有些定义可能比较复杂,需要考生进行深入思考,但选项可能比较简单,容易判断。
为了提高解答定义判断题的能力,考生需要多做练习,熟悉各种类型的定义和选项。
同时,考生也需要注重对各种概念的理解,提高自己的逻辑推理能力。

国家公务员考试行测定义判断冲刺试题及答案成公不等待决胜国考就现在!2017年国家公务员课程火热开售中>>二、定义判断。
每道题先给出定义,然后列出四种情况,要求你严格依据定义,从中选出一个最符合或最不符合该定义的答案。
注意:假设这个定义是正确的,不容置疑的。
请开始答题:91、文饰作用,又叫理由化的适应,是指一个人为了掩饰不符合社会价值标准、明显不合理的行为或不能达到个人追求目标时,往往在自己身上或从周围环境找一些理由来为自己辩护,把自己的行为说成是正当合理的,以隐瞒自己真实的动机或愿望。
根据上述定义,下列不属于文饰作用的一项是()A、张三期末考试考砸了,他认为是老师题目出得不好所导致的;B、李四在大一时没有获得一等奖学金,他认为原因是自己与辅导员的关系不好;C、王五做海鲜生意失败,就吃安眠药自杀了;D、周老师上英语课时讲错了题目,便解释说自己最近身体不好,思路不顺。
92、普通合伙企业是指依法在中国境内设立的由各合伙人订立合伙协议,共同出资、合伙经营、共享收益、共担风险,并对合伙企业债务承担无限连带责任的营利性组织。
其应当具备以下条件:(1)有两个以上的合伙人,并且都是依法承担无限责任者;(2)有书面合伙协议;(3)有各合伙人实际缴付的出资;(4)有合伙企业的名称;(5)有经营场所和从事合伙经营的必要条件。
根据以上定义,下列属于普通合伙企业的是()A、某村的“凤凰养鸡场”由该村的村民集资创办,并签订了书面协议,去年在村东头搭建了鸡棚,不到一年的时间就获利丰厚;B、刚刚大学毕业的小王想创业,但是资金不足,于是向朋友借了本钱,并达成了分期还款的协议,于是小王顺利地开办了一间外贸公司;C、在美国留学的小刘在网上遇到了远在加拿大的高中同学,聊天的过程中他们一拍即合,决定合伙成立一家公司,等公司业绩较好时,再转入国内进行发展;D、小陈从小就梦想自己做老板,大学毕业后他准备自己开个网络公司,并以自己的名字命名,现在整天和有着相同“创业梦”的朋友交流,但一直未确定下来。

行测定义判断强化练习带答案解析行测定义判断强化练习:1.定义:1请求谅解是立足于对方,请求对方宽恕的道歉表达方式。
2承担错误是承认自己的不对与过错,将责任归到自己身上,以减少对方的不满心理。
3责罚是以自我惩罚的方式承担责任与抵偿自己的罪过。
以下三个例证中,与定义相符的个数有几个?1不好意思,让你一个人受冷落了。
郑振环《天边有一簇圣火》2董炎:呀,路路,还在生我的气?今天都怪我不好,老舍《结婚一年间》3我对不起妈妈!我不是人。
电视剧《非常时代》A.0个B.1个C.2个D.3个2.定义:①科学性:指概念、原理、定义和论证等内容的叙述清楚、确切,历史事实、任务以及符号、专业术语和参考文献准确。
②艺术性:指人们反映社会生活和表达思想感情所达到的鲜明、生动的美好程度。
③实用性:指某项发明、某项技术等具有简便可行的可操作性,或者有着普遍推广意义,并且能够产生积极效果。
典型例证:1水蛭会吸血,中医认为把它晒干了入药能够活血化瘀;蚯蚓地龙在土壤里钻来钻去,中医认为它晒干了入药能够通络利尿。
2成功的备课是一项复杂而细致的工作,是整个教学过程中一个重要环节,备课也是教师对教材进行再加工再创造的过程。
3民族风情山歌戏《七彩畲乡》展示了社会主义新农村建设取得的辉煌成就,热情歌颂了新一代大学生村官热爱山乡、开拓进取的精神品格。
对上述典型例证与定义的关系判断正确的是。
A.例证1与定义①相符,例证2与定义②相符B.例证3与定义③相符,例证2与定义②不相符C.例证13分别与定义②①不相符D.例证12分别与定义②③相符3.定义:①赡养:晚辈亲属对长辈亲属的扶助和供养。
②抚养:长辈亲属对晚辈亲属或兄、姐对未成年弟、妹的扶助和供养。
③扶养:在各种社会关系中,针对“弱者”所发生的经济供养和生活扶助。
典型例证:1小张因失业没有收入,现由小张的弟弟为其无偿提供住宿和生活费用。
2出租车司机老李除了提供家庭日常生活费用外,还供养年老丧失劳动力的父母,天天忙得乐呵呵的。

2006年江苏省录用公务员考试《行政职业能力倾向测验》苏索培训模拟B4卷第一部分知觉速度与准确性(共60题,时限10分钟)一、同符查找(1~35题)1、YU^& LDJIU^%A、1B、2C、3D、42、KDHA DJSKIWA、1B、2C、3D、43、OUJI DKJSDOA、1B、2C、3D、44、KJCX ELJFPOA、1B、2C、3D、45、$#RV JKDSU^A、1B、2C、3D、06、OPWE JLDSFEA、1B、2C、3D、47、O*H$ K#DG$OA、1B、2C、3D、48、HYTS LOHMTSA、1B、2C、3D、49、KSY+ +IKHGYA、1B、2C、3D、410、BVGY VG&JOKA、1B、2C、3D、011、J*ED J*EDGVA、1B、2C、3D、412、DERT LOIUJKA、0B、2C、3D、413、HY^F ^FN*GHA、1B、2C、3D、414、&FUJ F&LMNJA、1B、2C、3D、415、VM$G V#GLPOA、1B、2C、3D、416、KIUJ JISXCDA、1B、2C、3D、417、SURT T%LOIKA、1B、2C、3D、418、JUYH UHYXSWA、1B、2C、3D、419、CDFG CFLKOIA、1B、2C、3D、420、HDIF KHFNGIA、1B、2C、3D、421、东南西北中左西东中可申申左南西A、1B、2C、3D、422、47285630 38240 0938A、1B、2C、3D、423、675938 96382 369A、1B、2C、3D、424、五中禾火夕歹禾木申五五禾多A、1B、2C、3D、425、空道KON人牢KN大首空K大空OA、1B、2C、3D、426、马丰WM69后马后W9丰M6右冯A、1B、2C、3D、027、JAKSON昌JAC吕KSC品A、0B、2C、3D、428、5021943 051293 2150A、1B、2C、3D、429、贞宝了分甲页宝分田了宝子分甲A、1B、2C、3D、430、47285630 38240 0938A、1B、2C、3D、431、连理枝头花正开连理枝花开连埋花A、1B、2C、3D、432、Y917Z23 YZ9123 9137A、1B、2C、3D、433、三五中禾火夕歹禾木申五五禾多A、1B、2C、3D、434、965831 56439 279084A、1B、2C、3D、435、301528 801479 09128A、1B、2C、3D、4二、数字区间定位(36~50题)36、1479 37、6984 38、2049 39、5473 40、5896 41、0912 42、6790 43、8930 44、4983 45、6347 46、5067 47、7788 48、9857 49、4999 50、6657三、字符替换(51~60题)51、数字表中对应标志的数字共有几个:A、4B、5C、6D、752、数字表中对应标志的数字共有几个:A、2 B C、4 D、553、数字表中对应标志的数字共有几个:A、1B、2C、3D、454、第7A、W B C、D55、第A BC D56标志的数字在哪几列:A、3,4,8B、1,7C、4,5,8D、1,7,857、数字表中对应的数字在那几行出现:A、1,2,3,B、3,4C、1,3,4D、2,3,458、第2A、B、C、D、59、哪一列中有三个数字相同,对应的标志是什么:A、第2B、第3列,C、第3D、第2列,60和M标志的数字分别有几个:A、5,4 4,2 C、5,3 D、4, 8第二部分 数量关系(共20题,参考时限15分钟)一、数字推理(61~70题)给你一个数列,但其中缺少一项,仔细观察数列的排列规律,选择你认为最合适的一个答案。

行测考试定义判断练习题及参考答案行测考试定义判断练习题1:1、矿产资源:是指一批由地质作用形成的,具有利用价值的,呈固态、液态、气态的自然资源。
根据上述定义,下列不是矿产资源的是()。
A.煤炭B.石油C.森林D.天然气2、行政实施是指从行政决策一经形成或最后批准时起,行政机关及其工作人员贯彻决策、实施决策的全部活动或整个过程。
下列不属于行政实施的一项是()。
A.行政部门为推行一项决策,检查行政决策是否与有关法律法规相抵触B.行政部门执行政策时遇上国庆,放假休息C.行政部门准备执行救灾措施所需要的经费和物资装备D.为推动群众爱卫护城自觉行动,县政府召开动员大会,发布动员令3、可再生资源:是指被开发利用后能再次生成的资源。
根据上述定义,下列不是可再生资源的是()。
A.空气B.森林C.水D.土地4、电子政务:是指政府机构在其管理和服务职能中运用现代网络技术,打破传统行政机关的时间、空间和部门分隔的制约,使各级政府的各项监管工作更加严密,服务更加便捷,从而把各级政府建设成廉洁、勤政、务实、高效的政府。
根据上述定义,下列不属于电子政务的行为内容的是()。
A.机关建立了自己的信息网站,所有非秘密信息都在网上看得到,网民也可以通过网络和政府对话B.机关的工作人员偶尔用计算机操作一些简单业务,比如打字、打印等C.各级政府之间通过网络技术进行业务和信息的互动,避免了信息的不对称性和不流畅性D.通过网络,各级政府接受社会的监督,也逐步实现了层级监督,政府更加高效和务实5、考核:是指各级行政机关根据法定的管理权限,在一定的时间内,对公务员的工作成绩和服务情形进行定期和不定期的考核与评价。
根据上述定义,下列属于考核的是()。
A.检察院规定工作人员要按时上下班,不可迟到早退B.美国实行工作标准考绩制,主要对公务员的工作数量、工作质量和工作适应能力进行考察评定C.人民代表大会上,部分代表谈了对提案的看法D.在机关组织的春游活动中,机关领导建议大家来一个对歌大赛参考答案:1、B2、B3、D4、B5、B行测考试定义判断练习题2:1、社会生活噪音:是指人为活动所产生的除工业噪音、建筑施工噪音和交通噪音之外的干扰周围生活环境的噪音。

陕西事业单位考试定义判断冲刺过关40题六在事业单位行测考试中,定义判断可谓是必考题型,也是考生复习的重中之重。
为您总结归纳出定义判断冲刺过关40题,祝您顺利通关!1.失语症:是指由于神经中枢病损导致抽象信号思维障碍,而丧失口语、文字的表达和领悟能力的临床症侯群。
根据上述定义,下列可能患失语症的是:( )A.“狼孩”回归社会后无法与人进行言语交流B.幼时高烧听力受损致使发音有极大缺陷,影响交流C.因受刺激精神失常,造成言语理解和表达上的困难D.因车祸头部受创,虽能模仿他人言语但经常答非所问2.流通加工:是指物品在从生产地到使用的过程中,根据需要施加包装、分割、计量、分拣、刷标志、帖标准、组装等简单作业的总称。
根据上述定义,下列属于流通加工的是:( )A.某工厂采购布匹、钮扣等材料,加工成时装并在市场上销售B.某运输公司在冷藏车皮中保存水果,使之在运到目的地时更新鲜C.杂货店将购时的西红柿按质量分成每斤1元和每斤2元两个档次销售D.某批发商在运输玻璃杯的过程中,为杯子加上防震外包装,以避免某碎裂3.危机公关:是指由于企业管理不善、同行竞争甚至遭遇恶意破坏或者是外界特殊事件的影响,而给企业或者品牌带来危机,企业针对危机所采取的一系列自救行动,包括消除影响、恢复形象等。
根据上述定义,下列属于危机公关的是:( )A.由于台风影响,某企业的户外广告牌被风吹倒,企业派员工前去修复B.某企业由于重要生产设备被盗,严重影响生产,高层领导召开紧急会议,研究对策C.某企业在行业竞争中失去领先地位,利润大幅下滑,企业高层领导决定转向新的领域D.某大型餐饮集团的一个连锁店由于卫生状况差被曝光后,该集团领导通过媒体向公众道歉,并借此机会发布新的企业卫生管理标准4.职业枯竭:是指人们在自己长期从事的工作重压之下,产生身心能量被工作耗尽的感觉。
根据上述定义,下列属于职业枯竭状态的是:( )A.老周不能胜任自己现有的工作,每天都会忙得焦头烂额B.刚参加工作的小李觉得这份工作太累,产生了跳槽的念头C.刘经理每天工作繁忙,缺乏充足的休息,情绪也越来越糟糕D.在从事过许多不同的职业之后,老王觉得所有工作都索然无味5.附加值:是附加价值的简称,是在产品原有价值的基础上,通过生产过程中的有效劳动新创造的价值,即附加在产品原有价值上的新价值。

公务员冲刺试题行政职业能力测试答案第二部分判断推理二、演绎推理:共10题,每题给出一段陈述,这段陈述被假设是正确的,不容置疑的。
要求你根据这段陈述,选择一个答案。
注意,正确的答案应与所给的陈述相符合,不需要任何附加说明即可以从陈述中直接推出。
【例题】某厂有五种产品:甲、乙、丙、丁、戊。
它们的年销售额之间的关系为:丙没有丁高,甲没有乙高,戊不比丁低,而乙不如丙高。
请问,哪种产品的年销售额最高?()A.甲B.乙C.丁D.戊【解答】从所给条件可以知道:戊丁丙乙甲。
因此,正确答案为D。
请开始答题:31.某县领导参加全县的乡计划生育干部会,临时被邀请上台讲话。
由于事先没有做调查研究,也不熟悉县里计划生育的具体情况,只能说些模棱两可、无关痛痒的话。
他讲道:“在我们县14个乡中,有的乡完成了计划生育指标;有的乡没有完成计划生育指标;李家集乡就没有完成嘛。
”在领导讲话时,县计划生育委员会主任手里捏了一把汗,因为领导讲的三句话中有两句不符合实际,真后悔临时拉领导来讲话。
以下哪项正确表示了该县计划生育工作的实际情况?()A.在14个乡中至少有一个乡没有完成计划生育指标B.在14个乡中除李家集乡外还有别的乡没有完成计划生育指标C.在14个乡中没有一个乡没有完成计划生育指标D.在14个乡中只有一个乡没有完成计划生育指标32.某市的红光大厦工程建设任务进行招标。
有四个建筑公司投标。
为简便起见,称它们为甲、乙、丙、丁。
在标底公布以前,各公司经理分别做出猜测。
甲公司经理说:“我们公司最有可能会中标,其他公司不可能。
”乙公司经理说:“中标的公司一定出自乙和丙两个公司之中。
”丙公司经理说:“中标的若不是甲公司就是我们公司。
”丁公司经理说:“如果四个公司中必有一个中标,那就非我们莫属了!”标底公开后得知,四人中只有一个人的预测成真了。
以下哪项判断最可能为真?()A.甲公司经理猜对了,甲公司中标了B.乙公司经理猜对了,丙公司中标了C.乙公司和丁公司的经理都说错了D.甲公司和乙公司的经理都说错了33.美国的一个动物保护组织试图改变蝙蝠在人们心目中一直存在的恐怖形象。

江西公务员考试定义判断高频考题含答案解析1.定义:①旷达:心胸开阔乐观。
②寂寞:冷清孤单。
③郁愤:忧郁愤恨。
典型例证:(1)烽火连三月,家书抵万金。
(2)四海无闲田,农夫犹饿死。
(3)海内存知己,天涯若比邻。
上述典型例证与定义存在对应关系的数目有()。
A.0个B.1个C.2个D.3个【答案】C【解析】第一步:抓住每个定义中的关键词旷达:心胸开阔乐观。
寂寞:冷清孤单。
2.泛化:是指某种特定刺激的条件反应形成后,另外一些类似的刺激,也会诱发同样的条件反应。
新刺激越近似于原刺激,条件反应被诱发的可能性就越大。
根据以上定义,以下可以称为泛化现象的是()。
A.杯弓蛇影B.草木皆兵C.四面楚歌D.一朝被蛇咬,十年怕井绳【答案】D【解析】第一步:抓住定义中的关键词关键词强调“受过某种特定刺激”、“类似的刺激”、“诱发同样的条件反应”。
第二步:逐一判断选项A项杯弓蛇影的含义是将映在酒杯里的弓影误认为蛇,比喻因疑神疑鬼而引起恐惧;B项草木皆兵的含义是把山上的草木都当做敌兵,形容人在惊慌时疑神疑鬼;C项四面楚歌的含义是比喻陷入四面受敌,处于孤立无援的窘迫境地,从ABC都看不出原先受到过类似的刺激,只有选项D给予明确提示,曾被蛇咬过,所以见到类似的井绳时,误以为是蛇而害怕,属于泛化现象,为合适选项,故正确选项为D。
3.代位求偿权:在财产保险中,由于第三者的过错致使保险标的发生保险责任范围内的损失的,保险人按照保险合同的约定给付了保险金后,得在其赔付金额的限度内代位行使被保险人对第三者请求赔偿的权利,即代位求偿权。
下列不属于行使代位求偿权的必要条件的是()。
A.保险标的超过80万元B.发生在财产保险之中C.被保险人因保险事故对第三人有损失赔偿请求权D.保险人已向被保险人给付赔偿金【答案】A【解析】第一步:抓住定义中的关键词题干指出行使代位求偿权的条件有“财产保险”,“损失是由于第三者的过错导致的”,“损失发生在保险责任范围内”,“保险人按照保险合同的约定给付了保险金”,“保险人得在其赔付金额的限度内代位行使被保险人对第三者请求赔偿的权利”。

公务员行测定义判断题及答案公务员行测定义判断题(一)1、焦虑障碍是指受不合乎现实或不合乎理性的害怕所困扰的状态,它所表现出的行为是多种多样的,但有一点是共同的——极度焦虑的体验。
根据上述定义,下列不属于焦虑障碍的是( )。
A、丽丽只要乘坐拥挤的火车,就害怕到站时下不了车,整个旅程一直焦躁不安B、东东只要听到打雷就浑身发抖,坐卧不宁,甚至出现呼吸急促、头晕的症状C、强强自从观看了某车祸视频后,经常梦到车祸现场,他因此日日酗酒D、亮亮不愿和周围人接触交往,常独坐一旁,总认为“自己活在世上是多余的人”2、直接调控是指政府利用手中掌握的资源,用行政办法对经济运行进行直接的调节和控制,以达到政府意愿目标。
下列选项中,不属于直接调控方式的是( )。
A、商品房价的市场供求规律自发调节B、银行贷款实行额度控制C、住房分配采取行政配给D、超缺物资实行定量供应3、循环经济是一种生态经济,它要求运用生态学规律而不是机械理论规律来指导人类社会的经济活动特征,是低开采低排放高利用的经济形态。
下列不属于循环经济做法的是( )A、变单程式经济为循环经济B、变消耗型经济为休养生息型经济C、变储备型经济为增长型经济D、退田还湖、退耕还林4、从权利:民事权利可分为主权利与从权利。
从权利是指在互有关联的两个民事权利中,其效力受另一效力制约的权利。
从权利随主权利的存在而存在或消灭而消灭。
下列属于从权利的是( )。
A、抵押权B、债权C、著作权D、上诉权5、赋、比、兴指的是诗歌的三种表现手法。
赋:铺陈直叙,把思想感情及其有关的事物平铺直叙的表达出来;比:类比,以彼物比此物,使此物更加生动具体、鲜明浅近;兴:先言他物,然后借以联想,引出诗人所要表达的事物、思想、感情。
根据上述定义,下列诗句中使用了“比”的是( )。
A、死生契阔,与子成说。
执子之手,与子偕老B、七月流火,九月授衣。
春日载阳,有鸣仓庚C、我心匪石,不可转也。
我心匪席,不可卷也D、手如柔荑,肤如凝脂。

江苏事业单位:定义判断冲刺过关40题五江苏事业单位考试除省属事业单位一年两次统一招考之外,各地市及相关部门也会根据实际情况陆续发布招聘公告,报名方式一般为规模大的采取网络报名,而人数少则现场报名或者提交指定材料发送至公告提及的报名邮箱。
江苏省事业单位考试分两个阶段,一是笔试,二是面试。
笔试科目针对招聘岗位的不同有所差异,一般考公共基础知识和行测、或公共基础,个别考公文写作,部分加专业测试,具体以招聘公告上说明为准。
为了帮大家把握好每个事业单位考试招考资讯,江苏公务员考试网持续为大家发布最新招聘信息,希望广大考生密切本网站。
1.复句是指由两个或几个意义上相关、结构上互不包含的单句形式组成的句子。
根据上述定义,下列属于复句的一项是( )。
A. 最后的结果证明,不能仅仅依靠聪明才智,还需付出努力才会成功B. 远山青翠,晚霞夕照,是这里最美的景色C. 小张原来是个工人,他搞技术开发,是受了师傅的指点的D. 树林里,三三两两的少先队员,正在分头采集蘑菇2.考试信度是指考试的客观性,指一个考试反映考生真实水平的程度。
根据上述定义,对考试信度影响不大的一项是( )。
A. 同一篇作文,王老师给了50分,李老师却只给了40分B. 许多女生都没有答对这道有关足球比赛的题目C. 考试这天天气特别闷热,使许多同学的发挥受到影响D. 考前李老师押中了两道大题,考后同学们都很高兴3.行政强制执行是指公民、法人或其他组织不履行法律规定的义务或行政机关依法所做出行政处理决定中规定的义务,有关国家机关依法强制其履行义务或达到与履行义务相同状态的行为。
根据上述定义,下列不属于行政强制执行行为的是( )。
A. 某税务机关对长期拖欠税费的商户店铺进行封闭,强制其缴纳税金B. 某市人民法院拍卖一个个体户的私有财产,保证与之相关的法律文书的执行C. 国家认监委正式对外公布了新的强制性产品认证制度,并强制执行D. 某法院没收了市公安局的警车一部,要求其按照法律文件对胜诉方进行赔偿4.绝对反义词:也称互补反义词,这类反义词在意义上互相排斥,肯定甲必否定乙,肯定乙必否定甲;同时,否定甲就必肯定乙,否定乙就必肯定甲。

青海公务员《行测》考前冲刺试题:定义判断二、定义判断。
每道题先给出一个概念的定义,然后分别列出四种情况,要求你严格依据定义从中选出一个最符合或最不符合定义的答案。
注意:假设这个定义是正确的,不容置疑的。
51心理学上的“皮格马利翁效应”,是指热切的期望与赞美能够产生奇迹:期望者通过一种强烈的心理暗示,使被期望者的行为达到他的预期要求。
它蕴含这样一个道理:赞美和期待具有一种超常的能量,能够改变一个人的行为与思想,激发人的潜能;如果向对方传递了一种消极的期望,则会让他变得自暴自弃,向着消极的一面发展。
根据上述定义,下列选项中不符合皮格马利翁效应的是:A. 受老师喜爱或关注的学生,一段时间内学习成绩或其他方面都有很大进步,而受老师漠视甚至是歧视的学生为了证明自己,也有可能逆流而上,取得好成绩B. 出生在贫民窟的小罗尔斯性格顽劣,而当校长对他说“你将来一定会是纽约州的州长”之后。
罗尔斯改掉了恶习,最终成为纽约州第一位黑人州长C. 美国钢铁大王卡内基选拔的第一任总裁查尔斯·史考伯说:“使一个人发挥能力的方法.是赞赏和鼓励。
再也没有比上司的批评更能抹杀一个人的雄心。
”D. 松下幸之助经常给下属打电话询问近况如何,下属回答还算顺利时,松下就会说:“很好.希望你好好加油。
”许多下属因此精神振奋、业绩优异参考答案:A解析:皮格马利翁效应的定义要点是:①赞美和期待具有一种超常的能量,能够改变一个人的行为与思想,激发人的潜能;②向对方传递了一种消极的期望,则会让他变得自暴自弃,向着消极的一面发展。
B、C、D三项均符合定义要点。
A项中受歧视的学生没有自暴自弃向消极方向发展,不符合定义要点②。
故答案选A。
52道路交通事故是指车辆在道路上因过错或者意外造成的人身伤亡或者财产损失的事件。
其中“道路”,是指公路、城市道路和虽在单位管辖范围但允许社会机动车通行的地方,包括广场、公共停车场等用于公众通行的场所。
“车辆”,是指机动车和非机动车。

黄金冲刺大题07 新定义综合(数列新定义、函数新定义、集合新定义)(精选30题)1.(2024·辽宁·二模)已知数列{}n a 的各项是奇数,且n a 是正整数n 的最大奇因数,34212n n S a a a a a =+++++L .(1)求620,a a 的值;(2)求123,,S S S 的值;(3)求数列{}n S 的通项公式.【答案】(1)63a =,205a =(2)12S =,26S =,322S =(3)423n n S +=【分析】(1)根据所给定义直接计算可得;(2)根据所给定义列出()1,2,3,,8i i a = ,即可得解;(3)当n 为奇数时2121n k a a k -==-()N *k ∈,即可求出13521n a a a a -++++ ,当n 为偶数时2n k ka a a ==()N *k ∈,从而得到246812nn a a a a a S -+++++= ,即可推导出114n n n S S ---=()2n ≥,再利用累加法计算可得.【详解】(1)因为6123=⨯⨯,所以63a =,又20145=⨯⨯,所以205a =;(2)依题意可得121a a ==,33a =,41a =,55a =,63a =,77a =,81a =,所以1122S a a =+=,2341211316a S a a a =+++=+++=,3123567481131537122S a a a a a a a a =++++++++=++++++=.(3)因为n a 是正整数n 的最大奇因数,当n 为奇数,即21n k =-()N *k ∈时2121n k a a k -==-,所以()()111352112113521242n n nn n a a a a ---+-++++=++++-=⨯= ,当n 为偶数,即2n k =()N *k ∈时2n k k a a a ==,所以当2n ≥时1246812223242222n n a a a a a a a a a a -⨯⨯⨯⨯⨯+++++=+++++ 1123412n n a a a a a S --=+++++= ,所以34212nn S a a a a a =+++++L ()()1352468212n n a a a a a a a a a -=++++++++++ 114n n S --=+,所以114n n n S S ---=()2n ≥且12S =,所以()()()()11221321n n n n n S S S S S S S S S S ---=-+-++-+-+ 12244442n n --=+++++ ()1414422143n n --+=+=-,当1n =时12S =也满足423n n S +=,所以数列{}n S 的通项公式为423n n S +=.【点睛】关键点点睛:本题关键是理解定义,第三问关键是推导出114n n n S S ---=()2n ≥且12S =,最后利用累加法求出n S .2.(2024·黑龙江双鸭山·模拟预测)已知数列12:,,,(3)N A a a a N ≥ 的各项均为正整数,设集合{j i T x x a a ==-∣,1}i j N ≤<≤,记T 的元素个数为()P T .(1)若数列A :1,3,5,7,求集合T ,并写出()P T 的值;(2)若A 是递减数列,求证:“()1P T N =-”的充要条件是“A 为等差数列”;(3)已知数列2:2,2,,2N A ,求证:(1)()2N N P T -=.【答案】(1){2,4,6},()3T P T ==.(2)证明见解析;(3)证明见解析【分析】(1)根据题意,结合集合的新定义,即可求解;(2)若A 为等差数列,且A 是递减数列,得到0d <,结合()i j a a j i d -=-,证得充分性成立;再由A 是递减数列,得到{}2131411,,,,N T a a a a a a a a =----L ,结合互不相等,得到21321N N a a a a a a --=-==- ,得到必要性成立,即可得证;(3)根据题意,得到(1)()2N N P T -≤,得出22ij j i a a --=,得到()()111222221221i j i i j i ---=-,不妨设12i i >,则()12112222121i i j i j i ----=-,推得2221j i --为奇数,矛盾,进而得证.【详解】(1)解:由题意,数列:1,3,5,7A ,可得312,514,716,532,734-=-=-=-=-=752-=,所以集合{2,4,6}T =,所以()3P T =.(2)证明:充分性:若A 为等差数列,且A 是递减数列,则A 的公差为(0)d d <,当1i j N ≤<≤时,()i j a a j i d -=-,所以{,2,3,,(1)}T d d d N d =- ,则()1P T N =-,故充分性成立.必要性:若A 是递减数列,()1P T N =-,则A 为等差数列,因为A 是递减数列,所以2131411N a a a a a a a a ->->->>- ,所以2131411,,,,N a a a a a a a a T ----∈L ,且互不相等,所以{}2131411,,,,N T a a a a a a a a =----L ,又因为324221N N a a a a a a a a ->->>->- ,所以232421,,,,N N a a a a a a a a T ----∈ 且互不相等,所以322142312,,,N a a a a a a a a a a -=--=-- 11N a a -=-,所以21321N N a a a a a a --=-==- ,所以A 为等差数列,必要性成立.所以若A 是递减数列,“()1P T N =-”的充要条件是“A 为等差数列”.(3)证明:由题意集合{}|,1j i T x x a a i j N ==-≤<≤中的元素个数最多为(1)2N N -个,即(1)()2N N P T -≤, 对于数列2:2,2,2N A ,此时22ij j i a a --=,若存在1122j i j i a a a a --=,则11222222j i j i -=-,其中1122,j i j i >>,故()()111222221221i j i i j i---=-,若12i i ≠,不妨设12i i >,则()12112222121i i j i j i ----=-,而1122,j i j i >>,故()1211221i i j i ---为偶数,2221j i --为奇数,矛盾,故12i i =,故12j j =,故由2:2,2,2N A 得到的j i a a -彼此相异,所以(1)()2N N P T -=.3.(2024·广西·二模)已知函数()ln f x x =,若存在()()g x f x ≤恒成立,则称()g x 是()f x 的一个“下界函数”.(1)如果函数()ln tg x x x=-为()f x 的一个“下界函数”,求实数t 的取值范围;(2)设函数()()12e e x F xf x x=-+,试问函数()F x 是否存在零点?若存在,求出零点个数;若不存在,请说明理由.【答案】(1)2(,e-∞-(2)函数F(x)是否存在零点,理由见解答【分析】(1)把恒成立问题转换为求2ln x x 的最小值问题,利用导数求出最小值即可;(2)把函数整理成()1111211ln e e e e e e e x x xxF x x x x x x ⎛⎫=-+≥--+=- ⎪⎝⎭,要判断是否有零点,只需看()F x 的正负问题,令1()e ex xG x =-,利用导数分析()G x 即可.【详解】(1)由()()g x f x ≤恒成立,可得ln ln tx x x -≤恒成立,所以2ln t x x ≤恒成立,令()2ln h x x x =,所以()21ln h x x '=+(),当1(0,)e x ∈时, ()0h x '<,()h x 在1(0,)e单调递减;当1()e x ∈+∞时, ()0h x '>,()h x 在1()e+∞,单调递增;所以()h x 的最小值为12()e e h =-,所以2e t ≤-,实数t 的取值范围2(,e]-∞-;(2)由(1)可知22ln e x x ≥-,所以22ln e x x ≥-,所以1ln e x x≥-,①又()()12e e x F xf x x =-+,所以1211211()ln (e e e e e e e x x xx F x x x x x x =-+≥--+=-,令1()e e x xG x =-,所以1()ex x G x -'=,当(0,1)x ∈时, ()0'<G x ,()G x 在(0,1)单调递减;当(1)x ∈+∞,时, ()0G x '>,()G x 在()1,∞+单调递增;所以()(1)0G x G ≥=,②所以1211211()ln ()0e e e e e e exx x xF x x x x x x =-+≥--+=-≥,又①②中取等号的条件不同,所以()0F x >所以函数没有零点.4.(2024·湖南长沙·模拟预测)设n 次多项式()121210()0n n n n n n P t a t a t a t a t a a --=+++++≠ ,若其满足(cos )cos n P x nx =,则称这些多项式()n P t 为切比雪夫多项式.例如:由cos cos θθ=可得切比雪夫多项式1()P x x =,由2cos 22cos 1θθ=-可得切比雪夫多项式22()21P x x =-.(1)若切比雪夫多项式323()P x ax bx cx d =+++,求实数a ,b ,c ,d 的值;(2)对于正整数3n …时,是否有()()()122n n n P x x P x P x --=⋅-成立?(3)已知函数3()861f x x x =--在区间()1,1-上有3个不同的零点,分别记为123,,x x x ,证明:1230x x x ++=.【答案】(1)4,0,3a b d c ====-(2)()()()112n n n P x x P x P x +-=⋅-成立(3)证明见解析【分析】(1)利用()()3cos cos3cos 2P θθθθ==+展开计算,根据切比雪夫多项式可求得,,,a b d c ;(2)要证原等式成立,只需证明()()cos 1cos 12cos cos n n n θθθθ++-=⋅成立即可,利用两角和与差的余弦公式可证结论成立;(3)由已知可得方程31432x x -=在区间()1,1-上有3个不同的实根,令()cos ,0,πx θθ=∈,结合(1)可是1cos32θ=,可得123π5π7πcos ,cos ,cos 999x x x ===,计算可得结论.【详解】(1)依题意,()()()223cos cos3cos 2cos2cos sin2sin 2cos 1cos 2sin cos P θθθθθθθθθθθθ==+=-=--()3232cos cos 21cos cos 4cos 3cos θθθθθθ=---=-,因此()3343P x x x =-,即32343ax bx cx d x x +++=-,则4,0,3a b d c ====-,(2)()()()112n n n P x x P x P x +-=⋅-成立.这个性质是容易证明的,只需考虑和差化积式()()cos 1cos 12cos cos n n n θθθθ++-=⋅.首先有如下两个式子:()()1cos cos cos cos sin sin n P n n n θθθθθθθ+=+=-,()()1cos cos cos cos sin sin n P n n n θθθθθθθ-=-=+,两式相加得,()()()11cos cos 2cos cos 2cos cos n n n P P n P θθθθθθ-++==,将cos θ替换为x ,所以()()()112n n n P x x P x P x +-=⋅-.所以对于正整数3n ≥时,有()()()122n n n P x x P x P x --=⋅-成立.(3)函数()3861f x x x =--在区间()1,1-上有3个不同的零点123,,x x x ,即方程31432x x -=在区间()1,1-上有3个不同的实根,令()cos ,0,πx θθ=∈,由()1知1cos32θ=,而()30,3πθ∈,则π33θ=或5π33θ=或7π33θ=,于是123π5π7πcos ,cos ,cos 999x x x ===,则123π5π7ππ4π2πcos cos cos cos cos cos 999999x x x ⎛⎫++=++=-+ ⎪⎝⎭,而4π2π3ππ3πππππcoscos cos cos 2cos cos cos 999999399⎛⎫⎛⎫+=++-== ⎪ ⎪⎝⎭⎝⎭,所以1230x x x ++=.5.(2024·浙江·模拟预测)已知实数0q ≠,定义数列{}n a 如下:如果{}2012222,0,1k k i n x x x x x =++++∈ ,0,1,2,,i k = ,则2012k n k a x x q x q x q =++++ .(1)求7a 和8a (用q 表示);(2)令12n n b a -=,证明:211n ni i b a -==∑;(3)若12q <<,证明:对于任意正整数n ,存在正整数m ,使得1n m n a a a <≤+.【答案】(1)23781,a q q a q=++=(2)证明见解析(3)证明见解析【分析】(1)观察题目条件等式中的系数可得答案;(2)112n n n b a q --==,分别计算1ni i b =∑和21n a -可证明结论;(3)先根据112n n a q --=无上界说明存在正整数m ,使得n m a a <,分1m -是偶数和1m -是奇数分别说明.【详解】(1)因为27122=++,所以271a q q =++;因为382=,所以38a q =;(2)由数列{}n a 定义得:112n n n b a q --==;所以2111nn i i b q q q -==++++∑ .而21211222n n --=++++ ,所以121211n nn i i a q q qb --==++++=∑ ;(3)当12q <<,由(2)可知,112n n a q --=无上界,故对任意n a ,存在m a ,使得m n a a >.设m 是满足m n a a >的最小正整数.下面证明1m n a a ≤+.①若1m -是偶数,设{}2121222,0,1,1,2,,kk i m x x x x i k -=+++∈= ,则2121222kk m x x x =++++ ,于是212111k m k m a x q x q x q a -=++++=+ .因为1n m a a -≥,所以111m m n a a a -=+≤+.②若1m -是奇数,设2221122222l l kl k m x x ++-=+++++++ ,则()()()()12221111111l l l l m m a a qq q q q q q q q q q +--=-++++=-++++-+++++< .所以111m m n a a a -<+≤+.综上所述,对于任意正整数n ,存在正整数m ,使得1n m n a a a <≤+.6.(2024·辽宁·三模)若实数列{}n a 满足*n ∀∈N ,有212n n n a a a +++≥,称数列{}n a 为“T 数列”.(1)判断2,ln n n a n b n ==是否为“T 数列”,并说明理由;(2)若数列{}n a 为“T 数列”,证明:对于任意正整数,,k m n ,且k m n <<,都有n m m ka a a a n m m k--≥--(3)已知数列{}n a 为“T 数列”,且202410i i a ==∑.令{}12024max ,M a a =,其中{}max ,a b 表示,a b 中的较大者.证明:{}1,2,3,,2024k ∀∈ ,都有20252023k M a M -≤≤.【答案】(1)数列{}n a 是“T 数列”,数列{}n b 不是“T 数列”;(2)证明见解析(3)证明见解析【分析】(1)根据“T 数列”的定义判断可得出结论;(2)由()1122,3,k k k a a a k -++≥= 可得出11k k k k a a a a +--≥-,利用累加法结合不等式的基本性质可得1m m m n a a a a n m +-≥--,以及1m km m a a a a m k--≤--,再结合11m m m m a a a a +--≥-可证得结论成立;(3)首先当1k =或2024时的情况,再考虑{2,3,,2023}k ∈ 时,结合(2)中结论考虑用累加法可证得结论.【详解】(1)因为()()22221222120n n n a a a n n n +++-=++-+=>,所以数列{}n a 是“T 数列”,因为()()22212ln ln(2)2ln(1)ln 2ln 210n n n b b b n n n n n n n +++-=++-+=+-++<,所以数列{}n b 不是“T 数列”;(2)令1n n n c a a +=-,因为数列{}n a 为“T 数列”,所以212n n n a a a +++≥从而211n n n n a a a a +++-≥-,所以1n n c c +≥因为1k m n ≤<<,所以()()()1121n n n n m m n m a a a a a a a a n m n m ---+-+-++--=-- 12()n n m m m c c c n m c c n m n m--+++-=≥=-- ,()()()1121m m m m k k m k a a a a a a a a m k m k ---+-+-++--=-- 1211()m m k m m c c c m k c c m k m k ----+++-=≤=-- 因为1m m c c -≥,所以n m m ka a a a n m m k--≥--.(3)当1k =或2024时,k k k a a a -≤≤,从而20252023k k k M M a a a M -≤-≤-≤≤≤,当{2,3,,2023}k ∈ 时,因为12024k <<,由第(2)问的结论得2024120241k k a a a a k k --≥--,可推得120242024120232023k k k a a a --≤+,从而1202412024202412024120241202320232023202320232023k k k k k k k a a a a a M M M ------≤+≤+≤+=对于1i k ∀<<,由第(2)问的结论得11k i i a a a a k i i --≥--,从而[]1111(1)(),1111i k k i k i a a a i a k i a i k k k --≤+=-+-=---也成立,从而11111111111(2)(1)(1)(2)(1)()112222k k k i k k k i i i k k k k k k a i a k i a a a a a k k ---===----⎡⎤⎡⎤≤-+-=+=+⎢⎥⎢⎥--⎣⎦⎣⎦∑∑∑对于2024k i ∀<<,由第(2)问的结论得20242024i i ka a a a i i k--≥--,从而[]2024202420241()(2024),202420242024i k k i k i a a a i k a i a k k k--≤+=-+----2024i =也成立,从而20242024202420241111()(2024)2024i k i k i k i k a i k a i a k =+=+=+⎡⎤≤-+-⎢⎥-⎣⎦∑∑∑20241(2025)(2024)(2023)(2024)202422k k k k k a a k----⎡⎤=+⎢⎥-⎣⎦2024(2005)(2023)22kk k a a --=+所以202420241(2005)(2023)22iki k k k aa a =+--≤+∑由条件20241202412024111(2)(2005)(2023)02222k i i k i k k ki i i k k k k k a a a a a a a a a -===+---==++≤++++∑∑∑1202420232025222k k ka a a -=++可得1202420252025202520232023202320232023k k k kk a a a M M M --⎛⎫⎛⎫≥-+≥-+=-⎪ ⎪⎝⎭⎝⎭,所以20252023k M a M -≤≤.【点睛】方法点睛:本题主要考查数列新定义的问题,处理此类问题时,通常根据题中的新定义,结合已知结论进行推导、求解;本题中,根据“T 数列”的定义“212n n n a a a +++≥”结合作差法、不等式的性质进行推理、证明不等式成立,并在推导时,充分利用已有的结论进行推导,属于难题.7.(2024·广东梅州·二模)已知{}n a 是由正整数组成的无穷数列,该数列前n 项的最大值记为n M ,即{}12max ,,,n n M a a a =⋅⋅⋅;前n 项的最小值记为n m ,即{}12min ,,,n n m a a a =⋅⋅⋅,令n n n p M m =-(1,2,3,n =⋅⋅⋅),并将数列{}n p 称为{}n a 的“生成数列”.(1)若3nn a =,求其生成数列{}n p 的前n 项和;(2)设数列{}n p 的“生成数列”为{}n q ,求证:n n p q =;(3)若{}n p 是等差数列,证明:存在正整数0n ,当0n n ≥时,n a ,1n a +,2n a +,⋅⋅⋅是等差数列.【答案】(1)()33213nn --(2)证明见解析(3)证明见解析【分析】(1)利用指数函数的性质判断数列的单调性,从而得出{p n }的通项,由分组求和法及等比数列的前n 项和公式进行求解即可;(2)根据数列的单调性,结合生成数列的定义进行证明即可;(3)根据等差数列的定义分类讨论进行证明即可.【详解】(1)因为3n n a =关于n 单调递增,所以{}12max ,,,3nn n n M a a a a =⋅⋅⋅==,{}121min ,,,3n n m a a a a =⋅⋅⋅==,于是33nn n n p M m =-=-,{}n p 的前n 项和()()()()()1231333333333313132n n nn P n n -=-+-++-=-=--- .(2)由题意可知1n n M M +≥,1n n m m +≤,所以11n n n n M m M m ++-≥-,因此1n n p p +≥,即{}n p 是单调递增数列,且1110p M m ==-,由“生成数列”的定义可得n n q p =.(3)若{}n p 是等差数列,证明:存在正整数0n ,当0n n ≥时,12n n n a a a ++⋯,,,是等差数列.当{}n p 是一个常数列,则其公差d 必等于0,10n p p ==,则n n M m =,因此{}n a 是常数列,也即为等差数列;当{}n p 是一个非常数的等差数列,则其公差d 必大于0,1n n p p +>,所以要么11n n n M a M ++>=,要么11n n n m a m ++=<,又因为{}n a 是由正整数组成的数列,所以{}n a 不可能一直递减,记2min ,{}n n a a a a = ,,,,则当0n n >时,有n n M m =,于是当0n n >时,0n n n n n p M m a a =-=-,故当0n n >时,0n n n a p a =+,…,因此存在正整数0n ,当0n n ≥时,12n n n a a a ++,,,…是等差数列.综上,命题得证.【点睛】方法点睛:常见的数列求和的方法有公式法即等差等比数列求和公式,分组求和类似于n n n c a b =+,其中{}n a 和{}n b 分别为特殊数列,裂项相消法类似于()11n a n n =+,错位相减法类似于n n n c a b =⋅,其中{}n a 为等差数列,{}n b 为等比数列等.8.(2024·浙江绍兴·二模)已知*k ∈N ,集合{0101222,0,k i i ik k X x x i i i ==++⋅⋅⋅+≤<<< 其中}01,,,k i i i ⋅⋅⋅∈N .(1)求2X 中最小的元素;(2)设13122a X =+∈,1b X ∈,且1a b X +∈,求b 的值;(3)记(12,2k n k nk k Y X +-+⎤=⋂⎦,*n ∈N ,若集合k Y 中的元素个数为n b ,求1112k mm m b +-=∑.【答案】(1)7(2)24b =或10(3)2k【分析】(1)根据集合新定义,确定2X 中最小的元素即可;(2)根据集合1X 中的元素可得132210a =+=,设22j i b =+,()0,i j i j ≤<∈N ,分别讨论当3j ≤时,当4j =时,当5j ≥时,b 的取值情况,即可得结论;(3)设k x Y ∈,则01222k i i i x =++⋅⋅⋅+,其中1k i k n =+-,01101k i i i k n -≤<<⋅⋅⋅<<+-,所以1C kn k n b +-=,根据组合数的运算性质确定1k S +与k S 的关系,即可求得1112k mm m b +-=∑的值.【详解】(1)2X 中的最小元素为0122227++=.(2)由题得132210a =+=,设22j i b =+,()0,i j i j ≤<∈N .①当3j ≤时,322212b =+=或312210b =+=或30229b =+=或21226b =+=或20225b =+=或10223b =+=.经检验,当10b =时,422022a b +==+,符合题意,所以10b =.②当4j =时,432224b =+=或422220b =+=或412218b =+=或402217b =+=.经检验,当24b =时,513422a b +==+,符合题意,所以24b =.③当5j ≥时,不符合题意.因此,24b =或10.(3)设k x Y ∈,则01222k i i i x =++⋅⋅⋅+,其中1k i k n =+-,01101k i i i k n -≤<<⋅⋅⋅<<+-,所以1C kn k n b +-=,设1112k m k m m b S +-==∑,则1222111C C C C 222k k k kkk k k k k S ++=+++⋅⋅⋅+.因为1111C C C k k k n n n ++--=+,所以1111111232122211111C C C C C 2222k k k k k k k k k k k k k S ++++++++++++=+++⋅⋅⋅++()()()()11111122222121211111C C C C C C C C C 2222k k k k k k k k k k k k k k k k k k k k +++++++++++=+++++⋅⋅⋅++++12221211111C C C C C 2222k k k k k k k k k k k k ++++⎛⎫=+++⋅⋅⋅++ ⎪⎝⎭111112*********C C C C 2222k k k k k k k k k k +++++++++++⋅⋅⋅++1122211111C C 222k k k k k k k k S S +++++⎛⎫=+-+ ⎪⎝⎭.因为()()()()()()()()1212221!22!21!21!11C C 02!1!21!1!!1!k k k k k k k k k k k k k k ++++++-+-=-⋅==++++,所以1112k k k S S S ++=+,所以12k k S S +=,又因为11211C 22S =+=,所以2kk S =.【点睛】方法点睛:解决以集合为背景的新定义问题,注意两点:(1)根据集合定义式,确定集合中元素的特点,结合指数运算确定指数的取值情况从而得集合k X 中的元素性质;(2)确定集合k Y 中的元素个数为n b 时,结合组合数的运算性质确定1112k mk m m b S +-==∑与1k S +的关系.9.(2024·山东潍坊·二模)数列{}n a 中,从第二项起,每一项与其前一项的差组成的数列{}1n n a a +-称为{}n a 的一阶差数列,记为(){}1n a ,依此类推,(){}1n a 的一阶差数列称为{}n a 的二阶差数列,记为(){}2n a ,….如果一个数列{}n a 的p 阶差数列(){}pna 是等比数列,则称数列{}na 为p 阶等比数列()*p ∈N .(1)已知数列{}n a 满足11a =,121n n a a +=+.(ⅰ)求()11a ,()12a ,()13a ;(ⅱ)证明:{}n a 是一阶等比数列;(2)已知数列{}n b 为二阶等比数列,其前5项分别为2037782151,,,,9999,求n b 及满足n b 为整数的所有n 值.【答案】(1)(ⅰ)()112a =,()124a =,()138a =;(ⅱ)证明见解析(2)当()91,N n k k =+∈时,n b 为整数.【分析】(1)(ⅰ)根据(){}1n a 的定义,结合通项公式求解即可;(ⅱ)根据递推公式构造()112n n n n a a a a +--=-即可证明;(2)由题意{}n b 的二阶等差数列{}(2)nb 为等比数列,设公比为q ,可得(2)1243n nb-=⨯,结合()11119b =进而可得()124127n n b n -=⨯-+,从而分析n b 为整数当且仅当14127n --为整数,再根据二项展开式,结合整除的性质分析即可.【详解】(1)(ⅰ)由11a =,121n n a a +=+易得2343,7,15a a a ===,……由一阶等差数列的定义得:()21112a a a =-=,()31224a a a =-=,()41338a a a =-=.(ⅱ)因为121n n a a +=+,所以当2n ≥时有121n n a a --=,所以1122n n n n a a a a +--=-,即()112n n n n a a a a +--=-,即()()1112,2n n a a n -=≥,又因为11a =,故(){}1n a 是以1为首项,2为公比的等比数列,即{}n a 是一阶等比数列.(2)由题意{}n b 的二阶等差数列{}(2)nb 为等比数列,设公比为q ,则(2)123b =,4q =,所以(2)1243n n b -=⨯.由题意()11119b =,所以()()()()()()1111211111111124199n n k k k k k n n b b b b b --+=-===-⨯+=++∑∑,所以()()()11111111214127n n k k k k k n n b b b n b b ---+==+-+===⨯-+∑∑,即()124127n n b n -=⨯-+.所以n b 为整数当且仅当14127n --为整数.由已知1n =时符合题意,2,3,4,5n =时不合题意,当6n ≥时,()111223311111141131C 3C 3C 3C 3n n n n n n n n ---------=+-=⨯+⨯+⨯++⨯ ,所以原题等价于12113C 9C 27n n --+为整数,因为()()()()121131113413C 9C 271829n n n n n n --⎡⎤-----+⎣⎦==⨯①,显然()311n --含质因子3,所以n 1-必为9的倍数,设()19,N n k k -=∈,则91n k =+,将91n k =+代入①式,当k 为奇数时,()311n --为偶数,①式为2的倍数;当k 为偶数时,n 为奇数,n 1-为偶数,①式为2的倍数,又因为2与9互质,所以①为整数.综上,当()91,N n k k =+∈时,n b 为整数.【点睛】方法点睛:(1)新定义的题型需要根据定义列出递推公式,结合等比等差的性质求解;(2)考虑整除时,可考虑根据二项展开式进行讨论分析.10.(2024·贵州黔西·一模)布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可运用到有限维空间并构成了一般不动点定理的基石,得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer).简单地讲就是:对于满足一定条件的连续函数()f x ,存在实数0x ,使得()00f x x =,我们就称该函数为“不动点”函数,实数0x 为该函数的不动点.(1)求函数()23x f x x =+-的不动点;(2)若函数()ln g x x b =-有两个不动点12,x x ,且12x x <,若212x x -≤,求实数b 的取值范围.【答案】(1)2log 3(2)2222ln 1e 1e 1b ⎛⎫-≤<- ⎪--⎝⎭【分析】(1)根据不动点定义求解即可;(2)根据题意问题转化为方程ln b x x =-有两个不等的实数根12,x x ,令()ln x x x ϕ=-,利用导数判断单调性极值,可得1b <-,且21x x -的值随着b 的值减小而增大,列式求出212x x -=时的b 值,得解.【详解】(1)设()f x 的不动点为0x ,则00023xx x +-=,解得02log 3x =,所以函数()f x 的不动点为2log 3.(2)函数()g x 有两个不动点12,x x ,即方程ln x b x -=,即ln b x x =-有两个不等的实数根12,x x ,令()ln x x x ϕ=-,则()111xx x xϕ-=-=',当()0,1x ∈时,()0x ϕ'>,当()1,x ∞∈+时,()0x ϕ'<,所以函数()x ϕ在()0,1上单调递增,在()1,∞+上单调递减,()()11x ϕϕ∴≤=-,且0x →时,()x ϕ∞→-,x →+∞时,()x ϕ∞→-,作出()x ϕ的大致图象如下:所以1b <-,且21x x -的值随着b 的值减小而增大,当212x x -=时,有1122ln ln b x x b x x =-⎧⎨=-⎩,两式相减得2211ln 2x x x x =-=,解得221e x x =,即221e x x =,代入212x x -=,解得122e 1x =-,所以此时2222ln e 1e 1b ⎛⎫=- ⎪--⎝⎭,所以满足题意的实数b 的取值范围为2222ln 1e 1e 1b ⎛⎫-≤<- ⎪--⎝⎭.11.(2024·河北沧州·一模)对于函数()y f x =,x I ∈,若存在0x I ∈,使得()00f x x =,则称0x 为函数()f x 的一阶不动点;若存在0x I ∈,使得()()00f f x x =,则称0x 为函数()f x 的二阶不动点;依此类推,可以定义函数()f x 的n 阶不动点.其中一阶不动点简称为“不动点”,二阶不动点简称为“稳定点”,函数()f x 的“不动点”和“稳定点”构成的集合分别记为A 和B ,即{}()A x f x x ==,{}(())B x f f x x ==.(1)若()ee (0)xf x x =>,证明:集合{}()A x f x x ==中有且仅有一个元素;(2)若()()212ln 1(1)exf x a x a x =+-+>-,讨论集合B 的子集的个数.【答案】(1)证明见解析(2)答案见解析【分析】(1)令e ()()e xg x f x x x =-=-,求导,可得函数()g x 的单调性,进而可得函数()g x 有唯一零点,可得结论;(2)由题意可知只需研究()f x 的不动点即可,令221()ln e F x x ax x=+-,求出其导数,判断其单调性,然后分类讨论a 的取值范围,判断()F x 的零点情况,即可判断()f x 的稳定点个数.,进而可得集合B的子集的个数.【详解】(1)令e()()e x g x f x x x =-=-,求导得e1()e 1ex g x '=-,令()0g x '=,可得e x =,当,e)x ∈-∞(,()0g x '<,当e,)x ∈+∞(,()0g x '>,所以min ()(e)0g x g ==,所以()g x 有唯一零点,所以集合{}|()A x f x x ==中有且仅有一个元素;(2)当1a >-时,由函数212ln ()(1)exf x a x x =+-+,可得导函数22121()(1)0e f x a x x'=+++⨯>,所以()f x 在0(,)+∞上单调递增,由反函数的知识,()f x 稳定点在原函数与反函数的交点上,即()f x 稳定点与()f x 的不动点等价,故只需研究212ln ()(1)exf x a x x =+-+的不动点即可;令221()()ln ,(0)e F x f x x x ax x x=-=+->,则22211()e F x a x x'=⨯++,则()F x '在0(,)+∞上单调递减,①当0a >时,()0F x '>恒成立,即()F x 在0(,)+∞上单调递增,当x 无限接近于0时,()F x 趋向于负无穷小,且2222221(e )ln e e 0e e F a =+⨯->,故存在唯一的20(0,e )x ∈,使得()0F x =,即()f x x =有唯一解,所以此时()f x 有唯一不动点;②当0a <时,即10a -<<时,22(1)10e F a '=++>,当1x 趋向无穷大时,2211211e x x ⨯+趋近于0,此时1()0F x '<,存在唯一1(0,)x ∈+∝,使得2211211()0e F x a x x '=⨯++=,此时()f x 在1(0,)x 上单调递增,在1()x +∞,上单调递减,故max 11112221121222()()ln ln e e eF x F x x ax x x x ==+-=--,当x 趋近于0时,()F x 趋向于负无穷大,当x 向正无穷大时,()F x 趋向负无穷大时,设22222()ln e eh x x x =--,则()h x 在0(,)+∞上单调递增,且22222222(e )ln e e e e h =--,又2211211e a x x =-⨯-在1(0,)x ∈+∞时单调递增,故(i )当max 1221222()ln 0e eF x x x =--=时,即21e x =,此时43e a =-,方程()0F x =有一个解,即()f x 有唯一不动点,所以集合B 的子集有2个;(ii )当max 1221222()ln 0e eF x x x =--<,即21e x <,此时431ea -<<-,方程()0F x =无解,即()f x 无不动点,所以集合B 的子集有1个;(iii )当max 1221222()ln 0e e F x x x =-->时,即21e x >,此时430e a -<<,方程()0F x =有两个解,即()f x 有两个不动点,所以集合B 的子集有4个;综上,当0a ≥时或43e a =-时,集合B 的子集有2个;当431e a -<<-时,集合B 的子集有1个;当430e a -<<时,集合B 的子集有4个.【点睛】方法点睛:本题属新定义题型,读懂题意是关键;研究方程根的个数问题常转化为判断函数零点的个数问题,利用导数研究含参函数的单调性,从而判断方程根(或函数零点)的个数问题.注意分类讨论思想的应用.12.(2024·山东聊城·二模)对于函数()f x ,若存在实数0x ,使00()1)(f x f x λ+=,其中0λ≠,则称()f x 为“可移λ倒数函数”,0x 为“()f x 的可移λ倒数点”.已知()e ,()(0)x g x h x x a a ==+>.(1)设2()()()x g x h x ϕ=为“()h x 的可移2-倒数点”,求函数()ϕx 的单调区间;(2)设(),0()1,0()g x x x x h x ω>⎧⎪=⎨<⎪⎩,若函数()x ω恰有3个“可移1倒数点”,求a 的取值范围.【答案】(1)单调递增区间为(,3),(1,)-∞--+∞,递减区间为()3,1--;(2)()2,e .【分析】(1)根据给定的定义,列式求出a 值,再利用导数求出函数()ϕx 的单调区间.(2)利用定义转化为求方程()()11x x ωω+=恰有3个不同的实根,再借助导数分段探讨零点情况即可.【详解】(1为“()h x 的可移2-倒数点”,得)21h h -=,即)21aa +=,整理()2210a a ++-=,即()()110a a +--=,解得1a =,由2()1)e (x x x ϕ=+的定义域为R ,求导得()()()()2e (1)2e 1e 13x x xx x x x x ϕ=+++=++',当(),3x ∞∈--时,()()0,x x ϕϕ'>单调递增;()3,1x ∈--时,()()0,x x ϕϕ'<单调递减;()1,x ∞∈-+时,()()0,x x ϕϕ'>单调递增,所以()x ϕ的单调递增区间为(,3),(1,)-∞--+∞,递减区间为()3,1--.(2)依题意,e ,0()1,0x x x x x aω⎧>⎪=⎨<⎪+⎩,由()x ω恰有3个“可移1倒数点”,得方程()()11x x ωω+=恰有3个不等实数根,①当0x >时,10x +>,方程()()11x x ωω+=可化为21e 1x +=,解得12x =-,这与0x >不符,因此在()0,∞+内()()10x x ωω+=没有实数根;②当10x -<<时,10x +>,方程()()11x x ωω+=可化为1e 1x x a +=+,该方程又可化为1e x a x +=-.设()1ex k x x +=-,则()1e 1x k x +='-,因为当()1,0x ∈-时,()0k x '>,所以()k x 在()1,0-内单调递增,又因为()()12,0e k k -==,所以当()1,0x ∈-时,()()2,e k x ∈,因此,当()2,e a ∈时,方程()()11x x ωω+=在()1,0-内恰有一个实数根;当(][)0,2e,a ∞∈⋃+时,方程()()11x x ωω+=在()1,0-内没有实数根.③当=1x -时,()10,1x x ω+=+没有意义,所以=1x -不是()()11x x ωω+=的实数根.④当1x <-时,10x +<,方程()()11x x ωω+=可化为1111x a x a ⋅=+++,化为()222110x a x a a ++++-=,于是此方程在(),1∞--内恰有两个实数根,则有()()()22221410211212110a a a a a a a ⎧+-+->⎪⎪+-<-⎨⎪-+++->⎪⎩,解得a >,因此当a >时,方程()()11x x ωω+=在(),1∞--内恰有两个实数根,当0a <≤时,方程()()11x x ωω+=在(),1∞--内至多有一个实数根,综上,a 的取值范围为()()2,e )2,e ∞⋂+=.【点睛】思路点睛:已知函数的零点或方程的根的情况,求解参数的取值范围问题的本质都是研究函数的零点问题,求解此类问题的一般步骤:(1)转化,即通过构造函数,把问题转化成所构造函数的零点问题;(2)列式,即根据函数的零点存在定理或结合函数的图象列出关系式;(3)得解,即由列出的式子求出参数的取值范围.13.(2024·湖南·二模)罗尔定理是高等代数中微积分的三大定理之一,它与导数和函数的零点有关,是由法国数学家米歇尔·罗尔于1691年提出的.它的表达如下:如果函数()f x 满足在闭区间[,]a b 连续,在开区间(,)a b 内可导,且()()f a f b =,那么在区间(,)a b 内至少存在一点m ,使得()0'=f m .(1)运用罗尔定理证明:若函数()f x 在区间[],a b 连续,在区间(,)a b 上可导,则存在0(,)x a b ∈,使得0()()()f b f a f x b a-'=-.(2)已知函数21()ln ,()12f x x xg x x bx ==-+,若对于区间(1,2)内任意两个不相等的实数12,x x ,都有1212|()()||()()|f x f x g x g x ->-成立,求实数b 的取值范围.(3)证明:当1,2p n >≥时,有111111[]1(1)p p p n p n n --<---.【答案】(1)证明见解析;(2)1ln 22b -≤≤;(3)证明见解析.【分析】(1)根据给定条件,构造函数()()F x f x tx =-,利用导数结合罗尔定理推导即得.(2)求出函数(),()f x g x 的导数,利用(1)的结论建立恒成立的不等式,再利用导数求出函数的值域即得.(3)构造函数1(),[1,]p h x x x n n -=∈-,求出导数结合(1)的结论,借助不等式性质推理即得.【详解】(1)令()()f b f a t b a-=-,则()()f b bt f a at -=-,令函数()()F x f x tx =-,则()(),()()F a F b F x f x t ''==-,显然()F x 在[],a b 上连续,且在(,)a b 上可导,由罗尔定理,存在0(,)x a b ∈,使得0()0F x '=,即00)(f x t '-=,所以0()()()f b f a f x b a-'=-.(2)依题意,()ln 1,()f x x g x x b ''=+=-,不妨令12x x >,则12121212()()()()||||f x f x g x g x x x x x -->--恒成立,由(1)得|()||()|,(1,2)f x g x x ''>∈,于是ln 1||x x b +>-,即1ln ln 1x b x x --<-<+,因此ln 1ln 1x x b x x --<<++,令()ln 1(12)x x x x ϕ=--<<,求导得1()0x x xϕ-'=>,函数()ϕx 在(1,2)上单调递增,则0()1ln 2x ϕ<<-,而函数ln 1y x x =++在(1,2)上单调递增,其值域为(2,3ln 2)+,则1ln 22b -≤≤,所以实数b 的取值范围是1ln 22b -≤≤.(3)令函数1(),[1,]p h x x x n n -=∈-,显然函数()h x 在(1,)n n -上可导,由(1),存在(1,)c n n ∈-,使得(1)()()(1)h n h n h c n n--'=--,又()(1)p h x p x -'=-⋅,则1111()(1)(1)p p p h c p c n n---'-=-=--,因此111111[]1(1)p p p p n n c ---=--,而11,1n c n p ≤-<<>,则p p c n <,即11p p c n >,所以111111[]1(1)p p p n p n n --<---.【点睛】思路点睛:涉及函数新定义问题,理解新定义,找出数量关系,联想与题意有关的数学知识和方法,构造函数,转化、抽象为相应的函数问题作答.14.(2024·安徽合肥·二模)在数学中,广义距离是泛函分析中最基本的概念之一.对平面直角坐标系中两个点()111,P x y 和()222,P x y ,记1212121212max ,11t x x y y PP x x y y ⎧⎫--⎪⎪=⎨⎬+-+-⎪⎪⎩⎭,称12t PP 为点1P 与点2P 之间的“t -距离”,其中{}max ,p q 表示,p q 中较大者.(1)计算点()1,2P 和点()2,4Q 之间的“t -距离”;(2)设()000,P x y 是平面中一定点,0r >.我们把平面上到点0P 的“t -距离”为r 的所有点构成的集合叫做以点0P 为圆心,以r 为半径的“t -圆”.求以原点O 为圆心,以12为半径的“t -圆”的面积;(3)证明:对任意点()()()111222333131223,,,,,,t t t P x y P x y P x y PP PP P P ≤+.【答案】(1)23;(2)4;(3)证明见解析.【分析】(1)根据所给定义直接计算即可;(2)依题意可得1max ,112xy x y ⎧⎫⎪⎪=⎨⎬++⎪⎪⎩⎭,再分类讨论,从而确定“t -圆”的图形,即可求出其面积;(3)首先利用导数说明函数()()01tf t t t=≥+的单调性,结合绝对值三角不等式证明即可.【详解】(1)由定义知,1224122||max ,max ,112124233tPQ ⎧⎫--⎪⎪⎧⎫===⎨⎬⎨⎬+-+-⎩⎭⎪⎪⎩⎭;(2)设(),P x y 是以原点O 为圆心,以12为半径的t -圆上任一点,则1max ,112x y x y ⎧⎫⎪⎪=⎨⎬++⎪⎪⎩⎭.若1112y x y x ≤=++,则11x y ⎧=⎪⎨≤⎪⎩;若1112x y xy≤=++,则有11y x ⎧=⎪⎨≤⎪⎩.由此可知,以原点O 为圆心,以12为半径的“t -圆”的图形如下所示:则“t -圆”的面积为224⨯=.(3)考虑函数()()01tf t t t=≥+.因为()210(1)f t t ='>+,所以()f t 在[)0,∞+上单调递增.又131223x x x x x x -≤-+-,于是1312231223131223122312231111x x x x x x x x x x x x x x x x x x x x x x x x --+---≤=++-+-+-+-+-+-+-1223122311x x x x x x x x --≤++-+-,同理,131223131223111y y y y y y y y y y y y ---≤++-+-+-.不妨设1313131311y y x x y y x x --≤+-+-,则13122313131223111t x x x x x x PP x x x x x x ---=≤++-+-+-1212232312122323max ,max ,1111x xy y x x y y x x y y x x y y ⎧⎫⎧⎫----⎪⎪⎪⎪≤+⎨⎬⎨⎬+-+-+-+-⎪⎪⎪⎪⎩⎭⎩⎭1223t t PP P P =+.【点睛】关键点点睛:本题关键是理解“t -距离”的定义,再结合不等式及导数的知识解答.15.(2024·广东深圳·二模)无穷数列1a ,2a ,…,n a ,…的定义如下:如果n 是偶数,就对n 尽可能多次地除以2,直到得出一个奇数,这个奇数就是n a ﹔如果n 是奇数,就对31n +尽可能多次地除以2,直到得出一个奇数,这个奇数就是n a .(1)写出这个数列的前7项;(2)如果n a m =且m a n =,求m ,n 的值;(3)记()n a f n =,*n ∈N ,求一个正整数n ,满足()()()()()()2024fn f n f f n f f f n <<<<个 .【答案】(1)11a =,21a =,35a =,41a =,51a =,63a =,711a =;(2)1m n ==;(3)202521n k =-(答案不唯一,满足()*212025,,m n k m m k =-≥∈N 即可)【分析】(1)根据数列{}n a 的定义,逐一求解;(2)根据数列{}n a 的定义,分1n =和1n >分别求解;(3)根据数列{}n a 的定义,写出()f n 的值,即可求解.【详解】(1)根据题意,()1311221a =⨯+÷÷=,2221a =÷=,()333125a =⨯+÷=,44221a =÷÷=,()4535121a =⨯+÷=,6623a =÷=,()7371211a =⨯+÷=.(2)由已知,m ,n 均为奇数,不妨设m n ≤.当1n =时,因为11a =,所以1m =,故1m n ==;当1n >时,因为314n n m +<≤,而n 为奇数,n a m =,所以312n m +=.又m 为奇数,m a n =,所以存在*k ∈N ,使得312km n +=为奇数.所以()33195231122k n n n m ++=+=+=.而95462n n n +<<,所以426k n n n <<,即426k <<,*k ∈N ,无解.所以1m n ==.(3)显然,n 不能为偶数,否则()2nf n n ≤<,不满足()n f n <.所以,n 为正奇数.又()111f a ==,所以3n ≥.设41n k =+或41n k =-,*k ∈N .当41n k =+时,()()341131414k f n k k n ++==+<+=,不满足()n f n <;当41n k =-时,()()341161412k f n k k n -+==->-=,即()n f n <.所以,取202521n k =-,*k ∈N 时,()()()()2025202420242202432113321132132122k k k f f n k -+⨯-+=⨯-<==⨯-()()()()20223202322023332113212k f f f n k ⨯-+<<==⨯- ()()()()2023220242024332113212k f f f n k ⨯-+<==⨯- 即()()()()()()2024fn f n f f n f f f n <<<< 个.【点睛】关键点点睛:第(3)问中,发现当41n k =-时,满足()n f n <,从而设202521n k =-,*k ∈N ,验证满足条件.16.(2024·湖南邵阳·模拟预测)对于定义在D 上的函数()f x ,若存在距离为d 的两条平行直线11:l y kx b =+和22:l y kx b =+,使得对任意的x D ∈都有12()kx b f x kx b +≤≤+,则称函数()()f x x D ∈有一个宽度为d 的通道,1l 与2l 分别叫做函数()f x 的通道下界与通道上界.(1)若e 1()e 1x x f x -=+,请写出满足题意的一组()f x 通道宽度不超过3的通道下界与通道上界的直线方程;(2)若()sin cos g x x x x =++,证明:()g x 存在宽度为2的通道;(3)探究2ln 3(),[1,)x h x x x +=∈+∞的通道?并说明理由.【答案】(1)1y =-与1y =;(2)证明见解析;(3)不存在,理由见解析.【分析】(1)求出函数()f x 的值域,再利用给定定义求解即得.(2)利用辅助角公式求出sin cos x x +的值域,再利用不等式的性质可得()x g x x ≤≤推理即得.(3)利用导数求出函数()h x 的值域,假定存在,设出通道下界与通道上界的直线方程,利用定义建立不等式,构造函数1()(),x h x k x x ϕ=-≥,按0,0,0k k k =><探讨函数值情况即可得解.【详解】(1)函数e 1()e 1x x f x -=+的定义域为R ,2()1e 1x f x =-+在R 上单调递增,而e 11x +>,则202e 1x<<+,即2111e 1x -<-<+,因此1()1f x -<<,取120,1,1k b b ==-=,得通道下界1l 的直线方程:1y =-,通道上界2l 的直线方程:1y =,显然直线1y =-与1y =的距离为2,因此通道宽度不超过3,所以通道下界与通道上界的直线方程分别为1y =-与1y =.(2)函数()sin cos g x x x x =++的定义域为R ,而πsin cos )[4x x x +=+∈,即sin cos x x ≤+,则()x g x x ≤≤取121,k b b ===1l 的直线方程:y x =2l 的直线方程:y x =,。
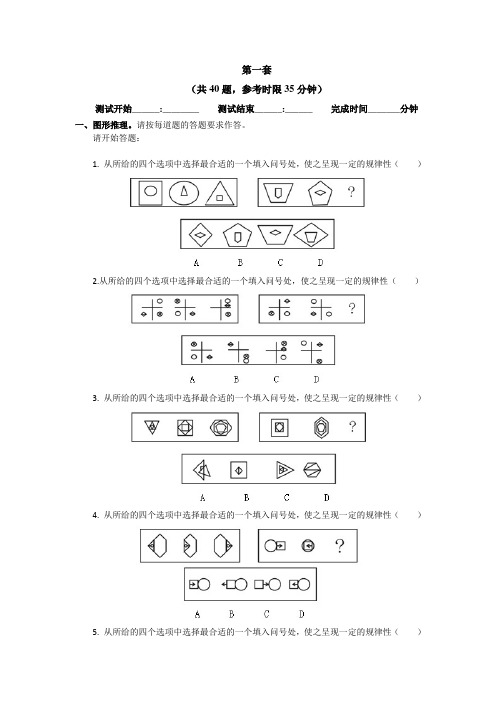
第一套(共40题,参考时限35分钟)测试开始______:________ 测试结束______:______ 完成时间_______分钟一、图形推理。
请按每道题的答题要求作答。
请开始答题:1. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()2.从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()3. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()4. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()5. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()6. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()7. 从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性()二、定义判断。
每道题先给出定义,然后列出四种情况,要求你严格依据定义,从中选出一个最符合或最不符合该定义的答案。
注意:假设这个定义是正确的,不容置疑的。
请开始答题:8. 人文关怀是指一种普通的人类自我关怀,表现为人格、人的价值、人的命运和尊严的关切,对人的生存状态和社会地位、人的进步需求、生活条件保障的关注,以及对理想人格的肯定和塑造。
根据上述定义,下列属于人文关怀的是()。
A. 对民众的博大的爱,深刻地理解和无私地付出B. 对人生存状况的关注,对人的生命和健康的呵护C. 对人的精神状态和人性的深切关怀,对人的情感、意志和价值的尊重D. 在强调国家利益的同时,关心个人的价值和利益及个人的困难和困境9. 社会责任是公民、企业和各种组织对国家或社会公共利益方面应尽的责任或义务。
社会责任就是行为主体对社会负有一定的责任,人是社会的动物,只有在社会中才能体现出人的真正本质。
根据上述定义,下列属于公民社会责任的是()。
A. 宪法法律规定以外的公民义务B. 公民应尽的非道德责任的责任C. 爱国守法、明礼诚信、敬业奉献D. 在工作单位应尽的一些岗位职责10. 公共意识是独立自由的个体所具有的一种整体意识或整体观念。

公务员考试定义判断高频考题含答案解析1.划分是把一个属概念分为他的各个种概念,以明确概念外延的一种思维方法。
正确的划分要求划分出的各项外延之和必须等于母项,而且要采用同一标准,子项的外延不相容,而且是同一层次的概念。
下列语句作为划分正确的是()。
A.直系亲属分为“双亲”“胞亲”“配偶”和“子女”B.战争分为常规战争和非常规战争C.地球分为南半球和北半球D.健康分为心理健康和生理健康【答案】C【解析】第一步:抓住定义中的关键词划分需按“统一标准”。
划分出的“子项外延之和必须等于母项”且“子项的外延不相容且是同一层次”,即子项应为全异关系。
第二步:逐一判断选项A中各项的外延之和不等于“直系亲属”,“双亲”、“子女”、“配偶”属于“直系亲属”,但“直系亲属”还应包括外祖父与外孙子女等,且“胞亲”不属于“直系亲属”;B中按使用的武器种类分为“常规战争”和“非常规战争”,但是它们的外延之和小于战争,因为战争还包括不使用武器的战争;C中“南半球”和“北半球”是按方位划分的,二者之和等于地球且二者是全异关系;D 中子项外延之和小于母项,因为健康包括心理健康、生理健康和道德健康。
故正确选项为C。
2.国际贸易是跨国界的交易活动,是一个国家同其他国家或地区间的商品、技术、劳务和信息等流通活动。
根据定义,下列属于国际贸易的是()。
A.以色列国防部向美国订购一批战斗机B.日本三菱公司向中国出口一批高级汽车C.澳大利亚人汤姆与印度某人才市场签订了劳务输出合同D.伊拉克过渡政府向德国某钢铁公司,购买了200吨钢材【答案】A【解析】解析:第一步:抓住定义中的关键词关键词强调“跨国界”、“一个国家同世界其他国家或地区”。
第二步:逐一判断选项B、C、D项均与定义中的“一个国家同世界其他国家或地区”不符。
故正确选项为A。
3.信息侵略指的是一个国家或民族试图利用自己在传媒和信息上的优势,将自己的核心价值观渗透和推广到其他国家或民族的传播体系和精神领域,最终达到嫁接和取代的目的。

公务员考试定义判断高频考题含答案解析1.思维是指人脑对客观间接的概括的反映。
根据思维过程中的凭借物或者思维状态的不同可以将思维分为(1)动作思维是指在思维过程中以实际动作作为支持的思维。
其特点是任务是直观的,以具体形式给予的,解决方式是实际动作;(2)形象思维是指用表象来进行分析、综合、抽象、概括的过程。
特点是借助鲜明、生动的客观形象;(3)抽象思维是指借助概念、判断、推理等形式来反映客观事物的运动规律,对事物的本质特征和内部联系加以认识的过程。
下列哪项符合动作思维的定义()。
A.福尔摩思通过在屋子找不到其他的出口,断定凶手一定是从屋顶的烟囱出去的,尽管烟囱很小B.洪熙官的儿子很小的时候就被要求每天看着父亲练功,渐渐地,他也能跟着父亲一起比划起来C.刘教授喜欢在他的文章中通过列举大量的实例来说明问题D.建筑系的学生在设计建筑方案时有时候需要先根据建筑图纸制作出一个模型来,这样似乎更有助于发展建筑设计的缺陷【答案】B【解析】第一步:判断考察的定义题目考查“动作思维”,所以在题干中仅需阅读“动作思维”。
第二步:抓住定义中的关键词关键词包括“实际动作”,“直观的,以具体形式给予的”。
第三步:逐一判断选项A中福尔摩思通过在屋子找不到其他的出口就断定凶手一定是从屋顶的烟囱出去,并没有涉及“实际动作”,因此不属于动作思维,而属于抽象思维;B中洪熙官的儿子每天看着父亲练功,完全符合关键词,因此属于动作思维;C中刘教授在他的文章中通过列举大量的实例来说明问题,不符合关键词“实际动作”,因此不属于动作思维,而属于形象思维;D中建筑系的学生根据建筑图纸制作出一个模型来,也不符合关键词“实际动作”,因此不属于动作思维,而属于形象思维。
综上所述,故正确选项为B。
2.激情是一种强烈的、短暂的、爆发式的情绪状态,它与心境、应激构成情绪的三种状态。
下列属于激情状态的是()。
A.惊慌失措,目瞪口呆B.手忙脚乱,陷入困境C.血压升高,怒发冲冠D.摆脱困境,化险为夷【答案】A【解析】第一步:抓住定义中的关键词关键词强调“强烈的、短暂的、爆发式的情绪状态”第二步:逐一判断选项A项惊慌失措的意思是吓得慌了手脚,不知如何是好。
在事业单位行测考试中,定义判断可谓是必考题型,也是考生复习的重中之重。
中公教育为您总结归纳出定义判断冲刺过关40题,祝您顺利通关!
1.仿生学是一门模仿生物的特殊本领,利用生物的结构和功能原理来研制机械或各种新技术的科学。
以下属于仿生学成果的是( )。
A.人们用掺和某些化学物质的方法得到类似生物光(如萤火虫)的冷光,作为安全照明用
B.科学研究表明:大猩猩的智力最接近人类,科学家据此猜测,大猩猩是人类始祖演变发展的一个分支
C.阿拉斯加犬被用来拉雪橇,因为它们坚韧耐劳,并且团结协作的精神强
D.一只鹦鹉非常聪明,它会说“欢迎光临”、“谢谢”等语句,成为某酒吧人见人爱的宠物
2.商品差价,是指同一商品由于流通环节、购销地区、购销季节以及质量不同而形成的价格差额。
下列属于商品差价的是( )。
A.春季白萝卜一块一斤,夏季胡萝卜五角一斤
B.奥迪轿车与奥拓轿车价值不同
C.春风出版社出版的《政治经济学》比秋雨出版社出版的同名书籍每本便宜5元钱
D.因为甲地产盐,每斤盐甲地比乙地的便宜2角钱
3.强迫障碍:是以反复出现强迫观念为基本特征的一类神经症性障碍。
强迫观念是以刻板形式反复进入患者意识领域的思想、表象或意向。
这些思想、表象或意向对患者来说,是没有现实意义的、不必要的或多余的;患者意识到这些都是他自己的思想,很想摆脱,但又无能为力,因而感到十分苦恼。
根据定义,以下可能属于“强迫障碍”的是( )。
A.张奶奶老是一个劲的叨念着:我儿子就要回来了
B.老李锁上门后又打开进去检查一遍再锁门……如此循环三次才放心离开
C.虽然已经打了三次电话了,赵某还是不放心,于是再一次拨通电话
D.明明已经确定带了那本书,小黄在路上还是忍不住检查好几回
4.职业素质是指劳动者在一定的生理和心理条件的基础上,通过教育、劳动实践和自我修养等途径而形成和发展起来的,在职业活动中发挥重要作用的内在基本品质。
根据以上定义,下列不属于职业素质的是( )。
A.声乐演唱家所具有的不同于一般人的生理遗传因素
B.作家对生活的敏锐的感觉力和较强的语言表达能力
C.画家所具有的不同于一般人的颜色辨别能力和空间想象能力
D.教师广博的知识和高尚的人格
5.行政复议:行政复议是公民、法人或者其他组织认为行政机关的具体行政行为或者行政不作为侵犯其合法权益的,对该行为或不作为提起行政复议。
下列不属于行政复议行为的是( )。
A.蔬菜市场摊主王某因不服区工商局的罚款处罚,向市工商局提出复议申请
B.刘某因打架斗殴被刑事拘留15天,释放后由于不服而向上级机关提出复议申请
C.某食品厂因违规操作而被吊销生产许可证,该厂向人民政府卑出复议申请
D.张某因不服超速驾驶被处以200元罚款的处罚,向上级公安交警部门提出复议申请
【答案及解析】
1.A【解析】根据定义,仿生学是模仿动物的特殊本领制造出的新技术。
B项是根据猩猩的智力接近人类而做出的一个猜测,C、D两项是利用动物的特殊本领而使之服务于人类,这三项都没有根据动物的结构和功能原理而作出什么新技术,因此都不是仿生学。
只有A 项是根据萤火虫的发光原理研制出的技术,所以选A。
2.D【解析】商品差价是同一商品的不同价格,A、B、C三项都是不同的商品,C项虽然都是《政治经济学》的书,但是是不同出版社出的同类的书,也不是同一商品。
D项是由于盐这一商品的购销地区的不同造成的价格差,因此选D。
3.D【解析】“这些思想,表象或意向对患者来说,是没有现实意义的、不必要的或多余的;患者意识到这些都是他自已的思想,很想摆脱,但又无能为力,因而感到十分苦恼。
”D 项中“检查好几回”是多余的,“忍不住”说明小黄“很想摆脱,但又无能为力”,故正确答案为D。
4.A【解析】根据定义的要件,职业素质是通过教育、劳动实践和自我修养等途径形成和发展起来的,所以只有A不符合这一要件,而是一种先天的遗传因素,故选A。
5.A【解析】由题干可知,行政复议包含一个要素是“侵犯了公民、法人或者其他组织的合法权益”,而B、C、D项中均为违反了法律法规收到了处罚,不属此类,故A项正确。