2020高考数学大二轮复习专题7立体几何第2讲综合大题部分增分强化练文

增分强化练1．(2019·泉州质检)在四棱锥P ­ABCD 中，PD ⊥平面ABCD ，AB ⊥AD ，AD ∥BC ，AB ＝1，AD ＝2BC ＝2，PD ＝ 3.(1)求证： 平面PBD ⊥平面PAC ；(2)M 为棱PB 上异于B 的点，且AM ⊥MC ，求直线AM 与平面MCD 所成角的正弦值． 解析：(1)证明：在Rt △ABC 与Rt △ABD 中，因为BC AB ＝22， AB AD ＝22， 所以BC AB ＝ABAD，∠ABC ＝∠DAB ＝90°，即△ABC ∽△DAB ，所以∠ABD ＝∠BCA .因为∠ABD ＋∠CBD ＝90°，所以∠BCA ＋∠CBD ＝90°，所以AC ⊥BD . 因为PD ⊥平面ABCD ，AC ⊂平面ABCD ，所以PD ⊥AC ， 又BD ∩PD ＝D ，所以AC ⊥平面PBD ， 又AC ⊂平面PAC, 所以平面PBD ⊥平面PAC .(2)过A 作AE ∥DP ，因为PD ⊥平面ABCD ，所以AE ⊥平面ABCD ，即AE ，AB ，AD 两两相垂直，以A 为原点，AB ，AD ，AE 所在的直线为x ，y ，z 轴，建立如图所示的空间直角坐标系，因为AB ＝1，AD ＝2BC ＝2，PD ＝3， 所以A (0,0,0)，B (1,0,0)，C ⎝ ⎛⎭⎪⎫1，22，0，D (0，2，0)，P (0，2，3)， AB →＝(1,0,0)，BP →＝(－1，2，3)，CB →＝⎝⎛⎭⎪⎫0，－22，0， 设BM →＝λBP →，λ∈(0,1]．则AM →＝AB →＋λBP →＝(1－λ，2λ，3λ)， CM →＝CB →＋λBP →＝(－λ，－22＋2λ，3λ).因为AM ⊥MC ，所以AM →·CM →＝0，即(1－λ)(－λ)＋2λ⎝ ⎛⎭⎪⎫－22＋2λ＋3λ2＝0，解得6λ2－2λ＝0，λ＝0或λ＝13.因为λ∈(0,1]，所以λ＝13.所以AM →＝⎝ ⎛⎭⎪⎫23，23，33，即M ⎝ ⎛⎭⎪⎫23，23，33.所以DC →＝⎝ ⎛⎭⎪⎫1，－22，0，DM →＝⎝ ⎛⎭⎪⎫23，－223，33，设n ＝(x 0，y 0，z 0)为平面MCD 的一个法向量，则⎩⎪⎨⎪⎧n ·DM →＝0n ·DC →＝0，所以⎩⎪⎨⎪⎧23x 0－223y 0＋33z 0＝0x 0－22y 0＝0，所以取n ＝⎝⎛⎭⎪⎫62，3，2， 设直线AM 与平面MCD 所成角为θ， 所以sin θ＝|cos 〈AM →，n 〉|＝63＋63＋6349＋29＋39·64＋3＋2＝23913，所以直线AM 与平面MCD 所成角的正弦值23913.2．(2019·济宁模拟)如图，在直角梯形ABED 中，AB ∥DE ，AB ⊥BE ，且AB ＝2DE ＝2BE ，点C 是AB 中点，现将△ACD 沿CD 折起，使点A 到达点P 的位置．(1)求证：平面PBC⊥平面PEB；(2)若PE与平面PBC所成的角为45°，求平面PDE与平面PBC所成锐二面角的余弦值．解析：(1)证明：∵AB∥DE，AB＝2DE，点C是AB中点，∴CB∥ED，CB＝ED，∴四边形BCDE为平行四边形，∴CD∥EB，又EB⊥AB，∴CD⊥AB，∴CD⊥PC，CD⊥BC，∴CD⊥平面PBC，∴EB⊥平面PBC，又∵EB⊂平面PEB，∴平面PBC⊥平面PEB.(2)由(1)知EB⊥平面PBC，∴∠EPB即为PE与平面PBC所成的角，∴∠EPB＝45°，∵EB⊥平面PBC，∴EB⊥PB，∴△PBE为等腰直角三角形，∴EB＝PB＝BC＝PC，故△PBC为等边三角形，取BC的中点O，连结PO，则PO⊥BC，∵EB⊥平面PBC，又EB⊂平面EBCD，∴平面EBCD⊥平面PBC，又PO⊂平面PBC，∴PO⊥平面EBCD，以O为坐标原点，过点O与BE平行的直线为x轴，CB所在的直线为y轴，OP所在的直线为z 轴建立空间直角坐标系如图，设BC ＝2，则B (0,1,0)，E (2,1,0)，D (2，－1,0)，P (0,0，3)，从而DE →＝(0,2,0)，PE →＝(2,1，－3)， 设平面PDE 的一个法向量为m ＝(x ，y ，z )， 则由⎩⎪⎨⎪⎧m ·DE →＝0m ·PE →＝0得⎩⎨⎧2y ＝02x ＋y －3z ＝0，令z ＝2得m ＝(3，0,2)，又平面PBC 的一个法向量n ＝(1,0,0)，则cos 〈m ，n 〉＝m ·n |m ||n |＝37＝217，平面PDE 与平面PBC 所成锐二面角的余弦值为217. 3．(2019·高考全国卷Ⅰ)如图，直四棱柱ABCD ­A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．(1)证明：MN ∥平面C 1DE ； (2)求二面角A ­MA 1­N 的正弦值． 解析：(1)证明：如图，连接B 1C ，ME . 因为M ，E 分别为BB 1，BC 的中点， 所以ME ∥B 1C ，且ME ＝12B 1C .又因为N 为A 1D 的中点，所以ND ＝12A 1D .由题设知A 1B 1綊DC ， 可得B 1C 綊A 1D ，故ME 綊ND ， 因此四边形MNDE 为平行四边形， 所以MN ∥ED . 又MN ⊄平面C 1DE ， 所以MN ∥平面C 1DE .(2)由已知可得DE ⊥DA ，以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系D ­xyz ，则A (2,0,0)，A 1(2,0,4)，M (1，3，2)，N (1,0,2)，A 1A →＝(0,0，－4)，A 1M →＝(－1，3，－2)，A 1N →＝(－1,0，－2)，MN →＝(0，－3，0)． 设m ＝(x ，y ，z )为平面A 1MA 的法向量，则⎩⎪⎨⎪⎧m ·A 1M →＝0，m ·A 1A →＝0，所以⎩⎨⎧－x ＋3y －2z ＝0，－4z ＝0，可取m ＝(3，1,0)．设n ＝(p ，q ，r )为平面A 1MN 的法向量， 则⎩⎪⎨⎪⎧n ·MN →＝0，n ·A 1N →＝0，所以⎩⎨⎧－3q ＝0，－p －2r ＝0，可取n ＝(2,0，－1)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝232×5＝155，所以二面角A ­MA 1­N 的正弦值为105. 4．(2019·高考全国卷Ⅱ)如图，长方体ABCD ­A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1.(1)证明：BE ⊥平面EB 1C 1；(2)若AE ＝A 1E ，求二面角B ­EC ­C 1的正弦值．解析：(1)证明：由已知得，B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1， 故B 1C 1⊥BE .又BE ⊥EC 1，B 1C 1∩EC 1＝C 1， 所以BE ⊥平面EB 1C 1.(2)由(1)知∠BEB 1＝90°.由题设知Rt △ABE ≌Rt △A 1B 1E ，所以∠AEB ＝45°，故AE ＝AB ，AA 1＝2AB .以D 为坐标原点，DA →的方向为x 轴正方向，|DA →|为单位长度，建立如图所示的空间直角坐标系D ­xyz ，则C (0,1,0)，B (1,1,0)，C 1(0,1,2)，E (1,0,1)，CB →＝(1,0,0)，CE →＝(1，－1,1)，CC 1→＝(0,0,2)． 设平面EBC 的法向量为n ＝(x 1，y 1，z 1)， 则⎩⎪⎨⎪⎧CB →·n ＝0，CE →·n ＝0，即⎩⎪⎨⎪⎧x 1＝0，x 1－y 1＋z 1＝0，所以可取n ＝(0，－1，－1)．设平面ECC 1的法向量为m ＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧CC 1→·m ＝0，CE →·m ＝0，即⎩⎪⎨⎪⎧2z 2＝0，x 2－y 2＋z 2＝0，所以可取m ＝(1,1,0)．于是cos 〈n ，m 〉＝n ·m |n ||m |＝－12.所以，二面角B ­EC ­C 1的正弦值为32. 增分强化练一、选择题1．已知直线l ⊥平面α，直线m ∥平面β，若α⊥β，则下列结论正确的是( ) A ．l ∥β或l ⊂β B ．l ∥m C ．m ⊥αD ．l ⊥m解析：当直线l ⊥平面α，α⊥β时，假设l ∩β＝A ，过A 在平面β内作a ⊥l ，根据面面垂直的性质定理可知：a ⊥α，这样过一点A 有两条直线a ，l 与平面α垂直，这与过一点有且只有一条直线与已知平面垂直相矛盾，故假设不成立，所以l ∥β或l ⊂β，故本题选A. 答案：A2．设m ，n 是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是( ) A ．若m ∥α，m ∥β，则α∥β B ．若m ⊥α，m ⊥n ，则n ⊥α C ．若m ⊥α，m ∥n ，则n ⊥α D ．若α⊥β，m ⊥α，则m ∥β解析：设m ，n 是两条不同的直线，α，β是两个不同的平面，则： 在A 中，若m ∥α，m ∥β，则α与β相交或平行，故A 错误； 在B 中，若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，故B 错误；在C 中，若m ⊥α，m ∥n ，则由线面垂直的判定定理得n ⊥α，故C 正确； 在D 中，若α⊥β，m ⊥α，则m ∥β或m ⊂β，故D 错误． 故选C. 答案：C3．(2019·蚌埠模拟)如图，在长方体ABCD ­A 1B 1C 1D 1中，AB ＝BC ＝2AA 1＝2，E ，F 分别在AB ，BC 上，则下列说法错误的是( )A ．直线AD 与A 1C 1所成的角为π4B ．当E 为中点时，平面A 1D 1E ⊥平面B 1C 1E C ．当E ，F 为中点时，EF ⊥BD 1 D ．当E ，F 为中点时，BD 1⊥平面B 1EF解析：对于A 选项，将A 1C 1平移到AC 如图所示，由于四边形ABCD 为正方形，故AD ，AC 所成角为π4，也即AD ，A 1C 1所成角为π4，故A 选项正确．对于B 选项，由于A 1E ＝B 1E ＝2，A 1B 1＝2，满足勾股定理，故A 1E ⊥B 1E ，而A 1E ⊥B 1C 1，故A 1E ⊥平面B 1C 1E ，所以平面A 1D 1E ⊥平面B 1C 1E ，故B 选项正确．对于C 选项，由于EF ∥AC ，故EF ⊥BD ，EF ⊥BB 1，由此证得EF ⊥平面BDD 1B 1，故EF ⊥BD 1，故C 选项正确．对于D 选项，虽然EF ⊥BD 1，但是BD 1与B 1E ，B 1F 不垂直，故D 选项说法错误．综上所述，本小题选D.答案：D4．(2019·咸阳模拟)在正方体ABCD ­A 1B 1C 1D 1中，E 、F 分别是AB 、B 1C 1的中点，则异面直线A 1E 、FC 所成角的余弦值为( )A.105 B.1010C.102D.45解析：取C 1D 1的中点G ，连接CG ，FG (图略)，因为正方体ABCD ­A 1B 1C 1D 1，且E ，G 分别是AB ，C 1D 1的中点， 所以A 1E ∥CG ，所以∠FCG 即为异面直线A 1E 、FC 所成角或其补角， 设正方体边长为2，则FC ＝CG ＝5，FG ＝2， 在△FCG 中由余弦定理得cos ∠FCG ＝5＋5－22×5×5＝45，所以异面直线A 1E 、FC 所成角的余弦值为45，故选D. 答案：D5．如图，在四棱柱ABCD ­A 1B 1C 1D 1中，E ，F 分别是AB 1、BC 1的中点，下列结论中正确的是( )A ．EF ⊥BB 1 B ．EF ⊥平面BCC 1B 1 C ．EF ∥平面D 1BCD ．EF ∥平面ACC 1A 1解析：连接B 1C 交BC 1于F ，由于四边形BCC 1B 1是平行四边形，对角线平分，故F 是B 1C 的中点．因为E 是AB 1的中点，所以EF 是△B 1AC 的中位线，故EF ∥AC ，所以EF ∥平面ACC 1A 1.故选D.答案：D6．如图，边长为2的正方形ABCD中，点E、F分别是AB、BC的中点，将△ADE，ΔBEF，△CDF分别沿DE，EF，FD折起，使得A、B、C三点重合于点A′，若四面体A′­EDF的四个顶点在同一个球面上，则该球的表面积为( )A．5π B．6πC．8π D．11π解析：由题意可知△A′EF是等腰直角三角形，且A′D⊥平面A′EF.三棱锥的底面A′EF扩展为边长为1的正方形，然后扩展为正四棱柱，三棱锥的外接球与正四棱柱的外接球是同一个球，正四棱柱的体对角线的长度就是外接球的直径，直径为1＋1＋4＝ 6.∴球的半径为62，∴球的表面积为4π·⎝ ⎛⎭⎪⎫622＝6π.故选B. 答案：B 二、填空题7．在直三棱柱ABC ­A 1B 1C 1中，若∠BAC ＝90°，AB ＝AC ＝AA 1则异面直线BA 1与AC 1所成的角等于________．解析：延长CA 到D (图略)，使得AD ＝AC ，则ADA 1C 1为平行四边形，∠DA 1B 就是异面直线BA 1与AC 1所成的角，又A 1D ＝A 1B ＝DB ＝2AB ，则△A 1DB 为等边三角形，∴∠DA 1B ＝60°. 答案：60°8．(2019·桂林、崇左模拟)在大小为75°的二面角α­l ­β内有一点M 到两个半平面的距离分别为1和2，则点M 到棱l 的距离等于________．解析：由题意，设垂足分别为A ，B ，则在△MAB 中，MA ＝1，MB ＝2，∠AMB ＝105°，∴AB 2＝1＋2－2×1×2×cos∠AMB ＝2＋3， ∴AB ＝2＋ 3.设M 到棱的距离为l ，则l ＝ABsin 105°＝2＋36＋24＝2.答案：2 三、解答题9．(2019·汕头模拟)如图，等边△PAC 所在平面与梯形ABCD 所在平面互相垂直，且有AD ∥BC ，AB ＝AD ＝DC ＝2，BC ＝4.(1)证明：AB ⊥平面PAC ； (2)求点D 到平面PAB 的距离．解析：(1)证明：取BC 中点M ，连接AM ， 则四边形AMCD 为菱形， 即有AM ＝MC ＝12BC,所以AB ⊥AC ，又AB ⊂平面ABCD ，平面ABCD ⊥平面PAC ，平面ABCD ∩平面PAC ＝AC ， ∴AB ⊥平面PAC .(2)由(1)可得PA ＝AC ＝23，所以∠ABC ＝60°，∠BAD ＝120°， 取AC 中点O ，连接PO ， 则PO ⊥AC ，PO ＝3，又PO ⊂平面PAC ，平面PAC ⊥平面ABCD ，平面PAC ∩平面ABCD ＝AC ∴PO ⊥平面ABCD ； 所以V D ­PAB ＝V P ­ABD ＝13S ABD ·PO＝13×12×2×2×sin 120°×3＝3， 由(1)有AB ⊥平面PAC ，得AB ⊥PA ， ∴S ΔPAB ＝12×2×23＝23，设点D 到平面PAB 的距离为d ， 由V D ­PAB ＝13S ΔPAB ·d .∴d ＝32.10.如图，E 是以AB 为直径的半圆上异于A 、B 的点，矩形ABCD 所在的平面垂直于该半圆所在的平面，且AB ＝2AD ＝2. (1)求证：EA ⊥EC ；(2)设平面ECD 与半圆弧的另一个交点为F . ①试证：EF ∥AB ；②若EF ＝1，求三棱锥E ­ADF 的体积． 解析：(1)证明：∵平面ABCD ⊥平面 ABE ，平面ABCD ∩平面ABE ＝AB ，BC ⊥AB ，BC ⊂平面ABCD ， ∴BC ⊥平面ABE .又∵AE ⊂平面ABE ，∴BC ⊥AE .∵E 在以AB 为直径的半圆上，∴AE ⊥BE ，又∵BE ∩BC ＝B ，BC 、BE ⊂平面BCE ， ∴AE ⊥平面BCE .又∵CE ⊂平面BCE ，∴EA ⊥EC .(2)①证明： ∵AB ∥CD ，AB ⊄平面CED ，CD ⊂平面CED ， ∴AB ∥平面CED .又∵AB ⊂平面ABE ，平面ABE ∩平面CED ＝EF ， ∴AB ∥EF .②取AB 中点O ，EF 的中点O ′，(图略)在Rt△OO ′F 中，OF ＝1，O ′F ＝12，∴OO ′＝32.由(1)已证得BC ⊥平面ABE ，又已知AD ∥BC ， ∴AD ⊥平面ABE .故V E ­ADF ＝V D ­AEF ＝13·S △AEF ·AD ＝13·12·EF ·OO ′·AD ＝312.11．如图1，在△ABC 中，C ＝90°，AC ＝2BC ＝4，E ，F 分别是AC 与AB 的中点，将△AEF 沿EF 折起，连接AC 与AB 得到四棱锥A ­BCEF (如图2)，G 为线段AB 的中点．(1)求证：FG ∥平面ACE ；(2)当四棱锥A ­BCEF 体积最大时，求F 与平面ABC 的距离． 解析：(1)证明：取AC 的中点H ，连接EH ，GH ，由于G 是AB 的中点， ∴GH ∥BC ，且GH ＝12BC ，又E ，F 分别为图1中AC 与AB 的中点， ∴FE ∥BC ，且FE ＝12BC ，∴FE ∥GH ，FE ＝GH ，∴四边形EFGH 为平行四边形， ∴FG ∥EH ，又FG ⊄平面ACE ，EH ⊂平面ACE ， ∴FG ∥平面ACE .(2)当四棱锥A ­BCF 体积最大时，AE ⊥平面BCEF ， 又EF ⊥EC ，AE ∩EF ＝E ， ∴FE ⊥平面AEC ，又FE ∥BC ， ∴BC ⊥平面ACE ∴BC ⊥EH ，又AE ＝EC ＝2，H 是AC 的中点，EH ⊥AC ，AC ∩BC ＝C ，∴EH ⊥平面ABC ，而EF ∥平面ABC ，∴F 到平面ABC 的距离即为E 到平面ABC 的距离，EH ＝EC ×sin 45°＝ 2.增分强化练考点一 利用空间向量证明平行与垂直如图所示，平面PAD ⊥平面ABCD ，ABCD 为正方形，△PAD 是直角三角形，且PA ＝AD ＝2，E ，F ，G 分别是线段PA ，PD ，CD 的中点．求证：PB ∥平面EFG .证明：∵平面PAD ⊥平面ABCD ，ABCD 为正方形，△PAD 是直角三角形，且PA ＝AD ，∴AB ，AP ，AD 两两垂直，以A 为坐标原点，AB ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系A ­xyz ，则A (0,0,0)，B (2,0,0)，C (2,2,0)，D (0,2,0)，P (0,0,2)，E (0,0,1)，F (0,1,1)，G (1,2,0)．∴PB →＝(2,0，－2)，FE →＝(0，－1,0)，FG →＝(1,1，－1)， 设PB →＝sFE →＋tFG →，即(2,0，－2)＝s (0，－1,0)＋t (1,1，－1)，∴⎩⎪⎨⎪⎧t ＝2，t －s ＝0，－t ＝－2，解得s ＝t ＝2，∴PB →＝2FE →＋2FG →，又∵FE →与FG →不共线，∴PB →，FE →与FG →共面． ∵PB ⊄平面EFG ，∴PB ∥平面EFG . 考点二 利用空间向量求空间角1．(2019·滨州模拟)如图，在三棱柱ABC ­A 1B 1C 1中，BC ＝BB 1，∠B 1BC ＝60°，B 1C 1⊥AB 1.(1)证明：AB ＝AC ；(2)若AB ⊥AC ，且AB 1＝BB 1，求二面角A 1­CB 1­C 1的余弦值． 解析：(1)证明：取BC 的中点O ，连结AO ，OB 1. 因为BC ＝BB 1，∠B 1BC ＝60°， 所以△BCB 1是等边三角形， 所以B 1O ⊥BC ，又BC ∥B 1C 1，B 1C 1⊥AB 1， 所以BC ⊥AB 1， 所以BC ⊥平面AOB 1，所以BC ⊥AO ，由三线合一可知△ABC 为等腰三角形 所以AB ＝AC .(2)设AB 1＝BB 1＝2，则BC ＝B 1C ＝2. 因为AB ⊥AC ，所以AO ＝1.又因为OB 1＝3，所以OB 21＋AO 2＝AB 21， 所以AO ⊥OB 1.以O 为坐标原点，向量OB →的方向为x 轴的正方向，建立如图所示的空间直角坐标系O ­xyz ，则O (0,0,0)，C (－1,0,0)，A 1(－1，3，1)，B 1(0，3，0)，CA →1＝(0，3，1)，CB →1＝(1，3，0)．设平面A 1B 1C 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧CA →1 ·n ＝0CB →1·n ＝0，即⎩⎨⎧3y ＋z ＝0x ＋3y ＝0，可取n ＝(3，－1，3)，由(1)可知，平面CB 1C 1的法向量可取OA →＝(0,0,1)，所以cos 〈OA →，n 〉＝OA →·n |OA →||n | ＝217，由图示可知，二面角A 1­CB 1­C 1为锐二面角， 所以二面角A 1­CB 1­C 1的余弦值为217. 2.已知四棱锥P ­ABCD 的底面ABCD 是直角梯形，AD ∥BC ，AB ⊥BC ，AB ＝3，BC ＝2AD ＝2，E 为CD 的中点，PB ⊥AE . (1)证明：平面PBD ⊥平面ABCD ；(2)若PB ＝PD ，PC 与平面ABCD 所成的角为π4，求二面角B ­PD ­C 的余弦值．解析：(1)证明：由ABCD 是直角梯形，AB ＝3，BC ＝2AD ＝2，可得DC ＝2，∠BCD ＝π3，BD ＝2，从而△BCD 是等边三角形， ∠BDC ＝π3，BD 平分∠ADC ，∵E 为CD 的中点，DE ＝AD ＝1，∴BD ⊥AE ， 又∵PB ⊥AE ，PB ∩BD ＝B ，∴AE ⊥平面PBD ， ∵AE ⊂平面ABCD ，∴平面PBD ⊥平面ABCD . (2)如图，作PO ⊥BD 于O ，连接OC ，∵平面PBD ⊥平面ABCD ，平面PBD ∩平面ABCD ＝BD ，∴PO ⊥平面ABCD ， ∴∠PCO 为PC 与平面ABCD 所成的角，∠PCO ＝π4，又∵PB ＝PD ，∴O 为BD 中点，OC ⊥BD ，OP ＝OC ＝3， 以OB ，OC ，OP 为x ，y ，z 轴建立空间直角坐标系，B (1,0,0)，C (0，3，0)，D (－1,0,0)，P (0,0，3)．PC →＝(0，3，－3)，PD →＝(－1,0，－3)，设平面PCD 的一个法向量n ＝(x ，y ，z )， 由⎩⎪⎨⎪⎧n ·PC →＝0，n ·PD →＝0得⎩⎨⎧3y －3z ＝0，x ＋3z ＝0，令z ＝1得n ＝(－3，1,1)，又平面PBD 的一个法向量为m ＝(0,1,0)， 设二面角B ­PD ­C 为θ，则|cos θ|＝|n ·m ||n |·|m |＝15×1＝55.所求二面角B ­PD ­C 的余弦值是55. 考点三 立体几何中的探索性问题1．(2019·桂林、崇左模拟)已知四棱锥S ­ABCD 的底面ABCD 是菱形，∠ABC ＝π3，SA ⊥底面ABCD ，E 是SC 上的任意一点．(1)求证：平面EBD⊥平面SAC；(2)设SA＝AB＝2，是否存在点E使平面BED与平面SAD所成的锐二面角的大小为30°？如果存在，求出点E的位置，如果不存在，请说明理由．解析：(1)证明：∵SA⊥平面ABCD，BD⊂平面ABCD，∴SA⊥BD.∵四边形ABCD是菱形，∴AC⊥BD.∵AC∩AS＝A，∴BD⊥平面SAC.∵BD⊂平面EBD，∴平面EBD⊥平面SAC.(2)当点E为SC的中点时，平面BED与平面SAD所成的锐二面角的大小为30°，理由如下：设AC与BD的交点为O，以OC、OD所在直线分别为x、y轴，以过O垂直平面ABCD的直线为z轴建立空间直角坐标系(如图)，则A (－1,0,0)，C (1,0,0)，S (－1,0,2)，B (0，－3，0)，D (0，3，0)． 设E (x,0，z )，则SE →＝(x ＋1,0，z －2)，EC →＝(1－x,0，－z )， 设SE →＝λEC →，∴⎩⎪⎨⎪⎧x ＝λ－1λ＋1z ＝2λ＋1，∴E ⎝⎛⎭⎪⎫λ－1λ＋1，0，2λ＋1，∴DE →＝⎝ ⎛⎭⎪⎫λ－1λ＋1，－3，2λ＋1，BD →＝(0,23，0)，设平面BDE 的法向量n ＝(x 1，y 1，z 1)， ∵⎩⎪⎨⎪⎧n ⊥DE→n ⊥BD→ ，∴⎩⎪⎨⎪⎧n ·DE →＝0n ·BD →＝0.求得n ＝(2,0,1－λ)为平面BDE 的一个法向量． 同理可得平面SAD 的一个法向量为m ＝(3，－1,0)， ∵平面BED 与平面SAD 所成的锐二面角的大小为30°，∴cos 30°＝|m ·n ||m ||n |＝|(3，－1，0)·(2，0，1－λ)|24＋(1－λ)2＝32，解得λ＝1. ∴E 为SC 的中点．2．如图，在三棱柱ABC ­A 1B 1C 1中，CA ＝CB ＝CC 1＝2，∠ACC 1＝∠CC 1B 1，直线AC 与直线BB 1所成的角为60°.(1)求证：AB 1⊥CC 1；(2)若AB 1＝6，M 是AB 1上的点，当平面MCC 1与平面AB 1C 夹角的余弦值为15时，求AMMB 1的值．解析：(1)证明：在三棱柱ABC ­A 1B 1C 1中，各侧面均为平行四边形， 所以BB 1∥CC 1，则∠ACC 1即为AC 与BB 1所成的角， 所以∠ACC 1＝∠CC 1B 1＝60°， 如图，连接AC 1和B 1C ， 因为CA ＝CB ＝CC 1＝2，所以△ACC 1和△B 1CC 1均为等边三角形， 取CC 1的中点O ，连AO 和B 1O ， 则AO ⊥CC 1，B 1O ⊥CC 1， 又AO ∩B 1O ＝O ， 所以CC 1⊥平面AOB 1，AB 1⊂平面AOB 1，所以AB 1⊥CC 1.(2)由(1)知AO ＝B 1O ＝3，因为AB 1＝6， 则AO 2＋B 1O 2＝AB 21，所以AO ⊥B 1O ， 又AO ⊥CC 1，所以AO ⊥平面BCC 1B 1，以OB 1所在直线为x 轴，OC 1所在直线为y 轴，OA 所在直线为z 轴，建立如图空间直角坐标系，则A (0,0，3)，C (0，－1,0)，C 1(0,1,0)，B 1(3，0,0)，AC →＝(0，－1，－3)，AB 1→＝(3，0，－3)，CC 1→＝(0,2,0)，设AM →＝tMB 1→，M (x ，y ，z )，则(x ，y ，z －3)＝t (3－x ，－y ，－z )． 所以x ＝3t t ＋1，y ＝0，z ＝3t ＋1，M (3t t ＋1，0，3t ＋1)， 所以CM →＝(3t t ＋1，1，3t ＋1)，设平面ACB 1的法向量为n 1＝(x 1，y 1，z 1)， 平面MCC 1的法向量为n 2＝(x 2，y 2，z 2)， 所以⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AB 1→＝0⇒⎩⎨⎧－y 1－3z 1＝0，3x 1－3z 1＝0，解得n 1＝(1，－3，1)， ⎩⎪⎨⎪⎧n 2·CC 1→＝0，n 2·CM →＝0⇒⎩⎪⎨⎪⎧2y 2＝0，3t t ＋1x 2＋y 2＋3t ＋1z 2＝0.解得n 2＝(1,0，－t )．所以|cos θ|＝|n 1·n 2||n 1|·|n 2|＝|1－t |5·1＋t 2＝15， 解得t ＝12或t ＝2，即AM MB 1＝12或AMMB 1＝2.增分强化练一、选择题1．在一个密闭透明的圆柱筒内装一定体积的水，将该圆柱筒分别竖直、水平、倾斜放置时，指出圆柱桶内的水平面可以呈现出的几何形状不可能是( )A．圆面B．矩形面C．梯形面D．椭圆面或部分椭圆面解析：将圆柱桶竖放，水面为圆面；将圆柱桶斜放，水面为椭圆面或部分椭圆面；将圆柱桶水平放置，水面为矩形面，所以圆柱桶内的水平面可以呈现出的几何形状不可能是梯形面，故选C.答案：C2．(2019·三明质检)如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为( )A.23πB．2πC.83π D．8π解析：由几何体三视图可知：该几何体为圆柱，且圆柱的底面圆半径为1，高为2，所以圆柱的体积为V＝π×12×2＝2π.故选B.答案：B3．(2019·新乡模拟)如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为( )A ．28B ．30C ．36D ．42解析：该几何体是由12个棱长为1的正方体组合而成的，所以S (前后)＝12＋12＝24，S (左右)＝3＋3＝6，S (上下)＝6＋6＝12，从而S (表面)＝24＋6＋12＝42.故选D. 答案：D4．某几何体的三视图如图所示，则该几何体的体积为( )A ．16π－323B ．16π－163C ．8π－323D ．8π－163解析：由三视图可知，该几何体是一个半圆柱挖去一个倒立的四棱锥，∴V ＝12×π×22×4－13×42×2＝8π－323.故选C.答案：C5．如图，网格纸的小正方形的边长是1，在其上用粗实线和粗虚线画出了某几何体的三视图，图中的曲线为半圆弧或圆，则该几何体的体积是( )A.2π3＋83B ．2π＋83C ．2π＋8D ．8π＋8解析：由题意可知几何体是组合体，由14的圆柱与一个四棱锥组成，如图：V ＝14×22×π×2＋13×2×2×2＝2π＋83.故选B.答案：B6．用一个平面去截正方体，则截面不可能是( ) A ．直角三角形 B ．等边三角形 C ．正方形D ．正六边形解析：用一个平面去截正方体，则截面的情况为：①截面为三角形时，可以是锐角三角形、等腰三角形、等边三角形，但不可能是钝角三角形、直角三角形；②截面为四边形时，可以是梯形(等腰梯形)、平行四边形、菱形、矩形，但不可能是直角梯形；③截面为五边形时，不可能是正五边形；④截面为六边形时，可以是正六边形．故选A. 答案：A7．某几何体的正视图和侧视图均为如图所示的等腰三角形，则该几何体的体积不可能是( )A ．πB ．2C ．4D ．6解析：几何体可能是圆锥，底面半径为1，高为3，几何体的体积为13×12×π×3＝π，排除A ；几何体如果是正四棱锥，底面是正方形边长为2，高为3，几何体的体积为13×22×3＝4，排除C ；几何体如果是三棱锥，底面是等腰三角形，底边长为2，三角形的高为2，三棱锥的高为3，几何体的体积为13×12×2×2×3＝2，排除B ，故选D.答案：D8．某四棱锥的三视图如图所示，某侧视图是等腰直角三角形，俯视图轮廓是直角梯形，则该四棱锥的各侧面中，面积的最大值为( )A ．8B ．4 5C ．8 2D ．12 2解析： 因为三视图复原的几何体是四棱锥，顶点在底面的射影是直角梯形的一个顶点，后面是等腰直角三角形，直角边为4，所以后面的三角形的面积为12×4×4＝8, 右面三角形是直角三角形，直角边长为42，4，三角形的面积为12×42×4＝8 2.前面三角形BC 边长为6，高为42，其面积为12×42×6＝122，左面也是直角三角形，直角边长为4，25，三角形的面积为12×4×25＝45，四棱锥的四个侧面中面积最大的是前面三角形的面积12 2.故选D. 答案：D9．(2019·宁德质检)直三棱柱ABC ­A ′B ′C ′的所有棱长均为23，则此三棱柱的外接球的表面积为( ) A ．12π B ．16π C ．28πD ．36π解析：由直三棱柱的底面边长为23，得底面所在平面截其外接球所成的圆O 的半径r ＝2，又由直三棱柱的侧棱长为23，则球心到圆O 的球心距d ＝3， 根据球心距，截面圆半径，球半径构成直角三角形， 满足勾股定理，我们易得球半径R 满足：R 2＝r 2＋d 2＝7， ∴外接球的表面积S ＝4πR 2＝28π. 故选C. 答案：C10．(2019·蚌埠模拟)榫卯是我国古代工匠极为精巧的发明，广泛用于建筑．榫卯是在两个构件上采用凹凸部位相结合的一种连接方式．榫卯结构中凸出的部分叫榫(或叫榫头)．已知某“榫头”的三视图如图所示，则该“榫头”的体积是( )A ．48B ．50C ．54D ．63解析：由三视图可知，该几何体是由两个直棱柱组合而成，其直观图如图所示，故体积为3＋62×3×3＋3＋62×3×1＝54.故选C.答案：C11．如图，在矩形ABCD中，EF∥DA，GH∥BC，BC＝2，AF＝FG＝BG＝1，现分别沿EF，GH将矩形折叠使得AD与BC重合，则折叠后的几何体的外接球的表面积为( )A.8π3B.16π3C．6π D．24π解析：由题意得，折叠后的几何体为正三棱柱，且该三棱柱的底面边长为1，高为 2.如图所示的正三棱柱ABC­A1B1C1.设上下底面的中心分别为O 1，O 2，则球心O 为O 1，O 2的中点，连OC ，O 2C ， 则O 2C ＝23×⎝ ⎛⎭⎪⎫32×1＝33，OO 2＝1，∴OC ＝O 2C 2＋O 2O 2＝ ⎝ ⎛⎭⎪⎫33 2＋1＝233， 即球半径R ＝233，∴该几何体的外接球的表面积为S ＝4πR 2＝4π×43＝16π3.故选B. 答案：B12．若长方体ABCD ­A 1B 1C 1D 1的顶点都在体积为288π的球O 的球面上，则长方体ABCD ­A 1B 1C 1D 1的表面积的最大值等于( ) A ．576 B ．288 C ．144 D ．72答案：B 二、填空题13．若圆锥底面半径为1，侧面积为5π，则该圆锥的体积是________． 解析：设圆锥的母线长为l ，圆锥底面半径为1，侧面积为5π， ∴5π＝πl ，即l ＝5， ∴圆锥的高h ＝5－1＝2，∴该圆锥的体积是V ＝13πr 2h ＝13π×2＝23π.314．(2019·长春质检)一个倒置圆锥形容器，底面直径与母线长相等，容器内存有部分水，向容器内放入一个半径为1的铁球，铁球恰好完全没入水中(水面与铁球相切)则容器内水的体积为________．解析：如图所示，作出轴截面，由题意，圆锥的底面直径与母线长相等，可得AP ＝AB ，则AP ＝2AC ，所以∠APC ＝30°，记铁球的半径为r ，即OC ＝OD ＝r ＝1，在△ODP 中，sin ∠OPD ＝OD OP ＝12，则OP ＝2r ＝2，所以PC ＝3r ＝3，因此AC ＝3r ＝3，PA ＝23r ＝23，所以铁球所在圆锥的体积为V 圆锥＝V 水＋V 铁球，即V 水＝V 圆锥－V 铁球＝13S 圆C ·PC －43πr 3＝13π(3)2·3－43π＝53π.315.已知所有棱长都相等的三棱锥的各个顶点同在一个半径为3的球面上，则该三棱锥的表面积为________．解析：构造一个各棱长为a 的正方体，连接各面的对角线可作出一个正四面体， 而此四面体的外接球即为正方体的外接球． 此球的直径为正方体的体对角线，即23，由勾股定理得到3a 2＝12⇒a ＝2，三棱锥的边长即为正方体的面对角线长为：22， 所以该锥体表面积S ＝4×12×(22)2×32＝8 3.答案：8 316．(2019·洛阳、许昌质检)在直三棱柱ABC ­A 1B 1C 1中，∠ACB ＝90°，AC ＝2，BC ＝CC 1＝2，P 是BC 1上一动点，则A 1P ＋PC 的最小值为________．解析：连接A 1B ，沿BC 1将△CBC 1展开与△A 1BC 1在同一个平面内(图略)， 在BC 1上取一点与A 1C 构成三角形， ∵三角形两边和大于第三边，∴A 1P ＋PC 的最小值是A 1C 的连线．作展开图，如图，由∠ACB ＝90°，AC ＝2，BC ＝CC 1＝2， 得AB ＝AC 2＋BC 2＝6， 又AA 1＝CC 1＝2，∴A 1B ＝AA 21＋AB 2＝2＋6＝22，BC 1＝2＋2＝2，A 1C 1＝AC ＝2， ∴∠A 1BC 1＝45°，∠CBC 1＝45°，∴∠A 1BC ＝90°， ∴A 1C ＝A 1B 2＋BC 2＝8＋2＝10.答案：10增分强化练考点一 空间线、面位置关系的判断1．在长方体ABCD ­A 1B 1C 1D 1中，AB ＝AD ＝2，AA 1＝2，则异面直线AB 1与BC 1所成角的余弦值为( )A.23 B.56 C.33D.66解析：画出图形，如图所示．连接AD 1，B 1D 1，则AD 1∥BC 1，所以∠B 1AD 1即为AB 1与BC 1所成的角或其补角． 在B 1AD 1中，AB 1＝AD 1＝6，B 1D 1＝2， 所以由余弦定理得cos ∠B 1AD 1＝6＋6－42×6＝23，所以异面直线AB 1与BC 1所成角的余弦值为23.故选A. 答案：A2．(2019·宝鸡模拟)异面直线a ，b 所成的角为π3，直线a ⊥c ，则异面直线b 与c 所成角的范围为( ) A.⎣⎢⎡⎦⎥⎤π3，π2B.⎣⎢⎡⎦⎥⎤π6，π2C.⎣⎢⎡⎦⎥⎤π3，2π3D.⎣⎢⎡⎦⎥⎤π6，5π6解析：作b 的平行线b ′，交a 于O 点(图略)，所有与a 垂直的直线平移到O 点组成一个与直线a 垂直的平面α，O 点是直线a 与平面α的交点，在直线b ′上取一点P ，作垂线PP ′⊥平面α，交平面α于P ′，∠POP ′是b ′与面α的夹角为π6，在平面α中，所有与OP ′平行的直线与b ′的夹角都是π6，在平面α所有与OP ′垂直的线，由于PP ′垂直于平面α，所以该线垂直于PP ′，则该线垂直于平面OPP ′，所以该线垂直于b ′，故在平面α所有与OP ′垂直的线与b ′的夹角为π2，与OP ′夹角大于0，小于π2的线，与b ′的夹角为锐角且大于π6，故选B.答案：B3．在直三棱柱ABC ­A 1B 1C 1中，CA ＝CB ＝4，AB ＝27，CC 1＝25，E ，F 分别为AC ，CC 1的中点，则直线EF 与平面AA 1B 1B 所成的角是( ) A ．30° B ．45° C ．60°D ．90°解析：连接AC 1，则EF ∥AC 1，直线EF 与平面AA 1B 1B 所成的角，就是AC 1与平面AA 1B 1B 所成的角；作C 1D ⊥A 1B 1于D ，连接AD ，因为直三棱柱ABC ­A 1B 1C 1中，CA ＝CB ＝4，所以底面是等腰三角形，则C 1D ⊥平面AA 1B 1B ，可知∠C 1AD 就是直线EF 与平面AA 1B 1B 所成的角，CA ＝CB ＝4，AB ＝27，CC 1＝25，可得C 1D ＝42－(7)2＝3，AD ＝(7)2＋(25)2＝33， 所以tan ∠C 1AD ＝C 1D AD ＝33， 所以∠C 1AD ＝30°. 故选A.答案：A考点二空间线面平行、垂直关系的证明1．(2019·晋城模拟)若a，b是不同的直线，α，β是不同的平面，则下列命题中正确的是( ) A．若a∥α，b∥β，a⊥b，则α⊥βB．若a∥α，b∥β，a∥b，则α∥βC．若a⊥α，b⊥β，a∥b，则α∥βD．若a∥α，b⊥β，a⊥b，则α∥β解析：A中若a∥α，b∥β，a⊥b，平面α，β可能垂直也可能平行或斜交；B中若a∥α，b∥β，a∥b，平面α，β可能平行也可能相交；C中若a⊥α，a∥b，b⊥α，又b⊥β，故α∥β，所以a∥b必有α∥β；D中若a∥α，b⊥β，a⊥b，平面α，β可能平行也可能相交．故选C.答案：C2．(2019·蚌埠模拟)如图，在以P为顶点，母线长为2的圆锥中，底面圆O的直径长为2，点C在圆O所在平面内，且AC是圆O的切线，BC交圆O于点D，连接PD，OD.(1)求证：PB ⊥平面PAC ；(2)若AC ＝233，求点O 到平面PBD 的距离．解析：(1)证明：因为AB 是圆O 的直径，AC 与圆O 切于点A ，所以AC ⊥AB . 又在圆锥中，PO 垂直底面圆O ，所以PO ⊥AC ，而PO ∩AB ＝O ， 所以AC ⊥平面PAB ，从而AC ⊥PB .在△PAB 中，PA 2＋PB 2＝AB 2，所以PA ⊥PB ，又PA ∩AC ＝A 所以PB ⊥平面PAC . (2)因为AB ＝2，AC ＝233，AC ⊥AB ，所以在直角△ABC 中，∠ABC ＝π6.又OD ＝OB ＝1＝PO ，则△OBD 是等腰三角形，所以BD ＝3，S △OBD ＝12×1×1×sin 2π3＝34.又PB ＝PD ＝2，所以S △PBD ＝12×3×52＝154，设点O 到平面PBD 的距离为d ，由V P ­OBD ＝V O ­PBD ， 即13S △OBD ·PO ＝13S △PBD ·d ，所以d ＝55. 考点三 空间中的翻折问题1．(2019·淮南模拟)正三角形ABC 的边长为a ，将它沿平行于BC 的线段PQ 折起(其中P 在边AB 上，Q 在AC 边上)，使平面APQ ⊥平面BPQC .D ，E 分别是PQ ，BC 的中点．(1)证明：PQ ⊥平面ADE ；(2)若折叠后，A ，B 两点间的距离为d ，求d 最小时，四棱锥A ­PBCQ 的体积． 解析：(1)证明：在△APQ 中，AP ＝AQ ，D 是PQ 的中点，所以AD ⊥PQ .又因为DE 是等腰梯形BPQC 的对称轴，所以DE ⊥PQ . 而AD ∩DE ＝D ，所以PQ ⊥平面ADE .(2)因为平面APQ ⊥平面BPQC ，AD ⊥PQ ，所以AD ⊥平面PBCQ ，连结BD ，则d 2＝AD 2＋BD 2. 设AD ＝x ，DE ＝32a －x (E 为BC 的中点)， 于是BD 2＝DE 2＋BE 2＝ ⎝⎛⎭⎪⎫32a －x 2＋14a 2. 因此d 2＝x 2＋BD 2＝x 2＋DE 2＋BE 2＝x 2＋⎝⎛⎭⎪⎫32a －x 2＋14a 2＝2⎝⎛⎭⎪⎫x －34a 2＋58a 2，当x＝34a时，d min＝104a.此时四棱锥A­PBCQ的体积为13×S梯形PBCQ×AD＝13×12⎝⎛⎭⎪⎫a2＋a×34a×34a＝364a3.2．如图1，在菱形ABCD中，AB＝2，∠DAB＝60°，M是AD的中点，以BM为折痕，将△ABM 折起，使点A到达点A1的位置，且平面A1BM⊥平面BCDM，如图2.(1)求证：A1M⊥BD；(2)若K为A1C的中点，求四面体M­A1BK的体积．解析：(1)证明：在图1中，∵四边形ABCD是菱形，∠DAB＝60°，M是AD的中点，∴AD⊥BM，故在图2中，BM⊥A1M，∵平面A1BM⊥平面BCDM，平面A1BM∩平面BCDM＝BM，∴A1M⊥平面BCDM，又BD⊂平面BCDM，∴A1M⊥BD.图1 图2(2)在图1中，∵ABCD 是菱形，AD ⊥BM ，AD ∥BC ，∴BM ⊥BC ，且BM ＝3， 在图2中，连接CM ，则VA 1－BCM ＝13S △BCM ·A 1M ＝13×12×2×3×1＝33，∵K 是A 1C 的中点，∴VM ­A 1BK ＝VK ­MA 1B ＝12VC ­MA 1B ＝12VA 1­BCM ＝36.增分强化练考点一 空间几何体的三视图1．日晷是中国古代利用日影测得时刻的一种计时工具，又称“日规”．通常由铜制的指针和石制的圆盘组成，铜制的指针叫做“晷针”，垂直地穿过圆盘中心，石制的脚盘叫做“晷面”，它放在石台上，其原理就是利用太阳的投影方向来测定并划分时刻．利用日晷计时的方法是人类在天文计时领域的重大发明，这项发明被人类沿用达几千年之久，下图是一位游客在故宫中拍到的一个日晷照片，假设相机镜头正对的方向为正方向，则根据图片判断此日晷的侧(左)视图可能为( )解析：因为相机镜头正对的方向为正方向，所以侧视图中圆盘为椭圆，又晷针斜向下穿盘而过，故其投影为下虚上实，故选D.答案：D2．“牟合方盖”是我国古代数学家刘徽在探求球体体积时构造的一个封闭几何体，它由完全相同的四个曲面构成，其直观图如图(其中四边形是为体现直观性而作的辅助线)．当“牟合方盖”的正视图和侧视图完全相同时，其俯视图为( )解析：∵相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖)．∴其正视图和侧视图是一个圆，俯视图是从上向下看，相对的两个曲面在同一个圆柱的侧面上，∴俯视图是有2条对角线且为实线的正方形，故选B.答案：B3．(2019·青岛模拟)某四棱锥的三视图如图所示，则该四棱锥的侧面为等腰直角三角形的个数为( )A．1 B．2C．3 D．4解析：由三视图可得直观图如图所示：由三视图可知：PD ⊥平面ABCD ， ∴PD ⊥AD ，PD ⊥DC ，PD ⊥AB ， 又PD ＝AD ＝2，PD ＝DC ＝2，∴△PAD 和△PDC 为等腰直角三角形． 又PD ⊥AB ，AD ⊥AB ， ∴AB ⊥平面PAD ， ∴AB ⊥PA ，又AB ＝1，PA ＝4＋4＝22， ∴ΔPAB 不是等腰直角三角形．∵PB ＝12＋22＋22＝3，BC ＝12＋22＝5，PC ＝22＋22＝22， ∴△PBC 不是等腰直角三角形，综上所述，侧面为等腰直角三角形的共有2个． 故选B. 答案：B考点二 空间几何体的表面积与体积1．用半径为3 cm ，圆心角为2π3的扇形纸片卷成一个圆锥筒，则这个圆锥筒的高为( )A ．1 cmB ．2 2 cm C. 2 cmD ．2 cm解析：设圆锥的底面半径为r cm ，由题意底面圆的周长即扇形的弧长，可得2πr ＝2π3×3，即底面圆的半径为1，所以圆锥的高h ＝32－1＝22，故选B. 答案：B2．(2019·中卫模拟)一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为( )A.16π3B.8π3C ．4 3D ．23π解析：由已知几何体的正视图是一个正三角形，侧视图和俯视图均为三角形，可得该几何体是有一个侧面PAC 垂直于底面，高为3，底面是一个等腰直角三角形的三棱锥，如图．则这个几何体的外接球的球心O 在高线PD 上，且是正三角形PAC 的中心，这个几何体的外接球的半径R ＝23PD ＝233.则这个几何体的外接球的表面积为S ＝4πR 2＝4π×⎝ ⎛⎭⎪⎫2332＝16π3.故选A. 答案：A3．某几何体的三视图如图所示，则该几何体的体积为( )A ．6＋3π2B ．6＋3πC ．2＋3π2D ．2＋3π解析：由题意，根据给定的三视图可知，该几何体左边表示一个底面为腰长为2的等腰直角三角形，高为3的直三棱柱，右边表示一个底面为半径为1的半圆，母线长为3的半圆柱，所以该几何体的体积为V ＝12×2×2×3＋12π×12×3＝6＋3π2，故选A.答案：A4．(2019·泰安模拟)如图，已知正方体ABCD ­A 1B 1C 1D 1的棱长为1，点P 为棱AA 1上任意一点，则四棱锥P ­BDD 1B 1的体积为________．解析：连结AC 交BD 于O (图略)，则有AO ⊥平面BDD 1B 1，。

立体几何（文）【考纲解读】1.掌握平面的基本性质 ( 三个公理、三个推论 ) ，理解确定平面的条件；会用字母、集合语言表示点、直线、平面间的关系 .2. 理解线线、线面平行的定义; 熟练掌握线线、线面及面面平行的判定和性质; 会运用线线、线面及面面平行的判定和性质进行推理和证明.3．能画出简单空间图形( 长方体、球、圆柱、圆锥、棱柱等简易组合三视图所表示的立体模型, 会画它们的直观图.) 的三视图, 能识别上述4．理解空间中线线、线面垂直定义及分类；理解空间中线线、线面、面面垂直的有关定理及性质；会运用线面平行与垂直的判定与性质定理进行证明和推理.5．认识柱、锥、台、球及简单几何体的结构特征, 并运用这些特征描述简单物体的结构; 了解柱、锥、台、球的表面积与体积的计算公式( 不要求记忆 ).【考点预测】1.对于空间几何体中点、线、面的位置关系及平行与垂直的性质和判定，高考中常在选择题中加以考查 . 解答题主要考查空间几体的点、线、面的位置关系的证明及探索存在性问题，着重考查学生的空间想象能力、推理论证能力，运用图形语言进行交流的能力及几何直观能力，难度中等 . 明年高考将仍以平行与垂直关系的证明探究为重点 , 注意命题题型的多样化、新颖化，如开放性、探索存在性题型 .2.三视图与直观图、空间几何体的表面积与体积，考查了学生通过直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及性质的基本能力，是每年高考必考内容，明年高考仍以三视图，空间几何体的表面积与体积为重点，在客观题中加以考查，其中表面积与体积也可能在解答题题后一问中出现。

【要点梳理】1.三视图：正俯视图长对正、正侧视图高平齐、俯侧视图宽相等.2.直观图 : 已知图形中平行于 x 轴和 z 轴的线段 , 在直观图中保持长度不变, 平行于 y 轴的线段平行性不变, 但在直观图中其长度为原来的一半.3.体积与表面积公式 :(1) 柱体的体积公式 : V柱Sh;锥体的体积公式:V锥1Sh;1h(S 34台体的体积公式 : V棱台SS S ) ;球的体积公式:V球r 3.33(2) 球的表面积公式 :S球4R2.4. 有关球与正方体、长方体、圆柱、圆锥、圆台的结合体问题，要抓住球的直径与这些几何体的有关元素的关系 .5. 平行与垂直关系的证明, 熟练判定与性质定理.【考点在线】考点一三视图例1. （ 2020 年高考海南卷文科第 8 题）在一个几何体的三视图中，正视图和俯视图如右图，则相应的侧视图可以为（）【答案】 D【解析】由主视图和府视图可知，原几何体是由后面是半个圆锥，前面是三棱锥的组合体，所以，左视图是 D.【名师点睛】本题考查三视图的基础知识.【备考提示】三视图是高考的热点之一 , 年年必考 , 所以必须熟练立体几何中的有关定理是解答好本题的关键 .练习 1:（2020年高考江西卷文科9) 将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（）【答案】 D【解析】左视图即是从正左方看，找特殊位置的可视点，连起来就可以得到答案.考点二表面积与体积例 2. . (2020 年高考安徽卷文科8) 一个空间几何体得三视图如图所示，则该几何体的表面积为( )【解析】 由三视图可知几何体是底面是等腰梯形的直棱柱 . 底面等腰梯形的上底为 2，下底为4 ， 高 为 4 ， 两 底 面 积 和 为 212 44 24 ， 四 个 侧 面 的 面 积 为24 4 2 2 17 24 8 17 ，所以几何体的表面积为 48 8 17 . 故选 C.【名师点睛】 本题考查三视图的识别以及空间多面体表面积的求法.【备考提示】： 表面积与体积的求解也是高考的热点之一，年年必考，大多以三视图为载体，在选择与填空题中考查，难度不大，也可能在解答题的一个问号上.练习 2：（2020 年高考湖南卷文科4) 设图１是某几何体的三视图，则3该几何体的体积为 ()A ． 9 42Ｂ． 3618 2Ｃ．912Ｄ．9 1822【答案】 D【解析】 有三视图可知该几何体是一个长方体和球构成的组合体，其体积 V4 （ 3 339 18 .32）+3 2=2考点三 球的组合体例 3.（ 2020 年高考辽宁卷文科 10) 己知球的直径 SC=4，A ， B 是该球球面上的两点． AB=2,ASC 45o , 则棱锥 SABC 的体积为 ( )(A)3(B)2 3(C)4 3 5 3(D)3正视图侧视图俯视图图 13 3 33【答案】 C【解析】取 SC的中点 D, 则 D为球心，则AD=BD=DS=2。

第2讲 综合大题部分1．(2018·高考全国卷Ⅱ)如图，在三棱锥P ­ABC 中，AB ＝BC ＝22，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且MC ＝2MB ，求点C 到平面POM 的距离．解析：(1)证明：因为AP ＝CP ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝2 3.如图，连接OB .因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形， 且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知，OP ⊥OB .由OP ⊥OB ，OP ⊥AC 知，PO ⊥平面ABC .(2)如图，作CH ⊥OM ，垂足为H ，又由(1)可得OP ⊥CH ，所以CH ⊥平面POM .故CH 的长为点C 到平面POM 的距离．由题设可知OC ＝12AC ＝2，CM ＝23BC ＝423，∠ACB ＝45°， 所以OM ＝253，CH ＝OC ·MC ·sin∠ACB OM ＝455. 所以点C 到平面POM 的距离为455. 2．(2018·高考全国卷Ⅲ)如图，矩形ABCD 所在平面与半圆弧所在平面垂直，M 是上异于C ，D 的点． (1)证明：平面AMD ⊥平面BMC .(2)在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．解析：(1)证明：由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM .因为M 为上异于C ，D 的点，且DC 为直径， 所以DM ⊥CM .又BC ∩CM ＝C ，所以DM ⊥平面BMC .而DM ⊂平面AMD ，故平面AMD ⊥平面BMC .(2)当P 为AM 的中点时，MC ∥平面PBD .证明如下：连接AC 交BD 于O .因为ABCD 为矩形，所以O为AC 中点．连接OP ，因为P 为AM 中点，所以MC ∥OP .又MC ⊄平面PBD ，OP ⊂平面PBD ，所以MC ∥平面PBD .3．(2018·高考全国卷Ⅰ)如图，在平行四边形ABCM 中，AB ＝AC ＝3，∠ACM ＝90°.以AC 为折痕将△ACM 折起，使点M 到达点D 的位置，且AB ⊥DA .(1)证明：平面ACD ⊥平面ABC ；(2)Q 为线段AD 上一点，P 为线段BC 上一点，且BP ＝DQ ＝23DA ，求三棱锥Q ­ABP 的体积．解析：(1)证明：由已知可得，∠BAC ＝90°，即BA ⊥AC .又BA ⊥AD ，所以AB ⊥平面ACD .又AB ⊂平面ABC ，所以平面ACD ⊥平面ABC .(2)由已知可得，DC ＝CM ＝AB ＝3，DA ＝3 2.又BP ＝DQ ＝23DA ， 所以BP ＝2 2.如图，过点Q 作QE ⊥AC ，垂足为E ，则QE 綊13DC .由已知及(1)可得，DC ⊥平面ABC ，所以QE ⊥平面ABC ，QE ＝1.因此，三棱锥Q ­ABP 的体积为V Q ­ABP ＝13×S △ABP ×QE ＝13×12×3×22sin 45°×1＝1.4．如图，在多面体ABCPE 中，平面PAC ⊥平面ABC ，AC ⊥BC ，PE ∥BC,2PE ＝BC ，M 是线段AE 的中点，N 是线段PA 上一点，且满足AN ＝λAP (0<λ<1)．(1)若λ＝12，求证：MN ⊥PC ； (2)是否存在λ，使得三棱锥M ­ACN 与三棱锥B ­ACP 的体积比为1∶12？若存在，求出λ的值；若不存在，请说明理由．解析：(1)证明：若λ＝12，则N 是线段PA 的中点． 因为平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，AC ⊥BC ，BC ⊂平面ABC ，所以BC ⊥平面PAC .因为M 是线段AE 的中点，N 是线段PA 的中点，所以MN ∥PE ，又PE ∥BC ，所以MN ∥BC ，所以MN ⊥平面PAC .因为PC ⊂平面PAC ，所以MN ⊥PC .(2)存在λ＝13，使得三棱锥M ­ACN 与三棱锥B ­ACP 的体积比为1∶12. 理由如下：由(1)知，BC ⊥平面PAC ，所以三棱锥B ­ACP 的体积V B ­ACP ＝13S △ACP ·BC ， 因为M 是线段AE 的中点，所以点M 到平面ACP 的距离等于点E 到平面ACP 的距离的一半，因为AN ＝λAP (0<λ<1)，所以S △ACN ＝λS △ACP ，又2PE ＝BC ，所以三棱锥M ­ACN 的体积V M ­ACN ＝13S △ACN ·(12PE )＝13λS △ACP ·(14BC )＝112λS △ACP ·BC .因为三棱锥M ­ACN 与三棱锥B ­ACP 的体积比为1∶12，所以112λS △ACP ·BC 13S △ACP ·BC ＝112，解得λ＝13.精美句子1、善思则能“从无字句处读书”。

第2讲 综合大题部分1. (2018·高考天津卷)如图，在四面体ABCD 中，△ABC 是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，AB ＝2，AD ＝23，∠BAD ＝90°. (1)求证：AD ⊥BC ；(2)求异面直线BC 与MD 所成角的余弦值； (3)求直线CD 与平面ABD 所成角的正弦值．解析：(1)证明：由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD ＝AB ，AD ⊥AB ，可得AD ⊥平面ABC ，故AD ⊥BC .(2)如图，取棱AC 的中点N ，连接MN ，ND . 又因为M 为棱AB 的中点，所以MN ∥BC .所以∠DMN (或其补角)为异面直线BC 与MD 所成的角． 在Rt △DAM 中，AM ＝1，故DM ＝AD 2＋AM 2＝13. 因为AD ⊥平面ABC ，所以AD ⊥AC . 在Rt △DAN 中，AN ＝1， 故DN ＝AD 2＋AN 2＝13. 在等腰三角形DMN 中，MN ＝1， 可得cos ∠DMN ＝12MN DM ＝1326.所以，异面直线BC 与MD 所成角的余弦值为1326. (3)如图，连接CM .因为△ABC 为等边三角形，M 为边AB 的中点，所以CM ⊥AB ，CM ＝ 3. 又因为平面ABC ⊥平面ABD ， 平面ABC ∩平面ABD ＝AB ，而CM ⊂平面ABC ，故CM ⊥平面ABD ， 所以∠CDM 为直线CD 与平面ABD 所成的角． 在Rt △CAD 中，CD ＝AC 2＋AD 2＝4. 在Rt △CMD 中，sin ∠CDM ＝CM CD ＝34. 所以，直线CD 与平面ABD 所成角的正弦值为34.2．(2018·高考北京卷)如图，在四棱锥P ­ABCD 中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA ＝PD ，E ，F 分别为AD ，PB 的中点．(1)求证：PE ⊥BC ；(2)求证：平面PAB ⊥平面PCD ； (3)求证：EF ∥平面PCD .证明：(1)因为PA ＝PD ，E 为AD 的中点， 所以PE ⊥AD .因为底面ABCD 为矩形， 所以BC ∥AD ，所以PE ⊥BC . (2)因为底面ABCD 为矩形， 所以AB ⊥AD .又因为平面PAD ⊥平面ABCD ， 所以AB ⊥平面PAD ， 所以AB ⊥PD . 又因为PA ⊥PD ， 所以PD ⊥平面PAB . 所以平面PAB ⊥平面PCD .(3)如图，取PC 的中点G ，连接FG ，DG .因为F ，G 分别为PB ，PC 的中点， 所以FG ∥BC ，FG ＝12BC .因为四边形ABCD 为矩形，且E 为AD 的中点， 所以DE ∥BC ，DE ＝12BC .所以DE ∥FG ，DE ＝FG .所以四边形DEFG 为平行四边形． 所以EF ∥DG .又因为EF ⊄平面PCD ，DG ⊂平面PCD ， 所以EF ∥平面PCD .3．(2017·高考全国卷Ⅰ)如图，在四棱锥P ­ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面PAB ⊥平面PAD ；(2)若PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ­ABCD 的体积为83，求该四棱锥的侧面积．解析：(1)证明：由∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD . 由于AB ∥CD ，故AB ⊥PD ， 又AP ∩PD ＝P ，从而AB ⊥平面PAD . 又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD . (2)如图所示，在平面PAD 内作PE ⊥AD ，垂足为E .由(1)知，AB ⊥平面PAD ，故AB ⊥PE ，可得PE ⊥平面ABCD . 设AB ＝x ，则由已知可得AD ＝2x ，PE ＝22x . 故四棱锥P ­ABCD 的体积V P ­ABCD ＝13AB ·AD ·PE ＝13x 3.由题设得13x 3＝83，故x ＝2.从而PA ＝PD ＝2，AD ＝BC ＝22，PB ＝PC ＝2 2.可得四棱锥P ­ABCD 的侧面积为12PA ·PD ＋12PA ·AB ＋12PD ·DC ＋12BC 2sin 60°＝6＋2 3.4. (2017·高考全国卷Ⅱ)如图，四棱锥P ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面PAD ；(2)若△PCD 的面积为27，求四棱锥P ABCD 的体积．解析：(1)证明：在平面ABCD 内，因为∠BAD ＝∠ABC ＝90°，所以BC ∥AD . 又BC ⊄平面PAD ，AD ⊂平面PAD ， 故BC ∥平面PAD .(2)如图，取AD 的中点M ，连接PM ，CM .由AB ＝BC ＝12AD 及BC ∥AD ， ∠ABC ＝90°得四边形ABCM 为正方形，则CM ⊥AD .因为侧面PAD 为等边三角形且垂直于底面ABCD ， 平面PAD ∩平面ABCD ＝AD ，所以PM ⊥AD ，PM ⊥底面ABCD . 因为CM ⊂底面ABCD ，所以PM ⊥CM . 设BC ＝x ，则CM ＝x ，CD ＝2x ，PM ＝3x ，PC ＝PD ＝2x . 如图，取CD 的中点N ，连接PN ，则PN ⊥CD ，所以PN ＝142x . 因为△PCD 的面积为27， 所以12×2x ×142x ＝27，解得x ＝－2(舍去)或x ＝2. 于是AB ＝BC ＝2，AD ＝4，PM ＝2 3. 所以四棱锥P ABCD 的体积V ＝13×＋2×23＝4 3.1. 在多面体ABCDEF 中，底面ABCD 是梯形，四边形ADEF 是正方形，AB ∥DC ，AB ＝AD ＝1，CD ＝2，AC ＝EC ＝ 5.(1)求证：平面EBC ⊥平面EBD ；(2)设M 为线段EC 上一点，且3EM ＝EC ，试问在线段BC 上是否存在一点T ，使得MT ∥平面BDE ，若存在，试指出点T 的位置；若不存在，请说明理由． 解析：(1)证明：∵EC ＝5，CD ＝2，ED ＝1. ∴EC 2＝CD 2＋ED 2，∴ED ⊥DC .又四边形ADEF 是正方形，所以AD ⊥DE ， 又AD ∩DC ＝D ， 所以ED ⊥平面ABCD .又BC ⊂平面ABCD ，所以ED ⊥BC .在梯形ABCD 中，过点B 作BH ⊥CD 于点H ，故四边形ABHD 是正方形，所以∠ADB ＝45°，BD ＝ 2. 在Rt △BCH 中，BH ＝CH ＝1，所以BC ＝2， 故BD 2＋BC 2＝DC 2，所以BC ⊥BD .因为BD ∩ED ＝D ，BD ⊂平面EBD ，ED ⊂平面EBD ， 所以BC ⊥平面EBD ，又BC ⊂平面EBC ，所以平面EBC ⊥平面EBD .(2)在线段BC 上存在一点T ，使得MT ∥平面BDE ，此时3BT ＝BC .连接MT ，在△EBC 中，因为BT BC ＝EM EC ＝13，所以MT ∥EB .又MT ⊄平面BDE ，EB ⊂平面BDE ，所以MT ∥平面BDE .2．如图①，正方形ABCD 的边长为4，AB ＝AE ＝BF ＝12EF ，AB ∥EF ，把四边形ABCD 沿AB 折起，使得AD ⊥底面AEFB ，G 是EF 的中点，如图②.图① 图②(1)求证：DE ∥平面AGC ； (2)求证：AG ⊥平面BCE . 证明：(1)由已知AB ∥DC ∥EF ， 又AB ＝DC ＝12EF ，G 是EF 的中点，所以CD 綊EG ，所以四边形DCGE 是平行四边形， 所以DE ∥CG .因为DE ⊄平面AGC ，CG ⊂平面AGC ， 所以DE ∥平面AGC . (2)连接BG (图略)，因为BC ∥AD ，AD ⊥底面AEFB ，所以BC ⊥底面AEFB ，又AG ⊂底面AEFB ， 所以BC ⊥AG .因为AB 綊EG ，AB ＝AE .所以四边形ABGE 为菱形，所以AG ⊥BE . 又BC ∩BE ＝B ，BE ⊂平面BCE ，BC ⊂平面BCE ， 所以AG ⊥平面BCE .3. 如图，在直三棱柱ADF ­BCE 中，AB ＝BC ＝BE ＝2，CE ＝2 2. (1)求证：AC ⊥平面BDE ；(2)若点K 在线段BE 上，且EK ＝23，求三棱锥K ­BDF 的体积．解析：(1)证明：在直三棱柱ADF ­BCE 中，AB ⊥平面BCE ，所以AB ⊥BE ，AB ⊥BC .又AB ＝BC ＝BE ＝2，CE ＝22，所以BC 2＋BE 2＝CE 2，且AC ⊥BD ，所以BE ⊥BC . 因为AB ∩BC ＝B ，所以BE ⊥平面ABCD . 因为AC ⊂平面ABCD ，所以BE ⊥AC . 因为BD ∩BE ＝B ，所以AC ⊥平面BDE . (2)由(1)可得，AD ⊥平面ABEF ， 因为AB ＝BC ＝BE ＝2，EK ＝23，所以S △KBF ＝12×⎝ ⎛⎭⎪⎫2－23×2＝43，所以V K ­BDF ＝V D ­KBF ＝13S △KBF ×DA ＝13×43×2＝89.4．如图，在四棱锥P ABCD 中，底面ABCD 是菱形，PA ＝PD ，∠BAD ＝60°，E 是AD 的中点，点Q 在侧棱PC 上．(1)求证：AD ⊥平面PBE ；(2)若Q 是PC 的中点，求证：PA ∥平面BDQ ； (3)若V PBCDE＝2V QABCD，试求CPCQ的值． 解析：(1)证明：由E 是AD 的中点，PA ＝PD 可得AD ⊥PE .又底面ABCD 是菱形，∠BAD ＝60°，所以AB ＝BD ，又E 是AD 的中点，所以AD ⊥BE ， 又PE ∩BE ＝E ，所以AD ⊥平面PBE . (2)证明：连接AC ，交BD 于点O ，连接OQ .因为O 是AC 的中点，Q 是PC 的中点， 所以OQ ∥PA ，又PA ⊄平面BDQ ，OQ ⊂平面BDQ ， 所以PA ∥平面BDQ .(3)设四棱锥P BCDE ，Q ABCD 的高分别为h 1，h 2. 所以V PBCDE＝13S 四边形BCDE h 1， V QABCD＝13S 四边形ABCD h 2. 又V P BCDE＝2V QABCD，且S 四边形BCDE ＝34S 四边形ABCD ，所以CP CQ ＝h 1h 2＝83.。

（文数）解答题强化专练——立体几何一、解答题（本大题共10小题，共120.0分）1.如图，在三棱锥S-ABC中，SA=SC，AB⊥AC，D为BC的中点，E为AC上一点，且DE∥平面SAB．求证：（1）直线AB∥平面SDE；（2）平面ABC⊥平面SDE．2.如图，在四棱锥P-ABCD的底面ABCD为矩形，点P在底面ABCD的射影O落在AD上．（1）求证：平面PAB⊥平面PAD；（2）若O、M分别是AD、PB的中点，且求三棱锥M-PDC的体积．3.如图所示，正方形ABCD与直角梯形ADEF所在平面互相垂直，∠ADE=90°，AF∥DE，DE=DA=2AF=2．（1）求证：AC∥平面BEF；（2）求四面体BDEF的体积．4.如图，将边长为2的正六边形ABDEF沿对角线BE翻折，连接AC、FD，形成如图所示的多面体，且AC=．（1）证明：平面ABEF⊥平面BCDE；（2）求三棱锥E-ABC的体积．5.如图，在矩形ABCD中，AB=2，BC=3，点E是边AD上的一点，且AE=2ED，点H是BE的中点，将△ABE沿着BE折起，使点A运动到点S处，且有SC=SD．（1）证明：SH⊥平面BCDE．（2）求四棱锥S-BCDE的体积．6.如图，已知多面体PABCDE的底面ABCD是边长为2的菱形，PA⊥底面ABCD，ED∥PA，且PA＝2ED＝2．(1)证明：平面PAC⊥平面PCE；(2)若∠ABC＝60°，求三棱锥P﹣ACE的体积．7.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA=PD，AB=AD，∠BAD=60°（1）求证：AD⊥PB；（2）若AB=PA=2，PB=，求点C到平面PBD的距离．8.如图，在长方体ABCD-A1B1C1D1中，O是B1D1中点，若AB=BC=2，AA1=．（1）求证：平面AB1D1⊥平面CB1D1；（2）求点O到平面AB1C的距离．9.在四棱柱ABCD-A1B1C1D1中，底面ABCD为平行四边形，AA1⊥平面ABCD．AB=2AD=4，．（1）证明：平面D1BC⊥平面D1BD；（2）若直线D1B与底面ABCD所成角为，M，N，Q分别为BD，CD，D1D的中点，求三棱锥C-MNQ的体积．10.如图，多面体ABCDB1C1是正三棱柱ABC-A1B1C1沿平面DB1C1切除部分所得，BC=CC1=1，点D为AA1的中点．（1）求证：BC1⊥平面B1CD；（2）求点B1到平面BCD的距离．答案和解析1.【答案】证明：（1）因为DE∥平面SAB，DE⊂平面ABC，平面SAB∩平面ABC=AB，所以DE∥AB，因为DE⊂平面SDE，AB⊄平面SDE，所以AB∥平面SDE，（2）因为D为BC的中点，DE∥AB，所以E为AC的中点．又因为SA=SC，所以SE⊥AC，又AB⊥AC，DE∥AB，所以DE⊥AC，∵DE⊂平面SDE，SE⊂平面SDE，DE∩SE=E，所以AC⊥平面SDE，因为AC⊂平面ABC，所以平面ABC⊥平面SDE．【解析】本题考查了线面平行的性质与判定，面面垂直的判定，属于中档题．（1）由线面平行可得DE∥AB，故而AB∥平面SDE；（2）证得SE⊥AC，DE⊥AC可得AC⊥平面SDE，故而平面ABC⊥平面SDE．2.【答案】（1）证明：依题意，PO⊥平面ABCD，又AB⊂平面ABCD，所以PO⊥AB．又AD⊥AB，AD∩PO=O，所以AB⊥平面PAD．又AB⊂平面PAB，所以平面PAB⊥平面PAD．（2）因为PO⊥平面ABCD，O是AD的中点，所以△PAD是等腰三角形，又AD=2，，所以PO=1．因为M是PB的中点，所以M到平面PDC的距离等于点B到平面PDC距离的一半，连接BD，所以=．【解析】（1）根据PO⊥平面ABCD可得PO⊥AB，结合AB⊥AD可得AB⊥平面PAD，于是平面PAB⊥平面PAD；（2）计算PO，根据计算棱锥的体积．本题考查了面面垂直的判定，棱锥的体积计算，属于中档题．3.【答案】证明：（1）设AC∩BD=O，取BE中点G，连接FG，OG，所以，OG∥DE，且OG=DE．因为AF∥DE，DE=2AF，所以AF∥OG，且OG=AF，从而四边形AFGO是平行四边形，FG∥OA．因为FG⊂平面BEF，AO⊄平面BEF，所以AO∥平面BEF，即AC∥平面BEF．解：（2）因为平面ABCD⊥平面ADEF，AB⊥AD，所以AB⊥平面ADEF．因为AF∥DE，∠ADE=90°，DE=DA=2AF=2所以△DEF的面积为S△DEF=×ED×AD=2，所以四面体BDEF的体积V=•S△DEF×AB=【解析】（1）设正方形ABCD的中心为O，取BE中点G，连接FG，OG，由中位线定理，我们易得四边形AFGO是平行四边形，即FG∥OA，由直线与平面平行的判定定理即可得到AC∥平面BEF；（2）由已知中正方形ABCD与直角梯形ADEF所在平面互相垂直，∠ADE=90°，我们可以得到AB⊥平面ADEF，结合DE=DA=2AF=2．分别计算棱锥的底面面积和高，代入棱锥体积公式即可求出四面体BDEF的体积．本题考查的知识点是直线与平面平行的判定及棱锥的体积，（1）的关键是证明出FG∥OA，（2）的关键是得到AB⊥平面ADEF，即四面体BDEF的高为AB．4.【答案】（1）证明：正六边形ABCDEF中，连结AC、BE，交点为G，由边长为2的正六边形ABCDEF的性质得AC⊥BE，且AG=CG=，在多面体中，由AC=，得AG2+CG2=AC2，∴AG⊥GC，又GC∩BE=G，GC，BE⊂平面BCDE，∴AG⊥平面BCDE，又AG⊂平面ABEF，∴平面ABEF⊥平面BCDE．（2）解：连结AE，CE，则AG为三棱锥A-BCE的高，GC为△BCE的高，在正六边形ABCDEF中，BE=2AF=4，∴，∴V E-ABC=V A-BCE==2．【解析】（1）连结AC、BE，交点为G，由边长为2的正六边形ABCDEF的性质得AC⊥BE，且AG=CG=，由勾股定理得AG⊥GC，从而AG⊥平面BCDE，由此能证明平面ABEF⊥平面BCDE．（2）连结AE，CE，则AG为三棱锥A-BCE的高，GC为△BCE的高，利用V E-ABC=V A-BCE，能求出三棱锥E-ABC的体积．本小题主要考查空间线面关系、面面垂直的证明、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．5.【答案】（1）证明：取CD的中点M，连接HM，SM，由已知得AE=AB=2，所以SE=SB=2，又点H是BE的中点，所以SH⊥BE．因为SC=SD，点M是线段CD的中点，所以SM⊥CD．又因为HM∥BC，所以HM⊥CD，从而CD⊥平面SHM，所以CD⊥SH，又CD，BE不平行，所以SH⊥平面BCDE．（2）解：由（1）知，，底面BCDE的面积为，所以四棱锥S-BCDE的体积．【解析】（1）取CD的中点M，连接HM，SM，证明SH⊥BE．SM⊥CD．HM⊥CD，推出CD⊥平面SHM，即可证明SH⊥平面BCDE．（2）求出棱锥的底面面积与高，即可求解几何体的体积．本题考查直线与平面垂直的判定定理的应用，几何体的体积的求法，如果是考试，可以参考评分细则：（1）第（1）问中，不管用哪种方法，证出结论得（6分）；（2）第（2）问，计算出高，得（2分），算出底面积S=4，得（2分），正确算出四棱锥的体积本小问共得（6分）．6.【答案】（1）证明：连接BD，交AC于点O，设PC中点为F，连接OF，EF．∵O，F分别为AC，PC的中点，∴OF∥PA，且OF=，∵DE∥PA，且，∴OF∥DE，且OF=DE．∴四边形OFED为平行四边形，则OD∥EF，即BD∥EF，因为PA⊥平面ABCD，BD⊂平面ABCD，∴PA⊥BD，∵四边形ABCD是菱形，∴BD⊥AC，∵PA∩AC=A，∴BD⊥平面PAC，∵BD∥EF，∴EF⊥平面PAC，∵EF⊂平面PCE，∴平面PAC⊥平面PCE．（2）解：∵∠ABC=60°，∴ABC是等边三角形，可得AC=2．又∵PA⊥平面ABCD，AC⊂平面ABCD，∴PA⊥AC．∴，∵EF⊥平面PAC，∴EF是三棱锥E-PAC的高．∵，∴=．【解析】本题考查平面与平面垂直的判定，三棱锥体积的计算，考查空间想象能力与思维能力，是中档题．（1）连接BD，交AC于点O，设PC中点为F，由已知结合三角形中位线定理可得四边形OFED为平行四边形，则OD∥EF，即BD∥EF．再由PA⊥平面ABCD，可得PA⊥BD．又四边形ABCD是菱形，得BD⊥AC．由线面垂直的判定可得BD⊥平面PAC，则EF⊥平面PAC．进一步得到平面PAC⊥平面PCE．（2）由∠ABC=60°，可得△ABC是等边三角形，得AC=2．再由PA⊥平面ABCD，得PA⊥AC．求出三角形PAC的面积，证得EF是三棱锥E-PAC的高，即可求出结果.7.【答案】解：（1）证明：∵AB=AD，且∠BAD=60°∴△ABD是等边三角形设O是AD的中点，连接PO，BO，则BO⊥AD，∵△APD是等腰三角形∴PO⊥AD，∵PO∩BO=O，∴AD⊥平面PBO，∴AD⊥PB；（2）设PB中点为E，连接DE，∵AB=PA=2，PB=，∴AP=PD=AD=BD=2，OB=，DE=1，DE⊥BP，∴OP=BO=，OP2+OB2=PB2∴OP⊥OB，∵OP⊥AD，AD∩OB=O，∴OP⊥面ABCD，S△BCD=S△ABD=•OB•AD==，S△BDP=•DE•BP=×1×=，设点C到平面PBD的距离为h，∵V P-BCD=V C-BDP∴×OP×S△BCD=×h×S△BDP，即××=×h×，解得h=．【解析】（1）设O是AD的中点，连接PO，BO，通过证明AD⊥平面PBO，证出AD⊥PB；（2）利用等体积法，即可求点C到平面PAB的距离本题考查空间直线、平面位置关系的判断，考查点面距离的计算，考查空间想象能力、推理论证、计算、转化能力8.【答案】（1）证明：在长方体ABCD-A1B1C1D1中，∵AB=AD=2，AA1=，∴B1C=D1C，∵O为D1B1的中点，∴CO⊥B1D1，同理AO⊥B1D1，∴∠AOC就是平面AB1D1与平面CB1D1所成二面角的平面角．在三角形AOC中，可得AO=OC==2，∵AC=2，∴AO2+OC2=AC2，即OC⊥OA．∴∠AOC=90°．即平面AB1D1⊥平面CB1D1；（2）解：由（1）知，OB1⊥平面AOC，△AOC为直角三角形，且AO=OC=2．∴V=V，∴．∵，=2．∴d=1，∴点O到平面AB1C的距离为1．【解析】（1）在长方体ABCD-A1B1C1D1中，由已知证明CO⊥B1D1，∴∠AOC就是平面AB1D1与平面CB1D1所成二面角的平面角．求解三角形可得OC⊥OA即可；（2）由（1）知，OB1⊥平面AOC，△AOC为直角三角形，然后利用等积法即可求解．本题考查直线与平面垂直的判定，考查空间想象能力与思维能力，训练了利用等积法求距离，是中档题．9.【答案】证明：（1）∵D1D⊥平面ABCD，BC⊂平面ABCD，∴D1D⊥BC．又AB=4，AD=2，，∴，∵AD2+BD2=AB2，∴AD⊥BD．又∵AD∥BC，∴BC⊥BD．又∵D1D∩BD=D，BD⊂平面D1BD，D1D⊂平面D1BD，∴BC⊥平面D1BD，而BC⊂平面D1BC，∴平面D1BC⊥平面D1BD．解：（2）∵D1D⊥平面ABCD，∴∠D1BD即为直线D1B与底面ABCD所成的角，即，而，∴DD1=2．，∴三棱锥C-MNQ的体积．【解析】（1）推导出D1D⊥BC，AD⊥BD，BC⊥BD．从而BC⊥平面D1BD，由此能证明平面D1BC⊥平面D1BD．（2）由D1D⊥平面ABCD，得∠D1BD即为直线D1B与底面ABCD所成的角，即，由，能求出三棱锥C-MNQ的体积．本题考查面面垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．10.【答案】解：（1）设BC1与B1C交于点E，连接DE，∵多面体ABCDB1C1是正三棱柱ABC-A1B1C1沿平面DB1C1切除部分所得，BC=CC1=1．∴四边形BB1C1C是正方形，四边形CC1DA，ABB1D均为直角梯形，且AB⊥AD，AC⊥AD．∵点D为AA1的中点．AA1=BB1，AA1∥BB1．∴，DC1=，∴BD=C1D．，BC1⊥DE，又∵BC1⊥B1C，B1C∩DE=E，∴BC1⊥平面B1CD；（2）设点B1到平面BCD的距离为d．∵，点D到面BCC1B1的距离即为△ABC边BC上的高，即为．∴∵．∴，S=，∴．即点B1到平面BCD的距离为．【解析】（1）设BC1与B1C交于点E，连接DE，可得BD=C1D，BC1⊥DE，即可证明BC1⊥平面B1CD；（2）利用等体积法求点B1到平面BCD的距离．本题考查了线面垂直的证明、点到面的距离，属于中档题．。

增分强化练一、选择题1．直线(1－2a )x －2y ＋3＝0与直线3x ＋y ＋2a ＝0垂直，则实数a 的值为( ) A ．－52B.72C.56D.16解析：∵直线(1－2a )x －2y ＋3＝0与直线3x ＋y ＋2a ＝0垂直，∴3(1－2a )－2＝0，∴a ＝16，故选D. 答案：D2．过点(1，－1)且与直线x －2y ＋1＝0平行的直线方程为( ) A ．x －2y －1＝0 B ．x －2y ＋1＝0 C ．x －2y －3＝0D ．2x ＋y －1＝0解析：由题意得所求直线的斜率为12，又直线过点(1，－1)，故所求直线的方程为y ＋1＝12(x－1)，即x －2y －3＝0.故选C. 答案：C3．已知直线l 1：(3＋m )x ＋4y ＝5－3m ，l 2：2x ＋(5＋m )y ＝8平行，则实数m 的值为( ) A ．－7 B ．－1 C ．－1或－7D.133解析：当m ＝－3时，两条直线分别化为：2y ＝7，x ＋y ＝4，此时两条直线不平行；当m ＝－5时，两条直线分别化为：x －2y ＝10，x ＝4，此时两条直线不平行；当m ≠－3，－5时，两条直线分别化为：y ＝－3＋m 4x ＋5－3m 4，y ＝－25＋m x ＋85＋m ，∵两条直线平行，∴－3＋m 4＝－25＋m ，5－3m 4≠85＋m ，解得m ＝－7.综上可得：m ＝－7.故选A. 答案：A4．在直线3x －4y －27＝0上到点P (2,1)距离最近的点的坐标是( ) A ．(5，－3) B ．(9,0) C ．(－3,5)D ．(－5,3)解析：根据题意可知：所求点即为过P 点垂直于已知直线的直线与已知直线的交点，因为已知直线3x －4y －27＝0的斜率为34，所以过P 点垂直于已知直线的斜率为－43，又P (2,1)，则该直线的方程为：y －1＝－43(x －2)即4x ＋3y －11＝0，与已知直线联立得⎩⎪⎨⎪⎧4x ＋3y －11＝0 ①3x －4y －27＝0 ②①×4＋②×3得25x ＝125，解得x ＝5， 把x ＝5代入①解得y ＝－3，所以⎩⎪⎨⎪⎧x ＝5y ＝－3，所以直线3x －4y －27＝0上到点P (2,1)距离最近的点的坐标是(5，－3)． 故选A. 答案：A5．圆x 2＋y 2＝8与圆x 2＋y 2＋4x －16＝0的公共弦长为( ) A ．8 B ．4 C ．2D ．1解析：两圆方程作差得x ＝2，当x ＝2时，由x 2＋y 2＝8得y 2＝8－4＝4，即y ＝±2， 即两圆的交点坐标为A (2,2)，B (2，－2)， 则|AB |＝2－(－2)＝4， 故选B. 答案：B6．过点(2,1)的直线中被圆(x －1)2＋(y ＋2)2＝5截得的弦长最大的直线方程是( )A ．3x －y －5＝0B ．3x ＋y －7＝0C ．x ＋3y －5＝0D ．x －3y ＋5＝0解析：∵过点(2,1)的直线中被圆(x －1)2＋(y ＋2)2＝5截得的弦长最大的直线方程经过圆心， ∴其直线方程为过点(2,1)和圆心(1，－2)的直线， ∴其方程为：y ＋2x －1＝1＋22－1， 整理，得3x －y －5＝0. 故选A. 答案：A7．圆C ：x 2＋y 2－2x ＝0被直线y ＝3x 截得的线段长为( ) A ．2 B. 3 C ．1D. 2解析：圆C ：x 2＋y 2－2x ＝0的圆心为(1,0)，半径为1，圆心到直线y ＝3x 的距离为d ＝|3|(3)2＋1＝32，弦长为2·1－⎝⎛⎭⎪⎫322＝1，故选C. 答案：C8．已知直线l ：y ＝kx ＋1与圆O ：x 2＋y 2＝2相交于A ，B 两点，则 “k ＝1”是“∠AOB ＝120°”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：由题意得圆心(0,0)到直线l ：y ＝kx ＋1的距离为d ＝11＋k2，若∠AOB ＝120°，则有11＋k2＝2·12，该方程等价于k 2＝1即k ＝±1，若k ＝1时，则∠AOB ＝120°，但∠AOB ＝120°时，k ＝－1或k ＝1，故选A. 答案：A9．(2019·青岛模拟)已知圆C ：x 2＋y 2＝1和直线l ：y ＝k (x ＋2)，在(－3，3)上随机选取一个数k ，则事件“直线l 与圆C 相交”发生的概率为( ) A.15 B.14 C.13D.12解析：直线l 方程为kx －y ＋2k ＝0， 当直线l 与圆C 相切时可得|2k |k 2＋1＝1，解得k ＝±33，∴直线l 与圆C 相交时，k ∈⎝⎛⎭⎪⎫－33，33， ∴所求的概率P ＝23323＝13.故选C. 答案：C10．(2019·威海模拟)已知圆(x －2)2＋y 2＝1上的点到直线y ＝3x ＋b 的最短距离为3，则b 的值为( )A ．－2或2B ．2或43＋2C ．－2或43＋2D ．－43－2或2解析：由圆(x －2)2＋y 2＝1，可得圆心坐标为(2,0)，半径r ＝1，设圆心(2,0)到直线y ＝3x ＋b 的距离为d ，则d ＝|23＋b |3＋1，因为圆(x －2)2＋y 2＝1上的点到直线y ＝3x ＋b 的最短距离为3，所以d －r ＝3，即|23＋b |3＋1－1＝3，解得b ＝2或b ＝－43－2，故选D.答案：D11．圆C 1：(x －1)2＋(y －3)2＝9和C 2：x 2＋(y －2)2＝1，M ，N 分别是圆C 1，C 2上的点，P 是直线y ＝－1上的点，则|PM |＋|PN |的最小值是( ) A ．52－4 B.17－1 C ．6－2 2D.17解析：圆C 1关于y ＝－1的对称圆的圆心坐标A (1，－5)，半径为3，圆C 2的圆心坐标(0,2)，半径为1，由图象(图略)可知当P ，C 2，A ，三点共线时，|PM |＋|PN |取得最小值，|PM |＋|PN |的最小值为圆A 与圆C 2的圆心距减去两个圆的半径和，即|AC 2|－3－1＝1＋49－4＝52－4.故选A. 答案：A12．设过点P (－2,0)的直线l 与圆C ：x 2＋y 2－4x －2y ＋1＝0的两个交点为A ，B ，若8PA →＝5AB →，则|AB |＝( ) A.855 B.463 C.665D.453解析：由题意，设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为x ＝my －2，由⎩⎪⎨⎪⎧x 2＋y 2－4x －2y ＋1＝0x ＝my －2，得(m 2＋1)y 2－(8m ＋2)y ＋13＝0，则y 1＋y 2＝8m ＋2m 2＋1，y 1y 2＝13m 2＋1，又8PA →＝5AB →，所以8(x 1＋2，y 1)＝5(x 2－x 1，y 2－y 1)，故8y 1＝5(y 2－y 1)，即y 2＝135y 1，代入y 1y 2＝13m 2＋1得：y 21＝5m 2＋1，故y 22＝16925×5m 2＋1，又(y 1＋y 2)2＝⎝ ⎛⎭⎪⎫8m ＋2m 2＋12，即y 21＋y 22＋2y 1y 2＝19425×5m 2＋1＋26m 2＋1＝⎝ ⎛⎭⎪⎫8m ＋2m 2＋12，整理得：m 2－40m ＋76＝0，解得m ＝2或m ＝38，又|AB |＝1＋m 2·(y 1＋y 2)2－4y 1y 2＝23m 2＋8m －12m 2＋1，当m ＝2时，|AB |＝855；当m ＝38时，|AB |＝855.综上，|AB |＝855.故选A. 答案：A 二、填空题13．若直线(a ＋2)x ＋(1－a )y －3＝0与(a －1)x ＋(2a ＋3)y ＋2＝0互相垂直，则a 为________． 解析：∵直线(a ＋2)x ＋(1－a )y －3＝0与(a －1)x ＋(2a ＋3)y ＋2＝0互相垂直， ∴(a ＋2)(a －1)＋(1－a )(2a ＋3)＝0， ∴(a －1)(a ＋2－2a －3)＝0， ∴(a －1)(a ＋1)＝0， ∴a ＝1或a ＝－1. 答案：±114．已知圆C 与y 轴相切，圆心在x 轴的正半轴上，并且截直线x －y ＋1＝0所得的弦长为2，则圆C 的标准方程是________．解析：设圆心为(t,0)，且t >0, ∴半径为r ＝|t |＝t ，∵圆C 截直线x －y ＋1＝0所得的弦长为2,∴圆心到直线x －y ＋1＝0的距离d ＝|t －0＋1|2＝t 2－1，∴t 2－2t －3＝0， ∴t ＝3或t ＝－1(舍)， 故t ＝3， ∴(x －3)2＋y 2＝9. 答案：(x －3)2＋y 2＝915．已知圆x 2＋y 2＝9被直线mx ＋y －2m －1＝0所截得弦长为32，则实数m 的值为________． 解析：因为圆x 2＋y 2＝9的圆心是(0,0)，半径为3， 根据弦长为32，所以圆心到直线的距离为d ＝9－⎝⎛⎭⎪⎫3222＝322， 所以d ＝|－2m －1|m 2＋1＝322，解得m ＝1或m ＝7.答案：1或716．已知点P (－1,2)及圆(x －3)2＋(y －4)2＝4，一光线从点P 出发，经x 轴上一点Q 反射后与圆相切于点T ，则|PQ |＋|QT |的值为________． 解析：点P 关于x 轴的对称点为P ′(－1，－2)，由反射的对称性可知，P ′Q 与圆相切于点T ，|PQ |＋|QT |＝|P ′T |， ∵圆(x －3)2＋(y －4)2＝4的圆心坐标为A (3,4)，半径r ＝2， ∴|AP ′|2＝(－1－3)2＋(－2－4)2＝52， |AT |＝r ＝2，∴|PQ |＋|QT |＝|P ′T |＝|AP ′|2－|AT |2＝4 3. 答案：4 3增分强化练考点一 圆锥曲线的定义及标准方程1．(2019·榆林模拟)已知抛物线y 2＝2px (p >0)上的点M 到其焦点F 的距离比点M 到y 轴的距离大12，则抛物线的标准方程为( )A ．y 2＝x B ．y 2＝2x C ．y 2＝4xD ．y 2＝8x解析：由抛物线y 2＝2px (p ＞0)上的点M 到其焦点F 的距离比点M 到y 轴的距离大12，根据抛物线的定义可得p 2＝12，∴p ＝1，所以抛物线的标准方程为y 2＝2x .故选B.答案：B2．(2019·株洲模拟)已知双曲线C ：x 2a 2－y 2b 2＝1的一条渐近线l 的倾斜角为π3，且C 的一个焦点到l 的距离为3，则双曲线C 的方程为( ) A.x 212－y 24＝1 B.x 24－y 212＝1 C.x 23－y 2＝1 D ．x 2－y 23＝1解析：由x 2a 2－y 2b 2＝0可得y ＝±b a x ，即渐近线的方程为y ＝±bax ，又一条渐近线l 的倾斜角为π3， 所以b a ＝tan π3＝ 3.因为双曲线C 的一个焦点(c,0)到l 的距离为3， 所以|bc |a 2＋b 2＝b ＝3，所以a ＝1，所以双曲线的方程为x 2－y 23＝1.故选D. 答案：D3．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，且椭圆C 的长轴长与焦距之和为6，则椭圆C的标准方程为( ) A.4x 225＋y26＝1 B.x 24＋y 22＝1 C.x 22＋y 2＝1 D.x 24＋y 23＝1 解析：依题意椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12得c a ＝12，椭圆C 的长轴长与焦距之和为6,2a ＋2c ＝6， 解得a ＝2，c ＝1，则b ＝3，所以椭圆C 的标准方程为：x 24＋y 23＝1，故选D.答案：D4．设F 1，F 2是椭圆E ：x 225＋y 216＝1的左右焦点，P 是椭圆E 上的点，则|PF 1|·|PF 2|的最小值是________．解析：由椭圆方程可知a ＝5，c ＝3，根据椭圆的定义，有|PF 2|＝2a －|PF 1|＝10－|PF 1|，故|PF 1|·|PF 2|＝|PF 1|·(10－|PF 1|)，由于|PF 1|∈[a －c ，a ＋c ]＝[2,8]注意到二次函数y ＝x (10－x )的对称轴为x ＝5，故当x ＝2，x ＝8时，都是函数的最小值，即最小值为2×8＝16. 答案：16考点二 圆锥曲线的性质1．已知椭圆C ：16x 2＋4y 2＝1，则下列结论正确的是( ) A ．长轴长为12B ．焦距为34 C ．短轴长为14D ．离心率为32解析：由椭圆方程16x 2＋4y 2＝1化为标准方程可得x 2116＋y 214＝1 ，所以a ＝12，b ＝14，c ＝34，长轴为2a ＝1 ，焦距2c ＝32，短轴2b ＝12，离心率e ＝c a ＝32.故选D. 答案：D2．(2019·九江模拟)已知双曲线C ：x 2a 2－y 2b2＝1(a ，b >0)的右顶点A 和右焦点F 到一条渐近线的距离之比为1∶2，则C 的渐近线方程为( ) A ．y ＝±x B ．y ＝±2x C ．y ＝±2xD ．y ＝±3x解析：由双曲线方程可得渐近线为：y ＝±bax ，A (a,0)，F (c,0)， 则点A 到渐近线距离d 1＝|ab |a 2＋b2＝ab c， 点F 到渐近线距离d 2＝|bc |a 2＋b2＝bcc＝b ， ∴d 1∶d 2＝ab c∶b ＝a ∶c ＝1∶2，即c ＝2a ，则b a ＝c 2－a 2a ＝a a＝1， ∴双曲线渐近线方程为y ＝±x . 故选A. 答案：A3．已知双曲线C ：x 2－y 2＝1，则点(4,0)到C 的渐近线的距离为________．解析：双曲线C ：x 2－y 2＝1(a ＞b ＞0)的渐近线方程y ＝±x ，点(4,0)到C 的渐近线的距离为|±4|2＝2 2. 答案：2 24．(2019·株洲模拟)已知F 1，F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左右焦点，B 是短轴的一个端点，线段BF 2的延长线交椭圆C 于点D ，若△F 1BD 为等腰三角形，则椭圆C 的离心率为________． 解析：如图，不妨设点B 是椭圆短轴的上端点，则点D 在第四象限内，设点D (x ，y )． 由题意得△F 1BD 为等腰三角形，且|DF 1|＝|DB |.由椭圆的定义得|DF 1|＋|DF 2|＝2a ，|BF 1|＝|BF 2|＝a ， 又|DF 1|＝|DB |＝|DF 2|＋|BF 2|＝|DF 2|＋a ， ∴(|DF 2|＋a )＋|DF 2|＝2a ，解得|DF 2|＝a2.作DE ⊥x 轴于E ，则有|DE |＝|DF 2|sin ∠DF 2E ＝|DF 2|sin ∠BF 2O ＝a 2×b a ＝b2，|F 2E |＝|DF 2|cos ∠DF 2E ＝|DF 2|cos ∠BF 2O ＝a 2×c a ＝c 2，∴|OE |＝|OF 2|＋|F 2E |＝c ＋c 2＝3c2，∴点D 的坐标为⎝⎛⎭⎪⎫3c 2，－b 2.又点D 在椭圆上，∴⎝ ⎛⎭⎪⎫3c 22a2＋⎝ ⎛⎭⎪⎫－b 22b2＝1，整理得3c 2＝a 2，所以e ＝c a ＝33. 答案：33考点三 直线与圆锥曲线的相关问题1．(2019·内江模拟)设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左右焦点分别为F 1、F 2，上下顶点分别为A 、B ，直线AF 2与该椭圆交于A 、M 两点．若∠F 1AF 2＝120°，则直线BM 的斜率为( )A.14B.34C.32D. 3解析：由题意，椭圆x 2a 2＋y 2b2＝1(a >b >0)，且满足∠F 1AF 2＝120°，如图所示，则在△AF 2O 中，|OA |＝b ，|AF 2|＝a ，且∠OAF 2＝60°，所以a ＝2b ， 不妨设b ＝1，则a ＝2，所以c ＝a 2－c 2＝3，则椭圆的方程为x 24＋y 2＝1，又由A (0,1)，F 2(3，0)，所以kAF 2 ＝－33，所以直线AF 2的方程为y ＝－33x ＋1，联立方程组⎩⎪⎨⎪⎧y ＝－33x ＋1x 24＋y 2＝1，整理得7x 2－83x ＝0，解得x ＝0或x ＝837，把x ＝837代入直线y ＝－33x ＋1，解得y ＝－17，即M ⎝ ⎛⎭⎪⎫837，－17 ， 又由点B (0，－1)，所以BM 的斜率为k BM ＝－17－(－1)837－0＝34，故选B.答案：B2．已知直线l ：y ＝2x ＋b 被抛物线C ：y 2＝2px (p >0)截得的弦长为5，直线l 经过C 的焦点，M 为C 上的一个动点，设点N 的坐标为(3,0)，则MN 的最小值为________．解析：(1)∵⎩⎪⎨⎪⎧y ＝2x ＋by 2＝2px ⇒4x 2＋(4b －2p )x ＋b 2＝0,则52＝(1＋22)⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫2b －p 22－4×b 42， 又直线l 经过C 的焦点，则－b 2＝p 2，∴b ＝－p ，由此解得p ＝2, 抛物线方程为y 2＝4x ，M (x 0，y 0)，∴y 20＝4x 0，则|MN |2＝(x 0－3)2＋y 20＝(x 0－3)2＋4x 0＝(x 0－1)2＋8, 故当x 0＝1时，|MN |min ＝2 2. 答案：2 23．已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)上的动点到其左焦点距离的最大值是最小值的3倍，且点P ⎝⎛⎭⎪⎫1，32在椭圆上．(1)求椭圆E 的标准方程；(2)过点G (0,1)作直线l 与曲线交于A ，B 两点，求△ABO 面积的最大值．解析：(1)由题意得，⎩⎪⎨⎪⎧a ＋c ＝3(a －c )a 2＝b 2＋c21a 2＋94b2＝1，解得a ＝2，b ＝3，∴椭圆的标准方程为x 24＋y 23＝1. (2)易知直线l 的斜率存在．设直线l 的方程为y ＝kx ＋1，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧y ＝kx ＋1x 24＋y23＝1，消去y 得(3＋4k 2)x 2＋8kx －8＝0，则x 1＋x 2＝－8k 3＋4k 2，x 1x 2＝－83＋4k2，∴|x 1－x 2|＝(x 1＋x 2)2－4x 1x 2＝46·1＋2k23＋4k2d ＝1k 2＋1，∴S △ABO ＝12×d ×1＋k 2|x 1－x 2|＝26·1＋2k 23＋4k 2， 令 1＋2k 2＝t ，∵k 2≥0，∴t ≥1， ∴S △ABO ＝26t 2t 2＋1＝262t ＋1t，易证y ＝2t ＋1t 在[1，＋∞)上单调递增，∴2t ＋1t≥3，∴S △ABO ≤263，∴△ABO 面积的最大值为263.增分强化练考点一 直线的方程1．直线mx ＋y －m ＋2＝0恒经过定点( ) A ．(1，－1) B ．(1,2) C ．(1，－2)D ．(1,1)解析：直线mx ＋y －m ＋2＝0，化为：m (x －1)＋y ＋2＝0，可知直线经过定点(1，－2)．故选C. 答案：C2．(2019·南昌模拟)唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为x 2＋y 2≤1，若将军从点A (2,0)处出发，河岸线所在直线方程为x ＋y ＝3，并假定将军只要到达军营所在区域即回到军营，则“将军饮马”的最短总路程为( ) A.10－1 B ．22－1 C ．2 2D.10解析：设点A 关于直线x ＋y ＝3的对称点A ′(a ，b )，AA ′的中点为⎝⎛⎭⎪⎫a ＋22，b 2，k AA ′＝b a －2，故⎩⎪⎨⎪⎧ba －2·(－1)＝－1a ＋22＋b 2＝3，解得⎩⎪⎨⎪⎧a ＝3b ＝1，所以A ′(3,1)．要使从点A 到军营总路程最短，即为点A ′到军营最短的距离，“将军饮马”的最短总路程为32＋12－1＝10－1，故选A. 答案：A3．过点(－2,4)且在两坐标轴上的截距互为相反数的直线的一般方程为________． 解析：①当在坐标轴上截距为0时，所求直线方程为：y ＝－2x ，即2x ＋y ＝0； ②当在坐标轴上截距不为0时，∵在坐标轴上截距互为相反数， ∴x －y ＝a ，将A (－2,4)代入得，a ＝－6， ∴此时所求的直线方程为x －y ＋6＝0. 答案：2x ＋y ＝0或 x －y ＋6＝04．平行线5x ＋12y －10＝0和mx ＋6y ＋2＝0的距离是________解析：由题意，两直线5x ＋12y －10＝0和mx ＋6y ＋2＝0平行，可得5m ＝126，解得m ＝52，即5x ＋12y ＋4＝0，由两平行直线之间的距离公式，可得d ＝|－10－4|52＋122＝1413. 答案：1413考点二 圆的方程1．方程x 2＋y 2＋x ＋y －m ＝0表示一个圆，则m 的取值范围是( ) A ．m >－12B ．m <－12C ．m ≤－12D ．m ≥－12解析：因为方程x 2＋y 2＋x ＋y －m ＝0要表示一个圆，所以2＋4m >0 解得：m >－12，故选A.答案：A2．点M ，N 是圆x 2＋y 2＋kx ＋2y －4＝0上的不同两点，且点M ，N 关于直线x －y ＋1＝0对称，则该圆的半径等于( ) A ．2 2 B. 2 C ．1D ．3解析：圆x 2＋y 2＋kx ＋2y －4＝0的圆心坐标为⎝ ⎛⎭⎪⎫－k2，－1，因为点M ，N 在圆x 2＋y 2＋kx ＋2y －4＝0上，且点M ，N 关于直线l ：x －y ＋1＝0对称，所以直线l ：x －y ＋1＝0经过圆心，所以－k2＋1＋1＝0，k ＝4. 所以圆的方程为：x 2＋y 2＋4x ＋2y －4＝0，圆的半径为：12 42＋22－4×(－4)＝3. 故选D.答案：D3．已知圆C ：(x －6)2＋(y ＋8)2＝4，O 为坐标原点，则以OC 为直径的圆的方程为( ) A ．(x －3)2＋(y ＋4)2＝100 B ．(x ＋3)2＋(y －4)2＝100 C ．(x －3)2＋(y ＋4)2＝25 D ．(x ＋3) 2＋(y －4)2＝25解析：由题意可知：O (0,0)，C (6，－8)，则圆心坐标为(3，－4)，圆的直径为62＋(－8)2＝10，据此可得圆的方程为(x －3)2＋(y ＋4)2＝⎝ ⎛⎭⎪⎫1022，即(x －3)2＋(y ＋4)2＝25.故选C.答案：C4．已知圆C 的圆心是直线x －y ＋1＝0与x 轴的交点，且圆C 与直线x ＋y ＋3＝0相切，则圆C 的方程是( )A ．(x ＋1)2＋y 2＝2 B ．(x ＋1)2＋y 2＝8 C ．(x －1)2＋y 2＝2 D ．(x －1)2＋y 2＝8解析：直线x －y ＋1＝0与x 轴的交点坐标为(－1,0)，因为圆C 与直线x ＋y ＋3＝0相切，所以半径为圆心到切线的距离，即r ＝d ＝|－1＋0＋3|12＋12＝2，则圆C 的方程为(x ＋1)2＋y 2＝2，故选A. 答案：A考点三 直线与圆的位置关系1．圆O 1：x 2＋y 2－2x ＝0和圆O 2：x 2＋y 2－4y ＝0的公切线条数是( ) A ．4条 B ．3条 C ．2条D ．1条解析：圆O 1：x 2＋y 2－2x ＝0的圆心(1,0)半径为1；圆O 2：x 2＋y 2－4y ＝0的圆心(0,2)半径为2，O 1O 2＝12＋22＝5，∵1＜5＜3，∴两个圆相交，所以圆O 1：x 2＋y 2－2x ＝0和圆O 2：x 2＋y 2－4y ＝0的公切线条数2.故选C.答案：C2．(2019·南宁模拟)已知直线l ：3x －4y －15＝0与圆C ：x 2＋y 2－2x －4y ＋5－r 2＝0(r >0)相交于A ，B 两点，若|AB |＝6，则圆C 的标准方程为( ) A ．(x －1)2＋(y －2)2＝25 B ．(x －1)2＋(y －2)2＝36 C ．(x －1)2＋(y －2)2＝16 D ．(x －1)2＋(y －2)2＝49解析：圆C ：x 2＋y 2－2x －4y ＋5－r 2＝0可化为(x －1)2＋(y －2)2＝r 2，设圆心(1,2)到直线l 的距离为d ，则d ＝|3－8－15|5＝4，又|AB |＝6，根据r 2＝32＋42＝25，所以圆C 的标准方程为(x －1)2＋(y －2)2＝25.故选A. 答案：A3．(2019·汕头模拟)已知直线l 与圆x 2＋y 2－4y ＝0相交于A ，B 两点，且线段AB 的中点P 的坐标为(－1,1)，则直线l 的方程为________．解析：因为圆x 2＋y 2－4y ＝0的圆心坐标为C (0,2)，又点P 坐标为(－1,1)， 所以直线CP 的斜率为k CP ＝2－10＋1＝1； 又因为AB 是圆的一条弦，P 为AB 的中点， 所以AB ⊥CP ，故k AB ＝－1，即直线l 的斜率为－1， 因此，直线l 的方程为y －1＝－(x ＋1)，即x ＋y ＝0. 答案：x ＋y ＝04．直线2x ＋y －3＝0与圆x 2＋y 2－2x －2y ＝0相交于A ，B 两点，O 为坐标原点，则|OA →＋OB →|＝________.解析：设A (x 1，y 1)，B (x 2，y 2)，AB 的中点为M ，联立直线方程与圆的方程⎩⎪⎨⎪⎧x 2＋y 2－2x －2y ＝0y ＝－2x ＋3，整理可得5x 2－10x ＋3＝0，故x 1＋x 2＝2，y 1＋y 2＝(－2x 1＋3)＋(－2x 2＋3)＝－2(x 1＋x 2)＋6＝2， 据此可得M (1,1)，|OM →|＝1＋1＝2，结合平面向量的运算法则有|OA →＋OB →| ＝|2OM →| ＝2 2. 答案：2 2增分强化练1．已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的右焦点F 为抛物线y 2＝4x 的焦点，P ，Q 是椭圆C 上的两个动点，且线段PQ 长度的最大值为4. (1)求椭圆C 的标准方程；(2)若OP ⊥OQ ，求△OPQ 面积的最小值． 解析：(1)∵y 2＝4x 的焦点为(1,0)， ∴椭圆C 的右焦点F 为(1,0)，即c ＝1， 又|PQ |的最大值为4，因此|PQ |＝2a ＝4， ∴a 2＝4，b 2＝a 2－c 2＝4－1＝3， 所以椭圆C 的标准方程为x 24＋y 23＝1.(2)①当P ，Q 为椭圆顶点时，易得△OPQ 的面积为12×2×3＝3，②当P ，Q 不是椭圆顶点时，设直线OP 的方程为y ＝kx (k ≠0)，由⎩⎪⎨⎪⎧y ＝kx x 24＋y23＝1，得x 2＝123＋4k 2，所以|OP |＝k 2＋1 123＋4k2， 由OP ⊥OQ ，得直线OQ 的方程为：y ＝－1kx ，所以|OQ |＝1k2＋1123＋41k 2＝ 1＋k 2123k 2＋4， 所以S △OPQ ＝12|OP |·|OQ |＝6(k 2＋1)2(3＋4k 2)(3k 2＋4)＝6(k 2＋1)212k 4＋25k 2＋12＝6 112＋k 2(k 2＋1)2，(k 2＋1)2k2＝k 2＋1k2＋2≥4，当且仅当k 2＝1时等号成立，所以0<k 2(k 2＋1)2≤14，所以127≤S △OPQ <3，综上，△OPQ 面积的最小值为127.2．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，F 1，F 2分别为椭圆C 的左、右焦点，点P (263，33)满足PF →1·PF →2＝0. (1)求椭圆C 的方程；(2)直线l 经过椭圆C 的右焦点与椭圆相交于M ，N 两点，设O 为坐标原点，直线OM ，直线l ，直线ON 的斜率分别为k 1，k ，k 2，且k 1，k ，k 2成等比数列，求k 1·k 2的值． 解析：(1)依题意F 1(－c,0)， ∴PF →1·PF →2＝－c 2＋3＝0，即c ＝3， ∵e ＝c a ＝32， ∴a ＝2， ∴b 2＝a 2－c 2＝1，∴椭圆C 的方程为x 24＋y 2＝1.(2)设直线l 的方程为y ＝k (x －3)，M (x 1，y 1)，N (x 2，y 2)，由⎩⎪⎨⎪⎧x 24＋y 2＝1y ＝k (x －3)，得(1＋4k 2)x 2－83k 2x ＋4(3k 2－1)＝0，则x 1＋x 2＝83k 21＋4k 2，x 1x 2＝12k 2－41＋4k 2，∵k 1，k ，k 2成等比数列，∴k 1·k 2＝k 2＝y 1y 2x 1x 2＝k 2(x 1－3)(x 2－3)x 1x 2，则3(x 1＋x 2)＝3， 即83k21＋4k 2＝3， 解得k 2＝14，故k 1k 2＝14.3．已知抛物线C ：y 2＝2px (0<p <1)上的点P (m,1)到其焦点F 的距离为54.(1)求C 的方程；(2)已知直线l 不过点P 且与C 相交于A ，B 两点，且直线PA 与直线PB 的斜率之积为1，证明：l 过定点．解析：(1)由题意，得2pm ＝1，即m ＝12p.由抛物线的定义，得|PF |＝m －(－p 2)＝12p ＋p2.由题意，知12p ＋p 2＝54，解得p ＝12或p ＝2(舍去)．所以C 的方程为y 2＝x . (2)证明：由(1)得P (1,1)．设l ：x ＝ny ＋t ，由于直线l 不过点P (1,1)， 所以n ＋t ≠1.由⎩⎪⎨⎪⎧y 2＝x ，x ＝ny ＋t消去x 并整理得y 2－ny －t ＝0.由题意，判别式Δ＝n 2＋4t >0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝n ，①y 1y 2＝－t ，②则k PA k PB ＝y 1－1x 1－1·y 2－1x 2－1＝y 1－1y 21－1·y 2－1y 22－1＝1y 1y 2＋(y 1＋y 2)＋1. 由题意，得y 1y 2＋(y 1＋y 2)＋1＝1， 即y 1y 2＋(y 1＋y 2)＝0，③将①②代入③得－t ＋n ＝0，即t ＝n .所以l ：x ＝n (y ＋1)．显然l 过定点(0，－1)．4．已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1、F 2，焦距为2，长轴的长为4.(1)求椭圆C 的标准方程；(2)设过点F 1的直线l 与椭圆C 交于E ，D 两点，试问：在x 轴上是否存在定点M ，使得直线ME ，MD 的斜率之积为定值？若存在，求出该定值及定点M 的坐标；若不存在，请说明理由．解析：(1)因为椭圆C 的焦距为2，长轴的长为4， 所以2c ＝2,2a ＝4，解得c ＝1，a ＝2， 所以b 2＝a 2－c 2＝3，所以椭圆C 的标准方程为x 24＋y 23＝1.(2)设E (x 1，y 1)，D (x 2，y 2)，M (m,0)．易知F 1(－1,0)，当直线l 的斜率存在时，设直线l 的方程为y ＝k (x ＋1)．联立方程，得⎩⎪⎨⎪⎧y ＝k (x ＋1)，x 24＋y23＝1，得(4k 2＋3)x 2＋8k 2x ＋4k 2－12＝0， 则x 1＋x 2＝－8k 24k 2＋3，x 1x 2＝4k 2－124k 2＋3.又y 1y 2＝k 2(x 1＋1)(x 2＋1)＝k 2(x 1x 2＋x 1＋x 2＋1)＝k 2(4k 2－124k 2＋3－8k 24k 2＋3＋1)＝－9k24k 2＋3，直线ME ，MD 的斜率k ME ＝y 1x 1－m，k MD ＝y 2x 2－m，则k ME ·k MD ＝y 1x 1－m ·y 2x 2－m ＝y 1y 2(x 1－m )(x 2－m )＝y 1y 2x 1x 2－m (x 1＋x 2)＋m 2＝－9k 24k 2＋34k 2－124k 2＋3－m (－8k 24k 2＋3)＋m 2＝－9k24k 2＋34k 2－12＋8mk 2＋4m 2k 2＋3m24k 2＋3 ＝－9k2(4m 2＋8m ＋4)k 2＋3m 2－12. 要使直线ME ，MD 的斜率之积为定值，需3m 2－12＝0， 解得m ＝±2.当m ＝2时，k ME ·k MD ＝－9k 2(4m 2＋8m ＋4)k 2＝－9k 236k 2＝－14；当m ＝－2时，k ME ·k MD ＝－9k 2(4m 2＋8m ＋4)k 2＝－9k 24k 2＝－94.当直线l 的斜率不存在时， 不妨设E (－1，32)，D (－1，－32)，此时，当m ＝2时，M (2,0)，k ME ·k MD ＝－14；当m ＝－2时，M (－2,0)，k ME ·k MD ＝－94.综上，在x 轴上存在两个定点M ，使得直线ME ，MD 的斜率之积为定值． 当定点M 的坐标为(2,0)时，直线ME ，MD 的斜率之积为定值－14；当定点M 的坐标为(－2,0)时，直线ME ，MD 的斜率之积为定值－94.增分强化练一、选择题1．双曲线x 23－y 29＝1的渐近线方程是( )A ．y ＝±3xB ．y ＝±13xC ．y ＝±3xD ．y ＝±33x 解析：因为x 23－y 29＝1，所以a ＝3，b ＝3，渐近线方程为y ＝±b ax ， 即为y ＝±3x ，故选C. 答案：C2．已知双曲线my 2－x 2＝1(m ∈R)与抛物线x 2＝8y 有相同的焦点，则该双曲线的渐近线方程为( ) A ．y ＝±3x B ．y ＝±3x C ．y ＝±13xD ．y ＝±33x 解析：∵抛物线x 2＝8y 的焦点为(0,2)，∴双曲线的一个焦点为(0,2)，∴1m ＋1＝4，∴m ＝13，∴双曲线的渐近线方程为y ＝±3x ， 故选A. 答案：A3．已知双曲线C ：x 2m 2－y 23＝1的离心率为2，则C 的焦点坐标为( )A ．(±2,0)B ．(±2，0)C ．(0，±2)D ．(0，±2)解析：由双曲线C ：x 2m 2－y 23＝1，离心率为2，可得m 2＋3m＝2，∴m 2＝1, 则c ＝m 2＋3＝2，故双曲线C 的焦点坐标是(±2,0)．故选A. 答案：A4．(2019·呼和浩特模拟)已知双曲线C 1：x 24－y 2k ＝1与双曲线C 2：x 2k －y 29＝1有相同的离心率，则双曲线C 1的渐近线方程为( ) A ．y ＝±32x B ．y ＝±62x C ．y ＝±34x D ．y ＝±64x 解析：由双曲线方程可知k >0，双曲线C 1：x 24－y 2k ＝1的离心率为4＋k2，双曲线C 2：x 2k －y 29＝1的离心率为k ＋9k，由题意得4＋k 2＝k ＋9k ，解得k ＝6, 双曲线C 1为x 24－y26＝1，则渐近线方程为y ＝±62x ， 故选B. 答案：B5．已知双曲线C 的一个焦点坐标为(3，0)，渐近线方程为y ＝±22x ，则C 的方程是( ) A ．x 2－y 22＝1 B.x 22－y 2＝1 C.y 22－x 2＝1 D ．y 2－x 22＝1解析：因为双曲线C 的一个焦点坐标为(3，0)，所以c ＝3，又因为双曲线C 的渐近线方程为y ＝±22x ，所以有b a ＝22⇒a ＝2b ，c ＝3，而c ＝a 2＋b 2，所以解得a ＝2，b ＝1，因此双曲线方程为x 22－y 2＝1，故选B.答案：B6．(2019·岳阳模拟)过抛物线x 2＝4y 的焦点F 作直线，交抛物线于P 1(x 1，y 1)，P 2(x 2，y 2)两点，若y 1＋y 2＝6，则|P 1P 2|＝( ) A ．5 B ．6 C ．8D ．10解析：x 2＝4y 的焦点为(0,1)，准线为y ＝－1，因为P 1(x 1，y 1)，P 2(x 2，y 2)两点是过抛物线焦点的直线与抛物线的交点，所以P 1(x 1，y 1)，P 2(x 2，y 2)两点到准线的距离分别是y 1＋1，y 2＋1，所以由抛物线的定义知|P 1P 2|＝|P 1F |＋|P 2F |＝y 1＋1＋y 2＋1＝y 1＋y 2＋2＝6＋2＝8，故选C. 答案：C7．(2019·洛阳、许昌质检)若双曲线x 2－y 2b2＝1 (b >0)的一条渐近线与圆x 2＋(y －2)2＝1至多有一个交点，则双曲线离心率的取值范围是( ) A ．(1,2] B ．[2，＋∞) C ．(1，3]D ．[3，＋∞)解析：双曲线x 2－y 2b2＝1(b >0)的一条渐近线方程是bx －y ＝0，由题意圆x 2＋(y －2)2＝1的圆心(0,2)到bx －y ＝0的距离不小于1，即2b 2＋1≥1，则b 2≤3，那么离心率e ∈(1,2]，故选A. 答案：A8．(2019·咸阳模拟)已知椭圆、双曲线均是以直角三角形ABC 的斜边AC 的两端点为焦点的曲线，且都过B 点，它们的离心率分别为e 1，e 2，则1e 21＋1e 22＝( )A.32 B ．2 C.52D ．4解析：以AC 边所在的直线为x 轴，AC 中垂线所在的直线为y 轴建立直角坐标系(图略)，设椭圆方程为x 2a 21＋y 2b 21＝1，设双曲线方程为x 2a 22－y 2b 22＝1，焦距都为2c不妨设|AB |>|BC |，椭圆和双曲线都过点B ， 则|AB |＋|BC |＝2a 1，|AB |－|BC |＝2a 2， 所以|AB |＝a 1＋a 2，|BC |＝a 1－a 2， 又因为△ABC 为直角三角形，|AC |＝2c ，所以(a 1＋a 2)2＋(a 1－a 2)2＝(2c )2，即a 21＋a 22＝2c 2，所以a 21c 2＋a 22c 2＝2，即1e 21＋1e 22＝2.故选B. 答案：B9．(2019·乌鲁木齐质检)已知抛物线C ：y 2＝8x 的焦点为F ，直线l 过焦点F 与抛物线C 分别交于A ，B 两点，且直线l 不与x 轴垂直，线段AB 的垂直平分线与x 轴交于点P (10,0)，则△AOB 的面积为( ) A ．4 3 B ．4 6 C ．8 2D ．8 6解析：设直线l ：x ＝ty ＋2，A (x 1，y 1)，B (x 2，y 2)，则由⎩⎪⎨⎪⎧y 2＝8x x ＝ty ＋2可以得到y 2－8ty －16＝0，所以AB 的中点M (4t 2＋2,4t )，线段AB 的垂直平分线与x 轴交于点P (10,0)，故t ≠0. 所以AB 的中垂线的方程为y ＝－1t (x －4t 2－2)＋4t ＝－1t ·x ＋8t ＋2t，令y ＝0可得x ＝8t 2＋2，解方程10＝8t 2＋2得t ＝±1. 此时AB ＝ 1＋t 2|y 1－y 2|＝81＋t 2t 2＋1＝16，O 到AB 的距离为d ＝21＋t2＝2，所以S ΔOAB ＝12×16×2＝8 2.故选C. 答案：C10．(2019·滨州模拟)已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F ，短轴的一个端点为P ，直线l ：4x －3y ＝0与椭圆C 相交于A ，B 两点．若|AF |＋|BF |＝6，点P 到直线l 的距离不小于65，则椭圆离心率的取值范围是( ) A.⎝ ⎛⎦⎥⎤0，59 B.⎝ ⎛⎦⎥⎤0，32 C.⎝ ⎛⎦⎥⎤0，53 D.⎝ ⎛⎦⎥⎤13，32 解析：如图所示，设F ′为椭圆的左焦点， 连接AF ′，BF ′，则四边形AFBF ′是平行四边形，∴6＝|AF |＋|BF |＝|AF ′|＋|AF |＝2a ，∴a ＝3.取P (0，b )，∵点P 到直线l ∶4x ＋3y ＝0的距离不小于65，∴|3b |16＋9≥65，解得b ≥2. ∴c ≤9－4＝5，∴0<c a ≤53. ∴椭圆E 的离心率范围是⎝⎛⎦⎥⎤0，53. 故选C. 答案：C11．(2019·济宁模拟)已知直线l 过抛物线C ：y 2＝3x 的焦点F ，交C 于A ，B 两点，交C 的准线于点P ，若AF →＝FP →，则|AB |＝( ) A ．3 B ．4 C ．6D ．8解析：如图所示：不妨设A 在第一象限，由抛物线C ：y 2＝3x 可得F ⎝ ⎛⎭⎪⎫34，0，准线DP ：x ＝－34.因为AF →＝FP →，所以F 是AP 的中点，则AD ＝2CF ＝3.所以可得A ⎝ ⎛⎭⎪⎫94，332，则k AF ＝3，所以直线AP 的方程为：y ＝3⎝ ⎛⎭⎪⎫x －34， 联立方程⎩⎪⎨⎪⎧y ＝3⎝ ⎛⎭⎪⎫x －34y 2＝3x，整理得：x 2－52x ＋916＝0所以x 1＋x 2＝52，则|AB |＝x 1＋x 2＋p ＝52＋32＝4.故选B.答案：B12．(2019·晋城模拟)已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点为F ，直线l 经过点F 且与双曲线的一条渐近线垂直，直线l 与双曲线的右支交于不同两点A ，B ，若AF →＝3FB →，则该双曲线的离心率为( ) A.52 B.62C.233D. 3解析：由题意得直线l 的方程为x ＝b ay ＋c ，不妨取a ＝1，则x ＝by ＋c ，且b 2＝c 2－1.将x ＝by ＋c 代入x 2－y 2b2＝1，(b ＞0)，得(b 4－1)y 2＋2b 3cy ＋b 4＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－2b 3c b 4－1，y 1y 2＝b4b 4－1.由AF →＝3FB →，得y 1＝－3y 2，所以⎩⎪⎨⎪⎧－2y 2＝－2b 3cb 4－1－3y 22＝b 4b 4－1，得3b 2c 2＝1－b 4，解得b 2＝14，所以c＝b 2＋1＝54＝52，故该双曲线的离心率为e ＝c a ＝52，故选A. 答案：A 二、填空题13．(2019·合肥质检)抛物线x 2＝8y 的焦点坐标为________．解析：由抛物线方程x 2＝8y 知，抛物线焦点在y 轴上，由2p ＝8，得p2＝2，所以焦点坐标为(0,2)． 答案：(0,2)14．已知过P (1,1)的直线l 与双曲线C ：x 2－y 2＝1只有一个公共点，则直线l 的条数为________． 解析：双曲线C ：x 2－y 2＝1的渐近线方程y ＝±x ， 其中一条渐近线y ＝x 过点P (1,1)，所以过点P (1,1)的直线x ＝1与双曲线右支相切，只有一个公共点，过P (1,1)与y ＝－x 平行的直线y ＝－x ＋2和双曲线右支相交，只有一个公共点， 综上共有2条直线符合要求． 答案：215．(2019·泰安模拟)抛物线C ：y 2＝4x 的焦点为F ，动点P 在抛物线C 上，点A (－1,0)，当|PF ||PA |取得最小值时，直线AP 的方程为________． 解析：设P 点的坐标为(4t 2,4t )， ∵F (1,0)，A (－1,0)，∴|PF |2＝(4t 2－1)2＋16t 2＝16t 4＋8t 2＋1， |PA |2＝(4t 2＋1)2＋16t 2＝16t 4＋24t 2＋1， ∴⎝ ⎛⎭⎪⎫|PF ||PA |2＝16t 4＋8t 2＋116t 4＋24t 2＋1＝1－16t 216t 4＋24t 2＋1＝1－1616t 2＋1t2＋24≥1－16216t 2·1t2＋24＝1－1632＝12，当且仅当16t 2＝1t 2，即t ＝±12时取等号，此时点P 坐标为(1,2)或(1，－2)，此时直线AP 的方程为y ＝±(x ＋1)，即x ＋y ＋1＝0或x －y ＋1＝0. 答案：x ＋y ＋1＝0或x －y ＋1＝016．抛物线C ：y 2＝2px (p >0)的焦点为A ，其准线与x 轴的交点为B ，如果在直线3x ＋4y ＋25＝0上存在点M ，使得∠AMB ＝90°，则实数p 的取值范围是________．解析：由题得A ⎝ ⎛⎭⎪⎫p 2，0，B ⎝ ⎛⎭⎪⎫－p2，0， ∵M 在直线3x ＋4y ＋25＝0上，设点M ⎝ ⎛⎭⎪⎫x ，－3x －254，∴AM →＝⎝ ⎛⎭⎪⎫x －p 2，－3x －254， BM →＝⎝⎛⎭⎪⎫x ＋p 2，－3x －254， 又∠AMB ＝90°，∴AM →·BM →＝⎝ ⎛⎭⎪⎫x －p 2⎝ ⎛⎭⎪⎫x ＋p 2＋⎝ ⎛⎭⎪⎫－3x －2542＝0，即25x 2＋150x ＋625－4p 2＝0， ∴Δ≥0，即1502－4×25×(625－4p 2)≥0， 解得p ≥10或p ≤－10，又p >0，∴p 的取值范围是[10，＋∞)． 答案：[10，＋∞) 三、解答题17．已知椭圆的焦点F 1(－4,0)，F 2(4,0)，过点F 2并垂直于x 轴的直线与椭圆的一个交点为B ，并且|F 1B |＋|F 2B |＝10，椭圆上不同的两点A (x 1，y 1)，C (x 2，y 2)满足条件：|F 2A |，|F 2B |，|F 2C |成等差数列． (1)求椭圆的方程； (2)求弦AC 中点的横坐标．解析：(1)由题意可知2a ＝|F 1B |＋|F 2B |＝10. 所以a ＝5，又c ＝4，所以b ＝a 2－c 2＝3， 所以椭圆方程为：x 225＋y 29＝1.(2)由点B (4，y B )在椭圆上，得|F 2B |＝|y B |＝95.由|F 2A |，|F 2B |，|F 2C |成等差数列， 得 (x 1－4)2＋y 21＋ (x 2－4)2＋y 22＝2×95，①点A (x 1，y 1)在椭圆x 2125＋y 219＝1上，得y 21＝925(25－x 21)，所以 (x 1－4)2＋y 21 ＝x 21－8x 1＋16＋925(25－x 21)＝ ⎝ ⎛⎭⎪⎫5－45x 12＝15(25－4x 1)，② 同理可得 (x 2－4)2＋y 22＝15(25－4x 2)，③将②③代入①式，得15(25－4x 1)＋15(25－4x 2)＝185，所以x 1＋x 2＝8，设AC 中点坐标为(x 0，y 0)，则横坐标x 0＝x 1＋x 22＝4.18．(2019·合肥质检)已知F 1，F 2分别为椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左，右焦点，点P ⎝⎛⎭⎪⎫1，22在椭圆C 上，且△PF 1F 2的面积为22. (1)求椭圆C 的方程；(2)设过点F 1的直线l 交椭圆于A ，B 两点，求F 2A →·F 2B →的取值范围． 解析：(1)由椭圆C 经过点P ⎝ ⎛⎭⎪⎫1，22，且△PF 1F 2的面积为22， 得1a 2＋12b 2＝1，且12×2c ×22＝22，即c ＝1. 又a 2－b 2＝c 2＝1，解得a 2＝2，b 2＝1. 所以椭圆C 的方程为x 22＋y 2＝1.(2)由(1)知F 1(－1,0)，F 2(1,0)．设A (x 1，y 1)，B (x 2，y 2)． 若直线l 的斜率不存在，可得点A ，B 的坐标为⎝ ⎛⎭⎪⎫－1，22，⎝ ⎛⎭⎪⎫－1，－22， 则F 2A →·F 2B →＝72.当直线l 的斜率存在时，设l ：y ＝k (x ＋1)，代入椭圆方程得(1＋2k 2)x 2＋4k 2x ＋2(k 2－1)＝0. 则Δ＝16k 4－8(1＋2k 2)(k 2－1)＝8k 2＋8>0恒成立． 所以x 1＋x 2＝－4k 21＋2k 2，x 1x 2＝2(k 2－1)1＋2k 2.所以F 2A →·F 2B →＝(x 1－1)(x 2－1)＋y 1y 2 ＝(1＋k 2)x 1x 2＋(k 2－1)(x 1＋x 2)＋k 2＋1＝7k 2－11＋2k 2＝72－92(1＋2k 2). 又k 2≥0，则F 2A →·F 2B →＝72－92(2k 2＋1)∈⎣⎢⎡⎭⎪⎫－1，72. 综上可知，F 2A →·F 2B →的取值范围为⎣⎢⎡⎦⎥⎤－1，72.增分强化练(三十一)考点一 范围、最值问题(2019·大连模拟)已知抛物线C ：x 2＝2py (p >0)，其焦点到准线的距离为2，直线l 与抛物线C 交于A ，B 两点，过A ，B 分别作抛物线C 的切线l 1，l 2，l 1与l 2交于点M . (1)求p 的值；(2)若l 1⊥l 2，求△MAB 面积的最小值．解析：(1)由题意知，抛物线焦点为：⎝ ⎛⎭⎪⎫0，p 2，准线方程为：y ＝－p2，焦点到准线的距离为2，即p ＝2. (2)抛物线的方程为x 2＝4y ，即y ＝14x 2，所以y ′＝12x ，设A (x 1，y 1)，B (x 2，y 2)，l 1：y －x 214＝x 12(x －x 1)，l 2：y －x 224＝x 22(x －x 2)，由于l 1⊥l 2，所以x 12·x 22＝－1，即x 1x 2＝－4.设直线l 方程为y ＝kx ＋m ，与抛物线方程联立，得⎩⎪⎨⎪⎧y ＝kx ＋m x 2＝4y ，所以x 2－4kx －4m ＝0，Δ＝16k 2＋16m >0，x 1＋x 2＝4k ，x 1x 2＝－4m ＝－4，所以m ＝1.即l ：y ＝kx ＋1，联立方程⎩⎪⎨⎪⎧y ＝x 12x －x 214y ＝x 22x －x224，得⎩⎪⎨⎪⎧x ＝2k y ＝－1，即M (2k ，－1)，M 点到直线l 的距离d ＝|k ·2k ＋1＋1|1＋k 2＝2|k 2＋1|1＋k 2， |AB |＝(1＋k 2)[](x 1＋x 2)2－4x 1x 2＝4(1＋k 2)，所以S ＝12×4(1＋k 2)×2|k 2＋1|1＋k 2＝4(1＋k 2)32≥4， 当k ＝0时，△MAB 面积取得最小值4. 考点二 定点、定值问题(2019·南昌模拟)已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)，点M 在C 的长轴上运动，过点M 且斜率大于0的直线l 与C 交于P ，Q 两点，与y 轴交于N 点．当M 为C 的右焦点且l 的倾斜角为π6时，N ，P 重合，|PM |＝2. (1)求椭圆C 的方程；(2)当N ，P ，Q ，M 均不重合时，记NP →＝λNQ →，MP →＝μMQ →，若λμ＝1，求证：直线l 的斜率为定值．解析：(1)因为当M 为C 的右焦点且l 的倾斜角为π6时，N ，P 重合，|PM |＝2，所以a ＝|PM |＝2，故b c ＝tan π6＝33， 因为a 2＝b 2＋c 2， 因此c ＝3，b ＝1，所以椭圆C 的方程为x 24＋y 2＝1.(2)证明：设l ：x ＝ty ＋m (m ≠0)，所以M (m,0)，N ⎝ ⎛⎭⎪⎫0，－m t ，所以k l ＝1t .因为斜率大于0，所以t >0，设P (x 1，y 1)，Q (x 2，y 2)，则NP →＝⎝ ⎛⎭⎪⎫x 1，y 1＋m t ，NQ →＝⎝ ⎛⎭⎪⎫x 2，y 2＋m t ，由NP →＝λNQ →得，x 1＝λx 2，①同理可得y 1＝μy 2，②①②两式相乘得，x 1y 1＝λμx 2y 2，又λμ＝1，所以x 1y 1＝x 2y 2，所以(ty 1＋m )y 1＝(ty 2＋m )y 2，即t (y 21－y 22)＝m (y 2－y 1)，即(y 2－y 1)[]m ＋t (y 1＋y 2)＝0，由题意k l >0，知y 1－y 2≠0，所以m ＋t (y 1＋y 2)＝0.联立方程组⎩⎪⎨⎪⎧ x ＝ty ＋m x 24＋y 2＝1，得(t 2＋4)y 2＋2tmy ＋m 2－4＝0，依题意，y 1＋y 2＝－2tmt 2＋4，所以m －2t 2mt 2＋4＝0，又m ≠0，所以t 2＝4，因为t >0，故得t ＝2，所以k l ＝1t ＝12，即直线l 的斜率为12.考点三 存在性问题已知抛物线y 2＝4x ，过点P (8，－4)的动直线l 交抛物线于A ，B 两点．(1)当P 恰为AB 的中点时，求直线l 的方程；(2)抛物线上是否存在一个定点Q ，使得以弦AB 为直径的圆恒过点Q ？若存在，求出点Q 的坐标；若不存在，请说明理由．解析：(1)设A ，B 两点坐标分别为(x 1，y 1)，(x 2，y 2)，当P 恰为AB 的中点时，显然x 1≠x 2，故k AB ＝y 1－y 2x 1－x 2＝4y 1＋y 2，又y 1＋y 2＝－8，故k AB ＝－12， 则直线l 的方程为y ＝－12x . (2)假设存在定点Q ，设Q ⎝ ⎛⎭⎪⎫y 204，y 0，当直线l 斜率存在时，设l ：y ＝k (x －8)－4(k ≠0)，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧ y 2＝4x y ＝k (x －8)－4，整理得ky 2－4y －32k －16＝0，Δ>0，y 1＋y 2＝4k ，y 1y 2＝－32－16k， 由以弦AB 为直径的圆恒过点Q 知QA →·QB →＝0，即⎝ ⎛⎭⎪⎫x 1－y 204⎝ ⎛⎭⎪⎫x 2－y 204＋(y 1－y 0)(y 2－y 0)＝0， 即⎝ ⎛⎭⎪⎫y 214－y 204⎝ ⎛⎭⎪⎫y 224－y 204＋(y 1－y 0)(y 2－y 0)＝⎣⎢⎡⎦⎥⎤(y 1＋y 0)(y 2＋y 0)16＋1(y 1－y 0)(y 2－y 0)＝0， 故(y 1＋y 0)(y 2＋y 0)＝－16，即y 1y 2＋y 0(y 1＋y 2)＋y 20＋16＝0，整理得(y 20－16)k ＋4(y 0－4)＝0，即当y 0＝4时，恒有QA →·QB →＝0，故存在定点Q (4,4)满足题意；当直线l 斜率不存在时，l ：x ＝8，不妨令A (8,42)，B (8，－42)，Q (4,4)，也满足QA →·QB→＝0，综上所述，存在定点Q (4,4)，使得以弦AB 为直径的圆恒过点Q .。

专题07 立体几何§7－1 点、直线、平面之间的位置关系【知识要点】1．空间直线和平面的位置关系：(1)空间两条直线：①有公共点：相交，记作：a∩b＝A，其中特殊位置关系：两直线垂直相交．②无公共点：平行或异面．平行，记作：a∥b．异面中特殊位置关系：异面垂直．(2)空间直线与平面：①有公共点：直线在平面内或直线与平面相交．直线在平面内，记作：a⊂α ．直线与平面相交，记作：a∩α ＝A，其中特殊位置关系：直线与平面垂直相交．②无公共点：直线与平面平行，记作：a∥α ．(3)空间两个平面：①有公共点：相交，记作：α ∩β ＝l，其中特殊位置关系：两平面垂直相交．②无公共点：平行，记作：α ∥β ．2．空间作为推理依据的公理和定理：(1)四个公理与等角定理：公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内．公理2：过不在一条直线上的三点，有且只有一个平面．公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．公理4：平行于同一条直线的两条直线互相平行．定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补．(2)空间中线面平行、垂直的性质与判定定理：①判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行．如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行．如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直．如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．②性质定理：如果一条直线与一个平面平行，那么经过该直线的任一个平面与此平面的交线与该直线平行．如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行．垂直于同一个平面的两条直线平行．如果两个平面垂直，那么一个平面内垂直于它们交线的直线与另一个平面垂直．(3)我们把上述判定定理与性质定理进行整理，得到下面的位置关系图：【复习要求】1．了解四个公理与等角定理；2．理解空间中线面平行、垂直的有关性质与判定定理；3．能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题． 【例题分析】例1 如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是AB ，AA 1的中点． 求证：(Ⅰ)E 、C 、D 1、F 四点共面；(Ⅱ)CE 、DA 、D 1F 三线共点．【分析】对于(Ⅰ)中证明“E 、C 、D 1、F 四点共面”，可由这四点连接成两条直线，证明它们平行或相交即可；对于(Ⅱ)中证明“CE 、DA 、D 1F 三线共点”，可证其中两条相交直线的交点位于第三条直线上．证明：(Ⅰ)连接D 1C 、A 1B 、EF ． ∵E ，F 分另是AB ，AA 1的中点，∴EF ∥A 1B ，,211B A EF =又A 1D 1∥BC ，A 1D 1＝BC ， ∴A 1D 1CB 是平行四边形． ∴A 1B ∥D 1C ，EF ∥D 1C ， ∴E 、C 、D 1、F 四点共面． (Ⅱ)由(Ⅰ)得EF ∥CD 1，,211CD EF =∴直线CE 与直线D 1F 必相交，记CE ∩ D 1F ＝P ， ∵P ∈D 1F ⊂平面A 1ADD 1，P ∈CE ⊂平面ABCD ， ∴点P 是平面A 1ADD 1和平面ABCD 的一个公共点． ∵平面A 1ADD 1∩平面ABCD ＝AD ， ∴P ∈AD ，∴CE 、DA 、D 1F 三线共点．【评述】1、证明多点共面、多点共线、多线共面的主要依据： (1)证明多点共面常用公理2及其推论；(2)证明多点共线常用公理3，即证明点在两个平面内，从而点在这两个平面的交线上； (3)证明多线共面，首先由其中两直线确定平面，再证其余直线在此平面内． 2、证明a ，b ，c 三线交于一点的主要依据：(1)证明a 与b 相交，c 与b 相交，再证明两交点重合； (2)先证明a 与b 相交于点P ，再证明P ∈c ．例2 在四棱锥P －ABCD 中，底面ABCD 是平行四边形，M ，N 分别是AB ，PC 的中点，求证：MN ∥平面P AD ．【分析】要证明“线面平行”，可通过“线线平行”或“面面平行”进行转化；题目中出现了中点的条件，因此可考虑构造(添加)中位线辅助证明．证明：方法一，取PD 中点E ，连接AE ，NE ．∵底面ABCD 是平行四边形，M ，N 分别是AB ，PC 的中点，∴MA ∥CD ，.21CD MA = ∵E 是PD 的中点， ∴NE ∥CD ，.21CD NE =∴MA ∥NE ，且MA ＝NE ， ∴AENM 是平行四边形， ∴MN ∥AE ．又AE ⊂平面P AD ，MN ⊄平面P AD ， ∴MN ∥平面P AD ．方法二取CD 中点F ，连接MF ，NF ． ∵MF ∥AD ，NF ∥PD ， ∴平面MNF ∥平面P AD ， ∴MN ∥平面P AD ．【评述】关于直线和平面平行的问题，可归纳如下方法：111111【分析】要证明“线线垂直”，可通过“线面垂直”进行转化，因此设法证明A1C垂直于经过BC1的平面即可．证明：连接AC1．∵ABC－A1B1C1是直三棱柱，∴AA1⊥平面ABC，∴AB⊥AA1．又AB⊥AC，∴AB⊥平面A1ACC1，∴A1C⊥A B．①又AA1＝AC，∴侧面A1ACC1是正方形，∴A1C⊥AC1．②由①，②得A1C⊥平面ABC1，∴A1C⊥BC1．【评述】空间中直线和平面垂直关系的论证往往是以“线面垂直”为核心展开的．如本题已知条件中出现的“直三棱柱”及“AB⊥AC”都要将其向“线面垂直”进行转化．例4在三棱锥P－ABC中，平面P AB⊥平面ABC，AB⊥BC，AP⊥PB，求证：平面P AC⊥平面PBC．【分析】要证明“面面垂直”，可通过“线面垂直”进行转化，而“线面垂直”又可以通过“线线垂直”进行转化．证明：∵平面P AB⊥平面ABC，平面P AB∩平面ABC＝AB，且AB⊥BC，∴BC⊥平面P AB，∴AP⊥BC．又AP⊥PB，∴AP⊥平面PBC，又AP 平面P AC，∴平面P AC⊥平面PBC．【评述】关于直线和平面垂直的问题，可归纳如下方法：(1)证明线线垂直：例5 如图，在斜三棱柱ABC －A 1B 1C 1中，侧面A 1ABB 1是菱形，且垂直于底面ABC ，∠A 1AB ＝60°，E ，F 分别是AB 1，BC 的中点．(Ⅰ)求证：直线EF ∥平面A 1ACC 1；(Ⅱ)在线段AB 上确定一点G ，使平面EFG ⊥平面ABC ，并给出证明． 证明：(Ⅰ)连接A 1C ，A 1E ．∵侧面A 1ABB 1是菱形， E 是AB 1的中点， ∴E 也是A 1B 的中点，又F 是BC 的中点，∴EF ∥A 1C ．∵A 1C ⊂平面A 1ACC 1，EF ⊄平面A 1ACC 1， ∴直线EF ∥平面A 1ACC 1． (2)解：当31=GA BG 时，平面EFG ⊥平面ABC ，证明如下： 连接EG ，FG ．∵侧面A 1ABB 1是菱形，且∠A 1AB ＝60°，∴△A 1AB 是等边三角形． ∵E 是A 1B 的中点，31=GA BG ，∴EG ⊥AB ． ∵平面A 1ABB 1⊥平面ABC ，且平面A 1ABB 1∩平面ABC ＝AB ， ∴EG ⊥平面ABC ．又EG ⊂平面EFG ，∴平面EFG ⊥平面ABC ．练习7－1一、选择题：1．已知m ，n 是两条不同直线，α ，β ，γ 是三个不同平面，下列命题中正确的是( ) (A)若m ∥α ，n ∥α ，则m ∥n (B)若m ⊥α ，n ⊥α ，则m ∥n (C)若α ⊥γ ，β ⊥γ ，则α ∥β (D)若m ∥α ，m ∥β ，则α ∥β 2．已知直线m ，n 和平面α ，β ，且m ⊥n ，m ⊥α ，α ⊥β ，则( ) (A)n ⊥β (B)n ∥β ，或n ⊂β (C)n ⊥α (D)n ∥α ，或n ⊂α3．设a ，b 是两条直线，α 、β 是两个平面，则a ⊥b 的一个充分条件是( ) (A)a ⊥α ，b ∥β ，α ⊥β (B)a ⊥α ，b ⊥β ，α ∥β (C)a ⊂α ，b ⊥β ，α ∥β (D)a ⊂α ，b ∥β ，α ⊥β 4．设直线m 与平面α 相交但不垂直，则下列说法中正确的是( ) (A)在平面α 内有且只有一条直线与直线m 垂直 (B)过直线m 有且只有一个平面与平面α 垂直 (C)与直线m 垂直的直线不可能与平面α 平行 (D)与直线m 平行的平面不可能与平面α 垂直 二、填空题：5．在三棱锥P －ABC 中，6==PB PA ，平面P AB ⊥平面ABC ，P A ⊥PB ，AB ⊥BC ，∠BAC ＝30°，则PC ＝______．6．在直四棱柱ABCD －A 1B 1C 1D 1中，当底面ABCD 满足条件______时，有A 1C ⊥B 1D 1．(只要求写出一种条件即可)7．设α ，β 是两个不同的平面，m ，n 是平面α ，β 之外的两条不同直线，给出四个论断： ①m ⊥n ②α ⊥β ③n ⊥β ④m ⊥α以其中三个论断作为条件，余下的一个论断作为结论，写出正确的一个命题______．8．已知平面α ⊥平面β ，α ∩β ＝l ，点A ∈α ，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α ，m ∥β ，给出下列四种位置：①AB ∥m ；②AC ⊥m ；③AB ∥β ；④AC ⊥β ， 上述四种位置关系中，不一定成立的结论的序号是______． 三、解答题：9．如图，三棱锥P －ABC 的三个侧面均为边长是1的等边三角形，M ，N 分别为P A ，BC 的中点．(Ⅰ)求MN 的长； (Ⅱ)求证：P A ⊥BC ．10．如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，且E 、F 分别是AB 、BD 的中点．求证：(Ⅰ)直线EF ∥平面ACD ； (Ⅱ)平面EFC ⊥平面BCD ．11．如图，平面ABEF ⊥平面ABCD ，四边形ABEF 与ABCD 都是直角梯形，∠BAD ＝∠F AB ＝90°，BC ∥AD ，AF BE AF BE AD BC 21,//,21==，G ，H 分别为F A ，FD 的中点．(Ⅰ)证明：四边形BCHG 是平行四边形；(Ⅱ)C ，D ，F ，E 四点是否共面?为什么?(Ⅲ)设AB ＝BE ，证明：平面ADE ⊥平面CDE ．§7－2空间几何体的结构【知识要点】1．简单空间几何体的基本概念：(1)(2)特殊的四棱柱：3．简单几何体的三视图与直观图：(1)平行投影：①概念：如图，已知图形F，直线l与平面α 相交，过F上任意一点M作直线MM1平行于l，交平面α 于点M1，则点M1叫做点M在平面α 内关于直线l的平行投影．如果图形F上的所有点在平面α 内关于直线l 的平行投影构成图形F1，则F1叫图形F在α 内关于直线l的平行投影．平面α 叫投射面，直线l叫投射线．②平行投影的性质：性质1．直线或线段的平行投影仍是直线或线段；性质2．平行直线的平行投影是平行或重合的直线；性质3．平行于投射面的线段，它的投影与这条线段平行且等长；性质4．与投射面平行的平面图形，它的投影与这个图形全等；性质5．在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．(2)直观图：斜二侧画法画简单空间图形的直观图．(3)三视图：①正投影：在平行投影中，如果投射线与投射面垂直，这样的平行投影叫做正投影．②三视图：选取三个两两垂直的平面作为投射面．若投射面水平放置，叫做水平投射面，投射到这个平面内的图形叫做俯视图；若投射面放置在正前方，叫做直立投射面，投射到这个平面内的图形叫做主视图；和直立、水平两个投射面都垂直的投射面叫做侧立投射面，投射到这个平面内的图形叫做左视图．将空间图形向这三个平面做正投影，然后把三个投影按右图所示的布局放在一个水平面内，这样构成的图形叫空间图形的三视图．③画三视图的基本原则是“主左一样高，主俯一样长，俯左一样宽”． 4．简单几何体的表面积与体积： (1)柱体、锥体、台体和球的表面积：①S 直棱柱侧面积＝ch ，其中c 为底面多边形的周长，h 为直棱柱的高．②'=ch S 21正棱锥形面积，其中c 为底面多边形的周长，h ＇为正棱锥的斜高． ③''+=h c c S )(21正棱台侧面积，其中c ＇，c 分别是棱台的上、下底面周长，h ＇为正棱台的斜高．④S 圆柱侧面积＝2πRh ，其中R 是圆柱的底面半径，h 是圆柱的高． ⑤S 圆锥侧面积＝πRl ，其中R 是圆锥的底面半径，l 是圆锥的母线长． ⑥S 球＝4πR 2，其中R 是球的半径． (2)柱体、锥体、台体和球的体积：①V 柱体＝Sh ，其中S 是柱体的底面积，h 是柱体的高．②Sh V 31=锥体，其中S 是锥体的底面积，h 是锥体的高． ③)(31'+'+=S SS S h V 台体，其中S ＇，S 分别是台体的上、下底面的面积，h 为台体的高．④3π34R V =球，其中R 是球的半径．【复习要求】1．了解柱、锥、台、球及其简单组合体的结构特征；2．会画出简单几何体的三视图，会用斜二侧法画简单空间图形的直观图； 3．理解球、棱柱、棱锥、台的表面积与体积的计算公式． 【例题分析】例1 如图，正三棱锥P －ABC 的底面边长为a ，侧棱长为b ．(Ⅰ)证明：P A ⊥BC ；(Ⅱ)求三棱锥P －ABC 的表面积； (Ⅲ)求三棱锥P －ABC 的体积．【分析】对于(Ⅰ)只要证明BC (P A )垂直于经过P A (BC )的平面即可；对于(Ⅱ)则要根据正三棱锥的基本性质进行求解．证明：(Ⅰ)取BC 中点D ，连接AD ，PD ． ∵P －ABC 是正三棱锥，∴△ABC 是正三角形，三个侧面P AB ，PBC ，P AC 是全等的等腰三角形． ∵D 是BC 的中点，∴BC ⊥AD ，且BC ⊥PD ， ∴BC ⊥平面P AD ，∴P A ⊥BC ．(Ⅱ)解：在Rt △PBD 中，,4212222a b BD PB PD -=-= ∴.442122a b a PD BC S PBC -==⋅∆ ∵三个侧面P AB ，PBC ，P AC 是全等的等腰三角形， ∴三棱锥P －ABC 的侧面积是.44322a b a- ∴△ABC 是边长为a 的正三角形，∴三棱锥P －ABC 的底面积是,432a∴三棱锥P －ABC 的表面积为⋅-+=-+)312(434434322222a b a aa b a a (Ⅲ)解：过点P 作PO ⊥平面ABC 于点O ，则点O 是正△ABC 的中心， ∴,63233131aa AD OD =⨯==在Rt △POD 中，,3332222a b OD PD PO -=-=∴三棱锥P －ABC 的体积为.3123334331222222a b a a b a -=-⨯⨯【评述】1、解决此问题要求同学们熟悉正棱锥中的几个直角三角形，如本题中的Rt △POD ，其中含有棱锥的高PO ；如Rt △PBD ，其中含有侧面三角形的高PD ，即正棱锥的斜高；如果连接OC ，则在Rt △POC 中含有侧棱．熟练运用这几个直角三角形，对解决正棱锥的有关问题很有帮助．例2 如图，正三棱柱ABC －A 1B 1C 1中，E 是AC 的中点．(Ⅰ)求证：平面BEC 1⊥平面ACC 1A 1；(Ⅱ)求证：AB 1∥平面BEC 1．【分析】本题给出的三棱柱不是直立形式的直观图，这种情况下对空间想象能力提出了更高的要求，可以根据几何体自身的性质，适当添加辅助线帮助思考．证明：(Ⅰ)∵ABC －A 1B 1C 1是正三棱柱，∴AA 1⊥平面ABC ， ∴BE ⊥AA 1．∵△ABC 是正三角形，E 是AC 的中点，∴BE ⊥AC ，∴BE ⊥平面ACC 1A 1，又BE ⊂平面BEC 1， ∴平面BEC 1⊥平面ACC 1A 1．(Ⅱ)证明：连接B 1C ，设BC 1∩B 1C ＝D ．∵BCC 1B 1是矩形，D 是B 1C 的中点， ∴DE ∥AB 1． 又DE ⊂平面BEC 1，AB 1⊄平面BEC 1， ∴AB 1∥平面BEC 1．例3 在四棱锥P －ABCD 中，平面P AD ⊥平面ABCD ，AB ∥DC ，△P AD 是等边三角形，已知BD ＝2AD ＝8，542==DC AB ．(Ⅰ)设M 是PC 上的一点，证明：平面MBD ⊥平面P AD ； (Ⅱ)求四棱锥P －ABCD 的体积． 【分析】本题中的数量关系较多，可考虑从“算”的角度入手分析，如从M 是PC 上的动点分析知，MB ，MD 随点M 的变动而运动，因此可考虑平面MBD 内“不动”的直线BD 是否垂直平面P AD ．证明：(Ⅰ)在△ABD 中，由于AD ＝4，BD ＝8，54=AB ，所以AD 2＋BD 2＝AB 2． 故AD ⊥BD ．又平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，BD ⊂平面ABCD ， 所以BD ⊥平面P AD ，又BD ⊂平面MBD ，故平面MBD ⊥平面P AD ． (Ⅱ)解：过P 作PO ⊥AD 交AD 于O ，由于平面P AD ⊥平面ABCD ，所以PO ⊥平面ABCD ． 因此PO 为四棱锥P －ABCD 的高，又△P AD 是边长为4的等边三角形．因此.32423=⨯=PO 在底面四边形ABCD 中，AB ∥DC ，AB ＝2DC ，所以四边形ABCD 是梯形，在Rt △ADB 中，斜边AB 边上的高为5585484=⨯，即为梯形ABCD 的高， 所以四边形ABCD 的面积为.2455825452=⨯+=S 故.316322431=⨯⨯=-ABCD P V例4 如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图．它的主视图和左视图在下面画出(单位：cm)(Ⅰ)画出该多面体的俯视图；(Ⅱ)按照给出的尺寸，求该多面体的体积； (Ⅲ)在所给直观图中连结BC ＇，证明：BC ＇∥平面EFG ．【分析】画三视图的基本原则是“主左一样高，主俯一样长，俯左一样宽”，根据此原则及相关数据可以画出三视图．证明：(Ⅰ)该几何体三视图如下图：(Ⅱ)所求多面体体积).cm (32842)2221(316442=⨯⨯⨯⨯-⨯⨯=-=正三棱锥长方体V V V (Ⅲ)证明：在长方体ABCD －A'B'C'D'中，连结AD'，则AD'∥BC'． 因为E ，G 分别为AA'，A'D'中点， 所以AD'∥EG ，从而EG ∥BC '．又BC'⊄平面EFG ， 所以BC'∥平面EFG ．例5 有两个相同的直三棱柱，底面三角形的三边长分别是3a ，4a ，5a ，高为a2，其中a ＞0．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的一个是四棱柱，求a 的取值范围．解：直三棱柱ABC －A 1B 1C 1的三个侧面的面积分别是6，8，10，底面积是6a 2，因此每个三棱柱的表面积均是2×6a 2＋6＋8＋10＝12a 2＋24．情形①：将两个直三棱柱的底面重合拼在一起，只能拼成三棱柱，其表面积为： 2×(12a 2＋24)－2×6a 2＝12a 2＋48．情形②：将两个直三棱柱的侧面ABB 1A 1重合拼在一起，结果可能拼成三棱柱，也可能拼成四棱柱，但表面积一定是：2×(12a 2＋24)－2×8＝24a 2＋32．情形③：将两个直三棱柱的侧面ACC 1A 1重合拼在一起，结果可能拼成三棱柱，也可能拼成四棱柱，但表面积一定是：2×(12a 2＋24)－2×6＝24a 2＋36．情形④：将两个直三棱柱的侧面BCC 1B 1重合拼在一起，只能拼成四棱柱，其表面积为：2×(12a 2＋24)－2×10＝24a 2＋28在以上四种情形中，②、③的结果都比④大，所以表面积最小的情形只能在①、④中产生．依题意“表面积最小的一个是四棱柱”，得24a 2＋28＜12a 2＋48，解得,352<a 所以a 的取值范围是⋅)315,0(例6 在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1，CD 的中点，求三棱锥F －A 1ED 1的体积．【分析】计算三棱锥F －A 1ED 1的体积时，需要确定锥体的高，即点F 到平面A 1ED 1的距离，直接求解比较困难．利用等积的方法，调换顶点与底面的方式，如1111EFD A ED A F V V --=，也不易计算，因此可以考虑使用等价转化的方法求解．解法1：取AB 中点G ，连接FG ，EG ，A 1G ． ∵GF ∥AD ∥A 1D 1，∴GF ∥平面A 1ED 1，∴F 到平面A 1ED 1的距离等于点G 到平面A 1ED 1的距离．∴.8183313132111111111a a a D A S V V V EG A EG A D ED A G ED A F =⨯⨯====⋅∆---解法2：取CC 1中点H ，连接F A 1，FD 1，FH ，FC 1，D 1H ，并记FC 1∩D 1H ＝K ．∵A 1D 1∥EH ， A 1D 1＝EH ，∴A 1，D 1，H ，E 四点共面． ∵A 1D 1⊥平面C 1CDD 1，∴FC ⊥A 1D 1．又由平面几何知识可得FC 1⊥D 1H ，∴FC ⊥平面A 1D 1HE ． ∴FK 的长度是点F 到平面A 1D 1HE (A 1ED 1)的距离． 容易求得.811053453131,1053321111a a a FK S V a FK ED A ED A F =⨯⨯===⋅∴∆- 练习7－2一、选择题：1．将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为( ) (A)2π (B)4π (C)8π (D)16π2．如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )(A)9π (B)10π (C)11π (D)12π3．有一种圆柱体形状的笔筒，底面半径为4 cm ，高为12 cm ．现要为100个这种相同规格的笔筒涂色(笔筒内外均要涂色，笔筒厚度忽略不计)．如果所用涂料每0.5 kg 可以涂1 m 2，那么为这批笔筒涂色约需涂料( ) (A)1.23 kg (B)1.76 kg (C)2.46 kg (D)3.52 kg 4．某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a 和b 的线段，则a ＋b 的最大值为( ) (A)22(B)32(C)4(D)52二、填空题：5．如图，正三棱柱ABC －A 1B 1C 1的每条棱长均为2，E 、F 分别是BC 、A 1C 1的中点，则EF 的长等于______．6．将边长为1的正方形ABCD 沿对角线AC 折起，使得BD ＝1，则三棱锥D －ABC 的体积是______．7．一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为3，底面周长为3，则这个球的体积为______．8．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件①：_______________________________________________________________； 充要条件②：_______________________________________________________________． (写出你认为正确的两个充要条件) 三、解答题：9．如图，在正四棱柱ABCD －A 1B 1C 1D 1中，E 是DD 1的中点．(Ⅰ)求证：BD 1∥平面ACE ；(Ⅱ)求证：平面ACE ⊥平面B 1BDD 1． 10．已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．(Ⅰ)求该几何体的体积V ； (Ⅱ)求该几何体的侧面积S ．11．如图，已知ABCD －A 1B 1C 1D 1是棱长为3的正方体，点E 在AA 1上，点F 在CC 1上，且AE ＝FC 1＝1．(Ⅰ)求证：E ，B ，F ，D 1四点共面； (Ⅱ)若点G 在BC 上，32=BG ，点M 在BB 1上，GM ⊥BF ，求证：EM ⊥面BCC 1B 1．习题7一、选择题：1．关于空间两条直线a 、b 和平面α ，下列命题正确的是( ) (A)若a ∥b ，b ⊂α ，则a ∥α (B)若a ∥α ，b ⊂α ，则a ∥b (C)若a ∥α ，b ∥α ，则a ∥b (D)若a ⊥α ，b ⊥α ，则a ∥b 2．正四棱锥的侧棱长为23，底面边长为2，则该棱锥的体积为( ) (A)8(B)38 (C)6 (D)23．已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则直线AB 1与侧面ACC 1A 1所成角的正弦值等于( ) (A)46 (B)410 (C)22 (D)23 4．已知某个几何体的三视图如下，根据图中标出的尺寸(单位：cm)，可得这个几何 体的体积是( )(A)3cm 34000 (B)3cm 38000 (C)2000cm 3 (D)4000cm 35．若三棱柱的一个侧面是边长为2的正方形，另外两个侧面都是有一个内角为60° 的菱形，则该棱柱的体积等于( ) (A)2 (B)22(C)23(D)24二、填空题：6．已知正方体的内切球的体积是π34，则这个正方体的体积是______．7．若正四棱柱ABCD －A 1B 1C 1D 1的底面边长为1，AB 1与底面ABCD 成60°角，则直线AB 1和BC 1所成角的余弦值是______． 8．若三棱锥的三条侧棱两两垂直，且侧棱长均为3，则其外接球的表面积是______．9．连结球面上两点的线段称为球的弦．半径为4的球的两条弦AB 、CD 的长度分别等于3472、，每条弦的两端都在球面上运动，则两弦中点之间距离的最大值为______．10．已知AABC 是等腰直角三角形，AB ＝AC ＝a ，AD 是斜边BC 上的高，以AD 为折痕使∠BDC 成直角．在折起后形成的三棱锥A －BCD 中，有如下三个结论： ①直线AD ⊥平面BCD ； ②侧面ABC 是等边三角形；③三棱锥A －BCD 的体积是.2423a 其中正确结论的序号是____________．(写出全部正确结论的序号) 三、解答题：11．如图，正三棱柱ABC －A 1B 1C 1中，D 是BC 的中点，AB ＝AA 1．(Ⅰ)求证：AD ⊥B 1D ；(Ⅱ)求证：A 1C ∥平面A 1BD ；(Ⅲ)求二面角B －AB 1－D 平面角的余弦值．12．如图，三棱锥P －ABC 中，P A ⊥AB ，P A ⊥AC ，AB ⊥AC ，P A ＝AC ＝2，AB ＝1，M 为PC 的中点．(Ⅰ)求证：平面PCB ⊥平面MAB ； (Ⅱ)求三棱锥P －ABC 的表面积．13．如图，在直三棱柱ABC －A 1B 1C 1中，∠ABC ＝90°，AB ＝BC ＝AA 1＝2，M 、N 分别是A 1C 1、BC 1的中点．(Ⅰ)求证：BC 1⊥平面A 1B 1C ； (Ⅱ)求证：MN ∥平面A 1ABB 1； (Ⅲ)求三棱锥M －BC 1B 1的体积． 14．在四棱锥S －ABCD 中，底面ABCD 为矩形，SD ⊥底面ABCD ，2=AD ，DC ＝SD ＝2．点M 在侧棱SC 上，∠ABM ＝60°．(Ⅰ)证明：M 是侧棱SC 的中点；(Ⅱ)求二面角S －AM －B 的平面角的余弦值．专题07 立体几何参考答案练习7-1一、选择题：1．B 2．D 3．C 4．B 二、填空题：5．10 6．AC ⊥BD (或能得出此结论的其他条件)7．②、③、④⇒①；或①、③、④⇒② 8．④ 三、解答题：9．(Ⅰ)解：连接MB ，MC ．∵三棱锥P －ABC 的三个侧面均为边长是1的等边三角形，∴23==MC MB ，且底面△ABC 也是边长为1的等边三角形． ∵N 为BC 的中点，∴MN ⊥BC ． 在Rt △MNB 中，⋅=-=2222BN MB MN (Ⅱ)证明：∵M 是P A 的中点，∴P A ⊥MB ，同理P A ⊥MC ．∵MB ∩MC ＝M ，∴P A ⊥平面MBC ， 又BC ⊂平面MBC ，∴P A ⊥BC ．10．证明：(Ⅰ)∵E 、F 分别是AB 、BD 的中点，∴EF 是△ABD 的中位线，∴EF ∥AD ．又EF ⊄平面ACD ，AD ⊂平面ACD ，∴直线EF ∥平面ACD ．(Ⅱ)∵EF ∥AD ，AD ⊥BD ，∴EF ⊥BD ．∵CB ＝CD ，F 是BD 的中点，∴CF ⊥BD ． ∵CF ∩EF ＝F ，∴BD ⊥平面CEF ．∵BD ⊂平面BCD ，∴平面EFC ⊥平面BCD ．11．(Ⅰ)由题意知，FG ＝GA ，FH ＝HD ，∴GH ∥AD ，,21AD GH =又BC ∥AD ，AD BC 21=，∴GH ∥BC ，GH ＝BC ， ∴四边形BCHG 是平行四边形． (Ⅱ)C ，D ，F ，E 四点共面．理由如下： 由BE ∥AF ，AF BF 21=，G 是F A 的中点， 得BE ∥FG ，且BE ＝FG ．∴EF ∥BG ．由(Ⅰ)知BG ∥CH ，∴EF ∥CH ，故EC ，FH 共面，又点D 在直线FH 上， 所以C ，D ，F ，E 四点共面． (Ⅲ)连结EG ，由AB ＝BE ，BE ∥AG ，BE ＝AG 及∠BAG ＝90°，知ABEG 是正方形， 故BG ⊥EA ．由题设知F A ，AD ，AB 两两垂直，故AD ⊥平面F ABE ，∴BG ⊥AD ． ∴BG ⊥平面EAD ，∴BG ⊥ED ． 又ED ∩EA ＝E ，∴BG ⊥平面ADF ． 由(Ⅰ)知CH ∥BG ，∴CH ⊥平面ADE ．由(Ⅱ)知F ∈平面CDE ，故CH ⊂平面CDE ，得平面ADE ⊥平面CDE ．练习7-2一、选择题：1．B 2．D 3．D 4．C 二、填空题： 5．5 6．122 7．3π48．答案不唯一，如“两组相对侧面分别平行”；“一组相对侧面平行且全等”；“对角线交于一点”；“底面是平行四边形”等． 三、解答题：9．证明：(Ⅰ)设AC ∩BD ＝O ，连结OE ．∵E 是DD 1的中点，O 是BD 的中点，∴OE ∥BD 1．又OE ⊂平面ACE ，BD 1⊄平面ACE ，∴BD 1∥平面ACE ．(Ⅱ)∵ABCD －A 1B 1C 1D 1是正四棱柱，∴底面ABCD 是正方形，∴AC ⊥BD ．又D 1D ⊥平面ABCD ，∴AC ⊥D 1D ，∴AC ⊥平面B 1BDD 1， ∵AC ⊂平面ACE ，∴平面ACE ⊥平面B 1BDD 1．10．解：由已知可得该几何体是一个底面为矩形，高为4，顶点在底面的射影是矩形中心的四棱锥P －ABCD ．(Ⅰ).644)68(3131=⨯⨯⨯==Sh V (Ⅱ)该四棱锥有两个侧面P AD 、PBC 是全等的等腰三角形，且BC 边上的高为：h 1＝.24)28(422=+ 另两个侧面P AB 、PCD 也是全等的等腰三角形， AB 边上的高为,5)26(4222=-+=h因此.22440)582124621(2+=⨯⨯+⨯⨯=S11．(Ⅰ)证明：在DD 1上取一点N 使得DN ＝1，连接CN ，EN ，显然四边形CFD 1N 是平行四边形，∴D 1F ∥CN ． 同理四边形DNEA 是平行四边形，∴EN ∥AD ，且EN ＝AD ． 又BC ∥AD ，且BC ＝AD ，∴EN ∥BC ，且EN ＝BC ， ∴四边形CNEB 是平行四边形，∴CN ∥BE ， ∴D 1F ∥BE ，∴E ，B ，F ，D 1四点共面．(Ⅱ)∵GM ⊥BF ，∴△BCF ∽△MBG ，∴,CF BGBC MB =即,2323=MB ∴MB ＝1．∵AE ＝1，∴四边形ABME 是矩形，∴EM ⊥BB 1．又平面ABB 1A 1⊥平面BCC 1B 1，且EM ⊂平面ABB 1A 1，∴EM ⊥平面BCC 1B 1．习题7一、选择题：1．D 2．B 3．A 4．B 5．B 二、填空题： 6．324 7．438．9π 9．5 10．①、②、③ 三、解答题：11．(Ⅰ)证明：∵ABC －A 1B 1C 1是正三棱柱，∴BB 1⊥平面ABC ，∴平面BB 1C 1C ⊥平面ABC ．∵正△ABC 中，D 是BC 的中点，∴AD ⊥BC ，∴AD ⊥平面BB 1C 1C ， ∴AD ⊥B 1D ．(Ⅱ)解：连接A 1B ，设A 1B ∩AB 1＝E ，连接DE ． ∵AB ＝AA 1， ∴ 四边形A 1ABB 1是正方形，∴E 是A 1B 的中点，又D 是BC 的中点，∴DE ∥A 1C ．∵DE ⊂平面A 1BD ，A 1C ⊄平面A 1BD ，∴A 1C ∥平面A 1BD ．(Ⅲ)解：建立空间直角坐标系，设AB ＝AA 1＝1， 则⋅-)1,0,21(),0,23,0(),0,0,0(1B A D设n 1＝(p ，q ，r )是平面A 1BD 的一个法向量， 则,01=⋅n 且,011=⋅B n 故.021,023=-=-r P q 取r ＝1，得n 1＝(2，0，1)． 同理，可求得平面AB 1B 的法向量是).0,1,3(2-=n 设二面角B －AB 1－D 大小为θ ，∵,515||||cos 2121==⋅n n n n θ∴二面角B －AB 1－D 的平面角余弦值为⋅51512．(Ⅰ)∵P A ⊥AB ，AB ⊥AC ，∴AB ⊥平面P AC ，故AB ⊥PC ．∵P A ＝AC ＝2，M 为PC 的中点，∴MA ⊥PC ．∴PC ⊥平面MAB ， 又PC ⊂平面PCB ，∴平面PCB ⊥平面MAB ．(Ⅱ)Rt △P AB 的面积1211==⋅AB PA S ．Rt △P AC 的面积.2212==⋅AC PA S Rt △ABC 的面积S 3＝S 1＝1．∵△P AB ≌△CAB ，∵PB ＝CB ，∴△PCB 的面积.632221214=⨯⨯==⋅MB PC S ∴三棱锥P －ABC 的表面积为S ＝S 1＋S 2＋S 3＋S 4＝.64+13．(Ⅰ)∵ABC －A 1B 1C 1是直三棱柱，∴BB 1⊥平面A 1B 1C 1，∴B 1B ⊥A 1B 1．又B 1C 1⊥A 1B 1，∴A 1B 1⊥平面BCC 1B 1，∴BC 1⊥A 1B 1． ∵BB 1＝CB ＝2，∴BC 1⊥B 1C ，∴BC 1⊥平面A 1B 1C ．(Ⅱ)连接A 1B ，由M 、N 分别为A 1C 1、BC 1的中点，得MN ∥A 1B ， 又A 1B ⊂平面A 1ABB 1，MN ⊄平面A 1ABB 1，∴MN ∥平面A 1ABB 1．(Ⅲ)取C 1B 1中点H ，连结MH ．∵M 是A 1C 1的中点，∴MH ∥A 1B 1，又A 1B 1⊥平面BCC 1B 1，∴MH ⊥平面BCC 1B 1，∴MH 是三棱锥M －BC 1B 1的高， ∴三棱锥M －BC 1B 1的体积⋅=⨯⨯⨯==⋅⋅∆321421313111MH S V B BC 14．如图建立空间直角坐标系，设A (2，0，0)，则B (2，2，0)，C (0，2，0)，S (0，0，2).(Ⅰ)设)0(>=λλ， 则),12,12,2(),12,12,0(λλλλλ++--=++BM M 又.60,),0,2,0(ο>=<-=BM BA BA 故,60cos ||||.οBM =即,)12()12()2(14222λλλ+++-+-=+解得λ ＝1． ∴M 是侧棱SC 的中点．(Ⅱ)由M (0，1，1)，A (2，0，0)得AM 的中点⋅)21,21,22(G 又),1,1,2(),1,1,0(),21,23,22(-=-=-=AM MS GB ∴,,,0,0AM AM ⊥⊥∴==⋅⋅∴cos,G 〈等于二面角S －AM －B 的平面角． Θ,36||||),cos(-==MS GB 即二面角S －AM －B 的平面角的余弦值是－36．。

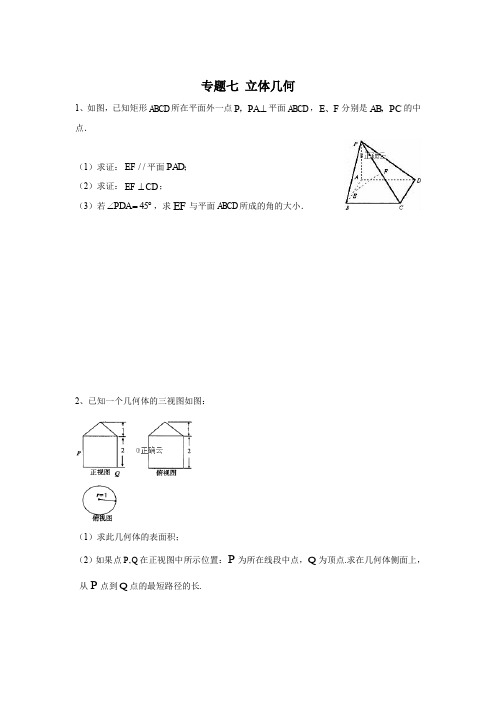
专题七 立体几何1、如图，已知矩形ABCD 所在平面外一点，⊥P PA 平面ABCD ，、E F 分别是，AB PC 的中点．（1）求证：//EF 平面；PAD （2）求证：⊥EF CD ；（3）若45∠=︒PDA ，求EF 与平面ABCD 所成的角的大小．2、已知一个几何体的三视图如图：（1）求此几何体的表面积；（2）如果点,P Q 在正视图中所示位置：P 为所在线段中点，Q 为顶点.求在几何体侧面上，从P 点到Q 点的最短路径的长.3、如图，PC ⊥平面ABC ，//DA PC ，90ACB ∠=︒，E 为PB 的中点，1AC AD BC ===，2PC =．（1）求证：//DE 平面ABC ； （2）求证：PD ⊥平面BCD ；（3）设Q 为PB 上一点PQ PB λ=uuu r uur，试确定λ的值使得二面角Q CD B --为45°．4、如图，在单位正方体1111-ABCD A B C D 中，O 是11B D 的中点. （1）求证1//B C 平面1ODC ；（2）求异面直线1B C 与OD 夹角的余弦值； （3）求直线1B C 到平面1ODC 的距离.5、已知直三棱柱111ABC A B C －中，112023BCA AB AC AA ∠︒＝，＝＝，＝， E 是BC 的中点，F 是1A E 上一点，且13A F FE ＝. （1）证明：AF ⊥平面1A BC ；（2）求二面角11B A E B －－余弦值的大小.6、四面体ABCD 及其三视图如图所示，过棱AB 的中点E 作平行于,AD BC 的平面分别交四面体的棱,,BD DC CA 于点,,F G H .（1）证明：四边形EFGH 是矩形；（2）求直线AB 与平面EFGH 夹角θ的正弦值.答案以及解析1答案及解析：答案：（1）取PD 中点Q ，连、，AQ QF 则//AE QF ， ∴四边形AEFQ 为平行四边形， ∴//EF AQ ，又∵AQ 在平面PAD 内，EF 不在平面PAD 内， ∴//EF 面PAD ；（2）证明：∵⊥CD AD ，⊥CD PA ，⋂=PA AD A ，PA 在平面PAD 内，AD 在平面PAD 内，∴⊥CD 面PAD ， 又∵AQ 在平面PAD 内， ∴⊥CD AQ ， ∵//EF AQ ， ∴⊥CD EF ；（3）解：∵45∠=︒PDA ， ∴PAD △为等腰直角三角形， ∴⊥AQ PD ， ∴45∠=︒QAD ，即AQ 与平面ABCD 所成角为45︒， 又∵//AQ EF ，∴EF 与平面ABCD 所成角45︒．2答案及解析：答案：（1）由三视图可知，此几何体是一个圆锥和一个圆柱的组合体，其表面积是圆锥的侧面积、圆柱的侧面积与圆柱的一个底面积之和.()()12222S =π=π圆锥侧，()()224S =ππ⋅=圆柱侧，S =π圆柱底，所以此几何体的表面积()2π4ππ25.S S S S a =++=+π++=表圆锥侧圆柱侧圆柱底（2）分别沿点P 与点Q 所在的母线剪开圆柱的侧面，并展开铺平，如图所示则()()2221πPQ AP AQ =+=+，所以,P Q 两点在该几何体的侧面上的最短路径的长为2π1+.3答案及解析：答案：（1）证明：建立如图所示的空间直角坐标系，则010101()()()002B D P ,,,,,,,,，10,,12E ⎛⎫ ⎪⎝⎭，11,,02DE ⎛⎫=- ⎪⎝⎭uuur .可知()0,0,2PC =uuu r为平面ABC 的一个法向量，0DE PC ⋅=u u u r u u u r Q ，DE BC ∴⊥uuu r uu u r ．DE ⊄Q 平面ABC ，//DE ∴平面ABC ．（2）证明：()1,0,1PD =-uuu r Q ，()0,1,0BC =uu u r ，()1,0,1CD =uuu r．0PD BC ∴⋅=u u u r u u u r ，0PD CD ⋅=u u u r u u u r．PD BC ∴⊥，PD CD ⊥．BC DC C ⋂=Q ，PD ∴⊥平面BCD ．（3）解：由（2）可知：()1,0,1PD =-uuu r为平面BCD 的法向量，()0,1,2PB =-uur Q ，()0,,2PQ PB λλλ==-uuu r uur，()0,1λ∈．()0,,22Q λλ∴-+．设平面QCD 的法向量为(),,n x y z r，由00n CD n CQ ⎧⋅=⎪⎨⋅=⎪⎩r uu u r r uu u r ，得()0220x z y z λλ+=⎧⎪⎨+-+=⎪⎩，令1z =，则1x =-，22y λ=-，()21,2,1,0,1n λλ⎛⎫∴=--∈ ⎪⎝⎭r ．cos 45n PD n PD⋅︒=⋅r uu u r r uu u r22222222λ==⎛⎫⨯+- ⎪⎝⎭，解得22λ=-．4答案及解析：答案：（1）法一：连接1A D ，则11//.B A C D 而1⊆A D 平面1ODC ，1⊄B C 平面1ODC ， 所以1//B C 平面1ODC .法二：设平面1ODC 的一个法向量为(,,)=n x y z ，由 1.0.0⎧=⎪⎨=⎪⎩n DO n DC ，得11022⎧++=⎪⎨⎪+=⎩x y z y z ，令1=y ，则1,1=-=z x ， 所以(1,1,1)=-n .又1(1,0,1)=--B C .从而1.0=n B C ， 所以1//B C 平面1ODC .（2）法一：由（1）知异面直线1B C 与OD 的夹角为1∠A DO 或其补角. 而1111==A D AC DC ，且O 为11A C 中点，故0130∠=A DO ， 所以两异面直线1B C 与OD 的夹角θ的余弦值为3COS 2θ=. 法二：设1B C 、DO 分别为直线1B C 与OD 的方向向量，则由1(1,01)=--B C ，11(,,1)22=DO ，得1,3cos 2<>=B C DO ，所以两异面直线1B C 与OD 的夹角θ的余弦值为3COS 2θ=. （3）由（1）知平面1ODC 的一个法向量为(1,11)=-n ，又(0,1,0)=DC ， 所以1B C 到平面1ODC 的距离33⋅==DC n d n.5答案及解析：答案：（1）连接,AE AF ，在ABC △中，11sin12022AB AC BC AE ⋅⋅=⋅°，故1AE =. 由于三棱柱111ABC A B C -是直三棱柱，故1AA ⊥平面1ABC AA AE ⇒⊥，直角三角形1A AE 中，因为13,1AA AE ==，所以1122A E EF =⇒=，又因1A EAE AFE EF AE =⇒∠为直角，即1A E AF ⊥，再由E 为BC 中点并且ABC △为等腰三角形可知AE BC ⊥，结合1AA BC ⊥，1AA AE A =I ，得BC ⊥平面1A AE BC AF ⇒⊥，综合1A E AF ⊥，BC AF ⊥，1BC A E E=I ，得到AF ⊥平面1A BC .（2）由于AE BC ⊥，如图以点E 为坐标原点建立空间直角坐标系，3tan 60AEBE ==°，故()()()()113,0,0,0,1,3,0,0,0,3,0,3B A E B --，()()()113,0,0,0,1,3,3,0,3EB EA EB =-==-u u r u u u r u u u r.设面1BA E 法向量为1111(,,)n x y z =u r，面11B A E 法向量为2222(,,)nx y z =u u r，111111030300n EB x y z n EA ⎧⎧⋅=-=⎪⎪⇒⎨⎨+=⋅=⎪⎪⎩⎩u r uu ru r uuu r ，取11z =，得1(0,3,1)n =-u r ，212221210330300n EB x z y z n EA ⎧⎧⋅=-+=⎪⎪⇒⎨⎨+=⋅=⎪⎪⎩⎩u u r uuu ru ur uuu r ，取21z =，得2(1,3,1)n =-u u r ，则二面角11B A E B --的余弦值1212425cos 545n n n n θ⋅===⋅⋅u r uu r u r u u r .6答案及解析：答案：（1）由该四面体的三视图可知，,BD DC ⊥,BD AD ⊥,AD DC ⊥BD DC ⊥，2BD DC ==，1AD =.由题知，//BC 平面EFGH ，平面EFGH ⋂平面BDC FG =，平面EFGH ⋂平面ABC EH =， ∴//BC FG ，//BC EH ，//FG EH . 同理//EF AD ，//HG AD ，∴//EF HG . ∴四边形EFGH 是平行四边形， 又AD DC ⊥，AD BD ⊥， ∴AD ⊥平面BDC ， ∴EF FG ⊥，∴四边形EFGH 是矩形.（2）方法一：如图，以D 为坐标原点建立空间直角坐标系，则()0,0,0D ，()0,0,1A ，()2,0,0B ，()0,2,0C .()0,0,1DA =，()2,2,0BC =-，(2,0,1)BA =-.设平面EFGH 的法向量(,,)n x y z =， ∵//EF AD ，//FG BC ，∴0n DA ⋅=，0n BC ⋅=，得0220z x y =-+=⎧⎨⎩，取()1,1,0n =，∴210sin cos ,552BA n BA n BA nθ⋅=〈〉===⨯.方法二：如图，以D 为坐标原点建立空间直角坐标系，()0,0,0D ，()0,0,1A ，()2,0,0B ，()0,2,0C .∵E 是AB 的中点，∴F 、G 分别为BD 、DC 的中点，得11,0,2E ⎛⎫⎪⎝⎭，()1,0,0F ，()0,1,0G . ∴10,0,2FE ⎛⎫= ⎪⎝⎭，(1,1,0)FG =-，(2,0,1)BA =-.设平面EFGH 的法向量(,,)n x y z =，则0n FE ⋅=，0n FG ⋅=，得 12z x y ⎧=-+=⎪⎨⎪⎩ ，取()1,1,0n =， ∴210sin cos ,552BA n BA n BA nθ⋅=〈〉===⨯.。

第2讲综合大题部分真题押题精练演练模拟| ［真题体验1.(2018 •高考全国卷I )如图，四边形ABCD^正方形，E, F分别为AD BC的中点，以DF为折痕把厶DFC折起，使点C到达点P的位置，且PF丄BF(1)证明：平面PEFL平面ABFD⑵求DP与平面ABFD所成角的正弦值.解析：⑴证明：由已知可得BF丄PF, BF丄EF,所以BF丄平面PEF又BF?平面ABFD所以平面PEFL平面ABFD⑵如图，作PH丄EF,垂足为H由⑴ 得，PH丄平面ABFD以H为坐标原点，希勺方向为y轴正方向，| BF为单位长，建立如图所示的空间直角坐标系H-xyz.由⑴可得，DEI PE又DP= 2, DE= 1,所以PE= 3.又PF= 1, EF= 2,所以PEL PF.31,- 1, 0 ,所以PH=2则 H(0,0,0)又帀为平面ABFD 勺法向量,设DP 与平面ABF ［所成角为0 ,所以DP 与平面ABFD 所成角的正弦值为)如图，在三棱锥 F -ABC 中, AB= BC= 2 2, PA= PB= PC= AC 4,O 为AC 的中点.(1)证明：POL 平面ABC⑵ 若点M 在棱BC 上，且二面角 MPAC 为30°,求PC 与平面PAM 所成角的正弦值. 解析：⑴ 证明：因为 PA= PC= AC= 4, O 为AC 的中点， 所以 OPL AC 且 OP= 2^3.如图，连接OB所以△ ABC 为等腰直角三角形， 1且 OBLAC , OB= q AC= 2. 由 OP + OB= PB 知 PC L OB由 OPL OB OPLAC , OBH AC= O,得 PO L 平面 ABC⑵ 如图，以O 为坐标原点，OB 勺方向为x 轴正方向，建立空间直角坐标系Oxyz .由已知得 Q 0,0,0) , B (2,0,0) , A (0, — 2,0) , C (0,2,0) , P (0,0 , 2护),辰(0,2,2 西). 取平面PAC 的一个法向量 OB= (2,0,0).设 Ma,2— a, 0)(0 < a w 2),贝 U AM = (a, 4 — a,0). 设平面PAM 勺法向量为n = (x , y , z ). 由 AP • n = 0 , AM ・ n = 0 得可取y = 3a ,得平面PAM 勺一个法向量为n = (.3( a — 4), .3 a, — a),2 羽 a-&2* a —1 2+ 3a 2 + a 2则sin葩5P1丽6p2. (2018 •高考全国卷n 2y + 2伍=0 , ©x +4 — a y = 0 ,所以 cos 〈 O B n > 因为AB= BC=由已知可得|cos 〈 O B n> | = cos 30所以2臂;4|a尋2a — 4 + 3a + a24解得 a =— 4(舍去)或a =3.又 PC= (0,2 , — 2 3)，所以 cos 〈P c , n 〉=¥• 所以PC 与平面PA 術成角的正弦值为电33. (2017 •高考全国卷I )如图，在四棱锥 RABCDK AB// CD 且/ BAP=Z CDP= 90(1) 证明：平面 PABL 平面PAD(2) 若 PA= PD= AB= DC / APD= 90°,求二面角 A PB C 的余弦值. 解析：⑴ 证明：由已知/ BAP=Z CDP= 90°, 得 AB 丄 AP, CDL PD由于 AB// CD 故 ABL PD 又 APA PD= P , 从而AE L 平面PAD又AB ?平面PAB 所以平面 PABL 平面PAD (2)在平面PAD 内作PF 丄AD 垂足为F .由(1)可知，AB 丄平面PAD 故AE L PF,可得PF 丄平面 ABCD以F 为坐标原点，F A 的方向为x 轴正方向，|AB 为单位长度，建立如图所示的空间直角 坐标系F -xyz .由(1)及已知可得，0，0，P 0，0，-2，B-22，1, 0，C —¥，1，0 .所以陀—与,1, — -2,6B = ( ,2, 0,0) , P A = -2, 0, — -2 , X B = (0,1,0) 设n = (X 1,屮,Z 1)是-3.4“33 ，平面PCE的法向量，则可取 n = (0，- 1,—2).设m = (X 2, y 2, Z 2)是平面PAB 的法向量，则4. (2018 •高考全国卷川)如图，边长为2的正方形ABCD 所在的平面与半圆弧 「丨:'所在平面.X — 垂直，M 是「「上异于C, D 的点.(1)证明：平面AM D 平面BMC⑵ 当三棱锥 MABC 体积最大时，求面 MAB^面MCC 所成二面角的正弦值.解析：(1)证明：由题设知，平面 CM D 平面 ABCD 交线为 CD 因为BC D CD BC ?平面ABCD所以BC D 平面 CMD 故BC D DM因为M 为「1 :'上异于C, D 的点，且DC 为直径， 所以DML CM 又BOH CM = C,所以DML 平面BMC 而DM ?平面AMD 故平面 AM D 平面BMC⑵ 以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所示的空间直角坐标系D-xyz .当三棱锥MABC 体积最大时，M 为「■!：'的中点.由题设得D (0,0,0) , A (2,0,0) , B (2,2,0) , C (0,2,0) , M 0,1,1),n • P C= 0, n • CB= 0,m- PA = 0,m- AB= 0,可取 m = (1,0,1)贝U cos 〈 n , m 〉n • m -申 护I n || m = 3x ^2 =-~所以二面角A -PBC 的余弦值为一A M = ( - 2,1,1) ,A E= (0,2,0) ,D A = (2,0,0)—2x+ y + z= 0 ,即＜2y= 0.可取n= (1,0,2) ,DA是平面MCD勺法向量，因此设n= (x , y , z)是平面MAB勺法向量,则押题预测1.如图所示，在平行四边形 ABCDK BC= 2AB= 4, / ABC= 60°, PAL AD E, F 分别为BCPE 的中点，AF 丄平面PED(1) 求证：PA!平面 ABCD(2) 求直线BF 与平面AFD 所成角的正弦值. 解析：⑴证明：连接AE 由 BC= 2AB= 4,Z ABC= 60°,••• AE= 2, ED- 2 3，从而有 AU + E D = AD ,所以AE! ED又AF P AE= A ,所以ED 丄平面PAE PA ?平面PAE 贝U ED L PA又 PA L AD ADA ED - D,所以 PA!平面 ABCD则 A (0,2,0) , D (2 .3 , 0,0),氏—.3 ,1,0), 因为AFL 平面PED 所以AF L PEcos 〈 n , D A >「艮仝,sin 〈n , D A >=罕.|n | |D A |55所以面MAB 与面MCC 所成二面角的正弦值是2：55⑵ 以E 为坐标原点，建立如图所示的空间直角坐标系，又F为PE的中点，所以PA= AE= 2 ,所以F(0,2,2) , F(0,1,1) , X F= (0，- 1,1) , K b= (2 3,—2,0) , B F= ( 3, 0,1),设平面AFb的法向量为n= (x, y, z),A F- n = 0, —y+ z= 0,由得X b- n = 0, 2 3x—2y= 0令x = 1,得n= (1 , 3, 3).设直线BF与平面AFb所成的角为0 ,小X I BF・ n l 2护J21贝U sin 0 = |cos 〈BF, n〉| = =———= ,|BF| n| 2p7即直线BF与平面AFD所成角的正弦值为亠g=45°, AD= AP= 2,2.如图所示，在四棱锥P-ABCDK 侧面PADL底面ABCD底面ABCD1平行四边形，/ ABC(1)求证：ADL PC⑵试确定点F的位置，使得直线EF与平面PDC所成的角和直线EF与平面ABC斷成的角相等.解析：(1)证明：如图所示，在平行四边形ABC呼，连接AC因为AB= 2 ,2 , BC= 2，/ ABC= 45°,由余弦定理得，A C=A B+B C— 2 - AB- BC- cos 45°= 4,得AC= 2,所以/ ACB= 90°, 即BC L AC又AD// BC 所以AD L AC 因为AD= AF= 2, DP= 2 2,所以PAL AD又AP n AC= A ,所以AC L 平面PAC 所以ADL PC⑵因为侧面PA L 底面ABCD PAL AD所以PA L 底面ABCD 所以直线 AC AD AP 两两互相垂直，以 A 为原点，直线 AD AC设兽入（入€ [0,1]）,则 PF = （2 入，2 入，一2 入），F （2 入，2 入，一2 入 + 2）, 所以矗（2入+ 1,2入一1,— 2入+ 2），易得平面ABCD 勺一个法向量为 设平面PDC 的法向量为n = （x , y , z ）,n • PC= 0 , 由Tn • PD= 0 ,EF 与平面PDC 所成的角和直线 EF 与平面ABC 斷成的角相等, < EF, m> | = |cos 〈 EF,n 〉| , 即I EF ・ m = | EF ・ n ||EF | m |EF | n 「2入所以 | — 2 入 + 2| =1二1 ,即，3| 入一1| = | 入 |(入 € [0,1]),3—V3PF 3—J3解得x=,所以PT —AP 为坐标轴，建立如图所示的空间直角坐标系A -xyz ，贝U A (0,0,0) ，Q — 2,0,0), C (0,2,0) ,B (2,2,0) , E ( — 1,1,0) , P (0,0,2)，所以归(0,2 , — 2),PD= ( — 2,0，—2) , PB= (2,2 , — 2).m ^ (0,0,1)得 2y — 2Z = 0, —2x — 2z = 0,令 x = 1,得 n = (1 , — 1,— 1).因为直线 所以|cos即当PB= 32討时，直线EF 与平面PDC 所成的角和直线EF 与平面ABC ［所成的角相等.3.如图，在二棱柱 ABC -A i BiC 中，/ AAB = 45 , AC= BC 平面 BBCC 丄平面 AABB, E 为CC 中点.(1)求证：BB 丄AC⑵ 若AA = 2, AB=P 2，直线AC 与平面ABBA 所成角为45°,求平面 ABE 与平面ABC 所成锐二面角的余弦值.解析：(1)证明：过点 C 做CC 丄BB 交BB 于Q 因为面BBCC 丄面AABB,BBCC Q 面 AAB i B = BB,所以 CQ_面 AABB , 故 CQL BB , 又因为 AC = BC QC= QC所以 Rt △ AQC2 Rt △ BQC 故 QA= QB 因为/ B i A A =Z 0B = 45°,所以 AQL BB , 又因为BB L CQ 所以BB L 面AOC 故 BB L AC⑵ 以Q 为坐标原点，QA QB QC 所在直线为x , y , z 轴，建立空间直角坐标 Q -xyz ,A 1 ,0,0) ,B (0,1 ,0) , Q0,0,1 ) , A l (1 , — 2,0) , B i (0 , — 1 ,0) , E (0 , — 1 , 1 ),设面ABE 的法向量为n = (x , y , zj ,—X 1 + y 1 + Z 1 = 0 ,Z 1 = 0 ,令 X 1= 1,得 n = (1,1,0).设面ABC 勺法向量为m = (X 2 , y 2 , Z 2),n • AE = 0 , 、n • BiE =—X 2 + y = 0,—X 2 + Z 2 = 0,令 X 2= 1，得 m= (1,1,1)，二 cos 〈 m n >面ABE 与面ABC 所成锐二面角的余弦值为4. （2018 •临沂模拟）如图①，在矩形 ABCDK AB= 3, BC = 4, E 是边AD 上一点，且 AE =3，把△ ABE 沿 BE 翻折，使得点 A 到A'满足平面 A BE 与平面BCDE 垂直（如图②）. （1）若点P 在棱A C 上，且CP= 3PA ，求证：DP//平面A BE;（2）求二面角 BA' E -D 的余弦值的大小.解析：（1）证明：在图②中，过 P 作PQ/ BC 交A' B 于点Q 连接QE因为BC = 4,所以PQ 1,因为DE/ BC DE= 1，所以DE 綊PQ所以四边形QED 为平行四边形，所以 DP// EQ 因为DF ?平面A BE EQ ?平面A BE,所以DP//平面A BE⑵在图②中，过A 作A F 丄BE 于点F ,因为平面 A BEL 平面BCDE 所以A F 丄平面BCDE因为/ BA E = 90°, A B = 3, A E = 3,33^3所以/ A EB= 30°, A F = 2, EF=W ,n r AC= 0, £ 7nr n 6 mm?=亍，因为 CP= 3PA'，所以 PQ _A _P -1BC = A 'C = 4过F 作FGL DE 交DE 的延长线于点 G 则 FG=9 E & 9.如图②，建立空间直角坐标系,D (0,0,0) ,E (1,0,0) , 04 , . 3, 0) , C (0 , . 3, 0),X)图②/13 3 ;343,2誓,0，则E A EF= 324(1,0,0)设平面A BE 的法向量n = (x , y , z ),94x + 即 9 x + .4可取 n = (1，——3, 0).设平面 A DE 的法向量m ^(x i , y i , z i ),X = 0,即 9x i + 芈y i + 2z i = 0, 可取 m = (0,2 , - 3).所以 cos 〈m n 〉=-2 3——=--^ . + 3 — 4+ 37因为二面角 BA' E- D 为钝角，所以二面角 BA' E-D 的余弦值的大小为一 -21n • EF ^ 0,则彳[n • E A = 0,叶 6E= o , 则 Am- E /A = 0,。

增分强化练（四十二）1．(2019·乌鲁木齐质检)在平面直角坐标系xOy中，直线l的参数方程为错误!(t为参数）．以坐标原点为极点，x轴的非负半轴为极轴的极坐标系中．曲线C的极坐标方程为ρ＝2错误!cos 错误!.(1)写出直线l的普通方程和曲线C的直角坐标方程；（2)判断直线l与曲线C的位置关系，并说明理由．解析：(1)消去参数t，则直线l的普通方程为x－2y＋2＝0，因为ρ＝2错误!cos错误!，故ρ＝2cos θ－2sin θ，即ρ2＝2ρcos θ－2ρsin θ,曲线C的直角坐标方程为x2＋y2－2x＋2y＝0。

(2)圆心(1，－1）到直线x－2y＋2＝0的距离d＝错误!>错误!，故直线l与曲线C是相离的位置关系．2．(2019·安阳模拟）在直角坐标系xOy中，曲线C的参数方程为错误!（α为参数）,以坐标原点为极点,x轴非负半轴为极轴建立极坐标系．直线l的极坐标方程为ρcos错误!＝2.（1)求C的普通方程和l的直角坐标方程；（2)设直线l与x轴和y轴的交点分别为A，B,点M在曲线C上，求△MAB面积的最大值.解析：（1)由错误!（α为参数）消去参数α可得曲线C的普通方程为x2＋y2＝16。

由ρcos错误!＝2得错误!ρcos θ＋错误!ρsin θ＝2,因为错误!，所以直线l的直角坐标方程为x＋错误!y－4＝0。

(2)由(1）得A（4，0)，B错误!，所以|AB｜＝错误!，设M（4cos α，4sin α)，则点M到直线AB的距离为d＝错误!＝错误!，当sin错误!＝－1时，d max＝6.故△MAB的面积的最大值为错误!×错误!×6＝8错误!。

3．（2019·济宁模拟）在平面直角坐标系xOy中，曲线C的参数方程为错误!(φ为参数)．（1）以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,求曲线C的极坐标方程；（2)若射线θ＝α与曲线C有两个不同的交点A，B,求错误!＋错误!的取值范围．解析：(1)曲线C的直角坐标方程为(x＋1)2＋(y－错误!）2＝1，即x2＋y2＋2x－23y＋3＝0,又x2＋y2＝ρ2，x＝ρcos θ，y＝ρsin θ，∴曲线C的极坐标方程为ρ2＋2ρ(cos θ－错误!sin θ)＋3＝0。

增分强化练(四十三)考点一 绝对值不等式的解法已知函数f (x )＝|2x ＋1|＋|x －1|.(1)求不等式f (x )≥3的解集；(2)若直线y ＝x ＋a 与y ＝f (x )的图象所围成的多边形面积为92，求实数a 的值． 解析：(1)由题意，可得函数f (x )＝⎩⎪⎨⎪⎧ 3x ，x ≥1x ＋2，－12＜x ＜1－3x ，x ≤－12，由f (x )≥3可知：①当x ≥1时，3x ≥3，即x ≥1； ②当－12＜x ＜1时，x ＋2≥3，即x ≥1，与－12＜x ＜1矛盾，舍去； ③当x ≤－12时，－3x ≥3，即x ≤－1； 综上可知，不等式f (x )≥3的解集为{x |x ≤－1或x ≥1}．(2)画出函数y ＝f (x )的图象，如图所示，其中A ⎝ ⎛⎭⎪⎫－12，32，B (1,3)，由k AB ＝1，知y ＝x ＋a 图象与直线AB 平行，若要围成多边形，则a ＞2.易得y ＝x ＋a 与y ＝f (x )图象交于两点C ⎝ ⎛⎭⎪⎫a 2，3a 2，D ⎝ ⎛⎭⎪⎫－a 4，3a 4， 则|CD |＝2·⎪⎪⎪⎪⎪⎪a 2＋a 4＝324a . 平行线AB 与CD 间的距离d ＝|a －2|2＝a －22， 且|AB |＝322，∴梯形ABCD 的面积S ＝322＋324a 2·a －22＝32＋34a 2·(a －2)＝92，(a ＞2)． 即(a ＋2)(a －2)＝12，∴a ＝4，故所求实数a 的值为4.考点二 与绝对值有关的参数范围问题(2019·淮南模拟)已知函数f (x )＝|x －2|＋2.(1)解不等式f (x )＋f (x ＋1)>f (7)；(2)设g (x )＝|2x －a |＋|2x ＋3|，若对任意x 1∈R ，都有x 2∈R ，使得g (x 1)＝f (x 2)成立，求实数a 的取值范围．解析：(1)不等式f (x )＋f (x ＋1)>f (7)等价于|x －2|＋|x －1|>3，①当x >2时，原不等式即为2x －3>3，解得x >3，所以x >3；②当1<x ≤2时，原不等式即为1>3，解得x ∈∅，所以x ∈∅；③当x ≤1时，原不等式即为－2x ＋3>3，解得x <0，所以x <0；所以不等式f (x )＋f (x ＋1)>f (7)的解集为{x |x <0或x >3}．(2)对任意x 1∈R ，都有x 2∈R ，使得g (x 1)＝f (x 2)成立，则{y |y ＝g (x )}⊆{y |y ＝f (x )}．因为g (x )＝|2x －a |＋|2x ＋3|≥ |(2x －a )－(2x ＋3)|＝ |a ＋3|，当且仅当(2x －a )(2x ＋3)≤0时取等号，又f (x )＝|x －2|＋2≥2，所以|a ＋3|≥2，从而a ≥－1或a ≤－5，所以实数a 的取值范围(－∞，－5]∪[－1，＋∞)．考点三 不等式的证明(2019·泉州质检)已知函数f (x )＝⎪⎪⎪⎪⎪⎪x －14＋⎪⎪⎪⎪⎪⎪x ＋14，M 为不等式f (x )≤2的解集． (1)求M ；(2)证明：当a ，b ∈M 时，21－ab ≥a －b .解析：(1)f (x )＝⎪⎪⎪⎪⎪⎪x －14＋⎪⎪⎪⎪⎪⎪x ＋14 ＝⎩⎪⎨⎪⎧ －2x ，x ≤－1412，－14<x <142x ，x ≥14，所以不等式的解集为M ＝[－1,1]．(2)证明：要证21－ab≥a－b，只需证21－ab≥|a－b|,即证4(1－ab)≥|a－b|2,只需证4－4ab≥a2－2ab＋b2，即4≥a2＋2ab＋b2,即证4≥(a＋b)2,只需证2≥|a＋b|，因为a，b∈M，所以|a＋b|≤2，所以所证不等式成立．。

第2讲 综合大题部分1．已知椭圆C ：x 2a2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1、F 2，焦距为2，长轴的长为4. (1)求椭圆C 的标准方程；(2)设过点F 1的直线l 与椭圆C 交于E ，D 两点，试问：在x 轴上是否存在定点M ，使得直线ME ，MD 的斜率之积为定值？若存在，求出该定值及定点M 的坐标；若不存在，请说明理由．解析：(1)因为椭圆C 的焦距为2，长轴的长为4， 所以2c ＝2,2a ＝4，解得c ＝1，a ＝2， 所以b 2＝a 2－c 2＝3，所以椭圆C 的标准方程为x 24＋y 23＝1.(2)设E (x 1，y 1)，D (x 2，y 2)，M (m,0)．易知F 1(－1,0)，当直线l 的斜率存在时，设直线l 的方程为y ＝k (x ＋1)．联立方程，得⎩⎪⎨⎪⎧y ＝k x ＋1，x 24＋y23＝1，得(4k 2＋3)x 2＋8k 2x ＋4k 2－12＝0， 则x 1＋x 2＝－8k 24k 2＋3，x 1x 2＝4k 2－124k 2＋3.又y 1y 2＝k 2(x 1＋1)(x 2＋1)＝k 2(x 1x 2＋x 1＋x 2＋1)＝k 2(4k 2－124k 2＋3－8k24k 2＋3＋1)＝－9k 24k 2＋3， 直线ME ，MD 的斜率k ME ＝y 1x 1－m，k MD ＝y 2x 2－m，则k ME ·k MD ＝y 1x 1－m ·y 2x 2－m＝y 1y 2x 1－mx 2－m＝y 1y 2x 1x 2－m x 1＋x 2＋m 2＝－9k 24k 2＋34k 2－124k 2＋3－m －8k 24k 2＋3＋m 2＝－9k 24k 2＋34k 2－12＋8mk 2＋4m 2k 2＋3m24k 2＋3 ＝－9k24m 2＋8m ＋4k 2＋3m 2－12. 要使直线ME ，MD 的斜率之积为定值，需3m 2－12＝0， 解得m ＝±2.当m ＝2时，k ME ·k MD ＝－9k 24m 2＋8m ＋4k 2＝－9k 236k 2＝－14； 当m ＝－2时，k ME ·k MD ＝－9k 24m 2＋8m ＋4k 2＝－9k 24k 2＝－94.当直线l 的斜率不存在时， 不妨设E (－1，32)，D (－1，－32)，此时，当m ＝2时，M (2,0)，k ME ·k MD ＝－14；当m ＝－2时，M (－2,0)，k ME ·k MD ＝－94.综上，在x 轴上存在两个定点M ，使得直线ME ，MD 的斜率之积为定值． 当定点M 的坐标为(2,0)时，直线ME ，MD 的斜率之积为定值－14；当定点M 的坐标为(－2,0)时，直线ME ，MD 的斜率之积为定值－94.2．(2018·高考某某卷)如图，已知点P 是y 轴左侧(不含y 轴)一点，抛物线C ：y 2＝4x 上存在不同的两点A ，B 满足PA ，PB 的中点均在C 上．(1)设AB 中点为M ，证明：PM 垂直于y 轴；(2)若P 是半椭圆x 2＋y 24＝1(x <0)上的动点，求△PAB 面积的取值X 围．解析：(1)证明：设P (x 0，y 0)，A (14y 21，y 1)，B (14y 22，y 2)．因为PA ，PB 的中点在抛物线上，所以y 1，y 2为方程(y ＋y 02)2＝4·14y 2＋x 02即y 2－2y 0y ＋8x 0－y 20＝0的两个不同的实根． 所以y 1＋y 2＝2y 0，因此，PM 垂直于y 轴．(2)由(1)可知⎩⎪⎨⎪⎧y 1＋y 2＝2y 0，y 1y 2＝8x 0－y 20，所以|PM |＝18(y 21＋y 22)－x 0＝34y 20－3x 0，|y 1－y 2|＝22y 20－4x 0. 因此，△PAB 的面积S △PAB ＝12|PM |·|y 1－y 2|＝324(y 20－4x 0)32.因为x 20＋y 204＝1(x 0<0)，所以y 20－4x 0＝－4x 20－4x 0＋4∈[4,5]，因此，△PAB 面积的取值X 围是[62，15104]．3．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝22，过右焦点F 且垂直于x 轴的弦长为2.(1)求椭圆C 的方程；(2)若直线l ：y ＝x ＋m 与椭圆C 交于M ，N 两点，求△MFN 的面积取最大值时m 的值．解析：(1)由题意知⎩⎪⎨⎪⎧c a ＝22，2b2a ＝2，a 2＝b 2＋c 2，解得⎩⎨⎧a ＝2，b ＝2，∴椭圆C 的方程为x 24＋y 22＝1.(2)联立方程得⎩⎪⎨⎪⎧x 24＋y 22＝1，y ＝x ＋m ，消去y ，得3x 2＋4mx ＋2m 2－4＝0，Δ＝16m 2－12(2m 2－4)＝－8m 2＋48>0，∴|m |< 6.设M (x 1，y 1)，N (x 2，y 2)， ∴x 1＋x 2＝－4m 3，x 1x 2＝2m 2－43，∴|MN |＝2|x 1－x 2|＝2×x 1＋x 22－4x 1x 2＝2×－4m 32－42m 2－43＝46－m 23. 又点F (2，0)到直线MN 的距离d ＝|2＋m |2，∴S △FMN ＝12|MN |·d＝23|2＋m |·6－m 2(|m |<6)． 令u (m )＝(6－m 2)(m ＋2)2(|m |<6)， 则u ′(m )＝－2(2m ＋32)(m ＋2)(m －2)， 令u ′(m )＝0，得m ＝－322或m ＝－2或m ＝2，当－6<m <－322时，u ′(m )>0；当－322<m <－2时，u ′(m )<0；当－2<m <2时，u ′(m )>0； 当2<m <6时，u ′(m )<0. 又u (－322)＝34，u (2)＝32，∴u (m )max ＝32，∴当m ＝2时，△MFN 的面积取得最大值，最大值为23×32＝83. 4．(2018·高考卷)已知抛物线C ：y 2＝2px 经过点P (1,2)，过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ，B ，且直线PA 交y 轴于M ，直线PB 交y 轴于N . (1)求直线l 的斜率的取值X 围；(2)设O 为原点，QM →＝λQO →，QN →＝μQO →，求证：1λ＋1μ为定值．解析：(1)因为抛物线y 2＝2px 过点(1,2)， 所以2p ＝4，即p ＝2. 故抛物线C 的方程为y 2＝4x .由题意知，直线l 的斜率存在且不为0. 设直线l 的方程为y ＝kx ＋1(k ≠0)，由⎩⎪⎨⎪⎧y 2＝4x ，y ＝kx ＋1得k 2x 2＋(2k －4)x ＋1＝0.依题意Δ＝(2k －4)2－4×k 2×1>0， 解得k <0或0<k <1.又PA ，PB 与y 轴相交，故直线l 不过点(1，－2)． 从而k ≠－3.所以直线l 的斜率的取值X 围是(－∞，－3)∪(－3,0)∪(0,1)． (2)证明：设A (x 1，y 1)，B (x 2，y 2)． 由(1)知x 1＋x 2＝－2k －4k 2，x 1x 2＝1k2.直线PA 的方程为y －2＝y 1－2x 1－1(x －1)． 令x ＝0，得点M 的纵坐标为y M ＝－y 1＋2x 1－1＋2＝－kx 1＋1x 1－1＋2. 同理得点N 的纵坐标为y N ＝－kx 2＋1x 2－1＋2. 由QM →＝λQO →，QN →＝μQO →，得λ＝1－y M ，μ＝1－y N . 所以1λ＋1μ＝11－y M ＋11－y N ＝x 1－1k －1x 1＋x 2－1k －1x 2＝1k －1·2x 1x 2－x 1＋x 2x 1x 2＝1k －1·2k 2＋2k －4k 21k 2＝2.所以1λ＋1μ为定值．。